Análisis energético de un sistema para calentamiento de agua con bomba de calor y evaporador inundado

INSTITUTO POLITÉCNICO NACIONAL

ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA

INGENIERÍA EN SISTEMAS AUTOMOTRICES

UNIDAD PROFESIONAL ADOLFO LÓPEZ MATEOS

Análisis energético de un sistema para calentamiento de

agua con

o a de alor y evaporador i u dado

TESIS

QUE PARA OBTENER EL TITULO DE:

INGENIERO EN SISTEMAS AUTOMOTRICES

PRESENTA:

ARTURO ALEJANDRO TORRES ARÉVALO

DIRECTORES DE PROYECTO:

DR. IGNACIO CARVAJAL MARISCAL

INGENIERO JUAN MANUEL MORENO RAMIREZ

ÍNDICE

Página

I. PLANTEAMIENTO DEL PROBLEMA

……….…

...4

II. OBJETIVO

……….

.

…….

.4

III. ALCANCE

………..…………

.

………..

.4

IV. CONTENIDO

……….………...……

Nomenclatura

………

Lista de Figuras

……….

Lista de Ta las………

Lista de Gráficas

………

Resumen

……….

Capítulos:

1. Marco

teóri o………..………..

1.1 Evaporador inundado

………

1.2 Bomba de calor

……….

1.3 Balance de energía

……….

1.4 Compresor

……….

1.5 Intercambiador de calor

...16

1.8 Transferencia de calor

………..

2. Descripción del sistema

………

20

2.1 Bomba de calor

………

2.2 Evaporador inundado

………..

2.2.1 Balance de energía para el fluido de trabajo

……….

2.2.2 Balance de energía para la placa de absorción

………

3. Análisis del sistema

……….

3.1 Análisis del evaporador inundado

………

3.1.1 Análisis del evaporador inundado para un día soleado

………..

3.1.2 Análisis del evaporador inundado para un día nublado

………..

3.1.3 Análisis del evaporador inundado para 8 días soleados

……….

3.1.4 Análisis del evaporador inundado para 8 días nublados

……….

3.2 Análisis de la bomba de calor

………..

3.2.1 Análisis de la bomba de calor para un día soleado

……….

3.2.2 Análisis de la bomba de calor para un día nublado

………

4. Análisis de resultados

………

4.1 Discusión

………

4.2 Conclusiones

………..

Apéndice 1: Programa para simular la bomba de calor en un día soleado

……

.74

Apéndice 2: Mapas tridimensionales de la bomba de calor

………..

Análisis de un sistema para calentamiento de agua con

bomba de calor y evaporador inundado

I.

PLANTEAMIENTO DEL PROBLEMA

La atmósfera presenta elevadas concentraciones de gases nocivos debido a los gases de

combustión emitidos por las máquinas térmicas. Asimismo, es necesario investigar y aplicar

fuentes alternas de energía debido a la crisis energética. Actualmente se ha registrado un

incremento en México en el uso de gas en el sector residencial [13]. Una fracción

importante del gas en los hogares se usa para el calentamiento de agua sanitaria.

Algunas tecnologías alternativas como el calentamiento de agua con bomba de calor y

evaporador inundado, no se han estudiado en México teóricamente ni se ha experimentado

con ellas hasta el momento.

II.

OBJETIVO

Analizar el comportamiento de un sistema de calentamiento de agua con bomba de calor,

cuando se incluye un evaporador inundado, aplicando el principio de funcionamiento del

evaporador inundado y describiendo el sistema de calentamiento de agua propuesto, con el

fin de proponer la tecnología del evaporador inundado y evaluar su implementación.

III.

ALCANCE

Este trabajo contiene 4 capítulos. En el primer capítulo se describen los conceptos y las

ecuaciones que ayudan a hacer el análisis. En el segundo capítulo hay una descripción del

sistema. En el tercer capítulo se analiza energéticamente el comportamiento del sistema

̇

̇

̇

̇ ̇

̇

)

)

Lista de figuras

Página

Figura 1. Evaporador inundado……….

Figura 2. Diagrama T-s para el ciclo ideal de refrigeración por compresión……….

Figura 3. Balance de energía para un compresor……….

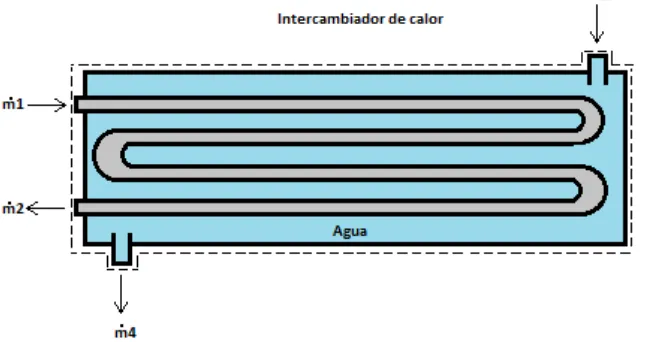
Figura 4. Balance de energía para un intercambiador de calor con dos entradas y dos

salidas……….16

Figura 5. Balance de energía para una válvula de regulación de presión………17

Figura 6. Diagrama de la bomba de calor………..21

Figura 7. Balance de energía para el fluido de trabajo……….22

Figura 8. Absorción de radiación solar por parte del fluido………..23

Figura 9. Transferencia de calor por conducción a través del fluido………..23

Figura 10. Transferencia de calor por conducción y convección a través de la pared…………24

Figura 11. Transferencia de calor por conducción y convección a través del vidrio………24

Figura 12. Balance de energía para la placa de absorción………..25

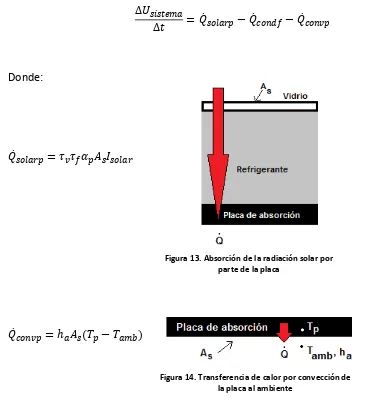
Figura 13. Absorción de la radiación solar por parte de la placa………26

Figura 14. Transferencia de calor por convección de la placa al ambiente………26

Figura 15. Acercamiento de la gráfica 20………..46

Lista de gráficas

Página

Gráfica 1. Transferencia de calor a través de la placa, la pared y el vidrio……….30

Gráfica 2. Transferencia de calor a través de la placa, la pared y el vidrio……….31

Gráfica 3. Temperatura ambiental, temperatura de la placa y transferencia de calor por convección desde la placa……….32

Gráfica 4. Absorción de radiación solar de la placa y transferencia de calor por convección desde la placa comparados con su temperatura………..33

Gráfica 5. Ganancias y pérdidas de calor que afectan al fluido y su cambio de temperatura………34

Gráfica 6. Ganancias y pérdidas de calor para el fluido de trabajo………..34

Gráfica 7. Transferencia de calor neta hacia el fluido y la placa cada 30 minutos……….35

Gráfica 8. Radiación solar incidente para un día nublado y un día soleado………36

Gráfica 9. Temperatura del fluido, del medio ambiente y de la placa………37

Gráfica 10. Absorción de radiación solar de la placa y transferencia de calor por convección desde la placa……….37

Gráfica 11. Ganancias y pérdidas de calor del fluido……….38

Gráfica 12. Transferencia neta de calor para la placa y el fluido de trabajo………..39

Gráfica 13. Temperatura de la placa a lo largo de 8 días……….40

Gráfica 14. Evaporación de masa y temperatura del fluido………..41

Gráfica 15. Energía absorbida por el fluido con respecto a la transmisividad del fluido……..42

Gráfica 16. Energía absorbida por el fluido con respecto al ancho de las paredes………43

Gráfica 17. Energía absorbida por el fluido con respecto al ancho de la placa………44

Gráfica 18. Temperatura de la placa para un ancho de la placa de 5mm………44

Gráfica 20. Energía absorbida por el fluido usando acero y polietileno para el material de la

placa……….46

Gráfica 21. Absorción de energía del fluido para una placa de absorción de polietileno...47

Gráfica 22. Temperatura de la placa para 8 días nublados………48

Gráfica 23. Temperatura del fluido en comparación con la masa de fluido evaporada en días

nublados………48

Gráfica 24. Absorción de energía del fluido con respecto a la transmisividad en días

nublados………49

Gráfica 25. Cantidad de energía absorbida por el fluido con respecto al ancho de las paredes

en días nublados………..50

Gráfica 26. Absorción de energía del fluido con respecto al ancho de la placa de absorción

en días nublados………..51

Gráfica 27. Absorción de energía del fluido con respecto a distintos materiales para días

nublados………52

Gráfica 28. Absorción de energía del fluido para una placa de polietileno en días

nublados………

Gráfica 29. Temperatura de la placa para el 8vo. día nublado………55

Gráfica 30. Temperatura y evaporación de masa del fluido refrigerante para el 8vo. día

soleado………56

Gráfica 31. Variación del ∆T del agua con diferentes flujos másicos………..57

Gráfica 32. ∆T del agua cuando el compresor tiene una relación de compresión igual a 2………..57

Gráfica 33. ∆T del agua cuando el compresor tiene una relación de compresión igual a 5………..58

Gráfica 34. ∆T del agua cuando el compresor tiene una relación de compresión igual a 10………59

Gráfica 35. ∆T del agua cuando se modifica la eficiencia isentrópica del compresor………….59

Gráfica 37. ∆T del agua con un evaporador de área superficial igual a 2 m2……….61

Gráfica 38. ∆T del agua con un evaporador de área superficial igual a 1 m2 y una

profundidad de 10 cm……….62

Gráfica 39. ∆T del agua con un evaporador de área superficial igual a 5 m2 y una

profundidad de 2cm………..62

Gráfica 40.Temperatura de la placa para el 8vo. día nublado……….63

Gráfica 41. Temperatura del fluido y evaporación de masa para el 8vo. día nublado…………64

Gráfica 42. ∆T del agua con distintos flujos másicos para un día nublado……….65

Gráfica 43. ∆T del agua con un evaporador de área superficial igual a 1 m2 y una

profundidad de 10 cm para un día nublado……….66

Gráfica 44. ∆T del agua con un evaporador de área superficial igual a 5 m2 y una

profundidad de 2 cm para un día nublado………66

Gráfica 45. Transferencia neta de calor al fluido con una velocidad baja del viento…………..77

Gráfica 46. Transferencia neta de calor al fluido con una velocidad alta del viento………

Gráfica 47. Transferencia neta de calor al fluido cuando la temperatura ambiente es menor a la temperatura de saturación del fluido de trabajo………78

Resumen

En el presente trabajo se estudia una bomba de calor para calentamiento de agua poniendo especial atención en el evaporador inundado, el cual es un colector solar que tiene la capacidad de aprovechar la energía del medio ambiente.

Para este estudio se realiza un análisis de primera ley; para el análisis del evaporador inundado se realizan balances de energía para la placa de absorción y el fluido de trabajo, tomando en cuenta la radiación solar y la transferencia de calor por convección. Para la bomba de calor se establecen los balances de energía de los demás dispositivos: el compresor, la válvula de expansión y el intercambiador de calor.

El evaporador inundado se simula en el software EES® bajo distintas condiciones ambientales. A partir de ahí se observa el comportamiento del evaporador y después se varían distintos parámetros, como son, el ancho de la placa de absorción, el ancho de las paredes, la profundidad del fluido refrigerante y los materiales para la placa de absorción. La bomba de calor se simula de la misma forma en EES® variando la relación de compresión, la eficiencia isentrópica del compresor, el área superficial del evaporador, la profundidad del fluido de trabajo y el flujo másico de agua que pasa a través del intercambiador de calor.

Se observa, que al variar algunos parámetros como el ancho de las paredes, la relación de compresión y la eficiencia isentrópica, el desempeño del evaporador inundado y de la bomba de calor no mejora notablemente. Por el contrario, cuando se disminuye el ancho de la placa de absorción y se aumenta el área superficial del evaporador inundado, manteniendo al mínimo la profundidad del fluido de trabajo, se puede ver una mejora notable en el desempeño del sistema. Esto trae beneficios en cuanto a ahorro de materiales.

CAPÍTULO 1.

1.1 Evaporador Inundado

Un evaporador inundado es un colector de energía solar que está diseñado para proveer grandes cantidades de calor para aplicaciones industriales a un costo que es competitivo con los combustibles fósiles [1].

Mediante la absorción directa de radiación solar por parte del fluido y por la transferencia de calor desde la placa de absorción (con la cual está en contacto directo), la temperatura del fluido incrementa, resultando en un cambio de fase de liquido a vapor. El transporte de energía térmica es logrado por el flujo del vapor hacia el extremo del usuario [3].

1.2 Bomba de calor

La bomba de calor es un dispositivo que transfiere calor desde un medio de baja temperatura a otro medio de alta temperatura. El objetivo de una bomba de calor, es mantener un espacio calentado a una temperatura alta. Esto se logra absorbiendo calor desde una fuente que se encuentra a temperatura baja [5].

El desempeño de las bombas de calor se expresa en términos del coeficiente de desempeño (COP), por sus siglas en inglés (Coefficient Of Performance), definido como [5]:

El ciclo de refrigeración por compresión de vapor es el que más se utiliza en refrigeradores, sistemas de acondicionamiento de aire y bombas de calor. Se compone de cuatro procesos [5]:

1-2 Compresión isentrópica en un compresor

2-3 Rechazo de calor a presión constante en un condensador

3-4 Estrangulamiento en un dispositivo de expansión

4-1 Absorción de calor a presión constante en un evaporador

Figura 2. Diagrama T-s para el ciclo ideal de refrigeración por compresión [5]

1.3 Balance de energía

El principio de conservación de la energía se expresa como: el cambio neto (aumento o disminución) de la energía total del sistema durante un proceso es igual a la diferencia entre la energía total que entra y la energía total que sale del sistema durante un proceso. Es decir:

En ausencia de efectos eléctricos, magnéticos y de tensión superficial, el cambio en la energía total del sistema durante un proceso es la suma de los cambios en sus energías interna, cinética y potencial, lo cual se expresa como [5].

En forma de tasa, el balance de energía para un sistema que experimenta cualquier clase de proceso se expresa como [5]:

̇ ̇

1.4 Compresor

Los compresores son los dispositivos encargados de hacer pasar el fluido frigorígeno desde la presión de evaporación, correspondiente a las condiciones del foco frío, a la presión de condensación del foco caliente, por lo que hay que hacer un aporte exterior de trabajo. El motor y el cilindro de trabajo forman una unidad compacta totalmente hermética denominada compresor. En el interior se encuentra el aceite necesario para su lubricación que se puede mezclar con el fluido frigorífero (principalmente en los arranques) durante el recorrido por el circuito frigorífico, volviendo nuevamente a depositarse, la mayor parte, en el compresor [8].

La eficiencia isentrópica de un compresor se define como la relación entre el trabajo de entrada requerido para elevar la presión de un gas a un valor especificado de una manera isentrópica y el trabajo de entrada real [5]:

Balance de energía para el compresor [5]:

̇

1.5 Intercambiador de calor

Los intercambiadores de calor son dispositivos donde dos corrientes de fluido en movimiento intercambian calor sin mezclado. Los intercambiadores de calor se usan ampliamente en varias industrias y su diseño es variado.

El calor se transfiere del fluido caliente al frío a través de la pared que los separa. Algunas veces el tubo interno tiene un par de vueltas dentro de la coraza para aumentar el área de transferencia de calor y, por consiguiente, la tasa de transferencia de calor [5].

Figura 3. Balance de energía para un compresor

Balance de energía para el intercambiador de calor [5]:

1.6 Válvula de regulación de presión

Las válvulas de estrangulamiento son dispositivos de diferentes tipos que restringen el flujo de un fluido provocando una caída relevante de presión. A diferencia de las turbinas, producen una caída de presión sin implicar trabajo. La caída de presión en el fluido suele ser acompañada de una gran disminución de temperatura, por esa razón los dispositivos de estrangulamiento son de uso común en aplicaciones de refrigeración y acondicionamiento de aire [5].

Balance de energía para la válvula de regulación de presión [5]:

1.7 Calor latente y calor sensible

Para fundir un sólido o vaporizar un líquido se requiere una gran cantidad de energía. La cantidad de ésta que es absorbida o liberada durante el proceso de cambio de fase se llama calor latente [5].

La porción de energía interna de un sistema asociada con la energía cinética de las moléculas es llamada calor sensible [6].

1.8 Transferencia de calor

La conducción es la transferencia de energía de las partículas más energéticas de una sustancia hacia las adyacentes menos energéticas, como resultado de interacciones entre esas partículas. La conducción puede tener lugar en los sólidos líquidos o gases [6].

La razón de conducción de calor a través de una capa plana es proporcional a la diferencia de temperatura a través de ésta y el área de transferencia de calor, pero es inversamente proporcional al espesor de esa capa (Ley de Fourier); es decir [6]:

̇

En el caso límite de la ecuación que acaba de darse se reduce a su forma diferencial [6]:

̇

La rapidez de la transferencia de calor por convección es proporcional a la diferencia de temperatura y se expresa en forma conveniente por la Ley de Newton de enfriamiento [6]:

̇

El número de Nusselt representa el mejoramiento de la transferencia de calor a través de una capa de fluido como resultado de la convección en relación con la conducción a través de la misma capa. Entre mayor sea el número de Nusselt, más eficaz es la convección. Un número de Nusselt de Nu=1 para una capa de fluido representa transferencia de calor a través de ésta por conducción pura [6]:

̇

̇

El número de Reynolds representa la relación de las fuerzas de inercia con las fuerzas viscosas en un fluido, es una cantidad adimensional, y se expresa como [6]:

Donde es el área superficial y es el perímetro [6].

El número de Prandtl adimensional relaciona a la difusividad molecular de la cantidad de movimiento con la difusividad molecular de calor [6]:

Si se considera convección forzada:

El número Nusselt promedio se obtiene mediante las siguientes ecuaciones [6]:

Laminar:

Turbulento: ,

La analogía eléctrica se puede emplear para resolver problemas más complejos que incluyan tanto resistencias térmicas en serie como en paralelo [7]:

_∑

La radiación suele considerarse como un fenómeno superficial para los sólidos que son opacos a la radiación térmica, como los metales, la madera y las rocas, ya que las radiaciones emitidas por las regiones interiores de un material de ese tipo nunca pueden llegar a la superficie, y la radiación incidente sobre esos cuerpos suele absorberse en unas cuantas micras hacia adentro de dichos sólidos [6].

Cua do u a superfi ie de e isividad ε y área superfi ial AS, a una temperatura

termodinámica TS, esta por completo encerrada por una superficie mucho más grande (o

negra), a una temperatura termodinámica Talred, y separada por un gas (como el aire) que

no interfiere con la radiación, la razón neta de la transferencia de calor por radiación entre estas dos superficies se da por [6]:

̇

Cuando la radiación choca contra una superficie, parte de ella es absorbida, parte de ella es reflejada y la parte restante, si la hay, es transmitida. La fracción de irradiación absorbida

por la superfi ie se lla a a sortividad α, la fra ió reflejada por la superficie recibe el

o re de refle tividad ρ, y la fra ió tra s itida es la tra s isividad τ [6]:

CAPÍTULO 2.

2.1 Bomba de calor

El sistema se compone de 4 etapas:

1-2 Absorción de calor en el evaporador

El evaporador absorbe la radiación solar por medio de la placa de absorción y del fluido de trabajo que en este momento se encuentra en estado líquido. La temperatura del fluido de trabajo aumenta. Al alcanzar el punto de ebullición una fracción del líquido se evapora y sale del evaporador inundado.

2-3 Compresión

El refrigerante se comprime, incrementando así su presión y su temperatura. Se considera que el compresor es adiabático y tiene diámetros de entrada y de salida idénticos, por lo tanto los cambios en la energía cinética se pueden despreciar.

3-4 Rechazo de calor en el condensador

El refrigerante entra como vapor sobrecalentado y rechaza calor al agua, después sale del condensador como liquido saturado.

4-1 Estrangulamiento

El estrangulamiento en la válvula provoca una caída de presión para ajustar la presión a la entrada del evaporador. También hay una disminución en la temperatura del refrigerante debido a la expansión del fluido.

2.2 Evaporador inundado

El evaporador inundado se analiza mediante un balance de energía aplicado al fluido de trabajo y a la placa de absorción, donde se toma en cuenta la transferencia de calor por convección y conducción.

2.2.1 Balance de energía para el fluido de trabajo:

Se parte del balance general de energía:

̇ ̇ Despreciando los cambios de energía cinética y potencial:

Cuando la temperatura del fluido es menor a la temperatura de saturación ( ), no hay evaporación de masa y la transferencia neta de calor al fluido resulta en un incremento o disminución en la energía interna del fluido.

̇ ̇ ̇ ̇

La transferencia de calor por radiación entre la placa y el fluido de trabajo es una cantidad mínima, ya que la diferencia de temperatura entre el sistema y sus alrededores es pequeña, por lo tanto es despreciable.

Donde:

̇

̇

Figura 9. Transferencia de calor por conducción a través del fluido

̇

̇

Por lo tanto el balance de energía para el fluido cuando ( ) es:

Cuando la temperatura del fluido es igual a la temperatura de saturación hay una evaporación de masa del fluido de trabajo, este flujo másico pasa por los diferentes dispositivos de la bomba de calor y regresa al evaporador inundado. Si la masa de fluido de

Figura 10. Transferencia de calor por conducción y convección a través de la pared

trabajo que entra al evaporador es igual a la que sale de este, entonces no hay acumulación de energía en el sistema:

Entonces las entradas y salidas de energía del sistema son iguales a cero:

̇ ̇ ̇ ̇ ̇ ̇

Si la entrada de masa al evaporador en forma de mezcla liquido-vapor es igual a la salida de masa en estado de vapor saturado _{̇ ̇} , entonces:

̇ ̇ ̇ ̇ ̇

Por lo tanto el balance de energía para el fluido cuando ( ) es:

̇

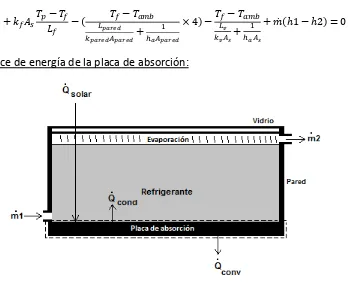
2.2.2 Balance de energía de la placa de absorción:

Debido a que la placa esta en reposo, el cambio de energía del sistema es igual al cambio de energía interna de la placa:

Donde el cambio de energía interna del sistema es igual a la transferencia neta de calor a la placa:

̇ ̇ ̇

Donde:

̇

̇

Por lo tanto el balance de energía para la placa de absorción es:

( ) (3)

Figura 13. Absorción de la radiación solar por parte de la placa

CAPÍTULO 3.

3.1 Análisis del evaporador inundado

Para el análisis del evaporador inundado se utilizan las ecuaciones presentadas en la sección 2.1, las cuales describen las entradas y salidas de energía del evaporador inundado. Para este análisis se utiliza el software EES® (Engineering Equation Solver), el cual como su nombre lo indica se utiliza para resolver ecuaciones. Su principal ventaja es que cuenta con librerías para calcular las propiedades termodinámicas de distintos refrigerantes, además de tener un entorno amigable para presentar gráficas de distintos tipos y diagramas de propiedades termodinámicas.

Con este software se resuelven las ecuaciones (1), (2) y (3) de la siguiente manera:

Primero se toma la ecuación (3), la cual describe el comportamiento de la placa, y se resuelve con respecto a la temperatura que alcanza la placa una vez que se da alguna transferencia de calor desde o hacia esta. La ecuación que se introduce al programa es de la siguiente forma:

( )

La ecuación (1) se resuelve de igual manera para encontrar la temperatura que alcanza el fluido después de que se da la transferencia de calor desde o hacia el fluido.

Se establece que la temperatura de saturación es similar a la temperatura ambiente, específicamente 20 °C ya que como es una bomba de calor, el evaporador inundado debe absorber energía de su medio cuando la temperatura ambiente sea mayor a la temperatura de saturación establecida.

Por lo tanto, cuando la temperatura del fluido de trabajo sea igual a la temperatura de saturación establecida se utiliza una condicional en EES® para que utilice la ecuación (2), la cual se relaciona con el calor latente de vaporización, y se resuelve para obtener el flujo másico del fluido de trabajo evaporado:

̇ ( ₎

3.1.1 Análisis del evaporador inundado para un día soleado

Primero se evalúan las ecuaciones con condiciones ambientales para un día soleado. Los datos de radiación solar, velocidad del viento y temperatura ambiental son obtenidos de la página de la Red Universitaria de Observatorios de la UNAM [11] para el Centro de Ciencias Atmosféricas el 26/05/2015. Esta fuente proporciona estas condiciones ambientales cada 30 minutos, es por esto que se evalúa el cambio de temperatura de la placa de absorción, el cambio de temperatura del fluido de trabajo y la evaporación de masa cada 30 minutos, empezando desde las 6:30 am, durante 24 horas. Se empieza la simulación a esa hora debido a que es cuando sale el sol.

El material propuesto para la placa de absorción y las paredes del evaporador es el acero, ya que es barato y al ser un buen conductor térmico, las transferencias de calor por conducción y convección se verán más marcadas. Por lo tanto se utilizan las propiedades del acero en las anteriores ecuaciones. Sin embargo se evalúan distintos materiales para la placa de absorción y las paredes en este trabajo.

El vidrio templado con bajo contenido de carbono es usado para colectores solares porque tiene una alta transmisividad de la radiación solar, pero tiene esencialmente cero

transmisividad de la radiación emitida por superficies calentadas por el sol (5.0- μ )[ ]. Por lo tanto las propiedades ópticas, el coeficiente de transferencia de calor por

conducción, así como la anchura de un vidrio templado con bajo contenido de carbono real son utilizadas a lo largo del análisis. Es importante hacer notar que se considera que la energía solar que no es transmitida por el vidrio es reflejada debido a que la absortividad de

los vidrios te plados e ge eral es uy aja→ % [10].

Las dimensiones propuestas para el inicio del análisis son un área superficial igual a 1 m2

distribuido en un área cuadrada, con una altura de 2 cm

.

Se utiliza el refrigerante 134a porque es amigable con el medio ambiente y porque no se requieren de grandes presiones (aproximadamente 570 kPa) para que se sature a 20 °C [5].

Para calcular el coeficiente de transferencia de calor por convección primero se obtiene la longitud característica para el área superficial del evaporador:

0 200 400 600 800 1000 1200 1400 -120

-100 -80 -60 -40 -20 0 20 40

t [min]

Q

[

W

]

Qconvp

Qconvp

Qconvpared

Qconvpared

Qconvv

Qconvv

Y de tablas de propiedades del aire [5] se obtiene el número Prandtl a temperatura ambiente. Para después obtener el número Nusselt para flujo laminar de la siguiente ecuación:

Y finalmente se obtiene el coeficiente de transferencia de calor por convección:

Al simular el sistema es claro que las pérdidas de calor por convección se muestran con signo negativo debido a que en realidad son ganancias de calor, ya que el aire ambiental está más caliente que los componentes del evaporador, como se observa en la gráfica 1.

Por este motivo es conveniente replantear las ecuaciones para que indiquen una ganancia de energía en vez de una pérdida debido al intercambio de calor con el exterior. Por lo tanto las ecuaciones se modifican en EES® de la siguiente manera:

0 200 400 600 800 1000 1200 1400 -40

-20 0 20 40 60 80 100 120

t [min]

Q

[

W

]

Qconvp

Qconvp

Qconvv

Qconvv

Qconvpared

Qconvpared

Para el fluido:

̇ ̇ ̇ ̇

Cuando:

Cuando:

̇ ( ₎

Para la placa:

̇ ̇ ̇

( )

Se grafica con las correcciones en la transferencia de calor y da como resultado la siguiente gráfica:

0 200 400 600 800 1000 1200 1400 -40 -20 0 20 40 60 80 100 12 14 16 18 20 22 24 26 t [min] Q [ W ] Qconvp Qconvp T [ °C ] Tamb Tamb Tp Tp

Se aprecia en la gráfica 2 como la transferencia de calor a través del vidrio es la cantidad más grande alcanzando un máximo de 102.3 W en el día, seguida de la transferencia de calor por convección hacia la placa, la cual alcanza un máximo de 83.58 W en el día. Por último se tiene la transferencia de calor desde las paredes, la cual es casi despreciable comparándola con las otras dos cantidades, alcanzando un máximo de 8.4 W en el día. La gráfica 3 relaciona a la temperatura ambiental con la transferencia de calor por convección desde la placa y con la temperatura de la placa.

Es interesante notar primeramente como la temperatura de la placa sube hasta alcanzar un máximo aproximadamente a los 800 minutos y después de ahí la temperatura se mantiene casi constante. La gráfica demuestra como poco después de los 900 minutos (9:00 pm) la temperatura de la placa y la temperatura ambiental son iguales, por lo tanto en ese punto no hay transferencia de calor, y es después de esa hora cuando la placa empieza a perder calor hacia el ambiente, de hecho se puede observar en la gráfica como la cantidad _̇ alcanza números negativos después de ese momento.

La gráfica 4 compara las ganancias que tiene la placa con la cantidad ̇ y ̇ las cuales son la transferencia de calor por convección desde placa y la cantidad de radiación

0 200 400 600 800 1000 1200 1400 -50 0 50 100 150 200 250 300 350 400 450 500 550 600 13 14 15 16 17 18 19 20 21 22 23 24 25 26 t [min] Q [ W ] Qsolarp Qsolarp Qconvp Qconvp T [ °C ] Tp Tp

Como se observa, la radiación solar absorbida por la placa es la que influye en mayor medida en el cambio de temperatura de la placa. En un posterior análisis se simula el sistema durante más de 24 horas para observar la temperatura de la placa a lo largo de varios días, ya que como se ve en la gráfica, las pérdidas de calor en la noche debido a una baja temperatura ambiental son mínimas y la temperatura de la placa casi no desciende, por lo tanto irá en aumento a lo largo de varios días hasta alcanzar un máximo.

En la gráfica 5 se compara al fluido con las diferentes transferencias de calor que lo afectan, como son la transferencia de calor por conducción desde la placa, la transferencia de calor por convección a través del vidrio y a través de las paredes.

Se observa como la temperatura después del minuto 1000 (aproximadamente las 11:00 pm) hasta que acaba el día se mantiene esencialmente constante. Es importante notar que el fluido no alcanza la temperatura de saturación (20 °C), por lo tanto no hay evaporación de masa del fluido de trabajo para este día.

0 200 400 600 800 1000 1200 1400 -20 0 20 40 60 80 100 120 140 160 180 200 220 240 260 280 t [min] Q [ W ] Qcondf Qcondf Qconvpared Qconvpared Qconvv Qconvv Qsolarf Qsolarf

0 200 400 600 800 1000 1200 1400

-20 0 20 40 60 80 100 120 13 14 15 16 17 18 19 20 21 22 23 24 25 26 t [min] Q [ W ] Qcondf Qcondf Qconvpared Qconvpared Qconvv Qconvv Tf [ °C ] Tf Tf

En la gráfica 6 se comparan todas las transferencias de calor que influyen en la temperatura del fluido.

Gráfica 6. Ganancias y pérdidas de calor para el fluido de trabajo

0 200 400 600 800 1000 1200 1400 -100

0 100 200 300 400 500 600 700

t [min]

Q

[

W

]

D Qf

D Qf

D Qp

D Qp

Como se puede observar, al igual que con la placa, la absorción de radiación solar es la que le aporta una mayor cantidad de energía al fluido, seguidas por la transferencia de calor por convección a través del vidrio, la conducción de calor de la placa al fluido y por último la transferencia de calor por convección a través de las paredes.

Si se suma la cantidad total de las transferencias netas de calor a lo largo de todo el día, se puede obtener la cantidad total de calor transferido a la placa y al fluido.

∑

∑

Las ecuaciones anteriores representan la sumatoria de 48 elementos de transferencia neta de calor calculadas cada 30 minutos, dando así la suma de las transferencias de calor por 24 horas.

0 200 400 600 800 1000 1200 1400 0

200 400 600 800 1000

t [min]

Q

[

W

]

Qsoleado

Qsoleado

Qnublado

Qnublado

3.1.2 Análisis del evaporador inundado para un día nublado

Para simular el día nublado se utilizan las condiciones ambientales para el día 05/06/2015 de la Escuela Nacional Preparatoria no. 9, de la Red Universitaria de Observatorios de la UNAM (PEMBU, CITA). Se utilizan las mismas dimensiones del evaporador, los mismos materiales y las mismas ecuaciones para calcular _̇ .

La gráfica 8 demuestra la comparación de la radiación solar incidente en el evaporador para el día soleado y el día nublado.

En la gráfica 9 se puede notar como la temperatura ambiente no tiene repercusiones notables en el cambio de temperatura del fluido ni de la placa, por ejemplo, del minuto 500 aproximadamente hasta el minuto 700 la temperatura ambiente tiene una caída de casi cuatro grados, lo mismo pasa del minuto 800 hasta el final del día, sin embargo, parece que las temperaturas no tienden a variar como lo hace la temperatura ambiente, por lo tanto es necesario comparar las distintas transferencias de calor hacia el fluido y la placa.

0 200 400 600 800 1000 1200 1400 15 16 17 18 19 20 21 22 23 24 25

t [min]

T

[

°C

]

0 200 400 600 800 1000 1200 1400

-100 0 100 200 300 400 t[i] Q [ W ] Qsolarp Qsolarp

D Qp

D Qp

Qconvp

Qconvp

Como se observa en la gráfica 10, la absorción de radiación solar aporta en mayor medida en la transferencia neta de calor hacia la placa. Algo a recalcar es que la temperatura ambiente al final del día no es mucho menor a la temperatura de la placa al final del día y

Gráfica 9. Temperatura del fluido, del medio ambiente y de la placa

0 200 400 600 800 1000 1200 1400 -100

-50 0 50 100 150 200 250

t [min]

Q

[

W

]

D Qf

D Qf

Qconvpared

Qconvpared

Qconvv

Qconvv

Qsolarf

Qsolarf

Qcondf

Qcondf

por lo tanto no se da una mayor transferencia de calor. También es importante notar que al final del día (aproximadamente a los 1400 minutos) no hay transferencia de calor por convección de la placa al ambiente, ya que según los datos ambientales, la velocidad del viento a esas horas es igual a cero, por lo tanto el coeficiente de transferencia de calor por convección es igual a cero y la transferencia de calor por convección es cero.

Se observa que para este día la transferencia de calor por convección a través del vidrio es similar a la absorción de radiación solar por parte del fluido, y que una vez más la transferencia de calor a través de las paredes es mínima y despreciable, al igual que la transferencia de calor de la placa al fluido.

La gráfica 12 demuestra que la placa tiene más ganancias y más pérdidas que el fluido de trabajo.

0 200 400 600 800 1000 1200 1400 -100

0 100 200 300 400

t [min]

Q

[

W

]

D Qp

D Qp

D Qf

D Qf

3.1.3 Análisis del evaporador inundado para 8 días soleados

El análisis del evaporador para 8 días soleados se hace de manera muy similar al análisis del evaporador para un día soleado, ya que se utiliza el mismo evaporador en cuestión a materiales y dimensiones, y además se utilizan las mismas condiciones meteorológicas que para el día soleado, pero ahora el programa resuelve las ecuaciones cada 30 minutos durante 8 días.

Este análisis se da con el fin de observar el progreso de la temperatura de la placa, la temperatura del fluido y la masa de fluido evaporada durante periodos más largos de tiempo, ya que como se observa en los análisis anteriores, la temperatura para el fluido y la placa en el primer día es mayor al final del día que al principio de este, por lo tanto es predecible que esta tiende a aumentar durante varios días hasta estabilizarse, además en el primer día no se da evaporación de masa del refrigerante para un día soleado, ni tampoco para un día nublado, ya que la temperatura del fluido de trabajo siempre se mantiene debajo de la temperatura de saturación ( . Además en este análisis se pretende mostrar el desempeño del evaporador inundado bajo distintos cambios en materiales y dimensiones, para que en un futuro se pueda dar un diseño óptimo para este dispositivo.

0 1440 2880 4320 5760 7200 8640 10080 11520 10

15 20 25 30 35 40

t [min]

T

[

°C

] _T

p

Tp

DÍA 1 DÍA 2 DÍA 3 DÍA 4 DÍA 5 DÍA 6 DÍA 7 DÍA 8

Éste análisis se basa en gran parte en el cálculo de , el cual es la cantidad que nos indica la transferencia total de energía al fluido durante un periodo determinado de tiempo, que en este caso son 8 días (por eso en la sumatoria se suman 384 elementos, ya que este es el número de divisiones de media hora que tienen 8 días):

(∑

)

Por lo tanto, a mayor , mayor será la masa de fluido evaporada y mejor será el desempeño del evaporador inundado.

La gráfica 13 muestra un interesante progreso en la temperatura de la placa, ya que en el primer día la temperatura al inicio del día y la final del día es muy diferente, pero a través de los días se observa que esta diferencia de temperatura gradualmente va disminuyendo y es por esto que la gráfica tiene esta forma. Para el día 7 y 8 la diferencia de temperatura de la placa al inicio y al final del día se va acercando a cero, esto se puede observar más claramente el último día. Entonces a partir del último día se puede decir que si siguen los días soleados la temperatura de la placa se mantendrá entre 30°C y 35°C.

Es importante notar que el número de minutos que tienen 8 días es 11520, es por esto que

0 1440 2880 4320 5760 7200 8640 10080 11520 10 15 20 25 30 35 40 0 0.0005 0.001 0.0015 0.002 0.0025 0.003 0.0035 0.004 t [min] T [ °C ] Tf Tf m [ k g ] mevap mevap

DÍA 1 DÍA 2 DÍA 3 DÍA 4 DÍA 5 DÍA 6 DÍA 7 DÍA 8

Lo que se pretende en la gráfica 14, es mostrar la temperatura del fluido y la masa evaporada cuando la temperatura del fluido es igual a la temperatura de saturación.

Como se observa en el análisis para un día soleado, la temperatura del fluido de trabajo no alcanza la temperatura de saturación (20°C), esto también se puede observar en esta gráfica en el DÍA 1. Sin embargo para el segundo día, la temperatura del fluido sigue aumentando hasta por fin alcanzar la temperatura de saturación aproximadamente a medio día. Después, la masa de fluido evaporada empieza a disminuir en lo que resta del día, hasta llegar a un valor de cero casi al final del primer día. Nótese que para el inicio del tercer día la temperatura del fluido ya es un poco menor a la temperatura de saturación, sin embargo esto no ocurre para los días siguientes, y por lo tanto el fluido se mantiene en saturación durante lo que resta de la simulación.

Con respecto a la masa de fluido evaporada, se puede ver que esta aumenta del día 3 al día 6, y se mantiene constante del día 6 al día 8.

La siguiente parte del análisis se enfoca en variar las dimensiones y los materiales en el evaporador para observar el efecto que tienen sobre la cantidad total de energía absorbida por el fluido de trabajo durante 8 días ( ).

0.54 0.56 0.58 0.6 0.62 0.64 0.66 0.68 22

23 24 25 26 27

t

Q

ta

lf

[k

W

-h

]

Profundidad del fluido

Hasta ahora la profundidad del fluido de trabajo se ha mantenido constante en 2cm, sin embargo, cuando la profundidad del fluido aumenta la absortividad del fluido también lo hace.

Para este trabajo se han considerado las propiedades ópticas (transmisividad, reflectividad y absortividad) del agua ya que el R134a (tetrafluoroetano) es transparente y posee una densidad similar a la del agua[3]:

Al variar la profundidad del fluido también lo hará la altura del evaporador, y con esto el área expuesta a la convección por las paredes.

Se observa en la gráfica 15 que la energía total absorbida por el fluido está en función de la

Profundidad del fluido (m)

0.02 0.04 0.06 0.08 0.1

τf 0.6756 0.6185 0.5858 0.5648 0.5498

Tabla 1. Transmisividad del fluido de trabajo a diferentes profundidades

0 0.01 0.02 0.03 0.04 0.05 22.51

22.51 22.51 22.51 22.51 22.51 22.51 22.51 22.51 22.51 22.51

L_pared [m]

Qto

ta

lf

[k

W

-h

]

pueda absorber, por lo tanto cuando hay una profundidad mayor, es decir que el evaporador inundado tenga una mayor altura, entonces el fluido absorberá mayor cantidad de calor. Esté análisis se hizo para profundidades pequeñas debido que el refrigerante es muy costoso y no es posible realizar diseños que contemplen mayores profundidades.

Ancho de las paredes

En este análisis, se varía el ancho de las paredes del evaporador.

Como se puede observar en la gráfica 16, la escala de muestra números idénticos para toda la escala, esto es debido a que la variación que presenta con respecto al ancho de las paredes está dado en Watts-hora, y por lo tanto no se refleja un cambio en una escala de kWh. Esto significa que las pérdidas y ganancias que tiene el evaporador por convección a través de las paredes son insignificantes. Aún así se observa que el fluido absorbe más energía cuando las paredes son delgadas. Por lo tanto, el ancho de las paredes se debe mantener lo más pequeño posible.

0 0.01 0.02 0.03 0.04 0.05 15

17 19 21 23 25

L

[m]

Q

ta

lf

[k

W

-h

]

10 15 20 25 30 35 40 45

T

[

°C

]

Tp@5mm

Tp@5mm

Ancho de la placa

En este análisis, se varía el ancho de la placa de absorción, esto a su vez varía la masa de la placa, incrementando o disminuyendo así el tiempo que esta tarda para calentarse.

Se puede observar como mejora mucho la cantidad de energía absorbida por el fluido cuando se disminuye el ancho de la placa.

La gráfica 18 muestra como al disminuir el ancho de la placa la temperatura de la placa varía más durante el día, además se observa cómo se estabiliza (es decir que la diferencia al inicio y al final del día es casi igual a cero) más rápidamente cuando disminuye el ancho de la placa, además la placa registra temperaturas de hasta 37°C. Al final todo esto repercute positivamente en la cantidad a lo largo de 8 días.

Materiales para la placa de absorción

La mayor parte de la tubería usada en la refrigeración y aire acondicionado está hecha de cobre. Sin embargo, el aluminio, acero, acero inoxidable, y los tubos plásticos también son utilizados. El polietileno es una de las sustancias más comunes utilizadas para manufacturar tubos plásticos [4].

Debido a que el tetrafluoroetano puede reaccionar con distintos elementos, solo se consideran los materiales utilizados para tuberías de refrigeración, ya que nos garantizan que no reaccionarán con el R134a.

Gráfica 19. Energía absorbida por el fluido utilizando distintos materiales para la placa

22.51 kWh 22.48 kWh

23.49 kWh

22.06 kWh

24.15 kWh

21 21.5 22 22.5 23 23.5 24 24.5

Acero Cobre Aluminio Acero inoxidable Polietileno

0 1440 2880 4320 5760 7200 8640 10080 11520 -100

0 100 200 300 400 500 600 700 800

t [min]

Q

[

W

]

D Qf ,acero

D Qf ,acero

D Qf polietileno

D Qf polietileno

Se observa como los metales demuestran un desempeño similar, a excepción del aluminio que tiene mejor desempeño. Sin embargo, al usar polietileno, la cantidad de energía absorbida por el fluido es la mayor.

0 0.01 0.02 0.03 0.04 0.05 18

19 20 21 22 23 24 25

L

[m]

Q

ta

lf

[k

W

-h

]

En la imagen anterior se observa que al usar polietileno la cantidad de energía absorbida por el fluido a medio día es mayor que para el acero, y que para las últimas horas del día, el fluido pierde más energía usando acero que usando polietileno.

La gráfica 21 demuestra como al igual que una placa de acero, la utilización de una placa de polietileno que tenga una menor anchura mejora la absorción de energía del fluido, incluso al comparar la gráfica 21 con la gráfica 17 se puede notar como para una anchura de 5mm la placa de polietileno muestra mejores resultados, ya que se obtienen aproximadamente 24.2 kWh con la placa de acero y 24.7 kWh con la placa de polietileno.

3.1.4 Análisis del evaporador inundado para 8 días nublados

Al igual que en el análisis del evaporador inundado para 8 días soleados este análisis se basa en las condiciones ambientales utilizadas para el análisis del evaporador para un día nublado. Por lo tanto las condiciones de velocidad del viento, radiación solar y temperatura ambiental son las mismas que en el día nublado, sin embargo estas se repiten durante 8 días para hacer el análisis transitorio de la temperatura de la placa y de la temperatura del fluido de trabajo durante un periodo mayor de tiempo.

0 1440 2880 4320 5760 7200 8640 10080 11520 16 18 20 22 24 26 28 30

t [min]

T

[

°C

]

DÍA 1 DÍA 2 DÍA 3 DÍA 4 DÍA 5 DÍA 6 DÍA 7 DÍA 8

15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 0 0.0002 0.0004 0.0006 0.0008 0.001 0.0012 0.0014 0.0016 0.0018 0.002 T [ °C ] Tf Tf m [ k g ] mevap mevap

DÍA 1 DÍA 2 DÍA 3 DÍA 4 DÍA 5 DÍA 6 DÍA 7 DÍA 8

La gráfica 22 muestra como la temperatura de la placa al igual que para un día soleado tiende a ir aumentando durante los días hasta que la diferencia de temperatura de la placa al inicio y al final del día se acerca a cero, esto pasa durante los 2 últimos días. Se observa como la placa alcanza un máximo de casi 25°C. Esto es aproximadamente 10°C menos que el valor de temperatura que alcanza la placa para los días soleados.

0.548 0.56 0.58 0.6 0.62 0.64 0.66 0.68 9

10 11 12 13

t

Q

ta

lf

[k

W

-h

]

Se puede ver en la gráfica 23 que al contrario de los días soleados, cuando hay días nublados consecutivos, la temperatura del fluido no se mantiene en saturación durante los siguientes días. Se observa que en los días soleados, para el segundo día el fluido no se mantiene en saturación durante la noche, sin embargo del 3er al 8vo día el fluido se mantiene en saturación. Este fenómeno no ocurre en los días nublados, ya que prácticamente ningún día el fluido se mantiene por completo a temperatura de saturación. Con respecto a la masa evaporada, se observa que se evapora un máximo de poco más de un gramo de fluido de trabajo cada segundo al medio día, esto es aproximadamente la mitad de lo que se evapora para un día soleado.

Profundidad del fluido

Este análisis utiliza la tabla 1 como en el análisis para la profundidad del fluido en días soleados. Esto significa que la transmisividad del fluido disminuye con respecto a un aumento en la profundidad.

0.01 0.02 0.03 0.04 0.05 8.308

8.308 8.308 8.308 8.308 8.309 8.309 8.309 8.309 8.309 8.309

L

[m]

Q

ta

lf

[k

W

-h

]

Al igual que en los días soleados, la cantidad de energía que absorbe el fluido de trabajo es mayor para profundidades mayores del fluido, donde la transmisividad es baja y la absortividad es mayor.

Ancho de las paredes

Al variar el ancho de las paredes desde 5mm hasta 5cm se puede notar que el cambio en la energía absorbida por el fluido disminuye conforme aumenta el ancho de las paredes. Al igual que en los días soleados, la cambio en la energía absorbida no es significativa cuando hay un aumento o disminución significativa en el ancho de las paredes, esto se puede observar en la escala de la gráfica 25, esto es debido a que el cambio se da en el orden de los Watts-hora.

0.01 0.02 0.03 0.04 0.05 5.5

6 6.5 7 7.5 8 8.5 9

L_p [m] Qto

ta

lf

[k

W

-h

]

Ancho de la placa

Se observa en la gráfica 26 como para los días nublados de igual manera que para los días soleados una disminución en la anchura de la placa repercute positivamente en la absorción de energía por parte del fluido.

Materiales para la placa de absorción

Los materiales analizados son los mismos que para el análisis de los días soleados: acero, acero inoxidable, cobre, aluminio y polietileno.

Al igual que en los días soleados una placa de absorción de polietileno es la que le da un mejor desempeño al evaporador, en comparación con los otros materiales, los cuales son metales. El aluminio es el único material que es ligeramente superior a los otros metales en este análisis.

0.01 0.02 0.03 0.04 0.05 5.5

6 6.5 7 7.5 8 8.5 9

Lp [m] Qto

ta

lf

[k

W

-h

]

Gráfica 27. Absorción de energía del fluido con respecto a distintos materiales para días nublados

En la gráfica 28 se observa como para anchos de placa menores, la absorción de energía del fluido es mayor, incluso si se compara esta gráfica con la gráfica 26 se puede notar como la placa de polietileno para un ancho de 5mm se desempeña ligeramente mejor que la placa de acero.

8.3 kWh 8.3 kWh

8.58 kWh

8.18 kWh

8.74 kWh

7.9 8 8.1 8.2 8.3 8.4 8.5 8.6 8.7 8.8

Acero Cobre Aluminio Acero inoxidable Polietileno

Materiales

3.2 Análisis de la bomba de calor

Para el análisis de la bomba de calor se toman las ecuaciones mostradas en el marco de referencia en las secciones 1.3, 1.4 y 1.5 ya que describen los balances de energía para el compresor, el intercambiador de calor y la bomba de expansión, además de la ecuación para la eficiencia isentrópica.

Para la simulación se toma en cuenta un compresor adiabático, por lo tanto el compresor no tiene pérdidas de calor y el balance de energía para el compresor es el siguiente:

La eficiencia isentrópica de un compresor adiabático con flujo estacionario es la siguiente:

Para la válvula de expansión el balance de energía es el mismo que el presentado en el marco de referencia:

Para el intercambiador de calor de calor el balance de energía es el siguiente:

Esto significa que la energía que pierda la bomba de calor va a ser una ganancia de energía para el agua que pase por el intercambiador de calor.

comercial (NOM-011-SESH-2012). La cual establece que se tiene que producir una diferencia mínima de temperatura entre el agua de entrada y de salida del boiler [9]:

La apa idad de ale ta ie to de e per itir elevar la te peratura del agua fría o o

mínimo 25 K (25 °C) proporcionando el flujo de agua que se establece en la placa o etiqueta de acuerdo a las especificaciones del fabri a te.

Es por esto que en los próximos análisis se contempla este como referencia. De la misma forma la NOM proporciona la siguiente ecuación para determinar la capacidad de calentamiento de un boiler (Diario Oficial de la Federación):

Esta ecuación representa el calor que absorbe una masa determinada de agua durante el tiempo de prueba para alcanzar una diferencia de temperatura.

Para los propósitos de este análisis se modifica esta ecuación de tal manera que describa la tasa de transferencia calor desde la bomba de calor hacia un flujo másico de agua:

̇ ̇

Donde:

̇ es el calor que le transfiere la bomba de calor al agua

̇ es el flujo másico de agua que atraviesa el intercambiador de calor

es el calor específico del agua

es la diferencia de temperatura que se produce debido a una transferencia de calor. Estas ecuaciones son programadas en EES® basándose en programas utilizados en la sección 3.1, de tal forma que este obtenga primeramente el calor absorbido por el evaporador inundado, después calcula mediante la eficiencia isentrópica y la relación de compresión las condiciones del refrigerante a la salida del compresor y finalmente considerando que la válvula de expansión es isoentálpica ( se obtiene el calor cedido al agua y la diferencia de temperatura del agua con las siguientes ecuaciones:

200 400 600 800 1000 1200 1400 30

31 32 33 34 35 36 37 38 39 40

t [min]

T

[

°C

]

Tp

Tp

_̇ ̇

3.2.1 Análisis de la bomba de calor para un día soleado

Para este análisis se utilizan las mismas condiciones ambientales (radiación solar, temperatura ambiental y velocidad del viento) que para el análisis del evaporador inundado para un día soleado (sección 3.1.1). Sin embargo para esta simulación se utilizan diferentes temperaturas iniciales para la placa y para el fluido, específicamente las del 8vo día, ya que para este día el fluido se encuentra siempre en saturación y se puede considerar que la temperatura de la placa al inicio y al final del día son casi las mismas como se muestra en las gráficas 29 y 30. Se hace esto debido a que se puede considerar que la temperatura de la placa se estabiliza para estos días y continuará casi constante en los días posteriores.

0 200 400 600 800 1000 1200 1400 14 16 18 20 22 24 26 28 30 0 0.0005 0.001 0.0015 0.002 0.0025 0.003 0.0035 t [min] T [ °C ] Tf Tf m [ k g ] mevap mevap

Como se menciona anteriormente el fluido siempre está en saturación en este día.

Flujo másico de agua

Si se varía el flujo másico de agua que pasa a través del intercambiador de calor el cambio de temperatura del agua varía enormemente, disminuyendo si se duplica el flujo másico y disminuyendo todavía más si se triplica como se observa en la gráfica 31.

Al observar la gráfica se puede notar hay una disminución en el tiempo que se mantiene el cambio de temperatura del agua mayor o igual a 25°C. Ya que por ejemplo para un flujo másico de 10 g/s está condición se mantiene casi 700 minutos, mientras que para un flujo másico de 30 g/s la condición se mantiene durante menos de 150 minutos. Por lo tanto se puede decir que el sistema es bastante sensible a un cambio en el flujo másico de agua que pasa por el intercambiador de calor.

Se observa como para un flujo másico de 20 g/s el tiempo puede incrementar bastante si se mejoran algunos aspectos de la bomba de calor, por lo tanto se usa este flujo másico para posteriores análisis.

0 200 400 600 800 1000 1200 1400 0

5 10 15 20 25

t [min]

D

Ta

g

u

a

[

°C

]

D Tagua@20g/s

D Tagua@20g/s

D Tagua@10g/s

D Tagua@10g/s

D Tagua@30g/s

D Tagua@30g/s

Relación de compresión

Para esté análisis como se había mencionado se utiliza un flujo másico de 20 g/s y se varía la relación de compresión para ver cómo se comporta el sistema, iniciando con una relación de compresión igual a 2 como se observa en la gráfica 32.

Gráfica 31. Variación del ∆T del agua con diferentes flujos másicos

Para la gráfica 32, 33 y las gráficas que siguen se sombrea un área con azul para distinguir el tiempo que la bomba de calor cumple con la condición .

Al aumentar la relación de compresión a 5 (gráfica 33) hay un incremento en el tiempo muy pequeño, ya que en la gráfica 32 se observa que se delimita de los 200 a los 600 minutos, esto sucede de la misma manera para la gráfica 33 pero con un ligero aumento en el tiempo.

Al simular el sistema con una relación de compresión igual a 10 se observa el mismo efecto (gráfica 34) ya que de la misma manera hay el tiempo en el que se mantiene la diferencia de temperatura del agua mayor o igual a 25 °C se delimita entre los 200 a los 600 minutos. Hay que tomar en cuenta que esta relación de compresión es 5 veces mayor a la planteada originalmente, y aún así no se da un incremento considerable en el área sombreada.

0 200 400 600 800 1000 1200 1400 0

5 10 15 20 25

t [min]

D

T

g

u

a

[

°C

]

D Tagua@0.6 D Tagua@0.6 D Tagua@0.8 D Tagua@0.8 D Tagua@0.9 D Tagua@0.9

h isen= 0.9

h isen= 0.8

h isen= 0.6

Eficiencia isentrópica

Al variar la eficiencia isentrópica del compresor se puede notar que el cambio en la temperatura del agua es despreciable.

Gráfica 34. ∆T del agua cuando el compresor tiene una relación de compresión igual a 10

Área superficial del evaporador inundado

Se modifica el área superficial del evaporador inundado, para que así este reciba mayor radiación solar. Anteriormente solo se había utilizado un área superficial igual a 1m2. La gráfica 36 muestra lo que ocurre cuando se incrementa en un 50% esta área.

Se observa como por fin el área sombrada rebasa los límites de 200 y 600 minutos, además se encuentra que hay otra sección sombreada en las horas de la tarde, lo cual significa que una vez más la bomba de calor produce un calentamiento adecuado del agua para estas horas.

Al duplicar el área superficial del evaporador inundado se observa un interesante aumento en el área sombreada, ya que el área sombreada se duplica comparada con el área sombreada de un evaporador de 1 m2. Es por esto que el área del evaporador inundado es una característica influyente en la bomba de calor.

Volumen de refrigerante

En la sección 3.1, la cual se dedico a analizar el evaporador inundado, se demuestra como al variar la profundidad del fluido refrigerante este absorbe más radiación solar y por lo tanto la ganancia de energía es mayor bajo esta condición. Sin embargo surge el cuestionamiento de si es mejor aumentar la profundidad del fluido refrigerante o el área superficial del evaporador inundado. Es por esto que se evalúan estas dos características con respecto al volumen de refrigerante, y se compara cual de las dos es más influyente para el sistema. Para la primera simulación se considera el área superficial del evaporador inundado igual a 1 m2 y se le aumenta la profundidad a 10 cm, dando así un volumen igual a 0.1 m3.

Para la segunda simulación se considera el área superficial del evaporador inundado igual a 5 m2 y la profundidad del fluido igual a 2cm para obtener así el mismo volumen de refrigerante igual a 0.1 m3.

Se puede notar a primera viste como al usar la misma cantidad de refrigerante el área sombreada es muchísimo mayor cuando el refrigerante se distribuye en un área superficial

Gráfica 38.∆T del agua con un evaporador de área superficial igual a 1 m2 y una profundidad de 10cm