Estudio de la influencia del ruido de impulso y del ruido blanco sobre un receptor en sistemas de comunicaciones

(1)

Escuela Superior de Ingeniería Mecánica y Eléctrica

Sección de Estudios de Postgrado e Investigación

Estudio de la influencia del ruido de impulso y del ruido

blanco sobre un receptor en sistemas de comunicaciones

T E S I S

Que para obtener el grado de MAESTRO EN CIENCIAS

CON LA ESPECIALIDAD DE INGENIERIA EN

TELECOMUNICACIONES

P R E S E N T A

Ing. Francisco Javier Tejeda López

Director de Tesis: Dr. Vladimir Kazakov Erasova

(2)

(3)

Po r h a b er m e per m i t i d o t er m i n a r est e l o g r o y h a b er m e d a d o l a o po r t u n i d a d d e d á r sel o a m i s pa d r es, a d em á s d e ser vi r m e d e i n spi r a ci ó n pa r a seg u i r a d el a n t e

A m i s pa d r es

Po r t o d o su a po yo y co m pr en si ó n , po r l eg a r m e l a h er en ci a m á s va l i o sa , qu e su ejem pl o m e h a ser vi d o pa r a su per a r m e en l a vi d a

A m i s h er m a n os

Po r so po r t a r m e t o d a s esa s n o ch es d e d esvel o y a n g u st i a s

A m i s a m i g os

Po r t o d o su a po yo i n co n d i ci o n a l y po r b r i n d a r m e su a m i st a d

A m i s pr ofesor es

Po r h a b er m e t r a n sm i t i d o su s co n o ci m i en t o s y ex per i en ci a s

A m i d i r ect or d e t esi s

Po r ser pa r a m i u n ejem pl o a seg u i r , po r ser u n g r a n ser h u m a n o y b r i n d a r m e su va l i o so t i em po a seso r a n d o

est e t r a b a jo , po r su pa ci en ci a y a m i st a d

A m i g l or i osa i n st i t u ci ón

Po r h a b er m e d a d o l a o po r t u n i d a d d e r ea l i z a r m i fo r m a ci ó n pr o fesi o n a l

A t od os el l os GR ACI AS

(4)

Establecer el régimen de funcionamiento que mejore la calidad

del receptor cuando en su entrada están presentes el ruido blanco

Gaussiano y el ruido de impulso, encontrando a través de la

probabilidad de error, su umbral óptimo.

Justificación:

(5)

Relación de Gráficas vii

Resumen x

Abstract xii Introducción xiv Antecedentes xvi

Capitulo 1

1

Modelos de ruidos que influyen en sistemas de

comunicaciones

1.1INTRODUCCIÓN 1

1.2FLUJO DE POISSON 1

1.3FDP PARA EL INTERVALO DE TIEMPO ENTRE DOS EVENTOS 4

1.4ECUACIONES DIFERENCIALES DE KOLMOGOROV PARA LAS CADENAS DE

MARKOV EN TIEMPO CONTINUO 6

1.5PROCESO BINARIO MARKOVIANO 9

1.6FDP DEL PROCESO DE SALIDA DE UN FILTRO LINEAL INFLUIDO POR EL

PBM 12

Capítulo 2:

15

Función de densidad de probabilidad de un filtro RC

influido por el Proceso Binario Markoviano y el

ruido blanco en el estado estacionario

2.1INTRODUCCIÓN 16

2.3MÉTODO DIRECTO 18

2.3MÉTODO DE LA FUNCIÓN CARACTERÍSTICA 19

2.4ANÁLISIS DE LOS RESULTADOS GRÁFICOS 22

(6)

Capítulo 3:

47

Probabilidad de error en un receptor

3.1INTRODUCCIÓN 47

3.2PROBABILIDAD DE ERROR CON LA PRESENCIA DEL RUIDO BLANCO

GAUSSIANO 48

3.3PROBABILIDAD DE ERROR CON PRESENCIA DEL RUIDO DE IMPULSO 54

3.4PROBABILIDAD DE ERROR CON LA PRESENCIA DEL RUIDO BLANCO Y EL

RUIDO DE IMPULSO 57

Conclusiones 63 Recomendaciones y sugerencias para trabajos futuros 64 A N E X O 65

ANEXO 1. 66 ANEXO 2. 68 ANEXO 3. 71 ANEXO 4. 72 ANEXO 5. 73 ANEXO 6. 73 ANEXO 7. 74 ANEXO 8. 75

(7)

Figura 1 Forma típica del ruido de impulso medido cerca de una caja registradora en la banda de frecuencia de 918 MHz.

xv Figura 2 Ruido de impulso producido por un horno de microondas en la banda

de 2.44 GHz. La separación entre el receptor y el horno de microondas es de 15 metros.

xv

Figura 3 Distribuciones de probabilidad de amplitud pico, determinadas de los datos obtenidos de lugares donde hay hornos, cajas registradoras y dentro de almacenes.

xv

Figura 4 Distribuciones de la duración de los pulsos para diferentes bandas. xv Figura 1-1 Intervalo de tiempo entre dos eventos. 4 Figura 1-2 Los dos eventos tienen la misma fdp. 5 Figura 1-3 Covarianza del Proceso Binario Markoviano. 13 Figura 1-4 Densidad espectral de potencia del Proceso Binario Markoviano 13 Figura 1-5 Esquema del PBM y su familia de fdps 14 Figura 2-1 Esquema del receptor con un filtro acoplado. 16 Figura 2-2 Esquema del receptor con un filtro RC. 16

Figura 2-3 Filtro RC. 17

Figura 2-4 Suma de dos fdps por el método de la suma dedos variables aleatorias. Caso simétrico. σ=1/8, λ1=2 y λ2=2.

23

Figura 2-5 Suma de dos fdps por el método de la suma de dos variables aleatorias. Caso asimétrico. σ=1/8, λ1=0.725 y λ2=3.

24

Figura 2-6 Método directo. Caso par. 25 Figura 2-7 Método de la función característica. Caso par. 25 Figura 2-8 Método directo. Caso Impar. 25 Figura 2-9 Método de la función característica. Caso Impar. 25 Figura 2-10 Método directo, λ1=λ2=1, σ2=1/64. 26

Figura 2-11 Método función característica, λ1=λ2=1, σ2=1/64. 27

Figura 2-12 Método directo, λ1=λ2=1.5, σ2=1/64. 27

Figura 2-13 Método función característica, λ1=λ2=1.5, σ2=1/64. 28

Figura 2-14 Método directo, λ1=λ2=2, σ2=1/64. 28

Figura 2-16 Método directo, λ1=λ2=3, σ2=1/64. 29

Figura 2-18 Método directo, λ1=0.5, λ2=2, σ2=1/64. 30

Figura 2-19 Método función característica, λ1=0.5, λ2=2, σ2=1/64. 31

Figura 2-20 Método directo, λ1=1, λ2=2, σ2=1/64. 31

Figura 2-21 Método función característica, λ1=1, λ2=2, σ2=1/64. 32

Figura 2-24 Método directo, λ1=1.5, λ2=3, σ2=1/64. 33

Figura 2-25 Método función característica, λ1=1.5, λ2=3, σ2=1/64. 34

Figura 2-26 Método directo, λ1=2, λ2=0.5, σ2=1/64. 34

(8)

Figura 2-32 Método directo, λ1=3, λ2=1.5, σ2=1/64. 37

Figura 2-33 Método función característica, λ1=3, λ2=1.5, σ2=1/64. 38

Figura 2-34 Fdps en función del parámetro α. λ1=λ2=1, σ2=1/64. 39

Figura 2-35 Fdps en función del parámetro α. λ1=λ2=1.5, σ2=1/64. 40

Figura 2-36 Fdps en función de la varianza del ruido blanco. λ1=λ2=1, α=0.3. 42

Figura 2-38 Fdps en función de la varianza del ruido blanco. λ1=λ2=1, α=1. 43

Figura 2-39 Fdps en función de la varianza del ruido blanco. λ1=λ2=1, α= 1.1. 43

Figura 2-41 Fdps en función de la varianza del ruido blanco. λ1=λ2=1.5, α=0.9. 44

Figura 3-1 Esquema del receptor. 46

Figura 3-2 Fdps Gaussianas. 47

Figura 3-3 Gráfica de la probabilidad de error para el filtro acoplado. 49 Figura 3-4 Gráfica de la probabilidad de error para el filtro RC. 50 Figura 3-5 Gráfica del factor ατ contra la relación señal a ruido, para el filtro RC. 52 Figura 3-6 Gráfica de la probabilidad de error contra el factor ατ, para el filtro

RC.

52

Figura 3-7 Caso simétrico. λ1=λ2=0.5. 53

Figura 3-8 Caso simétrico. λ1=λ2=1. 53

Figura 3-9 Caso simétrico. λ1=λ2=1.5. 53

Figura 3-10 Caso simétrico. λ1=λ2=3. 53

Figura 3-11 Señal de entrada del filtro. Suma del PBM y señal. 54 Figura 3-12 Proceso de salida del filtro RC, con sus respectivas fdps. 55 Figura 3-13 Gráfica de la probabilidad de error para el PBM. 57 Figura 3-14 Comparación de las curvas de la probabilidad de error cuando se

presenta el PBM.

58 Figura 3-15 Fdps del proceso de salida de un filtro influido por ruido blanco y

PBM, indicando el umbral óptimo. λ1=λ2=1.5, con una señal de entrada

de amplitud igual a 1.

59

Figura 3-16 Gráfica del umbral óptimo, para una señal de entrada de amplitud 1, con diferentes flujos de intensidades de Poisson.

60 Figura 3-17 Probabilidad de error en función del umbral, considerando el parámetro

de la amplitud de la señal de entrada. λ1=λ2=1, α=1, σ=1/64.

(9)

Estudio de la

influencia del ruido

de impulso y del

ruido blanco sobre

un receptor en

sistemas de

(10)

Resumen

El receptor de un sistema de comunicaciones consta de dos partes principales: el filtro y el dispositivo de umbral. La característica más importante del receptor es que él nos puede dar la probabilidad de error. Para calcularla es necesario conocer la función de densidad de probabilidad (fdp) del proceso de salida en el filtro RC bajo la influencia del ruido de impulso y el ruido blanco Gaussiano. Para poder analizar y entender el ruido de impulso, usamos el modelo matemático del Proceso Binario Markoviano (PBM), ya que es uno de los pocos modelos que nos permite hacer ciertas manipulaciones; de esta forma obtenemos algunas expresiones analíticas.

En el capítulo 1 es analizado detalladamente el flujo de Poisson, destacando sus características Markovianas. Posteriormente son definidas las ecuaciones diferenciales para las cadenas de Markov en tiempo continuo propuestas por Kolmogorov, las cuales dan origen al Proceso Binario Markoviano y al final de este capítulo es obtenida la fdp del proceso de salida de un filtro lineal (RC) influido por el PBM, definida por la distribución beta, la cual depende de los parámetros de entrada del proceso (intensidades del flujo de Poisson, la constante característica del filtro)

(11)

finalizar con la afectación que tienen los parámetros de entrada de los procesos en la forma de la fdp del proceso de salida.

(12)

Abstract

The receptor of a communication system is featured by two main components: the filter and the device threshold. The main characteristic of the receptor is that it can provide the error probability. In order to calculate it, is necessary to have knowledge about Probability Density Function (pdf) of the output process in the RC filter driven of impulse noise and Gaussian white noise. In order to analyze and understand the impulse noise, we use the mathematical model of Binary Markovian Process (BMP), due to is one of the few mathematical models that allow us to do manipulations, in that way we obtain some analytical expressions.

In the chapter 1, is analyzed carefully the Poisson’s flow, remarking their Markovian features. Afterwards are defined the differential equations for the Markov’s chains in continue time, proposed by Kolmogorov, which give the fundaments for the Binary Markovian Process; and at the end of this chapter is found the pdf of the output process in a lineal filter (RC) driven by the BMP defined by the beta distribution, which depends on the input process parameters (Poisson’s intensity flows, characteristic constant of the filter).

(13)

(14)

Introducción

Los sistemas de comunicaciones no son perfectos en lo que se refiere a inmunidad al ruido en sus tres partes principales: transmisor, línea o medio de comunicación y receptor. Por lo tanto, dependiendo de la calidad de construcción e instalación de un canal de comunicación, habrá siempre un mayor o menor grado de incertidumbre por la inevitable presencia de ruido, sobre todo en el medio de comunicación, que es donde se generan los llamados errores de transmisión.

En un canal de comunicación intervienen factores (naturales y artificiales) que afectan la transmisión de la señal, de manera que para el receptor sería prácticamente ininteligible. Desde este punto de vista podríamos tomar en consideración diferentes clases de efectos que influyen al canal de comunicación, de los cuales: el ruido blanco Gaussiano, atenuación, distorsión, ruido de impulso, etc.

(15)

telecomunicaciones, en donde se ha tratado de analizar diferentes tipos de modulación (QAM, PSK, ASK, etc.) en un ambiente de ruido de impulso para poder observar su comportamiento, encontrando la tasa de bits erróneos, tratando al mismo tiempo su eliminación, en la medida de lo posible mediante filtraje. Para llevar a cabo estas investigaciones se han hecho estudios en redes de telecomunicaciones de diferentes características (HFC, ADSL, etc.), en las que se ha puesto mucho énfasis por ser de alta velocidad, lo que implica un riesgo muy grande en su confiabilidad cuando se tiene la presencia del ruido de impulso. Incluso, el ruido de impulso se presenta en una acción tan sencilla como el conectar o desconectar algún equipo electrónico, el cual puede afectar su funcionamiento. De hecho el ruido de impulso puede ser tan cotidiano en los hogares, por ejemplo, al ver un televisor y al instante se enciende un automóvil, la ignición de su motor provoca ruido de impulso manifestándose con la imagen del televisor distorsionada, en fin se pueden enunciar innumerables ejemplos de ruido de impulso, que tal vez sean familiares.

(16)

Antecedentes

Se han propuesto varios modelos para analizar al ruido de impulso desde un punto de vista más práctico, cuyo objetivo es obtener expresiones sencillas de manejar. Uno de ellos es el propuesto por el Prof. Pierre Mertz (1961) [1, 2], en él involucra solo dos parámetros: la amplitud de los pulsos y su distribución en el tiempo. La distribución propuesta por este método para las amplitudes es muy simple. Consiste en sustituir simplemente una función parabólica por una función Gaussiana:

( )

(

)

m

h x

k x

p

+

= (1) donde p(x) es la fdp de la amplitud, x es la amplitud y k, h, m son constantes; la desviación estándar queda entonces definida como:

(

1

)(

2

)

2

− −

=

n n

h

σ (2) La distribución de impulsos en el tiempo es más laboriosa, la analiza mediante la distribución de errores en tiempo. Esto es principalmente porque son muy pocos los datos experimentales para esta distribución y en la mayoría de los casos se han medido errores que cruzan por un determinado umbral de amplitud.

Considera también que los impulsos o errores llegan al sistema de comunicaciones en paquetes, estos llegan aleatoriamente regidos por la distribución de Poisson.

(17)

forma empírica contra la distribución de Poisson. Las curvas más interesantes son las que obtuvo en la práctica, donde utiliza un circuito telefónico.

En 1980 B. I. Kuz’min [3], propone un estudio sobre las características estadísticas de la duración de pulsos de interferencia (ruido de impulso), en la salida de cuatro tipos fundamentales de filtros para las distribuciones de amplitudes de los pulsos de interferencia hiperbólica y log normal. Esta investigación utiliza resultados de Mertz, pero la diferencia radica en que Kuz’min obtiene bastantes expresiones analíticas.

Al mismo tiempo V. A. Smirnov y R. N. Efendiev (1980) [4], consideran el problema de la estimación de inmunidad al ruido de un receptor de señales discretas bajo un ambiente de pulsos de interferencia y ruido blanco. En esta investigación tratan el problema de filtración y el de síntesis, usando la teoría de Markov para filtros no lineales; utilizan señales con modulación ASK (Amplitude Shitft Keying), además de que obtienen expresiones bastante interesantes, ya que a partir de ellas consiguen calcular la probabilidad de error.

(18)

Figura 1. Forma típica del ruido de impulso medido cerca de una caja registradora en la banda de frecuencia de 918 MHz.

Figura 2. Ruido de impulso producido por un horno de microondas en la banda de 2.44 GHz. La separación entre el receptor y el horno de microondas es de 15 metros.

Obtiene resultados importantes debido a que encuentra las gráficas de la distribución de la probabilidad de la amplitud pico, para distintas frecuencias. Lo notable de este modelo es que es puramente experimental, ya que no tiene fundamentos matemáticos sólidos que puedan ser usados para una manipulación y obtener así, nuevos resultados que mejoren ciertos aspectos en la calidad del receptor.

Figura 3. Distribuciones de probabilidad de amplitud pico, determinadas de los datos obtenidos de lugares donde hay hornos, cajas registradoras y dentro de almacenes.

(19)

(20)

Capítulo 1:

Modelos de ruidos que influyen en sistemas de

comunicaciones

1.1 Introducción

En este capítulo comenzaremos describiendo los conceptos que dan origen a las ecuaciones propuestas por Kolmogorov que definen al PBM, obteniendo sus características estadísticas y su fdp en la salida de un filtro.

1.2 Flujo de Poisson

El flujo de eventos aleatorios es conocido como la secuencia de algunos eventos ocurridos en determinados instantes de tiempo. Geométricamente el flujo de eventos aleatorios es graficado por puntos sobre el eje de tiempo. Las principales características del flujo de Poisson son [6, 7, 8]:

1.- Ordinario: El flujo es llamado ordinario, si la probabilidad de que ocurran 2, 3, 4, ... eventos durante un pequeño intervalo de tiempo ∆t es despreciable en comparación con la probabilidad de que ocurra un evento:

( )

>> P

( )

i , i = 2,3,4,....

(21)

Físicamente la desigualdad (1-1) significa que el flujo de Poisson es relativamente raro en un flujo de eventos. Para un flujo arbitrario y para cualquier intervalo [t, t+τ], la siguiente expresión es valida:

( )

0

( )

1

( )

1

2 , , , + +

∑

= ∞ = i t t

t P P i

P _τ _τ _τ (1-2)

donde Pt, τ(0) es la probabilidad de que no haya ningún evento en el intervalo

[t, t+τ]. Tomando en cuenta (1-1) la expresión (1-2) será:

( )

0 _,

( )

1 1

, t + t t ≈

t P

P _∆ _∆ (1-3) Ahora calculemos el número promedio de eventos de un flujo ordinario sobre el intervalo [t, t+τ]:

( )

0 1

( )

1 2

( )

2 ....

( )

...

(

1

0⋅P_t_,_∆_t + ⋅P_t_,_∆_t + ⋅P_t_,_∆_t + +m⋅P_t_,_∆_t m + = P_t_,_∆_t

)

(1-4) Entonces el número promedio de eventos en la unidad de tiempo será:

( )

t P_t _t

∆

∆ 1

,

(1-5) Al tomar el límite de esta expresión, obtenemos la intensidad de un flujo ordinario:

( )

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ₌ → = segundo t P t

t t t 1 1

0 lim _, tiempo 1 ∆ ∆

λ ∆ (1-6)

Evidentemente λ(t) > 0.

Se presenta un caso especial cuando λ(t) = λ = constante, entonces se dice que el flujo es estacionario.

Las probabilidades Pt, τ(i) dependen de la longitud del intervalo [t, t+τ]

solamente y no depende de t.

(22)

cualesquiera τ1 y τ2, el número de eventos en uno de ellos no depende del

número de eventos del otro.

Usando ambas propiedades, podemos mostrar el número de eventos ocurridos en un intervalo [t, t+τ] del flujo no estacionario que estará determinado por la siguiente fórmula:

( )

[

( )

]

Λ( )τ

τ Λ τ ,

,

!

, m _t

t e

m t m

P = − (1-7) donde Λ(t, τ), es el número promedio de eventos ocurridos en el intervalo [t, t+τ]:

( )

τ = +

_∫

τλ

( )

Λ t

t

dt t

t, ' ' (1-8)

Λ(t,τ) es llamada también la función del flujo delantero. En el caso del estado estacionario:

( )

τ = Λ

( )

τ = +

_∫

τλ = λτ

Λ t

t dt

t, ' (1-9)

y entonces en lugar de (1-7), tenemos la conocida ley de distribución de Poisson:

( ) ( )

λτ

τ = λτ e−

m m

P

m

! (1-10) El flujo estacionario de Poisson es conocido como flujo simple.

Verifiquemos (1-10) y pongamos m = 0. Tenemos dos intervalos: (0, τ) y (τ,

τ+∆τ), ∆τ es pequeño. Como este flujo no tiene efecto secundario, podemos escribirlo para el intervalo (0, τ+∆τ):

( )

0 _τ

( ) ( )

0 _∆_τ 0

τ ∆

τ P P

P₊ = (1-11) Recordando la característica ordinaria (1-4):

( )

0 1 _∆_τ

( )

1

τ

∆ P

(23)

Tendremos en lugar de (1-12):

( )

0 _τ

( )

0 _τ

( ) ( )

0 _∆_τ 1

τ ∆

τ P P P

P₊ = − (1-13) y entonces:

( )

0 _τ

( )

0 _τ

( ) ( )

0 _∆_τ 1

τ ∆

τ P P P

P₊ − = − (1-14) dividimos (1-14) por ∆τ y tomemos el límite cuando ∆τ tiende a cero, por lo tanto:

( )

_{( )}

0 0

τ

τ _λ

τ P

d dP

−

= (1-15) La solución de esta ecuación diferencial con condiciones iniciales P0(0)=1 es:

( )

λτ

τ = e−

P 0 (1-16) Por supuesto, tenemos el mismo resultado de la fórmula (1-10) cuando m = 0, por lo que comprobamos nuestros resultados.

1.3 Fdp para el intervalo de tiempo entre dos eventos

Figura 1-1. Intervalo de tiempo entre dos eventos.

Consideremos un intervalo τ < T. La probabilidad de que no exista ningún evento en este intervalo τ esta determinada por la expresión (1-16). Pero esta probabilidad es la probabilidad de que la variable aleatoria T sea mayor que τ:

(

)

( )

λτ

τ

τ = = − > P e T

P 0 (1-17) Entonces la probabilidad del evento inverso T < τ, obviamente es igual a:

(

_T

)

_P

(

_T

)

_e T

(24)

Pero la probabilidad P(T<τ) es la integral de la ley de distribución de la variable aleatoria T. Tomando la derivada de P(T<τ) con respecto a τ obtenemos la fdp:

( )

τ =λe−λτ, τ>0

f (1-19) Tal ley es conocida como la ley de distribución exponencial. Esta fdp tiene una propiedad notable:

Si un tiempo τ1 ya ha pasado después del evento escogido, entonces la fdp de

la parte restante del intervalo θ=t-τ1 será la misma para cualquier τ1>0:

Figura 1-2. Los dos eventos tienen la misma fdp.

( )

_θ ₌ _λ −λθ

e

f (1-20) Probemos esta propiedad.

Siguiendo a (1-11), podemos escribir:

( )

0

( ) ( )

0 0

1

1 θ τ θ

τ P P

P ₊ = (1-21) según (1-10):

( )

λ(τ θ)

θ τ λτ

τ₁ 0 =e− 1,P₁+ 0 =e− 1+

P (1-22) de (1-21) y (1-22) encontraremos que:

( )

_{( )}

( )

λθ τ

θ τ

θ = + =e−

P P P

0 0 0

1

(1-23)

(25)

En realidad, la fdp f(θ) de la parte restante del intervalo (el futuro), no depende del intervalo (0, τ1) después de ocurrir el último evento (el pasado),

pero la fdp f(θ) depende del momento τ1 (el presente) porque el valor inicial

de θ coincide con τ1.

La ley exponencial es la única ley caracterizada por tales propiedades. Por lo tanto, el flujo de Poisson es el único flujo que determina los momentos de transiciones en sistemas Markovianos. El flujo de Poisson esta descrito por el parámetro λ (intensidad). En general, este parámetro puede depender del tiempo t y de los estados xi: λ(xi, t) (i =1, N).

1.4 Ecuaciones diferenciales de Kolmogorov para las cadenas de

Markov en tiempo continuo

Una importante observación es: los momentos de transición en el sistema Markoviano puede existir solo si el flujo de Poisson ocurre. Así que debemos conocer todas las intensidades λi(t), i=1, N, pero no es suficiente.

Porque la ocurrencia de algunos eventos con flujo de Poisson permite cualquier transición.

Para describir todas las posibles transiciones [7, 9], es necesario entrar a las probabilidades de transición condicionales qi,j(t) referida al evento del flujo de

Poisson. Si tal evento no ocurre, significa que el sistema se mantiene en el mismo estado. Entonces:

( )

t =0 paratodai

q_ij (1-24)

( )

∑

=

N

j

ij t q 1

1 (1-25)

Escojamos el estado xi y el correspondiente flujo de Poisson con un parámetro

(26)

( )

_{( )}

t t e

P_t _t λi t ∆t λ_i ∆

∆ 0 = − ≈1−

, (1-26)

( )

P

( )

t t

P_t_,_∆_t 1 =1− _t_,_∆_t 0 =λ_i ∆ (1-27) Después de que escribimos las probabilidades de transición del estado xi:

(

t t t

)

( )

t t

P_ii , + ∆ =1−λ_i ∆ (1-28)

(

t t t

)

( )

t tq

( )

t

P_ij , +∆ =λ_i ∆ _ij (1-29) La probabilidad incondicional del estado Pj(t+∆t) es igual:

(

t t

)

P

( )

t

[

( )

t t

]

P

( ) ( )

t t tq

( )

t

P _i _ij

N

i i j

j

j ∆ λ ∆

∑

λ ∆

= + − = + 1

1 (1-30)

Pasemos Pj(t) al lado izquierdo y dividamos ambas partes sobre ∆t y tomemos

el límite cuando ∆t tiende a cero. Esto produce:

( )

_{( ) ( )}

_{( ) ( ) ( )}

N ...., 2, 1, j , = + − =

∑

= t q t t P t P t dt t dP ij N i i i j j j 1 λ

λ (1-31)

Este sistema de ecuaciones esta caracterizado por la evolución de la probabilidad incondicional del estado. Este sistema es conocido como el sistema de ecuaciones de Kolmogorov.

Existe otra forma de describir este tipo de procesos. Anteriormente dimos un flujo especial con intensidad λi(t) y el conjunto de probabilidades

condicionales qij(t) para cada estado xi. Podemos usar otra aproximación: es

necesario tomar N-1 flujos de Poisson para cada estado. Estos flujos transfieren el sistema del estado xi al estado xj, y las correspondientes

intensidades serán designadas por dos subíndices xij(t). Podemos mostrar el

sistema de ecuaciones diferenciales para las probabilidades de transición Pij(t0,

t) tendremos:

( )

_{( ) ( )}

∑

= = N i il lj ij t t P t dt t t dP 1 0 0 , ,

(27)

Existe un sistema más de ecuaciones diferenciales:

( )

_{( ) ( )}

∑

= − = N i lj il ij t t P t dt t t dP 1 0 0 0 0 , ,

λ (1-33) Ambos sistemas, (1-32) y (1-33), fueron obtenidos por Kolmogorov y los llamo como sistemas de ecuaciones para las cadenas de Markov en tiempo continuo.

La primera de ellas (1-32) es llamada ecuación del sistema adelantado, porque el incremento de tiempo es tomado para el tiempo t. La segunda (1-33) es llamada ecuación del sistema atrasado, porque el incremento de tiempo es tomado para el tiempo t0.

Podemos obtener fácilmente las ecuaciones de las probabilidades incondicionales de estado Pj(t) del sistema de ecuaciones (1-32). En realidad,

multiplicaremos ambas partes de (1-32) por la probabilidad inicial Pi(t0) y

sumamos con respecto a i. Como resultado tendremos:

( )

_{( ) ( )}

∑

= = N i i ij j t P t dt t dP 1

λ (1-34)

involucrando a:

( )

_∑

( ) ( )

= = N i o ij i

j t P t P t t

P

1

, (1-35)

cuando λij(t) = λij = constante, el flujo de Poisson será estacionario y entonces

las probabilidades de transición no dependen del tiempo t. Tal proceso es llamado homogéneo y el sistema de ecuaciones (1-32) será un sistema de ecuaciones con coeficientes constantes:

( )

_{( )}

∑

= = N i i lj ij t P dt t dP 1

(28)

Para resolver (1-36) es necesario dar las probabilidades iniciales Pj(t0) (i = 1,

N), después el régimen de transferencia finaliza:

( )

0 = dt t dP_j (1-37) y tendremos un sistema de ecuaciones algebraicas en lugar del sistema de ecuaciones diferenciales:

∑

= = N i i ijP 1 0

λ (1-38) Similarmente a las cadenas de Markov en tiempo discreto, necesitamos añadir a (1-38) la ecuación de normalización:

∑

= = N i i P 1

1 (1-39)

1.5 Proceso Binario Markoviano

Consideremos una señal que tiene solo dos estados x1 y x2. Todas las

posibles transiciones son controladas por dos flujos de Poisson con intensidades λ1, λ2.

Escribamos las dos ecuaciones de Kolmogorov (1-36) para este caso [9]:

( )

_{( )}

t P t P dt t dP 2 2 1 1

1 =−λ +λ _(1-40)

( )

_{( )}

t P t P dt t dP 1 1 2 2

2 =−λ +λ _(1-41)

y de acuerdo con (1-39):

( )

₂

( )

1

1 t + P t =

P (1-42) suponemos que:

( )

λ ϑ λ

( )

λ β

(29)

Entonces, en lugar de (1-40) tenemos:

( )

₌₋_ϑ

_{( )}

₊_β

_{( )}

₌₋_ϑ

_{( )}

₊_β

₍

₋

_{( )}

_{) (}

₌₋ _ϑ₊_β

_{) ( )}

₊_β₌₋_γ

_{( )}

₊_β t P t P t P t P t P t P dt t dP 1 1 1 1 2 1 1 ₁ (1-44) donde β ϑ

γ= + (1-45) La ecuación (1-44) es una ecuación lineal de primer orden no homogénea. Su solución es (si la condición inicial es P1(t0)):

( )

_,

( )

( 0)

(

₁ ( 0)

)

0 1 0 1 t t t t e e t P t t

P = −γ − + − −γ −

γ β

(1-46)

o

( )

_,

( )

( 0)

(

₁ ( 0)

)

0 2 0 2 t t t t e e t P t t

P = −γ − + − −γ −

γ ϑ

(1-47)

si t →∞, entonces se presenta el caso estacionario.

( )

γ ϑ γ β ₌ ₌ =

= ₁ ₂ ₀ ₂

0

1 t ,t P , P t ,t P

P (1-48)

Después de calcular la esperanza matemática y la varianza:

( )

γ ϑ γ β ₂ 1 z z z P z t z i i

i = +

=

∑

(1-49)

si

z1 = -1; z2 = 1 (1-50)

así

( )

ϑ β ϑ β β ϑ β ϑ γ β ϑ + − = + − = − = 1 1 t

z (1-51)

(30)

( )

₁2 ₁ ₂2 ₂

( )

12

( )

12 1

2 ₌ ₊ ₌ ₋ ₊ ₊ ₌

γ ϑ γ β P z P z t

z (1-52)

y

( )

2 2 2 2 2 1 1 1 ⎟⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎝ ⎛ + − − = − = = ϑ β ϑ β

σ z& t z t z t (1-53)

Encontremos la función de covarianza de este proceso, para hacerlo, primero calcularemos la fdp bidimensional P(zi, zj, τ) para el régimen estacionario.

Escribamos el sistema de ecuaciones de las probabilidades de transición:

( )

_{( )}

₍

t t P t t P dt t t dP i i

i , _, _,

0 2 0

1 0

1 ₌₋_ϑ ₊_β

)

_(1-54)

( )

_{( )}

₍

t t P t t P dt t t dP i i

i , _, _,

0 2 0

1 0

2 ₌_ϑ ₋_β

)

_(1-55)

Podemos escribir la solución de estas ecuaciones, por ejemplo:

( )

_,

(

₁ ( 0)

)

( 0

0 11 t t t t e e t t

P = − −γ − + −γ −

γ

)

β

(1-56)

( )

_,

(

₁ ( 0)

)

0 12 t t e t t

P = − −γ −

γ ϑ

(1-57)

( )

_,

(

₁ ( 0)

)

( 0

0 22 t t t t _e e t t

P = − −γ − + −γ −

γ )

ϑ

(1-58)

( )

_t _t

(

_e (t to)

)

P = − −γ −

γ β

1 ,

0

21 (1-59)

donde t - t0 = τ; ahora ya podemos encontrar las probabilidades:

(

)

( )

(

γτ

)

γτ γ β γ β τ

τ = PP = −e− + e− z

z

P , , 1

2 2

11 1 1

1 (1-60)

(

)

(

)

( )

(

γτ

)

γ ϑβ τ τ τ

τ = P z z = PP = P P = −e− z

z

(31)

(

)

( )

(

γτ

)

γτ γ ϑ γ ϑ τ

τ = P P = −e− + e− z

z

P , , ₂ 1

2

22 2 2

2 (1-62)

Recordemos la expresión general para la función de covarianza:

( )

(

)

( )

2

,

, τ τ

τ z z P z z z k i j j i j i

z =

∑∑

− (1-63)

si z1 = z, z2 = z + a, encontraremos:

( )

γτ

γ ϑβ τ = a e−

k_z ₂

2

(1-64)

cuando z1 =-a, z2 = +a, tenemos:

( )

γτ

γ ϑβ τ = a e− k_z

2 2

4

(1-65)

Si calculamos la transformada de Wiener-Khichin, podemos encontrar la densidad espectral de potencia del Proceso Binario Markoviano:

( )

8 2 ₂ 1 ₂

γ ω γ ϑβ τ τ ω ωτ + = = ∞

_∫

∞ − − a d e k

s _z j (1-66)

cuando ϑ=β, entonces:

( )

_τ ₌_a2_e−2ϑτ

k_z (1-67)

( )

₂ 2 ₂

4 4 ϑ ω ϑ ω + = a

s (1-68)

El Proceso Binario Markoviano es un modelo matemático bastante conocido del ruido de impulso.

1.6 Fdp del proceso de salida de un filtro lineal influido por el

PBM

(32)

de los pulsos, la fdp de los intervalos entre pulsos y la fdp de la amplitud de los pulsos.

Cuando se presenta en la entrada de un receptor, en la salida de este tendremos un proceso binario, porque el receptor cuenta con circuitos limitadores que restringen su amplitud. Recordemos el esquema del receptor, el cual consta del filtro y del dispositivo de umbral. Cuando este proceso

(33)

Figura 1-4. Densidad espectral de potencia del Proceso Binario Markoviano.

binario sale del filtro, está definido por las intensidades del flujo de Poisson, que como acabamos de analizar, se trata del PBM.

Cuando el PBM está en la entrada de un filtro lineal, la fdp del proceso de salida estará definida por la distribución beta, dependiendo de las intensidades del flujo de Poisson; de tal manera que éstas intensidades determinaran la forma de la fdp.

( )

(

)

1

2 1 2 2 1 2 2 2 1 1 ; − − ₋ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = α λ α λ α λ α λ Γ α γ Γ x x x

f (1-69)

donde γ = λ1 + λ2, 0 ≤x2 ≤ 1, λ1 y λ2 son las intensidades del flujo de Poisson y

α es el ancho de banda del filtro lineal.

(34)

(35)

Capítulo 2:

Función de densidad de probabilidad de un filtro

RC influido por el Proceso Binario Markoviano y el

ruido blanco en el estado estacionario

2.1 Introducción

En lo que se refiere a este capítulo, analizaremos la fdp del proceso de salida de un filtro RC influido por ruido blanco y el PBM, tratando de encontrar una expresión analítica que la defina recurriendo a dos métodos: método directo y el método de la función característica.

2.2 Esquema del filtro acoplado y un filtro real

(36)

cuasi acoplado para una señal rectangular (figura 2-2). Por estas razones en nuestro análisis consideramos un filtro RC en la etapa de filtraje.

Figura 2-1. Esquema del receptor con un filtro acoplado.

Figura 2-2. Esquema del receptor con un filtro RC.

(37)

2.3 Método Directo

Supongamos que α=1/RC la constante de tiempo (parámetro del circuito) y que la densidad espectral de potencia del ruido blanco n(t) es N0/2.

El PBM ξ(t) esta descrito por los estados z1=0 y z2=1; y por las intensidades

del flujo de Poisson λ1 y λ2.

Figura 2-3. Filtro RC.

Para el caso estacionario debemos considerar el proceso de salida:

( )

t x

( )

t x

( )

t

y = ₁ + ₂ (2-1) donde: x1(t) es la componente del proceso de salida como resultado de la

influencia del ruido blanco, x2(t) es la componente del proceso de salida como

resultado de la influencia del PBM. La fdp de la variable Gaussiana x1es:

( )

(

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ − = 2 1 2 1 1 1 1 1 2 exp 2 1 σ π σ m x x

f (2-2)

( )

4 0 2 1 N T α

σ = (2-3)

m1≠0 cuando alguna señal esta presente.

La fdp de la variable x2 es la distribución beta, que está dada por (1-69):

( )

(

)

1

2 1 2 2 1 2 2 2 1 1 ; − − ₋ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = α λ α λ α λ α λ Γ α γ Γ x x x

f (2-4)

(38)

Tomando en cuenta que las dos variables aleatorias x1 y x2 son independientes,

podemos encontrar la ley de distribución del proceso de salida y(t) usando el teorema de la suma de dos variables aleatorias:

( )

( ) (

)

( )

₁

(

₂

) ( )

₂ ₂ ₂ 1 1 2 1 1 dx x f x y f y f dx x y f x f y f

∫

− = − = (2-5)

La principal desventaja de utilizar este método es que no podemos calcular las integrales (2-5) con (2-2) y (2-4) analíticamente, solo es posible calcularlas numéricamente. El resultado de este cálculo nos dará una solución exacta, que servirá de patrón para el siguiente método.

2.3 Método de la función característica

Las expresiones de las funciones características para las fdps (2-2) y (2-4) son conocidas:

( )

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = 2 exp 2 2 1 1 1 v v jm jv σ

φ (2-6)

( )

_∑

∞

( )

= _⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 0 1 1 2 ! k k k k k jv jv α γ Γ α λ Γ α λ Γ α γ Γ

φ (2-7)

La multiplicación de las fórmulas (2-6) y (2-7) da la función característica del proceso de salida y(t):

( )

jv

( ) ( )

jv jv y φ1 φ2

(39)

( )

( ) (

)

( )

jv jm v v

(

jvy

)

dv k k k dv jvy jv y f x k k y − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = = − =

∑

∫

∞ = ∞ ∞ − exp 2 exp ! 1 2 1 exp 2 1 2 2 1 0 1 1 σ α γ Γ α λ Γ α λ Γ α γ Γ π φ π (2-9) Usando tablas de integrales (ver fórmula (3.462.3) en [10]) podemos encontrar y calcular la integral en (2-9) (comparar con [11]):

( )

(

)

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ − =

∑

∞ = 2 2 2 0 1 1 2 2 2 2 2 1 ! 1 4 exp 2 1 σ σ β γ Γ β λ Γ β λ Γ β γ Γ σ π σ m y D k k k m y y f _k k k (2-10)

donde Dk(•) (ver secciones (9.24), (9.25) en [10]) es una función

parabólica cilíndrica.

Esta función puede representarse mediante los polinomios de Hermite Hk(•)

como (ver fórmula (9.253) en [10]):

( )

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = − 2 2 exp 2 2

2 ρ ρ

ρ _k

k

k H

D (2-11)

( ) ( )

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 2 exp 2 exp 1 2 2 _ρ ρ ρ ρ k k k k d d H

Entonces, en lugar de (2-10) tenemos:

( )

_{( )∑}

∞ = ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 0 2 2 2 2 1 ! 1 k k k k g m y H b k y f y f σ

(40)

donde: ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ = k k b_k α γ Γ α λ Γ 1 (2-13)

( )

(

)

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ₋ − = 2 2 2 2 2 2 exp 2 1 σ π σ m y y

f_g (2-14)

La expresión (2-12) es la bien conocida serie de Edgeworth [12], donde fg(y)

es la fdp Gaussiana, bk son los cuasimomentos y Hk corresponden a los

polinomios de Hermite.

Lo más notable de este resultado son los cuasimomentos que

usualmente se obtienen mediante la fdp, la cual debe ser aproximada por la

serie de Edgeworth. Generalmente no es tan sencillo calcularlos, debido a que

no hay ninguna expresión analítica de la fdp. Existe otro método para

encontrar dichos cuasimomentos, es a través de la definición del momento

inicial [13, 14, 15, 16]:

( )

=

_{∫ ∫}

t t

( ) ( ) (

_k −

) (

− _k

)

_k

k t g u g u t u t u du du

m

0 0

1 1

1 ... .... ...

.... ξ ξ (2-15)

donde g(•) es la respuesta al impulso del filtro y ξ(•) es el proceso de entrada. Es importante hacer notar la ventaja de calcular los cuasimomentos, ya

que su expresión es mucho más simple que la integral (2-15), que al aumentar

el número de términos se hace cada vez más compleja de resolver. Cabe hacer

la aclaración que los cuasimomentos son equivalentes a los momentos

iniciales hasta k = 6 aproximadamente. Además una característica interesante

en este caso es el hecho de que los cuasimomentos dependen de las

(41)

lo hace un caso raro dentro de la definición de los cuasimomentos bk en la

serie de Edgeworth.

2.4 Análisis de los resultados gráficos

Es posible obtener mediante la ecuación (2-15) algunos resultados

gráficos, sin embargo tenemos que hacer algunas consideraciones. Al tomar la

esperanza matemática y la varianza del primer y segundo cuasi momento

respectivamente, tenemos que:

b0=1, b1=0, b2=0

Es bastante simple demostrar este hecho. Los cuasimomentos están definidos

como: ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = σ σ H x m

b_n n _n (2-16)

donde n es el orden del cuasi momento, σ es la desviación estándar, Hn es el

polinomio de Hermite y m es la esperanza matemática. H0=1, H1=x y H2=x 2

-1,

es evidente que b0=1; entonces calculemos b1, según la definición:

( )

0

1

1 = − =

− =

=

= H x x x m x m b

σ σ σ

σ (2-17)

y para b2 tenemos:

( )

(

)

0

2 2 2 1 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 = + − = − + − = = − + − = − + − = = − + − = − = = σ σ σ σ σ σ σ σ m x m m x m x m x m xm x m xm x x x H b (2-18)

En general, cuando el PBM es simétrico, al calcular los cuasimomentos de n

-esimo orden y recordando que los operadores del momento y la varianza

corresponden integrales, tenemos que al multiplicar una función par (PBM

(42)

resultantes son iguales a cero, y cuando al multiplica una función impar (PBM

asimétrico) por una variable par en el integrando, los cuasimomentos

resultantes también son iguales a cero; este hecho reduce el número de

términos en la serie de Edgeworth.

Por otro lado, necesitamos conocer los polinomios de Hermite de un

orden relativamente alto:

H3=x 3

-3x;

H4=x 4

-6x2+3;

H5=x5-10x3+15x;

H6=x 6

-15x4+45x2-15;

H7=x 7

-21x5+105x3-105x;

H8=x 8

-28x6+210x4-420x2+105;

H9=x9-36x7+378x5-1260x3+945x;

H10=x10-45x8+630x6-3150x4+4725x2-945;

H11=x 11

-55x9+990x7-6930x5+17325x3-9450x;

H12=x 12

-66x10+1485x8-13860x6+51975x4-61425x2+9450;

H13=x13-78x11+2145x9-25740x7+135135x5-269325x3+132300x;

H14=x14-91x12+3003x10-45045x8+315315x6-945000x4+940275x2-132300;

H15=x 15

-105x13+4095x11-75075x9+675675x7-2836890x5+4720275x3

-2012850x;

H16=x 16

-120x14+5460x12-120120x10+1351350x8-7566615x6+18904725x4

-16173675x2+2012850;

H17=x17-136x15+7140x13-185640x11+2552550x9-18377415x7+64304415x5

-91792575x3+34360200x;

H18=x 18

-153x16+9180x14-278460x12+4594590x10-41350365x8+192946320x6

(43)

H19=x19-171x17+11628x15-406980x13+7936110x11-87296265x9+523749240x7

-1570992570x5+1962996525x3-653836050x;

H20=x 20

-190x18+14535x16-581400x14+13226850x12

-174593475x10+1309415625x8-5237237250x6+9817959375x4

-6542825625x2+653836050

Ahora bien, mediante el programa de MATLAB y usando el método

directo (la suma de dos variables aleatorias) como primera instancia, sumamos

la fdp del ruido blanco Gaussiano y la fdp del PBM. Podemos observar en las

figuras que cuando las intensidades de flujo de Poisson son iguales, la fdp del

PBM es simétrica, y como resultado tenemos a la salida del filtro una fdp

simétrica con respecto a su esperanza matemática. En este caso estamos

considerando a la esperanza matemática igual a cero en la fdp del ruido blanco

Gaussiano, lo cual quiere decir que no hay señal presente y consideramos

también una varianza muy pequeña, debido a que la suma de las dos variables

aleatorias se lleva a cabo mediante una integral (convolución) y entonces el

barrido de una fdp con respecto a la otra fdp debe ser completo.

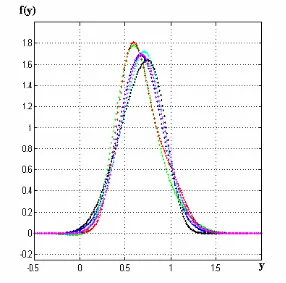
Figura 2-4. Suma de dos fdps por el método de la suma de dos variables aleatorias. Caso simétrico.

(44)

En la figura (2-4) tenemos un caso simétrico en el cual la fdp Gaussiana tiene

σ=1/8 y la fdp del PBM tiene las intensidades de flujo de Poisson iguales a

λ1=2 y λ2=2.

Cuando las intensidades del flujo de Poisson no son iguales, entonces la

fdp del PBM es asimétrica y la fdp del proceso de salida en filtro ya no se

comporta como en el caso simétrico, la fdp es ahora asimétrica también. Como

podemos observar en la figura (2-5), la fdp Gaussiana tiene σ=1/8 y la fdp del PBM tiene las intensidades λ1=0.725 y λ2=3. En todos los casos, la fdp

resultante debe cumplir con la ecuación de normalización, es decir, el área

bajo la curva tiene que ser igual a la unidad; si observamos con detalle en las

gráficas, es claro que esta condición se cumple por lo que podemos decir que

estamos en lo correcto.

Figura 2-5. Suma de dos fdps por el método de la suma de dos variables aleatorias. Caso asimétrico.

σ=1/8, λ1=0.725 y λ2=3.

Consideremos ahora nuestro resultado obtenido por el método de la

función característica, que describe la fdp del proceso de salida mediante la

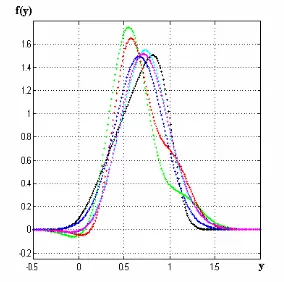
serie de Edgeworth. En las figuras (2-6) y (2-7) estamos comparando los dos

métodos empleados, para un caso simétrico, la figura (2-6) corresponde al

método directo, en la cual se puede observar la fdp de la componente del ruido

blanco, la fdp de la componente del PBM y la suma de estas componentes

(45)

utilizamos el método de la función característica, debido a que la serie de

Edgeworth es una suma infinita tiene que ser truncada, esa es la razón por la

que solo se toman algunos términos para cada curva. Lo que observamos es

que a medida que se incrementa el número de términos en la serie, la

discrepancia entre la curva exacta y la curva aproximada disminuye muy

lentamente, lo que quiere decir que la serie de Edgeworth converge muy

lentamente.

Figura 2-7. Método de la función característica. Caso par.

Figura 2-6. Método directo. Caso par.

Figura 2-9. Método de la función característica. Caso impar.

(46)

Las figuras (2-8) y (2-9) corresponden a un caso asimétrico comparando

nuevamente los dos métodos empleados. Una importante observación es que

en prácticamente todas las curvas obtenidas empleando el método de la

función característica presentan partes negativas, este hecho contradice a la

teoría de la probabilidad, por lo que estas curvas no pueden ser aceptadas

como fdps.

(47)

Figura 2-11. Método función característica, λ1=λ2=1, σ2=1/64.

(48)

Figura 2-13. Método función característica, λ1=λ2=1.5, σ2=1/64.

(49)

(50)

(51)

Figura 2-19. Método función característica, λ1=0.5, λ2=2, σ2=1/64.

(52)

Figura 2-21. Método función característica, λ1=1, λ2=2, σ2=1/64.

(53)

(54)

[image:54.612.166.450.72.355.2]

Figura 2-25. Método función característica, λ1=1.5, λ2=3, σ2=1/64.

[image:54.612.164.452.381.674.2]

(55)

[image:55.612.165.451.71.354.2]

Figura 2-27. Método función característica, λ1=2, λ2=0.5, σ2=1/64.

[image:55.612.164.452.383.675.2]

(56)

[image:56.612.166.450.72.354.2]

[image:56.612.164.452.380.674.2]

(57)

[image:57.612.165.451.71.355.2]

[image:57.612.164.452.380.674.2]

(58)

[image:58.612.165.451.71.354.2]

Figura 2-33. Método función característica, λ1=3, λ2=1.5, σ2=1/64.

En resumen podemos decir que [14, 15]:

i) Cuando el PBM es simétrico (λ1=λ2) la fdp del proceso de salida es

simétrica también;

ii) Cuando el PBM es asimétrico (λ1≠λ2) la fdp del proceso de salida es

asimétrica también;

iii) Cuando γ>α, la forma de la fdp tiende a la fdp Gaussiana.

Al mismo tiempo, podemos ver algunas características negativas. Estas son:

a) En la mayoría de los casos, prácticamente todas las curvas con el

número de términos restringido en la serie de Edgeworth tienen partes

(59)

b) Al incrementar el número de términos en la serie, la discrepancia entre

la curva exacta y la curva aproximada disminuye muy lentamente. Esto

significa que la serie de Edgeworth converge muy lentamente.

2.5 Fdp y la dependencia de los parámetros de entrada

Necesitamos conocer la dependencia de los parámetros de entrada de

los procesos, los cuales determinan la forma de la fdp del proceso de salida,

estos son: las intensidades de flujo de Poisson, la constante característica del

circuito RC y la varianza. A continuación se muestran algunas gráficas

variando estos parámetros, para ciertos casos escogidos al azar, tomando en

cuenta solo los casos simétricos, los cuales se tomarán en cuenta en el

[image:59.612.159.455.369.666.2]

próximo capítulo para encontrar la probabilidad de error.

(60)

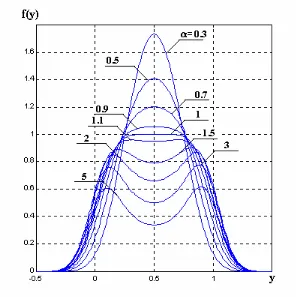
2.5.1 Dependencia del Ancho de banda del circuito RC

En la figura (2-34) se muestra la gráfica de la suma de las fdps de salida de los

procesos, dejando constante las intensidades del flujo de Poisson y la varianza,

variando únicamente la constante característica del circuito RC. Como

podemos observar, a medida que esta constante decrece, la amplitud de las

fdps también decrecen a tal punto que cuando la constante del circuito es muy

grande, las fdps obtenidas son bimodales. Este efecto se debe a que como

sabemos, la constante del circuito α representa el ancho de banda del filtro lineal, entonces cuando el ancho de banda del PBM es mucho menor al del

sistema, la fdp del proceso de salida tiende a dos funciones delta; pero cuando

el ancho de banda del PBM es mucho mayor al del filtro lineal, se presenta un

[image:60.612.165.451.405.687.2]

(61)

2.5.2 Dependencia de la varianza del ruido blanco Gaussiano

Consideremos ahora el caso cuando las intensidades del flujo de

Poisson y la constante del circuito son constantes y supongamos que están en

función de la varianza del ruido blanco Gaussiano, tomando en cuenta varios

casos.

Como se observa en las gráficas (2-36 – 2-43), es evidente la

dependencia de la varianza en la fdp del proceso de salida en el circuito,

notando que a medida que disminuye ésta, la fdp incrementa su amplitud

concentrándose en la media. Este efecto se puede explicar de la siguiente

manera; cuando la varianza del ruido blanco es mucho mayor a la varianza el

PBM, tomando en cuenta a los dos procesos independientemente, significa

que la amplitud del ruido blanco es mucho mayor que la amplitud del PBM en

la entrada del filtro lineal, esto quiere decir que al sumar las dos varianzas

correspondientes a cada ruido en la salida del filtro, la más predominante es la

del ruido blanco. El punto intermedio es la transición del cambio de la fdp,

cuando pasa de una forma Gaussiana a una forma bimodal (en ciertos casos,

depende de las intensidades del flujo de Poisson y de la constante del circuito),

esto es, en la entrada del filtro lineal la varianza del ruido de impulso tiene ya

cierto efecto con respecto a la varianza del ruido blanco. Y por último, ahora

estamos en el otro extremo, cuando ya no se distingue la influencia de una

varianza de la otra y la forma de la fdp dependerá de las características del

(62)

[image:62.612.165.451.72.355.2]

Figura 2-36. Fdps en función de la varianza del ruido blanco. λ1=λ2=1, α=0.3.

[image:62.612.165.452.399.679.2]

(63)

[image:63.612.165.451.72.353.2]

Figura 2-38. Fdps en función de la varianza del ruido blanco. λ1=λ2=1, α=1.

[image:63.612.166.451.401.676.2]

(64)

[image:64.612.165.451.72.354.2]

Figura 2-40. Fdps en función de la varianza del ruido blanco. λ1=λ2=1, α=1.5.

[image:64.612.166.452.399.680.2]

(65)

[image:65.612.166.451.71.349.2]

Figura 2-42. Fdps en función de la varianza del ruido blanco. λ1=λ2=0.5, α=1.5.

[image:65.612.167.450.392.670.2]

(66)

Capítulo 3:

Probabilidad de error en un receptor

3.1 Introducción

Es importante comparar la calidad de los filtros lineales con la presencia

del ruido blanco y el ruido de impulso por separado, para posteriormente hacer

un análisis con la suma de estos dos ruidos simultáneamente, variando los

parámetros de entrada para observar su comportamiento. En este capítulo

estudiaremos estas características para posteriormente obtener la probabilidad

de error.

Figura 3-1. Esquema del receptor.

El receptor en un sistema de comunicaciones, esta constituido por varias

etapas: etapa limitadora, etapa de filtraje, etapa de decisión, etc. Es importante

remarcar en que etapas del receptor puede afectar la presencia de ruido.

Cuando en la entrada del receptor se presenta una señal contaminada con

ruido, ya sea de impulso, blanco o ambos, pasan por circuitos limitadores de

amplitud, estos circuitos restringen la amplitud del ruido de impulso, por lo

(67)

binario, el cual analizamos con el modelo matemático del PBM. En la salida

del filtro podemos obtener la fdp del proceso de salida, en la figura (3-1)

representada por y(t), que entra en el dispositivo de umbral, en donde ya esta

preestablecido un umbral de decisión definido por h, finalmente en la salida el

dispositivo de umbral es el que toma la decisión de que la señal esta presente o

no.

3.2 Probabilidad de error con la presencia del ruido blanco

Gaussiano

Figura 3-2. Fdps Gaussianas.

Supongamos que tenemos un sistema de comunicaciones, en el receptor

podemos captar dos niveles 1 o 0, para nuestro caso, la señal observada

presenta ruido blanco, entonces la fdp que describe es Gaussiana con la media

igual a cero m=0 y la varianza igual a σ2=2E/N0. De acuerdo con esto

podemos construir la fdp de salida del filtro cuando no hay señal presente:

( )

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 2 2 0 2 exp 2 1 σ π σ y y

p (3-1)

La fdp en la salida del filtro cuando la señal esta presente, esta caracterizada

por una media igual a m=2E/N0 y una varianza igual a σ2=2E/N0 también.

( )

(

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ − = 2 2 1 2 exp 2 1 σ π σ m y y

(68)

Estas fpds se muestran en la figura (3-2), en donde se puede ver que el umbral

de decisión es h. Cuando y>h, se presenta una falsa alarma porque el receptor

decide que la señal está presente aunque en realidad no lo esté. La

probabilidad de este tipo de error corresponde al área sombreada del lado

derecho del umbral y puede ser calculada mediante la siguiente expresión:

dy y P h

∫

∞ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 2 2 0 2 exp 2 1 σ π σ

ε (3-3)

De igual manera, cuando y<h se presenta una falsa supresión, porque el

receptor decide que la señal está ausente aunque no lo esté. Este error

corresponde al área del lado izquierdo del umbral y puede calcularse por la

siguiente fórmula:

(

)

dy m y P h

∫

∞ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ₋ − = 2 2 1 2 exp 2 1 σ π σ

ε (3-4)

Ahora bien, no podemos sumar estas dos probabilidades de error por si solas,

debido a que cada una de ellas respetan diferentes leyes de distribución de

probabilidades. Para obtener una relación de estas dos probabilidades de error

necesitamos aplicar la ley de la probabilidad total:

1 1 0

0 ε ε

ε P P PP

P = + (3-5) La gráfica de la probabilidad de error para el filtro acoplado se traza en una

retícula de escala semi-logarítmica, en donde el eje de las abscisas

corresponde a su relación señal a ruido contra el logaritmo de la probabilidad

de error. La relación señal a ruido para el filtro acoplado es:

(69)

[image:69.612.169.438.67.349.2]

Figura 3-3. Gráfica de la probabilidad de error del filtro acoplado.

En la figura (3-3) se muestra la gráfica de la probabilidad de error. Se observa

que la máxima probabilidad de error es de 0.5 (log 0.5 = -0.3), esto se debe a

que en la expresión de la ley de la probabilidad total, la probabilidad a priori

toma un valor de 0.5 por ser las fdps simétricas con respecto a su media. A

medida que cambia la relación señal a ruido, se va desplazando el umbral y

por consiguiente también la media de la fdp de la salida del filtro cuando la

señal esta presente. Esto significa que la área de la probabilidad de error

disminuye con el aumento de la relación señal a ruido.

Tomemos en consideración el filtro bajo estudio, el filtro RC, y

comparémoslo con el filtro acoplado en cuestión de la probabilidad de error.

Notamos una diferencia, el filtro RC depende del factor ατ. Este factor influye notablemente en la calidad del filtro, ya que como podemos ver en la figura

(70)

ruido mayor, lo que implica más energía, por lo que no es lo suficientemente

[image:70.612.165.475.118.433.2]

eficiente como es el filtro acoplado.

Figura 3-4. Gráfica de la probabilidad de error del filtro RC.

Al graficar la relación señal a ruido con respecto al factor ατ, como se ilustra en la figura (3-5), vemos que la curva decrece muy lentamente y tiene

solo un máximo. Calculemos este máximo analíticamente. La relación señal a

ruido para el filtro RC esta definida como [17]: