Reconoces y realizas operaciones con distintos tipos de funciones

(1)

Introducción

general

Este libro fue diseñado para fungir como una herramienta importante dentro de la planeación didáctica y del aula; se combinan aspectos visuales, algebraicos y deductivos, además de la información proporcionada. Los ejemplos presentados se apegan a la realidad del aula y algunos están contextualizados, con el propósito de que se apliquen posteriormente..

El texto está basado completamente en el programa de Matemáticas IV (Precálculo) de la DGB. En el primer bloque se incluye la conceptualización de un tema muy importante para las matemáticas de la vida diaria y para una explicación más precisa de todo lo que nos rodea.

En el bloque dos se presentan las bases y las transformaciones de funciones, tema muy importante para la modelación con funciones.

Cada bloque contiene alguno de los siguientes elementos, cuya finalidad te permitirá mejorar los resultados obtenidos tanto dentro como fuera del aula:

Los desempeños del estudiante, es muy importante que pongas atención en esta información pues indica lo que debes saber hacer al finalizar el bloque éstos se verán reflejados en las evidencias de lo aprendido, y por consiguiente, estarás en condiciones de aplicar esos conocimientos.

(2)

Introducción

general

Actividad introductoria, cuya finalidad es que el estudiante establezca un contacto con sus conocimientos previos, así como iniciar a los nuevos conocimientos. Es recomendable que traten de contestar con honestidad y sin revisar la información contenida en el libro pues tiene la finalidad de verificar cuánto se sabe antes de empezar los temas. Puedes guardar tus respuestas en tu portafolio de evidencias, ya que al finalizar el bloque, podrás comparar tus conocimientos preliminares con lo desarrollado en el aula.

Problemas contextualizados, situaciones problemas de la vida cotidiana aplicados en el ámbito, laboral, familiar, empresarial y científico.

Autoevaluación, en la cual el estudiante verifique lo aprendido, en forma conceptual y práctica. Es recomendable que lo resuelva como una actividad guiada por el docente, donde ya sea en forma individual o por parejas, se ponga en juego todo lo aprendido, sin que el estudiante revise la información contenida en sus apuntes o en el presente libro.

Mi agradecimiento a todas aquellas personas que de una u otra forma hicieron posible este libro, en especial a Samantha mi musa inspiradora y a nuestro primer bebé que viene en camino, que con su apoyo y amor fueron mi motivación para terminar esta obra; a mi familia que siempre está conmigo, mis padres Melesio y Ruth, y mis queridos hermanos Ruth Rosalía, Maribel y Luis Ignacio, quienes siempre me echan porras y me exhortan para salir adelante; a Orissa que siempre está en mi corazón; a Claudia, porque se que siempre cuento con ella, en las buenas y en las malas; a Mauro, por su paciencia; a la maestra Amelia por su comprensión; a Martha Pestaña y Carmina Siliceo, por sus invaluables sugerencias y a Mario Jareda por su invaluable apoyo, recién llegado al cargo… Muchas gracias.

Por último, pongo a disposición de docentes, estudiantes y público en general, el correo electrónico librodgbmate4@hotmail.com para atender sus dudas, sugerencias y comentarios, que me permitan mejorar este libro.

(3)

BL

OQUE

Competencias a desarrollar

OBJE

TO

S DE

APRENDIZAJE

DESEMPEÑOS DEL ESTUDIANTE

1

Tiempo asignado: 8 horas

Reconoces y realizas

(4)

BL

OQUE

Competencias a desarrollar

OBJE

TO

S DE

APRENDIZAJE

DESEMPEÑOS DEL ESTUDIANTE

• Utiliza los criterios que definen a

una función para establecer si una

relación dada es funcional o no.

Describe una función empleando

• diferentes tipos de registros y

refiere su dominio y rango.

Emplea la regla de

• correspondencia de una función,

y los valores del dominio implícito

o explícito, para obtener las

imágenes correspondientes.

Aplica diferentes tipos de

• funciones en el análisis de

situaciones.

Utiliza operaciones entre

• funciones para simplificar

procesos a través de nuevas

relaciones.

Aplica las nociones de relación y

• función para describir situaciones

de su entorno.

Funciones.

• Relaciones.

• Dominio.

• Contradominio.

• Imagen.

• Regla de correspondencia.

•

Construye e interpreta modelos matemáticos •

mediante la aplicación de procedimientos aritméticos, algebraicos, geométricos y variacionales, para la comprensión y análisis de situaciones reales, hipotéticas o formales. Formula y resuelve problemas matemáticos, •

aplicando diferentes enfoques.

Explica e interpreta los resultados obtenidos •

mediante procedimientos matemáticos y los contrasta con modelos establecidos o situaciones reales.

Analiza las relaciones entre dos o más variables •

de un proceso social o natural para determinar o estimar su comportamiento.

Cuantifica, representa y contrasta experimental •

o matemáticamente las magnitudes del

espacio y las propiedades físicas de los objetos que lo rodean.

Interpreta tablas, gráficas, mapas, diagramas y •

(5)

�

B1

�

INTRODUCCIÓN

Las funciones se presentan en casi todos los aspectos de nuestra vida, ya que los cambios que sufren algunas variables repercuten en nuestras acciones, en la naturaleza y en el Universo. En el presente bloque encontrarás las bases para desarrollar las competencias en el uso y aplicación de las funciones, partiendo desde la terminología, sus definiciones y su conceptualización hasta llegar a su aplicación en diversos problemas de nuestro entorno real; además, encontrarás un proyecto cuyo fin es que a lo largo del curso vayas descubriendo las aplicaciones del conocimiento matemático de cada bloque, te recomiendo que vayas realizando las actividades conforma avances en tus conocimientos, y al finalizar presentes tus avances y descubrimientos en la clase.

Operaciones con números enteros y fraccionarios, uso de signos de agrupación. I. Realiza las siguientes operaciones

1. 2 5

3 6

− − =

2. 7 9

8 4+ =

−

3. 2 5. 7 6=

4. 7 1

9 3÷ =

5.

2

5 3

  =      

6. 2 8 7

3 5 6+ − =

7. 24 9 72

4 − −3 9 =

8. 3 7 2 5 3 5 22 6

9 7 11 12

      − _ − _ − _− −_ _ − ___=

    

 

(6)

�

Reconoces y realizas operaciones con distintos tipos de funciones

9.

50 17 5 3

10 16 2 7  ₋  ₋        − _ _+ =       10.   ₋  ₋ ₊       _ _{ } _    ₊     

4 ₁₂ 3 9 10

3 4 2 4

25 _{16 7}

10 5

Solución de ecuaciones

II. Resuelve las siguientes ecuaciones 1. 7x-8=0

2. 4 7(= x−4)

3. 2 4 3(7 ) 5 2

x − x

− = − +

4. 3 − −8 3 + =2 5 −16 4

x

x x

5. _x2₋₁₂_x₊₃₂₌

6. ₆_x2₋₅_x_{− =}_{4 0}

7. ₄_x2₋₁₆₌

Localización de puntos.

(7)

�

B1

�

2.

x y

-2 -13

-1 -10

0 -7

1 -4

2 -1

3 2

4 5

5 8

6 11

7 14

8 17

3.

x y

-4 -7

-3 0

-2 5

-1 8

0 9

1 8

2 5

3 0

4 -7

Transformación del lenguaje común al lenguaje matemático.

IV. Rrepresenta los siguientes enunciados en forma de expresión algebraica: 1. La tercera parte de un número.

2. El triple de un número. 3. El cuadrado de un número. 4. La suma de dos números.

5. La suma de dos números consecutivos. 6. La suma del cuadrado de dos números.

7. El doble de la diferencia de dos números por la suma de los mismos números. 8. La suma de dos números al cuadrado.

9. La suma del cubo de un número con el cuadrado de otro número.

(8)

�

Actividad

Proyéctate

Investiga:

¿Por qué flotan los globos?

¿Qué relación existe entre las funciones y las expresiones matemáticas utilizadas por la física para representar la flotación de un globo?

¿Cómo construir un globo aerostático casero? Consigue los materiales y constrúyelo

Consigue un cronómetro y sujeta tu globo con una cuerda de dos metros, vamos a suponer que nuestro globo asciende a velocidad constante y mediremos su velocidad simplemente dividiendo el largo del hilo y el tiempo que tarde en ascender esa distancia tu globo.

Ahora construye la ecuación que te permita determinar la distancia entre el globo y tú en cualquier momento de su ascensión, si tú te encuentras a 5 metros de distancia del punto de lanzamiento.

Construye globos de distinto tamaño y comprueba su velocidad de ascensión. Lanza 3 globos de helio y comprueba su velocidad de ascensión.

¿La velocidad de ascensión es la misma? ¿Por qué crees que se dan estos resultados?

¿Podrías establecer una ecuación para determinar la velocidad de ascensión según su tamaño y otra dependiendo del gas del que estén llenos?

(9)

�

B1

�

RELACIONES Y FUNCIONES

Diferencia entre variable y constante

Variable: es aquello que puede tomar diferentes valores, se representa mediante símbolos (por lo general, las últimas letras del abecedario: s, t, v, w, x, y, z) y toma sus valores de un conjunto específico.

Ejemplo: la velocidad (v) de un automóvil 10 m/s, 30 m/s, 50 m/s

Constante: es aquello cuyos valores no cambian, es decir, sólo tiene un valor. Por ejemplo, una cantidad numérica: 5, 10, π, e, etc. (en álgebra las constantes se pueden representar con las primeras letras del abecedario: a, b, c, d, e).

Variable independiente: es aquella variable cuyos valores no dependen de ninguna otra variable para cambiar.

Variable dependiente: es aquélla cuyos valores dependen de los valores de otra variable llamada independiente.

Diferencia entre relación y función

Relación: se establece cuando dos o más variables siguen una regla de correspondencia o asociación. En ella, a cada elemento del dominio se le puede asignar uno o más elementos del contradominio.

Ejemplos de relaciones

1. Los asientos de un teatro se identifican por una letra (fila) y un número de asiento.

Sabemos que un teatro está distribuido en filas y cada asiento se numera de forma consecutiva. La numeración vuelve a comenzar conforme cambiamos de fila, la variable independiente es el número de fila y la dependiente es el número de asiento.

(10)

�

Número de fila Número de asiento A 1 B 2 C 3

De esta manera, formamos los pares: A1, A2, A3, B1, B2, B3, C1, C2, C3; así que a cada elemento del conjunto A le corresponde todos los elementos del conjunto B; se establece una relación.

2. A cada automóvil se le asocia: un modelo, un número de serie, un número de placa, un número de tarjeta de circulación.

3. A cada persona se le asocia una edad, una estatura, un peso.

Función: es una relación tal que a cada elemento de la variable independiente le corresponde uno y sólo un valor de la variable dependiente.

Para establecer correctamente cuál es la relación entre las variables, es importante identificar la variable dependiente y la independiente. Los valores de la variable dependiente cambian sólo si lo hacen los de la independiente y, para saber si esta relación es función o no, a cada elemento de la variable independiente se le asociará uno y sólo un elemento de la variable dependiente. Si esta condición no ocurre, entonces se trata simplemente de una relación.

Ejemplos de funciones

1. El clima representativo está en función de la estación del año: La variable independiente: estación del año.

Valores: primavera, verano, otoño, invierno. Variable dependiente: clima representativo. Valores: soleado, caluroso, ventoso, frío.

Conforme cambian las estaciones, el clima representativo se va modificando, pero no ocurre de manera inversa, por ello; la variable independiente es estación del año.

Regla de correspondencia

Variable independiente Variable dependiente Estación del año Clima representativo Primavera Soleado Verano Caluroso Otoño Ventoso Invierno Frío

(11)

�

B1

�

2. El perímetro de una circunferencia está en función de su radio.

Si varía el radio de la circunferencia, también varía su perímetro, y no al contrario; de tal manera, que la variable dependiente es el perímetro de la circunferencia y la variable independiente, el radio.

Variable independiente: radio de la circunferencia.

Valores: Los valores que puede tomar el radio de la circunferencia son todos aquellos mayores a cero.

Variable dependiente: perímetro de la circunferencia.

Valores: todos los valores mayores a cero, pueden tomar el perímetro de la circunferencia.

Variable independiente Variable dependiente Radio de la circunferencia Perímetro de la circunferencia 1 2π

2 4π 3 6π 4 8π

3. El área de un cuadrado está en función de la magnitud (tamaño) de sus lados.

Cuando cambia la longitud del lado de un cuadrado, el área cambiará, por lo que la variable independiente es la magnitud del lado del cuadrado y la variable dependiente es el área del cuadrado.

Variable independiente: magnitud del lado del cuadrado.

Valores: todos los valores que puede tomar el lado de un cuadrado, mayores que cero.

Variable dependiente: área del cuadrado.

Valores: todos los valores mayores a cero que puede tomar el área del cuadrado.

(12)

�

Variable independiente Variable dependiente Magnitud del lado del cuadrado Área del cuadrado

1 1

2 4

3 9

4 16

Variables

De las siguientes funciones realiza un análisis como el anterior, identificando la variable independiente y la dependiente, así como los valores que pueden tomar y la regla de correspondencia.

1. El área de una circunferencia está en función de su diámetro.

2. La imagen de un espejo está en función del movimiento de la persona que se refleja en el espejo.

3. El tiempo de absorción de las medicinas en el cuerpo humano.

A partir de las definiciones de relación y función, podemos deducir que las funciones son un caso particular de las relaciones; es decir, un subconjunto de éstas, con la característica que a cada elemento del dominio le corresponde uno y sólo un elemento del contradominio. En una relación a cada elemento del dominio le puede corresponder uno o más elementos del dominio; por lo tanto, podemos concluir que todas las funciones son relaciones, pero no todas las relaciones son funciones.

Notación para funciones:

f(x)=y

“se lee f de x es igual a y”

En la notación f(x), la variable dentro del paréntesis nos indica cuál es la variable independiente, en este caso es x.

Regla de correspondencia: son las condiciones en las que están relacionadas dos variables, se puede representar por medio de una ecuación matemática.

Argumento: es a cada elemento de la variable independiente.

Imagen: se conoce con este nombre a cada elemento de la variable dependiente.

Actividad

(13)

�

B1

�

Intervalos

Intervalo: es el conjunto de valores comprendidos en un segmento de un eje real, llámese eje x o eje y o, simplemente, la recta de los reales.

Los intervalos se clasifican en:

Intervalo cerrado, se llama así, si incluye a los extremos. Intervalo abierto, se llama así, si no incluye a los extremos. Intervalo mixto:

a) intervalo mixto abierto-cerrado: si no incluye el extremo izquierdo, e incluye al extremo derecho.

b) intervalo mixto cerrado-abierto: se llama así, si incluye al extremo izquierdo y no incluye al extremo derecho.

c) intervalo semiabierto. d) intervalo semicerrado.

La notación de un intervalo puede presentarse en forma paréntesis y/o corchetes (tradicional), en forma de desigualdad y en forma gráfica; esta última casi no la usamos, por lo tanto sólo la mencionaremos.

Sean a y b dos números reales y a < b entonces:

Descripción Notación

paréntesis Desigualdad Se lee

Intervalo cerrado [a, b] a ≤ x ≤ b Intervalo _{cerrado a, b.}

Intervalo abierto (a, b) a < x < b Intervalo abierto a, b. Intervalo mixto

abierto-cerrado (a, b] a < x ≤ b

Intervalo abierto en a, cerrado en b. Intervalo mixto:

Cerrado- abierto [a, b) a ≤ x < b

Intervalo cerrado en a, abierto en b.

Intervalo semiabierto (-∞, b) -∞ < x < b

Intervalo abierto a la izquierda y en b.

Intervalo semicerrado (-∞, b] -∞ < x ≤ b

(14)

�

Descripción Notación

paréntesis Desigualdad Se lee

Intervalo semi abierto

(a, ∞) a < x < ∞

Intervalo abierto en a y a la derecha. Intervalo semi-cerrado

[a, ∞) a ≤ x < ∞

Intervalo cerrado en a y en el lado derecho.

Intervalo abierto (-∞, ∞) -∞ < x < ∞

Abierto en ambos lados, en este caso particular se representa a la recta numérica completa.

Tabla 1.1 La notación de un intervalo

Un intervalo se utiliza para señalar una porción de la función o para representar su dominio, incluso, sirve para representar el rango.

Notación de intervalos Completa la siguiente tabla:

Num. Intervalo Desigualdad Se lee Valores que incluye y

que excluye

1 [2,3] 2 ≤ x ≤ 3 Intervalo

cerrado de 2 a 3

Todos los valores entre 2 y 3 incluyendo los extremos.

2 (5,10] 5 < x ≤ 10 Intervalo

abierto en 5 y cerrado en 10

Todos los valores entre: 5, 6, 7, 8, 9 y10; incluyendo el 10,

excluyendo el 5.

(15)

�

B1

�

Num. Intervalo Desigualdad Se lee Valores que incluye y

que excluye

3 (-5,1) 5 < x < 1 Intervalo

cerrado de 5 a 1

Todos los valores entre -5, -4, -3, -2, -1, 0, 1;

excluyendo a 5 y 1.

4 [-3, ∞)

Todos los valores entre -3, -2,-1, 0, 1, 2, 3… hasta infinito; excluyendo: a ninguno.

5 2 ≤ x < 0

6 Intervalo _{abierto en 2 y}

abierto en 16.

7 Todos los valores entre 10, 9, 8, excluyendo a 8.

8 (∞, 3)

9 (20,15]

10 ∞<x≤15

11

Intervalo de ∞ abierto a la izquierda a -3 cerrado a la derecha.

(16)

�

Rango: es el conjunto de imágenes de una función asociadas a los valores de x que conforman el dominio; es decir, son aquellos valores reales que toma la variable dependiente.

Ejemplo

Determina el rango de la función cuya gráfica se muestra en la imagen en el intervalo de valores de x de [-6,6].

Debemos recordar que rango es el conjunto de imágenes (valores de y) asociadas a cada argumento (valores de x).

(17)

�

B1

�

De la misma manera, buscamos las imágenes asociadas a los extremos del intervalo de análisis. Observamos que para x = -6 es y = -1 y para x = 6 es y = 5; como la función no tiene variaciones en el intervalo, entonces el rango:

/ -1 5}

rango y R= ∈ ≤ y ≤

Se lee: "el rango está en los valores de y que pertenecen a los reales, tal que -1 menor o igual que y, menor o igual que 5".

La recta azul señala el rango en forma gráfica, el cual está comprendido en [-1, 5] se lee: "el intervalo de -1 a 5".

Ejemplo

Determina el rango de la función cuya gráfica se muestra en la imagen en el intervalo de valores de x de [0,4].

Solución

Tal vez te hayas quedado con la idea errónea de que para encontrar el rango de la función, necesitas, buscar las imágenes de los extremos del intervalo; pero no es así debido a que para x = 0 la imagen asociada es y = 0 y para x = 4 también la imagen asociada es y = 0. Sin embargo, puedes observar en la parte central otras imágenes mayores que cero y menores que cero. Por lo tanto al hacer el análisis dentro del intervalo, observamos que la menor de las imágenes es y = -3 y la mayor de las imágenes en el intervalo de análisis es y = 3. Por consiguiente, el rango queda:

rango={y R/-3 y 3}∈ ≤ ≤

Se lee: "el rango está en los valores de y que pertenecen a los reales, tal que -3 menor o igual que y menor o igual que 3".

(18)

�

La recta roja nos señala el rango comprendido en [-3, 3], que se lee "el intervalo de -3 a 3".

En cada una de las siguientes gráficas señala con rojo el rango solicitado, y en la línea de abajo represéntalo con la notación de desigualdad.

1. Obtener el rango de la función para los valores de x [-1. 1].

(19)

�

B1

�

2. Obtener el rango de la función para los valores de x [-3. 3].

3. Obtener el rango de la función para los valores de x [-5, -1].

(20)

�

Dominio: son todos los valores que puede tomar la variable independiente debido al contexto en el cual se creó, y que en una función generan imágenes reales. Los argumentos que no generan imágenes reales no pertenecen al dominio de la función.

El dominio de una función en cuya regla de correspondencia no tiene: exponentes negativos, exponentes fraccionarios, raíces pares o divisiones en donde la variable dependiente se localice en el denominador, es todos los valores de x que pertenecen a los reales.

Al analizar la definición de dominio, surge una pregunta obligada: ¿Cómo reconocer un argumento que no genera una imagen real?

Existen dos factores que limitan el dominio de la función: a) las imágenes no reales, b) el contexto de la función:

Supongamos que necesitas hacer jugo de zanahoria, si comparamos este hecho con nuestro tema podemos decir que: el conjunto de todas las zanahorias que usarás son el dominio de la función, a cada zanahoria le llamaremos argumento;

el extractor de jugos es la función, cada chorrito de jugo que salga de nuestro extractor debido a cada una de las zanahorias sería una imagen, el jugo en conjunto sería el rango de la función; pues bien, con esto puedes observar cómo es una función

zanahoria extractor jugode 1 zanahoria

argumento función imagen

Por ejemplo:

Dada la función _{f x}_{( )}₌_x2₊₅_x₋₈_{, evaluarla para x = 2:}

argumento función imagen

x = 2 _f_{(2) (2)}₌ 2₊_{5(2) 8 4 10 8 6}_{− = +} _{− =} _y₌₆

zanahorias extractor jugo

(21)

�

B1

�

Dada la función _{f x}_{( )}₌_x2₊₅_x₋₈_{, mostrar dominio y rango:}

dominio función rango

Todos los valores de xЄR _{f x}_{( )}₌_x2₊₅_x₋₈_{todos los valores}

de y ≥ -57/4 que Є R Si seleccionas una zanahoria, al meterla al extractor se transformará para obtener el jugo, si tomas una zanahoria podrida, al meterla al extractor lo que resultará será jugo en mal estado, algo que no deseas. Esta es la razón por la cual la zanahoria no pertenecerá al dominio de la función, porque al pasar por el procesador nos da una imagen no deseada, que es jugo en mal estado.

Si trabajas con funciones matemáticas y eliges un argumento, si lo sustituyes en la función y éste se transforma en una imagen no real, ya sea una indeterminación (∞) o una cantidad imaginaria, entonces este valor que tomó la variable independiente no pertenece al dominio de la función.

Debes recordar que obtenemos una indeterminación (∞) cuando se presenta la división entre cero (3/0, -5/0, 0/0), y las cantidades imaginarias se presentan principalmente al tratar de obtener una raíz par de un número negativo

(

₋_{4 ,}4₋_9,6₋₃

)

.

Por ejemplo: dada la función ( ) 2 , 1

x f x

x

=

+ hallar los valores de x que no

pertenecen al dominio de la función y verificar el resultado mediante su gráfica.

Solución

Al observar la función percibimos que es el cociente de dos funciones (función racional); por lo tanto, busquemos aquellos valores cuyo denominador se convierte en cero. Con este propósito utilizaremos la siguiente ecuación:

1 0 x+ =

Tal vez te preguntes por qué precisamente utilizar la ecuación significa que buscamos los valores de x que hacen que el denominador se haga cero y como no es posible hacer la división entre cero, al encontrar dichos valores de x, también estamos encontrando los valores de x que no pertenecen al dominio de la función (más adelante en el bloque seis profundizaremos en esta idea).

x + 1 = 0 resolviendo:

(22)

�

Comprobando que este valor de x produce la división entre cero:

2( 1) ( 1)

( 1) 1 2 ( 1)

0

f f

− − =

− + − − =

Por lo tanto, concluimos: x = -1 no pertenece al dominio de la función, porque es el único valor de x que produce la división entre cero. En consecuencia, el dominio de la función es:

Dominio={x R/∈ x≠ −1}

Todos los valores de x que pertenecen a los reales, excepto x = -1

Al obtener la gráfica de la función, observamos que justo cuando x toma el valor de -1, la función se corta en dos partes. Lo anterior significa que el valor de x mencionado no proporciona una imagen real.

La línea en rojo indica el dominio de la función. Observamos que en x = -1 no obtenemos una imagen real, por lo cual la gráfica se divide en dos partes iguales.

Ejemplo

Obtener el dominio de la siguiente función:

( ) 4

f x = x−

(23)

�

B1

�

x - 4 ≥ 0 Resolviendo la desigualdad:

x ≥ 4 Interpretando el resultado, obtenemos que: Dominio de la función:

Dominio={x R/∈ x≥4}

Se lee: "El dominio está en los valores de x que pertenecen a los reales; tal que x debe ser mayor o igual que cuatro".

La línea roja nos señala el dominio. Se observa que, efectivamente, éste comienza en x = 4 y continúa en todos los valores mayores.

Ejemplo

Halla el dominio de la función:

3 4

y= x+

Al analizar la regla de correspondencia de esta función, observamos que no tiene exponentes fraccionarios ni exponentes negativos ni raíces pares ni división en donde la x aparece en el denominador. Entonces, concluimos que su dominio es:

Dominio={x R/-∈ ∞ < < ∞x }

(24)

�

Halla el dominio de las siguientes funciones, realiza su gráfica con ayuda de un programa graficador y señala sobre el eje x, con rojo, el dominio de la función:

2

1. ( ) 2 3) 4. ( ) 5 3 2. ( ) 3 5. ( ) 5 7

2

3. ( ) 6. ( ) 5 4

f x x f x x x f x x f x x

x x

f x f x

x

= + = − +

= + = −

= =

+

3 2x 7

− +

Dominio de una función dependiendo del contexto

Analicemos el siguiente problema:

La posición de una pelota, arrojada desde lo alto de la torre Ánimas en Xalapa, Veracruz, cuya altura es de 62 m, se representa por la función: _{f x}_{( ) 62 4.9 ;}₌ ₋ _x2

donde f(x) es la posición de la pelota mientras va cayendo, en metros (m), y x es el tiempo de caída de la misma en segundos (s): a) halla el dominio de la función; b) realiza la gráfica que representa la caída de la pelota.

Si analizamos la función que representa la caída de la pelota observamos que es una función cuadrática; por consiguiente, asociamos esta expresión a la forma de su gráfica o a una parábola. También sabemos que el dominio de la función cuadrática son todos los valores de x pertenecientes a los reales, y su rango son todos los valores de y menores o iguales que 62.

Actividad

(25)

�

B1

�

Sin embargo, por el contexto del problema, como la variable independiente se presenta en segundos y el punto de caída de la pelota es de 62 m de altura, el dominio se ve limitado, en primera instancia, al tiempo que permanece la pelota en el aire desde que fue soltada hasta llegar al suelo; y, en segunda, porque el problema no puede tomar valores negativos, pues físicamente no es posible. En consecuencia, en una función cuya variable independiente es el tiempo, sólo se pueden considerar los valores positivos, incluyendo el cero.

2

( ) 62 4.9 para y=0, tenemos: 0 62 4.9

4.9 62 62 4.9 3.55

f x x x x

x

x s

= −

= − =

= ±

Por obvias razones tomamos el valor positivo x = 3.55 s; entonces, el dominio queda establecido de la siguiente manera: D =

{

x R∈ / 0≤ ≤x 3.55

}

, en conclusión, el dominio de nuestra función se modificó por el contexto del problema.

(26)

�

Dominio de funciones Contesta lo que se te pide.

Halla el dominio de la función

1. _{f a}_{( ) 4}₌ _{a a}₋ 2_{que nos permite conocer}

la magnitud de todos los lados del rectángulo cuya área es cuatro y su perímetro es ocho.

Un paracaidista se lanza en caída libre en posición horizontal, con las 2.

extremidades extendidas hacia el frente, desde una altura de 2,000 m. Si la función de su velocidad antes de abrir su paracaídas es: v t( ) 9.8= t, con la velocidad en m/s y el tiempo en segundos, determina el dominio de la función (en un salto con estas características el paracaídas se debe abrir a una distancia de 600 m del suelo; se sabe que debido a las condiciones de nuestra atmósfera la velocidad máxima terminal de un humano en caída libre es de aproximadamente 200 km/hr o 55.55 m/s). Realiza una tabla velocidad-tiempo y su respectiva gráfica.

Formas de representar una función

Existen cinco formas de representar una función algebraicamente, tabular, geométrica, sagital y verbalmente.

Algebraica, esta forma representa la regla de correspondencia de una •

función recurriendo al álgebra (fórmulas)

Tabular es la representación en forma de pares coordenados

• x y y de todos

los puntos obtenidos por la regla de correspondencia (numéricamente). Geométrica (gráfica) es la representación de todos los puntos del plano •

cartesiano que muestran al lugar geométrico, obtenidos por la regla de correspondencia de una función.

Sagital: representa a la regla de correspondencia tomando como base a la •

teoría de conjuntos.

Verbal: representa a la función por medio de un enunciado. •

Ejemplo

Dada la siguiente situación problema encuentra todas las formas de representar a la función:

Actividad

(27)

�

B1

�

La forma verbal.

La forma algebraica (regla de correspondencia). La forma tabular.

La forma geométrica (gráfica). La forma sagital.

Se desea construir una alacena rectangular, cuya área frontal en metros sea de un largo que exceda en 15 cm su altura, de tal manera que su área está en función de su largo, construye la función que represente las dimensiones de todas las alacenas que puedes construir con estas características.

a) La forma verbal de la función es: "el área está en función de su largo"

b) La forma algebraica la encontramos de la siguiente manera, primero convertimos a metros los 15 cm; lo cual nos da 0.15 m ahora definimos nuestras variables dependiente e independiente:

L = largo de la alacena, es la variable independiente, es decir, puede tomar distintos valores.

A = área de la alacena, es la variable dependiente, es decir, el área puede cambiar, sólo si cambiamos su largo

L -0.15 = es el alto de nuestra alacena, ya que es menor que el largo en 15 cm. Ahora construimos nuestra regla de correspondencia:

El área de un rectángulo de estas características es: largo por ancho, quedando así nuestra función:

( 0.15)

A L L= −

Es decir:

2 _0.15

A L= − L

c) Forma tabular: la encontramos dando valores a la variable dependiente y hallando los de la independiente:

L (m) A (m2₎

1 0.85

2 3.7

3 8.55

4 15.4

(28)

�

d) La forma gráfica la encontramos llevando estos valores y localizándolos en el plano cartesiano.

Como puedes observar, la gráfica es una parábola, sin embargo, el dominio de nuestra función está definido por el contexto, ya que no puede haber largos negativos, nuestro interés se centra en los valores positivos del eje x largo, en donde marcamos los puntos encontrados en la tabulación.

f) La forma sagital nos relaciona con la teoría de conjuntos, en este curso sólo la utilizaremos para representación.

(29)

�

B1

�

Por ejemplo, si medimos el tiempo que tarda un corredor de cien metros planos en recorrer una distancia determinada, obtenemos la siguiente tabla, es decir, nuestra función nace en forma de tabla:

Tiempo (s) Distancia (m)

0 0

1.87 10

2.97 20

3.95 30

4.94 40

5.88 50

6.81 60

7.69 70

8.62 80

9.61 90

10.62 100

Otro ejemplo es la gráfica obtenida del porcentaje de carbono en un acero y su dureza; en este caso la función nace en forma de gráfica.

Otro ejemplo es la Ley de Hooke, la cual establece que la deformación sufrida por un resorte es proporcional a la fuerza aplicada, en donde F es la fuerza aplicada (y) k= es la constante de proporcionalidad del resorte y x es la deformación que sufre el resorte:

F = kx

(30)

�

Es importante recalcar que en la medida en que tú transites de una forma a otra dentro de la función, tu conocimiento sobre ésta será más real; es decir, que si interpretas a partir de su forma algebraica o de su tabla o de su gráfica, podrás construir la expresión algebraica a partir de la tabla o de la gráfica, o de su forma verbal.

A partir de la forma de la función dada, encuentra las otras 4 formas de representar una función

1. El volumen de un cubo está en función de la magnitud de sus lados. 2. W=25D

W = Trabajo mecánico (joules) D = desplazamiento (metros)

3.

4.

t (tiempo en segundos)

d (distancia en metros)

0 0

1 20

2 40

3 60

4 80

5 100

6 120

(31)

�

B1

�

5.

Regla de la recta vertical para la determinación de una función de x

Esta regla nos permite determinar si una gráfica corresponde a una función o a una relación. Si trazamos una recta vertical que cruce la gráfica de la función y ésta toca sólo un punto, entonces es una función de x; si toca dos o más, entonces esta gráfica corresponderá a una relación.

Ejemplo

1. Determina si la siguiente gráfica corresponde o no a una función de x:

Al trazar rectas verticales a lo largo de la gráfica de la función, observamos que, efectivamente, se trata de una función de x, en virtud de que cada recta sólo corta en un punto la gráfica.

(32)

�

Al trazar rectas verticales, éstas intersectan en un solo punto de la gráfica; por lo tanto, concluimos que la gráfica corresponde a una función de x.

3. Determina si la siguiente gráfica corresponde o no a una función de x:

En este caso, se observa que al trazar las rectas verticales todas intersectan en dos puntos la gráfica, por lo cual concluimos que se trata de una relación.

Dadas las siguientes gráficas, usando la regla de la recta vertical, determina si corresponden a una función de x o sólo se trata de una relación y escribe tu respuesta en la línea inferior:

(33)

�

B1

�

1. __________________ 2. ___________________ 3. ___________________

4. ___________________ 5. ___________________ 6. ___________________

TIPOS DE FUNCIONES

Clasificación según la forma de expresar a una función

Funciones explícitas y funciones implícitas

Según la forma en que se expresan las funciones, se clasifican en explícitas e implícitas.

Funciones explícitas: son aquéllas en las cuales la variable dependiente está despejada.

Ejemplos

= + = − + = + − +

− =

−

2

3 2

2

1. 5 7

2. ( ) 8 16 3. ( ) 5 6 7 8

3 1 4.

2 8

y x f x x x

f x x x x

x y

x

(34)

�

2 2

1. 5 2 4 0 2. 9

3. 9 25 225 0 4. 5 9 45 0

x y x y x y x y + − = + = − − = + − =

Clasificación según el tipo de expresión que aparece en la regla de

correspondencia

               Constante Valor absoluto Identidad Lineal Cuadrática lg Cúbica Cuártica Polinomial Racional Irracional Seno Coseno Tangente Trigonométricas Cotangente Secante Cosencan A ebraicas Funciones Trascendentales                            _     _ _                  _   _  _    _  _    _   a te

Logaritmo de base10 (log) Logarítmicas Logaritmo de base a (log )

Logartimo natural o neperiano

Base 10 Exponenciales Base a

Base e b       

Esquema 1.1. Funciones algebraicas y funciones trascendentes

Clasificación según su monotonía

Funciones crecientes y decrecientes

Sean f y g dos funciones continuas en [a, b] y sean x₁ y x₂ dos argumentos dentro de ese intervalo, en donde x₁ < x₂_, y, y₁e y₂_, sus respectivas imágenes, diremos que f es:

a) Creciente en el intervalo si se cumple que y₁ < y₂

b) Decreciente en el intervalo si se cumple que y₁ > y₂

(35)

�

B1

�

Cuando sabemos si una función es creciente o decreciente en un intervalo, podemos entender la información de la misma.

Ejemplo

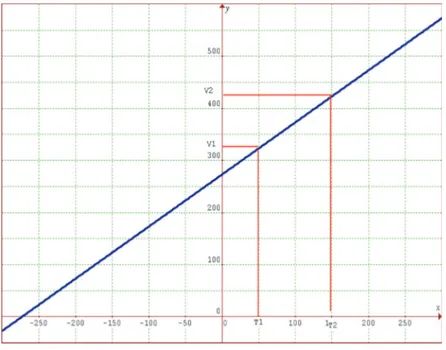
1. En la carrera de un pistón de un motor a gasolina, el fluido se enciende a alta presión, ¿qué pasa con el volumen y la temperatura cuando el pistón se desplaza hacia abajo?:

Los argumentos V1 y V2 cumplen con la condición V1< V2.

Las imágenes asociadas a esos argumentos cumplen con la condición P1>P2, por consiguiente la función es decreciente.

En el contexto del problema, estos datos nos indican que cuando en un pistón existe determinado volumen a alta presión y el pistón se desplaza hacia abajo, el volumen aumenta y la presión disminuye.

(36)

�

Tabla 1.2 Comportamiento de un gas ideal.

Los argumentos T1 y T2 cumplen con la condición T1 < T2; como T1 está a la izquierda de T2, la posición determina que sea menor a ella.

Las imágenes asociadas a esos argumentos cumplen con la condición V1< V2; en virtud de que V1 está por debajo de V2 y en el eje de las y, quienes ocupan esta posición son los que cumplen con la condición V1 es menor que V2.

Por lo tanto, se concluye que la función es creciente.

El contexto del problema indica que si la temperatura de un gas aumenta, su volumen también se incrementa.

Clasificación según el comportamiento de las funciones

Funciones continuas y discontinuas

Esta clasificación se puede realizar según el comportamiento de su gráfica. Una función es continua si al trazar su gráfica, ésta no sufre ni saltos ni interrupciones; de lo contrario, es discontinua.

(37)

�

B1

�

Ejemplos de funciones continuas y funciones discontinuas:

Función continua Función discontinua

En la primera gráfica, se observa que el trazo es “continuo” e ininterrumpido; en la segunda, que está dividida en dos partes debido a un valor de x que no pertenece al dominio de la función. P para este caso es x=0.

Función discontinua Función continua

En la primera gráfica, se observa que el trazo es “discontinuo”, interrumpido en x =-3, x = 0, x = 3; en la segunda, no existe interrupción alguna en todo el recorrido de la variable independiente.

Clasificación respecto a la relación que existe entre su dominio y

contradominio

Funciones inyectivas

También son llamadas funciones uno a uno o funciones biunívocas. Son aquéllas que a cada imagen (y) del codominio le corresponde uno y sólo un argumento (x) del dominio.

Prueba de la recta horizontal

(38)

�

uno y sólo un punto, entonces la función será inyectiva.

Funciones sobreyectivas

También son llamadas suprayectivas. Son aquéllas en las cuales el codominio y el dominio son conjuntos idénticos.

Prueba de la recta horizontal

Si trazamos una recta horizontal sobre la gráfica de una función, ésta la puede cortar en dos o más puntos.

Funciones biyectivas

Si una función es a la vez inyectiva y es sobreyectiva, entonces es biyectiva.

Ejemplo

1. Determinar si la siguiente función es: a) Inyectiva

b) Sobreyectiva c) Biyectiva

(39)

�

B1

�

b) También se observa que cada x es argumento de, al menos, una imagen (y) por consiguiente, es sobreyectiva.

c) Como la función es inyectiva y sobreyectiva a la vez, por lo tanto, también es una función biyectiva.

2. Determina si la siguiente función es: a) Inyectiva

b) Sobreyectiva c) Biyectiva

(40)

�

b) Se observa que cada x es argumento de, al menos, una imagen (y); por lo tanto, es sobreyectiva.

c) Como la función no es inyectiva, pero sí sobreyectiva, por lo tanto, no es una función biyectiva.

Con ayuda de un software para graficar, construye la gráfica de las siguientes funciones y determina si son inyectivas, biyectivas y sobreyectivas.

3 2

4

3

2 3

1. 6. 1 2. ( ) 2 3 7. ( ) 2 3. 8.

4. ( ) 16 9. ( ) 4 5.

y x y x

f x x f x x

y x y x

f x x f x x

= = −

= − = +

= =

= − = −

2 3 2

- 3 10 10. 7 12

y= x − x+ y x= − x + x

1. Explica por qué se puede afirmar lo siguiente: “toda función lineal es inyectiva, biyectiva y sobreyectiva a la vez”.

2. Verifica si se cumple la siguiente afirmación: la función es sobreyectiva; fundamenta tu respuesta.

(41)

�

B1

�

OPERACIONES CON FUNCIONES

Las funciones se pueden sumar, restar, multiplicar y dividir, a esta condición

también se le llama combinación de funciones; al combinarlas obtenemos

nuevas funciones que, a su vez, tienen sus propios rangos y dominios. Nos

permiten resolver problemas diversos, como la optimización al combinar

perímetros y áreas, o volúmenes y áreas. Por ejemplo, la función de venta

de autos nuevos más la suma de autos usados nos dará una nueva función,

cuyo significado es la venta total de autos y muchos más:

Dadas dos funciones f y g

Suma y resta

(f + g)(x)= f(x)+g(x)

(f - g)(x)= f(x)-g(x)

Multiplicación y división

(f · g)(x)= f(x) · g(x)

( )

( ) , donde g(x) 0 ( )

f f x x en g g x

 

= ≠

   

Ejemplo:

Sumar, restar, multiplicar y dividir las funciones:

2

( ) 4 ( ) 5 4

f x =x − y g x = x+

El dominio de la función f(x) son el conjunto de todos los valores

x

que

pertenecen a los reales, el dominio de la función g(x) son todos los valores

de

x

pertenecientes a los reales.

(42)

�

Suma:

2

( ) 4 ( ) 5 4 ( )( ) 4 5 4 5 ( )( ) 5

f x x y g x x f g x x x

x x f g x x x

= − = + + = − + +

= + + = +

El dominio de la nueva función también es el conjunto de los reales, porque

la regla de correspondencia de la función no tiene raíces, ni cocientes en

donde

x

se encuentre en el denominador.

Resta:

2 2 2 2 2

( ) 4 ( ) 5 4 ( )( ) 4 (5 4) 4 5 - 4 5 8 ( )( ) 5 8

x x x x f g x x x

= − = + − = − − +

= − − = − − − = − −

El dominio de la nueva función también es el conjunto de los reales, porque

la regla de correspondencia de la función no tiene raíces, ni cocientes en

donde

x

se encuentre en el denominador.

Multiplicación:

2

3 2

( ) 4 ( ) 5 4 ( . )( ) ( 4)(5 4) 5 4 20 16 ( . )( ) 5 4 20 16

x x x f g x x x x

= − = + = − +

= + − − = + − −

El dominio de la nueva función también es el conjunto de los reales, porque

la regla de correspondencia de la función no tiene raíces ni cocientes en

donde

x

se encuentre en el denominador.

División:

2

( ) 4 ( ) 5 4 4

( )

5 4

f x x y g x x f _x x

g x = − = +   − =   ₊  

(43)

�

B1

�

5 4 0 5 4

4

5

x x x

+ = = −

− =

Por lo tanto, concluimos que el dominio son todos los valores de x

pertenecientes a los reales, excepto

4

5

x=−

COMPOSICIÓN DE FUNCIONES

El maestro Carlos, de Física, mientras estudia con sus alumnos el tema

de calor y temperatura, observa que para ellos es difícil convertir los

grados Kelvin a Fahrenheit y viceversa, pues no existe una fórmula

que lo permita. Por esto solicita a sus alumnos que busquen la forma

de construir una fórmula para realizar estas conversiones. A Sara, una

alumna muy avanzada, se le ocurre el siguiente método a partir de sus

clases de matemáticas: piensa que es posible utilizando la composición

de funciones así que define sus funciones:

Sabemos que la ecuación empleada para convertir los grados centígrados

a grados Fahrenheit es:

9

32 5

F C

° = ° +

Y la ecuación para convertir los Kelvin a grados centígrados:

273

C K

° = −

Sara transforma estas ecuaciones y las convierte en funciones, resultando

de la siguiente manera:

9 ( ) 32

5

(44)

�

f(x) = es la temperatura en Fahrenheit y para esta función

x

= es la

temperatura en grados centígrados:

( ) 273

g x = −x

g(x) = es la temperatura en grados centígrados y

x

= es la temperatura en

kelvin.

Sara hace la composición de funciones:

Composición:

(f g x° )( )=f g x( ( ))

De acuerdo con esta simbología, en cada x que tenga la función f se va a sustituir la expresión algebraica de la función g, tal y como se ve a continuación:

9

si ( ) 32 y ( ) 273, entonces: 5

f x = x+ g x = −x

9

( )( ) ( ( )) ( 273) 32 5

f g x° =f g x = x− +

Después de hacer la sustitución, se efectúan las operaciones y se simplifican:

9

( )( ) ( ( )) ( 273) 32 5 9 9(273) 32 5 5 9 2457 32 5 5

9 2497 160

5 5 5

f g x f g x x x x x ° = = − + = − + = − + = − + 9 2337 5 5 9 2337 ( ( )) 5 5 x f g x x

= −

¿Qué significa, entonces, cada una de las variables de nuestra nueva función?:

( ( )) es la temperatura en grados farenheit

f g x =

Ahora, el rango de la nueva función es el conjunto de todas las temperaturas en grados Fahrenheit que se presentan en la naturaleza y el dominio de la función son todas las temperaturas en Kelvin que se presentan en la naturaleza.

(45)

�

B1

�

9 2337 ( ( ))

5 5

f g x = x−

9 2337 °F

5K 5

= −

I. Dados los siguientes pares de funciones, determina: a) (f g x+ )( )

b) (f g x− )( )

c) ( . )( )f g x

d)  _{ }

 ( )

f x g

e) f g x( ( )) f) g f x( ( ))

g) El dominio de cada función y su gráfica:

2

1. ( ) 5 2 y ( ) 8 2 2. ( ) 1 y ( ) 1

2 4

3. ( ) y g(x)=2x+4

f x x g x x x f x x g x x

x f x

x

= − = − +

= − = −

− =

h) Co-evaluación

II. Cada estudiante realizará un crucigrama y su clave, utilizando definiciones y conceptos de este libro. Al terminar, lo intercambiará con su compañero-pareja, para que lo califique y entregue el resultado de la evaluación.

(46)

�

III. Resuelve la siguiente sopa de letras, encuentra las 16 palabras ocultas pertenecientes al bloque estudiado.

o s a g i t a l p r s s e l d e E r n o i c n u f

f b j s u e b g a m g y o j f f g w t o a e n p h

c P c b f q a o f n f b n b f k a b g m c l d w c

b t f a r u n g b g d c z a r d e p y i n v x g o

f o a f v e f i d b a r g u m e n t o q a g p m n

a k e c g n p ñ x e z g l o e e y q r z h j d u t

g t f a l b w a s t a s o f k i a e n v w a o c r

j f m k s a o e b m f ñ c j c r y f c q g d y i a

a i h c f r k i h q u g n e s f w e e t j t ñ p d

g f e x p d f n m c x b f o a p a h q g i k d r o

a d f j q a i y a b z i a ñ e h x s b j e v z u m

o r e g l a d e c o r r e s p o n d e n c i a g i

f s p l d k h c i t a o b r e g e g w p f u e t n

i f a f g d o t v e g f h j g q a k s e a h v c i

a a b u c b t i j n g w g a b n p f c q l k e g o

g d w i y f h v o e a q f e u o j b l f p t w c h

f a e f y b v a q y u d h i r i a q o g n a r g f

h a f u s e h l r a g o f o a c t c p e b x o c h

r k a d a x c r e c i e n t e a o s i a f f e a f

a j c f h d i t u x a w a e k l k c x f p i b g i

l d f k o q f c i g f r m d a e e a c l a e d r d

u i e a e d o q k v ñ h b e d r v e d u i r y g h

b c t l t a k e q i a g j w c y d p b r f l g a d

a b c o u b u r y r l a c e k e t g a e k m q e j

t a h c m s o i n i m o d s a l g e b r a i c a f

IV. Relaciona correctamente ambas columnas:

1. ( ) segunda coordenada de un par ordenado a) variable dependiente 2. ( ) eje x

3. ( ) dominio b) variable independiente 4. ( ) eje y

5. ( ) contradominio

6. ( ) primera coordenada de un par ordenado

(47)

�

B1

�

V. Anota en la línea de abajo si la gráfica corresponde a una función o a una relación, utilizando la regla de la vertical.

___________ ___________ __________ __________ __________

VI. Encierra en un círculo rojo la gráfica o gráficas que corresponden a una función discontinua y en un círculo azul a una continua.

.

VII. Dada la siguiente gráfica, encuentra la forma sagital, la tabla y la regla de correspondencia (forma algebraica) (valor dos reactivos cada forma de la función).

(48)

�

3. Con verde señala sobre la gráfica de dónde a dónde la función es creciente. 4. Con naranja señala sobre la gráfica de dónde a dónde la función es

decreciente.

5. Encierra con café la imagen de x = 5

VIII. Realiza la suma, resta, multiplicación y división del dominio de la función resultante.

IX. Escribe cinco enunciados de funciones.