Ejercicios detallados del obj 3 Mat III 733

Capitulo III Matemática III (733)

Objetivo 3. Aplicar el cálculo integral a problemas de áreas, volúmenes, área de una superficie y longitud de arco de una curva dada en coordenadas cartesianas.

Ejercicio 1

Determina el área de la superficie de revolución generada al girar la

curva de ecuación 4 2

1 1

8 4

x y

y

= + , 1≤ ≤y 2 alrededor del eje OY.

Solución

Justificación: En este objetivo amiga y amigo estudiante es IMPORTANTE, que sepas deducir la fórmula que vas a usar, por 2 razones:

Cuando tu HACES, aprendes, y creeme, toda fórmula que deduzcas o sepas de donde proviene es muy difícil que se te olvide.

Los ejercicios de este objetivo requieren que construyas las integrales definidas que vas a resolver, y a lo largo de esta guía observaras que dichas integrales son relativamente sencillas de resolver el problema está en como construirlas.

Además de lo anterior, debes conocer por lo menos las gráficas más comunes, como rectas, parábolas, circunferencias, funciones exponenciales, logarítmicas y trigonométricas, entre otras.

Te daré algunos tip’s de cómo graficar rápidamente algunas de estas gráficas:

1) Rectas: Por ejemplo, graficar: y=3x+5

Función Corte con el eje x y, =0 Corte con el eje y x, =0

3 5

y= x+ 0 3 5 5

3

x x −

= + → = y=3 0

( )

+ =5 5

Gráfica de la recta

2) Parábolas: Por ejemplo, grafique: 2

2

y=x + −x y 2

6 x= − − +y y .

Una parábola SIEMPRE abre hacia arriba si el coeficiente de equis cuadrado es POSITIVO, por ejemplo: 2

2x 7 x

y= − + , o hacia abajo si el coeficiente de equis cuadrado es NEGATIVO, por ejemplo: 2

2x 7 x

y=− − + y abre SIEMPRE hacia la derecha si el coeficiente de ye cuadrado es POSITIVO, por ejemplo: 2

7y 1 y

x= + + y abre hacia la izquierda si el coeficiente de ye cuadrado es NEGATIVO, por ejemplo: 2

10 4y

x=− − +y .

Función

Derivando e igualando a cero: '

0 y =

Vértice

Evalúa el valor de la derivada en la función original

Corte con los ejes:

2

2 y=x + −x

'

2 1 0

1 2 y x x = + = − =

Para 1

2 x=−

2

1 1

2

2 2

1 5 2 20

4 2 8

18 9 8 4 y y y −   =  − −   − = − = − = = − 1 9 , 2 4

V_− − _

 

2

2 0

y=x + − =x

( )

( )( )

( )

2 2 1 2 1 2 4 2

1 1 4 1 2

2 1

1 1 8 1 9

2 2

1 3

1 3 2

1 3 2 2 2 1 2 4 2 2

b b ac

x a x x x x x x x − ± − = − ± − − − = − ± + − ± = = − +  =  − ±  =  − −  ₌   = =   −  _{= = −} 

Gráfica de la parábola 2

Función

Derivando e igualando a cero: '

0 x =

Vértice

Evalúa el valor de la derivada en la función original

Corte con los ejes:

2

6 x= − − +y y

'

2 1 0

1 2 x y y = − − = − =

Para 1

2 y= −

2

1 1

6

2 2

1 13 1 26

4 2 4

25 4 x x x −   = −_{ } + +   − + = − + = = 25 1 , 4 2

V_ − _

 

2

6 0 x= − − + =y y

( )

( )( )

( )

2 2 1 2 1 2 4 2

1 1 4 1 6

2 1

1 1 24 1 25

2 2

1 5

1 5 2

1 5 2 2 6 3 2 4 2 2

b b ac

x a y y y y y y y − ± − = ± − − − = − ± + ± = = − − +  =  ±  ₋ =  − −  ₌  ₋  = = −  ₋  −  _{= =}  ₋

Gráfica de la parábola 2

3) Funciones exponenciales: Por ejemplo x

y=e , x y=e− Estas graficas son conocidas y son:

Observa que siempre cortan al eje y en uno, y el eje equis es la asíntota horizontal de ambas. Además, siempre son positivas.

4) Funciones logarítmicas: son las funciones inversas de las exponenciales, por ejemplo: y=lnx

5) Circunferencias: Estas funciones se identifican cuando ambas variables (equis y ye) están elevadas al cuadrado y tienen coeficiente positivo e igual, por ejemplo:

2 2 4 x +y =

(

)

2 ₂

1 9

x− +y =

(

)

2 2

2 25

x + y+ =

A veces te dan estas ecuaciones desarrolladas, por ejemplo, si en la tercera desarrollo el producto notable, obtendría:

(

)

2 2

2 2

2 _{2 2 2}

2 25 4 4 25 4 4 25 0

4 21 0

x y x y y x y y

x +y y

+

+

+ = → + + + = → + + + − =

− =

Si llegas a toparte con una ecuación de este tipo, debes completar cuadrados y llevarla a la forma 2

(

)

2

2 25

x + y+ = .

Ahora bien, cuando las ecuaciones están así: 2 2 4 x +y = ,

(

)

2 ₂

1 9

x− +y = , 2

(

)

2

2 25

x + y+ = , debes compararla con la ecuación general de la circunferencia:

(

) (

2

)

2 2

x h− + y−k =r

Donde

( )

h k, es el centro de la circunferencia y r el radio.

Vamos a conseguir el centro y radio de las circunferencias dadas:

2 2

2

( , ) (0, 0) 4

4 4 2

c h k x y r r =  + = → = → = = 

(

)

2 2

2

( , ) (1, 0)

1 9

9 9 3

c h k

x y r r =  − + = → = → = = 

(

)

2 2

2

( , ) (0, 2)

2 25

25 25 5

c h k

x y r r = −  + + = → = → = = 

OJO: SIEMPRE SE CAMBIA EL SIGNO PARA ENCONTRAR LAS

COORDENADAS DEL CENTRO.

6) Funciones polinómicas: Cuando graficamos rectas y parábolas, éstas son funciones polinómicas, sin embargo, en algunas ocasiones nos encontramos con funciones polinómicas de grado 3 ó 4 e inclusive más, en estos casos nos indican los valores de las ordenadas o de las abscisas donde esta encerrada el área, y con éstos valores sustituidos en la educación original nos permiten conseguir 2 puntos, y sabiendo QUE TODA FUNCIÓN POLINOMICA ES CONTINUA unimos dichos puntos, teniendo cuidado que la función no cambie de signo en ese intervalo. El ejemplo de este caso es precisamente al que corresponde a éste ejercicio, por ende, cuando comience la resolución veras como se aplica lo comentado.

Para ambas funciones construye en la recta real (eje x) el conteo de 2 π

en 2 π

. Antes de continuar, quiero saber si sabes contar de 2 en 2 ó 5 en 5.

Probablemente, te enseñaron que contar de 2 en 2 es así: 2, 4, 6,8,10,12,14,16,18,...

Y contar de 5 en 5 era:

5,10,15, 20, 25, 30, 35, 40, 45, 50, 55,...

Pues, esto no es DEL TODO CIERTO. Cuando se te dice cuenta de 2 en 2, se refiere a contar, y que haces tú cuando se te dice en la vida, por ejemplo, cuéntame cuantos vasos hay, para ver si alcance el refresco para todos, tu ¿qué haces? Pues cuentas, dices, 1 vaso, 2 vasos, 3 vasos, 4 vasos, y así sucesivamente y das la respuesta, hay 12 vasos por ejemplo, bueno eso es contar.

Por tanto, cuando se te dice cuenta de 2 en 2, deberías contar así:

2, 2, 2, 2, 2, 2, 2,

1× 2× 3× 4× 5× 6× 7× 8×2,9×2,10×2,...

Observa que siendo en este caso el patrón el 2, contamos cuantos 2 hay, es decir, un dos, dos dos, tres dos, cuatro dos, así como cuando contaste los vasos. ¿Que sucede? Lo que te enseñaron en la escuela entonces ¿no esta bien? Si esta bien, pero no en aquel momento lo dicho no fue el cuento completo, fíjate porque, si el conteo de 2 en 2 lo multiplicas, es decir, un dos es uno por dos, dos dos es dos por dos, tres dos es tres por dos, y así

sucesivamente, obtienes:

1 2 2 2 3 2 4 2 5 2 6 2 7 2 2 2 2

2 4 6 8 10 12 14

8 9 10

16 18 20

2,

2,

2,

2,

2,

2,

2,

2,

2,

2,...

1

2

3

4

5

2, 4, 6,8,10,12,14,16,18

6

7

8

9

1

, 20

0

,...

× × × × × × × × × ×

×

×

×

×

×

×

×

×

×

×

↓ ↓ ↓

↓

↓

↓

↓

↓

↓

↓

Ahora, te preguntarás ¿qué tiene que ver esto con graficar el seno y el

coseno?, bueno recuerda que te mencione que contaras de 2 π

en 2 π

equis, si no te hubiera explicado lo que es contar, probablemente no hubieras contado de 2 π en 2 π

. Contemos pues, de 2 π

en 2 π

en el eje equis, observa:

2

2

2

1

1

,

2

,

3

,

4

,

5

,

6

,

7

,

8

,

,

,...

2

2

2

2

2

2

2

2

9

2

10

2

π π π

π

π

π

π

π

π

π

π

π

π

×

×

×

×

×

×

×

×

×

×

↓

↓

×

2 π

× ₃ 4

2 3 2 2

π π π ×

↓

↓

2

π × 2 5 3 2 6 5

π π π ×

↓

↓

2

π

× ₇ 8

2 7 4 2

π π π ×

↓

↓

2

π × 2 2 10 9 5 9

π π π ×

↓

↓

2

π

×

3

5

7

9

, ,

, 2 ,

, 3 ,

, 4 ,

, 5 ,...

2

2

2

2

2

π

_π

π

_π

π

_π

π

_π

π

_π

Así:

Luego de contar de 2 π

en 2 π

, en el eje y construye dos rectas paralelas

Ahora grafiquemos el seno de equis, esta curva siempre PARTE DEL ORIGEN, y cada 2π se repite la misma curva, porque el seno de equis es periódica, observa:

Ahora grafiquemos el coseno de equis, esta curva siempre PARTE DE 1 EN EL EJE Y, y cada 2π se repite la misma curva, porque el coseno de equis es periódico, observa:

Ahora vamos a deducir, la fórmula que usaremos para resolver el primer ejercicio planteado, además, será usada en los ejercicios donde se pida el calculo DEL ÁREA DE UNA SUPERFICIE EN REVOLUCIÓN.

Primero aclaremos que la palabra revolución en este objetivo se entenderá como sinónimo de giro o rotación, por ejemplo:

1)

En el ejercicio 1 se nos pide calcular el área de la superficie de revolución, la superficie de un sólido es el área total externa, por ejemplo:

Cubo

Un cubo tiene 6 caras, y cada cara es un cuadrado, por lo tanto el área de una cara de lado L es: L2.

Por ende, el área de toda su superficie será: 2

6 S = L

Ahora bien, los casos que enfrentaremos serán sólidos de revolución, es decir, curvas que giran o rotan alrededor de un eje fijo, que por lo general es el eje equis o eje ye.

Vamos, sin más preámbulo, a deducir la fórmula que nos permite calcular el área de una superficie en revolución.

Observemos la siguiente figura:

La figura 1, muestra el área plana que rotara, en este caso, alrededor del eje x, observa como se dibuja en esta figura el rectángulo típico azul, cuyo ancho inferior es dx, observa como a la parte superior del rectángulo le llame dL, esto porque asumí que como el rectángulo es muy fino o de ancho muy pequeño puedo aproximar la longitud superior del rectángulo a la longitud de la curva en ese segmento muy pequeño, observa ésta situación aumentada en la siguiente figura:

(como en un aro de matrimonio); se destaca en rojo la superficie de dicho disco.

Ahora imagina que extraemos ese disco y lo estiro, así como una cinta de ancho dL, haciendo esto, obtenemos el rectángulo rojo de la parte de abajo:

Ahora bien, se ve claramente como toda la superficie del disco, es ahora la superficie de este rectángulo rojo, es decir, el área de este rectángulo. Este rectángulo tiene largo y ancho, el ancho es dL tal como ya explique, pero el largo será la longitud de la circunferencia del disco, recuerda que la longitud de una circunferencia de radio R es:

2πR

Pero en este caso el radio es f x( ) por ser la altura del rectángulo típico azul por ende al estirar el disco formado de superficie roja, obtenemos que la longitud de la circunferencia del disco, es:

2π f x( )

Cual es el área de un rectángulo, pues ancho por largo, por lo tanto, la superficie o área del rectángulo rojo es:

(

)

[

arg

]

dA=dS = ancho × L o

Donde: dA=dS: es el diferencial de área o superficie.

Sustituyendo el ancho y el largo del rectángulo rojo se tiene: 2 ( )

dS= πf x dL

2 1 dy

dL dx

dx  

= +_{ }

 

También este diferencial de longitud se puede escribir:

(

_'

)

2

1 ( )

dL= + f x dx

Sustituyendo este diferencial de longitud en nuestra ecuación de diferencial de superficie, se tiene:

2 2 ( ) 1 dy

dS f x dx

dx

π

 

= +_{ }

 

Como y= f x( ) y ' dy y

dx

= se puede escribir:

( )

_' 2

2 1

dS = πy + y dx

Puedes observar en la figura 1 ó 2, que debemos sumar todos los subrectangulos típicos desde x=a hasta x=b, por lo tanto, aplicando integrales en ambos miembros, tenemos:

( )

_' 2

( )

_' 2

2 1 2 1

b b

a a

S=

∫

π

y + y dx=

π

∫

y + y dx

Que es la fórmula para calcular la superficie de un sólido en revolución. Si aplicas el mismo tratamiento anterior a una gráfica de la forma:

Obtendrás exactamente la misma fórmula, claro, con las variables invertidas, es decir:

2 2

2 1 2 1

d d

c c

dx dx

S x dy x dy

dy dy

π

 

π

 

= +  = + 

   

En resumen hay 2 casos:

1)

( )

' 2

2 1

b

a

S=

π

∫

y + y dx cuando la gráfica es de la forma:

2)

2

2 1

d

c

dx

S x dy

dy

π

 

= + 

 

∫

cuando la gráfica es de la forma:

Retomando el ejercicio plateado número 1, que trata sobre determinar el área de la superficie de revolución generada al girar la curva de ecuación

4 2

1 1

8 4

x y

y

= + , 1≤ ≤y 2 alrededor del eje OY, podremos ver claramente que

Desarrollando la fórmula del caso 2, se tiene:

Sustituyendo lo anterior en nuestra fórmula, se tiene: 2 2

4 3

2 3

1

1 1 1 1

2 1

8 4 2 2

S y y dy

y y

π

   

=  +  + − 

   

∫

( )

( )

( )

2

2 3 3

2 2 4 2 6 6

3 2 3

2

1 1

2 2

4 8 4 8 2 2

2 1 2 1

2 2 32 4

8 4

y y

y y y y

S dy dy

y y y

y

π  +   −  π  +   − 

= _{ } +_{ } =   + 

   

   

(

)

(

)

2

2

6 6

2 2 6 6

2 3 2 3

1 1

4 2 2 1 _{2 1}

2 1 2 1

32 4 8 2

y y _{y y}

S dy dy

y y y y

π  +   −  π  +   − 

= _{ } +_{ } =   + 

   

   

∫

∫

(

₆

)

2 ₆

( )

₆ 2 ₆

2 6 2 6

2 6 2 6

1 1

1 4 2 1

2 2

2 1 2

8 4 8 4

y y y y

y y

S dy dy

y y y y

π

 +  −

π

 +  + − +

=   + =  

   

∫

∫

( )

₆ 2 ₆

(

₆

)

2

2 6 2 6

2 6 2 6

1 1

2 1 1

2 2

2 2

8 4 8 4

y y y

y y

S dy dy

y y y y

π

 +  + +

π

 +  +

=   =  

   

∫

∫

(

₆

)

2

2 6 2 6 6

2 ₆ 2 3

1 1

1

2 2 1

2 2

8 ₄ 8 2

y

y y y

S dy dy

y _y y y

π

 +  +

π

 +   + 

=   =    

     

∫

∫

2 6 6 6 6 2 12 6

2 3 5

1 1

2 2 3 2

2 2

16 16

y y y y y y

S dy dy

y y y

π

 + + + 

π

 + + 

=   =  

   

∫

∫

2 12 6 2 12 2 6 2

5 5 5 5 5 5

1 1 1 1

3 2 3 2

2 2

16 16 16 16 16 16

y y y y

S dy dy dy dy

y y y y y y

π

 

π

  =  + +  =  + +     

∫

∫

∫

∫

12 2 y

S=

π

₅

16 y 2 6 1 3y dy+

∫

5 16 y

2 2 2 2 2

5 7 5

1 1 1 1 1

1 1 3 1

2

8 16 16 8

dy y dy−

π

y dy ydy y dy−

   

+ = + +

   

 



∫

∫



∫

∫

∫

8 ₂ 2 ₂ 4 ₂

1 3 1

2

1 1 1

16 8 16 2 8 4

y y y

S

π

−        =   +  +   −         

( )

8 8 2 2 4 4 8

4

1 2 1 3 2 1 1 2 1 1 2 1 3 4 1 1 1 1

2 2

16 8 8 16 2 2 8 4 4 16 8 16 2 8 4 2 4

S

π

π

− −           _  ₋   ₋  _{ } =   − +  − + ₋ + =  +  + _− + _               _{  }

1 256 1 3 3 1 1 2 255 3 1 1 16

2 1 3

16 8 16 2 32 16 16 8 2 2 16

S= π  − +   + − + = π  +   + − + 

           

   

( )

( )

4 255 16 9 15

255 9 15 1020 144 15 1179

8 8 2 32 8 32 8 32 8 32

S=π _ + + _=π + + =π _ + + _=π_ _

  _{ }    

1179 256

S= π

Respuesta: 1179 256

Ejercicio 2

Sea R la región del plano XY limitada por las curvas de ecuaciones y= x y y= −2 x. Calcula el volumen del sólido generado al girar la región R alrededor de la recta y= −1.

Solución

Justificación: En este caso, se nos pide calcular el volumen, y tal como hice en el ejercicio 1 que deduje la fórmula a utilizar, haré exactamente lo mismo aquí, con el mayor detalle posible, te recuerdo que lo hago, porque es vital que domines de donde salen las fórmulas, porque resolver los ejercicios requieren de saber construir las integrales y tomar correctamente los límites de integración, y todo esto depende precisamente de que realmente sepas lo que estas haciendo.

Para calcular el volumen hay 2 métodos que son: El método de las arandelas o discos y método de las capas cilíndricas, la diferencia principal entre éstos, es que en el método de las arandelas el rectángulo típico es

PERPENDICULAR AL EJE DE GIRO, mientras que en el método de las

capas cilíndricas el rectángulo típico es PARALELO AL EJE DE GIRO. Pasemos a deducir ambas fórmulas y a observar cuando aplicarlas.

Método de las arandelas (rectángulo típico

PERPENDICULAR

AL EJE

DE GIRO

En la figura 4, se observa el área encerrada por dos curvas f x( ) y ( )g x , siendo f x( )> ( )g x >0, f x( )> ( )g x quiere decir que f x( ) esta por encima de g x( ) y (>0) quiere decir que ambas son positivas; ésta área esta encerrada además de las funciones anteriores por dos rectas verticales x=a y x=b, el área de esta figura 4 a la cual me refiero la destaque subrayándola con líneas inclinadas.

En la figura inmediata anterior hemos llegado al volumen de la arandela, que no es más que el volumen de un cilindro hueco:

(

2 2

)

1 2 V =πh R −R

Sustituyendo en esta ecuación R₁=R_e = f x( ), R₂=R_i =g x( ) y la altura del cilindro h=dx se tendrá el diferencial de volumen de la arandela de la figura 5:

( ) ( )

(

2 2

)

(

(

) (

2

)

2

)

( ) ( )

e i

dV =π R − R dx=π f x − g x dx

Puedes observar en la figura 4 ó 5, que debemos sumar todos los subrectangulos típicos desde x=a hasta x=b, por lo tanto, aplicando integrales en ambos miembros, tenemos:

(

) (

)

(

2 2

)

(

(

) (

2

)

2

)

( ) ( ) ( ) ( )

b b

a a

V=

∫

π f x − g x dx=π

∫

f x − g x dx

Que es la fórmula para calcular el volumen del sólido en revolución formado al rotar el área rayada alrededor del eje equis, CON EL RECTÁNGULO TÍPICO PERPENDICULAR AL EJE DE GIRO.

NOTA: Esta fórmula se usa solo si el sólido de revolución gira

Y se solicita rotarla alrededor del eje Y la fórmula, al aplicar el análisis anterior sería:

(

) (

)

(

2 2

)

( ) ( ) d

c

V=π

∫

f y − g y dy

Si gira alrededor de otro eje, PARALELO AL EJE EQUIS (X) hay que tomar los radios internos

( )

R_i y externos

( )

R_e desde ese eje de giro. Esta situación se ilustra al resolver el ejercicio planteado número 2, donde hay que calcular el volumen generado al rotar la región R del plano XY limitada por las curvas de ecuaciones y= x y y= −2 x alrededor de la recta y= −1.

Método de las capas cilíndricas (rectángulo típico

PARALELO

AL EJE

DE GIRO

En la figura 7, se observa el área encerrada por dos curvas f x( ) y ( )g x , siendo f x( )> ( )g x >0, f x( )> ( )g x quiere decir que f x( ) esta por encima de g x( ) y (>0) quiere decir que ambas son positivas; ésta área esta encerrada además de las funciones anteriores por dos rectas verticales x=a y x=b, el área de esta figura 7 a la cual me refiero la destaque subrayándola con líneas inclinadas.

abscisas x_i−1 y xi son los extremos inferiores del rectángulo típico, tal como se muestra en la siguiente figura aumentada:

El incremento delta equis: ∆x, viene dado por la diferencia ∆ = −x x_i x_i−1, es decir, extremo mayor, menos extremo menor, pero cuando este delta equis tiende a cero, es decir, el ancho del rectángulo es muy pequeño, este ∆x se convierte en dx.

Ahora bien, ya todos sabemos que el volumen de un cilindro viene dado por el área de la base multiplicada por su altura, es decir:

Pero si el cilindro es hueco:

Su volumen es:

( )

2

( )

2

( ) ( ) ( )

2 2

1 2 1 2

Observando la figura 8 y 9, se tiene:

1

2 1

(1) (2)

( ) ( )

e i

i i

R R x R R x

h f x g x −

= =

 

= =



 _{= −}

 Entonces:

( ) ( ) (

2 2

)

( ) ( )

e i

dV =π_ R − R _ f x −g x

Recordando que:

( )

( )

(

)(

)

( )

( )

(

)(

)

2 2

2 2

e i e i e i

a a a

R R

b b

b

R R R R

− = + −

− = + −

Se tiene:

(

_{e i}

)(

_{e i}

)(

( ) ( )

)

dV =π R +R R −R f x −g x Sustituyendo (1) y (2) se puede escribir:

(

i i1

)(

i i1

)(

( ) ( )

)

Se tiene claramente que:

1

2

m i

x

R

=

x

₋

+

∆

Pero como: ∆ = −x x_i x_i−1, se obtiene:

1 1 1 1 1 1

1

1 1

2

2

1

2

2

2

2

2

1

i i i i i i i i i i

m

i

i i

i

x

x

x

x

x

x

x

x

x

x

x

x

x

R

=

x

₋

+

−

−

=

−

+

−

−

=

−

+ −

−

=

+

−

−

−

=

+

−

Por lo tanto:

(

)

1

1

2

2

i

m i

i

i m

x

x

x

R

=

+

−

∴

+

x

₋

=

R

Sustituyendo dx= −x_i x_i−1 y este radio medio

( )

R

m en nuestro

diferencial de volumen, se tiene:

(

i i1

)

(

xi i1

)

(

( ) ( )

)

dV =π x +x₋ −x₋ f x −g x

(

2 _m

)

( )

(

( ) ( )

)

dV =π R dx f x −g x

Y como en este caso, el giro es alrededor del eje ye, se tiene que

m

R

=

x

, y como el orden de los factores no altera el producto se puede

escribir:

(

)

2 ( ) ( )

dV = πx f x −g x dx

Puedes observar en la figura 7 ó 8, que debemos sumar todos los subrectangulos típicos desde x=a hasta x=b, por lo tanto, aplicando integrales en ambos miembros, tenemos:

(

)

(

)

2 ( ) ( ) 2 ( ) ( )

b b

a a

V =

∫

πx f x −g x dx= π

∫

x f x −g x dx

Que es la fórmula para calcular el volumen del sólido en revolución formado al rotar el área rayada alrededor del eje ye, CON EL RECTÁNGULO TÍPICO PARALELO AL EJE DE GIRO.

NOTA: Esta fórmula se usa solo si el sólido de revolución gira

Y se solicita rotarla alrededor del eje X la fórmula, al aplicar el análisis anterior sería:

(

)

2 ( ) ( ) d

c

V= π

∫

y f y −g y dy

Si gira alrededor de otro eje, PARALELO AL EJE YE (Y) hay que tomar el radio medio

( )

R_m desde ese eje de giro.

En resumen:

Cuando pidan el volumen de un sólido que gira alrededor de un eje

paralelo

al eje equis o al eje ye, se utilizan las siguientes fórmulas generales:

FÓRMULA GENARAL DEL MÉTODO DE LAS ARANDELAS

( ) ( )

(

2 2

)

b

e i

a

V =π

∫

R − R dx

FÓRMULA GENARAL DEL MÉTODO DE LAS CAPAS CILÍNDRICAS

(

)

2 ( ) ( )

b

m a

V = π

∫

R f x −g x dx

Cuando pidan el volumen de un sólido cuando gira alrededor del eje equis o del eje ye, se utilizan las siguientes fórmulas particulares:

(

) (

)

(

2 2

)

( ) ( ) b

a

V =π

∫

f x − g x dx (eje de giro: eje x)

(

) (

)

(

2 2

)

( ) ( ) d

c

V=π

∫

f y − g y dy (eje de giro: eje y)

FÓRMULA GENARAL DEL MÉTODO DE LAS CAPAS CILÍNDRICAS

(

)

2 ( ) ( ) b

a

V = π

∫

x f x −g x dx (eje de giro: eje y)

(

)

2 ( ) ( ) d

c

V = π

∫

y f y −g y dy (eje de giro: eje x)

¿Cuándo usar el método de las arandelas o capas cilíndricas?

Situación planteada en el ejercicio Eje de giro del ejercicio: Puedes aplicar

Puedes despejar x en función de y ó y

en función de x, en la o las funciones que te dan, por ejemplo:

5 3 5

3 y y= x− → =x +

2

9 9

y=x + → =x y−

Eje x ó eje y ó ejes paralelos al eje x o al eje y

Cualquier método

(Tu eliges si pondrás el

rectángulo típico paralelo o

perpendicular al eje de giro)

Tienes y en función de x, y no puedes despejar x en función de y, en la o las

funciones que te dan, por ejemplo:

2 4

3 5

y x x

x

= − + , y= +x sen x

( )

Eje x ó eje paralelo al eje x

Sólo el método de las arandelas

(Rectángulo típico perpendicular

al eje de giro)

Tienes y en función de x, y no puedes despejar x en función de y, en la o las

funciones que te dan, por ejemplo:

( )

ln

y= −x x , 2 x y=x +e

Eje y ó eje paralelo al eje y

Sólo el método de las capas cilíndricas

(Rectángulo típico paralelo al eje

de giro)

Tienes x en función de y, y no puedes despejar y en función de x, en la o las

funciones que te dan, por ejemplo:

( )

ln

x= −y y , y 3 x=e − y

Eje x ó eje paralelo al eje x

Sólo el método de las capas cilíndricas

(Rectángulo típico paralelo al eje

de giro)

Tienes x en función de y, y no puedes despejar y en función de x, en la o las

funciones que te dan, por ejemplo:

3

x=y −y, 2

2 1

x= y+y +

Eje y ó eje paralelo al eje y

Sólo el método de las arandelas

(Rectángulo típico perpendicular

Del cuadro anterior se desprende que debes saber aplicar ambos métodos, porque hay ejercicios donde solo podrás aplicar uno de los 2 métodos.

Recomendación: Una vez elegido el método, dibuja el rectángulo típico correspondiente y siempre usa las formulas generales, para que construir la integral, es decir, siempre usa:

( ) ( )

(

2 2

)

b

e i

a

V =π

∫

R − R dx (Arandelas)

(

)

2 ( ) ( )

b

m a

V = π

∫

R f x −g x dx (Capas cilíndricas)

Además te recomiendo encarecidamente que leas hasta entender la deducción de las fórmulas, las explique lo más detallado que pude, al hacer esto, cuando te enfrentes a un ejercicio llevaras la mitad del camino ganado.

A continuación resolveré en detalle el ejercicio número 2, y para que observes como aplicar cada UNO DE LOS MÉTODOS EXPLICADOS, resolveré el ejercicio con ambos métodos, ya que la situación me lo permite. (NO ES NECESARIO QUE LO RESUELVAS DE LAS 2 MANERAS, LO EJECUTO ASÍ A MANERA DIDACTICA).

Por supuesto que por ambos caminos debes llegar AL MISMO RESULTADO. Comencemos.

Se plantea calcular el volumen del sólido generado al girar la región R del plano XY limitada por las curvas de ecuaciones y= x y y= −2 x, alrededor

de y= −1.

PASO 1: Ubicar los puntos de intersección entre las curvas y los interceptas con los ejes coordenados de cada una de ellas, de ser necesario.

Esto te ayudará a graficar y obtener los límites de integración:

Tenemos dos curvas que llamare: f x( )= −2 x y g x( )= x , es indiferente a

quien llames efe o ge.

Dado que las funciones poseen la operación valor absoluto, debemos aplicar a cada una de ellas su definición:

( ) 0

( ) si ( )

( ) si ( ) 0

f x h

h x x

h x x

f

+

− <

≥



Aplicando esta definición a nuestras funciones, se tiene: si 0

0 si x x x x x + − < ≥  = 

Por lo tanto:

( )

( )

2 si 0 ( )

2 si 0

x x

f x

x x

− − <



=

− + ≥

 y

si 0 ( )

si 0

x x g x x x − <  = + ≥  Simplificando:

2 si 0 ( )

2 si 0

x x f x x x + <  = − ≥

 y

si 0 ( )

si 0

x x g x x x − <  = + ≥ 

Por lo tanto las intercepciones de las curvas son: Para x<0:

2 (1)

(2) y x y x = +   = − 

Resolviendo el sistema por el método de sustitución, sustituyendo (2) en (1) se tiene:

2

2 2 2 2 1

2

x x x x x x

− = + → − − = → − = ∴ = = − −

Por lo tanto la ordenada es: y= − → = − − =x y

( )

1 1

Y nuestro primer punto de intersección es:

( ) (

x y, = −1,1

)

Para x≥0:

2 (3)

(4) y x y x = −   = 

Resolviendo el sistema por el método de sustitución, sustituyendo (4) en (3) se tiene:

2

2 2 2 2 1

2 x= − → + = →x x x x= ∴ = =x

Por lo tanto la ordenada es: y= → =x y

( )

1 =1

Y nuestro segundo punto de intersección es:

( ) ( )

x y, = 1,1 PASO 2: Graficar.

Ahora bien, la gráfica de la función g x( )= x es conocida, porque se trata

del módulo de equis, y esta compuesta por las rectas obtenidas si 0

( )

si 0

x x g x x x − <  = + ≥

En cuanto a la gráfica f x( )= −2 x, observamos que debe pasar por los

puntos de intercepción ya calculados y además por el intercepto con el eje ye, que se calcula haciendo cero a la variable equis:

( )

2 0 2 0 2 0, 2 y= − = − = →

Uniendo ambas gráficas se tiene la región encerrada por f x( ) y g x( ):

PASO 3: Dibujar el eje de giro.

En este caso el eje de giro es la recta: y= −1, grafiquemos pues este eje:

Aplicando el método de las arandelas La fórmula general de este método es:

( ) ( )

(

2 2

)

b

e i

a

V =π

∫

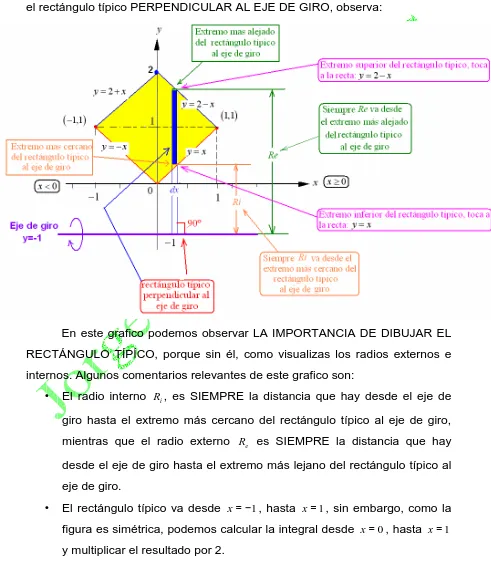
R − R dx

Por lo tanto, debemos saber quien es el radio externo R_e y quien el radio interno R_i, así como los límites de integración a y b, esto se deduce dibujando el rectángulo típico PERPENDICULAR AL EJE DE GIRO, observa:

En este grafico podemos observar LA IMPORTANCIA DE DIBUJAR EL RECTÁNGULO TÍPÍCO, porque sin él, como visualizas los radios externos e internos. Algunos comentarios relevantes de este grafico son:

• El radio interno R_i, es SIEMPRE la distancia que hay desde el eje de

giro hasta el extremo más cercano del rectángulo típico al eje de giro, mientras que el radio externo R_e es SIEMPRE la distancia que hay desde el eje de giro hasta el extremo más lejano del rectángulo típico al eje de giro.

[image:34.595.59.550.204.771.2]

• Muy importante es visualizar como en el primer cuadrante, es decir, desde x=0 hasta x=1 el rectángulo típico toca a la recta y= −2 x en su parte superior, mientras que toca a la recta y=x en su parte inferior. Ahora observa en el próximo gráfico cuanto valen los radios internos y externos:

Las distancias ye siempre se miden desde el eje equis hasta el extremo inferior y superior del rectángulo típico, y se coloca la ye que corresponde, es decir, si toca una recta, una parábola, etc.

El grafico inmediato anterior nos permite visualizar claramente que:

)

1

(

i

R

= +

x

(Radio interno)

(2

)

1

e

R

=

+

−

x

(Radio externo)

Se toma el 1 positivo y no negativo, porque estamos hablando de distancias, y las distancias siempre son positivas.

Los límites de integración serán: desde a=0 hasta b=1, y multiplicaremos toda la integral por 2.

Sustituyendo todo lo anterior en la ecuación general del volumen, se tiene:

(

) (

)

(

)

1

2 2

0

2 1 2 1

Calculando esta integral:

(

)

(

)

(

)

(

(

) (

)

)

1 1

2 2 2 2

0 0

2 3 1 2 2 9 6 1 2

V = π

∫

−x − + x+x dx= π

∫

− x+x − + x+x dx

(

)

(

)

(

)

1 1 1

2 2

0 0 0

2 9 6 1 2 2 8 8 2 8 1

V = π

∫

− x+ − −x x−x dx= π

∫

− x dx= π

∫

−x dx

2 ₁ 2 2

1 0 1 1 16

16 16 1 0 16 1 16 8

0

2 2 2 2 2 2

x

V = πx− = π − − − = π − = π  = π = π

   

 

   

Aplicando el método de las capas cilíndricas La fórmula general de este método es:

(

)

2 ( ) ( )

d

m c

V = π

∫

R f y −g y dy

Por lo tanto, debemos saber quien es el radio medio Rm, así como f x( ),

( )

g x y los límites de integración a y b, esto se deduce dibujando el rectángulo típico PARALELO AL EJE DE GIRO, observa:

En este grafico podemos observar LA IMPORTANCIA DE DIBUJAR EL RECTÁNGULO TÍPÍCO, porque sin él, como visualizas el radio medio. Algunos comentarios relevantes de este grafico son:

distintas, para el que esta mas abajo toca a la función x= y, y el que esta mas arriba toca a la función x= −2 y, siendo así las cosas, hay 2 radios medios, el radio medioR_m1 y el R_m2, que son SIEMPRE la distancia que hay desde el eje de giro hasta el rectángulo típico correspondiente.

• El rectángulo típico de abajo va desde y=0, hasta y=1, y el de más arriba va desde y=1, hasta y=2, claro está, como la figura es simétrica, podemos calcular las integrales generadas y multiplicar el resultado total por 2.

• Muy importante es visualizar como ambos rectángulos típicos tocan en su parte izquierda x=0.

• IMPORTANTE: Observa como se despejo ye en función de equis por estar los rectángulos típicos paralelos al eje equis.

• El grafico inmediato anterior nos permite visualizar claramente que:

1 1

2 2

1

1

1

1

m

m

R

y

y

R

y

y

= + = +

= +

= +

(Radios medios)

Se toma el 1 positivo y no negativo, porque estamos hablando de distancias, y las distancias siempre son positivas.

Los límites de integración serán: para la primera integral (rectángulo típico de abajo) desde c=0 hasta d =1, y para la otra integral desde c=1 hasta d =2, multiplicaremos la suma de las integrales por 2.

Sustituyendo todo lo anterior en la ecuación general del volumen, se tiene:

( ) (

1

)(

)

( ) (

2

)(

)

0 1

2 2 1 0 2 1 2 0

V =  π +y y− dy+ π +y − −y dy



∫

∫



Calculando esta integral:

( )

1

(

2

)

( ) (

2

)(

)

0 1

2 2 2 1 2

V =  π y+y dy+ π +y −y dy



∫

∫



(

)

(

)

2 2

2 3 2 3

2 2

1 1

1 1

4 2 2 4 2

0 0

2 3 2 3

y y y y

V π y y y dy π y y dy

     

=  + + − + − =  + + + − 

     



∫

 

∫



2 3 ₁ 2 3 ₂

4 2

0 1

2 3 2 3

y y y y

V π y

   

=  +  + + − 

   

( )

( )

2 3 2 3 2 3

1 1 2 2 1 1

4 0 2 2 2 1

2 3 2 3 2 3

V π

    

=  + − + + − − + − 

    

 

1 1 4 8 1 1 3 2 8 3 2

4 4 2 4 4 2 2

2 3 2 3 2 3 6 3 6

V = π + + + − − + − = π + + + − − + − 

         

   

5 8 1 5 36 8 12 1 41 8 13

4 6 2 4 4

6 3 6 6 3 6 6 3 6

V = π  + − − + = π + − − + = π − − 

       

     

( )

41 8 13 41 16 13 12

4 4 4 4 2 8

6 3 6 6 6

V = π_ − − _= π_ − − _= π_ _= π = π

     

Como ves, hemos llegado al mismo resultado. El sólido de revolución generado es:

Respuesta: V =8π .

Ejercicio 3

Un sólido tiene como base un círculo de diámetro AB cuya longitud es

2a. Halla el volumen del sólido si toda sección transversal perpendicular a AB

es un triángulo equilátero.

Solución

para volumen deducidas en el ejercicio anterior. En este caso procederemos así:

PASO 1. Esbozar la figura, incluyendo un eje perpendicular a las secciones de área conocida (es decir, un eje OX)

PASO 2. Escoger una sección perpendicular al eje OX, a una distancia equis x

del eje ye.

PASO 3. Expresar el área A x( ) de la base de la sección en términos de su posición x sobre el eje OX.

PASO 4. Integrar entre los límites apropiados.

En este paso obtendremos el producto del área A x( ) por el grosor de la

sección que se desplaza integrada en todo el recorrido de la sección, así:

( )

b

a

V =

∫

A x dx

PASO 2. Escoger una sección perpendicular al eje OX, a una distancia equis x

del eje ye.

En la figura anterior se visualiza que la sección seleccionada se ubica a una distancia x del eje ye, la sección es un triángulo equilátero (la longitud de sus lados es igual).

PASO 3. Expresar el área A x( ) de la base de la sección en términos de su posición x sobre el eje OX.

Para obtener el área en función de x, se procede a construir dos funciones:

FUNCIÓN DE LA BASE: En este caso, la base es circular de radio a y centro en el origen.

Recordando lo explicado en el ejercicio 1 de esta guía acerca de la gráfica de funciones, sabemos que la ecuación general de una circunferencia es:

(

) (

2

)

2 2

x h− + y−k =r

2 2 2 2 2

( , ) (0, 0) c h k

x y a

r a r a

=



→ + =



= → =



De aquí, se tiene:

2 2 2 2 2 2 2 2

x +y =a →y =a − ∴ = ±x y a −x

Por lo tanto:

FUNCIÓN DE LA SECCIÓN TRIÁNGULAR QUE SE DESPLAZA:

De la figura inmediata anterior se observa claramente que la longitud o distancia L es:

2 2 2 2 2 2

2

L= a −x + a −x = a −x

NOTA: Recuerda que las distancias son positivas, es decir: a pesar de

que la parte superior es 2 2

y= a −x y la inferior es: 2 2

y= − a −x , la distancia entre los dos extremos de la línea ele

( )

L es:

2 2 2 2 2 2 2 2 2 2

2

L= a −x + − a −x = a −x + a −x = a −x

Si dibujamos el triángulo equilátero de frente, tenemos:

Observa que en el triángulo equilátero de frente, exactamente en el triángulo destacado en rojo se puede aplicar el teorema de Pitágoras, así:

2 _{2 2 2 2 2 2}

2 2 2 2 4 3 3 3 3

2 4 4 4 4 4 2

L L L L L L L L

L =h +_{ }  →h = −L = − = ∴ =h = =  

Recuerda que buscamos la altura de este rectángulo, porque estamos buscando la función A x( ) y el área de un triángulo es base por altura entre dos:

Sustituyendo 3 2 L h= :

2

3 3

( )

2 2 2 4

L L L L

A x = h= =

Pero el área debe estar en función de equis, esto se logra sustituyendo: 2 2

2

L= a −x Finalmente:

(

)

2

₍

₎

2 2

2 2

3 2

( ) 3

4

a x

A x a x

−

= = −

PASO 4. Integrar entre los límites apropiados.

En este caso la sección triangular se mueve desde x= −a, hasta x=a, es decir, a lo largo de todo el diámetro AB tal como se observa en la figura esbozada en el paso 1, por lo tanto:

(

2 2

)

( ) 3

b a

a a

V A x dx a x dx

−

=

_∫

=

_∫

−

Resolviendo esta integral:

(

)

(

)

3

2 2 2 2 2

3 3 3

3

a a

a a

a x

V a x dx a x dx a x

a − −   = − = − = _ − _  ₋

∫

∫

( ) ( )

3

( ) ( )

3 3 3

2 2 3 3

3 3

3 3 3 3

a a a a

V a a a a a a

  ₋  _{  − }   = − − − −  = _ − − − −_{ }    _{ }     

3 3 3 3 3 3 3 3

3

3 2 3 2 2

3 3 3

3 3 3 3 3 3

a a a a a a a a

V =  − − − + a =  −− + =  −− 

     

     

3 3 3 3 3 3

2 2 2 2 4 4 3

3 3 3

3 3 3 3 3

a a a a a a

V = _ + _= _ + _= _ _=

      Respuesta: 3 4 3 3 a

V = .

Ejercicio 4

a) Dibujar la región R limitada por las gráficas:

(

)

2

( ) 2 1

f x = − −x , 2

( ) 1

Solución

Justificación: Para calcular área de regiones en el plano dibujaremos el rectángulo típico como se muestra en la figura:

De manera que el rectángulo típico es:

Como al área de un rectángulo es base por altura, un diferencial de área sería:

(

( ) ( )

)

dA= f x −g x dx

Tomando integrales en ambos miembros, y observando que el rectángulo típico se desplaza de a a b, se tiene:

(

( ) ( )

)

b

a

A=

∫

f x −g x dx

Nota: Se integra la curva de arriba menos la de abajo con respecto al rectángulo típico.

Nota: Se integra la curva de la derecha menos la de la izquierda con respecto al rectángulo típico.

Aplicando el análisis anterior, se tendría que el área es:

(

( ) ( )

)

d

c

A=

∫

f y −g y dy

Para dar respuesta al apartado “a”, del ejercicio 4 planteado, debemos graficas las funciones dadas; tal como te explique en el ejercicio 1, se observa

Función

Derivando e igualando a cero: '

0 y =

Vértice

Evalúa el valor de la derivada en la función original

Corte con los ejes:

(

)

2

2 1

y= − −x

variable equis elevada al cuadrado negativa, abre hacia abajo

(

)

(

)

'

2 1 0

1 0 1 y x x x = − − = − = =

Para x=1

(

)

( )

2 2

2 1

2 1 1

2 y x y y = − − = − − =

( )

1, 2

V

(

)

2

2 1 0

y= − −x =

que las funciones f x( ) y g x( ) son parábolas, por estar una de las variables elevada al cuadrado, por lo tanto, para realizar su gráfica se procede así:

Por lo tanto:

Gráfica de la parábola y= − −2

(

x 1

)

2

Para la otra parábola, se tiene:

Por lo tanto:

Gráfica de la parábola y= −1 x2 Función

Derivando e igualando a cero: '

0 y =

Vértice

Evalúa el valor de la derivada en la función original

Corte con los ejes:

2 1 y= −x variable

equis elevada al

cuadrado negativa, abre hacia

abajo

' 2

2 0

0

y x

x

= − =

=

Para x=0 2 2

1 1 0 1

y y x y

y = = −

= − =

( )

0,1

V

2

1 0

y= −x = 2

1 2

1 1 1

1 x x x x

= = ±

Ahora veremos si las parábolas se interceptan, igualándolas, éstas intercepciones nos darán los límites de integración, así:

( ) ( ) f x =g x

(

)

2 ₂

2− −x 1 = −1 x Resolviendo esta ecuación:

(

2

)

2 2 2 2 2

2− x −2x+ = −1 1 x → − +2 x 2x− = −1 1 x → − +1 x 2x− +1 x =0 2

1− x +2x− +1 x2 = →0 1+2x−1 0 2 0 0 0 2

x x

= → = ∴ = =

La ordenada o coordenada ye de este punto de intercepción se consigue sustituyendo x=0 en cualquiera de las funciones f x( ) ó g x( ), así:

2 2

0

1 1 0 1 0 1

x

y x

=

= − = − = − =

Por lo tanto el punto de intercepción es:

( )

0,1 . Tomando en cuenta

0

Área 1 VERDE

Podemos observar que el rectángulo típico toca en la parte inferior a 0

y= y en la parte superior a la función 2 ( ) 1

g x = −x y dicho rectángulo típico recorre el intervalo en el eje equis desde a= −1 hasta b= −1 2, entonces:

(

)

1 2 2 1 1 1 0

A x dx

−

−

=

_∫

− −

Resolviendo esta integral:

(

)

(

)

( )

3

3

1 2 3

2 1

1

1 2

1 2 ₁

1 1 2 1

3 3 3

1 x

A x dx x

− − − _{−  } − = − = − = − − − − −      −

∫

(

)

3

( )

(

)

3

1

3 3 2 1 2 ₁ 3 3 2 1 2 ₁

1 1

3 3 3 3

A = − − − − − − − = − − − − − + 

 

 

(

)

3

(

)

3

1

3 3 2 1 2 _{3 1} 3 3 2 1 2 ₂

3 3 3 3

A = − − − −_− + _= − − − −_− _

   

(

)

3

(

)

3

1

3 3 2 1 2 ₂ 3 3 2 1 2 2

3 3 3

A = − − − + = − − − +

( )

( )

( ) ( )

(

2 3

)

3 2 1

3 3 2 1 3 1 2 3 1 2 2 2

3 A

− − − + − +

=

( )

( ) ( )

2

1

3 3 2 1 3 2 3 2 2 2 2 5 3 2

3

A = − − + − + + = −

1 3 2

− + 6

( )

2

( )

2 3

− +

1

5 1 6 2 2 2 2 2 2 2 2

3 3 3

A = − − + =− + = −

Área 2 AZUL

Podemos observar que el rectángulo típico toca en la parte inferior a

(

)

2

( ) 2 1

f x = − −x y en la parte superior a la función 2

( ) 1

g x = −x y dicho

rectángulo típico recorre el intervalo en el eje equis desde a= −1 2 hasta 0

b= , entonces:

(

)

(

)

0 2 2 2 1 2

1 2 1

A x x dx

−

 

=

_∫

_ − − − − _

(

)

(

)

(

)

0 0

2 2 2 2

2

1 2 1 2

1 2 2 1 1 2 2 1

A x x x dx x x x dx

− −

   

=

_∫

_ − − − − + _ =

_∫

_ − − − + − _

(

)

0 0

2 2 2 2

2

1 2 1 2

1 2 1 1 2 1

A x x x dx x x x dx

− −

   

=

_∫

_ − − − + + _ =

_∫

_ − + − − _

2 1

A = − x2 + x2 −2x−1

(

)

0 0 0 2

1 2 1 2 1 2

0

2 2 2

2

1 2

x

dx x dx xdx

− − −       _{= − = − = −  }    ₋   

∫

∫

∫

(

)

2

2 2 1 2 0 2 2 2 2 A  ₋    = − _ − _=    

(

)

2

1 2

2

−

(

)

2

( )

2

1 2 1 2 2 2

 

 _{= − = − +}

 

 

 

2 1 2 2 2 3 2 2

A = − + = −

Área 3 ROJA

Podemos observar que el rectángulo típico toca en la parte inferior a 2

( ) 1

g x = −x y en la parte superior a la función f x( )= − −2

(

x 1

)

2 y dicho rectángulo típico recorre el intervalo en el eje equis desde a=0 hasta b=1, entonces:

(

)

(

)

1 2 2 3 0

2 1 1

A =

∫

_ − −x − −x _dx

Resolviendo esta integral:

(

)

1 1

2 2 2 2

3

0 0

2 2 1 1 2 2 1 1

A =

∫

_ − x − x+ − +x _dx=

∫

_ − +x x− − +x _dx

3 2

A = − x2 +2x−1−1+ x2

( )

1 1

0 0

2 2

dx x dx

  _{= =}

 

∫

∫

x₂2 1 2 1 2 2

1 0 1 0 1

0=x 0= − = − =

Área 4 GRIS

Podemos observar que el rectángulo típico toca en la parte inferior a

0

y= y en la parte superior a la función f x( )= − −2

(

x 1

)

2 y dicho rectángulo típico recorre el intervalo en el eje equis desde a=1 hasta b= +1 2, entonces:

(

) ( )

1 2

2 4

1

2 1 0

A x dx

+

 

=

_∫

_ − − − _

(

)

1 2 1 2 1 2

2 2 2

4

1 1 1

2 2 1 2 2 1 1 2

A x x dx x x dx x x dx

+ + +

     

=

_∫

_ − − + _ =

_∫

_ − + − _ =

_∫

_ − + _

(

_{) ( )}

3

3 ₂ 3

2 2

4

1 2 ₁

1 2

1 2 1 2 1 1

3 1 3 3

x

A = −x +x + = + − + + + − − +_ _

 

( )

( )

( ) ( )

(

₂ 2 3

)

₍

_{( )}

₎

3

2 2

4

1 3 1 2 3 1 2 2

1

1 2 1 2 2 2 1 1

3 3 A + + + _{ } = + − + + + − − +   

( )

( )

(

2

)

₍

₎

4

1 3 2 3 2 2 2

1

1 2 1 2 2 2 2

3 3 A + + + _{ } = + − + + + − −   

(

_{) ( )}

4

1 3 2 6 2 2 _{6 1}

1 2 3 2 2

3 3

A = + − + + + + + −_ − _

 

(

)

(

)

4

7 3 2 2 2 ₅ 7 5 2 5

4 3 2 4 3 2

3 3 3

A = + − + + − _{ }= + − + −

 

(

)

4

12 9 2 7 5 2 5 ₁₂

3

A = + − + − = +9 2−7 −5 2− 5 4 2

3 = 3

Finalmente el área total es:

1 2 3 4

2 2 2 4 2

3 2 2 1

3 3

T

A = +A A +A +A = − + − + +

2 2 2 4 2 6 2 2 6 2 2 12 6 2 10

4 2 2 4 2 2

3 3 3 3

T

A = − + + − = − + − = − + − =

Respuesta: 10 3 T A=A =

Ejercicio 5

a) Dibuja la región R del plano XY limitada por las curvas de ecuaciones:

(

2

)

3 3

y=x x − +x y=x2

b) Calcula el área de la región R descrita en al parte “a”. Solución

Justificación: En este caso tenemos la gráfica de una función de grado 3,

(

2

)

3 2

3 3 3 3

y=x x − + = −x x x + x y una parábola, por tanto, es recomendable