Después de introducir y trabajar con el Algebra de Boole, vamos a volver a los circuitos

Conalep Tehuacán 150

•

Nombre del Plantel:

Conalep Tehuacán 150

•

Nombre del módulo:

Operación de Circuitos de

Electrónicos

Apunte 4: Circuitos

Combinacionales

•

Ing. Jonathan Quiroga Tinoco

•

Grupo:

309

•

Carrera:

P.T.B. en SOMA

•

Ciclo Escolar:

Capítulo 4

CIRCUITOS COMBINACIONALES

4.1. Introducción

Después de introducir y trabajar con el Algebra de Boole, vamos a volver a loscircuitos digitales. Recordemos que son circuitos electrónicos que trabajan con números, y que con la tecnología con la que están realizados, estos números están representados en binario. En la figura 4.1 se muestra el esquema general de un circuito digital, que tiene m bits de entrada y n bits de salida.

Si tomamos un circuito genérico y miramos en su interior, podemos ver que está constituido por otros circuitos más simples, interconecados entre sí. En la figura 4.2 hay un ejemplo de un circuito con 4 bits de entrada y 3 de salida, constituido por otros dos circuitos más simples e interconectados entre ellos.

Estos subcircuitos se pueden clasificar en dos tipos:

Circuitos combinacionales

Circuitos secuenciales

Numeros de salida, en binario

.

.. ... Numeros de

entrada, en binario

Circuito Ditial E₀ E E E Em 1 2 3 S S S S₀ 1 2 3 Sn

Figura 4.1: Un circuito digital, con m bits de entrada y n de salida

E3

E₂ E1

E0

S₂ S₁

S₀ Circuito 1

Circuito 2

Figura 4.2: Un circuito digital constituido por otros dos circuitos interconectados

Así, podemos decir que todo circuito digital genérico tendrá una parte combinacionaly otra

parte secuencial. En este capítulo nos centraremos en loscircuitos combinacionales, que no tienen parte secuencial.Estos circuitos se caracterizan porque NO almacenan información. Las salidas están relacionadas con las entradas a través de una función booleana, como las vistas en el capítulo 3. Como veremos más adelante, los circuitos secuenciales son capaces de “recordar” números que han recibido anteriormente.

En un circuito combinacional, las salidas dependen directamente del valor de las entradas, y no pueden por tanto almacenar ningún tipo de información, sólo realizan transformaciones en las entradas. Estos circuitos quedan caracterizados mediante funciones booleanas.

Cada bit de salida de un circuito combinacional, se obtiene mediante una función booleana apli-cado a las variables de entrada. Así, si un circuito tiene n salidas, necesitaremos n funciones booleanas para caracterizarlo.

En la figura 4.3 vemos un circuito combinacional que tiene 3 entradas: A,B y C, y dos salidas F, G, que son dos funciones booleanas que dependen de las variables de entrada: F(A,B,C) y G(A,B,C). Por ejemplo, estas funciones podrían tener una pinta así:

Circuito Combinacional B

A C

F(A,B,C) G(A,B,C)

Figura 4.3: Un circuito combinacional de 3 entradas y 2 salidas

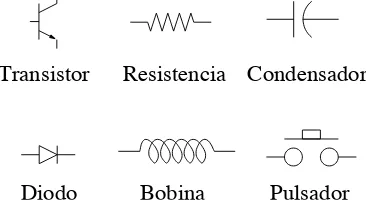
Transistor Resistencia Condensador

Diodo Bobina Pulsador

Figura 4.4: Algunos símbolos empleados en la electrónica analógica

construir estos circuitos, y cómo lasfunciones booleanaslas podemos realizar mediante puertas lógicas, lo que se denominaimplementación de funciones booleanas.

4.2. Puertas lógicas

En todas las ingenierías se utilizanplanosque describen los diseños. En ellos aparecen dibu-jos, letras y símbolos. Mediante estos planos o esquemas, el Ingeniero representa el diseño que tiene en la cabeza y que quiere construir.

Enelectrónica analógicase utilizan distintos símbolos para representar los diferentes compo-nentes: Resistencias, condensadores, diodos, transistores... Algunos de estos símbolos se pueden ver en la figura 4.4.

En electrónica digital se utilizan otros símbolos, los de las puertas lógicas, para representar las manipulaciones con los bits.

4.2.1. Puertas básicas

Puerta AND

A

Esta puerta implementa la operación del Algebra de Boole. La que se muestra en esta figura tiene dos entradas, sin embargo puede tener más. Lo mismo ocurre con el resto de puertas lógicas que veremos a continuación.

Puerta OR

A

B A+B

Implementa la operación + del Algebra de Boole. Puede tener también mas de dos entradas.

Puerta NOT(Inversor)

A A

Tiene sólo una entrada y realiza la operación de negación lógica. Esta puerta se conoce normalmente con el nombre deinversor.

Sólo con estos tres tipos de puertas se pueden implementar cualquier función booleana.

Ejemplo:

Analizar el siguiente circuito y obtener la expresión booleana de la salida:

A B C

F

El circuito está constituido por dos puertas, una AND de tres entradas y un inversor. A la salida de la puerta AND se tiene el producto de las tres variables de entrada y al atravesar el inversor se obtiene la expresión final de F, que es:

Ejemplo:

A B

C

F

El circuito está constituido por dos puertas AND, dos inversores y una puerta OR. La expre-sión de F es:

4.2.2. Otras puertas

Con las puertas básicas podemos implementar cualquier función booleana. Sin embargo exis-ten otras puertas que se utilizan mucho en electrónica digital.

Puerta NAND

A

B A.B

El nombre viene de la abreviación de NOT-AND, y la operación que realiza es la negación de un producto. Aplicando las leyes de DeMorgan vemos que la expresión a su salida es:

Esta puerta también puede tener más de dos entradas.

Las puertas NAND tienen una característica muy importante y es que sólo con ellas se puede implementar cualquier función booleana. Sólo hay que aplicar las propiedades del Algebra de Boole a cualquier expresión booleana para dejarla de forma que sólo existan este tipo de operaciones, como veremos en el apartado 4.3.3

Puerta NOR

A

Es una puerta OR negada (NOT-OR). Aplicando las leyes de DeMorgan:

Lo mismo que con las puertas NAND, con las puertas NOR se puede implementar cual-quier función booleana (ver apartado 4.3.4)

Puerta XOR

A

B A + B

Es la puerta que implementa la operación , definida en el apartado 3.8

Ejemplo:

Analizar el siguiente circuito y obtener la expresión booleana de la salida:

A

B F

A la salida de la puerta NAND tenemos la expresión: , que se introduce en una de las entradas de la puerta NOR, y por la otra B. El resultado es:

y aplicando las leyes de DeMorgan nos queda:

Es decir, que es un circuito nulo. Con independencia de lo que se introduzca por las entradas, a su salida siempre se obtendrá ’0’.

Ejercicios

Figura 4.5: Dos circuitos integrados, junto a una moneda de 1 euro

4.2.3. Circuitos integrados

¿Y si ahora queremos construir un circuito? ¿Cómo lo implementamos físicamente? Las

puertas lógicasse encuentra encapsuladas dentro decircuitos integradoso también conocidos como chips. En la figura 4.5 se muestra una foto de dos de ellos, junto a una moneda de 1 euro para apreciar su tamaño. Más coloquialmente, entre los alumnos, reciben el nombre de “cucarachas”, porque son negros y tienen patas.

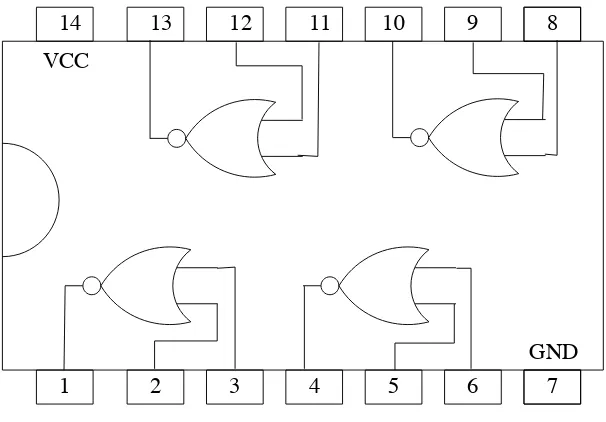
Hay una familia de circuitos integrados,74XX, que está estandarizada de manera que se ha definido la información que entra o sale por cada una de las patas. Así pueden existir multitud de fabricantes, pero todos respectando el mismo estándar. En la figura 4.6 se muestra un esquema del integrado 7402, que contiene en su interior 4 puertas NOR de dos entradas.

Por las patas denominadas VCC y GND se introduce la alimentación del chip, que normal-mente será de 5v, aunque esto depende de la tecnología empleada. Por el resto de patas entra o sale información binaria codificada según la tecnología empleda. Por ejemplo se puede asociar 5v al dígito ’1’ y 0v al dígito ’0’.

1 2 3 4 5 6 7 8 9

11 12

13

14 10

GND VCC

Figura 4.6: Esquema del integrado 7402

impreso, o por sus siglas en inglésPCB(printed circuito Board). En la figura 4.7 se muestra la parte inferior de una de estas placas. Por los agujeros se introducen las patas de los componentes y luego se sueldan. Los distintos agujeros están interconectados por pistas de cobre. Además existe una capa de un barniz verde para que las pistas no estén “al aire” y se puedan producir cortocircuitos.

4.2.4. Otras tecnologías

La electrónica ha avanzado muchísimo y en los chips en los que antes sólo se podían integrar una pocas puertas lógicas, ahora se pueden integrar muchísimas más. De esta manera, los chips tradicionalmente se han clasificado según el número de puertas que pueden integrar. Así tenemos la siguienteclasificación de chips:

SSI(Small Scale Integration). Chips con menos de 12 puertas

MSI(Medium Scale Integration). Entre 12 y 100 puertas.

LSI(Large Scale Integration). Entre 100 y 10.000 puertas.

VLSI(Very Large Scale Integration). Más de 10.000 puertas

Figura 4.7: Una placa de circuito impreso (PCB) vista desde abajo

con un microprocesador o microcontrolador yprogramarlos. Es decir, hacersoftwareen vez de

hardware.

Sin embargo, existen otras manera de implementar circuitos digitales sin utilizar los chips tradicionales, es decir, sin tener que recurrir a los chips de la familia 74XX. Esta nueva for-ma de diseñar se denominalógica programable. Existen unoscircuitos integrados genéricos

(PALs,GALs, CPLDs,FPGAS), que contienen en su interior muchas puertas lógicas y otros com-ponentes. El diseñador especifica los circuitos digitales que quiere diseñar utilizando un lengua-je de descripción hardware(Como por ejemplo el VHDL). Un herramienta software, conocida como sintetizador, convierte esta descripción en un formato que indica cómo se deben inter-conectar los diferentes elementos de este chip genérico. El chip “se configura” (es decir, realiza conexiones entre sus elementos internos) según se indica en el fichero sintetizado, de manera que

¡¡¡¡nuestra descripción del hardware se ha convertido en un circuito que hace lo que hemos indicado!!!!

¡¡¡Con esta técnica se pueden diseñar desde circuitos simples hasta microprocesadores!!! El hardware está siguiendo la misma tendencia que el software. Los diseñadores de ahora utilizan sus propios “lenguajes de programación” para especificar el hardware que están diseñando.

hardware, los conocimientos aquí adquiridos sirvan para ambos casos.

4.3. Diseño de circuitos combinacionales

4.3.1. El proceso de diseño

En Ingenieríase entiende pordiseñar el proceso por el cual se obtiene el objeto pedido a partir de unas especificaciones iniciales. Cuando diseñamos circuitos combinaciones, estamos haciendo lo mismo. Partimos de unas especificaciones iniciales y obtenemos unesquema, o pla-no, que indica qué puertas básicas u otros elementos hay que utilizar así como la interconexión que hay entre ellos.

Los pasos que seguiremos para el diseño son los siguientes:

1. Estudio de las especificaciones iniciales, para entender realmentequées lo que hay que diseñar. Este punto puede parecer una trivialidad, sobre todo en el entorno académico don-de las especificaciones son muy claras. Sin embargo, en la realidad, es muy difícil llegar a comprender o entender qué es lo que hay que diseñar.

2. Obtención de las tablas de verdad y expresiones booleanas necesarias. En el entorno académico este suele ser el punto de partida. Nos describen qué función es la que se quiere implementer y lo hacemos.

3. Simplificación de las funciones booleanas. ¡¡¡Este punto es importantísimo!!! No basta con implementar una función y ya está. ¡¡Somos ingenieros!!.Hay que implementar la mejor función, de manera que obtengamos el mejor diseño posible, reduciendo el número de puertas lógicas empleadas, el número de circuitos integrados o minimizando el retraso entre la entrada y la salida.

4. Implementación de las funciones booleanas utilizando puertas lógicas. Aquí podemos tener restricciones, como veremos. Puede ser que por especificaciones del diseño sólo se dispongan de puertas tipo NAND. O puede ser que sólo podamos utilizar puertas lógicas con el mínimo número de entradas. En ese caso habrá que tomar la función más simplifica-da y modificarla para asimplifica-daptarla a este tipo de puertas. El resultado de esto es la obtención de un esquema o plano del circuito.

físicamente el diseño. Esto se estudia en el laboratorio de esta asignatura, utilizando tec-nología TTL.

En este apartado veremos el punto 4, es decir, veremos cómo a partir de una función (que ya está simplificada) podemos obtener el circuito correspondiente, o cómo la podemos modificar para utilizar un tipo determinado de puertas lógicas.Esto se denomina implementar una función.

4.3.2. Implementación de funciones con cualquier tipo de puertas

El proceso es muy sencillo. Sólo hay que tomar la función que queremos implementar e ir sustituyendo las operaciones del Algebra de Boole por sus correspondientes puertas lógicas. Y como siempre, lo mejor es ver un ejemplo.

Ejemplo 1:

Implementar la siguiente función, utilizando cualquier tipo de puertas lógicas:

Se trata de implementar un circuito que tiene tres bits de entrada: A, B y C y como salida se quiere obtener la función F indicada. Se puede realizar de muchas formas, pero vamos a ir poco a poco. Primero nos fijamos que no tenemos ninguna restricción. Es decir, en el enunciado nos permiten utilizar cualquier tipo de puerta lógica, y con cualquier número de entradas. Tampoco vamos a simplificar la función, porque lo que queremos es ver cómo implementarla, aunque ya hemos visto que siempre hay que simplificar!!! (y de hecho, esta función se puede simplificar más, ¿como?, se deja como ejercicio). Vemos que en la función hay tres términos que van suma-dos: , , y . La puerta lógica que representa la suma es la OR, por lo que podemos escribir:

BC ABC

F A

C B C

B

El término lo obtenemos directamente a partir de un inversor:

C C

Para obtener el término , que es el último que nos falta, nos fijamos que es un producto de tres elementos, por lo que usaremos una puerta AND de tres entradas:

ABC B

A

C

y finalmente para obtener y usamos un par de inversores:

B A

B A

y ahora unimos todas las pierzas para obtener el circuito final:

Ejemplo 2:

Implementar la siguiente función, utilizando el menor número posible de puertas lógi-cas de cualquier tipo. La función está simplificada al máximo.

En este caso nos dicen que la función está simplificada al máximo, por lo que no hay que hacer. ¡¡¡Pero es una pregunta que siempre nos tendremos que hacer!! ¿Está simplificada al má-ximo?. También nos introducen una restricción: usar el menor número posible de puertas lógicas. Lo primero que se nos puede ocurrir es utilizar el método del ejemplo anterior, sustituyen-do las operaciones del Algebra de Boole por puertas lógicas. El circuito que obtenemos es el siguiente:

D C B A

F

Hemos utilizo las siguientes puertas lógicas:

4 inversores

2 puertas AND de dos entradas

1 puerta OR de cuatro entradas

La expresión de F que nos queda es la siguiente:

y si ahora implementamos el circuito:

A B C D

F

¡¡Sólo hemos utilizado 3 puertas!!. Una puerta NAND, una XOR y una OR, todas de dos entradas.

Ejercicios:

Hacer el ejercicio 2

4.3.3. Implementación de funciones con puertas NAND

Sólo con las puertas NAND es posible implementar cualquier función boolena. Para ello ha-brá que hacer transformaciones en la función original para obtener otra función equivalente pero que se pueda obtener sólo con puertas NAND. Para ver cómo podemos hacer eso, implementa-remos las puertas NOT, AND, OR y XOR usando sólo puertas NAND.

Para refrescar ideas, a continuación se muestra una puerta NAND de dos entradas y las formas de expresar el resultado:

A

B A.B = A+B

Implementación de una puerta NOT

Gráficamente:

A.A = A A

Tenemos un circuito por el que si introducimos una variable A, obtenemos a la salida su complementario , es decir, se comporta exactamente igual que un inversor.

Implementación de una puerta AND

Tenemos que diseñar un circuito con puertas NAND que implemente la función . Lo que haremos será aplicar propiedades del Algebra de Boole a esta función hasta dejarla de forma que la podamos implementar directamente con puertas NAND. Podemos hacer lo siguiente:

La expresión se implementa con una puerta NAND y la expresión será por tanto la negación de la NAND. Como ya sabemos como negar utilizando una puerta NAND, el circuito resultante es:

A B

A.B

A.B

Implementación de una puerta OR

La función que queremos implementar con puertas NAND es: . Aplicando pro-piedades del Algebra de Boole, esta expresión la convertimos en la siguiente:

A

B

A

B

A.B = A+B

Implementación de una puerta XOR

La función a implementar con puertas NAND es: . Podemos

modificarla de la siguiente manera:

No nos dejemos asustar por aparente complejidad de esta expresión. Fijémonos en que la expresión es la suma de dos términos negados, es decir, que tiene la forma de: . ¡¡Y esto es una puerta NAND!!, que lo podemos poner de la siguienet manera:

A.B A.B

F

El término tiene también la forma de una puerta NAND, puesto que es del tipo . Y lo mismo le ocurre al término . El circuito nos queda así:

A.B

F A

B A

B _A.B

A.B A

B

F

A.B B

A A

B

Ya tenemos implementada la función XOR sólo con puertasn NAND.

Ejemplo 1:

Implementar la siguiente función utilizando únicamente puertas NAND. La función está sim-plificada al máximo:

Tendremos que aplicar la propiedades del Algebra de Boole para dejar esta expresión de forma que la podamos implementar con puertas NAND. Como el enunciado no nos pone ninguna restricción, podremos usar puertas NAND con el número de entradas que queramos. Una puerta NAND de tres entradas puede realizar las siguientes operaciones:

Si aplicamos una doble negación a F y luego aplicamos sucesivamente las leyes de DeMorgan (o el teorema de Shannon):

A

C

B F

Ejemplo 2:

Implementar la siguiente función utilizando sólo puertas NAND de 2 entradas:

Es la misma función que la del apartado anterior, sin embargo, ahora tenemos la restricción de que sólo podemos usar puertas NAND de dos entradas. Si hacemos la misma transformación que antes, obtenemos:

que tiene la forma y que se implementa fácilmente con una NAND de dos entra-das:

F A+B+C

A+B+C

El problema ahora es cómo implementar los términos y . Vamos con el primero de ellos. Se puede escribir también de la siguiente forma (aplicando el “truco” de la doble negación):

A+B+C BC

A

El otro término lo podemos implementar de forma similar:

A+B+C AB

C

y ahora juntando todas las piezas e implementando lo que falta:

B A

C

F

Ejercicios:

Hacer el ejercicio x

4.3.4. Implementación de funciones con puertas NOR

Lo mismo que con las puertas NAND, con las puertas NOR se puede implementar cualquier función booleana. Vamos a ver cómo se pueden implementar el resto de puertas lógicas. Recor-demos que las expresiones a las salidas de las puertas NOR son:

A

Implementación de una puerta NOT

Se hace de la misma manera que con las puertas NAND. Si introducimos la misma variable por las dos entradas, obtenemos la variable negada:

A+A = A A

Implementación de una puerta OR

La función a implementar es: . Esta expresión la podemos poner de la siguente manera:

es decir, que podemos utilizar una puerta NOR y luego un inversor, que ya sabemos cómo implementarlo con puertas NOR. Lo que nos queda es:

A+B A

B A+B

Implementación de una puerta AND

La función a implementar es: . Podemos realizar las siguientes modificaciones para que pueda ser implementada con puertas NOR:

Y el circuito quedaría así:

A

B

A

B

Implementación de una puerta XOR

La función a implementar es: . Haciendo las siguientes modificaciones:

y de la misma manera que hemos hecho con las puertas NAND, vamos a ir implementando esta función poco a poco. Primero vemos que hay una puerta NOR cuyas entradas son y

, y que está negada:

A.B+A.B A.B

A.B F

A continuación implementamos y , teniendo en cuanta que los podemos reescribir de esta forma:

Gráficamente:

A.B A.B B

A

A B

A

B A.B+A.B

A.B A.B A B

F

Hemos implementado la puerta XOR sólo con puertas NOR.

Ejercicios:

Hacer el ejercicio x

4.4. Aplicación: Diseño de un controlador para un robot

se-guidor de línea

4.4.1. Introducción

En este apartadodiseñaremos un circuito digital que gobierne el comportamiento de un robot seguidor de línea. El objetivo es que el alumno vea cómo todo lo aprendido hasta ahora se puede aplicar, y obtener también algo de intuición sobre el tipo de circuitos digitales que se pueden diseñar.

Este apartado es opcional. El lector no interesado puede saltar directamente al apartado 4.6. Sin embargo los alumnos inquietos pueden utilizarlo de base para introducirse en el mundo de la robótica y de la electrónica digital práctica, para ver cómo se puede hacer un proyecto real.

Figura 4.8: El microbot Tritt

En la figura 4.9 se muestra el mismo microbot Tritt pero sin la tarjeta CT6811 que lleva el microcontrolador 6811. En vez de ella diseñaremos nuestro propio “cerebro digital”.

4.4.2. Especificaciones

Las especificaciones son:

Objetivo: Diseñar un circuito digital, capaz gobernar un microbot, haciendo que éste siga una línea negra pintada sobre un fondo blanco.

Sensores: El microbot está dotado de dos sensores digitales capacez de diferenciar el color negro del blanco. La salida de estos sensores es ’0’ cuando leen blanco y ’1’ cuando leen negro. Denominaremos a este bit comoC:

Sensor C

Color Blanco 0 Color Negro 1

Figura 4.9: Microbot Tritt sin la tarjeta CT6811

P S Motor

0 0 Parado

0 1 Parado

1 0 Giro derecha 1 1 Giro izquierda

El bit P es el bit de ’Power’. Indica si el motor está conectado o no. El bit S es el del sentido de giro. Según su valor el motor girará a la derecha o a la izquierda (siempre que el motor esté activado, con P=1).

Sensor 1 Sensor 2

Motor 1 Motor 2 Ruedas

Algoritmo: El algoritmo para seguir la línea negra es muy sencillo. Mientras los dos senso-res detecten negro, el robot deberá avanzar. Cuando el sensor de la derecha detecte blanco y el de la izquierda negro, el robot girará a la izquierda y cuando ocurra el caso contrario gi-rará a la derecha. Si ambos sensores leen blanco permanecerá parado. Esto se esquematiza en la siguiente figura:

Recto Giro izquierda Giro derecha

4.4.3. Diagrama de bloques

Como primera fase del diseño tenemos que entender qué es lo que se nos está pidiendo y determinar el aspecto que tiene el circuito que hay que realizar. El circuito tendrá dos entradas provenientes de los sensores, y , y cuatro salidas, dos para cada motor: , , y :

Sensor 2 Sensor 1

Circuito a diseñar

S P 1 1 S P 2 2 C₁

C2

Motor 1

4.4.4. Tabla de verdad

Ahora hay que definir el comportamiento del circuito, utilizando una tabla de verdad. Este comportamiento nos lo da el algoritmo de seguir la línea. La tabla de verdad es la siguiente:

0 0 x 0 x 0

0 1 0 1 1 1

1 0 1 1 0 1

1 1 0 1 0 1

Con una ’x’ se han marcado las casillas de la tabla de verdad que es indiferente su valor. Según nos convenga puede valer ’0’ ó ’1’.

4.4.5. Ecuaciones booleanas del circuito

Puesto que el circuito sólo tiene 2 variables de entrada, es inmediato obtener las expresiones

de , , y .

También se podría haber hecho Karnaugh:

P1 S1

C1

C₂ 0 0 1

1 C1

C₂ 0 0 1 1 S2 C1 C₂ 0 0 1 1 0 1 1

1 1 0

0 x

x 1

4.4.6. Implementación del circuito

El circuito, implementado con puertas lógicas básicas es el siguiente:

S₁

S₂

P2

P₁ C1

C2

Si lo construimos utilizando puertas TTL, necesitamos dos integrados, uno para los inversores y otro para la puerta OR. Si en vez de ello lo implementamos sólo con puertas NAND, el circuito es el siguiente:

C1

C2

S₁

S2

P1

P₂

Tiene también 3 puertas, pero ahora sólo es necesario un sólo circuito integrado.

4.5. Análisis de circuitos combinacionales

tabla. Iremos rellenando el valor de estos puntos intermedios hasta obtener el valor de la función. Y como siempre, lo mejor es ver ejemplos.

Ejemplo 1:

Obtener la tabla de verdad del siguiente circuito:

B A C

F

El problema se puede hacer de varias maneras. Y ese suele ser uno de los problemas. ¿Qué camino escojo para obtener la tabla de verdad?. Por un lado podemos obtener la expresión de F, pasando las puertas lógicas a operandos del Algebra de Boole y luego obtener la tabla de verdad. O podemos obtener directamente la tabla de verdad. Sea cual sea el camino elegido, lo primero que haremos será tomarpuntos intermedios:seleccionamos las salidas de las puertas lógicas y les asignamos una variable boolena:

B A C

F a

b

En este circuito hemos tomado dos puntos intermedios, ela y elb. Si decidimos obtener F usando el Algebra de Boole, la expresión que obtenemos es:

obtener la tabla de verdad directamente del diseño y luego aplicar karnaugh para obtener la expresión más simplificada de F, si fuese necesario. En la tabla de verdad dibujaremos nuevas columnas en las que aparecen los puntos intermedios, que nos permitirán ir anotando los cálculos intermedios para obtener F más fácilmente. La tabla de verdad sin rellenar es:

A B C

0 0 0

0 0 1

0 1 0

0 1 1

1 0 0

1 0 1

1 1 0

1 1 1

Y ahora vamos columna por columna, rellenando la información. Comenzaremos por la co-lumnaa. Hay que hacer la NAND de B y C. Para no confundirnos, nos dibujamos la tabla NAND para dos variables:

A B

0 0 0 1

0 1 0 1

1 0 0 1

1 1 1 0

y nos fijamos en que sólo vale ’0’ cuando ambas variables son 1. Recorremos las filas de B y C buscando el caso en el que B=1 y C=1, y anotamos un ’0’. Para el resto de casos a=’1’. Nos queda lo siguiente:

A B C

0 0 0 1

0 0 1 1

0 1 0 1

0 1 1 0

1 0 0 1

1 0 1 1

1 1 0 1

Se ha marcado con “negrita” los dos casos en los que B=1 y C=1. Para el resto de casos “no hemos tenido que pensar”, se puede rellenar de forma directa. Este método nos permite obtener las tablas de verdad de una manera muy rápida y cometiendo muy pocos errores.

Contiemos con la siguiente columna. En este caso hay que rellenar una columna con el pro-ducto entre B y A. Nuevamente nos fijamos en la tabla de la operación AND y vemos que el resultado sólo vale ’1’ cuando B=1 y A=1. Para el resto de casos se tendrá ’0’:

A B C

0 0 0 1 0

0 0 1 1 0

0 1 0 1 0

0 1 1 0 0

1 0 0 1 0

1 0 1 1 0

1 1 0 1 0

1 1 1 0 1

Y por último ya podemos obtener el valor de F, aplicando una operación OR a la columna

a con la b. Por la definición de la operación OR (mirando su tabla), sabemos que sólo vale 0 cuando ambos operandos son ’0’. Buscamos ese caso en la tabla y en el resto de filas ponemos un ’1’. La tabla final es:

A B C

0 0 0 1 0 1

0 0 1 1 0 1

0 1 0 1 0 1

0 1 1 0 0 0

1 0 0 1 0 1

1 0 1 1 0 1

1 1 0 1 0 1

1 1 1 0 1 1

1 1 1 1 1 00 01 11 10 0

1 A

BC

0 1 1

Podemos hacer los siguientes grupos:

1 1 1 1 1 00 01 11 10 0

1 A

BC

0 1 1

De los que obtenemos la expresión más simplificada de F:

Vemos que está más simplificada que la expresión inicial que obtuvimos aplicando el Algebra de Boole.

4.6. Resumen

Todo circuito digitalestá constituido en su interior porcircuitos combinacionalesy/o cir-cuitos secuenciales. Estos últimos son capaces de almacenar información. En este capítulo he-mos trabajado con circuitos combinaciones, en los que sus salidas dependen directamente de las entradas, y no son capaces de almacenar información ni recordar cuáles fueron las entradas anteriores.

Para la construcción de los circuitos combinacionales, se emplean las puertas lógicas, que permiten realizar electrónicamente las operaciones del Algebra de Boole. Las puertas lógicas básicas con AND, ORy NOT, pero también existen otras puertas lógicas que se usan mucho:

NAND,NORyXOR. Cualquier circuito combinacional se puede construir a partir de las puertas básicas, combinándolas adecuadamente. Sin embargo, también es posible implementar circuitos utilizando sólopuertas NAND, o sólopuertas NOR.

tecnología TTL. También es posible utilizar otras tecnologías para la construcción de circuitos digitales, como son los dispositivos lógicos programables o las FPGA’s.

El diseño de un circuito combinacional es sencillo. A partir de unas especificaciones se obtiene latabla de verdadde las salidas del circuito, y utilizando el método de simplificación deKarnaughobtendremos lafunción más simplificada. Las funciones así obtenidas se podrán implementar de diversas maneras, entre las que hemos visto, su implementación usando puertas básicas, sólo puertas NAND, o sólo puertas NOR.

Como ejemplo práctico, hemos diseñado un circuito combinacional que actúa de “cerebro” de un Microbot, controlándolo de manera que siga una línea negra sobre un fondo blanco.

Finalmente hemos visto cómo se analizanlos circuitos, obteniendo sus tablas de verdad o ecuaciones booleanas a partir de las puertas lógicas.

4.7. Ejercicios

Ejercicio 1:

Obtener las expresiones booleanas de las salidas de los siguientes circuitos (no hay que sim-plificar ni operar estas expresiones):

Circuito 1:

F C

B A

D

A B C D E

F

Circuito 3:

A B C D E

F

Ejercicio 2:

Implementar las siguientes función, utilizando cualquier tipo de puertas lógicas, sabien-do que todas las funciones están simplificadas al máximo.

1.

Ejercicio 2:

Implementar sólo con puertas NAND

Ejercicio 3:

Implementar sólo con puertas NOR

Ejercicio x:

Dada la función :

2. Implementar sólo con puertas NAND

3. Implementar sólo con puertas NOR

4. Aplicar la propiedad distributiva e implementar con cualquier tipo de puertas lógicas

C O M P U E R T A S L Ó G I C A S

D E F I N I C I O N E S :

C i r c u i t o s d i g i t a l e s e l e c t r ó n i c o s . S e l l a m a n c i r c u i t o s l ó g i c o s , y a q u e c o n l a s e n t r a d a s a d e c u a d a s e s t a b l e c e n c a m i n o s d e m a n i p u l e o l ó g i c o .

C o m p u e r t a. E s u n b l o q u e d e c i r c u i t e r i a q u e p r o d u c e s e ñ a l e s d e s a l i d a l ó g i c a ( ” 1 ” ó “ 0 ” ) s i s e s a t i s f a c e n l a s c o n d i c i o n e s d e l a s e n t r a d a s l ó g i c a s . L o s n o m b r e s , c i r c u i t o s d i g i t a l e s , c i r c u i t o s d e c o n m u t a c i ó n , c i r c u i t o s l ó g i c o s y c o m p u e r t a s s o n u s a d o s a m e n u d o p e r o s é h a r á r e f e r e n c i a a l o s c i r c u i t o s c o n c o m p u e r t a s .

T a b l a d e v e r d a d. E s u n a r e p r e s e n t a c i ó n e n f o r m a t a b u l a r d e t o d a s l a s c o m b i n a c i o n e s p o s i b l e s d e l a s v a r i a b l e s d e e n t r a d a .

U s o s . - C u a l q u i e r i n f o r m a c i ó n u s a d a p a r a c a l c u l a r o c o n t r o l a r , p u e d e s e r o p e r a d a p a s a n d o s e ñ a l e s b i n a r i a s a t r a v é s d e v a r i a s c o m b i n a c i o n e s d e c i r c u i t o s l ó g i c o s c o n c a d a s e ñ a l q u e r e p r e s e n t a u n a v a r i a b l e y t r a n s p o r t a u n b i t d e i n f o r m a c i ó n . D e f i n i m o s c o m o b i t l o s “ 1 ” ó “ 0 ” q u e p u e d e t o m a r u n a v a r i a b l e b i n a r i a .

L ó g i c a b i n a r i a . E x i s t e n t r e s o p e r a c i o n e s b i n a r i a s b á s i c a s : A N D , O R y N O T .

A N D . ( “ Y ” ): E s t a o p e r a c i ó n s e r e p r e s e n t a p o r u n p u n t o , u n a s t e r i s c o ó p o r u n a a u s e n c i a d e o p e r a d o r . X * Y = Z , l e í d o “ X y Y e s i g u a l a Z ” , i m p l i c a q u e Z = 1 s í y s o l o s í X = 1 y Y = 1 .

O R . ( “ O ” ): E s t a o p e r a c i ó n s e r e p r e s e n t a p o r e l s i g n o + . P o r e j e m p l o : X + Y = Z . S e l e e “ X o Y e s i g u a l a Z ” , q u e q u i e r e d e c i r q u e Z = 1 s í y s o l o s í X = 1 o Y = 1 o a m b a s .

N O T . ( “ I n v e r s o r ” ) : E s t a o p e r a c i ó n s e r e p r e s e n t a p o r u n a p ó s t r o f e ( ´ ) ( a l g u n a s v e c e s p o r u n a b a r r a ) . P o r e j e m p l o : X ´ = Z ( ó X = Z ) s e l e e “ n o X i g u a l a Z ” . E s d e c i r e n o t r a s p a l a b r a s , s í X = 1 e n t o n c e s Z = 0 , p e r o s í X = 0 e n t o n c e s Z = 1 .

L a l ó g i c a a r i t m é t i c a s e p a r e c e a l a a r i t m é t i c a b i n a r i a ( y a q u e l a s o p e r a c i o n e s A N D y O R t i e n e n s i m i l i t u d c o n l a m u l t i p l i c a c i ó n y l a s u m a r e s p e c t i v a m e n t e ) . P e r o n o c o n f u n d i r , u n a v a r i a b l e a r i t m é t i c a d e s i g n a u n n ú m e r o q u e p u e d e c o n s i s t i r e n m u c h o s v a l o r e s , m i e n t r a s q u e u n a v a r i a b l e l ó g i c a s i e m p r e e s 1 ó 0 .

E j e m p l o :

V a r i a b l e a r i t m é t i c a : 1 + 1 = 2 . L e í d o : u n o m á s u n o i g u a l a d o s . V a r i a b l e l ó g i c a : 1 + 1 = 1 . L e í d o : u n o O R u n o e s i g u a l a 1 .

T I P O S D E C O M P U E R T A S .

C O M E N T A R I O :

D I A G R A M A D E T I E M P O . E s l a r e p r e s e n t a c i ó n g r á f i c a d e l a s s e ñ a l e s d e e n t r a d a a l a c o m p u e r t a , e n l a c u a l s e i n c l u y e n t o d a s l a s c o m b i n a c i o n e s p o s i b l e s .

C O M E N T A R I O : E l c í r c u l o a l a s a l i d a d e l i n v e r s o r i m p l i c a u n c o m p l e m e n t o l ó g i c o ó n e g a c i ó n .

B U F F E R F = X X F 0 0 1 1

N O T A : U n b u f f e r e s u n a c o m p u e r t a q u e p u e d e a b s o r b e r m á s c o r r i e n t e q u e c u a l q u i e r p u e r t a c o n v e n c i o n a l y s e u t i l i z a c u a n d o s e r e q u i e r e u n a b a n i c o d e s a l i d a m a y o r q u e e l h a b i t u a l .

E n e s t e c i r c u i t o e x i s t e f u n c i ó n d e t r a n s f e r e n c i a p e r o n o h a y c a m b i o e n l a s e ñ a l d e e n t r a d a ( F = X ) . E s t e c i r c u i t o e s u s a d o s o l a m e n t e p a r a a m p l i f i c a c i ó n d e s e ñ a l d e p o t e n c i a , y e s t e e s e q u i v a l e n t e a c o n e c t a r d o s i n v e r s o r e s e n c a s c a d a .

S E P A R A D O R

( c t o . d e t e r c e r e s t a d o )

C O M E N T A R I O : L a f u n c i ó n N A N D e s e l c o m p l e m e n t o d e l a f u n c i ó n A N D y s u s í m b o l o e s e l d e l a c o m p u e r t a A N D a n e x á n d o l e u n c i r c u i t o a l a s a l i d a .

L a f u n c i ó n N O R e s e l c o m p l e m e n t o d e l a f u n c i ó n O R .

N O T A : L a s c o m p u e r t a s N A N D y N O R , s o n l a s m a s u s a d a s ( l l a m a d a s c o m p u e r t a s u n i v e r s a l e s ) , y a q u e b a s á n d o s e e n é s t a s s e p u e d e c o n s t r u i r c u a l q u i e r c i r c u i t o l ó g i c o .

C O M E N T A R I O S : L a c o m p u e r t a N O R - E X C L U S I V A ( X N O R ) e s e l c o m p l e m e n t o d e l a c o m p u e r t a X O R .

F = ( X .Y+ X . Y ) ’

F = ( X .Y) ’ . ( X . Y ) ’ F = ( X +Y) . ( X +Y) F = ( X + Y ) . ( X +Y)

F = X . X + X .Y+ Y . X + Y .Y

F = X .Y + Y . X

C O M P U E R T A S C O N V A R I A S E N T R A D A S .

U n a c o m p u e r t a p u e d e e x p a n d i r s e a m ú l t i p l e s e n t r a d a s s i l a o p e r a c i ó n b i n a r i a q u e r e p r e s e n t a e s c o n m u t a t i v a y a s o c i a t i v a .

X + Y = Y + X C o n m u t a t i v a

( X + Y ) + Z = X + ( Y + Z ) = X + Y + Z A s o c i a t i v a

Compuerta NAND de 3 entradas

Compuerta Y (NAND)

Compuerta NOR de 3 entradas

O

Compuerta (NOR)

1 2 3

4 1

2

3

1

2 3

1 2

3 4

L a s c o m p u e r t a s N O R y N A N D n o c u m p l e n l a l e y a s o c i a t i v a , e s d e c i r ,

( ( x + y ) ´ + Z ) ´ = ( X + ( Y + Z ) ´ ) ´

n o s e c u m p l e l a i g u a l d a d .

P o r l o t a n t o p a r a i m p l e m e n t a r c o m p u e r t a s N O R ó N A N D , d e v a r i a s e n t r a d a s s e u s a n c o m p u e r t a s A N D Y O R y l u e g o s e i n t r o d u c e u n i n v e r s o r .

L a s c o m p u e r t a s O R – E X C L U S I V A S y s u e q u i v a l e n c i a s o n a m b a s , c o n m u t a t i v a s y a s o c i a t i v a s y p u e d e e x t e n d e r s e a m á s d e d o s e n t r a d a s .

O b s e r v a c i o n e s :

1 . - L a c o m p u e r t a X O R n o r m a l m e n t e o p e r a c i ó n s e r e p r e s e n t a A m a s e l s i g n o d e s u m a e n c e r r a d o e n u n c í r c u l o y l a s e g u n d a v a r i a b l e B .

2 . - L o s v a l o r e s d e l a s c o m p u e r t a s e n f a m i l i a C M O S s e d a n e n l a s i g u i e n t e t a b l a .

N o m b r e N o . D e P a r t e

A N D 4 0 8 1

O R 4 0 7 1

N O T 4 0 6 9

B U F F E R 4 0 4 9

N A N D 4 0 1 1

N O R 4 0 0 1

X O R 4 0 3 0 , 4 0 7 0

X N O R -

O B T E N C I O N D E L A I N F O R M A C I O N D E U N A T A B L A D E V E R D A D

P a r a S a c a r l a i n f o r m a c i ó n c o n t e n i d a e n c u a l q u i e r t a b l a d e v e r d a d , e l m é t o d o d e S h a n n o n , e s t a b l e c e q u e :

1 . S i e l r e s u l t a d o s e o b t i e n e e n f u n c i ó n d e l o s u n o s d e l a t a b l a , e s t a t a b l a t e n d r á l a f o r m a d e d i s y u n c i ó n d e c o n j u n c i o n e s ( s u m a d e p r o d u c t o s ) . C a d a c o n j u n c i ó n i n c l u i r á l a s v a r i a b l e s c o n e l v a l o r q u e t i e n e l a t a b l a .

2 . S i l a f u n c i ó n s e o b t i e n e a p a r t i r d e l o s c e r o s d e l a t a b l a , e s t a t e n d r á l a f o r m a d e c o n j u n c i ó n d e d i s y u n c i o n e s ( p r o d u c t o s d e s u m a ) . C a d a d i s y u n c i ó n i n c l u i r á l a s v a r i a b l e s c o n e l v a l o r c o n t r a r i o a l q u e t i e n e l a t a b l a .

E j e m p l o : O b t e n g a l a i n f o r m a c i ó n d e l a s s i g u i e n t e s t a b l a s d e v e r d a d . a )

> D i s y u n c i ó n d e c o n j u n c i o n e s ( “ 1 ” ) F = A * B

* C o n j u n c i ó n d e d i s y u n c i o n e s ( “ 0 ” ) F = ( A + B ) . ( A + B) . ( A+ B )

b )

D i s y u n c i ó n d e c o n j u n c i o n e s F = A. B + A .B

C o n j u n c i ó n d e d i s y u n c i o n e s F = ( A + B ) . ( A+ B)

D e m u e s t r e q u e l a f u n c i ó n d e d i s y u n c i ó n d e c o n j u n c i o n e s e s l a m i s m a q u e l a c o n j u n c i ó n d e d i s y u n c i o n e s .

a ) ( A + B ) . ( A + B) . ( A+ B ) = A . B

( A . A + A .B+ B . A + B .B) . ( A+ B ) = A . B ( A + A . B+ B . A ) . ( A+ B ) = A . B

A . ( 1 + B+ B ) . ( A+ B ) = A . B A . ( A+ B ) = A . B

A . A+ A . B ) = A . B A . B = A . B

b ) A * B B * A A * B B * A B * A B * A B * B A * B B * A A * A B * A B * A ) B A ( * ) B A ( F

S i m p l i f i q u e e l s i g u i e n t e c i r c u i t o l ó g i c o :

F = ( X +Z) . ( Y . X + X . Z ) + ( X . Z +Z) .Z. Y

F = ( X . Y . X + X . X . Z +

Z

Z

F = X . Y ( 1 +

Z

T e c n o l o g í a s d e C i r c u i t o s I n t e g r a d o s

A p l i c a c i ó n :

M i l i t a r .

I n d u s t r i a l o C i e n t í f i c a . C o m e r c i a l .

F a m i l i a d e c i r c u i t o s i n t e g r a d o s p o r a p l i c a c i ó n :

1 . - Ci r c u i t o s In t e g r a d o s No Li n e a l e s . 2 . - Ci r c u i t o s In t e g r a d o s Di g i t a l e s .

a ) F a m i l i a d e C . I . T T L ( 7 4 / 5 4 X X # # # )

L a f a m i l i a T T L e s Ló g i c a T r a n s i s t o r y Tr a n s i s t o r ; e n e s t a f a m i l i a l o s t r a n s i s t o r e s s e u t i l i z a n c o m o i n t e r r u p t o r e s .

C A R A C T E R I S T I C A S : S o n m á s r á p i d o s q u e l o s C M O S .

D E S V E N T A J A S : C o n s u m e n m u c h a e n e r g í a

R E Q U E R I M I E N T O S D E O P E R A C I Ó N :

U t i l i z a n u n v o l t a j e r e g u l a d o d e 4 . 7 5 a 5 . 2 5 v o l t s d e C . C . o d e C D t í p i c a m e n t e 5 v o l t s d e C . C .

E l n i v e l d e s e ñ a l d e e n t r a d a n o d e b e e x c e d e r a V C C .

S e p u e d e i n t e r c o n e c t a r v a r i o s c i r c u i t o s i n t e g r a d o s , s i e m p r e y c u a n d o s e a n d e l a m i s m a f a m i l i a .

L o s C . I . s o n g e n e r a l m e n t e p a q u e t e s d e s i l i c ó n , d o n d e s e i n t e g r a n t r a n s i s t o r e s , r e s i s t e n c i a s , c o n d e n s a d o r e s , e t c . P a r a i d e n t i f i c a r l a s t e r m i n a l e s b a s t a c o n i d e n t i f i c a r e l l a d o d e l a m a r c a o s e m i c í r c u l o , e x t r e m o e n e l c u a l d e b e d e e x i s t i r u n p u n t o q u e i n d i c a e l c o m i e n z o d e l a n u m e r a c i ó n d e l o s p i n s d e l C . I .

b ) F a m i l i a d e C . I . C M O S ( Me t a l Ox i d o Se m i c o n d u c t o r

Co m p l e m e n t a d o)

L a f a m i l i a C M O S t r a b a j a b a j o e l p r i n c i p i o d e t r a n s i s t o r F E T IB< < IC .

F E T T r a n s i s t o r d e E f e c t o d e C a m p o .

C A R A C T E R I S T I C A S :

C o n s u m e n p o c a p o t e n c i a

S u v o l t a j e d e o p e r a c i ó n e s d e 3 - 1 5 v .

E l v o l t a j e d e e n t r a d a n o d e b e e x c e d e r V d d ( p o l a r i z a c i ó n ) . S u r e s p u e s t a a l o s c a m b i o s e s m á s l e n t a c o m p a r a d a c o n T T L . N u n c a c o n e c t e u n M O S a u n c i r c u i t o d e p o t e n c i a e n e s t a d o o f f ( s i n p o l a r i z a c i ó n ) .

P R E C A U C I O N E S :

D e b e p r o t e g e r s e d e l a e l e c t r i c i d a d e s t á t i c a .

N o s e a l m a c e n e C M O S e n p l á s t i c o s n o c o n d u c t o r e s .

M a n t é n g a s e e n v u e l t o s e n m a t e r i a l c o n d u c t o r , c o m o e l a l u m i n i o . U t i l i z a e l e q u i p o a d e c u a d o p a r a s u m a n e j o .

C a l c u l o d e l a r e s i s t e n c i a l i m i t a d o r a p a r a u n l e d i n d i c a d o r .

I M P L E M E N T A C I O N D E C I R C U I T O S M E D I A N T E C O M P U E R T A S U N I V E R S A L E S

S o n c o n s i d e r a d a s C o m p u e r t a s U n i v e r s a l e s l a s c o m p u e r t a s N o - Y y N o - O .

A B F B A F . A B F B A F

C o m o s e p u e d e v e r p a r a i m p l e m e n t a r m e d i a n t e c o m p u e r t a s N o - Y ( N A N D ) , t o d o d e b e q u e d a r e x p r e s a d o e n f o r m a d e p r o d u c t o s n e g a d o s . P a r a l a c o m p u e r t a N o - O , l a f o r m a d e b e s e r e n s u m a s n e g a d a s .

E J E M P L O S :

1 . - I m p l e m e n t a r l a f u n c i ó n m e d i a n t e c o m p u e r t a s N O - Y d e d o s e n t r a d a s .

z x y x

L . . S i a = x.y y b = x . z

b a b a z x y x

L . . ; P o r t e o r e m a d e M o r g a n m n= m . n

b a

L . =x.y.x.z

I m p l e m e n t e e l c i r c u i t o l ó g i c o .

2 . - I m p l e m e n t e l a f u n c i ó n K = a . b +a.b m e d i a n t e c o m p u e r t a s N O R d e d o s e n t r a d a s .

K = a . b +a.b

b a b a

K . . =a b a b=a b a b

3 . - I m p l e m e n t a r l a s s i g u i e n t e s f u n c i n e s m e d i a n t e c o m p u e r t a s u n i v e r s a l e s d e d o s e n t r a d a s .

C 1 = A.B A.B.C y C 2 = A.(B.C B.C) ( T A R E A )

P r o c e d i m i e n t o p a r a e l D i s e ñ o L ó g i c o C o m b i n a t o r i o .

U n c i r c u i t o c o m b i n a t o r i o e s t a c o n s t i t u i d o p o r c o m p u e r t a s l ó g i c a s , d o n d e e l v a l o r d e l a s s a l i d a s s e d e t e r m i n a d i r e c t a m e n t e d e l a c o m b i n a c i ó n p r e s e n t e e n l a s e n t r a d a s s i n t e n e r e n c u e n t a l o s e s t a d o s a n t e r i o r e s . E l d i s e ñ o d e c i r c u i t o s c o m b i n a t o r i o s c o m i e n z a d e s d e e l e n u n c i a d o d e l p r o b l e m a y t e r m i n a c o n e l d i a g r a m a d e l c i r c u i t o l ó g i c o . E l p r o c e d i m i e n t o e s :

1 . - P l a n t e a m i e n t o v e r b a l d e l p r o b l e m a .

2 . - D e t e r m i n a c i ó n d e l n ú m e r o d e v a r i a b l e s d e e n t r a d a y s a l i d a .

3 . - T a b u l a c i ó n d e l a s c o n d i c i o n e s d e l p r o b l e m a e n u n a t a b l a d e v e r d a d , q u e e s t a b l e s c a l a s r e l a c i o n e s r e q u e r i d a s e n t r e e n t r a d a s y s a l i d a s .

4 . - E n b a s e a l a t a b l a d e v e r d a d o b t e n e r l a f u n c i ó n l ó g i c a p a r a c a d a u n a d e l a s s a l i d a s .

5 . - A p l i c a r a l g u n a d e l a s t é c n i c a s d e s i m p l i f i c a c i ó n c o n o c i d a s , p a r a o b t e n e r e n c a d a c a s o l a m í n i m a e x p r e s i ó n a l g e b r a i c a .

6 . - C o n f i g u r a c i ó n d e l d i a g r a m a l ó g i c o q u e c o r r e s p o n d e a l a s

e x p r e s i o n e s s i m p l i f i c a d a s d e l a s s a l i d a s , d e a c u e r d o a l t i p o d e c o m p u e s t a s e s p e c i f i c a d a s p o r e l d i s e ñ o .

P r o b l e m a s d e A p l i c a c i ó n

1 . - E n c u e n t r e l a e c u a c i ó n l ó g i c a y e l d i a g r a m a q u e g o b i e r n e e l c o m p o r t a m i e n t o d e l s i g u i e n t e s i s t e m a c u a n d o s e a c t i v a e l b o t ó n W , s e a c t i v a e l m o t o r M , q u e c o n t r o l a e l l i m p i a d o r d e u n a u t o m ó v i l ; e l m o t o r d e b e d e a c t i v a r s e s o l o s i e l l i m p i a d o r e s t a a l a d e r e c h a y e l b o t ó n W e s t a a c t i v a d o .

W = 0 , i n t e r r u p t o r a b i e r t o m o t o r n o a c t i v a d o . S = 0 , e l l i m p i a d o r n o e s t a e n l a d e r e c h a .

M = 1 ( m o t o r a c t i v a d o ) , s i e l i n t e r r u p t o r W e s t a c e r r a d o y e l l i m p i a d o r e s t a e n l a d e r e c h a S = 1 .

2 . - E n u n c u r s o d e b e l l e z a d o n d e e x i s t e n 4 p e r s o n a s q u e i n t e g r a n e l j u r a d o , s e p i d e o b t e n e r l a e x p r e s i ó n l ó g i c a q u e g o b i e r n e e l c o m p o r t a m i e n t o d e u n c i r c u i t o q u e d e t e r m i n e c u a n d o e l n ú m e r o d e v o t o s s e n 1 2 o m á s v o t o s .

J e f e d e p r e n s a : S u v o t o v a l e e l d o b l e q u e e l d e l o s p e r i o d i s t a s ( v o t o u n i t a r i o ) .

J e f e d e e v e n t o s e s p e c i a l e s : s u v o t o v a l e e l d o b l e q u e e l d e l j e f e d e p r e n s a .

E j e c u t i v o d e T . V . : s u v o t o v a l e e l d o b l e q u e e l d e j e f e d e e v e n t o s . E l j u r a d o q u e d o i n t e g r a d o p o r u n p e r i o d i s t a , u n j e f e d e p r e n s a , u n j e f e d e e v e n t o s e s p e c i a l e s y u n e j e c u t i v o d e T . V .

F U N C I O N B O O L E A N A

E s t a d e f i n i d a c o m o u n a f u n c i ó n b i n a r i a q u e d e p e n d e d e n v a r i a b l e s d e t e r m i n a d a s .

F = f ( x , y , z ) ; l a f u n c i ó n d e p e n d e d e t r e s v a r i a b l e s , d o n d e z c o r r e s p o n d e a l L S B d e l a f u n c i ó n o r d e n a d a .

x . y . z P r o d u c t o c a n ó n i c o ( m i n i t e r m ) ( x + y + z ) S u m a c a n ó n i c a ( m a x t e r m )

L a F u n c i ó n B o o l e a n a s e p u e d e o b t e n e r d e l a s f o r m a s :

S u m a d e T é r m i n o s M í n i m o s ( D i s y u n c i ó n d e c o n j u n c i o n e s o f o r m a c a n ó n i c a d i s y u n t i v a ) . - P a r a n v a r i a b l e s b i n a r i a s s e p u e d e o b t e n e r 2n

t é r m i n o s m í n i m o s y c u a l q u i e r f u n c i ó n d e B o o l e p u e d e e x p r e s a r s e c o m o u n a s u m a d e t é r m i n o s m í n i m o s . L o s t é r m i n o s m í n i m o s c u y a s u m a d e f i n e l a f u n c i ó n d e B o o l e s o n a q u e l l o s q u e d a n l o s u n o s d e l a f u n c i ó n d e u n a t a b l a d e v e r d a d . S i u n a f u n c i ó n n o e s t a e n f o r m a d e s u m a d e t é r m i n o s m í n i m o s , s e p u e d e l l e g a a e l l a l l e v a n d o l a e x p r e s i ó n a u n a s u m a d e t é r m i n o s “ y ” u “ A N D ” o p r o d u c t o , l u e g o s e i n s p e c c i o n a c a d a t e r m i n o p a r a v e r s i c o n t i e n e t o d a s l a s v a r i a b l e s d e l a s c u a l e s d e p e n d e l a f u n c i ó n , s i l e h a c e f a l t a u n a o m á s v a r i a b l e s s e e x p a n d e e l t e r m i n o , a p l i c a n d o a l a f u n c i ó n “ y ” o p r o d u c t o u n a e x p r e s i ó n x ó n o x ( x + x) d o n d e x e s u n a d e l a s v a r i a b l e s f a l t a n t e s .

E J E M P L O S . - E x p r e s a r l a f u n c i ó n d e B o o l e F A B.C, c o m o s u m a s d e t é r m i n o s m í n i m o s .

C B A

F . = A(B B) B.C.(A A)= A.B A.B B.C.A BCA

F = A.B.(C C) A.B.(C C) A.B.C A.BC

7 6 5 4 5 1 1 1 1 1 1 0 1 0 1 1 0 0 1 0 1 0 0 1 F = A.B.C A.B.C A.B.C A.B.C A.B.C A.BC

f ( a , b , c ) = 3 ( 1 , 4 , 5 , 6 , 7 ) M i n i t e r m

F o r m a d e r e p r e s e n t a r e l M i n t e r m e n u n a t a b l a d e v e r d a d : E q u i v a l e n t e

d e c i m a l A B c F 0 0 0 0 1

1 0 0 1 0

2 0 1 0 0

3 0 1 1 0

4 1 0 0 1

5 1 0 1 1

6 1 1 0 1

7 1 1 1 1

P r o d u c t o d e T é r m i n o s M á x i m o s ( m a x t e r m o t é r m i n o m á x i m o o c o n j u n c i ó n d e d i s y u n c i o n e s c o m p l e t a ) . - e s a q u e l q u e n o s d a l o s c e r o s d e l a f u n c i ó n e n l a t a b l a d e v e r d a d . S i e n u n a f u n c i ó n l ó g i c a l o s p r o d u c t o s d e s u m a n o e s t á n c o m p l e t o s o n o s o n s u m a s c a n ó n i c a s , s e p u e d e l l e g a r a u n a f u n c i ó n c o m p l e t a , e x p a n d i e n d o l a f u n c i ó n . S e s u m a e l t e r m i n o x y n o x (x . x) , d o n d e x e s u n a d e l a s v a r i a b l e s f a l t a n t e s , f i n a l m e n t e s e a p l i c a l a l e y d i s t r i b u t i v a p a r a l a s u m a a + b . c = ( a . b ) . ( a + c ) .

E J E M P L O :

F = x . y +x.z= ( x . y + x) . ( x . y + z ) = ( x + x) ( y + x) . ( x + z ) . ( y + z ) F = ( x+ y ) . ( x + z ) . ( y + z ) = ( x+ y + z.z) . ( x + z + y.y) . ( y + z + x.x) 4 5 0 2 0 4 1 0 0 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 F = ( x+ y + z ) . ( x y z) . ( x + y + z ) . ( x + y+ z ) . ( x + y + z ) . (.x+ y + z ) ; S e c o n s i d e r a n v a l o r e s c o n t r a r i o s p a r a e v a l u a r l a f u n c i ó n . F ( x , y . z ) = 3( 0 , 2 , 4 , 5 ) M a x t e r m

x y z F

0 0 0 0

0 0 1 1

0 1 0 0

0 1 1 1

1 0 0 0

1 0 1 0

1 1 0 1

1 1 1 1

T a r e a . - E x p r e s a r l a s s i g u i e n t e s f u n c i o n e s e n s u m a d e t é r m i n o s m í n i m o s y p r o d u c t o d e t é r m i n o s m á x i m o s .

a ) F ( A , B , C ) =(A B).(B C)

b ) L ( X , Y , Z ) = 1