1
Detección de daño en
edificios
Ramsés Rodríguez Rocha
rrodriguezr@ipn.mx
Detección de daño en Edificios
2
Detección de daño en Edificios
3
Chi Chi, Taiwan, 1999
Detección de daño en Edificios
4
Detección de daño en Edificios
5
Chi Chi, Taiwan, 1999
Izmit Turquía, 1999
Yingxiu China, 2008.
Nivel I: Existencia
Nivel II: Localización
Nivel III: Magnitud
Nivel IV: Predicción de vida útil
Importancia de la
detección de daño
• Prevenir derrumbes y pérdidas humanas
• Reparación de estructuras
Proceso de la
detección de daño
*
*
Detección de daño
Instrumentación
Sin daño (estado base)
Con daño ( )
*
*k
k
Problema de la
detección de daño
•Estado previo, aún en la inspección visual
•Parámetros modales sin daño para reconstruir este estado
•
Problema:
Generalmente, no se tienen registros antes del daño
•Menos de 25 edificios instrumentados (Taborda et al, 2002)
Método de sensibilidades (Stubbs y Kim, 1996). Condiciones
iniciales-convergencia
Kharrazi et al., (2000). Sensibilidades; ajuste; extenso cálculo
Método de cocientes (Barroso y Rodríguez, 2004). Edificios de
cortante; Daño por entrepiso, no en elementos
Desarrollar un método que permita identificar daño
en edificios en los que no se conocen sus
parámetros modales base (sin daño)
Se propone el método de Rigideces Base, MRB.
Ventajas:
Detección de daño en edificios sin tener información modal previa
Reducción de gastos de instrumentación, sólo un proceso de
medición
No requiere de inspección visual
Método de rigideces base
Ts s i i i i
m
k
m
k
m
k
m
k
m
k
m
k
u
1
2 2 1 2 1 1
3 1 1 1h
EI
12
k
*
*
;configuración estructural; propiedadesgeométricas de elementos; tol. ;
K
B
K
a
Modelo
E=1
1 1k
p
3 2 1 i i 5 4 2 i 1 i 5 j 4 j 1 j i j iu
u
p
k
u
u
p
p
u
u
p
p
) (c
k
p
1
1Ajuste por flexión
1a
M
M
c
M
a
1 1
m
p
DDF,
k
i
B
ka
i
nek
iK
1 i
Principal
aportación
,
Rigideces base
Método de rigideces base
K
nex
ik
iKd
1 i
- - - -
K
-
K
d
x
K
s
x=0
,
No hay daño
x=1
, Daño total
ii
DVC
xs
x
i*
Indicadores de daño
K
d
aprox
K
d
tol
K
-
K
d
x
1
k
1
x
2
k
2
x
i
k
i
x
ne
k
neMétodo de rigideces base
x
iMediciones del
edificio con daño
Método de rigideces base
Procesamiento
de sañales
Rigidez lateral
del edificio
Estado base
Estado con
daño
K
I
N
R
K
100
K
d
K
M
Z
H
M
q
2q
TM
Efecto de la información
modal limitada y ruido
Ajuste. Baruch y Bar-Itzhack (1978)
N
N
TM
K
d
;
Variación de q y Ω
8 @ 3.75 m
4.15 m
3.42 m 3.00 m 4 @ 9.0 m
10 9 8 7 6 5 4 3 2 1
T 4.95 m
Efecto de la información
modal limitada y ruido
Edificio STC
1 3 5
21 23 25
48 50
46
1 3
5
Número de modos
Marco plano de dos pisos de cortante
k1 k2
m1
m2 e(%)
0.5 1 1.5 2 2.5
120
80
40
0
-40
s2/s1 s2=k2/m2
s1=k1/m1
-50 0 50 100
0.5 1 1.5 2
-50 -30 -10 10 30
0.5 1 1.5
e(%)
0.1 0.5 0.6
0.9
3 @ 3.5 m
6.0 m
1 2 3 4 5 6
7 8 9 -3.2 43.6 45 1 4 -1.0 84.0 85 8 -2.0 73.4 74 3 3 0.5 85.4 85 7 2 2.2 56.2 55 7 1 Error Relativo (%) Daño calculado (%) Daño simulado (%) Elemento dañado Estado de daño
Marco plano de tres niveles
(Fierro et
al
., 1999)
Estructura tridimensional
de dos niveles
(Sohn y Law, 1997)
1.7 35.6 35 1 4 0.8 55.4 55 5 1.7 35.6 35 2 3 0.8 50.4 50 3 2 1.4 40.6 40 1 1 Daño calculado (%) Daño simulado (%) Elemento dañado Estado de daño 14.6 m 21.9 m 7.3 m 1 2 3 4 Error Relativo (%) 0.8 55.4 55 2 5.2 15.8 15 3 1.4 40.6 40 4 2.1 30.6 30 5 0.6 60.4 60 6
Estructura tridimensional
de dos niveles
-10
0
10
20
30
40
1
2
3
4
5
6
7
8
Iteraciones
Error relativo (%)
5
2
6
1
4
3 1
2 3
Edificio de concreto reforzado
en Van Nuys California
Piso 4
Edificio de concreto reforzado
en Van Nuys California
Piso 4
Conclusiones
Se presentó el MRB para la detección de daño en edificios de los
que se desconoce su estado de referencia (sin daño).
El MRB se aplicó utilizando únicamente la información de la
estructura con daño.
Se localizó y estimó la pérdida de la rigidez en los elementos
dañados de las estructuras estudiadas.
Variaciones rigidez/masa menores que 10% produjo errores
menores que 10%. Estado base.
Edificio en California
Se localizó correctamente los elementos reportados como
dañados.
Primer modo de vibración de la estructura con daño para
ajustar su matriz de rigidez.
Dos primeros modos de vibración para calcular el estado
de referencia.
Marcos planos y estructuras tridimensionales, errores menores
que 7%. Ruido e información modal limitada.
Errores relativos mayores que 10% para niveles de ruido
mayores que 10%.
Marcos planos y estructuras tridimensionales, errores 0%. MRB
es numéricamente exacto, global.
Daño de 1% en zonas especificas. Discretización. Extremos.
Artículo arbitrado.
Independent Component Analysis
• Linear transformation method which
separates the sources from the
acquired data
• FT of this representation yields
clearer spectral analysis
Example. Four-story shear frame
(Bernal & Gunes, 2000)
Amplitude
Period (sec.) Amplitude
Period (sec.)
Utilizing ICA
Theoretical Computed by
ICA Error (%) 0.103 0.104 -1.0 0.038 0.036 5.3 0.025 0.025 0.0 0.020 0.020 0.0
Periods (sec.)
Example. Damage detection of a
three-story frame
1 2 3
4 5 6
7 8
9
(Biggs, 1964 )
1 2 3 4 5 6 7 8 9
For undamage and damage
cases D1, D2, e < 2% for
identified frequencies
utilizing ICA.
D1
10% 20
10
0 # of element
Loss of stiffness (%)
Baseline available
Example. Damage detection of a
three-story frame
1 2 3 4 5 6 7 8 9
0
1 2 3
4 5 6
7 8
9
0 30
3 4 5
Floor 4
Observed damage. (Trifunac et al., 1999)
Mode ICA FDD
1 0.66 0.72
2 1.35 1.37
Van Nuys building
Period (sec.) Amplitude
First peak Second peak
1.8 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 2.0
Third peak
Second peak
FDD ICA
FDD Frequencies (Hz)
Van Nuys building
7 4 S 6 5 3 2 15 cm<cracks<10 cm Cracks <1 cm Cracks > 10 cm Floor
34.2
9.0 8.3 11.1 16.0
29.9
8.1 6.7 19.3 11.5
45.4
4.6 4.0 3.7 6.4
22.3 15.1
10.4 74.2 21.2
88.8
6.5
66.3 87.0
3.1
43.9 62.6
60.8 11.3 10.0
91.6 66.4 30.8 9.7 61.8
42.9 81.4
27.8
FDD ICA
Conclusions
•
BSM was utilized for damage detection on the Van Nuys building(California, USA) without baseline modal parameters.
• Modal information from ICA and FDD was computed.
•Adequate results from both techniques with one iteration.
•BSM located crack smaller than 1 cm with moderate magnitude of damage using modal information from FDD.
•Better damage identification results when using FDD, although fewer false locations with ICA. Three iterations.
EFECTO DE LA INTERACCIÓN
SUELO-ESTRUCTURA EN LA
DETECCIÓN DE DAÑO,
USANDO EL MÉTODO DE
Introducción
• Se estudia la influencia de la Interacción
Suelo-Estructura (ISE) en la
determinación de daño en un modelo
numérico de 10 niveles con
Introducción
• El MRB se formula considerando que la
estructura está empotrada en la base.
• Se hace uso de Funciones de
Transferencia (FT) para restar la influencia
de la dinámica del suelo en las señales
Modelo ISE utilizado
• Modelo unidimensional de propagación de
ondas con FT de Wolf (1985) para efectos
de sitio.
• Interacción cinemática aproximada
(Kausel et al., 1978).
Descomposición en el Dominio
de la Frecuencia.
• De acuerdo con Brincker et. al. (2000) la
matriz espectral de potencia de la
respuesta
• [
Y(f)
]
es la respuesta transformada del
dominio del tiempo al de la frecuencia
para cada valor de frecuencia .
(
)
(
)
)
(
f
Y
f
Y
f
yy
G
T
Descomposición en el Dominio
de la Frecuencia.
• Expresada como una descomposición por
valores singulares (DVS):
• donde [
U
p
] es una matriz que contiene
vectores singulares y [
S
p
] una matriz
diagonal con los valores singulares.
T
p
p
p
S
U
U
f
yy
G
Método de Rigideces Base
• (Rodríguez et. al. 2010) detecta daño en
edificios sin información base (estado sin
daño).
• Mediante cocientes de rigidez y masa se
establece un estado de referencia.
Ts s i i i i
m
k
m
k
m
k
m
k
m
k
m
k
u
1
Función de Transferencia
• Para la Función de Transferencia:
• Se tiene que:
0, 00 , h Ae h a
0 2)
(
f
h
e
d
H
j f)
(
)
(
)
(
f
H
f
X
f
Y
f Xf Y f
Función de Transferencia
• Siendo Y(f) y X(f) las Transformadas de
Fourier de los registros sísmicos elegidos.
• Se usan dos FT para identificar la más
conveniente en detección de daño.
• FT-CL. En donde X(f) es el movimiento de
Campo Libre.
Función de Transferencia
• FT-CL. Resta efectos de sitio.
• FT-BC. Resta además componentes
horizontales de la ISE.
Casos de daño
• Para cada caso se evalúan las 2 FT
mencionadas, resultando en 6 casos de
estudio: D1-CL, D2-CL, D3-CL y D1-BC,
D2-BC, D3-BC.
D1
D2
D3
Elem. Dañado
1
2
5
Frecuencias encontradas (Hz) DDF
Modo D1-CL D2-CL D3-CL D1-BC D2-BC D3-BC
1 0.549 0.639 0.647 0.562 0.651 0.659
2 1.855 2.238 2.340 1.888 2.295 2.425
3 3.385 3.768 3.491 3.394 3.788 3.540
4 4.814 5.273 5.196 4.814 5.282 5.200
Detección de daño usando FT
-20% 0% 20% 40% 60% 80% 100% 1 2 3 4 5 6 7 8 9 10 Daño (%) N iv e l Modelo D1-FT-CL Simulado Calculado
0% 20% 40% 60% 80% 100%
1 2 3 4 5 6 7 8 9 10 Daño (%) N iv e l Modelo D2-FT-CL Simulado Calculado
0% 20% 40% 60% 80%
1 2 3 4 5 6 7 8 9 10 Daño (%) N iv e l Modelo D3-FT-CL Simulado Calculado
0% 20% 40% 60% 80% 100%
1 2 3 4 5 6 7 8 9 10 Daño (%) N iv e l Modelo D1-FT-BC Simulado Calculado
0% 20% 40% 60% 80% 100%
1 2 3 4 5 6 7 8 9 10 Daño (%) N iv e l Modelo D2-FT-BC Simulado Calculado
0% 20% 40% 60% 80% 100%
Detección de daño, con ISE
• Se seleccionaron, para el modelo D1 los
modos 1 y 2, para el modelo D2 los
modos 1 y 5 y para el modelo D3 los
modos 1 y 3.
0% 20% 40% 60% 80% 100%
1 2 3 4 5 6 7 8 9 10 Daño(%) N iv e l
Modelo D1 ISE
Simulado
Calculado
0% 20% 40% 60% 80% 100%
1 2 3 4 5 6 7 8 9 10 Daño (%) N iv e l
Modelo D2 ISE
Simulado
Calculado
0% 20% 40% 60% 80% 100%
1 2 3 4 5 6 7 8 9 10 Daño (%) N iv e l
Modelo D3 ISE
Simulado
Comentarios
• Para todos los casos (FT) el MRB
identifica correctamente el elemento
dañado.
• No se presentan elementos falsos.
Comentarios
• Para señales con ISE (García et al.,
2011), en D2 no se identificó el elemento
dañado y en D3 hubo elementos falsos.
Porcentajes de daño y error
D1-CL D2-CL D3-CL
Modos
Daño medido
Error
relativo Modos
Daño medido
Error
relativo Modos
Daño medido
Error relativo 1 y 2 11.05% 87.21% 1 y 5 80.73% -62.00% 1 y 3 69.87% -39.60%
D1-BC D2-BC D3-BC
Modos
Daño medido
Error
relativo Modos
Daño medido
Error
relativo Modos
Daño medido
Error relativo 1 y 2 57.95% 32.55% 1 y 5 88.47% -76.00% 1 y 3 90.07% -80.00%
D1-ISE D2-ISE D3-ISE *
Modos
Daño medido
Error
relativo Modos
Daño medido
Error
relativo Modos
Daño medido
Error relativo 1 y 2 73.47% 14.93% 1 y 5 -- -- 1 y 3 45.02% 9.96%
Conclusiones
• Usando ambas FT la localización del daño
mejoró con respecto a cuando se usan
señales sin deconvolucionar.
• No se presentaron elementos falsos.
• En D2 y D3 el error fue menor usando
FT-CL, mientras que para D1 disminuyó
Conclusiones
• El uso de FT para eliminar componentes
frecuenciales de la excitación e ISE
resulta en mejores resultados de
localización de daño.
• Ambas FT fueron eficientes para la
62
Objetivo
Proponer una metodología de localización de daño no destructiva basada en mediciones dinámicas utilizando una Red Neuronal Artificial Polinomial (RNAP).
Metodología
1.- Definir casos de estudio de edificios de cortante.
2.- Modelar numéricamente con base en la ecuación dinámica lineal para osciladores de múltiples grados de libertad edificios sujetos a carga sísmica, con la posibilidad de manipular la ubicación y magnitud de daño, reduciendo el porcentaje de rigidez de los elementos columna para simular el daño.
3.- Calcular la respuesta dinámica teórica por piso en términos de aceleraciones absolutas de un modelo de referencia (sin daño) y después generar la respuesta para el modelo sujeto a distintos casos de daño.
4.- Calcular los pesos por piso del modelo de referencia, así como los pesos de los distintos casos de daño con la RNAP utilizando como entradas de la misma, la respuesta dinámica teórica de los casos de estudio.
5.- Una vez que la RNAP obtiene los pesos que caracterizan la respuesta dinámica de los diferentes casos de estudio, se utiliza una métrica basada en la suma de la diferencia absoluta de los pesos para analizar una posible relación de daño entre los pesos del modelo de referencia y los modelos con distintos casos de daño.
Generalidades de una Red Neuronal Artificial
Las RNA son redes interconectadas masivamente en paralelo de elementos simples (usualmente adaptativos) y con organización jerárquica, las cuales intentan interactuar con los objetos del mundo real del mismo modo que lo hace el sistema nervioso biológico (Matich Damián J., 2001).
Entre sus principales características se encuentran las siguientes:
• Consisten de unidades de procesamiento que intercambian datos o información.
• Se utilizan para reconocer patrones, incluyendo imágenes, manuscritos y secuencias de tiempo.
• Tienen capacidad de aprender y mejorar su funcionamiento.
Principalmente las RNA se componen de tres elementos, tres capas o tres niveles que son:
• Capa de Entrada: Es en donde se guarda la información proveniente de las fuentes externas de la red.
• Capa Oculta: No tiene contacto con el exterior, puede tener un número elevado de capas y pueden estar interconectadas de distintas maneras, lo que determinara la tipología de la red.
• Capa de Salida: Transfiere información de la red hacia el exterior.
Figura 1.3 Esquema de una red neuronal antes del entrenamiento.
Se modeló numéricamente un edificio de dos grados de libertad a partir del principio de masas y rigideces (Figura 3.1.1). El cual no ha sufrido cambios en las rigideces para simular el daño.
Figura 3.1.1 Modelo lineal de masas y rigideces
En la tabla 3.1.1 se muestran las propiedades del Modelo de la Figura 3.1 con diferentes combinaciones de daño, que son las siguientes:
CASO 1.- No hay cambios en la rigidez.
CASO 2.- La rigidez del primer entrepiso se redujo al 10% CASO 3.- La rigidez del segundo entrepiso se redujo al 10%
CASO 4.- La rigidez del primer y segundo entrepiso se redujeron al 10%
Tabla 3.1.1 Propiedades del Modelo con diferentes casos de daño y degradación de rigidez al 10 %.
En estos experimentos se entrenó a la RNAP introduciendo dos respuestas consecutivas como si fuese sólo una, primeramente utilizamos las respuestas del modelo de referencia (sin daño-sin daño) como se muestra en la Figura 3.1.2 y después se entrenó utilizando la señal sin daño con cada una de las señales dañadas (sin daño-con daño).
Figura 3.1.2 Señales consecutivas del modelo de referencia (sin daño-sin daño).
69
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Resultados
En la Figura 3.1.3 se muestran los resultados del entrenamiento de la RNAP comparados sobre poniéndolos con la respuesta original. Se puede notar que las series o señales son tan similares que parece que en la figura se mostrará sólo una serie.
0 2000 4000 6000 8000 10000 12000 14000 16000 18000 -0.2 0 0.2 0.4 0.6 0.8 1 1.2
Número de muestras
En la Figura 3.1.4 se muestra un acercamiento de la Figura 3.1.3 para un rango de 1673 y 1685 muestras de la serie para mostrar que el entrenamiento de la RNAP es muy adecuado.
Figura 3.1.4 Acercamiento de la Figura 3.1.3 del entrenamiento de la RNAP.
1.674 1.676 1.678 1.68 1.682 1.684
x 104 0.48 0.485 0.49 0.495 0.5 0.505
Número de muestras
Así también en la Figura 3.1.5 se muestran los resultados de la prueba también comparados sobre poniéndolos con la respuesta original. Donde también se puede notar que las series o señales son tan similares que parece que en la figura se mostrará sólo una serie.
Figura 3.1.5 Resultados de prueba de la RNAP.
0 100 200 300 400 500 600 700 800 900 0.46 0.47 0.48 0.49 0.5 0.51 0.52 0.53
Número de muestras
En la Figura 3.1.6 se muestra un acercamiento de la Figura 3.1.5 para un rango entre las 250 y 400 muestras de prueba para mostrar que la predicción de la RNAP es muy adecuada.
Figura 3.1.6 Acercamiento de la Figura 3.5 en la fase de prueba de la RNAP.
250 300 350 400
0.486 0.488 0.49 0.492 0.494 0.496 0.498 0.5 0.502 0.504 0.506
Número de muestras
En la Figura 3.1.7 se muestra la evolución de los pesos con respecto a las muestras de entrenamiento. Se observó que hay un periodo de estabilización entre las 6000 y 11000 muestras y a continuación se observa un periodo de oscilación hasta la muestra 15000, para terminar otra vez con un periodo de estabilización.
Figura 3.1.7 Evolución de los pesos respecto a las muestras de entrenamiento de la serie.
0 2000 4000 6000 8000 10000 12000 14000 16000 18000 -0.5
0 0.5
0 2000 4000 6000 8000 10000 12000 14000 16000 18000 -2
0 2
0 2000 4000 6000 8000 10000 12000 14000 16000 18000 0
2 4
0 2000 4000 6000 8000 10000 12000 14000 16000 18000 -0.5
0 0.5
0 2000 4000 6000 8000 10000 12000 14000 16000 18000 -1
0 1
0 2000 4000 6000 8000 10000 12000 14000 16000 18000 -1
0 1
Número de muestras
En la Figura 3.1.8 se muestran los resultados obtenidos del análisis utilizando la suma de la diferencia absoluta y cuando la rigidez se degrado 10 %, obteniendo una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.1479 y 0.0961 cuando el daño está en el primer nivel (caso dos) y una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.0545 y 0.2745 cuando el daño está en el segundo nivel (caso tres). Estos resultados muestran que la métrica es mayor en el nivel dañado. Así mismo para el caso cuatro la métrica nos supone el daño en el segundo nivel.
En la Figura 3.1.9 se muestran los resultados obtenidos cuando la rigidez se degrado 20 %, obteniendo una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.2015 y 0.1349 cuando el daño está en el primer nivel (caso dos) y una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.0455 y 0.2872 cuando el daño está en el segundo nivel (caso tres). Estos resultados muestran que la métrica es mayor en el nivel dañado. También se muestra en comparación a la figura anterior que el caso cuatro guarda la relación de localización y magnitud de daño.
Figura 3.1.9 Magnitud de los pesos en los diferentes casos de estudio con 20% de daño.
En la Figura 3.1.10 se muestran los resultados obtenidos cuando la rigidez se degrado 30 %, obteniendo una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.2893 y 0.2055 cuando el daño está en el primer nivel (caso dos) y una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.0506 y 0.2445 cuando el daño está en el segundo nivel (caso tres). Estos resultados muestran que la métrica es mayor en el nivel dañado. Además para el caso cuatro se puede notar que la relación en cuanto a la localización del daño cambio al aumentar la degradación de rigidez, arrojándonos como resultado que el valor de la métrica mayor se encuentra en el primer nivel y no en el segundo como en los experimentos anteriores.
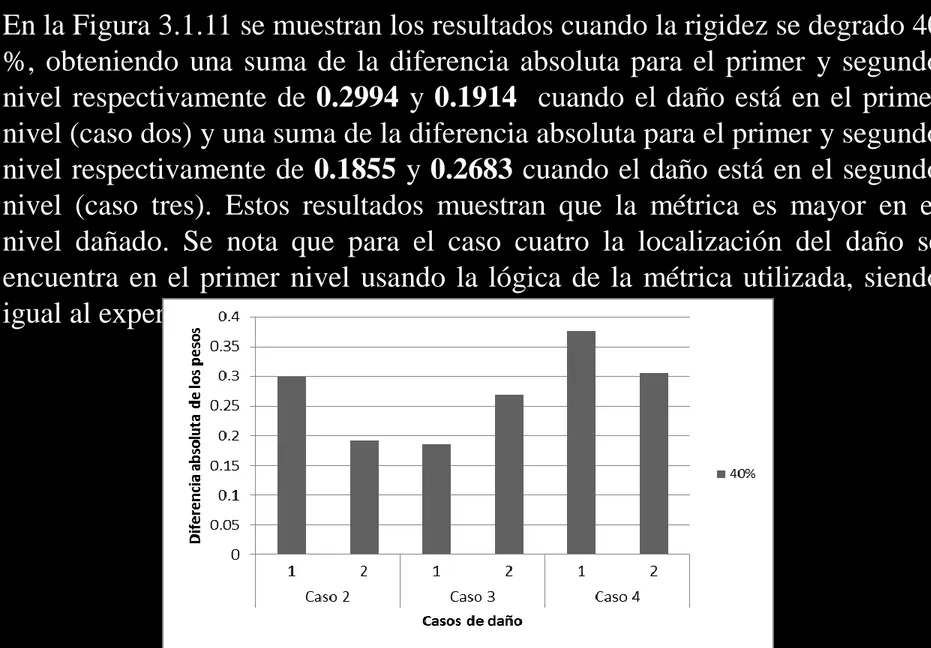
En la Figura 3.1.11 se muestran los resultados cuando la rigidez se degrado 40 %, obteniendo una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.2994 y 0.1914 cuando el daño está en el primer nivel (caso dos) y una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.1855 y 0.2683 cuando el daño está en el segundo nivel (caso tres). Estos resultados muestran que la métrica es mayor en el nivel dañado. Se nota que para el caso cuatro la localización del daño se encuentra en el primer nivel usando la lógica de la métrica utilizada, siendo igual al experimento anterior.
En la Figura 3.1.12 se muestran los resultados cuando la rigidez se degrado 50 %, obteniendo una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.2956 y 0.1332 cuando el daño está en el primer nivel (caso dos) y una suma de la diferencia absoluta para el primer y segundo nivel respectivamente de 0.3702 y 0.3283 cuando el daño está en el segundo nivel (caso tres). Estos resultados ya no guardan la relación de localización de daño debido a que en el caso tres el daño se encuentra en el segundo nivel y la métrica nos indica que el nivel dañado es el primero.
Figura 3.1.12 Magnitud de los pesos en los diferentes casos de estudio con 50% de daño.
En las siguientes figuras se muestra la aportación de los pesos, así como su magnitud cada vez que se aumentó el daño.
En la Figura 3.1.13 se muestra la magnitud de la diferencia los pesos del modelo de referencia (sin daño-sin daño) y los pesos para los casos de daño del primer nivel cuando el daño se simula en este mismo primer nivel cada vez que se aumenta la degradación de la rigidez. Se nota que hay una relación de comportamiento cuando se aumenta el daño y que el peso cuatro es el más representativo.
En la Figura 3.1.14 se muestra la magnitud la diferencia los pesos del modelo de referencia (sin daño-sin daño) y los de los otros casos de daño del segundo nivel cuando el daño se incrementa en el primer nivel en los diferentes porcentajes de daño. Se puede observar que los valores son mayores en los pesos del 1er nivel y que podría existir una relación en cuanto el incremento de daño de no ser por que el peso cuatro es mayor cuando se degrada el 30% que el mismo peso cuando se degrada la rigidez en 40%.
Así mismo se muestra en la Figura 3.1.15 la magnitud de la diferencia de los pesos del primer nivel cuando el daño esta en el 2º nivel, observándose primeramente que el peso cuatro es el mas representativo y que la relación entre el aumento de daño y los pesos no es muy clara o contundente.
Figura 3.1.15 Magnitud de la diferencia de los pesos del primer nivel cuando se aumenta el daño en el segundo nivel.
En la Figura 3.1.16 se muestra la magnitud de la diferencia los pesos cuando el daño esta en el segundo nivel y como también el peso cuatro es el más representativo, sin embargo aunque en magnitud los pesos son mas grandes que los pesos del 1er nivel, la relación en cuanto al incremento de daño no es muy clara, refiriéndonos a que el valor del peso cuatro que es el más representativo no guarda relación al aumento de daño del 10%, 20%, 30% y 40% respectivamente.
Figura 3.1.16 Magnitud de los pesos del segundo nivel cuando se aumenta el daño en este nivel.
84
Modelo para identificar una relación de daño
Se modelo un edificio de dos niveles y analizando la norma entre las respuestas dinámicas se buscó identificar alguna relación de daño, sus características son las siguientes; m1=0.40775 , k1=200 ton/cm, m2=0.40775
k2=200 ton/cm, cuando se degrada la rigidez en los siguientes porcentajes; 0.25, 0.50 y 0.75%.
En la Figura 3.2.1 se muestra la variación del error de las respuestas de cada piso respectivamente, calculado como la norma. Se puede observar que la magnitud del error es mayor para el piso 2 aún cuando el daño está en el piso 1.
/cm
s
85 En la Figura 3.2.2 se muestra la variación del error del piso 1, se observa que primero incrementa cuando se aumenta el daño hasta en 50 % pero luego disminuye cuando el daño es de 75% y el error en el piso 2 incrementa conforme aumenta el daño.
86 En la Figura 3.2.3 se comparan los errores de las respuestas del mismo piso 1, cuando el daño está en uno y cuando el daño está en 2. Se observa una tendencia de incremento del error para el piso 1 cuando el daño está en 1, pero el error aumenta y disminuye en el caso del piso 2 cuando se aumenta el daño.
87 Como en el caso anterior en la Figura 3.2.4 se muestra la tendencia del piso 2 cuando el daño está en el piso1 y cuando está en el piso 2, observándose una tendencia a aumentar cuando el daño está en el piso 2 y se aumenta el daño, pero no cuando el daño está en el piso 1.
88
Conclusiones
• La detección de daño en edificios como en otras obras civiles a través de los años en México ha tomado más importancia debido a la alta sismicidad que ocurre periódicamente y esto afecta directamente en las propiedades estructurales de los edificios, por lo que después de los eventos sísmicos se realizan revisiones para saber el estado de integridad de los elementos estructurales de los edificios, pero los métodos para realizar dichas revisiones aún no son totalmente adecuadas, por estas razones en este trabajo se propone una nueva metodología que ayude a realizar evaluaciones para la detección de daño, concluyendo que aún se deben hacer mejoras a su procedimiento para que la metodología sea adecuada.
• En algunos experimentos los pesos que la RNAP calcula tienen la relación suficiente con la localización del daño hasta 40% de degradación de rigidez.
89
• En algunos experimentos se muestra cómo se localizó el daño para los casos dos y tres cuando se incrementaba el porcentaje de daño, sin embargo cuando se incrementó al 50% o más, la localización de daño no fue adecuada. Por lo que se concluyó que utilizando el modelo lineal de la ecuación de movimiento los pesos calculados por la RNAP no tienen suficiente relación con la localización del daño.
• En todos los experimentos, los errores de entrenamiento y de prueba resultaron muy adecuados, y por esa razón la predicción que hace la RNAP se puede suponer como efectiva. Para ejemplificar en el caso del experimento de la sección anterior, los errores de entrenamiento oscilan entre 1.85E-06 y 2.7169E-06 y los de prueba entre 2.1943E-07 y 3.6801E-07. Observándose que son valores muy pequeños y que podrían equivaler a cero para fines ingenieriles.
• La RNAP tiene un mejor aprendizaje cuando se le aporta una mayor cantidad de datos de entrada.
• Fijando un umbral para los máximos y mínimos de salida se puede tener mejores resultados y menores errores de predicción.
• Cuando se aumenta la potencia de los polinomios homogéneos se puede determinar una mejor aproximación en la predicción, sin embargo la potencia 2 es aceptable y se obtienen buenos resultados.
• Resulta una mejor aproximación de predicción cuando se utilizan exponentes fraccionarios.
• El número de valores previos puede variarse para intentar un mejor entrenamiento de la RNAP, sin embargo esto puede ser innecesario, ya que los valores de los errores entre un modelo entrenado con dos valores previos son demasiado similares a otros entrenados con más de dos valores anteriores.
Dr. Francisco José Rivero Ángeles Dr. Eduardo Gómez Ramírez Dr. José Alberto Escobar Sánchez
Dr. Roberto Gómez Martínez
Dr. Maria I. Todorovska Universidad del Sur de California
AGRADECIMIENTOS
Muchas
gracias
DETECCIÓN DE DAÑO EN
SOLDADURA DE RISERS RÍGIDOS EN
AGUAS PROFUNDAS, UNA
Detección de daño en soldadura de risers rígidos en aguas profundas, una metodología propuesta
Grieta
Sección transversal dañada del riser.
7.00E+07 7.50E+07 8.00E+07 8.50E+07
0 5 10 15 20
Rig id e z a f le x ió n d a ñ a d a K* ( N -m 2 )
Profundidad de grieta "a" (mm)
Detección de daño en soldadura de risers rígidos en aguas profundas, una metodología propuesta
Daño en 900m
-0.25 -0.2 -0.15 -0.1 -0.05 0 0.05 0.1 0.15 0.2 0.25
0 1000 2000 3000
A c e le ra c ió n ( m /s 2 ) Tiempo (s) Sin daño Con daño Degradación de rigidez a flexión: 15%
Aceleración de sensor localizado a 1800m
Detección de daño en soldadura de risers rígidos en aguas profundas, una metodología propuesta
Periodos teóricos y periodos obtenidos con el método DDF, ambos estados.
Detección de daño en soldadura de risers rígidos en aguas profundas, una metodología propuesta
Modos extraídos con el DDF.
900 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
697 1197 1697 2197 2697
Des p la za m ie n to m o d a l Longitud (m)
Modos sin daño Modos con daño
Detección de daño en soldadura de risers rígidos en aguas profundas, una metodología propuesta
-1.00E-04 4.00E-05 1.80E-04
600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800
(DF
M
)
Longitud (m)
Paso 6 – Verificar la localidad de daño a través del método de Diferencia de Formas Modales (DFM).
-2.50E-06
600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800
(DPM
)
Longitud (m)
-4 1
600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800
(ID Ph
i´
)
Longitud (m)
Detección de daño en soldadura de risers rígidos en aguas profundas, una metodología propuesta
Daño en 1600m, 10 % de degradación en rigidez
-1.1E-05 -6E-06 -1E-06
600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800
(DFM
)
DFM y DPM para el modo con periodo de 7.74s con daño en 1600m
-1.19E-07 -6.90E-08 -1.90E-08 3.10E-08 8.10E-08
600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800
(DPM
)
Longitud (m)
Paso 6 - Verificar la localidad de daño a través del método de Diferencia de Formas Modales (DFM).
1611m 1 %
Detección de daño en soldadura de risers rígidos en aguas profundas, una metodología propuesta
SCR 2000, daño en 360m, 16.8 % K*
Ubicación de sensores en el SCR 2000
0 200 400 600 800 1000 1200 1400 1600 1800 2000
0 500 1000 1500
A ltu ra de l fon do m a rino (m )
Distancia horizontal (m)
Daño
Detección de daño en soldadura de risers rígidos en aguas profundas, una metodología propuesta
-0.058 -0.008 0.042
300 600 900 1200 1500 1800 2100 2400 2700
(DFM
)
DFM y DPM para el modo con periodo de 9.94s.
-0.0007 -0.0002 0.0003
300 600 900 1200 1500 1800 2100 2400 2700
(DPM
)
Longitud (m)
Paso 5 y 6 – Verificar la localidad de daño a través del método de Diferencia de Formas Modales (DFM).
325m 10 %