10 Integrales dobles 3. Complemento.pdf
Texto completo
Figure




Documento similar
El método propuesto modela las curvas de carga mediante las llamadas integrales fracciónales o acumulativas de una función objetivo f(t) que debe determinarse. Las curvas de
Se dice que la integral impropia de Riemann de f es convergente en I si son convergentes las integrales impropias de las funciones Re( f ) y Im( f ) en I en cuyo caso la
Los estados de situación financiera consolidados intermedios al 31 de marzo de 2021 y 2020 y los estados consolidados de resultados integrales intermedios, de
Se concluye que es necesaria la contratación de la "CONSTRUCCIÓN DE PROYECTOS INTEGRALES AP Y S EN JALOA EL GUASMO, HUALCANGA SAN NICOLAS, LUIS LÓPEZ Y MOCHAPATA - CANTÓN
Otros resultados integrales antes de impuesto a la renta (369) 610 Impuesto a la renta relacionado con otros resultados integrales (668) 13 Total otros resultados integrales que
(b) Try to draw the graph of a continuous function with domain and range in that does not have a fixed point.. What is
En diciembre de 2004, gracias al impulso del movimiento feminista y después de décadas de lucha, entra en vigor la Ley Orgánica de Medidas de Protección Integral contra
usando una terminologia muy extendida por la ciencia Economie^, la R.A. no - puede reducirse a unos simples cambios conyunturales, puesto que ella, en el fondo, debe irapulsar

![Figura 7: Subdivisi´ on del sector de corona circular determinado por r ∈ [a, b], θ ∈ [α, β].](https://thumb-us.123doks.com/thumbv2/123dok_es/5704466.136078/14.918.326.564.485.694/figura-subdivisi-on-sector-corona-circular-determinado-θ.webp)


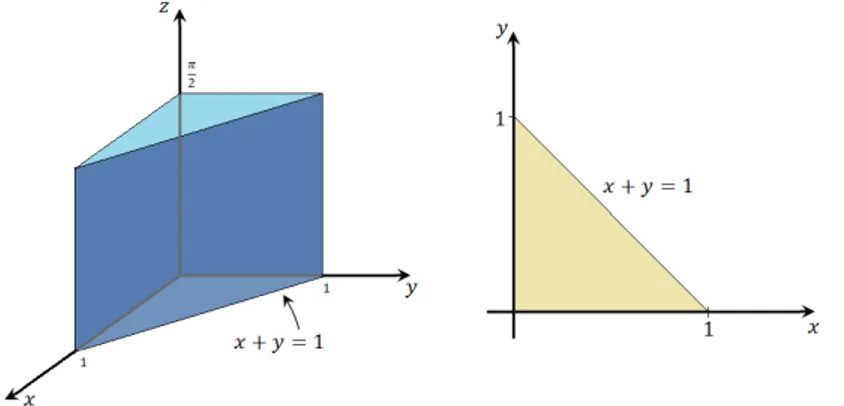
![Figura 11: “Caja cil´ındrica” determinada por r ∈ [a, b], θ ∈ [α, β], z ∈ [s, t].](https://thumb-us.123doks.com/thumbv2/123dok_es/5704466.136078/30.918.366.523.270.480/figura-caja-cil-ındrica-determinada-por-θ-α.webp)