TOPOLOGÍ A FRACTAL DE M ATERI ALES
COM PACTADOS ALEATORI AM EN TE
TESI S
QUE PARA OBTENER EL GRADO DE
DOCTOR EN CI EN CI AS
CON ESPECI ALI DAD EN
I N GEN I ERÍ A M ECÁN I CA
PRESENTA
M. en I . Rolando Cort és Mont es de Oca
DI RECTOR
Dr. Alexander Balankin
México, Dist rit o Federal, Junio de 2010
SECCIÓN D E ESTU D IOS D E POSGRAD O E IN VESTIGACIÓN ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
DEDICATORIAS:
A MI FAMILIA:
A mi esposa Lilia Flores Por su apoyo y compresión.
A mis hijos Lilia Lizbeth y Rolando Daniel
Por acompañarme y construir un estímulo para seguir adelante.
A MIS PADRES:
Dionisio Cortés Montes
Guillermina Montes de Oca Calzada
Con agradecimiento por educarme y transmitirme valores que me orientaron a seguir y alcanzar metas.
A MIS HERMANOS:
Al Instituto Politécnico Nacional y a la Sección de Estudios de Posgrado e Investigación de la Escuela Superior de Ingeniería Mecánica y Eléctrica, por haberme brindado la oportunidad de instruirme.
Al Dr. Alexander Balankin en primer instancia por ser una persona de gran calidad moral y seguidamente por su apoyo incondicional en dirigirme mi doctorado.
Índice
Resumen………... Abstract………. Objetivo………. Metas……….. Justificación……….
Capítulo 1 Introducción………..……….
Capítulo 2 Estado del Arte……….………..…
Capítulo 3 Metodología Experimental…..………
3.1 Metodología Experimental………
3.2 Desarrollo de la investigación……….. 3.2.1 Material utilizado para la investigación………..
3.2.2 Elaboración de probetas de papel……….. 3.3 Relajación de la deformación………..
3.4 Dimensión fractal de masa………...
3.5 Geometría del papel arrugado……….
3.6 Rugosidad de las bolas de papel y de las hojas extendidas………..
3.7 Perforación de las bolas de papel a lo largo de su diámetro……….
3.8 Dimensión fractal global………...
Capítulo 4 Análisis y Discusión de Resultados ………..
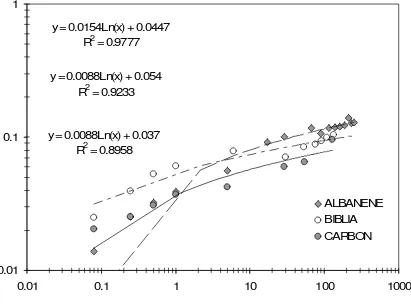
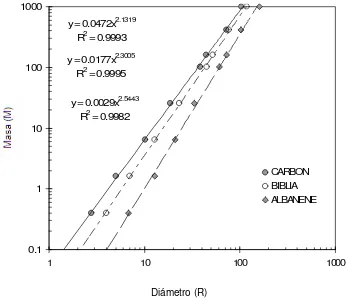
4.1 Cálculo de la velocidad de relajación………. 4.2 Obtención de dimensión fractal de masa de las bolas de 3 tipos de papel…
4.3 Análisis de la geometría de la rugosidad del papel………. 4.4 Determinación de dimensión fractal global de bolas atravesadas por hilos…
8 9 10 11 12
16
32
37
37
37
38
38
41
42
43
45
47
49
51
51
55
59
Conclusiones………...
Anexo 1 Datos de la relajación de esfuerzos………. Anexo 2 Diámetros y masa de los papeles………. Anexo 3 Publicaciones derivadas de la tesis……….
68
69
Lista de figuras
1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1.10 1.11 1.12 1.13 1.14 1.15 1.16 3.1 3.2 3.3 3.4Hoja delgada arrugada anualmente………...
Plegado de (a) Corteza terrestre (b) una roca en varias capas………...
Fotos de un planificador de doblez en un artón………...
Doblamiento chino y japonés (Origami)………...
Forma de arrugamiento característico de (a) papalote (b) doble cono…...
Muestra una de hoja de papel que ha sido ligeramente arrugada con las
manos……….
Muestra pliegues y vértices en estado arrugado………
El cono-d aparece cuando una fuerza F de abajo empuja el centro de una
plana inicialmente contra el borde de un recipiente cilíndrico. Dos
conjuntos de sistemas de coordenadas son mostradas………...
Esquema de la región céntrica de un cono-d. El área creciente es
mostrada en blanco. Directores negros se muestran como líneas. Varios
directores o líneas convergen alrededor de la punta de la creciente……...
Máquina de plegado continúo de hojas delgadas………..………
Padrón Chevron doblada desde una hoja delgada………..
Diferentes tipos de patrones de papel………..
Patrón de cobre………
Patrón de aluminio………..
Dos tipos diferentes de patrones de material compuesto……….
Proceso de doblado de hojas delgadas de aluminio y papel y ejemplo de
aplicaciones, como decoración y absorción de impactos……….
Tamaños de las hojas de papel para generar superficies arrugadas….……
Conjunto de bolas de papel arrugadas o comprimidas manualmente………
Representación esquemática de la medición de los incrementos del
diámetro en función del tiempo para obtener la deformación ε…………...
3.5
3.6
3.7
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
Configuración experimental de la geometría de los dobleces, donde ni
representa a cada uno de los nodos y li a las líneas………
Esferas arrugadas con hilos que cruzan a lo largo de su diámetro mayor y
a lo largo de diámetros aleatorios………
Trayectoria de los hilos en las hojas de papel extendidas………..
Comportamiento de la relajación de los tres tipos de papeles……….
M contra R, que determina la dimensión fractal de masa de los papeles..
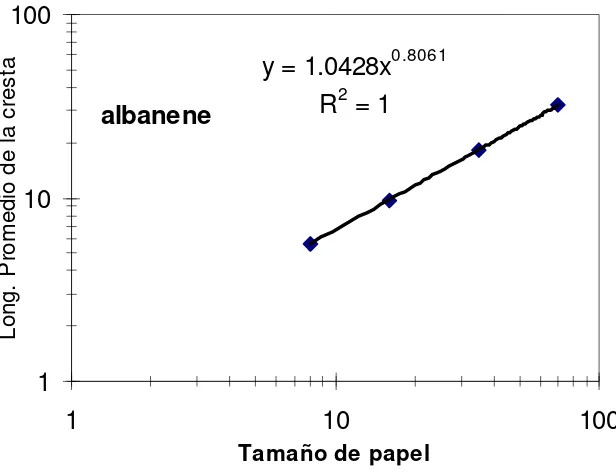
Longitud promedio de las crestas entre nodos por tamaño de papel……….
Longitud total promedio de los dobleces en todo el papel………
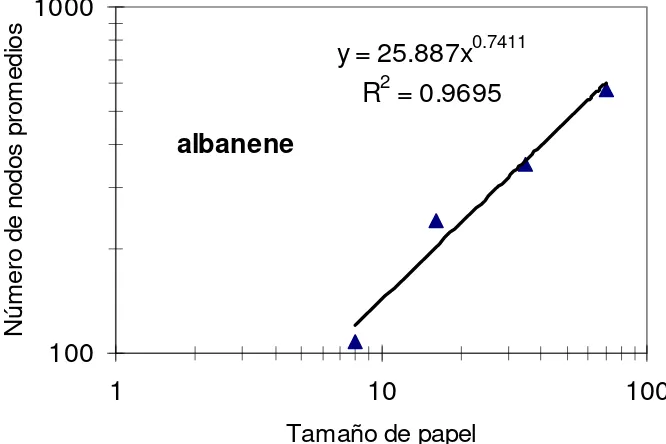
Número de nodos por tamaño de papel ………..
B
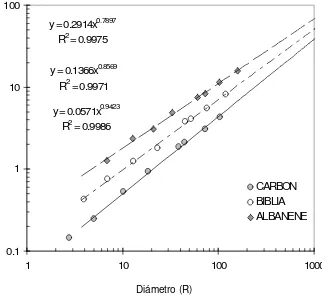
σ contraR para los tres tipo de papel………
Red de dobleces formados durante el proceso de arrugamiento para hojas de papel albanene de tamaño L=8 (1), 16 (2) y 35 (3)………..
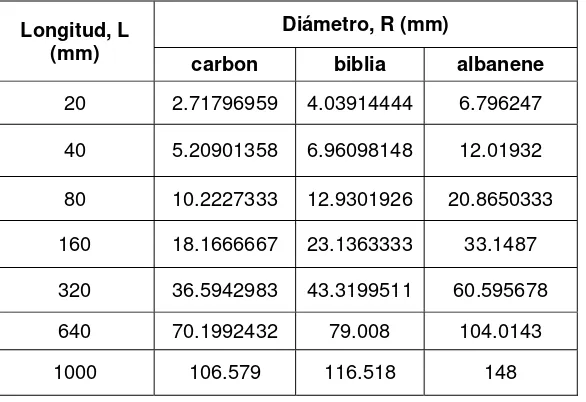
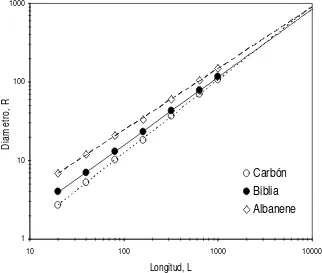
Diámetro R contra Longitud L para los tres tipo de papel………. 45
47
48
54
58
60
61
61
64
64
66
Lista de tablas
3.1
3.2
3.3
3.4
4.1
4.2
4.3 4.4
4.5
4.6 4.7
4.8
4.9
4.10
4.11
Características del papel utilizado………
Forma, dimensiones y cantidades de las probetas de los 3 tipos de
papel……….
Espesor (h),densidad de superficie (ρA), Módulo de Young (EL, ET),
Esfuerzo de cedencia (σYl, σYT)………
Forma, dimensiones y Cantidades de Probetas de papel albanene…….
Incremento en la longitud del diámetro en 9 días………..
Incremento en la deformación en las bolas en los 9 días………...………
Datos de los diámetros y pesos de las bolas con L=70………..… Datos de los diámetros y pesos de las bolas con L=35………..
Diámetros promedio (R) y masas promedio (M) de los papeles..………..
Datos estadísticos del papel albanene..……….
Dobleces en cada nodo, tamaño 80x80 mm2………
Dobleces en cada nodo, tamaño 160x160 mm2………
Dobleces en cada nodo, tamaño 350x350 mm2………
Diámetros de los papeles y su correspondiente desviación estándar…...
Tamaño L de los papeles y sus diámetros promedios R………...
38
41
43
48
52
53
56
57
58
59
62
62
63
63
Nomenclatura
λ D ε A ε B ε C ε 0 d f d 0 t Δ i t Δ t h YL σ YL σ M D L E T E L A ρ R M T lFactor de escalamiento
Diámetro de las bolas de los papeles arrugados (m)
Deformación (adimensional)
Deformación en bolas de papel albanene (adimensional)
Deformación en bolas de papel biblia (adimensional)
Deformación en bolas de papel carbón (adimensional)
Diámetro inicial de la bola de papel antes de la relajación (mm)
Diámetro final de la bola de papel después de la relajación (mm)
Intervalo de tiempo (s)
Subintervalo de tiempo (s)
Tiempo total de relajamiento (s)
Espesor de los papeles (albanene, biblia y carbón)
Esfuerzo de cedencia longitudinal (MPa)
Esfuerzo de cedencia transversal (MPa)
Dimensión fractal (adimensional)
Módulo de Young longitudinal (MPa)
Módulo de Young transversal (Mpa)
Tamaño de los lados de la probeta cuadrada de papel (cm)
Densidad de superficie (g/mm2)
Longitud aleatoria del diámetro de las bolas de papel (mm)
Masa de las bolas de papel (gr)
n
n
N
Número de nodos o intersecciones de la rugosidad (adimensional)
Resumen
Este trabajo presenta un estudio, sobre el efecto de los dobleces (arrugas) en
láminas de papel, que han sido sometidas a un proceso irreversible de arrugamiento;
así como las propiedades de escalamiento de hojas arrugadas aleatoriamente de
diferentes tipos de papel en los estados doblados y desdoblados. El reporte presenta
también la geometría estadística de las redes de crestas dobladas, que se observan
claramente después de que se aplana la hoja doblada. Para este estudio se
analizaron varios tipos de especimenes de bolas de papel arrugadas, con diferentes
tamaños de hoja que fueron desde L0 =2 hasta 100 cm, de longitud con la relación de escalamiento L=λL0 donde, L es el tamaño de la hoja (cm). Los factores de
escalamiento fueron λ =1, 2, 4, 8, 16, 20, 32 y 50; y por lo menos 30 hojas de cada
tamaño y de cada tipo de papel fueron usadas. El análisis experimental se realizó por
medio del estudio estadístico de la red de dobleces, de las bolas arrugadas de tres
tipos de papel, (albanene, biblia y carbón), para posteriormente determinar la
dimensión fractal de masa de cada una de las bolas de papel, que son DM =2.54
para el papel albanene; DM =2.30 para el papel biblia y DM =2.13 para el papel
carbón. También, se encontró, por medio del estudio de estadística de la red de
dobleces, que la distribución en la longitud de los pliegues se ajusta mejor, por la
distribución normal-log. Además, se llevó a cabo el estudio de la propiedad de
auto-similitud en bolas de papel al insertar algunos hilos de seda a través de todas las
bolas en su diámetro máximo y otros hilos al azar para analizar su estructura interna.
También se realizó éste análisis experimental por medio del estudio estadístico de la
red de dobleces, determinando de esta manera la dimensión global fractal del
conjunto de bolas insertadas por los hilos de seda. Los resultados fueron: para papel
Abstract
This work introduces a study, about the effects of the folds (Wrinkles) in sheets of
paper, which have been submitted to an irreversible process of creasing, as well as
the scaling properties of randomly crumpled sheets of different kinds of paper in
folded or unfolded states. The report also presents the statistical geometry of folded
ridged networks, clearly seen after the folded sheet is flattened. For this study
numerous kinds of specimens of crumpled paper balls in diverse sizes were analized.
This was from L0 =2 to 100 cm, long with the scaling relationL=λL0, where L is the size of the sheet (cm). The scaling factors were λ=1, 2, 4, 8, 16, 20, 32 and 50;
and at least 30 sheets of each size for each kind of paper were folded. The
experimental analysis was performed by using a statistical study of the network of
folds from the crumpled balls in three kinds of paper, (albanene, biblie y carbon); to
later determine the fractal dimension of mass from each one of the paper balls. It was
54 . 2 = M
D for the albanene paper; DM =2.30 for the biblie paper; and DM =2.13 for
the carbon paper. It was also found, through the statistical study of the network of the
folds, that the distribution in the length of the folds is best suited with a log-normal
distribution. Besides, the study of the property of self-similarity in paper balls was
carried out by inserting some silk threads throughout the balls in their maximum
diameter and other silk threads random to analize their internal structure. This
experimental analysis was also performed by means of a statistical study of the
network of folds, determining in this manner the global fractal dimension of the set of
balls inserted by the silk threads. The results were: for the albanene paper D=0.94;
Objetivo
Estudiar el comportamiento topológico fractal de hojas delgadas de papel
comprimidas aleatoriamente, en los estados doblados y desdoblados.
Estudiar las propiedades de escalamiento de la estructura interna de las hojas
Metas
• Calcular la velocidad de relajación de la deformación en las bolas de papel.
• Determinar el tiempo que dura la relajación de esfuerzos en bolas de los tres tipos de papeles analizados.
• Determinar la dimensión fractal de masa, de las bolas de papel de los tres tipos.
• Calcular el número de líneas, el número de bordes así como el número de conexiones de las líneas que llegan a cada borde, en hojas de papel de diferentes tamaños después de ser desarrugadas y desdobladas.
• Determinar la longitud de las líneas o rugosidad existente en las hojas de papel.
• Est ipular el núm ero t ot al de int ersecciones en las hoj as de papel, cuando ést as han sido at ravesadas por hilo a lo largo de su diám et ro
• Det erm inar la dist ancia de ent rada y de salida de los hilos que at raviesan a las bolas de papel.
• Calcular la relación exist ent e ent re los diferent es t am años de bolas de papel aguj eradas con respect o al núm ero t ot al de aguj eros.
Justificación.
En los últimos 20 años, tres conceptos han aparecido sistemáticamente en las
ciencias físico-matemáticas y naturales, incluyendo la biología; a saber, la
complejidad, la fractalidad y el caos. Estos conceptos, íntimamente relacionados
entre si, han dado lugar a una nueva rama de la ciencia que bien pudiera llamarse la
ciencia de los sistemas complejos. En muchos casos se dice que un sistema es
complejo cuando su comportamiento y evolución en el tiempo, son muy sensibles a
las condiciones iniciales o a perturbaciones pequeñas, de manera que las posibles
trayectorias a lo largo de las cuales que pueda evolucionar, sean variadas y
complejas. Por consiguiente, dentro de la complicada evolución de éstos sistemas a
través del tiempo, suelen formarse estructuras geométricas irregulares o “patrones
irregulares” cuyas características geométricas no se pueden describir por la
geometría euclidiana convencional [1].
Por lo que hay una nueva herramienta geométrica que puede hacer frente a éste tipo
de formas irregulares. La Teoría Fractal, originalmente propuesta por Mandelbrot.
Como formas irregulares, tenemos las nubes en el cielo, las líneas de una costa en
un mapa, los árboles y las montañas por mencionar algunos ejemplos. La teoría
Fractal de Mandelbrot, nos provee de un mecanismo para extraer una regla o la
regularidad oculta en las formas irregulares. [2].
Una hoja elástica es un ejemplo de un sistema físico simple, la hoja elástica será
deformada para crear una estructura singular espontánea, el complejo
comportamiento de la hoja de papel, llega cuando fuerzas externas son ejercidas
sobre él, transformándose en una bola, la deformación de la hoja se convierte en
energía, que se centra en sólo algunas regiones, distribuidas de manera uniforme a
través de la hoja. Sorprendentemente dos estructuras singulares llamadas vértices y
crestas son generadas, las cuales juegan un papel importante en la estructura de la
estructuras son consecuencia de dos o mas vértices, donde también hay
concentración de energía [3].
En la década pasada, ha habido un gran interés en los procesos de arrugamiento,
que van desde el plegamiento de las membranas de las células de la sangre, hasta
el pandeo de la corteza terrestre. En particular, la geometría estadística de
membranas arrugadas aleatoriamente, al igual que las hojas arrugadas azar [4,5,6].
Se sabe, que mediante el estudio del arrugamiento del papel, es posible conocer
hoy en día, el comportamiento de muchas casos de las que nos encontramos
rodeados y que sin darnos cuenta, éstas están completamente vinculadas con los
procesos que lleva consigo el arrugar el papel [7].
Anteriormente se ha visto que se ha adoptado el término fractal, para objetos
geométricos irregulares con la propiedad de autosimilitud e invarianza bajo
concentración y expansión. Posteriormente se señaló que los fractales abren un
nuevo campo entre el excesivo orden geométrico Euclidiano y el caos geométrico de
la rugosidad y de la fragmentación. Esta geometría encuentra su base en las
estructuras, superficies o curvas complejas que ocupan espacio mediante el
plegamiento, ramificación y que presentan la propiedad de la autosimilitud. La
autosimilitud es una propiedad intrínseca y genérica del conjunto fractal y se refiere a
que cada parte de una forma es geométricamente similar al todo, o a que sus
momentos estadísticos son similares e independientes del submuestreo, sin
embargo, ésta propiedad nunca se verificó para la materia doblada aleatoriamente.
Es por ello el estudio de éstos fenómenos, la aplicación de la geometría fractal en
bolas de papel arrugadas, que como se sabe se han venido estudiando
ampliamente en las últimas décadas [8].
Durante varios, años, se han realizado un considerable número de investigaciones
teóricos y experimentales, para entender la geometría del doblez y su efecto en el
intrigantes fenómenos mecánicos es que casi todos los materiales deformados
exhiben cambios dimensionales en direcciones laterales, sin corresponder a las
tensiones. Este fenómeno es conocido como efecto de Poisson. Por lo que en éste
REFERENCIAS
[1] Jayanth R. Banavar1, Amos Maritan2, Cristian Micheletti2 & Flavio Seno3., ”Geometrical aspects of protein folding” (2005).
[2] M. Daniel, S. Baskar and M. M. Latha “Fractal dimension and Tertiary
Structure of Proteins”, Physica Scripta. Vol 60 (1999).
[3] T A Witten “How soft matter correlates: three examples”, J. Phys: Condens. Matter 17 (2005).
[4] K. A. Matan, R. B. Williams, T. A. Witten and S. R. Nagel. “Crumpling a Thin Sheet”. 2002. Physical Review Letters. Page 076101-1 - 076101-4
[5] Blair Daniel L. and Kudrolli Arshad., “Goemetry of Crumpled Paper” PRL 94,166107 (2005).
[6] Sultan Eric and Boudaoud Arezki., “Statistics of Crumpled Paper” Phisical Review Letters (2006).
[7] Sahraoui Chaieb and Francisco Melo., “From creases to conical defletions in a buckled thin sheet: stress focusing vs singularities in strong deformations of a thin elastic sheet” Journal of the Mechanics and Physics of Solids 48 (2000).
[8] Eric M. Kramer and Tomas A. Witten., “Stress condentation in crushed elastic manifols” 2005
[9] B. A. DiDonna and T. A. Witten. ”Anomalous Strenght of Membranes with
Capitulo 1 Introducción
La física de materiales condensados, tradicionalmente se ocupa del estudio de
objetos “duros”; sin embargo, existen materiales suaves, como los polímeros y otros
sistemas complejos; el estudio de ellos constituye un nuevo campo de investigación
al que se ha denominado “materiales condensados suaves”, existen ejemplos de
cómo la materia condensada ha crecido más allá de su inicial dominio de los
polímeros, coroides, soluciones surfatantes y cristales líquidos. Hay otros tres
ejemplos sobre la materia condensada suave: primero una hoja elástica es un
ejemplo de un sistema físico simple. Aquí una simple hoja de materia elástica puede
ser deformada para crear una estructura singular espontánea llamada Cone-d. El
complejo comportamiento de una hoja de papel llega cuando fuerzas externas son
ejercidas sobre él, quedando arrugada la hoja en forma esférica. La deformación de
la hoja se convierte en energía que se centró en sólo algunas regiones distribuidas
de manera uniforme a través de la hoja. Sorprendentemente dos estructuras
singulares llamadas vértices y crestas juegan un papel importante. Un vértice es la
concentración de energía y esfuerzos. La cresta de las estructuras es consecuencia
de dos o más vértices como se puede observar en la figura 1.1. Un segundo caso es
el de una estructura denominada membrana líquida, y por último se tienen los materiales granulares que recientemente han despertado el interés de los físicos en
cuestiónde materia suave [1].
Un asunto común de la investigación en la física condensada de la materia, es la
forma o la manera en la cual la energía externa se almacena o se comprime en una
sustancia o elemento particular. Si se habla de una energía externa sobre un sistema
y ésta es una perturbación débil o uniforme, se puede decir que entonces la energía
será almacenada uniformemente sobre una sustancia. Pero si este fenómeno de
perturbación es fuerte, sucede a menudo que este fenómeno es llamado
condensación. En estos casos la perturbación de la energía se condensa en
espacios muy pequeños del sistema. Muchas personas arrugamos al día muchas
cosas, pero la pregunta que se debe hacer es: ¿Qué estructuras internas se han
modificado para absorber la energía que se ha introducido y cuanto trabajo se tuvo
realmente que hacer para efectuar este cambio? Como se sabe las hojas arrugadas
son más fuertes y resistentes, que las que no lo son, las propiedades de
escalamiento explican que las arrugas son condensaciones de cadenas y por lo tanto
de energías que hacen que una hoja arrugada sea más resistente; de ahí la
importancia de analizar el arrugamiento de las mismas [2].
El arrugar un pedazo de papel por ejemplo; la tensión en las crestas y los picos
puede llegar a ser tan grande que el efecto de arrugamiento puede ser irreversible
hasta un punto, ya que si posteriormente el papel es extendido sobre una superficie
plana, este mostrará algunas arrugas visibles a simple vista, otra característica
importante es que la rigidez de la membrana aumenta de forma rápida y efectiva
incrementando el grado de arrugamiento. El último límite para arrugar una membrana
seria prensarlo de forma uniforme correspondiente únicamente al volumen de la
membrana. En la práctica este límite no puede ser alcanzado ya que al apretar un
pedazo de papel tan duro entre las manos, los resultados suelen ser una bola de
papel que contiene alrededor de 75% de aire [3].
Es sabido que el relleno de papel arrugado tiene una propiedad muy interesante;
esta propiedad es que es resistente a la compresión. Esto es que en un papel
arrugado tiene en cada arruga energía almacenada que tiende a enderezarse de
puede tener grandes aplicaciones. En este sentido, en los últimos años ha habido un
gran interés en el estudio del plegado de papeles [4].
Por lo que se hará mención de la evolución sobre el estudio de plegamientos. La
corteza terrestre sufre un proceso de plegamiento, el calor es un factor importante en
las profundidades del manto terrestre y puede convertir las rocas de frágiles a
dúctiles, que son factores de plasticidad y rigidez de la roca, estos factores influyen
en el comportamiento mecánico de la roca. La cantidad de tiempo en que las rocas
están sometidas a tensión es también importante, así como la temperatura; ver
figuras 1.2 (a) y (b) [5,6].
(a)
(b)
La piel es otro material arrugado, las arrugas o pliegues aparecen cuando la piel se
deforma debido a la contracción muscular. Extensas investigaciones han establecido
que durante el proceso de envejecimiento, la estructura y las propiedades mecánicas
de la piel son modificadas. Las arrugas y los pliegues son muy delgados en una piel
joven y vistosa en una piel de más edad. Otro ejemplo son las frutas como las
manzanas y las ciruelas, éstas se componen de una piel fina que rodea un interior
suave de agua, proteínas, lípidos, carbohidratos, ácidos orgánicos, fibra y algunos
materiales más. Cuando la fruta se seca, el agua es extraída del fruto y el volumen
de la parte blanda de los frutos disminuye y como resultado se encoje la piel, dando
lugar a las arrugas. Las ciruelas pasas son un claro ejemplo de este fenómeno [7].
El plegado es un proceso muy común en nuestras vidas, y va desde el nivel
macroscópico (plegado de papel para envolver un regalo) hasta el nivel
microscópico (plegado de proteínas). El estudio del plegado es desde una
perspectiva de planificación de movimiento. Es decir, determinar una secuencia de
movimiento, para transformar una superficie plana en una determinada forma. El
objetivo no es sólo doblar por doblar sino, analizar el proceso de doblado. El objetivo
principal es estudiar y analizar, cómo la naturaleza realiza este proceso, simplemente
con mirar a nuestro alrededor, se puede dar uno cuenta de que el mundo está
compuesto por una infinidad de pliegues; las plantas, los animales, nosotros
mismos, nuestro planeta, por mencionar algunos. En la figura 1.3 se muestra la
secuencia de doblez de una hoja transformándola en un forma [8].
El origami es el antiguo arte de doblamiento chino y japonés. Este arte viene desde
épocas muy lejanas. En la geometría del plegado del papel, una línea recta se
convierte en un pliegue, en la figura 1.4 se muestra el doblamiento chino y japonés.
De una manera más sencilla de explicar, los mapas origami, son una serie de pasos
o dobleces sucesivos llevados a cabo de una forma sistemática para la obtención de
una estructura [9,10,].
Figura 1.4 Doblamiento chino y japonés (Origami)
Otro estudio sobre el doblado del papel a la mitad, más de siete u ocho veces fue
resuelto por Britney Gallivan [11]. En éste reto era comúnmente sabido que era
imposible de hacer, durante muchos años este problema había sido discutido por
mucha gente, incluso por matemáticos. A Britney se propuso doblar a la mitad 12
veces cualquier cosa, después de muchos experimentos ella pudo doblar una lámina
de oro 12 veces a la mitad, desarrollando así una ecuación para determinar los
límites del plegamiento en cualquier dimensión dada. La ecuación es la siguiente:
L=(πt/6)(2n+4)(2n-1)---(1) Donde :
n=número de dobleces que se quiere hacer
t= grosor del papel
Esta ecuación dice que dependiendo de la cantidad de dobleces que se requiere
hacer y el grosor del papel, es posible obtener el tamaño mínimo que debe tener el
papel para poder doblarlo esa cantidad de veces. La base del problema es el grosor
del papel y el número de capas, que crece de forma exponencial a medida que se va
doblando a la mitad [11].
El arrugamiento de una pieza de papel deja marcas permanentes, mostrando una
concentración de tensión. Es necesario examinar como responden los materiales a
fuerzas externas. De esta forma, los materiales responden a dichas fuerzas con una
deformación elástica (en la que el material vuelve a su tamaño y forma original
cuando se elimina la fuerza externa), una deformación permanente a una fractura. La
elasticidad es la propiedad de un material que le hace recuperar su tamaño y su
forma original después de ser comprimido o estirado por una fuerza externa. La
distancia entre las moléculas de un material no sometido a esfuerzos depende de un
equilibrio entre las fuerzas moleculares de atracción y repulsión. Cuando se aplica
una fuerza externa que crea una tensión en el interior del material, las distancias
moleculares cambian y el material se deforma. Si las moléculas están firmemente
unidas entre sí, la deformación no será grande incluso con un esfuerzo elevado. En
cambio si las moléculas están poco unidas, una tensión relativamente pequeña
causará una deformación grande. Por debajo del límite de elasticidad, cuando se
deja de aplicar la fuerza, las moléculas vuelven a su posición de equilibrio y el
material elástico recupera su forma original. Más allá de su límite de elasticidad, la
fuerza aplicada separa tanto las moléculas, que no pueden volver a su punto de
partida, y el material queda permanentemente deformado o se rompe. La plasticidad
es aquella propiedad que permite al material soportar una deformación permanente
sin fracturarse. También, una fuerte deformación de una hoja de material sólido,
frecuentemente deja en ésta un estado arrugado, teniendo o dejando puntos con
curvaturas marcadas sobre el material. En estas curvas marcadas, hay crestas de
tamaños variables. En estos puntos, hay flexión y estiramiento del material, esta
energía se concentra en fracciones de la hoja. Los puntos de deformación parecen
apareciendo cuando la fuerza externa actúa sobre ellos. Se pueden ver ciertas
formas de arrugamiento característico. En forma de cono, de doble cono, de
papalote. Estas formas van a depender del ángulo y la fuerza que se aplique al
material, así como también de los enlaces microscópicos del tipo del material, en la
figura 1.5 (a) y (b) se muestran estas formas [12,13].
(a) (b)
Figura 1.5 Forma de arrugamiento característico de (a) Papalote (b) Doble cono
El arrugamiento de una hoja de papel delgado es un fenómeno que se puede
encontrar en la vida cotidiana; sin embargo, los sistemas que rigen éste fenómeno,
es muy complejo si antes no se tiene una drástica simplificación como base. Al
mismo tiempo éste fenómeno exhibe una serie de comportamientos intrigantes para
la física moderna que estudia la materia blanda como son transición de fase, el
escalamiento y la condensación de energía. Se puede ver también el arrugamiento
de una hoja como una colección de crestas y vértices, en los que cada uno
representa energía. Es decir; son caminos que la energía toma en las membranas
para pasar de un estado de arrugamiento a otro. Por lo tanto, para entender el
arrugamiento; es necesario comprender la fuerza y la rigidez de las crestas, en la
Figura 1.6 Muestra una hoja de papel que ha sido ligeramente arrugada con las manos
Figura 1.7 Muestra pliegues y vértices en estado arrugado
.
Hojas delgadas elásticas sometidas bajo presión isotrópica, conduce a la formación
de complejos patrones de plegamiento a lo largo de varias escalas de longitud, así
como también la autosimilitud. La complejidad de los patrones resultantes ha
generado un amplio interés entre mecánicos físicos y matemáticos [16,17].
Otra propiedad de la cresta es, la creciente singularidad del desarrollamiento de un
de la punta empujada y curvatura domina toda la región exterior, dos tipos de
tensiones en la región exterior son identificados y mostrados a diferentes escalas.
Cuando se arruga un pedazo de papel con las manos, dos tipos de estructuras
singulares aparecen en el papel arrugado que son: las crestas y vértices. Las
energías se condensan en una red de dichas singularidades, en conclusión se han
explorado las propiedades de la singularidad cónica de un cono-d desarrollable. Las
leyes de escalamiento gobiernan la energía y el tamaño de la cresta, en las figuras
1.8 y 1.9 se muestra el desarrollo del cono-d [18,19,20].
Figura 1.9 Esquema de la región céntrica de un cono-d. El área creciente es mostrada en blanco. Directores negros se muestran como líneas. Muchos directores o líneas convergen alrededor de la punta de la creciente.
El arrugamiento también juega un papel importante en el comportamiento mecánico,
para el embalaje o empaquetamiento de material y en la disipación de la energía de
colisión en las zonas arrugadas de los automóviles. Propiedades mecánicas de las
placas elásticas delgadas macroscopicas, experimentan grandes deformaciones que
son importantes en ingeniería, en la seguridad de algunas estructuras y en el
desarrollo de material que es utilizado en el embalaje [21,22].
Por otro lado, se ha investigado una innovadora teoría a cerca de plegamiento de
hojas para la absorción de impacto, hojas planas son dobladas para absorber
energía, está claro; dependiendo de la energía ha ser absorbida, del material, del
número de dobleces por unidad de longitud, el numero de capas apiladas etc. El
plegamiento de este tipo de hojas en que se basa la teoría, está basado en un
patrón tridimensional. Esta investigación se basa en un patrón que se genera a partir
de una hoja de material plano llamado Chevron. Para generar este patrón, la hoja de
material se alimenta a través de varios conjuntos de rodillos que predoblan el
material y finalmente el último conjunto de rodillos forman los pliegues que dan la
Figura 1.10 Maquina de plegado continuo de hojas delgadas
[image:31.612.165.470.71.303.2]
Figura 1.11 Padrón Chevron Doblada desde una Hoja Delgada
Este patrón puede ser producido utilizando diferentes materiales laminados como
son: papel Kraft, aluminio, cobre, acero, materiales compuestos y plásticos [23,24].
Una nueva teoría geométrica genera repetitivos patrones de plegamientos que
transforma una hoja de material en estructuras poligonales. Amplios patrones pueden
se han formado con hojas planas de aluminio, cobre, acero, compuestos y papel.
Algunos ejemplos son mostrados a continuación (ver figuras 1.12, figura 1.13, figura
1.14, y figura 1.15)
Figura 1.13 Patrón de cobre Figura 1.14 Patrón de aluminio
Figuras 1.15 Dos tipos diferentes de patrones de material compuesto
Existe una gran variedad de aplicaciones del plegamiento de hojas de papeles en el mundo real, algunos ejemplos son los siguientes [25,26]:
1. En infraestructuras civiles: En adornos de pisos, decoración de entradas, barreras en los caminos, paredes preensambladas y disipadores de energía en las columnas de las construcciones,ver figura 1.16 [26].
2. Empaquetamientos: Cajas para la absorción de impactos,ver figura 1.16 [26].
3. Aeroespacial y automotores: Endurecedores, paneles para puertas, sustitución de bolsas de aire [26].
REFERENCIAS
[1Cap.1] T. A. Witten, “How Soft Matter correlates: three examples”. 2005. Journal of Physics: Condensed Matter. Page S1651-S1658
[1Cap.2] A. J. Wood. “Witten´s Lectures on Crumpling”, Special issue of Physical A 313,83 (2002)
[1Cap.3] J. A. Aström, J. Timonen and Mikko Karttunen, “Crumpling of a Stiff Tethered Membrane” Physical Review Letter. Page 244301-1-244301-4
[1Cap.4] Crumple Physics, “A Crash Barrier of Crumpled Sheet Metal”. 200
http://www.Science-Projects.com, Page 1-2
[1Cap.5] C. J. Budd and M. A. Peletier, “Approximate Self-Similarity in Models of Geological Folding”, Page 1-26
[1Cap.6] H-B. Muhlhatus, L. N. Moresi, B. Hobbs, and F. Dufour. “Large Amplitude Folding in Finely Layered Viscoelastic Rock Structures”. hans@ned.dem.ciro.au
[1Cap.7] Jan Genzer and Jan Groenewoldb, “Soft matter with hard skin: From skin
wrinkles to templating and material characterization”. 2006. Soft
matter.Page 310-323.
[1Cap.8] G. Song and N. M. Amato. “How Does If fold?”. 2000. Technical Report 00-014. Page 1-17.
[1Cap.9] Paper Folding. “Paper folding Geometry”. 2007.http://www.cut- theknot.org/pythagorasPaperFolding /index.shtml. Page 1-5
[1Cap.10] E. D. Demaine and J. S. B. Mitchell. “Reaching Folded States of a Rectangular piece of Paper”. jsbm@ams.sunysb .edu. Page 1-3
[1Cap.11] L. Carroll, “Folding Paper in Half 12 Times”. 2006.
http:/www.pomonahistorical. org/12 times .htm
[1Cap.12] M. Ben Amar and Y. Pomeau. “Crumpled Paper”. 1997. The Royal Society 453, Page 729-755.
[1Cap.14] B. A. DiDonna and T. A. Witten. ”Anomalous Strenght of Membranes with Elastic Ridges”. 2001. Physical Review Letter. Page 206105-1-206105-4
[1Cap.15] B. A. DiDonna. “Scaling of the buckling transition of ridges in thin shets”.2002. Physical Review E 66. Page 016601-1 – 016601-25
[1Cap.16] S. Conti and F. Maggi. “Confining thin elastic sheets and folding paper”.2005. page 1-35
[1Cap.17] Sergio Conti, Antonio DeSimone and Stefan Müller. “Self-similar holding patterns and scaling in compressed elastic sheets”. 2004. Page 2534-2549
[1Cap.18] Tao Liang and Thomas A. Witten. “Crescent singularities in crumpled sheet”. 2005. Physical Review E 71. Page 016612-1- 016612-11
[1Cap.19] BY E. Cerda1,2 and L. Mahadevan2. “Confined developable elastic surfaces: cylinders, cones and the Elastica”. 2004. Proc. R. A 461. Page 671-700
[1Cap.20] Tao Liang and Thomas A. Witten. “Spontaneous curvature cancellation in forced thin sheets”. 2006. Page 1-13
[1Cap.21] Shankar C. Venkataramani. “Lower bounds for the energy in a crumpled elastic Sheet-A minimal ridge”. 2002. Page 1-15
[1Cap.22] Alexander E. Lobkovsky and T. A. Witten. “Properties of Ridges in Elastic Membranes”. 2006. Page 1-14
[1Cap.23] E. A. Elsayed and Basily B. Basily. “A Continuous Folding Process for Sheet Materials” Page 1-19
[1Cap.24] Laure LaRue, Basily B. Basily and E. A. Elsayed. “Cuishiong Systems for Impact Energy absorption”. Page 1-19
[1Cap.25] Basily B. Basily and E. A. Elsayed. “Design and Develoment of Lightweight sandwich structures with Innovative Sheet Folded Cores” Page 1-9
Capítulo 2 Estado del Arte
Algunos, investigadores han Realizado estudios sobre el plegado de hojas de papel tales como:
Gomes (1986) [1] estudia la geometría fractal de las bolas de papel arrugadas, el análisis destaca algunos aspectos físicos, matemáticos, e introduciendo el concepto de dimensión fractal que es la base de muchas áreas de la física moderna. Los fractales son ahora un tema de interés general y aquí describe un interesante ejemplo del exponente de la dimensión fractal definida a través de la Relación entre la masa y el tamaño.
Gomes, Vasconcelos y Nacimiento (1987) [2] investigan el área negra de bolas de papel arrugadas de dimensión D=2.5 obtenidas a través de la inmersión de tales objetos en una solución negra con la ayuda de la técnica de pintura balística.
Gomes, Braga y Castro (1989) [3] investigan la relación entre la masa, M, y el tamaño, R, para autoeditar superficies aleatorias.
Gomes, Soares (1989) [4] propone el uso de resistencia eléctrica , en función de la deformación de las superficies arrugadas de papel grafito, estos resultados los comparan con preacciones teóricas.
Gomes, Ren, Rodrigues y Furtado (1989) [5] determinan la deformación de bolas de papel de aluminio, cuando son sometidas a diferentes cargas. Para este efecto, describen el comportamiento de ocho relaciones escalares, relacionándolas con las cargas, deformaciones, superficies escalares y variables de la geometría de la superficie arrugada.
Gomes, Jyh y Ren (1990) [6] en éste trabajo se enfocan en configuraciones no-equilibradas de superficies fractales arrugadas, obtenidas de la compresión aleatoria e irreversible de colectores bidimensionales.
García, Gomes, Jyh y Ren (1990) [7] propiedades estadísticas y geométricas de superficies arrugadas en desequilibrio (cs) y cables arrugados (cw), son investigadas y comparadas. Se estudia la relación entre la distancia geodesica “x” y la distancia pitagórica “r” en cs y cw y su dependencia lineal del tamaño L (desarrugada).
Lima, Oliveira y Gomes (1992) [8] muestran un simple experimento cinemático y pedagógico para medir la dimensión fractal D de masa-tamaño de superficies arrugadas presentadas. La experimentación está inspirada en el conocido experimentos galeanas con los órganos de rodadura sobre planos inclinados.
determinarse a partir del conocimiento de la velocidad V que alcanzó la bola al rodarse en un plano inclinado.
Bevilacqua (2002) [10] en este Artículo trata de las membranas artificiales densamente dobladas, las membranas densamente dobladas aun no han tenido la atención suficiente a pesar de que frecuentemente aparecen en la naturaleza. Las hojas con el mismo espesor, pero áreas arbitrarias se doblan proporcionando una geometría que conserva la energía de densidad constante. Una cuestión importante es determinar la forma de cómo la energía de escalamiento hace referencia a la geometría de escalamiento.
(2004) [11] en éste reporte habla sobre el arrugamiento de hojas de papel de dos dimensiones las cuales son transformadas a bolas de papel de tres dimensiones, para lo cual hace una breve historia sobre el concepto de dimensión, que a su vez, describe el proceso de arrugamiento y determina la dimensión fractal de la bola.
(2005) [12] en esta carta muestra el procedimiento experimental y la determinación de la dimensión fractal de una variedad de materiales arrugados.
(2007) [13] en éste reporte muestran algunos estudios de nuevos arrugamientos, como el estudio de las películas de crema que se forman el arrugado de leche caliente, café con leche, otros estudiaron el arrugado de papel y hojas de polímeros arrugadas. Las investigaciones encontraron que el relleno tiene una dimensión fractal de aproximadamente 2.5.
Jearl Walter [14] este articulo presenta un problema aplicado a la participación de regresión lineal, basado en la Geometría Fractal en Bolas de Papel Arrugadas. La masa m de el papel y el diámetro D, están relacionadas por la dimensión d de acuerdo con la ecuación (1), se puede determinar d desde una gráfica de datos. Sin embargo, en vez de trazar los datos según la ecuación (1), se transforma esa ecuación en una ecuación lineal. Entonces se puede hacer una regresión lineal sobre los datos, es decir, encontrar la línea recta que mejor se adapte a una parcela de datos. Porque la dimensión d se expresa como una potencia en la ecuación (1), transformando la ecuación (1) en una ecuación lineal tomando logaritmo natural de ambos lados de la ecuación.
(2005) [15] éste reporte muestra el procedimiento de bolas de papel, es decir, muestra la metodología de la fabricación de dichas bolas. Una vez hechas las bolas se toman varias medidas del diámetro de esas bolas, para posteriormente tomarles el peso, con estos datos se grafica y se determina la dimensión fractal.
(2005) [17] en éste reporte dice que la geometría de las bolas de papel arrugadas, son investigadas. Muestra que estos sistemas son fractales y sus características son estudiadas.
(2004) [18] en éste trabajo muestra un estudio de las bolas en una cadena de embalaje en dos dimensiones.
Bowick y sus Cols. (2004) [19] en esta carta muestran una amplia variedad de estructuras de membranas, incluyendo aquellas membranas que engordan cuando se estiran. Materiales parecidos a la goma, que fácilmente cambian de forma, al ser más delgados, en su corte transversal, es cuando son estirados. Esto es descrito por la relacion de Poisson”s
Blair Daniel L. and Kudrolli. (2005) [20] en éste trabajo, reportan nuevos experimentos diseñados para medir directamente la geometría del papel arrugado usando topografia de reconstrucción no-invasiva por láser-guiado.
Boué, Adda-Bedia, Boudaoud, Cassani, Couder, Eddi, and Trejo (2006) [21] en éste articulo muestran el estudio de los patrones espirales en el embalaje de estructuras flexibles, tanto en sistemas geométricos cónicos (Sistema para embalaje cónico) como en sistemas geométricos cilíndricos (Sistema para embalaje cilindrico).
Sultan and Boudaoud (2006) [22] este articulo investiga las propiedades estadística de las configuraciones del papel arrugado.
Andresen C. A., and Hansen A., (2007) [23] este trabajo apunta a la descripción de la red de crestas formadas durante un proceso de arrugamiento con la mano de algunos tipos de papeles y espesores. Los resultados obtenidos fueron la obtención de algunas propiedades de la red así como también algunas propiedades geométricas, de igual forma se determinó la rugosidad de los mismos, que han demostrado un comportamiento auto-afin.
REFERENCIAS
[2Cap.1] Gomes, M. A. F., ”Fractal geometry in crumpled paper balls”, Am. J. Phys. 55(7), July, (1987).
[2Cap.2] Gomes, M. A. F., G. L. Vasconcelos y C. C. Nacimiento., “Blackish fractal balls”, J. Phys. A: Math. Gen. 20 (1987).
[2Cap.3] Gomes, M. A. F., I. J. S. Braga y C. A. F. Castro., “Random surfaces on hard spheres”, J. phys. A: Math. Gen. 22 (1989).
[2Cap.4] Gomes, M. A. F., y J. H. P. Soares., “Electrical resistance of crumpled surfaces”,J. Phys. D: Appl. Phys. 22 (1989).
[2Cap.5] Gomes, M. A. F., T. I. Jyh, T. I. Ren, I. M. Rodrigues y C. B. S. Furtado., “Mechanically deformed crumpled surfaces”, J. Phys. D. Appl. Phys. 22 (1989).
[2Cap.6] Gomes, M. A. F., T. I. Jyh, T. I. Ren., “ The crumpled state of some non-equilibrium fractal surfaces”, J. Phys. A: Math. Gen. 23 (1990).
[2Cap.7] Garcia, J. B. C., Gomes, M. A. F., T. I. Jyh, T. I. Ren., “ Critical properties of non-equilibrium crumpled systems”, J. Phys A: Math. Gen. 25 (1992).
[2Cap.8] F. F., V. M. Oliveira y M. A. F. Gomes., “A Galilean experiment to measure a fractal dimension”, Am. J. Phys. 61 (5), May (1993).
[2Cap.9] Kirk T. McDonald., “The fractal Dimension of a Ball of Aluminum Foil”
[2Cap.10] Bevilacqua Luiz., “The fractal Nature of Energy-Geometry Scaling in Densely Folded
Membranes”, Multi-Scale (2002).
[2Cap.11] Experiment-Crumpling.doc “Crumpled” (2004).
[2Cap.12] http://www.uow.edu.au/eng/phys/students/fractals/experiment.htm “Experimental Procedure” (2005).
[2Cap.13] www.sciencemag. “Crumpling: A new Wrinkle”(2007).
[2Cap.14] Jearl Walker at www. wiley.com/college/hrw“Fractal Dimension of Paper Ball ”
[2Cap.16] http://clsses.yale.edu/fractals/FracAndDim/BoxDim/PowerLaw/CrumpledPap er. html “Power Law Relations” (2006).
[2Cap.17] http:www.iop.org/EJ/ abstract “Paper crushes fractally”,(2005).
[2Cap.18] http:www.scopus.com/scopus/record/display.url? view = basic ”Beads –on -a- string packing in two dimensions” (2006).
[2Cap.19] Bowick and Lakes R., “news and views” and Abroader view of membranes” Macmillan Magazines Ltd, (2001).
[2Cap.20] Blair Daniel L. and Kudrolli Arshad., “Goemetry of Crumpled Paper” PRL 94, 166107 (2005).
[2Cap.21] Boue L., Adda-Bedia M., Boudaoud A., Cassani D., Couder Y., Eddi A., and Trejo M., “Spiral Patterns in the Packing of Flexible Structures” Phisical Review Letters (2006).
[2Cap.22] Sultan Eric and Boudaoud Arezki., “Statistics of Crumpled Paper” Phisical Review Letters (2006).
[2Cap.23] Andresen C. A., and Hansen A., “Ridge Network in Crumpled Paper” 67084 Strasbourg, France (2007).
Capítulo 3 Metodología Experimental
3.1 Metodología Experimental.
La investigación es el análisis de fenómenos científicos fundamentales. En la
investigación en ingeniería se desarrollan experimentos y se efectúan mediciones
para dar soporte a, o confirmar nociones teóricas. Las mediciones forman la columna
vertebral de la ciencia y la ingeniería, porque las descripciones del mundo físico son
imposibles sin ellas.
Sin embargo, muchas fuentes contribuyen al error experimental, además de los
errores de medición, análisis y muestreo, por ejemplo, pueden contribuir variables
tales como la temperatura ambiente y humedad, destreza, antigüedad del material,
estado del equipo, etc. Por estas razones, se hicieron varios experimentos bajo las
mismas condiciones de tal manera que se pueda obtener mejores resultados.
3.2 Desarrollo de la investigación
La geometría de las bolas de papel arrugadas son examinadas. El análisis destaca
algunos aspectos físicos, matemáticos e intuitivos del problema, introduciendo el
concepto de dimensión fractal que es la base de muchas áreas de la física moderna
[1].
En este trabajo de investigación, se estudia el fenómeno de arrugamiento, para lo
cual, se hará uso para este estudio de algunos tipos de papeles. Como se sabe el
papel es un material poroso, con estructura anisotrópica asociada con una
orientación asimétrica en la distribución de sus fibras debido a su proceso de
fabricación.
3.2.1 Material utilizado para la investigación.
El papel en general es un producto compuesto obtenido de la pasta de fibras
vegetales, de forma delgada y flexible. Algunas de las propiedades físicas del papel
son sensibles a los cambios como la humedad y la temperatura; sin embargo, para
este estudio, dichas propiedades se tomaron en consideración dichos efectos.
Para realizar este trabajo experimental, sobre la topología fractal de materiales
delgados compactados aleatoriamente, se utilizaron los siguientes tipos de papeles:
Albanene, Biblia y Carbón.
Las ventajas de trabajar con papeles son las siguientes: que se puede obtener sin
ningún problema, manejo sencillo, almacenaje sencillo, factible para hacer estudios
de rugosidad, elaboración rápida de probetas, elaboración práctica de varias
probetas y sobretodo económicos.
3.2.2 Elaboración de probetas de papel.
En esta investigación se llevó un análisis de superficies arrugadas de materiales
delgados en el que se utilizaron papeles, debido al fácil manejo que se puede tener
con este material y a su bajo costo. Se utilizaron 3 tipos diferentes de papel, de
diferente grosor (ver tabla 3.1).
Tabla 3.1 Características del papel utilizado, espesor (h), densidad superficial (ρA).
Nota: Todo el papel tiene la misma densidad de masa ρ=ρA/h= 900±50 Kg/m3 .
Nombre comercial de papel Carbón Biblia Albanene
Espesor, h (mm) 0.024 ±0.004 0-039±0.002 0.068±0.005 Densidad, ρA (gr/m
2
En primer lugar, para estudiar el fenómeno de rugosidad presentado; y con el objeto
de obtener la dimensión fractal, se prepararon para cada tipo de material, probetas
de hojas cuadradas de 4 diferentes tamaños, como se ilustra en la figura 3.1,
8 cm
8 cm 16 cm
16 cm
35 cm 35 cm
70 cm
70 cm
S1 S2
S3
S4
8 cm
8 cm 16 cm
16 cm
35 cm 35 cm
70 cm
70 cm
S1 S2
S3
S4
Figura 3.1. Tamaños de las hojas de papel para generar superficies arrugadas.
Y manteniendo la siguiente relación de escalamiento:
L=λL0 (3.1)
Donde, L es el tamaño de la hoja (en cm); para el factor de escalamiento λ =1, 2, 4,
8, 16, 25,35 y 50; y L0 =2 hasta 100
Para cada tamaño de hojas de papel, se hicieron treinta probetas, (N=30 hojas de
papel). Estas probetas fueron comprimidas mediante una compactación aleatoria
realizada con ambas manos hasta tener una forma aproximadamente esférica, con
Figura 3.2Conjunto de bolas de papel arrugadas o comprimidas manualmente con tamaños L=
λ
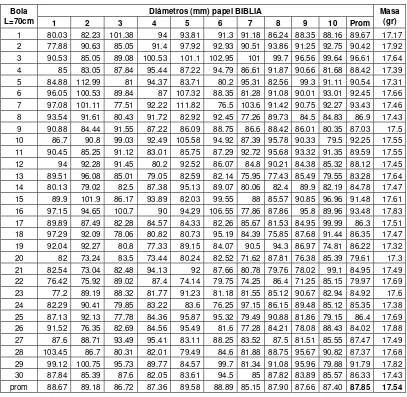
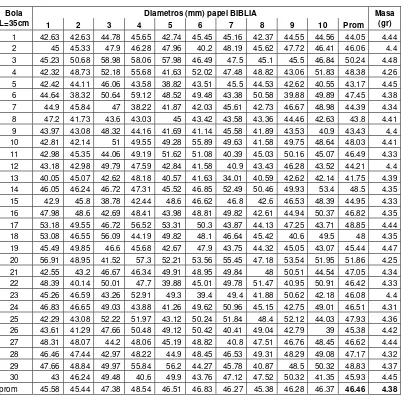
L0Inmediatamente después de obtener las bolas de papel, se miden sus diámetros en
10 direcciones tomadas aleatoriamente, y se calcula el diámetro promedio (mediana)
de ellos para cada una de las bolas de papel de la siguiente manera:
∑
= n i i
j L n R
R ( ) (1/ ) (3.2)
Donde, R(L) es el diámetro de cada bola de papel; n representa a cada una de las 10 direcciones en que se midieron los diámetros; Ri es cada una de las mediciones
del diámetro a lo largo de n. Además se calculó el promedio general del diámetro en
cada tamaño de papel L, con la siguiente relación:
) ( )
(L R L
R = j (3.3)
Donde, los corchetes denotan el promedio de N =30 bolas del mismo tamaño.
Tabla 3.2Forma, dimensiones y Cantidades de Probetas de los 3 tipos de papel Forma Papel albanene No. De Piezas Papel biblia No. De Piezas Papel carbon No. De Piezas cuadrado 80X80 mm 30 80X80 mm 30 80X80 mm 30 cuadrado 160X160 mm 30 160X160 mm 30 160X160 mm 30 cuadrado 350X350 mm 30 350X350 mm 30 350X350 mm 30 cuadrado 700X700 mm 30 700X700 mm 30 66X66 mm 30
3.3 Relajación de la deformación
El diámetro en las bolas de papel aumenta con el tiempo durante los próximos 6 a 9
días inmediatamente después de formar la bola [1,2], ya que existe una relajación de
la deformación, por lo que se tomaron mediciones del incremento de diámetro en
función del tiempo, a diversos intervalos para conocer con mayor detalle la relajación
de la deformación y puntos de inflexión donde se presentan cambios en la velocidad
de deformación, en la figura 3.3 se muestra el incremento del diámetro en las esferas
para los tres tipos de papeles que se utilizaron en éste trabajo, los cuales son:
albanene, biblia y carbón. Para cada tipo de papel se prepararon cinco piezas con
dimensión de, 32 cm X32 cm. cada una; cada pieza de papel es arrugada a través de
una compactación realizada con ambas manos, hasta obtener una forma
aproximadamente esférica, e inmediatamente se mide su diámetro inicial, ya que en
ese instante inicia su relajación y el diámetro se incrementa continuamente hasta que
termina de disiparse la energía acumulada en los dobleces.
Una vez que el estado de esfuerzos en cada bola de papel entra en equilibrio el
incremento del diámetro se detiene, es decir ya no existe relajamiento en la
análisis y en los resultados, se esperó hasta después del décimo día después de ser
comprimidas, para realizar las demás mediciones, cuando con certeza se puede
saber que no hay relajación de esfuerzos y entonces se procede nuevamente a
medir los diámetros en cada una de las bolas de papel, y se continúa con las demás
mediciones y análisis, como se verá en el siguiente tópico.
Figura 3.3. Representación esquemática de la medición de los incrementos del diámetro en función del tiempo para obtener la deformación ε
3.4 Dimensión fractal de masa
Las hojas cuadradas de papel con diferentes tamaños como los que se muestran en
la figura 3.1 son bidimensionales, en cambio, un cubo sólido de papel es
tridimensional, ahora bien, de acuerdo a la geometría fractal, se convierte una hoja
de papel por medio de arrugamiento y comprimiéndola hasta llevarla a un bola,
sucede que su superficie bidimensional es embebida en tres dimensiones [3,4,5] y la
hoja de papel tiene dimensión fractal DM, que oscila entre 2.0 y 3.0; la masa M del
papel y el diámetro R de la bola de papel comprimida determinan la dimensión fractal de acuerdo a la siguiente relación [1]:
M
D kR
M = (3.4)
Donde k, es una constante desconocida. Para obtener la dimensión fractal, primero
0 ,
0 Δt=
se obtuvo la masa para cada una de las treinta bolas de papel y de cada tamaño
diferente elaborado de acuerdo a la ecuación (3.1) y se midieron también sus
diámetros para los cuatro tamaños de papel (ver anexo 2) y al graficar estos datos se
obtiene la DM de cada tipo de papel, expresados como una potencia.
3.5 Geometría del papel arrugado
El comprimir una hoja de papel manualmente hasta convertirla en un volumen en
forma esférica, trae como consecuencia una red de dobleces permanentes formados
durante el proceso de arrugamiento. A estos dobleces, cuando la hoja recobra una
forma original, es decir, desdoblada la hoja, se les denomina superficie arrugada, que
presenta líneas en los papeles, con ramificaciones que pueden estar
interconectadas, a los puntos de interconexión donde convergen dos o más
dobleces, se les denomina nodos. Cada línea que une dos nodos, es siempre recta
y la cantidad de líneas y nodos, dependen de la fuerza aplicada al papel al ser
arrugado. El propósito de este trabajo es, determinar los parámetros estadísticos
que rigen la morfología de estos dobleces y la relación de escalamiento que guardan
con respecto al tamaño de las piezas de papel que son sometidas al proceso de
arrugamiento. El papel utilizado para este análisis experimental es el albanene. Los
datos y propiedades mecánicas del papel albanene están dados en la tabla 3.3
Tabla 3.3 Espesor (h), Densidad de superficie (ρA), Modulo de Young (EL, ET),
Esfuerzo de cedencia (σ YL, σY T)
Tipo de papel Albanene
Espesor, h,(mm) 0.068±0.005
Densidad de superficie, ρA, (g/m2) 63±1
Modulo de Young longitudinal, EL, (MPa) 7102±200
Modulo de Young transversal, ET, (MPa) 4036±87
Esfuerzo de cedencia longitudinal, σYL, (MPa) 56.8±3
Primeramente se prepararon, 30 probetas para cuatro tamaños de papel albanene en
forma cuadrada con dimensiones de (80x80 mm2, 160x160 mm2, 350x350 mm2, y
700x700 mm2), en total fueron 120 piezas de papel. A cada una de ellas se le somete
a un proceso de arrugamiento aleatorio, aplicando la mayor fuerza posible con las
manos, hasta convertir cada pieza de papel en un volumen en forma esférica.
Posteriormente, cada pieza volumen de papel es desarrugado, retornándolo a su
forma original, de manera que el proceso de desarrugamiento consiste en abrir el
volumen hasta quedar parcialmente extendido, teniendo cuidado de no romper el
papel.
Después, se realiza un análisis de la geometría de cada una de las superficies
arrugadas. Se midió con un calibrador la longitud de cada una de las arrugas, se
realizó luego una sumatoria de cada una de ellas para determinar la longitud total, y
después se contabiliza el número de nodos; todo este proceso se lleva acabo para
cada una de las superficies arrugadas, que respectivamente son encontradas
mediante el uso de las siguientes expresiones:
Ltotal =
∑
=
n
i l
1
i (3.5)
N nodos =
∑
=n
i n
1
i (3.6)
Donde l y n , representan a cada una de las líneas y los nodos en la superficie
arrugada de la pieza de papel analizada. Una representación esquemática de la
configuración geométrica de las superficies arrugadas es mostrada en la figura 3.4 y
Figura 3.4 Representación esquemática de la geometría de los dobleces
Figura 3.5 Configuración experimental de la geometría de los dobleces, donde ni
representa a cada uno de los nodos y li a las líneas
3.6 Rugosidad de las bolas de papel y de las hojas extendidas
A continuación se describe la caracterización de la rugosidad de las superficies de
las bolas. Para ello se utiliza la desviación estándar de cada una de las medidas del
diámetro tomadas a cada una de las bolas según la expresión (3.2) que es calculada
de la siguiente manera:
(
)
[
2]
1/2) (
/
1
∑
−= ni i
S n R R
La desviación estándar fue determinada de las mediciones a lo largo de n=10
direcciones tomadas al azar en cada bola. También se determinó la desviación
estándar de la expresión (3.3) que corresponde a las mediciones de las N =30
bolas de papel para cada tamaño y se obtuvo con la siguiente relación:
(
)
[
2]
1/2 ) (/
1
∑
−= Nj j
B N R R
σ (3.8)
Con los datos obtenidos, y con las dos fórmulas anteriores se obtiene el exponente
de rugosidad global αS de las bolas esféricas al graficar las desviaciones estándar
contra los diámetros:
S
R S B
α σ
3.7 Perforación de las bolas de papel a lo largo de su diámetro.
También se estudiaron las propiedades de escalamiento en la estructura interna de
hojas elastoplásticas dobladas aleatoriamente haciendo cruzar hilos de diferentes
colores a través del diámetro de las bolas de papel arrugadas, con el objeto de ver el
número de capas que cruza el hilo cuando éste atraviesa por su diámetro mayor,
para ello la esfera es desarrugada y extendida nuevamente. El mismo procedimiento
se realizó con otros hilos, pero ésta vez se cruzó a lo largo de diámetros aleatorios y
con ángulo diferentes, para verificar las veces que cruza en las capas una vez
extendida la hoja de papel como se ilustran en las figuras 3.6 y 3.7
Figura 3.7. Trayectoria de los hilos en las hojas de papel extendidas
Para lo cual también se usaron hojas cuadradas de 3 diferentes tipos de papeles
(carbón, Biblia y albanene) ver figura 3.1. El tamaño de la hoja varía de Lo = 2 hasta
100 cm, con la relación L=λL0 (3.1) y por un factor de escalamiento λ =1, 2, 4, 8,
16, 32 y 50.
Por lo menos 30 hojas de cada tamaño y de cada papel, se arrugaron con la mano,
hasta formar bolas de papel ver figura 3.6. Para reducir las incertidumbres causadas
por las variaciones en la fuerza de compresión y la relajación de tensión, después de
retirada de la fuerza de doblez, todas las mediciones fueron tomadas 10 días
después de que las bolas se doblaron, hasta que no se observaron cambios en las
dimensiones de las bolas, en la tabla 3.4 se muestra la forma, dimensiones y
cantidades de probetas de papel albane.
Tabla3.4Forma,dimensiones y CantidadesdeProbetas de papel albanene
Forma Papel Abanene No. de Probetas
Cuadrada 70X70 cm. 30
Cuadrada 35X35 cm. 30
Cuadrada 16X16 cm. 30
3.8 Dimensión fractal global
La dimensión fractal global “D” se determinó usando la relación (3.10)
δ α
−
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
Yh F h
L h
R 2/D
(3.10)
Para los conjuntos de las hojas dobladas aleatoriamente de los diferentes tamaños
de papel. El conjunto medio del diámetro de las bolas para las hojas de tamaño L
se definió como R(L)= Rj(L) , donde los paréntesis denotan un promedio mayor a
N =30 bolas de diámetro Rj(L)=(1/n)
∑
inRi y Ri son diámetros medidos a travésREFERENCIAS
[3Cap.1]
[3Cap.2]
[3Cap.3]
[3Cap.4]
[3Cap.5]
[3Cap.6]
A. Balankin, O. Susarrey, R. Cortés, D. Samayoa, J. Martínez and M. Mendoza, “Intrinsically Anomalous Roughness of Ramdomly Crumpled Thin Sheets”, Physical Review E. 74, 061602 (2006).
R. F. Alburqueque, M. A. F. Gomes, “Stress relaxation in Crumpled Surfaces”, Physica A, 310, 377-383 (2002).
M. A. F. Gomes, “Fractal Geometry in Crumpled Paper Balls”, Am J. Physical 55, 649, (1987)
J. Walker, “Fractal Dimension of Paper Ball”, Jear Walker at www.wiley.com/college/hrw
R. H. Ko and C. P. Bean, “A Simple Experiment that Demostrates Fractal Behaviour”, The Physics Teacher, 29, 78-79, (1991)
Capítulo 4 Análisis y Discusión de Resultados
4.1 Cálculo de la velocidad de relajación
Cuando las hojas de papel son comprimidas hasta convertirlas en bolas, trae como consecuencia una red de dobleces permanentes, formados durante el proceso de arrugamiento al ser comprimidas en forma manual [1,2,3,4], de manera instantánea el diámetro de las bolas se incrementa, debido a que en los dobleces formados se acumula la energía aplicada al comprimirlas, misma que empieza a disiparse, lo que provoca una relajación en la deformación de las bolas de papel, hasta que la energía se disipa totalmente es cuando se detiene la deformación [5].
La deformación que sufren las bolas de papel, se define con la siguiente relación:
0 0)/ (df −d d =
ε (4.1)
Donde d0 y df son el diámetro inicial y final (en cada intervalo de tiempo) de cada
una de las bolas de papel analizadas.
El intervalo de tiempo necesario para realizar las mediciones de las deformaciones en las bolas de papel se fijó en;
hrs
t =8
Δ (4.2)
Sin embargo, durante la primera hora se necesitó incrustar un sub-intervalo de tiempo con el objeto de determinar la velocidad de relajación [2] que se presenta al inicio de la disipación de la energía:
La expresión anterior fue necesaria debido a que durante la relajación se observó que en la primera hora, existía una velocidad mucho mayor en la deformación.
El tiempo total de la medición del incremento en los diámetros para cada uno de tres tipos de papel fue de 9 días (t =216hrs) [6], debido a que fue el tiempo necesario para que concluyera la disipación de la energía, la medición es realizada con el esquema mostrado en la figura 3.3. Los datos obtenidos durante las mediciones, definen cada uno de los incrementos en la longitud del diámetro para cada periodo de tiempo. La tabla 4.1, muestra los datos de los resultados de los diámetros para siete intervalos de tiempo en las mediciones realizadas en cada tipo de papel, los demás datos de los incrementos de los diámetros, se presentan en el anexo 1 de esta tesis.
Tabla 4.1 Incremento en la longitud del diámetro (Δd0), en los 9 días
Tiempo (hrs)
Diámetro promedio de tres papeles R (mm)
Albanene Biblia Carbón
0.00 69.91 45.04 31.48
0.08 70.88 46.16 32.12
0.25 71.68 46.82 32.28
0.50 72.17 47.42 32.46
1.00 72.62 47.79 32.66
5.00 73.80 48.00 32.81
90.00 77.39 49.24 33.47