Aplicación de un Controlador Difuso de Complejidad Reducida al Prototipo: Viga Bola Edición Única

Texto completo

(1)TESIS QUE PARA OPTAR EL GRADO DE MAESTRO EN CIENCIAS EN SISTEMAS DE MANUFACTURA PRESENTA. JUAN EMILIO PÉREZ HERNÁNDEZ Asesor:. Comité de tesis:. Invitados especiales:. Dr. ALEJANDRO ACEVES LÓPEZ. Dr. JESÚS ULISES LICEAGA CASTRO Dr. REYNALDO FÉLIX ACUÑA. Dr. JOSEPH AGUILAR MARTIN M. en C. VIRGILIO VÁSQUEZ LÓPEZ. Jurado:. Dr. JESÚS ULISES LICEAGA CASTRO, Dr. REYNALDO FÉLIX ACUÑA, Dr. ALEJANDRO ACEVES LÓPEZ, Dr. JOSEPH AGUILAR MARTIN, M. en C. VIRGILIO VÁSQUEZ LÓPEZ,. Atizapán de Zaragoza, Edo. Méx., 05 de Agosto del 2004. Presidente Secretario Vocal Vocal Vocal.

(2) DEDICATORIAS. Dedico con cariño este trabajo: A mis padres: Emilio Pérez y María Teresa Hernández A mi hermana: Bárbara A mi novia: Nancy Belinda Bravo A mis familiares y amigos.. "Solo el mejor momento para ser feliz es ahora " - anónimo.

(3) AGRADECIMIENTOS. A DIOS que me permitió hacer realidad algo que alguna vez fuese un sueño. Al ITESM-CEM por el financiamiento otorgado para estudiar el posgrado. Al Dr. Aceves por su paciencia y gran don de enseñanza. Al Dr. Liebermann por su gran apoyo y consejos. A los miembros del jurado que me han evaluado..

(4) RESUMEN El Controlador Lógico Natural es una alternativa dentro del control difuso orientado a controlar procesos multivariables. Aún se encuentra en fase de desarrollo y prueba en sistemas sencillos y monovariables. Las características principales del Controlador Lógico Natural son: i) utiliza los límites o restricciones naturales que los procesos poseen para crear los dominios de discurso necesarios que nos permitirán el control del proceso; ii) independientemente del número de variables de entrada, utiliza las reglas difusas completamente opuestas y solo dos conjuntos difusos por cada variable de entrada. El sistema utilizado en este trabajo es el viga-bola, un prototipo del laboratorio de control del ITESM-CEM. El ajuste del controlador se hizo en forma experimental e iterativa, arrojando buenos resultados. Una vez desarrollada la propuesta de sintonización o ajuste del Controlador Lógico Natural, se procedió a aplicarlo en tiempo real al viga-bola. Para conocer el grado de robustez del Controlador Lógico Natural y su desempeño contra controladores Proporcional - Derivativos, se decidió aplicar ciertas pruebas en tiempo real al prototipo. De ellas se concluyó que el Controlador Lógico Natural es una buena alternativa de control, con resultados equiparables a los obtenidos con los PD's diseñados con el mismo objetivo, pero con la ventaja de hacer que la acción de control sea mucho más suave y por ende que el gasto de energía sea menor que en estos últimos. Cabe aclarar que no se tiene la finalidad de decidir qué tipo de controlador es mejor, solo es un análisis comparativo entre ellos. Bajo los resultados obtenidos se invita a la continuación del desarrollo de este controlador para conocer mejor sus limitantes, incrementando el grado de dificultad de las pruebas o aplicándolo en sistemas de mayor complejidad..

(5) ÍNDICE LISTA DE FIGURAS. 3. LISTA DE TABLAS. 4. OBJETIVO GENERAL. 5. OBJETIVOS PARTICULARES. 5. INTRODUCCIÓN GENERAL. 6. PARTE I. ASPECTOS TEÓRICOS. 10. CAPITULO 1. GENERALIDADES DEL CONTROLADOR DIFUSO. 11. 1.1 INTRODUCCIÓN 11 1.2 FUNDAMENTOS DE LA LÓGICA DIFUSA 12 1.2.1 CONJUNTOS DIFUSOS 12 1.2.1.1 Conceptos básicos asociados con los conjuntos difusos 17 1.2.2 OPERADORES SOBRE CONJUNTOS DIFUSOS 19 1.2.2.1 Intersección difusa. Operador de conjunción 19 1.2.2.2 Unión difusa. Operador de disyunción 20 1.2.2.3 Complemento difuso 22 1.2.2.4 Familia de t-normas de Frank 23 1.2.3 RELACIONES DIFUSAS 25 1.2.4 VARIABLES LINGÜÍSTICAS Y REGLAS SI-ENTONCES 25 1.3 CONTROLADORES DIFUSOS 30 1.3.1 CONVERTIDOR DE ENTRADAS NUMÉRICAS A ENTRADAS DIFUSAS 31 1.3.2 BASE DE REGLAS DIFUSAS 32 1.3.3 INFERENCIA DIFUSA 34 1.3.4 CONVERTIDOR DE ENTRADAS DIFUSAS A SALIDAS NUMÉRICAS 35 1.3.5 EL CONTROLADOR DIFUSO DE MAMDANI 36 1.3.6 EL CONTROLADOR DIFUSO USADO COMO UNA FUNCIÓN NO LINEAL. ...38 1.3.6.1 Los sistemas difusos como aproximadores universales 39 1.4 ASPECTOS SOBRE EL CONTROL DIFUSO MULTIVARIABLE 41 CAPITULO 2. EL CONTROLADOR LÓGICO NATURAL. 43. 2.1 ANTECEDENTES 43 2.1.1 LAS TÉCNICAS QUE UTILIZAN ALGÚN TIPO DE DESACOPLAMIENTO Y/O REGULACIÓN DESCENTRALIZADA 44 2.1.2 LAS TÉCNICAS QUE UTILIZAN ALGÚN MECANISMO DE APRENDIZAJE. ..45 2.1.3 MEDIANTE LA IDENTIFICACIÓN E INVERSIÓN DE UN MODELO DIFUSO. 47 2.1.4 REDUCIENDO LA COMPLEJIDAD DEL CONTROLADOR DIFUSO 48 2.1.4.1 El controlador difuso de Hao Ying, William Siler y James J. Buckley 50 2.1.4.2 La propuesta de Vidolov & Mélin 52 2.2 EL CONTROLADOR LÓGICO NATURAL (CLN) 54 2.1.1 DEFINICIÓN DEL CLN 55.

(6) 2. 2.2.1.1 2.2.1.2 2.2.1.3 2.2.1.4. Subconjuntos difusos Reglas difusas de control Método de inferencia Defuzzyficación. PARTE II.-EXPERIMENTACIÓN. 57 57 60 60 63. CAPITULO 3. CONDICIONES PARA LA EXPERIMENTACIÓN CON EL VIGA-BOLA ....64 3.1 INTRODUCCIÓN 3.2 EL MODELO MATEMÁTICO DEL VIGA-BOLA 3.2.1 MODELO MATEMÁTICO DEL BLOQUEA 3.2.2 MODELO MATEMÁTICO DEL BLOQUE B 3.4 EXPERIMENTACIÓN 3.4.1 FASE DE DISEÑO 3.4.2 FASE DE COMPARACIÓN 3.4.3 FASE DE PRUEBA CAPITULO 4. RESULTADOS Y COMPARACIONES EN EL VIGA-BOLA 4.1 INTRODUCCION 4.2 CONTROLADORES CLÁSICOS 4.2.1 CONTROLADOR PD DISCRETO PARA EL LAZO INTERNO 4.2.2 CONTROLADOR PD DISCRETO PARA EL LAZO EXTERNO 4.3 CONTROL A TRAVÉS DEL CLN 4.3.1 LAS RESTRICCIONES NATURALES DEL ÁNGULO DE LA VIGA 4.3.2 RESTRICCIONES NATURALES PARA LA POSICIÓN DE LA BOLA 4.4 EXPERIMENTACION 4.5 METODOLOGIA PROPUESTA PARA SINTONIZAR EL CLN 4.6 RESULTADOS CAPITULO 5. CONCLUSIONES Y PERSPECTIVAS 5.1 5.2. CONCLUSIONES GENERALES PERSPECTIVAS. 64 65 66 67 70 70 71 71 74 74 76 79 80 82 82 86 90 95 97 99 99 101. ANEXO. 102. BIBLIOGRAFÍA. 104.

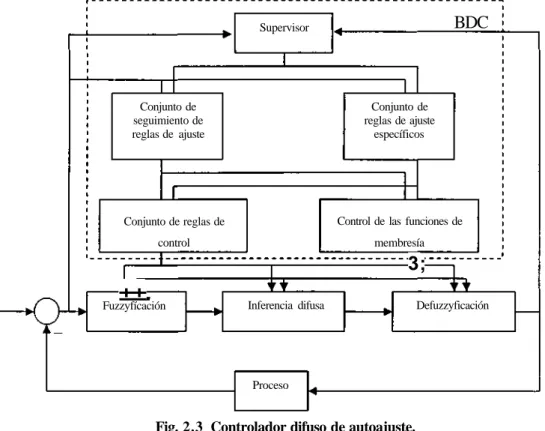
(7) LISTA DE FIGURAS Fig. 1. 1 Universo de discurso y conjuntos clásicos 13 Fig. 1. 2 Conjuntos difusos joven y adulto 14 Fig. 1. 3 Conjunto difuso algunos 15 Fig. 1. 4 Temperaturas que corresponden a "fría" desde el punto de vista de dos personas distintas 15 Fig. 1. 5 Tipos estándar de la función de membresía 16 Fig. 1. 6 Conjunto singleton 17 Fig. 1. 7 Centros de conjuntos difusos 18 Fig. 1. 8 Altura de los conjuntos difusos 18 Fig. 1. 9 Conjunto difuso convexo de números reales 19 Fig. 1.10 La variable lingüística Temperatura con sus valores lingüísticos 26 Fig. 1.11 Implicación difusa 29 . 12 Esquema básico de un controlador difuso 31 Fig. 31 Fig. . 13 Bloque R, generador de las señales de entrada al Fuzzyficador 32 Fig. . 14 Grado de veracidad del peso de David 32 Fig. . 15 Fuzzyficador tipo singleton 33 Fig. . 16 Base de reglas completa 35 Fig. . 17 Defuzzyficación del conjunto verano 36 Fig. . 18 Representación del Defuzzyficador de centro de promedios 40 Fig. . 19 Controladores difusos tipo PID 41 Fig. . 20 Interacción de lazo en un sistema de dos entradas y dos salidas Fig. 21 Sistema difuso tipo MISO 42 Fig. 2. 1 Sistema desacoplado en lazo cerrado 44 Fig. 2. 2 Sistema descentralizado 45 Fig. 2. 3 Controlador difuso de autoajuste 46 Fig. 2. 4 Identificación del proceso por medio de un modelo difuso 48 Fig. 2. 5 Inversión del modelo difuso 48 Fig. 2. 6 Pasos para la reducción de la complejidad de un sistema difuso 49 Fig. 2. 7 El controlador difuso de Hao Ying 50 Fig. 2. 8 Conjuntos difusos de las entradas y la salida del controlador difuso 50 Fig. 2. 9 Los conjuntos difusos de las entradas e y de para el controlador de Vidolov y Mélin....52 Fig. 2. 10 Superficies resultantes de los controladores de a) Ying et. al y b) Vidolov y Mélin, para dos entradas al controlador 53 Fig. 2. 11 Configuración de control del CLN para una sola entrada - una sola salida 54 Fig. 2. 12 Partición difusa para el CLN 57 Fig. 2. 13 Caso especifico de dos entradas al CLN 61 Fig. 2. 14 Superficies resultantes del CLN con dos entradas al variar X y la t-norma 62 Fig. 3. 1 Motor, leva y resorte que maneja el ángulo de la viga 65 Fig. 3. 2 Diagrama de bloques del viga-bola 65 Fig. 3. 3 Gráfica de la posición angular de la viga cuando v(/)=l 67 Fig. 3. 4 Bloque A 67 Fig. 3. 5 Fuerzas actuantes sobre el sistema 67 Fig. 3. 6 Diagrama de bloques del viga-bola 68 Fig. 3. 7 Lazo abierto del viga-bola 68 Fig. 3. 8 Diagrama de bloques del viga-bola para determinar el valor de G 69.

(8) 4. Fig. 3. 9 Lugar de las raíces en función de Ke 69 Fig. 3. 10 Diagrama de bloques simplificado del viga-bola 70 Fig. 3. 11 Prueba 1. Cambio de posición 72 Fig. 3. 12 Prueba 2. Perturbación en la acción de control 72 Fig. 3. 13 Prueba 3. Perturbación en la salida del sistema 72 Fig. 3. 14 Prueba 4. Seguimiento de referencia con variación paramétrica 73 Fig. 4. 1 Lazo cerrado del servomotor 74 Fig. 4. 2 Diagrama de bloques del viga- bola, en cascada 75 Fig. 4. 3 Diagrama de bloques real con la cancelación de las ganancias de la tarjeta de adquisición de datos 76 Fig. 4. 4 Diagrama de bloques para determinar el Bode de lazo cerrado 77 Fig. 4. 5 Lazo cerrado del lazo externo 77 Fig. 4. 6 Lazo cerrado del lazo interno 78 Fig. 4. 7 Diagrama de bloques discreto del sistema en cascada del viga-bola 78 Fig. 4. 8 Diagrama de bloques del lazo interno con el controlador PD discreto 79 Fig. 4. 9 LGR del lazo interno discreto 79 Fig. 4. 10 Simulación de la salida del sistema de control del ángulo de la viga 80 Fig. 4. 11 Diagrama de bloques del lazo externo con el PD discreto 80 Fig. 4. 12 LGR del lazo externo 81 Fig. 4. 13 Simulación de la posición de la bola sobre la viga, utilizando el PD discreto 81 Fig. 4. 14 Variables de entrada al CLN 82 Fig. 4. 15 Posición de referencia del ángulo de la viga y suposición real 83 Fig. 4. 16 Límites naturales de la derivada del error del ángulo de la viga 83 Fig. 4. 17 Diagrama de boques y cuadro de parámetros del CLN para la simulación del lazo interno 84 Fig. 4. 18 Simulación resultante del lazo interno con los límites naturales 84 Fig. 4. 19 Simulación del viga-bola controlado con el CLN ajustado a una entrada escalón unitario 86 Fig. 4. 20 Restricciones naturales del error 87 Fig. 4. 21 La derivada del error de posición de la bola 87 Fig. 4. 22 Diagrama de bloques del sistema completo con el CLN 87 Fig. 4. 23 Simulación del viga-bola a una entrada escalón unitario con las restricciones naturales X = 0 y la t-norma Probabilística 88 Fig. 4. 24 Simulaciones resultantes con los límites ajustados: para una entrada escalón unitario 90 Fig. 4. 25 Diagrama de flujo propuesto para el ajuste de los intervalos de las restricciones naturales 96. LISTA DE TABLAS Tabla 1. 1 Operador compuesto max-min Tabla 1. 2 Familia de t-normas y t-conormas de Frank. 23 24.

(9) OBJETIVO GENERAL Aplicar el Controlador Lógico Natural en un prototipo de laboratorio y comparar su desempeño contra el obtenido mediante técnicas clásicas de control para sustentar su utilidad en el control de sistemas más complejos.. OBJETIVOS PARTICULARES •. Analizar en simulación y experimentalmente los efectos de los parámetros propios del Controlador Lógico Natural y emitir recomendaciones de diseño.. •. Comparar los desempeños obtenidos contra controladores clásicos (Proporcional Derivativos) y entender sus fortalezas.. •. Establecer bases para continuar la investigación, desarrollo y uso del Controlador Lógico Natural en procesos más complejos..

(10) INTRODUCCIÓN GENERAL. El control difuso de procesos es una alternativa para el control de sistemas cuando estos últimos no pueden ser controlados adecuadamente mediante técnicas de control clásico o moderno. Tal es el caso de los sistemas que son fuertemente no lineales o difíciles de modelar, ya que plantear sus modelos matemáticos resulta ser muy difícil o casi imposible de obtener. Como ejemplo tenemos: los hornos de cemento, plantas de tratamiento de agua, procesos de manufactura, incineradores multicapas, entre otros. En estos casos resulta adecuada la implantación de controladores difusos. El control difuso también es utilizado para controlar sistemas lineales de bajo grado de dificultad o no difíciles de modelar, sustituyendo las acciones de corrección que un "operador experto" realizaría. Un controlador difuso no requiere de modelos matemáticos complicados para su implementación, sino más bien de la información cualitativa de la dinámica del proceso que un operador experto conoce basándose en su experiencia en acciones correctivas aunque sean poco precisas. Resulta entonces interesante usar el controlador difuso porque permite combinar la información difusa del conocimiento experto con la información precisa proveniente de los sensores para poder realizar tareas de regulación de procesos. Es importante aclarar que a lo largo de este trabajo de investigación se hará mención al controlador difuso como una función no lineal que contiene ciertas dinámicas internas. La forma usual de representar al controlador difuso será: e{t). u(t). Donde: e(t) es una señal escalar dependiente del tiempo. R representa un conjunto de ecuaciones (normalmente lineales diferenciales) que producen un conjunto de señales dependientes de e(t) y organizadas en un vector columna é. f(.) es una función no lineal estática y sin memoria que combina el vector columna de señales é en un solo escalar u(t)..

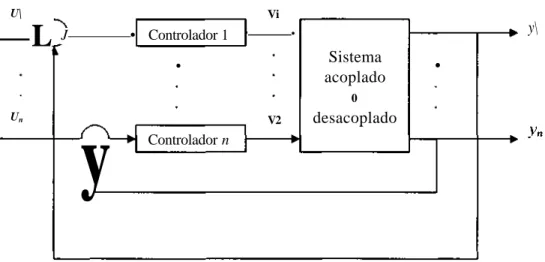
(11) También es importante señalar que cuando nos refiramos a un sistema difuso, nos referiremos al mapeo no lineal (estático) representado precisamente por f(.). Nótese entonces que un controlador difuso será considerado como la combinación de un bloque lineal dinámico R y un sistema difuso estático f. La señal u(í) es la señal de control que se envía al proceso a controlar, pero también es considerada la salida del sistema difuso. Por otro lado, el vector de señales é es considerado la entrada al sistema difuso pero que depende de una señal escalar e(í) construida a partir de las señales provenientes de los sensores del proceso. En forma general, un controlador difuso está integrado por cuatro bloques: el primero, que convierte los valores cuantitativos provenientes de la planta en valores cualitativos o difusos; el segundo, en el cual se concentran todas las reglas que se emplearán para la ejecución de la acción de control; el tercero, el bloque en donde interactúan los valores o datos difusos de entrada con las reglas, dando como resultado un valor difuso; y el cuarto bloque, que convierte el valor difuso obtenido en un valor cuantitativo que la planta aceptará como acción de control. Es importante señalar que la cantidad de parámetros que se requieren definir para un sistema difuso varía en función de la cantidad de variables de entrada al proceso, de las variables que entrarán al controlador difuso, de los conjuntos difusos que se creen por cada variable del sistema difuso, pero sobre todo por la cantidad de reglas difusas que se necesitarán, las cuales dependen de la cantidad de variables del sistema difuso y de sus conjuntos difusos creados. Como se observa, son muchos los parámetros que se requieren especificar. Un problema mayor se presenta cuando se requiere regular un proceso multivariable, no solo por la inmensa cantidad de parámetros del controlador difuso (R, f) a ajustar, sino también por la dificultad de encontrar a un experto que sea capaz de regular tales procesos. Es por eso que la búsqueda de alternativas resulta indispensable. Existen alternativas presentadas en la literatura englobadas en cuatro grandes ejes: i.. Las técnicas que utilizan algún tipo de desacoplamiento y/o regulación descentralizada [30, 34, 60]. Debido a que todas las entradas de un proceso están acopladas y afectan a todas y cada una de las salidas, la finalidad del desacoplamiento es hacer que para cada entrada al proceso solo sea afectada su salida correspondiente eliminando así la interacción existente. La descentralización se refiere al hecho de crear un controlador difuso por cada par entrada - salida acoplada o desacoplada.. ii.. Las técnicas que utilizan algún mecanismo de aprendizaje [13, 16, 35, 58, 61, 65]. En estas técnicas se aplican mecanismos de optimización matemática o de adaptación con redes neuronales o algoritmos genéticos, los cuales le dan al sistema la capacidad de adaptarse (o auto-sintonizarse) a la situación real.. iii.. Mediante la identificación e inversión de un modelo difuso [24, 62], En esta alternativa se busca crear un modelo de la planta a través de una descripción de la.

(12) 8 misma por medio de reglas difusas, y una vez creado el modelo, buscar la forma de invertir su efecto. iv.. Reduciendo la complejidad del controlador difuso [1, 3, 50, 57, 63]. Dos clases de técnicas existen: aquellas que reducen la complejidad de un primer controlador difuso muy complejo, ya sea reduciendo el número de conjuntos difusos por variable y/o el número de reglas difusas; y aquellas que construyen un controlador inicialmente de complejidad reducida, buscando crear el controlador difuso más simple. En ambos casos la idea principal es disminuir la cantidad de parámetros a ajustar y hacer más fácil la sintonización.. Setnes presentó un algoritmo para reducir la complejidad del controlador difuso [50]. Esta propuesta tiene el inconveniente de tener que conocer de manera inicial una base de reglas completa, para que a partir de ella se eliminen conjuntos o reglas difusas sin que el funcionamiento del controlador difuso se vea perjudicado. Otras investigaciones proponen el uso de controladores difusos inicialmente simplificados; tal es el caso del trabajo realizado por Hao Ying [63], quien propuso utilizar solamente dos variables de entrada al controlador difuso con solo dos conjuntos difusos por variable, creando así la base difusa completa de cuatro reglas difusas. Un trabajo similar al anterior es el de Vidolov & Mélin [57], salvo que ellos consideraron solamente utilizar las reglas completamente opuestas, obteniendo resultados muy parecidos a los que Hao Ying obtuvo. Por su parte, Aguilar & Hernández crearon un controlador difuso al que denominaron Controlador Lógico Natural (CLN) [6]. La característica principal de éste era que poseía solo un conjunto difuso y una sola regla. En el año de 1999, Aceves & Aguilar analizaron al CLN y concluyeron que presentaba problemas de simetría y de estabilidad, por lo que decidieron definir una segunda versión del CLN [3]. En esta nueva versión se especifican solamente dos conjuntos difusos por variable y solo dos reglas difusas. La idea es limitar sabiamente el grado de libertad del controlador difuso para alcanzar un diseño más sencillo. El presente trabajo se desarrollará en base a esta segunda versión, al controlador se le seguirá llamando Controlador Lógico Natural. Esta tesis forma parte de una serie de estudios sobre el CLN, éste será diseñado para controlar en tiempo real la posición de una bola sobre una viga. La metodología heurística para ajustar los parámetros del CLN es uno de los objetivos de este trabajo, estableciendo así la primer metodología de diseño. La metodología propuesta en esta tesis parte del hecho de conocer las restricciones físicas naturales del sistema: la saturación de la acción de control y de los rangos de operación del sistema. Como no es posible aplicar métodos analíticos para determinar su grado de robustez, se aplicarán una serie de pruebas en tiempo real para analizar su comportamiento. Con este trabajo se espera entender un poco más las ventajas y desventajas del CLN para el control de procesos y dejar las bases para futuros trabajos..

(13) El presente trabajo está dividido en dos partes: los aspectos teóricos del Controlador Lógico Natural y, la experimentación. La primera parte de esta tesis se subdivide en dos capítulos: el capítulo 1 presenta un resumen de los principios de la lógica difusa y las generalidades del controlador difuso. De igual forma, el capítulo 2 presenta los antecedentes, la definición y características del CLN. La segunda parte de esta tesis está compuesta de los siguientes capítulos: el capítulo 3 que describe el prototipo del viga-bola: su modelo matemático, la estrategia de control aplicada, los requisitos de diseño y la definición de las pruebas que se aplican a dicho sistema real. El capítulo 4 presenta el diseño de los controladores convencionales, la propuesta de diseño del CLN, los resultados de las pruebas y un análisis comparativo del desempeño obtenido con el CLN y con los controladores clásicos. El capítulo 5 contiene las conclusiones y perspectivas a las cuales se han llegado. En este capítulo se establecen bases para continuar la investigación, desarrollo y uso del CLN en procesos más complejos. Finalmente en el anexo se presenta el código de Matlab® del programa del Controlador Lógico Natural utilizado para realizar todas las pruebas tanto en simulación como en tiempo real (utilizando la tarjeta AD-512), todo con simulink®..

(14) 10. PARTE I. ASPECTOS TEÓRICOS.

(15) 11. CAPITULO 1. GENERALIDADES DEL CONTROLADOR DIFUSO.. 1.1. INTRODUCCIÓN.. Los sistemas difusos han sido aplicados en diversos campos, tanto en comunicaciones como en manufactura, medicina, sicología, sistemas de negocios, etc. Pero en donde ha habido un mayor interés es en el control de procesos. Un sistema difuso puede ser utilizado en sistemas de control de lazo abierto o de lazo cerrado. Cuando es utilizado como controlador en lazo abierto, el sistema difuso usualmente ajusta algunos parámetros de control y el proceso funciona de acuerdo a dichos parámetros. Pero cuando se usa como controlador de lazo cerrado, el sistema difuso mide las salidas del proceso y toma las acciones de control sobre el proceso en forma continua. Podemos encontrar ejemplos de aplicaciones de los sistemas difusos en las referencias [19, 32, 46, 59], de entre ellos tenemos los siguientes: a. Ajuste de equipos electrónicos. Ajusta los potenciómetros de un equipo tomando como antecedentes las magnitudes eléctricas medidas. b. Control de robots móviles autónomos. Controla la tracción y dirección de un robot móvil para que siga una determinada trayectoria. c. Lavadoras. Evalúa el tipo y grado de suciedad, la cantidad de ropa, el tipo de tejido y ajusta el mejor ciclo de lavado. d. Reguladores de agua caliente para grifos domésticos. Dependiendo de la temperatura deseada y el caudal de la misma regula la temperatura del agua. e. Ascensores. Midiendo el tráfico de usuarios se reduce el tiempo de espera y se precisa el aviso de llegada del ascensor..

(16) 12 Estas son solo algunas de las aplicaciones que en el campo del control automático se han desarrollado. Pero para poder entender cómo se aplican los sistemas difusos, es preciso conocer las bases que han hecho de estos sistemas una buena alternativa de control de procesos, así que la intención del presente capítulo es dar a conocer algunos de los principios que rigen al controlador difuso y por consiguiente al Controlador Lógico Natural. Aquí se ven conceptos básicos de la lógica difusa y posteriormente se define al controlador difuso con cada uno de los elementos que lo integran.. 1.2 FUNDAMENTOS DE LA LÓGICA DIFUSA.. La palabra difuso tiene la siguiente definición: "Adjetivo. Extenso, poco preciso" [44]. Sin embargo, nosotros lo a vamos a ver como un adjetivo técnico ya que los sistemas difusos son sistemas bien definidos y el control difuso es una clase de control no lineal claramente definido. El nombre de difuso fue propuesto por el profesor Lotfi A. Zadeh, quien formuló las bases iniciales de la Teoría de Conjuntos Difusos y con ello la base de la lógica difusa. La lógica difusa es una extensión de la lógica clásica. Esta última califica a sus enunciados con dos valores: falso o verdadero. Aunque la lógica clásica ha modelado satisfactoriamente gran parte del razonamiento "natural" del ser humano, es cierto que éste utiliza valores de verdad que no necesariamente son falso o verdadero. Por ejemplo, al calificar que "el cielo es azul", una persona a diferencia de otra puede graduar en base a su criterio qué tan azul lo está, e igualmente, si "un vehículo se mueve rápido", hay que considerar qué tan rápido es el vehículo, aunque esto último no implique necesariamente cuantificar la velocidad del vehículo con toda precisión. Desde un punto de vista optimista, lo difuso puede entenderse como la posibilidad de asignar más valores de verdad a los enunciados que los clásicos/íz/so o verdadero. Si a verdadero se da el valor 1 y a falso el valor 0, en la lógica difusa se permiten valores intermedios entre 0 y 1, que ni son totalmente falsos ni totalmente ciertos. Se trata entonces de una lógica multivalor en vez de una lógica clásica con solo dos valores. Los sistemas difusos y el control difuso tienen su punto de partida en la lógica difusa y ésta a su vez en la Teoría de Conjuntos Difusos. A continuación se definen una serie de conceptos, características y propiedades matemáticas para los conjuntos difusos.. 1.2.1. CONJUNTOS DIFUSOS.. Un universo de discurso es la colección de todos los elementos que conciernen a un contexto o aplicación en particular. También es llamado espacio de entrada y se representa con la letra U. Un conjunto clásico es un grupo en el cual se incluye o se excluye totalmente un elemento del universo de discurso. Los representaremos con una letra mayúscula en cursiva, por ejemplo, el conjunto A..

(17) 13. Fig. 1. 1 Universo de discurso y conjuntos clásicos.. En la figura anterior se muestra un universo de discurso U y dos conjuntos A y B que contienen una colección de objetos. Una forma de definir a cada conjunto es por medio de la función de membresía. La función de membresía es una forma de identificar a los elementos de un conjunto, sea clásico o difuso. También es llamada función de pertenencia y es denotada por /.IA(X), de tal forma que: "1 six e A MA(X)=. J) si x i. A JLÍA(X). Definiremos a la variable x como aquella que puede ser igual a cualquier elemento de U y tomará el valor 1 si la variable x pertenece a A o adquirirá el valor 0 si no pertenece a A. Una forma de denotar a un conjunto es a través de la siguiente relación:. = {(x,Mx))\. ):. U. La cual se lee: El conjunto A está compuesto por todas las parejas x, una función que relaciona al universo con el conjunto {0,1}.. JLIA(X),. donde ¿LIA(X) es. En un conjunto clásico la función de membresía solo toma los valores opuestos: cero o uno, falso o verdadero, fuera del conjunto o dentro del conjunto. Pero en conjuntos difusos la pertenencia a los conjuntos es gradual. Por lo tanto, un conjunto difuso en el universo de discurso í / e s un conjunto sin límites abruptos ni claramente definidos y puede contener elementos con solo un grado parcial de pertenencia. Los conjuntos difusos pueden clasificarse como continuos o discretos: Conjunto difuso continuo. Cuando el universo en discurso es continuo, el conjunto A es comúnmente escrito como:.

(18) 14 A. ¡MA(X)/X. =. u Donde el signo integral denota la colección de todos los elementos x que pertenecen a U que están asociados con la función de pertenencia JUA(X) * 0. El siguiente ejemplo tomado de la referencia [59] muestra dos conjuntos difusos continuos: Sea U el intervalo [0, 100] que representa la edad de un humano ordinario. Podemos definir los conjuntos difusosyoven y adulto de la siguiente forma: 25. 50. O. 25. r.,.. ^. "r *-50 2 , adulto = |(l + ( ) ) Ix 5. 50. Cuya gráfica es:. joven 1. adulto. /. 'i|. ^ ~. 0,5 ¡. 0J. ^-,— edad. Fig. 1. 2 Conjuntos difusos^ove/i y adulto.. Conjunto difuso discreto. Cuando t/es discreto, A es comúnmente escrito como:. Donde el signo de suma representa la colección de todos los puntos x que pertenecen a U que están asociados con la función de pertenencia ^(x) ^ 0. El siguiente ejemplo tomado de la referencia [59] muestra un conjunto difuso discreto: Sea U el intervalo [0,10] de números enteros. El conjunto difuso algunos puede estar definido como:.

(19) 15 algunos = 0-5/ + 0.8/ + 1/ + 1 / + 0.8/ + 0.5^ Cuya gráfica es: algunos M. 1.5 1 -! 0.5 0 0. 1• —2* 3. 4. 5. 6. 7. 8. 9. 1 0. Fig. 1. 3 Conjunto difuso algunos.. El siguiente ejemplo muestra una aplicación de los conjuntos difusos y su relación con la función de membresía: Se desea caracterizar la temperatura "fría" mediante la apreciación de dos personas de diferente región geográfica. El conjunto difuso A será utilizado para caracterizar o modelar todas las temperaturas bajas. La función de membresía nos ayuda a caracterizar al conjunto A y relaciona todas las temperaturas contra su grado de pertenencia al conjunto correspondiente. Una forma sencilla de visualizar una función de membresía es mediante una gráfica, como la que se muestra en la Fig. 1.4. 1,1 0,9 0,7 0,5 0,3 '°'1-10. 1.1 09 0.7 •. 0.5 i 0.3 ,;. \ X \ \ -5. 0. 5. 10. Grados Centígrados. 15. 20. x. -10. -5. 0. 5. 10. 15. 20. v. Grados Centígrados. Fig. I. 4 Temperaturas que corresponden a "fría" desde el punto de vista de dos personas distintas.. Para una persona, a partir de 15° centígrados comienza a sentirse el frío, en el intervalo de centígrados la temperatura es un poco fría, y desde 5o centígrados hacia abajo, la temperatura es completamente fría. En cambio para la otra persona, la temperatura fría comienza a los 5o centígrados, entre esta temperatura y 3o centígrados es un poco más fría, pero a partir de la última ya es completamente fría. De la primer gráfica podemos decir que para x = 3o C. tenemos /ii\(x) =0.7; en cambio en la segunda para el mismo valor de temperatura, JLI,I(X) = I..

(20) 16 De lo anterior podemos decir que los conjuntos difusos son una herramienta para modelar matemáticamente lo impreciso de una observación. La función de membresía debe ser determinada dependiendo del tipo de aplicación. Sin embargo, esta tarea suele ser tediosa. Para evitar este trabajo se tienen formas de la función de membresía ya estandarizadas como S, Z, triangular, trapezoidal, campana y singleton, las cuales se muestran en la Fig. 1.5. Función de membresía tipo Z. Función de membresía tipo S. juA(x) 1.5 1 0.5 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 1 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 1 0. Función de membresía tipo trapezoidal. Función de transferencia tipo triangular 1.5 1 0.5 0 1. 3. 5. 7. 9. 11. 13. 15. 1. 3. 5. 7. 9. 11 13 15 17 19. Función de membresía tipo campana. Función de membresía tipo singleton 1.5. 1 0.5. 0. 1. 3. 5. 7. 9. 11 13 15 17. Fig. 1. 5 Tipos estándar de la función de membresía.. En la siguiente subsección se definen algunos conceptos útiles asociados a los conjuntos difusos..

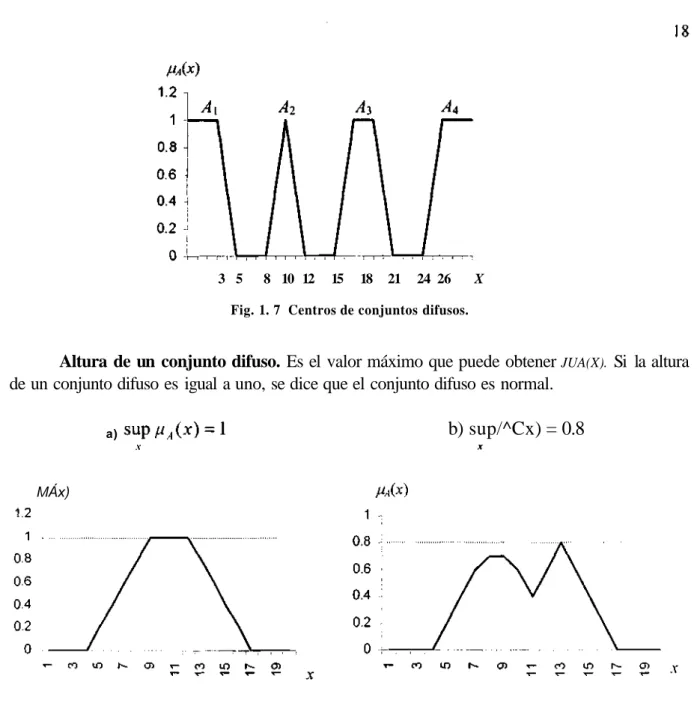
(21) 17 1.2.1.1. Conceptos básicos asociados con los conjuntos difusos.. Soporte de un conjunto difuso. Es un conjunto que contiene todos los elementos del universo de discurso í/cuya función de membresía es distinta de 0. Esto es:. Supp<Á)={xeU\MA(x)>0} Como ejemplo tenemos que el soporte del conjunto difuso algunos (Fig. 1.3) es el conjunto de números enteros {3,4,5,6,7,8}. Si el soporte de un conjunto difuso carece de elementos, se dice que el conjunto difuso es vacío. Si el soporte de un conjunto difuso solo tiene un elemento, se le conoce como conjunto singleton. Como ejemplo de un conjunto singleton tenemos: Sea A = {(3,0.6) | JUA(X): U —> {0,1}}, cuyo gráfico es:. 1.2 1. 0.8 0.6 0.4 0.2. 0. Fig. 1. 6 Conjunto singleton.. Centro de un conjunto difuso. El centro de un conjunto difuso se define dependiendo del tipo de conjunto que se trate (ver Fig. 1.7). Cuando el conjunto se extiende hacia el infinito negativo (A\), el centro es el elemento más grande de todos los elementos que alcanzan el máximo valor de la función de membresía; cuando el conjunto se extiende hacia el infinito positivo (A4), el centro es el elemento más pequeño de todos los puntos que alcanzan el máximo valor de la función de membresía; cuando los conjuntos son finitos {Ai y A3), el centro es el valor promedio o centroide de aquellos que alcanzan el máximo valor de la función de membresía. Para observar el centro de un conjunto difuso se tiene el siguiente ejemplo: En la Fig. 1.7 podemos observar que el centro del conjunto A\=3, el centro de A2=\0, el centro de A-s, = 18 y el centro de .¿4=26..

(22) 3 5. 8 10 12. 15. 18. 21. 24 26. X. Fig. 1. 7 Centros de conjuntos difusos.. Altura de un conjunto difuso. Es el valor máximo que puede obtener JUA(X). Si la altura de un conjunto difuso es igual a uno, se dice que el conjunto difuso es normal. a). b) sup/^Cx) = 0.8. MÁx). Fig. 1. 8 Altura de los conjuntos difusos.. Conjunto difuso convexo. Para que un conjunto difuso sea convexo es necesario que su gráfico tenga solamente una cumbre, como por ejemplo la Fig. 1.9..

(23) 1.2 1. 0.8-I. 0.6 0.4 0.2 0 1. 3. 5. 7. 9. 11. 13. 15. 17. JC. Fig. 1. 9 Conjunto difuso convexo de números reales.. Un ejemplo de un conjunto difuso no convexo lo visualizamos en la Fig. 1.8 b). Los conjuntos convexos son muy utilizados en la teoría de control difusa. Las definiciones anteriores solo son aplicables a un solo conjunto difuso. En la siguiente sección se verán las operaciones básicas entre conjuntos difusos.. 1.2.2. OPERADORES SOBRE CONJUNTOS DIFUSOS.. Los operadores que se aplican a los conjuntos difusos son los mismos que se aplican en la lógica clásica: Operador de disyunción, de conjunción y de negación. Estos hacen posible obtener la unión, la intersección y el complemento de los conjuntos difusos. Definimos los conjuntos difusos A y B dentro del mismo universo de discurso U.. 1.2.2.1. Intersección difusa. Operador de conjunción.. La intersección de A y B es un conjunto difuso, denotado como AP\B y su función de membresía es el resultado de un operador matemático entre fxA{x) y ¿UB(X) que se denotará como. Así, la intersección de A y B se puede denotar de la siguiente forma:. Donde el operador / se define como:.

(24) 20. Y se lee como un mapeo que transforma las funciones de membresía de los conjuntos difusos Ay B en la función de membresía de la intersección de A y B. Para que una función t sea considerada como intersección, debe de satisfacer los siguientes cuatro axiomas [59]: Axioma t i . Condiciones de frontera y de elemento neutro. t(jiA(x),\) = t(\, f.iA{xj) = //-i(.v)/ ¿(0,0) = 0. Axioma t2. Condición de conmutatividad. Í(JJA(X), fdB(x)) = t(jiB(x), MA(X)). Axioma t3. Condición de no decremento o de monotonía. Si MA{X) ^ f¿A(x ') y /-iB{x) - MB(X '), entonces t(jiA(x), /JB(X)) < t(i¿A(x% Axioma t4. Condición de asociatividad. t(t(jiA(x), JUB(X)), pidx)) = t(juA{x),t(¿iB(x), /.idx))). Cualquier función / que satisfaga los axiomas anteriores es llamado operador de conjunción. Estos son conocidos como t-normas o normas triangulares [29]. Existen varias clases de operadores de conjunción [59], pero solamente las siguientes son de utilidad para esta tesis: a) clase Zadeh o del mínimo.. b) clase Probabilística o producto algebraico. MAnüix) = juA(x) c) clase Lukasiewicz o producto limitado. = max(0, ¿iA(x) + /JB{x) -1) Podemos encontrar en la literatura más operadores de conjunción, por ejemplo en la referencia [59].. 1.2.2.2. Unión difusa. Operador de disyunción.. La unión de A y B es un conjunto difuso en U, denotado por AVJB y cuya función de membresía es el resultado de un operador matemático entre /.iA(x) y //«(*) que se denotará como. Así, la unión de A y B se puede denotar de la siguiente forma:.

(25) 21. Donde el operador s se define como: s: [0,1] x [0,1] ->[0,l] Lo cual se lee como un mapeo que transforma las funciones de membresia de los conjuntos difusos Ay B en la función de membresia de la unión deAyB Para que una función 5 sea calificada como una unión, debe satisfacer los siguientes cuatro axiomas [59]: Axioma si. Condición de frontera o elemento neutro. s(\,\) - 1; 5(0, /uA(x)) = s(juA(x),0) = fiA(x). Axioma s2. Condición conmutativa. s(¿iA(x), /.tB(x)) = S(/.IB(X), f.iA{x)). Axioma s3. Condición de no decremento o de monotonía. Si juA(x) </-iA(x') y JUB(X) </.¿B(X '), entonces s(/.iA{x), juB(x)) < s(juA(x'\ /J.B(X')). Axioma s4. Condición asociativa. s(s(/.iA(x), /.IB(X)), MC(X)) = s(/.iA(x), S(/IB(X), /.idx))). Cualquier función 5 que satisfaga esos axiomas es llamado operador de disyunción. Estos operadores son conocidos como t-conormas o s-normas [29]. Existen varias clases de operadores de disyunción [59], pero solamente las siguientes serán de utilidad para el presente trabajo: a) clase Zadeh o del máximo. MA^B(X). = max(j.iA(x),. b) clase Probabilística o suma algebraica.. c) clase Lukasiewicz o suma limitada. MAVB(X). = min(/.iA(x).

(26) 22 1.2.2.3. Complemento difuso.. El complemento o negación de A es un conjunto difuso en U, denotado por Á y cuya función de membresía (la más utilizada en sistemas difusos) es el resultado de un operador matemático denotado como c{.). El complemento o negación de A se puede denotar de la siguiente forma: C(JIA(X))=. /IA{X). Donde el operador c se define como: c: [0,1]-* [0,1] Y se lee como un mapeo que transforma la función de membresía del conjunto difuso A a la función de membresía de su complemento. Para que la función c sea calificada como un complemento difuso debe satisfacer estos tres axiomas [59]: Axioma el. Condiciones de contorno. c(0) = 1 y c(l) - 0. Axioma c2. Ordenación inversa. Para toda /¿A(X), MB(X) c{f.iA{x)) > c{f.iB{x)). e. [0,1], si f-uix) < MB(X), entonces. Axioma c3. Involución. Para toda juA(x) e [0,1], c(c(juA(x))) = juA(x) Cualquier función c que satisfaga los tres axiomas anteriores es llamada complemento difuso. Podemos encontrar diversos tipos de complementos difusos en la referencia [59], pero el que se utilizará en el presente trabajo está definido como:. La intersección difusa de A y B es el conjunto difuso más pequeño que contiene a ambos conjuntos. La unión difusa es el conjunto más grande que contiene tanto a A como a B. En la lógica clásica la combinación entre la unión, la intersección y el complemento se da por las leyes de De Morgan, las cuales también se aplican a los conjuntos difusos. Si A y B son dos conjuntos difusos, entonces: AvB=AnB. y. AnB=AuB.

(27) 23. Los operadores de conjunción, de disyunción y de complemento se pueden relacionar entre sí a través de las leyes de De Morgan de la siguiente manera: = t{c{fiA{x)), c(juB(x))). c(s(jiA(x),. A lo que se conoce como clase asociada o dualidad de las normas [59]. Los operadores de disyunción, de conjunción y el complemento difuso son utilizados para analizar la base de reglas difusa. Sin embargo, en ocasiones el criterio evaluado no corresponde ni completamente a uno u otro operador. Cuando esto sucede, se utilizan los operadores compuestos [49]. Estos se denotan por la letra v y se representan como:. Donde X es un parámetro entre cero y uno que puede ser elegido dependiendo de las necesidades. Como ejemplo, si MA\X)~()A y fiB\x)~^m°t aplicando el operador compuesto max-min, generamos la siguiente tabla: Tabla 1.1 Operador compuesto max-min.. X X max \fu A (x. 0 0.2 0.4 0.5 0.6 0.8 1. ))+ (l - ¡V)min ( /.iA{x\^H(x)). min(0.4, 0.8) = 0.4 0 2(0.8) + 0.8(0.4) = 0 .48 0 4(0.8) + 0.6(0.4) = 0 .56 0 5(0.8) + 0.5(0.4) = 0 .60 0 6(0.8) + 0.4(0.4) = 0 .64 0 8(0.8) + 0.2(0.4) = 0 .72 max(0.4, 0.8) = 0.8. Otros tipos de operadores compuestos podemos encontrar en [38, 59], pero no se utilizarán en el presente trabajo.. 1.2.2.4. Familia de t-normas de Frank.. Desde que se desarrolló la teoría de normas triangulares y conormas triangulares [29] se ha extendido su uso en la teoría de control difuso para ser utilizadas en la intersección y unión de conjuntos difusos. Muchos investigadores han presentado varios tipos de operadores para el mismo propósito. Los operadores convencionales "son los de Zadeh (min y max), los cuales han sido utilizados en casi todos los diseños de controladores difusos. Sin embargo, algunos estudios experimentales y teóricos indican que los otros tipos de operadores pueden trabajar mejor en.

(28) 24 algunas situaciones. Para cada tipo de operación, las funciones correspondientes pueden ser divididas en dos categorías. Una son las funciones no paramétricas, como la clase Zadeh, la clase probabilística o la clase Lukasiewicz; y la otra son las funciones paramétricas, en las cuales se utilizan parámetros para ajustar la fuerza de las operaciones correspondientes. Dentro de esta última categoría existe una t-norma llamada de Frank, la cual se define como [1]:. mí n I 9>M¡. = 1 - - - log <P. \ i I. 1 + U(e ' - l j. Y su t-conorma o s-norma se define como: /r. n\. <P M Donde [lP e [0,1 ]" Esta t-norma agrupa en un solo operador las t-normas y s-normas más frecuentemente utilizadas al variar el parámetro (p, creando así la familia de t-normas de Frank: Tabla 1. 2 Familia de t-normas y t-conormas de Frank.. t-norma. t-conorma sv(\ip). Zadeh ((p-> -oo). Probabilística (q>->0) Lukasiewicz ((p —> +oo). mhf=1(^)). ma?. Cl(/^(e*)) m 1. n^(6*) Í=I. m m a ^ l - w + Z j.ip(e, ),0) /=!. \. i-ni-//P(E/) ;=l m. min( Z /uP{&¡ ),1). Además de esta familia de t-normas existen otras que pueden ser encontradas en [23. 29, 531, las cuales no se utilizarán en esta tesis. Cuando trabajamos con distintos universos de discurso requerimos relacionar los conjuntos de los distintos universos, lo cual se logra a través de las relaciones difusas..

(29) 25 1.2.3. RELACIONES DIFUSAS.. El producto cartesiano de dos universos no difusos U y V, denotado por U x V, es el conjunto no difuso de todos los pares (M,V) tales que los u pertenezcan a U y los v a V, es decir [59]:. UxV= {(«,v)|«e U y ve V} En una forma generalizada, si existen n universos: U\ x Uix ... x Un ={(i/i, u2,..., un) I u¡ e U\, u2e U2,...„ wn e £/„} Una relación no difusa Q entre los universos U\, U2,..., Un es un subconjunto del producto cartesiano U\ x U2 x ... x Un y se puede especificar como:. QiUi.U2....,. Un)czUlxU2x...xUtt. Como una relación es en sí un conjunto, podemos aplicarle todas las operaciones y propiedades mencionadas. Además, podemos utilizar la siguiente función de pertenencia para representar una relación: f 1 si (MI, M2, ..., un) e Q(U\, U2,..., U,,) llQÍU\,U2,...,Un)=. i. [_ 0 de otra forma Una relación difusa es un conjunto difuso Q definido como: Q =. { ( ( i / i , M 2 , ..., U n ) , M Q ( U U. U 2 , ..., Un)) I ( M i , M 2 , ..., II,,) €. U\ X f/ 2 X . . . X U,,\. Donde:. Cuando solamente hablamos de dos universos, U y V, la relación difusa [/x Kse llama relación difusa binaria. El uso de las relaciones difusas se aplica la máquina de inferencia difusa. Pero para poder llegar a esta última es preciso conocer lo que son las variables lingüísticas y la base de reglas que regirán al sistema difuso.. 1.2.4. VARIABLES LINGÜISTICAS Y REGLAS SI - ENTONCES.. El control difuso es un sistema basado en un conjunto de reglas de conocimientos, del tipo: "SI pasa esto ENTONCES haz esta acción". De aquí que hablemos de las reglas SI - ENTONCES como parte importante de un sistema difuso. La sintaxis correcta de esta regla es:.

(30) 26 SI <propos¡c¡ón difusa> ENTONCES <proposic¡ón difusa> Antes de entrar en este tema se definen los conceptos de variable lingüística y proposición difusa. En la vida diaria hablamos de variables que pueden ser medibles o no, por ejemplo, podríamos hablar de la variable temperatura, ésta puede tener un valor de 25° C. o cualquier otro, siempre y cuando contemos con un termómetro para saberlo; pero cuando no es así solamente decimos que la temperatura es alta o regular o baja, pero ¿qué tan alta? o ¿qué tan baja?. Cuando la variable toma palabras como su valor, estamos hablando de variables lingüísticas. Las palabras son caracterizadas por conjuntos difusos definidos en el universo de discurso en donde la variable está definida. Una variable lingüística está caracterizada por los elementos x, T, U, M; donde: x es el nombre de la variable lingüística. Tes el conjunto de los valores lingüísticos que x puede tomar. U es el dominio físico en el que la variable lingüística x toma sus valores de cantidad. Mes la regla que relaciona a cada valor de Tcon un conjunto difuso en U. Por ejemplo, x es la Temperatura; Tpuede ser {fría, fresca, confortable, cálida, caliente}; U podría ser el intervalo [-10°, 35o] y; M relaciona "fría", "fresca", "confortable", ""cálida" y "caliente" con la función de membresía de la Fig. 1.10. P fría. -10. fresca. 3. 5. confortable. cálida. 12 15 17 22 25 28. caliente. 35. °C.. Fig. 1. 10 La variable lingüística Temperatura con sus valores lingüísticos.. Definimos una proposición difusa como una oración que va a relacionar una o varias variables lingüísticas con uno o varios valores lingüísticos. Las proposiciones pueden ser de dos tipos: a) Atómicas: x es A.

(31) 27 Donde x es la variable lingüística y A es el valor lingüístico de x. b) Compuestas:. (xesS AND xisNOTF) OR xesM Son proposiciones atómicas con conectores AND, OR y NOT, estos se representan por los operadores de conjunción, disyunción y negación respectivamente. Sus variables lingüísticas pueden o no ser diferentes. Para determinar el valor de la función de membresia de las proposiciones se aplican las siguientes relaciones. •. Cuando utilizamos el conector AND se usan intersecciones difusas. Por ejemplo, sean x y y variables lingüísticas en los universos de discurso U y V respectivamente; A y B los conjuntos difusos en U y V, entonces la proposición compuesta difusa: x es A. AND. yesB. Es interpretada como una relación difusa Ar\B en Ux Kcon la función de membresia: MA^B (x>y) = ^MA (X)>MB (y)]. Donde / es un operador lógico de conjunción. •. Para el conector OR se usan uniones difusas. Si la proposición difusa es: x es A OR. y es B. La relación difusa AuB en U x V tiene la siguiente función de membresia:. Donde 5 es un operador lógico de disyunción. Para el conector NOT se usa el complemento difuso. Si la proposición difusa es: x. es A. La función de membresia correspondiente es:.

(32) 28 Donde c es un operador lógico de negación.. Regresando a la sintaxis de una regla difusa: SI <proposición difusa> ENTONCES <proposición difusa> Podemos ejemplificarla como: SI. xesA. ENTONCES y es B. A la parte SI de la regla (x es A) se le llama antecedente o premisa, mientras que a la parte ENTONCES de la regla (y es B) se le llama consecuente o conclusión. Tanto el antecedente como el consecuente de una regla difusa pueden tener proposiciones compuestas, como por ejemplo: SI x es A y y es B yz es C ENTONCES y es B y z es Cy w es D En cuyo caso todas las proposiciones son calculadas y resueltas simultáneamente usando los operadores lógicos, resultando en un único valor para el antecedente y un único valor para el consecuente: SI xesA' ENTONCES y es B' Una vez que se conocen los valores del antecedente y del consecuente se aplica la operación lógica denominada implicación difusa, la cual se especifica como: A->B Una regla difusa (o implicación difusa) modela el conocimiento adquirido. Considere la siguiente expresión que representa el conocimiento: "Un ser humano morirá". Esto significa que cualquier ser que sea identificado como humano tendrá inevitablemente que morir. Considere ahora el siguiente ejemplo: "Si la temperatura es baja y el caudal de agua es bajo entonces abrir el agua caliente". Esta afirmación es cierta pero maneja información imprecisa y por lo tanto puede ser modelada mediante conjuntos difusos. Una regla difusa o implicación difusa relaciona elementos de un espacio hacia elementos de otro espacio..

(33) 29. U. V Una regla. Fig. 1.11 Implicación difusa.. En la literatura [59] podemos encontrar diversas funciones de implicación, como por ejemplo las siguientes: Sea SI <FP\> ENTONCES <FP2> una relación difusa QenUxV, donde FP\ y FP2 son proposiciones difusas. Se asume que FP\ es una relación difusa definida en U = U\ x ... x {/„.. FP2 es una relación difusa definida en V- V\ x ... x Vm, y x y y son variables lingüísticas en Uy V, respectivamente. Se tienen las siguientes implicaciones: Implicación de Lukasiewicz. La función de membresía para Q es: jiio(x,y) = min[l, 1- MFI\ (*) + MFP2 (y) ] Implicación de Zadeh. La función de membresía para Q es: Po(x,y) = max[min[ MFI\ M , MFP2 (y) ], 1- MFP, (X) ] Implicación de Mamdani. La función de membresía para Q es: Mo(x,y) = min[ MFI\ M , MFP2 (y) ]. o bien. nQ{x,y) = MFF\ (X) MFP2 (y). No son los únicos tipos de implicación, pero de todas, la implicación de Mamdani es la más utilizada en el control difuso. En los sistemas difusos, el conocimiento humano tiene que ser representado en la forma de las reglas difusas SI - ENTONCES y son necesarias varias reglas para especificar qué es lo que debe de hacer un sistema. Una vez teniendo todas las reglas evaluadas por separado es preciso tomar todos los conjuntos difusos que representan la salida para cada regla y combinarlos en un solo conjunto; a este paso se le conoce como agregación difusa [7]. El objeto de obtener un solo conjunto difuso final es el de transformarlo en un valor no difuso para que sea utilizado por el proceso a controlar..

(34) 30. Prácticamente toda la información que se manipula diariamente, ya sea en la casa o en el trabajo, está frecuentemente incompleta o con un cierto grado de incertidumbre, sin embargo, esto no nos impide tomar decisiones. Todos los conceptos de la lógica difusa están matemáticamente bien fundamentados, lo que la hace ser una herramienta muy útil que al manejar grados de verdad permite modelar lo incompleto de una información o lo impreciso de una observación. Con estas bases se parte para afirmar que la lógica difusa se puede aplicar en la supervisión de procesos industriales y en aplicaciones de control. En este último campo, se pueden diseñar controladores difusos, los cuales son otra alternativa de control de procesos. Lo que se persigue con ellos es que a través de algún algoritmo matemático se ejecuten lo mejor posible las acciones de control que un operador experto realizaría bajo determinadas condiciones del proceso. En la siguiente sección se definirá al controlador difuso, sus partes y características principales.. 1.3. CONTROLADORES DIFUSOS.. Los controladores convencionales y los controladores difusos tienen en común que ambos producen una señal de control u{t) a partir de una señal de error e{t), entre la salida real y(t) y la referencia r{t). Sin embargo ellos difieren en el tipo de herramientas para su diseño. Los primeros necesitan una descripción de las dinámicas del proceso mediante ecuaciones diferenciales mientras que los segundos requieren una descripción lingüística de las dinámicas del proceso. Las variables y este conocimiento se representan en forma de conjuntos difusos. En los controladores difusos intervienen cuatro bloques: El que convierte los valores numéricos (observaciones) a valores difusos, llamado Fuzzyficador; el que contiene la base de reglas o de conocimientos sobre el sistema que se desea controlar, llamado Base de reglas difusas; el que genera las salidas difusas en función de las entradas y reglas difusas, llamado Inferencia difusa y; el que convierte las salidas difusas en valores numéricos que serán aplicados a la planta (conclusiones), llamado Defuzzyficador (Fig. 1.12). A continuación se verá cada uno de estos bloques con mayor detalle. Cabe mencionar que la palabra Fuzzyficador es un término híbrido generalmente aceptado. Actualmente la comunidad científica de habla hispana aún no se ha puesto de acuerdo en el término más adecuado para su traducción, en inglés es "Fuzzyfier". De igual manera sucede con la palabra Defuzzyficador ("Defuzzyfier")..

(35) 31. Fig. 1. 12 Esquema básico de un controlador difuso.. El bloque R recibe la señal del error e del lazo cerrado y genera las señales de entrada necesarias del Fuzzyficador (Fig 1.13). Es función del diseñador elegir las señales adecuadas que alimentarán al Fuzzyficador.. d 2 e/dr. Fig. 1. 13 Bloque R, generador de las señales de entrada al Fuzzyfícador.. 1.3.1 CONVERTIDOR DE ENTRADAS NUMÉRICAS A ENTRADAS DIFUSAS. Como las entradas a un controlador difuso son valores numéricos reales, necesitamos de un tipo de interfase entre el controlador difuso y dichos valores. Esta es la acción del Fuzzyficador. En otras palabras, el Fuzzyficador es un operador que construye un conjunto difuso a partir de un valor (u observación). También podemos expresar que el Fuzzyficador es un operador que asigna una distribución de certitud a una medida o-una expresión. Por ejemplo, la apreciación del peso de una persona puede ser: David pesa 70 Kg. Sin embargo, el peso exacto de David puede no ser exactamente 70 Kg. Para definir el grado de certitud de dicha expresión, se le asigna una distribución de veracidad:.

(36) 32. 70. w. Fig. 1. 14 Grado de veracidad del peso de David.. La cual captura lo incierto o impreciso de una afirmación u observación. Por ejemplo la lectura de un termómetro electrónico muy sofisticado puede ser T= 32.427° C. Considerando que el instrumento es muy preciso entonces se puede asignar una distribución de verdad de tipo singleton, la cual modela lo preciso de una medición.. 32.427°. Fig. 1. 15 Fuzzyficador tipo singleton.. Para Fuzzyficar un valor real se puede utilizar cualquiera de las funciones de membresía que se han visto anteriormente. Las funciones de membresía más utilizadas en el control difuso son la gaussiana, la triangular y la singleton, pero esta última es la más comúnmente utilizada porque simplifica los cálculos que se hacen en la inferencia difusa.. 1.3.2. BASE DE REGLAS DIFUSAS.. Para trabajar con sistemas difusos, el conocimiento humano tiene que ser representado en forma de reglas difusas SI - ENTONCES. Son necesarias varias reglas para especificar qué es lo que debe de hacer un sistema. A todo el conjunto de reglas difusas se le conoce como Base de reglas difusas. Esta base se puede definir como: Re(/): SI x, es Al\ y ... y xm es Aln, ENTONCES y es B1 Donde Re'"es la regla /-ésima; A'j, y B1 son conjuntos difusos de los universos de discurso U, c S.K y V c S.H respectivamente para la /-ésima regla; x¡, ;c2, ... , x,, e U son las variables lingüísticas de entrada al sistema difuso y y e Fes la variable de salida del mismo sistema; /V/es.

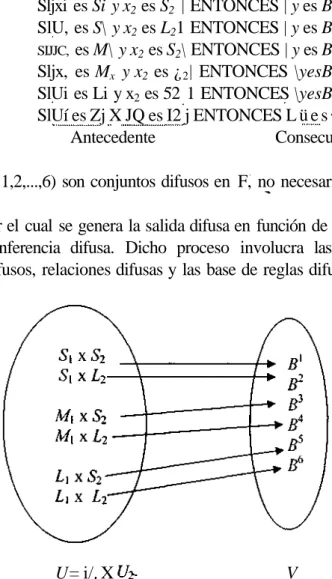
(37) 33. el número de reglas en la base de reglas difusas, para / = 1,2,..., M; n es el número de conjuntos difusos por cada variable lingüística de entrada. La cantidad de reglas Mde la base de reglas difusa depende del número m de variables de entrada y del número de conjuntos difusos n que se formen por cada variable de entrada. Se dice que una base de reglas es "completa" si el número de reglas difusas es igual a la multiplicación del número de conjuntos difusos de cada variable. Si el número de conjuntos para cada variable de entrada fuera el mismo, se tendría que M = nm. Por ejemplo, se puede considerar un sistema difuso con 2 entradas y una salida, con U = U\ x U2 = [0,1] x [0,1] y V - [0,1]. Se definen tres conjuntos difusos S\, M\ y L\ en U\, y dos conjuntos difusos £2 y L2 en U2. Una base de reglas completa está compuesta por todas las posibles combinaciones entre los conjuntos de U\ y U2. El número de reglas M - 3 x 2 =6 reglas y son: Sljxi es Si y x2 es S2 | ENTONCES | y es B1 SlU, es S\ y x2 es L21 ENTONCES | y es B2 3 SIJJC, es M\ y x2 es S2\ ENTONCES | y es B Sljx, es Mx y x2 es ¿ 2 | ENTONCES \yesB4 SlUi es Li y x2 es 52 1 ENTONCES \yesB3 SlUí es Zj X JQ es I2 j ENTONCES L ü e s ^ Antecedente Consecuente Donde B1 (/= 1,2,...,6) son conjuntos difusos en F, no necesariamente diferentes entre sí. El proceso por el cual se genera la salida difusa en función de las entradas y reglas difusas es conocido como inferencia difusa. Dicho proceso involucra las funciones de pertenencia, operadores lógicos difusos, relaciones difusas y las base de reglas difusas.. U= i/. X. V. Fig. 1.16 Base de reglas completa..

(38) 34 1.3.3. INFERENCIA DIFUSA.. El proceso por el cual se obtiene una conclusión a partir de una observación y de un conocimiento se le llama inferencia. Por ejemplo, se sabe que "todo ser humano morirá" y se sabe que "Pedro es humano" por lo tanto se puede inferir que "Pedro morirá". En el caso de observaciones imprecisas y conocimiento impreciso también se puede inferir una conclusión imprecisa, por ejemplo, sea la siguiente expresión una regla de inferencia: "un tomate rojo está maduro". Considere ahora la siguiente observación: "este tomate está un poco rojo". Entonces la conclusión inferida es: "este tomate está un poco maduro". A este proceso también se le conoce como mecanismo de inferencia difusa, motor de inferencia difusa o sistema de inferencia difusa [7]. En la inferencia difusa, los principios de la lógica difusa se utilizan al combinar la base de reglas difusas en el mapeo del conjunto difuso A en U al conjunto de salida B en V. Hemos visto que una sola regla SI - ENTONCES es interpretada como una relación difusa y emplea la función de implicación. Pero como sabemos, necesitamos de más de una sola regla, las cuales van a inferir en el conjunto difuso de salida. Al proceso de unir las salidas para cada regla en una sola, es decir, tomar todos los conjuntos difusos que representan la salida para cada regla y combinarlos en un solo conjunto para después utilizarlo en el proceso de Defuzzyficación, se le conoce como agregación difusa [7]En la agregación todas las reglas de la base de reglas difusa son combinadas para formar una sola relación difusa del tipo U x V, la cual será vista como una sola regla difusa SI ENTONCES. Los pasos para realizar la inferencia difusa y encontrar el conjunto difuso de salida dado el conjunto difuso de entrada son: 1. Para cada regla determinar la función de membresía del lado del antecedente y del lado del consecuente. 2. Aplicar la implicación para obtener la función de membresía para cada regla. 3. Para realizar la agregación de las reglas se pueden ver inicialmente a cada regla de forma independiente y para combinar las reglas utilizar el operador unión. Para poder obtener el conjunto difuso de salida, se pueden aplicar los distintos tipos de inferencias difusas que hay en la literatura, los distintos tipos de implicaciones y los diferentes operadores para las t-normas y sus t-conormas; lo que crea una amplia gama de máquinas de inferencia difusa [23, 59]. Su uso varía entre una y otra aplicación pero en general se busca que.

(39) 35. sea simple al efectuar los cálculos y que se adecué al razonamiento del humano experto. Las máquinas de inferencia más utilizadas en el control difuso son: Máquina de inferencia del producto, máquina de inferencia del mínimo, máquina de inferencia de Lukasiewicz, máquina de inferencia de Zadeh, entre otras [23,59]. Una vez generado el conjunto difuso de salida, es preciso convertirlo a un valor numérico para que sea utilizado como acción de control por la planta del sistema, como se verá en la sección siguiente.. 1.3.4. CONVERTIDOR DE ENTRADAS DIFUSAS A SALIDAS NUMÉRICAS.. A este proceso se le llama Defuzzyficación. El cual es el paso inverso a la Fuzzyficación, es decir, consiste en eliminar la información que modela la incertidumbre y obtener un valor preciso y exacto. Algunos autores lo interpretan como el "mejor" escalar que representa a un conjunto difuso. Por ejemplo, la época de verano se puede modelar mediante un conjunto difuso cuya función de membresía podría ser:. 1° Junio. Io Ju|io. Io Agosto. Io Sep. 10 de Julio. Dias del año (d). Fig. 1. 17 Defuzzyficación del conjunto verano.. El mejor día que representa al verano puede ser el 10 de julio. El Defuzzyficador está definido como un mapeo de un conjunto difuso B en V c S.R proveniente de la máquina de inferencia difusa a un valor numérico real y* e V. En otras palabras, la tarea del Defuzzyficador es encontrar un valor en V que sea el que mejor represente al conjunto difuso B. De entre los Defuzzyficadores [59], uno de los más utilizados es: El Defuzzyficador de centro de promedios. Como el conjunto B es la unión o intersección de M conjuntos difusos podemos obtener mejor el peso promedio de los centros de los Mconjuntos difusos por medio de:. y* =.

(40) 36 Donde y, es el centro del /-ésimo conjunto difuso y w¡ es la altura o valor máximo de la función de membresía del /-ésimo conjunto difuso (Fig. 1.18).. Fig. 1. 18 Representación del Defuzzyficador de centro de promedios.. Existen otros Defuzzyficadores como el del centro de gravedad o el máximo [59], pero no serán de utilidad para esta tesis. Una vez definidos los elementos que integran a un controlador difuso, podemos mencionar un ejemplo de controlador difuso: el controlador de Mamdani, el cual es base del controlador que atañe a esta tesis.. 1.3.5. EL CONTROLADOR DIFUSO DE MAMDANI.. Una de las primeras aplicaciones de la lógica difusa en el control de procesos fue propuesta en 1975 por Ebrahim Mamdani y su equipo para el control del motor de vapor. Su controlador, conocido como Controlador difuso de Mamdani [7, 49] está basado en la experiencia humana, obtenida de ingenieros de control o por operadores de planta. Esta experiencia es traducida en reglas difusas, con su apropiada interfaz de Fuzzyficación y de Defuzzyficación. Las reglas de control son expresadas de la forma que ya conocemos: Re (/): SI jt| es A\ y ... y xn es A'n, ENTONCES y es Bl Donde x\, ..., xn son la variables reales de entrada al controlador; Aln y Bl son los conjuntos difusos, y es la variable de salida difusa. Su esquema de funcionamiento es: •. Generación del conjunto difuso correspondiente a cada regla.. •. Agregación mediante la unión de los conjuntos difusos de las salidas individuales, generando un conjunto difuso por cada variable de salida..

(41) 37. La ventaja del controlador de Mamdani radica en que está ampliamente aceptado dentro del control difuso [17, 22].. Una vez que se definen las funciones de membresía, las reglas difusas, las funciones de asociación de reglas, el mecanismo de inferencia y la función de defuzzyficación, el controlador difuso se convierte en una función no dinámica y no lineal:. Para definir dicha función, es necesario definir los universos de discurso de cada variable. Sea u una variable escalar que adquiere valores dentro de un subconjunto convexo de los números reales: M € E\j C 5R. Sea x un vector variable de escalares en donde cada escalar adquiere valores dentro de un subconjunto convexo de los reales: x¡ e EjCVl. A cada variable escalar se le divide en N subconjuntos difusos, los cuales son caracterizados por sus respectivas funciones de membresía: Para*:. MÁ-Y Ej ^ [0,1] j=\...N. Paraw:. /${.):£{/-> [0,1]. Supóngase que se cuenta con M reglas difusas que relacionan el espacio compuesto de .v con el espacio de U: {E\ xE2x ... x En) ->• Eu Según las reglas de inferencia de la lógica difusa, el grado de veracidad de cada regla es igual al grado de veracidad de cada antecedente. Para calcular el grado de veracidad de cada antecedente se debe realizar una operación de asociación lógica de ellos mediante: /.(•): [0,1]" -> [0,1] Sean entonces W\ los grados de veracidad (o de activación) de cada regla, donde /=1,2,...,M La función de defuzzyficación es un mapeo:.

(42) 38 Eu De esta forma se puede escribir que:. = fD V. M. Primero debemos notar que las operaciones de Fuzzyficación, asociación y Defuzzyfícación están descritas de forma simple mediante una función matemática. Sin mirar con detalle todo el vocabulario y considerando únicamente el resultado final, el controlador difuso es simplemente una función no lineal. Un controlador difuso puede ser expresado como:. u=fx(x) Donde x es un vector de dimensión n, X representa todos los parámetros estructurales del controlador, y u es un escalar. El controlador difuso puede ser considerado como una alternativa para representar una función no lineal estática. Se puede considerar que el controlador difuso es una tabla finita de datos que son interpolados mediante alguna metodología. Cada regla difusa corresponde a un dato de la tabla; las funciones de membresía, la Fuzzyficación, la asociación, la Defuzzyfícación son en su conjunto el mecanismo de interpolación. Todos los controladores difusos tienen características no lineales que se derivan de las propiedades no lineales de la estructura misma del controlador [22].. 1.3.6 EL CONTROLADOR DIFUSO USADO COMO UNA FUNCIÓN NO LINEAL. Toda función que sí cumpla con las propiedades de linealidad {Propiedad aditiva o superposición y Propiedad de homogeneidad o de escalado) es considerada como función lineal. Si algún elemento de la estructura de la función es no lineal (de acuerdo a las propiedades vistas), se dice que toda la función es no lineal. Considérese el uso de un controlador difuso con tan solo una regla: SI x es A ENTONCES u es B.

(43) 39 Donde A y B son los conjuntos difusos o valores lingüísticos tomados para la variable x y la acción de control u. La Fuzzyficación de x\ y X2 es hallar /JU(*I) y MA(X2)- Para que sea lineal se requiere que: = x MA(XÍ) + MA(X2) MA(X\ + i), lo cual no siempre es cierto. Queda claro que una fuente de no linealidad del controlador difuso se encuentra en las funciones de membresía, pero esta no es la única. Otra fuente importante de no linealidad es la función de Defuzzyfícación, pero la más importante se encuentra en las características de cada regla difusa. Cada regla difusa nos permite granear un punto de una función, para que exista una muy buena aproximación de un sistema difuso con dicha función, se requiere de un elevado número de reglas difusas que nos permitan granear todos los puntos consecutivos y así tener una exactitud mayor en la aproximación a la función que se esté manejando.. 1.3.6.1. Los sistemas difusos como aproximadores universales.. Los controladores difusos son sistemas basados en reglas lingüísticas y se consideran como un mapeo no lineal, que en algunos casos pueden ser representados por fórmulas compactas, como por ejemplo [59]: M. i=\. No en todos los casos se pueden representar de esa forma. El problema de los controladores difusos radica en que por lo menos existen tres tipos de Fuzzyfícadores, tres de Defuzzyficadores y, cinco máquinas de inferencia difusa, lo cual nos lleva a cuando menos 5 x 3 x 3 = 45 posibles combinaciones, sin tomar en cuenta los distintos tipos de implicaciones para la interpretación de las reglas difusas, ni las diferentes formas de funciones de membresía. Habrán algunas combinaciones que sean efectivas al aplicarlas en determinados casos, mientras que en otros no lo sean. Pero se ha demostrado que el controlador difuso puede ser una buena aproximación a cualquier función continua no lineal con un cierto grado de exactitud, siempre y cuando se cree un número suficientemente elevado de conjuntos difusos y una base de reglas difusas lo suficientemente completa para aproximar lo más posible el resultado obtenido al resultado esperado, reduciendo el margen de error sin importar el tipo de aplicación que se le dé. De aquí que el controlador difuso sea considerado como un aproximador universal. Teorema de Aproximación Universal [59]. Supóngase que el universo de discurso de entrada (/es un conjunto compacto en 9T. Entonces, para cualquier función real continua g(x) en U y una arbitraria exactitud 8 > 0, existe un sistema difusoyí.x) que cumple:.

(44) 40. Dada una función continua, su aproximación a través de sistemas difusos puede ser alcanzada si el número de conjuntos difusos y de reglas difusas se puedan incrementar tan grandes como sea posible. Sin embargo, el alcanzar una mejor aproximación a expensas de un mayor número de conjuntos difusos y de reglas difusas no es deseable en la práctica. Nótese que el controlador difuso sigue requiriendo la construcción de varias señales a partir de la señal del error entre la salida real y la referencia. En el caso del diseño de controladores difusos para sistemas de una sola entrada - una sola salida (SISO), se suelen utilizar las señales. , }e(')d' las cuales son inyectadas. dt. "'. o. al controlador. Ta Tal es el caso de los controladores difusos SISO de tipo Proporcional - Integral Derivativo (PID).. e(t). e(t) •. d dt. •. d dt. CD. CD. i2. dt2. 0. e(t) d dt 2. ri dt 2 '. CD. •. /dt 0. Fig. 1. 19 Controladores difusos tipo PID.. No se debe caer en el error de que diseñar un controlador difuso para un sistema SISO es cosa trivial, pues se requiere del correcto ajuste de los parámetros del controlador (universo de discurso, conjuntos difusos, reglas, operadores lógicos, Fuzzyficadores y Defuzzyficadores). En la práctica se suelen utilizar métodos heurísticos. Las complicaciones aumentan Quando se desean diseñar controladores difusos para sistemas de múltiples entradas - múltiples salidas (MIMO). Por esta razón se encuentran en la literatura muy pocos controladores difusos MIMO exitosos..