Análisis de componentes principales y su aplicación

Texto completo

(1)1. UNIVERSIDAD NACIONAL SAN AGUSTIN DE AREQUIPA. FACULTAD DE CIENCIAS NATURALES Y FORMALES ESCUELA PROFESIONAL DE MATEMÁTICAS. ANÁLISIS DE COMPONENTES PRINCIPALES Y SU APLICACIÓN. Tesis presentado por la Bachiller: MADELEYNE YAJA LEON Para optar el título profesional de Licenciada en Matemáticas. ASESOR: Dr. Daniel Octavio Roque Roque AREQUIPA 15 DE MAYO DEL 2018.

(2) 2. INDICE. PRÓLOGO: RESUMEN: CAPÍTULO I: CONCEPTOS PRELIMINARES Pág. 1. 1 Combinación lineal de vectores………………………………………………… 5 1.2 Autovalores y autovectores de una matriz cuadrada ……………………….....…7 1.3 Matriz de varianza- covarianza “∑”…………………………………………….15 1.4 Autovalores y autovectores de una matriz de varianza-covarianza …………….19 1.5 Distribución normal multivariante ……………………………………………...20 CAPÍTULO II: COMPONENTES PRINCIPALES 2.1 Introducción……………………………………………………………………...24 2.2 Enfoque descriptivo de componentes principales………………………………..24 2.3 Componentes principales en una población……………………………………...25 2.4 Proporción de variación total mediante autovalores de la matríz  ……………..35 2.5 Componentes principales en una distribución normal……………………………37 2.6 Análisis de componentes principales de dos variables…………………………...39 CAPÍTULO III. APLICACIONES. 3.1 Introducción………………………………………………………………………46 3.2 Utilización de componentes principales en datos meteorológicos……………….46 CONCLUSIONES: BIBLIOGRAFIA:.

(3) 3. PRÓLOGO Cuando tomamos medidas sobre una población u objetos, frecuentemente se incluyan muchas variables como posibles resultados, y cualquiera de estas variables puede ser que tenga un futuro relevante. Generalmente, las variables originales cuando se presentan correlacionadas entre sí en mayor o menor grado, estas correlaciones son como un velo que impiden evaluar adecuadamente el papel que juega cada variable en el fenómeno estudiado, por lo que, hay necesidad de transformar las variables originales correlacionadas en un nuevo conjunto de variables denominadas componentes principales que se caracterizan por estar incorrelacionadas entre sí. El análisis en componentes principales es una técnica de análisis estadístico multivariable que se clasifica entre los métodos de reducción de la cantidad de variables originales, que se aplica cuando se dispone de un conjunto elevado de variables con datos cuantitativos persiguiendo obtener un menor número de variables como combinación lineal de las variables originales, posteriormente su interpretación de las componentes principales permitirá un análisis más simple del problema estudiado. Si las variables originales son incorrelacionadas entre sí, en ese caso, el número de los componentes principales coincide con la cantidad de variables originales. Así que, el análisis de componentes principales se tratará de una técnica para el análisis de la interdependencia. En el presente trabajo se propone los siguientes objetivos: 1. Estudiar teóricamente los componentes principales, con fundamento matemático. 2. Presentar mediante una aplicación que las componentes principales son combinaciones lineales de las variables originales y son no correlacionadas. Para cumplir con los objetivos propuestos, la estructuración del presente trabajo de tesis es como sigue. En el Capítulo I se desarrolla: combinación lineal de vectores, autovalores y autovectores de una matriz cuadrada, matriz de varianza-covarianza, autovalores y autovectores de una matriz ∑ y distribución normal multivariante. En el Capítulo II se estudia el enfoque descriptivo de componentes principales, componentes principales en una población, proporción de variación total mediante autovalores de la matriz de varianza-covarianza, componentes principales en una distribución normal y análisis de componentes principales de dos variables. Finalmente en el Capítulo III, se desarrolla una aplicación a variables meteorológicas. La autora..

(4) 4. RESUMEN El análisis en Componentes Principales permite describir, de un modo sintético, la estructuración y las interrelaciones de las variables originales en el fenómeno que se estudia a partir de las componentes obtenidas que, naturalmente, habrá que interpretar. Es razonable pensar que si en la investigación se quedara con todas las variables originales correlacionadas no simplificaría el problema, por lo que deberá seleccionarse sin mayor pérdida de información pocas variables y fácil de interpretar..

(5) 5. CAPÍTULO I: CONCEPTOS PRELIMINARES 1.1 COMBINACIÓN LINEAL DE VECTORES En varias partes de la matemática se presentan conjuntos donde tiene sentido y resulta interesante considerar las “combinaciones lineales” de los elementos de dichos conjuntos. Para ser más preciso en este tema, debemos conocer lo que es Espacio Vectorial. Definición 1.1 Sea un conjunto V  . Se dice que V es un espacio vectorial sobre R si satisface las siguientes condiciones: 1. Para v i w en V, se tiene que v+w  V. 2. Sean v, w en V; v + w = w + v (propiedad conmutativa) 3. Sean v, w, z en V; v+(w+z) = (v+w)+z (propiedad asociativa) 4. Existe un único elemento 0 en V, llamado vector nulo, tal que v + 0 = v 5. Para cada elemento v de V, existe un único –v en V, tal que v + (-v) = 0. 6. Sea   R, v V, se tiene v  V. 7. Para todo v de V, se tiene que 1v = v. 8. Sean  y  en R y v de V; ()v = (v). 9. Sean v i w de V, R; (v+w) = v + w 10. Sean  y  en R y v de V; (+)v = v+v. Definición 1.2 Un vector v de V se dice combinación lineal de los vectores v1, v2, …, vn en V, si existen escalares 1, 2, …, n de R tales que v = 1v1 + 2v2 + …+ nvn = ∑𝑛𝑖=1 𝛼𝑖 𝑣𝑖 Ejemplo 1.1 Dado v = (a, b) en V, (2, 5) y (3, 7) elementos de V. Sean  y  de R. Entonces podemos escribir que: (a, b) = (2, 5) + (3, 7), Lo cual genera un sistema de dos ecuaciones lineales: {. 𝑎 = 2𝛼 + 3𝛽 𝑏 = 5𝛼 + 7𝛽.

(6) 6. En algunas aplicaciones de Algebra Lineal, se necesitan vectores que tengan ciertas definiciones tales como uno en el i-ésimo lugar, o sea: vi = ei , para i = 1, 2, …, n; 0. = [1] . 0 de modo que: 𝑒𝑘𝑡 ei = {. 1 , 𝑠𝑖 𝑘 = 𝑖 0 , 𝑠𝑖 𝑘 ≠ 𝑖. En este caso, el vector ei se llama vector unitario. Lema 1.1 (Desigualdad de Cauchy - Schwarz). Sean dos vectores b y d de orden p1 cada uno. Entonces (btd)2  (btb)(dtd) La igualdad se cumple si y solo si b = rd (o d = rb) para algún escalar rR. Demostración. Si b = 0 o d = 0, cumple la igualdad, excluimos ese caso. Consideremos el vector b – rd  0, para rR, entonces 0 < |b-rd|2 = (b-rd)t(b-rd) = btb – rdtd - bt(rd) + r2dtd = btb – 2r(btd) + r2(dtd) = btb = btb -. (𝑏 𝑡 𝑑)2 𝑑𝑡 𝑑. (𝑏 𝑡 𝑑)2 𝑑𝑡 𝑑. +. (𝑏 𝑡 𝑑)2 𝑑𝑡 𝑑. – 2r(btd) + r2(dtd). + (dtd)[𝑟 −. 𝑏𝑡𝑑. 2. ] . 𝑑𝑡 𝑑. 𝑏𝑡𝑑. Hagamos r = 𝑑𝑡 𝑑 , entonces 0 < btb -. (𝑏 𝑡 𝑑)2 𝑑𝑡 𝑑.  (btd)2  (btb)(dtd). si b  rd, rR. En caso que b – rd = 0  0 = (b-rd)t(b-rd)  (btd)2 = (btb)(dtd)  En la siguiente sección veremos la extensión de la desigualdad de Cauchy-Schwarz..

(7) 7. 1.2 AUTOVALORES Y AUTOVECTORES DE UNA MATRIZ CUADRADA. En general, una matriz A de orden mn, es decir, de m filas y n columnas es un ordenamiento de números tal como: 𝑎11 𝑎12 … 𝑎1𝑛 𝑎 𝑎22 … 𝑎2𝑛 ] A = [ 21 . . . … 𝑎𝑚1 𝑎𝑚2 𝑎𝑚𝑛 𝑚×𝑛 En donde 𝑎𝑖𝑗 es un elemento de R. Decimos que A es una matriz cuadrada si m = n. Esto es: 𝑎11 𝑎12 … 𝑎1𝑛 𝑎22 … 𝑎2𝑛 ] A = [𝑎21 . . . 𝑎 𝑎 …𝑎 𝑛1. 𝑛2. 𝑛𝑛 𝑛×𝑛. Ejemplo 1.2 La Sra. Phelips y el Sr. Jhosonn son representantes de ventas de una agencia de automóviles que ofrece sólo dos modelos. Agosto fue el último mes para los modelos de este año, y los modelos del próximo año se ofrecerán a partir de setiembre. Las ventas brutas de cada mes se presentan en las siguientes matrices: Ventas de agosto 𝑆𝑟𝑎. 𝑃ℎ𝑒𝑙𝑖𝑝𝑠 𝑆𝑟. 𝐽ℎ𝑜𝑠𝑜𝑛𝑛. 𝐶𝑜𝑚𝑝𝑎𝑐𝑡𝑜 𝐷𝑒 𝑙𝑢𝑗𝑜 $. 6 000 $. 12 000 [ ] $. 12 000 0. =𝐴. Ventas de setiembre 𝑆𝑟𝑎. 𝑃ℎ𝑒𝑙𝑖𝑝𝑠 𝑆𝑟. 𝐽ℎ𝑜𝑠𝑜𝑛𝑛. 𝐶𝑜𝑚𝑝𝑎𝑐𝑡𝑜 𝐷𝑒 𝑙𝑢𝑗𝑜 $. 24 000 $. 48 000 [ ] $. 30 000 $. 36 000. = B.. (Por ejemplo, la Sra Phelips tuvo una venta de $. 6 000 en automóviles compactos en agosto y, el Sr. Jhosonn tuvo una venta de $. 36 000 en automóviles de lujo en setiembre) a) ¿Cuáles fueron las ventas combinadas en Agosto y setiembre por cada persona y cada modelo?. b) ¿Cuál fue el aumento en las ventas de agosto a Setiembre? c) Si los dos representantes recibieron 5% de comisiones sobre las ventas brutas, calcule la comisión de cada persona por cada modelo vendido en setiembre. Solución. a) Se tiene:.

(8) 8. 𝐶𝑜𝑚𝑝𝑎𝑐𝑡𝑜 𝐷𝑒 𝑙𝑢𝑗𝑜 A + B = $. 30 000 $. 60 000 𝑆𝑟𝑎. 𝑃ℎ𝑒𝑙𝑖𝑝𝑠 [ ] 𝑆𝑟. 𝐽ℎ𝑜𝑠𝑜𝑛𝑛 $. 42 000 $ 36 000 b) En este caso hacemos la diferencia. 𝐶𝑜𝑚𝑝𝑎𝑐𝑡𝑜 𝐷𝑒 𝑙𝑢𝑗𝑜 B - A = $. 18 000 $. 36 000 [ ] $. 18 000 $ 36 000. 𝑆𝑟𝑎. 𝑃ℎ𝑒𝑙𝑖𝑝𝑠 𝑆𝑟. 𝐽ℎ𝑜𝑠𝑜𝑛𝑛. c) Aplicamos la multiplicación de un vector por un escalar. 0.05B = [. (0.05)($. 18 000) (0.05)($. 36 000) ] (0.05)($. 18 000) (0.05)($ 36 000). 𝐶𝑜𝑚𝑝𝑎𝑐𝑡𝑜 𝐷𝑒 𝑙𝑢𝑗𝑜 = $. 1 200 $. 2 400 [ ] $. 1 500 $ 1 800. 𝑆𝑟𝑎. 𝑃ℎ𝑒𝑙𝑖𝑝𝑠 𝑆𝑟. 𝐽ℎ𝑜𝑠𝑜𝑛𝑛. Para estudiar autovalores y autovectores de una matriz cuadrada, necesitamos conocer algo de transformaciones lineales. En buena cuenta, una transformación lineal T es una aplicación de un espacio vectorial V en W en los reales R. Definimos por: T:V. W. que para cada wW , existe v V tal que T(v) = w, en esas condiciones T es una aplicación. Definición 1.3 Dados V y W dos espacios vectoriales en R. Sea T una aplicación de V en W. Se llama T una transformación Lineal dada por T:V v. W T(v) = w. Si cumple dos condiciones siguientes: 1) T(v1 + v2) = T(v1) + T(v2), para v1 y v2 de V. 2) T(v1) = T(v1), para  R, v1V. Ejemplo 1.3 Sea −1 2 A=[ 2 1. 0 ] R32 3. Definimos una transformación lineal por T(v) = Av, vR31. Comprobar que T es una transformación lineal. Solución. Sea.

(9) 9. 𝑣1 v = [𝑣2 ], 𝑣3 Entonces −1 2 T(v) = Av = [ 2 1. 𝑣1 −𝑣1 + 2𝑣2 0 𝑣 ] [ 2] = [ ] 2𝑣2 + 𝑣2 + 3𝑣3 3 𝑣 3. Es una transformación lineal. En efecto: 1) Sea x i y dadas por. 𝑥1 𝑦1 x = [𝑥2 ] , y = [𝑦2 ]; 𝑥3 𝑦3 dos elementos de R31, entonces 𝑥1 𝑦1 −1 2 0 𝑥 𝑦 T(x + y) = A(x + y) = [ ] ([ 2 ] + [ 2 ]) 2 1 3 𝑥 𝑦 3. =[. 3. 𝑥1 + 𝑦1 −1 2 0 𝑥 + 𝑦 ][ 2 2] 2 1 3 𝑥 +𝑦 3 3. =[. −𝑥1 − 𝑦1 + 2𝑥2 + 2𝑦2 + 0 ] 2𝑥1 + 2𝑦1 + 𝑥2 + 𝑦2 + 3𝑥3 + 3𝑦3. =[. (−𝑥1 + 2𝑥2 + 0) + (−𝑦1 + 2𝑦2 + 0) ] (2𝑥1 + 𝑥2 + 3𝑥3 ) + (2𝑦1 + 𝑦2 + 3𝑦3 ). −𝑦 + 2𝑦2 + 0 −𝑥1 + 2𝑥2 + 0 ]+[ 1 ] 2𝑥1 + 𝑥2 + 3𝑥3 2𝑦1 + 𝑦2 + 3𝑦3 𝑥1 𝑦1 −1 2 0 𝑥 −1 2 0 𝑦 =[ ] [ 2] + [ ] [ 2] 2 1 3 𝑥 2 1 3 𝑦 3 3 =[. = Ax + Ay = T(x) + T(y). 2. Sea  R, x  R31. Entonces 𝑥1 −1 2 0 𝑥 T(x) = A(x) = [ ]([ 2 ]) 2 1 3 𝑥 3. 𝑥1 −1 2 0 𝑥 =[ ] [ 2] 2 1 3 𝑥 3 =[. −𝑥1 + 2𝑥2 + 0 ] 2𝑥1 + 𝑥2 + 3𝑥3. =[. (−𝑥1 + 2𝑥2 + 0) ] (2𝑥1 + 𝑥2 + 3𝑥3 ).

(10) 10. =[. −𝑥1 + 2𝑥2 + 0 ] 2𝑥1 + 𝑥2 + 3𝑥3. 𝑥1 −1 2 0 𝑥 =  ([ ] [ 2 ]) 2 1 3 𝑥 3 = (𝐴𝑥) = T(x). Definición 1. 4 Sea V un espacio vectorial sobre R y sea T una transformación lineal sobre V. a) Un autovalor de T es un escalar R, tal que existe un vector no nulo vV que satisface T(v) = v. b) Cualquier vector vV que satisface T(v) = v se llama un autovector de T asociado al autovalor . Teorema 1.1 Sea T un operador lineal sobre un espacio vectorial V de dimensión finita y sea  un escalar. Las siguientes afirmaciones son equivalentes: a)  es un autovalor de T b) det(T - I) = |T - I| = 0. Observación - Supongamos que en lugar de T tengamos una matriz cuadrada A, entonces la parte b) del teorema 1.1 es: det(A - I) = 0 = |A - I|. Definición 1.5 Sea A una matriz cuadrada de orden n sobre R. El número R se llama autovalor de A si existe un vector vRn no nulo tal que Av = v, y este vector v se llama autovector de A correspondiente al autovalor . Apoyándonos en el teorema anterior podemos tener que: det(A - I) = 0, donde I es la matriz identidad cuadrada de orden n. Ejemplo 1.4 Sea 3 1 −1 A = [2 2 −1] 2 2 0 Hallar el autovalor  y su correspondiente autovector v. Solución. Aplicando la observación anterior tendremos: 3− | 2 2. 1 2− 2. −1 −1| = 0 −. Si y sólo si 2− (3-)| 2. −1 2 −1 2 2− | + 1| | + (-1) | |=0 − 2 − 2 2.

(11) 11.  (3- ) ( -2 + 2 +2) +(-2+2) -(4-4+2) = 0  -6+32+6+22 - 3 -2 -2+2-2 = 0  3-52+8-4 = 0  ( -1)( -2)2 = 0. De donde se tiene que 1 y 2 son los autovalores. Ahora encontremos los autovectores correspondientes. Si  = 1, entonces 𝑥1 3 1 −1 𝑥1 𝑥 𝑥 Ax = 1x  [2 2 −1] [ 2 ] = [ 2 ] 𝑥3 2 2 0 𝑥3 3𝑥1 + 𝑥2 − 𝑥3 = 𝑥1  {2𝑥1 + 2𝑥2 − 𝑥3 = 𝑥2 2𝑥1 + 2𝑥2 = 𝑥3 { {. 2𝑥1 + 𝑥2 − 2𝑥1 − 2𝑥2 = 0 2𝑥1 + 𝑥2 − 2𝑥1 − 2𝑥2 = 0. 𝑥2 = 0 2𝑥1 = 𝑥3. Si x1 = 1, entonces x3 = 2. Luego, el autovector correspondientes es (1, 0 , 2). Si  = 2, entonces 𝑥1 3 1 −1 𝑥1 Ax = 2x  [2 2 −1] [𝑥2 ] =2 [𝑥2 ] 𝑥3 2 2 0 𝑥3 3𝑥1 + 𝑥2 − 𝑥3 = 2𝑥1  {2𝑥1 + 2𝑥2 − 𝑥3 = 2𝑥2 𝑥1 + 𝑥2 = 𝑥3 { {. 𝑥1 + 𝑥2 − 𝑥1 − 𝑥2 = 0 2𝑥1 − 𝑥1 − 𝑥2 = 0. 0=0 𝑥1 = 𝑥2. Supongamos que x1 = 1 = x2, entonces x3 = 2. Luego, el autovector correspondientes es (1, 1, 2). En el siguiente lema, veremos una extensión importante de la desigualdad de Cauchy-Schwarz. Pero antes, veremos algunas propiedades de la descomposición espectral de matrices. Por ejemplo, sobre la raíz cuadrada de una matriz definida positiva A de orden pp, para lo cual, vamos a suponer que la matriz A tiene como autovalores 1, 2, …, p y sus respectivos autovectores normalizados e1, e2, …, ep ( vectores unitarios). Así se tiene que: A = ∑𝑝𝑖=1 𝑖 𝑒𝑖 𝑒𝑖𝑡 = PPt,.

(12) 12. donde P = [e1, e2, …, ep] de modo que PPt = PtP = I de orden pp, y. 1.  = [ 0. 0. 0. … 0 … 0] . .  0 𝑝 𝑝×𝑝. 2 . 0. con i > 0 para i = 1, 2, …, p. Y finalmente podemos obtener que: 1. A-1 = P-1Pt = ∑𝑝𝑖=1  𝑒𝑖 𝑒𝑖𝑡 . 𝑖. Además se puede verificar que: (P-1Pt)(PPt) = (PPt)(P-1Pt) = PPt = 𝐼𝑝×𝑝 . Denotamos: √1 1/2 =. 0 . [ 0. 0. … 0. √ 2 . 0. … 0 . .  0 √ 𝑝]. La matriz definida por. A1/2 = ∑𝑝𝑖=1 √𝑖 𝑒𝑖 𝑒𝑖𝑡 = P1/2Pt Se llama matríz de raíz cuadrada, cuyas propiedades son: 1. (A1/2)t = A1/2 ( esto es A!/2 es simétrica). 2. A1/2 A1/2 = A. 3. (A1/2 )-1 = ∑𝑝𝑖=1. 1 𝑒 𝑒𝑡 √ 𝑖 𝑖 𝑖. = P-1/2Pt, donde -1/2 es una matriz diagonal con 1/√𝑖 en la. i-ésima elemento diagonal. 4. A1/2A-1/2 = A-1/2A1/2 = 𝐼𝑝×𝑝 y A-1/2A-1/2 = A-1 donde A-1/2 = (A1/2)-1. Lema 1.2 (Extensión de la Desigualdad de Cauchy-Schwarz). Sean b y d dos vectores cualquiera de orden p1 y sea B una matriz definida positiva de orden pp. Entonces (btd)2  (btBb)(dtB-1d). La igualdad se da cuando b =rB-1d ó d = rBb para rR. Demostración. La igualdad se cumple cuando b = 0 ó d = 0. Sea B1/2 una matriz de raíz cuadrada definida en términos de los autovalores i, y autovectores normalizados ei, como B1/2 = ∑𝑝𝑖=1 √𝑖 𝑒𝑖 𝑒𝑖𝑡 y B-1/2 = ∑𝑝𝑖=1. 1 𝑒 𝑒𝑡 √ 𝑖 𝑖 𝑖. Por otro lado se tiene que: btd = btId = btB1/2B-1/2d = (B1/2b)t(B-1/2d)  (btd)2 = [(B1/2b)t(B-1/2d)]2. Entonces, aplicando el lema 1.1 se tiene:.

(13) 13. (btd)2 = [(B1/2b)t(B-1/2d)]2  (B1/2b)t(B1/2b)(B-1/2d)t(B-1/2d) = (btBb)(dtB-1d) o sea, (btd)2  (btBb)(dtB-1d). La igualdad se da cuando b = rB-1d ( ó d = rBb) para algún r R.  Lema 1.3 (Maximización) Sea B una matriz definida positiva, d un vector de orden p1. Entonces para cualquier vector arbitrario x diferente de cero y de orden p1 se tiene: (𝑥 𝑡 𝑑)2. máx. 𝑥 𝑡 𝐵𝑥. = dtB-1d, x  0.. El máximo alcanza cuando x = rB-1d para cualquier r  0. Demostración. Según el lema 1.2 se tiene: (xtd)2  (xtBx)(dtB-1d), x 0 . (𝑥 𝑡 d)2 𝑥 𝑡 Bx.  dtB-1d. Observamos que en esta desigualdad, la expresión dtB-1d es la cota superior, entonces existe el máximo y es igual a dtB-1d. O sea, (𝑥 𝑡 d)2. máx. 𝑥 𝑡 Bx. = dtB-1d, x 0.. Este valor de máximo se da para x = rB-1d para cualquier r  0.  Teorema 1.2 Sea B una matriz definida positiva con autovalores 1  2  … p asociado a los autovectores e1, e2, .., ep. Entonces 𝑚á𝑥 ⏟ 𝑥≠0. 𝑚á𝑥 ⏟ 𝑥≠0. 𝑥 𝑡 𝐵𝑥 𝑥𝑡𝑥 𝑥 𝑡 𝐵𝑥 𝑥𝑡𝑥. = 1, alcanza cuando x = e1 = p, alcanza cuando x = ep. Además, 𝑚á𝑥 ⏟ 𝑥 𝑒1 ,…,𝑒𝑘+1. 𝑥 𝑡 𝐵𝑥 𝑥𝑡𝑥. = k+1, alcanza cuando x = ek+1, k = 1, 2, …, p-1.. donde el símbolo  representa perpendicularidad entre vectores..

(14) 14. Demostración. Sea P una matriz ortogonal cuyas columnas son los autovectores e1, e2,…, ep y  es la matriz diagonal con autovalores 1, 2, …, p en toda la diagonal. Sea B1/2 = P1/2Pt y, sea y = Ptx de orden p1 con x  0 implica y  0. De modo que, tendremos: 𝑥 𝑡 𝐵𝑥 𝑥𝑡𝑥. = = =. 𝑥 𝑡 𝐵1/2 𝐵1/2 𝑥 𝑥 𝑡 𝑃𝑃 𝑡 𝑥. ; pues I = PPt. 𝑥 𝑡 P1/2 P𝑡 P1/2 P𝑡 x 𝑦𝑡𝑦 𝑦 𝑡 𝑦 𝑦𝑡𝑦 𝑝. =. ∑𝑖=1 𝑖 𝑦𝑖2 𝑝. ∑𝑖=1 𝑦𝑖2 𝑝. ∑.  1∑𝑖=1 𝑝. 𝑦𝑖2. 𝑦2 𝑖=1 𝑖. = 1 ,. O sea, 𝑥 𝑡 𝐵𝑥 𝑥𝑡𝑥.  1 .. (2.1). Haciendo x = e1 nos dá 1 0 y = Pte1 = [ ] : 0 como 1, 𝑘 = 1 𝑒𝑘𝑡 𝑒1= { 0, 𝑘 ≠ 0 Por esta elección de x, yty/yty = 1/1 = 1, o sea 𝑒1𝑡 𝐵𝑒1 𝑒1𝑡 𝑒1. 𝑒 𝑡 𝐵𝑒. = 𝑒1𝑡 𝐵𝑒1 = 1  máx 𝑒1𝑡 𝑒 1 = 1. 1 1. Un argumento similar nos dá la segunda parte, 𝑚á𝑥 ⏟. 𝑥 𝑡 𝐵𝑥. 𝑥≠0. 𝑥𝑡𝑥. = p, alcanza cuando x = ep.. Ahora si x = Py = y1e1 + y2e2 + … + ypep, así x e1 , …, ek implica 0 = 𝑒𝑖𝑡 𝑥 = y1𝑒𝑖𝑡 𝑒1 + y2𝑒𝑖𝑡 𝑒2 + …+ yp𝑒𝑖𝑡 𝑒𝑝 = yi, i  k. En consecuencia, para x perpendicular a los primeros k autovectores ei, el lado izquierdo de la desigualdad de (2.1) se convierte. 𝑥 𝑡 𝐵𝑥 𝑥𝑡𝑥. 𝑝. =. ∑𝑖=𝑘+1 𝑖 𝑦𝑖2 𝑝 ∑𝑖=𝑘+1 𝑦𝑖2.  k+1 . 𝑚á𝑥 ⏟ 𝑥 𝑒1 ,…,𝑒𝑘+1. 𝑥 𝑡 𝐵𝑥 𝑥𝑡𝑥. = k+1.

(15) 15. Tomando yk+1 = 1, yk+2 = …, = yp = 0.  1.3 MATRIZ DE VARIANZA-COVARIANZA “∑” Sea Xt = (X1, X2, …,Xp) un vector aleatorio de n componentes, donde X1, X2, …,Xp son variables aleatorias discretas definidas sobre un mismo espacio muestral. Una función real pX definida en ∏𝑝𝑖=1 𝑅𝑋𝑖 , será una función de cuantía multivariada ( o una cuantía multivarida de las variables X1, X2, …,Xp) si: 1) 𝑝𝑥 (𝑥1 , 𝑥2 , … , 𝑥𝑝 )  0, para todo (𝑥1 , 𝑥2 , … , 𝑥𝑝 ) ∏𝑝𝑖=1 𝑅𝑋𝑖 = 𝐷𝑝𝑋 2) ∑(𝑥1 ,𝑥2 ,…,𝑥𝑝 ) ∈𝐷𝑝 𝑝𝑥 (𝑥1 , 𝑥2 , … , 𝑥𝑝 ) = 1 𝑋. Donde xi, para i = 1, 2,…, p son valores de las variables aleatorias Xi. Si las variables aleatorias son continuas, en ese caso se dice que tenemos una función de densidad multivariada fX definida en Rp, para lo cual debe satisfacer dos condiciones: 1) 𝑓𝑥 (𝑥1 , 𝑥2 , … , 𝑥𝑝 )  0, para todo (𝑥1 , 𝑥2 , … , 𝑥𝑝 ) 𝑅 𝑝 = 𝐷𝑓𝑋 ∞. ∞. 2) ∫−∞. … ∫−∞ 𝑓𝑥 (𝑥1 , 𝑥2 , … , 𝑥𝑝 )𝑑𝑥1 … 𝑑𝑥𝑝 = 1. Definición 1.6 La matriz ∑ = E[(X-E(X))t(X-E(X))] Se llama matriz de varianza-covarianza, donde X es una vector columna de p componentes (o sea, Xt = X1p). La matriz  en forma desarrollada es:  = E[(X-E(X))t(X-E(X))] 𝑋1 − 𝐸(𝑋1 ) 𝑋 − 𝐸(𝑋2 ) =E ( 2 ) (𝑋1 − 𝐸(𝑋1 ), … , 𝑋𝑝 − 𝐸(𝑋𝑝 ) : [ 𝑋𝑝 − 𝐸(𝑋𝑝 ) ] … 𝐸(𝑋1 − 𝐸(𝑋1 ))(𝑋𝑝 − 𝐸(𝑋𝑝 )) 𝐸(𝑋1 − 𝐸(𝑋1 ))2 : : : =[ ] … 𝐸(𝑋1 − 𝐸(𝑋1 ))(𝑋𝑝 − 𝐸(𝑋𝑝 )) 𝐸(𝑋𝑝 − 𝐸(𝑋𝑝 ))2 𝜎12 𝜎 = [ 21 : 𝜎𝑝1. 𝜎12 𝜎22 : 𝜎𝑝2. 𝜎1𝑝 … … 𝜎2𝑝 … : ] : 𝜎𝑝2. Se tiene 𝜎𝑖𝑗 = 𝜎𝑗𝑖 ; para todo i, j = 1, 2,…, p, la matriz  es una matriz cuadrada y simétrica. Además  es una matriz definida positiva. Y la matriz de correlación es.

(16) 16.  = (𝜌𝑖𝑗 )𝑛×𝑛. 1 𝜌21 =[ … 𝜌𝑛1. 𝜌12 1 … 𝜌𝑛2. 𝜌 … … 𝜌1𝑛 2𝑛 … …] … 1. donde 𝜌𝑖𝑗 = 𝜌𝑗𝑖 , para todo i, j = 1, 2, …,n. Esta matriz es también cuadrada y simétrica. Además -1 ≤ 𝜌𝑖𝑗 ≤ 1. Para todo i, j = 1, 2, …,n. Un caso particular ocurre cuando tenemos que X tiene dos componentes, esto es: X = X21 = [. 𝑋1 ] 𝑋2. y, sea una combinación lineal aX1 + bX2 Entonces E[aX1 + bX2] = aE[X1] + bE[X2] = a1 + b2 𝜇1 = [a, b][𝜇 ] 2 = Ct y, como la Var[X] = E[(X - )2], eso implica que Var[aX1 + bX2] = E[((aX1 + bX2) – (a1 + b2))2] = E[(a(X1 - 1) + b(X2 - 2))2] = E[a2(X1- 1)2 + b2(X2 - 2)2 + 2ab(X1- 1)(X2 - 2)] = a2E[(X1- 1)2] + b2E[(X2 - 2)2] + 2abE[(X1- 1)(X2 - 2)] = a2Var[X1] + b2Var[X2] + 2abCov[X1, X2] = a211 + b222 + 2ab12 𝜎11 𝜎12 𝑎 = [a, b][𝜎 ][ ] 12 𝜎22 𝑏 = CtC. Este resultado se generaliza para p variables, así: Var[c1X1+ c2X2 + … + cpXp] = CtC.. (1.1). donde Ct = (c1, c2, …, cp). Ahora, supongamos que tenemos q combinaciones lineales de las p variables aleatorias X1, X2, …, Xp, Z1 = c11X1 + c12X2 + … + c1pXp Z2 = c21X1 + c22X + … + c2pXp ………………………………………………………..

(17) 17. Zq = cq1X1 + cq2X2 + … + cqpXp Entonces: Cov(Zi, Zj) = 𝐶𝑖𝑡 𝐶𝑗. (1.2). para i, j = 1, 2, …, q. Ejemplo 1.5 La función fX definida por: 1. fx(x1, x2) = {. (6 − 𝑥1 − 𝑥2 ); 0 < 𝑥1 < 2; 2 < 𝑥2 < 4 0 ; 𝑒𝑛 𝑜𝑡𝑟𝑜 𝑐𝑎𝑠𝑜. 8. es una función de densidad conjunta de dos variables aleatorias X1, X2. Encontrar la matriz de covarianzay matriz de correlación. Solución. Determinemos el vector de medias: ∞. ∞. ∞. ∞ 1. E[𝑋1] = ∫−∞ ∫−∞ 𝑥1 fx(x1, x2)d𝑥1 𝑑𝑥2 = ∫−∞ ∫−∞ 8 𝑥1 (6 − 𝑥1 − 𝑥2 )d𝑥1 𝑑𝑥2 4. 1. 2. = 8 ∫2 ∫0 (6𝑥1 − 𝑥12 − 𝑥1 𝑥2 )d𝑥1 𝑑𝑥2 4. 1. =8 ∫2 [3𝑥12 − =. 4 ∫ [12 8 2 1. 𝑥13 3. 3. 2. 2. 𝑥2 ] 𝑑𝑥2 0. − 3 − 2𝑥2 ] 𝑑𝑥2. 1 28. = 8[. 𝑥12. 8. = 8 [ 3 𝑥2 − 𝑥22 ] 1 112. −. − 16 −. 4 2 56 3. 1 56. 5. + 4] = 8 [ 3 − 12]= 6 = 1.. De la misma forma calculamos: ∞. ∞. E[𝑋2] = ∫−∞ ∫−∞ 𝑥2 fx(x1, x2)d𝑥1 𝑑𝑥2 1. 4. 2. 17. = 2.. = 8 ∫2 ∫0 (6𝑥2 − 𝑥2 𝑥1 − 𝑥22 )d𝑥1 𝑑𝑥2 =. 6. Luego el vector de medias es: 5. 17. 6. 6.  = ( , ). Ahora calculamos las varianzas: 5. Var[𝑋1 ] = 𝜎12 = E[(X1- 6)2] 5 2. = E[𝑥12 ] - (6).

(18) 18 4. 2. 1. 25. = ∫2 ∫0 (𝑥1 )2 8 (6 − 𝑥1 − 𝑥2 )d𝑥1 𝑑𝑥2 - 36 1. 4. 1. 4. 2. 25. = 8 ∫2 ∫0 (6𝑥12 − 𝑥13 − 𝑥12 𝑥2 )d𝑥1 𝑑𝑥2 - 36 = 8 ∫2 [2𝑥13 −. 𝑥14. −. 4. 4. 1. 𝑥13 3. 2. 25. 𝑥2 ] d𝑥2 - 36 0. 8. 25. = 8 ∫2 [16 − 4 − 3 𝑥2 ]d𝑥2 - 36 1. 4 25. 4. = 8 [12𝑥2 − 3 𝑥12 ] - 36 2. 1. = 8 [48 −. 64 3. − 24 +. 1. 16 3. 25. ]- 36. 25. = 8 [24 − 16]- 36 25. 11. = 1- 36 = 36 = 𝜎12 . De la misma forma se calcula: Var[𝑋2] = 𝜎22 = E[(X2-. 17 2 )] 6. 17 2. = E[𝑥22 ] - ( 6 ) 4. 2. 1. = ∫2 ∫0 (𝑥2 )2 8 (6 − 𝑥1 − 𝑥2 )d𝑥1 𝑑𝑥2 11. = 36 = 𝜎22 . Ahora calculamos: 𝜎12 = Cov(X1, X2) = E[X1X2]-E[X1]E[X2] 1. 4. 1. 4. 2. 5 17. = 8 ∫2 ∫0 x1 𝑥2 (6 − 𝑥1 − 𝑥2 )d𝑥1 𝑑𝑥2 - 6 6 𝑥13. = 8 ∫2 [3𝑥12 𝑥2 − =. 4 [12𝑥2 ∫ 8 2 1. 3. 𝑥2 −. 2. 2. 5 17. 𝑥22 ] d𝑥2 - 6 6 0. 8. 5 17. − 3 𝑥2 − 2𝑥22 ]d𝑥2 - 6 6. 4 28. 1. 𝑥12. 5 17. =8 ∫2 [ 3 𝑥2 − 2𝑥22 ]d𝑥2 - 6 6 1 14. 4 5 17. 2. = 8 [ 3 𝑥22 − 3 𝑥23 ] -6 6 2. 1 224. = 8[. 3. −. 128 3. 1 240−184. = 8[ =. 3. 1 56 8. −. 56 3. +. 16 3. 5 17. ] -6 6. 5 17. ] -6 6. 5 17. [ 3 ] -6 6. 7 5 17. 7. 85. = 3 -6 6 = 3 − 36 = Por lo tanto, la matriz de covarianza. 84−85 36. 1. = -36 = 𝜎21. 289 36.

(19) 19 11. −1. 36  = [−1. 36 11 ].. 36. 36. Mientras que, para la matriz de correlación, primero determinemos que: 𝜎. 𝜌12 = 𝜎 12 = 𝜎 1 2. −1⁄ 36. 1. = - 11 = 𝜌21 11. 11 36 36. √ √. Ahora si: −1. 1. 11.  = [−1. 1. 11. ].. 1.4 AUTOVALORES Y AUTOVECTORES DE UNA MATRIZ DE VARIANZACOVARIANZA “∑”. Sabemos que, la matriz de covarianza  es: 𝜎12  = [𝜎21 : 𝜎𝑛1. 𝜎12 𝜎22 : 𝜎𝑛2. 𝜎1𝑛 … … 𝜎2𝑛 … : ] : 𝜎𝑛2. Se tiene 𝜎𝑖𝑗 = 𝜎𝑗𝑖 ; para todo i, j = 1, 2,…,n, la matriz  es una matriz cuadrada y simétrica. En algunas ocasiones se utiliza que 𝜎12 = 11, 𝜎22 = 22, …, 𝜎𝑝2 = pp. Los autovalores  se encuentran resolviendo. 𝜎12 − 𝛼 | - I| = 0  | 𝜎21 : 𝜎𝑛1. 𝜎12 −𝛼 : 𝜎𝑛2. 𝜎22. … … … :. 𝜎1𝑛 𝜎2𝑛 : |=0 2 𝜎𝑛 − 𝛼. Ejemplo 1.6 Sea la matriz de covarianza 1  = [−1 0. −1 0 2 −2]. −2 1. Encontrar los autovalores y autovectores de esta matriz. Solución. Sea  el autovalor que buscamos, para cual tenemos: 1−𝛼 −1 0 | - I| = 0  | −1 2−𝛼 −2 | = 0 0 −2 1−𝛼 2−𝛼 −2 −2 −1 −1 2 −   (1- )| |+(-1) | | +0| |=0 −2 1−𝛼 1−𝛼 0 0 −2  (1- 𝛼)[(2- )(1- ) - 4] -1[0 +1(1- )] + 0 = 0  (1 - )(2-3-2) +1-  = 0.

(20) 20.  (-1)(2 -3 -1) = 0  1 = 1  2 =. −3+√13 2.  3 =. −3−√13 2. .. Vamos obtener, el autovector correspondiente a 1 = 1. 𝑥1 1 −1 0 𝑥1 𝑥 𝑥 x = 1x  [−1 2 −2] [ 2 ] = [ 2 ] 𝑥3 0 −2 1 𝑥3 𝑥1 − 𝑥2 = 𝑥1 𝑥2 = 0  {−𝑥1 + 2𝑥2 − 2𝑥3 = 𝑥2  {𝑥1 = −2𝑥3 −2𝑥2 + 𝑥3 = 𝑥3 𝑥3 = 𝑥3 Por tanto, el autovector correspondientes (-2, 0, 1). De manera similar se hallan los demás autovectores. 1.5 DISTRIBUCIÓN NORMAL MULTIVARIANTE. En primer lugar debemos tener presente que un vector aleatorio puede ser definida como X = (X1, X2, …, Xp) Entonces, 𝑋1 𝑋 Xt =( ⋮2 ) 𝑋𝑝 En esta oportunidad, vamos a considerar que 𝑋1 𝑋2 X = ( ⋮ )  Xt = (X1, X2, …, Xp). 𝑋𝑝 Un vector aleatoria. Una función de densidad conjunto de las variables aleatorias X1, X2, …, Xp (componentes de X) se define por: 1. −1. fX(x1, x2,…, xp) = (2𝜋)𝑝/2 ||1/2 𝑒 2. (𝑋−𝜇)𝑡 −1 (𝑋−𝜇). donde  es la matriz de varianza-covarianza del vector aleatorio X,  es el vector de medias y, - < xi <  para todo i = 1, 2,…, p, se denomina densidad normal multivariada de las variables aleatorias X1, X2, …, Xp. Ejemplo 1.7 Sea fX una función de densidad normal conjunta de las variables aleatorias X1, X2 (Normal bivariada). a) ¿Cuántos parámetros tiene esta densidad?. b) Si las variables aleatorias X1, X2 fuesen independientes, ¿qué forma tiene la densidad?. Obtenga las marginales..

(21) 21. Solución. a) Para Xt = (X1, X2), tenemos: −1. 1. fX(x1, x2) = (2𝜋)2/2 ||1/2 𝑒 2. (𝑋−𝜇)𝑡 −1 (𝑋−𝜇). donde t = E[X] = (E[X1], E[X2]) = (1, 2). Luego: 𝑋 − 𝜇1  = E[(X-)(X-)t] = E[( 1 ) (𝑋1 − 𝜇1 , 𝑋2 − 𝜇2 )] 𝑋2 − 𝜇2 𝐸((𝑋1 − 𝜇1 ))2 𝐸((𝑋1 − 𝜇1 )(𝑋2 − 𝜇2 )) =[ ] 𝐸((𝑋2 − 𝜇2 )(𝑋1 − 𝜇1 )) 𝐸((𝑋2 − 𝜇2 ))2 =[. 𝜎12 𝜎21. 𝜎12 ] 𝜎22. Sabemos que: 𝜎. 𝜎21 = 𝜎12 y 𝜌12 = 𝜎 21  𝜎12 = 𝜎1 𝜎2 𝜌12 𝜎 1 2. = 𝜎1 𝜎2 𝜌 = 𝜎21 . Haciendo que, 𝜌 = 𝜌12 = 𝜌21 . Ahora sí: 𝜎2 || = | 1 𝜎21 =|. 𝜎12 | 𝜎22. 𝜎12 𝜎1 𝜎2 𝜌. 𝜎1 𝜎2 𝜌 | 𝜎22. = 𝜎12 𝜎22 - 𝜎12 𝜎22 𝜌2 = 𝜎12 𝜎22 (1- 𝜌2 ). También calculamos la inversa de . 1 1. -1 = 1−𝜌2 [. 𝜎12 −𝜌. −𝜌 𝜎1 𝜎2 1 ]. 𝜎22. 𝜎1 𝜎2. Entonces. 1. (X - )t -1 (X- ) = (x1- 1, x2- 2) 1−𝜌2 [. 1. −𝜌. 𝜎12 −𝜌. 𝜎1 𝜎2 1 ]. 𝜎1 𝜎2. 𝜎22. 𝑥1 −  (𝑥 − 1 ) 2. 2.

(22) 22 𝑥1 −𝜇1 2. 1. = 1−𝜌2 [(. ) − 2𝜌. 𝜎1. (𝑥1 −𝜇1 )(𝑥2 −𝜇2 ) 𝜎1 𝜎2. 𝑥2 −𝜇2 2. +(. 𝜎2. ) ].. De modo que:. fX (x1, x2) =. 1 2𝜋𝜎1 𝜎2 √1−𝜌2. 𝑒. −1 1 . 2 1−𝜌2. (𝑥 −𝜇 )(𝑥 −𝜇 ) 𝑥 −𝜇 2 𝑥 −𝜇 2 [( 1 1 ) −2𝜌 1 1 2 2 +( 2 2 ) ] 𝜎1. 𝜎1 𝜎2. 𝜎2. de donde observamos, que esta función de densidad tiene 5 parámetros. 1, 2 , 𝜎12 , 𝜎22 y 𝜌. b) Si X1 y X2 son independientes, entonces Cov(X1, X2) = 0. Por tanto 𝜌 = 0. Luego la densidad normal bivariada presenta la siguiente forma: −1. 1. fX (x1, x2) = 2𝜋𝜎. 1 𝜎2. 𝑒2. 𝑥 −𝜇 2 𝑥 −𝜇 2 .[( 1 1 ) +( 2 2 ) ] 𝜎1. 𝜎2. que se puede expresarse como el producto de dos densidades marginales, en razón a que las variables aleatorias X1, X2 son independientes.. fX (x1, x2) =. 1 √2𝜋𝜎1. 𝑒. −1 𝑥1 −𝜇1 2 .( ) 2 𝜎1. 𝑒. −1 𝑥1 −𝜇1 2 .( ) 2 𝜎1. 1 √2𝜋𝜎2. 𝑒. −1 𝑥2 −𝜇2 2 .( ) 2 𝜎2. = f(x1).f(x2).. 𝑒. −1 𝑥2 −𝜇2 2 .( ) 2 𝜎2. = f(x1).f(x2).. O, sea:. fX (x1, x2) =. 1 √2𝜋𝜎1. 1 √2𝜋𝜎2. O, sea:. fX (x1, x2) =. 1 √2𝜋𝜎1. 𝑒. −1 𝑥1 −𝜇1 2 .( ) 2 𝜎1. 1 √2𝜋𝜎2. 𝑒. −1 𝑥2 −𝜇2 2 .( ) 2 𝜎2. = f(x1).f(x2).. O, sea:. f1 (x1) = y,. 1 √2𝜋𝜎1. 𝑒. −1 𝑥1 −𝜇1 2 .( ) 2 𝜎1. , - < x1 < .

(23) 23 −1 𝑥2 −𝜇2 2 .( ) 𝜎2. f2 (x2) = 𝑒 2 Son las densidades marginales.. , - < x2 < ..

(24) 24. CAPÍTULO II: COMPONENTES PRINCIPALES 2.1 INTRODUCCIÓN El estudio del análisis de componentes principales se inicia a partir de la estructura de la matriz de varianza-covarianza, formando una combinación lineal de las variables originales, en la cual se tiene como objetivo reducir la cantidad de variables participantes y su interpretación. Supongamos que se tiene p variables originales, los cuales pueden ser reducidos a k  p variables llamados componentes principales cumpliendo cierta estructura matemática. La información contendida en p variables originales, puede ser explicada simple y llanamente con k componentes principales, por lo que; estas k componentes principales reemplazan a las p variables originales en n mediciones que conforman la muestra. 2.2 ENFOQUE DESCRIPTIVO DE COMPONENTES PRINCIPALES. Algebraicamente, los componentes principales son combinaciones lineales particulares de los p variables aleatorias X1, X2, …, Xp. Geométricamente, estas combinaciones lineales representan la selección de un nuevo sistema de coordenadas obtenidas por rotación del sistema original X1, X2, …, Xp como ejes coordenadas. Los nuevos ejes representan las direcciones con máxima variabilidad y al mismo tiempo proveen un simple y más asequible descripción de la estructura de covarianza. Como veremos, los componentes principales dependen solamente de la matriz de varianzacovarianza  ( o de la matriz de correlación ). Su desarrollo no requiere suponer una población normal multivariada. Si consideramos, los componentes principales sobre una población normal multivariada tendremos útiles interpretaciones en términos de la constante de densidad elipsoidal. Además se puede realizar inferencias de la muestra. Sea el vector aleatorio Xt = [X1, X2, …, Xp ] tiene matriz de varianza-covarianza  con autovalores 1, 2, …, p  0. Consideremos las combinaciones lineales Y1 = 𝑙1𝑡 𝑋 = l11X1 + l21X2 + …+ lp1Xp Y2 = 𝑙2𝑡 𝑋 = l12X1+ l22X2 + … + lp2Xp ……………………………………… Yp = 𝑙𝑝𝑡 𝑋 = l1pX1 + l2pX2 + …+ lppXp.

(25) 25. Entonces, usando (1.1) y (1.2) tenemos. Var(Yi) = 𝑙𝑖𝑡  li , i = 1, 2, …, p;. (2.1). y, Cov(Yi, Yk) = 𝑙𝑖𝑡  lk , i, k = 1, 2, …, p.. (2.2). los componentes principales son estas combinaciones lineales no correlacionadas Y1, Y2, …, Yp cuyas varianzas en (2.1) sean los más grandes posibles. La primera componente principal es la combinación lineal de variables originales con máxima varianza. Esto es, se debe maximizar Var(Y1) = 𝑙1𝑡 l1, esto puede ser posible si multiplicamos a cualquier li por alguna constante real positiva. Para eliminar este inconveniente restringimos nuestra atención a vectores coeficientes de norma uno. Así: Primera componente principal = 𝑙1𝑡 𝑋; con Máx(Var(𝑙1𝑡 𝑋)) y sujeta 𝑙1𝑡 𝑙1= 1. Segunda componente principal = 𝑙2𝑡 𝑋; con Máx(Var(𝑙2𝑡 𝑋)) y sujeta 𝑙2𝑡 𝑙2= 1 y Cov(𝑙1𝑡 𝑋, 𝑙2𝑡 𝑋) = 0. La i-ésima componente principal = 𝑙𝑖𝑡 𝑋 ; con Máx(Var(𝑙𝑖𝑡 𝑋)) , sujeta a 𝑙𝑖𝑡 𝑙𝑖 = 1 y Cov(𝑙𝑘𝑡 𝑋, 𝑙𝑖𝑡 𝑋) = 0 para k < i. 2.3 COMPONENTES PRINCIPALES EN UNA POBLACIÓN. Cuando se recoge la información de una muestra de datos, lo más frecuente es tomar el mayor número posible de variables. Si tomamos demasiadas variables sobre un conjunto de objetos, por ejemplo 20 variables, tendremos que considerar (. 20 ) = 190 2. Posibles coeficientes de correlación; si son 40 variables dicho número aumento hasta 780. Evidentemente, en este caso es difícil visualizar relaciones entre las variables. Otro problema que se presenta es la fuerte correlación que muchas veces se presentan entre las variables; si tomamos demasiados variables (cosa que en general sucede cuando no se sabe demasiado sobre los datos o sólo se tiene ánimo exploratorio), lo normal es que estén relacionados o que miden lo mismo bajo distintos puntos de vista. Por ejemplo, en estudios médicos, la presión sanguínea a la salida del corazón y a la salida de los pulmones están frecuentemente relacionados. Se hace necesario, pues, reducir el número de variables. Es importante resaltar el hecho de que el concepto de mayor información se relaciona con el de mayor variabilidad o varianza. Cuando mayor sea la variabilidad de los datos (varianza) se considera que existe mayor información. Teorema 2.1 Sea  la matriz de varianza-covarianza asociada con el vector aleatorio Xt = [X1, X2,…, Xp]..

(26) 26. en una muestra de tamaño n, cuyos autovalores - autovectores formados por los pares (1, e1), (2, e2),…, (p, ep) donde 1  2  …  p  0 y e1, e2, …, ep son autovectores unitarios correspondientes a cada autovalor i para todo i. La i-ésima componente principal está dada por 𝑡 Yi = 𝑒𝑝𝑖 𝑋 = e1iX1 + e2iX2 +… + epiXp; i = 1, 2,…, p.. Entonces, Var(Yi) = 𝑒𝑖𝑡 ei = i ; i = 1, 2, …, p Cov(Yi , Yk) = 𝑒𝑖𝑡 ek = 0 ; i  k. Demostración. Por el teorema 1.2, con B = , 𝑚á𝑥 ⏟ 𝑙≠0. 𝑙𝑡  𝑙 𝑙𝑡 𝑙. = 1, se dá cuando l = e1. Donde 𝑒1𝑡 𝑒1 = 1 ya que los autovectores son normalizados. Así: 𝑚á𝑥 ⏟ 𝑙≠0. 𝑙𝑡  𝑙 𝑙𝑡 𝑙. = 1 =. 𝑒1𝑡 𝑒1 𝑒1𝑡 𝑒1. = 𝑒1𝑡 𝑒1 = Var (Y1).. De la misma forma se obtiene que: 𝑙𝑡  𝑙. 𝑚á𝑥 ⏟ 𝑙𝑒1 ,𝑒2 ,…,𝑒𝑘. 𝑙𝑡 𝑙. = k+1 , k = 1, 2, …, p-1.. Para la elección 𝑡 l = ek+1, con 𝑒𝑘+1 𝑒𝑖 = 0; i = 1, 2, …, k y k = 1, 2, …, p-1. k+1 =. 𝑡 𝑒𝑘+1  𝑒𝑘+1 𝑡 𝑒 𝑒𝑘+1 𝑘+1. =. 𝑡 𝑒𝑘+1  𝑒𝑘+1. 1. 𝑡 = 𝑒𝑘+1  𝑒𝑘+1 = Var (Yk+1).. Ahora, por otro lado sabemos que.  𝑒𝑘 = kek ; k = 1, 2,…., p Para todos los autovalores 1, 2, …, p y autovectores normalizados e1, e2, …, ep de  con 𝑒𝑖𝑡 𝑒𝑘 = 0, para i  k. Entonces Cov(Yi , Yk) = 𝑒𝑖𝑡 kek = k 𝑒𝑖𝑡 ek = 0 ; i  k.  Según este teorema podemos decir que los componentes principales son no correlacionadas y tienen como varianza igual a los autovalores de la matriz varianza-covarianza ..

(27) 27. Teorema 2.2 Sea Xt = [X1, X2, …,Xp] que tiene como matriz de varianza-covarianza , con pares de autovalores y autovectores (1, e1), (2, e2), …, (p, ep), donde 1  2  , …, p  0. Sean Y1 = 𝑒1𝑡 𝑋; Y2 = 𝑒2𝑡 𝑋; …; Yp = 𝑒𝑝𝑡 𝑋 los componentes principales. Entonces 11 + 22 +… + pp = ∑𝑝𝑖=1 𝑉𝑎𝑟(𝑋𝑖 ) = 1 + 2 + , …, + p = ∑𝑝𝑖=1 𝑉𝑎𝑟(𝑌𝑖 ). Demostración Sabemos que 11 + 22 +… + pp = tr(), ponemos A = , para obtener  = PPt, donde  es la matriz diagonal de autovalores y P = [e1, e2, …,ep] así que PPt = PtP = I. Luego se tiene: tr() = tr(PPt) = tr(PtP) = tr() = 1 + 2 + , …, + p .  Este resultado nos dice que, la varianza de la población total es 11 + 22 +… + pp = 1 + 2 + , …, + p, y en consecuencia, la proporción de la variabilidad total de la población debido (o explicada por) a la i-ésima componente principal es 𝑃𝑟𝑜𝑝𝑜𝑟𝑐𝑖ó𝑛 𝑑𝑒 𝑙𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑖𝑙𝑖𝑑𝑎𝑑 𝑑𝑒 𝑙𝑎 𝑝𝑜𝑏𝑙𝑎𝑐𝑖ó𝑛  ( ) = 1 + 2 +𝑖 ,…,+ p , i = 1, 2, …, p 𝑑𝑒𝑏𝑖𝑑𝑜 𝑎 𝑙𝑎 𝑖 − é𝑠𝑖𝑚𝑎 𝑐𝑜𝑚𝑝𝑜𝑛𝑒𝑛𝑡𝑒 𝑝𝑟𝑖𝑛𝑐𝑖𝑝𝑎𝑙 Proposición 2.3.- Sea vRp un autovector de  asociado a un autovalor  no nulo (  0), sea aRn. Entonces ata = 0  ata = 0..

(28) 28. Demostración. () Se tiene 0 = ata = ata = ata  ata = 0, pues   0. () Se tiene 0 = ata = at. 𝑎 1 = at a .  ata = 0. . Por tanto, en aplicación de este resultado Cov(atX, Z1) = 0  ata1 = 0. El hecho de que ata1 = 0 significa que los vectores a1 y a2 son ortogonales, si y solo si, Cov(atX, Z1) = 0, o sea, las componentes Z1 y Z2 son incorrelacionadas. Es así que, podríamos definir que la segunda componente principal es la combinación lineal de las variables de X que tiene mayor varianza entre las combinaciones lineales normalizadas e incorrelacionadas con la primera componente principal y en general entre todos los componentes principales. Según los resultados anteriores, formalizamos mediante una definición lo que se llama componentes principales. Definición 2.1 Se definen las p componentes principales de X como las variables aleatorias (Z1, Z2, …, Zn) tales que Z1 = 𝑎1𝑡 X, Z2 = 𝑎2𝑡 X , …, Zn = 𝑎𝑛𝑡 X ; a1, a2, …, an  Rn Var(Z1) = max{Var(atX): aRn, ata = 1} Var(Z2) = max{Var(atX): aRn, ata = 1, 𝑎1𝑡 a = 0} …………………………………………………. 𝑡 Var(Zn) = max{Var(atX): aRn, ata = 1, 𝑎1𝑡 a = 0, 𝑎1𝑡 a = 0, 𝑎2𝑡 a = 0,…, 𝑎𝑝−1 a = 0}.. Si la variabilidad de la población es explicada en un 70 a 90% a lo largo de las p variables, entonces podemos atribuirlas a los primeros componentes, o sea, al primero, segundo hasta tercer componente tal vez que represente a las p variables originales sin mayor pérdida de información que contienen dichas p variables originales. Ejemplo 2.1 Supongamos que deseamos conocer cuáles son los factores relacionados con el riesgo de enfermedad coronaria. Del conocimiento previo sabemos que el riesgo es la presión arterial, la edad, la obesidad, el tiempo que se ha sido hipertenso, el pulso y el estrés. Para la.

(29) 29. investigación seleccionamos al azar 20 pacientes hipertensos en los que medimos las siguientes variables: X1: Presión arterial media (mm Hg). X2: Edad (años) X3: Peso (Kg) X4: Superficie corporal (m2) X5: Duración de la Hipertension (años) X6: Pulso (pulsaciones/minutos) X7: Medida del estrés. Tratamos de estudiar la situación del grupo de pacientes en relación a los factores de riesgo y las posibles interrelaciones entre las distintas variables. Inicialmente queremos describir el conjunto de pacientes utilizando simultáneamente todas las variables. Los datos obtenidos se muestran en la tabla siguiente..

(30) 30. Tabla: 1: Presentación de datos de enfermedad coronaria. Nº X1. X2 X3. X4. X5. X6 X7. 1. 105 47 85.4. 1.75 5.1. 63 33. 2. 115 49 94.2. 2.10 3.8. 70 14. 3. 116 49 95.3. 1.98 8.2. 72 10. 4. 117 50 94.7. 2.01 5.8. 73 99. 5. 112 51 89.4. 1.89 7.0. 72 95. 6. 121 48 99.5. 2.25 9.3. 71 10. 7. 121 49 99.8. 2.25 2.5. 69 42. 8. 110 47 90.9. 1.90 6.2. 66 8. 9. 110 49 89.2. 1.83 7.1. 69 62. 10 114 48 92.7. 2.07 5.6. 64 35. 11 114 47 94.4. 2.07 5.3. 74 90. 12 115 49 94.1. 1.98 5.6. 71 21. 13 114 50 91.6. 2.05 10.2 68 47. 14 106 45 87.1. 1.92 5.6. 67 80. 15 125 52 101.3 2.19 10.0 76 98 16 114 46 94.5. 1.98 7.4. 69 95. 17 106 46 87.0. 1.87 3.6. 62 18. 18 113 46 94.5. 1.90 4.3. 70 12. 19 110 48 90.5. 1.88 9.0. 71 99. 20 122 46 95.7. 2.09 7.0. 75 99. En este problema estamos trabajando con 7 variables, o sea, la dimensión es 7, pero ¿ es posible describir el conjunto de datos utilizando con un número menor de dimensiones, aprovechando las interrelaciones entre las variables?. Según la teoría desarrollada en esta tesis, la respuesta es afirmativa en el sentido que; si es posible describir el problema con un número menor de dimensión. Las interrelaciones entre variables quedan reflejadas en la matriz de covarianza , el procedimiento en general será obtenida mediante el programa estadístico SPSS versión 22. En primer lugar vamos a estudiar la relacion existente de las siete variables de dos en dos. Mediante el programa SPSS version 22 se tiene:.

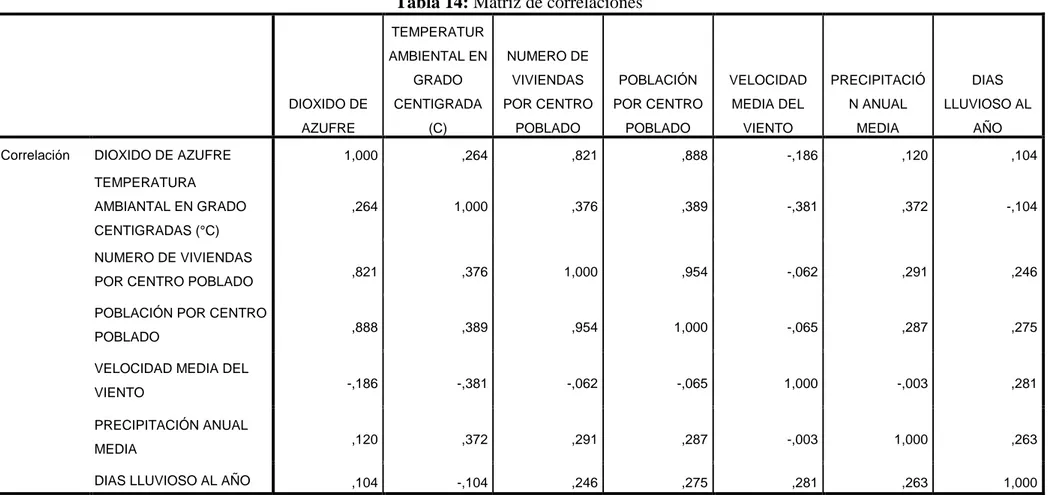
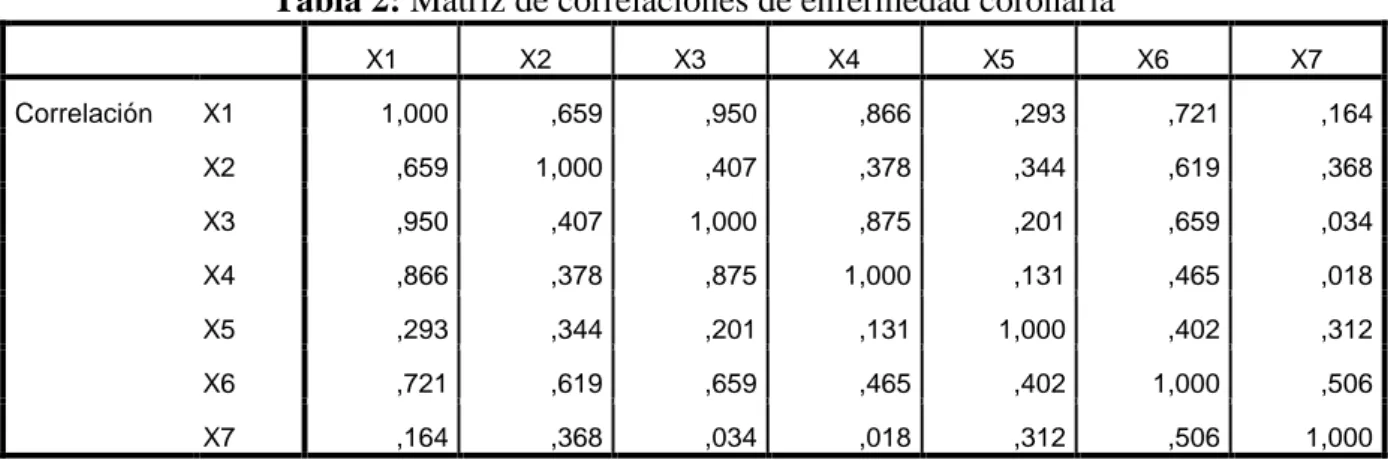
(31) 31. Tabla 2: Matriz de correlaciones de enfermedad coronaria X1 Correlación. X2. X3. X4. X5. X6. X7. X1. 1,000. ,659. ,950. ,866. ,293. ,721. ,164. X2. ,659. 1,000. ,407. ,378. ,344. ,619. ,368. X3. ,950. ,407. 1,000. ,875. ,201. ,659. ,034. X4. ,866. ,378. ,875. 1,000. ,131. ,465. ,018. X5. ,293. ,344. ,201. ,131. 1,000. ,402. ,312. X6. ,721. ,619. ,659. ,465. ,402. 1,000. ,506. X7. ,164. ,368. ,034. ,018. ,312. ,506. 1,000. En la Tabla 2 se observa que la correlación de Pearson r es como sigue: r1 = Corr(X1, X2) = 0.659 = 12 r2 = Corr(X1, X3) = 0.950 = 13 r3 = Corr(X1, X4) = 0.866 = 14 r4 = Corr(X1, X5) = 0.293 = 15 r5 = Corr(X1, X6) = = 0.721 = 16 r6 = Corr(X1, X7) = 0.164 = 17 r7 = Corr(X2, X3) = 0.407 = 23 r8 = Corr(X2, X4) = 0.378 = 24 r9 = Corr(X2, X5) = 0.344 = 25 r10 = Corr(X2, X6) = 0.619 = 26 r11 = Corr(X2, X7) = 0.368 = 27 r12 = Corr(X3, X4) = 0.875 = 34 r13 = Corr(X3, X5) = 0.201 = 35 r14 = Corr(X3, X6) = 0.659 = 36 r15 = Corr(X3, X7) = 0.034 = 37 r16 = Corr(X4, X5) = 0.131 = 45 r17 = Corr(X4, X6) = 0.465 = 46 r18 = Corr(X4, X7) = 0.018 = 47 r19 = Corr(X5, X6) = 0.402 = 56 r20 = Corr(X5, X7) = 0.312 = 57 r21 = Corr(X6, X7) = 0.506 = 67.

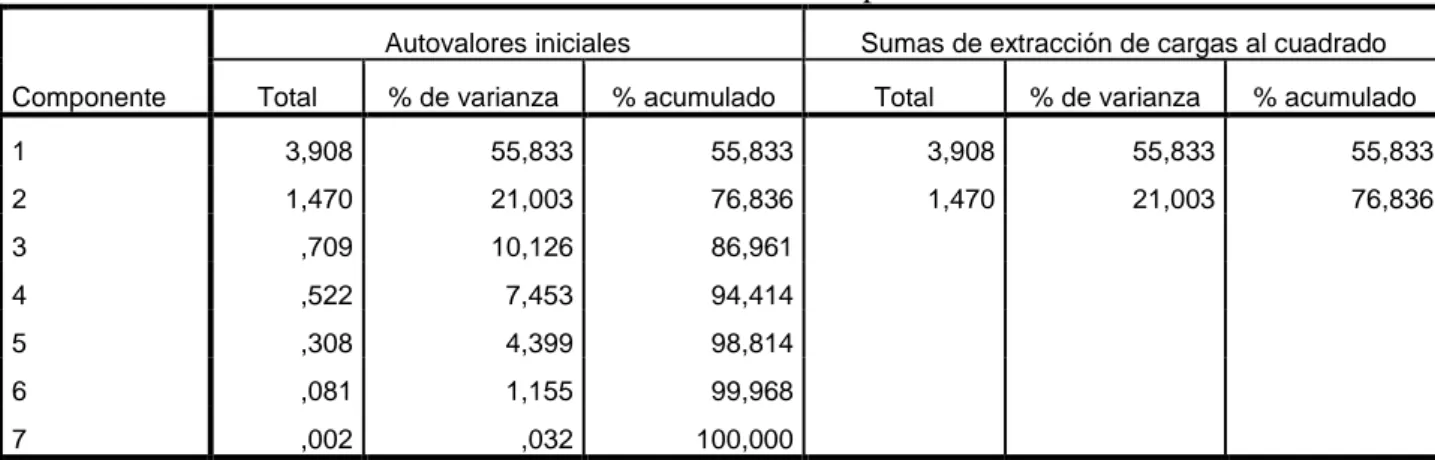
(32) 32. Existe una formula matemática que da el numero exacto de relaciones entre dos variables 7! 7 ( ) = 2!5! = 21 2. En el análisis anterior tenemos las siguientes correlaciones altas: r2 = Corr(X1, X3) = 0.950 = 13 r3 = Corr(X1, X4) = 0.866 = 14 r12 = Corr(X3, X4) = 0.875 = 34 significa que la variable X1 con X3 tienen una correlación de 95%, o sea, esas variables están fuertemente correlacionadas, lo cual significa que la presión arterial. está fuertemente. correlacionada con el peso del individuo. Las variables X1 y X4 tienen su correlación que equivale a 86.6% en donde también están fuertemente correlacionadas. Lo cual indica la presión arterial está fuertemente correlacionadas con la superficie corporal del individuo. De la misma forma observamos que las variables X3 con X4 tiene una correlación de 87.5%, lo cual indica que el sobrepeso de una persona está fuertemente correlacionadas con la superficie corporal. Con respecto a las correlaciones bajas podemos decir. r15 = Corr(X3, X7) = 0.034 = 37 r18 = Corr(X4, X7) = 0.018 = 47 Tenemos que las variables X3 con X7 tienen una correlación de 3.4%, eso significa que el peso de una persona no tiene mucha correlación con el estrés del individuo. De la misma forma podemos deducir que las variables X4 y X7 con 1.8% de correlación, o sea, la superficie corporal de una persona no tiene tanta correlación con el estrés de dicha persona. Tabla 3: Varianza total explicada Autovalores iniciales Componente. Total. % de varianza. Sumas de extracción de cargas al cuadrado. % acumulado. Total. % de varianza. % acumulado. 1. 3,908. 55,833. 55,833. 3,908. 55,833. 55,833. 2. 1,470. 21,003. 76,836. 1,470. 21,003. 76,836. 3. ,709. 10,126. 86,961. 4. ,522. 7,453. 94,414. 5. ,308. 4,399. 98,814. 6. ,081. 1,155. 99,968. 7. ,002. ,032. 100,000. A partir de esta tabla podemos decir que la varianza total (VT) es.

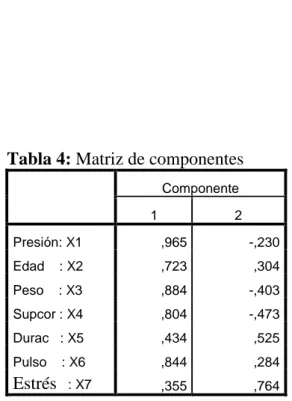
(33) 33. VT = 3.908 + 1.470 + 0.709 + 0.522 + 0.308 + 0.081 + 0.002 = 7 entonces 7  100% 3.908  x% de modo que: x1% =. 3.908 ×100% 7. = 55.83%. Esto significa que, la primera componente principal explicará el 55.83% de información contenida en las variables originales. Del mismo modo se tiene: 7  100% 1.470  x2% De modo que: x2% =. 1.470 ×100% 7. = 21%,. la segunda componente principal explicará o contendrá el 21% de información contenida en las variables originales. Sumando los dos resultados tendremos: x1% + x2% = 21% + 55.83% = 76.83%  77% En este caso, las dos primeras componentes recogen aproximadamente el 77% de la variabilidad, más aun recogen las fuentes de variabilidad más importantes de los datos. El resto de los datos ofrecen aproximadamente un 33% de variabilidad de información que contienen las variables originales. Una vez reducida la cantidad de variables originales participantes, obtenemos ciertas variables nuevas llamada componentes principales. Como ésta nuevas variables son calculadas a partir de las variables originales, en consecuencia, queda solamente determinar la información recogida por dichas componentes principales, en otra palabras, qué variables explican la similitud de los individuos en el sub-espacio de representación final. La interpretación se hace a partir de las correlaciones entre las variables observadas y las componentes. Dichas correlaciones se muestran en la tabla siguiente. (las componentes también se llaman factores)..

(34) 34. Tabla 4: Matriz de componentes Componente 1. 2. Presión: X1. ,965. -,230. Edad. : X2. ,723. ,304. Peso. : X3. ,884. -,403. Supcor : X4. ,804. -,473. Durac : X5. ,434. ,525. Pulso. ,844. ,284. ,355. ,764. Estrés. : X6 : X7. Observamos como la primera componente está altamente correlacionada con todas las variables salvo Duración y estrés, es decir, la primera componente muestra, fundamentalmente aspectos relacionados con el aumento de la presión arterial y de las variables determinantes del riesgo de enfermedad coronaria. La segunda componente está más correlacionada con el estrés y algo menos con la duración, por lo que mostrará las diferencias en el índice de estrés. En muchas ocasiones el investigador se enfrenta a situaciones en las que, para analizar un fenómeno, dispone de información de muchas variables que están correlacionadas entre sí en mayor o menor grado. Estas correlaciones son como un velo que impide evaluar adecuadamente el papel que juega cada variable en el fenómeno estudiado. Por lo que, el método de reducción de variables permite pasar a un nuevo conjunto de variables llamadas componentes principales, que se caracterizan por no ser correlacionadas, o sea, variables incorrelacionadas entre sí y que pueden ordenarse de acuerdo con la información que llevan incorporada. La cantidad de información incorporada en una componente esta medida por su varianza. Es decir, cuanto mayor sea su varianza mayor es la información que lleva incorporada en dicha componente. Por esta razón se selecciona como primera componente aquella que tenga mayor varianza, mientras que, por el contrario, la última es la de menor varianza. En general, la extracción de componentes principales se efectúa sobre variables tipificadas para evitar.

(35) 35. problemas derivados de escala, aunque también se puede aplicar sobre variables expresadas en desviaciones respecto a la media. Si p variables están tipificadas, la suma de las varianzas es igual a p, ya que la varianza de una variable tipificada es por definición igual a 1. El nuevo conjunto de variables que se obtiene por el método de componentes principales es igual en números al de variables originales. Es importante destacar que la suma de sus varianzas es igual a la suma de las varianzas de las variables originales. Las diferencias entre ambos conjuntos de variables estriban en que, como ya se ha indicado, las componentes principales se calculan de forma que estén incorrelacionadas entre sí. Cuando las variables originales están muy correlacionadas entre sí, la mayor parte de su variabilidad se puede explicar con muy pocas componentes. Si las variables originales estuvieron completamente incorrelacionadas entre sí, entonces el análisis de componentes principales carecería por completo de interés, ya que en ese caso las componentes principales coincidirían con las variables originales. Si la correlación muestral es nula entre el conjunto de variables, entonces las componentes principales coincidirán exactamente con las variables originales. Así pues, para aplicar este análisis hay que partir del supuesto de que las variables están correlacionadas entre sí Desde el punto de vista de su aplicación, el método de componentes principales es considerado como un método de reducción, es decir, un método que permite reducir la dimensión del número de variables que inicialmente se ha considerado en el análisis. Cada componente de los vectores coeficientes 𝑒𝑖𝑡 = [e1i, e2i, …,eki, …, epi] también inspeccionan los méritos de la variables dadas en los componentes. Por ejemplo, la magnitud de eki mide la importancia de la k-ésima variable de la i-ésima componente principal respecto al otro variable. En particular, eki es proporcional al coeficiente de correlación entre Yi y Xk.. 2.4 PROPORCIÓN DE VARIACIÓN TOTAL MEDIANTE AUTOVALORES DE LA MATRIZ DE . En muchas aplicaciones estaremos interesado en saber, qué variables y en qué proporciones aportan informaciones en la estructuración como en la elaboración de Componentes Principales, para sacar conclusiones y así poder hacer interpretaciones respectivas de las componentes respectos a las variables originales. Teorema 2.3 Si Y1 = 𝑒1𝑡 X, Y2 = 𝑒2𝑡 X, …, Yp = 𝑒𝑝𝑡 X son los componentes principales obtenidos a partir de la matriz varianza-covarianza , entonces.

(36) 36. 𝑌 ,𝑋𝑘 = 𝑖. 𝑒𝑘𝑖 √𝑖 √𝜎𝑘𝑘. ; i, k = 1, 2, …, p. son los coeficientes de correlación entre los componentes Yi y la variable Xk. Aquí (1, e1), (2, e2) , …, (p, ep) son pares de autovalores y autovectores de . Demostración Hagamos 𝑙𝑘𝑡 = [0,…,0,1,0,…,0] para tener Xk = 𝑙𝑘𝑡 X, y Cov(Xk, Yi) = Cov(𝑙𝑘𝑡 X, 𝑒𝑘𝑡 X) = 𝑙𝑘𝑡 ei. Por otro lado, tenemos ei = iei , Cov(Xk, Yi) = Cov(𝑙𝑘𝑡 X, 𝑒𝑘𝑡 X) = 𝑙𝑘𝑡 ei = 𝑙𝑘𝑡 iei = ieki Por el teorema 2.1 sabemos que: Var(Yi) = i y Var(Xk) = kk Entonces. 𝑌 ,𝑋𝑘 = 𝑖. = =. 𝐶𝑜𝑣(𝑌𝑖 ,𝑋𝑘 ) √𝑉𝑎𝑟(𝑌𝑖 )√𝑉𝑎𝑟(𝑋𝑘 ) 𝑖 e𝑘𝑖 √𝑖 √𝑘𝑘 𝑒𝑘𝑖 √𝑖 √𝜎𝑘𝑘. ; i, k = 1, 2, …, p . Ejemplo 2.2 Supongamos que las variables aleatorias X1, X2 y X3 tienen como matriz de covarianza 1  = [−2 0. −2 0 5 0] 0 2. Encuentre los coeficientes de correlación entre los componentes principales Yi y las variables Xk para i, k = 1, 2, 3. Solución. Primero encontremos los autovalores i y autovectores ei de . 1 = 5.83  𝑒1𝑡 = [0.383, -0.924, 0] 2 = 2  𝑒2𝑡 = [0, 0, 1] 3 = 0.17  𝑒3𝑡 = [0.924, 0.383, 0] Por tanto, los componentes principales son:.

(37) 37. Y1 = 𝑒1𝑡 𝑋 = 0.383X1 -0.924X2 Y2 = 𝑒2𝑡 𝑋 = X3 Y3 = 𝑒3𝑡 𝑋 = 0.924X1 + 0.383X2 Según la matriz  se observa que la variable X3 no está correlacionada con las otras dos variables. Por otro lado, se verifica las primeras componentes principales. Var[Y1] = Var[0.383X1 -0.924X2] = (0.383)2 Var[X1] + (- 0.924)2Var[X2] + 2(0.383)(-0.924)Cov(X1, X2) = 0.147(1) +0.854(5)-0.708(-2) = 5.83 = 1, Cov(Y1, Y2) = Cov(0.383X1-0.924X2 , X3) = 0.383Cov(X1, X3) – 0.924Cov(X2, X3) = 0.383(0) – 0.924(0) = 0. También se verifica que: 11 +  22 + 33 = 1 + 5 + 2 = 1 + 2 + 3 = 5.83 + 2.00 + 0.17 = 8 Ahora, la proporción de la variación total de la población respecto a la primera componente es 1 1 +2 +3. =. 5.83 8. = 0.73. Continuando, con las primeras dos componentes principales, la proporción de variabilidad es 1 +  2 1 +2 +3. =. 5.83+2 8. = 0.98.. Respecto a la varianza poblacional. En este caso, los componentes Y1 y Y2 puede ser reemplazado por las variables originales, sin mucha pérdida de información. Finalmente. 𝑌1 , 𝑋1 = =. 𝑒11 √1 √11 0.383√5.83 √1. = 0.925. 𝑌1 , 𝑋2 = =. 𝑒21 √1 √22 0.924√5.83 √5. = 0.998. Esto significa, que las variables aleatorias X1, X2, por separado tienen igual importancia para las primeras componentes principales. También.

(38) 38. 𝑌2 , 𝑋1 = 𝑌2 , 𝑋2 = 0, y,. 𝑌2 , 𝑋3 = =. √2 √2. √ 2 √33. = 1.. Puede ser que los resultados de la correlación no sean tomadas en cuenta en vista que la tercera variable no es significativa. 2.5 COMPONENTES PRINCIPALES EN UNA DISTRIBUCIÓN NORMAL. Sea X una variable aleatoria normal multivariable, por lo que X  N(, ) donde  es un vector de medias de orden p1 y  es una matriz de varianza-covarianza de orden pp. Sabemos que la densidad de X es constante sobre la elipsoide centrada en , esto es: (x - )t -1(x- ) = c2 La cual tiene como ejes c√𝑖 𝑒i ; i = 1, 2,…, p donde (i, ei) son los pares de autovalores- autovectores de . Un punto fuera de los ejes de la elipsoide tienen coordenadas proporcionales a 𝑒𝑖𝑡 = [e1, e2, …,ep] en el sistema coordenado la cual tiene como origen el  y los ejes son paralelos a los ejes originales x1, x2, …, xp es muy conveniente tener  = 0, sin pérdida de generalidad podemos tomar W = X -   E[W] = 0, y, Cov(X) = Cov(W). Así tendremos que c2 = xt -1x 1. 1. 1. 2. 1. =  (𝑒1𝑡 𝑥)2 +  (𝑒2𝑡 𝑥)2 + …+ (𝑒𝑝𝑡 𝑥)2 𝑝. donde 𝑒1𝑡 𝑥, 𝑒2𝑡 𝑥, …, 𝑒𝑝𝑡 𝑥 son los componentes principales de x, lo cual ponemos como: 𝑦1 = 𝑒1𝑡 𝑥, y2 =𝑒2𝑡 𝑥, …, yp = 𝑒𝑝𝑡 𝑥 luego tenemos c2 =. 1. 1. 1. 1. (𝑦1)2 +  (𝑦2 )2 + …+ (𝑦𝑝 )2 , i > 0, i = 1, 2,…,p 2. 𝑝.

(39) 39. y, esta ecuación define un elipsoide en un sistema de coordenadas de ejes y1, y2, …,yp con direcciones diferentes a los ejes x1, x2, …,xp. Como 1 es el autovalor más grande, entonces el eje mayor está en la dirección de e1. Los otros ejes de menor tamaño están en la dirección de e2, …,ep. Los componentes principales 𝑦1 = 𝑒1𝑡 𝑥, y2 =𝑒2𝑡 𝑥, …, yp = 𝑒𝑝𝑡 𝑥 están en las direcciones de los ejes de un elipsoide de densidad constante. En consecuencia, cualquier punto sobre el i-ésimo eje elipsoidal tiene x coordenada proporcional a 𝑒𝑖𝑡 = [e1i, e2i, …, epi] y, cualquier coordenada de la componente principal es de la forma [0, …,0, yi, …,0]. Cuando   0, entonces yi es un componente principal centrado de media con yi = 𝑒𝑖𝑡 (𝑥 − ); i = 1, 2, …, p con media cero y esta en la dirección de ei. Como caso particular tomaremos para un vector de distribución normal bidimensional con  = 0 y  = 0.75 dada en la siguiente figura. x2 y2 = 𝑒2𝑡 x y1 = 𝑒1𝑡 x x1. Fig. 2.1. Componente principal en la densidad bidimensional Como caso particular, en la siguiente sección, vamos a estudiar componentes principales de dos variables. 2.6 ANALISIS DE COMPONENTES PRINCIPALES DE DOS VARIABLES Para comprender mejor lo dicho en la sección anterior, ilustraremos para el caso bidimensional mediante un ejemplo, ya que, la formalización analítica se hará para el caso general de nvariables. Para mayor facilidad en cuanto a la operacionalidad matemática y presentación gráfica y, a modo de familiarizarse con el programa estadístico SPSS, versión 22, utilizaremos en este ejemplo el mencionado programa..

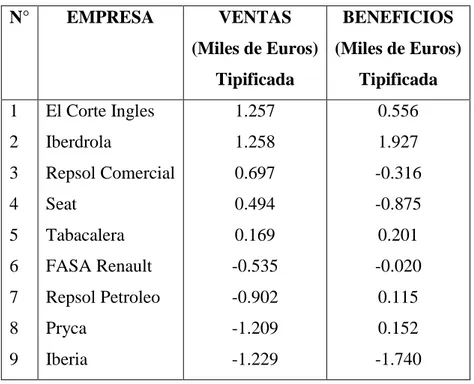
(40) 40. Ejemplo 2.3 Consideremos un caso de dos variables para dar una visión intuitiva del método. Para tal efecto se tiene la tabla siguiente:. Table 5: Empresas y Ventas-Beneficios N°. EMPRESA. VENTAS. BENEFICIOS. (Miles de Euros) (Miles de Euros) 1. El Corte Ingles. 775.104. 23.795. 2. Iberdrola. 775.218. 58.778. 3. Repsol Comercial. 700.963. 1.531. 4. Seat. 674.063. -12.756. 5. Tabacalera. 631.003. 14.729. 6. FASA Renault. 537.744. 9.059. 7. Repsol Petroleo. 489.155. 12.541. 8. Pryca. 448.465. 13.495. 9. Iberia. 445.853. -34.824. En primer lugar, veamos el diagrama de puntos mediante el programa SPSS.. Tabla 6: Correlaciones de ventas-beneficios Ventas Ventas. Correlación de Pearson. Beneficios 1. Sig. (bilateral) N Beneficios. ,495 ,175. 9. 9. Correlación de Pearson. ,495. 1. Sig. (bilateral). ,175. N. 9. 9.

(41) 41. Fig 2.2: Ilustración gráfica de Ventas-beneficios Observamos en la tabla 6 que la correlación positiva es igual a 0.495. Esto significa que existe una correlación moderada entre las variables de beneficios y ventas en sentido positivo. Podemos tipificar las dos variables, para lo cual necesitamos conocer la media y desviación estándar y así: z=. 𝑉𝑒𝑛𝑡𝑎𝑠− ̅̅̅̅̅̅̅̅̅̅ 𝑉𝑒𝑛𝑡𝑎𝑠 𝜎𝑉𝑒𝑛𝑡𝑎𝑠. , z=. ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 𝐵𝑒𝑛𝑒𝑓𝑖𝑐𝑖𝑜𝑠− 𝐵𝑒𝑛𝑒𝑓𝑖𝑐𝑖𝑜𝑠 𝜎𝐵𝑒𝑛𝑒𝑓𝑖𝑐𝑖𝑜𝑠. Tabal 7: Estadísticos Ventas-beneficios Ventas N. Válido. 9. 9. Perdidos. 0. 0. 608,61867. 11,92756. 132,391864. 21,607924. 17527,606. 466,902. Media Desviación estándar Varianza. Beneficios. Luego se tiene los valores tipificados o estandarizados..

(42) 42. Tabla 8: Valores tipificado de ventas-beneficios. N°. EMPRESA. VENTAS. BENEFICIOS. (Miles de Euros) (Miles de Euros) Tipificada. Tipificada. 1. El Corte Ingles. 1.257. 0.556. 2. Iberdrola. 1.258. 1.927. 3. Repsol Comercial. 0.697. -0.316. 4. Seat. 0.494. -0.875. 5. Tabacalera. 0.169. 0.201. 6. FASA Renault. -0.535. -0.020. 7. Repsol Petroleo. -0.902. 0.115. 8. Pryca. -1.209. 0.152. 9. Iberia. -1.229. -1.740. El diagrama de dispersión de los valores tipificados se observa en el siguiente gráfico, ubicados o distribuidos entre los campos negativos y positivos.. Fig 2.3: Ilustración gráfica de Ventas-beneficios tipificados.

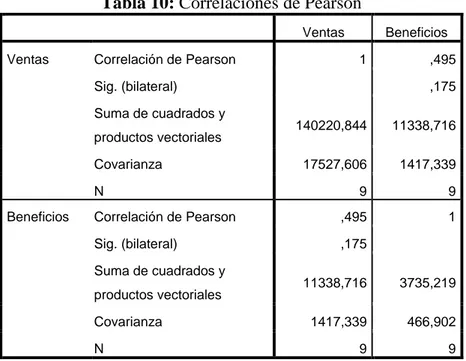
(43) 43. Cuando se tipifican las observaciones, entonces la matriz de covarianzas es precisamente la matriz de correlación y, por lo tanto, la varianza de cada variable tipificada es igual a 1.. Tabla 9: Correlaciones de los valores tipificados. VentasT VentasT. Correlación de Pearson. BenefT 1. ,546. Sig. (bilateral). ,128. N BenefT. 9. 9. Correlación de Pearson. ,546. 1. Sig. (bilateral). ,128. N. 9. 9. Y, la matriz de correlación para las dos variables tipificadas es: R=[. 1 0.546. 0.546 ] 1. Al aplicar el método de componentes principales, la suma de las varianzas de todas las componentes principales es igual a la suma de las varianzas de las variables originales. En consecuencia, en el caso de dos variables tipificadas esta suma debe ser igual a 2. Tabla 10: Correlaciones de Pearson Ventas Ventas. Correlación de Pearson. Beneficios 1. Sig. (bilateral) Suma de cuadrados y. ,175 140220,844. 11338,716. 17527,606. 1417,339. 9. 9. Correlación de Pearson. ,495. 1. Sig. (bilateral). ,175. productos vectoriales Covarianza N Beneficios. ,495. Suma de cuadrados y productos vectoriales Covarianza N. 11338,716. 3735,219. 1417,339. 466,902. 9. 9.

(44) 44. La matriz de covarianza cuando las variables no son tipificadas es: 17527.61 1417.34 =[ ] 1417.34 466.90 La aplicación del procedimiento de componentes principales requiere calcular los autovalores y los autovectores de la matriz de covarianza. Para tal efecto se tiene: 17527.61 −  | 1417.34. 1417.34 | = 0  (17527.61-)(466.90-) - (1417.34)2 = 0 466.90 −   8183641.11 – 17994.51 + 2 -2008852.68 = 0  2 – 17574.51 + 6174788.43 = 0. {. {. 1 =. 17574.51+√308863401.7−24699153.72. 2 =. 17574.51−√308863401.7−24699153.72. 2(1) 2(1). 1 = 17215.84 2 = 358.670. Son los autovalores de la matriz . Cuando se tipifican las observaciones, entonces la matriz de covarianza es precisamente la matriz de correlaciones y, por lo tanto, la varianza de cada variable tipificada es igual a 1. En este caso tendremos la matriz R= [. 1 0.546. 0.546 ] 1. luego el polinomio característico es: 1− | 0.546. 0.546 | = 0  (1-)2 - 0.2981 = 0 1−  1-2 + 2 - 0.2981 = 0  2 – 2 + 0.7019 = 0. {. {. 1 =. 2+√4−2.81. 2 =. 2− √4−2.81. 2(1) 2(1). 1 = 1.545 2 = 0.455.

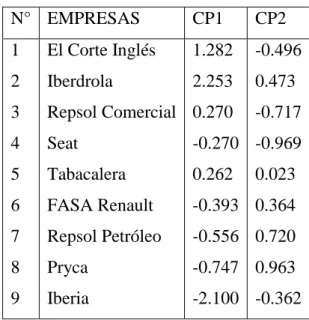
(45) 45. Y, según el programa SPSS tenemos. Tabla 11: Autovalores iniciales mediante SPSS Autovalores iniciales Componente. Total. % de varianza. Sumas de extracción de cargas al cuadrado. % acumulado. 1. 1,546. 77,313. 77,313. 2. ,454. 22,687. 100,000. Total 1,546. % de varianza. % acumulado. 77,313. 77,313. La varianza de cada componente principal es igual al valor de cada autovalor asociado. En el caso de bidimensional tipificada, la varianza de la primera componente principal es igual a 1 (que es la varianza de una de las variables tipificadas), más el 0.54603, que es el coeficiente entre las dos variables. La segunda componente principal su varianza es el resto de 1. O sea, estas varianza se determinan así:  var(1° componente principal) = var(z)+0.54603 = 1 + 0.54603 = 1.54603 = 1  var(2° componente principal) = var(z)-0.54603 = 1 – 0.54603 = 0.45397 = 2 Por algebra lineal sabemos que cada autovalor tiene asociado un autovector. En el caso de 2 variables supongamos que estos autovectores tienen la forma de 𝑢11 𝑢21 u1 = [𝑢 ] y u2 = [𝑢 ] 12. 22. sujeta a: 2 2 𝑢11 +𝑢12 =1 2 2 𝑢21 +𝑢22 =1. y que se cumple 𝐮𝐭𝟏 u2 = 0 O sea, son unitarios y ortogonales, estos vectores se llaman ortonormales o se denominan bases ortonormales. Cuando los datos están tipificados los vectores que se obtienen, independientemente de los valores que tengan los autovalores, son los siguientes: u1 = [. 0.7071 −0.7071 ] y u2 = [ ] 0.7071 0.7071. como puede comprobarse, estos vectores cumplen con las restricciones dadas:.

(46) 46. (0.7071)2 + (0.7071)2 = 1 y 0.7071 𝒕 −0.7071 𝐮𝐭𝟏 u2 = [ ] [ ] 0.7071 0.7071 = [ 0.7071, 0.7071] [. −0.7071 ] =0 0.7071. Los coeficientes o los elementos de los vectores u1 y u2 son los coeficientes que hay aplicar a las variables originales para obtener las respectivas componentes principales. Así: Z1 = u11X1 + u12X2 Z2 = u21X1 + u22X2 En nuestro caso, como en todos los casos de dos variables tipificadas, las combinaciones lineales para la obtención de componentes son los siguientes: Z1 = 0.7071X1 + 0.7071X2 Z2 = - 0.7071X1 + 0.7071X2 O sea, Z1 = 0.7071(1.257) + 0.7071(0.556) = 1.282 Z2 = - 0.7071(1.257) + 0.7071(0.556) = - 0.496 luego tenemos la siguiente tabla. Tabla 12: Componentes principales 1 y 2 N° EMPRESAS. CP1. CP2. 1. El Corte Inglés. 1.282. -0.496. 2. Iberdrola. 2.253. 0.473. 3. Repsol Comercial 0.270. 4. Seat. -0.270 -0.969. 5. Tabacalera. 0.262. 6. FASA Renault. -0.393 0.364. 7. Repsol Petróleo. -0.556 0.720. 8. Pryca. -0.747 0.963. 9. Iberia. -2.100 -0.362. -0.717. 0.023.

(47) 47. Los coeficientes de combinaciones lineales de Z1 y Z2 son precisamente los senos y los cosenos del ángulo de rotación entre los ejes de las componentes principales y los ejes correspondientes a las variables originales. Cuando se trata de variables tipificadas el ángulo de rotación es siempre de 45°. Así: Primer eje principal: cos45° = 0.7071, sen45° = 0.7071 Segundo eje principal: cos135° = -0.7071, sen135° = 0.7071..

(48) 48. CAPÍTULO III: APLICACIONES 3.1 INTRODUCCIÓN. Cuando se miden muchas variables aleatorias de un gran número de unidades experimentales, a menudo se presentan que las variables en estudio están siempre están interrelacionadas en mayor o menor proporción, tal como indica la matriz de correlación lineal, si por decir están interrelacionadas, para que no haya superposición de información es preferible que las nuevas variables que son combinación lineal de las variables originales, sean no dependientes, o sea, no correlacionadas y que expliquen la mayor variabilidad de información, esas nuevas variables se llaman componentes principales. En ese sentido tenemos la siguiente aplicación de componentes principales. 3.2 APLICACION A VARIABLES METEOROLÓGICAS. Uno de los objetivos del cálculo de componentes principales es la identificación de los mismos, es decir, averiguar qué información de la muestra resumen. Sin embargo este es un problema difícil que a menudo resulta subjetivo. Habitualmente, se conservan sólo aquellos componentes que recogen la mayor parte de la variabilidad, según visto o desarrollado en el Capítulo II. En los distritos de Aplao y Andagua, se propone estudiar segun los resultados de los autovalores con sus respectivas varianzas, el nivel de variabilidad y al mismo tiempo la correlacion de mayor coeficiente entre los factores predeterminados. Para lo cual se toma una muestra de 42 datos con las siguientes variables . Centro Poblado del Distrito de Aplao y Andagua de la Provincia de Castilla Departamento de Arequipa.. . Dióxido de azufre-SO2. . Temperatura ambiental en Grados Centígradas.. . Número de viviendas de cada centro poblado.. . Población de cada centro poblado.. . Velocidad media del viento.. . Precipitación pluvial media por año.. . Días lluviosos al año..

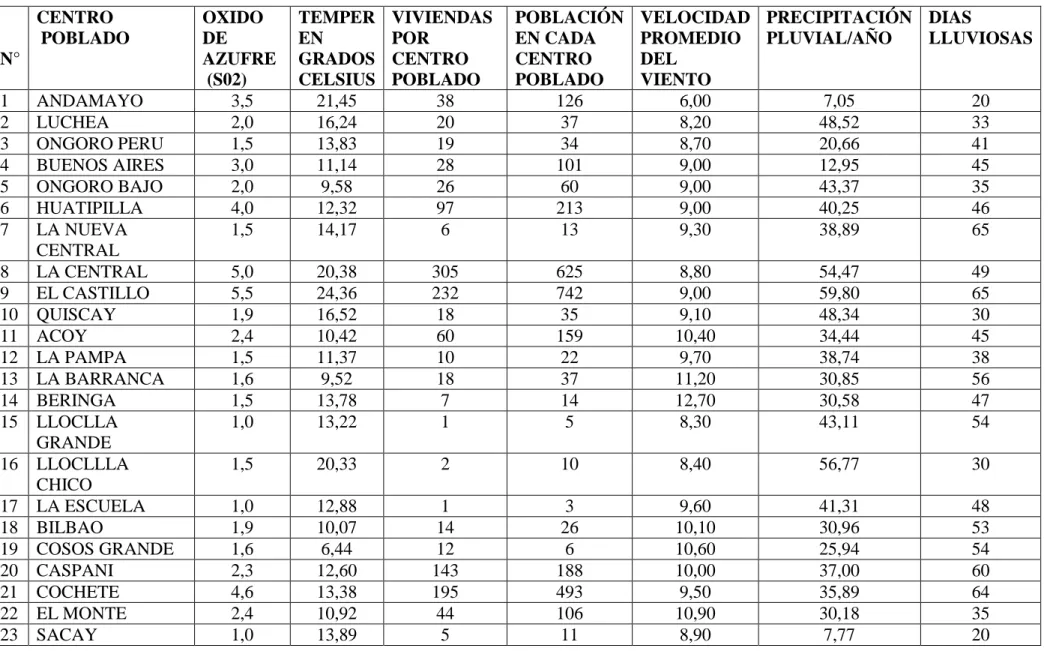
(49) 49. Tambien se analizar tres componentes principales segun los resultados obtenidos de mayor valor en lugar de analizar 8 variables originales. Para tal efecto la información ha sido proporcionada por el Instituto Nacional de Estadística e Informática (INEI) de la región de Arequipa..

(50) 50. TABLA N° 13: Matriz de datos de elementos que aportan en la generación de SO2. CENTRO POBLADO N° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23. ANDAMAYO LUCHEA ONGORO PERU BUENOS AIRES ONGORO BAJO HUATIPILLA LA NUEVA CENTRAL LA CENTRAL EL CASTILLO QUISCAY ACOY LA PAMPA LA BARRANCA BERINGA LLOCLLA GRANDE LLOCLLLA CHICO LA ESCUELA BILBAO COSOS GRANDE CASPANI COCHETE EL MONTE SACAY. OXIDO DE AZUFRE (S02) 3,5 2,0 1,5 3,0 2,0 4,0 1,5. TEMPER EN GRADOS CELSIUS 21,45 16,24 13,83 11,14 9,58 12,32 14,17. VIVIENDAS POR CENTRO POBLADO 38 20 19 28 26 97 6. POBLACIÓN EN CADA CENTRO POBLADO 126 37 34 101 60 213 13. VELOCIDAD PRECIPITACIÓN DIAS PROMEDIO PLUVIAL/AÑO LLUVIOSAS DEL VIENTO 6,00 7,05 20 8,20 48,52 33 8,70 20,66 41 9,00 12,95 45 9,00 43,37 35 9,00 40,25 46 9,30 38,89 65. 5,0 5,5 1,9 2,4 1,5 1,6 1,5 1,0. 20,38 24,36 16,52 10,42 11,37 9,52 13,78 13,22. 305 232 18 60 10 18 7 1. 625 742 35 159 22 37 14 5. 8,80 9,00 9,10 10,40 9,70 11,20 12,70 8,30. 54,47 59,80 48,34 34,44 38,74 30,85 30,58 43,11. 49 65 30 45 38 56 47 54. 1,5. 20,33. 2. 10. 8,40. 56,77. 30. 1,0 1,9 1,6 2,3 4,6 2,4 1,0. 12,88 10,07 6,44 12,60 13,38 10,92 13,89. 1 14 12 143 195 44 5. 3 26 6 188 493 106 11. 9,60 10,10 10,60 10,00 9,50 10,90 8,90. 41,31 30,96 25,94 37,00 35,89 30,18 7,77. 48 53 54 60 64 35 20.

(51) 51. 24 25 26 27 28. LOS PUROS 2,2 8,74 CUCULI 1,0 8,46 MARANCITO 2,5 12,32 MARAN GRANDE 3,8 9,91 QUERULPA 4,0 10,92 CHICO 29 QUERULPA 1,1 12,66 GRANDE 30 RESCATE 1,2 10,30 31 ONGORO 1,8 10,08 32 HUATIAPILLA 1,5 16,58 BAJO 33 HUAYRA PUNCO 1,0 15,34 34 ALTO LA 2,1 19,15 BARRANCA 35 MASCAPAMPA 1,0 20,66 36 APLAO 1,0 10,64 37 MISTIHUASI 1,1 15,29 38 SAN ANTONIO 1,9 14,45 39 CHARCA 1,5 10,70 40 SAN ISIDRO DE 2,6 12,99 TAUCA 41 VIRGEN DEL 2,8 7,67 ROSARIO 42 CCALLUA 1,9 8,29 Para encontrara los componentes principales, se procede:. 25 3 13 57 65. 59 5 40 187 266. 8,80 12,40 7,10 10,90 8,60. 33,36 36,11 39,04 34,99 37,01. 35 40 45 48 64. 16. 41. 9,60. 39,93. 58. 12 34 25. 41 103 77. 9,40 10,60 9,20. 36,22 42,75 49,10. 54 39 62. 5 35. 8 100. 7,90 10,90. 46,00 35,94. 58 49. 17 7 6 9 11 22. 7 8 28 35 11 52. 10,80 8,70 10,60 7,60 9,40 6,10. 48,19 15,17 44,68 42,59 38,79 40,75. 56 60 55 45 58 40. 35. 149. 11,80. 29,07. 59. 12. 56. 12,60. 39,50. 58.