El trato igual y la plena oportunidad de hacer valer los derechos : regla fundamental en el arbitraje

Texto completo

(1),,-,. fu e O(XCO 00 9 O\ °I. ¡Qqf. 2t- l(J.

(2) INSTITUTO TECNOLOGICO Y DE ESTUDIOS SUPERIORES DE MONTEREY CAMPUS EUGENIO GARZA SADA. ESTUDIO DEL EFECTO DE UN MODELO DE ENSEÑANZA DE LA MATEMATICA BASADO EN PROCESOS CON DOSIFICACION DE. CONTENIDO SOBRE EL RENDIMIENTO DE LOS ESTUDIANTES DE PROFESIONAL EN EL ITESM CAMPUS TAMPICO. Tesis presentada como requisito parcial para optar al título de Maestro en Educación con especialidad en Matemáticas. Autor: lng. Norma Cervantes Rosales. Asesor: Dra. Margarita A. de Sánchez.. Monterrey, N.L. 15 de Noviembre de 1991.

(3) ESTUDIO DEL EFECTO DE UN MODELO DE ENSEÑANZA DE. LA. MATEMATICA. BASADO. EN. PROCESOS. CON. DOSIFICACION DEL CONTENIDO SOBRE EL RENDIMIENTO DE LOS ESTUDIANTES DE PROFESIONAL EN EL ITESM CAMPUS TAMPICO.. lng. Norma Cervantes Rosales.. Trabajo de Grado aprobado en nombre del Instituto Tecnológico. y. de. Estudios. Superiores. de. Monterrey,. Campus Eugenio Garza Sada, por el siguiente Jurado:. Dra. Margarita A. de Sánchez. Dra. Zenaida Ramos. Dr. Ramón Núf\ez Doval.

(4) A mi esposo:. Ruben momento. Ricardo. estuvo. Martínez. a mi. lado. Vi/legas,. brindándome. que su. en. todo. apoyo. y. comprensión.. A mis padres:. Arturo Cervantes Infante y Ma. del Carmen Rosales de Cervantes, quienes con su ejemplo me han enseñado a esforzarme por alcanzar las metas anheladas..

(5) Reconocimientos. A la Dra. Margarita A. de Sánchez por su valiosa asesoría en la realización de este trabajo y por su entusiasmo y aliento que me ayudaron a esforzarme en la elaboración de este trabajo de tesis. A la Lic. Dora Estela Rodríguez, directora de la maestria en educación del ITESM Campus Eugenio Garza Sada por el apoyo administrativo necesario para la realización de este trabajo de tesis. Al lng. Jorge Elizondo Montalvo, director del ITESM Campus Tampico por la oportunidad de estudiar la mestría en educación . Al lng. Fortunato Méndez E., director de la división de Ingeniería del ITESM Campus Tampico, por el apoyo brindado durante todo el tiempo que estudié la maestría en educación . Al Lic. Rafael Díaz Guerra, por sus valiosas sugerencias en la parte estadística de este trabajo..

(6) RESUMEN. En este trabajo de tesis se presenta un modelo de enseñanza de la Matemática basado en procesos con dosificación del contenido. Para diseñar dicho modelo, se realizó una revisión bibliográfica acerca de la enseñanza de la Matemática desde una perspectiva no tradicional que se ubica en la didáctica de la Matemática centrada en procesos. Para determinar el efecto del modelo de enseñanza propúesto sobre el aprendizaje de los alumnos, se condujo una investigación cuasiexperimental con dos grupos intactos de Matemáticas I para las Ciencias Sociales en el ITESM Campus Tampico. Uno de los grupos fue el experimental, en donde se aplicó el modelo de enseñanza, y el otro grupo recibió la metodología convencional. Teniendo en cuenta que la muestra no fue seleccionada al azar, no es posible realizar inferencia estadística hacia toda la población, sin embargo los resultados obtenidos indican que los alumnos que recibieron el modelo de enseñanza propuesto tuvieron un rendimiento superior en los dos tipos de exámenes aplicados que los estudiantes del grupo control. Asimismo, los estudiantes del grupo experimental presentaron un nivel completamente satisfactorio de razonamiento matemático. Se concluyó que la utilización del modelo en el grupo experimental mejoró tanto su rendimiento como su nivel de razonamiento matemático. Se recomienda realizar futuras investigaciones, donde se lleve a cabo un muestreo aleatorio que permita realizar la inferencia estadística..

(7) INDICE GENERAL. PR ESENT ACION .................................................................... . RECONOCIMIENTOS............................................................... iv. RESUMEN.................................................................................. V. INDICE GENERAL ........................................................•........... vi LISTA DE TABLAS ..........................•....................................... ix. INTRODUCCION ........................................................................ 1. 1. ANTECEDENTES Y DEFINICION DEL PROBLEMA ................ 4. 1.1. ANTECEDENTES ........................................................... 4 1.2. DIAGNOSTICO GLOBAL ...............................................7 1.3. SELECCION DE UNA NECESIDAD .............................. 23 1.4. DEFINICION DEL PROBLEMA ..................................... 24 1.4.1. Enunciado ............................•..........................25 1.4.2. Delimitación .................................................. 26. 1.4.3. Justificación .................................................27 1.5. OBJETIVOS Y METAS DEL PROYECTO ..................... 27 1.6. ESTRATEGIA GENERAL ............................................ 28 1.7. LIMITACIONES DEL TRABAJO ................................. 29. 2. MARCO TEORICO CONCEPTUAL. ....................................... 30.

(8) 2.1. SELECCION Y ORGANIZACION DEL CONTENIDO DEL CURRICUL0 .......................................................31. 2.2. PRINCIPIOS QUE ORIENTAN LA CONDUCCION DEL PROCESO DE ENSEÑANZA-APRENDIZAJE DE LA MATEMATICA DESDE LA PERSPECTIVA TRADICIONAL ...........................................................69 2.3. PRINCIPIOS QUE ORIENTAN LA CONDUCCION DEL PROCESO DE ENSEÑANZA-APRENDIZAJE DE LA MATEMATICA DESDE LA PERSPECTIVA NO-TRADICIONAL ................................................•..82 2.4.. EVALUACION DEL APRENDIZAJE ......................... 106. 2.5. LINEAMIENTOS CURRICULARES ...........................122. 3. UNA ALTERNATIVA DE SOLUCION: MODELO DE ENSEÑANZA BASADO EN PROCESOS CON DOSIFICACION DEL CONTENID0 .............................................................. 131. 3.1.ANALISIS DEL PROGRAMA ANALITICO DEL CURSO MATEMATICAS I PARA LAS CIENCIAS SOCIALES ................................................................ 132. 3.2. IDENTIFICACION DE LAS CARACTERISTICAS ACADEMICAS DE LOS ESTUDIANTES INSCRITOS EN EL CURSO .......................................................... 135. 3.3. REDISTRIBUCION DEL CONTENIDO DEL CURSO ... 137 3.4. DEFINICION DE LA METODOLOGIA DE ENS ENANZA ............................................................. 139 3.5. DETERMINACION DE LA FORMA DE EVALUACION.

(9) DE LOS ESTUDIANTES......................................... 145 3.6. SUPUESTOS GENERALES QUE JUSTIFICAN EL MODELO .............................................................146. 4.ESTRATEGIA METODOLOGICA ....................................... 147 4.1. METODO DE INVESTIGACION UTILIZADO ............. 147 4.2. POBLACION Y MUESTRA ........................................ 149 4.3. DISEÑO DEL EXPERIMENTO ................................... 149 4.4. METODO DE RECOLECCION DE DATOS .................. 150 4.5. HIPOTESIS.............................................................. 154 4.6. METODO DE PROCESAMIENTO DE LOS DATOS ...... 155. 5. ANALISIS DE DATOS Y PRESENT ACION DE RESULTADOS ....•.........•...•.......................................... 157 5.1. DESCRIPCION DE LA MUESTRA ............................ 157 5.2. ESTADISTICOS DESCRIPTIVOS ........................... 158 5.3. ANALISIS DE LOS DATOS ...................................... 166. 6. SINTESIS, CONCLUSIONES Y RECOMENDACIONES ....... 170 6.1. SINTESIS .•...•......•............................. .............. ........ 170. 6.2. CONCLUSIONES .........•.••...•........•••.••..•........••........... 173 6.3. RECOMENDACIONES ................................................ 174. 7. ANEXOS ............................................................................176. 7.1. ANEXO A .................................................................. 177 7.2. ANEXO B .................................................................... 181.

(10) e. 196. 7.4. ANEXO D. 197. 7.5. ANEXO E. 199. 7.6. ANEXO F. 207. 7.7. ANEXO G. 215. 7.8. ANEXO H. 242. 7.9. ANEXO. 258. 7.10. ANEXO J. 260. 7.11. ANEXO K. 262. 7.12. ANEXO L. 263. 7.3. ANEXO. 8. BIBLIOGRAFIA ...................................................................... 264.

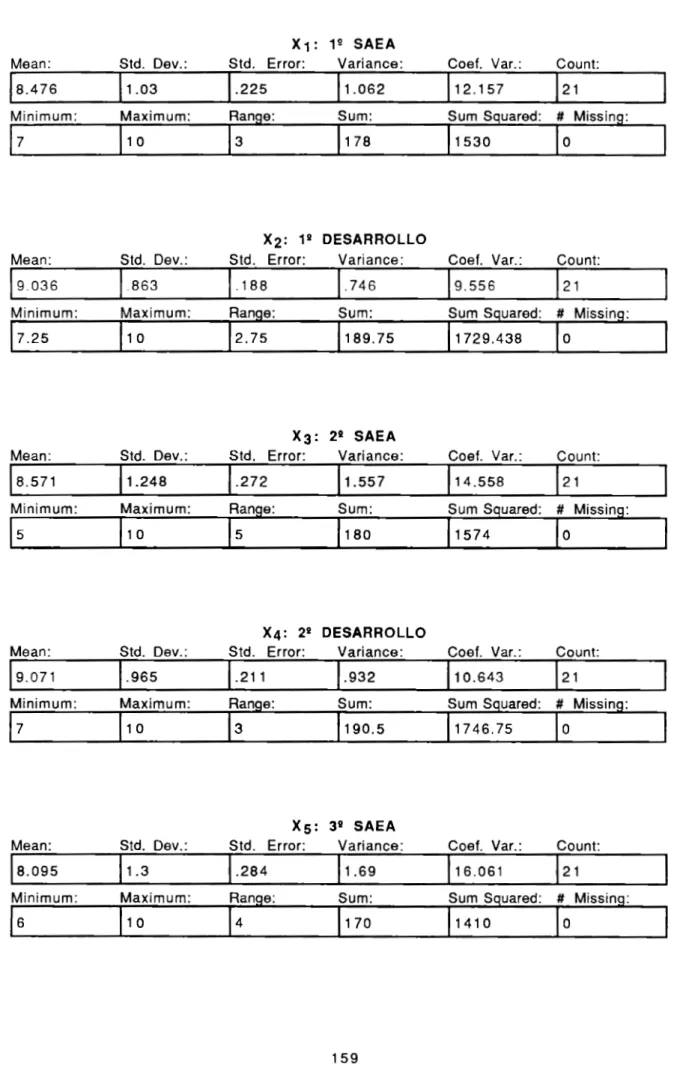
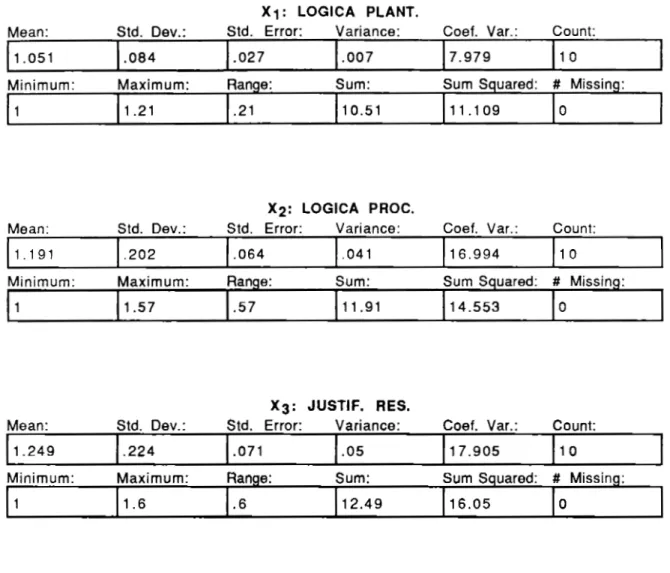
(11) INDICE DE TABLAS. PAG. TABLA. Estadísticos descriptivos de las califica-. 1. ciones Grupo Experimental ................................... 159. 2. Estadísticos descrptivos de las calificaciones Grupo Control ............................................... 161. 3. Estadísticos descriptivos del Análisis de razonamiento Grupo Experimental ................. 163. 4. Estadísticos descriptivos del Análisis de razonamiento Grupo Control ............................. 164. 5. Resumen de las medias de calificaciones a comparar entre ambos grupos ...................... 167. 6. Resumen de las medias y nivel de satisfacción en las variables de razonamiento matemático a comparar entre ambos grupos .................................................................... 167. 7. Medias en los exámenes SAEA y los de. desarrollo a comparar en cada grupo ....... 167.

(12) INTRODUCCION. Entre las funciones principales de la educación superior, se encuentra la de formar profesionistas capaces de asumir en la sociedad. responsabilidades. importantes que contribuyan. a su. desarrollo social, económico y cultural. Mucho se ha hablado acerca de la necesidad de preparar cuadros profesionales acordes con el avance tecnológico de los últimos tiempos. Desde esta perspectiva, destaca el importante papel de la ciencia y la técnica en la transformación acelerada de los procesos productivos.. Incluso se afirma, que el futuro a nivel. internacional está determinado por la ciencia y su incorporación directa a la producción. Si se considera que la Matemática es instrumento y lenguaje de la ciencia, se tiene entonces que el desarrollo científico y tecnológico y la educación en Matemática son inseparables. En este sentido, José Adem (1991 ), reconocido matemático mexicano, afirma que la enseñanza de la matemática ocupa una posición estratégica en el sistema educativo, y el nivel de la preparación científica y tecnológica puede elevarse más fácilmente si. los. conocimientos. matemáticos. se. imparten. oportuna. y. adecuadamente. Esto implica un estudio cuidadoso de los programas actuales de los cursos, y una revisión de los métodos de enseñanza a todos los niveles: elemental, medio y superior. En la mayoría de las instituciones educativas se presenta el problema del bajo rendimiento que los alumnos presentan en los distintos cursos de Matemática que se imparten, lo cual es un motivo de preocupación constante para todos los involucrados en el 1.

(13) quehacer educativo: autoridades educativas, docentes, padres de familia, alumnos, etc. Existen. muchas. interpretaciones. reduccionistas. que. pretenden explicar el problema mencionado, las cuales, en algunas ocasiones asignan toda la responsabilidad a los alumnos (no estudian, son flojos, tienen malos hábitos de estudio, traen malas bases, etc.); en otros casos la responsabilidad recae en los docentes (no saben explicar, no estan bien preparados, no saben evaluar, etc.). En ambos casos, se trata de una explicación, en extremo simple, de una situación que es sumamente compleja y que, por sus negativas consecuencias, requiere de un planteamiento más global. Teniendo en cuenta la importancia de la enseñanza de la Matemática para el desarrollo científico y tecnológico de una sociedad y los problemas que se presentan en su enseñanza, es necesario. buscar. alternativas. que. mejoren. el. proceso. de. enseñanza-aprendizaje de esta disciplina. González (sin fecha) afirma que cuando se aborda el proceso de enseñanza-aprendizaje, se observa que en él confluye un conjunto de elementos que, de alguna manera, afectan el rendimiento de los estudiantes. Entre las principales variables implicadas en este proceso se pueden señalar las siguientes:. 1.. Características. académica,. motivación. personales para. el. del. estudiante:. aprendizaje,. actitud. habilidad hacia. la. asignatura, hábitos de estudio, etc.. 2.. Características. académica,. formación. personales. del. pedagógica, actitud 2. docente:. capacitación. hacia la asignatura,.

(14) concepción del proceso educativo, concepción de la asignatura.. 3. Prerequisitos de los objetivos a desarrollar: nivel de dominio de los contenidos curriculares previstos y de los procesos cognitivos requeridos para tener éxito en el aprendizaje.. 4.. Modalidad. en. la que. se. presentan. los. contenidos. curriculares: verbal, gráfica, pictórica, simbólica, etc.. 5. Naturaleza del tópico a enseñar en cuanto a su extensión, complejidad y nivel de abstracción.. 6. Variables del proceso instruccional: estructura de la clase, técnica de la pregunta, retroalimentación correctiva y distribución del tiempo.. Teniendo en cuenta las gran cantidad de variables que influyen en el proceso de enseñanza-aprendizaje, puede afirmarse que el bajo rendimiento en Matemática no depende sólo de los alumnos o de los profesores; este problema debe verse en forma más comprensiva, tratando de abarcar las diferentes variables que convergen en el proceso, especialmente las que tienen que ver con el proceso instruccional, que compete directamente a los docentes.. 3.

(15) CAPITULO 1. 1. ANTECEDENTES Y DEFINICION DEL PROBLEMA. En el Instituto Tecnológico y de Estudios Superiores de Monterrey. (ITESM). Campus. Tampico,. el. proceso. de. enseñanza-aprendizaje de la Matemática, al igual que en muchas otras instituciones educativas, presenta problemas relacionados con las diferentes variables que influyen en el mismo, mencionadas en la introducción de este trabajo. En este primer capítulo se presentan los antecedentes y el diagnóstico global del proceso de enseñanza-aprendizaje de la Matemática en la institución educativa mencionada. Asimismo,. como resultado del diagnóstico realizado,. se. presenta una serie de necesidades que permitieron definir el problema de investigación de este trabajo de tesis.. 1.1. ANTECEDENTES. El sector curricular de Matemáticas del ITESM Campus Tampico está constituido por 8 cursos de Matemáticas: 4 del área de Ingeniería y 4 del área de Licenciatura, los cuales tienen una secuencia vertical, ya que cada curso es requisito del seguiente. Tanto en el área de Ingeniería como de Licenciatura, los cursos forman parte del tronco común de diferentes carreras profesionales. Entre las de Ingeniería se encuentran: Ingeniero industrial y de sistemas, Ingeniero. en sistemas computacionales, Ingeniero en. electrónica y comunicación, Ingeniero mecánico, entre otras. En el 4.

(16) caso de Licenciatura, se encuentran: Licenciado en Administración de Empresas, Contador Público, Licenciado en Economía, entre otras. Una de las actividades tradicionales al. inicio de cada. semestre escolar en el ITESM Campus Tampico es la llamada "junta de inducción", donde el director del Campus se reúne con todos los maestros que impartirán clases en el semestre que esté por iniciarse. Entre las actividades que se llevan a cabo en estas reuniones destaca la lectura que realiza alguno de los directivos del Campus del documento llamado: "Guía para facilitar el desempeño de la labor docente de los profesores", que en el apartado referente al Programa Analítico dice textualmente:. "Revise el programa de su materia y cumpla estrictamente con todos los objetivos. El sistema Tecnológico de Monterrey en toda la República tiene como norma indiscutible, impartir los mismos programas de estudio de todas y cada una de las materias, de cada carrera en todos los Campus. Por lo tanto, no es posible que un profesor modifique el programa de la materia que imparte; antes bien, deberá apegarse estrictamente al nivel marcado en los objetivos específicos de aprendizaje de cada tema. Cualquier observación para mejorar el programa será considerada por su director de departamento, como sugerencia que llevará al comité encargado de actualizar los programas ".. Entre las estrategias institucionales diseñadas para asegurar el cumplimiento de los programas analíticos por parte de los profesores destaca el llamado Sistema de Ayuda para la Evaluación del. Aprendizaje. (SAEA),. que. a. partir. del. semestre. Agosto-Diciembre de 1988 fue implantado en el ITESM Campus Tampico. en. el. área. de. Matemáticas 5. y. Estadística. a. nivel.

(17) profesional. Este. sistema. consiste. en. una. serie. de. exámenes. departamentales de opción múltiple que son generados con la ayuda de una computadora que tiene almacenado un banco de reactivos, los cuales. han sido elaborados por un grupo de profesores de. Matemáticas del. Campus. Monterrey,. teniendo. en. cuenta. los. objetivos específicos de aprendizaje que contienen los programas analíticos de las materias de Matemáticas y Estadística. Al inicio de cada semestre , se le entrega a cada profesor el programa analítico de la materia que va a impartir, el cual tiene marcado hasta que objetivo específico de aprendizaje debe cubrirse en cada período de acuerdo con el examen SAEA , de tal manera que para el examen final (que también es del sistema SAEA) se haya cubierto todo el programa. De lo expuesto en esta sección se puede concluir que en el sistema educativo ITESM se valora el estricto cumplimiento de los contenidos especificados en cada programa de las diferentes materias que se imparten, · de ahí que se hayan desarrollado aseguren el cumplimiento de los. estrategias institucionales que. programas, como es el caso del sistema SAEA. Si. bien. lo. expuesto. acontecimiento educativo,. refleja. el. aspecto. normativo. del. la pregunta natural que surge es, ¿de que. manera se lleva a cabo en la práctica el cumplimento de esta norma institucional?,. ¿cómo. se. afecta. el. proceso. de. enseñanza-aprendizaje?, ¿qué hacen los maestros y alumnos para cumplir con ella?. Para responder la preguntas planteadas, se presenta en la siguiente. sección. el. diagnóstico 6. global. del. proceso. de.

(18) enseñanza-apredizaje de la Matemática en el ITESM Campus Tampico, en donde se describen las situaciones deseada observada. y. con respecto a diferentes variables que inciden en dicho. proceso y se extraen conclusiones al comparar ambas situaciones.. 1.2. DIAGNOSTICO GLOBAL. El. diagnóstico. global. de. todo. el. sector curricular. de. Matemáticas de profesional del ITESM Campus Tampico, se llevó a cabo en cuatro etapas: 1. Descripción de la situación observada. 2. Descripción de la situación deseada. 3. Comparación entre la situación observada y la deseada. 4. Identificación de necesidades.. Los factores que se consideraron para realizar el diagnóstico fueron: 1.. La formación docente de los profesores de Matemáticas.. 2.. El programa analítico de los cursos de Matemáticas y Estadística.. 3.. El método de enseñanza utilizado.. 4.. La evaluación del desempeño del alumno.. En los siguientes apartados se detallan cada una de las etapas del diagnóstico en relación a mencionados.. 7. cada uno de los factores.

(19) 1.2.1. DESCRIPCION DE LA SITUACION OBSERVADA. Con el propósito de describir la situación observada relación. en. a los factores considerados en el diagnóstico, se tomaron. en cuenta tanto la perspectiva del maestro como la del alumno. La información relativa a cada factor se obtuvo de las siguientes fuentes: 1.. Cuestionario de opinión aplicado a los profesores.. 2. Investigación exploratoria de carácter etnográfico con un grupo, en donde se realizaron: observación participativa de la clase, entrevistas con el maestro y los alumnos y cuestionario de opinión a los alumnos.. 1.2.1.1.. Información. proveniente. del. cuestionario. de. opinión aplicado a los profesores. Se aplicó un cuestionario de opinión (Anexo A) a todos los profesores de Matemáticas del Campus Tampico, cuyos objetivos son los siguientes:. 1. Conocer la formación académica del maestro que imparte Matemáticas en profesional en el ITESM Campus Tampico y además determinar si posee algÚna formación didáctica para la enseñanza de la disciplina.. 2. Contrastar la opinión del docente con respecto al proceso 8.

(20) de enseñanza-aprendizaje de la Matemática antes y después de la implantación del sistema SAEA. Los factores que se utilizaron para hacer la comparación fueron: cumplimiento del programa analítico, métodos de enseñanza y formas de evaluación del desempeño de los alumnos.. Dado que en el Campus solamente hay 6 maestros de Matemáticas en profesional, incluyendo a la tesista, se les aplicó a todos (excepto a la tesista) el cuestionario y se obtuvieron los siguientes resultados:. 1. En cuanto a la formación académica y pedagógica de los maestros, se encontró lo siguiente: Sólo uno de los cinco maestros entrevistados tiene una formación académica específicamente en el área de Matemáticas (Licenciado en Matemáticas), los cuatro maestros restantes son ingenieros: dos son Ingenieros industriales y de sistemas y los otros. dos Ingenieros químicos administradores. Tres de los cinco maestros han tomado los talleres de. Microenseñanza. y Objetivos específicos de aprendizaje, impartidos. por el sistema ITESM con duración de 8 horas cada uno. En dichos cursos se proporcionan a los participantes herramientas básicas para la actividad docente: estructuración de la clase, formulación de. preguntas,. elaborar. retroalimentación. a los. estudiantes,. forma de. exámenes en relación a los objetivos del programa, etc.. Ninguno. de. los. cinco. maestros. ha. recibido. cursos. relacionados específicamente con la didáctica de la Matemática.. 9.

(21) 2.. En. relación. implantación del. a. la situación. sistema SAEA,. los. observada antes resultados se. de. la. presentan. ordenados de acuerdo a las siguientes variables:. 2.1. Cumplimiento del programa analítico de los cursos de Matemáticas. Antes de la implantación del sistema de evaluación SAEA, ninguno de los maestros encuestados cumplía estrictamente con el programa analítico de la materia de Matemáticas o Estadística que impartían. La. razón. principal. que argumentan. situación, es que el número de clases semestre. no. era. suficiente. para. para explicar esta. de que disponían durante el cubrir. todos. los. objetivos. específicos de aprendizaje que incluía el programa, de ahí que cubrían la cantidad de objetivos que el tiempo de clases les permitía, en promedio un 90% del total del programa,. y dado que. ellos. únicamente. mismos. elaboraban. sus. propios. exámenes,. evaluaban aquel material que había sido cubierto en clase.. 2.2. Métodos de enseñanza utilizados. Todos los profesores entrevistados indicaron que antes de la implantación del sistema SAEA, utilizaban una combinación de metodologías de enseñanza expositiva y participativa. Los profesores señalaron que utilizaban esta combinación de metodologías porque consideran que es necesario asegurarse de que, una vez visto un tema, los alumnos han comprendido y pueden resolver los problemas vistos.. 1O.

(22) 2.3. Evaluación del desempeño del alumno. Todos los maestros entrevistados, al calificar los exámenes que. ellos. mismos. procedimiento. como. elaboraban el. tomaban. resultado. de. los. en. cuenta. tanto. problemas,. el. ya que. consideran que es necesario ver los procedimientos que sus alumnos utilizan para resolver los problemas. para saber cuáles errores son. los que cometen. Además consideran que el hecho de elaborar ellos mismos los exámenes y evaluar tanto el procedimiento como el resultado de los problemas, les permitía llevar un seguimiento más personal de cada alumno.. 3. En relación a la situación observada después de la implantación. del. sistema. SAEA,. los resultados. se presentan. ordenados de acuerdo a las siguientes variables:. 3.1. Cumplimiento del programa analítico de los cursos de Matemáticas. Todos. los. maestros. encuestados. cubren. el. 100%. del. contenido de los programas analíticos, sin embargo, tres de los cinco maestros, tienen que dar en promedio dos clases extra por período. parcial,. para. terminar. de. cubrir. el. material. correspondiente. Además, todos los maestros proporcionan asesoría extra clase a sus alumnos, a la cual asisten, en promedio, el 30% de sus alumnos.. 11.

(23) 3.2. Métodos de enseñanza utilizados. Todos. los. maestros. señalaron. que. utilizan. tanto. la. metodología de enseñanza expositiva como participativa, ya que consideran que es necesario asegurarse de que los alumnos han comprendido lo que el maestro ha explicado.. 3.3 Evaluación del desempeño del alumno. Todos los maestros encuestados coinciden en que el grado de dificultad de muchos (un 70%) de los reactivos del examen SAEA es bajo. Además todos afirmaron que existen diferentes alternativas que utilizan sus alumnos para resolver el examen, cuando no saben hacer los problemas que les plantean, entre las que se. encuentran:. adivinar, sustituir las respuestas en la ecuaciones, derivar las cuatro opciones de resupesta cuando no pueden. resolver la integral. que se les presenta, etc. Todos los maestros consideran que las calificaciones del examen SAEA no siempre son representativas del aprendizaje de sus alumnos ya que en algunas ocasiones los alumnos no estudian y aprueban el examen contestándolo al azar.. 3.4. Aprendizaje del estudiante. Todos los maestros encuestados señalaron que la mayoría de sus alumnos utilizan un aprendizaje por repetición, memorizando los procedimientos de los problemas tipo, sin razonar lo que están haciendo. Además, señalaron que la retención de lo aprendido es a corto plazo, en la mayoría de los casos, sólo para presentar los exámenes. 12.

(24) 1.2.1.2.. Información. proveniente. de. la. investigación. exploratoria. La tesista llevó a cabo una investigación exploratoria con un grupo de. Matemáticas 111. de. Ingeniería durante el semestre. Agosto-Diciembre'90, la cual proporcionó información acerca de dos de los cuatro factores considerados para realizar el diagnóstico global, éstos son: el programa analítico del curso y el método de enseñanza utilizado. La. metodología. de. dicha. investigación,. consistió. en. observación participativa realizada por la tesista en un período de tiempo de 3 semanas, durante las cuales se observó la clase de Matemáticas 111 de Ingeniería del Campus Tampico impartida por una maestra de planta. El grupo estaba formado por 26 alumnos que cursaban el tercer semestre del tronco común de Ingeniería. Con. el. fin. de validar. los. resultados. obtenidos. en. la. observación participativa se realizaron entrevistas abiertas con la maestra y con los alumnos, se aplicaron cuestionarios de opinión a los alumnos y se recabaron algunos documentos como: programa analítico del curso, listas de asistencia y de calificaciones y exámenes de los alumnos. Entre los resultados más importantes obtenidos con este trabajo, se encuentra la forma en que la maestra y sus alumnos "sobrellevaban" el programa por objetivos tan extenso del curso de Matemáticas 111. La maestra, por su parte, distribuía los objetivos específicos 13.

(25) de aprendizaje de cada período parcial en el número de clases disponible y para cada clase, planificaba con anticipación los objetivos que debía cubrir, lo cual siempre ocurría, es decir, siempre exponía en clase los objetivos que traía preparados, sin considerar si los alumnos entendían o no. La situación anterior, se comprobó cuando se entrevistó a la maestra para conocer sus procesos de diagnóstico, al preguntarle: ¿De qué manera decides que los alumnos están en capacidad de pasar de un tema al siguiente?, a lo que respondió: ¡Sinceramente no lo tomo en cuenta, me baso en los objetivos del programa, cuando termino de explicar un objetivo paso al siguiente sin considerar si entendieron o no, pues de lo contrario no terminaría el programa, estoy segura que la asimilación del contenido ocurre después de la clase, cuando el alumno estudia por su cuenta los apuntes! Ante esta situación, los alumnos ya se acostumbraron, mientras su maestra escribe y escribe en el pizarrón, resolviendo los problemas en voz alta hablando -para sí misma-, los alumnos se concretan a copiar lo que ella escribe, y en muy pocas ocasiones intervienen en la clase. Sólo dos alumnos intervenían regularmente y cuando lo hacían era para corregir alguna operación equivocada del problema que estaba resolviendo la maestra. Al entrevistar a los alumnos, éstos manifestaron que les gustaría que su maestra explicara más despacio, pues casi nunca logran entender, dada la rapidez con la que explica, y también que les gustaría que profundizara un poco más en los temas más difíciles pues a veces sólo pone uno o dos ejemplos que no son suficientes para resolver la tarea. Los alumnos también opinaron que el problema no estaba en 14.

(26) la maestra, que lo que pasa es que el programa tiene muchos objetivos y el tiempo no es suficiente para cubrir todo, un alumno afirmó: "Son demasiados objetivos y hay muy poco tiempo para verlos, aunque se alcancen a ver todos rápidamente, se ven muy superficialmente y por lo tanto se olvidan después".. 1.2.2. DESCRIPCION DE LA SITUACION DESEADA. A continuación se describe la situación deseada para cada uno de los factores considerados en el diagnóstico global.. 1. La formación docente de los profesores de Matemáticas. De acuerdo con Morris Kline (Sin fecha), el profesor de Matemáticas ideal no sólo debería saber lo que enseña, sino también a quienes se lo enseña. Se necesitan, profesores de amplios conocimientos. académicos. y. educativos,. por. oposición. al. investigador especializado y autocentrado. Tales profesores tendrán que haberse formado en los departamentos de Matemáticas de las escuelas de graduados. Este autor destaca la necesidad de profesores que tengan amplios conocimientos de Matemáticas, y de sus aplicaciones, y además que sean educadores. Esto último significa que tendrán que saber qué demostraciones y qué abstracciones pueden manejar los jóvenes, y cuáles son sus intereses. Además, la amplitud y apertura de juicio deseable en el profesor ideal requerirían que él viese también las matemáticas desde un punto de vista no matemático y que pudiese apreciar así las actitudes y problemas de los jóvenes. En cuanto al profesor de Matemáticas deseable a nivel de. 15.

(27) educación superior, José Adem (1991) divide los alumnos de este nivel en dos grupos, ya que considera que en cada caso los requisitos que deben cumplir los profesores son diferentes. Dichos grupos son: a) Alumnos que cursan Matemáticas en el primer o en los dos primeros años de educación superior. En este grupo están incluidos los estudiantes de biología y bioquímica, ingenierías, arquitectura, química, agricultura, economía y administración. De acuerdo con este autor, los profesores que imparten clases a este grupo de alumnos deben tener como mínimo el título de Licenciado en Matemáticas. b) Los estudiantes que cursan Matemáticas durante todos o casi todos los años de la carrera. En este grupo quedan incluidos los estudiantes de ciencias exactas y los de las Escuelas Normales Superiores, con especialidad en Matemáticas. El autor señala que los profesores que impartan clase a este grupo de estudiantes, deben tener el grado de Maestro o de Doctor en Ciencias. El autor citado señala que los programas de formación tanto de Licenciados como Maestros y Doctores en Matemáticas deberán incluir cursos de Matemática aplicada y práctica docente, lo cual capacitaría a los egresados para trabajar en la docencia. Al igual que los autores citados, González (Sin fecha), afirma que el docente en Matemáticas ha de ser experto en el contenido propio de su asignatura, pero, además, también debe ser experto en aquellos procesos que el. alumno. contenido y operar con el mismo.. 16. requiere. para adquirir ese.

(28) 2. El programa analítico de los cursos de Matemáticas y Estadística. Con respecto a los contenidos de los programas, es deseable que exista un equilibrio apropiado entre su amplitud y profundidad. Es deseable,. concebir. las. materias de. Matemáticas y. Estadística como una manera ordenada de establecer relaciones importantes entre los hechos y las ideas fundamentales de la d1sc1p11na, en contraposición a la concepción de la materia como una acumulación o colección de hechos descriptivos específicos, ya que ésto último conduce a abarcar un contenido tan. amplio que. prácticamente impide dedicar tiempo a los procesos mentales. Al respecto Hilda Taba (1987) señala que la profundidad de los contenidos significa comprender plena y claramente ciertos principios, ideas o conceptos básicos y su aplicación. Para lograr conocimientos profundos, es necesario analizar con sumo cuidado las. ideas y en. suficiente detalle como. para comprender su. significado total, para relacionarlas con otras ideas y aplicarlas. a. nuevos problemas y situaciones. La. misma autora menciona que esta conceptualización. sugiere la posibilidad de lograr un equilibrio razonable entre la amplitud del contenido y su profundidad mediante la selección de una serie de ideas adecuadas, fácilmente aplicables y transferibles, al estudio de las cuales se dedicará el tiempo suficiente.. 3. El método de enseñanza utilizado. Es deseable adoptar el enfoque de la enseñanza de la Matemática basada en procesos, donde se intenta establecer un. 17.

(29) equilibrio entre el proceso cognoscitivo y el contenido implicados en cada uno de los objetivos que se formulan en el programa de estudio. En este enfoque de procesos, el maestro se considera como un mediador entre el contenido curricular (estímulo) y el alumno para hacer. posible el proceso de aprendizaje. Por su parte, el alumno se. concibe como un ser activo capaz no sólo de recibir información, sino de transformarla para crear nueva información y de participar consciente y activamente en su propio proceso de aprendizaje. Es. deseable. que. los. alumnos. logren. aprender. significativamente el contenido de los cursos de Matemáticas, entendiendo por aprendizaje significativo, la concepción de Ausubel (1990), que afirma: "El aprendizaje significativo por recepción involucra la adquisición de significados nuevos. Requiere tanto de una actitud de aprendizaje significativo como de la presentación al alumno de material potencialmente significativo. La última condición, en cambio, presupone: 1. que el material de aprendizaje en sí puede estar relacionado de manera no arbitraria (plausible, sensible y no azarosamente) y sustancial (no al pie de la letra) con cualquier estructura cognoscitiva apropiada ( que posea significado "lógico") , y 2. que la estructura cognoscitiva del alumno particular contiene ideas de afianzamiento relevantes con las que el nuevo material puede guardar relación. La interacción entre los significados potencialmente nuevos y las ideas pertinentes de la estructura cognoscitiva del alumno da lugar a los significados reales o psicológicos" (46).. 4. La evaluación del desempeño del alumno. González (Sin fecha), señala que dado que la enseñanza de la 18.

(30) Matemática tiene como eje la solución de problemas, el énfasis debe estar colocado más en el proceso que conduce a la solución que en la solución propiamente dicha. Desde esta perspectiva, a los errores debe dárseles un tratamiento distinto del que se le da habitualmente en el enfoque tradicional, en este sentido, una buena respuesta no supone que el alumno comprenda la fundamentación conceptual que subyace al proo1ema correspona1ente; al contrario, puede haoer s100 omeniaa. por azar, o mediante la aplicación mecánica de algún algoritmo o la transposición de algún procedimiento aplicado con anterioridad o, simplemente, a través de la repetición memorística; en cualquiera de estos casos, la buena respuesta oculta el hecho real de que el alumno no tiene un conocimiento comprensivo de la información matemática requerida por el problema. Tomando en cuenta lo anterior, es desable combinar el instrumento de evaluación SAEA con exámenes elaborados por el mismo maestro, que además de evaluar el resultado, evalúen el procedimiento, lo cual permitiría que el profesor conociera cuáles son las dificultades que presentan sus alumnos en la resolución de problemas para tomarlas en cuenta en el momento de explicar los temas y de ofrecer retroalimentación.. 1.2.3. COMPARACION ENTRE LA SITUACION OBSERVADA Y LA SITUACION DESEADA. Al igual que en la descripción de las situaciones observada y deseada, la comparación entre ambas, se llevará a cabo siguiendo el. 19.

(31) orden de los factores que han sido considerados para realizar el diagnósitco global. 1. La formación docente de los profesores de Matemáticas. En cuanto a los conocimientos matemáticos que debe tener el docente, se tiene que el 80% de los maestros de Matemáticas del ITESM Campus Tampico no tienen la formación académica requerida para impartir clases de Matemáticas a nivel superior, ya que de acuerdo a los autores consultados, los docentes de este nivel educativo deben tener como mínimo la Licenciatura en Matemáticas. En cuanto a la formación educativa, el 60% de los maestros han recibido dos cursos de herramientas básicas para la docencia, sin embargo,. ninguno a recibido capacitación específica en la. didáctica de la Matemática . Ninguno de los maestros tiene la formación. pedagógica que los autores citados consideran tan. necesaria para que el docente pueda desempeñar mejor su labor.. 2. El programa analítico de los cursos. En los programas analíticos de los cursos de Matemáticas, no existe un equilibrio apropiado entre la amplitud y los contenidos,. la profundidad de. lo cual conduce a abarcar un contenido tan amplio. que practicamente. impide dedicar tiempo. a los procesos de. razonamiento. Si bien, con la implantación del sistema SAEA se logró que los maestros cumplieran con la norma institucional de cubrir el 100% de los contenidos de los cursos que imparten, esta situación tiene repercusiones importantes en el aprendizaje de los alumnos, ya que el hecho de que se expongan todos los temas del programa no. implica que el alumno los aprenda.. 20.

(32) La investigación exploratoria proporciona evidencia de que el profesor cumple con. todos. considerar si los alumnos. los contenidos del. programa sin. están comprendiendo lo que él expone. rápidamente.. 3. El método de enseñanza utilizado. Aunque todos los maestros señalaron que utilizan como1nac1on. oe. meroaolog1a. ae. ensenanza. una. expositiva. y. participativa, la concepción de enseñanza participativa de estos profesores. consiste. en. que. los. alumnos. puedan. repetir los. problemas que se explicaron, es decir, que los alumnos sigan los algoritmos. presentados,. lo. cual. conduce. al. aprendizaje. memorístico, en donde el alumno repite algo que no entiende, algo que no sabe como aplicar y que olvidará rápidamente una vez que haya pasado el momento de la prueba que requiere ese conocimiento. Lo anterior no coincide con la situación deseada en la enseñanza de la Matemática basada en procesos, donde el alumno participa activamente en su proceso de aprendizaje, es decir, donde se concibe al alumno como un ser activo, capaz no sólo de recibir información, sino de transformarla para crear nueva información. La investigación. exploratoria y las entrevistas con. los. alumnos indican que el maestro se ha convertido en un expositor de los temas, preferenciando más el cumplimiento de los objetivos del programa que el aprendizaje de los alumnos.. 4. La evaluación del desempeño del alumno. Los exámenes de opción múltiple SAEA, donde sólo se califica la respuesta, no son los más apropiados para conocer el aprendizaje 21. •.

(33) real de los alumnos, ya que de acuerdo a lo dicho en la situación deseada, una buena respuesta no supone que el alumno comprenda la fundamentación conceptual que subyace al problema correpondiente, ya que pudo ser obtenida por azar, o mediante la aplicación mecánica. de. algún. algoritmo. o. a. través. de. la. repetición. memorística. Todos los maestros entrevistados conocen. las diferentes. rorrnas que utilizan sus alumnos para cumestar un proo1ema cuanao. no saben resolverlo, entre las que se encuentran : el azar, sustituir valores, descartar opciones, etc.. 1.2.4. IDENTIFICACION DE NECESIDADES. De. la comparación. entre. las. situaciones. observada. y. deseada, se identificó la siguiente lista de necesidades: 1. Capacitar a los maestros de Matemáticas del ITESM Campus Tampico en tres aspectos: a) Conocimientos fundamentales de la disciplina desde un punto de vista más formal para abordar más rigurosamente el conocimiento matemático en las carreras de ingeniería. b). Matemáticas. aplicadas. a. las. diferentes. áreas,. principalmente a aquellas donde se tengan carreras profesionales: administración, economía, computación, ingeniería industrial, entre otras. c) Capacitación docente, en donde se aborde la situación educativa. desde un punto de vista integral, es decir, que no se. limite a dar procedimientos estándares para impartir clases, sino más bien, proporcionar al docente conocimientos acerca de las 22.

(34) diferentes teorías de aprendizaje, métodos de enseñanza, teoría y diseño curricular y evaluación del aprendizaje.. 2. Programar adecuadamente el contenido de los cursos de Matemáticas teniendo en cuenta el tiempo de clases de que se dispone en un semestre escolar, de manera tal que el maestro tenga oportunidad de verificar el aprendizaje a niveles de comprensión y protund1zación del contenioo y aoemas µu1::aa µ, uµu, c,u, 'ª'. a. ;:,u;:,. estudiantes una retroalimentación significativa para el logro de la internalización de las habilidades matemáticas que se pretenden desarrollar.. 3. Buscar alternativas de enseñanza de la Matemática que promuevan el aprendizaje significativo por parte de los alumnos.. 4.. Diseñar instrumentos de evaluación que proporcionen. información confiable acerca del aprendizaje de los alumnos, y que ésta información se utilice para mejorar la enseñanza.. 1.3. SELECCION DE UNA NECESIDAD. Dado que una preocupación constante del profesor es el aprendizaje de sus alumnos, se seleccionó la necesidad relacionada con la programación adecuada del contenido de los cursos de Matemáticas. De todo lo expuesto en el diagnóstico, se presume que la. 23.

(35) programación. de. los. cursos. influye. en. el. proceso. de. enseñanza-aprendizaje de la Matemática, ya que debido a la amplitud de contenido que presentan los programas, se fortalece una enseñanza tradicional que hace énfasis en el contenido que debe enseñarse descuidándose o ignorándose el proceso de razonamiento asociado con. el conocimiento. la comunicación. y enfatizando. unidireccional por parte del docente (emisor, agente activo) hacia el a1umno (recepmr, suJeto pasivo). De esta manera la enseñanza de la Matemática se convierte sólo en la transmisión de información. a ser adquirida por el alumno. mecánicamente,. De. programar. sin. comprenderla.. adecuadamente. Matemáticas,. en. donde. los. aquí. contenidos. se establezca. la. de. un. necesidad los. cursos. equilibrio. entre. de de el. contenido que debe enseñarse y los procesos de razonamiento asociados con el mismo.. 1.4. DEFINICION DEL PROBLEMA. En base a la necesidad planteada se precisa hacer una planificación adecuada del programa de Matemáticas, que permita al profesor utilizar una metodología de enseñanza participativa, donde el alumno intervenga consciente y activamente en su propio proceso de. aprendizaje .. A. continuación. se. investigación de esta tesis.. 24. define. el. problema. de.

(36) 1.4.1. ENUNCIADO DEL PROBLEMA. ¿De qué manera una dosificación adecuada del contenido del programa analítico y la aplicación de una metodología participativa para impartir Matemáticas influye sobre el rendimiento de los alumnos?. Las vanao1es involucraaas en este proo1ema son:. 1. Variables independientes: a). Dosificación. adecuada del. contenido. del. programa,. entendiendo por esto, la distribución del contenido en las sesiones de clase disponibles en el semestre escolar teniendo en cuenta el tiempo requerido para lograr el equilibrio entre el conocimiento y el proceso de razonamiento asociado con el mismo. b) Metodología de enseñanza participativa, en donde el maestro. actúa como. mediador del. aprendizaje. y el. alumno. interviente activamente en su proceso de aprendizaje.. 2. Variable dependiente: Rendimiento de los alumnos, la cual tendrá los siguientes indicadores: a) Puntaje obtenido en el examen SAEA, donde sólo se califica el resultado de los problemas. b) Puntaje obtenido en el examen de desarrollo elaborado por la tesista, donde se determinará el nivel de razonamiento de los estudiantes, calificando tanto el procedimiento como el resultado de los problemas.. 25.

(37) 1.4.2. DELIMITACION DEL PROBLEMA. La situación problemática presentada se ubica en el sector curricular. correspondiente. al. área. de. Matemáticas. a. nivel. profesional en el Campus Tampico. Como se mencionó en los antecedentes, este sector está constituído por 8 cursos de Matemáticas: 4 del área de Ingeniería y 4 ae1 área de. C1t:11~1c1;:, So~1c111;¡;:,.. Aunque lo ideal sería hacer un estudio de todo el sector, dado el tiempo del que se dispone para elaborar el trabajo de tesis, fue necesario seleccionar uno de los cursos del área de Ciencias Sociales: Matemáticas l. La elección de la materia Matemáticas I para las Ciencias Sociales, obedeció a los siguientes criterios: a) Experiencia de la tesista en la impa·rtición. de este curso,. el cual ha sido dictado 6 veces. b) Unico curso en donde se disponía de dos grupos en el semestre Enero-Mayo de 1991.. Para. contestar. la. pregunta. planteada. se. condujo. un. experimento de campo con dos grupos de profesional de la materia Matemáticas I para las Ciencias Sociales en el semestre Enero-Mayo de 1991 en el ITESM Campus Tampico.. 26.

(38) 1.4.3. JUSTIFICACION DEL PROBLEMA. El problema planteado queda justificado con el diagnóstico global presentado en secciones anteriores. Hasta el momento, los maestros del ITESM Campus Tampico se han concretado en cubrir todo el programa de la materia que imparten, en la mayoría de los casos, solo a nivel expositivo y aunque están conscientes de la necesidad de hacer algo al respecto, no se ha realizado ninguna investigación que permita conocer más acerca. de. la. situación. problemática. con. el. fin. de. buscar. alternativas de solución, de ahí que el presente trabajo sea un intento por explorar dicha situación para tener un referente confiable que ayude a determinar. más. una alternativa de solución. viable.. 1.5. OBJETIVOS Y METAS DEL PROVECTO. Los objetivos que se pretenden alcanzar con el presente trabajo de tesis son los siguientes:. 1. Demostrar que una dosificación adecuada del contenido del programa analítico del curso de Matemáticas I para las Ciencias Sociales y la aplicación de la metodología de enseñanza basada en procesos,. mejora. y. permite. desarrollar. las. habilidades. de. razonamiento de los alumnos.. 2. Determinar si existe diferencia en el puntaje obtenido por los alumnos entre el examen SAEA y el examen de desarrollo. 27.

(39) elaborado por el propio profesor.. 3.. Determinar. la cantidad. de. objetivos. específicos. de. aprendizaje adecuada para ser cubierta en el número de horas disponibles en el semestre teniendo en cuenta que el maestro además de exponer los temas, verifique si está ocurriendo el aprendizaje. de. profundización,. sus de. tal. alumnos manera. al que. nivel los. de. comprensión. pueda. y. retroaIImentar. significativamente para que éstos logren la internalización. de las. habilidades matemáticas que se persiguen en el curso.. 4. Proporcionar con el marco teórico diferentes maneras de seleccionar y organizar el currículo de Matemáticas.. 1.6. ESTRATEGIA GENERAL. Para el logro de los objetivos se trabajó con 2 grupos de alumnos. de. Matemáticas. en. el. semestre. Enero-Mayo'91,. considerando a uno como grupo experimental y al otro como grupo control. En el grupo experimental se utilizó un modelo de enseñanza basado en procesos con disminución del contenido, el cual se describe en el tercer capítulo de este trabajo y se fundamenta con el marco teórico presentado en el segundo capítulo. determinar el efecto de la utilización del modelo de. Para enseñanza. basado en procesos con disminución del contenido sobre. el rendimiento. de los alumnos se aplicaron 2 tipos de. 28. exámenes: el.

(40) SAEA y uno de desarrollo elaborado por la tesista. El examen de desarrollo también permitirá analizar el nivel de. razonamiento. que. utilizan. los. alumnos. para. resolver los. problemas.. 1.7. LIMITACIONES DEL TRABAJO. Con los resultados del presente trabajo se tendrá un referente que. permitirá conocer más. acerca de. la. situación. problemática presentada, aunque para efectos de una generalización a todo el sector curricular será necesario hacer un estudio del resto de los cursos que lo componen, es decir, los resultados de este trabajo únicamente servirán como un indicador de lo que sucede en los otros cursos del sector. Otra de las principales limitaciones del trabajo, consiste en que dado que se está trabajando con alumnos inscritos formalmente en el curso, el cual a su vez es requisito para Matemáticas 11, es necesario cubrir todo el programa, de ahí que el modelo de enseñanza basada en procesos con dosificación del contenido que se propone en este trabajo, se podrá aplicar solamente en los tres períodos parciales, ya que para el examen final se deberá cubrir con todo el programa.. 29.

(41) CAPITULO 2. 2. MARCO TEORICO CONCEPTUAL. En este capítulo se presentan los aspectos teóricos más relevantes relacionados con el problema de investigación, objeto de esta tesis. Teniendo en cuenta las variables involucradas en el problema de investigación presentado en el capítulo anterior, el marco teórico conceptual que sustenta este trabajo se compone de los siguientes aspectos: 1. Selección y organización del contenido del currículo. 2. Principios que orientan la conducción del proceso de enseñanza-aprendizaje desde dos perspectivas: a) Tradicional; b) No-tradicional. 3. Evaluación del desempeño del estudiante, de acuerdo a los métodos de evaluación : a) Convencional; b) No-Convencional.. De los aspectos teóricos presentados se desprenderán los lineamientos curriculares. que orientarán el modelo de enseñanza. basado en procesos con dosificación de contenido que se propone en este trabajo.. 30.

(42) 2.1. SELECCION Y ORGANIZACION DEL CONTENIDO DEL CURRICULO. Antes. de. desarrollar. lo. referente. a. la. selección. y. organización del contenido del currículo, es conveniente precisar a qué llamamos currículo, y ante esta interrogante nos encontramos con una gran variedad de acepciones acerca del concepto que ponen de. manifiesto. los. diferentes. enfoques. ideológicos,. psicopedagógicos, filosóficos, políticos, económicos, etc., que lo orientan. Sin embargo, existe cierto concenso entre diferentes autores, que lo conceptualizan como proceso, es decir, como una propuesta educativa sujeta a transformaciones y adaptaciones a la realidad educativa de una institución, en este sentido Gimeno Sacristán (Sin fecha) afirma: "Cuando definimos el currículum, estamos describiendo la concreción de las funciones de la propia escuela y la forma particular de enfocarlas en un momento histórico y social determinado, para un nivel o modalidad de educación, en un entramado institucional, etc ... EI currículum es una praxis antes que un objeto estático emanado de un modelo coherente de pensar la educación o los aprendizajes necesarios de los niños y de los jóvenes, que tampoco se agota en la parte explícita del proyecto de socialización cultural en las escuelas... Es una práctica en la que se establece un diálogo, por decirlo así, entre agentes sociales, elementos técnicos, alumnos que reaccionan ante él, profesores que lo modelan, etc. Desarrollar esta acepción del currículum como ámbito práctico tiene el atractivo de poder ordenar en torno a este discurso las funciones que cumple y el modo como. 31.

(43) las realiza, estudiándolo procesualmente: una práctica y toma significado dentro de alguna medida previa y que no sólo currículum, sino de otros determinantes. la práctica al tiempo que contextualizado. se expresa en una práctica en es función del Es contexto de por ella" (16).. Esta concepción práctica del currículo permite entenderlo como. algo. que. se construye,. teniendo. en. cuenta que esta. construcción no puede ser independiente del contexto ideológico, cultural, social, político y económico en el que se desarrolla, de ahí que para entender el currículo en un sistema educativo se requiere tener en cuenta las prácticas políticas y administrativas que se expresan. en. su. desarrollo,. las. condiciones. estructurales,. organizativas, materiales, dotación de profesorado, bagage de ideas y significados que le dan forma y que lo modelan en sucesivos pasos de transformación. Todo lo anterior pone de manifiesto la compleja naturaleza del currículo, misma que no se puede reducir únicamente a la práctica pedagógica de la enseñanza, ya que se presenta como un territorio. donde se. intersectan diversos subsistemas políticos,. administrativos, de supervisión, de producción de medios, de creación intelectual, etc., que generan fuerzas diversas que inciden en la acción pedagógica. Si bien la conceptualización de Gimeno Sacristán, atiende a una visión macrosocial del currículo al ubicarlo como un cruce de prácticas que inciden en la acción pedagógica, algunos otros autores aunque toman en cuenta la necesidad de conceptualizar el currículo sin desligarlo de su contexto. macrosocial,. 32. hacen. énfasis en.

(44) vincularlo con lo que sucede en las aulas. Entre los autores que comparten esta perspectiva, tenemos a Stenhouse (1984) que señala: " Un currículum es una tentativa para comunicar los principios y rasgos esenciales de un propósito educativo, de forma tal que permanezca abierto a discusión crítica y pueda ser trasladado efectivamente a la práctica"(29). Stenhouse destaca la necesidad de la retroalimentación del currículo a través de la práctica educativa; conceptualiza el currículo como una propuesta educativa que puede ser modificada de acuerdo a lo que sucede en las aulas. En este sentido, encontramos otra definición de currículo planteada por el mismo autor antes citado, "todos los currícula son verificaciones hipotéticas de tesis acerca de la naturaleza del conocimiento y de la naturaleza de la enseñanza y del aprendizaje. Tales currícula son medios en los que las ideas se expresan en formas que las hacen comprobables por los profesores en los laboratorios que denominamos aulas"(100). De acuerdo a lo anterior, es importante la investigación de acción desempeñada por los docentes, a partir de la cual, éstos van. construyendo el currículo. tomando en cuenta su propia práctica docente y el desempeño de sus alumnos, así como también la práctica de otros profesores. Todo esto reafirma la idea de Stenhouse: "los currícula son hipotéticos y siempre defectuosos"(101 ). Por otra parte,. Coll. (1986). hace. una distinción. entre. proyecto o diseño curricular y desarrollo del currículo: el diseño curricular es el proyecto, en sentido estricto, que preside las. 33.

(45) actividades educativas, que proporciona informaciones concretas sobre sus intenciones (qué enseñar) y sobre la manera de llevarlas a cabo (cuándo y cómo enseñar y también qué, cuándo y cómo evaluar). Por su parte, el desarrollo del currículo es la puesta en práctica del proyecto. con. las. necesarias. adecuaciones,. modificaciones. y. enriquecimientos sin fin, que comporta inevitablemente el hecho de contrastar un proyecto educativo con la realidad de las aulas. Esta propuesta de Coll coincide con el modelo de currículo conceptualizado como proceso, tal y como lo menciona Stenhouse. Al igual que Stenhouse, Coll propone que el desarrollo del currículo proporciona. elementos. que. permiten. reelaborar,. revisar. y. enriquecer el diseño curricular; de ahí que el diseño curricular y su desarrollo sean aspectos curriculares indisociables que se nutren mutuamente. Siguiendo con esta misma idea que presupone la necesidad de tomar en cuenta, cuando se diseña un currículo, los aspectos derivados de la puesta en práctica del proyecto educativo en las aulas,. Hilda Taba. (1987). menciona lo siguiente:. "Existe. un. fundamento razonable para creer que, si la secuencia en la evolución del currículo. se. invirtiera --es decir,. si. los. maestros fueran. invitados primero a experimentar con aspectos específicos del currículo y luego, sobre la base de tales experiencias, se planeara su estructura--, la elaboración del currículo adquiriría una nueva dinámica" (23). Por su parte, Coll plantea un concepto del docente, alejándolo de la visión tradicional que lo considera como un agente externo al. 34.

(46) currículo, remitiéndolo a la simple ejecución de los programas, desde esta perspectiva, el maestro es un agente inherente a la elaboración del currículo, según lo exresado por el autor mismo: "el currículm no puede suplantar la iniciativa y la responsabilidad profesional. de. los. profesores,. convirtiéndolos. en. meros. instrumentos de ejecución de un plan previamente establecido hasta sus más mínimos detalles. Como proyecto que es, el currículum debe estar abierto a la consideración de los múltiples factores presentes en cada una de las situaciones educativas particulares, factores que solo el profesor está en condiciones de contemplar e integrar plenamente en su práctica pedagógica". (9).. En síntesis, los autores citados coinciden en conceptualizar el currículo como una propuesta educativa que al ponerse en práctica debe adecuarse, modificarse, enriquecerse con la realidad áulica, destacando la importante participación del maestro en este proceso de construcción del currículo, a través de la investigación de acción que puede llevar a cabo en su práctica docente. Retomando la diferenciación que señala Coll entre diseño curricular y desarrollo del currículo, para efectos de este trabajo, se considerará el primer aspecto: el diseño curricular. Este se entenderá como la propuesta educativa, el proyecto que preside las actividades educativas, que proporciona informaciones concretas sobre sus intenciones (qué enseñar) y sobre la manera de llevarlas a cabo (cuándo y cómo enseñar y también qué, cuándo y cómo evaluar) . Para el. diseño curricular existen. diferentes propuestas. metodológicas que incluyen varias etapas que van desde la. 35.

(47) fundamentación del proyecto curricular hasta su evaluación. Por ejemplo, Díaz Barriga (1984) propone las siguientes etapas del proceso del diseño curricular:. 1. Fundamentación de la carrera profesional. Incluye la investigación de las necesidades que pueden ser abordadas por el profesionista, el mercado ocupacional, las instituciones nacionales o extranjeras que ofrecen carreras afines a la propuesta, el análisis de los principios y lineamientos universitarios pertinentes y de la población estudiantil. 2. Determinación del perfil profesional.. Una vez establecida. una fundamentación sólida de la carrera que se va a. crear, es. necesario. alcanzar. establecer. las. metas. que. se. quieren. determinando el tipo de profesionista que se intenta formar. 3. Organización y estructuración del currículo.. El perfil. profesional elaborado en la etapa anterior, proporciona las bases para decidir cuáles van a ser los contenidos que se incluirán en el plan curricular, y bajo que organización y estructura se diseñará dicho plan. 4. Evaluación continua del currículo.. Se diseña una plan de. evaluación continua del currículo, ya que el plan curricular no se considera como algo estático, sino que está basado en necesidades que pueden ser cambiantes y en avances disciplinarios.. Otra de las propuestas metodológicas de diseño curricular, muy similar a la presentada por Díaz Barriga es la de Hilda Taba. 36.

(48) (1987) que incluye las siguientes etapas:. 1. Diagnóstico de las necesidades. 2. Formulación de objetivos. 3. Selección del contenido. 4. Organización del contenido. 5. Selección de las actividades de aprendizaje. 6. Organización de las actividades de aprendizaje. 7. Determinación de lo que se va a evaluar y de las maneras y medios para hacerlo.. En ambas metodologías propuestas por estos autores se observa que una de las etapas del diseño curricular es precisamente la selección y organización del contenido, conceptualizará en los siguientes apartados.. sobre. la que se. En la propuesta de. Díaz Barriga, ésta constituye la tercera etapa, llamada organización. y estructuración del currículo, mientras que en la de Hilda Taba corresponde. a las. etapas. 3. y 4 denominadas selección. y. organización del contenido.. 2.1.1.SELECCION DEL CONTENIOO DEL CURRICULO. Este apartado se desarrollará a través de diferentes niveles de generalidad que se diferencian de acuerdo con el alcance de la conceptualización curricular que realizan los autores consultados,. 37.

(49) estos niveles son:. 1. La selección del contenido del currículo a nivel general, en donde no se hace énfasis en ningún nivel educativo en especial, los autores que se encuentran en este nivel son: Hilda Taba, lmídeo Nérici y Robert. Gagné.. 2. La selección del contenido del currículo a nivel profesional en México, en donde se citarán los siguientes autores: María de lbarrola, Raquel Glazman y Armando Rugarcía.. 3. La selección del contenido del currículo de Matemáticas, donde se trabajarán las aportaciones del matemático mexicano José Adem.. 2.1.1.1. Selección del contenido del currículo a nivel general. Hilda Taba (1987) considera que la selección del contenido, junto con las experiencias de aprendizaje inherentes a éste, es una de las decisiones curriculares más importantes, de ahí que se requiera de un método racional para llevar a cabo esta tarea. Sin embargo, esta misma autora afirma que existen varios problemas. a los que se enfrenta el. diseñador curricular al. emprender esta tarea, entre los que se encuentran:. 38.

(50) 1. La falta de acuerdo entre los diseñadores en cuanto a lo que debe incluirse o no, a nivel de contenidos, en un currículo.. Las. propuestas sobre lo que debe incluirse en el currículo o excluirse de él, contienen diversidad de criterios, algunas de los cuales son o insuficientes o irracionales o bien ambas cosas a la vez. Debido a esta situación, los mismos educadores parecen hallarse confundidos en cuanto a los criterios por medio de los cuales decidir qué contenido debe incluir el currículo.. 2. La explosión del conocimiento ha hecho imposible la clásica simplicidad de las materias escolares.. A medida que. aumenta el conocimiento especializado, es necesario o bien agregar más asignaturas o asignar nuevas prioridades a las materias corrientes para dar lugar a los nuevos conocimientos y conceptos.. 3. La extensión de los objetivos de la educación exige nuevos campos para el aprendizaje que no formaban parte del currículo clásico, tales como las materias que tratan sobre la sociología de la familia o la evolución personal, el desarrollo del pensamiento creativo o la comprensión objetiva de las culturas universales.. 4.. El. crecimiento. desproporcionado. relación a la escasez de recursos y de maestros.. 39. del. alumnado. con.

(51) Con relación a estos problemas, Hilda Taba (1987) señala: "cuando se trata de enseñar un contenido cada vez más diverso en la misma cantidad de tiempo, se vuelve imposible preservar la unidad, la profundidad o la secuencia en el aprendizaje. es válido decir que, bajo estas condiciones cuanto más se "abarca" menos se aprende. Si bien los nuevos contenidos y los nuevos puntos de insistencia son necesarios, también es importante evitar que el currículo se convierta en una especie. oe. carncerIa,. una. misceláneas en lugar de aprendizaje "(348). La. IIIezc1a. I110IgerrnIe. oe. una dieta sistemática de. misma autora señala que uno de los aspectos más. importantes en la determinación de los criterios para la selección del contenido del currículo es el de establecer la diferencia entre el contenido y las experiencias de aprendizaje, u operaciones mentales que los estudiantes emplean para aprender el contenido. La selección del contenido define criterios estructurales del currículo que brinda los elementos necesarios para alcanzar los objetivos. referidos. a. la. adquisición. del. conocimiento:. los. conceptos, las ideas y los hechos que deben ser aprendidos. Por el contrario, el logro de objetivos tales como el pensamiento, las capacidades y las actitudes no es posible mediante la mera selección y organización del contenido. Para ello, los estudiantes necesitan pasar por ciertas experiencias que les permitan poner en práctica la conducta deseada. En este sentido es que se habla de las experiencias de aprendizaje. Como se señaló con anterioridad, la selección y organización del contenido del currículo es una de las etapas del diseño. 40.

(52) curricular, de ahí que los criterios que se aplicarán en esta etapa se derivan de las necesidades y. fases anteriores relativas al diagnóstico de las a la formulación de los objetivos del currículo, al. respecto Hilda Taba (1987) afirma: "la formulación y la aplicación de criterios para la selección y la organizac1on del currículo es, esencialmente, un recurso por medio del cual trasladar 1as cons1aerac1ones aer1vaaas ae1 estua10 ae 1as ruemes. para la elaboración del currículo a un currículo en funcionamiento. Estos criterios deben, por consiguiente, abarcar e integrar todo lo que implican los puntos de vista con relación a la función de la escuela en la sociedad, el estudio de las necesidades y las exigencias de la comunidad, el estudio del alumnado y los procesos del aprendizaje y el análisis de la naturaleza del conocimiento y de las asignaturas"(352).. Los criterios para la selección del contenido propuestos por esta autora son:. La validez y relevancia del contenido. El contenido del currículo es válido y significativo en la medida en que refleja el conocimiento científico contemporáneo, sin embargo, al hablar sobre. la. validez. del. contenido. es. necesario. seleccionar. lo. fundamental del conocimiento teniendo en cuenta que los hechos específicos es lo menos fundamental, mientras que la verdadera esencia de las materias escolares reside en las ideas básicas, los conceptos y las formas de pensamiento acontecimientos concretos.. 41. que organizan. los hechos y.

(53) Hilda Taba sugiere centrar el estudio de los contenidos sobre un número limitado de principios cuidadosamente seleccionados que constituyen el núcleo de la materia y luego emplear estas ideas como criterios para ejemplificar más bien que para abarcar el contenido más específico necesario para desarrollarlas. Estas ideas podrían ser consideradas los elementos esenciales del currículo. En el caso de la Matemática, las ideas, conceptos y leyes fundamentales se consideran como la "estructura de la asignatura" y en los. nuevos currícula de Matemática se a visto que es necesario. combinar. materias. que. antes. se. estudiaban. por. separado:. Aritmética, Algebra, Geometría y Cálculo. La tarea de desarrollar un currículo cuyo contenido sea válido, significativo y fundamental va más allá de la selección de las. ideas. básicas.. También. existe. el. problema. de. esta. significatividad en el acto de la adopción de decisiones menores tales como la elección de temas o actividades particulares. Esto significa. que. los. hechos. particulares. del. contenido. deben. representar también la estructura de la materia. Hilda Taba considera que es difícil trasladar este criterio de validez y relevancia del contenido a la práctica, ya que los maestros, al igual que los diseñadores curriculares no siempre están. suficientemente. familiarizados. con. los. límites. del. conocimiento en las materias que enseñan, de ahí que en la práctica se cometan tantos errores, como el de perder el tiempo exponiendo conceptos. que. son. insuficientemenete. comprendidos. por. los. alumnos, y que, por consiguiente, sólo pueden ser memorizados, así. 42.