Codificación aritmética
Es útil cuando se tienen fuentes con alfabetos pequeños.
En el código Huffman si el alfabeto es grande, la probabilidad del símbolo más probable es pequeña y la desviación de la rata de código de la entropía (redundancia) es pequeña. Al contrario si el alfabeto es pequeño en donde la redundancia del código Huffman es grande. Esto se resuelve generando un código extendido pero esto a veces es impráctico porque se generan alfabetos demasiado grandes, se requieren grandes cantidades de memoria y tiempos y recursos exagerados en la decodificación.
Ejemplo:
Considere una fuente que pone letras independientes e idénticamente distribuidas (𝒊𝒊𝒅) desde un alfabeto
𝑨 = {𝒂𝟏, 𝒂𝟐, 𝒂𝟑}
Con el modelo de probabilidad
𝑷(𝒂𝟏) = 𝟎. 𝟗𝟓
𝑷(𝒂𝟐) = 𝟎. 𝟎𝟐
𝑷(𝒂𝟑) = 𝟎. 𝟎𝟑
La entropía para esta fuente es 𝟎. 𝟑𝟑𝟓 𝒃𝒊𝒕𝒔/𝒔í𝒎𝒃𝒐𝒍𝒐. Un código Huffman para esta fuente está dado en la tabla 1
Letra código
𝒂𝟏 𝟎
𝒂𝟐 𝟏𝟏
𝒂𝟑 𝟏𝟎
Tabla 1: Código Huffman para un alfabeto de tres letras
La longitud promedio para este código es 𝟏. 𝟎𝟓 𝒃𝒊𝒕/𝒔í𝒎𝒃𝒐𝒍𝒐. La diferencia entre la longitud promedia de código y la entropía, o redundancia, para este código es 𝟎. 𝟕𝟏𝟓 𝒃𝒊𝒕/𝒔í𝒎𝒃𝒐𝒍𝒐, lo que es el 𝟐𝟏𝟑% de la entropía. Esto significa que para codificar esta secuencia necesitaríamos más del doble del número de bits prometidos por la entropía.
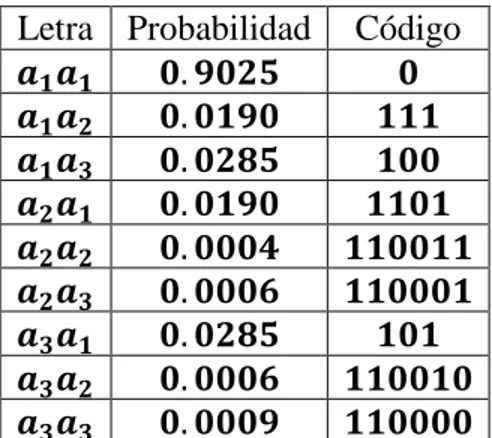
Letra Probabilidad Código
𝒂𝟏𝒂𝟏 𝟎. 𝟗𝟎𝟐𝟓 𝟎
𝒂𝟏𝒂𝟐 𝟎. 𝟎𝟏𝟗𝟎 𝟏𝟏𝟏
𝒂𝟏𝒂𝟑 𝟎. 𝟎𝟐𝟖𝟓 𝟏𝟎𝟎
𝒂𝟐𝒂𝟏 𝟎. 𝟎𝟏𝟗𝟎 𝟏𝟏𝟎𝟏 𝒂𝟐𝒂𝟐 𝟎. 𝟎𝟎𝟎𝟒 𝟏𝟏𝟎𝟎𝟏𝟏 𝒂𝟐𝒂𝟑 𝟎. 𝟎𝟎𝟎𝟔 𝟏𝟏𝟎𝟎𝟎𝟏 𝒂𝟑𝒂𝟏 𝟎. 𝟎𝟐𝟖𝟓 𝟏𝟎𝟏 𝒂𝟑𝒂𝟐 𝟎. 𝟎𝟎𝟎𝟔 𝟏𝟏𝟎𝟎𝟏𝟎 𝒂𝟑𝒂𝟑 𝟎. 𝟎𝟎𝟎𝟗 𝟏𝟏𝟎𝟎𝟎𝟎
Tabla 2: Código Huffman para un alfabeto extendido
La rata promedio para el alfabeto extendido es 𝟏. 𝟐𝟐𝟐 𝒃𝒊𝒕𝒔/𝒔í𝒎𝒃𝒐𝒍𝒐. La rata adicional sobre la entropía es aún cerca del 𝟕𝟐% de la entropía. Si se continúa poniendo bloques de más símbolos encontramos que la redundancia cae a un valor aceptable cuando hacemos bloques de 𝟖 𝒔í𝒎𝒃𝒐𝒍𝒐𝒔. El tamaño de alfabeto correspondiente a este nivel es de 𝟔𝟓𝟔𝟏, lo cual hace que el tamaño de este código sea impráctico por varias razones:
El tamaño de la memoria necesario para almacenar este código puede que no esté disponible.
La decodificación de un código de este tamaño puede ser un proceso altamente ineficiente y consumidor de tiempo.
Si la estadística cambia aunque sea ligeramente puede hacer que el código sea ineficiente.
Problema: para codificar una secuencia de longitud 𝒎 en Huffman se requieren palabras de código para todas las posibles secuencias de longitud 𝒎.
En la codificación aritmética se asigna un identificador único o tag a la secuencia a codificar, el cual es una fracción binaria a la que se le asigna posteriormente un código binario.
Se asigna un código aritmético único a una secuencia de longitud 𝒎 sin que sea necesario generar palabras de código para todas las posibles secuencias de longitud 𝒎.
Codificando una secuencia
Una manera de codificar con un identificador único a cada secuencia es asignarle un número en el intervalo [𝟎, 𝟏), lo cual da un conjunto infinito de identificadores.
La variable aleatoria 𝑿 se toma como la asignación de un número a las letras o símbolos de la fuente
𝑿(𝒂𝒊) = 𝒊 𝒂𝒊∈ 𝑨
Siendo 𝑨 = {𝒂𝟏, 𝒂𝟐, ⋯ , 𝒂𝒎} el alfabeto de la fuente.
El mapeo supone que se dispone de un modelo de probabilidad de la fuente 𝑷 y de la función densidad de probabilidad de la variable aleatoria, tal que
𝑷(𝑿 = 𝒊) = 𝑷(𝒂𝒊)
Y la función distribución acumulativa
𝑭𝑿(𝒊) = ∑ 𝑷(𝑿 = 𝒌) 𝒊
𝒌=𝟏 Ejemplo:
Considere el alfabeto de tres letras 𝑨 = {𝒂𝟏, 𝒂𝟐, 𝒂𝟑} con 𝑷(𝒂𝟏) = 𝟎. 𝟕, 𝑷(𝒂𝟐) = 𝟎. 𝟏 ,
𝑷(𝒂𝟑) = 𝟎. 𝟐.Usando el mapeo propuesto 𝑭𝑿(𝟏) = 𝟎. 𝟕, 𝑭𝑿(𝟐) = 𝟎. 𝟖, 𝑭𝑿(𝟑) = 𝟏 Esto parte el intervalo unitario como se muestra en la ilustración 1.
Ilustración 1: Restringiendo el intervalo que contiene el identificador para la secuencia
{𝒂𝟏, 𝒂𝟐, 𝒂𝟑}
el símbolo es 𝒂𝟑 el identificador estará entre [𝟎. 𝟖, 𝟏. 𝟎]. Una vez el intervalo que contiene el identificador ha sido determinado, el resto del intervalo unidad es descartado y el intervalo restringido es dividido otra vez en las mismas proporciones del intervalo original. Suponga que el primer símbolo fue 𝒂𝟏 . El identificador estaría contenido en el sub intervalo[𝟎, 𝟎. 𝟕]; Este sub intervalo es luego dividido en exactamente las mismas proporciones como el intervalo original, dando los sub intervalos [𝟎. 𝟎, 𝟎. 𝟒𝟗], [𝟎. 𝟒𝟗, 𝟎. 𝟓𝟔]
,[𝟎. 𝟓𝟔, 𝟎. 𝟕] la primera partición corresponde al símbolo 𝒂𝟏, la segunda al símbolo𝒂𝟐 y así sucesivamente. El proceso iterativo puede visualizarse en la ilustración 1.
La aparición de cada nuevo símbolo de la secuencia restringe el identificador a un nuevo subintervalo que es disjunto de cualquier otro subintervalo que pueda haber sido generado usando este proceso, luego cualquier miembro de este subintervalo puede ser usado como identificador. Una escogencia popular es el límite inferior pero también puede ser el medio del intervalo.
Hay un procedimiento recursivo para calcular los límites inferior y superior del intervalo para una secuencia de longitud 𝒏.
En general, se puede mostrar que para cualquier secuencia 𝑿 = (𝒙𝟏𝒙𝟐⋯ 𝒙𝒏)
𝒍(𝒏)= 𝒍(𝒏−𝟏)+ (𝒖(𝒏−𝟏)− 𝒍(𝒏−𝟏)) ∗ 𝑭𝑿(𝒙𝒏 − 𝟏)
𝒖(𝒏)= 𝒍(𝒏−𝟏)+ (𝒖(𝒏−𝟏)− 𝒍(𝒏−𝟏)) ∗ 𝑭𝑿(𝒙𝒏)
En donde se supone que 𝒍(𝟎) = 𝟎 y 𝒖(𝟎) = 𝟏.
Observe que a través de este proceso no necesitamos calcular explícitamente cualquier probabilidad conjunta.
Si se usa el punto medio del intervalo para el identificador, entonces
𝑻̅𝑿(𝑿) =𝒖
(𝒏)+ 𝒍(𝒏)
𝟐
Ejemplo: Generando un identificador
Considere una fuente que genera los símbolos 𝒔𝟏 con probabilidad 𝑷(𝒔𝟏) = 𝟎. 𝟖, 𝒔𝟐 con probabilidad 𝑷(𝒔𝟐)=0.02 y 𝒔𝟑 con probabilidad 𝑷(𝒔𝟑) = 𝟎. 𝟏𝟖. Se define la variable aleatoria 𝑿(𝒔𝒊) = 𝒊. Se supone que se va a codificar la secuencia 𝟏 𝟑 𝟐 𝟏. Del modelo de probabilidad sabemos que
𝑭𝑿(𝒌) = 𝟎 𝒌 ≤ 𝟎, 𝑭𝑿(𝟏) = 𝟎. 𝟖, 𝑭𝑿(𝟐) = 𝟎. 𝟖𝟐, 𝑭𝑿(𝟑) = 𝟏,
Usando las ecuaciones que permiten calcular los limites inferior y superior de manera iterativa y suponiendo 𝒍(𝟎) = 𝟎 y 𝒖(𝟎) = 𝟏 . El primer elemento de la secuencia 𝟏 resulta en la siguiente actualización:
𝒍(𝟏) = 𝟎 + (𝟏 − 𝟎) ∗ 𝟎 = 𝟎
𝒖(𝟏) = 𝟎 + (𝟏 − 𝟎) ∗ 𝟎, 𝟖 = 𝟎, 𝟖
O sea, el identificador de la secuencia estará en el intervalo [𝟎, 𝟎. 𝟖). El segundo elemento de la secuencia es 𝟑. Usando las ecuaciones de actualización tenemos:
𝒍(𝟐) = 𝟎 + (𝟎. 𝟖 − 𝟎) ∗ 𝑭𝑿(𝟐) = 𝟎 + (𝟎. 𝟖 − 𝟎) ∗ 𝟎. 𝟖𝟐
= 𝟎. 𝟔𝟓𝟔
𝒖(𝟐) = 𝟎 + (𝟎. 𝟖 − 𝟎) ∗ 𝑭𝑿(𝟑) = 𝟎 + (𝟎. 𝟖 − 𝟎) ∗ 𝟏
= 𝟎. 𝟖
Por consiguiente, el intervalo que contiene el identificador de la secuencia 𝟏 𝟑 es
[𝟎. 𝟔𝟓𝟔, 𝟎. 𝟖]. El tercer elemento es 𝟐, lo que resulta en las siguientes ecuaciones de actualizacion:
𝒖(𝟑)= 𝟎. 𝟔𝟓𝟔 + (𝟎. 𝟖 − 𝟎. 𝟔𝟓𝟔) ∗ 𝑭𝑿(𝟐) = 𝟎. 𝟔𝟓𝟔 + (𝟎. 𝟖 − 𝟎. 𝟔𝟓𝟔) ∗ 𝟎. 𝟖𝟐 = 𝟎. 𝟕𝟕𝟒𝟎𝟖
Y por lo tanto el intervalo que contiene la secuencia 𝟏 𝟑 𝟐 es [𝟎. 𝟕𝟕𝟏𝟐, 𝟎. 𝟕𝟕𝟒𝟎𝟖). Continuando con el último elemento, las ecuaciones de actualización dan lo siguiente:
𝒍(𝟒)= 𝟎. 𝟕𝟕𝟏𝟐 + (𝟎. 𝟕𝟕𝟒𝟎𝟖 − 𝟎. 𝟕𝟕𝟏𝟐) ∗ 𝑭𝑿(𝟎) = 𝟎. 𝟕𝟕𝟏𝟐 + (𝟎. 𝟕𝟕𝟒𝟎𝟖 − 𝟎. 𝟕𝟕𝟏𝟐) ∗ 𝟎. 𝟎
= 𝟎. 𝟕𝟕𝟏𝟐
𝒖(𝟒) = 𝟎. 𝟕𝟕𝟏𝟐 + (𝟎. 𝟕𝟕𝟒𝟎𝟖 − 𝟎. 𝟕𝟕𝟏𝟐) ∗ 𝑭𝑿(𝟏) = 𝟎. 𝟕𝟕𝟏𝟐 + (𝟎. 𝟕𝟕𝟒𝟎𝟖 − 𝟎. 𝟕𝟕𝟏𝟐) ∗ 𝟎. 𝟖 = 𝟎. 𝟕𝟕𝟑𝟓𝟎𝟒
𝑻̅𝑿(𝟏 𝟑 𝟐 𝟏) =𝒖
(𝟒)+ 𝒍(𝟒)
𝟐 =𝟎. 𝟕𝟕𝟑𝟓𝟎𝟒 + 𝟎. 𝟕𝟕𝟏𝟐
𝟐
= 𝟎. 𝟕𝟕𝟐𝟑𝟓𝟐
Generando una secuencia binaria
Para codificar el identificador se toma la representación binaria del número y se trunca a
𝒍(𝒙) = ⌈𝒍𝒐𝒈(𝟏 𝑷(𝒙)⁄ )⌉ + 𝟏
En donde 𝑷(𝒙) es la probabilidad de la secuencia. Ejemplo:
Considere la fuente 𝐴 que genera los símbolos 𝑨 = {𝒂𝟏, 𝒂𝟐, 𝒂𝟑, 𝒂𝟒} con probabilidades
𝑷(𝒂𝟏) = 𝟏 𝟐⁄ 𝑷(𝒂𝟐) = 𝟏 𝟒⁄ 𝑷(𝒂𝟑) = 𝟏 𝟖⁄ 𝑷(𝒂𝟒) = 𝟏 𝟖⁄
Se puede generar un código binario para esta fuente como se muestra en la tabla 3. La cantidad 𝑻̅̅̅𝒙 se obtiene usando la ecuación (𝟒. 𝟑). La representación binaria de 𝑻̅̅̅𝒙 se trunca a ⌈𝒍𝒐𝒈 (𝟏/𝑷(𝑿)) ⌉ + 𝟏 𝒃𝒊𝒕𝒔 para obtener el código binario.
Símbolo 𝑭𝑿 𝑻̅𝑿 En Binario ⌈𝒍𝒐𝒈𝟐(
𝟏
𝑷(𝒙))⌉ + 𝟏 Código
𝟏 . 𝟓 . 𝟐𝟓 . 𝟎𝟏𝟎 𝟐 𝟎𝟏
𝟐 . 𝟕𝟓 . 𝟔𝟐𝟓 . 𝟏𝟎𝟏 𝟑 𝟏𝟎𝟏
𝟑 . 𝟖𝟕𝟓 . 𝟖𝟏𝟐𝟓 . 𝟏𝟏𝟎𝟏 𝟒 𝟏𝟏𝟎𝟏
𝟒 𝟏. 𝟎 . 𝟗𝟑𝟕𝟓 . 𝟏𝟏𝟏𝟏 𝟒 𝟏𝟏𝟏𝟏
Tabla 3: Código binario para un alfabeto de 4 símbolos
Descifrando un identificador
Dado el identificador obtenido en el ejemplo anterior trataremos de imitar al codificador para obtener la secuencia representada por este identificador. El valor del identificador es
𝟎. 𝟕𝟕𝟐𝟑𝟓𝟐. El intervalo que contiene este identificador es un subconjunto de todos los intervalos contenidos en el proceso de codificación. La estrategia de decodificación será decodificar los elementos en la secuencia de tal manera que los limites inferior 𝒖(𝒌) 𝒚 𝒍(𝒌)
𝒍(𝟏) = 𝟎 + (𝟏 − 𝟎)𝑭𝑿(𝒙𝟏− 𝟏) = 𝑭𝑿(𝒙𝟏− 𝟏)
𝒖(𝟏) = 𝟎 + (𝟏 − 𝟎)𝑭𝑿(𝒙𝟏)
= 𝑭𝑿(𝒙𝟏)
En otras palabras, el intervalo que contiene el identificador es [𝑭𝑿(𝒙𝟏− 𝟏), 𝑭𝑿(𝒙𝟏)). Necesitamos encontrar el valor de 𝒙𝟏 para el cual 𝟎. 𝟕𝟕𝟐𝟑𝟓𝟐 está en el intervalo
[𝑭𝑿(𝒙𝟏− 𝟏), 𝑭𝑿(𝒙𝟏)). Si hacemos 𝒙𝟏 = 𝟏, el intervalo es [𝟎, 𝟎. 𝟖), Si hacemos 𝒙𝟏= 𝟐, el intervalo es [𝟎. 𝟖, 𝟎. 𝟖𝟐), Si hacemos 𝒙𝟏 = 𝟑, el intervalo es [𝟎. 𝟖𝟐, 𝟏). Como 𝟎. 𝟕𝟕𝟐𝟑𝟓𝟐
esta en el intervalo [𝟎, 𝟎. 𝟖) escogemos 𝒙𝟏= 𝟏. Repetimos este procedimiento para el segundo elemento 𝒙𝟐, usando los valores actualizados para 𝒍(𝟏) 𝒚 𝒖(𝟏)
𝒍(𝟐) = 𝟎 + (𝟎. 𝟖 − 𝟎)𝑭𝑿(𝒙𝟐− 𝟏) = 𝟎. 𝟖𝑭𝑿(𝒙𝟐− 𝟏)
𝒖(𝟐) = 𝟎 + (𝟎. 𝟖 − 𝟎)𝑭𝑿(𝒙𝟐)
= 𝟎. 𝟖𝑭𝑿(𝒙𝟐)
Si hacemos 𝒙𝟐= 𝟏, el intervalo actualizado es [0, 0.64), el cual no contiene el identificador. Luego 𝒙𝟐 no puede ser 𝟏. Si hacemos 𝒙𝟐= 𝟐, el intervalo actualizado es [0.64, 0.656), el cual tampoco contiene el identificador. Si hacemos 𝒙𝟐= 𝟑, el intervalo actualizado es [0.656, 0.8), el cual sí contiene el valor 𝟎. 𝟕𝟕𝟐𝟑𝟓𝟐 del identificador. Luego el segundo elemento en la secuencia es 𝟑. Sabiendo cual es el segundo elemento de la secuencia, podemos actualizar los valores de 𝒍(𝟐) y 𝒖(𝟐) y encontrar el elemento 𝒙𝟑, el cual nos dará un intervalo que contiene el identificador:
𝒍(𝟑) = 𝟎. 𝟔𝟓𝟔 + (𝟎. 𝟖 − 𝟎. 𝟔𝟓𝟔)𝑭𝑿(𝒙𝟑− 𝟏)
= 𝟎. 𝟔𝟓𝟔 + 𝟎. 𝟏𝟒𝟒𝑭𝑿(𝒙𝟑− 𝟏)
𝒖(𝟑) = 𝟎. 𝟔𝟓𝟔 + (𝟎. 𝟖 − 𝟎. 𝟔𝟓𝟔)𝑭𝑿(𝒙𝟑)
= 𝟎. 𝟔𝟓𝟔 + 𝟎. 𝟏𝟒𝟒𝑭𝑿(𝒙𝟑)
Sin embargo, las expresiones resultantes son cansonas en esta forma. Para hacer las comparaciones más fáciles, podriamos restar el valor de 𝒍(𝟐) tanto de los limites como del identificador. O sea, encontramos el valor de 𝒙𝟑 para el cual el intervalo [𝟎. 𝟏𝟒𝟒 ∗ 𝑭𝑿(𝒙𝟑− 𝟏), 𝟎. 𝟏𝟒𝟒 ∗ 𝑭𝑿(𝒙𝟑)) contiene 𝟎. 𝟕𝟕𝟐𝟑𝟓𝟐 − 𝟎. 𝟔𝟓𝟔 = 𝟎. 𝟏𝟏𝟔𝟑𝟓𝟐. O, podríamos hacerlo aún más simple y dividir el valor del identificador residual de 𝟎. 𝟏𝟏𝟔𝟑𝟓𝟐 por 𝟎. 𝟏𝟒𝟒
para obtener 𝟎. 𝟖𝟎𝟖, y encontrar el valor de 𝒙𝟑 para el cual 𝟎. 𝟖𝟎𝟖 cae en el intervalo
[𝑭𝑿(𝒙𝟑− 𝟏), 𝑭𝑿(𝒙𝟑)) . Inmediatamente vemos que el único valor de 𝒙𝟑 para el cual es posible esto es 𝟐. Substituyendo 𝟐 para 𝒙𝟑 en las ecuaciones de actualización, podemos hallar los nuevos valores de 𝒍(𝟑) 𝒚 𝒖(𝟑). Podemos ahora encontrar el elemento 𝒙
𝒍(𝟒) = 𝟎. 𝟕𝟕𝟏𝟐 + (𝟎. 𝟕𝟕𝟒𝟎𝟖 − 𝟎. 𝟕𝟕𝟏𝟐)𝑭𝑿(𝒙𝟒− 𝟏) = 𝟎. 𝟕𝟕𝟏𝟐 + 𝟎. 𝟎𝟎𝟐𝟖𝟖𝑭𝑿(𝒙𝟒− 𝟏)
𝒖(𝟒) = 𝟎. 𝟕𝟕𝟏𝟐 + (𝟎. 𝟕𝟕𝟒𝟎𝟖 − 𝟎. 𝟕𝟕𝟏𝟐)𝑭𝑿(𝒙𝟒)
= 𝟎. 𝟕𝟕𝟏𝟐 + 𝟎. 𝟎𝟎𝟐𝟖𝟖𝑭𝑿(𝒙𝟒)
Otra vez podemos restar 𝒍(𝟑) del identificador para conseguir 𝟎. 𝟕𝟕𝟐𝟑𝟓𝟐 − 𝟎. 𝟕𝟕𝟏𝟐 =
𝟎. 𝟎𝟎𝟏𝟏𝟓𝟐 y encontrar el valor de 𝒙𝟒 para el cual el intervalo [𝟎. 𝟎𝟎𝟐𝟖𝟖 ∗ 𝑭𝑿(𝒙𝟒− 𝟏), 𝟎. 𝟎𝟎𝟐𝟖𝟖 ∗ 𝑭𝑿(𝒙𝟒)) contiene a 𝟎. 𝟎𝟎𝟏𝟏𝟓𝟐. Para hacer las comparaciones más simples, podemos dividir el valor residual del identificador por 𝟎. 𝟎𝟎𝟐𝟖𝟖 para conseguir 𝟎. 𝟒 y encontrar el valor de 𝒙𝟒 para el cual 𝟎. 𝟒 está contenido en [𝑭𝑿(𝒙𝟒− 𝟏), 𝑭𝒙(𝒙𝟒)). Podemos ver que aquel valor es 𝒙𝟒 = 𝟏 y hemos decodificado la secuencia completa. Observe que nosotros sabíamos la longitud de la secuencia anticipadamente y, por lo tanto, sabíamos cuando parar.
El algoritmo de decodificación:
1. Inicialice 𝒍(𝟎) = 𝟎 𝒚 𝒖(𝟎)= 𝟏 𝒚 𝒕(𝟎) = 𝒕𝒂𝒈 𝒚 𝒌 = 𝟏
2. Para cada 𝒌 encuentre 𝒕(𝒌) = (𝒕(𝒌−𝟏)− 𝒍(𝒌−𝟏))/(𝒖(𝒌−𝟏)− 𝒍(𝒌−𝟏)) 3. Encuentre el valor de 𝒙𝒌 para el cual 𝑭𝑿(𝒙𝒌− 𝟏) ≤ 𝒕(𝒌) ≤ 𝑭𝑿(𝒙𝒌) 4. Actualice 𝒖(𝒌) 𝒚 𝒍(𝒌) 𝒆 𝒊𝒏𝒄𝒓𝒆𝒎𝒆𝒏𝒕𝒆 𝒌
5. Continúe en 2) hasta que la secuencia completa haya sido decodificada Hay dos maneras de saber que la secuencia completa ha sido decodificada:
El decodificador puede conocer la longitud de la secuencia Si un símbolo particular se denota como fin de transmisión.
Comparación con el código Huffman
Si se codifican los símbolos uno a la vez el código Huffman se comporta mejor que la codificación aritmética. Sin embargo a medida que se codifican secuencias más largas la codificación aritmética va mejorando (ver tabla 4).
¿Cuantas muestras tenemos que agrupar para hacer que el esquema de codificación aritmético se desempeñe mejor que el código Huffman? Podemos tener alguna idea mirando los límites en la rata de codificación.
Los límites en la longitud promedio de la codificación aritmética son
No toma muchos símbolos en una secuencia antes que la rata de codificación para el código aritmético llegue a estar cerca de la entropía. Sin embargo, recordando que para los códigos Huffman, si tomamos bloques de m símbolos juntos, la rata de codificación es
𝑯(𝑿) ≤ 𝒍𝑯≤ 𝑯(𝑿) + 𝟏 𝒎⁄
Mensaje 𝑃(𝑥) 𝑇̅𝑋(𝑥) 𝑇̅𝑋(𝑥) en binario ⌈𝑙𝑜𝑔 1
𝑃(𝑥)⌉ + 1 Código
𝟏𝟏 . 𝟐𝟓 . 𝟏𝟐𝟓 . 𝟎𝟎𝟏 𝟑 𝟎𝟎𝟏
𝟏𝟐 . 𝟏𝟐𝟓 . 𝟑𝟏𝟐𝟓 . 𝟎𝟏𝟎𝟏 𝟒 𝟎𝟏𝟎𝟏
𝟏𝟑 . 𝟎𝟔𝟐𝟓 . 𝟒𝟎𝟔𝟐𝟓 . 𝟎𝟏𝟏𝟎𝟏 𝟓 𝟎𝟏𝟏𝟎𝟏
𝟏𝟒 . 𝟎𝟑𝟐𝟓 𝟎. 𝟒𝟔𝟖𝟕𝟓 . 𝟎𝟏𝟏𝟏𝟏 𝟓 𝟎𝟏𝟏𝟏𝟏
𝟐𝟏 . 𝟏𝟐𝟓 𝟎. 𝟓𝟔𝟐𝟓 . 𝟏𝟎𝟎𝟏 𝟒 𝟏𝟎𝟎𝟏
𝟐𝟐 . 𝟎𝟔𝟐𝟓 . 𝟔𝟓𝟔𝟐𝟓 . 𝟏𝟎𝟏𝟎𝟏 𝟓 𝟏𝟎𝟏𝟎𝟏
𝟐𝟑 . 𝟎𝟑𝟏𝟐𝟓 . 𝟕𝟎𝟑𝟏𝟐𝟓 . 𝟏𝟎𝟏𝟏𝟎𝟏 𝟔 𝟏𝟎𝟏𝟏𝟎𝟏
𝟐𝟒 . 𝟎𝟑𝟏𝟐𝟓 . 𝟕𝟑𝟒𝟑𝟕𝟓 . 𝟏𝟎𝟏𝟏𝟏𝟏 𝟔 𝟏𝟎𝟏𝟏𝟏𝟏
𝟑𝟏 . 𝟎𝟔𝟐𝟓 . 𝟕𝟖𝟏𝟐𝟓 . 𝟏𝟏𝟎𝟎𝟏 𝟓 𝟏𝟏𝟎𝟎𝟏
𝟑𝟐 . 𝟎𝟑𝟏𝟐𝟓 . 𝟖𝟐𝟖𝟏𝟐𝟓 . 𝟏𝟏𝟎𝟏𝟎𝟏 𝟔 𝟏𝟏𝟎𝟏𝟎𝟏
𝟑𝟑 . 𝟎𝟏𝟓𝟔𝟐𝟓 . 𝟖𝟓𝟏𝟓𝟔𝟐𝟓 . 𝟏𝟏𝟎𝟏𝟏𝟎𝟏 𝟕 𝟏𝟏𝟎𝟏𝟏𝟎𝟏
𝟑𝟒 . 𝟎𝟏𝟓𝟔𝟐𝟓 . 𝟖𝟔𝟕𝟏𝟖𝟕𝟓 . 𝟏𝟏𝟎𝟏𝟏𝟏𝟏 𝟕 𝟏𝟏𝟎𝟏𝟏𝟏𝟏
𝟒𝟏 . 𝟎𝟔𝟐𝟓 . 𝟗𝟎𝟔𝟐𝟓 . 𝟏𝟏𝟏𝟎𝟏 𝟓 𝟏𝟏𝟏𝟎𝟏
𝟒𝟐 . 𝟎𝟑𝟏𝟐𝟓 . 𝟗𝟓𝟑𝟏𝟐𝟓 . 𝟏𝟏𝟏𝟏𝟎𝟏 𝟔 𝟏𝟏𝟏𝟏𝟎𝟏
𝟒𝟑 . 𝟎𝟏𝟓𝟔𝟐𝟓 . 𝟗𝟕𝟔𝟓𝟔𝟐𝟓 . 𝟏𝟏𝟏𝟏𝟏𝟎𝟏 𝟕 𝟏𝟏𝟏𝟏𝟏𝟎𝟏
𝟒𝟒 . 𝟎𝟏𝟓𝟔𝟐𝟓 . 𝟗𝟖𝟒𝟑𝟕𝟓 . 𝟏𝟏𝟏𝟏𝟏𝟏𝟏 𝟕 𝟏𝟏𝟏𝟏𝟏𝟏𝟏
Tabla 4: Codificación aritmética para secuencias de dos símbolos.
Aplicaciones
El estándar 𝑱𝑩𝑰𝑮 (𝑹𝒆𝒄𝒐𝒎𝒆𝒏𝒅𝒂𝒄𝒊ó𝒏 𝑰𝑻𝑼 − 𝑻 𝑻. 𝟖𝟐) (Joint Bi-level Image processing Group)
En este estándar se recomienda la codificación aritmética como parte de la codificación de imágenes binarias.
Este grupo se forma en 𝟏𝟗𝟖𝟖 para la codificación progresiva de imágenes de dos niveles. El estándar 𝑱𝑩𝑰𝑮 consta de dos algoritmos:
El algoritmo de transmisión progresiva El algoritmo de codificación sin pérdidas.
La compresión sin pérdidas:
Muchas imágenes bi_nivel tienen una gran cantidad de estructura local.
Por ejemplo en la transmisión de texto hay grandes porciones de la imagen en donde se encuentran píxeles blancos con probabilidad de ocurrencia cerca de uno. En otras porciones de imagen sucede lo contrario, hay grandes probabilidades de encontrar píxeles negros. Se pueden hacer suposiciones razonables de la situación para un determinado píxel conociendo los valores de los píxeles vecinos al píxel que está siendo codificado. Por ejemplo si la mayoría de los píxeles vecinos son blancos hay grandes probabilidades de que este también lo sea y viceversa.
Cada caso nos da una probabilidad asimétrica, lo que es ideal para la codificación aritmética. Si se trata cada caso separadamente usando un codificador aritmético diferente para cada una de las dos situaciones, se podría obtener una mejora sobre el caso donde usamos el mismo codificador aritmético para todos los píxeles.
Ejemplo:
Suponga que la probabilidad de encontrar un píxel negro es 𝟎. 𝟐 y la de encontrar un píxel blanco es 𝟎. 𝟖, la entropía en este caso es 𝑯(𝑺) = 𝟎. 𝟕𝟐𝟐
Si se usa un solo codificador para codificar esta fuente se conseguirá una rata de bit cercana a 𝟎. 𝟕𝟐𝟐 𝒃𝒊𝒕/𝒑í𝒙𝒆𝒍.
probabilidad de encontrar un píxel negro es 𝟎. 𝟕. La entropía de estos conjuntos es 𝟎. 𝟐𝟖𝟔 y
𝟎. 𝟖𝟖𝟏 respectivamente.
Si usamos dos codificadores aritméticos para los dos conjuntos con tablas de frecuencia acopladas a las probabilidades, conseguiríamos ratas cercanas a 𝟎. 𝟐𝟖𝟔 cerca del 𝟖𝟎% del tiempo y cercanas a 𝟎. 𝟖𝟖𝟏 cerca del 𝟐𝟎% del tiempo. La rata promedio sería cerca de
𝟎. 𝟒𝟎𝟓 𝒃𝒊𝒕𝒔/𝒑í𝒙𝒆𝒍 la cual es casi la mitad de la rata requerida si usáramos un solo codificador aritmético.
Si usamos solamente píxeles en la vecindad de aquellos que ya han sido transmitidos al receptor para hacer nuestra decisión acerca de cual codificador usar, el decodificador puede mantenerse informado acerca de cual codificador fue usado para codificar un píxel particular. La codificación aritmética es particularmente atractiva para el uso de codificadores múltiples, todos ellos usando la misma maquinaria computacional con cada codificador usando un conjunto diferente de probabilidades.
El algoritmo 𝑱𝑩𝑰𝑮 hace uso de esta característica de la codificación aritmética. En vez de chequear para ver si la mayoría de los píxeles en la vecindad son blancos o negros, el codificador 𝑱𝑩𝑰𝑮 usa el patrón de píxeles en la vecindad o contexto para decidir cuál conjunto de probabilidades usar en la codificación de un píxel particular (ver ilustración 2). Si la vecindad consiste de 𝟏𝟎 𝒑í𝒙𝒆𝒍𝒆𝒔 con cada píxel capaz de tomar uno de dos valores diferentes, el número de patrones diferentes posibles es 𝟏𝟎𝟐𝟒, el codificador 𝑱𝑩𝑰𝑮 usa de
𝟏𝟎𝟐𝟒 𝒂 𝟒𝟎𝟗𝟔 codificadores, dependiendo de si una capa de baja o alta resolución está siendo codificada.
Ilustración 2: Configuración de los vecinos en el estándar 𝑱𝑩𝑰𝑮
El píxel X es el que va a ser codificado, mientras que los que van a ser usados como templates (plantillas) son marcados como O o A, los cuales son previamente codificados y están disponibles tanto para el codificador como para el decodificador.
El píxel A puede pensarse como un miembro flotante de la vecindad. Su colocación es dependiente de la entrada que esta siendo codificada. Suponga que la imagen tiene líneas verticales separadas 𝟑𝟎 𝒑í𝒙𝒆𝒍𝒆𝒔. El pixel 𝑨 puede ser movido alrededor en orden a capturar cualquier estructura que pueda existir en la imagen. Esto es especialmente útil en las imágenes halftone en las que los pixeles 𝑨 son usados para capturar la estructura periódica. La ubicación y movimiento del pixel 𝑨 es transmitida al decodificador como información lateral.
En la siguiente ilustración 3 los símbolos en la vecindad han sido reemplazados por 𝟎𝒔 y
𝟏𝒔. El cero corresponde a píxeles blancos mientras que el uno corresponde a píxeles negros. El pixel a codificar esta encerrado en una caja sombreada.
Ilustración 3: contextos de (a) tres líneas, (b) dos líneas
El patrón de 0s y 1s es interpretada como un numero binario el cual es usado como un índice para el conjunto de probabilidades. El contexto en el caso de la vecindad de tres líneas (leyendo de izquierda a derecha y de arriba abajo) es 𝟎𝟎𝟎𝟏𝟎𝟎𝟎𝟏𝟏𝟎, el cual corresponde a un índice de 𝟕𝟎. Para la vecindad de dos líneas el contexto es 𝟎𝟎𝟏𝟏𝟏𝟎𝟎𝟎𝟎𝟏 o 𝟐𝟐𝟓. Como hay 𝟏𝟎 𝒃𝒊𝒕𝒔 en este template tendremos 𝟏𝟎𝟐𝟒 diferentes codificadores aritméticos.
En el estándar 𝑱𝑩𝑰𝑮 los 𝟏𝟎𝟐𝟒 codificadores son una variación del codificador aritmético conocido como el codificador QM.
En la descripción del codificador aritmético previa hemos estado actualizando el intervalo de identificador al actualizar los extremos del intervalo
u
n yl
n .De igual manera se podría haber mantenido un extremo y el tamaño del Intervalo. Esta es la aproximación adoptada en el codificador QM, el cual conserva el extremo inferior y el tamaño del intervalo
A
n
u
n
l
nSe puede obtener una ecuación de actualización de
A
n
n n n X n X n nx
P
A
x
F
x
F
A
A
1 11
1
1
1
n X n n nx
F
A
l
l
En vez de tratar directamente con 0s y 1s puestos por la fuente, el codificador QM los mapea en el símbolo más probable (MPS) y en el símbolo menos probable (LPS).
Si 0 representa un píxel negro y 1 representa un píxel blanco entonces en una imagen mayormente negra el 0 será el MPS y el uno el LPS.
Denotando la probabilidad de ocurrencia del LPS en el contexto C por
q
c y mapeando el MPS al subintervalo mas bajo la ocurrencia de un símbolo MPS resulta en las siguientes ecuaciones de actualización: n
n1l
l
c n nq
A
A
11
Mientras que la ocurrencia de un LPS resultara en las siguientes ecuaciones de actualización:
c n n nq
A
l
l
1
11
c n n
q
A
A
1Para hacer la implementación del codificador más simple el comité 𝑱𝑩𝑰𝑮 recomendó varias desviaciones del algoritmo de codificación estándar, evitando las multiplicaciones al asumir que
A
n tiene un valor cercano a uno lo que simplifica las ecuaciones de actualización tomandoA
n =1.Si
A
n cae por debajo de 0.75 se hace un proceso de reescalamiento hasta que el valor de n
A
sea mayor o igual a 0.75.reescalado al límite inferior. Los bits que salen fuera del buffer que contiene el valor del límite inferior constituyen la salida del codificador.
Mirando las ecuaciones de actualización para el codificador QM podemos ver que la rescalizacion ocurrirá cada vez que ocurre un LPS. La ocurrencia de un MPS podrá o no resultar en un re escalamiento dependiendo del valor de
A
n .La probabilidad
q
c del LPS para el contexto C se actualiza cada vez que el reescalamiento toma lugar y el contexto C es activo. Una lista ordenada de valores es hecha en una tabla parac
q
. Cada vez que tiene lugar un reescalamiento el valor deq
c es cambiado al próximo valor más bajo o más alto en la tabla dependiendo de si el reescalamiento fue causado por la ocurrencia de un LPS o de un MPS.En una situación no estacionaria puede suceder que el símbolo asignado al LPS ocurra más frecuentemente que el símbolo asignado al MPS lo cual es detectado cuando
q
c
A
n
q
c . En esta situación se reversa la asignación. Esta prueba debe realizarse cada vez que una rescalizacion toma lugar.El decodificador QM opera de manera similar al codificador descrito. La transmisión progresiva
Busca poder transmitir imágenes de más baja resolución utilizando menos bits.
El estándar 𝑱𝑩𝑰𝑮 recomienda generar un píxel de más baja resolución por cada bloque de 2*2 en la imagen de más alta resolución. El número de imágenes de más baja resolución (llamadas capas) no se especifica en el estándar.
Un método directo para generar una capa de más baja resolución es reemplazar cada bloque de 2*2 con el valor promedio de los cuatro píxeles, reduciendo la resolución por dos en las direcciones vertical y horizontal. El problema es cuando la mitad de los píxeles es blanco y la mitad negra.
Ilustración 4: pixeles utilizados para determinar el valor del pixel de más bajo nivel
Los círculos representan los píxeles de la capa de más baja resolución y los cuadrados representan los píxeles de la capa de más alta resolución.
Cada píxel contribuye un poco al índice. La tabla se forma calculando la expresión
b
d
f
h
a
c
g
i
B
C
A
e
2
3
4
Si el valor de esta expresión es mayor a 4.5 el píxel X es tentativamente declarado 1. Las imágenes de más baja resolución pueden ser usadas para codificar las imágenes de más alta resolución. La especificación 𝑱𝑩𝑰𝑮 hace esto usando los píxeles de más baja resolución como parte del contexto para codificar las imágenes de más alta resolución (ver ilustración 5).
Se usan diez píxeles en cada contexto. Si se incluyen los 2 bits requeridos para indicar el t𝑒𝑚𝑝𝑙𝑎𝑡𝑒 que está siendo usado, se usaran 12 bits para indicar el contexto, lo cual indica que habrá 4096 contextos diferentes.
El desempeño de la codificación aritmética se puede observar en las tablas 5 y 6 obtenidas a partir de la codificación de las imágenes de la ilustración 6.
Ilustración 6: imágenes usadas para la codificación aritmética.
Imagen Bits/pixel Tamaño (bytes)
Rata de compresión (aritmética)
Rata de compresión (Huffman)
Sena 6.52 53431 1.23 1.16
Sensin 7.12 58306 1.12 1.27
Tierra 4.67 38248 1.71 1.67
Omaha 6.84 56061 1.17 1.14
Imagen Bits/pixel Tamaño (bytes)
Rata de compresión (aritmética)
Rata de compresión (Huffman)
Sena 3.89 31847 2.06 2.08
Sensin 4.56 37387 1.75 1.73
Tierra 3.92 32137 2.04 2.04
Omaha 6.27 51393 1.28 1.26