2012
–
2013
Índice
Plano tangente
1
Planos tangentes a superficies
1
Aproximación lineal a una función f
(
x,
y
)
4
La diferencial total
5
La función diferencial total
5
Funciones de más de dos variables
6
Trabajo práctico
7
Ejemplos con Sage
8
Planos tangentes y aproximación lineal
8
Plano tangente
Planos tangentes a superficies
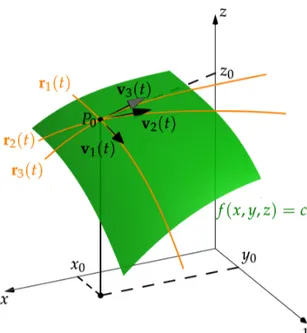
Figura1: dada una superficie de nivel f(x,y,z) = c, todas las curvas suavesr(t), sobre la superficie de nivel, y que pa-san por el puntoP0(x,0,y0,z0),
tendrán vectores tangentes
Curvas sobre una superficie de nivel f(x,y,z) =c
f(x,y,z) =ces una superficie de nivel de una funciónderivable
f.
r1(t),r2(t)yr3(t)son curvassuaves, sobre f(x,y,z) = c, que pasan por P0.
v1(t),v2(t)yv3(t)sonsiempretangentes a las curvas, porque
v1(t) = ddtr1, etc.
El gradiente∇f es normal a todas las tangentesv(t)
En general las curvas seránr(t) =g(t)i+h(t)j+k(t)k.
Sobre la superficie de nivel tendremos f g(t),h(t),k(t) =c
Derivando ambos lados de la ecuación queda
d
dtf g(t),h(t),k(t)
= d dt(c) d f
dx dg dt +
d f dy
dh dt +
d f dz
dk dt =0 d f
dxi+ d f dyj+
d f dzk
| {z }
∇f
·
dg
dti+ dh dtj+
dk dtk
| {z }
v(t)=dr/dt
=0
Entonces, en cada punto de la curva,∇f es ortogonal al vector velocidad.
Figura2: dada una superficie de nivel f(x,y,z) = c, el plano
tangente porP0tiene vector
El plano tangente a la superficie de nivel f(x,y,z) =c
Definición1. Elplano tangente a la superficie de nivel f(x,y,z) =c, en
P0, es normal al vector(∇f)P0.
Entonces una ecuación del plano será
fx(P0)(x−x0) +fy(P0)(y−y0) + fz(P0)(z−z0) =0 Ejemplo1. Obtener el plano tangente a la superficie
f(x,y,z) =x2+y2+z−9=0 (una paraboloide circular) en el puntoP0(1, 2, 4)
1. El plano tangente pasará porP0y será perpendicular al gradien-te de f enP0. El gradiente es
(∇f)P0 = 2xi+2yj+k
(1,2,4)=2i+4j+k 2. Por lo tanto, el plano tangente será
2(x−1) +4(y−2) +1(z−4) =0 2x+4y+z=14
Figura3: dada la funciónw =
f(x,y,z) = x2 +y2+z−9,
su superficie de nivelx2+y2+ z−9 = 0 tiene plano tangen-te 2x+4y+z =14 en el punto
P0(1, 2, 4). Plano tangente al gráfico de z= f(x,y)
1. Ahora queremos obtener el plano tangente al gráfico dez =
f(x,y), en un puntoP0(x0,y0,z0)conz0= f(x0,y0). 2. La ecuación f(x,y) =zes equivalente a f(x,y)−z=0.
3. Esto quiere decir quez= f(x,y)es lasuperficie de nivel cerode la funciónF(x,y,z) = f(x,y)−z.
4. Las derivadas parciales deFson
Fx= ∂
∂x f(x,y)−z
= fx−0= fx
Fy= ∂
∂y f(x,y)−z
= fy−0= fy
Fz= ∂
∂z f(x,y)−z
=0−1=−1
5. La ecuación del plano tangente
Fx(P0)(x−x0) +Fy(P0)(y−y0) +Fz(P0)(z−z0) =0
se simplifica entonces a
fx(x0,y0)(x−x0) +fy(x0,y0)(y−y0) + (−1)(z−z0) =0
Definición2. Elplano tangente al gráfico z = f(x,y)de una función derivable f en el puntoP0(x0,y0,z0) = x0,y0,f(x0,y0)es
Ejemplo2. Encontrar el plano tangente a la superficiez= xcosy−
yexen el punto(0, 0, 0).
1. Las derivadas parciales de f(x,y)son
fx(0, 0) = (cosy−yex)(0,0)=1−0·1=1 fy(0, 0) = (−xsiny−ex)(0,0)=0−1=−1
2. Entonces el plano tangente es
1·(x−0)−1·(y−0)−(z−0) =0 x−y−z=0
Aproximación lineal a una función f
(
x,
y
)
¿Para qué linealizar una función f(x,y)?
Las funciones de dos variables f(x,y)pueden ser complicadas. . . A veces necesitamos reemplazarlas por otras funciones, más simples, que den una precisión requerida.
Cualquier función f(x,y)puede seraproximadao reemplazada siemprepor una función simpleL(x,y).
Sin embargo, esta aproximación introduciráun error.
Siempre y cuando trabajemos con la función L(x,y)adecuada, ¡el error será tan pequeño que no nos importará!
x y
(x0,y0)
(x0+∆x,y0+∆y)
∆x=x−x0
∆
y
=
y
−
y0
Figura4: si f es derivable en
(x0,y0), entonces el valor de f en cualquier punto cercano
(x,y)es aproximadamente
f(x0,y0) + fx(x0,y0)(x−x0) + fy(x0,y0)(y−y0).
Linealización de f(x,y)
Tenemos una función f(x,y)complicada.
Elegimos un punto fijo(x0,y0)del dominio de f.
Definición3. Lalinealizaciónde una función f(x,y)en un punto (x0,y0)donde f es derivablees la función
L(x,y) = f(x0,y0) + fx(x0,y0)(x−x0) + fy(x0,y0)(y−y0)
Entonces
f(x,y)≈L(x,y)
es laaproximación linealde f en el punto(x0,y0).
Observaciones acerca de la función L(x,y)
El gráficoz= L(x,y)es
z= f(x0,y0) +fx(x0,y0)(x−x0) + fy(x0,y0)(y−y0) z=z0+fx(x0,y0)(x−x0) +fy(x0,y0)(y−y0)
0= (z0−z) +fx(x0,y0)(x−x0) +fy(x0,y0)(y−y0)
La ecuación del plano tangente a f(x,y)en(x0,y0)es
0= fx(x0,y0)(x−x0) + fy(x0,y0)(y−y0)−(z−z0)
¡Entonces la función aproximadaL(x,y)es igual al plano tangen-te a f(x,y)en(x0,y0)!
Entonces elerror de aproximaciónserá cada vez más pequeño a
medida que(x,y)→(x0,y0).
Ejemplo3. Encontrar la aproximación lineal de la función f(x,y) =
x2−xy+1/2y2+3 en el punto(3, 2).
1. Primero evaluamos f, fx, fyen el punto(x0,y0) = (3, 2)
f(3, 2) =x2−xy+1/2y2+3
(3,2)=8 fx(3, 2) = ∂
∂x
x2−xy+1/2y2+3
(3,2)= (2x−y)(3,2)=4 fy(3, 2) = ∂
∂y
x2−xy+1/2y2+3
(3,2)= (−x+y)(3,2)=−1 2. Entonces la aproximación lineal queda
L(x,y) = f(x0,y0) + fx(x0,y0)(x−x0) +fy(x0,y0)(y−y0)
=8+4·(x−3) + (−1)·(y−2) =4x−y−2
La diferencial total
La función diferencial total
Diferencia en en valor de f(x,y)Tenemos una función f(x,y).
Supongamos que f, fx, fypueden calcularse en un punto(x0,y0).
Si nos movemos a un punto cercano(x0+∆x,y0+∆y), la diferen-ciaen el valor de la función será
∆f = f(x0+∆x,y0+∆y)−f(x0,y0) Diferencia en el valor de L(x,y)
Haciendo un cálculo sencillo, para la función linealizadaL(x,y)
quedará
∆L=L(x0+∆x,y0+∆y)−L(x0,y0)
= fx(x0,y0)∆x+fy(x0,y0)∆y
Con frecuencia se dice que losdiferenciales dxydyson
La diferencial total d f
Definición4. Si nos movemos de un punto(x0,y0)a un punto
cercano(x0+dx,y0+dy), el cambio resultante en el valor de f d f = fx(x0,y0)dx+fy(x0,y0)dy
se llamadiferencial total de f.
Entonces la diferencial total es la función decuatro variables inde-pendientes d f(x0,y0,dx,dy).
Ejemplo4. Se diseño una lata cilíndrica para tener un radior = 10 cm y una alturah=50 cm.
Pero resultó que el radiory la alturahtienen un errordr= +0,2 cm ydh=−1 cm.
Calcular el cambio absoluto en el volumen de la lata. 1. Para estimar el cambio enV(r,h) =πr2husamos
∆V≈dV =Vr(r0,h0)dr+Vh(r0,h0)dh
2. ConVr(r,h) =2πrhy conVh(r,h) =πr2nos queda
dV=2πr0h0dr+πr20dh=2π·10·50·0,2+π·102·(−1)
=200π−100π=100π≈314 cm3
Funciones de más de dos variables
La aproximación lineal y la diferencial total de f(x,y,z)
Definición5. Laaproximación linealde f(x,y,z)en el puntoP0(x0,y0,z0)
es
L(x,y,z) = f(P0) +fx(P0)(x−x0) + fy(P0)(y−y0) +fz(P0)(z−z0)
Definición6. Si las segundas derivadas parciales de f son
conti-nuas, y six,y,zse cambian desdex0,y0,z0en pequeñas cantidades dx,dy,dz, entonces ladiferencial total
d f = fx(P0)dx+fy(P0)dy+fz(P0)dz
nos dará una buena aproximación del cambio resultante en f.
Ejemplo5. Obtenga la aproximación linealL(x,y,z)de
f(x,y,z) =x2−xy+3 sinz
en el punto(x0,y0,z0) = (2, 1, 0).
1. Luego de calcular las tres derivadas parciales primeras de f nos quedará
f(2, 1, 0) =2 fx(2, 1, 0) =3 fy(2, 1, 0) =−2 fz(2, 1, 0) =3 2. Por lo tanto
Trabajo práctico
1. En cada caso, encuentre la ecuación del plano tangente a la su-perficie indicada en el puntoP0.
a) x2+y2+z2=3 P
0(1, 1, 1)
b) 2z−x2=0 P
0(2, 0, 2)
c) cosπx−x2y+exz+yz=4 P0(0, 2, 2)
d) x+y+z=1 P0(0, 1, 0)
2. En cada caso, encuentre la ecuación del plano tangente al gráfico de la función indicada, en el punto especificado.
a) z=ln x2+y2
(1, 0, 0)
b) z=e−(x2+y2) (0, 0, 1)
c) z=√y−x (1, 2, 1)
d) z=4x2+y2 (1, 1, 5)
3. En cada caso, obtenga la aproximación linealL(x,y)de la fun-ción en los dos puntos indicados.
i) f(x,y) =x2+y2+1 a)(0, 0) b)(1, 1) ii) f(x,y) = (x+y+2)2 a)(0, 0) b)(1, 2) iii) f(x,y) =excosy a)(0, 0) b)(0,π/2)
iv) f(x,y) =e2y−x a)(0, 0) b)(1, 2)
4. En cada caso, obtenga la aproximación linealL(x,y,z)de la función en los tres puntos indicados.
i) f(x,y,z) =xy+yz+xz a)(1, 1, 1) b)(1, 0, 0) c)(0, 0, 0) ii) f(x,y,z) =px2+y2+z2 a)(1, 0, 0) b)(1, 1, 0) c)(1, 2, 2) iii) f(x,y,z) = sinxy
z a)(π/2, 1, 1) b)(2, 0, 1)
Ejemplos con Sage
.
El código Sage en los siguientes recuadros puede ser seleccionado, copiado y pegado en una hoja de trabajo de Sage, para ejecutarlo y así obtener los resultados y los gráficos.Planos tangentes y aproximación lineal
Ecuación del plano tangente a f(x,y,z) =0
# definir f(x,y,z) =cosπx−x2y+exz+yz−4
# la superficie es f(x,y,z) =0
f(x,y,z)=cos(pi*x)-x*x*y-exp(x*z)+y*z-4
show(f)
# calcular el gradiente de f
fx = f.diff(x); fy = f.diff(y); fz = f.diff(z); x0 = 0; y0 = 2; z0 = 2
P0 = vector((x0,y0,z0)) show(P0)
A = fx(x0,y0,z0); B = fy(x0,y0,z0) C = fz(x0,y0,z0)
plano = A*(x-x0)+B*(y-y0)+C*(z-z0)==0
show(plano)
.
Puede utilizar estos ejemplos de código Sage como base para compro-bar los resultados de los ejercicios del trabajo práctico.Ecuación del plano tangente a z= f(x,y)
# definir f(x,y) =4x2+y2
# la superficie es z= f(x,y)
f(x,y)=4*x*x+y*y
# calcular el gradiente de f
fx = f.diff(x); fy = f.diff(y) show(f)
x0 = 1; y0 = 1
z0 = f(x0,y0)
P0 = vector((x0,y0,z0)) show(P0)
A = fx(x0,y0); B = fy(x0,y0); C = -1
plano = A*(x-x0)+B*(y-y0)+C*(z-z0)==0
show(plano)
Calcular la aproximación lineal L(x,y)en(x0,y0)
# definir f(x,y) =x3y4
f(x,y)=x**3*y**4
# calcular el gradiente de f
fx = f.diff(x); fy = f.diff(y) show(f)
x0 = 1; y0 = 1
P0 = vector((x0,y0)) show(P0)
z0 = f(x0,y0)
# definir la aproximación lineal