EXPERIMENTAÇÃO NUMÉRICA NO FENÔMENO DE VAPORIZAÇÃO RETRÓGRADA DUPLA: UM ESTUDO SOBRE A CURVA CRÍTICA DO SISTEMA NÃO LINEAR Libotte G  B

12º CONGRESSO IBEROAMERICANO DE ENGENHARIA MECANICA

Guayaquil, 10 a 13 de Novembro de 2015

EXPERIMENTAÇÃO NUMÉRICA NO FENÔMENO DE VAPORIZAÇÃO

RETRÓGRADA DUPLA: UM ESTUDO SOBRE A CURVA CRÍTICA DO SISTEMA

NÃO-LINEAR

Libotte, G. B.*, Platt, G. M.º

*º Universidade do Estado do Rio de Janeiro, Brasil *e-mail: gustavolibotte@gmail.com

Palavras-chave: Vaporização retrógrada dupla, Equilíbrio de fases, Curva crítica, Sistema de equações não-lineares, Método de Newton

RESUMO

INTRODUÇÃO

Com a expansão da indústria do petróleo e a necessidade cada vez maior de novos recursos no ramo da engenharia, a procura por soluções robustas e eficientes que possam otimizar a produção se faz cada vez mais necessária. Uma área muito explorada nesse sentido é a do estudo de fluidos supercríticos, pois muitas aplicações industriais envolvem a diluição de solutos em solventes desse tipo. O conhecimento aprofundado de propriedades termodinâmicas, a compreensão de comportamentos próximos a regiões críticas e a capacidade de predição de fenômenos físicos são de extrema importância. Nesse contexto, um fenômeno termodinâmico com características muito peculiares e que apresenta comportamento totalmente não-linear é a vaporização retrógrada dupla.

Essa particularidade é caracterizada em misturas que normalmente encontram-se em altas faixas de pressão e para uma pequena porção da composição do sistema em questão, porém pode causar a redução da solubilidade do componente menos solúvel e não possui efeito adverso na solubilidade do componente mais solúvel da mistura. Dessa forma, o fenômeno da vaporização retrógrada dupla pode ser utilizado para aumentar a eficiência de extrações supercríticas de fluidos, como mostrado por [1].

Ainda de acordo com [1], a vaporização retrógrada dupla é um fenômeno que ocorre próximo a pontos críticos de misturas muito diluídas compostas por um soluto não volátil e um solvente volátil com grande diferença molecular entre eles. No problema de coexistência de fases, essa característica resulta em um comportamento de domo duplo, o que produz quatro pontos de orvalho para uma dada fração molar e pressão. Em sistemas binários, essa característica surge no instante em que a temperatura da mistura alcança uma faixa superior a temperatura crítica do solvente, no entanto a vaporização retrógrada dupla também pode ocorrer em temperaturas abaixo da temperatura crítica do solvente puro, quando as curvas do ponto de bolha e orvalho se aproximam, passando a ter o comportamento de uma substância pura.

Descrito inicialmente por [2], nesse trabalho serão analisadas as características relacionadas ao fenômeno de vaporização retrógrada dupla no sistema binário composto por etano + limoneno. Esse problema é representado por um sistema de equações algébricas não-lineares e resolvido a partir do método de Newton (com a contribuição de algumas estratégias de amortecimento) e a utilização de diferenças divididas finitas centradas como aproximação para o cálculo das derivadas. A equação de estado de Peng-Robinson com as regras clássicas de mistura de van der Waals mostram-se absolutamente capazes de predizer tal comportamento no cálculo do equilíbrio de fases da mistura.

Outro aspecto a ser apresentado, também em relação ao sistema composto por etano + limoneno, é a criação da curva crítica do problema. Nesse caso específico, os pontos críticos são os quais a matriz Jacobiana do sistema não-linear não são invertíveis. Cada um desses pontos é calculado através de um método de Newton após identificadas mudanças de sinal no cálculo do determinante da matriz Jacobiana do sistema. A curva crítica é, portanto, construída através de um método de continuação, análoga a metodologia utilizada em [3].

MODELO TERMODINÂMICO E DETERMINAÇÃO DO PROBLEMA

Para o cálculo do equilíbrio líquido-vapor da mistura será utilizada a equação de estado de Peng-Robinson [4], assim como realizado em [5, 6]. Na sua forma explícita em relação a pressão, a equação de estado de Peng-Robinson é dada por

) ( )

( m m m

m

b V b b V V

a b

V RT P

    

 . (1)

Como mencionado por [4], o parâmetro a_m é a medida da força de atração intermolecular e b_mestá relacionado ao tamanho molecular dos componentes da mistura. Tais valores são obtidos através das propriedades críticas dos componentes puros, calculados por

a P

T R a

i i c

c i

2 2

45724 . 0

 e

i i c

c i

P RT

O termo de correção  é uma função adimensional que depende de T_R e . Considerando que T_R T T_c, então  é calculado através de





[

1



k

(

1



T

_R

)]

2, com k0.374641.54226i0.26992i2.

Quando a Eq. (1) é utilizada para o cálculo do equilíbrio de fases de uma mistura, como é o caso deste estudo, é conveniente aplicar-se as regras clássicas de mistura de van der Waals. Com isso, para uma mistura de c componentes, os parâmetros a_m e b_m são definidos por



  c i j i ij m a xx

a 1 e



  c i i i m bx

b

1

, (3)

onde a_ij é uma média geométrica definida como a_ij  a_i_ia_j_j



1k_ij



. Por sua vez, o coeficiente empírico ij

k é um parâmetro de mistura binário associado a interação intermolecular entre um par distinto de moléculas. De acordo com [4], o uso desse parâmetro traz melhorias significativas ao grau de predição da equação de estado, porém o seu descarte não traz prejuízos ao resultado final dos cálculos, de fato. Portanto, o seu uso foi desconsiderado na abordagem em questão.

Após calculados os parâmetros da mistura referentes à Eq. (3), é possível obter os termos que constituem os coeficientes da forma polinomial da equação de estado de Peng-Robinson, os quais são definidos por

2 2 T R P a A m e

RT P b

B m

.

(4)

A forma polinomial da equação de estado de Peng-Robinson é, portanto, dada por



1



2



2 3 2

 

2 3



0

3_{        }

B B AB Z B B A Z B

Z , (5)

com ZPV RT. Então, a Eq. (5) pode ser resolvida e três raízes serão obtidas. No caso estudado, se todas as raízes calculadas forem reais, a de menor magnitude é referente ao fator de compressibilidade da fase líquida e a maior delas está relacionada a fase vapor. A raiz intermediária não possui significância física.

De posse das raízes calculadas a partir da Eq. (5), é possível obter os coeficientes de fugacidade de cada um dos componentes do sistema computado pela equação de estado de Peng-Robinson com o auxílio das regras de mistura de van der Waals por

 











_



_

_                           B Z B Z b b a a x B A B Z Z b b m i m c j j ij m i i 2 1 2 1 ln 2 2 ln 1 ˆ

ln 1 . (6)

Problema do cálculo de ponto de orvalho

Especificando uma temperatura e fração molar para a fase líquida do sistema, o problema de cálculo de ponto de orvalho objetiva encontrar a pressão e a composição da fase vapor coexistindo em equilíbrio com a fase líquida da mistura. Sabendo que

P z

fˆi ˆi i , (7)

a coexistência de fases em um sistema não reativo de c componentes acarreta no sistema de equações algébricas não-lineares de equilíbrio

   

ˆ ln ˆ 0

ln  iL 

V

i f

parai1,,c, além das restrições de somas unitárias 1 1

c

i xi e 1 1 c

i yi . Os sobrescritos L e V se referem às fases  , líquida e vapor respectivamente. Simplificando o termo da pressão em ambos os lados da Eq. (7), podemos reescrevê-la como

   

ˆ ln ˆ 0

ln  i 

L i i V

i y  x



.

(9)

Portanto, temos c2 equações para um sistema termodinâmico de 2c2 variáveis



xi,yi,TeP



. Com

isso, especificando a temperatura T e c1composições da fase vapor y_i, o sistema, composto pelas Eq. (8) e as restrições de somas unitárias, não possui graus de liberdade. Para um sistema binário, neste caso composto por etano + limoneno, espeficicando-se a fração molar de um dos componentes na fase vapor e a temperatura do sistema é possível calcular a composição líquida e a pressão no problema de ponto de orvalho, haja vista que as frações molares são complementares em sistemas binários.

As variáveis do problema de ponto de orvalho podem ser representadas, portanto, na forma vetorial por



x1,x2, ,xc1,P



 

 . Se considerarmos xc 1ic_11xie  

 11

1 ci i

c y

y , teremos apenas c equações de equilíbrio e o problema toma sua forma final como

 

















                       

 1 11

1 1 1 2 2 2 2 1 1 1 1 1 ˆ ln 1 ˆ ln ) ˆ ln( ) ˆ ln( ) ˆ ln( ) ˆ ln( c i i L c i i V L V L V x y x y x y F         (10)

Assim sendo, o problema a ser resolvido consiste em encontrar os zeros da função descrita pela Eq. (10), ou seja,

 

 0

F .

Quando as composições líquida e vapor estão na mesma proporção, os coeficientes de fugacidade também são iguais para ambas as fases. Tem-se, nesses casos, a solução trivial para o sistema não-linear (solução sem relevância física). Situação semelhante ocorre quando as frações molares se aproximam de zero ou de um, ou seja, quando o sistema passa a ter somente um elemento constituinte.

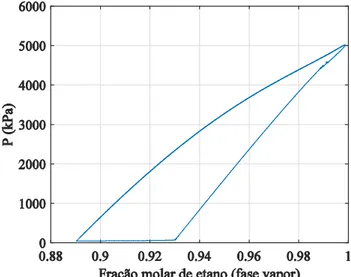
Como dito anteriormente, os resultados obtidos neste trabalho são referentes à mistura binária composta por etano + limoneno. Essa mistura apresenta o fenômeno de vaporização retrógrada dupla para composições próximas ao etano puro, mais precisamente quando yetano 0.998966e T 307.4K, ou seja, T Tc. Nessas condições, o sistema apresenta um comportamento de domo duplo, como pode ser observado na Fig. 1. As propriedades críticas e fator acêntrico do etano e limoneno são, respectivamente Tc(K)



305.3,660



,



4872,2750



) (kPa 

Pc e 



0.1,0.313



.

Para uma pequena porção da fração molar do etano na fase vapor, compreendida no intervalo

998992 . 0 998961

.

0  yetano aproximadamente, a curva apresenta quatro interseções, indicando que o problema apresenta quatro mínimos globais, ou seja, as quatro raízes do problema de ponto de orvalho. Essas raízes estão listadas na Tab. (1).

Tabela 1: Raízes do problema de ponto de orvalho

o e

x tan Pressão (kPa)

0.1567 619.24

0.9829 4859.5

0.9918 4931.2

Fig. 1: Comportamento de domo duplo do problema de ponto de orvalho

ASPECTOS DA CURVA CRÍTICA E RESULTADOS

A obtenção da curva crítica é parte essencial na resolução do problema da Eq. (10) com o método de inversão de funções do plano no plano, referido em [7]. O procedimento para o seu cálculo se inicia com a procura de pontos consecutivos em uma malha quadrangular nos quais os sinais do determinante nesses pontos sejam distintos.

Algoritmo 1: Pontos com inversão de sinal na malha de determinantes

1: funçãoCurvaCritica( )

2: nTamanho da malha

3: x₁Faixa de procura da fração molar 4: PFaixa de procura da pressão 5: matDetMatriz de determinantes 6: para i1até n faça

7: para j1 até n faça

8: matDet(i,j)det





x1(i),P(j)





det denota o determinante da matriz

9: fim para 10: fim para

11: CMatriz que armazena parte da curva 12: curvaCritMatriz da curva crítica 13: para i1até n faça

14: para j1 até n1 faça

15: se sign



matDet

 

i,j



sign



matDet



i,j1





então sign denota a função sinal 16: x₁*Newton





x1

   

i,P j





17: CCalculaCurvaCritica





x ,1* P

 

j





18: curvaCrit

 

i,j C

19: fim se

20: fim para 21: fim para

22: retorna curvaCrit

Algoritmo 2: Cálculo da curva crítica

1: função CalculaCurvaCritica(r) 2: passoTamanho do incremento 3: r0 r

4: r_{t }







J

 

r



x 



J

 

r



T



t

     

 det det

0 1

1 0

1 J denota a matriz Jacobiana

5: r1r



passort



6: flag10

7: enquanto flag10 faça

8: nsec



2passo



r₀r₁





norm



r₀r₁



norm denota a norma Euclidiana 9: flag2 0

10: cont0

11: enquanto flag2 0 e contn1 faça 12: qr0nsec

13: _

  

 

     

 



 sec

0 1

1 0

n q

q_a

14: _

  

 

        

 sec

0 1

1 0

n q

q_b

15: se sign



det



J

 

q_a





sign



det



J

 

q_b





então

16: flag2 1

17: senão

18: nsecnsec 2

19: fim se

20: contcont1

21: fim enquanto 22: se contn₂ então 23: t



0 1



24: se det



J

 

qa



det



J

 

q



0então

25: mqa

26: senão

27: mq_b

28: fim se

29: nq

30: rk 





1tk



m

 

 tkn



31: t_mCalculaRaiz

 

r_k

32: r





1tm



m

 

 tmn



33: C

 

i,j r

34: r1r0

35: r0 r

36: senão

37: flag11

38: fim se 39: fim enquanto 40: retorna C

Quando detectadas, essas coordenadas servem de ponto de partida para o cálculo de cada uma das partes que compõem a curva crítica como um todo. Esse mecanismo é repetido até que todos os pontos da malha com inversão de sinal sejam detectados e a curva crítica possa ser construída através da composição de todas as partes calculadas separadamente, como mostra o Alg. 1.

Para o cálculo de cada um dos segmentos que estruturam a curva crítica, primeiro é computado o vetor rt, tangente ao ponto r, rotando-se o vetor gradiente pertinente ao determinante da matriz Jacobiana. Em seguida, esse vetor tangente é utilizado para realizar o cálculo de um ponto “quase crítico”, denotado por r₁.

A obtenção da curva crítica propriamente dita é feita a partir de uma método preditor-corretor. Na etapa preditora, é calculado o vetor secante nsec, que por sua vez é utilizado para obter o ponto q e consequentemente os vetores q_a e q_b, que se tratam do próprio vetor q rotado em 90 para direções opostas, como pode ser observado no Alg. 2. Com isso, se os sinais do determinante da matriz Jacobiana de q_a e q_b não forem distintos, o vetor secante é refinado. O processo se repete até que os sinais do determinante da matriz Jacobiana de q_a e q_b sejam diferentes ou, como essa não é uma condição com ocorrência obrigatória, até que a etapa atinja uma quantidade predefinida de iterações. Na etapa corretora, dois pontos m e n são selecionados, novamente de acordo com o sinal do determinante da matriz Jacobiana de q_a e q_b. O algoritmo, então, calcula um ponto crítico no segmento entre m e n . Para esse cálculo, é computada a raiz do segmento em questão. Na abordagem realizada em [8], foi utilizado o método de Van Wijngaarden-Dekker-Brent, que combina os métodos da bisseção, da secante e interpolação quadrática inversa. Na presente abordagem, é importante salientar que apenas o método da bisseção foi utilizado e, apesar de ser uma técnica simples, mostrou-se suficiente na obtenção de todos os resultados.

A porção da curva crítica calculada é armazenada e a etapa corretora é repetida até que toda a parcela da curva crítica referente ao segmento entre m e n seja computada. Cada uma das frações da curva crítica calculadas, referente a cada um dos pontos detectados na malha quadrangular, é armazenada até que toda a curva seja produzida. Os conceitos mais aprofundados da metodologia podem ser encontrados em [9], assim como uma de suas aplicações, abordada por [8].

A curva crítica computada foi explorada no intervalo 0x1, como pode ser comprovado na Fig. 2. No entanto, esse fato não descarta a possibilidade de haver outras curvas críticas para o mesmo problema fora desse intervalo. Todavia, mesmo que seja uma possibilidade matemática plausível, o problema físico em questão só se aplica para frações molares que possibilitem a coexistência de substâncias na mistura binária.

Fig. 2: Curva crítica da mistura etano + limoneno

CONCLUSÕES

A obtenção da curva crítica é o primeiro passo na solução de problemas através da técnica de inversão de funções do plano no plano, que fornece uma metodologia robusta e pode ser aplicada na resolução de problemas reais de engenharia, onde muitas vezes métodos conhecidos não são capazes de computar as soluções corretas e com certa acurácia.

Além disso, a curva crítica pode ser útil para o melhor entendimento do comportamento de problemas com alto grau de não-linearidade, através de análises relacionadas com a localização geométrica das soluções e o comportamento de bacias de atração, por exemplo. Ainda, é possível fazer a análise do problema em regiões próximas a curva crítica, nas vizinhanças onde, possivelmente, se torna ainda mais complicada a solução dos problemas por outras metodologias.

SÍMBOLOS E UNIDADES

P pressão absoluta

 

kPa

R constante universal dos gases



kJmol1K1



T temperatura absoluta

 

K

V volume molar



m3mol1



m

a parâmetro de atração



kPamol2m6



m

b parâmetro de repulsão



m3mol1



c

T temperatura crítica

 

K c

P pressão crítica

 

kPa

 termo de correção do parâmetro de atração (adimensional) R

T temperatura reduzida (adimensional)

 fator acêntrico (adimensional)

x fração molar na fase líquida



mol mol



y fração molar na fase vapor



mol mol



ij

k parâmetro de interação binária (adimensional)

Z fator de compressibilidade



kPam3kJ1



z fração molar



mol mol



ˆ _{coeficiente de fugacidade (adimensional)}

REFERÊNCIAS

1. RAEISSI, Sona. On the phenomenon of Double Retrograde Vaporization: Within a study on Supercritical Deterpenation of Orange Oils with Ethane. TU Delft, Delft University of Technology, 2004.

2. RAEISSI, S.; PETERS, C. J. On the phenomenon of double retrograde vaporization: multi-dew point behavior in the binary system ethane+ limonene. Fluid phase equilibria, v. 191, n. 1, p. 33-40, 2001.

3. GUEDES, Aline L.; MOURA NETO, Francisco D.; PLATT, Gustavo M. Prediction of azeotropic behaviour by the inversion of functions from the plane to the plane. The Canadian Journal of Chemical Engineering, v. 93, n. 5, p. 914-928, 2015.

4. PENG, Ding-Yu; ROBINSON, Donald B. A new two-constant equation of state. Industrial & Engineering Chemistry Fundamentals, v. 15, n. 1, p. 59-64, 1976.

5. PLATT, G. M.; BASTOS, I. N.; DOMINGOS, R. P. Calculation of double retrograde vaporization:

Newton’s methods and hyperheuristic approach. Journal of Nonlinear Systems and Applications, v. 107, p.

120, 2012.

6. RAEISSI, S.; PETERS, C. J. Simulation of double retrograde vaporization using the Peng–Robinson equation of state. The Journal of Chemical Thermodynamics, v. 35, n. 4, p. 573-581, 2003.

7. MALTA, Iaci; SALDANHA, Nicolau; TOMEI, Carlos. The numerical inversion of functions from the plane to the plane. Mathematics of Computation of the American Mathematical Society, v. 65, n. 216, p. 1531-1552, 1996.

8. SILVA, E. T. wx2x2: um software para sistemas não lineares. 2007. 54 f. Dissertação (Mestrado em Matemática Aplicada). Pontifícia Universidade Católica, Rio de Janeiro. 2007.