CAPITULO III: VARIABLE COMPLEJA

(1)

AURELIO HERNÁNDEZ RAMÍREZ ENERO – JUNIO 2012 133

Capitulo III

VARIABLE COMPLEJA

3.1 Números complejos

El sistema numérico, tal como se conoce, es el resultado de una evolución gradual, tal como se indica en la siguiente descripción:

1. Los números naturales, 1, 2, 3, 4,…, o enteros positivos, fueron usados primero para contar. Los símbolos han cambiado con las épocas, pues los romanos, por ejemplo, utilizaban I, II, III, IV,…. La suma y el producto o de dos números naturales y son también números naturales, lo cual se suele expresar diciendo que el conjunto de los números naturales es cerrado respecto de las operaciones de adición, multiplicación, o que cumple la propiedad de clausura con relación a éstas operaciones.

2. Los números negativos y el cero, denotados por -1, -2, -3,… y 0, respectivamente, que permiten resolver ecuaciones como con y naturales, llevan a la operación de sustracción o inversa de la adición, que se escribe . El conjunto de los enteros positivos y negativos con el cero se llama el conjunto de los enteros y es cerrado bajo las operaciones de adición, multiplicación y sustracción.

3. Los números racionales o fracciones, tales como , ,…permiten resolver ecuaciones de la forma para enteros cualesquiera y , con , los cuales conducen a la operación de división o inversa de la multiplicación, que se representa como o (llamado el cociente de y ) donde es el numerador y el denominador. El conjunto de los enteros es un subconjunto de los números racionales, puesto que los enteros corresponden a los números racionales con . El conjunto de números racionales es cerrado bajo las operaciones de adición, sustracción, multiplicación y división, excluyendo la división por cero.

4. Los números irracionales, tales como √ y son números que no son racionales, es decir, no pueden ser expresados como , donde y son enteros y . El conjunto de números racionales e irracionales es llamado el conjunto de los números reales.

5. Los números complejos. No existe un número real que satisfaga la ecuación polinómica

. Para resolver éste tipo de ecuaciones, es necesario introducir los números complejos.

3.1.1 Definición de números complejos

Los números complejos, denotados por la letra , se definen como pares ordenados:

(2)

de números reales y , los cuales indican una parte real y una parte imaginaria de respectivamente. Lo anterior puede ser escrito como:

de lo anterior se deduce que los números complejos de la forma ( ) se llaman números imaginarios puros.

Otra simbología1 utilizada para definir a los números complejos es:

Los números complejos y son iguales, , si ( ) ( ) y

( ) ( ).

3.1.2 Representación geométrica

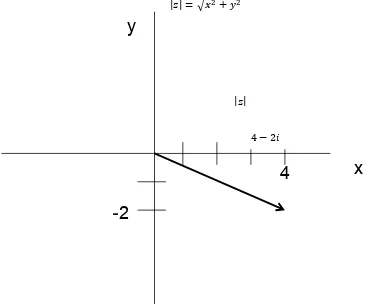
[image:2.612.125.500.339.643.2]

Es común asociar el número complejo ( ) , con un punto en el plano cartesiano, cuyas coordenadas son y . Cada número complejo corresponde sólo a un punto y recíprocamente. El plano se denomina plano complejo o plano , de donde el eje recibe el nombre de eje real y el eje el de eje imaginario. Por ejemplo el número está representado por el punto ( ) como lo muestra la Figura 1. Como se puede ver en la misma figura, el número complejo se le puede asemejar a un vector, en éste caso con componentes y y módulo o valor absoluto | |, definido como:

| | √

Figura 1. Representación esquemática del número complejo

1_{Algunos autores utilizan la letra}_{para designar a la parte imaginaria.}

y

x

4 -2

(3)

3.1.3. Operaciones fundamentales, propiedades y leyes con números

complejos

Teniéndose dos números complejos; y , sus operaciones fundamentales son:

1. Adición o suma

( ) ( ) ( ) ( )

2. Sustracción o resta

( ) ( ) ( ) ( )

3. Multiplicación

( )( ) ( ) ( )

de donde: ( )( ) ( )( )

4. División

( ) ( )

( )

Si son números complejos, son válidas las siguientes propiedades y leyes: a) | | | || | o | | | || | | |

b) | | | |

| | si

c) | | | | | | o | | | | | | | |

d) | | | | | | o | | | | | |

e) Ley de la clausura y pertenecen al conjunto de los números complejos

f) Ley conmutativa de la adición

g) Ley asociativa de la adición ( ) ( )

h) Ley conmutativa de la multiplicación

i) Ley asociativa de la multiplicación ( ) ( )

j) Ley distributiva ( )

(4)

l) Para cualquier número complejo , existe un número único en el conjunto de los números complejos tal que ; se llama el opuesto (o recíproco) de con respecto a la adición y es denotado por .

m) Si es un número complejo, entonces el número que se obtiene al cambiar el signo de su parte imaginaria se denomina complejo conjugado; simbolizado por ̅, por ejemplo: si

, entonces ̅ . De Ia definición de suma se demuestra fácilmente que el conjugado de una suma de dos números complejos es Ia suma de los conjugados:

̅̅̅̅̅̅̅̅̅ ̅ ̅

Además se tienen las siguientes propiedades:

̅̅̅̅̅̅̅̅̅ ̅ ̅ ̅̅̅̅̅̅ ̅ ̅ (̅̅̅̅̅̅) ̅ ̅

Las definiciones de suma y multiplicación muestran que la suma y el producto de un número complejo y su conjugado ̅ son también números reales:

̅ ( ) ( ) ̅ ( )( )

̅ ( ) ( )

Como ( ) y ( ) y combinando la suma y diferencia de y ̅ se tienen las siguientes fórmulas:

( ) ̅ y ( ) ̅

n) Para cualquier , existe un número único en el conjunto de los números complejos tañ que ; se llama el inverso (o recíproco) de con respecto a la multiplicación y es denotado por o .

Ejemplo:

Si y , encuentre: y

Sumando las partes imaginarias y reales de los dos números, se obtiene:

( ) ( ) ( ) ( )

Utilizando la ley distributiva:

( )( ) ( )( ) ( )( )

Ejemplo:

Si y , encuentre: y

En ambas partes de este ejemplo se multiplican tanto el numerador como el denominador por el conjugado del denominador y entonces se la multiplicación:

3.1.4 Forma polar y exponencial de los números complejos, Teorema de

De Moivre y formula de Euler.

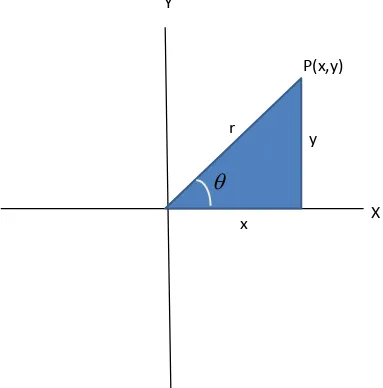
Si P es un punto en el plano complejo correspondiente al número complejo ( ) o , entonces se puede observar según la Figura 2 que:

(5)

donde √ | | se llama el módulo o valor absoluto de y ( ) llamado amplitud o argumento de (denotado por ), es el ángulo en radianes, que forma la recta que une el origen con el punto P y la del eje positivo x. Se deduce que:

( ( ) ( ))

llamada la forma polar del número complejo, y r y se llaman coordenadas polares.

[image:5.612.146.529.205.593.2]

Para cualquier número complejo corresponde solamente a un valor de en . No obstante, cualquier otro intervalo de longitud , por ejemplo , se puede emplear.

Figura 2. Representación de un número complejo en forma polar.

Si ( ( ) ( )) y ( ( ) ( )), se demuestra que:

[ ( ) ( )] [ ( ) ( )]

una generalización de lo anterior conduce a:

[ ( ) ( )]

P(x,y)

y

r

x



Y

(6)

Y si , la expresión anterior queda:

[ ( ( ) ( ))] [ ( ) ( )]

que se llama frecuentemente el teorema de De Moivre.

Una variante de la forma polar se obtiene al tener en cuenta la conocida fórmula de Euler: _{( ) ( )}

para Esto nos permite escribir un número complejo en la forma siguiente, denominada forma exponencial:

| |

Esta nueva forma es especialmente cómoda para expresar productos y cocientes ya que sólo hay que tener en cuenta las propiedades de la función exponencial (para multiplicar se suman exponentes y para dividir se restan). En particular, para potencias con exponentes enteros se tiene:

| |

Esto nos permite dar una nueva expresión para el inverso de un complejo no nulo en la forma.

_{| |} _{[ ( ) ( )]}

Ejemplo:

Si , encuentre su módulo | |

| | √ ( ) √

Ejemplo:

Exprese √ en forma polar

Con y √ , se obtiene | | √( ) ( √ ) y ( √ ) , por lo

tanto el número complejo expresado en forma polar será:

* ( ) ( )+

3.1.5 Potencias y raíces

Las potencias enteras de un número complejo ( ( ) ( )) , diferente de cero están dadas por la fórmula:

_{[ ( ) ( )]}

(7)

Se dice que un número es una raíz n-ésima de un número complejo no nulo si . Si

[ ( ) ( )] y [ ( ) ( )] son las formas polares de y , entonces

se convierte en:

[ ( ) ( )] [ ( ) ( )]

de aquí se concluye que y y

( ) ( ) ( ) ( )

igualando las partes real e imaginaria se tiene de ésta última ecuación:

( ) ( ) y ( ) ( )

éstas igualdades implican que , donde es un entero. Entonces

Al tomar valores enteros sucesivos , se obtienen raíces distintas con el mismo módulo pero con diferentes argumentos. Pero para se obtienen las mismas raíces debido a que el seno y el coseno son periódicos cada . Para ver esto, se supone que , donde entonces:

( )

y así

( ) ( ), ( ) ( )

A continuación se sintetiza éste resultado. Las raíces n-ésimas de un número complejo no nulo

[ ( ) ( )] vienen dadas por:

[ ( ) ( )]

donde .

Ejemplo:

Calcule para √

Con , √ , | | √( ) ( √ ) , ( √ ) y , se tiene:

(8)

Ejemplo:

Encuentre las tres raíces cúbicas de .

Con , , √( ) ( ) √ , ( ) , la forma polar del número indicado

es: √ [ ( ) ( )] y , se tiene:

(√ ) [ ( ) ( )]

Por lo tanto, las tres raíces son:

√ [ ( ) ( )] √ [ ( ) ( )] √ [ ( ) ( )]

Ejercicios

a) En los siguientes problemas, exprese el número indicado en la forma 1. ( ) ( )

2. 3.

4. ( ) ( )( ) 5. ( )( )_{( )( )}

b) En los siguientes problemas sea . Encuentre la expresión indicada. 1. ( )

2. ( ̅ ) 3. ( )

c) En los problemas encuentre un número complejo que cumpla con la ecuación indicada. 1. ( )

2.

3. ̅

d) Escriba en forma polar el número complejo indicado. 1.

2. 3.

4. √ 5.

e) Encuentre y y escriba el número complejo en la forma

1. * ( ) ( )+ * ( ) ( )+

(9)

1. ( √ )

2. * ( ) ( )+

3. ( √ )

4. ( )

5. *√ ( ( ) ( ))+

g) Encuentre todas las soluciones de la ecuación indicada.

1.

2.

h) Exprese el resultado en forma polar y de forma

1. * ( ) ( )+ * ( ) ( )+

2. * (

) ( )+

* () ()+

3.2 Funciones analíticas

Uno de los conceptos más importantes en matemáticas es el de una función. Se puede recordar de cursos previos que una función es cierto tipo de correspondencia entre dos conjuntos; más específicamente: una función de un conjunto A a un conjunto B es una regla de correspondencia que asigna a cada elemento de A un único elemento en B. Si b es el elemento del conjunto B asignado al elemento a del conjunto A a través de , se dice que b es Ia imagen de a y se escribe

( ). El conjunto A se denomina el dominio de Ia función . El conjunto de todas las imágenes de B se denomina el rango de la función.

Cuando el dominio A de la anterior definición de función es un conjunto de números complejos , se dice que es una función de una variable compleja o, en forma abreviada, una función compleja. La imagen de un número complejo z es algún número complejo , esto es,

( ) ( ) ( )

donde y son las partes real e imaginaria de , y son funciones de valores reales. En forma inherente al postulado matemático anterior está el hecho de que no se pueden dibujar una gráfica de una función compleja ( ) puesto que una gráfica así requeriría de cuatro ejes en un sistema coordenado de cuatro dimensiones. Algunos ejemplos de funciones de una variable compleja son:

( ) , es cualquier número complejo

( )

, y

( ) ( ) es cualquier número complejo

Cada una de éstas funciones podría expresarse en la forma ( ) ( ) ( ). Por ejemplo:

( ) ( ) ( ) ( ) ( )

(10)

AURELIO HERNÁNDEZ RAMÍREZ ENERO – JUNIO 2012 142 Límite de una función

Suponer que la función está definida en una vecindad de , excepto posiblemente en el mismo . Entonces se dice que posee un límite en , escrito como:

( )

Expresándolo con otras palabras, el ( ) significa que los puntos ( ) se pueden acercar arbitrariamente al punto , si se elige el punto suficientemente cercano, aunque no igual, al punto . La diferencia fundamental entre ésta definición y el concepto de límite en variables reales radica en la comprensión de que . Para una función de una variable real ,

( ) significa que ( ) se acerca a al acercarse a , ya sea por su derecha o por su izquierda, sobre la línea de números reales. Pero como y son puntos en el plano complejo, cuando se dice que existe el ( ) se entiende que ( ) se acerca a cuando el punto se acerca a desde cualquier dirección.

Suponer que ( ) y ( ) , entonces se tienen las siguientes propiedades de los límites:

1) [ ( ) ( )] 2) [ ( ) ( )]

3)

(

( )

( ))

Continuidad en un punto

Una función es continua en un punto si ( ) ( ). Como consecuencia de las propiedades de los límites, se tiene que si dos funciones y son continuas en un punto , entonces su suma y su producto son continuos en . El cociente de las dos funciones es continuo en siempre y cuando ( ) .

Derivada

La derivada de una función compleja se define en términos de un límite. El símbolo utilizado en la siguiente definición es el número complejo .

Suponer que la función compleja se define en la vecindad de un punto . La derivada de en es:

( )

( ) ( )

Siempre y cuando existe dicho límite, se dice que la función es derivable en . La derivada de una función ( ) también se escribe

.

Las reglas de derivación son las mismas que en el cálculo de variables reales. Si y son derivables en un punto y es una constante compleja, entonces:

Reglas de la constante:

(11)

Regla de la suma:

[ ( ) ( )] ( ) ( ) Regla del producto: * ( )_{( )}+ ( ) ( ) _{[ ( )]}( ) ( )

Regla de la cadena: ( ( )) ( ( )) ( )

Regla de potencias de :

_{, siendo} _{un entero.}

Ejemplo:

Derive 1) ( ) y 2) ( )

1) ( )

2) ( ) [( ) ] [ _{( )} ] _{( )}

Ejemplo:

Demuestre que la función ( ) no es derivable en punto alguno.

Considerando se tiene

( ) ( ) ( ) ( )

y por lo tanto:

( ) ( )

Ahora, si se considera que a lo largo de una línea paralela al eje , entonces y el valor del límite es 1. Por otro lado, si se considera que a lo largo de una línea paralela al eje , entonces y el valor del límite es 4. Por lo tanto, ( ) no es derivable en ningún punto .

Funciones analíticas

Si bien los requerimientos para que una función sea derivable son severos, existe una clase de funciones sumamente importante, cuyos miembros cumplen incluso con condiciones más severas. Estas funciones se denominan funciones analíticas.

“Se dice que una función compleja ( ) es analítica en un punto si es derivable en y en todo punto de alguna vecindad de ”. Una función es analítica en un dominio D si es analítica en todos los puntos de D. La definición se debe leer cuidadosamente. La analiticidad en un punto es una propiedad de vecindad. La analiticidad en un punto no es, por lo tanto, sinónimo de derivabilidad en un punto.

3.2.1 Ecuaciones de Cauchy-Riemann

(12)

. Este requisito es más estricto que simplemente Ia derivabilidad en un punto, ya que una función compleja puede ser derivable en un punto aunque no sea derivable en todos los demás.

En las Ecuaciones de Cauchy-Riemann se observa que si una función ( ) ( ) ( ) es derivable en un punto , entonces las funciones y deben satisfacer un par de ecuaciones que relacionan sus derivadas parciales de primer orden. Este resultado es una condición necesaria para Ia analiticidad.

Suponer que ( ) ( ) ( ) es derivable en un punto . Entonces existen las derivadas parciales de primer orden de y en el punto que cumplen con las Ecuaciones de Cauchy-Riemann. Comprobación

Como ( ) existe se sabe que

( )

( ) ( )

Escribiendo ( ) ( ) ( ) y , se tiene:

( )

( ) ( ) ( ) ( )

Puesto que éste límite existe, puede tender a 0 desde cualquier dirección conveniente. En particular, si horizontalmente, entonces y por lo tanto se convierte en:

( ) ( ) ( ) ( ) ( )

Como ( ) existe, también existe los dos límites. Pero por definición, los límites son las primeras derivadas parciales de y respecto a , con lo cual queda:

( )

Si ahora se hace que verticalmente, entonces queda como:

( ) ( ) ( ) ( ) ( )

que es lo mismo que

( )

(13)

AURELIO HERNÁNDEZ RAMÍREZ ENERO – JUNIO 2012 145 Ejemplo:

Demostrar que la ( ) ( ) cumple con las ecuaciones de Cauchy-Riemann.

De la función se tiene:

( ) ( )

Con las ecuaciones de Cauchy-Riemann se comprueba:

Ejemplo:

Demuestre que la función ( ) ( ) ( ) no es analítica en punto alguno.

Se tiene: ( ) ( )

Se ve que

pero la igualdad

se cumple únicamente sobra a línea .

Criterio para la analiticidad

Suponer que las funciones reales ( ) y ( ) son continuas y tienen derivadas parciales de primer orden continuas en un dominio D. Si y cumplen con las ecuaciones de Cauchy-Riemann en todos los puntos D, entonces la función compleja ( ) ( ) ( ) es analítica en D.

Ejemplo:

Para la función ( )

se tiene: ( ) ( )

En otras palabras, las ecuaciones de Cauchy-Riemann se cumplen excepto en el punto donde

, esto es, en . Se concluye de acuerdo al criterio de analiticidad que ( ) es analítica en cualquier dominio que no contenga al punto .

(14)

En ésta sección se examinan las funciones exponenciales, logarítmicas, trigonométricas e hiperbólicas de una variable compleja , llamadas funciones elementales. Aunque la definición de éstas funciones complejas se deduce a partir de sus análogas para variables reales, las propiedades de éstas funciones complejas contienen algunos puntos interesantes.

3.3.1 Función exponencial

De variables reales la función exponencial ( ) tiene las propiedades

( ) ( ) ( ) ( ) ( )

Desde luego, se desea que la definición de la función compleja ( ) , donde , se reduzca a para y que posea las mismas propiedades antes mencionadas. Ya se ha utilizado anteriormente una función exponencial con un exponente imaginario puro; la fórmula de Euler,

_{( ) ( )}_{, donde} _{es un número real}

Para es razonable esperar que

y por lo tanto se define la función exponencial como:

_{[ ( ) ( )]}

Ejemplo:

Calcule

Con y se tiene:

_{( )} _{( )}

Finalmente [ ( ) ( )]

3.3.2 Función logarítmica

El logaritmo de un número complejo , ,se define como la inversa de la función exponencial, esto es,

( )

Se observa que ( ) no está definido para , ya que no existe un valor de para el cual

. Para encontrar las partes real e imaginaria de ( ) se escribe y se utiliza la definición de la función exponencial:

(15)

de ésta expresión se tiene que ( ) y ( ). Se pueden despejar y de estas dos últimas expresiones. Primero, elevándolas al cuadrado y sumándolas, se tiene:

_{| |}

y así

| | | |

donde | | denota el logaritmo natural real del módulo de . En segundo lugar, para despejar se dividen las dos ecuaciones y se obtiene:

( )

Ésta última ecuación significa que es un argumento de , es decir, ( ). Pero como no existe un único argumento de un número complejo determinado , si es un argumento de

, entonces también lo es

La definición del logaritmo de un número complejo es:

Para y ( ),

( ) | | ( )

Ejemplo:

Encuentre los valores de 1) ( ), 2) ( ) y 3) ( ) 1) Con (

) ( ) y ( ) | | , se tiene:

( ) ( )

2) Con ( ) ( ) y ( ) | | , se tiene:

( ) ( )

3) Con (

) ( )

y ( ) | | , se tiene:

( ) ( )

Ejemplo:

Encuentre todos los valores de tales que √

Se tiene que (√ ), |√ | , (

√ ) , lo cual conduce a:

(16)

3.3.3 Función trigonométrica

Si es una variable real, entonces la fórmula de Euler indica que:

_{( ) ( )} _{( ) ( )}

Restando y sumando éstas expresiones, se observa que las funciones reales ( ) y ( ) pueden expresarse con una combinación de funciones exponenciales:

( )

quedando la definición de las funciones trigonométricas para cualquier número complejo :

( )

Como en trigonometría se definen cuatro funciones adicionales en términos de ( ) y ( ):

( ) ( )

( ) ( ) ( ) ( ) ( ) ( ) ( )

Derivadas

Como (

) se deduce a partir de la regla de cadena que ( ) y ( ) , por lo tanto,

( )

De hecho, se puede demostrar que la forma de las derivadas de las funciones trigonométricas complejas es igual a la de las funciones reales. Se sintetizan a continuación los resultados:

( ) ( ) ( ) ( )

( ) ( ) ( ) ( ) ( ) ( )

Identidades

Las identidades trigonométricas comunes también son las mismas en el caso complejo.

( ) ( ) ( ) ( )

(17)

( ) ( ) ( ) ( ) ( )

( ) ( ) ( ) ( ) ( ) ( )

Ceros

Para encontrar los ceros de ( ) y ( ) se necesita expresar ambas funciones en la forma

. Antes de proceder, debe recordarse que si es real, entonces el seno y el coseno hiperbólicos se definen en términos de las funciones reales exponenciales y :

( ) ( )

Ahora, de la definición de funciones trigonométricas y de la fórmula de Euler se obtiene, después de algunas simplificaciones,

( ) ( ) ( )

( ) (

) ( ) ( )

quedando:

( ) ( ) ( ) ( ) ( )

y en una forma similar:

( ) ( ) ( ) ( ) ( )

Combinando las expresiones anteriores y ( ) ( ), se encuentra que:

| ( )| ( ) ( )

Ahora, un número complejo es 0 si, y sólo si, | | . Así pues, si ( ) , entonces se debe tener que ( ) ( ) . Esto implica que ( ) y ( ) y por lo tanto ,

. Así, los únicos ceros de ( ) son los números reales En forma similar se infiere que ( ) únicamente cuando ( )

Ejemplo:

Calcular el ( )

Se tiene: ( ) ( ) ( ) ( ) ( )

Ejemplo:

(18)

La expresión se puede reescribir como: . Multiplicando ésta última ecuación por se

obtiene la ecuación cuadrática en :

resolviendo se encuentra que √ . Entonces, para se tiene que

( √ ) . Dividiendo entre y utilizando ( √ ) ( √ ), las soluciones de la ecuación indicada se expresan como: ( √ ).

3.3.4 Funciones hiperbólicas.

El seno y el coseno hiperbólicos complejos se definen en forma análoga a las definiciones reales dadas en las funciones trigonométricas, para cualquier número complejo :

( ) ( )

Las funciones tangente, cotangente, secante y cosecante hiperbólicas se definen en términos de

( ) y ( ):

( ) ( )

( ) ( ) ( ) ( ) ( ) ( ) ( )

El seno y coseno hiperbólicos son funciones enteras, y las funciones definidas anteriormente son analíticas excepto en los puntos donde los denominadores son 0. Utilizando la definición de seno y coseno hiperbólicos que:

( ) ( ) ( ) ( )

Es interesante observar que, en contraste con el cálculo real, en cálculo complejo las funciones trigonométricas e hiperbólicas se relacionan entre sí, si se sustituye por en todos los lugares de la definición de funciones hiperbólicas y se comparan los resultados con la definición de funciones trigonométricas, se ve que ( ) ( ) y ( ) ( ). Estas ecuaciones permiten expresar ( ) y ( ) en función de ( ) y ( ), respectivamente. En forma similar se tendrían las siguientes expresiones:

( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )

Ceros

Las relaciones anteriores permiten deducir igualdades para las funciones hiperbólicas utilizando los resultados de las funciones trigonométricas. Por ejemplo, para expresar ( ) en la forma , se escribe ( ) ( ) como ( ) quedando:

(19)

como ( ) ( ) y ( ) ( ), lo anterior se simplifica a:

( ) ( ) ( ) ( ) ( )

En forma semejante,

( ) ( ) ( ) ( ) ( )

También se deduce que los ceros de ( ) y ( ) son imaginarios puros y son, respectivamente,

y ( )