O USO DO MÉTODO DA VELOCIDADE RADIAL NA MENSURAÇÃO DA MASSA DE PLANETAS

Texto completo

(1)O USO DO MÉTODO DA VELOCIDADE RADIAL NA MENSURAÇÃO DA MASSA DE PLANETAS. Richard Assis da Silva 1 Elaine Cristina Ferreira Silva Fortes 2. Resumo: Existem vários métodos para a obtenção das massas aproximadas de exoplanetas, cada um com suas peculiaridades. Neste trabalho serão mencionados três métodos: o da terceira lei de Kepler, o da velocidade radial e, o do trânsito. O primeiro limita-se aos planetas ou aos exoplanetas que possuem satélites naturais, já os demais, podem ser utilizados tanto para planetas que possuem satélites como para os que não possuem. A terceira Lei de Kepler ou Lei dos Períodos trata-se de um método simples para a obtenção de massas aproximadas de planetas e de exoplanetas que possuem satélites naturais. O método da velocidade radial, também conhecido como método de espectroscopia Doppler e de método Wobble, é um dos mais populares métodos de descoberta de exoplanetas, é responsável pela descoberta de cerca de 70%. O método de trânsito é responsável pela descoberta de cerca de 23% de exoplanetas e, também é um método eficaz para a obtenção das massas de exoplanetas da classe "Hot Jupiters".. Palavras-chave: Lei dos Períodos, espectroscopia Doppler, Trânsito. Modalidade de Participação: Iniciação Científica. O USO DO MÉTODO DA VELOCIDADE RADIAL NA MENSURAÇÃO DA MASSA DE PLANETAS 1 Aluno de graduação. richardassisdasilva@outlook.com. Autor principal 2 Docente. elainefortes@unipampa.edu.br. Orientador. Anais do 10º SALÃO INTERNACIONAL DE ENSINO, PESQUISA E EXTENSÃO - SIEPE Universidade Federal do Pampa | Santana do Livramento, 6 a 8 de novembro de 2018.

(2) O USO DO MÉTODO DA VELOCIDADE RADIAL NA MENSURAÇÃO DA MASSA DE PLANETAS 1 INTRODUÇÃO O céu sempre fascinou a humanidade. Não é à toa que ele vem sendo estudado há tanto tempo. Essa curiosidade levou o homem, no decorrer da história, a questionar-se, estudar e criar teorias que explicassem todas suas perguntas. No estudo de planetas, Ptolomeu, Copérnico, Kepler, Galileu e Newton são os primeiros nomes que nos remetemos, tanto que as três Leis de Kepler e a Gravitação de Newton são utilizadas em vários problemas até hoje. A Terra exerce uma força de atração nos objetos que estão sobre sua superfície. Newton deu-se de conta que essa força estendia-se até a Lua e produzia uma aceleração centrípeta necessária para mantê-la em órbita (OLIVEIRA FILHO, 2014). O Sol também produz essa aceleração em relação aos planetas que o orbitam. Em 2006 a União Astronômica Internacional (IAU) ± sigla em inglês para International Astronomical Union ± aprovou uma resolução definindo planetas e planetas anões. De acordo com IAU (2006), um planeta é definido GH DFRUGR FRP WUrV FULWpULRV ³i) está orbitando o Sol, ii) possui forma determinada pelo equilíbrio hidrostático (arredondado) resultante do fato que sua força gravitacional supera a força de coesão dos materiais que o constituem, iii) e tenha varrido sua vizinhança composta por objetos menores em sua órbita. Um planeta anão, segundo IAU (2006), é um corpo celestial que orbita o Sol, possui forma determinada pelo equilíbrio hidrostático (arredondado) resultante do fato que sua força gravitacional supera a força de coesão dos materiais que o constituem, não possue uma vizinhança limpa, não é um satélite. Com isso, Plutão passou a ser considerado um planeta anão e o Sistema Solar passou a ter oito planetas. Vale ressaltar que existem exoplanetas, que possuem as mesmas definições de planetas, porém orbitam estrelas fora do Sistema Solar. Existe ainda, de acordo com HAAS (2016) uma classe peculiar de planetas que não orbitam estrelas, mas são ligados diretamente às galáxias das quais fazem parte. Existem vários métodos para detecção de planetas e exoplanetas, entre eles citamos os métodos da velocidade radial (70%), o método de trânsito (23%), detecção visual direta (2.9%), microlentes gravitacionais (2.3%) e o método das variações temporais (1.9%). Os números entre parênteses indicam o percentual de descobertas para exoplanetas, (KITCHIN, 2012). O método da velocidade radial, também conhecido como método de espectroscopia GRSSOHU RX PpWRGR GH ³:REEOH´ p XP GRV PDLV EHP-sucedidos métodos para a detecção de exoplanetas, (KITCHIN, 2012). Com as técnicas deste método, é possível obter as massas de planetas e exoplanetas, que possuem ou não satélites naturais. Outro método bastante importante na detecção de planetas e exoplanetas é o método de trânsito. Ele é baseado na redução do brilho de uma estrela hospedeira quando seu exoplaneta passa na sua frente, percorrendo o seu disco, com relação à linha de visada, SANTOS (2017). Trata-se de um método eficaz para a obtenção das massas de exoplaneWDV GD FODVVH ³+RW -XSLWHUV´ TXH VHJXQGR 0,6/,6 VmR FODVVHV GH H[RSODQHWDV TXH SRVVXHP FDUDFWHUtVWLFDV físicas semelhantes às de Júpiter e têm períodos orbitais muito curtos (< 10 dias) e orbitam muito próximos de suas estrelas. O propósito deste estudo é ilustrar os métodos usados no cálculo das massas de alguns planetas do Sistema Solar que possuem satélites enfatizando o método da velocidade radial e, diferenciar este da Lei dos Períodos e do método de Trânsito. 2 METODOLOGIA 2.1 LEI DOS PERÍODOS Tycho Brahe (1546-1601) foi um astrônomo que fez observações sobre o movimento do sistema planetário. Esses dados foram interpretados por Johannes Keppler (1571-1630). Este Anais do 10º SALÃO INTERNACIONAL DE ENSINO, PESQUISA E EXTENSÃO - SIEPE Universidade Federal do Pampa œ Santana do Livramento, 6 a 8 de novembro de 2018.

(3) descobriu importantes regularidades no movimento dos planetas, que o levaram a elaborar três leis que governam o movimento dos planetas, entre elas a lei dos períodos. A terceira Lei de Kepler ou Lei dos Períodos trata-se de um método simples e de grande eficácia para a obtenção de massas aproximadas de planetas que possuem satélites naturais. Tal método diz que o quadrado do período de revolução de um planeta (ou exoplaneta) ao redor do Sol (ou de outra estrela) é diretamente proporcional ao cubo do raio médio de sua órbita (OLIVEIRA FILHO, 2014), como é mostrado na Equação 1: 26 L -4 7 (Eq. 1) Sendo P o período sideral do planeta, R a distância média entre o planeta e o Sol, e K uma constante. Newton, após vários estudos sobre as leis de Kepler encontrou um valor para a constante K, (OLIVEIRA FILHO, 2014), Onde, ) L xáxy : sr?55. - L À:Æ>à; 8 .. à/ ÄÚ æ.. (Eq. 2). é a constante gravitacional, M é a massa do Sol, e m é a massa. do planeta, como é exposto pela Equação 2: Substituindo o K na Equação 1, temos:. 26 L À:Æ; 4 7 . 8 .. (Eq. 3). Note que a Equação 3 leva em consideração o fato que M << m. 2.2 VELOCIDADE RADIAL O método da velocidade radial é um dos mais populares métodos de descoberta de exoplanetas. Este método envolve a obtenção de medidas precisas da velocidade radial de uma estrela utilizando um telescópio óptico, CLUBB (2008). Se um exoplaneta estiver presente em um sistema, uma estrela-mãe exibirá mudanças periódicas de velocidade radial por causa de seu movimento orbital sobre um centro de gravidade comum com a amplitude, K. Isto é proporcional a massa mínima do planeta, m sin i, e inversamente proporcional ao período orbital do planeta, P, à excentricidade, e, e a massa da estrela, M*, (HRUDKOVÁ, 2009). A Equação 4 é a equação da velocidade radial para planetas e exoplanetas que possuem órbitas excêntricas. 8Ll. à 5 ¾6 À p l / .p l . p É ¥ÆŽ ¥:5?Ø . ;. /. (Eq. 4). Sendo, V a velocidade radial da estrela, P o período orbital do planeta, m a massa do planeta, e M* a massa da estrela. Astrônomos obtêm as velocidades radiais utilizando o efeito Doppler com as características do espectro estelar, (HASWELL, 2010). A variação do comprimento de onda é dado pela Equação 5: Ï ¿ L (Eq. 5) Ö 8 Onde c é a velocidade da luz (c=3 x 10 m/s). A Equação 6 é uma variação da Equação 4, pois sendo K = Vsin i e, se i § ƒ consequentemente K = V. Caso a órbita do exoplaneta ao redor de sua estrela tiver a forma mais próxima de um círculo, pode-se adotar a Equação 7 para os cálculos. -Ll. à 5 ¾6 À p l / .p l . p É ¥ÆŽ ¥:5?Ø . ;. /. -Ll. à ¾6 À p l / .p É ¥ÆŽ. /. Anais do 10º SALÃO INTERNACIONAL DE ENSINO, PESQUISA E EXTENSÃO - SIEPE Universidade Federal do Pampa œ Santana do Livramento, 6 a 8 de novembro de 2018. (Eq. 6) (Eq. 7).

(4) 2.3 TRÂNSITO O método de trânsito, expresso na Equação 8, é uma técnica baseada na redução do brilho de uma estrela quando o exoplaneta passa na sua frente percorrendo o seu disco, com relação à linha de visada , (SANTOS, 2017). Trata-se de um método que tem como base a Lei dos Períodos, como pode ser visto na Equação 8.. 6 L ÀÆŽ k4 Ž …‘• Ü4ãß oá (Eq. 8) Onde, T é o tempo de duração do trânsito, apl, a distância média entre o centro de massa da estrela e o centro de massa do planeta, M* e R*, respectivamente, a massa e o raio da estrela, Rpl, o raio do planeta, e Üo ângulo da latitude estelar. De acordo com MISLIS (2010), quando o planeta passa entre sua estrela hospedeira e o observador, o fluxo da estrela diminui moderadamente, pois uma parcela de sua luz é bloqueada pelo planeta. Cada sistema planetário tem uma curva de luz própria, torna-se possível obter, através do método de trânsito, as características físicas de cada exoplaneta de determinado sistema. A equação característica desse método é a Equação 9, conhecida como a equação da SUREDELOLGDGH JHRPpWULFD SDUD D GHWHFomR GH H[RSODQHWDV GR WLSR ³+RW -XSWHUV´ H[SRVWD SRU (MISLIS, 2010). à ËŽ É 2) L rátuz @ A @ A @ A (Eq. 9) ÆŽ å × Onde PG § R*/r é a probabilidade geométrica, expressa através de R* e r, M* e m são, respectivamente, as massas da estrela e do planeta, R* e r são, respectivamente, o raio da estrela e a distância entre o centro de massa da estrela e o centro de massa do planeta, ambos em UA, e o período orbital, P, exposto em dias. ¥8ÔÛ×. .. 3 RESULTADOS e DISCUSSÃO 3.1 LEI DOS PERÍODOS Calculou-se a massa de Júpiter utilizando seu satélite Europa, com período orbital de 3,06 x 105 s e distância do centro de Júpiter de 6,70 x 108 m. Dados: P = 3,06 x 105 s; R = 6,70 x 108 m; G= 6,67 x 10-11m³/Kg s². vè 6 r :xáyr : sr< I;7 /Ã L n 7 I :uárx : sr9 O;6 xáxy : sr?55 -C O 6. /Ã N sá{r:sr6; -CX Pode-se também obter sua massa utilizando outro satélite, Ganímedes, com período orbital P= 6,19 x 105 s e distância do centro de Júpiter R= 1,07 x 109 m. Neste caso, resulta que MJ = 1,90 x1027 Kg. Com a Terceira Lei de Kepler pode-se calcular a massa de qualquer planeta ou exoplaneta que possua pelo menos um satélite natural. 3.2 VELOCIDADE RADIAL Para testar o método da velocidade radial optou-se por fazer uso de dados referentes aos planetas Saturno e Júpiter. Para isso, a Equação 7 foi utilizada. Dados de Saturno: K = 2,5 m/s; M* = 1,98 x 1030 Kg; P = 1,94 X 107 s. A órbita de Saturno é aproximadamente circular, tem-se que K = V sin i H VHQGR L § ƒ ORJR . 9. Anais do 10º SALÃO INTERNACIONAL DE ENSINO, PESQUISA E EXTENSÃO - SIEPE Universidade Federal do Pampa œ Santana do Livramento, 6 a 8 de novembro de 2018.

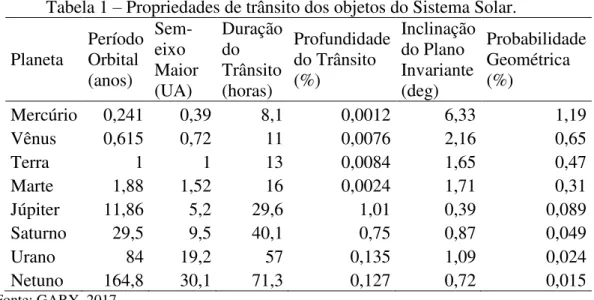
(5) /Ì L táw. I/ / §:sá{z:sr74 ÄÚ ;6 © O. sá{u : sr; O. tè lxáxy : sr?55. I7 p GC O 6. /Ì N vász:sr6: -CX Para o cálculo da massa de Júpiter, tem-se que: K = 12,5 m/s; M* = 1,98 x1030 Kg; P = 3,15 X 107 s. /Ã L. stáwà / / §:sá{z:sr74 ÄÚ ;6 © O6. 3.3 TRÂNSITO. uáyv : sr< O. tè lxáxy : sr?55. /Ã N sá{r:sr6; -C. I7 p -C O 6. Para o cálculo das massas de Saturno e de Júpiter foram utilizados dados da Tabela 1, que fornece informações sobre propriedades de trânsito dos objetos do Sistema Solar. Para Saturno, PG = 0,049%; R* = 0,00465 UA; r = 9,50 UA; M* = 1,98 X 1030 Kg e; P = 4332,58 d. rárrvxw 7# sryxyáwr @ /Ì pl pl p vá{r:sr?8 L rátuz l 74 {áwr 7# @ íUõô y sr -C /Ì N yáyw:sr6: -C. Para Júpiter, PG = 0,089%; R* = 0,00465 UA; r = 5,20 UA; M* = 1,98 X 1030 Kg e; P = 4332,58 d. /Ã rárrvxw 7# vuutáwz @ pl pl p zá{:sr?8 L rátuz l 74 wátr 7# @ íUõô y sr -C /Ã N sá{s:sr6; -Cä Com o método de trânsito utilizando a equação da probabilidade geométrica obtém PDVVDV DSUR[LPDGDV GH ³+RW -XSLWHUV´ Tabela 1 ± Propriedades de trânsito dos objetos do Sistema Solar. SemDuração Inclinação Período Profundidade Probabilidade eixo do do Plano Planeta Orbital do Trânsito Geométrica Maior Trânsito Invariante (anos) (%) (%) (UA) (horas) (deg) Mercúrio 0,241 0,39 8,1 0,0012 6,33 1,19 Vênus 0,615 0,72 11 0,0076 2,16 0,65 Terra 1 1 13 0,0084 1,65 0,47 Marte 1,88 1,52 16 0,0024 1,71 0,31 Júpiter 11,86 5,2 29,6 1,01 0,39 0,089 Saturno 29,5 9,5 40,1 0,75 0,87 0,049 Urano 84 19,2 57 0,135 1,09 0,024 Netuno 164,8 30,1 71,3 0,127 0,72 0,015 Fonte: GARY, 2017.. Anais do 10º SALÃO INTERNACIONAL DE ENSINO, PESQUISA E EXTENSÃO - SIEPE Universidade Federal do Pampa œ Santana do Livramento, 6 a 8 de novembro de 2018.

(6) 4 CONSIDERAÇÕES FINAIS Três técnicas foram citadas neste trabalho, a lei dos períodos, o método de trânsito utilizando a equação da probabilidade geométrica e o método da velocidade radial, utilizando o desvio Doppler da luz emitida pela estrela. Independentemente do tamanho do planeta ou exoplaneta e, se possui ou não satélites naturais, até o presente momento, o método de mais sucesso na descoberta e na obtenção de massas de planetas e exoplanetas é o da velocidade radial. Aqui ilustramos a sua funcionalidade para o cálculo de massa de dois planetas do sistema solar e comparamos os resultados obtidos com o método de trânsito. REFERÊNCIAS CLUBB, I.K. A detailed derivation of the radial velocity equation. San Francisco, San Francisco State University, 2008. GARY, D. E. Search for extrasolar planets. 2017. Disponível <https://web.njit.edu/~gary/320/Lecture10.html>. Acesso em 01 jan 2018.. em:. HAAS, G. Megacurioso. Fora de órbita: você sabia que a maioria dos planetas não orbita estrelas?. 2016. Disponível em: <https://www.megacurioso.com.br/astronomia/39431-fora-deorbita-voce-sabia-que-a-maioria-dos-planetas-nao-orbita-estrelas-.htm>. Acesso em: 16 set 2017. HASWELL, A.C. Transiting exoplanets. 1st ed. Cambridge, Cambridge University, 2010. HRUDKOVÁ, M. Planets by other suns. Thesis (Ph. D) ± Faculty of Mathematics and Physics, Charles University, Prague, 2009. IAU. Resolution B5: Definition of a Planet in the Solar System. 2016. Disponível em: < https://www.iau.org/static/resolutions/Resolution_GA26-5-6.pdf>. Acesso em: 30 ago 2017. KITCHIN, C. Exoplanets: finding, exploring, and understanding alien worlds. New York, Springer, 2012. MISLIS, D. Theory and applications for transiting extrasolar planets. Thesis (Ph.D for Science), University of Hamburg, Germany, 2010. OLIVEIRA FILHO, K.S.; SARAIVA, M.F.O. Astronomia e astrofísica. 3.ed. São Paulo, Blume, 2014. SANTOS, W.C.; AMORIM, R.G.G. Descoberta de exoplanetas pelo método de trânsito. Revista Brasileira de Ensino de Física, São Paulo, v. 39, n.2, p. e2308, 2017.. Anais do 10º SALÃO INTERNACIONAL DE ENSINO, PESQUISA E EXTENSÃO - SIEPE Universidade Federal do Pampa œ Santana do Livramento, 6 a 8 de novembro de 2018.

(7)