Actividades lúdicas en el desarrollo lógico matemático

Texto completo

(1)Porta. UNIVERSIDAD DE GUAYAQUIL FACULTAD DE FILOSOFÍA, LETRAS Y CIENCIAS DE LA EDUCACIÓN CARRERA MERCADOTECNIA Y PUBLICIDAD. TÍTULO DEL TRABAJO DE INVESTIGACIÓN PRESENTADO ACTIVIDADES LÚDICAS EN EL DESARROLLO LÓGICO MATEMÁTICO. TALLERES EDUCATIVOS. AUTORAS: PATRICIA ELIZABETH FERNÁNDEZ CEDEÑO ANA MELISSA MACIAS BARBA. TUTOR: LCDA. DELFA MANTILLA PACHECO MSc.. Guayaquil, septiembre del 2019.

(2) ii. FACULTAD DE FILOSOFÍA, LETRAS Y CIENCIAS DE LA EDUCACIÓN CARRERA MERCADOTECNIA Y PUBLICIDAD. DIRECTIVOS. Dr. Santiago Galindo Mosquera, MSc.. DECANO. Lic. Pilar Huayamave Navarrete, MSc.. DIRECTORA DE CARRERA. Dr. Pedro Rizzo Bajaña, MSc.. VICE-DECANO. Ab. Sebastián Cadena Alvarado. SECRETARIO.

(3) iii. FACULTAD DE FILOSOFÍA, LETRAS Y CIENCIAS DE LA EDUCACIÓN CARRERA MERCADOTECNIA Y PUBLICIDAD.

(4) iv. FACULTAD DE FILOSOFÍA, LETRAS Y CIENCIAS DE LA EDUCACIÓN CARRERA MERCADOTECNIA Y PUBLICIDAD.

(5) v. FACULTAD DE FILOSOFÍA, LETRAS Y CIENCIAS DE LA EDUCACIÓN CARRERA MERCADOTECNIA Y PUBLICIDAD.

(6) vi. DEDICATORIA. Principalmente a mis padres, docentes, pareja y amigos que estuvieron junto a mí apoyándome durante todo el proceso.. Melissa Macias Barba. Principalmente a Dios, mi familia, esposo e hijos, docentes, amigos que estuvieron acompañándome en este largo camino de enseñanza.. Patricia Fernández Cedeño.

(7) vii. AGRADECIMIENTO. Agradezco a mis padres y pareja que me apoyaron tanto económicamente como emocional a lo largo de esta etapa, al igual que a nuestra tutora que nos supo guiar en este proceso.. Melissa Macias Barba. Agradezco a todas las personas que estuvieron conmigo apoyándome incondicionalmente en este proceso educativo, que fue largo, a mis padres que me acompañaron desde el primer día de clases, a mi esposo por su apoyo incondicional a mis hijos y amigos, especialmente a mi amiga y compañera de este proyecto y a mi tutora que nos supo guiar.. Patricia Fernández Cedeño.

(8) viii. ÍNDICE Portada…………………………………………………………………………………………………………………………...i Directivos……………………………………………………………………………………………………………………….ii Certificado de aprobación……………………………………………………………………………………………..iii Informe revisión final…………………………………………………………………………………………………….iv Licencia…………………………………………………………………………………………………………………………..v Dedicatoria…………………………………………………………………………………………………………………….vi Agradecimiento………………………………………………………………………………………………………..…..vii Índice……………………………………………………………………………………………………………………………viii Índice de cuadros…………………………………………………………………………………………………………..ix índice de tablas……………………………………………………………………………………………………………...x índice de imágenes…………………………………………………………………………………………………………xi índice de anexos…………………………………………………………………………………………………………...xii Resumen……………………………………………………………………………………………………………………...xiii Abstract……………………………………………………………………………………………………………………….xiv Introducción………………………………………………………………………………………………………………….xv CAPÍTULO I: EL PROBLEMA 1.1 Planteamiento del problema de investigación……………………………………………………..1 1.2 Formulación del problema…………………………………………………………………………………..6 1.3 Sistematización……………………………………………………………………………………………………6 1.4 Objetivos de la Investigación……..……………………………………………………………………….6 1.5 Justificación e importancia…………………………………………………………………………………..7 1.6 Delimitación del Problema…………………………………………………………………………………..8 1.7 Premisas de la Investigación…………………………………………………………………………….....9 1.8 Operacionalización de las variables…………………………………………………………………...10 CAPÍTULO II: MARCO TEÓRICO 2.1 Antecedentes del estudio………….……………………………………………………………………...12 2.2 Marco Teórico - Conceptual ……………..……………………………………………………………...13.

(9) ix. Porta..................................................................................................................................... i CAPÍTULO I ...................................................................................................................... 1 EL PROBLEMA ............................................................................................................... 1 1.1. Planteamiento del problema de investigación ........................................... 1. 1.2. Formulación del problema............................................................................... 6. 1.3. Sistematización .................................................................................................. 6. 1.4. Objetivos de la Investigación ......................................................................... 6. Objetivo General............................................................................................................. 6 1.5. Justificación e Importancia ............................................................................. 7. 1.6. Delimitación del problema ............................................................................... 8. 1.7. Premisas de la investigación .......................................................................... 9. 1.8. Operacionalización de las variables ........................................................... 10. CAPÍTULO II ................................................................................................................... 12. ÍNDICE DE CUADROS Cuadro Nº 1 Operacionación de las variables .......................................................... 10 Cuadro Nº 2 Plan de trabajo .................................................................................... 71.

(10) x. ÍNDICE DE TABLAS. Tabla Nº 1 Población de la Unidad Educativa Universitaria Francisco Huerta Rendón...................38 Tabla Nº 2 Estratos de la muestra de la Unidad Educativa Universitaria Francisco Huerta Rendón………………………………………………………………………………………………………………………………………38 Tabla Nº 3 Muestra de la Unidad Educativa Universitaria Francisco Huerta Rendón……………….….39 Tabla Nº 4 Nivel de conocimiento académico con la relación de la lógica matemática ……………...41 Tabla Nº 5 Frecuencia de las actividades complementarias dentro de la clase............................. 42 Tabla Nº 6 Componentes numéricos…………………………………………………………..................................43 Tabla Nº 7 Materiales didácticos................................................................................................... 44 Tabla Nº 8 Problemas matemáticos.............................................................................................. .45 Tabla Nº 9 Estudio matemático……………………………....................................................................... 46 Tabla Nº 10 Metodología matemática…………………………………….....................................................47 Tabla Nº 11 Nivel de conocimiento en el pensamiento lógico matemático……............................. 48 Tabla Nº 12 Beneficios en el desarrollo de talleres educativos….................................................. 49 Tabla Nº 13 Interacción del docente en talleres educativos.......................................................... 50 Tabla Nº 14 Nivel académico apropiado para impartir la lógica matemática................................ 51 Tabla Nº 15 Aplicación de actividades lúdicas durante la clase..................................................... 52 Tabla Nº16 Metodología empleada en clases................................................................................ 53 Tabla Nº 17 Apoyo del material empleado para la planificación y preparación de la clase...........54 Tabla Nº 18 Preparación de evaluaciones...................................................................................... 55 Tabla Nº 19 Las capacitaciones le ayudaran a aplicar las actividades lúdicas................................56 Tabla Nº 20 Problemas relevantes de la práctica docente............................................................ 57 Tabla Nº 21 Desarrollo de metodologías acorde al ritmo y estilo del estudiante......................... 58 Tabla Nº 22 Implementación de talleres educativos en el fortalecimiento del proceso formativo en el área de matemática ………………………………………………………………………………………….………………59 Tabla Nº 23 Promover talleres educativos a los estudiantes en el área lógico matemático......... 60 Tabla Nº 24 Resultado general de la evaluación a estudiantes..... ……………………………………….…….61 Tabla Nº 25 Presupuesto................................................................................................................69.

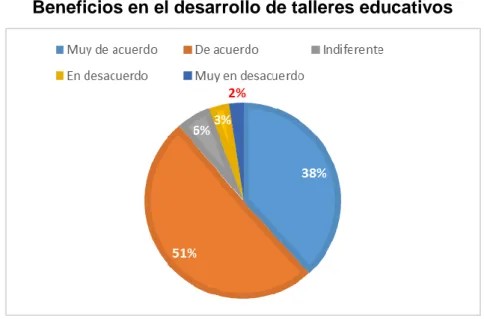
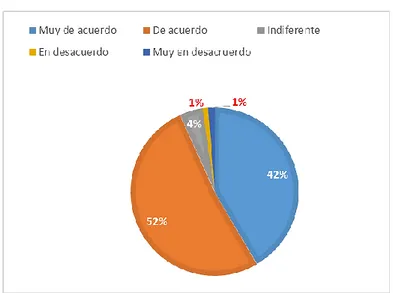
(11) xi. ÍNDICE DE GRÁFICOS. Gráfico Nº 1 Nivel de conocimiento académico con la relación de la lógica matemática….....…....41 Gráfico Nº 2 Frecuencia de las actividades complementarias dentro de la clase......................... 42 Gráfico Nº 3 Componentes numéricos………………………………………………………….............................. 43 Gráfico Nº 4 Materiales didácticos................................................................................................ 44 Gráfico Nº 5 Problemas matemáticos.............................................................................................45 Gráfico Nº 6 Estudio matemático…………………………….................................................................... 46 Gráfico Nº 7 Metodología matemática…………………………………….....................................................47 Gráfico Nº 8 Nivel de conocimiento en el pensamiento lógico matemático……............................ 48 Gráfico Nº 9 Beneficios en el desarrollo de talleres educativos….................................................. 49 Gráfico Nº 10 Interacción del docente en talleres educativos....................................................... 50 Gráfico Nº 11 Nivel académico apropiado para impartir la lógica matemática............................. 51 Gráfico Nº 12 Aplicación de actividades lúdicas durante la clase.................................................. 52 Gráfico Nº 13Metodología empleada en clases............................................................................. 53 Gráfico Nº 14 Apoyo del material empleado para la planificación y preparación de la clase........54 Gráfico Nº 15 Preparación de evaluaciones.................................................................................. .55 Gráfico Nº 16 Las capacitaciones le ayudaran a aplicar las actividades lúdicas.............................56 Gráfico Nº 17 Problemas relevantes de la práctica docente......................................................... 57 Gráfico Nº 18 Desarrollo de metodologías acorde al ritmo y estilo del estudiante....................... 58 Gráfico Nº 19 Implementación de talleres educativos en el fortalecimiento del proceso formativo en el área de matemática …………………………………………………………………………………….……………………59 Gráfico Nº 20 Promover talleres educativos a los estudiantes en el área lógico matemático...... 60 Gráfico Nº 21 Resultado general de la evaluación a estudiantes..... …………………………………….…….61. ÍNDICE DE IMÁGENES Imagen Nº 1 Imagotipo................................................................................................ 69 Imagen Nº 2 Significado de los colores utilizados........................................................ 70 Imagen Nº 3 Afiche...................................................................................................... 72 Imagen Nº 4 Portada del folleto de los talleres............................................................ 73 Imagen Nº 5 Bolígrafo.................................................................................................. 74 Imagen Nº 6 Pulseras.....................................................................................................74.

(12) xii. ÍNDICE DE ANEXOS Anexo 1: Formato de evaluación de la propuesta........................................................................ 125 Anexo 2: Acuerdo del Plan de Tutoría ......................................................................................... 126 Anexo 3: Informe de avance de la gestión tutorial ...................................................................... 127 Anexo 4: Envío de informe a directora de la carrera …………........................................................ 128 Anexo 5: Rúbrica de evaluación trabajo de titulación ................................................................. 129 Anexo 6: Certificado de porcentaje de similitud ......................................................................... 130 Anexo 7: Rúbrica de evaluación memoria escrita ....................................................................... 131 Anexo 8: Carta de la carrera dirigida al plantel ........................................................................... 132 Anexo 9: Carta del colegio de autorización.................................................................................. 133 Anexo 10: Evidencias de la aplicación de la encuesta y test de conocimientos a los estudiantes................................................................................................................................... 134 Anexo 12: Evidencias de la entrevista a la autoridad ...................................................................135 Anexo 13: Certificado de práctica docente ..................................................................................136 Anexo 14: Certificado de vinculación .......................................................................................... 138 Anexo 15: Formato de los instrumentos de investigación .......................................................... 140 Anexo 16: Evidencias de tutorías ................................................................................................. 144 Anexo 17: Ficha de registro de tesis .............................................................................................145.

(13) xiii. UNIVERSIDAD DE GUAYAQUIL FACULTAD DE FILOSOFÍA, LETRAS Y CIENCIAS DE LA EDUCACIÓN CARRERA MERCADOTECNIA Y PUBLICIDAD TÍTULO DEL TRABAJO DE INVESTIGACIÓN PRESENTADO ACTIVIDADES LUDICAS EN EL DESARROLLO LOGICO MATEMATICO.TALLERES EDUCATIVOS. Autor(es): Melissa Macias y Patricia Fernández Tutor(a): Lic. Delfa Mantilla Pacheco. Msc. Guayaquil, agosto del 2019. RESUMEN La presente investigación se centra en analizar la influencia de las actividades lúdicas en el PEA mediante la investigación de campo y de un estudio bibliográfico para identificar el nivel de desarrollo lógico matemático de los estudiantes de octavo grado, de la Unidad Educativa Universitaria Francisco Huerta Rendón, por lo cual se profundizo el estudio de las variables: actividades lúdicas en el desarrollo lógico matemático, desde un enfoque cuali-cuantitativo debido a que se realizó un estudio bibliográfico y de campo, en el cual se emplearon instrumentos de investigación tales como test de conocimiento, encuestas, docentes y estudiantes y entrevista a la autoridad, se detectó que los docentes valoran la aplicación de estrategias de aprendizaje activo, sin embargo en la práctica y al relacionar con los resultados del test aplicado a los estudiantes nos muestra un nivel muy bajo de dominio cognitivo basado en el desarrollo del pensamiento lógico, aplicado a las matemáticas. Por esa razón, se proponen talleres educativos en los que a través de diversas actividades basadas en la pedagogía activa, desarrollen las habilidades cognitivas de los estudiantes, como un complemento de las clases en el área de las matemáticas.. Palabras Claves: Lúdicas, Lógica, Matemáticas, Talleres.

(14) xiv. UNIVERSITY OF GUAYAQUIL FACULTY OF PHILOSOPHY, LETTERS AND EDUCATION SCIENCES CAREER MARKETING AND ADVERTISING TITLE OF RESEARCH WORK PRESENTED LUDIC ACTIVITIES IN MATHEMATICAL LOGICAL DEVELOPMENT. EDUCATIONAL WORKSHOPS. Author(s): Melissa Macias y Patricia Fernández Advisor: Lic. Delfa Mantilla Pacheco. Msc. Guayaquil, august of 2019. ABSTRACT This research focuses on analyzing the influence of recreational activities in the PEA through field research and a bibliographic study to identify the level of mathematical logical development of eighth grade students, of the Francisco Huerta Rendón University Educational Unit, for which the study of the variables was deepened: recreational activities in the mathematical logical development, from a qualitative-quantitative approach because a bibliographic and field study was carried out, in which research instruments such as knowledge test were used , surveys, teachers and students and an interview with the authority, it was detected that teachers value the application of active learning strategies, however in practice and when relating to the results of the test applied to students it shows us a very low level of cognitive domain based on the development of logical thinking, applied to mathematics Attics For this reason, educational workshops are proposed in which, through various activities based on active pedagogy, students develop cognitive skills, as a complement to the classes in the area of mathematics. Keywords: Playful, Logic, Mathematics, Workshops.

(15) xv. Introducción. La presente investigación se refiere al desarrollo lógico matemático que se pueden definir como la inferencia mediante la construcción de sistemas formales. Estos sistemas capturan las características esenciales de las inferencias válidas en los lenguajes naturales, pero al ser estructuras formales susceptibles de análisis matemático, permiten realizar demostraciones rigurosas sobre ellas. Cabe recalcar que la deficiencia. de. estos. conocimientos. no. posibilita. un. correcto. desenvolvimiento dentro del aula de clases causando limitaciones.. Este proyecto tiene como objetivo principal diagnosticar cuales son los factores que afectan directamente sobre el desarrollo lógico matemático en los estudiantes y docentes de 8vo de EGB del Unidad Educativa Universitaria “Francisco Huerta Rendón” y su influencia directa con el rendimiento escolar, mediante instrumentos de investigación como: encuestas, entrevistas y test de conocimientos para conocer más a fondo la problemática.. Para el desarrollo de esta investigación, se aplicó el método de, bibliográfica, campo, cuali-cuantitativa, descriptivo y explicativo por esta razón se obtuvo una muestra representativa de la población total que integra la problemática, respectivo a 89 estudiantes de octavo año de EGB, un docente y por último a una de las autoridades de dicho establecimiento.. Capítulo I: entre otros aspectos puede abarcar planteamiento del Problema, formulación y sistematización del mismo, objetivos de la investigación,. justificación,. delimitación,. investigación y su operacionalización.. hipótesis. o. premisas. de.

(16) xvi. Capítulo II: en el cual se incorporan los antecedentes de la investigación, Marco Teórico, marco contextual, marco conceptual, marco legal, entre otros.. Capítulo III: el cual debe abarcar los aspectos metodológicos empleados en el desarrollo del trabajo de titulación.. Capítulo IV: comprende el desarrollo de la Propuesta de la investigación. Conclusiones. Recomendaciones, Referencias Bibliográficas. Anexos..

(17) CAPÍTULO I. EL PROBLEMA 1.1. Planteamiento del problema de investigación. Internacionalmente el programa TIMSS (Estudio Internacional de Tendencias en Matemáticas y Ciencias) un trabajo de Investigación de la IEA (Asociación Internacional para la Evaluación del Rendimiento Educativo) que se lleva a cabo en más de 60 países con el fin de comparar sistemas educativos en dos edades diferentes, cuarto grado (entre 9 y 10 años de edad) y octavo básico (entre 13 y 14 años).. Más de 600.000 estudiantes participaron en los tests cuyos resultados dieron a notar que los estudiantes de Singapur, Hong Kong, Corea del Sur, Taiwán y Japón siguen en los primeros lugares respecto a las Matemáticas.. TIMSS demostró una vez más que los recursos del hogar son un predictor relevante del rendimiento académico.. "La diferencia de puntaje entre los estudiantes de familias de bajo nivel socioeconómico y de los pertenecientes a una de alto nivel es de 78 puntos en promedio". (BBC Mundo, 2016). "Y eso demuestra la importancia de implementar la Ley de Inclusión, principal herramienta de la reforma educacional". (BBC Mundo, 2016). La inversión en la educación ha aumentado considerablemente en la última década a 5.57% del PBI 2017, sim embargo es importante verificar la forma en la que se está administrando y financiando cada institución.. 1.

(18) Según el ministerio de educación de cada 100 jóvenes que empiezan la secundaria solo 40 terminan a tiempo y 10 con retraso denlo cuales la otra mitad lo abandona.. En matemáticas casi 80% de los estudiantes de las escuelas públicas no dominan la materia en cambio en escuelas privadas fue solo la mitad, esto demuestra una gran brecha que se halla entre las escuelas privadas y pública.. Parte de la responsabilidad se encuentran entre las distintas reglas de gestión y formas de financiamiento educativo, quizás al corregir esto habría más equidad en el ambiente educativo.. En la gestión, es importante que los directores se profesionalicen y tengan la posibilidad de manejar los recursos humanos y físicos para poder hacerse responsables de sus resultados. Con respecto al financiamiento no todos los países, cuentan con instituciones privadas que den la oportunidad a familia de escasos recursos a optar por una mejor educación.. El programa de la OCDE es de gran aporte en más de 80 países, y el cual se ampliará a 90 a finales del 2018. La OCDE ha coordinado tipos de estudios sobre estudiantes, docentes, directores y escuelas: PISA que estudia las habilidades cognitivas y socio-afectivas de los estudiantes y TALIS que aporta información sobre características de directores y docentes, así como de algunos procesos educativos y pedagógicos que se dan en los centros de estudios.. El informe también señala constantemente la desigualdad de género. Los varones tienen más posibilidades que las mujeres de repetir curso, abandonar los estudios y no entrar a la Universidad. Sin embargo, a pesar. 2.

(19) de su mejor desempeño académico, las mujeres continúan obteniendo bajos resultados en términos de empleo e ingresos.. Las mujeres siguen teniendo menos probabilidades de matricularse y graduarse en ámbitos bien remunerados en el Universidad. Por ejemplo, a pesar de la gran demanda de conocimientos de ingeniería que existe en la actualidad, solo el 6% de las mujeres con titulación universitaria han finalizado un grado de ingeniería, a comparación de los hombres con un 25%. En México la situación es distinta ya que muestra un mayor equilibrio entre hombres y mujeres, con un 11% de mujeres con titulación universitaria en el ámbito de la ingeniería.. También existen marcadas diferencias respecto al logro de la equidad en los resultados de aprendizaje: en todos los países de la OCDE, el rendimiento en matemáticas de los alumnos de 15 años de edad está estrechamente relacionado con el estatus socioeconómico de los estudiantes y la ubicación, urbana o rural, de sus centros educativos. En la mayoría de países, esta asociación se ha mantenido inalterada durante la última década.. El informe Panorama de la Educación proporciona estadísticas nacionales comparables que miden el estado de la educación en todo el mundo. El informe analiza los sistemas educativos de los 36 países miembros de la OCDE, así como de Argentina, Brasil, China, Colombia, Costa Rica, India, Indonesia, Federación Rusa, Arabia Saudí y Sudáfrica.. El Ecuador participó por primera vez en la prueba PISA-D 2018. El 70,9% de los estudiantes de Ecuador no alcanzó en Matemáticas el nivel 2, categorizado como el nivel de desempeño básico. El desempeño promedio de Ecuador fue de 377 sobre 1.000.. 3.

(20) En Ecuador, la muestra consistió en 6.108 estudiantes de 173 colegios fiscales, fiscomisionales, municipales y privados de todo el país, de zonas urbanas y rurales. PISA-D se realizó con la participación de Ecuador y ocho países más: Bután, Camboya, Guatemala, Honduras, Panamá, Paraguay, Senegal y Zambia. Todos estos países participaron por primera vez, son de ingresos medios y bajos, con tasas de pobreza, analfabetismo y desempleo mayores que los de los países de la OCDE.. Entre los países que participaron en PISA-D, Ecuador tuvo el mejor desempeño en todas las materias. Sin embargo, es importante considerar que la mayor parte de los estudiantes no llegaron al nivel 2 en Matemáticas ni en Ciencias.. Por competencias En Ecuador, el 49 % de los estudiantes alcanzó el nivel mínimo de Competencia en Lectura, el 29 % en Matemáticas y el 43 % en Ciencias.. Por género Las niñas tienen 8 puntos más que los niños en lectura. Mientras que en matemáticas los niños tienen 20 puntos más que las niñas.. Mejor condición Los estudiantes con un nivel socioeconómico alto tienen 3,2 veces más probabilidad de alcanzar, por lo menos, el nivel 2 en matemáticas.. Rurales y urbanos Los estudiantes de colegios urbanos tienen un mejor desempeño que estudiantes de colegios rurales. En lectura la diferencia es de 19 puntos. Repetir año 4.

(21) Los niños en Ecuador tienen 1,6 veces mayor probabilidad que las niñas de repetir grado en Ecuador. La repetición escolar está vinculada a un bajo desempeño. (El Universo, 2019). Las causas que conllevan esta problemática tiene un enfoque en la falta de hábitos de concentración y estudios que dan paso a un bajo rendimiento académico, por eso es muy poca la actualización en el proceso de enseñanza-aprendizaje.. El hecho científico se encuentra en el proceso de enseñanzaaprendizaje es lo más importante con respecto a la calidad de la educación, un rendimiento académico bajo, tiene mucho que ver con el manejo de la metodología de enseñanza del docente en la asignatura, esto definirá el origen del problema, en diversas situaciones la causa principal más frecuente es el desinterés por parte del estudiante por la poca motivación del docente quien enseña de manera tradicional en el área de matemáticas, muchas veces los docentes explican los temas tal y como se encuentran en el texto educativo y envían deberes más complejos que el explicado en clase lo cual trae como resultado la copia de tareas entre compañeros.. La ausencia de las actividades lúdicas da a relucir el nulo interés y motivación en el razonamiento lógico de manera proactiva, la continua catedra ajustada al libro y la pizarra crea un ambiente monótono durante las clases, el docente al no innovar la asignatura de matemática no capta el interés del estudiante lo cual conlleva la carencia del desarrollo del razonamiento lógico.. El mal manejo de la tecnología y los insumos en las aulas de clases afecta al estudiante, si bien es cierto el manejo de la pizarra y el marcador es lo que comúnmente se encuentra dentro del aula, por lo cual los 5.

(22) estudiantes suelen recurrir a comprender de una mejor forma un ejercicio mediante videos en línea.. 1.2. Formulación del problema. ¿De qué manera influyen las actividades lúdicas en el desarrollo lógico matemático del estudiante de octavo año de Educación Básica en la Unidad Educativa Universitaria Francisco Huerta Rendón año 2019-2020?. 1.3. Sistematización. ¿De qué manera influyen las actividades lúdicas en el PEA? ¿Cómo incide el desarrollo lógico matemático en el proceso educativo del estudiante? ¿En qué aporta el contenido de los talleres educativos con actividades lúdicas a la formación integral del estudiante?. 1.4. Objetivos de la Investigación. Objetivo General. Diagnosticar la importancia de las actividades lúdicas en el desarrollo lógico matemático del estudiante de octavo año de Educación Básica de la Unidad Educativa Universitaria Francisco Huerta Rendón, mediante una investigación bibliográfica y de campo con encuestas, entrevistas y test de conocimientos para el desarrollo de niveles educativos.. 6.

(23) Objetivos Específicos. 1. Analizar la influencia de las actividades lúdicas en el PEA realizando un estudio bibliográfico.. 2. Identificar el nivel de desarrollo lógico matemático que demuestran los estudiantes mediante un estudio de campo, encuestas, entrevistas y test de conocimientos.. 3. Validar el contenido de talleres educativos con actividades lúdicas para potencializar la formación escolar a partir de los resultados obtenidos en la investigación.. 1.5. Justificación e Importancia. La presente investigación tiene como propósito diagnosticar el déficit académico de los estudiantes relacionado al desarrollo de habilidades matemáticas, identificar posibles nudos que afectan el PEA.. La importancia de emplear actividades lúdicas en el desarrollo lógico matemático del estudiante Actualmente es importante para los beneficiaros que serán los estudiantes de octavo año de EGB del colegio experimental Francisco Huerta Rendón ya que consiente en. integrar al proceso de. enseñanza y aprendizaje estrategias que potencialicen las actividades lúdicas como parte del PEA. dentro del salón de clases gracias la. adquisición de poder ampliar y desarrollar sus conocimientos y habilidades por aprender algo totalmente dinámico. Está investigación es conveniente para la sociedad educativa en general como docentes y estudiantes en primer plano ya que de esta 7.

(24) manera pueden adquirir nuevos saberes con la finalidad de establecer programas donde los adolescentes participen exponiendo su capacidades, habilidades y destrezas al momento de realizar una proyecto que tenga relación absoluta con el tema anteriormente expuesto siendo relevante porque el permite atraer conocimientos de manera transformadora, estimulando así al estudiante a desarrollar en el ámbito personal y profesional gracias a la integración de actividades lúdicas. Básicamente en implicación práctica se indagará la influencia que genera las actividades lúdicas en el desarrollo lógico matemático de los estudiantes para lo cual se propone el diseño de talleres educativos que permitan. implementar. estrategias. que. potencialicen. la. formación. académica que integren la cotidianidad de los procesos mentales cognitivos en los estudiantes. El valor teórico de la investigación es lograr que en las instituciones en especial en el Colegio Francisco Huerta Rendón tengan conocimientos los docentes y estudiantes sobre cómo realizar y emplear actividades lúdicas que permitan reconocer el desarrollo lógico matemático como herramienta principal en el ámbito educativo.. 1.6. Delimitación del problema. Campo:. Educación. Área:. Matemática. Aspectos:. Actividades lúdicas, lógica matemática, talleres educativos.. Título:. Actividades lúdicas en el desarrollo lógico matemático. Propuesta: Talleres educativos. Contexto:. Unidad Educativa Universitaria Dr Francisco Huerta Rendón.. 8.

(25) 1.7. Premisas de la investigación. 1. Los aspectos que impulsan las actividades lúdicas ayudan a estimular el desarrollo lógico matemático. 2. Los campos de las actividades lúdicas mejoran el desarrollo lógico matemático. 3. Los beneficios de la actividad lúdica optimizan el desarrollo lógico matemático. 4. Las funciones de las actividades lúdicas estimulan las habilidades y potencialidades con el fin de obtener un buen desarrollo integral 5. Conectores del desarrollo lógico matemático. 6. Las etapas de Piaget influyen en el desarrollo lógico matemático de acuerdo a los estadios evolutivos de los estudiantes. 7. Los factores que favorecen el desarrollo lógico matemático son los diferentes recursos didácticos y actividades adecuadas que se presentan en la etapa de educación Infantil 8. Los elementos del desarrollo. lógico. matemático desarrollan. determinadas funciones cognitivas que van a derivar en la adquisición de conceptos básicos. 9. Los talleres educativos integran actividades didácticas con la finalidad de fortalecer el Desarrollo integral del educando. 10. Los talleres educativos ayudan a desarrollar las habilidades, capacidades y razonamiento lógico matemático.. 9.

(26) 1.8. Operacionalización de las variables Tabla. No. 1. Variables. Dimensión. Dimensión. Conceptual. operacional. Teoría. Indicadores. Teorías Piaget. del. juego . Emoción. . Sensación. . Autoestima. . Creatividad. . Psicología. . Física. de. . Autoconfianza. actividad. . Autonomía. . Personalidad. de. . Integradora. las actividades. . Rehabilitadora. Aspectos que es aquello que se impulsan. las. puede realizar en el actividades tiempo libre, con el lúdicas 1.Variable Independien te. objetivo de liberar tensiones, huir de la rutina diaria y de las Campos preocupaciones,. N° 1 Actividades Lúdicas. para. obtener. poco. de. diversión. que. y influyen en las un actividades. placer, lúdicas y. entretenimiento, así como. otros Beneficios. beneficios. la. (Significados, 2018). lúdica. Funciones. lúdicas 10.

(27) Éste es una relación creada. Conectores del. internamente la cual desarrollo se. constituye. descubrir. al lógico y matemático.. . Razonamiento. . . Inteligencia. . Capacidad. . Sensoriomotora. . Preoperacional. . Cognitivo. . Socioafectivo. . Ambiente. establecer relaciones entre los objetos. relaciones Etapas. de. igualdad, Piaget. que. de semejanza. y influyen en el. diferencia. El niño desarrollo 2. Variable. no puede construir lógico. Dependiente. la. relación. de matemático.. diferencia si no es No 2 Desarrollo lógico matemático. capaz de observar e identificar. las Factores. distintas. que. favorecen. el. propiedades en los desarrollo objetos hacen. que. lo lógico. de. aprendizaje. diferentes. matemático. En este sentido, los docentes necesitan aplicar. el. conocimiento físico Elementos del. . para establecer en desarrollo el. niño. estructura. una lógico lógico- matemático. Enseñanzaaprendizaje. . Conocimiento. . Habilidad. matemática. (Frutos, 2012) Fuente: Unidad Educativa Universitarias Francisco Huerta Rendón Elaborado: (Patricia Fernández, Melissa Macias, 2019). 11.

(28) CAPÍTULO II. MARCO TEORICO. 2.1. Antecedentes del Estudio. Este apartado traerá investigaciones referentes al tema que se está estudiando, con el propósito de analizar cómo ha sido tratado el tema, en el cual se recopilara de diferentes fuentes de información como tesis, monografías, artículos científicos y escritos de editores reconocidos:. Según (Reyes, 2016), el cual en su investigación que fue realizada para la obtención del grado de Licenciada en Ciencias de la Educación, Mención: Psicología Infantil y Educación Parvulario, que hace referencia a Las actividades lúdicas para desarrollar el pensamiento lógico-matemático de las niñas y niños, dando como resultado que la falta de actividades lúdicas genera el desinterés; para resolver esta problema propone un taller de actividades lúdicas que consiste en que los pequeños puedan participar y aprender con materiales interesantes que les permitan adquirir un nuevo conocimiento.. Según (Ortega, 2013), en su investigación termina dando como resultado que los maestros tienen conocimientos sobre la motivación a los estudiantes mediante las actividades lúdicas, pero no se aplica como una estrategia que permita desarrollar el pensamiento lógico matemático de los estudiantes, por ello hay que orientar a los docentes para concienciar sobre la importancia que tienen las actividades lúdicas en el desarrollo del pensamiento lógico matemático de los estudiantes. 12.

(29) 2.2. Marco Teórico - Conceptual. Definiciones de Lúdicas. Según Jiménez (2002) La lúdica es más bien una condición, una predisposición del ser frente a la vida, frente a la cotidianidad. Es una forma de estar en la vida y de relacionarse con ella en esos espacios cotidianos en que se produce disfrute, goce, acompañado de la distensión que producen actividades simbólicas e imaginarias con el juego.. Para Motta (2004) la lúdica es un procedimiento pedagógico en sí mismo. La metodología lúdica existe antes de saber que el profesor la va a propiciar. La metodología lúdica genera espacios y tiempos lúdicos, provoca interacciones y situaciones lúdicas. La lúdica se caracteriza por ser un medio que resulta en la satisfacción personal a través del compartir con la otredad.. En cambio para Waichman (2000) es imprescindible la modernización del sistema educativo para considerar al estudiante como un ser integral, participativo, de manera tal que lo lúdico deje de ser exclusivo del tiempo de ocio y se incorpore al tiempo efectivo de y para el trabajo escolar.. Importancia de las técnicas lúdicas Dávila (2003) menciona que María Montessori fue una de las primeras en utilizar juegos básicos y ejercicios lúdicos para desarrollar la discriminación perceptiva y táctil. Para ella, el juego es una actividad libre, ordenada de tal manera que conduzca a una finalidad definida.. 13.

(30) El docente debe profundizar en las actividades lúdicas, acercándose más al educando, dándole confianza y estimulándolo en prácticas que le generen seguridad y confianza personal. Para obtener unos resultados positivos y motivantes, el docente debe actualizarse constantemente adquiriendo conocimientos especializados, como es la docencia por medio de juegos, para mejorar el proceso de enseñanza-aprendizaje de las ciencias naturales en los educandos. (Paz, 2013). Características de las Técnicas Lúdicas De acuerdo con la investigación de Baena & Ruiz (2016) estas son Las siguientes características de las técnicas lúdicas: . La creatividad es una de las características más importantes del juego.. . Permite un desarrollo integral del infante.. . Conduce a un aprendizaje cooperativo, porque se lo puede realizar en equipo.. . Contienen reglas que permite que los niños y niñas participen ordenadamente, sin eliminar a sus integrantes.. . A traen experiencias de la vida cotidiana.. . Mayor desarrollo social, elevando la tolerancia, sinceridad y seguridad.. . Es lúdico y placentero.. . Tienen que ser supervisados por adultos.. Tipos de Técnicas Lúdicas Según Patricia Laffaurie (2017) la cual cita a Elsa Skrypiel en su libro (Psicología, 1990, págs. 103-104) propone la siguiente clasificación: 14.

(31)  Juegos constructivos  Juegos de argumento  Juegos al aire libre  Juegos didácticos  Juegos intelectuales. Juegos. constructivos:. son. de. carácter. individual. y. más. característicos de los párvulos en donde no se da importancia a la construcción de algo determinado, sino varía de acuerdo al material utilizado, por lo que este sufre y cobra forma diferente al proceso del mismo juego, en los cuales pueden mencionar cubos, arena, juegos de ensamble.. Juegos de argumento: estos ocupan un lugar importante en la formación de la personalidad del niño(a), debido a que se juegan sobre las diferentes situaciones de la vida, por lo que el infante asume e interpreta fenómenos de la vida, es aquí donde intervienen la expresión libre y la creatividad del niño/a, por medio del dibujo, pintura y dramatización (juegos de representación).. Juegos al aire libre: Dichos juegos se distinguen por su contenido intelectual, por medio de gestos y movimientos que desarrollan el aspecto físico emocional que siempre está presente en el juego al aire libre, ejemplo: La gallinita ciega, las escondidas, etc. Esto se desarrolla por medio de rondas, cantos y juegos grupales.. Juegos didácticos: Por su contenido, sus reglas y métodos a utilizar para su desarrollo, son elaborados por los(as) educadores(as) con fines instructivos; con frecuencia no reciben el nombre de juego, sino de clases lúdicas, es decir ven en ellos una forma especial del proceso docente, 15.

(32) llevando a cabo mediante el método del juego, estos juegos se utilizan fundamentalmente en el trabajo con niños de edad preescolar. Por ejemplo rompecabezas, juegos de memoria, etc.. Juegos intelectuales: por su naturaleza psicológica hacen recordar al juego didáctico y puede considerarse como una determinada etapa de desarrollo. Se diferencian en que se basan totalmente en la libre creación e iniciativa de los (as) niños / as como ejemplo se puede citar adivinanzas, preguntas y respuestas sobre temas escogidos. Se utilizan en edad escolar.. Ventajas de las Técnicas Lúdicas Las ventajas que los docentes obtendrían con implementar juegos según el Equipo Elige Educar (2014) son:. 1. Desarrolla la inteligencia práctica y el pensamiento divergente 2. Integran y valoran la diversidad dentro de un grupo 3. Facilitan la participación de estudiantes introvertidos 4. Vinculan la educación con el entretenimiento 5. Permiten adecuar rápidamente diversas modificaciones en los contenidos 6. Proporcionan una evaluación periódica y sistemática de aprendizajes 7. Ayudan a aprovechar el tiempo libre 8. Fomentan un “rol facilitador” por parte del profesor 9. Potencian el trabajo en equipo y sus habilidades asociadas 10. Proporcionan práctica y retroalimentación apropiada. 16.

(33) Fundamentaciones Fundamentación Epistemológica La epistemología es la ciencia que trata de conocer la naturaleza del conocimiento humano, en sus principios reales y en su funcionamiento real, los tipos o clases de conocimiento y los caminos o métodos que pueden conducir a su realización correcta en cada caso.. La fundamentación epistemológica de acuerdo a Carlos Morales (2014, pág. 6) relata que la relación que existe entre el pensamiento crítico con la epistemología, anunciando lo siguiente: Es así como el pensamiento crítico nace siendo una crítica epistemológica, un examen de la razón y de sus métodos.. Según Carlos Gallegos & Gerardo Rosales (2012, pág. 1)La Epistemología crítica es una propuesta epistémica, que entiende la construcción del conocimiento como un proceso centrado en la recuperación de las perspectivas históricas planteadas por y desde los sujetos subalternos, por sus demandas en el presente, así como sus expectativas frente al futuro. Siempre en el marco de una disputa por la definición de su identidad, su colocación social y su práctica.. Es una propuesta nacida de la necesidad del pensamiento crítico de reflexionar cómo construir y cómo producir conocimiento científico opuesto a los paradigmas neoliberales dominantes, desarrollada por científicos sociales latinoamericanos influidos teórica y analíticamente por: Karl Marx, Friedrich Engels, Antonio Gramsci, Theodor W. Adorno, Max Horkheimer, Herbert Marcuse, Ernst Bloch, Fernand Braudel, Walter Benjamin, Alfred Schütz y George Gurvitch hasta Michel Foucault, Cornelius Castoriadis, 17.

(34) Pierre Bourdieu e Immanuel Wallerstein entre los autores más importantes. (Gallegos Elias & Rosales Carranza, 2012) La epistemología es simplemente una teoría del conocimiento, nos da a entender cuál es la posición del saber propio de cada disciplina. La epistemología nos dice que clase de conocimiento es la Teoría de la educación.. Tratando de relacionar la fundamentación epistemológica con el estudio de la aplicación de las técnicas lúdicas, se puede dar a conocer que los docentes para brindar un buen servicio, deben estar muy bien preparados con los suficientes conocimientos para poder dar sus clases, tomando en cuenta que para el uso de herramientas y recursos dentro del proceso de enseñanza aprendizaje, es necesario tener la capacidad para dominarlos.. Fundamentación Psicológica La fundamentación psicológica de acuerdo al tema planteado este puede variar dependiendo de los factores que se puedan presentar; esto haciendo referencia que, cada uno de los alumnos son un mundo diferente en donde tienen diversas maneras de comprensión y de recibir la información que se les da; un factor importante del cual hablar es la motivación, ya que de eso influye para que el estudiante preste atención, se concentre y pueda lograr captar los conocimientos; la persona idónea para elevar el nivel de motivación es el docente, a través de diversos métodos durante su jornada laboral.. De acuerdo a la investigación de Wilfredo Moreno & Miriam Velásquez (2016, pág. 5) afirma que: Lev Vygotsky (1978) es uno de los teóricos que 18.

(35) asume la psicología como estudio de la conciencia, y pone énfasis en el ser y su interacción social, destacando la importancia del entorno social en el desarrollo de los procesos psicológicos superiores: el lenguaje, el pensamiento y el razonamiento desde una postura socio-histórica. Tal como menciona el autor, la psicología estudia la interacción entre los individuos, es decir, que la construcción del pensamiento crítico forma parte esencial para el desarrollo integral del estudiante; además, permite estudiar la conducta de cada uno de los niños y niñas ante sus demás compañeros, considerando que las técnicas lúdicas se las consigue a través del aprendizaje cooperativo.. Fundamentación Sociológica Raquel Suriá (2010, pág. 2) cita a (Zanden, 1986) argumentando que él hace referencia a la interacción, porque se trata de un proceso bidireccional: el individuo recibe influencias del medio y a su vez él también influye sobre este.. Suriá (2010, pág. 2) también cita a (Guy, 1990) En este enfoque, consideramos que los individuos receptan los elementos socio-culturales los cuales influyen en su personalidad y es así como al adquirir esa nueva información se adaptan al nuevo entorno social.. En base a las definiciones anteriores citadas por Suriá (2010, pág. 2) y aplicándolas en nuestra investigación podemos referirnos a los docentes como guías de la Institución quienes logran trasmitir sus ideales, valores, creencias, conductas aceptables; y para la Psicología se puede afirmar que. 19.

(36) toda actividad en la que participe el estudiante se verá reflejado en su personalidad.. Raquel Suriá (2010, pág. 5), cita a (Bandura, 1982) en su teoría del Aprendizaje Social donde afirma que las personas aprenden la mayor parte de su conducta a través de la observación de modelos: al observar a los demás uno se hace a la idea de cómo se efectúan las conductas nuevas y, posteriormente, esa información nos sirve como guía de acción.. LA TEORIA DEL APRENDIZAJE SOCIAL. Según (Bandura, 1982) La exposición a un modelo puede producir uno de los tres siguientes efectos:. 1. Modelado. Aprendizaje de respuestas nuevas que el observador desconoce. 2. Inhibición o desinhibición de respuestas aprendidas previamente. Las respuestas existen en el repertorio del sujeto. No tienen por qué ser exactamente iguales que las del modelo. 3. Facilitación o provocación de respuestas existentes en nuestro repertorio de conductas. La observación puede provocar imitación porque la percepción de esos actos funciona como “disparador” de respuestas de la misma clase.. En base al aprendizaje vicario que se mencionó anteriormente podemos decir que al aplicarlo en una Institución serían los estudiantes los 20.

(37) que al observar al docente adquieren, experiencias de las actividades que realizan, lo cual les sirve de guía para efectuar las acciones que crean pertinentes.. Procesos. del. aprendizaje. vicario. Según. Bandura. (1982),. el. aprendizaje vicario está controlado por 4 procesos:. 1. Atención; 2. Reproducción; 3. Retención; 4. Motivación. Fundamentación Pedagógica El aprendizaje humano se define como el cambio relativamente invariable de la conducta de una persona a partir del resultado de la experiencia. Este cambio es conseguido tras el establecimiento de una asociación entre un estímulo y su correspondiente respuesta. (Pérez & Gardey, 2008). . Concepción idealista-platónica. Entre la gran variedad de creencias sobre las relaciones entre las matemáticas y sus aplicaciones y sobre el papel de éstas en la enseñanza y el aprendizaje, podemos identificar dos concepciones extremas. Una de estas concepciones, que fue común entre muchos matemáticos profesionales hasta hace unos años, considera que el 21.

(38) alumno debe adquirir primero las estructuras fundamentales de las matemáticas de forma axiomática. Se supone que una vez adquirida esta base, será fácil que el alumno por sí solo pueda resolver las aplicaciones y problemas que se le presenten.. Según esta visión no se puede ser capaz de aplicar las matemáticas, salvo en casos muy triviales, si no se cuenta con un buen fundamento matemático. La matemática pura y la aplicada serían dos disciplinas distintas; y las estructuras matemáticas abstractas deben preceder a sus aplicaciones en la Naturaleza y Sociedad. Las aplicaciones de las matemáticas serían un "apéndice" en el estudio de las matemáticas, de modo que no se producirían ningún perjuicio si este apéndice no es tenido en cuenta por el estudiante.. Las personas que tienen esta creencia piensan que las matemáticas son una disciplina autónoma. Podríamos desarrollar las matemáticas sin tener en cuenta sus aplicaciones a otras ciencias, tan solo en base a problemas internos a las matemáticas.. Esta. concepción de las matemáticas se designa como "idealistaplatónica". Con esta concepción es sencillo construir un currículo, puesto que no hay que preocuparse por las aplicaciones en otras áreas. Estas aplicaciones se “filtrarían”, abstrayendo los conceptos, propiedades y teoremas matemáticos, para constituir un dominio matemático “puro”. . Concepción constructivista. Otros matemáticos y profesores de matemáticas consideran que debe haber una estrecha relación entre las matemáticas y sus aplicaciones a lo largo de todo el currículo. Piensan que es 22.

(39) importante mostrar a los alumnos la necesidad de cada parte de las matemáticas antes de que les sea presentada. Los alumnos deberían ser capaces de ver cómo cada parte de las matemáticas satisfacen una cierta necesidad. Ejemplo: Poniendo a los niños en situaciones de intercambio les creamos la necesidad de comparar, contar y ordenar colecciones de objetos. Gradualmente se introducen los números naturales para atender esta necesidad. En. esta visión, las aplicaciones, tanto externas como internas, deberían preceder y seguir a la creación de las matemáticas; éstas deben aparecer como una respuesta natural y espontánea de la mente y el genio humano a los problemas que se presentan en el entorno físico, biológico y social en que el hombre vive.. Los. estudiantes. axiomatización,. la. deben. ver,. generalización. por y. la. sí. mismos,. abstracción. que. la. de. las. matemáticas son necesarias con el fin de comprender los problemas de la naturaleza y la sociedad. A las personas partidarias de esta visión de las matemáticas y su enseñanza les gustaría poder comenzar con algunos problemas de la naturaleza y la sociedad y construir las estructuras fundamentales de las matemáticas a partir de ellas. De este modo se presentaría a los alumnos la estrecha relación entre las matemáticas y sus aplicaciones.. La elaboración de un currículo de acuerdo con la concepción constructivista es compleja, porque, además de conocimientos matemáticos, requiere conocimientos sobre otros campos. Las estructuras de las ciencias físicas, biológicas, sociales son relativamente más complejas que las matemáticas y no siempre hay un isomorfismo con las estructuras puramente matemáticas. Hay una abundancia de material disperso sobre aplicaciones de las matemáticas. en. otras. áreas,. pero. la. tarea. de. selección, 23.

(40) secuenciación e integración no es sencilla. (Gómez, Molano, & Rodriguez, 2015). Según Zabalsa (1991)se considera que “el aprendizaje se ocupa básicamente de tres dimensiones: como constructo teórico, como tarea del alumno y como tarea de los profesores, esto es, el conjunto de factores que pueden intervenir sobre el aprendizaje.. 2.3. Marco Contextual El proyecto se fundamentó en una problemática presentada en la. Unidad Educativa Universitaria „„Francisco Huerta Rendón‟‟, institución fiscal, fundada en 1971, con el objetivo de que los estudiantes de la Universidad de Guayaquil, Facultad de Filosofía, Letras y Ciencias de la Educación puedan realizar las prácticas docentes de educación media. Puesto que, el anterior colegio anexo, Francisco Campos Coello, fue fiscalizado por la dictadura militar.. Al principio hubo un gran grupo de estudiantes inscritos, que por razones políticas habían sido expulsados de otras instituciones fiscales. El curso lectivo 1971 – 1972, inicio con tres cursos de ciclo básico y dos secciones. Más adelante, hubo mayor demanda de matrículas, por ende era necesario tener más espacio físico y se crearon dos extensiones más.. Actualmente la institución está ubicada en la avenida Las Agua, cerca de la institución educativa Espíritu Santo y la Facultad de Ingeniera Industrial de la Universidad de Guayaquil. Cuenta con 1141 estudiantes, 35 docentes y 4 autoridades. También poseen tres laboratorios de 24.

(41) computación, una biblioteca, tres canchas para realizar diferentes actividades deportivas como fútbol, básquet o vóley y tres bares.. Además, cuentan con una banda de guerra formada por los estudiantes de los diferentes cursos de la institución, dirigidos por un docente, y se presentan en las diferentes festividades que haya en la ciudad como las del mes de Julio y Octubre o alguna actividad que sea necesaria su aparición como el cambio de abanderados, el juramento a la bandera, entre otras.. En otro aspecto, la unidad educativa posee 95 computadoras distribuidas en los laboratorios de computación, de las cuales 6 están sin funcionar y en cada uno hay un proyector perenne para que los jóvenes puedan apreciar de mejor forma los procesos que se realicen en los programas a enseñar por parte del docente. Solo uno ellos posee una pizarra interactiva, que fue equipada por el Estado, pero no es utilizada debido a que no cuentan con el programa que les permita manipularla.. El acceso a internet es limitado dentro de los laboratorios, debido a que solo se lo activa cuando es necesario en la clase, mediante antenas de wi-fi, pero en uno de los bares hay una computadora con acceso a internet e impresoras, a la cual los docentes y estudiantes pueden dar uso para imprimir documentos o sacar copias, tomando en cuenta que para ello, hay que pagar.. Por otra parte hay 4 proyectores extras que pueden ser utilizados por los educadores y colegiales para proyectar vídeos, diapositivas, imágenes o algún recurso de apoyo, en alguna exposición que los jóvenes realicen. 25.

(42) Anteriormente, está unidad educativa contaba con un auditorio pero por el aumento de estudiantes que ha habido, fue transformado en aulas de clases, en la actualidad las actividades que se realizaban en ese lugar, se efectúan en la biblioteca debido a que posee mayor espacio y las condiciones del lugar permiten que se puedan realizar proyecciones y presentaciones.. 2.4. Marco Legal. Constitución de la República del Ecuador (2008) Título II Derechos Capítulo II Derechos del buen vivir Sección II Ambiente sano Art. 15.- El Estado promoverá, en el sector público y privado, el uso de tecnologías ambientalmente limpias y de energías alternativas no contaminantes y de bajo impacto. La soberanía energética no se alcanzará en detrimento de la soberanía alimentaria, ni afectará el derecho al agua. Se. prohíbe. el. desarrollo,. producción,. tenencia,. comercialización,. importación, transporte, almacenamiento y uso de armas químicas, biológicas y nucleares, de contaminantes orgánicos persistentes altamente tóxicos, agroquímicos internacionalmente prohibidos, y las tecnologías y agentes biológicos experimentales nocivos y organismos genéticamente modificados perjudiciales para la salud humana o que atenten contra la soberanía alimentaria o los ecosistemas, así como la introducción de residuos nucleares y desechos tóxicos al territorio nacional.. 26.

(43) Sección III Comunicación e información Art. 18.- Todas las personas, en forma individual o colectiva, tienen derecho a: 1. Buscar, recibir, intercambiar, producir y difundir información veraz, verificada, oportuna, contextualizada, plural, sin censura previa acerca de los hechos, acontecimientos y procesos de interés general, y con responsabilidad ulterior. 2. Acceder libremente a la información generada en entidades públicas, o en las privadas que manejen fondos del Estado o realicen funciones públicas. No existirá reserva de información excepto en los casos expresamente establecidos en la ley. En caso de violación a los derechos humanos, ninguna entidad pública negará la información.. Sección V Educación Art. 27.- La educación se centrará en el ser humano y garantizará su desarrollo holístico, en el marco del respeto a los derechos humanos, al medio ambiente sustentable y a la democracia; será participativa, obligatoria, intercultural, democrática, incluyente y diversa, de calidad y calidez; impulsará la equidad de género, la justicia, la solidaridad y la paz; estimulará el sentido crítico, el arte y la cultura física, la iniciativa individual y comunitaria, y el desarrollo de competencias y capacidades para crear y trabajar.. 27.

(44) La educación es indispensable para el conocimiento, el ejercicio de los derechos y la construcción de un país soberano, y constituye un eje estratégico para el desarrollo nacional.. Art. 28.- La educación responderá al interés público y no estará al servicio de intereses individuales y corporativos. Se garantizará el acceso universal, permanencia, movilidad y egreso sin discriminación alguna y la obligatoriedad en el nivel inicial, básico y bachillerato o su equivalente.. Es derecho de toda persona y comunidad interactuar entre culturas y participar en una sociedad que aprende. El Estado promoverá el diálogo intercultural en sus múltiples dimensiones. El aprendizaje. se. desarrollará. de forma. escolarizada. y no. escolarizada.. La educación pública será universal y laica en todos sus niveles, y gratuita hasta el tercer nivel de educación superior inclusive.. Título VII Régimen del Buen Vivir Capítulo I Inclusión y Equidad Sección I Educación Art. 349. El Estado garantizará al personal docente, en todos los niveles y modalidades, estabilidad, actualización, formación continua y mejoramiento pedagógico y académico; una remuneración justa, de acuerdo a la profesionalización, desempeño y méritos académicos. La ley 28.

(45) regulará la carrera docente y el escalafón; establecerá un sistema nacional de evaluación del desempeño y la política salarial en todos los niveles. Se establecerán políticas de promoción, movilidad y alternancia docente.. Reglamento general a la ley orgánica de educación intercultural (2015) Título IX De la carrera Educativa Capítulo VII De la oferta de formación permanente para los profesionales de la educación Art. 311.- De los procesos de formación permanente para los profesionales de la educación. El Nivel Central de la Autoridad Educativa Nacional, con el objeto de mejorar las competencias de los profesionales de la educación, certifica, diseña y ejecuta procesos de formación en ejercicio, atendiendo a las necesidades detectadas a partir de los procesos de evaluación y a las que surgieren en función de los cambios curriculares, científicos y tecnológicos que afecten su quehacer.. Art. 312.- Programas y cursos de formación permanente. El programa de formación permanente es un conjunto o grupo de cursos relacionados entre sí que se orientan al logro de un objetivo de aprendizaje integral y puede. vincular. acciones. de. acompañamiento. posterior. para. la. implementación de lo aprendido.. El curso de formación es una unidad de aprendizaje relacionada con un tema o una tarea específica.. 29.

(46) Art. 313.- Tipos de formación permanente. La oferta de formación en ejercicio para los profesionales de la educación es complementaria o remedial.. La formación permanente de carácter complementario se refiere a los procesos de desarrollo profesional, capacitación, actualización, formación continua, mejoramiento pedagógico y académico para que provean a los docentes de conocimientos y habilidades distintas de las aprendidas en su formación inicial.. La formación permanente de carácter remedial es obligatoria y se programa para ayudar a superar las limitaciones que tuviere el docente en aspectos específicos de su desempeño profesional. Código de la niñez y adolescencia (2014) Titulo l Definiciones Capítulo III Derechos relacionados con el desarrollo Art. 45.- Derecho a la información.- Los niños, niñas y adolescentes tienen derecho a buscar y escoger información; y a utilizar los diferentes medios y fuentes de comunicación, con las limitaciones establecidas en la ley y aquellas que se derivan del ejercicio de la patria potestad. Es deber del Estado, la sociedad y la familia, asegurar que la niñez y adolescencia reciban una información adecuada, veraz y pluralista; y proporcionarles orientación y una educación crítica que les permita ejercitar apropiadamente los derechos señalados en el inciso anterior. Capítulo VI Deberes, capacidad y responsabilidad de los niños, niñas y adolescentes. 30.