UNIVERSIDAD POLITÉCNICA DE
ESCUELA TÉCNICA SUPERIO
DE
CAMINOS CANALES Y PUERTOS
INYECCIÓN DE GRANDES GRIETAS
CON RESINA EPOXI
UNiVtRSlDíD FOLIT CN!GA DE MADRID
ETS. ING.:M!ERO.Í .r. CAV.iNOS B I P- L I O T E :. A RTRO. E T K A A 30 A-^Q» N. üoCU^^AÍ - \ 0
N." EJ-/v\PL4if¡
SiGNATURA M..Í....<C. .2^:3^.-..^ -.-=-:-:-::::::PÍE.
ADEL MOHAMED FATHY^ ABI^ELAZIZ
INGENffiRO CIVILFACULTAD DE INGENIEROS, UNIVERSIDAD DE AIN SHAMS EL CAIRO, EGIPTO
DIRECTOR DE TESIS
JAIME PLANAS ROSSELLO
DOCTOR INGENIERO DE CAMINOS CANALES Y PUERTOS
Presidente
: fJa^^^^^ tlic^^ Gu
Vocales: \\or)p C V v f ^ ^ ^ ( l r e Í h '
^j^í^^--=^
Vocal Secretario : Q^ ^ ^ T W O V^, 6 J )
€^VN3AGRADECIMIENTOS
Mi agradecimiento, en primer lugar, a RODIO, Cimentaciones Especiales S. A., que no sólo financió una buena parte de la investigación sino que propuso las líneas generales del tema de estudio. Gracias especialmente a D. José Luis Rojo que alentó e impulsó el proyecto desde sus inicios, a D. Pietro de Porcellinis cuyo asesoramiento en el manejo y propiedades del material ha sido fiíndamental en mi trabajo, y a D. Juan Secadas, que aportó su experiencia en obra para concretar los problemas reales y circunscribir el análisis a lo prácticamente realizable.
Deseo también agradecer al Catedrático Dr. D. Manuel Ellees Calafat la constante ayuda que de él he recibido para superar las dificultades de todo tipo surgidas durarnte la realización de este trabajo. Es para mí un ejemplo por su continua lucha para mantener su departamento en primera línea investigadora.
Igualmente agradezco a todos los miembros del equipo científico, personal docente y no docente, del Departamento de Ciencia de Materiales de esta Escuela la inestimable ayuda y amistad recibida sin la cual hubiera sido muy difícil realizar este trabajo. En especial deseo hacer mención de los Sres. Dr. D. José Ygnacio Pastor, D. Tomás Beleña Parrilla, D. José Miguel Martínez, D. David Culebras (exjefe del taller mecánico), D. Juan Serrano , D. Pascual Colas y D. Francisco Gálvez, por su colaboración en diversas partes de este proyecto.
También deseo agradecer a la Agencia Española de Cooperación Internacional y al Ministerio de Educación Egipcio por la beca que me ha permitido desarrollar este trabajo.
Finalmente, deseo expresar mi más profundo agradecimiento al estimado Catedrático Dr. D. Jaime Planas Rosselló por su constante apoyo, orientación, estímulo y noble exigencia durante la realización de esta Tesis. Me siento orgulloso por haber sido uno de los muchos alumnos que han tenido el privilegio de haber aprendido, gracias a un gran profesor como él, a analizar y resolver un problema científico.
ÍNDICE
Resumen 1
1 Introducción y antecedentes 5
1.1 Introducción 5 1.2 Objetivo general del estudio 6
1.3 Planteamiento general del problema . 10
1.3.1 Grietas estables 12 1.3.2- Grietas cerradas 12 1.3.3 Grietas activas 13 1.3.4 Acoplamiento con el problema de mecánica de fluidos . . 14
1.4 El comportamiento reológico de la resina 14 1.4.1 Ecuaciones constitutivas para fluidos 15
1.4.2 Influencia de la temperatura en las propiedades reológicas:
Equivalencia t - T 21 1.4.3 Influencia de la presión 25
1.4.4 Influencia del tiempo de curado 26
1.5 El flujo de la resina en la grieta 31 1.5.1 Flujo de fluidos newtonianos en una grieta lisa 32
1.5.2 Flujo de fluidos newtonianos en grietas rugosas abiertas 34 1.5.3 Flujo de fluidos newtonianos en grietas comprimidas . . . 40
1.6 Objetivos concretos de la tesis 44
2.1 Aplicación de la mecánica de la fractura a problemas de inyección 48
2.1.1 Fundamentos de la aproximación 48 2.1.2 Fundamentos de mecánica de fractura elástica y lineal . . 49
2.1.3 Extensión de la zona abierta por la inyección 51 2.1.4 Inyección axisimétrica puntual ^. 53
2.1.5 Inyección axisimétrica con presión de inyección constante 55
2.1.6 El caso axisimétrico general 56 2.1.7 Fundamento del cálculo de la apertura de fisura 58
2.1.8 Distribución de aperturas para un proceso de inyección . . 60
2.2 Teoría del flujo en inyecciones axisimétricas 60
2.2.1 Ecuación de continuidad 61 2.2.2 Ecuación de Darcy generalizada 62
2.2.3 Ecuación de avance del frente de inyección 63
2.2.4 Ecuaciones de contomo 64 2.3 Inyección de grietas de caras paralelas con fluidos newtonianos . 67
2.3.1 Inyección de una grieta de caras paralelas y estáticas . . . 68
2.3.2 Inyección de una grieta de caras paralelas móviles 70 2.4 Inyección de un macizo deformable con un fluido newtoniano . . 72
2.4.1 Análisis cualitativo del proceso de inyección 72
2.4.2 Ecuaciones generales 74 2.4.3 Modelo simplificado 7^ 2ÁÁ Análisis por el método de elerriientos finitos 77
2.5 Inyección de fluidos newtonianos generalizados potenciales . . . 85
2.5.1 Ley de Darcy generalizada 85
2.5.2 Flujo radial 86 2.5.3 Inyección de ima grieta de caras paralelas y estáticas . . . 87
2.5.4 Inyección de una grieta de caras paralelas móviles 88 2.5.5 Inyección de u n macizo deformable: modelo simplificado 89
3 Estudio experimental 91
3.1 Descripción general de la experimentación 91 3.2 Ensayos de viscosimetría de placa y cono 93
3.2.1 Principio de funcionamiento 93
3.2.2 Equipo experimental 94 3.2.3 Ejecución de los ensayos 101 3.2.4 Proceso de datos y presentación de resultados 102
3.2.5 Resultados básicos de la experimentación 105
3.3 Ensayos de viscosimetría de flujo radial 108 3.3.1 Principio de ftmcionamiento 109
3.3.2 Equipo experimental 110 3.3.3 Ejecución de los ensayos 117 3.3.4 Proceso de datos y presentación de resultados 120
3.4 Ensayos de flujo radial en grieta rugosa 124 3.4.1 Principio de funcionamiento 124
3.4.2 Equipo experimental 126 3.4.3 Fabricación de las plaquetas de mortero 127
3.4.4 Montaje de las losetas en la máquina 133
3.4.5 Ejecución de los ensayos 135 3.4.6 Proceso de datos y presentación de resultados 136
4 Análisis y discusión de resultados 139
4.1 Reología de la resina 139 4.1.1 Resina sin endurecedor 140
4.1.2 Extensión de la equivalencia t-T 141 4.1.3 Influencia de la temperatura y del tiempo en la resina con
endurecedor 143 4.2 Flujo radial de la resina 148
4.2.1 Análisis de los ensayos de viscosimetría radial 148 4.2.2 Resultados de los ensayos de flujo entre placas rugosas . . 156
4.3.2 Comparación con el modelo simplificado newtoniano . . . 165 4.3.3 Análisis dimensional del modelo simplificado potencial. . 167
4.3.4 Estudio paramétrico 168
5 Conclusiones y trabajo futuro 175
5.1 Conclusiones 175 5.2 Trabajo futuro 177
Bibliografía 179
APÉNDICES
A Detalles analíticos 191
A.l Determinación de la apertura de grieta 191 A. 1.1 Principios de cálculo de la apertura de grieta 191
A. 1.2 Expresión de la apertura para fisura axisimétrica 194 A. 1.3 Determinación de la apertura para inyección con presión
uniforme 195
B Ensayos de viscosimetría de placa y cono 197
C Ensayos de viscosimetría de flujo radial 249
D Ensayos de flujo radial en placas rugosas _ 271
RESUMEN
Una grieta en una presa o en otra gran estructura, incluyendo macizos rocosos,
supone un riesgo para la seguridad y la funcionalidad. En muchos casos una
solución del problema consiste en inyectar con resina epoxi, que fluye en la grieta
y luego endurece y la sella, adhiriendo las dos caras de la fisura.
Para conseguir una buena adherencia, es preciso ua buen contacto entre la
resina y las caras de la grieta. Esto puede cor\seguirse usando una resina muy
viscosa inyectada a gran presión sobre áreas muy pequeñas. La elevada presión
abre ligeramente la grieta, la limpia y fuerza a un contacto muy íntimo entre
la resina y el hormigón o la roca. Si el tamaño de la zona que se presuriza es
pequeño comparado con las dimensiones de la estructura, el procedimiento es
completamente seguro aunque las presiones locales sean elevadas.
Este trabajo trata de este tipo de inyecciones, y busca un método general para
cuantificar la evolución de las variables involucradas en el proceso. Para ello se
necesitan ecuaciones que describan el flujo de la resina en la grieta y la apertura
producida por la presión de inyección, así como métodos para resolverlas.
Las propiedades de la resina, como ingrediente básico del proceso, han sido
investigadas teórica y experimentalmente. Específicamente, se han realizado
ensayos viscométricos para encontrar una ecuación constitutiva adecuada para
la resina, que incluya el efecto de la velocidad de deformación, de la temperatura
y del tiempo de curado. El resultado más importante en este campo es que la
resina no es newtoniana y puede ser aproximada por im fluido viscoso potencial
para todas las temperaturas y estados de curado investigados.
El flujo de la resina en la grieta se ha investigado también teórica y
experi-mentalmente. Se han hecho experimentos de flujo radial en grietas tanto lisas
como rugosas. Los resultados muestran que las ecuaciones teóricas describen
consistentemente las observaciones experimentales para fisuras de caras lisas y
permiten proponer una fórmula que incorpora las modificaciones inducidas en
abordado mediante el método de los elementos finitos y modelos simplificados
en el caso idealizado de ima gran grieta en un medio elástico. El componente
esencial del método consiste en la aplicación de técnicas y conceptos de mecánica
de la fractura para desarrollar ima fórmula que permita calcular la apertura de la;
grieta cuando se conoce la distribución de presiones de inyección. Esta relación,
junto con las ecuaciones de flujo, determina completamente el problema.
El sistema resultante de ecuaciones integro-diferenciales, definido sobre un
dominio cuyo contomo es móvil, ha sido resuelto numéricamente para varios
casos usando un programa de elementos finitos especialmente desarrollado para
ello. En paralelo, se ha creado una técnica semi-analítica que reduce el problema
a un sistema de 5 ecuaciones diferenciales no lineales, con lo que se ha conseguido
un método simplificado y muy rápido para analizar el proceso de inyección que
da resultados razonablemerite próximos a los conseguidos mediante el método
de elementos finitos.
Uno de los resultados esenciales del análisis es que, cuando se inyecta a
cau-dal constante, la presión aumenta primero rápidamente, alcanza un máximo y
después decrece lentamente. Esto significa que la parte de la estructura que
descansa sobre la grieta actúa como una válvula de seguridad sin que ello
im-plique desplazamientos globales de la estructura. Muy al contario, la reducción
de presión es debida exclusivamente a deformaciones locales y la estructura es
siempre perfectamente estable.
El modelo simplificado se ha utilizado para realizar un análisis paramétrico
de los factores que influyen^n la presión de pico, y se han creado abacos de
ABSTRACT
Cracks in dams and other huge structures, including rock foimdatioris, may be of a major safety concern. In many cases a good solution of the problem is grouting with epoxy resins that flow into the crack and then harden, bonding the two faces of the crack.
In order to achieve a good bonding, an intímate contact between the crack faces and the resin is needed. This can be achieved by using a highly viscous resin at high pressures over small crack áreas. The high pressure slightly and locally opens the crack, cleans the zone and makes the resin to get into very intímate contact with the concrete or rock on both sides of the crack. If the extensión of the pressurized zone is kept small compared to the overall structure dimensions, the procedure is completely safe even though the local pressures are high.
This work deals with this kind of grouting, seeking a general procedure to quantify the evolution of the various variables involved in the process. To this end, equations are needed to describe the flow of the resin in the crack, and the crack opening produced by the grouting pressure.
The properties of the resin as the basic ingredient of the process have been investigated both theoretically and experimentally. Specifically, viscometric tests have been performed to ascertain a suitable constítutive equation for the resin including the effect of velocity gradient, temperature, and gelation time. The most important results in this field is that the resin is non newtonian and can be approximated by a power law viscous fluid over the range of temperatures and gelation times investigated.
elastic médium, has been investigated using fínite elements and simplified
mod-els. The essential ingredient of the approach consists in using fracture mechanics
concepts to develop a formula delivering the crack opening as a function of the
grouting pressure.
This, together with the flow equations, completely determines the problem.
The resulting set of integrodifferential equations defined over a región with
mov-ing boundaries has been numerically solved for a numbered of cases usmov-ing a
specially developed finite element program. Simultaneously, a semi-analytical
procedure has been devised that reduces the problem to a set of 5 nonlinear
differential equations, thus providing a simplified and very fast procedure to
analyze the grouting problem that has been shown to give results reasonably
cióse to those delivered by the finite element method.
One of the essential results of the analysis is that during grouting at constant
flow rate the pressure first increases sharply, goes through a peak and then
decreases slowly. This means that the part of the structure lying on the crack
acts as a relief valve; however, this relief is produced by local deformations, not
by overall displacements; therefore the structure is always perfectly stable.
The factors goveming the pressure peak have been parametrically
investi-gated by means of the simplified model and a series of design plots are given
Capítulo 1
Introducción y antecedentes
1.1 Introducción
En esta tesis se aborda el problema ingenieril de la inyección de grandes grietas con resinas epoxi. Este tipo de inyecciones involucra a tres componentes que in-teraccionan dando lugar a un comportamiento conjunto relativamente complejo. Estos componentes son
1. La resina: Es el componente base cuyo objetivo es rellenar y sellar la grieta. Es un componente "vivo" que se inyecta en estado fluido y debe distribuirse adecuadamente en el interior de la grieta para luego endurecer sirviendo de puente entre las dos caras de la grieta.
2. La grieta: Es el componente cuyos efectos negativos se quieren eliminar me-diante la inyección. Sus dimensiones y topología, en particular su apertura y su rugosidad, y las condiciones en que se encuentra (limpia, inundada, drenada, etc.) condicionan totalmente el movimiento de la resina en su seno.
Estos tres componentes del sistema interaccionan de forma dinámica durante
la inyección, al menos en el tipo de inyecciones que en este trabajo consideramos,
ya que se producen a presiones suficientes como para que la grieta se abra
lo-calmente debido a la deformación provocada por la presión de la resina. La
abertura local modifica los parámetros de la grieta que a su vez modifica la
condiciones de flujo de la resina. Todo ello da lugar a un sistema de ecuaciones
acopladas altamente no lineales cuyo estudio abordamos, para casos sencillos
pero representativos, en este trabajo.
En este capítulo pretendemos delimitar el objeto de esta tesis, y acotar, en
base a otros trabajos y experiencias previas los objetivos concretos del estudio
teórico que se desarrolla en el Capítulo 2 y de la experimentación que se presenta
en el Capítulo 3. En el Capítulo 4 se discuten los resultados, tanto teóricos como
experimentales, y en el Capítulo 5 se resumen las conclusiones fundamentales y
se dibujan las posibilidades de futuros trabajos.
1.2 Objetivo general del estudio
En esta tesis consideramos la inyección de grandes grietas: grietas de decenas o
centenares de metros en dimensiones lineales y de centenares de metros
cuadra-dos de superficie. Son grietas que se dan en grandes presas o en macizos rocosos,
no las que se dan en estructuras más habituales como las de edificación o las de
puentes o pasos elevados.
Por sus dimensiones, su sellado requiere cantidades de resina que se miden
en toneladas y es prácticamente imposible efectuar la inyección en una sola
operación tal como puede hacerse con una grieta de unos pocos decímetros o
metros cuadrados.
Aunque es teóricamente posible hacer la inyección con resina de gran fluidez
que puede rellenar grietas ordinarias por simple gravedad o por inyección a muy
baja presión, ésta resulta una técnica poco fiable en el caso de grandes grietas
1.2. Objetivo general del estudio 7
1. Para hacer vina inyección a baja presión con resina muy fluida y
asegu-rar que la resina llena completamente la grieta es preciso garantizar que
la resina no puede escaparse de la grieta antes de endurecer. Esto exige
sellar todos los posibles caminos de escape de la resina, lo que en una gran
grieta es muy difícil, ya que en muchos casos no se conocen en detalle
las ramificaciones y conexiones en zonas profundas: la grieta puede, por
ejemplo, atravesar un dren a profundidad tal que esa vía de escape pase
desapercibida hasta que es demasiado tarde.
2. Para este tipo de inyecciones es preciso también que se efectúe una
in-yección ascendente para que la resina desaloje el aire o agua que haya en
la grieta, y hay que disponer purgas en los puntos en que la grieta-forme
un sifón. Sin embargo, ésto es muy difícil porque en una grieta de gran
tamaño la topología no suele ser conocida con detalle.
3. La colada de resina fluida puede rellenar adecuadamente una grieta
pe-queña, limpia y abierta, adheriendo convenientemente las dos caras de
la grieta. Pero si hay polvo, barro, agua, o la grieta está cerrada a trozos,
como puede suceder en una presa a bajo nivel de embalse, en el que la grieta
está comprimida por el peso propio, es difícil que una resina inyectada en
grandes superficies a baja presiónpueda eliminar los residuos o penetrar
en las zonas comprimidas y establecer un contacto íntimo con el hormigón
o roca sano en ambas caras de la grieta.
Es posible que existan soluciones a algunos de los problemas anteriores, como
efectuar una limpieza previa de la grieta con agua a presión. Pero el proceso es
complejo, caro y difícil de garantizar. Y ciertamente los problemas se multiplican
si la grieta está sumergida y el agua circula por ella, como es muy habitual: la
resina fluida es inmediatamente "lavada" por la corriente de agua, antes de que
pueda efectuar el sellado, a menos que se corte previamente, con otra técnica, la
corriente de agua.
realiza-Figura 1.2.1: Esquema de inyección de una grieta desde galería con múltiples puntos de
in-yección.
Figura 1.2.2: Esquema de inyección de una grieta desde superficie. Desde cada taladro de
inyección se inyecta una superficie relativamente pequeña.
ción de inyecciones de resina muy viscosa —casi pastosa— a presiones elevadas y
secuencialmente en muchos puntos. La inyección puede efectuarse desde galería
tal como esquematiza la Fig. 1.2.1 o desde superficie, como indica la Fig. 1.2.2.
El punto clave de este tipo de inyecciones es que conjugan alta viscosidad y
alta presión con poca superficie inyectada de una sola vez, del orden de unas
decenas de metros cuadrados. Al ser la presión elevada —superior en general
a la presión de tierras y ciertamente superior a la presión del agua que pueda
haber en la grieta— se desaloja con facilidad la suciedad y el aire y se consigue
im buen contacto de la resina con la roca sana. Si además la presión es suficiente,
1.2. Objetivo general del estudio
Figura 1.2.3: Esquema tridimensional de la inyeccón de una grieta en un punto
incluyendo zonas que en inyecciones a baja presión estarían en contacto y no quedarían bien selladas.
Aunque la presión es elevada, si la inyección se diseña adecuadamente la estabilidad de la estructura no se ve amenazada. Esto es debido a que la superficie activamente inyectada (i.e., bajo presión) es muy pequeña comparada con el tamaño de la estructura. Debe subrrayarse que aunque esquemas bidimensio-nales como los de las figuras anteriores ayudan a hacerse una idea del método, el proceso de inyección es realmente tridimensional tal y como se esquematiza en la Fig. 1.2.3, por lo que si las dimensiones lineales de la zona inyectada son del orden de, por ejemplo, 10 veces inferiores a las dimensiones lineales de la estructura, la relación de áreas es de 1 a 100.
Esta diferencia de escala implica que aunque la presión de inyección sea relativamente elevada, la fuerza resultante de esta presión es muy inferior a las fuerzas involucradas en el equilibrio de la estructura (peso propio y empuje de aguas, por ejemplo). "Además, aunque las deformaciones locales pueden ser elevadas (veremos que la grieta puede durante la inyección abrirse del orden de un milímetro), los corrimientos se anulan con la distancia r como P^lr^, donde R es el radio de la zona bajo presión, por lo que a tres o cuatro veces el radio de
inyección prácticamente no se dejan sentir.
hemos expuesto. Sin embargo, se carece de tina metodología de análisis
cuan-titativo de este proceso. El objetivo general de esta tesis es iniciar el camino
para el establecimiento de análisis cuantitativos de este tipo de inyecciones. Más
concretamente, el objetivo es buscar las relaciones que permiten cuantificar cómo
avanzará la resina en la grieta y cómo se deformará la estructura cuando se haga
una inyección de una forma determinada (por ejemplo, a caudal constante).
Para este análisis es obviamente preciso conocer las propiedades relevantes
de la resina, particularmente su ecuación constitutiva, conocer las leyes de flujo
de la resina en la grieta, y conocer cómo se deforma la estructura por efecto de
la presión.
Ninguno de estos aspectos a conocer es trivial y en una primera aproximación
hay que simplificar y acotar debidamente los objetivos de la investigación. Esto
es lo que se hace en los apartados siguientes de este Capítulo. En primer lugar
centramos un poco más el problema en cuanto a la grieta y la deformación de la
estructura; a continuación analizamos las teorías disponibles para la descripción
del comportamiento reológico de la resina y para la descripción del flujo de la
resina en la grieta; finalmente concretamos los objetivos a cubrir en el trabajo.
1.3 Planteamiento general del problema
De acuerdo con lo expuesto en la sección anterior, se pretende estudiar procesos
de inyección a alta presión, efectuados secuencialmente en zonas de pequeña
ex-tensión. La presión de inyección produce deformaciones que es preciso calcular.
En una primera aproximación parece lógico hacer un análisis simple suponiendo
un comportamiento elástico lineal del material de la estructura.
Supongamos entonces que del análisis de mecánica de fluidos conocemos
la distribución de presiones en las caras de la grieta. Se trata de determinar
las deformaciones de la estructura en elasticidad lineal. Sin embargo aunque
supongamos que el comportamiento del material es elástico, el comportamiento
1.3. Planteamiento general del problema 11
particular, pero muy especialmerite del tipo de grieta que tengamos y de la
localizacióri de la inyeccióri. Desde este pimto de vista, podemos clasificar las
grietas en tres tipos básicos:
1. Grietas activas. Son aquellas generadas por causas permanentes que están
todavía en acción de forma que la grieta está todavía creciendo o en estado
crítico (creciendo-a velocidad muy pequeña). Un ejemplo típico son las
grietas generadas por deformaciones diferenciales (expansión química,
re-tracción, entumecimiento, asientos diferidos) que han estado aumentando
hasta el momento del estudio.
2. Grietas estables. Son aquellas generadas por causas que han finalizado
su acción dejando la grieta abierta. Es el caso límite del caso anterior y los
ejemplos son los mismos con la condición de que cesaran con suficiente
antelación al estudio.
3. Grietas cerradas. Son aquellas que se abrieron por acciones extraordinarias
y luego volvieron a cerrarse debido a las cargas permanentes, teniendo en el
momento del estudio sus caras comprimidas. Es el caso de grietas creadas
por accidentes de todo tipo, en particular grietas horizontales producidas
durante un terremoto.
Desgraciadamente la clasificación no es independiente de las condiciones de
contomo, y una misma grieta puede pasar de una a otra situación al
modifi-car esas condiciones. Por ejemplo, una grieta en una presa puede ser activa
a embalse lleno, estar estabilizada cuando el nivel se encuentra entre el 50 y
el 90% del máximo, y estar cerrada cuando el nivel desciende por debajo del
50%. Obviamente en la práctica puede resultar difícil saber en qué situación
nos encontramos, y uno de los objetivos a largo plazo es ver qué ensayos de
campo pueden realizarse para detectar la situación. La pertenencia a ima de las
tres clases es fundamental para el estudio de la inyección, como vamos a ver a
continuación, y permite hacer una definición más operativa de las clases
es el único realmente lineal, siendo los otros dos no lineales. Por esto vamos a
comenzar la exposición por este tipo de grietas.
1.3.1 Grietas estables
Desde el punto de vista de la inyección, la grieta es estable si la inyección no
va a provocar el crecimiento de la grieta. Eñ esta situación, pueden admitirse
como fijas todas las cargas menos las presiones de inyección. Puesto que no hay
cambios de geometría porque, por definición, en este caso ni crece la grieta ni
se cambian las condiciones de contacto-no contacto entre las caras de la grieta,
la deformación provocada por la presión de inyección es lineal, y uno puede
escribir
I Í ; ( X ) = I Í ; O + / G^(x,xXx')dA (1.3.1)
JSi
donde WQ es la apertura inicial de la fisura debida a las cargas permanentes,
G„(x, x') es la apertura en el punto x provocada por una fuerza unidad en el
punto x', p(x') es la presión en el punto x' y la integral está extendida a la zona
de inyección. Por supuesto la función de Green Gtü(x, x') es fija para un
proble-ma dado (no cambia con el proceso de inyección). La superficie de inyección se
obtiene como parte de la solución del problema completo. Para este caso
par-ticular, todo el problema en su aspecto estructural consiste en obtener (calcular)
la función de Green Gyj{^, x'), un problema que abordaremos como parte de la
tesis en el Capítulo 2.
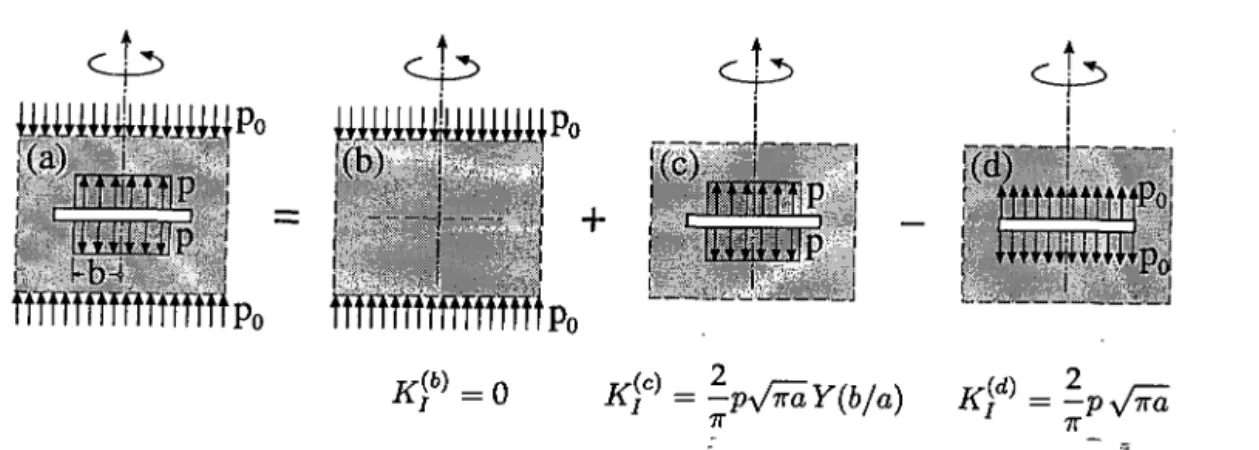
1.3.2 Grietas cerradas
Cuando la grieta está cerrada (en sentido mecánico, no hidráulico), la variación
de presión de contacto debe tenerse en cuenta y el problema deja de ser lineal
porque el contacto es siempre no lineal ya que no permite tracciones. En este
caso todo sucede como si la inyección estuviera produciendo una grieta, puesto
que el fluido separa los dos labios que estaban en contacto sobre un área que
ad-1.3. Planteamiento general del problema 13
'' ;; ;' Po
-J
PoFigura 1.3.1: Grieta inicialmente cerrada por una presión po abierta por efecto de la presión de
resina. Sa es el área en que se ha perdido el contacto y Si el área donde actúa la presión de la
inyección.
mitimos que, aunque la grieta esté mecánicamente cerrada al principio, el fluido
tiene una cierta capacidad de penetración debido al espacio que queda entre
asperezas, tendremos una cierta apertura media inicial WQ. Sea po la presión que
se ejerce entre las caras de la fisura antes de iniciarse la inyección (Fig. 1.3.1). Es
posible demostrar (Capítulo 2) que la apertura de fisura debe venir dada por una
ecuación del tipo
w (x) = WQ+ I G(x, x'; SM-^)dA - f G{x, x', Sa)po{^')dA (1.3.2)
JSi JSa
donde Sa es el área sobre la cual se ha perdido el contacto, y ahora la función
de Green G(x, x', Sa) depende de este área y por tanto se pierde totalmente la
linealidad. Veremos en el Capítulo 2 que para determinar el área sobre la que se
ha perdido el contacto, una nueva incógnita, se puede hacer uso, con ventaja, de
los conceptos de mecánica de la fractura.
1.3.3 Grietas activas
Cuando la grieta es activa, la inyección hará que esa grieta crezca. Incluso en
la hipótesis simplificada de que el crecimiento de la grieta puede describirse
lineal. La posición del nuevo frente de grieta debe determinarse como parte de
la solución y, debido al tipo de inyección que estamos considerando, es evidente
que el tratamiento tiene que ser tridimensional.
Obviamente este último caso es extremadamente complejo y está relacionado
con problemas de hidrofracturación. Pero es incluso más complicado porque
requiere la modelización detallada de toda la estructura. En particular, exige
conocer la geometría de toda la fisura con cierto detalle y las condiciones de
contorno reales, lo que en la práctica es extremadamente difícil. Dejaremos el
estudio de situaciones como ésta fuera de un primer análisis de los procesos de
inyección, ya que no permiten simplificaciones apreciables ni son susceptibles
de generalización.
1.3.4 Acoplamiento con el problema de mecánica de fluidos
Como acabamos de ver, un dato básico para la determinación del efecto
estruc-tural es la distribución de presiones de la resina, que debe obtenerse del análisis
de mecánica de fluidos de la resina en la grieta. El resultado depende de la
reología de la resina y de las características de la grieta, particularmente de su
apertura, y también de las condiciones de bombeo de la resina. Por consiguiente
es preciso buscar modelos para la resina y para la grieta antes de poder
com-pletar el análisis. En las dos secciones siguientes resumimos los conocimientos
disponibles sobre estos temas antes de concretar los objetivos de la investigación.
1.4 El comportamiento reológico de la resina
Antes de poder acotar los objetivos de la tesis, es preciso tener una idea del tipo de
conocimiento que necesitamos acerca del comportamiento de la resina. La resina
es un fluido polimérico que puede presentar un comportamiento no newtoniano
y su respuesta reológica es muy dependiente de la temperatura. Además es
un material que gelifica —endurece— y debemos ser capaces de predecir el
1.4. El comportamiento teológico de la resina 15
someramente los modelos disponibles para describir la respuesta mecárüca de
la resina, y su dependencia respecto de la temperatura y del tiempo.
El énfasis está puesto en buscar información sobre la estructura matemática
de las ecuaciones, no en la búsqueda de valores aplicables a una resina o familia
de resinas concretas, fundamentalmente porque la reología de la resina puede
cambiar en varios órdenes de magnitud usando los aditivos apropiados. Se parte
pues de la base que los valores concretos de los parámetros que aparezcan en las
ecuaciones deberán ser determinados experimentalmente para cada resina.
1.4.1 Ecuaciones constitutivas para fluidos
Consideremos en primer lugar aquellas ecuaciones en las que la temperatura
no aparece explícitamente: se trata formalmente de fluidos atérmicos, pero en
términos físicos corresponden a fluidos que evolucionan en condiciones
isoter-mas o casi isoterisoter-mas. Aún con esta simplificación existen multitud de ecuaciones
constitutivas para fluidos, más específicamente líquidos, desde la más simple de
líquido newtoniano incompresible (véase por ejemplo Malvern, 1969) hasta la
más sofisticada formulación de funcionales con memoria (Coleman y Noli 1961,
1963; Truesdell 1978; Tanner 1985; Bird, Armstrong y Hassager 1987; Larson
1988; Utracki 1990)
Sería ciertamente ideal que las resinas de alta viscosidad utilizadas en el tipo
de inyecciones que estamos analizando tuvieran un comportamiento
newtonia-no. Desgraciadamente ésto no es así. Como ejemplo, la Fig. 1.4.1 muestra la
dependencia de la viscosidad con la velocidad de deformación para una resina
viscosa típica (la curva ha sido determinada y suministrada por el fabricante de
la resina). Se observa claramente que la viscosidad decrece notablemente cuando
la velocidad de deformación aumenta, lo que indica que el modelo newtoniano
no es aplicable a esta resina. Los resultados experimentales que nosotros hemos
obtenido para un intervalo más amplio de velocidades de deformación (Capítulo
«o
{ = •
tí
JO o o
00
velocidad de deformación (s )
Figura 1.4.1: Reograma de una resina de alta viscosidad. En ordenadas la viscosidad está
referida a la viscosidad a una velocidad de deformación tangencial de 5 s~^.
Una vez aceptado que el modelo a utilizar no es newtoniano, debemos
bus-car un modelo más sofisticado que permita describir el comportamiento de la
resina. La Tabla 1.4.1 es una traducción simplificada de la que Bird, Armstrong
y Hassager (1987) incluyen en su obra, que tiene la particularidad poco usual de
incluir las aplicaciones principales de los distintos modelos.
Como puede observarse, Bird, Armstrong y Hassager clasifican los
mode-los en 5 grandes grupos, ordenados de arriba hacia abajo por orden de
com-plejidad. El primer grupo es el de los fluidos newtonianos generalizados, cuya
propiedad fiíndamental es que no tienen memoria de forma: Su estado tensional
depende sólo de su velocidad de deformación en el instante considerado. Todos
los demás modelos incorporan fenómenos de memoria, desde los viscoelásticos
en pequeñas deformaciones (que no es aplicable a nuestro caso por esta misma
limitación) hasta los integrales, que tienen memoria de largo alcance, pasando
por los diferenciales que dependen de las derivadas sucesivas del tensor de
1.4. El comportamiento teológico de la resina 17
Tabla 1.4.1: Modelos para fluidos no newtonianos
M o d e l o
Fluidos newtonianos generalizados Fluidos Viscoelásticos Fluidos de Rivlin-Ericksen polinómicos Fluidos de Rivlin-Ericksen (diferenciales) Modelos integrales Ejemplos Modelo potencial Modelo de Bingham Modelo de Carreau Modelo de Maxwell Modelo de Jeffreys Maxwell gralizado. Fluido 2° orden Fluido Ser. orden
Maxwell convect. Jeffreys convect. White-Metzner Oldroyd Giesekus
Líquido de Lodge Rivlin-Sawyers Fluido de K-BKZ
Condición Flujo estacionario Pequeñas deformaciones Pequeñas velocidades deformación Cualquier flujo Cualquier flujo Aplicaciones Presión-caudal Fuerza-velocidad Cálculos ingeiüeriles Estructura-propiedad Caracterización Control de calidad Mov. gotas y burbujas Partículas en suspensión Flujos secundarios Análisis de estabilidad Simulación de flujos
viscoelásticos
Modelización procesado
ínter-relación de datos Simulación de flujos
Como se deduce de la columna 'Aplicaciones', la familia a elegir para estudiar la relación entre presión aplicada y caudal es la de los materiales newtonianos generalizados. Las otras familias de modelos son demasiado complejas para ser utilizadas en im problema como el que nos ocupa, por lo menos en una primera aproximación.
Las magnitudes que intervienen en la definición de un fluido newtoniano generalizado son el tensor de tensiones de Cauchy cr y el tensor de velocidad de deformación D. El tensor D se define a partir del campo de velocidades v como la parte simétrica del tensor gradiente de velocidad:
1 1 D = - [grad v + (grad v)^] , A,- = :^ivij + Vj,i) (1.4.1) donde la segunda expresión es la definición en componentes, en la que A j y Vi son las componentes cartesianas de D y v y la coma en el subíndice indica
derivación parcial:
. . . . ^ (1.4.2, donde {xi, X2, X3) son las coordenadas cartesianas de u n punto. Para un fluido
incompresible se verifica que la traza o primer invariante del tensor de defor-mación es nula:
trD = Da = VÍ^Í = div v = O , para u n fluido incompresible. (1.4.3)
donde las igualdades intermedias son expresiones equivalentes del mismo con-cepto.
Un fluido en el'que la tensión depende linealmente de la velocidad de defor-mación se llama newtoniano. Para líquidos incompresibles, la ecuación corres-pondiente es
a = -pl + 2r]T) (1-4.4)
1.4. El comportamiento Teológico de la resina 19
de tensiones a' definido por
(T' = a+pl (1.4.5)
con lo que queda
a' = 2r/D (1.4.6)
Un fluido en el que la viscosidad se deja depender del segiindo invariante del tensor de velocidad dr-deformación es un fluido newtoniano generalizado. Conviene definir una velocidad de deformación equivalente 7, relacionada con el segundo invariante por:
7 = 2 / Ü D = \/2trD2 (1.4.7) donde J / D = \ trD^ es el segundo invariante de D. Con esta definición el líquido
newtoniano generalizado queda definido por
a' = 27y(7)D (1.4.8)
donde mantenemos la denominación de r; para la viscosidad, que ahora depende de la velocidad de deformación equivalente. Por otra parte, es conveniente definir también, como en plasticidad, ima tensión tangencial equivalente, que llamamos r, definida por
r=y^^tror'2 (1.4.9) Elevando al cuadrado (1.4.8) y tomando trazas, resulta ima relación entre la
tensión y velocidad de deformación equivalentes:
r = 77(7) 7 = ^(7) (1.4.10)-donde se ha definido la f imción ij) que da la relación entre la tensión y la velocidad de deformación equivalente. Evidentemente las propiedades viscosas del fluido quedan totalmente caracterizadas por la función •^(7) a la que denominaremos en general relación T-7.
-»• 1 .
F Vo X.
í-7 ^
Figura 1.4.2: Esquema de un flujo tangencial puro en que vi = voxz/h y t;2 = Í;3 = 0.
flujo tangencial puro, como el de la figura 1.4.2. En dicho caso
r = 0-12 = — , 7 = 2Di2 = fi,2 = -r (1.4.11)
donde, como ilustra la figura, F es la fiierza aplicada a la placa móvil, Ay voel área y velocidad de dicha placa, y hel espesor de la capa de líquido.
Existen en la literatura varias ecuaciones particulares de fluidos newtonianos generalizados. Una de las más generales es la dada por Utracki (1990) y Elbirly yShaw(1985):
r = 77oc7 + (^0 - í7oo) [1 + (¿07)"^]^""'^^"^ 7 (1-4.12) donde r]oo,Vo,to,'iT^y i^ son coristantes del material. Nótese que el material
de-pende de 5 constantes independientes, demasiadas probablemente para que sea útil en nuestro problema. Una ecuación de complejidad intermedia es la usada por Williams (1966) y por Carreau (1972), idéntica a la (1.4.12) con m = 2:
r = VooÍ+ ivo - ^oo) [l + (ío7)'J 7 (1-4.13)
Esta ecuación, llamada de Carreau, tiene 4 parámetros, lo cual sigue siendo excesivo. Cuando ío7^ es grande frente a uno, puede aproximarse por la ley de tres parámetros
T = ?7o7 + c 7 " (1.4.14) que es la suma de una ley lineal y una ley de potencia. Cuando la parte lineal es
despreciable se obtiene la ley potencial
r = c 7 " (1.4.15) Esta ley sólo tiene 2 parámetros y ajusta razonablemente bien los resultados
1.4. El comportamiento teológico de la resina 21
deformación. Tiene muchas ventajas de tipo matemático que no tienen las otras.
Como veremos en el Capítulo 2, la ventaja más importante está en que las leyes
de semejariza o escala son muy simples. Por ejemplo, es fácil demostrar que la
relación entre la diferencia de presión y el caudal que circula por un dispositivo
es siempre del tipo Ap a Q, cualquiera que sea la forma y dimensiones del
dispositivo.
Los fluidos potenciales en los cuales n < 1 se denominan, en general,
seu-doplástícos, y se caracterizan por disminuir su viscosidad al aumentar la
ve-locidad de deformación. Los fluidos poliméricos se ajustan bien a este tipo de
comportamiento (véase la Fig. 1.4.1). Los fluidos cuya viscosidad aumenta con
la velocidad de deformación se denominan dilatantes. Los fluidos poliméricos
normales no son dilatantes. Solamente cuando hay sólidos en suspensión con
concentraciones elevadas se presenta este tipo de comportamiento.
La tesis se ha desarrollado en la hipótesis de que, en primera aproximación,
la resina se comporta como un fluido newtoniano generalizado potencial con
n < 1, lo que, como veremos en los Capítulos 3 y 4, se ha podido comprobar
experimentalmente.
1.4.2 Influencia de la temperatura en las propiedades reológicas:
Equivalencia t-T
En todos los tratados sobre polímeros se subraya la gran influencia que la
tem-peratura tiene en las propiedades reológicas de estos materiales (Bueche 1962;
Lee y Neville 1967; Ferry 1970; Chang 1975; Larson 1988; Riande 1985a, 1985b;
Tanner 1988; Keimings 1990; Utracki 1990). La mayoría de los análisis existentes
se refieren a la influencia de la temperatura en la viscosidad, lo que supone que
o bien se considera un material newtoniano, o se refieren a condiciones estándar,
normalmente extrapolaciones a velocidad de deformación nula basadas en un
Una aproximación directa y puramente fenomenológica para el caso de un
fluido newtoniano generalizado sería escribir que la función r-7 que caracteriza al
fluido, depende explícitamente de la temperatura. Esto significa que la ecuación
(1.4.10) se rescribiría como
T = '0(7,T) (1.4.16)
donde T es la temperatura.
Aunque esta formulación es posible, es difícil de manejar en la práctica,
porque supone la determinación empírica de una función de dos variables
es-calares, que es bastante compleja. Afortunadamente la experiencia indica que la
estructura matemática de la dependencia es, para muchos polímeros, mucho más
simple —al menos en tina primera aproximación— y permite la determinación
experimental con mucho menos esfuerzo.
La forma, relativamente general, de abordar el problema es utilizar una
equi-valencia temperatura-tiempo que establece simplemente que a igualdad de
solic-itación los procesos ocurren más rápido cuanto mayor es la temperatura. De
las equivalencias temperatura-tiempo la más conocida es la semi-empírica de
Williams, Landel y Ferry (WLF), que relaciona la viscosidad 77 a la temperatura
T con la viscosidad TJQ a la temperatura TQ mediante la relación
77 = 770 e x p
Ci(r-ro)
C2 + ( T - r o ) (1.4.17)
donde C\ y C2 son constantes (que dependen, en general, de la temperatura de
referencia TQ).
Aunque ésta es la expresión más habitual de la equivalencia
temperatura-tiempo, no es directamente aplicable a resinas epoxi que sean no newtonianas.
Para poder generalizar la equivalencia a cualquier ecuación constitutiva, es
pre-ciso generalizar la relación anterior a fluidos no newtonianos. Una forma
ele-gante de hacer la generalización es la inicialmente propuesta por Morland y
Lee (1960) (véase Tanner 1985) que consiste, muy en el espíritu de las teorías
1.4. El comportamiento teológico de la resina 23
definir un tiempo intrínseco ^ relacionado con el tiempo real por la ecuación
d^ = ^ (1-4.18)
donde ÜTÍT) es el factor de equivalencia temperatura-tiempo.
Para que esta ecuación sea unívoca es preciso definir la escala del tiempo
intrínseco, lo que se hace de forma convencional estableciendo que los tiempos
intrínseco y ordinario coinciden para una cierta temperatura de referencia TQ, lo
que significa que, por convenio,
aT{To) = l (1.4.19)
Una vez establecido el concepto de tiempo intrínseco, la generalización de
una ecuación constitutiva se hace estableciendo que si la ecuación constitutiva
se formula en términos del tiempo intrínseco, entonces la ecuación constitutiva
no depende explícitamente de la temperatura. Los materiales que cumplen esta
condición se denominan termorreológicamente simples.
Para los fluidos newtonianos generalizados, todo el problema se reduce a
definir velocidades respecto del tiempo intrínseco y así definiríamos una
ve-locidad intrínseca como v* = dx/d^ y a partir de este campo definiríamos una
velocidad de deformación intrínseca D* y una velocidad de deformación
equiva-*
lente intrínseca 7, de forma que la tensión tangencial equivalente estaría definida
por una ecuación del tipo
r = V(7) (1.4.20)
donde ahora la función tjj no depende de la temperatura^
Evidentemente, pasar del tiempo intrínseco al tiempo real es inmediato a
partir del cambio de variables definido en (1.4.18) con el resultado
* dt
7= 7 ^ = ariT) 7 (1.4.21)
con lo que la ecuación constitutiva queda reducida a
lo que desde el punto de vista experimental requiere la determinación de dos
funciones de una variable: V y C'T', un problema mucho menos complejo que el
de determinar una función de dos variables.
Nota: Para ser más preciso, además de la modificación de la escala temporal implicada por
(1.4.18) debería incluirse también im cambio de escala en teiisiones relacionada con el cambio
de densidad del material (Tanner 1985); esto se hace definiendo ima "tensión intrínseca" S,
relacionada con la tensión real a por
a = - ^ S (1.4.23)
PoTo
donde p es la densidad en el estado real y po es la densidad en el estado de referencia. En general
esta corrección es muy pequeña y se desprecia.
En el caso newtoniano la función V'(-) es lineal, por definición, y se obtiene,
por tanto
r = r/oaT(r)7 (1.4.24)
donde evidentemente el producto 770 es la viscosidad para el estado de referencia
y la viscosidad se escribe entonces
V = VoaT{T) (1.4.25)
que es la forma más habitual en que aparece expresada la viscosidad en función
de la temperatura.
De forma análoga, la ecuación r-7 para el fluido con ley potencial es
T = co [aT(T)7]" (1.4.26)
donde coy n son constantes independientes de la temperatura y de la presión.
Nótese que de acuerdo con la equivalencia t — T, los exponentes de las leyes
potenciales no cambian. La experiencia indica que aunque pequeña, la variación
de los exponentes es mensurable, por lo que las ecuaciones anteriores deben
tomarse sólo como aproximadas.
En general a^ depende exponencialmente de la temperatura. La forma
1.4. El comportamiento teológico de la resina 25
(1.4.17) con (1.4.25); el resultado es
ariT) = exp Ci(T-To) C2 + {T-%)
Otros autores utilizan la forma más simple de Arrhenius
(1.4.27)
ariT) = exp (1.4.28)
donde H es la energía de activación aparente (constante del material) y i? la
constante universal de los gases ideales. Nótese que la formula de Arrhenius
se puede escribir como la de la ecuación de WLF con Ci = H/RTQ y C2 = TQ.
La forma de WLF (con C2 distinto de TQ) es aplicable a temperaturas
relativa-mente próximas a la temperatura de transición vitrea (hasta 100 °C por encima);
para temperaturas superiores la forma de Arrhenius suele ser suficientemente
aproximada (Tarmer 1985).
1.4.3 Influencia de la presión
La presión a la que se encuentra sometido el líquido influye también en la
vis-cosidad. La teoría del volumen libre, que se desarrolla en el Tanner (1985) y
es originada por Batchinsky, permite llegar a la conclusión de que a presiones
pequeñas comparadas con el módulo de compresibilidad del fluido, la
viscosi-dad puede escribirse como
77 = 7/0 exp (p//i) (1.4.29)
donde 770 es la viscosidad a presión atmosférica (y a la temperatura considerada),
fj, es una constante con dimensiones de presión, y;? es la presión manométrica.
Aunque no hemos conseguido en la literatura datos concretos para resinas epoxi,
los datos para otros polímeros indican que // varía entre 30 y 80 MPa
aproximada-mente.
El concepto de fluido termo-reológicamente simple puede extenderse para
incluir el efecto de la presión. El desarrollo es análogo al del apartado anterior
factor de equivalencia tiempo-temperatura-presión orp análogo a ax, pero que depende también de la presión.
Una ecuación muy general para axp es (Utracki 1990) C i ( r - T o - ^ p )
o^Tp = exp C2 + {T-TQ-ep) (1.4.30) donde 6p es una función de la presión que en general puede aproximarse por (Utracki 1990):
, ^ . C 3 l n l ± ^ + a i n i ^ (1.4.31) 1 + C4P0 1 + CePo
Nótese, en primer lugar, que la expresión del factor de equivalencia T — p — t es idéntico al de William, Landel y Ferry (1.4.27) con la temperatura reducida en 6p. Por tanto, el efecto de la presión es equivalente a un enfriamiento. Por otra
parte, la ecuación para 6p es relativamente compleja y está destinada a describir el comportamiento a presiones muy elevadas (de varios miles de atmósferas, o varios centenares de MPa). Para presiones relativamente pequeñas (del orden de decenas de MPa) puede adoptarse una aproximación lineal en la que, tomando Po — 1 atm = 0.1 MPa, y tomando p com^o presión manométrica resulta
OpP^Cip (1.4.32)
donde la constante C3 es del orden de imas décimas de grado por MPa.
1.4.4 I n f l u e n c i a d e l t i e m p o d e c u r a d o
Las ecuaciones anteriores son útiles para polímeros estables, cuyas propiedades a temperatura constante no cambian —o cambian lentamente— con el tiempo. Las resinas epoxi endurecen con relativa velocidad y su viscosidad cambia en pocos minutos u horas desde valores relativamente bajos hasta valores prácticamente infinitos, cuando se convierte en u n sólido.
1.4. El comportamiento Teológico de la resina 27
La ecuación más simple y extendida para describir la evolución de la vis-cosidad de resinas epoxi con el tiempo en condiciones isotermas, es la simple exponencial (HoUands y Kalnin 1970; Roller 1975):
V = VOT e'^' (1.4.33)
donde rjor es la viscosidad inicial a la temperatura T a la que se hace el ensayo y kr una constante cinética también a la temperatura correspondiente.
De acuerdo con ésto, el gráfico 77-í en un diagrama semilogarítmico debe ser lineal. Pero la experimentación demuestra que la curva no se ajusta a este esquema más que en la fase inicial, de forma que el crecimiento de la viscosidad con el tiempo es más que exponencial; basten para muestra los dos ejemplos que siguen.
Como primer ejemplo, la Fig. 1.4.3 recoge los resultados de Roller (1975) para una resina epoxi erisayada a 170 °C. Como puede verse la curva log 77-í es cóncava hacia arriba, lo que indica un crecimiento más rápido que el exponencial. Roller resuelve el problema usando dos exponenciales, una para tiempos cortos y otra para estadios más avanzados de la reacción, como indican las líneas de trazos, una solución a todas luces insatisfactoria desde el punto de vista científico.
El segundo ejemplo corresponde a los resultados de Dusi et al. (1987) que en-sayaron una resina a varias temperaturas, entre 140 y 170 °C. Las correspondien-tes curvas 77-í en un diagrama semilogarítmico son las mostradas en la Fig. 1.4.4. De nuevo se aprecia una variación sobre-exponencial de la viscosidad con la temperatura.
Volviendo a la exponencial (1.4.33), es preciso definir la dependencia con la temperatura de las dos constantes que allí aparecen. La forma más usual es suponer que tanto 77or como hp siguen una forma de Arrhenius (HoUand y Kalnin 1970; Roller 1975). De esta manera la ecuación de variación de la viscosidad con la temperatura y el tiempo (en condiciones isotermas) queda
77 = 770 e x p H 1 1
«2 CU
^^ T 3
«i
J2
o
o cfl
"> 100
10
1 '
•^. o. , , 1
170 °C X
/ /
^
o/-yf
¡?>/
o ^ /
^^
J3
0.5 1 1.5
t (min)
2.5
Figura 1.4.3: Aumento de la viscosidad de una resina epoxi con el tiempo cuando se cura en
condiciones isotermas a 170 °C (Roller 1975).
100
10
.•2 1 O
O
0.1
0.01
O 10 20 30 40 50 60 70 80 tiempo (min)
Figura 1.4.4: Aumento de la viscosidad de una resina epoxi con el tiempo de curado para varias
1.4. El comportamiento reológico de la resina 29
donde 770 es la viscosidad inicial a la temperatura TQ, yH,H'y koo son coiistantes; R es la constante tiniversal de los gases ideales.
Esta teoría es sólo válida para procesos isotermos. Para procesos anisotermos, RoUer (1985) propuso cambiar el factor exponencial e'^^* de (1.4.33) y (1.4.34) por una exponencial e^ donde
X=fkTdt (1.4.35)
con kr dado por la segunda ecuación de (1.4.34).
En formulaciones más recientes la variable x de la ecuación anterior ha sido sustituida por una magnitud con un sentido físico directo: el grado de curado a. El grado de curado mide la fracción de resina que ha gelificado y su
de-terminación analítica está relacionada con la ecuación que rige la cinética de la reacción; su determinación experimental se hace mediante calorimetría de bar-rido. El grado de curado viene dado por la integral:
a = /* h{T)^ dt (1.4.36)
donde h(T) es una función de la temperatura, característica del material, y /? es la derivada temporal de ¡3, el grado de reacción isoterma , cuya evolución (velocidad de reacción) está determinada por una ecuación diferencial del tipo
P = kp{p,T) (1.4.37)
donde la función k0{-) caracteriza la cinética de la reacción.
El caso más sencillo es aquel en que la velocidad de reacción a temperatura constante es también constante (en este caso se dice que la reacción es de orden cero). En dicho caso el grado de curado a tiene una expresión muy sencilla:
a= ¡\{T)kB{T)dt (1.4.38)
JO
La semejanza de esta ecuación con la (1.4.35) es patente.
Lee, Loos y Springer (1982) y Dusi et al. (1987) proponen que la evolución de la viscosidad con el tiempo esté relacionada con la temperatura y con el grado de curado por la ecuación
El. _ J_
'Rf~¥o
donde K es una constante (independiente de la temperatura).
Evidentemente, para una reacción de orden cero y condiciones isotermas, esta
ecuación jimto con la (1.4.38) lleva a la expresión exponencial (1.4.34) si se toma
kr = Kh{t)kp{T). Si el proceso es anisotermo se obtiene la expresión integral de
RoUer, Ec. (1.4.35).
Dusi et al. utilizan, para describir la evolución de su resina, una cinética de
reacción de orden superior:
/¿=(A;l + A;2/?"^)(l-/5)^ ki = Aiexp{-Hi/RT) {i = 1,1.) (1.4.40)
donde Ai,A2,Hi,H2,myq son constantes que se determinan a partir de ensayos
de calorimetría diferencial. Combinando esta ecuación con la (1.4.36) en la que
h{T) —determinada por calorimetría diferencial de barrido— es una función
lineal en T para temperaturas inferiores a 480 °K, Dusi et al. pueden calcular
la evolución de a a lo largo del tiempo y representar la evolución de la
viscosi-dad frente a dicha variable. La Fig. 1.4.5 muestra la curva resultante para una
temperatura de 140 °C. Como puede verse, la condición de que la viscosidad
evolucione de forma exponencial con a no es aproximada más que para valores
de a por debajo de 0.15 aproximadamente.
De acuerdo con ésto, puede decirse que aunque la idea de relacionar la
vis-cosidad con el grado de curado, más que con el tiempo, es muy atractiva y
científicamente más correcta, la dependencia exponencial supuesta por los
au-tores no es válida más que para los instantes iniciales.
Por otra parte, no se ha encontrado en la literatura ningtin análisis que
con-sidere resinas con comportamiento no newtoniano. Por ello, en el Capítulo 2
ex-tenderemos la idea de los materiales termo-reológicamente simples para incluir
de forma sistemática el efecto de la gelificación en materiales no newtonianos,
1.5. El flujo de la resina en la grieta 31
100
0.01
0.05 0.1 0.15 0.2
grado de curado, a
0.25 0.3
Figura 1.4.5: Alimento de la viscosidad de una resina epoxi con el grado de curado para 140 °C
(Dusietal. 1987).
1.5 El flujo de la resina en la grieta
En esta sección revisamos los conocimientos disponibles sobre las ecuaciones
que gobiernan, o pueden gobernar, el flujo de la resina en tina grieta, desde un
punto de vista macroscópico. Esto significa que las ecuaciones deben ser capaces
de representar aproximadamente el flujo sin requerir la modelización explícita
de los detalles microscópicos de la grieta.
Esta última condición es necesaria porque no parece razonable ni posible
hacer una modelización de una estructura de gran tamaño, con una zona
inyec-tada del orden de metros, que requiera afinar detalles geométricos del orden de
centésimas de milímetro, como sería necesario para representar adecuadamente
la rugosidad de la grieta.
Con esta premisa en mente, se ha encontrado que de las distintas
metodo-logías de investigación de procesos de inyección de la bibliografía, el grupo de
aporta métodos aplicables a nuestro caso, porque un aspecto fundamental en
los problemas de moldeo es la complejidad geométrica del molde, que debe
describirse pormenorizadamente (White y Dee 1974; Wu, Huang y Gogos 1974).
Otro grupo de investigadores importante analiza el flujo de fluidos de tipo
newtoniano entre placas paralelas desde el punto de vista de la estabilidad del
flujo (Couder 1988; Deustcher 1988; Hinch 1988; Vicsek 1988a, 1988b). En
parti-cular analizan el flujo radial entre placas paralelas de un fluido que se inyecta en
otro fluido de mayor viscosidad (célula de Hele-Shaw, véase p.ej. Vicsek 1988a).
En dicho caso se observa que se producen inestabilidades y la inyección pierde
la simetría de revolución adoptando una estructura en pétalos ramificados. Sin
embargo, éste no es el problema que se nos plantea a nosotros porque de haber
algún fluido en la grieta, éste sería agua, y la resina tiene una viscosidad
va-rios órdenes de magnitud superior a la del agua, por lo que el problema de la
inestabilidad no nos afecta.
El tercer grupo está formado por investigaciones sobre circulación de agua o
suspensiones acuosas (lechada de cemento) en grietas, juntas o diaclasas,
natu-rales o artificiales, en rocas y hormigón. Aunque los resultados cuantitativos no
pueden ser aplicados a nuestro caso, las investigaciones de este grupo contienen
conceptos que son de interés para nuestro problema y vamos a describirlos con
cierto detalle.
Por cuestión metodológica comenzaremos por describir el flujo de un líquido
newtoniano en ima grieta lisa (es decir, entre placas de caras paralelas) y
pasare-mos luego a estudiar la influencia de la rugosidad.
1.5.1 Flujo de fluidos newtonianos en una grieta lisa
Consideremos en primer lugar el caso de flujo rectilíneo (y laminar) entre placas
paralelas horizontales, tal como esquematiza la Fig. 1.5.1, en la que suponemos
que la distancia entre placas w es mucho menor que las dimensiones en el plano
de las mismas. Este problema es clásico y está resuelto en la mayoría de libros
1.5. El flujo de la resina en la grieta 33
(a)
w/2 w/2
(b)
I-Figura 1.5.1: Flujo rectilíneo entre placas paralelas o en fisura lisa (a) y ejes asociados a la fisura
(b).
La solución es que el perfil de velocidades es parabólico y que el gradiente de presión en la dirección de la corriente está relacionada con la velocidad media por
(1.5.1) dp 12r)_
donde 77 es la viscosidad, w la separación entre placas y vi la velocidad media (promediada en el espesor de la capa de fluido):
1 f^n
-•wjl
Cuando se despeja la velocidad media, el resultado es una ecuación similar a la ecuación de Darcy para el flujo en materiales porosos:
1 /•^"/2
Vi^ — Vi{x3)dX3 W J-w/2
(1.5.2)
Vi = k / dp k' = w (1.5.3)
dxi ' •" 1277
donde k' es un coeficiente de conductividad.
Es conveniente definir la densidad media de corriente por vmidad de ancho de placas, que, en este caso, viene dada por
-wjl
Qi
rw/2
= W f l = / Vi(x3)dX3
J-w/2
(1.5.4) Con esta definición, la ecuación de Darcy se rescribe como
Qi = k-— , k = 7 ^ ^ = ke (1.5.5)
'dxi ' •• 1277
Nótese que en la mayoría de los trabajos que hacen refencia a flujo de agua, se utiliza el gradiente hidráulico en lugar del gradiente de presión. La única modificación es u n factor pg, donde p es la derisidad del fluido y ^ la aceleración de la gravedad.
Las ecuaciones anteriores, que se han escrito para u n flujo paralelo al eje xi pueden generalizarse tomando dos ejes cartesianos x\ y X2 en el plano medio de la fisura (Fig. 1.5.1b). En este caso se tiene
w
qi = kp^i, ^ = T2~ i = 1,2 (1.5.6)
donde los subíndices se refieren a los dos ejes contenidos en el plano de la fisura y hemos abreviado escribiendo dp/dxi = p_i.
La ecuación de flujo (1.5.6) se denomina muchas veces la ley cúbica debido a que la transmisividad k varía con el cubo de la apertura w de la grieta.
1.5.2 F l u j o d e fluidos n e w t o n i a n o s e n grietas r u g o s a s abiertas
Varios autores han intentado adaptar la ley cúbica anterior, válida sólo para régimen laminar y placas lisas, a grietas rugosas y a flujo turbulento. En nuestro caso, en que la viscosidad de la resina es enorme, las condiciones son siempre de régimen laminar, por lo que ignoraremos los desarrollos para flujo turbulento, aunque sí recogeremos los límites en el que el flujo permanece laminar.
De acuerdo con Amadei e lUangasekare (1992) hay tres fiíentes de modifi-cación en la ley cúbica: La micro-rugosidad debida a las imperfecciones superfi-ciales en pequeña escala, la tnacro-rugosidad debida a las ondulaciones grandes de la superficie, y el zigzagueo de la corriente debido a zonas de contacto y / u oclusión.
1.5. El flujo de la resina en la grieta 35
0.1
>
T3 ni
."2
O 0.01
0.001
•N
laminar ley cúbica modificada
\ \
\
100
\
laminar ley cúbica
X
turbulento
1000 Re^ = 2300 numero de Reynolds
10^
Figura 1.5.2: Zonas de flujo laminar (segiin Louis 1969, simplificado)
(1.5.7) de Reyriolds Re y de la rugosidad relativa e, definidas como
2pg h
-ríe — , £ —
TT-rj 2w
donde p es la densidad del fluido, q el caudal por unidad de anchura antes definido y 77 su viscosidad; h es la rugosidad absoluta o valor medio de la altura de las asperezas y IÜ es la apertura de la grieta.
Para régimen laminar, Louis (1969) obtuvo que para pequeñas rugosidades relativas (e < 1/30) la ley cúbica es suficientemente aproximada. Para mayo-res rugosidades relativas la ley de flujo sigue siendo lineal en qi y p^i, pero la transmisividad se reduce según la ley
k^ w^ (1.5.8)
1277 l + 8.8£i-5
Figura 1.5.3: Esquema de la simulación de la micro-rugosidad mediante pegado de granos de
arena a placas lisas (según Amadei e lUangasekare 1992)
La ecuación correspondiente para la transmisividad en régimen laminar es ,.3 1
k = w (1.5.9)
1277 1+At&^-^
donde // = 17 para los ensayos de Lomize (1951), /x = 8.8 para los ensayos de
Louis (1969) y /í = 42 para los ensayos de Amadei e lUangasekare (1992). Según
estos últimos autores, las diferencias entre unos y otros coeficientes pueden
es-tribar en la diferente forma de simular la rugosidad en los distintos experimentos.
Basándose en sus propios experimentos, Amadei e lUangasekare proponen
otra expresión que tiene una forma muy similar a la anterior y puede ser
analí-ticamente conveniente. Dicha expresión es la siguiente:
{w - l.lhf
k = w (1 - l.leY (1.5.10)
1277 12?7
La ventaja de esta ecuación estriba en que la forma matemática es idéntica a
la de la fisura lisa sin más que un cambio de origen en la apertura de grieta.
La Fig. 1.5.4 ilustra la tendencia de las curvas anteriores comparados con los
resultados experimentales de Amadei e lUangasekare (1992).
Los resultados anteriores se refieren a grietas planas en promedio y de caras
paralelas, y la rugosidad debee entenderse como micro-rugosidad, es decir,
ru-gosidades de tamaño inferior al de la apertura de la grieta. A pesar de ello algunos
autores sugieren que la fórmula de Louis puede tener en cuenta simultáneamente
los efectos de la micro-rugosidad, de la macro-rugosidad u ondulación y de los
1.5. El flujo de la resina en la grieta 37 1.0 0.8 0.6 ^ \ \ 0.4 0.2 0.0
"x^--^
- cbov \ >^ \ ) \ - \
\ " - ^ V \ \
vv ° ""
D ^ ^ v \ \
o V A A "^
k i ^ = ( l - 2 . 2 e ) ^ w
h (mm) o 0.292 D 0.579 A 1.21 ^ / fx = 8.8 (Louis)
^ i/
^ C /11 = 17 (Lomize) /
-^y ^-^
^ ^ ~~"-• " - .^
Sw "^^
V ^ A A ^ ^ A - ^ ^ ^
^ ^ ^ ^ ^ ^ ^ = 42 Amadei e /^"•^-^^^^ ~" lUangasekare ^ —
0.0 0.1
rugosidad relativa e = 0.2
_h_ 2w
0.3
Figura 1.5.4: Curvas de variación de la transmisividad con la rugosidad. Las curvas de trazos corresponden a la ecuación (1.5.9) y la curva continua a la (1.5.10). Datos experimentales de Amadei e lUangasekare (1992).
Sin embargo, Louis (1969) y Amadei e lUangasekare (1992) indican que las ondulaciones de la grieta alargan el camino recorrido por el fluido y, en conse-cuencia, disminuyen la transmisividad aparente. La diferencia entre la micro- y la macro-rugosidad puede verse en la Fig. 1.5.5. Louis propuso que el ángulo 9 puede ser un cuantificador de la macro-rugosidad. Tsang y Witherspooñ (1983) llegaron a proponer que la macro-rugosidad y el desplazamiento tangencial re-lativo de las caras de la grieta son en realidad los que controlan el flujo, y que la micro-rugosidad sólo produce ruido de fondo.
Sharp (1970) representó la macro-rugosidad como una distribución de dientes de sierra como los mostrados en la Fig. 1.5.6a. Para este modelo, si se desprecian las pérdidas de carga localizadas en los codos, la transmisividad disminuye en u n factor igual a la cuarta potencia del coseno del ángulo que forman los dientes con la dirección media de la grieta:
k =