Cálculo de parámetros de mecánica de la fractura empleando la simulación mediante elementos finitos

Texto completo

(1)Universidad Central “Marta Abreu” de Las Villas Facultad de Ingeniería Mecánica Centro de Investigaciones de Soldadura. Trabajo de Diploma Título: Cálculo de parámetros de mecánica de la fractura empleando la simulación mediante elementos finitos. Autor: Luis Angel Camacho Duménigo. Tutor: Dr. Juan Alberto Pozo Morejón.. Santa Clara 2013.

(2) Pensamiento. En la tierra hacen falta personas que trabajen más y critiquen menos, que construyan más y destruyan menos, que prometan menos y resuelvan más… que digan mejor ahora que mañana.. CHE.

(3) Dedicatoria. Les dedico este Trabajo de Diploma a mis padres Ania y Luis Gualberto, a mis hermanos, José Antonio y Endy Marlon. A toda mi familia, mis abuelos, tíos y primos. A mi novia Glenda, por ser parte importante de este sueño hecho realidad..

(4) Agradecimiento. Le doy muchas gracias a mis padres por todo lo que han hecho para que yo esté aquí, haberme educado por el buen camino y por haberme dado los hermanos tan maravillosos que tengo. Le agradezco a toda mi familia, por su apoyo, en especial a mi novia Glenda, por luchar a mi lado por este sueño. Le doy muchas gracias a mi tutor el Dr. Juan Alberto Pozo Morejón por su apoyo incondicional. Les agradezco, a todos mis profesores y personas que tuvieron que ver para la realización de este trabajo, en especial, a Zenaida, Nicolai y Alexis. Le doy muchas gracias a nuestro comandante y a la Revolución cubana por darme la oportunidad de cumplir mi meta. A todos muchas gracias por creer en mí..

(5) Resumen Resumen. En el presente trabajo se realiza una revisión bibliográfica acerca del tema de la mecánica de la fractura lineal elástica y elasto-plástica, determinándose las expresiones analíticas de cálculo del factor de intensidad de tensiones (FIT) para diferentes casos de piezas. Se implementa y valida una metodología para el cálculo del FIT y la Integral J en piezas fisuradas empleando los “métodos de integral de domino” e “integral de interacción”, de ANSYS, a través de modelos en 2D y 3D. En todos los casos abordados el error de los resultados que brindan los modelos de elementos finitos, respecto a los obtenidos por expresiones analíticas de la literatura, no supera el 7 %, por lo que se considera aceptable..

(6) Abstract Abstract. In this paper a review is made Bibliographic about the subject of linear fracture mechanics of elastic and elasto-plastic, determining analytical expressions for calculating the stress intensity factor (FIT) for different cases of parts. It implements and validates a methodology for calculating the J Integral and FIT cracked into pieces using the "domino integral methods" and "interaction integral" ANSYS, through 2D and 3D models. In all cases discussed error results provided by the finite element models with respect to those obtained by analytical expressions literature, no more than 7%, which is acceptable..

(7) Índice. Índice Introducción ..................................................................................................................... 1 Capítulo I: Fundamentación teórica sobre la mecánica de la fractura ............................. 4 1.1 Algunos aspectos teóricos sobre la mecánica de la fractura lineal elástica............... 4 1.1.1 Factor de intensidad de tensiones (K) en la mecánica de la fractura lineal elástica ................................................................................................................... 5 1.1.2. Factor de intensidad de tensiones crítico (Kc) ..................................................... 13 1.2 Algunos aspectos teóricos sobre la mecánica de la fractura elastoplástica .......................................................................................................................... 17 1.2.1 La “Integral J” ....................................................................................................... 18 1.3 Métodos de integral de dominio y de integral de interacción de ANSYS ................. 22 Capítulo II: Materiales y métodos de investigación........................................................ 23 2.1 Procedimiento de determinación de la “integral J” y el factor de intensidad de tensiones “K” en piezas agrietadas empleando la modelación por elementos finitos en 2D ........................................................................................... 23 2.1.2 Procedimiento de cálculo de la “integral J” mediante método de integral de dominio ..................................................................................................................... 24 2.2 Procedimiento de determinación de la “integral J” y el factor de intensidad de tensiones “K” en piezas agrietadas empleando la modelación por elementos finitos en 3D ........................................................................................... 36 2.3 Metodología para la implementación del comando CINT empleando el “método de integral de dominio” .................................................................................... 40 2.4 Metodología para la implementación del comando CINT empleando el “método de integral de interacción” ............................................................................... 43 Capítulo III: Cálculo de la “integral J” y el factor de intensidad de tensiones mediante el método de elementos finitos (MEF) ........................................................... 44.

(8) 3.1 Determinación del factor de intensidad de tensiones a través del “método de integral de dominio” y modelación en 2D de “probeta compacta” fisurada ............... 44 3.2. Determinación del factor de intensidad de tensiones a través del “método de integral de dominio” y modelación en 2D en placa de acero de grandes dimensiones con grieta central ........................................................................ 48 3.3 Determinación del factor de intensidad de tensiones a través del “método de integral de dominio” y de “integral de interacción” mediante la modelación en 3D (probeta compacta) ............................................................................................. 51 3.4 Determinación del factor de intensidad de tensiones a través del “método de integral de interacción”, en placa de grandes dimensiones con grieta central inclinada pasante, modelada en 3D ................................................................... 57 3.5 Determinación del factor de intensidad de tensiones a través del “método de integral de interacción”, en bloque de grandes dimensiones, con grieta semicircular superficial en 3D ........................................................................................ 61 Conclusiones ................................................................................................................. 64 Recomendaciones ......................................................................................................... 65 Referencias Bibliográficas ............................................................................................. 66.

(9) Introducción Introducción La Mecánica de la Fractura es un tema novedoso, prácticamente se puede decir que no existía antes de la Segunda Guerra Mundial. A pesar de su juventud es ya una disciplina establecida. La mayoría de las universidades en el mundo que forman ingenieros de la rama mecánica ofrecen al menos un curso de Mecánica de la Fractura en el nivel de pregrado; cada vez un mayor número de graduados trata de. adquirir. conocimientos en este campo a través de diferentes variantes de superación. La Mecánica de la fractura es una rama de la mecánica de sólidos deformables ocupada del estudio de la estabilidad estructural de materiales, considerando la formación y propagación de grietas o defectos en materiales y analizando condiciones tensionales con la concentración de tensiones debida a dichos defectos. Los problemas de la fractura los ha estado enfrentando la sociedad humana prácticamente desde el mismo momento en que se empezó a construir. Este problema se hace más agudo en nuestros días, respecto a los siglos anteriores, debido al alto grado de complejidad tecnológica de nuestra sociedad donde barcos, aviones, automóviles y otros ingenios mecánicos son parte de nuestra cotidianeidad. Afortunadamente, y gracias a los avances experimentados en el campo de la Mecánica de la Fractura, nuestra comprensión de la manera en que fallan los materiales y nuestra habilidad para prevenir este fallo se ha incrementado respecto a épocas anteriores. La mecánica de la fractura utiliza métodos analíticos derivados de otras ramas de la mecánica y la ciencia de materiales para estudiar los mecanismos de formación y propagación de defectos, y métodos experimentales relativos a la mecánica de sólidos para determinar las resistencias relativas del material a la fractura. Esta permite mejorar el diseño de productos, así como procesos de fabricación e inspección para controlar la propagación de defectos que podrían llevar al fallo de sus componentes, pero sin la necesidad de usar coeficientes de seguridad injustificados. Aplica las teorías de elasticidad. 1.

(10) Introducción y plasticidad, a los defectos cristalográficos microscópicos de los materiales para predecir la fractura macroscópica mecánica en los cuerpos. La fractografía es altamente utilizada en la mecánica de fractura para entender las causas de falla y verifica las predicciones teóricas identificando las fallas reales. En el Centro de Investigaciones de Soldadura existe el precedente de una tesis de grado realizada por Silverio (Silverio, 2012) sobre la determinación del factor de intensidad de tensiones (FIT) en probetas empleando la simulación mediante elementos finitos y el “método de extrapolación de desplazamientos”. Con el desarrollo del presente trabajo se busca dar continuidad a dichos estudios, ahora empleando la simulación y los métodos de “integral de dominio” (para el cálculo de la “integral J”) y de “integral de interacción”. Se persigue además resolver problemas en 3D de mayor complejidad en el cálculo del factor de intensidad de tensiones. Problema práctico: En el CIS no se ha implementado una metodología para el cálculo del factor de intensidad de tensiones a través de los métodos de “integral de dominio” y de “integral de interacción”, en piezas fisuradas de cualquier geometría y dimensión, mediante el empleo de la modelación por elementos finitos empleando el software ANSYS. Problema científico: Se desconoce si la implementación del cálculo del factor de intensidad de tensiones en piezas fisuradas en 2D y 3D, a través de los métodos de “integral de dominio” y de “integral de interacción”, mediante el empleo de la modelación por elementos finitos y el software ANSYS conduce a resultados precisos. Hipótesis: Es posible garantizar el cálculo preciso del factor de intensidad de tensiones a través de los métodos de “integral de dominio” y de “integral de interacción”, mediante el empleo de la modelación por elementos finitos y el software ANSYS, en piezas en 2D y 3D.. 2.

(11) Introducción Objetivo: Implementar y validar la metodología de cálculo del factor de intensidad de tensiones a través de los métodos de “integral de dominio” y de “integral de interacción”, mediante la modelación por elementos finitos de problemas de piezas fisuradas en 2D y 3D. Objetivos específicos: 1.- Elaborar la fundamentación teórica la mecánica de la fractura lineal elástica y elasto-plástica. 2.- Implementar y validar la metodología de cálculo del factor de intensidad de tensiones a través de los métodos de “integral de dominio” y de “integral de interacción” mediante la modelación por elementos finitos para problemas de piezas fisuradas en 2D y 3D. Tareas de Investigación: 1.- Se ejecuta un estudio bibliográfico sobre el cálculo del factor de intensidad de tensiones a través de los métodos de “integral de dominio” y de “integral de interacción”. 2.- Se realiza un entrenamiento en el empleo del software ANSYS en la modelación de problemas de mecánica de la fractura. 3.- Se construyen mallas de elementos finitos, del tipo tela de araña, para el cálculo del factor de intensidad de tensiones de probetas en 3D, con frentes de grieta recto o circunferencial. 4.- Se implementa y valida la metodología de cálculo del factor de intensidad de tensiones a través de los métodos de “integral de dominio” y de “integral de interacción” mediante la modelación por elementos finitos para problemas de piezas fisuradas en 2D y 3D.. 3.

(12) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura. Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura En el presente capítulo se abordan los fundamentos teóricos que sirven de base a la investigación, se parte de conceptos básicos relacionados con el tema de la Mecánica de la Fractura Lineal elástica y elasto-plástica. Se explica todo lo relacionado con el Factor de intensidad de tensiones (K) utilizado en la Mecánica de la Fractura Lineal elástica y la “integral J” ó “integral de Rice” aplicada tanto a la mecánica de fractura lineal elástica, como elasto-plástica. 1.1 Algunos aspectos teóricos sobre la Mecánica de la Fractura Lineal elástica La mecánica de fractura lineal elástica (‘’Linear Elastic Fracture Mechanics’’) surgió sobre la base de las limitaciones en la aplicación de los conceptos tradicionales para predecir el comportamiento de los materiales ante la presencia de discontinuidades internas y superficiales. Es una ciencia que estudia los mecanismos y procesos de propagación de grietas en sólidos, así como la distribución de tensiones y deformaciones que ocurren en un material agrietado o con discontinuidades, sometidos a cierta tensión externa. Esta ciencia comenzó su desarrollo con los trabajos fundamentales de Griffith sobre criterio de propagación de grietas en sólidos, basados en conceptos de transformación de energía elástica en energía de superficie y por esta razón se conoce como una formulación energética de la mecánica de la fractura (Guillermo, 2005). Según los criterios de resistencia tradicionales para el diseño de un elemento o para la selección de un material, se manejan solo dos variables; de modo que se puede asegurar que un elemento cualquiera resiste la carga que le está siendo aplicada, si al comparar la Tensión Real Aplicada con la Tensión Admisible se comprueba que la segunda es mayor o a lo sumo igual a la primera. Ejemplo de ello es la siguiente condición para evaluar la resistencia de un elemento cargado (Ramos, 2007):. 4.

(13) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura  real. (1.1).  [ t ]. La Mecánica de la Fractura maneja el criterio de que hay tres variables interrelacionadas entre sí: la carga aplicada, la talla del defecto y la tenacidad a la fractura. La tenacidad a la fractura crítica de un material en deformación plana y modo “I” de carga “KIC” es una propiedad fundamental que depende de muchos factores, entre los cuales los más influyentes son la temperatura, la velocidad de deformación y la microestructura. La magnitud KIC disminuye al aumentar la velocidad de deformación y disminuir la temperatura. El KIC es una propiedad del material que aparece en la literatura y constituye el “Factor de Intensidad de Tensiones Crítico”, que tiene una estrecha relación con la magnitud KI, que es Factor de Intensidad de Tensiones (FIT) que realmente actúa en la punta de la grieta. Para que una pieza no falle se tiene que cumplir la condición KI ≤ KIC, de manera que cuando el KI que actúa en la punta de la fisura se iguala al KIC ocurre la falla catastrófica de la estructura. 1.1.1 Factor de intensidad de tensiones (K) en la Mecánica de la Fractura Lineal Elástica Existen dos alternativas para el análisis de fractura: 1.. El criterio de la energía.. 2.. El criterio de la concentración de tensiones. El criterio de la energía establece que la extensión de la grieta ocurre cuando la. energía disponible para el crecimiento de la grieta es suficiente para sobrepasar la resistencia del material. El criterio de la concentración de tensiones se basa en el establecimiento del parámetro KI el que es llamado como factor de intensidad de tensiones y que caracteriza las condiciones en el extremo de una grieta para un material lineal elástica (Félix, 2007).. 5.

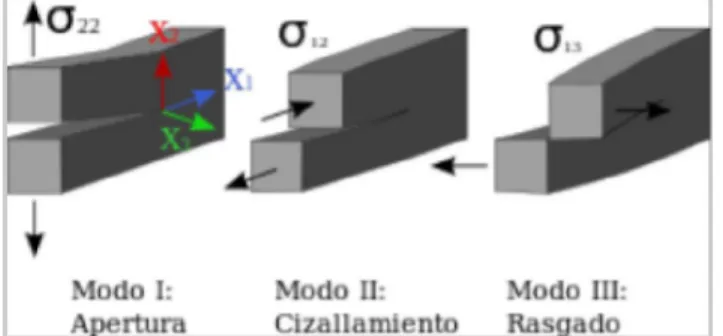
(14) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura Campo de tensiones en la punta de la grieta Existen tres tipos de carga que puede experimentar una grieta, como ilustra la figura 1.1 (Anderson, 1991): Fractura Modo I – Modo de apertura (Se produce un esfuerzo tensional perpendicular a la grieta) (Figura 1.1) Fractura Modo II – Modo de cizallamiento (Esfuerzos tangenciales actúan paralelos a las caras en la grieta pero en direcciones opuestas) (Figura 1.1) Fractura Modo III – Modo de rasgado (Esfuerzos tangenciales que actúan paralelos pero perpendiculares a la cara de la placa y opuestos entre sí) (Figura 1.1). Figura 1.1. Modos de factura con los ejes de referencia y las tensiones respecto a las caras de la grietas.. En la Mecánica de la Fractura Lineal Elástica, el campo de tensiones en torno a punta de la grieta puede ser descrito por la ecuación 1.2: m.   k   ij    fij ( )   Am r 2 gij m ( )  r m 0. (1.2). Donde ij, es el tensor de esfuerzos, r y  y se definen en la figura 1.2, k es una constante y fij es una función adimensional de  (Wu, 2002).. 6.

(15) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura. Figura 1.2. Campo de tensiones en la punta de la grieta.. En la ecuación 1.2 los términos de orden superior dependerán de la geometría, pero la solución para cualquier configuración dada contiene un término inicial que es proporcional a 1 / √r. En la medida que r tiende a cero el término inicial tiende al infinito y los otros términos permanecen finitos o nulos. Así, las tensiones en las proximidades de la punta de la grieta tienden a ser infinitamente grandes cuando r se aproxima a cero. Este carácter inusual de las tensiones en la punta de la grieta se conoce como singularidad de tensión en la punta de grieta. Para el tipo I de carga, los campos de tensión y desplazamiento en la punta de la grieta pueden ser descritos por las ecuaciones siguientes (Wu, 2002):.  xx . KI        3 cos  1  sin   sin  2r  2  2  2.   . (1.3).  yy . KI        3 cos  1  sin   sin  2r  2  2  2.   . (1.4). ux . KI 2. r       cos    k  1  2 sin 2    2  2   2 . (1.5). uy . KI 2. r       sin   k  1  2 cos 2   2  2   2 . (1.6). Donde xx, yy, Ux, Uy son tensiones y desplazamientos en la punta de la fractura, respectivamente. La variable  es el módulo en cortante, k = 3 - 4 para deformación plana y k = (3 -) / (1 +) ( coeficiente de Poisson) para tensión plana. La consideración del campo de tensiones en la punta de la grieta en modo I de carga, sobre el plano de la. 7.

(16) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura grieta, donde  = 0. De acuerdo a las ecuaciones 1.3 y 1.4 las tensiones en las direcciones “x” y “y” son iguales como muestra la siguiente ecuación (Wu, 2002):.  xx   yy . KI 2r. (1.7). Cabe señalar que la ecuación 1.7 es válida solamente cerca de la punta de la grieta, donde la singularidad de las tensiones domina el campo de tensión. La figura 1.3 es un diagrama esquemático de yy, tensión normal al plano de grieta, en función de la distancia radial desde la punta de la grieta (Wu, 2002).. Figura 1.3. Tensión normal al plano de la grieta en Modo I de carga.. El factor de intensidad de tensiones (KI), conocido también como FIT, se emplea en la mecánica de la fractura para el estado de tensiones cerca de la punta de una grieta, causada por cargas remotas. El factor (K) es una construcción teórica usualmente aplicada a materiales lineales estáticos y homogéneos y es usado para suministrar criterios de fallas en materiales frágiles. Este concepto también puede aplicarse a materiales que presentan fluencia a pequeña escala en la punta de grieta. La magnitud de (K) depende de: . La geometría. . La muestra. . La dimensión. 8.

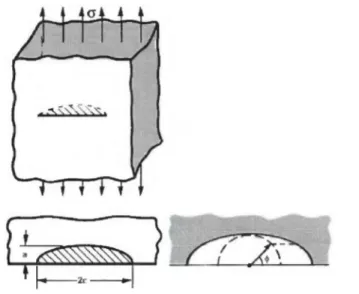
(17) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura . La ubicación de la grieta. . La magnitud modal de cargas sobre el material. Las unidades en las que se expresa este factor serían Pa. , relacionado con las. tensiones en la dirección “y” en la zona de singularidad de la punta de la grieta puede ser descrito por la relación (Wu, 2002):. . K I  lim   yy 2r. .    . (1.8). r 0. Las tensiones en la región de singularidad de tensión en la punta de grieta pueden ser determinadas mediante el modelado por elementos finitos. El Factor de Intensidad de Tensiones puede ser determinado por el trazado de la cantidad entre corchetes en la ecuación 1.8, respecto a la distancia a la punta de la grieta, y extrapolándola para r tendiendo a cero. Por otra parte, KI puede ser evaluado a partir de una extrapolación similar del desplazamiento de apertura de grieta (Wu, 2002):. KI .  2 2  lim   u yy k  1 r0  r .    . (1.9). Puesto que los desplazamientos se pueden determinar con un mayor grado de precisión que las tensiones en un modelo de elementos finitos, la ecuación 1.9 tiende a dar una estimación más precisa de la solución intensidad de tensiones KI. El valor de K modificado por Irwin, para el caso de una placa infinita con una grieta central sometida a una tensión de tracción remota, se define de forma general por la siguiente expresión (Anderson, 1991):. K   a (1.10) Donde K es FIT,  es la tensión aplicada y a es la semilongitud de la grieta analizada. El FIT no solo es modificado por los modos de fractura, también es influenciado por la geometría que se analice. La expresión siguiente fue publicada por Víctor E. Saouma. 9.

(18) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura (Saouma, 2000) para la determinación del factor de intensidad de tensiones en una placa de ancho finito con una grieta central, sometida a una tensión uniforme. Por la mayor complejidad del polinomio empleado se considera brinda mayor precisión que otras reportadas por otros autores (Silverio, 2012). 2 3  a a a  K I  1  0.256   1.152   12.2   a W  W   W   . (1.11). Donde KI es el factor de intensidad de tensiones, a es la mitad de la dimensión de grieta, W es el ancho de la placa y  es la tensión aplicada. La norma ASTM E647 (ASTM, 2000) que regula la determinación experimental de la razón de crecimiento de grietas a fatiga en diferentes materiales, brinda la siguiente expresión, para determinar el factor de intensidad de tensiones KI en una “probeta compacta” (ver Figura 1.4).. KI . P(2 ) B W(). 3 2. (0.886 4.64 13.322 14.723 5.44 ). Donde “KI” representa el Factor de Intensidad de Tensiones (Pa. (1.12) ); P la carga (N);. B es el espesor de la probeta (m); W es la distancia desde el centro del agujero hasta el final de la probeta (m); “a” es la distancia desde el centro del agujero hasta la punta de la grieta (m);  es la razón a/W (adimensional) (ASTM, 2000).. Figura 1.4. Geometría de probeta compacta.. 10.

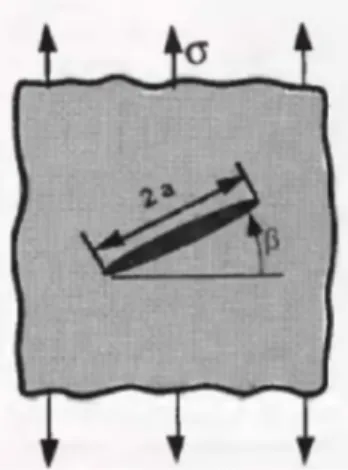
(19) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura Por otra parte para el cálculo de FIT en una placa de ancho infinito (ver Figura 1.5) con una grieta central inclinada, sometida a una tensión uniforme, autores como Néstor y Anderson (Pérez, 2004; Anderson, 1991; ANSYS INC; 2011) proponen las siguientes expresiones analíticas:. K I   cos 2  a K II   cos  sen. (1.13). a. (1.14). Donde KI y KII representan el factor de intensidad de tensiones para los diferentes modos de fractura, a es la mitad de la dimensión de grieta y. . es la tensión aplicada.. Figura 1.5. Geometría de la placa infinita con una grieta central inclinada.. Para una geometría 3D de grieta semielíptica superficial en bloque de grandes dimensiones (figura 1.6) Anderson propone las siguientes expresiones analíticas (Anderson, 1991).. =. ,. ∗ ∗√. ( ) = (sin. =. +. ( ) cos. (1.15). )1/4. (1.16). +. (1.17). 11.

(20) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura. Figura 1.6. Grieta semielíptica superficial sobre bloque.. De manera que para grieta semicircular superficial las expresiones 1.15 a 1.17 se convierten en:. =. ,. ∗ ∗√. (1.18). De manera que para geometrías conocidas y sencillas en la literatura especializada se pueden encontrar expresiones para la determinación de K, como las referenciadas anteriormente, o las expuestas por Anderson en tabla 2.4 (Anderson, 1991). Sin embargo en la práctica industrial se presentan un sin número de configuraciones y dimensiones de piezas, con distintas configuraciones y dimensiones de grietas para las que no existen expresiones analíticas de cálculo del factor de intensidad de tensiones. Es por esto que en la actualidad se recurre a una importante herramienta en manos de los ingenieros que constituyen los códigos de análisis por elementos finitos, a través de los cuales se puede resolver la anterior interrogante tanto para geometrías en 2D o 3D. Precisamente en esta tarea se centra el presente estudio. Las expresiones anteriores 1.11 a 1.18 tendrán en el presente trabajo una gran relevancia, ya que los resultados del FIT “K” obtenidos mediante la simulación por elementos finitos de las respectivas geometrías de piezas, serán validados contra los resultados que dichas expresiones arrojan.. 12.

(21) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura 1.1.2. Factor de Intensidad de Tensiones crítico (Kc) La fractura de un material ocurre cuando KI  KC. Para el caso especial de deformación plana, KC se convierte en KIC y es considerado una propiedad del material. El subíndice "I" representa el modo de fractura. De forma que la condición para que ocurra una falla queda (Ramos, 2007): KI  KIC KII  KIIC KIII  KIIIC Se debe destacar que la mayoría de los materiales son más susceptibles a falla en modo I de carga, por lo que la vasta mayoría de aplicaciones prácticas en mecánica de fractura considera solo este modo de carga. De manera que generalmente KIIC y KIIIC presenta mayores valores que KIC. No obstante se debe tener en cuenta que en ciertos casos particulares pueden ser de interés estos otros modos de carga (Ramos, 2007). Estado de tensión plana (plain stress) Un estado de tensión plana existe cuando una de las tensiones principales (1, 2, 3) es nula. Esto ocurre usualmente en elementos estructurales cuando una dimensión es muy pequeña comparada con las otras dos. En este caso las tensiones son despreciables con respecto a la menor dimensión ya que ellas no son capaces de desarrollarse dentro del material y son pequeñas comparadas con las tensiones en el pla. no.. En este caso el elemento estructural puede ser analizado como bidimensional, como por ejemplo las estructuras de pared delgada tales como placas sujetas a cargas en el plano, o cilindros delgados sujetos a presión. Los otros tres componentes no nulos del estado tensional permanecen constantes a lo largo del espesor, de manera que se puede reducir el análisis a dos dimensiones (ver figura 1.6) (WIKIPEDIA, 2012).. 13.

(22) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura. Figura 1.6. Estado de tensión plana en un sólido.. Según Anderson las expresiones matemáticas que aplican para este estado tensional son las siguientes (Anderson, 1991):. E [(1  v) xx  v yy (1  v)(1  2v) E  yy  [(1  v) yy  v xx (1  v)(1  2v) E  xy  2G xy   xy 1 v.  xx . (1.19) (1.20) (1.21).  zz  v ( xx   yy ). (1.22).  zz   xz   yz   xz   yz  0. (1.23). Donde  y  son los componentes de tensión normal y tangencial respectivamente, E es el módulo de Young, G es modulo en cortante, v es el coeficiente de Poisson. Estado de deformación plana (plain strain) Si una dimensión es muy grande comparada con las otras dos, la deformación principal en la dirección de la mayor dimensión está limitada y puede ser considerada como nula lo que conyeva a un estado tensional plano (ver figura 1.7). En este caso a pesar de que. 14.

(23) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura todas las tensiones principales son diferentes de cero, la tensión principal en la dirección de la dimensión mayor puede ser despreciada para los cálculos. De esta manera un cuerpo en un estado de deformación plana es aquel que se puede analizar descomponiendo el cuerpo en rebanadas idénticas y estudiar sobre cada rebanada la distribución de deformaciones como problema bidimensional usando dos coordenadas para la posición de cada punto sobre cada una de las rebanadas. (WIKIPEDIA, 2012).. Figura 1.7. Estado de deformación plana en un sólido.. De manera que en este estado tensional la deformación en el eje “Z” es nula y las ecuaciones que lo describen son las siguientes (Anderson, 1991):. E [ xx  v  yy 1  v2 ……………………………... (1.24) E  [ yy  v xx (1.25) 1  v2 ……………………..…………….  xx   xx.  xy  2G xy .  zz . E  xy (1.26) 1 v ……………….……………………. v ( xx   yy ) (1.27) 1 v …………………………………….. Efecto de las dimensiones de la probeta El factor de intensidad de tensiones crítico es solamente una constante del material cuando ciertas condiciones se cumplen. En otros casos el KC puede ser dependiente de la geometría. Las dimensiones de la zona plástica deben ser pequeñas comparadas al espesor de la probeta para garantizar condiciones de deformación plana en el extremo de. 15.

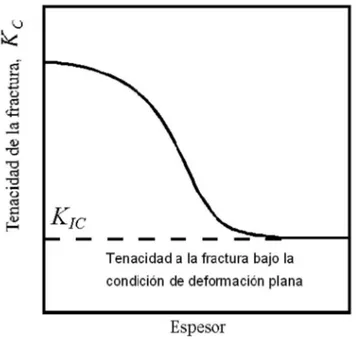
(24) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura la grieta. Si el espesor es muy pequeño o si la zona plástica es muy grande entonces la constricción en el extremo de la grieta se relaja. En la figura 1.8 se ilustra cómo influye el espesor de la probeta en el factor de intensidad de tensiones crítico para el modo I de carga. Los menores espesores se corresponden con el estado tensional de tensión plana. La Tenacidad a la fractura decrece con el espesor hasta que se alcanza un comportamiento horizontal de la curva, es decir deja de variar el KI con el espesor y ese valor es el que se corresponde precisamente con el KIC del material (Anderson, 1991).. Figura 1.8. Comportamiento de la Tenacidad a la Fractura respecto al espesor.. De manera que el Factor Crítico de Intensidad de Tensiones de un material en estado de deformación plana, que caracteriza la tenacidad a la fractura del mismo, constituye el KIC del material, y es una constante independiente de la geometría de la probeta. Los restantes valores críticos pueden ser de interés para aplicaciones puntuales. De acuerdo a las normas de la American Society for Testing and Materials (ASTM E647, 2000) para el ensayo de KIC, las dimensiones requeridas de las probetas para obtener un valor de KIC válido se calculan como:. 16.

(25) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura.  KI    2 . 5  a, B, (W-a)   YS . 2. (1.28). Esta ecuación fue obtenida de la observación de resultados experimentales de la dependencia entre la talla de la probeta y la tenacidad a la fractura en aluminio y aceros. Estas dimensiones garantizan condiciones de deformación plana y por lo tanto el KI caracteriza las condiciones en el extremo de la grieta. Esta ecuación satisface los requerimientos necesarios para una fractura lineal elástica y deformación plana. El valor de KIC resultante es válido ya que no depende de la geometría del cuerpo agrietado. Cuando el comportamiento elasto-plástico del material se manifieste de manera pronunciada, se debe apelar a otros parámetros que tomen en cuenta este tipo de comportamiento. Efecto del material en las propiedades de fractura La mayoría de los trabajos que inicialmente se realizaron en el campo de la Mecánica de la Fractura, eran solo aplicables a materiales con comportamiento lineal elástico bajo condiciones casi estáticas, avances posteriores en estos estudios fueron incorporando otros tipos de comportamiento del material (Ramos, 2007). El comportamiento típico de algunos materiales, de los más empleados en ingeniería, ante la fractura es el siguiente: Aceros de alta resistencia ---- Lineal elástico. Aceros de baja y mediana resistencia ---- Elasto-plástico / Totalmente plástico. Aceros inoxidables austeníticos ---- Totalmente plástico. Aluminio endurecido por precipitación ---- Lineal elástico. 1.2 Algunos aspectos teóricos sobre la Mecánica de la Fractura elasto-plástica La Mecánica de la Fractura Lineal Elástica es solo válida en la medida que la deformación no lineal del material (deformación plástica) es confinada a una región. 17.

(26) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura pequeña alrededor del extremo de la grieta. En muchos materiales es imposible caracterizar el comportamiento a la fractura del material, a través de este comportamiento y se requiere entonces de un modelo alternativo de fractura. Generalmente, los materiales que presentan valores altos de tenacidad, generan grandes inconvenientes a la hora de caracterizarlos mediante la mecánica de fractura elástica lineal (MFLE). Las restricciones en el espesor de las probetas necesarias para los ensayos, hacen poco viable su uso en materiales que presentan grandes deformaciones antes de la fractura. En estos casos, es recomendable el uso de la mecánica de fractura elasto-plástica (MFEP) que nos va a permitir determinar parámetros que nos describen la situación en el frente de la grieta. La Mecánica de la Fractura elasto-plástica surgió debido a las limitaciones en la aplicación del criterio KIc, de la Mecánica de Fractura Lineal Elástica, en los materiales dúctiles, donde el tamaño significativo de la zona plástica en relación con el espesor invalida las consideraciones de que la tensión elástica en la punta de la grieta controla el proceso de fractura. La Mecánica de la Fractura Elasto Plástica aplica a materiales que exhiben un comportamiento no lineal e independiente del tiempo (ejemplo la deformación plástica). En tales situaciones, la mecánica de fractura elasto-plástica utiliza varios métodos para hacer frente a relaciones no lineales entre el campo de tensiones y deformaciones, como,. por ejemplo, el CTOD (crack tip opening displacement) y la. “integral J”. Ambos parámetros describen las condiciones en el extremo de la grieta en materiales elasto-plásticos y cada uno puede ser usado como criterio de falla (Azterlan, 2010). 1.2.1 La “Integral J” A mediados de la década de 1960 James R. Rice (entonces en la Universidad de Brown) y GP Cherepanov desarrollaron independientemente una nueva medida de la tenacidad para describir el caso en que existe suficiente deformación en la punta de la grieta, de manera que la pieza ya no obedece a la aproximación lineal-elástica. Los análisis de Rice, que asume la deformación por delante de la punta de la grieta. 18.

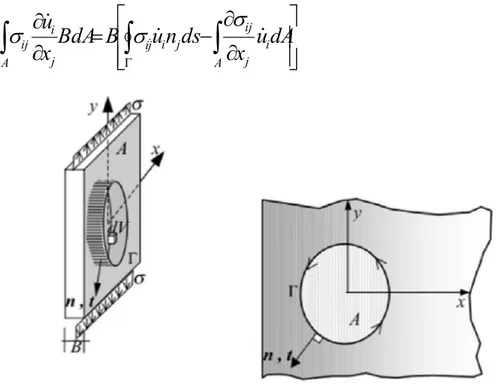
(27) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura como no linear elástica (teoría de la deformación plástica), se designan como “integral J”. Este análisis se limita a situaciones en las que la deformación plástica en la punta de la grieta no se extiende al borde más alejado de la parte cargada. También exige que el comportamiento no lineal elástico, sea una aproximación razonable en la forma y magnitud de la respuesta de carga de los materiales reales. En un campo bidimensional, la integral J se define por medio de una integral de línea. En el contexto del cálculo por el Método de los Elementos Finitos, es preferible realizar la integración sobre un área, lo que no es sino una extensión natural de las integraciones que se realizan sobre cada elemento finito durante la generación de la matriz del elemento. El método de la integral ‘’J’’ introduce un tratamiento matemático a los campos de tensiones y esfuerzos sobre un camino alrededor de la punta de la grieta. Este término tiene aplicación en la mecánica de fractura lineal elástica y elasto-plástica. En tales situaciones, la mecánica de fractura elasto-plástica utiliza varios métodos para hacer frente a relaciones no lineales entre el campo de tensiones y deformaciones. Con vistas a modelar el comportamiento elasto-plástico de los materiales se introdujeron dos parámetros: el desplazamiento de la abertura en el extremo de la grieta, CTOD y la integral de contorno J, J integral. Este método basado en una integral de contorno fue propuesto por Rice para estudiar el crecimiento de una fisura desde un enfoque energético. La integral de Rice es una herramienta de cálculo muy importante para la definición del factor de intensidad de tensión aun en el caso que exista plasticidad en la cabeza de la fisura. Esto permite su utilización en problemas de fractura frágil como así también en fractura dúctil (Sergio, 2001). Para determinar la expresión de la integral de Rice se transforma la integral que evalúa la energía interna U acumulada en un volumen V, en otra integral curvilínea que evalúa el trabajo realizado por la tensión completa en la frontera Γ del dominio que encierra dicho volumen. Para esto se considera una pieza delgada de volumen V =B A, donde B es el espesor y A el área plana de la pieza, sometida a tensión plana. En esta pieza se evalúa la. 19.

(28) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura variación temporal de la energía interna y su transformación mediante el teorema de la divergencia (Gauss). Esto es:. ij A.   ij ui BdA Bijui nj ds  ui dA xj xj   A. 1.29. Figura 1.9. Plana sometida a un estado de tensión plano.. Teniendo en cuenta el equilibrio del tetraedro elemental entre las tensiones  ij y fuerzas de superficie ti =  ij nj, donde nj es la normal saliente a la curva Γ, además el equilibrio elemental de Cauchy entre la divergencia de la tensión y las fuerzas de volumen fi =  ij x j. y la condición cinemática que define la relación entre el campo de. desplazamiento ui y deformación εij =  ij x j , se puede reescribir la ecuación anterior como:.   para fi o BijijdA Btiui ds  fiui dA  BijijdA Btiuuds    A A A. 1.30. Haciendo la integral en el tiempo sobre los dos miembros de la ecuación anterior, para evaluar el trabajo con el instante actual, resulta:. 20.

(29) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura. 1.31. BU dA BUt ds A. . El primer miembro de la ecuación anterior representa la energía actual acumulada en el volumen V=BA encerado por la curva Γ, y el segundo miembro representa el trabajo que realizan las tensiones sobre el área AΓ =B Γ. Para un problema elástico U   U e (ver Figura 1.9), dejándose de cumplir la igualdad 1.31 y resultando de esta un trabajo descompensado ΔW. Esto es:. 1 W  U dA Ut ds  0 B A . 1.32. Figura 1.10. Placa plana con una fractura, sometida a un estado de tensión plano.. Particularizando el sistema de referencias en x=x1, y=x2, y considerando ahora el cambio de esta energía descompensada a lo largo del eje x de crecimiento de la fisura, resulta una expresión conocida como la integral de Rice:. JI .  u  1 W  U dy ti i dtds  0 B x x    t. 1.33. Esta expresión representa la variación de la energía a lo largo del eje de una fisura. Aunque la integral de Rice mide la tasa incremental de trabajo absorbido por la fisura, es equivalente a la medición de la energía relajada por Griffith. Por este motivo, en fractura. 21.

(30) Capítulo I: Fundamentación teórica sobre la Mecánica de la Fractura lineal se cumple en el estado último la igualdad entre la integral de Rice (Rice, 1968) y la energía de fractura, Jic=Gf, resultando de aquí la relación entre Jic y el factor de intensidad de tensión crítico: Tensión plana:. f . EGf. a. . EJIC KIC  a a. 1.34. KIC  EGf  EJIC. . Deformación plana:. f . EGf. . EJIC KIC  1v2 a a. 1v a  2. . . KIC . EJIC 1v2. . . 1.35. De esta manera la “integral J” tiene la ventaja de que es aplicable para el caso de comportamiento elasto-plástico y lineal-elástico. Aunque ya está explicito cuando se habla de KI las ecuaciones 1.34 y 1.35 solo aplican al modo I de carga en estado tensional lineal elástico. La expresión 1.35 tiene suma relevancia para el presente trabajo ya que es la que se empleará para calcular KIC a partir del valor de JIC, determinado por el método de integral de dominio de ANSYS. 1.3 Métodos de integral de dominio y de integral de interacción de ANSYS Los “métodos de integral de dominio”, para el cálculo de la integral J, y de “integral de interacción” para el cálculo del FIT de ANSYS aplican la integración de áreas y volúmenes para problemas 2D y 3D respectivamente (ANSYS INC, 2011). En comparación con el “método de extrapolación de desplazamientos” para el cálculo del FIT, empleado por Silverio (Silverio, 2012) estos son más precisos, exigen menos requerimientos de malla y son sencillos de usar. Por no haber sido abordado con anterioridad en el Centro de Investigaciones de Soldadura de la UCLV, el presente trabajo se centra en la implementación y validación de una metodología para el cálculo del FIT mediante estos dos métodos, a través del empleo del comando “CINT”.. 22.

(31) Capítulo II: Materiales y Métodos de Investigación Capítulo II: Materiales y Métodos de Investigación En el presente capítulo se exhibe una metodología para el cálculo de la “integral J” y el factor de intensidad de tensiones “K” en piezas fisuradas, en 2D y 3D, utilizando la modelación por elementos finitos y el software ANSYS Versión 14.0. El cálculo de elementos finitos se basa en los métodos de “integral de dominio” y de “integral de interacción”, implementados en ANSYS. Un análisis de fractura es una combinación de un análisis de tensión y el cálculo de los parámetros de la mecánica de fractura. El análisis de tensiones es un análisis lineal elástico o un análisis elasto-plástico y se emplea la suposición de tensión plana (plane stress) o deformación plana (plane strain). 2.1 Procedimiento de determinación de la “Integral J” y el factor de intensidad de tensiones “K” en piezas agrietadas empleando la modelación por elementos finitos en 2D ANSYS tiene implementado los métodos de integral de dominio, para el cálculo de la integral J, y de integral de interacción para el cálculo del FIT, a través del empleo del comando “CINT” (ANSYS INC, 2011). En algunos casos debido a la simetría del problema, sólo se analiza la mitad o un cuarto de modelo, lo que reduce el tiempo de cálculo. El mallado en la región cercana a la punta de la grieta, zona de concentración de tensiones, se realiza utilizando una malla refinada. Se recomienda realizar un análisis de convergencia con vistas a determinar que el tamaño de elemento no está afectando el resultado. Se recomienda emplear un mallado alrededor de la punta de la grieta o frente de grieta del tipo “tela de araña”, con elementos de segundo grado.. 23.

(32) Capítulo II: Materiales y Métodos de Investigación 2.1.2 Procedimiento de cálculo de la “integral J” mediante método de integral de dominio Todo este procedimiento se inicia otorgándole un nombre a la tarea, procediendo de la siguiente forma: Utility Menu>File>Change Jobname... La siguiente ventana aparece:. Escriba un nombre en el espacio en blanco, el que desee, y haga clic en OK. También debe seguir el mismo procedimiento para cambiar el directorio lo que le dará la posibilidad de que el trabajo quede guardado donde usted elija: Utility Menu>File>Change Directory. Etapa de Preprocesamiento 1-Definir el tipo de elemento Para definir el tipo de elemento a emplear en el modelo se debe seguir la secuencia de comandos siguiente: Main Menu>Preprocessor>ElementType>Add/Edit/Delete. Se abrirá la ventana 'Element Types'. Haga clic en el botón Add…. 24.

(33) Capítulo II: Materiales y Métodos de Investigación Seguidamente aparece la ventana 'Library of Element Types'.. Seleccione 'Solid' que es el tipo de elemento que se recomienda para estos casos. En la parte derecha aparecerán diferentes elementos, el tipo de elemento recomendado para un modelo de fractura 2D es “PLANE183”, un elemento sólido cuadrático de 8-nodos. (ANSYS INC, 2011): Haga clic en OK. Usted debe ver `Element Types', ventana donde aparecerá el elemento escogido.. Para la definición del comportamiento del tipo de elemento debe proceder de la siguiente manera: Haga clic en el botón “Options”, y en la ventana de arriba seleccione “Plane strain” o “Plane stress” para el comportamiento de elementos “K3”, en dependencia. 25.

(34) Capítulo II: Materiales y Métodos de Investigación de lo que necesite (debe tener en cuenta que se utiliza “Plane stress' solo en casos donde la relación entre el espesor de la chapa y la longitud de la grieta sea muy pequeño) y haga clic en OK. (En los espacios en blanco aparecerá el tipo de elemento y en el negro y azul “Plane strain” o “Plane stress” en dependencia al seleccionado). Haga clic en el botón Close en la ventana “Element Types” (ANSYS INC, 2011).. 2-Definir las propiedades del material Para definir las propiedades del material se debe emplear la siguiente secuencia: Main Menu>Preprocessor>Material Props>Material Models.. En el lado derecho de la ventana “Define Material Model Behavior“que se abre, haga doble clic en “Structural“, en “Linear“', en “Elastic“, y finalmente en “Isotropic“. Lo anterior para materiales de comportamiento lineal elástico.. 26.

(35) Capítulo II: Materiales y Métodos de Investigación Seguidamente aparece la ventana que se muestra a continuación.. A continuación introduzca los valores para el módulo de Young (EX) y la relación de Poisson (PRXY) del material de la muestra. Haga clic en OK y luego cierre la ventana “Define Material Model Behavior“. 3-Definir los Keypoint A la hora de definir los Keypoints es fundamental para el dibujo del modelo geométrico en 2D. Siempre se colocará un Keypoint en la punta de la grieta. La secuencia de comandos es: Main Menu>Preprocessor>Modeling>Create>Keypoints>In Active CS. Se definen varios Keypoint de la siguiente manera: Para crear un Keypoint, escriba el # del Keypoint (1, 2, 3, etc.) en el espacio en negro, y en los espacios inferiores escriba las coordenadas en los dos ejes cartesianos. Vea siguiente ventana. Haga clic en “Apply” cada vez que declare un Keypoint. Tenga en cuenta que debe hacer clic en OK en lugar de “Apply” después de introducir los datos del último keypoint que defina (ANSYS INC, 2011).. 27.

(36) Capítulo II: Materiales y Métodos de Investigación 4-Definir las líneas Realice los siguientes pasos para definir las líneas: Main Menu>Preprocessor>Modeling>Create>Lines>Lines>InActiveCoord Para esto debe elegir el Keypoint # 1, después el keypoint 2 (1,2) para crear una línea que los conecte, esto creara la línea 1, después 2 y 3 (2,3) esto creará la línea 2 y así sucesivamente hasta terminar la figura deseada. Haga clic en OK para cerrar las líneas de la ventana “Lines in Active Coord”. Seleccione Utility Menu>PlotCtrls>Numbering a continuación aparece una ventana, en esta seleccione las casillas “Keypoint numbers” y “Line numbers” como se muestra, a continuación, haga clic en OK para activar la numeración de los puntos y las líneas (ANSYS INC, 2011).. Seleccione Utility Menu>Plot>Lines. Su ventana de gráficos debe tener un aspecto similar al que aparece a continuación (depende de la figura creada).. 28.

(37) Capítulo II: Materiales y Métodos de Investigación. 5-Discretizar líneas Esta operación depende de las líneas que se deseen seleccionar y el grado de refinamiento de la malla que se desee obtener, para ello se debe hacer lo siguiente: MainMenu>Preprocessor>Meshing>SizeCntrls>Manual Size>Lines>Picked Lines Debe elegir las líneas que desea seleccionar y seguidamente hacer clic en OK. Luego se abre la siguiente ventana. 29.

(38) Capítulo II: Materiales y Métodos de Investigación. Escriba el número de las divisiones en que desee dividir los elementos en la casilla en negro (este número de divisiones ayudará en la construcción del mallado), haga clic en “Apply”. Aparece de nuevo la misma ventana pero en esta ocasión de manera ampliada como se muestra a continuación.. En la casilla en negro debe poner la relación de tamaño (es la relación de tamaño del elemento pequeño con respecto al grande) cuando se quiera que la malla varíe el tamaño. 30.

(39) Capítulo II: Materiales y Métodos de Investigación de manera gradual. Si se deja en blanco dividirá la línea a espacios iguales (ANSYS INC, 2011). 6-Definir el Keypoint de Punta de la grieta El paso que viene a continuación es fundamental por la importancia que representa la región de la punta de la grieta y para construir los elementos singulares de manera automática mediante el comando “KSCON”, lo que constituye una ventaja que ofrece el software. Su realización consta de los siguientes pasos: Main Menu>Preprocessor>Meshing>Size Cntrls>Concentrat KPs>Create Se define el Keypoint en la punta de la grieta y se presiona OK, en la ventana que aparece a continuación, debe aparecer el número del Keypoint de la punta de la grieta como punto clave de concentración.. Para obtener resultados razonables, la primera fila de elementos alrededor de la punta de la grieta debe tener un radio de aproximadamente a / 8 o más pequeño, donde a es la longitud de la fisura. En “KCTIP midside node position” es necesario seleccione “Not Skewed 1/2pt”, que ubica el nodo a esta distancia de la punta de grieta y haga clic en OK (ANSYS INC, 2011). 7-Crear Área Para la creación del área se procede de la siguiente forma: Main Menu>Preprocessor>Modeling>Create>Areas>Arbitrary>By Lines. 31.

(40) Capítulo II: Materiales y Métodos de Investigación Para realizar esta función satisfactoriamente se deben seleccionar todas las líneas, luego haga clic en OK. 8-Aplicar condiciones de frontera Las condiciones de frontera a definir son las condiciones (restricciones) de simetría del modelo, y/o las demás restricciones que son necesarias aplicar, de acuerdo a las condiciones de los apoyos y para evitar el movimiento del cuerpo como un sólido rígido. Esto último puede provocar que el programa aborte. Para aplicar estas condiciones de simetría se deben seguir los siguientes pasos: Menu>Preprocessor>Loads>DefineLoads>Apply>Structural>Displacement>Symmet ry B.C.>.with Area Se seleccionan las líneas donde se quiera aplicar la simetría, seguido a esto haga clic en “Apply”. Seleccione el área. Haga clic en “Apply”. 9-Mallado del modelo Para realizar el mallado se sigue la siguiente secuencia: Main Menu>Preprocessor>Meshing>Mesh>Areas>Free Seleccione el área y haga clic en OK. Debe aparecer en la ventana de ANSYS, una malla similar a la que se muestra a continuación. (Depende de la figura y los valores que haya utilizado a lo largo de la modelación) (ANSYS INC, 2011).. 32.

(41) Capítulo II: Materiales y Métodos de Investigación 10-Aplicar cargas Para aplicar las cargas correctamente se debe seguir la siguiente secuencia: MainMenú>Preprocessor>Loads>DefineLoads>Apply>Pressure>Lugar donde desee aplicar la carga Esta secuencia se usa en el caso de que la carga se aplique en forma de tensión, y de ser en forma de fuerza siga los pasos siguientes: MainMenú>Preprocessor>Loads>DefineLoads>Apply>Force/Moment >Lugar donde desee aplicar la carga Seleccionar el lugar donde desee aplicar la carga (línea, keypoint, etc.) y seguidamente haga clic en OK. A continuación aparece la siguiente ventana. En la primera casilla seleccione “Constant value” para aplicar una carga constante y seleccione “Apply”, en la segunda introduzca el valor de la carga y haga clic en OK. Se debe tener en cuenta que para modelos en 2D en condición de “deformación plana” la fuerza se introduce por unidad de espesor de probeta P/B (Donde P es la carga y B el espesor de la probeta).. 33.

(42) Capítulo II: Materiales y Métodos de Investigación Etapa de Solución Para realizar la solución del sistema de ecuaciones se deben seguir los siguientes pasos: MainMenu>Solution>AnalysisType>NewAnalysis Seguidamente asegúrese de que “Static” está seleccionada (representa que se hace una corrida estática) y haga clic en OK. Posteriormente continúe de la siguiente manera: MainMenu>Solution>Solve>CurrentLS y revise sus opciones de soluciones que figuran en la ventana del comando `/ STATUS’, haga clic en el botón OK en la ventana “Solve Current Load Step”. Haga clic en el botón “Yes” en la ventana “Verify”. Usted debe ver el mensaje `Solution is done' en la ventana que aparece. Cerrar `Note' y el comando / STATUS (ANSYS INC, 2011). Para calcular la integral “J” o el FIT es necesario introducir una serie de comandos entre estos dos pasos de la etapa de solución, que utilizan el comando “CINT”. Este comando tiene la desventaja de que no se puede acceder por el “menú”. En el epígrafe 2.3 se explica el modo de utilización de este comando. Etapa de Postprocesamiento El funcionamiento de la siguiente etapa está marcado por el comando PRCINT, este tiene la limitante de que no se puede acceder a él por el “menú”, su objetivo es mostrar los resultados calculados de la integral J o del FIT en la etapa de solución Este comando funciona teniendo en cuenta la siguiente secuencia PRCINT, ID, Node, DTYPE Dónde: ID: Es el que identifica el número de la Grieta. Node: Es el número del nodo de la punta de la Grieta (por defecto = ALL). Esto se usa sólo para los problemas en 3D. Este comando por defecto entrega los resultados de “J” para todos los nodos del frente de grieta.. 34.

(43) Capítulo II: Materiales y Métodos de Investigación DTYPE: Es el que especifica el tipo de datos de salida, JINT - integral-J y de esta manera se obtienen los valores de la Integral J. K1, K2, K3 – Plotea los valores calculados de KI, KII y KIII respectivamente. Para salir de ANSYS y guardar todos los datos emplee la siguiente secuencia Utility Menu>File>Exit... En la ventana que se abre, seleccione “Save Everything“y haga clic en OK. Existe una forma de guardar el programa o secuencia de comandos de ANSYS, que permitirá en cualquier otro momento volver a correrlo o modificarlo a conveniencia. Para ello debe realizar los pasos siguientes: File>Write DB log file: Aparece la siguiente ventana.. En esta ventana en la parte izquierda se declara el nombre del fichero y la extensión, que debe ser “txt”, en la derecha debe seleccionar la dirección donde va a guardar. Debajo seleccionar que guarde los comandos esenciales solamente. Al terminar haga clic en OK. Es importante trabajar todo el modelo con unidades base del Sistema Internacional, o sea, “m”, “N”, “Pa”, de manera que la unidad de “J” en el resultado sea “Pa.m”, para que posteriormente el resultado final de “K” quede expresado en “Pa. 35. ”..

(44) Capítulo II: Materiales y Métodos de Investigación Etapa de postprocesamiento fuera del software Se debe definir cuál de los resultados de la integral J que el software reporta, desde el contorno más interno hasta el más externo, es el más preciso. Para esto se calcula el error relativo entre los valores sucesivos, comenzando por el contorno interior y se asume como resultado preciso aquel en que el error relativo sea el más pequeño. Luego a partir del valor de J, se calcula el factor de intensidad de tensiones, para el caso de estado tensional lineal – elástico y condición de deformación plana, mediante la expresión 1.35. 2.2 Procedimiento de determinación de la INTEGRAL “J” y el factor de intensidad de tensiones “K” en piezas agrietadas empleando la modelación por elementos finitos en 3D El procedimiento en 3D es similar en su inicio al 2D explicado anteriormente, específicamente hasta el paso 8 “mallado”, de la etapa de preprocesamiento. La filosofía que se recomienda para modelos 3D de caras planas y paralelas y grietas pasantes es la de construir un modelo 2D, mallarlo de manera automática y extruirlo en la dimensión del espesor, hasta obtener el modelo 3D deseado. De esta manera se aprovecha el mallado automático en 2D de ANSYS y se obtiene de manera sencilla el modelo 3D mallado correctamente. ANSYS no posee en la versión empleada un comando para mallado automático en 3D. Etapa de Preprocesamiento En esta etapa solo lo nuevo es que cuando se define el tipo de elemento además del elemento 2D se declara el elemento que se emplea en el modelo 3D. El tipo de elemento recomendado para modelos 3D es SOLID186, un elemento ladrillo de 20 nodos. En 3D no es necesario declarar la condición de “Plane strain” o “Plane stress”, ya que el elemento 2D solo se emplea para construir el modelo geométrico, pero no en la corrida de solución. A partir del paso 8 se crea el volumen.. 36.

(45) Capítulo II: Materiales y Métodos de Investigación Crear un volumen El volumen se crea a través de la extrusión de un área en el eje “Z”. Para extruir se siguen los siguientes pasos: Preprocessor>Modeling>Operate>Extrude>ElemExt Opts, a continuación aparece la siguiente ventana:. En la parte que esta negra completa debe aparecer el tipo de elemento escogido, en la que se encuentra en blanco y negro coloque el número de elementos a través del espesor que quiera lograr. Al terminar haga clic en OK. Seguidamente proceda de la siguiente forma (ANSYS INC, 2011): Preprocessor>Modeling>Operate>Extrude>Areas>Along Normal, Luego seleccione el área y haga clic en OK, debe aparecer la siguiente ventana.. 37.

(46) Capítulo II: Materiales y Métodos de Investigación En el espacio en negro debe introducir el valor de la longitud de extrusión (espesor de pieza) que desea realizar, al terminar haga clic en OK. Una vez extruida el área ya queda el volumen 3D completamente mallado. Se debe tener en cuenta, que al realizar la extrusión quedan los elementos 2D presentes en la superficie de la malla, que se deben eliminar, pues su presencia puede ser causa de errores. Para ello siga los siguientes pasos (ANSYS INC, 2011): Select> Entities> Elements> By Elements Name> Plane 183 Meshing>Mesh Tool>Se selecciona el área>Clear. De esta forma quedan solamente los elementos 3D. Luego Select>Everythink permite continuar el trabajo. A continuación se declaran las condiciones de frontera y las cargas de manera muy similar a la descrita en epígrafe anterior. La etapa de solución, postprocesamiento y postprocesamiento fuera del Software también es muy similar.. 2.2.1 Pasos para la construcción de modelo mallado de volumen tipo bloque con grieta semicircular superficial en 3D Una tarea con un grado de dificultad mayor al abordar problemas de mecánica de la fractura mediante simulación por MEF es la construcción de la malla para piezas con grietas semicirculares superficiales. Esta tarea es más compleja que la descrita anteriormente de piezas con fisuras pasantes. Se recomienda en la literatura que siempre la malla alrededor del frente de grieta tenga una configuración clásica del tipo “Tela de araña” (ANSYS INC, 2011). A continuación se describe la secuencia de pasos del procedimiento elaborado para la construcción de este tipo de malla de elementos finitos. Pasos para creación de malla de “tela de araña” en bloque con grieta semicircular superficial en la etapa de preprocesamiento: -. Se crea el volumen de bloque.. -. Se crea volumen de ¼ de “toro”. Este volumen se construye elaborando primero una área de forma semicircular y posteriormente extruyendo dicha área a lo largo. 38.

(47) Capítulo II: Materiales y Métodos de Investigación de una línea, que en este caso es una semicircunferencia que pasa por el centro del círculo pero en una plano perpendicular al mismo. -. Se resta del volumen del bloque el volumen del cuarto de toro, manteniendo el volumen de este último.. -. Se malla el área de la cara de dicho cuarto de toro auxiliándose de comando KSCON, que define el centro del área circular como “keypoint de concentración” y se malla con elementos cuadriláteros, obteniéndose la conocida “tela de araña”.. -. Luego se extruye el área mallada de cara del cuarto de toro a lo largo de línea empleando secuencia de comandos siguientes, previamente definidas las opciones de extrusión. Modeling – Operate – Extrude - Elem Ext Opts (esta secuencia de comandos declara el número de divisiones o elementos a lo largo de línea de extrusión). Modeling – Operate – Extrude – Areas - Along Lines Finalmente se obtiene un cuarto de toro mallado con elementos hexaédricos.. -. Se eliminan los elementos cuadriláteros del área circular.. -. Se malla con elementos tetraédricos el volumen restante del bloque con la opción de mallado libre.. -. Se reflejan los volúmenes creados, de manera que se crean volúmenes y mallas simétricos. Se crea el volumen del tipo semitoro que rodea el frente de grieta. Modeling – Reflect – Volumes, luego se declara el plano de simetría.. -. Se seleccionan los nodos sobre el plano de simetría que se encuentran del frente de grieta hacia afuera, pero incluyéndolo. Se mezclan los nodos, que se encuentran en la misma ubicación pero en volúmenes a ambos lados del plano de simetría.. -. Se seleccionan los nodos fuera del plano de simetría y se mezclan los nodos coincidentes.. De esta manera se concluye la construcción de modelo mallado. En capítulo III aparece un ejemplo de malla construida según este procedimiento.. 39.

(48) Capítulo II: Materiales y Métodos de Investigación 2.3 Metodología para la implementación del comando CINT empleando el “método de integral de dominio” La evaluación de la integral “J” se realiza a través del comando CINT y el “método de integral de dominio” (ANSYS INC, 2011) el que es compatible con los siguientes elementos: PLANE182, PLANE183, SOLID185, SOLID186, SOLID187. Dicha evaluación soporta los comportamientos de material de elasticidad isotrópica lineal y plasticidad isotrópica. El cálculo de la Integral “J” se efectúa siguiendo una serie de pasos: Paso 1: Iniciar un nuevo Cálculo de la Integral “J”. Paso 2: Definir la Información de la grieta. Paso 3: Especifique el número de contornos para calcular. Paso 4: Definir una condición de simetría de la grieta. Paso 5: Especificar controles de salida. Paso 1: Iniciar un nuevo Cálculo de la Integral “J”: Para iniciar un cálculo de la Integral “J”, utilice la opción del comando CINT NEW y proporcionar un número para identificar la información de entrada para el cálculo de la Integral-J. La sintaxis del comando es la siguiente: CINT, NEW, n Donde n es el número de identificación de este cálculo de la integral “J”. Paso 2: Definir la información sobre la grieta: El nodo de la punta de la grieta y la dirección de extensión de grieta son necesarios para el cálculo de la Integral-J. Dos métodos utilizan el comando CINT, están disponibles para especificar los valores: Definir el nodo de la punta de la grieta y el plano normal a la grieta. Este enfoque se aplica tanto para geometrías de grietas 2D como también para geometrías de grietas planas en 3D. Ofrece una forma sencilla de definir un cálculo en 3D de la Integral-J, ya que sólo es necesario definir el nodo en la punta de la fisura y la normal al plano de la grieta. Este método se debe utilizar cuando el plano de la grieta posee configuración plana.. 40.

(49) Capítulo II: Materiales y Métodos de Investigación Definir el componente nodo de extensión de grieta y la dirección de extensión de grieta. Este enfoque se aplica para planos curvos de grieta en 3D donde una normal única no existe. Sin embargo se puede definir el nodo componente de extensión de grietas y la dirección de extensión de grieta en cada ubicación de nodo de punta de grieta. Se debe utilizar este método cuando el plano de la grieta es curvo, o cuando un conjunto de nodos forman la punta de la grieta, como en el caso de mallas de punta de grietas colapsadas. Para definir el nodo de la punta de la grieta y el plano normal a la grieta en geometrías 2D se debe establecer un componente de nodo de punta de grieta (por lo general un nodo situado en la punta de la grieta). También se puede definir un grupo de nodos alrededor de la punta de la grieta, incluido el nodo en el extremo de la fisura. ANSYS utiliza este grupo de nodos como los nodos de partida para formar la información necesaria para la integración de contorno de forma automática. En geometría de grieta plana en 3D se debe definir un componente de nodo de punta de grieta que incluya todos los nodos a lo largo del frente de la fisura. En cada ubicación de nodo, sin embargo, sólo un nodo puede existir. Todos los nodos en el componente de nodo de grietas deben poder conectarse, y deben formar una línea sobre la base de la conectividad y elementos asociados con ellos. Esta línea es el frente de la grieta que ANSYS utiliza para determinar automáticamente los elementos para la integración de contorno. El procedimiento es similar en geometrías 2D de grietas, y se realiza a través de todos los nodos a lo largo del frente de la grieta. La sintaxis del comando es la siguiente: CINT, CTNC, CMNAME Después de que el componente de nodo de punta de grieta se define se debe utilizar la opción de comando CINT NORM para definir la normal del plano de la grieta. El programa convierte automáticamente este en el vector extensión de grieta, en base a la información del elemento. El vector extensión de grieta se toma a lo largo de la dirección perpendicular al plano formado por la normal al plano de grieta y la dirección tangente al nodo de punto de grieta y se normaliza a un vector unitario.. 41.