El calor de las finanzas : La Ecuación de Black-Scholes-Mertón

Universidad Nacional de Ingeniería Facultad de Ciencias

Escuela Profesional de Matemática

Tesis para Optar el Título Profesional de

Licenciado en Matemática

El Calor de las Finanzas: La Ecuación de

Black-Scholes-Merton.

Heinz Guillermo ROQUE L0Y0LA

Asesores:

aplicada nace de la curiosidad intelectual.

Dedicatoria

Índice General.

Índice de Gráficas.

Índice de Tablas.

Motivación.

Introducción.

1. Algunos Elementos de Teoría de la Probabilidad. 1.1. Introducción ... .

1. 1.1. Paradoja de Bertrand . 1.2. Espacio de Probabilidad. 1.3. Variable Aleatoria . . . 1.4. Procesos Estocá ticos. . . 1.5. Medidas de Dispersión.

1.6. La Distribución ormal y Lognormal 1.6.1. Regla 68-95-99 .

1.7. Integrales. . ... . 1.8. amino Aleatorios. .

111 VI VII 1

7

11 1 2 1 2 14 20 2 3 25 28 38 39

43

2. El Movimiento Browniano 47

2.1. Breve Reseña Histórica d 1 Movimiento Browniano Estándar. 48 2.2. 2.3. 2.4. 50 5 2 54 5 6 El Movimiento Browniano Estándar. . . . . .

2.2.1. Propiedad s del Movimiento Browniano Estándar. 2.2.2. Filtracion s d 1 Movimiento Browniano Estándar . El Proceso de Wi ner . . . . . . . . . . .

2.3.1. Condicion s de quivalencia entre el Proceso d Wi n r 5 7 . . . . 58 y el Movimiento Browniano . .

3. Elementos del Cálculo Estocástico 61

3.1. Martingalas. . . 6 1

3.2. Integral de Wiener. . . 68

3.3. lnt grales Estocá ticas. 76

3.3.1. Motivación. . . 76

3.3.2. Definición de Integrales Estocásticas. 82 3.3.3. Ejemplo de Integral Estocá ticas. . 90 3.3.4. Sumas de Riemann e Integrales Estocásticas. 9 4

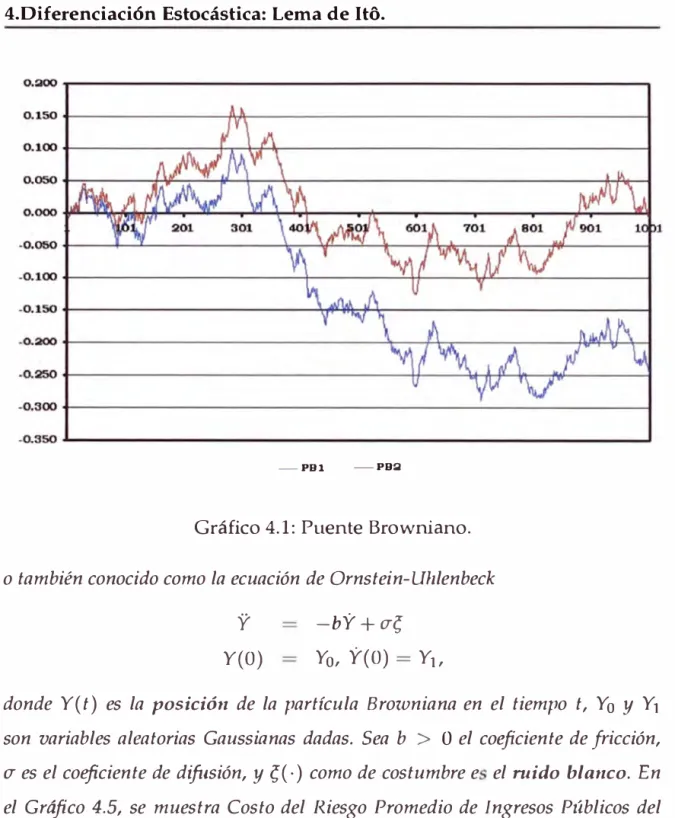
4. Diferenciación Estocástica: Lema de lt6. 96

4.1. Regla del Producto de lto. . . 97 4.2. El Lema de lto . . . 99 4.3. Ecuaciones Diferenciales Estocásticas. 100 4.3.1. Alguno Ejemplo . . . 10 1 4.3.2. La Desigualdad d Bellman-Gronwall. . 111 4.3.3. Teorema de Exi tencia y Unicidad. 114

4.4. Descripción del Proceso d lto . . . 12 3

S. El Modelo de Black-Scholes-Merton 127

5.1. Economía Financiera . . . . . . 128

5.1.1. Deri ado Financi ro . . . 130 5.2. Opciones Financieras. . . 13 2

5.2.1. Posiciones de una Opción Financiera. 13 2

5.2.2. Formas de jercer una Opción Financiera. . 13 3 5.2.3. Tipos de Riesgo . . . 13 3 5.2.4. Tipos d Opciones Financieras. 13 4 5.2.5. Objetivo d las Opciones. . . . 13 5

5.3. La Ecuación de alor en las Finanzas . 13 6

5.3.1. Evolución de la Valoración de Opcione Financiera 13 6 5.3.2. Valuación de una all Europea . . . 139 5.3.3. Factores qu det rminan el Precio de la Opcione . 15 4

5.3.4. Ventajas d 1 Modelo de Black-Scholes-Merton. 15 5 6. Análisis de Demandas Contingentes y Aplicaciones 156

6.1. Introducción . . . 157

6.2. Pasivos Corporativo como Opcione 158

6.3. Garantía como una Opción de Venta 160

6.4. Valoración . . . 160 6.5. Valoración de la Garantía de Cr dito Parcial por medio d 1

go d D uda y el quity de la Empresa . . . . . . . . 167 6.7. Análi i de Activos Contingentes y Warrants . . . . . . . 170 6.8. Análi is de Activos Contingentes y Bonos Convertibles con

Opción de Prepago . . . 171 6.9. Análisis de Activo Contingentes y LYO s ... . . 17 3

7. Conclusiones 175

Futuras Línea de Investigación. 178

A. Tiempo Continuo 181

A.l. La Tasa de Descuento. . . 181

A.1.1. El Interé es contabilizado una ez al año. . . 182 A.1.2. El interé es contabilizado dos veces al año. . 18 3 A.1.3. El interé e contabilizado n veces al año. . . 185 A.1.4. El interés s contabilizado de manera continua. 186 B. Visual Basic: Valoración de Opciones Europeas 191 B.1. Simulación de un Movimiento Browniano Estándar. 191 B.2. Simulación de un Movimi nto Browniano Geométrico. 192 B.3. Valoración de una Opción ompra . . . . . . . . . 19 3 B.4. Valoración de una Opción Venta . . . . . . . . . . 194 B.5. Simulación del Modelo d B&M para una Opción de Compra 194 B.6. Simulación del Modelo de B&M para una Opción de Venta 195

/

Indice de Gráficas

l. l. Paradoja de Bertrand: Prim r ca o. 1.2. Paradoja de Bertrand: S gundo caso. 1.3. Paradoja de Bertrand: Tercer caso. 1.4. El Problema de la aguja de Buffon. 1.5. Trayectoria d un proce o estocá tico . . 1.6. Regla 68-95-99. . . . .

13 13 14 20 25 39 2.1. Movimiento Browniano de un par de partículas 48

2.2. Movimiento Browniano Estándar . . 51

2.3. Movimiento Geom trico Browniano . . 59

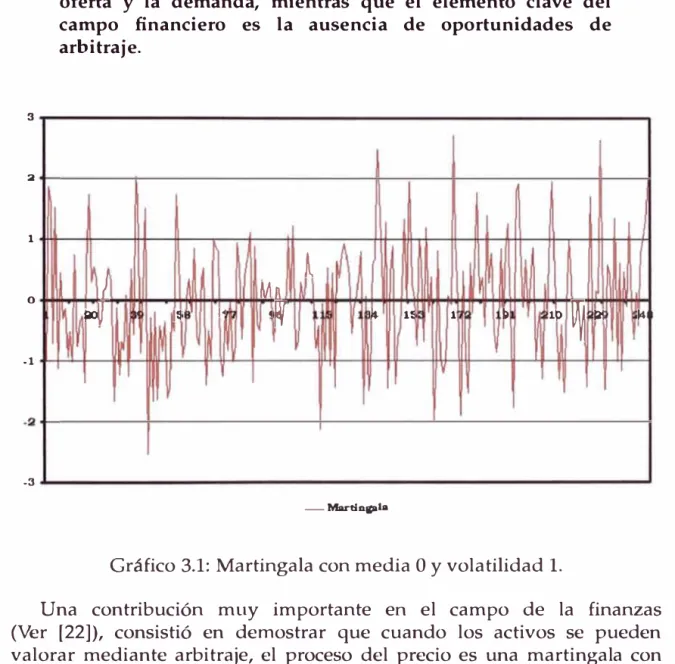
3.1. Martingala con media O y volatilidad l. 62 4.1. Puente Browniano. . . 105 4.2. Costo del Rie go Promedio de Ingr os Públicos del

Proyec-to: Proceso con Reversión a la Media 106

6.1. Valor Futuro de los Activos. 158

4.1. Caja d multiplicaci n d lto . . . 98 5.1. Re umen de lo fecto obre el precio de una opción sobre

acti os incrementando una variable y dejando fijas las demás 155 6.1. El interé , 1 principal, el cupón y el importe del IFC por año 162 6.1. El interés, el principal, el cupón y 1 importe del IFC por año 16 3 6.2. Proyección d lo Fluj de Caja eto para el IFC . . . 16 3 6.2. Proyección de los Flujos de Caja eto para el IFC . . . 164 6.3. IFC de la Garantía de Riesgo de Crédito empleando Black y

Schole (En$ millones) ... 166 A.1. Valore futuro cuando d contabiliza una vez al año .... 182

.2. Valores presentes d scontados al contabilizar una vez al año 18 3 A.3. Valore futuros cuando d contabiliza una vez al año . . . . 184 A.4. Valores presentes descontados al contabilizar una vez al año 185 A.5. Valores futuro cuando e contabiliza

n

vece al año . . . 18 7

A.6. Valores presentes descontados al contabilizar n veces al año 188

Motivación

El 14 de Octubre la Real Academia de Ciencias de Suecia decidió otorgar el

Premio del Banco de Suecia para las Ciencias Económicas en Memoria de Alfred

Nobel, 1997, a los profesores Robert C.

Merton, de la Universidad de Harvard,

Cambridge, USA, y Myron S.

Scholes de la Universidizd de Stanford, USA, por

haber desarrollado un nuevo método para determinar el valor de los derivativos,

el cual se conoce como la fórmula de Black-Scholes-Merton

1

(en adelante B&S).

A í lo informaba el diario El Comercio, en u edición del 15 de Octubre del mismo año. Este anuncio, aunque recortado, estaba a la vista de todos aquello que transitaban por el corr dor de la Escuela de Matemática. Cuando lo vi, esto dio respuesta a una pr gunta que yo tenía desde el primer día que ingre e a la UNI, ¿La matemática como carrera profesional, tiene alguna aplicación práctica en la vida real? Esto daba respuesta a una inqui tud temprana, pero a u ez motivó una pregunta adicional ¿Que son las opciones financieras y los derivativos? y ¿Por qué su valoración mereció el Premio obel?

La formulación de B&S es una a tuta y elegante repre entación matemática, que e fundam nta en la conocida cuación de calor desarrollada por Fourier n 1822, y utilizada por Ein tein en 1905 precisamente en la explicación formal del movimiento browniano, que e uno de los pilares de las finanzas modernas. Por consiguiente, la finanzas modernas y la física moderna si están con ctadas. De ahí pro iene el título de la tesis que presento a continuación.

del precio de las opciones n particular y en general de todo derivado financiero que sigue proce o estocásticos relativamente estandarizados. Desafortunadamente, en los dos artículos seminales, el primero de Fischer Black y Myron Scholes (1973) The Pricing of Options and Corporate Liabilities publicado en el Joumal of Political Economy 81 (3): 637-654 en su edicione de mayo-junio 1973 y el segundo de Robert C. Merton (1973) Theory of Rational Option Pricing publicado en el desaparecido Bell Joumal of Economics and Management Science 4 (1): 141-183 de la primavera (Spring) de 1973, el desarrollo de los principios matemáticos y particularmente de la conexión con la ecuación de calor no son directos, rigurosos y menos intuitivo .

Durante el año 2008, mi motivación inicial de inve tigar sobre los principios matemáticos de la formulación de B&S, se ha incrementado de manera importante debido a do razones. La primera razón, es la actual crisis financiera que está viviendo el mundo y que se gatilló a partir de los problemas que ha vivido el mercado de hipotecas en Estados Unidos. La segunda razón, se relaciona con Perú, y se vincula con el substancial déficit relativo de infraestructura que ive mi paí .

Crisis Financiera

En efecto, de acuerdo a ari analista especializado 2, los grandes culpables de la actual crisis financiera internacional on las denominadas ventas cortas y los seguros contra impagos (CDS). Ambas e relacionan directamente con los supue tos y las aplicaciones iniciales de B&S.

estrategia ganadora, qu el precio del activo estará más barato cuando deba recomprarlo. Así, él lo vende caro, y lo recompra barato. Ahí está su ganancia.

Cuando los inversionistas tienen temor que grandes compañías de seguros o bancos d inv rsión pueden colapsar, se desata una ola de ventas cortas, precisamente especulando con que esas acciones en un tiempo más valdrían muy poco. Eso contribuye a hacer bajar fuertemente las acciones, sobre todo de instituciones financieras, generando una mayor sensación de pánico financiero. Estados Unidos3_{, siguiendo los} mismos pasos que otra decena d países, resolvió en septiembre del 2008 suspender las ventas cortas sobre 799 acciones financieras, para poner fin a las especulaciones. La existencia d la estrategia de ventas corta permite construir carteras o portfolios libres de riesgos, compuestos por acciones y opciones, y constituye la base de la valoración de B&S.

Por otra parte, una pregunta valida de plantearse es cómo fue posible que las hipotecas de alto riesgo (también denominadas subprime4_{, en} inglés) despertaran una alta demanda por parte de los inversionistas. Las hipotecas subprime lograron entrar al mercado gracias a la securitización, mecanismo donde se empaquetan un grupo de activos (en este caso hipotecas) y se venden como garantía de un bono5 _{que se paga con el flujo}

3_{Securities and Exchange Commission, Informe N}º _{34-58592, Septiembre 18, 2008} 4_{Subprime: esta palabra, con la que se ha bautizado a la crisis, fue el}

egida en el año 2007 como la palabra del afio por la Sociedad Americana de Dialectos, dedicada al estudio de la lengua inglesa en EE.UU. Este adjetivo inglés se utiliza para describir un préstamo, hipoteca o inversión de alto riesgo, lo que está dado por la situación del deudor (bajos ingresos, poco trabajo y poco patrimonio). Cuando se clasifica el riesgo, a la hipoteca se le asigna un puntaje. La hipoteca prime, con bajo riesgo de impago, e aquella clasificada entre 850 y 620 puntos.

pero para colocar las subprime se crea un producto llamado obligaciones de deuda colaterizadas -CDO (Collateralized Debt Obligations). Este tipo de productos se dividen en niveles (o tranches, en inglés), de modo que en un mismo bono se empaquetan hipotecas de distinto riesgo. Por lo tanto, en el mismo producto hay hipotecas prime y subprime, y entre todas ellas se asegura el flujo al inversionista que compra el bono. Asegurado el pago del flujo, las agencias de clasificación de riesgo las catalogan con altos niveles de seguridad.

En el contexto anterior, aparecen los Credit Default Swap (CDS), que son sofisticados contratos de seguros mediante los cuales se busca proteger contra los riesgos de impago que pueda tener un bono. Para ello, el comprador del bono le paga a un asegurador - mediante un sistema de primas anuales, usualmente por cinco años- para que en caso de default6 de la empresa que emitió el bono el asegurador cubra los pagos que corresponden a dicho bono.

Estos contratos de garantías, a su vez, son transables en el mercado. Las espectaculares condiciones financieras hasta antes del 2008, llevaron a que se creara un gigantesco mercado de CDS, el que de acuerdo con algunas estimaciones llega a la impresionante cifra de US$ 62 trillones. La forma de colocarle precio a estos instrumentos garantizadores (CDS), es a través de modelos de riesgos de default, cuya principal familia de modelación sigue la formulación de B&S.

Es fácil darse cuenta que gracias a la existencia de estos seguros contra impago, el mercado de los bonos ligados a hipotecas subprime (los CDO) incrementaron aún más la demanda de los inversionistas por este tipo de bonos, ya que se hicieron más seguros. El problema es que estos seguros no se transan de manera competitiva en los mercados formales sino directamente entre las partes, por lo que no había una regulación específica y determinar su valoración y precio exacto es muy complejo.

Lo que sigue no es difícil intuirlo. Al caer el valor de las propiedades y comenzar las ejecuciones hipotecarias, disminuye el valor del activo que está en garantía y que respalda el valor de los bonos hipotecarios. Ello provoca una desvaloración del bono hipotecario, y por supuesto arrastra también al seguro que lo respalda (CDS), el que también se desvaloriza (pues aumenta el riesgo de impago).

Déficit

de

Infraestructura

en

Perú,

Participación Privada y Garantías Estatales

Según el Informe Global de Competitividad 2008 - 2009, publicado el 08 de octubre del 2008, por el Foro Económico Mundial7_{, ubica al Perú en} el puesto 83 del ranking, mejorando 3 posiciones con relación al reporte del año anterior. Por su lado, Chile descendió 2 posiciones siendo, de igual forma, el mejor posicionado de la región.

Por su parte, en oviembre del 2008, se desarrolló en la ciudad de la Lima las cumbres de Líderes y Empresarial del Foro de Cooperación Económica Asia Pacífico (APEC), donde se resaltó la importancia de la inversión pública y privada en los proyectos de infraestructura, como medida para enfrentar la crisis financiera internacional. Pero, cuando un Estado necesita desarrollar obras de infraestructura, y no cuenta con los medios económicos, ni los recursos de gestión para ello, entonces surgen las denominadas Asociaciones Público-Privadas (APPs).

En Perú, las APPs se clasifican en proyectos cofinanciados y autofinanciados, los que según sea el caso pueden necesitar garantías financieras estatales, los que se transforman en pasivos contingentes para el gobierno. Cabe señalar, que la característica de contingente proviene del hecho que estos pasivos se tienen que pagar únicamente bajo la ocurrencia de un evento específico. Una de las formas de valorar estos pasivos contingentes, es a través, de una técnica denominada Análisis de Activos Contingentes (AAC), cuyo fundamento central está basado en las proposiciones de Black, Scholes y Merton. Por esta razón, en el capítulo final se desarrolla los principales aspectos y algunas aplicaciones del AAC.

profesores de Tesis, Don Sergio Hinojosa, quien me ha enseñado y me ha guiado en las aplicaciones de las finanzas y los procesos estocásticos en el mundo real. El segundo es Don Patricio Mansilla, quien me ha motivado y alentado en complementar mi aprendizaje de matemáticas con la teoría económica y particularmente con la economía financiera. Con ellos, estoy trabajando, entre otras materias, en aplicaciones de op­ ciones financieras, opciones reales y flexibilidad al crecimiento económico.

Introducción

Uno de los desarrollos más notables en los mercados financieros, ha sido la comercialización de instrumentos derivados. En efecto, en el año 2007, el volumen total de transacciones en estos instrumentos ascendió a 516 mil millones de dólares8_{, de los cuales más de la mitad correspondió a} derivados de tasas de interés y dónde diariamente se negocian 5 mil millones de dólares (Bank of Internacional Settlements (2007), Salazar (2008)).

Los derivados son instrumentos financieros cuyo precio no sólo varía en función de los tradicionales parámetros como riesgo y plazo, sino que, también depende de la cotización que alcance en el mercado otro activo, al que se denomina subyacente. En este sentido su precio se "deriva" de la evolución del precio y de la cantidad de otro activo relacionado. Existen una serie de instrumentos derivados que se clasifican en categorías y en tipologías de uso. Entre los más importantes, clasificados por categorías, se encuentran los futuros, contratos a plazo (forwards), swaps, opciones de venta y compra, garantías. Mientras que los clasificados por tipologías, se encuentran los derivados de tipos de interés, acciones, índices, tipo de cambio, cobre, bienes agrícolas, metales, petróleo, crédito.

Extensa información para la enseñanza y comprensión sobre este tipo de instrumentos se encuentra en la literatura y en libros formales de la academia. Dentro de los más citados y usados en la enseñanza de derivativos, a nivel intermedio y avanzado se encuentran en primer lugar Hull (2002), y lo siguen libros como Kolb (1997), Miller (1997), Durban (2005) y Das (1994), entre otros. Esta literatura carece de desarrollos explicativos detallados de los principios y fundamentos de la matemática,

sobre-simplificación formal que se detecta en estos textos de estudio la que ha contribuido en su justa medida, a mi juicio, a explicar la actual crisis financiera internacional. En los programas formales de MBA y de diplomas especializados en el mundo y por cierto en Perú, los fundamentos matemáticos no son mencionados, y su tratamiento es el mismo que se entrega al desarrollo de una fórmula, por ejemplo, como la derivación de la solución a la ecuación polinómica de segundo grado por todos conocidas y enseñada en la educación secundaria.

El caso más ilustrativo al respecto, es el artículo seminal para la valoración moderna de derivados financieros, escrito en 1973 por el matemático Fischer Black y el economista Myron Scholes. En este artículo, se muestra una fórmula directa para valorar opciones financieras usando para ello como fundamento central la formulación de la ecuación de calor de Fourier. Esta ecuación es solamente citada, más no desarrollada ni menos explicada. La prescripción del paper es una fórmula matemática, que es la que se presenta en los cursos de finanzas y programas de negocios especializados, y es la que los traders y operadores de derivados usan de manera usual en las valoraciones de miles de millones de dólares anualmente. Se trata de colocarle un precio a un instrumento derivado, y por lo tanto comercializarlo en un mercado primario o secundario, que esencialmente contiene variables aleatorias que siguen procesos estocásticos. Para lo anterior, es necesario conocer, evidentemente una serie de principios y fundamentos de teoría de probabilidades y de movimientos estocásticos estandarizados o semi estandarizados. Asimismo, es necesario conocer principios básicos de cálculo estocástico, algunos teoremas y lemas y algunos principios de matemática para la física aplicada. A partir de esos elementos anteriores, recién es posible comprender el desarrollo por etapas, de la valoración financiera de instrumentos derivados y sus aplicaciones.

En lo que sigue, en el presente documento se desarrollan de una manera etápica y consistente, los principales elementos de la matemática y de la física necesarios para comprender la valoración de instrumentos financieros derivados y sus aplicaciones. El documento se organiza como sigue:

espacios de probabilidad y variables aleatorias, que es la base para las siguientes secciones de la tesis. Con estas herramientas, se hace una revisión acerca de los procesos estocásticos y medidas de dispersión, para efectos de análisis con respecto a la curva normal.

Además se revisan las definiciones de la Integral de Riemann y la Integral de Riemann-Stieltjes, con la finalidad de definir la integral

1

b

f ( t)

dg(

t), para cualquier función continua f y

g

sobre el intervalo

[a, b].

Aún cuando,

f

=

g

no resulta ser un problema no trivial. En realidad, no existe una respuesta definitiva. Es por ello, para poder responder a esta inquietud, se considera el estudio de los caminos aleatorios.

En el Capítulo 2, en base al marco teórico del Capítulo 1, se procede de definir al Movimiento Browniano Estándar, que fue la pieza clave para el estudio sobre opciones financieras que realizo Bachelier (1900). Así como también, definimos lo que es un Proceso de Wiener y realizamos su equivalencia con el Movimiento Browniano Estándar. Con estas ideas en mente, se desarrolla el Movimiento Geométrico Browniano, el cual fue introducido por Samuelson (1965) y que además juega un rol muy importante en el campo de las finanzas, en la valoración de derivados financieros.

En el Capítulo 3, con las definiciones del movimiento browniano, se estudia como este proceso juega un papel preponderante en la definición de las Martingalas, la Integral de Wiener, e Integrales Estocásticas.

Capítulo 4, todo lo anterior, se resume en la diferenciación estocástica, en particular, en el Lema de Ito. Las cuales forman la estructura de la modelación de instrumentos financieros, los cuales fueron posibles estudiarlos, gracias a la fórmula de Ito.

valoración de opciones financieras europeas.

En el Capítulo 7, empezamos explicado que es un análisis de deman­ das contingentes, y aplicarlo a la valoración de garantías financieras en un proyecto de infraestructura por medio de la fórmula de B&S para una opción de venta, para diferentes escenarios de volatilidad. Así como también, como el Análisis de Activos Contingentes, se aplica en Warrants, Bonos Convertibles y LYO s.

Algunos Elem.entos de Teoría de la

Probabilidad.

En la vida diaria, nos enfrentamos a menudo, a situacion s que muestran nuestra ignorancia respecto al futuro (lo cual es natural). Como, cuando intentamos prever la densidad del tráfico, la cotización en la bolsa de valores del precio de las acciones la proxima semana, los resultados de las próximas elecciones y a menudo no conocemos la respuesta con certeza. En su lugar, estamos obligados a suponer, o estimar nuestra posible respuesta.

probabilidad, se originaron en el siglo XVII. En 1654, el caballero de Mére, un jugador parisino, pregunto a Blaise Pascal sobre algunas situaciones relacionadas con la probabilidad que se dan en los juegos de azar, tales como la probabilidad de ganar que tendría cada jugador si se continuara un juego de azar detenido a la mitad. Interesado en el tema, Pascal inició una intensa correspondencia con el matemático y abogado Pierre de Fermat. Posteriormente Pascal escribió la obra Traité du Triangle Arithmetique, donde describe los coeficientes binomiales ( el triángulo de Pascal) y la distribución binomial de probabilidad.(Para mayores detalles ver, [36], [54])

1.1. Introducción.

La definición formal de probabilidad se inicia con el espacio muestral oespacio total, generalmente representado por O. El espacio muestral es un conjunto que incluye todos los posibles resultados de un experimento o situación. Con esta finalidad, se presenta el siguiente ejemplo1_:

1.1.1. Paradoja de Bertrand

Dado un circulo de radio 2m., elijamos una cuerda de este circulo de manera aleatoria. ¿Cuál es la probabilidad que esta cuerda intersecte al circulo de

radio 1m., el cual es concéntrico con el circulo de radio 2m.?

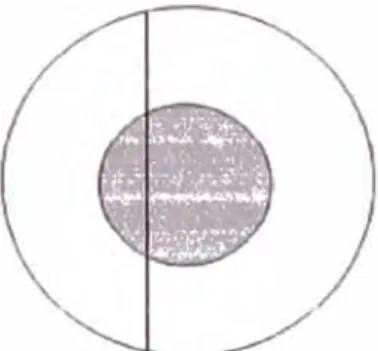
l. Solución Nºl: Cualquier cuerda (siempre que no pase por el centro) se encuentra únicamente determinado por la localización de su punto medio.

Así,

1.Algunos Elementos de Teoría de la Probabilidad.

Gráfico 1.1: Paradoja de Bertrand: Primer caso.

Probabilidad de pasar por el centro área del circulo interior área del circulo exterior

¡·

2. Solución N°2: Por la simetría de la rotación inferior podernos asumir que la cuerda es vertical. El diámetro del circulo mayor es 4m. y la cuerda pasara por el círculo pequeño si cae dentro de su diámetro de 2m ..

Gráfico 1.2: Paradoja de Bertrand: Segundo caso.

Por lo tanto

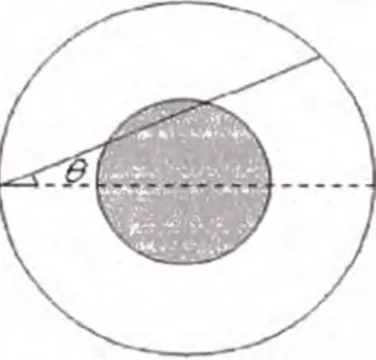
3. Solución N 3 Por imetría podemos asumir que los extremos de la cuerda se encuentra bastante separados. El ángulo 0 que hace la cuerda con la recta horizontal se encuentra entre

±

;

y la cuerda

1[ pasara por el circulo interior si 0 e encuentra entre

±

_6.

Gráfico 1.3: Paradoja de Bertrand: Tercer caso. Por lo tanto

La probabilidad de que pase por el circulo interior

2n

- ₁

6 -2n

3

2

□

Oservación 1.1 Este ejemplo muestra que debemos tener mucho cuidado al momento de definir que significado tiene el término aleatorio. La manera correcta de hacer esto es introducir a continuación la estructura matemática

precisa de un espacio de la probabilidad.

1.2. Espacio de Probabilidad.

1.Algunos Elementos de Teoría de la Probabilidad.

cuando son utilizadas precisamente en Teoría de la Probabilidad.

En lo sucesivo se entenderá por O, como un conjunto fijo al cual se le denominará, espacio total y al conjunto P (O) se le denominará el conjunto potencia de O. Además, recibirá el nombre de una sucesión de conjuntos, a toda aplicación d N en P(O). El cual se representará por {An}nelN C P(O).

Dado que la probabilidad, no puede ser definida sobre una colección cualquiera de sucesos, sino que la clase de subconjuntos del espacio muestra!, sobre la que puede establecerse una probabilidad debe tener una estructura nuruma, que se denomina sigma álgebra (cr-álgebra). Por consiguiente, una clase de sucesos constituye una sigma álgebra si cumple con las siguientes propiedades:

Definición 1.1 Dado el espacio total O, una clase U

e

P (O) tiene una estructura de cr-álgebra si y sólo si

(i) O E U.

(ii) Para todo A E U, se verifica que Ac _{E U.}

(ii) Dado cualquier sucesión {An}nelN

e

U se verifica que

LJ

Ak E U. k=l

Donde Ac

:=O\

_{A es el complemento de A.} Propiedades

1. 0EU.

En efecto: Es claro que 0

=

oc

y

como O E _{U por} ( _i)

y

( _{ii) se tiene que} oc _{= 0 E U.}

2. Para cualquier sucesión {An}nelN con An E U, V n EN, se tiene que

íl

An EU.

En efecto: Al ser An E U, Vn EN se tiene por (ii) que A� E U, \:/n EN. Por (iii)

LJ

A� E U, y por (ii)

nE

( LJ

A�) c

E U nEN

Finalmente como

se tiene el resultado enunciado.

3. Para cualquier sucesión { _Akh=1, ... _,n con _Ak E U,\:/ k

=

1, ... , n, se verifica que

LJ

Ak E U. k=1

En efecto: La sucesión A1, ... , A₁₁, 0, ... es una sucesión infinita de elementos de U. Por (iii), se tiene

n n

LJ

Ak U 0 U · · · U 0 U · · ·

=

LJ

Ak E U.

k=1 k=1

4. Para cualquier sucesión { _Akh=l, ... _,n con Ak E U, V k

=

1, ... , n, se

verifica que

n

n

Ak E U. k=1

En efecto: La sucesión A1, ... , An, O, O,... es una sucesión infinita de elementos de U y por la propiedad

_(2),

que se acaba de demostrar

n n

1.Algunos Elementos de Teoría de la Probabilidad.

5. La ínter ección de o--álgebras definidas sobre el mismo espacio total es un o--álgebra.

En efecto: Sea T la familia de o--álgebras dada por

T

={U:

_{U es una o--álgebra y U}

e

P(O)}

Se establecerá que

1-í=

n

u

UET

es una o--álgebra. Para ello se verá que se verifican las

condiciones que caracterizan a las o--álgebras:

a) O E 1-í, por ser las U E T o--álgebras y ser O E U,\/ U E T.

b) Si A E 1-í, entonces A E U, \/ U E T, entonces, por ser U una o--álgebra, Ac _{E U,\/ U E T y como consecuencia}

Ac _E

íl

_{U= 1-í.} UET

c) Si A11 E 1í se tiene que A11 E U, \/ U E T. Por lo tanto,

U

An E U,\/ U E T. En consecuencia

nE

U

An E

íl

U =1-í.

nEN ne

Definición 1.2 Sea U un o--álgebra de subconjuntos de O. Llamamos a

P: U�

[O, 1]

(i)

P(0)

=

O,

P(O)

= 1.

(ii) Dado cualquier ucesión {An}nEN

e

U se verifica que

00 00

P(

u

_Ak)

<

L

P(Ak)-k=1 k=1

(iii) Dado cualquier ucesión di junta { An }nEN

e

U se verifica que

00 00

P(

u

Ak)

=

L

P(Ak)-k=1 k=1

Se concluye que si A, B E U, entonces

A C B implica P(A)

<

P(B).

Definición 1.3 _{La terna (O,U,} P) es llamado un espacio de probabilidad siempre que O es un conjunto cualquiera, U es una (T-álgebra de subconjuntos de O y P es una medida de probabilidad sobre U.

Terminología.

(i) Un conjunto A E U es llamado un evento; y lo punto w E O son llamados puntos de la muestra.

(ii) _P(A) es la probabilidad del evento A.

(iii) Una propiedad el cual es cierto, excepto para un evento de probabilidad cero es llamado casi seguramente ( usualmente abreviado c.s.).

Ejemplo 1.1 Sea O

=

{

w1, W2, ... , WN} _{un conjunto finito, y supongamos que} están dados los numeras O

<

_Pj

<

1 para j

=

1, ... , N, sati ifaciendo

E

_Pj

=

1. Tomaremos U para abarcar todos los subconjuntos de O. Para cada conjunto A= {wji,Wh,···,wjm} E U,con 1

<

h

<

h

<

...

<

jm

<

N,definimos

1.Algunos Elementos de Teoría de la Probabilidad.

Ejemplo 1.2 La menor (]'-álgebra que contiene a todos los subconjuntos abiertos de JR11 _{es llamado la (]'-álgebra de Borel, denotado por B. Supongamos que f es} función integrable y no negativa, tal que f f dx

=

1. Definimos

ÍIR.11

P(B)

:=

h

f (x)dx

para cada B E B. Entonces (JR11_{, B, P) es un espacio de probabilidad. Llamaremos}

a f la densidad de la medida de probabilidad P.

Ejemplo 1.3 Supongamos que en vez de fijar un punto z E JR11, definimos

P(B)

:=

_{{ 01} si

z

E B si z

</.

B

para conjuntos B E B. Entonces (JR11_{,B,P) es un espacio de probabilidad.} Llamaremos a P la masa de Dirac concentrada en el punto z, y escribiremos P

=

Óz.

Ejemplo 1.4 Problema de la Aguja de Buffon, es un problema de probabilidad geométrica planteado y resuelto en 1777 por el matemático y naturalista francés Georges-Louis Lecher, Conde de Buffon. El problema se presenta con un plano dividido en rectas paralelas equidistantes en 2cm. y con una aguja de longitud de

1cm. que se deja caer en forma aleatoria sobre el plano. ¿Cuál es la probabilidad de que esta aguja corte a al_guna de estas rectas?

Primero debemos encontrar algún espacio de probabilidad apropiado (O,U, P). Para esto, sea

Gráfico 1.4: El Problema de la aguja de Buffon.

Esto determina completamente la posición de la aguja, hasta la traslación y la

reflexión. Tomemos

0=

T[

[O, 2)

"--v-'

valores de 0

X

[O, 1)

� valores de h

,

U= Subconjuntos de Borel de O,

P(B) __ 2 · área de B para ca da BE U T[

Denotaremos por A el evento que la aguja corta a una recta horizontal.

Podemos comprobar que esto sucede siempre que

s!e

<

}.

Por consiguiente, sin0

A= {(0,h) E O: h

<

-2-},ypor lo tanto:

P(A)

=

2(area de A) _rr

=

�

_rr

_l

(

_o

i

!

₂ sinBdB

=

.!__

_rr

1.3. Variables Aleatorias.

Podemos pensar acerca del espacio de probabilidad O, como una construcción matemática esencial, el cual no es directamente observable.

Por lo tanto, estamos interesados en introducir aplicaciones X : O -+ IR.11_,

1.Algunos Elementos de Teoría de la Probabilidad.

B denota la colección de subconjuntos de Borel de ]Rn, el cual es la menor CT-álgebra de subconjuntos de ]Rn conteniendo a todos los conjuntos abiertos.

Definición 1.4 Sea (O.U, P) un espacio de probabilidad. Una aplicación

X: O ----+- JRn

es llamado una variable aleatoria n-dimensional si para cada B E B, tenemos

Equivalentemente decimos que X es U-medible.

Nota 1.1 Usualmente escribiremos X y no X(w). Es costumbre dentro de la teoría de la probabilidad no exhibir la dependencia de las variables aleatorias sobre la muestra w E O. También denotaremos P(X-1_{(B)) como P(X E B), la} probabilidad que X esta en B.

Emplearemos letras capitales para denotar las variables aleatorias. Las letras en negrilla usualmente significan una aplicación vectorial.

Ejemplo 1.5 Sea A E U. Entonces la función indicador de A.

XA(w)

es una variable aleatoria.

-- { 01

siw E A si w <$. A,

Ejemplo 1.6 En general, si A1, A2, ... , Am E U, con O

números reales a_1, a_{2, .•• ,} a_m, entonces

X_{= LªiXA;} i=l

es una variable aleatoria, llamada una función simple.

U

A¡, y los

Lema 1.1 Sea X : O -t ]R. una variable aleatoria. Entonces

U(X)

:=

_{X-

1

_(B):

BE B}

es un cr-álgebra, llama.da la cr-álgebra generada por X. Está es la menor sub-cr­ álgebra de U con respecto a, el cual X es medible.

Oservación 1.2 Es importante entender en términos probabilísticos que la cr-álgebra U(X) puede ser interpretada como aquella que contiene toda la

información relevante acerca de la variable aleatoria.

En particular, si una variable aleatoria Y es una función de X, es decir, si

y=

<t>(X)

para alguna función razonable

<t>,

entonces Y es U(X)-medible.

Recíprocamente, supongamos que Y : O -t 1R es U(X)-medible. Entonces existe una función <t> tal que

y=

_<t>(X).

Por lo tanto, si Y es U(X)-medible. Y es en realidad una función de X. Por consiguiente, si conocemos el valor de X( w

),

en principio sabemos también que

Y(w)

=

<t>(X(w)), aunque no podemos tener una manera práctica de construir <t>.

□

Oservación 1.3 Se entenderá por variables aleatorias distribuidas idénticamente e independientemente, si cada una de ellas tiene la misma distribución de probabilidad y son mutuamente independientes.

1.Algunos Elementos de Teoría de la Probabilidad.

probabilidad (O, F, P), y la función de distribución Fx de X y la función de

distribución Fy de Y son las mismas: Fx

=

Fy.

Una colección de variables aleatorias X_¡, se dice que está idénticamente e

independientemente distribuida, si los X_¡ son idénticamente distribuidas y

mutuamente independiente (cada subfamilia finita de X_¡ es independiente).

1.4. Procesos Estocásticos.

Sea:

X : [O,

oo]

---+ 1R

t � X(t)

=

Xt

una función real de variable real. Por ejemplo, la función Xt puede describir la velocidad o la acel ración d un cuerpo solido en función del tiempo t. Pero X_t, también pued r pres ntar el precio de un activo financiero en el tiempo, llamada trayectoria del activo financiero X. Sin embargo, exi te una diferencia fundamental entre estas dos interpretaciones. En el prim r caso, X como una función de t, es una función suave, no olo continua (natura non facit saltus!2), sino que también (a menudo) es dH renciable. Para esta clase de funciones, existen herramientas conocidas d 1 cálculo clásico. Empleando la notación Xt

:=

dX

d/ para la derivación de Xt con resp cto al tiempo t, tan común en física,

la relación entre la diferenciación y la int gración puede ser formulada de la siguiente manera:

Xt

=

Xo

+

fo

1

X

5ds ó

Sea F E C2 _{(1R) una función r al dos v ces continuamente dif renciable} sobre 1R. Entonces, por el 1i or ma de Taylor (Ver [28], [56]), se llega a la siguiente expresión:

6F(Xt)

=

F(Xt+í.').t)-F(Xt)

=

F'(Xt)6Xt

+

�F"(Xr)(6Xt)2

con 6.Xt

=

Xt+6t -Xt y algún f E [t, t + 6.t]. Tomando el límite cuando

,6.t-+ O, obtenemos:

o, equivalentemente,

dF(Xt)

=

F'(Xt)dXt

F(Xt)

=

F(Xo)

+

fot F'(Xs)dXs

donde, para una función suave Xt, 6.Xt -+ dXt

=

Xtdt, y el término de mayor orden, que son de orden (dt)2_{, se anulan.}

Sin embargo, esta clásica relación no se aplica para aquellas funciones reales, que describen las trayectorias de los activos financieros, como ocurre en la matemática financiera. Cuando en el siglo XIX, el matemático alemán Weierstrass, construyó una función real continua, pero que no era diferenciable en ninguna parte, esta función fue considerada como una curiosidad matemática. Desafortunadamente, esta curiosidad se encuentra en el corazón de la matemática financiera. Las trayectorias de las tasas de cambio, las tasas de interés, y los activos líquidos son prácticamente continuos, debido a la alta frecuencia de los datos. Pero ellas no son de variación acotada, en cada intervalo de tiempo dado. En particular, ellos no son diferenciables en ninguna parte, por lo tanto la función de Weierstrass representa una posible gráfica financiera. Por consiguiente, el cálculo clásico requiere una extensión hacia las funciones de variación acotada, una tarea que fue pasada por alto, durante mucho tiempo. Este vacío, fue cubierto con el desarrollo del cálculo estocástico, el cual puede ser considerado como la teoría de diferenciación e integración de los procesos estocásticos, el cual es el objetivo de esta sección. Antes, definamos variables aleatorias que dependen del tiempo.

Definición 1.5 Sea (O.U, P) un espacio de probabilidad:

(i) Una colección de variables aleatorias {X(t) : t

>

O} es llamado un proceso

estocástico.

(ii) Para cada punto w E O, la aplicación t 1-r X(t,w) es la correspondiente

1.Algunos Elementos de Teoría de la Probabilidad.

so.---,

0+---.---.---.---1

o 10 20 30 40 50 60 70 80 90

-Serlel -Serie2 -Serie3 -Serie4

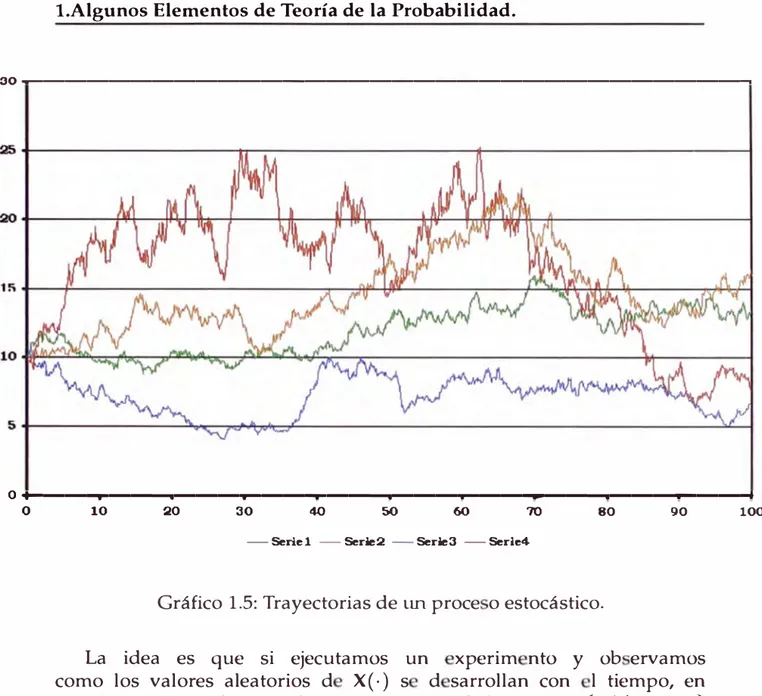
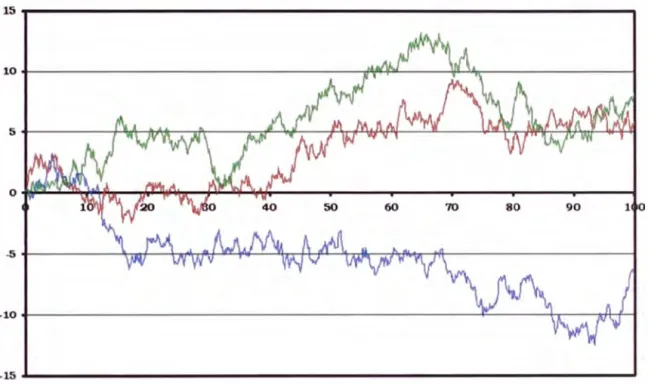
Gráfico 1.5: Trayectorias de un proce o estocástico.

La idea es que si ejecutamos un xperim nto y ob ervamos como los valores aleatorios d X(·) s d sarrollan con 1 tiempo, en realidad estarna observando una trayectoria de la muestra

{X(t)

: t

>

O} para algún w E O fijo. i volvemo a efectuar el experimento, observaremos en general una nu va trayectoria para la mue tra, tal como se indica en el Gráfico 1.5.

1.5. Medidas de Dispersión.

Una explicación intuitiva de la definición de la esperanza, e basa precisamente en la int rpretación de la probabilidad como límite de frecuencias relativas; es decir, sea X es una variable aleatoria, con función de probabilidad p(x¡). Tal qu X una

caracteástica numérica del resultado de un experimento, supongamos que vamos a repetir (por lo menos conceptualmente) el experimento una cantidad finita n de veces, independientemente, al observar los valores de esa característica numérica. Si el tamaño del experimento, n, es un valor muy grande, las observaciones tomarán el valor Xi con una frecuencia relativa aproximadamente igual a p (Xi), para todo i. Es decir, Xi aparecerá más o menos una cantidad np(x¡) de veces, en las n observaciones. Por consiguiente, el valor promedio esperado en estos n ensayos del experimento, es decir, la media aritmética de los n valores observados, será aproximadamente igual a:

1

-¿]xi·

np(xi)]

=¿]xi·

p(xi)]

n ₁ . ₁ .

Este valor será el límite cuando n -)- oo, i.e., el valor medio obtenido en n ensayos del experimento convergerá a lE (X) cuando n -)- oo. (Está es una versión de la Ley de los Grandes Números3). Por lo tanto, podemos decir que esperamos obtener un valor medio lE(X). (Ver [3])

Definición 1.6 Llamaremos a

lE(X) := fo XdP

la esperanza o valor esperado4 de X, siempre que exista la

integral.

La varianza, es una medida que en promedio, cuantifica el nivel de dispersión o de variabilidad de los valores de una variable cuantitativa con respecto a su valor promedio. La concentración de los datos alrededor de su valor promedio, es proporcional al valor de la varianza.

Definición 1.7 Llamaremos a

3La Ley de los Grandes Números, afirma que la m dia aritmética de los n valores observado es aproximadamente igual a IE(X) cuando n es muy grande.

1.Algunos Elementos de Teoría de la Probabilidad.

Var(X)

:=

lo

IX - JE(X) l2dP

la varianza de X, donde 1 · 1 denota la norma Euclidiana y siempre que la integral

exista.

Observemos que

Var(X)

=

JE(IX -JE(X) 12)

=

JE(IXl2) -IJE(X) 12•

La desviación estándar o volatilidad, es una medida de dispersión que nos indica cuánto tienden a alejarse los valores de una variable cuantitativa, del promedio en una distribución, es decir, es el promedio de la distancia de cada punto respecto del promedio.

Definición 1.8 Llamaremos a

o-(X)

=

✓

var(X)

la desviación estándar o volatilidad de X.

A continuación se enunciaran sin demostración al_gunas propiedades, acerca de las medidas de dispersión, donde X es una variable aleatoria, para su demostración se puede consultar [3], [30], [59], [ 62] y [ 67].

Proposición 1.1

Var(X)

= JE(X

2) -JE(X)2

Proposición 1.2

Var(aX

+

b)

=

a2Var(X)

Proposición 1.3

Cov(X, Y)

=

JE(XY) -JE(X)JE(Y)

Proposición 1.4

Proposición 1.5

Cov(X,

Y)

=

Cov(Y,X)

Proposición 1.6

Nota 1.2 _{La Proposición 1.6, puede ser enunciada de manera equivalente, en} términos del algebra lineal, de la siguiente manera:

Var

(t

W¡X¡)

=

w'Vw 1=1

donde:

w

=

vector columna de los valores W¡, para i

=

1, ... , n.

w'

=

transpuesta de w, un vector fila.

V= matriz cuadrada de dimensión n de las covarianzas Cov(X¡

,Xj)-Proposición 1.7

( 11 ) 11

Cov � W¡X¡, Y

=

�

w¡Cov(X¡,

Y)

Lema 1.2 _{Seaµ= IE(X) y} íT

=

S(X). Definimos

X=

X -µ. Entonces (T

IE(X)

=

O y Var(X)

=

CT(X)

=

l.

1.6. La Distribución Normal y Lognormal

1.Algunos Elementos de Teoría de la Probabilidad.

Notal.3 _{Sea x}

=

_{(x1, ...} 1X_n) E lRn,e y

=

(y1,•••,Y_n) E lRn. Entonces

x<y

significa que Xi

<

Yi, para i = 1, ... , n.

Definición 1.9 Sea (O.U, P) un espacio de probabilidad. La función distribución de la variable aleatoria X es la función

Fx : lRn ----+

[O, 1]

x 1---+ Fx(x) :=

_P(X

<

x), V x E lRn

Definición 1.10 Sea X _{una variable aleatoria y F}

=

Fx su función distribución. Si existe una función integrable, no negativa f : lR -+ lR tal que

F(x) =

J:

00 f (x)dy,

entonces f es llamado la función densidad para la variable aleatoria X.

Se concluye entonces que:

P(X E B)

=

hf(x)dx, \/BE B (1.1)

La distribución normal fue considerada por primera vez por De Moivre en 1753, pero quedó en el olvido, hasta que a principios del siglo XIX Gauss y Laplace la pusieron de actualidad y por ello en la literatura estadística se la conoce también con el nombre de distribución de Laplace-Gauss (Ver [5], [30]).

Su importancia se da, porque aparece ( de manera aproximada) en muchas situaciones, como en los campos de la física, economía y las finanzas, por citar algunos. En general, la distribución normal, surge siempre que los resultados de un experimento sean debidos a un conjunto muy grande de causas independientes que actúan sumando efectos, siendo cada efecto individual, de poca importancia respecto al conjunto.

Siempre que una variable aleatoria pueda ser expresada como producto de pequeños factores independientes, entonces, diremos que es­ ta es modelada por una distribución Lognormal, como es el caso del re­ torno a largo plazo de un proyecto de inversión. Es decir, Si X es una vari­ able aleatoria con distribución normal, entonces ex tiene una distribución

Lognormal.

Oservación 1.4 Sea X una variable aleatoria la cual se distribuye normalmente, entonces X puede tomar cualquier valor positivo o negativo. Sin embargo, si X es una variable aleatoria la cual se distribuye lognormalmente sólo puede ser positiva, con media, moda y mediana todas diferentes. Esto es sumamente importante cuando se desea valorar activos financieros, dado que es imposible que un activo adquiera un valor negativo, por lo que suponer que los mismos se distribuyen normalmente es una grave falencia5

A continuación se enunciara la definición formal de la distribución normal y lognormal, así como alguna de sus propiedades más importantes.

Definición 1.11 La distribución normal de parámetros 1'- y

(T,

que representan la media y la volatilidad respectivamente, (-oo

<

1'-

<

oo y

(T

>

O), se representará abreviadamente por N('fl,

(T),

es el modelo de probabilidad caracterizado por la función de densidad:

1 -(x-�)2

f(x)

=

--e 20" , para todo x E JR.

�(T

1.Algunos Elementos de Teoría de la Probabilidad.

Oservación 1.5 (Distribución Normal Estándar). Si la variable aleatoria X

tiene distribución normal N(µ, o-2_{), entonces, la variable aleatoria estándar}

Z

=

X -µ, tiene distribución normal N (O, 1), con media µ

z

=

O y varianza O'

o-¾= 1

Definición 1.12 Se dice que una variable aleatoria no negativa X tiene una distribución lognormal, si la variable aleatoria

Y

=

ln(X)) tiene una distribución normal. La función de densidad de probabilidad de una variable aleatoria lognormal cuando ln(X) tiene una distribución normal con parámetros µ y o-es

Proposición 1.8

J(x)

=

{

1 -(Ln(x)-µ)2 ---e iu2

../2iro-x

o

,

X> 0

,

X< 0

Joo 1 -(x-µ)2

../2ir

e :iu2 dx

=

1 Vx E lR -00 O'

Prueba. Primero supongamos que _µ

=

_O y o-

=

_1. Sea

Entonces:

a2

a=

!

00 --e-Zdx1 -x2 -00

../2ir

!

00

!

00 1 x2 1 -v2 --e-Z--eT dxdy -00 -00

../2ir

../2ir

=

2_

f

00

f

00

e -(x2ti) dxdy 2rr: -00 -00

a2 -1

la2rr la

oo

eTrdrd0,-2

= -

₁

la2rr

[

-eT ,2

l

d0

00

2n

o o

2n

o

0

1

la2rr

1

-

_[

_O

_-

_(-1)]d0

₌

_-(2rr)

2n

o

2n

=

1

Dado que a

>

O, y como se ha probado que a2

=

1, entonces se tiene que a

=

l.

Para el caso general, se aplica la siguiente transformación:

x-µ

y=

_(T

dy

=

dx _(T

¡

oo 1 _-(x-p}2

--e 2.u-r dx

=

-oo ../2'iicr

{

oo

_{_}1

_e=f-cr

dy

J-oo ../2'iicr

Proposición 1.9

¡

00 1

-t?---eT

_dy

-00 ../2'ii

1

¡

oo 1 -(x-µ)2 x

../2'ii e 2tr2 dx

=

µ V x E lR -oo 27rCT

Prueba. Supongamos que µ

=

O y CT

=

l.

x--e--,:-dx

=

¡

oo 1 _-x2

-00 ../2'ii

lím --1

J"

xe--,:--x:2dx n-oo

...f2'ii

_-n

--1 lím

[

-e--,:-_{_,.}2

l

n

.Jzii:

n-oo

1.Algunos Elementos de Teoría de la Probabilidad.

¡

00 1 _,._2

x--e----r dx

-00 _fin - lím (-e----r) - (-e----r) 1

[ -n2 -n2 l

fin

n-+oo

-1- lím O

fin

n-+oo

=

o

Para el caso general, se aplica la siguiente transformación:

Proposición 1.10

x-µ

y=

_(T dy

=

dx (T

/ 00

(µ

+

O"Y) � e? O"dy

Í-oo _2TCO"

µxl+O"xO

Por la Proposición 1.8

µ

¡

oo 1 _-(x-µ)2

x2--e 2u2 _dx

=

_µ2

+

�

_Vx E lR -00 _fin(T

□

Entonces:

x2_--eTdx

¡

00 1 x2

-00

v'2rr

f(n)g(n) - f(-n)g(-n) - J:

nf'gdx _112 _112 ¡n -x2 (-ne-r) -_(ne-r) - _l

-n-e-rdx -n2

¡n

-x2

-2ne---r dx - -e---Z-dx -n

¡n -x2 _112 l-_n-e---rdx -2ne---r

--1 lím

J"

x2_e---r -x2 _dx

y'2rr

n--+oo -n

--

_y'2rr

1 _11--+00 lím [111 _-ne-r -x2 dx -2ne---r -112

l

¡

00 1 -x2 -112

--e---Z-dx - lím 2ne---r -oo

y'2rr

n--+oo

_,,2 1- lím _n--+oo 2ne-r Por la Proposición 1.8

Queda por demostrar que el límite converge a O, por la re l.a de L'H8spital, se tiene:

lím _2ne

=#-

=

lím 2n

=

lím -2-

=

O

n--+oo n--+oo � _eT n--+oo _neT � Para el caso general, se aplica la siguiente transformación:

X- 1l

1.Algunos Elementos de Teoría de la Probabilidad.

f

00 x2

Jzrr

e

-<;;;:¡•l'

dx

Í

-

oo

2rro-¡

00

1

:::.i.

(µ + o-y)

2 _�

_e

₂

_o-dy

-oo

2rro-¡

oo

1

-(x-_µ)2

x

2

--e

2o-2

_dx

=

µ

2

x

1 +

_2µo-

x

O+

_o-

2

x

1

-00

�0-Por la Proposición 1.8 y 1.9

µ2

+

a-2

Proposición 1.11

Si

X

es

N[µ,o-2],

entonces

(X)=µ

y Var(X)

= o-2.

Prueba.

lE(X)

Var(X)

Var(X)

¡

oo

1

-(x-_µ)2

x--e

2u2

_dx

=

_µ

-00

'1iiio-Por la Proposición 1.9

lE(X2_{) -} lE(X)2

Por la Proposición 1.1

¡

oo

1

_-(x-i,¡

2

x

2

--e

2u

dx

-

µ

2 -00

-/i'iio-µ2

+

a-2 _ µ2

Por la Proposición 1.1 O

o

Proposición 1.12 La función de densidad de probabilidad de LN(µ, cr ) es:

1 -(log(x)-µ)2

---e 2u2 Vx E R

X�(T

Prueba. Supongamos que la variable aleatoria X es LN(µ,cr2_). Entonces X= eY_{, donde Y es N(µ, cr2}

). Entonces:

Prob(X

<

k)

=

Prob(eY_<k)

=

_Prob(Y

<

_ln(k))

Aplicando la transformación:

1

x

=

eY, y= ln(x), dy

=

-dx X

¡

k 1 _-(Ln(x)-µ)2 ---e 2.u2 dx

-oo X�(T

Lema 1.3 Sea X : O � R.11 _{una variable aleatoria, y supongamos que su función} distribución F

=

Fx tiene una densidad f. Supongamos que

es integrable. Entonces

En particular,

g

; R_ll --t _R

X f----+ g(X)

=

Y

E(Y)

=

{ _{g(x)f (x)dx.} }F.11

E(X) = { xf (x)dx

1.Algunos Elementos de Teoría de la Probabilidad.

Prueba. Supongamos primero que g es una función simple sobre 1Rn:

Entonces

Pero también

g = LbiXB;

i=l

(B

¡ E

B).

E(g(X))

=

tbi

1

XB;(X)dP

=

tb¡P(X E Bi). i=l f1 i=l

Á g(x)f (x)dx

=

t

b¡ Á f(x)dx

IR" _i=l B;

(l)

t

_b

¡P(X E Bi) i=l

Por lo tanto, la fórmula se cumple para todas las funciones simples g y, por la

aproximación, se verifica por lo tanto para cualquier función g en general.

□

A continuación enunciaremo algunos re ultado sobr variables aleatorias que se distribuy n normal e tándar, que serán de gran utilidad para la construcción del movimiento Browniano.

Lema 1.4 Supongamos que X es una variable aleatoria el cual se distribuye normal estándar. Entonces, para todo x

>

O,

x _{1 e-x2-12}

_<

_IP{X

_>

_x}

_<

_{.!___l e-x}212. x2

+

₁

'1fir

-

-

_X

_'1fii

Prueba. La desigualdad del lado derecho se obtiene mediante la siguiente estimación

1

100

u 2¡ 1 1 ?¡

IP{X > x}

< --

-e-u 2du

=

---e-x- 2.

'1fii

x X X

'1fii

Para la desigualdad del lado izquierdo definimos la siguiente

función:

2

100

2

f(x)

=

xe-x 12- _(x2

+

₁₎

De la definición se observa que f(O)

<

O

y

lím f (x) =O.Además,

X-too

(

r

oo

2 e-x2/2)

-2x

lx e-u 12du - x ,

el cual es positivo para x

>

O, por la primera parte. Por consiguiente f (x)

<

O,

probando el lema.

□

1.6.1. Regla 68-95-99

Aunque existen muchas curvas normales, todas ellas tienen propiedades comunes. En particular, todas las distribuciones normales cumplen las propiedades de la Regla 68-95-99. Para cualquier variable aleatoria que se distribuye normalmente con mediaµ. y volatilidad (T, se cumple lo siguiente

■ El 68 % de todas las ob ervaciones encuentran dentro del intervalo

µ.±(T.

P(µ. -(T <X<µ.+ (T)

=

0.6827

=

68.27%

■ El 95 % de todas las observaciones se encuentran dentro del intervalo µ.

±

2(T.

P(µ. -2(T

<

X

<

µ.

+

2(T)

=

0.9545

=

95.45 %

■ El 99.7% de todas las observaciones se encuentran dentro del inter­

valo µ.

±

3(T.

P(µ. - 3(T <X<µ.+ 3(T)

=

0.9973

=

99.73 %

Además, de la simetría de la función de probabilidad f ( x),

P(X

>

µ.)

=

P(X < µ.)

=

0.5

=

50%.

1.Algunos Elementos de Teoría de la Probabilidad.

95%

µ-3u µ-2u µ-a µ

Jl+a µ+2u µ+3u

Gráfico 1.6: Regla 68-95-99.

1.7.

_Integrales.

Primero revisaremos la definiciones de la integral de Riemann en cálculo y la integral de Riemann-Stieltjes en cálculo avanzado (Para mayores detalles ver [561).

l. Integral de Riemann. Una función acotada f definida sobre un intervalo cerrado y finito

[a, b]

es llamado Riemann

Integrable si el siguiente límite existe:

l

b

n

f ( t)dt

=

lím

L

f _{( T¡) (} t¡ - t¡_1 ), ll.1.nll--+O i=l

donde !).n

=

{

to, t1, ... , tn-1, tn} es una partición del intervalo [a,

b]

con la siguiente convención

a

=

to

<

t1

<

· · ·

<

tn-1

<

tn

=

b,

y T¡ es un punto de evaluación en el intervalo [t¡_1, t¡), i.e. T¡ E

Riemann integrable. Además, se sabe que una función acotada sobre

[a, b]

es Riemann integrable si y sólo si, es continua casi en todas partes con respecto a la medida de lebesgue (Ver [30]).

2. Integral Riemann-Stieltjes. Sea

g

una función monótona creciente sobre un intervalo cerrado y finito

[a, b].

Una función acotada f definida sobre el intervalo

_{[a, b]}

se dice que es Riemann-Stieltjes integrable con respecto a

g

si el siguiente límite existe:

l

b

n

f(t)dg(t)

=

lím LÍ(T¡)(g(t¡) -g(t¡_1)),

a _{116,dl-+O i=l} (1.2)

donde la partición l:).n y los puntos de evaluación T_¡ siguen la definición anterior. Se sabe que: las funciones continuas sobre [ a,

b]

son Riemann-Stieltjes integrables con respecto a cualquier función monótona creciente sobre

_{[a, b].}

Supongamos que la función f monótonamente creciente y continua y la función

g

es continua. Entonces, podemos emplear la fórmula de integración por partes para definir:

l

b

f(t)dg(t)

=

f(t)g(t)

]! -

l

b

g(t)df(t), (1.3) donde la integral del la derecho es definido como en la Ecuación (1.2) con f y

g

intercambiando. Esto nos conduce a la siguiente pregunta.

Para cualquier función continua

f

y

g

sobre el intervalo

[a, b],

¿Es

posible definir la integral

l

b

_{f (t)dg(t)} por la Ecuación (1.2)?

Consideremos el caso especial f = g, i.e., la integral:

l

b

f(t)df(t).

Sea l:).n

=

{

to, t1, ... , tn} una partición sobre el intervalo [ a,

_b].

Sea Ln y Rn las cuales denotan las correspondientes sumas de Riemann con los puntos de evaluación T_¡

=

t¡_1 y T¡

=

t_¡, respectivamente, i.e.,

n