Segunda aproximación en coalescencia perturbada aplicada a una aleación de Fe Mn Ti Si

Texto completo

(1)Universidad Central “Marta Abreu” de Las Villas. Facultad de Matemática-Física-Computación. TRABAJO DE DIPLOMA. Título: Segunda aproximación en coalescencia perturbada aplicada a una aleación de Fe-Mn-Ti-Si. Autor: Angel Luis Leiva Stable. Tutor: Lic. Roberto Silva González..

(2) Dedicatoria Quiero dedicar este trabajo a mis familiares en especial a mi madre Rosa Stable Álvarez por su lucha incansable durante mi desarrollo estudiantil y por siempre sentirse orgullosa de que su hijo estudiara la carrera de Licenciatura en Física..

(3) Agradecimientos Quiero agradecer el desarrollo de este trabajo a mi tutor Roberto Silva González por su apoyo incondicional , por su entrega y dedicación, también a los profesores del departamento de Física, en especial al profesor René Manso Montenegro por su gran influencia en mi carrera estudiantil, también a mis compañeros Carlos Fernández Noa y William Carreras Oropesa quienes fueron mis fuerzas para mi desarrollo durante estos cinco años, a todos mis familiares y amigos que de manera indirecta han contribuido a mi formación. Muchas gracias a todos..

(4) Resumen Comprobada experimentalmente la influencia de una segunda transformación de fase sobre el proceso de Maduración de Ostwald y la desviación de la función de distribución real del sistema de precipitados respecto al caso libre (teoría de Lifshitz-Slezov-Wagner); se pudo resolver la ecuación de continuidad a través del método de aproximaciones sucesivas. El método iterativo aplicado a la primera aproximación para los distintos tiempos de revenido isotérmico mostró una significativa mejoría en la descripción de los histogramas experimentales cuando existe una mayor influencia de la segunda transformación de fase. Se realizó el cálculo de la segunda aproximación del esquema de aproximaciones sucesivas de Picard, mostrándose, que la mejoría en la descripción de los histogramas experimentales de los precipitados metaestables e isomorfos de Fe3Si se logra con los procesos iterativos y no con el cálculo de términos más elevados en la serie se aproximaciones. Se logró calcular para cada tiempo de revenido isotérmico, la constante de velocidad en la ley de crecimiento del radio crítico del sistema de precipitados, el volumen total transformado de la segunda fase y su radio reducido máximo..

(5) II. Abstract The influence of a second phase transformation on the Ostwald process and the deviation of the real distribution function of the precipitate system from the free case (Lifshitz-Slezov-Wagner theory) were experimentally verified; it was possible to solve the continuity equation through the method of successive approximations. The process of iterative improvement of the first approximation for the different times of isothermal tempering showed a significant improvement in the description of the experimental histograms when there is a greater influence of the second phase transformation. The calculation of the second approximation of Picard's successive approximation scheme was carried out, showing that the improvement in the description of the experimental histograms of the metastable and isomorphic precipitates of Fe3Si is achieved with the iterative processes and not with the calculation of more terms High in the series are approximations. The rate constant in the growth rate of the critical radius of the precipitate system, the total transformed volume of the second phase and its maximum radius were calculated for each isothermal tempering time..

(6) III. Tabla de Contenido. Resumen .......................................................................................................................................... I Abstract .......................................................................................................................................... II Tabla de magnitudes fundamentales. ........................................................................................ VI Introducción .................................................................................................................................. 1 CAPÍTULO#1: DESCRIPCIÓN CINÉTICA DE LA MADURACIÓN DE OSTWALD ..... 5 1.1 Introducción .......................................................................................................................... 5 1.2 Teoría de Lifshitz-Slezov-Wagner ........................................................................................ 6 1.3 Ecuación cinética .................................................................................................................. 7 1.4 Ecuación de continuidad ..................................................................................................... 13 1.5 Evolución de los tamaños críticos....................................................................................... 14 1.6 Estimación de las constantes de velocidad 𝐊𝐋𝐒 y 𝐊𝐖 ...................................................... 23 CAPÍTULO #2: MATERIALES Y MÉTODOS ...................................................................... 24 2.1 Introducción ........................................................................................................................ 24 2.2 Elaboración de las aleaciones y preparación de las probetas .............................................. 24 2.3 Tratamientos térmicos y análisis de la composición química de los precipitados .............. 25 2.4 Técnicas generales de observación y estudio. Estudio por microscopía electrónica .......... 25 2.5 Determinación de la segunda transformación de fase......................................................... 26 2.6 Métodos de cálculo. Correcciones ...................................................................................... 26 2.7 Construcción de los histogramas experimentales. .............................................................. 28 CAPÍTULO. #3:. COALESCENCIA. PERTURBADA. POR. UNA. SEGUNDA. TRANSFORMACIÓN DE FASE. ............................................................................................. 29 3.1 Introducción ........................................................................................................................ 29.

(7) IV. 3.2 Velocidad de crecimiento de los precipitados en la teoría PLSW ...................................... 30 3.3 Dependencia temporal de 𝒓𝒈 en la teoría PLSW ............................................................... 31 3.4 Velocidad de crecimiento canónica de los precipitados en la teoría PLSW ....................... 32 3.6 Análisis cualitativo de la influencia de una segunda transformación de fase sobre la cinética de OR ........................................................................................................................... 36 3.7 Análisis cuantitativo de la cinética de OR. Aproximación de Born ................................... 37 3.8 Corroboración experimental de la aproximación de Born en la teoría PGLSW ................. 39 3.9 Estimación de la constante de velocidad 𝑲𝑷𝑳𝑺 y la 𝒖𝒎á𝒙 en la teoría PLSW ................ 42 3.9 Ajuste de la PSD a los histogramas experimentales. Obtención de la segunda aproximación en la teoría PLSW ..................................................................................................................... 44 CAPÍTULO# 4: RESULTADOS EXPERIMENTALES Y SU DISCUSIÓN ....................... 48 4.1 Introducción ........................................................................................................................ 48 4.2 Estudio cinético de la aleación Fe- 9.1 at. % Mn – 4.7 at. % Si – 2.5 at. % Ti. ................. 49 4.3 Resultados y su Discusión .................................................................................................. 54 4.4 Segunda aproximación. ....................................................................................................... 59 Conclusiones ................................................................................................................................ 63 Recomendaciones ........................................................................................................................ 64 Bibliografía .................................................................................................................................. 65 ANEXOS ......................................................................................................................................... i ANEXO #1. Obtención de la velocidad de crecimiento radial para precipitados en coalescencia ................................................................................................................................. i A.1.1-Partícula aislada en una matriz infinita. ......................................................................... i A.1.2- Sistema de precipitados en coalescencia perturbado por drenaje de soluto ................ v ANEXO # 2: Análisis cuantitativo de la coalescencia libre .................................................... viii ANEXO # 3: Principio de las transformaciones de contracción.............................................. xix.

(8) V. A3.1. Principio de Cacciopolli-Banach. .............................................................................. xix A3.2. Aplicación del principio de las transformaciones de contracción (Principio de Cacciopolli-Banach) a la teoría perturbada de la maduración de Ostwald. ......................... xxi A3.3.Aproximación n-ésima para la coalescencia perturbada. .......................................... xxvi A3.4. Características generales de la solución para la coalescencia perturbada. .............. xxvii ANEXO #4: Obtención de la segunda aproximación en coalescencia perturbada por segundas transformaciones de fase. ....................................................................................................... xxix.

(9) VI. Tabla de magnitudes fundamentales.. MAGNITUDES 𝜇𝛼 (𝑝, 𝑇) 𝜇𝛽 (𝑝, 𝑇, 𝐶) 𝜎. SIGNIFICADO FISICO Potencial químico de una fase macroscópica Potencial químico de la solución Energía específica en la interface matrizprecipitado. 𝜔. Volumen molar del componente segregado. 𝑅. Constante de los gases. 𝑇. Temperatura. 𝐽. Flujo difusivo de los monómeros disueltos por unidad de área de la superficie del precipitado. 𝐷𝑣. Coeficiente de difusión en el volumen de la matriz del elemento que controla la cinética del crecimiento del precipitado. 𝜏𝑑𝑖𝑓. Tiempo característico de establecimiento del estado estacionario del flujo del material disuelto. 𝜏𝑐ℎ. Tiempo característico de variación del radio del precipitado. ∆0 𝑓(𝑟, 𝑡). Sobresaturación inicial de la matriz Función de distribución de los radios de un sistema de precipitados.

(10) VII. Continuación de la tabla de magnitudes fundamentales. 𝑄0. Sobresaturación inicial total. 𝑛. Número de precipitados por unidad de volumen. 𝑓𝑤 (𝑢) 𝐾𝑊. Función de distribución de Wagner Constante de. velocidad de la ley de. crecimiento para el mecanismo de Wagner 𝑘′. Volumen transformado máximo que alcanza la fase precipitada para tiempos asintóticos. 𝜏0. Tiempo en que comienza la influencia de la segunda transformación de fase. 𝑍0. Factor de escala teórico en la teoría PLSW. 𝜙(𝑡). Fracción transformada de la segunda fase. 𝑟𝑔0. Radio máximo inicial de la población de precipitados. 𝑀. Valor donde se alcanza el máximo del histograma experimental. 𝑢𝑀. Valor del radio reducido correspondiente al máximo del histograma experimental.

(11) 1. Introducción La aleación estudiada (Fe- 9,1 at. % Mn – 4,7 at. % Si – 2,5 at. % Ti) dado su contenido en manganeso presenta después del temple una estructura martensítica y con el revenido isotérmico a temperaturas medias muestra que la misma es susceptible de sufrir entre otras transformaciones de fase, un proceso de coalescencia de un precipitado metaestable isomorfo del Fe3Si el cual se ve afectado por la difusión en el volumen de la matriz del elemento gammágeno (manganeso) hacia las fronteras de los listones martensíticos. Este fenómeno de coalescencia ya no obedece a un simple crecimiento libre de las partículas gobernado por el exceso de energía superficial, sino que ahora este proceso de Ripening del precipitado metaestable esta perturbado por una segunda reacción que utiliza el mismo soluto que necesita la fase metaestable para coalescer. La descripción cinética de la coalescencia perturbada por segundas transformaciones de fase ha sido realizada con anterioridad. La obtención de la función de distribución que caracteriza al sistema de precipitados se ha realizado en términos de un operador integro-diferencial que satisface las condiciones del principio de las transformaciones de contracción. Como función de partida del esquema de aproximaciones sucesivas se ha tomado la distribución de LifshitzSlezov-Wagner (LSW) con el objetivo de garantizar la convergencia rápida de la serie a la función de distribución real del ensemble de precipitados. Durante la aplicación del método iterativo a la aproximación de Born (Primer término de la serie de aproximaciones) se ha planteado la necesidad de mejorar el ajuste a los histogramas experimentales mediante el cálculo de la segunda aproximación del método de aproximaciones sucesivas. El ajuste iterativo de la primera aproximación (Aproximación de Born) a los histogramas experimentales generó una notable mejoría para los tiempos de revenido donde es más el efecto de la segunda transformación de fase, no resultando así para los estadíos iniciales y finales de la segunda transformación. En el presente trabajo se realiza el cálculo de la segunda aproximación de la secuencia de aproximaciones sucesivas y se comprueba como la nueva función de distribución de tamaños de partículas mejora el ajuste a la realidad experimental. Para la descripción cuantitativa del proceso de coalescencia perturbado se buscó la solución de la ecuación de continuidad en el espacio.

(12) 2. dimensional de los radios reducidos, debido a que dicha ecuación no es soluble por el método de separación de variables, lo que fue resuelto por métodos numéricos. El cálculo de la segunda aproximación del método de aproximaciones sucesivas al estudio de la influencia de una segunda transformación de fase sobre el fenómeno de coalescencia brinda una oportunidad, hasta la fecha no tratada en la literatura consultada, de analizar el comportamiento del fenómeno de coalescencia en una aleación (Fe-Mn-Si-Ti) cuando está afectada por una segunda reacción que usa el mismo soluto para su evolución. Lo cual constituye la situación problémica que valida la presente investigación. Al considerar lo antes mencionado, el problema científico de esta investigación se define de la manera siguiente: ¿Cómo contribuir mediante un modelo matemático basado en el método de aproximaciones sucesivas a describir la evolución del fenómeno de coalescencia, cuando este se ve afectado por una segunda transformación de fase? En esta investigación se planteó como hipótesis general la siguiente: Si se aplica el método de aproximaciones sucesivas y en particular la segunda aproximación al estudio de la influencia de una segunda transformación de fase, para contribuir a una mejor descripción de los histogramas experimentales. Para la validación de la hipótesis investigativa se planteó como objetivo general: Proponer un modelo matemático que basado en el método de aproximaciones sucesivas evalúe cuantitativamente la influencia de una segunda transformación de fase sobre el fenómeno de coalescencia. Como objetivos específicos: . Profundizar en el estudio y aplicación de la teoría general de las transformaciones de fase en el estado sólido.. . Realizar un estudio matemático y experimental, rigurosos, del proceso de coalescencia que tiene lugar en una aleación monofásica Fe-Mn-Si-Ti durante el revenido isotérmico haciendo uso del principio de las transformaciones de contracción..

(13) 3. . Obtener un método general a partir del cálculo perturbativo para la solución de la ecuación de continuidad que describa cuantitativamente la coalescencia perturbada por una segunda transformación de fase.. . Investigar las características del proceso de coalescencia y su relación con las transformaciones de fase analizadas.. En la presente investigación el objeto de la investigación es el estudio del fenómeno de la coalescencia. Campo: Teoría de las transformaciones de fase en el estado sólido. Población: Teoría de la coalescencia perturbada por segundas transformaciones de fase. Muestra: Sistema de precipitados metaestables de Fe3Si. Para dar solución al problema científico planteado y validar la hipótesis, se aplicó un conjunto de métodos, tanto teóricos como empíricos. Dentro de los métodos teóricos se destacan el análisis y la síntesis, empleado en todo el proceso de investigación para el estudio crítico de la literatura especializada en la temática objeto de estudio, así como en la evaluación de la información obtenida por otras fuentes, con vistas a comprender y obtener una visión más amplia del tema; el histórico-lógico con el fin de analizar la evolución, superación y aportes más relevantes de la teoría vinculada al fenómeno de coalescencia de precipitados, desde una perspectiva teóricapráctica, donde se precisó de esta manera el estado del arte de esta área del conocimiento, así como el inductivo-deductivo para el análisis, uso y tratamiento de la información y los datos que se utilizan con frecuencia en la investigación. En cuanto a los métodos empíricos se utilizó: la observación directa e indirecta de los hechos, mediante la obtención de datos relacionados al fenómeno en cuestión haciendo uso de técnicas experimentales para caracterizar el campo de aplicación, así como búsqueda y selección de datos e información primaria. También se emplearon técnicas tales como los métodos de resolución de ecuaciones en derivadas parciales, programas de cálculo digital y el procesamiento digital de señales..

(14) 4. La Novedad Científica del presente trabajo radica en la propuesta de un modelo matemático que basado en la aplicación del método de aproximaciones sucesivas, demuestra que la aproximación de segundo orden no mejora el ajuste de los histogramas experimentales para el estudio del fenómeno de coalescencia. En nuestro trabajo primeramente se describe la cinética de la Maduración de Ostwald, luego se expondrán los materiales y técnicas empleados para la descripción del proceso, se expondrá la obtención de la velocidad de crecimiento de los precipitados cuando la coalescencia libre de LSW se encuentra débilmente perturbada por la acción de una segunda transformación de fase. Segundo, se obtiene la forma teórica de la aproximación de Born y se realiza su validación experimental. Tercero, se realiza la obtención de la segunda aproximación de la secuencia de aproximaciones sucesivas para describir las situaciones de: (i) influencia fuerte de la segunda transformación de fase sobre la coalescencia de los precipitados en la matriz o, (ii) la no correspondencia entre la curva teórica de la aproximación de Born y los histogramas experimentales del sistema de precipitados. En estudios precedentes se ha realizado una descripción de este fenómeno pero en condiciones ideales, es por ello que se considerará que el sistema es débilmente perturbado y se formará una nueva fase que utiliza el mismo soluto, una vez realizado este proceso se analizarán los resultados obtenidos..

(15) 5. CAPÍTULO#1:. DESCRIPCIÓN. CINÉTICA. DE. LA. MADURACIÓN DE OSTWALD 1.1 Introducción Una solución sólida sobresaturada, en un estado metaestable, tiene una energía libre mayor que la energía libre de sus fases de equilibrio. En este escenario aparecen fuerzas motrices asociadas a la formación y crecimiento de regiones de nuevas fases en forma de diferentes compuestos químicos, que dan lugar a una transición del sistema a un estado heterofásico de equilibrio y la correspondientereducción de su energía libre de superficie [1,2,3,4,5]. La descomposición difusiva es el mecanismo que conduce a la creación de estructuras heterogéneas en un sólido, con una distribución de volumen finita de sus precipitados, o la destrucción de estructuras optimizadas [6].La formación de nuevas fases durante el proceso de descomposición difusiva ocurre fundamentalmente por dos mecanismos diferentes: la descomposición spinodal y posteriormente el crecimiento de las regiones discretas de las nuevas fases o el mecanismo de nucleación de una nueva fase [1,2, 5, 6]. La reducción de la energía libre de un sistema metaestable, descompuesto por el mecanismo de nucleación de una nueva fase, puede dividirse en tres etapas [1, 2, 5, 6]. La etapa inicial de la descomposición, cuando la sobresaturación de la matriz es alta, se caracteriza por la formación intensiva de centros de nucleación (precipitados de una segunda fase, poros, lazos de dislocación y cavidades llenas de gas) cuyos tamaños exceden el tamaño crítico [3,4]. La etapa de transición de la descomposición comienza cuando la cantidad de material en la nueva fase es comparable a la cantidad inicial, y la sobresaturación comienza a disminuir; en este estadío el número de precipitados es virtualmente constante y el volumen de la nueva fase aumenta debido al crecimiento de los precipitados [1, 2, 3, 4]. Finalmente, cuando los núcleos alcanzan tamaños que permiten aplicar a ellos conceptos estadísticos macroscópicos y la baja sobresaturación de la matriz hace posible que las fluctuaciones de composición ya no sean significativas, comenzará a jugar un papel determinante la redistribución de soluto entre los precipitados [5, 6,7]. Esta última etapa, conocida como Maduración de Ostwald (Ostwald’s Ripening) o Coalescencia, es un proceso de transformación de fase observado en una gran variedad de sistemas metálicos y no metálicos, donde los precipitados con varios tamaños se encuentran.

(16) 6. dispersos en la matriz. Durante el proceso de Ostwald el ensemble contará con una distribución no uniforme de tamaños de precipitados. Su naturaleza lo llevará espontáneamente a reducir la energía libre superficial disolviendo aquellos precipitados menores que los que determinan su población media y transfiriendo su masa hacia los precipitados de mayor tamaño. El resultado es una reducción del número de partículas con tamaños pequeños predominando aquellas de mayores radios [1, 2, 3, 4]. Este fenómeno juega un importante papel en la estabilidad de los sistemas polidispersos [3,4], el endurecimiento de fases por precipitación y la formación de estructuras superficiales [6, 8, 9]. En la actualidad, existen múltiples aplicaciones en la síntesis de nanocristales, semiconductores y nanoclusters con propiedades ópticas de forma y composición predefinidas [10, 11, 12], así como en la generación de energía, la optoelectrónica, la biología y la metalurgia [13]. En este capítulo, se tratarán los aspectos fundamentales de la teoría propuesta por Lifshitz y Slezov [1, 3, 4] y en un trabajo posterior por Wagner [2, 3, 4, 5], los cuales constituyen el marco teórico conocido como teoría LSW.. 1.2 Teoría de Lifshitz-Slezov-Wagner Cualquier sistema de precipitados dispersos, de tamaños diferentes y estadísticamente distribuidos en un medio que posee cierta solubilidad, tiende a ser termodinámicamente inestable debido al exceso de su energía superficial. La primera descripción cualitativa correcta de este fenómeno fue dada por Wilhelm Ostwald en el año 1900 para precipitados en una matriz con una alta movilidad. Para determinadas condiciones termodinámicas del sistema la fuerza motriz de este proceso es la diferencia en solubilidad entre las partículas polidispersas debido al efecto Gibbs-Thomson [3,4]. El tratamiento cuantitativo del fenómeno de la Maduración de Ostwald (OR) es estadístico por naturaleza debido a que las datas experimentales son esencialmente estadísticas [14]. Para describir este fenómeno en el caso ideal donde no se consideran la interacción directa entre los precipitados, los efectos de no coherencia entre los precipitados y la matriz, o los efectos de una fracción volumétrica finita de los precipitados; es necesario extraer la información que nos brinda el sistema de ecuaciones conformado por: (i). Una ley cinética que describe la velocidad de crecimiento/disolución de los precipitados situados en la matriz..

(17) 7. (ii). Una ecuación de continuidad que nos brinda información de cómo evoluciona en el tiempo la función de densidad de probabilidad para los radios de los precipitados.. (iii). Una condición de conservación de soluto, la cual debe ser satisfecha, por la ecuación cinética y la ecuación de continuidad.. Los resultados más significativos en la descripción del fenómeno de OR [3,4] fueron alcanzados en los comienzos de los años 60' del siglo pasado. Trabajos relacionados de Lifshitz y Slezov para el caso de la transferencia de materia mediante la difusión en el volumen de la matriz [1,3,4] y de Wagner para la adherencia de átomos a la superficie de los precipitados debido a una reacción de primer orden en su interface con la matriz [2,3,4], permitieron realizar predicciones cuantitativas del comportamiento asintótico de un ensemble de precipitados en coalescencia. Este marco teórico, conocido como teoría LSW, constituye el referente con respecto al cual las distintas modificaciones posteriores en la descripción del fenómeno son comparadas [5]. Mientras que el análisis LS utiliza la conservación del soluto intercambiado entre los precipitados, resuelve el problema para el caso donde la sobresaturación de la matriz es baja y los tiempos de revenido isotérmico muy grandes; el enfoque de Wagner asume que la fracción de volumen transformado de los precipitados es una cantidad conservada. En nuestra exposición de los fundamentos del fenómeno de OR, se tomará el enfoque seguido por V.V Slezov, aunque sea un poco más complejo su desarrollo.. 1.3 Ecuación cinética En el presente epígrafe se expone la descripción cinética del crecimiento de los precipitados. Nos proponemos encontrar una ley para la velocidad de crecimiento/disolución del tamaño de los precipitados. En la formulación del problema se considera una solución sólida de dos componentes, uno de los cuales, con concentración C, segrega y forma precipitados. La condición de equilibrio para la coexistencia estable de la fase macroscópica que evoluciona con el potencial químico 𝜇𝛼 (𝑝, 𝑇) y la solución macroscópica con potencial químico 𝜇𝛽 (𝑝, 𝑇, 𝐶) satisface la relación: 𝜇𝛼 (𝑝, 𝑇) = 𝜇𝛽 (𝑝, 𝑇, 𝐶∞ ) En (1.1) 𝐶∞ representa la concentración de la solución.. (1.1).

(18) 8. Para un precipitado de tamaño finito, que se encuentre en equilibrio con la solución, la condición (1.1) adquiere la forma: 𝜇𝛼 (𝑝𝛼 , 𝑇) = 𝜇𝛽 (𝑝, 𝑇, 𝐶𝑟 ).. (1.2). En (1.2) 𝐶𝑟 es la concentración de las partículas segregadas en la solución, requeridas para satisfacer las condiciones necesarias de equilibrio termodinámico. La presión en un precipitado de tamaño crítico se relaciona con la presión de la solución que lo rodea, la tensión superficial en la interface matriz-precipitado 𝜎, y el radio del precipitado 𝑟, a través de la ecuación de Young-Laplace: 𝑝𝛼 − 𝑝 =. 2𝜎 𝑟. (1.3). Realizando una expansión en serie de Taylor del potencial químico que caracteriza al precipitado de radio 𝑟, se obtiene: 𝜇𝛼 (𝑝𝛼 , 𝑇) ≅ 𝜇𝛼 (𝑝, 𝑇) + (. 𝜕𝜇𝛼 ) 𝜕𝑝 𝑝. 𝛼. 2𝜎 2𝜎𝜔 = 𝜇𝛼 (𝑝, 𝑇) + 𝑟 𝑟 =𝑝. (1.4). En la expresión (1.4), 𝜔 representa el volumen molar del componente segregado. Asumiendo que la solución se puede describir como una solución perfecta: 𝜇(𝑝, 𝑇, 𝐶) = 𝜇0 + 𝑅𝑇 ln 𝐶 ,. (1.5). y considerando a 𝑅 como la constante de los gases; podemos utilizar la condición de equilibrio (1.1) para una interface plana y así obtener la conocida ecuación de Gibbs-Thomson, la cual en su aproximación lineal asume la forma: 𝛼 𝐶𝑅 ≅ 𝐶∞ + 𝑟. (1.6). En (1.6), 𝛼 está relacionada a la tensión en la interface matriz-precipitado 𝜎 mediante la ecuación siguiente: 𝛼=. 2𝜎𝜔𝐶∞ 𝑅𝑇. (1.7).

(19) 9. El análisis de (1.7) permite concluir que la concentración de equilibrio en la superficie de los precipitados de menor tamaño excede a la que existe en la superficie de los precipitados de mayor tamaño. Esta diferencia de concentraciones asociada al radio de los precipitados genera la existencia de gradientes de concentración, los cuales, inducen flujos del componente disuelto desde los precipitados pequeños hacia la matriz y desde la matriz hasta los precipitados de mayor tamaño. Despreciando la interacción difusiva directa entre los precipitados, es decir, asumiendo que el radio medio de la población 𝑟̅ es pequeño comparado con la distancia media 𝑙 ̅ entre los mismos (aproximación de campo medio), se obtiene para el flujo difusivo de los monómeros disueltos por unidad de área de la superficie del precipitado:. 𝐽 = −𝐷𝑣 (. 𝜕𝐶 ) 𝜕𝑅 𝑅=𝑟. (1.8). donde 𝐷𝑣 es el coeficiente de difusión en el volumen de la matriz del elemento que controla la cinética del crecimiento del precipitado. La variación en el volumen está determinada por el flujo de átomos disueltos que por unidad de tiempo arriban a la superficie de los precipitados: 𝑑 4𝜋 3 𝜕𝐶 ( 𝑟 ) = −4𝜋𝑟 2 𝐽 = 4𝜋𝑟 2 𝐷𝑣 ( ) 𝑑𝑡 3 𝜕𝑅 𝑅=𝑟. (1.9). De la razón de cambio del radio de los precipitados en el tiempo, se obtiene la siguiente relación: 𝑑𝑟 𝜕𝐶 = 𝐷𝑣 ( ) 𝑑𝑡 𝜕𝑅 𝑅=𝑟. (1.10). La relación entre el tiempo característico de establecimiento del estado estacionario del flujo del material disuelto 𝜏𝑑𝑖𝑓 ~ 𝑟̅ 2 ⁄𝐷𝑣 , y el tiempo característico de variación del radio del precipitado 𝜏𝑐ℎ ~ 𝑟̅ 2 ⁄𝐷𝑣 ∆0 está dado por: 𝜏𝑑𝑖𝑓 ~∆0 ≪ 1 𝜏𝑐ℎ. (1.11). Donde ∆0 es la sobresaturación de la matriz. La relación entre los tiempos característicos permite descartar el solapamiento de las regiones de drenaje de soluto asociada a los precipitados y el.

(20) 10. choque directo de los mismos (aproximación de campo medio). En estas condiciones las variaciones temporales de la concentración de soluto son muy lentas, pudiéndose obtener una expresión. para el flujo de soluto resolviendo el correspondiente problema de difusión en. régimen estacionario: 𝛻 2 𝐶(𝑟, 𝑡) = 0. (1.12). La solución general de (1.12) en el sistema de coordenadas esféricas resulta:. 𝐶𝑅 = 𝐵 −. 𝐴 𝑟. (1.13). Para partículas esféricas de una fase en una matriz α, la solución (1.13) debe satisfacer las condiciones de frontera (CF): 𝛼 𝑙𝑖𝑚 𝐶𝑟 = 𝐶𝑚. 𝑪𝑭: { 𝑟→∞. 𝐶𝑅 |𝑅=𝑟 = 𝐶𝑟𝛼. donde: 𝛼 𝐶𝑚 : es la concentración media de la matriz cuando comienza el proceso de coalescencia. 𝛼 𝐶𝑟𝛼 : es la concentración en la interface matriz-precipitado, la cual está relacionada con 𝐶𝑚 a. través de la ecuación de Gibbs-Thomson. Aplicando las CF a la solución (1.13) se obtiene:. 𝛼 𝛼 𝐶𝑟 = 𝐶𝑚 − (𝐶𝑚 − 𝐶𝑟𝛼𝑖 ). 𝑟𝑖 𝑟. (1.14). Sustituyendo (1.14) en (1.10), la expresión para el flujo del material disuelto adquiere la forma:. 𝐽 = −𝐷𝑣. 𝜕 𝛼 𝑟𝑖 𝛼 [𝐶𝑚 − (𝐶𝑚 − 𝐶𝑟𝛼𝑖 ) ]| 𝜕𝑟 𝑟 𝑟=𝑟𝑖. Desarrollando las operaciones contenidas en (1.15), se obtiene:. (1.15).

(21) 11 𝛼 𝜕𝐶𝑚 𝜕 𝑟𝑖 𝛼 𝐽 = −𝐷𝑣 | + 𝐷𝑣 [(𝐶𝑚 − 𝐶𝑟𝛼𝑖 ) ∙ ]| 𝜕𝑟 𝑟=𝑟𝑖 𝜕𝑟 𝑟. (1.16) 𝑟=𝑟𝑖. 𝛼 El primer término en la expresión (1.16) se anula pues 𝐶𝑚 es independiente de 𝑟, entonces se. obtiene:. 𝛼 𝐽 = 𝐷𝑣 (𝐶𝑚 − 𝐶𝑟𝛼𝑖 )𝑟𝑖. 𝜕 1 1 𝛼 ( )| = −𝐷𝑣 (𝐶𝑚 − 𝐶𝑟𝛼𝑖 )𝑟𝑖 ( 2 )| 𝜕𝑟 𝑟 𝑟=𝑟𝑖 𝑟 𝑟=𝑟𝑖. (1.17). Simplificando y evaluando la expresión (1.17), se obtiene para el flujo atómico del material disuelto: −𝐽 = 𝐷𝑣 (. 𝜕𝐶 𝐷𝑣 𝛼 𝐷𝑣 𝛼 (𝐶𝑚 − 𝐶𝑟𝛼 ) = ) = (Δ(𝑡) − ). 𝜕𝑟 𝑟=𝑟𝑖 𝑟 𝑟 𝑟. (1.18). De acuerdo con la ecuación (1.10) para el cambio temporal del radio de los precipitados, se obtiene: 𝑑𝑟 𝐷 𝛼 = −𝐽 = (Δ(𝑡) − ) 𝑑𝑡 𝑟 𝑟. (1.19). El análisis de la ecuación (1.19) permite prever que en cada instante de tiempo existe un radio crítico, que depende de la sobresaturación de la matriz, 𝑟𝑐 = 𝛼 ⁄Δ(𝑡) para el cual los precipitados se encuentran en equilibrio con la solución. Este simple mecanismo permite prever que los precipitados crecen cuando 𝑟 > 𝑟𝑐 y se disuelven cuando 𝑟 < 𝑟𝑐 , además indica que la velocidad de crecimiento de los precipitados depende de la sobresaturación de la matriz Δ(𝑡) en cada instante de tiempo. Por lo tanto, la existencia de tal radio crítico 𝑟𝑐 implica la disolución de los precipitados más pequeños y el drenaje del soluto disuelto hacia los más grandes. La sobresaturación Δ(𝑡) y la función que describe el comportamiento del radio crítico 𝑟𝑐 (𝑡) son funciones explícitamente dependientes del tiempo. Un análisis cualitativo de la ecuación (1.19) anterior permite extraer los siguientes resultados concernientes al fenómeno de la coalescencia:.

(22) 12.  Los precipitados con 𝑟 = 𝑟𝑐 se encuentran en equilibrio con la solución. Tienen una velocidad de crecimiento nula, o sea, ni crecen ni se disuelven.  Cuando 𝑟 < 𝑟𝑐 los precipitados se disuelven con una velocidad que aumenta al disminuir su radio.  Cuando 𝑟 > 𝑟𝑐 crecen, alcanzando una velocidad de crecimiento máxima cuando 𝑟 = 2𝑟𝑐 .  El número total de precipitados y la velocidad de crecimiento disminuye progresivamente en el transcurso del tiempo. El radio medio de la población aumenta, y el límite del proceso es un precipitado de radio igual al tamaño de la matriz.  Las partículas de 𝑟 > 2𝑟𝑐 siguen creciendo pero a una velocidad más pequeña que para 𝑟 = 2𝑟𝑐 y eventualmente esa población tenderá a desaparecer..  Para tiempos avanzados, los volúmenes de las partículas deben crecer linealmente con el tiempo. De forma independiente a Lifshitz y Slezov; Wagner en su tratamiento del crecimiento controlado por la reacción en la interface matriz-precipitado [2], asume que la velocidad de transferencia de átomos es proporcional a la diferencia entre la concentración de equilibrio 𝐶𝑟𝛼 , 𝛼 para un precipitado de radio 𝑟, y la concentración media de soluto en la matriz 𝐶𝑚 :. 𝑑𝑟 𝛼) = −𝛽(𝐶𝑟𝛼 − 𝐶𝑚 𝑑𝑡. (1.20). En la expresión (1.20), 𝛽 es cierto coeficiente cinético que está relacionado con el carácter de no equilibrio de los procesos que ocurren en la interfaz matriz-precipitado. Asumiendo que el volumen total de los precipitados permanece constante: 𝑁. 4𝜋 ∑ 𝑟𝑖2 𝑖=1. 𝑑𝑟𝑖 = 0, 𝑑𝑡. (1.21). y combinando las expresiones (1.20) y (1.21), junto con la ecuación de Gibbs-Thomson (1.6) y la definición de radio crítico, podemos hallar la velocidad de crecimiento de un precipitado independiente cuando el mecanismo de crecimiento es tratado como una reacción química que tiene lugar en la superficie del precipitado durante el proceso de formación de enlaces interatómicos: 𝑑𝑟 1 1 = 𝛼𝛽 ( − ) 𝑑𝑡 𝑟𝑐 𝑟. (1.22).

(23) 13. 1.4 Ecuación de continuidad La descripción estadística de la evolución en el tiempo de los radios de un sistema de precipitados se puede realizar en términos de la función de densidad de probabilidad 𝑓(𝑟, 𝑡). Esta formulación, sobre la base de una función que caracteriza la distribución de los radios, tiene claras ventajas: primero, algunas microestructuras consisten en dominios cercanamente esféricos de una fase primaria β dispersa en una matriz α; segundo, solo es necesario el radio de cada esfera y la localización de su centro para localizar su frontera y cuantificar la curvatura de su interfaz. Este enfoque minimiza la cantidad de información necesaria para especificar el problema de frontera durante la descomposición difusiva [5, 6,14]. En la primera parte de este capítulo se obtuvo la ley cinética que expresa como varían los radios de los precipitados en el tiempo (Ec. (1.19)). En el análisis siguiente utilizaremos las variables adimensionales 𝜌 = 𝑟⁄𝑟𝑐 , 𝑡´ = 𝑡⁄𝑇; 𝑟𝑐0 = 𝛼 ⁄∆0 y 𝑇 = 𝑟𝑐0 3 ⁄𝛼𝐷, siendo Δ0 la sobresaturación inicial y 𝑟𝑐0 es el radio crítico inicial. Realizando los cambios anteriores se obtiene: {. 𝑑𝜌3 ⁄𝑑𝑡 = 3(𝜌⁄𝑥 − 1) , 𝑥(𝑡) = 𝑟𝑐 ⁄𝑟𝑐0. (1.23). donde 𝑥(𝑡) es el radio crítico adimensional, cumpliéndose la evidente relación 𝑥(0) = 1. Sea 𝑓(𝑟, 𝑡) la función de distribución de los radios de un sistema de precipitados; definida como: 𝜌(𝑟, 𝑟 + ∆𝑟, 𝑡) Δ𝑟→0 ∆𝑟. 𝑓(𝑟, 𝑡) = lim. , {. 𝑓(𝑟, 𝑡)|𝑟=∞ = 0 , 𝑓(𝑟, 𝑡)|𝑡=0 = 𝑓0 (𝑟). (1.24). En la expresión (1.24), 𝜌(𝑟, 𝑟 + ∆𝑟, 𝑡) representa el número de precipitados por unidad de volumen, que en el instante de tiempo 𝑡 tienen sus radios en la clase de tamaños entre 𝑟 𝑦 𝑟 + 𝑟.Introduciendo la función de distribución 𝑓(𝜌, 𝑡) respecto a los tamaños reducidos 𝜌 y considerando a 𝑣𝜌 = 𝑑𝑟⁄𝑑𝑡 como la velocidad de crecimiento de los precipitados en el espacio de los tamaños, podemos formular ecuaciones para la determinación de las funciones incógnitas 𝑓(𝜌, 𝑡) y 𝑥(𝑡) [3,4]. La forma de la función 𝑓(𝜌, 𝑡) depende del mecanismo de transferencia de soluto que tome lugar en la matriz y se obtiene resolviendo la correspondiente ecuación de Fokker - Planck en su forma simplificada, cuando la influencia del término difusivo 𝜕𝜌𝜌 [𝐷𝑣 (𝜌)𝑓(𝜌, 𝑡)] resulta insignificante. La ecuación de Fokker - Planck obtenida mediante esta.

(24) 14. simplificación se conoce como ecuación de continuidad, y en el espacio de los radios reducidos resulta: 𝜕𝑓 𝜕 + (𝑓𝑣𝑝 ) = 0 𝜕𝑡 𝜕𝜌. (1.25). El sistema de ecuaciones formado por la ecuación para la velocidad de crecimiento/disolución de los precipitados (Ecs. (1.19) y (1.22)), la ecuación de continuidad en el espacio de los tamaños reducidos (Ec. (1.25)) y una ley de conservación para el soluto intercambiado en la matriz, constituye un sistema completo para la caracterización del fenómeno de OR. La ley de conservación para el soluto intercambiado en la matriz se obtiene imponiendo que: ∞. 𝑄0 = Δ0 + 𝑞0 = Δ + 𝑞. ,. 𝑞=. 3 (4𝜋⁄3)𝑅𝑐0 ∫ 𝑓𝜌3. 𝑑𝜌. (1.26). 0. En (1.26) 𝑄0 representa la sobresaturación inicial total, que incluye el volumen inicial 𝑞0 del material en los precipitados. Teniendo en cuenta que 𝑥(𝑡) = Δ0 ⁄∆, entonces, a partir de (1.26) se obtiene: ∞. Δ0 1= + 𝑘 ∫ 𝑓𝜌3 𝑑𝜌 𝑄0 𝑥(𝑡). (1.27). 0. 3 ⁄ Donde 𝑘 = (4𝜋⁄3) 𝑅𝑐0 𝑄0 .. En las ecuaciones (1.25) y (1.27), 𝑓 está normalizada a la unidad de volumen y por consiguiente ∞. 𝑛 = ∫0 𝑓 𝑑𝜌 representa el número de precipitados por unidad de volumen.. 1.5 Evolución de los tamaños críticos Nuestro objetivo es encontrar una solución a las ecuaciones (1.25) y (1.27) con la condición inicial 𝑓(𝜌, 0) = 𝑓0 (𝜌). Para resolver el problema propuesto es necesario conocer el comportamiento asintótico del radio crítico, el cual, estará determinado por la función 𝑥(𝑡) o alternativamente por la sobresaturación Δ(𝑡) = Δ0 ⁄𝑥(𝑡) . El patrón de movimiento del punto 𝜌, que representa los radios reducidos de los precipitados, a lo largo del eje de las abscisas; ocurre de la siguiente manera: los puntos a la izquierda de 𝑥(𝑡) son acelerados hacia la izquierda y desaparecen al alcanzar el origen.

(25) 15. (disolución completa de los precipitados); los puntos localizados inicialmente a la derecha de 𝑥(𝑡) se mueven aun en esa dirección (precipitados en crecimiento), pero al trasladarse hacia la derecha decrece el valor de la sobresaturación y los tamaños críticos 𝑥(𝑡) de los precipitados tiende a aumentar. Los puntos resultantes de este crecimiento comienzan a moverse en la dirección opuesta y también desaparecen cuando alcanzan el origen. El movimiento ocurre de una forma ordenada por lo cual la secuencia original de puntos es preservada [4]. Si analizamos la ecuación 𝑥(𝑡) = 𝑟𝑐 ⁄𝑟𝑐0 y el significado físico de la variable 𝑥(𝑡), el radio dividido por el radio crítico se puede escribir en términos de 𝜌 de la forma siguiente: 𝑢=. 𝜌 𝑥(𝑡). (1.28). Cuando 𝑡 → ∞, la sobresaturación ∆(𝑡) de la matriz tiende a cero y el radio crítico, correspondientemente tiende a infinito. Por lo tanto, cuando 𝑡 varía de 0 a ∞, la cantidad 𝜏 = 3 ln 𝑥(𝑡) varía monótonamente de 0 a ∞ y se puede tomar como una nueva medida de tiempo. O sea: 𝜏 = ln 𝑥 3. (1.29). Sustituyendo las ecuaciones (1.29) y (1.28) en (1.19) se obtiene la velocidad de crecimiento de los volúmenes reducidos de los precipitados: 𝑑𝑢3 = 𝛾(𝑢 − 1) − 𝑢3 , 𝑑𝜏. (1.30). donde: 𝛾 = 𝛾(𝜏) = 3. 𝑑𝑡 . 𝑑𝑥 3. (1.31). La solución de la ecuación (1.30) con la condición inicial 𝑢𝜏=0 = 𝑣 puede ser escrita en la forma 𝑢(𝑣, 𝜏). Teniendo en cuenta que 𝜌(𝑣, 𝜏) = 𝑥𝑢(𝑣, 𝜏) ;𝑥(0) = 1 y 𝜏𝑡=0 = 0, la cantidad total 𝑞 de materia en los precipitados se podrá expresar en términos de la función de distribución original 𝑓0 (𝜌)como: ∞. 𝑞 = 𝑘𝑄0 ∫ 𝑣0 (𝜏). 𝑓0 (𝑣)𝑢3 (𝑣, 𝜏)𝑑𝑣 ,. (1.32).

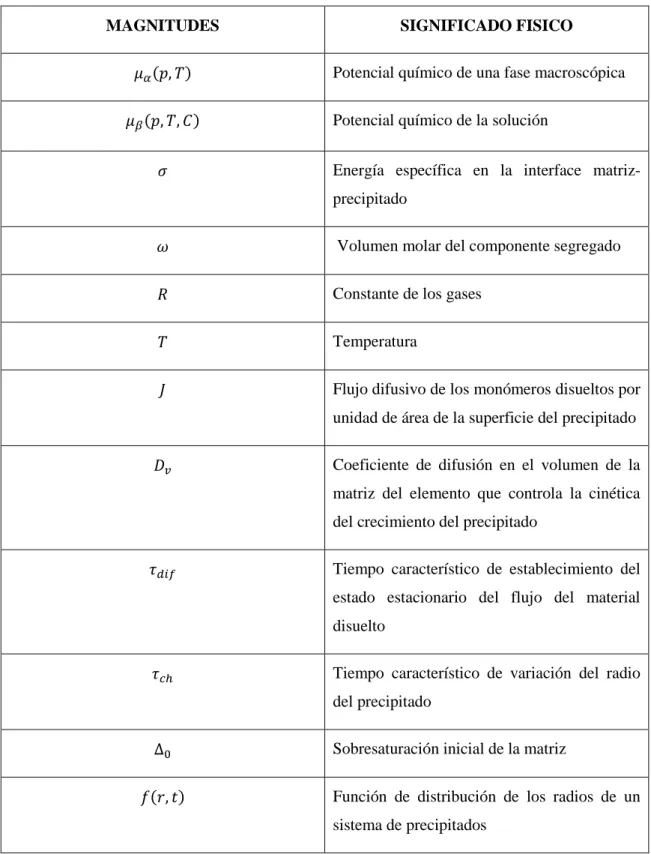
(26) 16. aquí 𝑣0 (𝜏) es la solución de la ecuación 𝑢(𝑣0 (𝜏), 𝜏) = 0, y por lo tanto, el límite inferior del tamaño inicial de los precipitados que permanece indisoluble en un tiempo 𝜏. Notando que 𝑥 3 = exp(𝜏), se puede reescribir la ecuación de conservación de materia (1.27) de la siguiente forma: 1 − exp(− 𝜏⁄3) = 𝑘 exp(𝜏) ∫. ∞. 𝑓0 (𝑣)𝑢3 (𝑣, 𝜏)𝑑𝑣. (1.33). 𝑣0 (𝜏). Las ecuaciones (1.30) y (1.33) proporcionan un sistema completo de ecuaciones, con 𝛾(𝜏) = 3 𝑑𝑡⁄𝑑𝑥 3 como función incógnita, para determinar y obtener, la función desconocida 𝑥(𝑡). Existen tres tipos posibles de comportamiento asintótico para la función 𝛾(𝜏), cuando 𝜏 → ∞; (i) 𝛾(𝜏) → ∞; (ii) 𝛾(𝜏) → 𝑐𝑜𝑛𝑠𝑡; (iii) 𝛾(𝜏) → 0. Comenzaremos el análisis detallado de las posibilidades anteriores con el caso 𝛾(𝜏) → 𝑐𝑜𝑛𝑠𝑡. Dependiendo del valor de 𝛾(𝜏) , el gráfico de la velocidad 𝑑𝑢3 ⁄𝑑𝜏 vs.𝑢, puede tocar al eje de las abscisas (cuando 𝛾(𝜏) = 𝛾0 = 27⁄4), pasar por debajo de este eje (𝛾(𝜏) < 𝛾0 ) o tener un segmento de valores positivos (𝛾(𝜏) > 𝛾0 ).. 3. Fig. 1.1: 𝑑𝑢 ⁄𝑑𝜏 como función de u para diferentes valores de γ..

(27) 17. Ahora consideraremos diferentes situaciones: (a) cuando 𝛾 > 𝛾0, todos los puntos a la izquierda de 𝑢1 se desvanecen al acercarse al origen; todos los puntos a la derecha de 𝑢1 se moverán hacia el punto 𝑢2 acercándose asintóticamente a él desde la izquierda o desde la derecha. La integral del miembro derecho de la ecuación (1.33) cuando𝜏 → ∞, se aproxima a un valor constante: ∞. 𝐼0 =. 𝑢23. ∫ 𝑓0 (𝑣)𝑑𝑣. ,. (1.34). 𝑢1. mientras que el volumen total de los precipitados 𝑞 aumenta cuando exp(𝜏) lo hace, observándose la siguiente relación: 𝑞 = 𝑘𝐼0 𝑒 𝜏 → ∞. ;. 𝜏→∞. (1.35). De este modo, la ecuación (1.33) no se satisface. El hecho que un valor constante de 𝛾 > 𝛾0 se logre solo asintóticamente no pone en riesgo ni contradice las condiciones anteriores, solo debemos desplazar el origen del tiempo y relacionar la expresión 𝑓0 (𝑣) al momento cuando 𝛾(𝜏) se acerque a su valor asintótico. (b) Cuando 𝛾 < 𝛾0, todos los puntos se moverán hacia la izquierda y alcanzaran el origen en un tiempo finito. Para el tiempo 𝜏, de acuerdo con la ecuación (1.30), todos los precipitados con tamaño más pequeño que 𝑣0 (𝜏) se disolverán y el valor de 𝑣0 (𝜏) está dado por la ecuación: 𝑣0 (𝜏). ∫ 0. 3𝑢2 𝑑𝑢 =𝜏 𝑢3 − 𝛾(𝑢 − 1). (1.36). Cuando 𝜏 → ∞, se cumple que 𝑣0 (𝜏) = exp(𝜏⁄3). Por lo tanto, el volumen total precipitado está determinado por la cola de la distribución original 𝑓0 (𝑣): ∞ 𝜏. 𝑞(𝜏) = 𝑘𝑒 ∫ 𝜏. 𝑒 ⁄3. ∞. 𝑓0 (𝑣)𝑢3 (𝑣, 𝜏)𝑑𝑣 ≈ 𝑘 ∫ 𝜏 𝑓0 (𝑣)𝑣 3 𝑑𝑣. (1.37). 𝑒 ⁄3. Cuando 𝑣 → ∞ entonces 𝑓0 (𝑣) ≥ 𝑣 −𝑛 con 𝑛 > 4(debido a que 𝑢(𝑣; 𝜏) ≈ 𝑒. −𝜏⁄ 3 ).. en este caso se aproxima a cero y entonces la ecuación (1.33) no tiene solución.. Por tanto, 𝑞(𝜏).

(28) 18. Las consideraciones anteriores con respecto a los casos donde 𝛾 > 𝛾0 y 𝛾 < 𝛾0 se extienden también para los casos cuando 𝛾 → ∞ y 𝛾 → 0 respectivamente. Así, solo el caso donde se cumpla que 𝛾(𝜏) → 𝛾0 = 27⁄4 se considerará una solución físicamente razonable. Cuando la condición 𝛾(𝜏) = 𝛾0 es satisfecha, todos los puntos a la derecha del punto 𝑢0 (blocking point) en su movimiento hacia la izquierda no pueden pasar a través del punto de contacto y terminan empotrados en él. En este caso la expresión (1.33) para la conservación del soluto en la matriz no es satisfecha. Este resultado sugiere que 𝛾(𝜏) debe aproximarse a 𝛾0 desde abajo, i.e, se puede proponer la relación 𝛾(𝜏) = 𝛾0 (1 − 𝜀(𝜏)).Los puntos que se acercan a 𝑢0 desde la derecha pasan con velocidad de crecimiento negativas a través de este punto. La velocidad de migración a través de 𝑢0 es determinada por el valor de 𝜀(𝜏) y la ecuación de movimiento (1.30). Esta forma de la función 𝛾(𝜏) es obligatoria para un movimiento ordenado de los precipitados de derecha a izquierda en variables canónicas lo cual corresponde a 𝑑𝑢⁄𝑑𝜏 < 0 para todo 𝑢[4]. Por otra parte, no debe existir migración en el espacio de tamaños reducidos, desde la derecha hacia la región a la izquierda del blocking point 𝑢0 , y cuando 𝑟𝑐 = 𝛾⁄Δ(𝑡) → ∞con𝜏 → ∞,Δ(𝑡) → 0, la cantidad de materia aumenta indefinidamente, lo cual es imposible. La migración debe ocurrir de forma tal que la función de distribución asegure que el balance de materia tenga tiempo suficiente para evolucionar. Como es observado, la cantidad de materia a la derecha del blocking point es despreciable, esto significa que 𝜀 2 (𝜏) debe ser igual a cero junto a la función de distribución para 𝑢 > 𝑢0 . Precisamente a esta simplificación, se le denomina aproximación de orden cero en la aproximación hidrodinámica de la ecuación de continuidad (1.25). La velocidad 𝑑𝑢⁄𝑑𝜏 debe tener un cero de segundo orden en esta aproximación; entonces, tomando en cuenta 𝜀 2 (𝜏) = 0, se arriba a los valores asintóticos de 𝑢0 y 𝛾0 y por tanto a los valores asintóticos para los radios reducidos críticos y la sobresaturación. Expresar matemáticamente las consideraciones anteriores conduce a dos condiciones para la función 𝑑𝑢⁄𝑑𝜏: 𝑑𝑢 ) =0 𝑑𝜏 𝑢=𝑢0 𝑑 𝑑𝑢 ( ) =0 {𝑑𝜏 𝑑𝜏 𝑢=𝑢0 (. (1.38). La solución del sistema de ecuaciones (1.38) permite determinar los valores asintóticos.

(29) 19. 𝑢0 = 3⁄2 y 𝛾0 = 27⁄4. Una vez determinados los valores para 𝑢0 y 𝛾0 se resuelve la ecuación de continuidad (1.25), a través del método de Fourier, para conocer la forma definitiva de la función de distribución de los radios reducidos y la ley asintótica para la evolución del radio crítico. Proponiendo la separación de variables: 𝑓(𝑢, 𝜏) = ℎ(𝜏)𝑔(𝑢). (1.39). Sustituyendo (1.39) en la ecuación de continuidad (1.25) y dividiendo entre el producto ℎ(𝜏)𝑔(𝑢), se obtiene el sistema de ecuaciones −. 1 𝑑ℎ 1 𝑑 𝑑𝑢 = ( 𝑔) = 𝛽 ℎ 𝑑𝜏 ℎ 𝑑𝑢 𝑑𝜏. (1.40). Si se utiliza la expresión (1.30), el miembro izquierdo de (1.40) depende solo de 𝜏 , y el miembro derecho solo depende de 𝑢. Ambos son iguales, de forma independiente, a la constante de separación 𝛽. La solución de la ecuación (1.40) (Ver Anexo#2) para la función de distribución en el espacio de los radios reducidos resulta: 1 𝑑𝑢 𝑑𝑢 −1 𝑔(𝑢) = exp (3 ∫ ( ) 𝑑𝑢), 𝑔0 𝑑𝜏 𝑑𝜏. (1.41). donde 𝑔0 es un factor de normalización. La función de distribución 𝑔(𝑢) se obtiene sustituyendo (1.30) en (1.41); la integración de la ecuación resultante es posible si el polinomio de tercer grado en el denominador del término subintegral tiene tres raíces reales (criterio de Hurwitz), de las cuales, dos coincidan (Condición de unimodalidad). El resultado es: 𝑢2 𝑢2 𝑑𝑢 𝑔(𝑢) = 𝑔0 exp (−3 ∫ ) (𝑢 − 3⁄2)2 (𝑢 + 3) (𝑢 − 3⁄2)2 (𝑢 + 3). (1.42). Resolviendo la integral a través del método de coeficientes indeterminados, luego de algunas operaciones elementales, se obtiene la función de distribución para los radios reducidos en la forma: 𝑔(𝑢) =. 1 𝑢2 3 exp ( ), ⁄ ⁄ 7 3 11 3 𝑔0 (𝑢 + 3) (3⁄2 − 𝑢) 2𝑢 − 3. donde la constante de normalización 𝑔0 es determinada numéricamente de la condición:. (1.43).

(30) 20 𝑢0. ∫ 𝑔(𝑢)𝑑𝑢 = 1. →. 𝑔0 = 0.014419. 0. La gráfica de la función normalizada se muestra en la Figura 2:. .. Fig.1.2: Dependencia. de la función de densidad P (u) de LS respecto al radio reducido 𝑢 = 𝑟⁄𝑟𝑐. La forma definitiva de la función de densidad de probabilidad para los radios reducidos de los precipitados se puede expresar utilizando la separación de variables propuesta en (1.39) para el método de Fourier y la forma particular de las funciones ℎ(𝜏) y 𝑔(𝑢), resultando:. 𝑓(𝑢, 𝜏) =. 𝐴𝑟 −3 { 𝑐. 𝑢2 3 exp ( ) ⁄ ⁄ 7 3 11 3 (𝑢 + 3) (3⁄2 − 𝑢) 2𝑢 − 3 0. , 𝑢 < 𝑢0. .. (1.44). , 𝑢 > 𝑢0. Para corroborar experimentalmente la relación (1.44) es necesario eliminar el factor 𝐴 dependiente del tiempo, que encierra el volumen del material observado y que no influirá en la forma de la distribución, este objetivo se logra imponiendo para todo tiempo la condición de normalización: 𝑃(𝑢) =. 𝑓(𝑢, 𝜏) ∞ ∫0 𝑓(𝑢, 𝜏)𝑑𝑢. (1.45). La probabilidad de que el tamaño reducido de un precipitado tomado al azar esté entre 𝑢 y 𝑢 + 𝛿𝑢 resulta:.

(31) 21 𝑢+𝑑𝑢. 𝑝(𝑢) = ∫ 𝑃(𝑢)𝑑𝑢. (1.46). 𝑢. Una vez obtenida la función densidad de probabilidad 𝑃(𝑢), se puede discutir algunos aspectos del fenómeno de coalescencia cuando el mecanismo de transferencia de masa es la difusión de soluto en la matriz. La función de distribución 𝑓(𝑢, 𝜏), se empleaen la determinación de los valores medios de las magnitudes utilizadas para describir el estado del ensemble de precipitados. La dispersión ⟨𝑟 2 ⟩ − ⟨𝑟⟩2, el radio reducido medio ⟨𝑟⟩ y el área bajo la curva están determinados por los momentos de la distribución. Su determinación se realiza a través de la relación: ∫⟨⋯ ⟩𝑓(𝑢, 𝜏)𝑑𝑢 ̅̅̅̅̅ ⟨⋯ ⟩ = ∫ 𝑓(𝑢, 𝑡)𝑑𝑢. (1.47). Evaluando numéricamente la integral en (1.47), se demuestra que, el radio medio de la población de precipitados coincide con su radio crítico. Considerando la relación entre la sobresaturación de la matriz y el radio crítico, se obtiene la ley para la evolución de la tercera potencia del radio crítico de la población de precipitados con el tiempo: 4 3 𝑟𝑐3 = 𝑟𝑐0 + 𝐷𝛼𝑡 9. (1.48). y la ley de evolución de la sobresaturación ∆(𝑡)de la matriz: 4𝐷 −1⁄3 ∆(𝑡) = ( 2 𝑡) 9𝛼. (1.49). También se puede predecir la variación del número de precipitados presentes en la matriz con el transcurso del tiempo a través de la expresión: ∞. ∫ 𝑓(𝑟, 𝑡)𝑑𝑟 = 𝑁(𝑡) 0. (1.50).

(32) 22. Resultando: 3 2⁄3 𝐴 𝑁(𝑡) = ( ) 2 𝑡. (1.51). 3 En (1.51) 𝐴 = 0.22 𝑄0 ⁄𝑟𝑐0 es una constante, que depende del radio crítico inicial 𝑟𝑐0 de la. población de precipitados y la sobresaturación inicial de la matriz 𝑄0 . Es importante notar, que las relaciones obtenidas para la variación temporal de la sobresaturación ∆(𝑡), el número de precipitados 𝑁(𝑡) y el radio crítico de la población de precipitados 𝑟𝑐 (𝑡) son solo válidas para el estado asintótico. Realizando un procedimiento similar al de Lifshitz y Slezov [5;8], pero considerando que la transferencia de soluto está determinada por el flujo de átomos que cruzan la interface precipitado - matriz y son depositados en la superficie del precipitado en la unidad de tiempo, se obtiene una función de distribución para los radios de los precipitados. Los resultados de este enfoque, debido a Wagner, permiten predecir una función de distribución de tamaños de precipitados más simétrica y una ley de crecimiento cuadrática para el radio crítico de la población. En el estado asintótico, se obtiene, para la función de distribución de Wagner: 𝑓𝑤 (𝑢) =. 𝑢 6 exp (− ) (2 − 𝑢)5 2−𝑢. Fig.1.3: Dependencia. (1.52). de la función de densidad P (u) para el mecanismo de Wagner respecto al radio reducido 𝑢 = 𝑟⁄𝑟𝑐 .. Y para la ley de crecimiento del radio crítico de los precipitados:.

(33) 23. 2 𝑟𝑐2 − 𝑟𝑐0 =. 1 𝛼𝛽𝑡 2. (1.53). 1.6 Estimación de las constantes de velocidad 𝐊 𝐋𝐒 y 𝐊 𝐖 En el caso de buena correlación entre las curvas teóricas de la teoría de Lifshitz y Slezov y Wagner [5;8;13] con los histogramas experimentales, se puede predecir la evolución temporal del radio crítico, a través de las relaciones(1.48) y (1.53): 2 𝑟𝑐2 − 𝑟𝑐𝑜 = 𝐾𝑊 𝑡 ,. (1.54). donde la constante de velocidad de la ley de crecimiento es 𝐾𝑊 = 𝛼𝛽 ⁄2 Determinando el radio de los precipitados para un instante de tiempo específico, conocidas la temperatura del revenido isotérmico y el valor de la constante 𝛼𝛽 ⁄2 , se puede estimar el valor de la constante de velocidad 𝐾𝑊 . Análogamente, cuando existe predominio del mecanismo de Lifshitz y Slezov, se puede escribir para la ley de crecimiento: 3 𝑟𝑐3 − 𝑟𝑐𝑜 = 𝐾𝐿𝑆 𝑡 ,. (1.55). donde la constante de velocidad resulta 𝐾𝐿𝑆 = 4𝐷𝛼 ⁄9. El valor de la constante 𝐾𝐿𝑆 puede calcularse a través del ángulo de inclinación en la dependencia 𝑟𝑐3 vs.𝑡. Se debe comprender que el cálculo a través de la metodología propuesta produce solo valores estimados de las constantes de velocidad [8, 9, 10]. Finalmente, la determinación experimental de las constantes 𝐾𝐿𝑆 y 𝐾𝑊 , permite hallar una relación entre los coeficientes 𝐷𝑣 y 𝛽 : 𝐾𝐿𝑆 3 𝐷𝑣 = . 𝐾𝑊 2 𝛽. (1.56). Por tanto, resulta suficiente contar con el valor de alguno de los coeficientes arriba mencionados para poder calcular el valor numérico del otro. Con los valores experimentales de los coeficientes 𝐷𝑣 y 𝛽, y los valores de las constantes 𝐾𝐿𝑆 y 𝐾𝑊 que pueden obtenerse de la data experimental del proceso de OR, se puede estimar el valor de la energía específica de superficie 𝜎: 𝜎=. 𝐾𝐿𝑆 𝑅𝑇 𝛼 𝜔2𝐷 𝐶∞ 𝑣. (1.57).

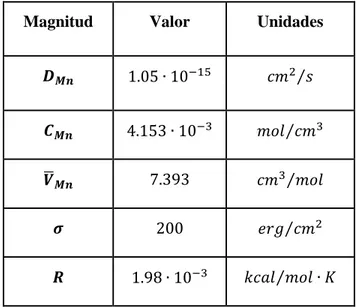
(34) 24. CAPÍTULO #2: MATERIALES Y MÉTODOS 2.1 Introducción Para el estudio de la cinética de la maduración de Ostwald en aleaciones ferrosas susceptibles de endurecer por precipitación metaestable, y de sufrir segundas transformaciones de fase durante el revenido isotérmico, fue elaborada una aleación: Fe- 9,1 at. % Mn – 4,7 at. % Si – 2,5 at. % Ti. En el presente capítulo se exponen las técnicas de observación, estudio y cálculo utilizadas para construir los histogramas experimentales de los precipitados metaestables e isomorfos de Fe3Si.. 2.2 Elaboración de las aleaciones y preparación de las probetas Las aleaciones bajo estudio fueron elaboradas por [15] siguiendo el procedimiento siguiente. Se prepararon lingotes de 5 kg en un horno de inducción Balzers, trabajando bajo presión parcial de argón, y siendo colocados en lingoteras paralelepípedas de 20 x30 mm2 de sección transversal. Las aleaciones han sido analizadas por métodos químicos clásicos y por análisis puntual con la ayuda de una microsonda de Castaing. A través de este análisis se obtuvo la siguiente composición química: Aleación: Fe – 9,1 at. % Mn – 4,7 at. % Si – 2,5 at. % Ti En la aleación, el análisis químico realizado en los laboratorios de investigaciones de la nueva sociedad de Aceros de Pompey, Francia [15], reflejó un contenido de oxígeno menor que 180ppm, de nitrógeno menor que 10ppm, y de carbono menor que 300ppm. El lingote de la aleación ha sido laminado en caliente entre 1150 0C y 1200 0C estando limitada a 50 % la reducción de espesor. Posteriormente el mismo fue cortado en probetas paralelepípedas de 6 mm de espesor, para la microscopía óptica, los análisis radiocristalográficos, la microscopía electrónica, y los ensayos de dureza. Se realizó un pulido electrolítico utilizando ácido perclórico al 5 % y éter monobutílico del etilenglicol al 95 %, con una tensión de 16 Volt..

(35) 25. 2.3 Tratamientos térmicos y análisis de la composición química de los precipitados Las probetas de la aleación han sido homogeneizadas durante 2 h a 1150 0C, en un horno vertical al vacío de 10-5 torr. El mismo posee un dispositivo que permite efectuar un temple rápido en agua al final del tratamiento. Los tratamientos térmicos consecutivos al temple son efectuados en un horno vertical con atmósfera de argón, para el revenido isotérmico hasta 520 0C (efectuados en la Escuela Superior de la Metalurgia, Nancy Francia).La temperatura de revenido isotérmico no oscila más de 3 0C del valor medio, para tiempos de revenido superiores a 12 h. La microsonda utilizada es la MS 46 CAMECA (de la Escuela Superior de la Metalurgia en Nancy, Francia). La misma permite realizar un análisis cuantitativo puntual y semicuantitativo por barrido, así como la obtención de imágenes X. Las muestras utilizadas son pulidas cuidadosamente hasta 3 µm, pues los desniveles (ralladuras) superiores a 3µm pueden provocar errores importantes en el análisis. Al poseer las aleaciones más de dos elementos, los resultados son corregidos por el método ZAF programado en la computadora.. 2.4 Técnicas generales de observación y estudio. Estudio por microscopía electrónica Después de cada tratamiento térmico de la aleación, fueron preparadas láminas delgadas de 800 a 1000 Å de espesor. Las mismas se obtuvieron cortando primero láminas de 1 mm de espesor, después reduciéndolas por abrasión mecánica hasta 0.01 mm de espesor, y por último llevándolas por adelgazamiento electrolítico hasta el espesor deseado. Las mejores condiciones de adelgazamiento electrolítico fueron obtenidas con una solución de 5% de ácido perclórico en el éter monobutílico del etilenglicol 95%, bajo una tensión de aproximadamente 16 volt y una temperatura media del electrólito de 160C. Las láminas delgadas fueron posteriormente observadas en los siguientes microscopios electrónicos: . Philips EM 300, que posee una anticontaminador de nitrógeno líquido y un goniómetro. asociado al portamuestra. . Hitachi HU-ll-A, usando la mesa con anticontaminador de nitrógeno líquido.. . Tesla BS-500..

(36) 26. 2.5 Determinación de la segunda transformación de fase La identificación de fases en las aleaciones masivas por difracción de rayos X ha sido realizada a partir de difractogramas obtenidos en un difractómetro con monocromador, utilizando la radiación Kα1 del cobalto (λKα1 = 1.7889 ·10-10 m). La misma provoca la fluorescencia del manganeso, que es eliminada por un conjunto de discriminación de impulsos (equipo de la Escuela Superior de la Metalurgia en Nancy, Francia). Para el estudio de la evolución de la transformación en las aleaciones, fue utilizado un difractómetro URS 50 (del CENIC), trabajando en este caso con el doblete Kα del cobalto λKα=1.7902·10-10 m ,eliminado en parte la fluorescencia del manganeso a través de filtros de aluminio de espesores conveniente elegidos.. 2.6 Métodos de cálculo. Correcciones La microfotografía electrónica en transmisión sobre láminas delgadas de una muestra no es más que la proyección del volumen de la misma sobre el plano de la fotografía. Este hecho provoca que cuando se realice un conteo directo de las partículas en la foto, no se obtenga la distribución verdadera de las partículas en la muestra. Pueden cometerse, fundamentalmente, dos tipos de errores: (i) Que se cuenten como partículas pertenecientes a la muestra algunas que la interceptan, pero cuyos centros no pertenecen a ese volumen. (ii) Que no se cuenten como partículas de la muestra aquellas pequeñas que resultan solapadas por otras mayores. La corrección del primer error se llamará: corrección por intersección y a la del segundo, corrección por solapamiento. Nos referiremos a un precipitado esférico, y para obtener la distribución verdadera de las partículas emplearemos el método desarrollado por [16] que permite relacionar las propiedades de la imagen proyectada con las de las partículas en la muestra. Sea 𝑁(𝐷)𝑑𝐷 el número de esferas por unidad de volumen cuyos diámetros 𝐷 se encuentran entre 𝐷 y 𝐷 ± 𝑑𝐷⁄2. El número esperado de tales esferas con centros en el interior de la muestra de espesor 𝑍 es 𝑍𝑁(𝐷)𝑑𝐷, por unidad de área y en ausencia de solapamiento; estas esferas pueden ser proyectadas como círculos del mismo diámetro. Las esferas cuyos centros están fuera.

(37) 27. de la muestra, pero que la interceptan, serán proyectadas como círculos de diámetros menores que los diámetros de las esferas. Si la distribución de círculos de intersección es 𝜇(𝑑), entonces, la distribución observada, 𝑁(𝑑) de diámetros imágenes es: 𝑁(𝑑) = 𝑍𝑁(𝐷)|𝐷=𝑑 + 𝜇(𝑑) − 𝑀(𝑑). (2.1). En (2.1) 𝑀(𝑑) representa la corrección por solapamiento, o sea, el número de proyecciones de diámetros entre 𝐷 y 𝐷 ± 𝑑𝐷⁄2 por unidad de área e intervalo de diámetro, pérdidas por solapamiento. Las correcciones dependen del espesor 𝑍 de la muestra; cuando éste espesor es mucho mayor que el diámetro medio de los precipitados debe predominar la corrección por solapamiento, mientras que cuando ocurre lo contrario, la corrección por intersección será la más importante. ̅ ≫ 1 y de muestras delgadas 𝑍⁄𝐷 ̅ < 2. Se tomará como criterio de muestras gruesas 𝑍⁄𝐷 ̅ como el diámetro medio de la población de precipitados. Donde se ha tomado a 𝐷 Se demuestra en [17] que el término de la corrección por intersección es el más importante a baja fracción volumétrica (que en nuestro sistema siempre es menor que 0.005 ver [15]) debido a que dicha corrección es proporcional a la probabilidad de que un plano trazado al azar en la muestra corte a varios precipitados a la vez en dirección horizontal, mientras que la corrección por solapamiento es proporcional a la probabilidad de que varios precipitados sean cortados verticalmente por un plano trazado al azar en la muestra. La adopción de dicho criterio se ̅ < 2. Por ese motivo se utilizó un programa confirma además al cumplirse la condición 𝑍⁄𝐷 elaborado por [15] para evaluar la expresión correspondiente a esta corrección: 𝑑𝑚á𝑥. 𝑁(𝐷𝐶 ) = 𝑍𝑁(𝐷)|𝐷=𝑑 + ∑ 𝑑(𝐷2 − 𝑑 2 )−1⁄2 𝑁(𝐷)∆𝐷. (2.2). 𝐷=𝑑. Debido a que el número de precipitados a corregir 𝑁 (𝐷) se encuentra dentro de la expresión de suma en (2.2) se hace necesario utilizar un método iterativo para su obtención, esto se llevó a cabo en el Software especializado Wolfram Mathematica v.11 [19]. Como resultado, se obtuvo las frecuencias corregidas para cada grupo de precipitados en cada intervalo de paso 0.1 definido en los histogramas experimentales correspondientes a los distintos tiempos de revenido isotérmico..

(38) 28. 2.7 Construcción de los histogramas experimentales. Los histogramas experimentales se construyeron a partir de los radios de la población de precipitados obtenidos de las microfotografías electrónicas en transmisión de las muestras revenidas y los resultados de las correcciones para el número de precipitados, realizadas a través de (2.2). En el eje de las ordenadas de los histogramas se representa la magnitud 𝑃(𝑢) la cual es proporcional a la probabilidad de encontrar una partícula con radio reducido 𝑢 entre 𝑟⁄𝑟𝑔 y 𝑟⁄𝑟𝑔 + ∆𝑟⁄𝑟𝑔 ; y ésta es igual al número de precipitados por unidad de volumen de la muestra dentro de algún intervalo ∆𝑟 . En el eje de las abscisas se grafica 𝑟⁄𝑟𝑔 con un paso en 𝑢 = 𝑟⁄𝑟𝑔 de 𝑢 = 0.1..

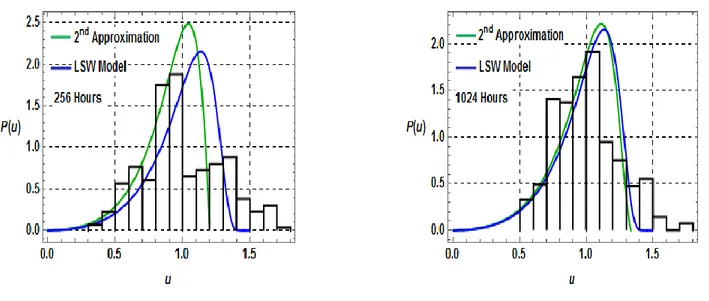
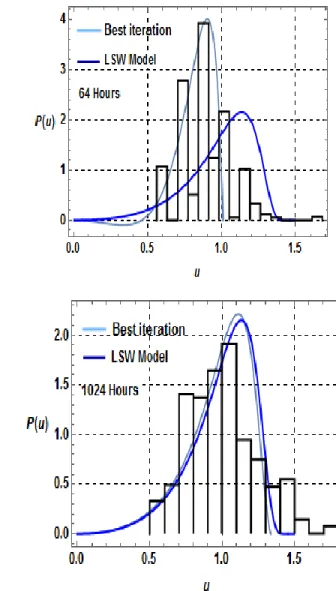
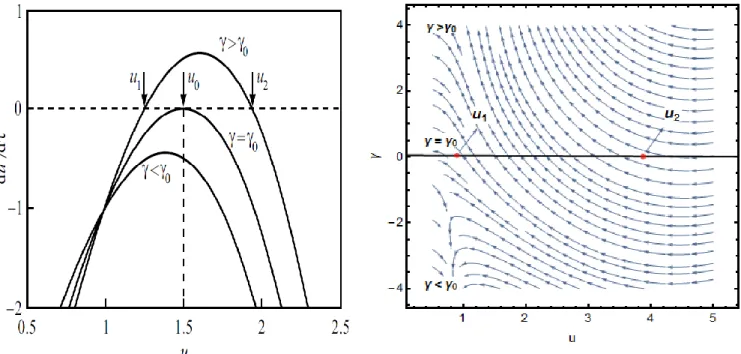
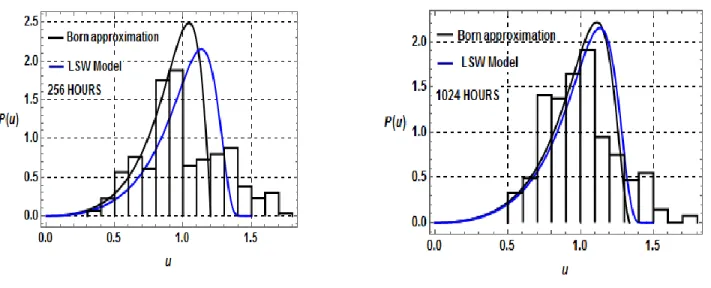
(39) 29. CAPÍTULO #3: COALESCENCIA PERTURBADA POR UNA SEGUNDA TRANSFORMACIÓN DE FASE. 3.1 Introducción La aleación bajo estudio es susceptible de endurecer por precipitación metaestable, y de sufrir segundas transformaciones de fase durante el revenido isotérmico. En estas condiciones la cinética de coalescencia de los precipitados metaestables isomorfos de Fe3Si se encuentra modificada respecto al caso libre de LSW. Teniendo en cuenta varias de las hipótesis fundamentales de la teoría LSW se puede intentar realizar una descripción del fenómeno de la maduración de Ostwald asociado a un primer proceso de precipitación, asumiendo que éste se desarrolla simultáneamente con una segunda transformación de fase. Estas últimas condiciones se ajustan a infinidad de situaciones experimentales, ya que con frecuencia, para gobernar las propiedades de una aleación, se busca la ocurrencia de una secuencia de transformaciones de fase, y en los sistemas de más de dos elementos es habitual la coexistencia simultánea de más de dos fases que se pueden utilizar para la optimización de las propiedades físico-mecánicas, durante el diseño de las aleaciones. En consecuencia, el objeto de estudio del presente capítulo es la obtención de la función de distribución que caracteriza a la dispersión de precipitados en una matriz donde la transferencia de soluto, que se realiza mediante la difusión de soluto en el volumen de la matriz, se encuentra débilmente perturbada (𝑓(𝜙̇) > 0), por una segunda transformación de fase que utiliza para su evolución el mismo soluto que los precipitados en OR. Este tratamiento perturbativo (PLSW) de la teoría LSW en una primera aproximación (Aproximación de Born) fue realizada en trabajos precedentes [20]. La superposición de la función de distribución a los histogramas experimentales plantea la necesidad del cálculo de la segunda aproximación de la secuencia utilizada para hallar las soluciones de la ecuación de continuidad (1.25)..