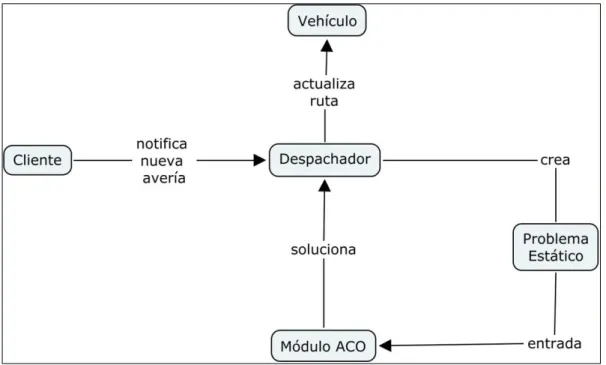
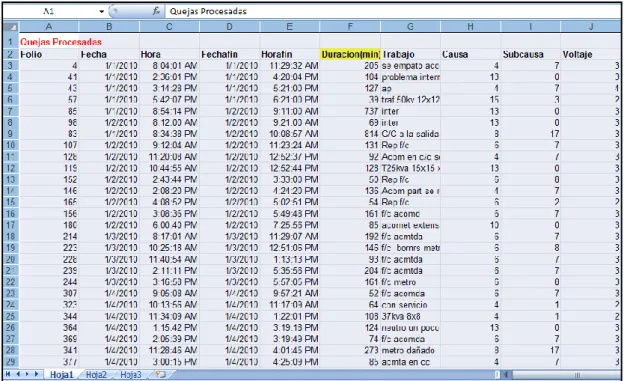
Optimización basada en colonias de hormigas en el ruteo de vehículos para la reparación de averías eléctricas

Texto completo

(1)Universidad Central “Marta Abreu” de Las Villas Facultad de Matemática, Física y Computación. Trabajo para optar por el Título de Licenciado en Ciencias de la Computación Optimización basada en colonias de hormigas en el ruteo de vehículos para la reparación de averías eléctricas Autor Dairon Hernández Pérez Tutores Dr. C. Amilkar Yudier Puris Cáceres Ms. C. Yasel Jose Costa Salas. 2011 “Año 53 de la Revolución”.

(2) Declaración de autoría. Hago constar que este trabajo ha sido realizado en la facultad de Matemática, Física y Computación de la Universidad Central “Marta Abreu” de las Villas como parte de la culminación de los estudios de la Licenciatura en Ciencias de la Computación, autorizando a que el mismo sea actualizado por la institución para los fines que estime conveniente, tanto de forma total como parcial y que además no podrá ser presentado en eventos ni publicado sin previa autorización de la universidad. ___________________ Firma del Autor. Los abajo firmantes, certificamos que el presente trabajo ha sido realizado según acuerdo de la dirección de nuestro centro, y que el mismo cumple con los requisitos que debe tener un trabajo de esta envergadura referido a la temática señalada. ___________________. ___________________. Firma del Tutor. Firma del Tutor ___________________ Firma del Jefe del. Seminario de Inteligencia Artificial.

(3) Dedicatoria. A toda mi gran familia, incluyendo a los que ya no están En especial a mis padres Edelis y Nelson.

(4) Agradecimientos. Agradezco a todas las personas que han contribuido al desarrollo de este trabajo: A toda mi ejemplar familia, por estar siempre pendiente de mí en cada paso que doy en la vida y apoyarme en todo. A mi novia Yaimit. A mis tutores por sus ideas, consejos y el tiempo dedicado. A todos mis compañeros de estudio.

(5) Resumen. Resumen A diario en el sector empresarial surgen problemas que deben resolverse con técnicas eficientes para obtener buenos resultados. La Optimización Basada en Colonias de Hormigas representa en el área de la Inteligencia Artificial una poderosa metaheurística para la solución de problemas complejos en distintos dominios de aplicación. En el campo de los Problemas de Enrutamiento de Vehículos esta metaheurística ha sido aplicada con éxito. En la presente investigación se desarrolló el algoritmo Sistemas de Colonias de Hormigas y una extensión de este con múltiples colonias, las cuales colaboran e intercambian información en el proceso de búsqueda de las soluciones. Estos fueron aplicados al clásico problema de los m Agentes Viajeros y a un problema real de enrutamiento de vehículos de reparación de averías eléctricas en la Organización Básica Eléctrica (OBE) de Santa Clara. Los algoritmos implementados demostraron su efectividad a partir de las pruebas realizadas..

(6) Abstract. Abstract Daily in the business sector there are problems to be solved with efficient techniques to obtain good results. The Ant Colony Optimization represents in the area of Artificial Intelligence a powerful metaheuristic for solving complex problems in different application domains. In the field of Vehicle Routing Problems with this metaheuristic has been applied successfully. In this research the algorithm was developed Ant Colony Systems and an extension of this multiple colonies, which they collaborate and exchange information in the process of finding solutions. These were applied to the classic Multiple Traveling Salesman Problem and a real problem routing vehicle repair electrical faults in the Basic Electric Company (BEC) in Santa Clara. The algorithms implemented demonstrated their effectiveness from the tests..

(7) Tabla de contenidos. Tabla de contenidos Introducción ........................................................................................................................................... 1 Capítulo I Marco Teórico y Referencial de la Investigación ..................................................................... 6 1.1 Introducción ................................................................................................................................. 6 1.2 Problemas de Ruteo de Vehículos ................................................................................................. 6 1.2.1 Características de los problemas ............................................................................................ 7 1.2.2 Algunas extensiones............................................................................................................ 10 1.2.3 Problemas Dinámicos de Ruteo de Vehículos ...................................................................... 11 1.3 Enrutamiento de vehículos en el servicio de reparación de averías eléctricas en Cuba .................. 12 1.4 Métodos de solución para VRP ................................................................................................... 13 1.5 Optimización Basada en Colonias de Hormigas ........................................................................... 16 1.5.1 Modo de funcionamiento general ........................................................................................ 17 1.5.2 Principales algoritmos ......................................................................................................... 19 1.6 ACO con múltiples colonias ....................................................................................................... 19 1.6 Consideraciones parciales ........................................................................................................... 20 Capítulo II Optimización Basada en Colonias de Hormigas para el diseño de rutas en la reparación de averías eléctricas .................................................................................................................................. 22 2.1 Introducción ............................................................................................................................... 22 2.2 Modelación del problema mediante ACO .................................................................................... 22 2.3 Descripción del algoritmo ACS para el problema de diseño de rutas en la reparación de averías eléctricas .......................................................................................................................................... 23 2.4 Descripción del algoritmo M-ACS para el problema de diseño de rutas en la reparación de averías eléctricas .......................................................................................................................................... 27 2.5 Selección del mejor algoritmo: ACS vs M-ACS .......................................................................... 29 2.5.1 Caso de estudio: Problema de los m Agentes Viajeros.......................................................... 29 2.5.2 Análisis estadístico y explicación de los resultados .............................................................. 31 2.6 Tratamiento de la dinamicidad .................................................................................................... 32 2.7 Conclusiones parciales................................................................................................................ 36 Capítulo III Caso de estudio: Servicio de reparación de averías eléctricas en la Organización Básica Eléctrica (OBE) de Villa Clara.............................................................................................................. 37 3.1 Introducción ............................................................................................................................... 37 3.2 Caracterización de la Empresa Eléctrica de Villa Clara ................................................................ 37.

(8) Tabla de contenidos. 3.3 Descripción del caso de estudio................................................................................................... 38 3.4 Formulación matemática resumida del problema objeto de estudio .............................................. 39 3.4 Obtención de los datos reales ...................................................................................................... 40 3.4.1 Ubicación geográfica de las averías y el cálculo de las distancias entre estas ........................ 41 3.5 Descripción de las instancias creadas .......................................................................................... 42 3.6 Resultados de las pruebas y comparación con los datos de la empresa .......................................... 43 3.6.1 Análisis de los resultados .................................................................................................... 43 3.7 Análisis de sensibilidad de parámetros ........................................................................................ 44 3.8 Descripción del software implementado ...................................................................................... 49 3.9 Conclusiones parciales................................................................................................................ 50 Conclusiones generales ......................................................................................................................... 51 Recomendaciones ................................................................................................................................. 52 Referencias bibliográficas ..................................................................................................................... 53.

(9) Introducción. Introducción “Algo le llamó la atención desde el suelo. Algo vivo se movía sobre su mano: era un ser quitinoso que le causó admiración; lo recordaba por haberlo visto en otros tiempos. La hormiga sujetaba una pequeña partícula blanca entre sus mandíbulas, y la miró alejarse. Las hormigas no eran muy inteligentes como especie, pero al menos habían logrado sobrevivir.” Philip K. Dick, La penúltima verdad En el sector industrial y empresarial se realizan enormes esfuerzos por resolver diversos problemas que se presentan a diario. En la mayoría de las ocasiones estos problemas caen dentro del área de la optimización. La optimización trata de elegir una decisión adecuada para maximizar (ganancias, velocidad, eficiencia, etc.), o minimizar (costos, tiempo, riesgo, error, etc.) un criterio determinado. Los problemas de optimización se dividen en dos categorías: aquellos problemas con variables continuas, en los cuales generalmente se buscan números reales o una función, y los problemas con variables discretas, en los cuales se buscan permutaciones, integraciones, grafos, etc. Se pueden encontrar una gran cantidad de problemas de optimización, tanto en la industria como en la ciencia. Desde los clásicos problemas de diseño de redes de telecomunicación u organización de la producción hasta los más actuales en ingeniería y re-ingeniería de software, existe una infinidad de problemas teóricos y prácticos que involucran a la optimización. Algunas clases de problemas de optimización son relativamente fáciles de resolver. Este es el caso, por ejemplo, de los problemas lineales, en los que tanto la función objetivo como las restricciones son expresiones lineales. Sin embargo, existen muchos problemas que por su propia naturaleza, no pueden ser resueltos mediante un procedimiento de búsqueda completo (Nemhauser and Wolsey, 1998), ya sea porque tal método no exista o porque su complejidad crece de manera no polinomial. De hecho la mayor parte de los que se encuentran en la práctica pertenecen a este tipo de problemas. Debido a esto se ha visto un enorme crecimiento al desarrollo de procedimientos eficientes para encontrar soluciones aproximadas que sean competentes, donde la rapidez del proceso de búsqueda de la solución es tan importante como la calidad de esta. Estos procedimientos son conocidos como heurísticos. En (Díaz et al., 1996) se 1.

(10) Introducción. recogen hasta tres definiciones diferentes de algoritmo heurístico, entre las que destacamos la siguiente: Un método heurístico es un procedimiento para resolver un problema de optimización bien definido mediante una aproximación intuitiva, en la que la estructura del problema se utiliza de forma inteligente para obtener una buena solución. En contraposición a los métodos exactos que proporcionan una solución óptima del problema, los métodos heurísticos se limitan a proporcionar una buena solución no necesariamente óptima. Lógicamente, el tiempo invertido por un método exacto para encontrar la solución óptima de un problema difícil 1, si es que existe tal método, es de un orden de magnitud muy superior al del heurístico (pudiendo llegar a ser tan grande en muchos casos, que sea inaplicable). En las últimas décadas han aparecido un conjunto de métodos bajo el nombre de metaheurísticos con el propósito de obtener mejores resultados que los alcanzados por los heurísticos tradicionales. El término metaheurística fue introducido en (Glover, 1977) por Fred Glover. Los profesores Osman y Kelly en (Kelly and Osman, 1996) introducen la siguiente definición: Los procedimientos meta-heurísticos son una clase de métodos aproximados que están diseñados para resolver problemas difíciles de optimización combinatoria, en los que los heurísticos clásicos no son efectivos. Los meta-heurísticos proporcionan un marco general para crear nuevos algoritmos híbridos combinando diferentes conceptos derivados de la inteligencia artificial, la evolución biológica y los mecanismos estadísticos. Los procedimientos metaheurísticos se sitúan conceptualmente “por encima” de los heurísticos en el sentido que guían el comportamiento de éstos. Así, al enfrentarnos a un problema de optimización, podemos escoger cualquiera de estos métodos para diseñar un algoritmo específico que lo resuelva aproximadamente. La Optimización Basada en Colonias de Hormigas (Dorigo and Stutzle, 2004, Dorigo et al., 1999), es una metaheurística que pertenece a la categoría de algoritmos bioinspirados o de vida artificial y de inteligencia colectiva, ya que la potencialidad de. 1. Podemos decir que un problema de optimización difícil es aquel para el que no podemos garantizar el encontrar la mejor solución posible en un tiempo computacional razonable.. 2.

(11) Introducción. estos modelos para resolver problemas está dada por la cooperación entre individuos de una forma directa o indirecta. Los algoritmos de ACO se inspiran directamente en el comportamiento de las colonias de hormigas naturales. Se basan en una colonia de hormigas artificiales, esto es, unos agentes computacionales simples que trabajan de manera cooperativa y se comunican mediante rastros de feromona2 artificiales. Esta estrategia ha mostrado ser eficiente en la solución de Problemas de Enrutamiento de Vehículos (Andrés, 2008). Problemas de Enrutamiento de Vehículos es un nombre genérico dado a un conjunto de problemas reales, enfocados a la configuración de rutas para vehículos. Estos problemas en su mayoría pertenecen a la clase de problemas NPhard (Lenstra and Rinnooy, 1981), por lo que es vital para su solución la aplicación de técnicas aproximadas. En la industria y en el sector de servicios, el costo del transporte representa una parte importante del valor final de la mercadería o del servicio brindado. El problema de distribuir productos o de brindar servicios desde ciertos depósitos a sus usuarios finales juega un papel central en la gestión de algunos sistemas logísticos y su adecuada planificación puede significar considerables ahorros. En (Toth and Vigo, 2002) se estima que los costos del transporte representan entre el 10% y el 20% del costo final de los bienes. Esos potenciales ahorros justifican en gran medida la utilización de técnicas de Investigación Operativa como herramientas de ayuda a la toma de decisiones. El carácter cambiante del entorno empresarial provoca que las decisiones a tomar sean cada vez más complejas. Muchas organizaciones se enfrentan en la actualidad con problemas relacionados con el movimiento de personas, mercancías o información. El transporte pretende satisfacer los deseos de movilidad, constituyendo una función de creciente importancia estratégica para las industrias. Las redes y los flujos se deben diseñar y gestionar de modo que se alcancen objetivos tales como los deseados resultados. económicos. de. las. empresas. distribuidoras,. los. requerimientos. medioambientales y la demanda de servicio de los clientes. El proceso de reparación de averías adjudica un peso significativo en el sector eléctrico, el cual juega un papel crucial en la economía de cualquier país, ya que constituye la base para el desarrollo industrial y social. Las ventajas que aporta a la sociedad y la. 2. Sustancia química olorosa utilizada por algunas especies de animales para intercambiar información.. 3.

(12) Introducción. toma de medidas para su uso racional, trae aparejado considerables mejoras económicas. Muchas de las empresas cubanas actuales presentan muchas deficiencias en cuanto a la organización de las rutas de sus vehículos. Tal es el caso de la Organización Básica Eléctrica (OEB) del municipio de Santa Clara. Por lo anteriormente expuesto, se plantea el siguiente problema de investigación: El proceso decisional vinculado con la reparación de averías eléctricas, usualmente, se basa en el aseguramiento, profesional, técnico y tecnológico, en el desempeño de las redes de distribución, presentando significativas limitaciones en cuanto a la planificación de los recorridos realizados para tales reparaciones dado por la inexistencia de un procedimiento que fundamentado sobre bases algorítmicas permita asistir la toma de decisiones relativas al enrutamiento de vehículos de reparación de averías eléctricas de manera eficiente. El Objetivo General de la Investigación consiste en implementar y comparar el comportamiento de algoritmos que sean capaces de asistir la toma de decisiones relativas al enrutamiento de vehículos en la reparación de averías eléctricas para:  Disminuir los costos implicados en tales procedimientos  Disminuir los tiempos de respuestas a los clientes A través de los Métodos de Optimización Basados en Colonias de Hormigas. Este objetivo general fue desglosado en los objetivos específicos siguientes: 1. Modelar el problema objeto de estudio para su solución mediante la metaheurística de Optimización Basada en Colonias de Hormigas. 2. Seleccionar e implementar los algoritmos de la metaheurística ACO. 3. Realizar. un estudio. estadístico,. donde. se. comparen. los. algoritmos. implementados de acuerdo a la calidad de las soluciones obtenidas. 4. Solucionar un caso de estudio real y evaluar el comportamiento de los algoritmos diseñados en para su solución. 5. Insertar los algoritmos implementados en una herramienta computacional para solucionar el caso de estudio. 6. Realizar un ajuste de parámetros en los algoritmos propuestos.. 4.

(13) Introducción. Durante el análisis del problema surgieron las Preguntas de Investigación expresadas a continuación: 1. ¿Cómo realizar la modelación del problema de ruteo de vehículos existentes en la OEB de Santa Clara, para su resolución mediante la metaheurística ACO? 2. ¿Qué variantes de la metaheurística ACO serán las escogidas para dar solución al problema? 3. ¿Qué ventajas proporcionará el desarrollo de procedimientos que ayuden a la toma de decisiones relativas al enrutamiento de vehículos? La hipótesis de la actual investigación es la siguiente: Si se emplea la Optimización Basada en Colonias de Hormigas en la planificación de rutas relativas a la reparación de averías eléctricas, se pueden obtener algoritmos que logren reducir los costos de las rutas y los tiempos de servicios, mejorando de esta forma las soluciones obtenidas por los especialistas de las empresas. El valor práctico consiste en el desarrollo de algoritmos que ayudan el proceso de enrutamiento de vehículos, y pueden ser aplicados en la empresa eléctrica como forma de brindar un mejor servicio al cliente, logrando así un mejor desempeño de la empresa. El valor social de la investigación se sustenta fundamentalmente en dos aspecto, el primero en lo que respecta al aporte en el área de la optimización con la introducción de algoritmos a la categoría de métodos aproximados y, en un segundo aspecto, en el planteamiento de nuevos métodos que permiten resolver problemas reales específicamente en temas tan sensibles para la sociedad como la del restablecimientos en menor plazo del servicio eléctrico. Para la presentación de esta investigación, se estructuró de la forma siguiente. Una Introducción, donde en los esencial se caracteriza la situación problémica y se fundamenta el problema científico a resolver. Un Capítulo I, que contiene el marco teórico-referencial que sustentó la investigación. A continuación, el Capítulo II, en el que se describen los algoritmos propuestos. Por último, el Capítulo III, donde se trata un caso de estudio real, y se prueban los algoritmos propuestos en su solución. También un cuerpo de Conclusiones, Recomendaciones y Bibliografía consultada derivadas de la investigación realizada.. 5.

(14) Capítulo I. Capítulo I Marco Teórico y Referencial de la Investigación 1.1 Introducción En el presente capítulo se presenta un acercamiento global a los Problemas de Enrutamiento de Vehículos. Se describen las características de los problemas estáticos y dinámicos de enrutamiento de vehículos así como los métodos de solución conocidos en la literatura, enfatizando en los métodos heurísticos y metaheurísticos. Además se aborda acerca de cómo se realiza el enrutamiento de vehículos de reparación de averías en la red eléctrica de nuestro país. También se trata la metaheurística de optimización basada en colonias de hormigas.. 1.2 Problemas de Ruteo de Vehículos Problemas de Ruteo de Vehículos (Vehicle Routing Problem, VRP) es un nombre genérico dado a una gran familia de problemas relacionados con la entrega (o recogida) de personal, bienes o servicios, a un conjunto de clientes mediante una flota de vehículos. Los primeros estudios realizados en esta área se remontan a finales de la década del 50. En 1959 Dantzig y Ramser (Dantzing and Ramser, 1959) propusieron por primera vez un algoritmo aproximado y formulación de programación matemática aplicada al despacho de camiones distribuidores de combustible en estaciones de servicio en Pennsylvania. Cinco años más tarde Clarke y Wright (Clarke and Wright, 1964) propusieron el primer algoritmo que resultó realmente efectivo: el popular Algoritmo de Ahorros. A partir de estos trabajos, el área de ruteo de vehículos ha crecido de manera explosiva. Por un lado, hacia modelos que incorporen cada vez más características de la realidad, y, por otro lado, en la búsqueda de algoritmos que permitan resolver los problemas de manera eficiente. El avance en estos modelos y algoritmos se debe en gran medida al desarrollo de los sistemas informáticos y tecnológicos en general. El crecimiento en el poder de cómputo y la baja en sus costos, ha permitido disminuir los tiempos de ejecución de los algoritmos. Por otro lado, el desarrollo de los Sistemas de Información Geográfica (Geographical Information Systems, GIS), el equipamiento de comunicaciones (telefonía inalámbrica) y el Sistemas de Posicionamiento Global (Global Positioning 6.

(15) Capítulo I. System, GPS), resultan fundamentales para lograr una adecuada interacción de los modelos y algoritmos con los planificadores, y a la vez estos con los choferes. Existen una amplia gama de aplicaciones de los VRP entre las que se destacan las siguientes: Distribución de combustible, alimentos y bienes materiales. La planificación del transporte público urbano. La planificación del transporte escolar. Entrega y/o recogida de la correspondencia. Servicios de emergencia: bomberos, ambulancias, policía. Servicio de taxis o radio taxi metropolitano. Servicio de mantenimiento o reparaciones de averías eléctricas (tratado en la presente investigación). El interés que reviste el área no es del todo práctico. Los VRP son Problemas de Optimización Combinatoria y pertenecen, en su mayoría a la clase NP-hard (Lenstra and Rinnooy, 1981). La motivación académica por resolverlos radica en que no es posible construir algoritmos que encuentren soluciones para cualquier instancia en un tiempo computacional razonable.. 1.2.1 Características de los problemas A grandes rasgos un VRP consisten en dado un conjunto de clientes y depósitos dispersos geográficamente y una flota de vehículos determinar un conjunto de rutas de costo mínimo que comiencen y terminen en los depósitos, para que los vehículos visiten a los clientes. Las características de los clientes, depósitos y vehículos, así como diferentes restricciones operativas sobre las rutas, dan lugar a diferentes variantes del problema. En la Figura 1.1 se muestra un escenario típico donde se asignan rutas a tres camiones que deben servir a 12 clientes.. 7.

(16) Capítulo I. Figura 1.1. Ejemplo de VRP Clásico. A continuación se describen las principales características que presentan los clientes, depósitos, vehículos y la red de transporte. Los clientes: Cada cliente tiene una demanda que deberá ser satisfecha por alguno de los vehículos. Puede además existir la restricción de que dicha demanda deba ser satisfecha por un único vehículo o que exista la posibilidad de que más de un vehículo visite a los clientes. También los clientes pueden ser proveedores y lo que se desea es recoger la mercancía y trasportarla al depósito. En otros casos la demanda no es un bien sino un servicio: el cliente debe ser visitado solamente por el vehículo. Los clientes también pudieran tener restricciones relativas a su horario de servicio. Usualmente estas restricciones se expresan en forma de intervalos de tiempo (llamados ventanas de tiempo) en los que se puede arribar al cliente. En problemas con varios vehículos diferentes podrían existir restricciones de compatibilidad entre éstos y los clientes. Los depósitos: tanto los vehículos como las mercancías (si las hubiera) suelen estar ubicadas en depósitos. Usualmente se exige que cada ruta comience y finalice en un mismo depósito, aunque este podía no ser el caso en algunas aplicaciones (por ejemplo, pudiera darse el caso de que el viaje debiera finalizar en el domicilio del conductor).. 8.

(17) Capítulo I. Pueden existir uno o más depósitos. En los problemas con múltiples depósitos podría ocurrir que cada vehículo tenga una flota de vehículos previamente asignada o que la asignación sea parte de los que se desea determinar. Los depósitos al igual que los clientes, podrían tener ventanas de tiempo asociadas. En algunos casos debe considerarse el tiempo necesario para cargar, descargar o preparar un vehículo antes de que comience su ruta, o el tiempo invertido en su limpieza al regresar. Por limitaciones de los depósitos también podría querer evitarse que demasiados vehículos estén operando en un mismo depósito a la vez (es decir, la congestión del depósito). Los vehículos: la capacidad de un vehículo puede tener varias dimensiones, como por ejemplo peso y volumen. En general cada vehículo tiene asociado un costo fijo en el que se incurre al utilizarlo y un costo variable proporcional a la distancia que recorra. Regularmente tienen asociado un tiempo de trabajo. Los problemas en que los atributos de los vehículos son iguales se denominan de flota homogénea, y, si hay diferencias, de flota heterogénea. La cantidad de vehículos podría ser un dato de entrada o una variable de decisión. Regulaciones legales podrían imponer restricciones sobre el tiempo máximo de que un vehículo puede estar en circulación. Usualmente se asume que cada vehículo recorre una sola ruta en el período de planificación, pero últimamente se han estudiado modelos en los que un mismo vehículo puede recorrer más de una ruta. La red de trasporte: en algunas instancias, existe vía de comunicación entre todo par de clientes, mientras que en otras la red vial no es completa. También pueden existir restricciones en cuanto al sentido de las vías. Las funciones de costo que pueden ser consideradas son las siguientes: Minimizar el tiempo total de trasporte. Minimizar la distancia total recorrida. Minimizar la suma de los tiempos de espera de los clientes. Minimizar el número de vehículos.. 9.

(18) Capítulo I. 1.2.2 Algunas extensiones Diferentes variaciones del VRP se han propuesto en la literatura con el interés de acercarse a contextos reales de aplicación, estos problemas incluyen la adición de variables y restricciones. El Problema del Agente Viajero (Traveling Salesman Problem, TSP) (Gutin and Punnen, 2002) puede verse como la variante más simple de la amplia gama de problemas de enrutamiento. En este se dispone de un solo vehículo que debe visitar a todos los clientes en una sola ruta y a costo mínimo. No suele haber un depósito y si lo hubiera no se distingue de los clientes. No existen demandas asociadas a los clientes ni tampoco restricciones temporales. La mayor parte de los VRP son generalizaciones del TSP. El Problema de los m Agentes Viajeros (Multiple Traveling Salesman Problem, m-TSP) (Bektas, 2006) es una generalización del TSP en la cual existe un depósito y m vehículos. El objetivo es construir exactamente m rutas, una para cada vehículo, de modo que cada cliente sea visitado una vez por uno de los vehículos. El Problema con Capacidades (Capacited Vehicle Routing Problem, CVRP) es una variante del m-TSP en la cual cada cliente tiene asociada una demanda y cada vehículo tiene una capacidad determinística (la flota es homogénea). En este problema la cantidad de rutas no es fijada de antemano como en el TSP y m-TSP. Consiste en construir rutas de longitud mínima para la entrega de bienes que comiencen y terminen en el depósito, satisfaciendo la demanda de todos los clientes. Un cliente solo puede ser atendido por un vehículo y la suma de las demandas de los clientes visitados por un vehículo no puede exceder la demanda de dicho vehículo. El Problema con Ventanas de Tiempo (Vehicle Routing Problem With Time Windows, VRPTW) es uno de los más conocidos. En esta variante del problema, además de capacidades, cada cliente tiene asociada una ventana de tiempo que consiste en un tiempo de inicio (ready time) y un tiempo de fin (due time) en la que puede ser atendido, estableciendo un horario de servicio permitido para que cada vehículo arribe a él y un tiempo de servicio o demora. Las ventanas de tiempo pueden considerarse duras cuando no es posible realizar la entrega al cliente fuera de los períodos establecidos, mientras que se consideran suaves cuando si pueden realizar entregas fuera de período de tiempo pero con una penalización. 10.

(19) Capítulo I. Existe una variante conocida como (Vehicle Routing Problem with Backhaul, VRPB), la cual se distingue de CVRP en que además de tener clientes que demandan la entrega de bienes (linehaul), existen también otros que demandan su recolección (backhaul). Incluyéndole restricciones en cuanto al tiempo de entrega o recolección se obtiene una extensión conocida como (Vehicle Routing Problem with Backhaul and Time Windows, VRPBTW). El Problema con Entrega y Recolección (Vehicle Routing Problem with Pickup and Delivery, VRPPD) es una variante en la que además de entregas realizadas a los clientes, de manera simultánea se realizan recogidas, retornando algún tipo de producto. El Problema de Enrutamiento Estocástico (Sochastic Vehicle Routing Problem, SVRP) corresponde a una familia de problemas donde alguna o varias variables del problema son aleatorias y varían en el tiempo. Se conocen tres enfoques principales de este problema, estos son los siguientes: 1. (Vehicle Routing Problem with Sochastic Demands, VRPSD), en donde solo son conocidas las demandas de los clientes con una distribución de probabilidad. 2. (Vehicle Routing Problem with Sochastic Customers, VRPSC), en el que la variable aleatoria son los clientes. 3. (Vehicle Routing Problem with Sochastic Times, VRPST), aquí los tiempos de viaje y de servicio son variables estocásticas. Cuando el problema tiene varios depósitos de los que parten los vehículos es conocido como (Multiple Deposits Vehicle Routing Problem, MDVRP). En la literatura consultada existen otras extensiones de VRP que han sido estudiadas. En (Toth and Vigo, 2002) se puede consultar un trabajo detallado sobre la variantes mencionadas anteriormente.. 1.2.3 Problemas Dinámicos de Ruteo de Vehículos El Ruteo Dinámico de Vehículos (Dinamic Vehicle Routing Problem, DVRP) es un término genérico enfocado al ruteo y planificación en ambientes dinámicos (que varían en el tiempo). Psaraftis (Psaraftis, 1995) se refiere a un DVRP como aquel problema en el que su solución no es un conjunto de rutas sino que percibe como las rutas deben evolucionar en tiempo real en función de las nuevas órdenes que se van conociendo. En 11.

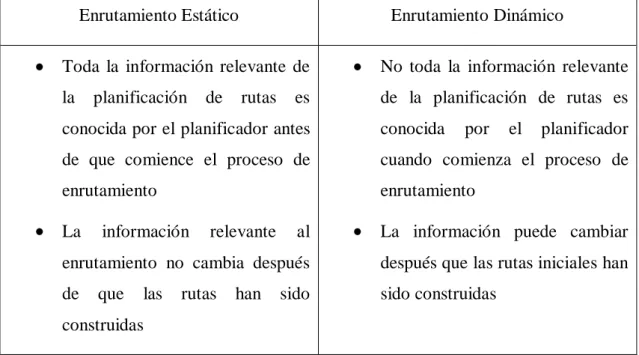
(20) Capítulo I. (Larsen, 2001) se define DVRP como un problema de ruteo donde todos o una parte de los requerimientos no es conocido de antemano sino que llegan a medida que se ejecuta el plan inicial de rutas. En la Tabla 1.1 se describe las características de los problemas estáticos y dinámicos de ruteo de vehículos. Enrutamiento Estático. Enrutamiento Dinámico. Toda la información relevante de. No toda la información relevante. la. de la planificación de rutas es. planificación. de. rutas. es. conocida por el planificador antes. conocida. de que comience el proceso de. cuando comienza el proceso de. enrutamiento. enrutamiento. La. información. el. planificador. al. La información puede cambiar. enrutamiento no cambia después. después que las rutas iniciales han. de. sido construidas. que. las. relevante. por. rutas. han. sido. construidas Tabla 1.1. Características de los problemas de enrutamiento estáticos y dinámicos.. 1.3 Enrutamiento de vehículos en el servicio de reparación de averías eléctricas en Cuba Por lo general, para realizar la reparación de averías se cuenta con un número limitado de vehículo, dicha flota puede ser heterogénea tomando en consideración las posibilidades técnicas y de capacidad que puede presentar cada vehículo. Por otra parte, las averías que se pueden presentar en una red de distribución eléctrica tienen, en la mayoría de los casos, prioridades de reparación diferente, este aspecto además de complejizar el proceso de optimización es de extraordinaria importancia para el análisis de la factibilidad en las soluciones alcanzadas. Al existir diferentes tipos de averías esto implica desigualdad significativa en los tiempos de reparación de dichas averías. Otra de las particularidades de relevancia en este tipo de problemática es la ocurrencia de una avería inesperada, es decir, una vez que ya fueron planificados los recorridos, para aquellos vehículos que realizan las reparaciones, ocurre inesperadamente una avería con cualquier nivel de prioridad. Este tipo de suceso exige la inserción lógica, económica y técnicamente factible de la avería inesperada por el método de 12.

(21) Capítulo I. optimización que sea propuesto. Como se puede apreciar esta problemática presenta sus propias características, las cuales precisan de la concepción y desarrollo de modelos de optimización que posibiliten brindar soluciones factibles y de calidad, acordes con el tiempo real del que se disponga para tomar tales decisiones. Diversas investigaciones se han enfocado al estudio de la reparación de averías en redes eléctricas, aunque en su mayoría, en los aspectos técnicos y tecnológicos que estas reparaciones implican. Los estudios que más sobresalen en esta área son los relacionados con el aseguramiento de medios técnicos y tecnológicos, regulaciones en las longitudes de las líneas de distribución y la superación profesional de los encargados de tales actividades. A pesar de las acciones y disposiciones existentes en el proceso de reparación de averías, se aprecian significativas deficiencias en cuanto a: La Unión Eléctrica de Cuba no ha emitido disposiciones para el proceso decisional relativo a la planificación de recorridos en la reparación de averías que presentan frecuentemente sus redes de distribución. Los estudios en el campo de las reparaciones de averías en redes de distribución eléctrica se han enfocado principalmente al aseguramiento material que implica el adecuado funcionamiento de las mismas, no considerando que la oportuna e inmediata reparación resulta un elemento de extraordinaria importancia en la calidad del servicio brindado.. 1.4 Métodos de solución para VRP Diferentes métodos se han propuesto para solucionar el VRP, estos se clasifican en exactos y aproximados. Varias propuestas de algoritmos exactos son apropiadas en problemas pequeños, según (Olivera, 2004) hasta 50 clientes aproximadamente, pero dado el alto costo computacional no son adecuadas para instancias mayores y en estos casos se usan algoritmos aproximados. Entre los métodos exactos aplicados al VRP se destacan los algoritmos de ramificación y acotación (Branch and Bound, BB). Este es un algoritmo de propósito general en el que se realizan sistemáticas enumeraciones de las soluciones. Subconjuntos de la solución son evaluados respecto a su contribución a la función objetivo, se definen unas cotas inferiores y superiores para cada problema, dependiendo del valor de estas cotas. 13.

(22) Capítulo I. calculado para cada posible subconjunto de solución se decide si se ramifica o no el árbol de soluciones (Nemhauser and Wolsey, 1988). Padberg y Rinaldi (Padberg and Rinaldi, 1991) propusieron un mejoramiento del BB clásico integrándole el método de corte de planos (Branch and Cut, BC). Por otro lado, la combinación del algoritmos de generación de columnas con el BB origina el algoritmo conocido como (Branch and Price, BP) (Christiansen and Lysgaard, 2007). Bard et al (Bard et al., 2002) propusieron un algoritmo BC para solucionar el VRPTW, mientras que Christiansen y Lysgaard (Bard et al., 2002) trataron el VRPSD, para solucionar este problema propusieron un algoritmo BP basado en la descomposición de Dantzig-Wolfe. Otros métodos exactos que destacan en la solución de VRP involucran la relajación langrangiana (Jing-Quan, 2009) y programación dinámica (Righini and Salanil, 2009). Para un compendio completo de métodos exactos para Problemas de Ruteo de Vehículos, puede consultarse los trabajos de Laporte (Laporte, 1992) y de (Kallehauge, 2008), este último hace una revisión de los algoritmos exactos propuestos en las últimas tres décadas para la solución del VRPTW. Debido a la complejidad computacional que presentan los VRP, los métodos aproximados (heurísticos y metaheurísticos) han sido los más estudiados. Los primeros algoritmos empleados en solucionar VRP y que resultaron eficientes fueron los heurísticos. A pesar de que estos no garantizan encontrar la solución óptima, encuentran soluciones cercanas a los óptimos a través de una exploración limitada del espacio solución, para cualquier instancia del problema, en un tiempo generalmente moderado. Las soluciones mostradas por estos métodos pueden ser mejoradas con procedimientos de búsqueda más sofisticados, pero incurriendo en elevados tiempos de ejecución. En esta área destacan el Algoritmo de Ahorro de Clarke y Wright (Clarke and Wright, 1964) y las heurísticas de inserción como las desarrolladas en (Mole and Jameson, 1976) y (Christofides et al., 1979), estos tienen la característica de ser algoritmos constructivos los cuales construyen las soluciones de manera secuencial. Otras heurísticas relevantes son los algoritmos de dos fases. En una primera fase realizan un agrupamiento para después aplicar otro método para la asignación de las rutas a los vehículos. La heurística de barrido (sweep) (Wren, 1971) y la heurística de asignación generalizada de Fisher y Jaikumar (Fisher and Jaikumar, 1981). 14.

(23) Capítulo I. Las heurísticas de búsqueda local son métodos de mejora iterativa en los que generalmente se define una solución inicial o semilla, y una estructura de vecindario; se exploran los vecindarios evaluando su contribución a la función objetivo. Las soluciones se obtienen aplicando procedimientos simples usualmente llamados movidas. En VRP estas movidas pueden ser de una ruta y multi-rutas. En (Olivera, 2004) tratan de manera detallada los procedimientos de búsqueda local aplicados a VRP. Los algoritmos metaheurísticos presentan un mejor desempeño que las heurísticas simples. Estas técnicas realizan una mejor exploración del espacio de soluciones. Existen tres grupos de metaheurísticas que se destacan en la resolución de VRP. Estas son los algoritmos de enjambres, los algoritmos evolutivos y los sistemas inmunes artificiales. Los algoritmos enmarcados en la inteligencia de enjambres, son métodos bioinspirados en el comportamiento de las colonias de insectos generalmente hormigas, abejas y termitas. Estos algoritmos replican el comportamiento colaborativo de estos agentes naturales, lo que les permite realizar tareas complejas que exceden la capacidad de un solo individuo. Dentro de esta categoría de algoritmos se encuentran: la Optimización Basada en Colonias de Hormigas (Ant Colony Optimization, ACO) y la Optimización de Enjambre de Partículas (Particle Swarm Optimization, PSO) (Kennedy and Eberhart, 1995). Existe una amplia relación de trabajos donde aplican ACO a la resolución de VRP estáticos (Chen, 2007b, Chen, 2007a, Colorti and Roizzoli, 2007) y en (Runka, 2009) se aplica a problemas dinámicos. También en (Ai and Kachitvichyanukul, 2009) se aplica PSO al VRP con resultados satisfactorios. Los algoritmos evolutivos imitan el proceso de evolución natural en los que sobreviven los individuos con mayor capacidad de adaptación mientras que los más débiles tienden a extinguirse. Diferentes clases de algoritmos evolutivos han sido aplicados a la solución del VRP destacándose los Algoritmos Genéticos (Alvarenga and Mateus, 2004, Qinghua, 2008, Hanshar and Ombuki, 2005). Los sistemas inmunes artificiales se inspiran en los sistemas inmunes naturales aprovechando la capacidad que tienen para determinar patrones y memorizar para dar rápidas respuestas en el futuro. En esta rama se destacan los trabajos (Hu and Li, 2008, Ma and Hu, 2006) que combinaron sistemas inmunes con algoritmos evolutivos. 15.

(24) Capítulo I. En la actualidad existe una gran cantidad de trabajos que giran sus investigaciones hacia la hibridación (Flisberg, 2009), es decir, combinar diferentes algoritmos para buscar mejores soluciones. Por otro lado, desde hace unos años se ha introducido y examinado exitosamente el concepto de hiperheurísticas en diferentes problemas. Las hiperheurísticas se pueden concebir como una herramienta o metaheurística de alto nivel que permiten controlar adaptativamente varias heurísticas o metaheurísticas de bajo nivel. Estos procedimientos se encargan de elegir en cada momento cual es la metaheurística apropiada y no la solución a un problema. En (Garrido, 2010) se propone una hiperheurística para solucionar un DVRP, obteniendo excelentes resultados.. 1.5 Optimización Basada en Colonias de Hormigas La Optimización Basada en Colonias de Hormigas (Dorigo et al., 1999) (Dorigo and Stutzle, 2004) pertenece a la rama de la Inteligencia Colectiva (Bonabeau, 1999). La Inteligencia Colectiva es un conjunto de técnicas inspiradas en el estudio de comportamientos colectivos presentes en sistemas de la naturaleza, generalmente de carácter descentralizado y auto organizativo. Dicho comportamiento social define los movimientos de las variables de decisión en el espacio de búsqueda y las orienta hacia soluciones óptimas. La expresión “Inteligencia Colectiva” fue introducida por Gerardo Beni, Suzanne Hackwood y Jing Wang en 1989, en el contexto de sistemas robóticos celulares. La principal característica de los algoritmos basados en la Inteligencia Colectiva viene determinada por la estrecha colaboración social que presentan a través del sistema de comunicación que surge entre los individuos del colectivo. La metaheurística ACO tiene su fuente de inspiración en el comportamiento de colonias de hormigas reales. A pesar de las limitadas capacidades de cada hormiga, la colonia logra en forma colectiva realizar tareas de gran complejidad a través de la coordinación entre los individuos. Una de las maneras de comunicación que utilizan las hormigas para lograr tal coordinación de tareas es en forma indirecta y consiste en realizar modificaciones en su entorno3. Como las hormigas tienen una visión escasa, la comunicación se realiza mediante el marcado en el suelo de rastros que sirven de. 3. A este concepto se le llama stigmergy en la literatura científica y se suele traducir al castellano como estigmergia.. 16.

(25) Capítulo I. referencia a otras hormigas, a través de la liberación de una sustancia química llamada feromona4. Este procedimiento se basa en una colonia de hormigas artificiales; esto es, unos agentes computacionales simples que trabajan de manera cooperativa y se comunican mediante rastros artificiales de feromona. Los algoritmos de ACO son esencialmente métodos constructivos: en cada iteración del algoritmo, cada hormiga construye una solución al problema. Las hormigas. construyen. las. soluciones. de. manera. probabilística. teniendo en cuenta dos tipos de información: Información heurística, mide la preferencia heurística de moverse desde el nodo r hasta el nodo s; es decir, la propensión a recorrer la arista ars. Se denota por ηrs. Las hormigas no modifican esta información durante la ejecución del algoritmo. Información de los rastros artificiales de feromona, mide la “deseabilidad aprendida”5 del movimiento de r a s. Imita de forma numérica a la feromona real que depositan las hormigas naturales. Esta información se modifica durante la ejecución del algoritmo dependiendo de las soluciones encontradas por las hormigas. Se denota por τrs.. 1.5.1 Modo de funcionamiento general El modo de operación básico de un algoritmo de ACO (Dorigo and Stutzle, 2003, Dorigo and Stutzle, 2004, Dorigo et al., 2006) es como sigue: las m hormigas (artificiales) de la colonia se mueven, concurrentemente y de manera asíncrona, a través de los estados adyacentes del problema (que puede representarse en forma de grafo con ponderaciones o sin ellas). Este movimiento se realiza siguiendo una regla de transición que está basada en la información local disponible en las componentes (nodos). Esta información local incluye la información heurística y memorística (rastros de feromona) para guiar la búsqueda. Las hormigas construyen incrementalmente soluciones al moverse por el grafo de construcción. Opcionalmente, las hormigas pueden depositar feromona cada vez que crucen un arco (conexión) mientras que construyen la solución (actualización en línea paso a paso de los rastros de feromona). Una vez que cada hormiga ha generado una 4. La intensidad de esta sustancia disminuye a través de un proceso de evaporación que ocurre en el tiempo de manera constante. 5 Nótese que las hormigas solo se comunican de manera indirecta, a través de modificaciones del espacio físico que perciben. Esta forma de comunicación se denomina Estimergia Artificial.. 17.

(26) Capítulo I. solución, ésta se evalúa y el agente puede depositar una cantidad de feromona en dependencia de la calidad de su solución (actualización en línea de los rastros de feromona). Esta información guiará la búsqueda de las otras hormigas de la colonia en el futuro. Además, el modo de operación genérico de un algoritmo de ACO incluye dos procedimientos adicionales, la evaporación de los rastros de feromona y las acciones del demonio. La evaporación de feromona la lleva a cabo el entorno y se usa como un mecanismo que evita el estancamiento en la búsqueda y permite que las hormigas busquen y exploren nuevas regiones del espacio. Las acciones del demonio son acciones opcionales (que no tienen un contrapunto natural) para implementar tareas desde una perspectiva global que no pueden llevar a cabo las hormigas por la perspectiva local que ofrecen. Ejemplos son: observar la calidad de todas las soluciones generadas y depositar una nueva cantidad de feromona adicional sólo en las transiciones/componentes asociadas a algunas soluciones, o aplicar un procedimiento de búsqueda local a las soluciones generadas por las hormigas antes de actualizar los rastros de feromona. En ambos casos el demonio reemplaza la actualización en línea a posteriori de feromona y el proceso pasa a llamarse actualización fuera de línea de rastros de feromona. La estructura general de ACO es como sigue (Dorigo and Stutzle, 2004): Procedimiento meta-heurística ACO; Actividades Programadas Construir Soluciones de las Hormigas Actualizar Feromonas Evaporación de la Feromona Acciones del Demonio (opcional) Fin de las Actividades Programadas Fin del Procedimiento Figura 1.2. Procedimiento general de ACO Este procedimiento se anida en el siguiente procedimiento iterativo:. 18.

(27) Capítulo I. Paso1: Inicializar los valores de feromona iteracionActual=1 Paso2: Repetir Procedimiento meta-heurística ACO iteracionActual = iteracionActual +1 Hasta que: criterio de parada Figura 1.3. Estructura genérica de ACO Para los métodos de ACO existen distintos criterios de parada (Dorigo and Stutzle, 2003), entre los que se encuentran: Se alcanza un número máximo de iteraciones o ciclos. Se obtiene una solución con una calidad deseada. Se alcanza un tiempo límite o predeterminado de procesamiento. Se obtiene un número máximo de evaluaciones de la función objetivo.. 1.5.2 Principales algoritmos En la literatura se han propuesto diversos algoritmos que siguen la metaheurística ACO. Entre los algoritmos de ACO disponibles para problemas de optimización combinatoria NP-hard, se encuentran el Sistema de Hormigas (Ant System, AS) (Dorigo et al., 1996), el Sistema de Colonia de Hormigas (Ant Colony System, ACS) (Dorigo and Gambardella, 1997), el Sistema de Hormigas Max-Min (Max-Min Ant System) (Stützle and Hoos, 2000), el AS con Ordenación (Rank-Based Ant System) (Bullnheimer et al., 1999), el Sistema de la Mejor-Peor Hormiga (Best-Worst Ant System) (Cordón et al., 2000) entre otros.. 1.6 ACO con múltiples colonias El esfuerzo realizado por mejorar el desempeño de ACO se ha reflejado en diferentes investigaciones. En (Puris et al., 2006) se propone la división del procedimiento de trabajo de las hormigas en dos etapas. Existen otras estrategias que se basan en la utilización de múltiples colonias, las cuales cooperan entre sí de manera paralela, intercambiando “algún” tipo de información. Este enfoque ofrece buenos desempeños 19.

(28) Capítulo I. en espacios de búsqueda considerablemente grandes (Aljanaby et al., 2010). En el proceso de búsqueda realizada por las colonias las mejores experiencias encontradas por unas son trasmitidas a otras cada un cierto número de iteraciones. En la literatura revisada existen muy pocos trabajos que apliquen esta estrategia a problemas de ruteo, la mayoría de estos están enfocados a la paralelizar ACO y a la resolución de problemas multi-objetivos donde cada colonia se encargaría de optimizar un objetivo. El primer trabajo de la utilización de múltiples colonias en el área de ruteo de vehículos se recoge en (Gambardella et al., 1999). Se trabaja con dos colonias de hormigas, una de ellas (ACS-VEI) tiene como objetivo minimizar la cantidad de rutas utilizadas y la otra (ACS-TIME) minimizar la longitud total de la solución. Las dos colonias evolucionan en paralelo y cuando alguna encuentra una solución que utiliza menos vehículos que la mejor solución encontrada, ambas son reiniciadas. Un trabajo más reciente es el encontrado en (Ortega et al., 2009), este se asemeja al anterior. En (Yudel, 2010) se introducen algoritmos basados en ACO multicolonias aplicados a problemas de selección de rasgos con múltiples fuentes de datos, obteniéndose excelentes resultados.. 1.6 Consideraciones parciales 1. Los Problemas de Enrutamiento de Vehículos constituyen un campo abierto de investigación que presenta gran importancia en diferentes entornos logísticos, creciendo cada vez más el conjunto de aplicaciones que aparecen en la práctica, trayendo aparejado lo difícil que se hace resolverlos. 2. Los algoritmos de Optimización Basada en Colonias de Hormigas han sido ampliamente estudiados y aplicados a una serie de problemas, incluyendo los Problemas de Enrutamiento de Vehículos, obteniéndose resultados satisfactorios. 3. El proceso decisional vinculado con la reparación de averías eléctricas, usualmente se basa en el aseguramiento profesional, técnico y tecnológico de adecuados niveles de desempeño en las redes de distribución, presentando significativas limitaciones en la concepción e incorporación de las particularidades presentes en la planificación de recorridos que implican tales reparaciones. Además, usualmente se basa en la experiencia y habilidad del personal encargado de esta tarea, debido esencialmente al desconocimiento de herramientas con basamento matemático, las cuales permitan la obtención de soluciones de calidad, acordes con las particularidades de dichas decisiones. 20.

(29) Capítulo I. 4. En el problema de la planificación de rutas para la reparación de averías eléctricas surgen averías en un momento inesperado una vez que ya se ha establecido una planificación inicial, por esta causa constituye un problema dinámico. 5. La variantes ACO con múltiples colonias ha sido pobremente utilizada en la solución de los problemas de ruteo de vehículos pero solamente enmarcadas en la optimización de múltiples objetivos, o en los intentos de paralelizar de ACO.. 21.

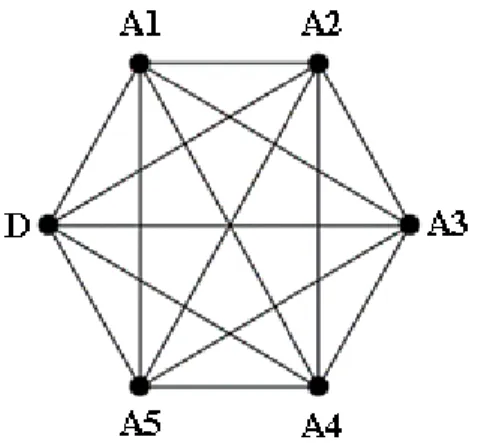
(30) Capítulo II. Capítulo II Optimización Basada en Colonias de Hormigas para el diseño de rutas en la reparación de averías eléctricas 2.1 Introducción En el presente capítulo se detallan los algoritmos de la metaheurística ACO empleados para dar solución al problema de diseño de rutas en la reparación de averías eléctricas. Estos algoritmos son: el Ant Colony System (ACS) y una variante de este, en la que se utilizan múltiples colonias de hormigas cooperando entre sí (M-ACS). Se realiza un estudio comparativo entre los resultados alcanzados por los algoritmos anteriormente mencionados, con el objetivo de seleccionar el algoritmo que brinde mejores resultados.. 2.2 Modelación del problema mediante ACO Todo problema de optimización que pretenda resolverse mediante algoritmos de la metaheurística ACO debe representarse como un grafo ponderado G = (V, A), donde A es el conjunto de aristas que conectan al conjunto de vértices V.. El grafo G se. denomina grafo de construcción, ya que las hormigas construyen las soluciones a través de este. En el problema tratado, el grafo de construcción va ha ser completo, debido a que existen conexiones entre cada par de vértices. El conjunto de vértices lo conforman en primer lugar, el centro de despacho de vehículos, y en segundo lugar el conjunto de averías. El conjunto de aristas va a estar formada por las vías de conexión entre cada par de localizaciones, y va a contener la información útil que será utilizada por las hormigas en el proceso de búsqueda de las soluciones.. Figura 2.1. Grafo completo que representa un posible escenario del problema. A diferencia de las modelaciones que se han hecho de ACO para el TSP, donde se debe encontrar una sola ruta o secuencia de nodos a visitar, en el problema tratado se deben 22.

(31) Capítulo II. encontrar m rutas, una para cada vehículo disponible. Por eso es necesario que las hormigas tengan una estructura de memoria m dimensional, es decir una memoria por cada vehículo. En cada paso realizado por las hormigas estas incorporan a su memoria m nuevos nodos. La matriz de distancia se asume como una matriz simétrica . Cada hormiga debe comenzar su recorrido en el vértice 0, el cual corresponde al despacho. La función heurística se definió de la siguiente forma:. ij. 1 Dist ij Pj. (2.1). donde Pj representa la prioridad de reparación en el nodo j. Esta función permite que se tenga un equilibrio entre la distancia a que se encuentra el nodo j y la prioridad de reparación dada por el nivel de afectación que tenga esta. Esto provoca que el movimiento de la hormiga no se restringa a nodos cercanos, sino que tenga en cuenta la prioridad en cada nodo, siendo esto un factor de gran importancia en el servicio de reparación de averías eléctricas.. 2.3 Descripción del algoritmo ACS para el problema de diseño de rutas en la reparación de averías eléctricas El ACS (Dorigo and Gambardella, 1997) es uno de los primeros sucesores del AS (Dorigo et al., 1996) que introduce modificaciones importantes con respecto a dicho algoritmo de ACO. Este utiliza una regla de transición, denominada regla proporcional pseudo-aleatoria basada en un parámetro q0, que determina la importancia relativa de la explotación frente a la exploración. Esta regla funciona de la siguiente manera: se genera un número aleatorio q de manera que si es menor o igual que q0 se escoge el mejor arco de acuerdo con la expresión de explotación como bien se muestra en la expresión (2.2), de lo contrario, se escoge el mecanismo de exploración dado por la expresión (2.3).. EXPT. arg max EXPR. i, j. i, j. si q dlc. q0. (2.2). 23.

(32) Capítulo II. EXPR. (i, j ) [ (i, j )] (i, j ) [ (i, j )]. si. EXPR J k i (2.3). j J k (i ). 0. dlc. donde:. EXPT : Elección de un arco i, j mediante la explotación (ver expresión 2.2). EXPR : Elección de un arco i, j mediante la exploración (ver expresión 2.3). : Valor de la feromona en el arco i, j . : Valor de heurística hasta nodo j en el arco i, j , (ver Pseudocódigo 2), referido al objetivo de mínimo recorrido. : Parámetro que determina la importancia relativa de la feromona vs heurística.. q : Número aleatorio entre [0,1].. q0 : Parámetro entre [0,1] que determina la importancia relativa de la explotación vs exploración. i : Nodo actual.. j : Nodo a visitar.. J k (i) : Conjunto de nodos que le falta visitar a la hormiga k posicionada en el nodo " i ". Como puede observarse, la regla tiene una doble intención: cuando q ≤ q0, utiliza en gran medida el conocimiento disponible (explotar), eligiendo la mejor opción con respecto a la información heurística y los rastros de feromona. Sin embargo, si q > q0 se aplica una exploración controlada, tal como se hacía en el AS. La condición de finalización del algoritmo se realiza cuando se ha alcanzado un número fijado de iteraciones. A continuación se muestra el algoritmo en forma de pseudocódigo: Pseudocódigo 1: Procedimiento General ACS 1. Fase de inicialización - Inicializar parámetros del Sistema de Colonia de Hormigas y del problema. 24.

(33) Capítulo II. nn. - Obtener una solución inicial gb. -. nn. gb. , donde. con la heurística del Vecino más Cercano. , es la mejor solución global. - L gb ← Longitud total de la ruta perteneciente a la mejor solución. Inicialmente es Lnn - Inicializar el nivel de feromona - Para cada par de nodos i, j :. i, j. 0,. donde,. 0. (n Lnn ). 1. 2. Ciclo realizado por cada hormiga k Do Until IT = N For each Hormiga k k. - Construir una solución empleando If Lk. Lgb. (nueva–hormiga-activa).. j. k. Lgb Then Lk :. gb. k. End if End for IT = IT + 1 Loop 3. Actualización - Realizar actualización global de la feromona. i, j. 1. i, j. / L gb. i, j. gb. N: Cantidad de iteraciones IT: Iteración actual. : Nivel de evaporación global de la feromona. gb. : Mejor recorrido.. Figura 2.2. Pseudocódigo del procedimiento general del Sistema de Colonias de Hormigas. Las hormigas aplican una actualización en línea paso a paso de los rastros de feromona que favorece la generación de soluciones distintas a las encontradas. También realiza una actualización fuera de línea de los rastros de feromona (acción del demonio), donde el ACS sólo considera una hormiga concreta, la que generó la mejor solución global.. 25.

(34) Capítulo II. Pseudocódigo 2: Procedimiento de Nueva Hormiga Activa 1. Inicialización - Ubique la hormiga k en el despacho: - Inicialice Tiempo - actualk. 0. 2. Ciclo para que cada hormiga construya su recorrido. Para la hormiga k ubicada en el nodo i (inicia en el despacho), se determina el conjunto N ik de nodos. Si el nodo i no es el despacho, incluirlo en el conjunto. For each i For each v. N ik. V. - Calcule el nivel de deseabilidad para ambos objetivos de la siguiente manera:. Distij = Máx(1, Re corridoij ) - Seleccione probabilísticamente el siguiente nodo a visitar j empleando. ij. de acuerdo con los mecanismos de explotación y exploración. Expresiones 2.2 y 2.3 - Actualice la ruta v:. k v. - Acumule recorrido: Lk. k. j. v. Lk. Re corridoij. - Actualice localmente la feromona empleando la siguiente ecuación.. i, j. 1. i, j. 0. End for End for V: Cantidad de vehículos. : Nivel de evaporación local de la feromona.. Figura 2.3. Pseudocódigo del procedimiento Nueva Hormiga Activa. La actualización de la feromona se lleva a cabo evaporando primero estos rastros en todas las conexiones utilizadas por la mejor hormiga global (es importante recalcar que, en el ACS, la evaporación de la feromona sólo se aplica a las conexiones de la solución, que es también la usada para depositar feromona). La feromona inicial se calculo a través de la heurística del vecino más cercano de la como indica la expresión 2.4, donde. 0 es. el valor de feromona inicial y Lnn es el valor total. de recorrido a través de la heurística del vecino más cercano (ver Pseudocódigo 2).. 0. (n Lnn ). 1. (2.4) 26.

(35) Capítulo II. Es necesario aclarar que en cada iteración una hormiga encuentra una configuración de recorridos para cada vehículo de los disponibles.. 2.4 Descripción del algoritmo M-ACS para el problema de diseño de rutas en la reparación de averías eléctricas El M-ACS es una forma de Inteligencia Colectiva más avanzada que ACS ya que a diferencia de este cooperan en la búsqueda de una solución m colonias. Este está inspirado en ACS multi-tipo (Nowé et al., 2004). La cooperación se realiza intercambiando los rastros de feromona, es decir, la información memorística. Cada colonia tiene dos matrices de rastros de feromona, una primera que está enfocada a contener los rastros de las soluciones encontradas por las hormigas que pertenezcan a ella, y otra matriz que contiene los rastros de feromona relacionados con las soluciones encontradas por las hormigas de las restantes colonias. La experiencia ganada, expresada mediante los rastros de feromona, se trasmite a las demás colonias. Adicionalmente las colonias intercambian su rastro "frecuentemente". De manera similar al ACS multi-tipo se extienden las expresiones (2.2) y (2.3) como sigue en (2.5) y (2.6):. EXPT. arg max. i, j. i, j. EXPR. si q q0 dlc. (i, j ) [ (i, j )] (i, j ) [ (i, j )]. EXPR. i, j. i, j i. j. si. En estas fórmulas,. EXPR J k i (2.6). j J k (i ). 0. (2.5). dlc. i, j. representa la cantidad promedio de rastro de feromona. perteneciente a otras colonias en el arco i, j . Este es el promedio de todos los rastros de feromona dejado otras hormigas en diferentes colonias realizando la misma tarea para otros conjuntos de datos. La potencia. indica la sensibilidad de la hormiga para. seguir su propia experiencia o la experiencia ganada por el resto de las colonias. Este es un parámetro a ser estudiado, pero claramente si a. se le asigna valor cero las hormigas. calcularán la probabilidad basada en la heurística del problema y la feromona de su propia colonia, tal como el algoritmo original siendo ignorado el rastro de feromona de 27.

(36) Capítulo II. las otras colonias. Si. es incrementado, la probabilidad de seleccionar un nodo se. convertiría cada vez más dependiente de la experiencia del resto de las colonias. En el pseudocódigo siguiente se muestra la descripción del algoritmo. Pseudocódigo 3: Procedimiento General M-ACS 1. Fase de inicialización - Inicializar parámetros nn. - Obtener una solución inicial gb. -. nn. , donde. gb. con la heurística del Vecino más Cercano. , es la mejor solución global. - L gb ← Longitud total de la ruta perteneciente a la mejor solución. Inicialmente es. Lnn For each Colonia s - Inicializar el nivel de feromona - Para cada par de nodos i, j :. i, j. i, j. 0,. donde,. 0. (n Lnn ). 1. End for 2. Ciclo realizado por cada hormiga k Do Until IT = N If IT % N = F Then -Realizar intercambio de feromona entre todas las colonias End if For each Colonia m For each Hormiga k k. - Construir una solución empleando If Lk. Lgb. (nueva–hormiga-activa).. j. k. Lgb Then Lk :. gb. k. End if End for End for IT = IT + 1 Loop 3. Actualización - Realizar actualización global de la feromona. i, j. 1. i, j. / L gb. i, j. gb. 28.

(37) Capítulo II. N: Cantidad de iteraciones IT: Iteración actual F: Frecuencia de intercambios de feromona. : Nivel de evaporación global de la feromona. gb. : Mejor recorrido. Figura 2.4. Pseudocódigo del procedimiento general M-ACS.. El intercambio de la feromona se realiza cada una determinada cantidad de iteraciones realizadas. Este intercambio se realiza como sigue, M representa la cantidad de colonias y el subíndice s la colonia actual:. s. i, j. m m M ;m s. i, j. (2.7). M 1. El procedimiento realizado por cada hormiga es el mismo descrito en el epígrafe anterior en el Pseudocódigo 2.. 2.5 Selección del mejor algoritmo: ACS vs M-ACS Los resultados experimentales encontrados al estudiar algoritmos de la metaheurística ACO a diferentes problemas de enrutamiento de vehículos, son de excelente calidad (Olivera, 2004). La variante de ACO en la que se utilizan múltiples colonias de hormigas ha sido pobremente aplicada a estos problemas. Por esto surge la necesidad de realizar un estudio comparativo entre ACS y M-ACS en cuanto a la calidad de las soluciones encontradas por estos. De esta forma se puede conocer cuál de estas dos variantes obtiene mejores desempeños para luego en el Capítulo III aplicarla a un caso de estudio real. Ambos algoritmos fueron implementados en el lenguaje java JDK 1.6, como entorno de desarrollo (IDE) se utilizó NetBeans 6.5 y fueron ejecutados en un procesador Intel(R) Pentium(R) D a 3.0 GHz, con 1 GB de RAM.. 2.5.1 Caso de estudio: Problema de los m Agentes Viajeros Como se explica en el epígrafe 1.1.2, el m-TSP es una generalización del TSP. Este problema suele ser más complejo de solucionar que el TSP, y el espacio de búsqueda de las soluciones es mucho mayor. El caso especial que será resuelto en esta sección se 29.

(38) Capítulo II. puede definir como: dado N ciudades, M viajeros y la matriz de distancia , donde. , cada viajero puede partir de cualquier ciudad y no tiene la. necesidad de regresar a la ciudad de partida, solo que estas pueden ser visitadas una vez y por un solo viajero. Todas las ciudades deben ser visitadas. El objetivo es minimizar la suma de las distancias recorridas por cada viajero. Las instancias de pruebas utilizadas son citadas en la librería TSPLIB6, y el número de viajeros es de 3, 5, y 7 respectivamente. Debido a la característica estocástica de los algoritmos de ACO, es necesario tener en cuenta que los parámetros pueden influir significativamente en la calidad de las soluciones encontradas por estos. Tanto para ACS como para M-ACS los parámetros fueron:. como se muestra en la expresión (2.3), β = 5, q0 = 0.8, ρ = 0.1 y α = 0.1. El. número de hormigas que se utilizó fue de 10 por cada colonia de M-ACS y 30 para ACS. El algoritmo M-ACS presenta dos parámetros que son cruciales en su comportamiento. Estos son la cantidad de colonias que van a cooperar, y la frecuencia de intercambios de feromona entre estas. Ambos deben ser valores pequeños debido a que valores medianamente grandes pueden disparar la complejidad computacional para encontrar una solución. Se realizó un estudio con 2, 3 y 4 colonias, y frecuencia de intercambio de feromona cada 5%, 10% y 15% del número total de iteraciones, realizando 1000 iteraciones del algoritmo. En la Tabla 2.1 se muestran los resultados obtenidos como promedio en 10 corridas para cada una de las instancias bier127, t225 y rat783 con 3, 5, 7 agentes viajeros cada una. De esta se puede concluir que la mejor configuración se obtiene con 3 colonias y frecuencia de intercambio de feromona cada 10% del número de iteraciones, por los que fueron estos los escogidos para comparar el comportamiento entre ACS y M-ACS.. 6. Accesible desde http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/. 30.