Control PD con compensación precalculada para robots manipuladores

Texto completo

(1)

(2) INSTITUTO TECNOLOGICO Y DE ESTUDIOS SUPERIORES DE MONTERREY CAMPUS MONTERREY DIVISION DE GRADUADOS E INVESTIGACION PROGR.AMA DE GRADUADOS EN INGENIERIA. CONTROL. PD CON COMPENSACION PRECALCULADA PARA ROBOTS MANIPULADORES. TESIS PRESENTADA COMO REQUISITO PARC1AL PARA OBTENER EL GRADO ACADEMICO DE MAESTRO EN CIENCIAS ESPECIALIDAD EN INGENIERIA DE CONTROL. LUIS RlCARDO SALGADO GARZA. DICIEMBRE 1992.

(3) INSTTTUTO TECNOLOGICO Y DE ESTUDIOS SUPERIORES DE MONTERREY CAMPUS MONTERREY DIVISION DE GRADUADOS E INVESTIGACION PROGRAMA DE GRADUADOS EN INGENIERIA. CONTROL PD CON COMPENSACION PRECALCULADA PARA ROBOTS MANIPULADORES. TESIS. PRESENTADA COMO REQUISITO PARCIAL PARA OBTENER EL GRADO ACADEMICO DE MAESTRO EN CIENCIAS ESPECIALIDAD EN INGENIERIA DE CONTROL. LUIS RICARDO SALGADO GARZA. DICIEMBRE DE 1992. 507046.

(4) INSTITUTO TECNOLOGICO Y DE ESTUDIOS SUPERIORES DE MONTERREY CAMPUS MONTERREY DIVISION DE GRADUADOS E INVESTIGACION PROGRAMA DE GRADUADOS EN INGENIERIA. Los miembros del comité de tesis recomendamos que la presente tesis del Ing. Luis Ricardo Salgado Garza sea aceptada como requisito parcial para obtener el grado academico de Maestro en Ciencias especialidad en: INGENIERIA DE CONTROL Comité de tesis. Dr. Rafael Kelly Mtz.. Dr. Rogelio Soto Rdz.. ASESOR. SINODAL. Dr. Jorge A. Olvera Rdz SINODAL. APROBADO POR UNANIMIDAD. Dr. Federico Viramontes Director del Programa de Graduados en Ingenieria Diciembre de 1992.

(5) i. Resumen El presente documento establece una metodología de sintonización para las ganancias del controlador PD con compensación precalculada para robots manipuladores, mostrando en forma explícita las directivas de diseño del controlador. Un primer acercamiento de la utilización de este controlador en robots manipuladores se presenta en el estudio del controlador aplicado a una articulación rotacional, en donde utilizando el método directo de Lyapunov se logra finalmente concluir la estabilidad asintótica local del origen de la ecuación en malla cerrada. La teoría de sistemas perturbados se utiliza para plantear un análisis preliminar sobre la robustez de este controlador ante incertidumbre paramétrica. Para el análisis del controlador aplicado a robots de n grados de libertad se utiliza una nueva función de Lyapunov, con la cual se efectúa un análisis riguroso para concluir la estabilidad asintótica local del origen del sistema en malla cerrada..

(6) ii. Dedicatoria. A Dios, nuestro señor, por darmee la oportunidad de llegar hasta este punto de mi vida.. A mis padres, que tanto los quiero.. A la memoria de mis abuelos maternos.. A mis abuelos paternos..

(7) iii. Agradecimientos. Quiero expresar mi especial agradecimiento al Dr. Rafael Kelly, por su invaluable ayuda en la dirección de esta tesis. Deseo remarcax el profesionalismo del Dr. Kelly, ya que a pesar de su cambio del Instituto su entusiasmo en este estudio nunca disminuyo.. Deseo hacer patente mi agradecimiento al Dr. Rogelio Soto, cuyas sugerencias enriquecieron el contenido de este documento.. Un cordial agradecimiento al Dr. Jorge A. Olvera, cuyo apoyo en el transcurso de mi maestría me ha dado la confianza para seguir adelante en mi vida profesional.. Agradezco a mis companeros de la maestría por sus oportunos comentarios sobre mi trabajo de tesis..

(8) Capitulo 1 Introduccion Durante la decada de los 80's, la creciente demanda por mayor rapidez y precision de los sistemas involucrados en los procesos de manufactura hicieron evidente la necesidad de incrementar la investigation destinada a introducir tecnologias mas eficientes en la produccion. El gran impulso que durante los liltimos anos ban recibido los campos teoricos y aplicados de la robotica es debido a que un gran numero de industrias han incorporado robots manipuladoree en operaciones tan diversas como: pintura automatizada, pulido y ensamblado de piezas, etc. La importancia de optimizar la operation de los robots manipuladores estriba en que entre mas exactos scan sus movimientos se obtendra mayor calidad en los productos que se fabriquen. De este modo, el area de control de robots manipuladores es de gran importancia para los procesos de produccion y, desde cl punto d« vista academico, plantea un problema interesante de control. Un robot manipulador puede ser analizado desde dos perspectives Para la ingonierfa mecanica, un robot es un sistema mecanico constituido por eslabones conectados a traves de uniones formando una cadena cinematica. Por otra parte, desde el punto de vista de control automatico, un robot manipulator es un sistema dinamico no-lineal, multivariable. De esta forma, el control de un robot manipulador plantsa un problema interesante: determinar las condiciones bajo las cuales un esquema de control puede hacer cumplir los requerimientos de funcionamiento que el usuario indique para un robot especifico. Durante la decada de los 80's, diversos investigadores propusieron estrategias avanzadas de control para robots manipuladores, entre las que se pueden mencionar: • Control adaptable de robots. • Control de robots con eslabones flexibles. • Control de robots con uniones flexibles. • Control de fuerza. • Control de impedancia. 1.

(9) 2. Capitulo 1. Introduction. Sin embargo, existen metodologfas motivadas en dos objetivos clasicos y primordiales, control de posicion y control de movimiento. Entre los controladores de robots capaces de satisfacer dichos objetivos de control, podemos mencionar: Control par calculado, Control PD con compensacion (Slotine y Li (1987)), Control PD+ (Paden y Panja (1988)), Control PD con compensacion precalculada y retroalimentacion no-lineal (Sadegh y Horowitz (1990)) y Control PD con compensacion precalculada; sin embargo, con excepcion del ultimo, para los restantes ha podido ser comprobada la estabilidad asintotica (o exponencial) global del origen, en malla cerrada. La importancia del controlador PD con compensacion precalculada estriba en que reduce el niimero de operaciones aritmeticas en tiempo real. Basicamente, los unices parametros de diseno de este controlador lo constituyen sus ganancias proporcional y derivativa, incorporadas en una estructura PD convencional. Por otra parte, esta ley de control incluye terminos derivados de la estructura del manipulador, siendo posible calcular sus valores fuera de linea, simplificandose asi su implementation para el caso en que las trayectorias son repetitivas. Es notable el hecho de que el controlador PD con compensacion precalculada se reduce al control PD con compensacion de gravedad para el caso de control de posicion. Diversos estudios sobre la estabilidad del control PD con compensacion precalculada ban sido realizados por Wen y Bayard (1988), Paden y Riedle (1988) y Wen (1990). En general, las conclusiones derivadas en estos trabajos pueden resumirse como sigue: el origen del sistema de control en malla cerrada es local exponencialmente estable si las ganancias proporcional y derivativa se seleccionan lo suficienlemente grandes. Algunos trabajos experimentales realizados por An et al (1988) y Kokkinis y Stoughton (1991), confirman los resutados teoricos sobre las ganancias del controlador, obteniendose desempenos no solo superiores a la estrategia PD convencional, sino comparables en exactitud a los obtenidos usando par calculado. A pesar de ello, estos trabajos no determinan en forma explfcita las directives de diseno del controlador, por lo que es necesario establecer una metodologia de diseno consistente en la obtencion de sus parametros y a la vez simple en su estructura. El objetivo del presente estudio es mostrar una metodologia mediante la cual se puedan obtener valores explfcitos de diseno para los parametros del controlador PD con compensacion precalculada aplicado a robots manipuladores de n grades de libertad (g.d.l.), en forma tal que pueda demostrarse rigurosamente la estabilidad asintotica local del origen del sistema en malla cerrada, estudiando especificamente el caso de control de movimiento. El material que cubre este documento pretende estar autodocumentado en lo relative a la metodologia matematica empleada en la derivation de propiedades; sin embargo, la presentation del modelo generalizado de robots utiliza propiedades que pueden ser consultadas en la literatura existente sobre este topico, por ello linicamente se incluyen las demostraciones cuya localization no sea inmediata en las fuentes de information externas. El resto del presente documento de tesis esta organizado de la siguiente manera..

(10) El capitulo 2, presenta en forma condensada la metodologia para la obtencion del modelo dinamico de robots, basada en las expresiones para las energfas cinetica y potencial de la estructura mecanica del manipulador; adicionalmente, se incluyen algunas de las propiedades del modelo general y ejemplos de la derivation de los parametros de tres modelos de robots. El capitulo 3 presenta un analisis riguroso sobre la estabilidad del controlador PD con compensation precalculada aplicado a una articulacion rotacional, de donde se obtienen los parametros del controlador que garantizan la estabilidad asintotica y exponencial local en malla cerrada, incluyendose simulaciones y un estudio preliminar sobre la estabilidad de este esquema de control ante incertidumbre parametrica en el modelo. El capitulo 4 aborda el estudio de la estabilidad del control PD con compensation precalculada aplicado al caso de robots de n g.d.l., obteniendose los parametros del controlador que garantizan la estabilidad asintotica local del sistema en malla cerrada; para corroborar los resultados teoricos, se presentan simulaciones computacionales con robots de 2 y 3 g.d.l. Las conclusiones finales sobre este trabajo estan contenidas en el capitulo 5, en donde, adicionalmente, se destacan algunos de los temas mas relevantes que podrian servir como futures topicos de investigation. Finalmente, las referencias y los apendices se presentan al lector como extension y apoyo al material utilizado en este estudio..

(11) Capitulo 1. Introduction.

(12) Contenido 1 Introducción. 1. 2 Modelado dinámico y propiedades 2.1 Modelado dinámico 2.1.1 Ecuaciones de movimiento de Lagrange 2.1.2 Ecuación dinámica de robots de n g.d.l 2.2 Propiedades 2.3 Casos de estudio 2.3.1 Articulación rotacional 2.3.2 Robot manipulador de 2 g.d.l 2.3.3 Robot manipulador de 3 g.d.l. 5 6 6 6 8 11 12 13 15. 3 Control PD con compensaci6n precalculada de una articulación rotacional 3.1 Ecuación en malla cerrada 3.2 Análisis de estabilidad asintótica 3.2.1 Equilibrio único 3.2.2 Estabilidad asintótica 3.3 Estabilidad exponencial 3.4 Robustez ante incertidumbre paramétrica 3.5 Simulaciones con una articulación rotacional 3.5.1 Simulación: modelo sin incertidumbre paramétrica 3.5.2 Simulación: modelo con incertidumbre parametrica. 19 19 20 21 22 27 32 34 34 37. 4 Control PD con compensacion precalculada de robots de n g.d.l. 4.1 Modelado dinamico y propiedades 4.2 Ecuacion en malla cerrada 4.3 Unicidad del equilibrio 4.4 Estabilidad asintotica 4.5 Simulaciones 4.5.1 Robot de 2 g.d.l 4.5.2 Robot de 3 g.d.l. 39 40 41 42 43 46 46 50. Conclusiones. 55 V.

(13) vi. Contenido. Apendices. 57. A. 57. B. 63. C. 69. D. 71. E. E.I E.2 E.3 E.4. 75 Listado: Articulacion rotacional 75 Listado: Articulacion rotacional con incertidumbre parametrica . . . 76 Listado: Robot de 2 g.d.l 77 Listado: Robot de 3 g.d.l 83. Referencias. 93. Vita. 95.

(14) Capftulo 2 Modelado dinamico y propiedades Un robot manipulador es un sistema mecanico formado por eslabones unidos mediante articulaciones. Para nuestro estudio, nos restringiremos al analisis de robots manipuladores cuyos eslabones formen una cadena cinematica abierta. Antes de iniciar el estudio de estabilidad del controlador PD con compensation precalculada debemos contar con una ecuacion que represente el modelo matematico del sistema de estudio, para ello tenemos dos herramientas: el modelo cinematico y el modelo dinamico de un robot. Ambos modelos son indispensables para llevar a cabo una aplicacion; sin embargo, sus cualidades como herramientas de diseno son sumamente distintas. El modelo cinematico de un robot establece las relaciones matematicas entre las posiciones, velocidades y aceleraciones angulares de cada articulation y sus correspondientes contrapartes en el espacio cartesiano. Este modelo es utilizado en simulaciones y en aplicaciones donde se requieren efectuar operaciones en el espacio cartesiano. Por otra parte, una herramienta muy util en el analisis de estabilidad de una estrategia de control es el modelo dinamico del sistema, ya que describe las relaciones entre la cinematica del robot y las fuerzas y pares que actiian sobre cada articulacion. Para entender el modelo dinamico de un robot manipulador se debe estar familiarizado con dos cantidades fisicas: la energia cinetica y la energia potencial. Estas cantidades se utilizan para obtener las ecuaciones dinamicas del sistema, empleando para ello las ecuaciones de movimiento de Lagrange (Spong y Vidyasagar (1989)). Esta section presentara la metodologfa general para la obtencion del modelo dinamico de un robot manipulador, obteniendose una ecuacion dinamica para el caso general. Finalmente, se presentan algunas de las propiedades mas relevantes del modelo general, que seran de utilidad en la demostracion de teoremas en los capitulos subsiguientes..

(15) 6. 2.1. Capitulo 2. Modelado dinamico y propiedades. Modelado dinamico. La estructura de los robots considerada en este estudio consiste en n eslabones unidos a traves de articulaciones, en donde a cada una corresponde uno de los n grades de libertad (g.d.l.) del manipulator. Los eslabones se numeran en orden creciente a partir del eslabon unido al piso (eslabon 1); asf mismo, las articulaciones se numeran respecto a los eslabones que unen, es decir, la articulacion i conecta los eslabones t e t — 1. Es necesario saber que el robot posee dispositivos mecanicos o electronicos, asociados a cada articulacion que generan informacion sobre las posiciones, velocidades y aceleraciones angulares (g,- € 5R, <fr € SR, q\ € 3t, donde t = l,...,n, respectivamente) . Antes de presentar la ecuacion dinamica generalizada para robots de n g.d.l. se presenta la metodologia para la obtenci6n de las ecuaciones de movimiento de la Lagrange, en funcion de las energias cinetica y potencial asociadas a un robot.. 2.1.1. Ecuaciones de movimiento de Lagrange. La energia total E de un robot manipulator de n g.d.l. se compone de la suma de sus energias cinetica K y potencial U:. donde q(t) = (qi (t),.. .,qn(t)f. Sea q(t) G 8?" y q(t) € 3?n, el Lagrangeano L(g, q) de un robot esta dado por la diferencia entre su energia cinetica y su energia potencial de la siguiente forma: (2.1). Utilizando el Lagrangeano se puede derivar la ecuacion de torques para cada articulacion, esta expresion esta dada por: dL. ¥. = r< 1=. 11. ....."'. (2.00 2).. '. donde r,- representa las fuerzas y pares actuantes sobre cada articulacion.. 2.1.2. Ecuacion dinamica de robots de n g.d.l.. La energia cinetica de un robot manipulador de n g.d.l., cuyas articulaciones carecen de friccion y elasticidad, esta dado por la siguiente expresion:.

(16) 2.1 Modelado dinamico. 7. donde H (q) es una matriz simetrica definida positiva, con dimension n x u, llamada matriz de inercia. De esta forma, el Lagrangiano queda determinado por:. Ahora, la ecuacion de torques articulares (2.2) puede expresarse como:. Por otra parte, es inmediato comprobar que:. — (-•TH( } • } -i' 3 Sustituyendo las expresiones anteriores, la ecuacion de movimiento toma la forma. 'U(A. d<i " simplificando se obtiene. donde. Es importante notar que la ecuacion (2.3) es una ecuacion vectorial diferencial no-lineal en el estado [q q]. El vector C(q, q)q tiene dimension n x 1 y es llamado vector de fuerzas centrifugas y de Coriolis, g (q) es un vector de n x 1 conocido como vector de fuerzas o pares gravitacionales y r es un vector de n x 1 llamado vector de fuerzas externas generalizadas..

(17) 8. Capitulo 2. Mode/ado dinamico y propiedades. 2.2. Propiedades. Los terminos del modelo dinamico (2.3) exhiben caracterfsticas que son utiles durante su manipulation algebraica en el diseno de controladores. En seguida se presentan algunas de las propiedades que seran utilizadas en los subsiguientes capftulos de este estudio. Propiedad 2.1 La matriz de inertia H (q) es una matriz simetrica defmida positiva de n x n, cuyos elementos son funciones unicamente de q. Asimismo, la matriz H (q)~ existe y es definida positiva. VVV. Propiedad 2.2 La matriz de fuerzas centrifugas y de Coriolis C (q, q) posee como elementos funciones de q y q. Ademas, la matriz C (q, q) satisface las siguientes propiedades:. 3kc>0:\\C(q,q)\\<kc \\q. • La matriz de inercia H (q) y la matriz C (q, q) estan relacionadas por la siguiente expresion:. donde la matriz ^H (q) — C (q, q) es una matriz antisimetrica, por lo cual es posible obtener la siguiente relacion:. VVV. Propiedad 2.3 El vector de pares gravitacionales g (q) depende solo de las posiciones articulares q. El vector g (q) es acotado si q tambien es un vector acotado. VVV. Las propiedades enunciadas anteriormente se cumplen para robots manipuladores de n g.d.l. y se utilizaran extensivamente a lo largo de este estudio; sin embargo, es.

(18) 2.2 Propiedades. 9. necesario establecer propiedades adicionales que nos ayudaran a establecer cotas superiores sobre expresiones que resultan de especial interes. Antes de presentar estas propiedades es necesario mencionar tres lemas que se utilizaran en su demostracion. Lema 2.1 Considerese el vector x e !Rn. La norma Euclidiana \\x\\ satisface: \\x\\ < n ( m a x < | ar,- |). vvv Lema 2.2 Considerese la matriz siraetrica A = AT € R n x n y sea otj su ij-esimo elemento. La nonna Euclidiana \\A\\ de la matriz A satisface: \\A\\ =. T. max(A. A) < n 2 (max tj \ % I). VVV Lema 2.3 Considerese la matriz A €. !Rnxn y siendo ay a su ij-esimo elemento, Sean AI, ..., An sus valores propios. Entonces se satisface que: I A,- |< n2 (max <j | ay |). Vi = 1,..., n. VVV Otro resultado importante que sera empleado en esta seccion es el teorema del valor medio, cuyo enunciado se presenta a continuation. Teorema 2.1 Teorema del valor medio. Considerese la funcion continua / : §£n —» 3?. Si / (zi,z2,..., zn} tiene derivadas parciales continuas, entonces para dos vectores constantes x, y € 3?" se tiene que:. - y) donde £ € 8?" es un vector convenientemente seleccionado en el segmento de h'nea que une los vectores x y y, y que en consecuencia satisface: £ = x + a (y — x). para algiin a en el intervalo [0,1]. Notese que la norma de £ satisface:. lltll < Ml + llv - *ll VVV.

(19) Capitulo 2. Mode/ado dinamico y propiedades. 10. A continuacion se presentan propiedades referentes al acotamiento de algunos de los terminos de la ecuacion de malla cerrada. Propiedad 2.4 Sea H (q) la matriz de inercia de un robot evaluada en q, donde q (E 5R". Para todo vector a:, y, z e SJ" se cumple que: \\H(x}z-H(y}z\\<kH\\x-y\\ \\z\\ donde: 'CH > n2 (max <jiJt>,. VVV. Propiedad 2.5 Sea C (g, q) la matriz de fuerzas centripetas y de Coriolis de un robot evaluada en (g, g), donde g, q € R n . Para todo vector v, x, y, z, w € 3?" se cumple que: ||C Or, *) „, - C (y, v) w\\ < kCl \\z - v\\ \\w\\ + kCt (\\z\\ + \\v-z\\) \\x - y\\ \\w\\ donde las constantes no negativas k^ y kc, toman la forma: kci kCy. n. (max. Ckij (q)\) dCkii (q) = n 3 [max IJiMi, dqi. =. VVV Propiedad 2.6 Sea g (q) el vector de terminos gravitacionales de un robot evaluado en q, donde q € 9£n. Para todo vector x, y, z € §?n se cumple que: \\9(x)-g(y)\\<kg. \\x-y\\. donde: kga>nl max. dqj. VVV.

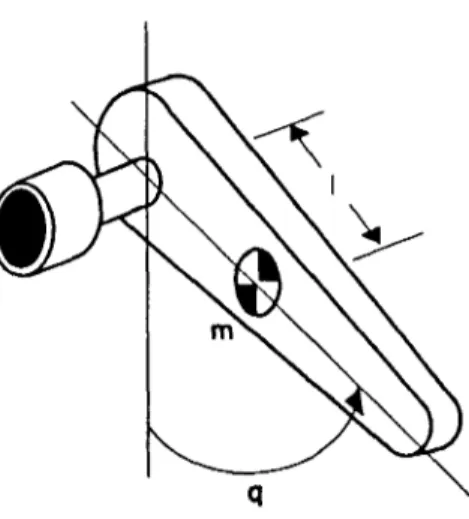
(20) 2.3. Casos de estudio. 11. Figura 2.1: Esquema mecanico de una articulacion rotacional. Las demostraciones de estas propiedades pueden ser consultadas en detalle en el apendice B de este documento.. 2.3. Casos de estudio. Hasta ahora, se ban presentado los preliminares matematicos que se utilizaran en la demostracion de estabilidad del controlador PD con compensacion precalculada, dejando hasta este apartado la presentacion inicial de problemas especlficos de diseno. A pesar de que el contenido teorico de este documento es aplicable al caso general de robots manipuladores de n g.d.l. (en con figuacion de cadena cinematica abierta), resulta de especial interes corroborar los resultados mediante simulaciones computacionales de los sistemas de estudio. Aunque se podrfan generar un sinumero de ejemplos de robots, es importante analizar la estabilidad del controlador aplicado a las tres configuraciones mas basicas de manipuladores: una articulacion rotacional, un robot de 2 g.d.l. y un robot de 3 g.d.l..

(21) 12. Capitulo 2. Mode/ado dindmico y propiedades. El analisis de estabilidad inicia en esta seccion con la presentation de los parametros A;/,, fcc,, kc2 y kg correspondientes a cada una de las estructuras de los casos de estudio.. 2.3.1. Articulacion rotacional. El caso mas simple de control de un robot manipulador lo constituye el control de una articulacion rotacional. En este caso, el sistema robotico esta formado por un unico eslabon, a cuyo eje de rotacion se encuentra acoplado un motor (figura 2.1). Sean m la masa del eslabon, / la distancia entre el eje de giro y el centro de masas del eslabon, q la posicion angular del eslabon respecto a la vertical y g la acceleration de la gravedad. La energfa cinetica K (9, q) y potencial U (q) del sistema quedan expresadas como:. K(q,q) U(q). = -mf =. mgl(l-cos(q)). Aplicando la ecuacion (2.1) se obtiene:. , q) =. m. ^ ~ m9l (1 ~ cos. de donde se pueden obtener las siguientes expresiones:. dL -z-r = mq dq. 9L. I / A -— = -mglBen (q) dq.

(22) 2.3 Casos de estudio. 13. Figura 2.2: Esquema mecanico de un robot de 2 g.d.l. Asi, la ecuacion de movimiento (2.2) toma la siguiente forma: mq + mglsen (q) = r donde r representa la fuerza ejercida sobre el eje de la articulacion. Es importante senalar que en este caso, la rnatriz de incercia H (q) como el vector de terminos gravitacionales g (q) se reducen a una constante y especificamente no existen terminos de Coriolis asociados a la ecuacion, de modo que los parametros de este sistema quedan expresados de la siguiente forma: kH. = 0. kCl. = 0. kc> = 0 kg = mgl. 2.3.2. (2.4). Robot manipulador de 2 g.d.l.. Otra estructura de robotica de interes es la formada por dos eslabones unidos mediante una articulacion rotacional; en este caso, unc de los eslabones posee otro eje de giro en el extremo opuesto al que se une con el segundo eslabon, formando asf un robot de 2 g.d.l. (figura 2.2). Considerese m,- la masa del eslabon i, L,- la longitud total del eslabon z, /Ci la distancia entre el eje de giro y el centro de masas del eslabon i, /,• el momento de inercia del eslabon i, g la aceleracion de la gravedad, para i = 1,2; donde q 6 9ft2 representa el vector de posiciones articulares. La energia cinetica y potencial del robot estan dadas por:.

(23) 14. Capitulo 2. Modelado dinamico y propiedades. donde: 2. Cj. (q\ + qiq. cos (q2). 2/2(91+92). U\(q) = U2 (q) = m20(Lisen (qi) + /^sen (91 + 92)) Obteniendo el Lagrangeano (2.1), la ecuacion de movimiento toma la forma (2.3), en donde la matriz de inercia H (q), la matriz de Coriolis C (q, q) y el vector de tenninos gravitacionales g (q) estan dados por:. (H Hnn(q) (q) \H2i(q). H12 (q)\..+ /C H Cnn(q,q) (q,q) 12(q)\ H22(q)J \C2i(q,q). Ci (q,q)\ C 122(q,q)\ C22(q,q)J q. 9l(q). donde: #ii(9) = (q2) + I\ + I2 #12 (q) = ™2l^ + m2L1/Cjcos (q2) + I2 H2\ (q) = m2/J + mîl^cos (q2) + I2 H22 (q) = m2^ + 72. 219,9 = m ^ s e n C22(q,q) = 0 gi(q) = miglClcos(qi) +m2glcjcos(qi +q2) g2(q) =.

(24) 2.3 Cases de estudio. 15. Asimismo, el vector de terminos de Coriolis C (q, q) q puede descomponerse de la siguiente fonna: T. '. /maL^senCfc). v. o. 0\. o;. De las expresiones anteriores, con n = 2 (2 g.d.l.) y de las propiedades 2.4, 2.5 y 2.6 se pueden obtener los siguientes parametros:. kg. =. kg = 2g(milCl + m2Li + m2/c2). 2.3.3. (2.5). Robot manipulador de 3 g.d.l.. En general, las operaciones de los robots industrials no se restringen a movimientos en un piano (2 dimensiones) sino que se definen en el espacio tridimencional, es por ello la importancia de analizar manipuladores de 3 o mas grados de libertad. Para efectos de esta simulacion, considerese una estructura robotica formada por tres eslabones rigidos y tres articulaciones rotacionales. El eslabon 1 se une al suelo mediante la articulacion 1, la cual puede girar sobre un eje perpendicular al piso (eje de giro 1). La articulacion 2 une los eslabones 1 y 2 de modo que puede rotar sobre un eje 2, perpendicular al eje de giro 1. Finalmente, la articulacion 3 une a los eslabones 2 y 3, realizando rotaciones sobre un eje 3, paralelo al eje de giro 2 (figura 2.3). Sea m,- la masa del eslabon f , L,- la longitud total del eslabon i, /Ci. la distancia entre el eje de giro y el centro de masas del eslabon t , /,• el momento de inercia del eslabon i, g la aceleracion de la gravedad, para t = 1, 2, 3; donde q 6 9ft3 representa el vector de posiciones articulares. En este caso, los momentos de inercia de los eslabones superiores afectan la dinamica del eslabon unido a la base, de modo que las energia cinetica y potencial del robot estan dadas por:. K(q,q). U(q). donde:. =. K^fi. = Ul(q) + U2(q) + U3(q. 527941.

(25) Capitulo 2. Modelado dinamico y propiedades. 16. Figura 2.3: Esquema mecanico de un robot de 3 g.d.l.. .(«,*) = \h% (q, q) = - ((/3 + m3L32) sen2 (q2 + q3) + m3L22sen2 (q2) +2m3L2/C3sen (q2) sen (q2 + q3)) q\ + m3/c,2 + m3L22 4- 2m3L2/Cjcos(93) q\. + m3/C3 + m3L2/C3cos ( Ui (q) = mi0/Cl + m2g (l^cos (q2) + LI) +m3g (L2cos (q2) + lC3cos (q2 + q3) + LI ) Con estos datos se puede expresar el Lagrangeano en forma compacta como: L(q,q) = K, (q,q) + K2(q,q) + K3(q,q) - U, (q) - U2(q) - U3(q) De esta ultima expresion se puede obtener la ecuacion dinamica de movimiento, que para este manipulador toma la forma de la ecuacion (2.3), donde H (9), C (q, q) €E g(q) eft 3 ..

(26) 17. 2.3 Casos de estudio. La matriz de inercia H (q) es simetrica definida positiva y esta constituida por los siguientes elementos: #11 (q) = Ii + (/2 + m2/c,2) sen2 ( ft ) + (/3 + m3/cj2sen2 (q2 + ft)) m3L22sen2 (g2) + 2m3L2/Cjsen (q2) sen (g2 + q3) m3/C32 + m3L22 #22 (?) = #23 (?) = /a + m3/cj2 + m3£,2fc,cos (q3) #33(9) = /3 donde los terminos restantes son cero. El vector de fuerzas centrffugas y de Coriolis C (0> 9) 9 puede expresarse como: ft. ft. 92. 92. ft,. \. ,ft. ft 92 : ft,. 9i 9.2. ft, 9i. f. 331. 92. •. ft. '. 92. V \ft,. i Oi 3J ,. donde: + m3/c,,2) sen (q2. Ci12 = (I2m2l^) sen m3L22sen(<72)cos C Ui. cos. q3). m3L2/Cjsen. s~% — t/i,_. m3L22) sen (?2) cos (/3 + m3/cj2) sen (g2 + ^3) cos (q2 + C223. + m3L2/Cjcos (?2) sen (q2 + ft) +. m3L2/C3sen (^2) cos (q2 + q3) = -m3L2/C3sen(?3) -Tn3L2lC3seu(q3). ^332. =. (fs + ™31C32) sen (q2. cos (q2 + q3). +m3L2lC3sen (q2) cos. q3) - m3L2/C3sen (q3). ^332.

(27) 18. Capitulo 2. Modelado dinamico y propiedades. y los elementos no mencionados son cero. El vector de terminos gravitacionales g (q) tiene como elementos: 9i (?) = 0. Haciendo uso de las propiedades 2.4, 2.5 y 2.6 se obtienen las siguientes constantes para el manipulador: ka = 1. kg = S^â/Q+mgLa + mg^). (2.6).

(28) Capftulo 3 Control PD con compensation precalculada de una articulacion rotacional El objetivo de este capftulo es analizar en detalle el control PD con compensation precalculada del mas sencillo artefacto robotico: una articulacion rotacional. Aunque sorprendente por la aparente sencillez del objetivo formulado, este planteamiento no ha sido abordado en forma rigurosa con anterioridad en la literatura. Igualmente, parece razonable resolver primeramente tal formulacion como requisite previo al problema de robots manipuladores de n grades de libertad. Los resultados que se presentan al final del capftulo permiten, en forma clara y concisa, establecer polfticas de diseno que garantizan la estabilidad asintotica del sistema de control en malla cerrada. Especfficamente, se proporcionan condiciones sobre las ganancias de posicion y velocidad, las cuales dependen, por supuesto, del modelo dinamicc de la articulacion rotacional.. 3.1. Ecuacion en malla cerrada. En este capftulo se considera el caso mas sencillo de un dispositive robotico: una articulacion rotacional, cuyo modelo dinamico esta dado por: m!2q + mgl sen(g) = r. (3.1). donde q € 3? denota la posicion angular del eslabon de la articulacion rotacional con respecto a la vertical, m es la masa del eslabon, / es la distancia entre el eje de giro y el centro de masa del eslabon, g es la aceleracion de la graveded y T es el par aplicado en la articulacion. 19.

(29) Capitulo 3. Control de una articulation rotational. 20. Controlador]-*-. Figura 3.1: Esquema del controlador PD con compensacion precalculada Para este modelo dinamico en particular, la ley de control PD con compensacion precalculada toma la forma: T = kpq + kvq + m/2^ + mgl sen(^). (3.2). donde kp y kv son los parametros de diseno del controlador los cuales deben ser conveuientemente seleccionados y q = qj, — q denota el error de posicion con qj siendo la posicion angular deseada (generalmanete es una funcion continua en el tiempo). Un esquema de la ecuacion del controlador en malla cerrada se visualiza en la figura 3.1, donde se puede apreciar que las ganancias proporcional y derivativa del controlador afectan directamente a la entrada de voltaje del motor. En las siguientes secciones se presentara en detalle un estudio de la ecuacion de malla cerrada que caracteriza el comportamiento de la articulacion rotacional (3.1) bajo el control PD con compensacion precalculada (3.2). El estudio de dicha ecuacion ha sido realizado con anterioridad por Kelly et ol (1991) pero aqui es presentado empleando un enfoque diferente que permite obtener lineamientos explfcitos de diseno.. 3.2. Analisis de estabilidad asintotica. La representation en variables de estado de la ecuacion de malla cerrada de la ley de control PD con compensacion precalculada (3.2) aplicada a la articulacion rotacional (3.1) resulta:.

(30) 3.2 Equilibria unico. 21. (3.3) donde las variables de estado representan los errores de posicion (q = qd — q) y de velocidad (q = qd — q). Notese que esta ecuacion tiene un equilibrio en el origen [q q] = 0- Sin embargo, pueden existir equilibrios adicionales \q q] = [s 0] donde 5 es solucion de: kps + mgl (sen(gw) - &en(qd - s)) = 0. Es bien sabido que si existen mas de un equilibrio, entonces ninguno de ellos podra ser global asintoticamente estable.. 3.2.1. Equilibrio unico. Ya que la ecuacion de malla cerrada (3.3) puede tener multiples equilibrios, ninguno de ellos puede ser global exponencialmente estable; sin embargo, para una seleccion suficientemente grande de fcp, puede demostrarse que el origen [99] = 0 es el unico equilibrio de la ecuacion de malla cerrada (3.3). Para demostrar lo anterior, primeramente se presenta el siguiente lema. Lema 3.1 Considerese una funcion f(t, q) : 8?+ X 8?n —> 3?" la cual satisface f ( t , 0) = 0 para todo t > 0. Si existe una funcion h(q) : 3?" —» 3? tal que:. h(0') h(q) \\f(t,q)\\. = 0 > 0 VgÔ > h(q) V«€»". V<6»f. entonces f(t, q) = 0 para todo t > 0 si y solo si q = 0, esto es, q = 0 € S" es la unica solucion de /(t, q) = 0 para todo t > 0.. VVV Ahora bien, notese que cualquier equilibrio de la ecuacion de malla cerrada (3.3) satisface q = 0 (q = </</), mientras que q es solucion de:. = o.. (3.4). donde g(q) = mgl sen(q) y g(qd) = mgl sen(qd). A continuacion se usara el lema 3.1 para demostrar que con una seleccion adecuada de kp, q — 0 es la linica solucion de (3.4) y de esta manera se garantiza que el origen es el unico equilibrio de la ecuacion de malla cerrada..

(31) 22. Capitulo 3. Control de una articulation rotational. Recordando que dado cualquier vector a, b € SR", y numeros reales como caso particular, se tiene que:. donde ||-|| denota la norma Eucludiana que en el caso de numeros reales equivale al valor absolute. En consecuencia, la norma (valor absolute) ||/(£, q)\\ de la funcion (3.4) satisface: \\kpq-(g(q)-9(qd)}\\. > \\kpq\\ - \\g(q) - g(qd)\\. > k, \\g\\-mgi\m > (kp - mgl) \\q\\. donde se han usado la desigualdad ||m<7/ [sen(<7j — q) — sen(qj)]\\ < mgl \\q\\. Claramente, si kp se selecciona de manera que: kp > mgl. (3.5). entonces, de acuerdo al lema 1, la funcion (3.4) tiene como unica solucion q = 0, lo que garantiza finalmente la unicidad del equilibrio. Si la constante kp satisface (3.5) y la constante kv es seleccionada adecuadamente, entonces, mediante el empleo de una funcion de Lyapunov conveniente, podria potencialmente intentarse demostrar la estabilidad asintotica global del origen \q q] = 0. A continuacion sera presentado el estudio de estabilidad asintotica (local) para este esquema de control.. 3.2.2. Estabilidad asintotica. Para estudiar las propiedades de estabilidad del origen \q q| = 0 de la ecuacion de malla cerrada (3.3), considerese la siguiente funcion candidata de Lyapunov:. La norma || q \\ se define en este caso como el valor absolute \q\..

(32) 3.2 Equilibria unico. 23. La constante positiva e$ se selecciona arbitrariamente. Las constantes de diseno kp y kv se seleccionan de modo que:. kp > 2mgl + ^p- + 4e2m/2 + e0. (3.7). ^ > kv > 4e0m/2 + 1. (3.8). •. Notese de (3.7) que: kp > £0mJ2 + £Q > e^ml2 de donde:. >£. (3.9). 3 10. /S °. <- '. La funcion candidata de Lyapunov (3.6) es una funcion definida positiva debido a que:. V^>£o>°. v<. 7e»n.. (3.ii). Para demostrar que bajo la condicion anterior, la funcion (3.6) es definida positiva, se precede en dos pasos. Primeramente, notese que la desigualdad (3.11) implica que:. i.. > £2 > 0. V q e 3T. debido a que e2, > e2, donde e = £o/(l+ \\ q ||). Esto a su vez, implica que la expresion kp — e2m/2 resulta ser un escalar positive. Por otro lado, la funcion (3.6) puede re-escribirse como: V(q, q) = ^ [^ + eg] ml2 [$ + eq] + -q [kp - £ 2 m/ 2 ] q. (3.12). la cual es definida positiva debido a que tanto m/ 2 , como kp — e2ml2 son escalares positives..

(33) 24. Capitulo 3. Control de una articulation rotational. Continuando con el estudio de estabilidad, la derivada temporal de la funcion candidata de Lyapunov (3.6) esta dada por: V(q, q) = -q [kpq + kvq] - q [g(qd) - g(q)] + qkpq + £qml2q - eq [kpq + kvq] - £q [g(qd) - g(q)] + £qml2q.. (3.13). Simplificando, la derivada temporal V(q, q) toma la forma: ^(<?>q) = ~qkvq - q[g(qd) - g(q)] + sqml2q - eqkpq - eqkv'q - eq [9(qd) - g(q)] + ei la cual puede ser reescrita como:. -9(q)} -eq\g(qj-g(q)].. (3.14). Ahora bien, debido a que g(q) = mgl sen(g) es una funcion Lipschitz, puede demostrarse que las siguientes desigualdades se satisfacen: < mgl \\q\\ U\\. - g(q)} < mgls \\q\\2 . Por otro lado, tambien es inmediato verificar que: £qml2q < \ eqml2q \ II q II ( 1 + I U I I X II q II (1+ II q II). -. £ ° 1+llff. 2. II q II II 'q II II q II II ml2* ||. II k II 2 m. (3.15) Empleando la desigualdad anterior, la ecuacion de V(q, q) en (3.14) satisface: < ~qkvq + eqml2q - eqkpq - eqkvq + emgl \\q\\* + £Qml2 |g| + mgl \\q\\ ||g la cual puede a su vez ser escrita como:. i /?\ T (ekp 2. A). \£kv. £k. A (q. kv ) \qt. - - [kp - 2mgl] \\q\\2 1 r,. - g r» - 4£°m + mgl \\q\\ \q\. .oi ii tJi2. (3.16).

(34) 3.2 Equilibria unico. 25. donde se ban usado —qkvq < -\qkvq- *£\\q ||2 y -qkpq < -\qkpq- \ || q ||2. Otra forma de visualizar (3.17) es mediante una suma de terminos cuadraticos, de modo que se tendria:. T. q\\\. Qi e[kp-2mgl] -mgl. -mgl. \f\\q. ^kv-4£oml*J\\\q. Qi. Para que V(q, q) sea una funcion definida negativa, es necesario que las matrices Qi y <?2 scan matrices simetricas definidas positivas, es decir, Q\ = Qf > 0 y Qi = Q% > 0- Para Piue Qi cumpla con esta condicion se requiere:. ekpkv -. lo es implicado si:. > kv. ya que entonces:. y en consecuencia kp — ekv > 0 y ekp — e2kv > 0.. (3.18).

(35) 26. Capitulo 3. Control de una articulation rotational. For otra parte, para que la matriz Q2 sea definida positiva, se tienen que cumplir las siguientes desigualdades: kp > 2mgl KJT [kp — 2mgl] [kv — 4e0"i/2] — (mgl)2 > 0. La ultima desigualdad es satisfecha para todo ||g|| < 6' si kp y kv se seleccionan de manera que: kp > 2mgl +. So. -. (3.19). +1. (3.20). . - 4e0m/2] - 1.. (3.21). y donde 6' > 0 esta dada por:. Para demostrar la afirmacion anterior, notese que las desigualdades (3.19) y (3.20) implican a su vez:. kv -. respectivamente. For supuesto, la multiplicacion de los miembros izquierdos de las desigualdades anteriores es mayor que la unidad, por lo que entonces:. (mgl)'. ;[kp - 2mgl][kv - 4e0m/2] - 1 > 0. lo cual garantiza que 6' definida en (3.21) sea positiva. Usando ahora la definicion de 8' y como se ha considerado 8' > ||g||, se tiene que: -. 4£. om/2] -\ = 8'> \\q\\. lo cual implica que: e(kp - 2mgl][kv£0ml2] - (mglf > 0 que es justamente lo que se deseaba demostrar..

(36) 3.3. Estabilidad exponential. 27. Del desarrollo precedente, la constante kv debe entonces satisfacer simultaneamente las desigualdades (3.18) y (3.20): ^ > kv > 4e0m/2 + 1 £Q. (3.22). mientras que kp ademas de verificar (3.11) y (3.19) debe ser tal que -£- > 4£Qml2 + 1 para de este modo asegurar que existe kv que satisfaga (3.22), por lo tanto: 2. kp > 2mgl +. v(mal) y. ' + 4^m/2 + e0.. £o. A manera de resumen, las constantes kp, kv y £Q que aseguran la estabilidad asintotica local del sistema en malla cerrada deberan ser seleccionadas conforme a los siguientes criterios: a) e0 > 0 b) kp > 2mgl Con la selection anterior se satisface entonces que: V(q,q)<0 para todo 6' > y g2 + q > 0 y en consecuencia, el origen [g q] = 0 es un equilibrio asintoticamente estable (localmente).. 3.3. Estabilidad exponencial. La estabilidad exponencial de un equilibrio en un sistema de control en lazo cerrado permite establecer algunas hipotesis sobre el funcionamiento de una version adaptable de dicho esquema de control; adicionalmente, establecer su estabilidad exponencial ofrece ciertas garantias sobre la robustez del sistema frente a perturbaciones. Esto ultimo servira como base para el analisis de incertidumbre parametrica en el modelo de la articulacion rotacional. Esta seccion presenta la demostracion de la estabilidad exponencial del controlador PD con compensacion precalculada aplicado a una articulacion rotacional, haciendo uso de la funcion de Lyapunov propuesta en la seccion anterior. El estudio de estabilidad exponencial del origen para el esquema de control propuesto inicia con el siguiente teorema converso de Lyapunov (Sastry y Bodson (1989)): Teorema 3.1 Asumiendo que f ( t , x ) : 9ft+ x 3?" —> 3?" es continua y sus primeras derivadas parciales en x acotadas y continuas por partes en t para toda x 6 Bh,t > 0. Entonces los siguientes estatutos son equivalentes:.

(37) 28. Capitulo 3. Control de una articulation rotational. a) x = 0 es un punto de equilibrio exponecialmente estable de: 4- — x — yf(t ^ t , xT\ ^. f(i \ — T xîgy — XQ. (1 9^ {o.£dj. b) Existe una funcion v(t,x), y constantes h', c\, 02, €3 y c4, estrictamente positivas tales que, para toda x € B/,», t > 0: ||2. (3.24). (3.25). dv_ dx. (3.26). vvv Podemos notar que la funcion de Lyapunov propuesta en (3.6) se puede re-escribir como: V(q,q) = -xPx. donde:. x=. P= De esta forma se puede verificar que la funcion V(q, q) cumple con las siguientes desigualdades:. || * ||2< \xTPx < c2 || x x f< \xTPx < ÂMAX Como vemos, las constantes c\ y GZ pueden calcularse a partir de los eigenvalores de la matriz P, asegurando el cumplimiento de la condicion (3.24)..

(38) 29. 3.3 Estabilidad exponential. Para obtener el valor de la constante 03 utilizaremos la expresion (3.17), la cual por ser una funcion definida negativa puede escribirse simplemente en funcion de Q\ y del vector de estados rr como: -C3. x. T. < -x Qix De esta forma, el eigenvalor mfnimo de la matriz Qi debera ser positivo para cumplir con la condicion (3.25). La obtencion de la constante c4 se inicia a partir de la siguiente representation de la funcion V(q, q): (3.27). Obteniendo la partial con respecto al vector de estados, tenemos:. dV(x). 2. dx. = xTPPx < (AMAX(P))2 N Aplicando raiz cuadrada en ambos lados obtenemos:. \\dV(x) <. C4W. La expresion anterior determina el valor de c\ en funcion del eigenvalor maximo de P, con lo cual se cumple la condicion (3.26) y finalmente se concluye la estabilidad exponencial del origen, para este esquema de control. Hasta aqui, hemos derivado una solucion analftica para la obtencion de las constantes mencionadas en el teorema 1; sin embargo, es necesario presentar resultados mas especificos que sirvan como base para la obtencion explfcita de los parametros del controlador para una articulacion rotacional, es por ello que a continuacion se expondra un proceso simple para la obtencion de las constantes mencionadas. Sabemos que las constantes de interes estan determinadas por las siguientes expresiones: a) ci = U min (P) b) c2 = |AMAX(P) c) c3 = A min (Qi) d) c4 = A MAX (P).

(39) 30. Capitulo 3. Control de una articulation rotational. Las expresiones para los eigenvalores anteriores resultan ser sumamente complicados, de modo que por simplicidad seria mas conveniente obtener los rangos en los cuales se localizan cada uno de los eigenvalores. Para obtener los rangos para cada uno de los eigenvalores haremos uso del teorema de Gersgorin (Horn y Johnson (1990)), el cual se enuncia a continuation:. Teorema 3.2 Sea A € ftnxn, y sea. j = 1 3 * f. la sumatoria de los terminos del renglon i, que no pertencen a la diagonal principal de A. Entonces todos los eigenvalores de A se localizan en la union de n discos, es decir: \J{\eC:\\-aii\<Pfi(A)} = t=l. vvv Haciendo uso del teorema 3.2, tenemos que del primer y del segundo renglon de la matriz P:. 1+ - ml2 \<. *:° ,m/ 2 < £oml2 + II 9 II. 1l.

(40) 3.3 Estabilidad exponencial. 31. Como kp > eoml2 es inmediato que kp > m/ 2 , y por lo tanto, la primera condition establece el limite superior sobre los eigenvalores, mientras que la siguiente determina el limite inferior, de modo que:. >. 1/. ". 1. - eo > 0. ,.... -2 \(kP a + enml ) > - Co > 0. A paxtir de los renglones de Q\ se obtienen: \X-£kp\<eKv. | X-kv\<eKv de modo que c$ > min{e(A;p — kv), kv(l — e)}. Esta selection de 03 se debe realizar en forma local, para ello se utiliza la cota maxima sobre los valores de || q \\ en forma tal que se obtenga una nueva expresion en funcion de la 6' definida en (3.21), esta nueva expresion se puede escribir como:. De esta ultima expresion se derivan dos condiciones que, en conjunto con las ya obtenidas en esta seccion, permiten asegurar la estabilidad exponencial del origen en malla cerrada. Estas dos expresiones permiten que la constante 03 sea positiva, la primera de ellas es: aj fcp .> KV Adicionalmente se requiere que e — -^r < 1, lo cual se satisface si se cumple lo siguiente: b) £Q < 1.

(41) 32. Capitulo 3. Control de una articulation rotational. Finalmente sabemos que la constante c\ corresponde al eigenvalor maximo de P, de modo que queda expresada como: (kp + £0ml2) > c4 > 0 El analisis anterior plantea rangos de confiabilidad dentro de los que se localizan las constantes de interes para asegurar la estabilidad exponencial local del origen del sistema en malla cerrada. El desarrollo matematico completo y las expresiones finales exactas para ci, 02, 03 y 04 pueden ser consultadas en el apendice C.. 3.4. Robustez ante incertidumbre parametrica. La ecuacion de malla cerrada con incertidumbre parametrica en la masa del eslabon es: mPq + mglsen(q) = kpq + kvq + moPqj + ml qd — ml q + mglsen(q) = kpq 4- kvq + mo/ Definase m = mo — m, entonces:. d_i* * j/. \ ~7^ [kp§ +k»Q + m'2& ~ mglsen(q). q mglsen(qd)] ). mglsen(qd}} En la seccion anterior se demostro que el sistema / (q, q\ es local exponencialmente estable. El estudio de la robustez del sistema en malla cerrada ante incertidumbre parametrica en el modelo puede ser considerado como un caso particular del analisis del sistema de control ante perturbaciones. En seguida se aplica una metodologfa para obtener una cota maxima sobre el termino de perturbacion g(t, q, q) y, de esta forma, definir un limite superior sobre los errores de posicion y velocidad de una articulacion rotacional.. < (3.28).

(42) 3.4 Robustez ante incertidumbre parametrica. 33. Basandose en el lema 4.8 de Khalil (1991) podemos establecer una cota superior sobre el termino de perturbacion, la cual queda expresada como:. <1 donde. < r ; adicionalmente sabemos que c\ <. D, tal que. < 1, con lo cual podemos simplificar la expresion y obtener finalmente una cota para la perturbacion: C ^r. (3.29). de (3.28) y (3.29) podemos derivar la siguiente expresion: m. Despejando la aceleracion deseada maxima tenemos: g <. - . c3 MAX < 04. La expresion exacta para el valor maximo de la perturbacion se obtiene al sustituir las formulas para los valores de las constantes cy y 04, presentados en el Apendice C; sustituyendo estos valores obtenemos:. - 1. MAX| <. + m/. 2. (3.30). 2. - m/2) - 4. En resumen, para el caso de incertidumbre parametrica en la masa se puede asegurar que los equilibrios del sistema de control en malla cerrada permanecen acotados dentro de una region <$', esto bajo las condiciones de que el termino de perturbacion y la aceleracion maxima deseada esten tambien acotados, y se cumplan las condiciones establecidas en las secciones 3 y 4 de este capitulo..

(43) Capitulo 3. Control de una articulation rotational. 34. Tabla 3.1: Parametros de la articulacion Distancia al centro de masas Masa del eslabon Aceleracion de la gravedad. 3.5. notation 1 m g. valor unidades m 0.5 2 kg m/seg2 9.8. Simulaciones con una articulacion rotacional. Para corroborar la validez de los resultados expuestos con anterioridad se realizaron dos simulaciones del controlador PD con compensacion precalculada aplicado a una articulacion rotacional. La primera se centra en la verification de los objetivos de control de posicion y movimiento; la segunda simulation aborda el caso de robustez ante incertidumbre parametrica en la masa del eslabon, utilizando para ello los conceptos expuestos en las secciones anteriores. En esta section se muestran los parametros utilizados en la simulacion, asi como los resultados obtenidos.. 3.5.1. Simulacion: modelo sin incertidumbre parametrica. El sistema que se simulo representa una articulacion rotacional simple (fig. 2.1), cuyo modelo esta expresado por la ecuacion (3.3). Para la realization de la simulacion se fijaron los parametros mostrados en la tabla 3.1. Sea SQ = 10, de las desigualdades (3.7) y (3.8) se obtiene:. I • kv = 23. Bajo estas condiciones se puede demostrar que existen constantes I, 02, 03, 04 y 6' para las cuales el sistema de control es asintoticamente estable..

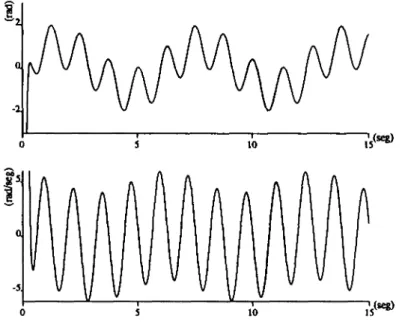
(44) 35. S.SSimulaciones con una articulacion rotational. 10. 10. 15. Figura 3.2: Referencias de posicion (arriba) y velocidad (abajo).. -z 10. 10. :(seg). 15. '(**). Figura 3.3: Salidas de posicion (arriba) y velocidad (abajo)..

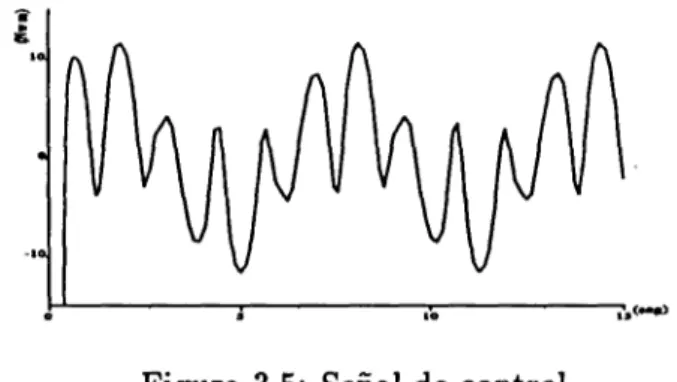
(45) 36. Capitulo 3. Control de una articulation rotational. 10. (seg). Figura 3.4: Errores de posicion (om'&o) y velocidad (06070). Para este ejemplo se fijo una condicion inicial q = 50. Las funciones de entrada de referenda de posicion, velocidad (figura 3.2) y aceleracion fueron las siguientes: • qj = sen(<) + e~3t + cos(5i) • qd = cos(t) - 3e~3' - 5sen(5«) • qd = -sin(t) + 9e~3' - 25cos(5<) Los resultados de la simulacion muestran que las salidas de posicion y velocidad (figura 3.3) siguen perfectamente a sus entradas de referenda, excepto al principle, en donde se observa un error transitorio debido a la condicion inicial establecida. Un analisis mas detallado sobre las graficas de los errores de posicion y de velocidad (figura 3.4) muestran el comportamiento exponencial de soluciones del sistema y su paulatina estabilizacion en el origen. Un aspecto interesante sobre el funcionamiento de esta estrategia de control es analizar el comportamiento de la serial de control que, como se puede apreciar en la figura 3.5, se mantiene en actividad para poder realizar el seguimiento de la serial de referenda. La simulacion realizada corrobora los resultados teoricos relatives a la obtencion de los parametros del controlador que aseguren que el origen del sistema en malla cerrada es asintoticamente estable. De esta forma, se ban presentado resultados de simulacion que verifican el cumplimiento de los objetivos de control y movimiento para la ley de control PD con compensation precalculada..

(46) S.SSimuladones con una articulation rotational. 37. Figura 3.5: Serial de control.. 3.5.2. Simulacion: modelo con incertidumbre parametrica. Dado que un gran numero de robots manipuladores realizan tareas de transporte de piezas, resulta interesante analizar el efecto de la incertidumbre en el modelo del robot. En este apartado, abordaremos el caso de incertidumbre en el valor de la masa del eslabon asociado a la articulacion rotacional. Considerense los valores mostrados en la tabla 3.1 como los parametros reales de la articulacion, sea mo el valor de la masa medido por el usuario. Entonces, bajo las mismas condiciones de simulacion que en el apartado anterior, tomando 9dMAX = 35m/seg2 y r = 700: m = 2.2 Los resultados obtenidos mediante simulacion se muestran en la figura 3.6, verificandose que incluso con un error tan grande en la estimation de la masa del eslabon, los errores de posicion y velocidad del sistema permanecen acotados..

(47) 38. Capitulo 3. Control de una articulation rotational. 70(*g). 10/Kg). Figura 3.6: Errores de posicion (arriba) y velocidad (abajo)..

(48) Capitulo 4. Control PD con compensacion precalculada de robots de n g.d.l.. En general, los resultados obtenidos del analisis realizado en el capftulo 3 brindan una base teorica para iniciar el estudio del controlador PD con compensacion precalculada aplicado a robots de n g.d.l.; sin embargo, el analisis requerido es mas elaborado ya que la dinamica de cada articulacion resulta del efecto combinado de toda la estructura del robot.. El estudio de estabilidad que se presenta en este capftulo establece limites inferiores para las ganancias proporcional y derivativa del controlador, las cuales garantizan que los errores articulares de posicion y velocidad decrecen asintoticamente a cero; de esta forma se logran satisfacer los objetivos de control de posicion y movimiento. La metodologia utilizada en este analisis requiere el empleo de una nueva funcion de Lyapunov, cuyos elementos dependen de la estructura del robot.. Como etapa preliminar al estudio de estabilidad consideraremos el modelo dinamico de un robot manipulator y estableceremos algunas propiedades adicionales a las delineadas en el capftulo 2. 39.

(49) 40. 4.1. Capitulo 4. Control de robots de n g.d.l.. Modelado dinamico y propiedades. El modelo simplificado de un robot manipulador, despreciando la friccion y otras perturbaciones, esta dado por la ecuacion (2.3) (Spong y Vidyasagar (1989)). Adicionalmente a las propiedades establecidas en el capftulo 2, podemos extraer otras cuatro, que nos ayudaran en el analisis de estabilidad que se presentara mas adelante. Propiedad 4.1 Existe una constante kjj tal que para todo x, j/, z, v y w 6 3?" se cumple la siguiente desigualdad: (z + vf[H(x)w-H(y)w]. < kH \\w\\ \\z + v\\ < kH \\z\\2 \\w\\ + ka \\v\\ \\w\\ \\z\\. VVV. Propiedad 4.2 Existen constantes positivas kct y kcy tales que para todo x, j/, z, u, v y w e SR" se cumple la siguiente desigualdad: (v + w)T[C(x,z)u-C(y,u)u}. < {kCl\\u\\ \\y\\ + kCl (\\z\\ \\y\\) \\x\\ \\u\\} \\x\\ + \\y\\ < kCl (\\u\\ \\v\\ \\w\\+ kCl \\u\\ HI2) |ti|| |H|2. HI HI INI donde v = x — y y w = z — u.. VVV. Propiedad 4.3 Existe una constante k^ tal que para todo x, t/, z y w € §?n se satisface:. < kc> \\z\f IH + fceJMI2 Ikll +kCl\\v\\ HI NI+*e,NI Ikll 2 donde v = y + w. VVV.

(50) 4.2. Ecuacion en malla cerrada. 41. Propiedad 4.4 Existe una constante kg tal que para todo x, y, z y w (E K" se satisface: (z + w)T(g(x)-q(y)}. < kg ||z||2 + kg \\z\\ \\w\\. donde z = y — x.. VVV. 4.2. Ecuacion en malla cerrada. Considerese la ley de control PD con compensation precalculada, que para robots de n g.d.l. puede escribirse como: T = Kpq + Kv'q + H(qd) qd + C(qd,qd) qd + g (qd). (4.1). donde Kp y Kv son matrices de diseo, que deben ser simetricas definidas positivas de dimension n x n; qd, qd y qd 6 &" son las posiciones, velocidades y aceleraciones articulares deseadas, respectivamente; H(qd), C(qd,q<i} y <?(?<*) representan la matriz de inercia, la matriz de fuerzas centrifugas y de Coriolis y el vector de terminos gravitacionales respectivamente, evaluados en los parametros de posicion y velocidad deseados. Los vectores q y q expresan los errores angulares de posicion y velocidad respectivamente ([q = qd — q] y \q = qd — q\). Esta ley de control guarda cierta similitud con la ley de control de Linearization con Retroalimentacion (Slotine y Li, (1990)); sin embargo, la ley de control PD con compensation precalculada utiliza los vectores de referencia q,i, qd y qd como los argumentos y factores para la matriz de inercia y los vectores de Coriolis y el de pares gravitacionales, a diferencia de la estrategia de linearization con retroalimentacion que utiliza las variables q,qyq obtenidas en tiempo real mediante sensores colocados en el robot. De lo anterior es posible visualizar el hecho de que que la estrategia de linearization requiere realizar cierto niimero de operaciones en durante la operation del robot; por otra parte, la ley de control PD con compensation precalculada puede realizar algunos de estos calculos fuera de Hnea, almacenarlos en tablas dentro del controlador y utilizar estos datos precalculados para generar la action de control, de esta forma se reduce la cantidad de operaciones matematicas en tiempo real y se aligera la carga del controlador..

(51) 42. Capitulo 4. Control de robots de n g.d.l.. Igualando las ecuaciones de movimiento (2.3) y la ley de control (4.1) se obtiene la ecuacion del controlador en malla cerrada: ~. .. Tt =. 9. jtq =. -H(q)-. q. , q)~C (qd, qd)] qd + C (q, q)'q-[g (q) - 9. en la cual se sustituye q = qd — qyq = qd — q para llegar a una ecuacion en funcion de estados del sistema: d _ q. Tt = d •„. "TT? at. =. i. q _ _x r. ~-^ (?d ~ 9). _. i,. i -î>9 + KvQ — [H (qd — q) — H (qd)\ qd *•. ~q,qd-q)-C (qd ~q,qd- q)] qd + C (qd -q,qd~q)q. -[9(qd-q)-g(qd)]}Es inmediato verificar que el origen [q q]T = [0 0]T es un equilibrio de la ecuacion de malla cerrada (4.2); sin embargo, puede no ser el linico.. 4.3. Unicidad del equilibrio. Notese que cualquier equilibrio de la ecuacion de malla cerrada (4.2) satisface q = 0 (q — qd) mientras que q es solucion de:. Kpq - [H (q) - H (qd)} qd - [C (q,q) - C (qd, qd)] qd - (g (q) - g (qd)} = 0 (4.2). Dado lo anterior, precede fijar las condiciones para las cuales el origen es el linico equilibrio de la ecuacion de malla cerrada..

(52) 4.4.. Estabilidad asintotica. 43. Recordando que dado cualquier vector a, b, c, d € 3ftn se tiene que: \\a-b- c-d\\> \\a\\-\\b\\-\\4dado que la norma ||/(i, q)\\ de la funcion rectorial (4.2) satisface: \\Kpq - [H (q) - H (ft)] ft - [C (q, q) - C (qd, qd)} qd - (g (q) - g (qd)}\\ <. \\Kpq\\-\\[H(q)-H(qd)]qd\\ - \\(C(q,q) - C (ft,ft)]ft|| - || [g(q) - g (ft)]|| < Am,-n(^)||g1|-^||gd|| ||9||-fccJ|rf Mil -kg\\q\\ < (Am,-n (Kp) - kH Hftll - fcc, Hftll 2 - *^) ||9|| < (Am,-n (A-,) - ka Hftll -fcc2Hftll 2 - *f) Ikll. donde se han utilizado las propiedades 2.4, 2.5 y 2.6. De la ultima expresion se puede apreciar que si Kp se selecciona de manera que Amt-n (Kp) satisfaga: Am,-n (Kp) > kH Hftll + kc, H^li 2 + kg. (4.3). entonces, de acuerdo al lema 3.1, la funcion (4.2) tiene como unica solucion 9 = 0, lo cual garantiza la unicidad del origen como equilibrio de la ecuacion (4.2).. 4.4. Estabilidad asintotica. Una vez establecidos los criterios bajo los cuales el origen es el unico equilibrio, podemos iniciar el estudio sobre la estabilidad del sistema en malla cerrada, utilizando para ello el segundo metodo de Lyapunov. Considerese la siguiente funcion candidata de Lyapunov: -q) + Kp + Kv H(qd-q). H(qd-q)\(q\ H(qd-q))(q). la cual es una funcion definida positiva ya que H (q), Kp y Kv son matrices definidas positivas..

(53) 44. Capitulo 4. Control de robots de n g.d.l.. La derivada temporal de la funcion candidata de Lyapunov (4.4) esta dada por:. V(q,q). = q qTH(qd-q)'q + qTT. ••. \ • T CL. •. +q H(qd-q)q+-q — (H(qd-q))q. sustituyendo. obtenemos:. H(qd-q}q-qrKpq-qTKvq T. q-]. [H(qd-q)-H(qd)]qd. (qd - q, qd - q) - C (qd, qd)] qd q) C(qd-q,qd-q)q. 9). [9(qd-g)-g(qd)}. la cual, mediante el uso de las propiedades 4.1, 4.3, 4.2 y 4.4, puede ser reducida a la siguiente desigualdad: V(q,q). < (q + q) H (qd - q) 'q - qT Kpq - '? Kvq. + [kH M + *&, IMI + kc, Uf + k9] \\g\\* + [ka \\qa\\ + 2*&, ||^|| + kCy \\q\\* + kg] \\q\\ \\ij\\ \\qd\\ + kCl] \\q\\2 \\ij\\. (4-5).

(54) 4.4 Estabilidad asintotica. 45. Sea: ci = kH\\qd\\+2kCl\\qd\\+kCl \\q\\* + kg c2 = 2kCl \\qj\\ + kCl ca = kCl\\qd\\ Sustituyendo estos valores en la desigualdad (4.5) se obtiene la siguiente expresion: H(qd-q)'q-qTKpq-'qTKvq. c2 |k~||. (4.6). 9. adicionalmente se sabe que:. 02 f I^|. (q + qf H(q}'q< A MA x (H) \\q\\ \q\ + A MA x Finalmente, Sustituyendo estos valores en la ecuacion (4.6) obtenemos:. V(q,q). < \uAx(H)M. \t\ + ^MAX (H) \qf - A min (Kp) \\q\\2 - A min (^) \\ij. ~ 03] Ikl + Cl |k~||. + C3. 9. |k1|2 +. 9. + 2c2. la cual puede escribirse en forma compacta como:. Para asegurar que el origen es local asintoticamente estable bastariaque Q (9, q\ > 0, para ello se require garantizar que: 3Amin (Kp) , A min (Kv). tales que Q (q, q) > 0. donde:. Sea a = — ^ + c3 — Q; entonces, para asegurar que Q (q,q) podemos establecer las siguientes condiciones:.

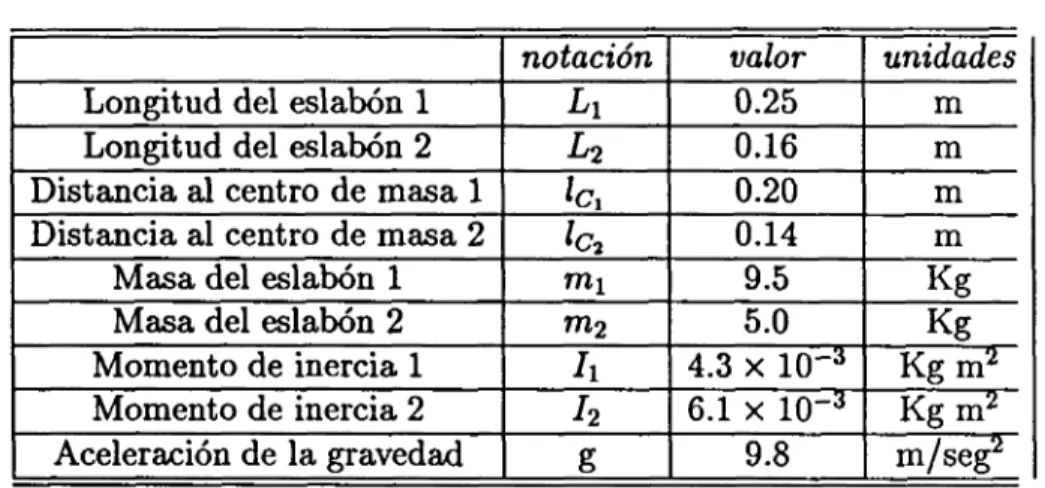
(55) 46. Capitulo 4. Control de robots de n g.d.l. a) A min (Kp) > -a. [. ^—. H -iii ^ "-" > 0. despejando A m i n (Kv): \~\\\2 + AMAX (H) + — + 03 Partiendo de la ecuacion (4.7) se puede verificar que: llffll I* < *2 de modo que la expresion para el valor propio mmimo de Kv esta dado por: +2c262)2 x. ~T a). ,m,c*,r. H A M AX (-W J + — + C3. 1. Con lo cual se garantiza la estabilidad asintotica local del origen de la ecuacion de malla cerrada, para una region. < 6. Es interesante observar que el valor \\ propio mmimo de Kp no depende de 8. A manera de resumen, las ganacias del controlador PD con compensation precalculada deben elegirse de acuerdo a las siguientes directives: q. • a) Amin (Kp) > -a 4(Ami,,(Ar,)+a)— + A MAX (H) + ^ + c3 donde 8 > 0 se define en (4.7) y : C 2 ,. 4.5. Simulaciones. Esta ultima seccion del capftulo presenta los resultados obtenidos de simulaciones computacionales realizdas sobre los modelos dinamicos de dos robots. Los resultados corroboran que el origen es local asintoticamente estable en malla cerrada y brindan intuicion sobre el comportamiento global del sistema.. 4.5.1. Robot de 2 g.d.l.. Los valores numericos de los parametros del robot de esta simulation ban sido adaptados de Ozaki et al (1991). El manipulador considerado en esta seccion posee dos articulaciones rotacionales, una de las cuales sujeta al eslabon 1 de una pared, mientras que la otra se encarga de unir al eslabon 1 con el 2. Los valores de los parametros del robot se muestran en la Tabla 4.1..

(56) 4.5 Simulaciones. 47. Tabla 4.1: Parametros del robot de 2 g.d.l. notation Longitud del eslabon 1 Li Longitud del eslabon 2 LI Distancia al centre de masa 1 lCt Distancia al centre de masa 2 'ft m! Masa del eslabon 1 Masa del eslabon 2 7712 Momento de inercia 1 h Momento de inercia 2 It Aceleracion de la gravedad g. valor unidades 0.25 m 0.16 m 0.20 m 0.14 m 9.5 Kg 5.0 Kg 4.3 x 10-3 Kgm 2 6.1 x 10-3 Kgm 2 9.8 m/seg2. Sean XA, yd, £<*, yd, %d y Vd las referencias de position, velocidad y aceleracion que sirvan como de entrada al robot, y esten definidas por: xd(t) = yd(t) =. 0.075sin(47rt) 0.075cos(47rt). y sus derivadas. Resolviendo la cinematica inversa de este manipulador se obtienen las siguientes cotas: ||&||MAX = 164.13rad/seg2 y ||<fa||MAX = 7.5rad/seg. Utilizando las constantes derivadas en el capitulo 2 (2.5) y aplicando el procedimiento de diseno visto en la seccion anterior, se pueden extraer los siguientes valores para las ganancias del controlador: Am,-B(jg = 391.95 =. 488.78. Para el caso de este manipulador se eligieron las siguientes matrices: Kp = diag[1500] Kv = diag[500].

(57) Capitulo 4. Control de robots de n g.d.l.. 48. y 0.4. 0.2. ai. 0.1. 0.2. 0.4. Figura 4.1: Trayectoria del robot de 2 g.d.l. sobre el plano(ar, y).. Las referencias de posicion seleccionadas hacen que el extremo final del robot trace un circulo en el piano cartesiano (x, y), a una frecuencia de 2 revoluciones por segundo y centre en (0.2,0.2). Los resultados de la simulation (figura 4.1) muestran que el extremo del robot parte de las condiciones iniciales de posicion, para finalmente seguir una trayectoria circular. Una mejor visualization sobre la evolucion de los errores de posicion y velocidad se muestra en las figuras 4.2 y 4.3. Los errores de posicion, en ambas articulaciones, poseen un transitorio en donde el controlador debe llevar al robot desde sus condiciones iniciales hasta la referenda, despues de este perfodo de ajuste los errores de posicion llegan a cero y permanecen en este valor. Los errores de velocidad tambien poseen un breve transitorio, debido a las condiciones iniciales, para finalmente estabilizarse en cero. El comportamiento de las senales de control para cada articulacion puede apreciarse en la figura 4.4, de donde se pueden extraer las magnitudes de los esfuerzos de control que pudieran servir para el diseno electronico del controlador. Un aspecto interesante de esta simulacion es la solucion de la cinematica inversa del robot mediante un sistema dinamico. El algoritmo utilizado fue propuesto por Colbaugh et al (1990) y presenta una metodologfa para la solucion dinamica de este problema, evitando el analisis geometrico de la estructura del manipulador necesario para extraer las ecuaciones de su cinematica. La base teorica que sustenta a este algoritmo es presentada en detalle en el Apendice D..

(58) 49. 4.5 Simulaciones. 0.4 0.2. a -0.2 -O.4. (. «* 0.2 0 -OJ. -0.4. Figura 4.2: Errores de posicion: q\ y 92 (<ê arriba hacia abajo).. fo.4.. I 1 =•02. Q -0.2 -0.4. 804,. ^0.2. 0. -0.2. -0.4.. !(seg). Figura 4.3: Errores de velocidad: q^ y q2 (de arriba hacia abajo)..

(59) Capitulo 4. Control de robots de n g.d.l.. 50. a I. ~5(seg). a -I. i(seg). Figura 4.4: Manipulation: r\ y TI (de arriba hacia abajo).. 4.5.2. Robot de 3 g.d.l.. El robot manipulador considerado en esta seccion esta formado por tres eslabones rigidos, unidos mediante tres articulaciones rotacionales. Los valores numericos para los parametros del manipulador ban sido adaptados de Stoten (1990), y se muestran en la Tabla 4.2. Utilizando los valores obtenidos en la seccion de modelado dinamico del capitulo 2 (2.6) y aplicando el procedimiento de diseno previo, podemos encontrax las matrices de ganancia del controlador; sin embargo, estas ganancias dependeran de la trayectoria que se desee controlar. En seguida se muestran las ecuaciones de las trayectorias utilizadas para esta simulation:. xd(i) = yd(i) = zd(i) =. 0.075sin(7rt/2) 0.075sin(7rt/2) 0.075cos(7rt/2). Estas referencias de position hacen que la primera articulation (base) gire 45 grades y que las otras dos articulaciones se muevan de modo que el extreme final trace un circulo, a una frecuencia de 0.25 revoluciones por segundo y centrado en (0.2,0.2) sobre los pianos (y, z) y (x,z). En este caso, tomese el eje z como el que se origina perpendicular a la base o piso y en direccion hacia el primer eslabon, mientras que los otros ejes completan el sistema coordenado..

(60) 51. 4.5 Simulaciones Tabla 4.2: Parametros del robot de 3 g.d.l.. Longitud del eslabon 1 Longitud del eslabon 2 Longitud del eslabon 3 Distancia al centro de masa 1 Distancia al centro de masa 2 Distancia al centro de masa 3 Masa del eslabon 1 Masa del eslabon 1 Masa del eslabon 2 Momento de inercia 1 Momento de inercia 2 Momento de inercia 3 Aceleracion de la gravedad. notation Li. L2 L3 bt Ic2 Ic3 m\ 7712. ma /i h h g. valor unidades 0.50 m 0.25 m 0.16 m 0.25 m 0.16 m 0.13 m 15.0 Kg 9.5 Kg 5.0 Kg 3 Kgm 2 8.0 x 10~ 4.3 x 10~3 Kgm 2 6.1 x 10~3 Kgm 2 m/seg2 9.8. Resolviendo la cinematica inversa del manipulador se pueden obtener las cotas maximas para las velocidades y aceleraciones angulares, que para este ejemplo son: H^HMAX = O-^ rad/seg y ll&Hjif^x = 1-4 rad/seg2. Aplicando la metodologia de diseno se determinan los eigenvalores minimos para las matrices de ganancias:. 191.12 1154.30. para las cuales se especifico una las siguientes matrices:. = 5. Para efectos de la simulacion, se definieron. Kp = diag[3000] Kv = diag[1200].

(61) Capitulo 4. Control de robots de n g.d.l.. 52. Figura 4.5: Movimiento del robot en el espacio tridimensional.. Q •O.S. -1. 10. as o -as -i 10. t '. ~0.5. 0,. -0.5. -1. 70(seg). Figura 4.6: Errores de posicion: ?i, 92 y 93 (de arriba hacia abajo)..

(62) 53. 4.5 Simulaciones. If2 •=• a. -2 0. ?<*«*>. ?2 •=• a. -2. Figura 4.7: Errores de velocidad: qlt q2 y q3 (de arriba hacia abajo).. a ^. e I. -To. To. (««). (Kg). Figura 4.8: Manipulacion: TI, T% y TS (de arriba hacia abajo)..

(63) 54. Capitulo 4. Control de robots de n g.d.l.. La figura 4.5 muestra el movimiento del extremo del manipulator en el espacio tridimensional. Para analizar a detalle la evolution de los errores de posicion y de velocidad, se pueden consultar las figuras 4.6 y 4.7 respectivamente. En estas graficas, se puede apreciar como los errores parten de un estado inicial y se mueven paulatinamente hasta llegar a cero, en donde permancen a partir t = 1.5 seg de simulation. Los esfuerzos de control se muestra en la figura 4.8, de donde es necesario resaltar que mientras las senales de control de la segunda y tercer articulation se mantienen activas, la senal de la base del robot posee un transitorio y se estabiliza despues de haber girado 45° sobre su eje. Los resultados de estas simulaciones confirman la validez de la teorfa expuesta en este capftulo, con lo cual se corrobora que el controlador PD con compensation precalculada cumple con los objetivos de control de movimiento y seguimiento, llevando los errores de posicion y velocidad a cero en un corto tiempo..

(64) Conclusiones. La relativa de sencillez de la estrategia de control PD con compensacion precalculada la hace un tema interesante de estudio dentro del area de control de robots manipuladores. En cuanto a su implementation, este controlador posee terminos que pueden ser calculados fuera de linea, con lo cual se reduce el numero de operaciones a efectuar en tiempo real, haciendolo muy adecuado para trayectorias repetitivas. Los antecedentes de este trabajo no brindan politicas explicitas de diseno. Este documento ha propuesto una metodologiapara la sintonizacion de los parametros del controlador, de manera que se garantice la estabilidad del origen en malla cerrada. En el capitulo 3 se establecio un procedimiento de diseno para garantizar la estabilidad asintotica local del controlador aplicado a una articulacion rotacional. Adicionalmente, se abordo en forma incipiente el estudio de la robustez del controlador frente a incertidumbre parametrica en el modelo; como resultado de este analisis se concluyo que este esquema de control mantiene acotados los errores de posicion y velocidad, en proportion a la incertidumbre en los parametros del eslabon. Para el caso de robots de n g.d.l., se demostro la estabilidad asintotica local del controlador; mientras que utilizando este procedimiento (alterno al mostrado en el capitulo 3) pudo garantizarse que para el caso especifico de una articulacion rotacional este controlador es global asintoticamente estable, ya que de acuerdo a la metodologia empleada en el capitulo 4 las restricciones para la estabilidad asintotica dependen de los terminos de Coriolis y para este caso especifico los efectos de las fuerzas de Coriolis son cero. Las simulaciones corroboraron los resultados teoricos obtenidos, mostrando que el controlador PD con compensacion precalculada cumple con los objetivos de control de posicion y control de movimiento, para los que fue disenado. 55.

(65) 56. Conclusiones. En este punto, resulta necesario presentar en forma condensada las contribuciones mas relevantes de este trabajo en el area de control de robots; sobresale la importancia del estudio de las condiciones para garantizar la unicidad del origen como equilibrio de la ecuation de malla cerrada, lo cual establece una etapa previa al analisis de estabilidad que no habia sido planteado previamente en la literatura; asimismo, es relevante el hecho de que la funcion de Lyapunov propuesta en el analisis de estabilidad del controlador para robots n g.d.l. resulto de una modification a la propuesta para el controlador PD con compensation precalculada y retroalimentacion nolineal, dada la adaptation realizada para este estudio la funcion propuesta en el Capitulo 4 debe considerarse como una funcion original; finalmente, el estudio de robustez ante incertidumbre parametrica, aunque abordado en forma preliminar para el caso de una articulation rotational, establece una nueva Hnea de investigation en el area de control de robots manipuladores. Como trabajos futures dentro de este tema de investigation se proponen: la demostracion de la estabilidad asintotica global de este controlador para robots de n g.d.l., asf como el estudio de la robustez de este esquema de control ante incertidumbre parametrica..

(66) Apendice A. Este apendice contiene un resumen de las propiedades de matrices mas importantes dentro del area de control de robots.. Matrices cuadradas Considerese A e 3?nXn una matriz cuadrada de dimension n y x e 9£n un vector de dimension n. 1. ATA, AAT y A + AT son matrices simetricas. 2. ATA es simetrica y semidefinida positiva. • A,- (ATA\ para todo i = 1,..., n.. 3. ||4| =. • \\A\\ = 0 <=> A,- (ATA) = 0 para todo t = 1,..., n. • \\A\\ = 0 <^=» A = 0 € »nS. . HAH = 1^1 U^ll = |U^| = \\A\f. 57.

(67) 58. Apendice A.. 4. det (A) = det (AT) • A,- (A) = A, (AT) para todo i — 1,..., n 5. Si |a,-,-| > X)"=ij^,- |°ij| Para t°do i = 1,..., n entonces det(^4) ^ 0 6. det(A) = nr=1 A,-(A) 7. nn/2(max,-J-|a,j|)n > |det(4)| 8. nmaxjj |a,-j| > |Aj.(>l)| para todo k = 1,..., n 9. det(.A) 7^ 0 •<=>• yl es no singular •$=>• A,-(yl) 7^ 0 para todo i = 1,..., n 10. ±xTAx = xT(A + AT)x = xT(A + AT)x 11. Si A,-(>1) = 0 para algiin i, entonces A es singular. 12.fcA,-(>l)es valor propio de kA para todo real k ^ 0 13. (A,-(>l))r es valor propio de Ar, con r un entero positivo. 14. l/\i(A) es valor propio de A~l siempre y cuando A sea no singular. 15. A es definida positiva (A > 0) si xTAx > 0 para todo x ^ 0 e 9ft" 16. Si A y B son matrices cuadradas no singulares, entonces (AB)~l = B~Â~l.

(68) 59. Martices simetricas Sea A •= AT (E 9ft nxn una matriz cuadrada simetrica de dimension n y x (E 9ft" un vector de dimension n. 1. Ak es simetrica para todo k = 1,2,... 2. Si A es no singular, entonces A~l es simetrica. 3. A,-(A) 6 9ft para todo i = 1,..., n. 4. \M\x(ATA) = AMAX(A2) = max,- |A/(,4)|2 5. Xm-m(A)xTx < xTAx < XM\x(A)xTx 6. A min (A) > 0 <=^> A > 0 7. n maxjj |a,j| > |A^(>1)| para todo k = 1,...,n.. 8. \\A\\ = \\A\\ = /AMAx^ 2 ) = max,- |A,-. \\A\\ = n 9. Sea B = BT £ 3ftn. -AMAX(#) - A min (£) < AMAX(^ + B) < • A-B>0^ Xm\n(A) - AMAX(B) > 0 • AB no necesariamente es simetrica. 10. det(A)<nr=ia,, XX.. ~j7*Z'. j\.X —•— ^3T. s\£ ^— ^J7. ^T.37.

(69) 60. Apendice A.. Matrices simetricas definidas positivas Sean A = AT € !Rnxn y B = BT 6 3ff nxn matrices simetricas definidas positivas de dimension n y x € §ftn un vector de dimension n.. 1. A + B >0 2. A - B <{=* J3-1 - A~l > 0 3. A - B <=* det(A) > det(B) 4. A - B => Xk(A) > Xk(B) para k = 1,..., n 5. [det(A + B)]l/n > (det(A))1/n + (det(£))1/n 6. AB no necesariamente es definida positiva.. 7. A > 0 «=* A~l > 0 8. \i(A) > 0 para todo i = 1,..., n 9. \\A\\ =. 10. p11. a,-,- > 0 es una condicion necesaria para que A > 0 12. Para cualquier C1 € ftnXn,CTAC > 0 13. Afc > 0, para todo k entero positive. 14. Existe C e 3?nxn no singular tal que A = CTC. 15. \xTAy\2 < (|MAX)_Amiii A MAX + Am,-n)2 (xTAx). «•(». (y?'Ay).

(70) 61. 17. Sean Ay C matrices simetricas. Entonces:. A * (BT. B G) > 0 = = ^ > ° . C">0, 4-BC~ 1 B T > 0, C-BTA~1B. (A * Ur <det(,4)det(B).

(71) 62. Apendice A..

(72) Apendice B. Lema 2.1 Sea x 6 SR", la norma Euclidiana para el caso vectorial se define como:. < y nmax ,- (x,-2) rnax. «:c' < -y/n max ,- (|ar,-|) < n max ,-(|:r,-|). O T. nx. Lema 2.2 Considerese una matriz simetrica A = A € 3? " y sea a,j su jj-esimo elemento. Partiendo del Lema 2.1, podemos considerar a la matriz A como un vector de vectores, de modo que:. ^ i/n (max. i \renglonj\). < < n f max ,• < n f max ,• <. O T. T. Lema 2.3 Considerese la matriz A = A € §£" y sea A = [AjAa - . . A n ] el vector de sus eigenvalores. Es inmediato verificar que: 63.

(73) Apendice B.. 64. IIA/H < Podemos comprobar que:. asi, podemos llegar a la siguiente expresion:. < n 2 (max ,j|a t j|). Vf =. O. Propiedad 2.4 Sea H (q) la matriz de inercia de un robot y x, y, z € 9fc", entonces podemos aplicar el teorema del valor medio (teorema 2.1) de la siguiente forma: t. =. \. 9Hii(l) I. II* - y\\ < n2 I max. 19=90. de esta forma podemos llegar a la siguiente desigualdad: dHij(q)\. Ik - y\\ Ml.