Desarrollo de un Elemento Finito Placa Basado en una Forma Especial de Representación de Solución

Texto completo

(1)INSTITUTO TECNOLÓGICO Y DE ESTUDIOS SUPERIORES DE MONTERREY CAMPUS ESTADO DE MÉXICO. DESARROLLO DE UN ELEMENTO FINITO PLACA BASADO EN UNA FORMA ESPECIAL DE REPRESENTACIÓN DE SOLUCIÓN.. TESIS QUE PARA OPTAR EL GRADO DE MAESTRO EN CIENCIAS EN SISTEMAS DE MANUFACTURA PRESENTA. GUILLERMO PINEDA HERNÁNDEZ. Asesor:. Dr. OLEKSANDER TKACHENKO. Comité de tesis:. Dr. SERGEI KANAOUN MIRONOV Dr. SADEGH BABAII KOCHEKSERAII. Jurado:. Dr. SERGEI KANAOUN MIRONOV Dr. SADEGH BABAII KOCHEKSERAII Dr. OLEKSANDER TKACHENKO. Atizapán de Zaragoza, Edo. Méx.,a 30 de Julio de 2004. Presidente Secretario Vocal.

(2) RESUMEN. En el presente trabajo se desarrolla un nuevo elemento rectangular para placas en la teoría de Kirchhoff. Dicho elemento es compatible y tiene 12 grados deflexiones y rotaciones dentro del elemento y en sus bordes se definen modificación de polinomios de Hermite. Las modificaciones se realizan restricciones sobre sus segundas derivadas.. delgadas basado de libertad. Las por medio una por el uso de. Para comprobar las características del elemento se resuelven algunos problemas clásicos en la teoría de placas como son: 1. Placa rectangular sometido a una carga uniformemente distribuida con 4 lados empotrados. 2. Placa rectangular sometido a una carga uniformemente distribuida , simplemente apoyada. 3. Placa rectangular sometido a una carga uniformemente distribuida con 2 lados empotrados y 2 lados simplemente apoyados. 4. Placa simplemente apoyada, sometido a un momento distribuido en 2 de sus lados. 5. Placa empotrada en uno de sus lados (cantilliver), sometido a un momento distribuido en el otro extremo, donde a > b relación 10/1. 6. Placa empotrada en uno de sus lados (cantillever), sometido a una fuerza distribuida en el otro extremo, donde a > b relación 10/1. 7. Placa empotrada en uno de sus lados (cantillever), sometido a una fuerza distribuida en el otro extremo, donde a > b relación 2/1. Para los primeros 4 casos se utiliza una placa rectangular con distintos tamaños de malla, para estos ejemplos se utiliza simetría. En los otros 3 casos restantes se muestran el comportamiento con un arreglo del elemento definido por las dimensiones a que es el largo de elemento y b como el ancho. Con estos ejemplos se obtiene: una gráfica de error contra densidad de malla, velocidad de convergencia del error relativo con respecto a los grados de libertad utilizados, y la representación grafica de la deflexión, momentos y cortantes. Finalmente se realiza una comparación con otros elementos placa desarrollados, debido a que es necesario comprobar el comportamiento del elemento con resultados obtenidos con respecto a otras formulaciones, esta comparación sirve como parámetro de validación del trabajo hecho..

(3) 3. ÍNDICE LISTA DE FIGURAS.................................................................................................................... 5 LISTA DE TABLAS...................................................................................................................... 7 LISTA DE GRAFÍCAS................................................................................................................. 8 CAPITULO 1.. INTRODUCCIÓN ....................................................................................... 10. 1.1 Antecedentes.................................................................................................................. 10 1.2 Métodos para el análisis de placas................................................................................. 11 1.2.1 Solución analítica de placas................................................................................... 12 1.2.1.1 Método de Navier (Solución de series dobles).................................................. 12 1.2.1.2 Método de Levy (Solución de series simple). ................................................... 13 1.2.2 Métodos numéricos para el Análisis de placas..................................................... 13 1.2.3 Métodos directos ................................................................................................... 13 1.2.3.1 Método de diferencias finitas (FDM). ............................................................... 14 1.2.3.2 Método de elementos de frontera (BEM). ......................................................... 14 1.2.4 Métodos indirectos ................................................................................................ 15 1.2.4.1 Método de los elementos finitos (FEM). ........................................................... 15 1.3 Planteamiento del problema .......................................................................................... 17 1.4 Campo de estudio ......................................................................................................... 18 1.5 Objetivos........................................................................................................................ 19 CAPITULO 2.. MARCO TEÓRICO.................................................................................... 20. 2.1 Análisis de esfuerzos ..................................................................................................... 20 2.1.1 Relaciones Esfuerzo-deformación......................................................................... 20 2.1.2 Relaciones deformación -desplazamiento ............................................................. 21 2.2 Conceptos generales sobre placas.................................................................................. 22 2.2.1 Teoría de placas ..................................................................................................... 23 2.2.2 Teoría de placas de Kirchhoff ............................................................................... 28 2.2.3 Teoría de placas de Mindlin .................................................................................. 28 CAPITULO 3.. DESARROLLO DEL NUEVO ELEMENTO FINITO PLACA ............ 30. 3.1 Funciones de forma e interpolación............................................................................... 30 3.1.1 Grados de continuidad ........................................................................................... 31 3.1.1.1 Interpolación C 0 .............................................................................................. 31 3.1.1.2 Interpolación C 1 ............................................................................................... 33 3.2 Funciones de forma con polinomios de Hermite........................................................... 34 3.3 Funciones de forma con polinomios de Hermite modificados. ..................................... 36 3.4 Matriz de rigidez............................................................................................................ 48 3.4.1 Principio de la energía potencial ........................................................................... 48 3.4.2 Vector de carga...................................................................................................... 51 3.4.2.1 Carga uniformemente distribuida ...................................................................... 52 3.4.2.2 Momento flexionate........................................................................................... 53 3.4.2.3 Fuerza cortante .................................................................................................. 54.

(4) 4 CAPITULO 4.. ANÁLIS DE EJEMPLOS NUMERICOS ................................................. 55. 4.1 Comparaciones con otros elementos finitos tipo placas................................................ 57 4.1.1 Elemento DKQ ...................................................................................................... 57 4.1.2 Elemento ARS-Q12............................................................................................... 57 4.1.3 Elemento ANSYS SHELL-63 ............................................................................... 57 4.2 Placa rectangular sometido a una carga uniformemente distribuida con 4 lados empotrado .................................................................................................................................. 58 4.3 Placa rectangular sometido a una carga uniformemente distribuida , simplemente apoyada...................................................................................................................................... 61 4.4 Placa rectangular sometido a una carga uniformemente distribuida con 2 lados empotrados y 2 simplemente apoyados ..................................................................................... 66 4.5 Placa simplemente apoyada, sometido a un momento distribuido en 2 de sus lados... 71 4.6 Placa empotrada en uno de sus lados (cantilliver), sometido a un momento distribuido en el otro extremo, donde a > b relación 10/1......................................................................... 76 4.7 Placa empotrada en uno de sus lados (cantillever), sometido a una fuerza distribuida en el otro extremo, donde a > b relación 10/1 .............................................................................. 81 4.8 Placa empotrada en uno de sus lados (cantillever), sometido a una fuerza distribuida en el otro extremo, donde a > b relacion 2/1. ............................................................................... 86 CAPITULO 5.. CONCLUSIONES ....................................................................................... 92. REFERENCIAS Y BIBLIOGRAFÍA........................................................................................ 93 ANEXOS A................................................................................................................................... 94 ANEXOS B................................................................................................................................. 102 ANEXOS C................................................................................................................................. 108 ANEXOS D................................................................................................................................. 114 ANEXO E ................................................................................................................................... 122.

(5) 5. LISTA DE FIGURAS Figura. 1.1 Figura. 2.1. Figura 3.10 Figura 3.11 Figura 3.12. Dimensiones de una placa, así como su plano medio De un rectángulo infinitesimal, a) esfuerzo normal en la dirección x , b) esfuerzo normal en dirección y , c) Esfuerzo cortante Notación para los componentes de rotación normales a la mitad de la superficie Elemento placa típico con nodos en cada esquina Sección de una placa deformada vista desde la dirección y las líneas del espesor se asumen que permanecen rectas. .Esfuerzos y fuerza lateral distribuida q . Momentos fuerzas cortantes transversales asociados con los esfuerzos de la (a). a) Interpolación lineal y funciones de forma, b) Interpolación cuadrática y funciones de forma. a) La línea sólida es una interpolación cúbica C 0 que se ajusta a los 4 puntos de la ordenada de la línea tocada , b) Una curva de Interpolación cúbica fundamentada sobre lo ordenada y información de la pendiente de sus puntos finales. Funciones de forma de una curva cúbica ajustada a las ordenadas y a la pendiente en x = 0 y x = L . Representación de una curva de Hermite y sus componentes. Funciones de Hermite de primer orden. Placa rectangular con 12 grados de libertad Función de forma N 1 . Función de forma N 2 . Función de forma N 3 . Función de forma N 4 . Función de forma N 5 . Función de forma N 6 .. Figura 3.13 Figura 3.14 Figura 3.15 Figura 3.16 Figura 3.17 Figura 3.18 Figura 4.1 Figura 4.2. Función de forma N 7 . Función de forma N 8 . Función de forma N 9 . Función de forma N 10 . Función de forma N 11 . Función de forma N 12 . Distintos tipos de malla Relación de malla a/b. Figura. 2.2 Figura 2.3 Figura 2.4. Figura 2.5a Figura 2.5b Figura 3.1 Figura 3.2. Figura 3.3 Figura 3.4 Figura 3.5 Figura 3.6 Figura 3.7 Figura 3.8 Figura 3.9. 11 21 23 24 25 26 27 32 33. 34 34 35 36 40 41 41 41 42 42 42 43 43 43 44 44 56 56.

(6) 6 Figura 4.3 Figura 4.4 Figura 4.5 Figura 4.6 Figura 4.7 Figura 4.8 Figura 4.9. Placa rectangular 4 lados empotrados bajo una carga uniformemente distribuida Placa rectangular simplemente apoyada bajo una carga uniformemente distribuida Placa rectangular 2 lados empotrados, 2 lados simplemente apoyados bajo una carga uniformemente distribuida Placa simplemente apoyada, sometido a un momento distribuido en 2 de sus lados Placa empotrada en uno de sus lados (cantilliver), sometido a un momento distribuido en el otro extremo, donde a > b relación 10/1 Placa empotrada en uno de sus lados (cantillever), sometido a una fuerza distribuida en el otro extremo, donde a > b relación 10/1 Placa empotrada en uno de sus lados (cantillever), sometido a una fuerza distribuida en el otro extremo, donde a > b relación 2/1. 58 61 66 71 76 81 86.

(7) 7. LISTA DE TABLAS. Tabla 3.1. Valores de los coeficiente de Gauss. Tabla 4.1. Resultados de desplazamiento en el centro de la placa con respecto a 56 la densidad de malla para el ejemplo 4.2 60 Comparación del elemento para el ejemplo 4.2. Tabla 4.2 Tabla 4.3 Tabla 4.4 Tabla 4.5 Tabla 4.6 Tabla 4.7 Tabla 4.8 Tabla 4.9 Tabla 4.10 Tabla 4.11 Tabla 4.12 Tabla 4.13 Tabla 4.14. 49. Resultados de desplazamiento en el centro de la placa con respecto a la 61 densidad de malla para el ejemplo 4.3 65 Comparación del elemento para el ejemplo 4.3 Resultados de desplazamiento en el centro de la placa con respecto a la 66 densidad de malla para ejemplo 4.4 70 Comparación del elemento para el ejemplo 4.4 Resultados de desplazamiento en el centro de la placa con respecto a la 71 densidad de malla para el ejemplo 4.5 75 Comparación del elemento para el ejemplo 4.5 Resultados de desplazamiento en el extremo de la placa con respecto a 76 la densidad de malla para el ejemplo 4.6 80 Comparación del elemento para ejemplo 4.6 Resultados de desplazamiento en el extremo de la placa con respecto a 81 la densidad de malla para el ejemplo 4.7 85 Comparación del elemento para el ejemplo 4.7 Resultados de desplazamiento en el extremo de la placa con respecto a 86 la densidad de malla para el ejemplo 4.8 90 Comparación del elemento para el ejemplo 4.8.

(8) 8. LISTA DE GRAFÍCAS Grafica 4.1. Error relativo VS Densidad de malla ejemplo 4.2. 59. Grafica 4.2. 59. Grafica 4.7 Grafica 4.8. Velocidad de convergencia en la norma de error relativo de deflexión en el centro de la placa versus numero de grados de libertad para una placa cuadrada empotrada bajo carga uniformemente distribuida Deflexión en el un cuarto de placa bajo una carga uniformemente distribuida, ejemplo 4.2 Error relativo VS Densidad de malla, ejemplo 4.3 Velocidad de convergencia de error relativo para la deflexión en el centro de la placa versus numero de grados de libertad en escala logarítmica para una placa cuadrada simplemente apoyada bajo un carga uniformemente distribuida Deflexión en un cuarto de placa bajo una carga uniformemente distribuida, ejemplo 4.3 Representación de momento M X , normalizado, ejemplo 4.3 Representación de momento M y , normalizado, ejemplo 4.3. Grafica 4.9 Grafica 4.10. Representación del cortante Q x , normalizado, ejemplo 4.3 Representación del cortante Q y , normalizado, ejemplo 4.3. 64 65. Grafica 4.11 Grafica 4.12. 67 67. Grafica 4.13 Grafica 4.14 Grafica 4.15. Error relativo VS Densidad de malla, ejemplo 4.4 Velocidad de convergencia en la norma de error relativo de deflexión en el centro de la placa versus numero de grados de libertad en escala logarítmica para una placa cuadrada 2 lados simplemente apoyados y 2 empotrados bajo un carga uniformemente distribuida Deflexión en un cuarto de placa Representación de momento M X , normalizado, ejemplo 4.4 Representación de momento M y , normalizado, ejemplo 4.4. Grafica 4.16 Grafica 4.17. Representación del cortante Q x , normalizado, ejemplo 4.4 Representación del cortante Q y , normalizado, ejemplo 4.4. 69 70. Grafica 4.18 Grafica 4.19. Error relativo VS Densidad de malla, ejemplo 4.5 72 Velocidad de convergencia en la norma de error relativo de deflexión 72 en el centro de la placa versus numero de grados de libertad en escala logarítmica para una placa cuadrada simplemente apoyada bajo un par en 2 de sus extremos. Grafica 4.20 Grafica 4.21 Grafica 4.22. Deflexión en un cuarto de placa Representación de momento M X , normalizado, ejemplo 4.5 Representación de momento normalizado M y , ejemplo 4.5. Grafica 4.3 Grafica 4.4 Grafica 4.5. Grafica 4.6. 60 62 62. 63 63 64. 68 68 69. 73 73 74.

(9) 9. Grafica 4.23 Grafica 4.24. Representación de momento normalizado Q x , ejemplo 4.5 Representación del cortante Q y , normalizado, ejemplo 4.5. 74 75. Grafica 4.25 Grafica 4.26. Error relativo VS Densidad de malla 77 Velocidad de convergencia en la norma de error relativo de deflexión 77 en el extremo de la placa versus numero de grados de libertad en escala logarítmica para una placa empotrada en uno de sus lados (cantilliver), sometido a un momento distribuido en el otro extremo, donde a > b. Grafica 4.27 Grafica 4.28 Grafica 4.29. Deflexión a lo largo de la placa Representación de momento M X , normalizado, ejemplo 4.6 Representación de momento normalizado M y , ejemplo 4.6. 78 78 79. Grafica 4.30. Representación de momento normalizado M x y , ejemplo 4.6. 79. Grafica 4.31 Grafica 4.32. Error relativo VS Densidad de malla 82 Velocidad de convergencia en la norma de error relativo de deflexión 82 en el extremo de la placa versus numero de grados de libertad en escala logarítmica para una placa empotrada en uno de sus lados (cantilliver), sometido a un par en el otro extremo, donde a > b. Grafica 4.33 Grafica 4.34 Grafica 4.35. Deflexión a lo largo de la placa, ejemplo 4.7 Representación de momento M X , Máximo, ejemplo 4.7 Representación de momento Máximo M y , ejemplo 4.7. 83 83 84. Grafica 4.36. Representación de momento Máximo M x y , ejemplo 4.7. 84. Grafica 4.37 Grafica 4.38. Error relativo VS Densidad de malla 87 Velocidad de convergencia en la norma de error relativo de deflexión 87 en el extremo de la placa versus numero de grados de libertad en escala logarítmica para una placa empotrada en uno de sus lados (cantilliver), sometido a un par en el otro extremo, donde a > b. Grafica 4.39 Grafica 4.40 Grafica 4.41. Deflexión a lo largo de la placa, ejemplo 4.8 Representación de momento M X , normalizado o, ejemplo 4.8 Representación de momento normalizado M y , ejemplo 4.8. 88 88 89. Grafica 4.42. Representación de momento normalizado M x y , ejemplo 4.8. 89.

(10) 10. CAPITULO 1. INTRODUCCIÓN 1.1 ANTECEDENTES Las placas y las láminas no son más que una forma particular de un sólido tridimensional. La teoría de placas delgadas se basa en la hipótesis formalizada por Kirchhoff en 1850 cuyo nombre se asocia con esta teoría, sin embargo Sophie Germain presentó una versión anterior en 1811. Reissner introdujo en 1945 una representación de las hipótesis de Kirchhoff al igual que Mindlin de manera ligeramente diferente en 1951. Estas teorías modificadas amplían el campo de las aplicaciones a placas gruesas y se asocia este nombre con los postulados de Reissner-Mindlin. Las propiedades de deflexión de una placa dependen en gran medida de su espesor si se compara con sus otras dimensiones. Las placas se clasifican en tres grupos de acuerdo a la relación a , h donde a es una dimensión de la placa y h es el espesor de la placa, como se ve en la figura 1. Estos grupos son: 1. El primer grupo el de placas gruesas con un relación a ≤ 10 . El análisis de este grupo de h placas incluye todos los componentes de esfuerzo, deformación y desplazamientos para cuerpos sólidos haciendo uso de las ecuaciones de elasticidad. 2. El segundo grupo se refiere a placas cuya relación sea a ≥ 100 . Este tipo de placas son h llamadas membranas. 3. El tercer grupo representa un tipo de placa intermedio llamada placa delgada con una relación 10 ≤ a ≤ 100 dependiendo del valor w . Que es la relación de deflexión h h máxima con respecto a su espesor, Este grupo se divide en dos grupos. . Placas rígidas. Una placa puede clasificarse como placa rígida si w ≤ 0.2 . Las cargas h aplicadas, principalmente producen flexiones internas, momentos torsores y fuerzas cortantes transversales. El plano medio deformado se considera despreciable..

(11) 11 . Placas flexibles. Si la deflexión de la placa esta mas allá de cierto nivel, w ≥ 0.3 , luego, h la deflexión lateral estará acompañada de un alargamiento del plano medio, dichas placas se denominan como placas flexibles. Estas placas representan una combinación de placas rígidas y membranas sometidas a cargas externas debido a la acción combinada de momentos internos, fuerzas cortantes y fuerzas axiales. Dichas placas debido a su a su favorable relación peso - carga, son ampliamente usadas en la industria automotriz. Cuando el valor de la deflexión máxima es considerablemente mas grande que el espesor de la placa, predomina la acción de una membrana.. x(u ). h z (w) a. x(u ) b. z (w) Plano medio. y (v ) Figura. 1.1.Dimensiones de una placa, así como su plano medio La clasificación antes mencionada esta condicionada a un u otro grupo de placa, depende de la exactitud de la placa, tipo de carga, condiciones de frontera, etc.. 1.2 MÉTODOS PARA EL ANÁLISIS DE PLACAS En la teoría de elasticidad, las ecuaciones que rigen a los esfuerzos, deformaciones y desplazamientos pueden presentarse en forma diferencial, sin embargo esta no es la única formulación posible para encontrar un comportamiento esfuerzo – deformación de un cuerpo. También puede reducirse por algunas integrales definidas para una u otro tipo de funciones llamadas funcionales. Las técnicas matemáticas para dicho proceso se llama calculo varacional..

(12) 12 1.2.1. SOLUCIÓN ANALÍTICA DE PLACAS. La teoría clásica de placas considera la solución matemática en forma exacta de series trigonométricas simples y dobles aplicadas a placas rectangulares por lo menos con 2 lados opuestos simplemente apoyados y aplicando cargas transversales. Algunos métodos de solución analítica son los siguientes: 1. Método de Navier (Solución de series trigonométricas dobles). 2. Método de Levy (Solución de series trigonométricas simples). 1.2.1.1 Método de Navier (Solución de series dobles). La Solución de la ecuación diferencial que rige a la flexión de una placa en coordenadas cartesianas esta definida como: ∂ 4 wx ∂4 w ∂4 w p +2 2 2 + = ∂ x4 ∂x ∂y ∂ y4 D. (1.1). La flexión es expresada como w ( x , y ) y la carga distribuida p ( x , y ) tienen una forma de serie de Fourier infinita de la siguiente forma: ∞. ∞. w ( x , y ) = ∑∑ wmn Sin m =1 m =1. mπx nπy Sin a b. mπx nπy p ( x , y ) = ∑∑ p mn Sin Sin a b m =1 m =1 ∞. ∞. (1.2). Donde wmn y p mn representan los coeficientes a ser determinados. La solución por series infinitas para la deflexión de placas generalmente converge rápidamente; por lo tanto una exactitud satisfactoria es obtenida considerando solo algunos términos. Puesto que los esfuerzos resultantes son obtenidos por la segunda y tercera derivada de la flexión w ( x , y ) , la convergencia de la serie expresada para las fuerzas y momentos internos es menos rápida, especialmente en la proximidad de los ejes de la placa, esta lenta convergencia es acompañada por una menor precisión en los cálculos. Las series para momentos flexionantes y consecuentemente para los esfuerzos así como para las fuerzas cortantes pueden divergen directamente en el punto de aplicación de una carga concentrada, llamado punto singular, por lo tanto es necesario usar una técnica más eficiente, especialmente sí el máximo esfuerzo ocurre en la proximidad del punto singular. Por lo tanto el determinar una correcta distribución de esfuerzos cerca de un punto singular es un proceso que está en desarrollo..

(13) 13 1.2.1.2 Método de Levy (Solución de series simple). En 1900 Levy desarrolla un método para resolver problemas de deflexión de placas rectangulares con un par de soportes a los ejes opuestos y con condiciones arbitrarías de soporte usando series de Fourier. Este método es más práctico ya que facilita la implementación de cálculos numéricos para series simples que para series dobles y también es bastante aplicable con distintos tipos de condiciones de frontera. La solución se expresa en términos complementarios wh y particulares w p , el método consiste en que las series de Fourier simples en donde las funciones desconocidas son determinadas a partir de las condiciones de frontera preescritas que se expresan de la siguiente forma:. w = wh + w p. (1.3). La solución particular w p se expresa en una serie de fourier simple como ∞. w p ( x, y ) = ∑ g m ( y ) sin m =1. mπx a. (1.4). La carga distribuida p ( x, y ) se denomina como ∞. p( x, y ) = ∑ p m ( y ) Sin m =1. mπ x a. (1.5). La solución teórica de placas está limitada por una geometría simple, la configuración de la carga y los tipos de soportes. Si este tipo de condiciones se vuelven demasiado complicados, los métodos de análisis clásicos se vuelven demasiado compleja, tediosos y en algunos casos hasta imposibles. 1.2.2. MÉTODOS NUMÉRICOS PARA EL ANÁLISIS DE PLACAS. Por las desventajas que presenta la solución analítica, los métodos aproximados son los únicos procedimientos que pueden emplearse en la solución de la mayoría de problemas de placas. Existen varios métodos aproximados que son ampliamente usados para el análisis de placas, estos métodos pueden dividirse en dos grupos: métodos directos y métodos indirectos. 1.2.3. MÉTODOS DIRECTOS. Estos métodos permiten obtener valores numéricos de funciones desconocidas, la discretización directa de la ecuación diferencial que rigen al correspondiente valor de frontera del problema. Algunos ejemplos son: método de diferencias finitas, método de elementos de frontera..

(14) 14 1.2.3.1 Método de diferencias finitas (FDM).. Este es un método para solucionar problemas de valor en la frontera de una ecuación diferencial, la esencia del FDM se expresa como: 1. El plano medio de la placa es cubierto por una red rectangular o triangular, dependiendo de la geometría de la placa. Esta red se nombra malla de diferencia finita y los puntos de intersección se llaman puntos nodales. 2. La ecuación diferencial que rige dentro del dominio de la placa es remplazada por ecuaciones de diferencias finitas actuando sobre los puntos de la malla usando operadores de diferencias finitas. 3. Las condiciones de frontera se incluyen en los operadores de diferencias finitas de los puntos de la malla en los limites de la placa. Como resultado del mencionado reemplazo, se obtiene un conjunto de ecuaciones algebraicas lineales escritas para cada punto nodal dentro de la placa. Resolviendo este sistema de ecuaciones se obtiene un campo numérico de desplazamientos nodales. Ventajas: a) Es un método fácil de entender y aplicar. b) Se puede aplicar a problemas lineales y no lineales. c) Se ajusta para aplicaciones en computadora. Desventajas: a) Se necesita mucho trabajo para lograr una completa automatización dentro de un programa. b) La matriz del sistema aproximado de una ecuación algebraica lineal es asimétrica, causando algunas dificultades en la solución numérica del sistema. c) En aplicaciones donde se necesitan geometrías muy complicadas, causa serias dificultades. 1.2.3.2 Método de elementos de frontera (BEM).. El método de elementos de frontera es usado para el análisis en dos y tres dimensiones para cuerpos elásticos, homogéneos, una ventaja importante es que únicamente se discretiza la frontera. El BEM satisface adecuadamente fronteras complicadas debido a discontinuidades externas o condiciones de frontera mixtas. El BEM permite convertir el problema con valor de la frontera, en forma de ecuaciones diferenciales parciales a forma integral sobre la frontera de la placa, luego se obtiene una solución aproximada resolviendo dicha integral..

(15) 15 Ventajas: a) Puede adaptarse fácilmente a geometrías muy complicas y condiciones de frontera arbitrarias como el método de los elementos finitos, sin embargo a diferencia de este método permite reducir la dimensión del problema dando como consecuencia una disminución del orden de la malla. b) El método de elementos de frontera es fácil de programar para una configuración de placa, carga y condiciones de frontera arbitrarías. c) La exactitud numérica del elemento en la frontera generalmente es mayor que la del método de los elementos finitos u otro método numérico debido a que la discretización numérica del método al establecer un sistema lineal de ecuaciones algebraicas. El error de la solución aproximada introducido por el método de elementos de frontera puede estimarse posteriormente cuando el problema en consideración ha sido solucionado. d) El método se ha adaptado bien para la solución de problemas con singularidades, como defectos por grietas, placas con esquinas, etc. Desventajas: a) Solo se utiliza para materiales homogéneos. b) Su aplicación primaria es para problemas lineales. c) El método requiere que la solución fundamental de la ecuación diferencial se represente en una forma analítica. La solución fundamental es mas complicada para problemas de flexión de placas por lo tanto la formulación del método del elemento de la frontera y su aproximación numérica se vuelve menos eficiente. d) La matriz del sistema lineal de ecuaciones algebraico es completa, a diferencia del método de los elementos finitos donde causa algunas dificultades en la implementación numérica. 1.2.4. MÉTODOS INDIRECTOS. Estos métodos usan el principio varacional o métodos de residuos pesados para determinar el campo numérico de las funciones desconocidas (deflexiones, fuerzas internas y momentos), evitando la ecuación diferencial de la placa. Como es el caso del método de elementos finito. 1.2.4.1 Método de los elementos finitos (FEM).. El método de los elementos finitos es basado en el concepto que se puede remplazar un continuo por una simple unión de elementos, con el que quedan definidos cargas y desplazamientos. Conforme al FEM, una placa se discretiza en un numero finito de elementos, llamados elementos finitos y conectados por nodos a lo largo de su frontera. Parámetros desconocidos (deflexiones, fuerzas internas y momentos) son asignadas en forma de valores sin determinar a los nodos. Las condiciones de equilibrio y continuidad deben ser satisfechas en cada nodo a lo largo de las fronteras entre elementos finitos. Para determinar las funciones desconocidas antes mencionadas se utiliza el principio varacional, como resultado se obtiene un sistema de ecuaciones algebraicas. Esta solución determina el estado esfuerzo y deformación de una placa..

(16) 16 El procedimiento para resolver un problema por FEM, se explica a continuación. a) Para cada elemento finito se tiene un numero “e” así como una numeración para cada nodo y desplazamiento, una fuerza nodal {Q}e y matrices de rigidez {k }e son determinadas en un sistema de coordenadas locales. La transición de las matrices de un sistema local a un sistema global es llevada a cabo por medio de un ensamble de matrices. b) Las ecuaciones que gobiernan al sistema son formadas donde la matriz global {K } y {Q} son generadas por los elementos como: {K }= ∑ e [k ] e y {Q}= ∑ e {Q}e . c) Las condiciones de frontera son insertadas en la matriz global de rigidez y se forman las ecuaciones que forman completamente a la placa. d) Las ecuaciones formadas son resueltas. e) Los datos obtenidos son calculados. La flexión del elemento, fuerzas internas, momentos, así como los componentes de esfuerzo calculados en todos los puntos nodales.. Ventajas: a) La solución por medio de elementos finitos se obtiene sin el uso de ecuaciones diferenciales que rigen al sistema. b) El método tiene un claro y directo significado mecánico y puede formularse en términos prácticos y conocidos para los ingenieros. c) El método puede ser aplicado exitosamente para condiciones de frontera y cargas arbitrarias. d) El método puede aplicarse a análisis de esfuerzos para estructuras combinadas, que consisten en varios elementos estructurales como placas, cascarones, vigas, etc. Desventajas a) El método de los elementos finitos requiere de computadoras con considerable velocidad y capacidad del almacenamiento. b) Es difícil verificar la exactitud de los resultados numéricos cuando se analizan grandes sistemas estructurales. c) El método difícilmente se adapta a la solución cuando existe un problema de singularidad, por ejemplo placas con grietas, puntos en las esquinas, discontinuidad interna y problemas con dominios infinitos. d) El método presenta muchas dificultades asociadas con la continuidad y elementos no conformes en el análisis de placas.

(17) 17. 1.3 PLANTEAMIENTO DEL PROBLEMA El análisis de placas y láminas fue una de las primeras aplicaciones del método de elementos finitos, Desafortunadamente la mayoría de estos elementos son muy débiles cuando son usados en modelos de estructuras delgadas, resultando lejana a la solución exacta. Desde el inicio los elementos para placa han estado plagados de problemas como; una rigidez sobre estimada haciendo que los desplazamientos calculados sean menores que de lo que deberían ser, ocasionando un fenómeno definido como esfuerzos parásitos1, que necesitan alto orden de grados de libertad, uso de muchos nodos, inestabilidad, restricciones de forma, continuidad o simplemente pobre desempeño. Numerosos elementos finitos para flexión de placas han sido desarrollados a través de los años, esto implica que sé esta llevando a cabo una fuerte investigación entorno a estos tipos de elementos. El principal detalle en los elementos usados en la actualidad es él gran numero de grados de libertad y nodos utilizados ya que un numero grande de nodos tiene como consecuencia el ensamble de una matriz de rigidez muy grande incrementando el tiempo de calculo y por el contrario, el uso de pocos nodos tiene como consecuencia una pobre aproximación de problema a resolver. En este trabajo se desarrolla un nuevo elemento rectangular compatible para placas delgadas basado en la teoría de Kirchhoff. Dicho elemento tiene 3 grados de libertad por nodo para su desarrollo se usa una modificación de los polinomios de Hermite. En su formulación tradicional el uso de los polinomios de Hermite requiere de cuatro parámetros por nodo definidos como deflexión (w) , rotación en x ( wx ) , rotación en y ( w y ) y torsión ( wx y ) . Para poder desarrollar el nuevo elemento se coloca una restricción sobre la función de deflexión w ( x , y ) y se expresa como:. ∂2 ∂2 + w ( x , y ) w ( x, y ) = Ax + B y + C x y + D ∂ x2 ∂ y2. (1.3). En este caso los momentos flexionantes se aproximan a funciones lineales de coordenadas x y y . De esta manera se obtienen relaciones que permiten expulsar el termino w xy por medio de los parámetros w , wx , w y , reduciendo el número de grados de libertad a 3 por nodo.. 1. Se utiliza este nombre en el presente trabajo al termino Shear locking.

(18) 18. 1.4 CAMPO DE ESTUDIO El análisis de placas y láminas fue una de las primeras aplicaciones del método de elementos finitos en los inicios de los años 60. En los últimos años el uso de materiales compuestos en aplicaciones estructurales ha hecho del método de los elementos finitos una herramienta para analizar el comportamiento de estas estructuras bajo diferentes configuraciones de cargas y restricciones. Como resultado de estas aplicaciones muchos elementos finitos para placas han sido desarrollados basados en sus desplazamientos, desafortunadamente la mayoría de estos elementos son muy débiles, resultando en una solución alejada de la solución exacta. Inicialmente los elementos para placa han estado plagados de problemas como esfuerzos parásitos definido anteriormente, que necesita alto orden de grados de libertad o uso de muchos nodos, inestabilidad, restricciones de forma o simplemente pobre desempeño. Numerosos elementos finitos para flexión de placas han sido desarrollados a través de los años, [8] cita cerca de 88 diferentes elementos, esto implica que sé esta llevando a cabo una fuerte investigación entorno a estos tipos de elementos placa, por ejemplo:. 1. Elemento DKQ, elemento rectangular de Kirchhoff de 12 grados de libertad con un nodo en cada esquina y tres grados de libertad por nodo, utiliza funciones de forma cúbica es el elemento rectangular más conocido para el análisis de placas delgadas, la formulación comienza con una independencia en el desplazamiento lateral y una rotación en la línea normal a la mitad de la superficie. En este aspecto los elementos DKQ asemejan a los elementos Mindlin. Sin embargo los elementos Mindlin están implícitamente acoplados por el cortante transversal y la rigidez del material, mientras los elementos DKQ están explícitamente acoplados para cumplir un esfuerzo cortante transversal iguala a cero en sitios selectos. [9] 2. Los elementos Mindlin aparecen después como forma especial de elementos isoparametricos para sólidos de 3D. El elemento placa inicial es un sólido de 8 nodos, el elemento sólido tiene 8 × 3 = 24 grados de libertad. El elemento placa Mindlin y su elemento sólido inicial están sometidos a los mismos desordenes como esfuerzos parásitos cuando el elemento es muy delgado. Así, no es fácil obtener un elemento Mindlin lo suficientemente robusto. [9] 3. Elemento MITC4, es un elemento placa rectangular, este elemento tiene una alta capacidad de predecir cuando es usado en una distorsión geométrica, realiza análisis lineales y no lineales que calcula desplazamientos transversales y esfuerzos flexionantes bastante bien, pero los esfuerzos cortantes no son muy satisfactorios particularmente cuando se analizan placas muy delgadas. [5].

(19) 19 4. Elemento ARS-Q12, elemento placa rectangular de 12 grados de libertad, basado en la teoría de Reissner-Mindlin para el análisis de placas gruesas y delgadas de gran desempeño. Primero las funciones de rotación y el esfuerzo cortante a lo largo de cada elemento es determinado bajo la teoría de vigas de Timoshenko, después la rotación y los esfuerzos cortantes en el dominio del elemento son determinados usando un método de interpolación mejorado y finalmente la matriz de rigidez es calculada por el procedimiento estándar.[6] Los problemas que presentan la mayoría de elementos desarrollados hasta la actualidad son enfocados a la continuidad que debe existir, esto es que los elementos deben permanecer conectados a sus nodos comunes ocasionando que no exista una convergencia apropiada a la solución que se busca. Otro detalle en los elementos usados en la actualidad es él numero de grados de libertad y nodos utilizados ya que un gran numero de nodos ocasiona el ensamble de una matriz de rigidez muy grande aumentando considerablemente el tiempo de calculo y en el caso contrario, el uso de pocos nodos al momento de hacer él calculo tiene como consecuencia una pobre aproximación de problema a resolver. Los ejemplos mencionados no pretenden ser una referencia esto significa que existe una prioridad al desarrollo de nuevos elementos Al diseñar este nuevo elemento finito placa de 16 grados de libertad que son flexión w , rotación en x w x , rotación en y w y , y la torsión w xy ; Partiendo de las funciones de forma que hacen uso de una modificación de los polinomios de Hermite para integrar el grado de libertad w(x , y ) a la función de forma considerando sus efectos, obteniendo de esta manera un elemento de 12 grados de libertad que es más sencillo de resolver debido a que se reduce el número de matrices de rigidez a calcular y ensamblar.. 1.5 OBJETIVOS Desarrollar un nuevo elemento finito placa por medio de una modificación de los polinomios de Hermite, que se aproxime a la solución exacta y mantenga las características de continuidad adecuadas.. •. Desarrollo de un nuevo elemento finito, análisis, estudio y su comportamiento en diversas aplicaciones. •. Comprobar el comportamiento del nuevo elemento finito placa con respecto a problemas analizados analíticamente.. •. Comparar al nuevo elemento finito con otros elementos.

(20) 20. CAPITULO 2. MARCO TEÓRICO 2.1 ANÁLISIS DE ESFUERZOS Algunos elementos pueden formularse utilizando métodos directos, ya sea en barras y vigas pero en general la formulación de elementos para mecánica estructural confía en herramientas ya establecidas de análisis de esfuerzos como son: esfuerzo-deformación, deformacióndesplazamiento y métodos de energía. 2.1.1. RELACIONES ESFUERZO-DEFORMACIÓN. Se define {σ} como un arreglo de esfuerzos y {ε}como un arreglo de deformaciones. Los subíndices cero indican valores iniciales. La matriz constitutiva [E] contiene las constantes elásticas. Para condiciones de linealidad elástica, las relaciones esfuerzo deformación pueden establecerse en forma matricial.. {σ} = [E]{ε} + {σ 0 } {σ 0 } = − [E]{ε 0 }. (2.1). Esta relación es valida en una, dos o tres dimensiones. En dos dimensiones, con x y y . En el plano de coordenadas la ecuación 2.1 es ⎧ σ x ⎫ ⎡ E11 ⎪ ⎪ ⎢ ⎨σ y ⎬ = ⎢ E11 ⎪τ ⎪ ⎢ E ⎩ x y ⎭ ⎣ 11. E11 E11 E11. E11 ⎤ E11 ⎥⎥ E11 ⎥⎦. ⎧ ε x ⎫ ⎧σ x 0 ⎫ ⎪ ⎪ ⎪ ⎪ ⎨ ε y ⎬ + ⎨σ y 0 ⎬ ⎪γ ⎪ ⎪τ ⎪ ⎩ xy ⎭ ⎩ x y 0 ⎭. (2.2).

(21) 21 La matriz constitutiva [E] es ⎤ ⎡ 1 ν 0 ⎥ ⎢ [E] = E 2 ⎢ν 1 0 ⎥ 1 −ν ⎢ 1 −ν ⎥ ⎥ ⎢0 0 2 ⎦ ⎣. (2.3). Donde ν es la razón de Poisson, Las deformaciones iniciales {ε 0 }son ocasionadas por diferentes situaciones, incluyendo cambio de temperatura y engrandecimiento debido a la humedad o la radiación. 2.1.2 RELACIONES DEFORMACIÓN -DESPLAZAMIENTO Un campo de desplazamiento describe como un cuerpo se deforma tanto como este se desplaza. Las relaciones deformación-desplazamiento juegan un role prominente en la formulación común de elementos finitos. Para obtener las formulas , se usa la definición ingenieril de deformación. la deformación normal en una dirección dada se define como el cambio unitario de longitud de una línea que estaba originalmente orientada según la mencionada dirección. Es positiva si el cambio en la longitud un consiste en un alargamiento, y negativa si se trata de un acortamiento. La deformación tangencial es el cambio de valor en el ángulo como se muestra en la figura 2.1, la cual proporciona las deformaciones ε x , ε y y γ x y en el plano xy . Generalmente la dirección x representa el desplazamiento u y la dirección y el desplazamiento v que son función de las coordenadas : u = u ( x, y ) y v = v( x, y ) por consiguiente se utilizan ecuaciones diferenciales parciales. εx =. ∆u ∆x. εy=. ∆u. ∆x ∆y. ∆v ∆y. ∆v ∆u. γ xy =. ∆x. ∆x ∆u ∆y. ∆y. ∆u ∆ v + ∆y ∆ x. ∆v. ∆y. ∆v ∆x a). b). c). Figura. 2.1. De un rectángulo infinitesimal, bajo las condiciones a) esfuerzo normal en la dirección x , b) esfuerzo normal en dirección y , c) Esfuerzo cortante.

(22) 22 Se obtienen la relaciones deformación-desplazamiento.. εx =. ∂u ∂x. εy =. ∂u ∂y. γ xy =. ∂u ∂u + ∂x ∂ y. (2.4). En tres dimensiones, el desplazamiento sucede en tres coordenadas x , y , y z son: u = u ( x, y, z ) , v = v ( x, y, z ) y w = w ( x, y, z ) definidas como:. εz =. ∂w ∂z. γ yz =. ∂v ∂w + ∂z ∂ y. γ zx =. ∂w ∂u + ∂x ∂z. (2.5). En forma matricial para dos y tres dimensiones las relaciones deformación-desplazamiento son:. ⎡∂ ⎢ ⎧ ε x ⎫ ⎢ ∂x ⎪ ⎪ ⎢ ⎨ε y ⎬ = ⎢ 0 ⎪γ ⎪ ⎢ ⎩ xy ⎭ ∂ ⎢ ⎣⎢ ∂y. ⎤ 0⎥ ⎥ ∂ ⎥ ⎧u ⎫ ⎨ ⎬ ∂y ⎥ ⎩v ⎭ ∂⎥ ⎥ ∂x ⎥⎦. ⎡∂ ⎢ ∂x ⎢ ⎢0 ⎧εx ⎫ ⎢ ⎪ε ⎪ ⎢ ⎪ y⎪ ⎢0 ⎪⎪ ε y ⎪⎪ ⎢ ∂ ⎨ ⎬=⎢ ⎪γ x y ⎪ ⎢ ∂y ⎪γ yz ⎪ ⎢ ⎪ ⎪ ⎢0 ⎪⎩γ zx ⎪⎭ ⎢ ⎢ ⎢∂ ⎢ ⎣ ∂z. 0 ∂ ∂y 0 ∂ ∂x ∂ ∂z 0. ⎤ 0⎥ ⎥ 0⎥ ⎥ ∂⎥ ∂z ⎥⎥ 0⎥ ⎥ ∂⎥ ⎥ ∂y ⎥ ∂⎥ ∂⎥ ⎥ ∂x ⎦. ⎧u ⎫ ⎪ ⎪ ⎨v ⎬ ⎪ w⎪ ⎩ ⎭. (2.6). 2.2 CONCEPTOS GENERALES SOBRE PLACAS Por placa se entiende un cuerpo delgado cuyo espesor es mucho mas pequeño con respecto a sus otras dimensiones, los elementos de tres dimensiones no se utilizan en el análisis de placas. Si los elementos en tres dimensiones se hicieran delgados únicamente en dirección del espesor, estos ocasionarían problemas de esfuerzos parásitos y mal condicionamiento, se debe evitar el uso de muchos grados de libertad, basándose en la teoría de placas En general las placas desarrollan momentos flexionantes en dos direcciones y un momento torsor..

(23) 23 Teoría de placas. 1. Teoría de placas delgadas o teoría de Kirchhoff, la cual prohíbe la deformación por cortante transversal y solo se toma el esfuerzo normal en dirección del espesor. 2. La teoría de placas gruesas o teoría de Mindlin, que toma en cuenta la deformación por cortante transversal y el esfuerzo normal en dirección del espesor. Se toma la siguiente notación:. ux = θ x z. ∂w ∂x ∂w wy = ∂y. wx =. θx =ψ y. uy = θy z. θ y =ψ x. θx =ψ y. z. θ y = −ψ x. θy. ψy. θx. z. z. ψx. wy = y. ∂w ∂y. wx =. ∂w ∂x y. y. x. x. x. Figura. 2.2. Notación para los componentes de rotación normales a la mitad de la superficie. 2.2.1 TEORÍA DE PLACAS. Para una placa con un espesor “ t ” se considera una superficie a la mitad de la placa una distancia de t desde una superficie lateral. Para iniciar el análisis se localiza el plano xy a la 2 mitad de la superficie considerada, con z = 0 .Como se ve en la figura 2.3.

(24) 24. z 4. 1. 2. y. 3. x. Figura 2.3. Elemento placa típico con nodos en cada esquina .. La teoría elemental de flexión de placas, asume que la flexión en una placa homogénea hace que la superficie a la mitad de la placa se vuelva una superficie neutral, esto es que:. εx = εy = γxy = 0. z=0. (2.7). Si se presenta un plano de carga, tal vez asociado con una deflexión lateral muy grande, las deformaciones en la mitad de la superficie de la placa no se consideran como cero. El comportamiento de una placa es idealizado cuando se toma una línea recta y normal a la superficie de la placa antes de aplicar una carga esta permanece recta pero no necesariamente normal a mitad de la superficie deformada. La rotación en esta línea recta tiene componentes ψ x y ψ y . De esta manera un punto diferente a la superficie media tiene un desplazamiento µ en dirección x . Una sección transversal similar, visto desde una dirección − x , proporciona un desplazamiento ν en dirección y Como se muestra en la figura 2.4.

(25) 25 u = − zψ x. ψx. z, w. P. z w wx. x, u. Figura 2.4.Sección de una placa deformada vista desde la dirección y las líneas del espesor se asumen que permanecen rectas. Para pequeños desplazamientos y rotaciones, de las relaciones deformación – desplazamiento en forma matricial se tiene: ⎡∂ ⎢ ⎧ ε x ⎫ ⎢ ∂x ⎪ ⎪ ⎢ ⎨εy ⎬ = ⎢ 0 ⎪γ ⎪ ⎢ ⎩ xy⎭ ∂ ⎢ ⎣⎢ ∂y. ⎤ 0⎥ ⎥ ∂ ⎥ ⎧u ⎫ ⎨ ⎬ ∂y ⎥ ⎩ν ⎭ ∂⎥ ⎥ ∂x ⎥⎦. Simbólicamente:. {ε} = [∂]{u}. (2.8). Por lo tanto se obtienen las siguientes deformaciones:. u = − zψ x v = − zψ y. (2.9). ε x = − zψ x, x. ε y = − zψ y,y. (2.10). γ xy = − z (ψ x,y + ψ y,x ). γ yz = w, y − ψ y γ zx = w, x − ψ x. (2.11).

(26) 26 ( ,); denota diferenciación y w ; es la deflexión lateral en dirección z a la superficie media de la placa. Estas ecuaciones son la base de la teoría de placas de Mindlin, que permite la deformación transversal por cortante, esto es que γ y z y γ z x necesitan no ser diferente a cero. En la teoría de placas de Kirchhoff, la línea normal media de la placa sin deformar se asume que permanece recta a la superficie media de la placa. Por lo tanto w, y = ψ y y w, x = ψ x la deformación transversal por cortante es cero durante la teoría de placas de Kirchhoff, sin embargo las fuerzas cortantes permanecen presentes. Muchas placas se basan en el modelo de Kirchhoff, debido a que son suficientemente delgadas para que la deformación transversal por cortante pueda ser despreciada. Los esfuerzos sobre las secciones transversales son descritos en las figuras 2.5a, 2.5b, donde es muy común asociar estos esfuerzos con momentos y fuerzas por unidad de longitud en el plano x y.. Mx = ∫. t. My = ∫. t. σ x z dz. 2. −t. 2. 2 t − 2. σ y z dz. (2.12). t. Mxy = ∫ t2 τ x y z dz −. 2. Donde Mx y My son momentos flexionantes y Mxy es un momento torsor.. z. q y. τ yz. σy. x. τzx. σx. τxy. τxy. Figura 2.5a.Esfuerzos y fuerza lateral distribuida q ..

(27) 27 t. Qx = ∫ t2 τ z x dz −. 2. (2.13). t. Qy = ∫ τ y z dz 2 −t 2. Donde Qx y Qy son fuerzas cortantes transversales.. z. Qy. q. My. Qx. Mxy Mx. x. t. Mxy Figura 2.5b.Momentos fuerzas cortantes transversales asociados con los esfuerzos de la (a).. La deformación descrita en la figura 2.4, en el cual la línea normal a la superficie media se asume que permanece recta, produce esfuerzos σ x , σ y y τ x y varia linealmente con z se muestra en la figura 2.5a. Para un material homogéneo produce esfuerzos ± 6 Mx t 2 , ± 6 My t 2 , ± 6 Mxy t 2 en la superficie z = ± t 2 . Por costumbre σ z es considerado como despreciable en comparación con σ x , σ y y τ x y . Por lo tanto para un material lineal elástico e isotropico, la relación esfuerzo-deformación en cada capa de la placa es la expresión de esfuerzo plano:. ⎧σ x ⎫ E ⎪ ⎪ ⎨σ y ⎬ = 2 ⎪τ ⎪ 1 − ν ⎩ xy⎭. ⎡ ⎤⎛ ⎞ 1 0 ν ⎢ ⎥ ⎜ ⎧ ε x ⎫ ⎧ ε x 0 ⎫⎟ ⎪ ⎪ ⎪ ⎪ ⎢ν 1 0 ⎥ ⎜ ⎨ ε y ⎬ − ⎨ ε y 0 ⎬⎟ ⎢ 1 − ν 2 ⎥ ⎜⎜ ⎪γ ⎪ ⎪γ ⎪ ⎟⎟ ⎢0 0 ⎥ ⎩ x y ⎭ ⎩ x y 0 ⎭⎠ 2 ⎦⎝ ⎣. (2.14).

(28) 28 2.2.2 TEORÍA DE PLACAS DE KIRCHHOFF. La deformación transversal por cortante es prohibida, así w, x = ψ x y w, y = ψ y de las ecuaciones 2.5. Ahora ε x = − z w, x x , ε y = − z w, yy y γ xy = −2 z w, x y . Estas relación esfuerzo-curvatura se. sustituye en la ecuación 2.8. Por lo tanto la relación momento-curvatura para una placa homogénea e isotropica es:. {M} = −[D]({k}) ⎡ ⎧ Mx ⎫ ⎢D νD ⎪ ⎪ ⎨ My ⎬ = − ⎢⎢ν D D ⎪Mxy⎪ ⎢ 0 ⎩ ⎭ 0 ⎢⎣. ⎤ 0 ⎥ ⎧ w, x x ⎫ ⎪ ⎪ 0 ⎥ ⎨ w, y y ⎬ ⎥ (1 − ν ) D ⎥ ⎪2 w, ⎪ xy⎭ ⎩ 2 ⎥⎦. (2.15). (2.16). Donde D se llama rigidez a la flexión. D=. E t3 12(1 − ν ). (2.17). 2.2.3 TEORÍA DE PLACAS DE MINDLIN. Los tres campos w , ψ x , ψ y cada uno debe ser expresado en términos de x y y para describir el estado de esfuerzo-deformación sobre la placa de Mindlin. Con w , ψ x , ψ y se guardan como cantidades independientes en las ecuaciones 2.3-2.5, el proceso que se utilizo para obtener la ecuación 2.10 se repite. Así de para una material homogéneo, isotropico y lineal produce una relación analógica para la placa de Mindlin: ⎡D νD ⎧ Mx ⎫ ⎢ν D D ⎪ My ⎪ ⎢ ⎪⎪ ⎪⎪ ⎢ 0 = − Mxy 0 ⎨ ⎬ ⎢ ⎪ Qx ⎪ ⎢ 0 0 ⎪ ⎪ ⎢ ⎪⎩ Qy ⎪⎭ 0 ⎣ 0. 0 0 (1 − ν ) D 2 0 0. 0 0 0 k Gt 0. 0 ⎤ ⎛ ⎧ ψ x, x ⎫⎞ ⎜⎪ ⎥ ⎪⎟ 0 ⎥⎜ ψ y y , ⎪⎟ ⎪ ⎜ ⎪ψ + ψ ⎪ ⎟ ⎥ 0 ⎜ ⎨ x, y y , x ⎬⎟ ⎥ ⎪ ⎪ ⎜ 0 ⎥ ⎪ ψ x − w, x ⎪ ⎟ ⎜ ⎟ ⎥ k G t ⎦ ⎜⎝ ⎪⎩ ψ y − w, y ⎪⎭ ⎟⎠. (2.18).

(29) 29 El factor k calcula la variación de distribución del esfuerzo cortante en dirección z y k t puede considerarse como el espesor efectivo para la deformación transversal por cortante. Se acepta un valor de k para una placa homogénea es k = 5 6 . En la teoría de Mindlin, no solo existen tres campos, pero el campo de deflexión lateral es acoplado con los campos de rotación xy , únicamente por la deformación transversal por cortante. Tal teoría parece muy complicada que la teoría de Kirchhoff, pero de hecho es mucho mas fácil obtener una variedad de elementos finitos, sin embargo existen algunas dificultades como lo son los esfuerzos parasitos..

(30) 30. CAPITULO 3. DESARROLLO ELEMENTO FINITO PLACA. DEL. NUEVO. A lo largo de este capitulo se estudia el caso mas general de interpolación de una función, se ven algunas definiciones de continuidad, posteriormente se desarrolla una modificación de los polinomios de Hermite, necesarios para definir las funciones de forma del elemento que se esta desarrollando. 3.1. FUNCIONES DE FORMA E INTERPOLACIÓN. La interpolación es la forma en que una función continua satisface condiciones preescritas en un numero finito de puntos. En el análisis por elemento finito los puntos son nodos de un elemento, y las condiciones preescritas son valores nodales de un campo de cantidades. Los valores nodales son raramente exactos y incluso cuando lo son, la interpolación generalmente proporciona valores aproximados de otras ubicaciones. En el análisis de elementos finitos la función de interpolación es casi siempre un polinomio, el cual proporciona automáticamente en un valor único y continuo. Para generalizar se toma que ai como grado de libertad, el polinomio de interpolación con variable dependiente φ y la variable independiente x puede escribirse como: n. φ = ∑ ai x i. or. (3.1). φ = [X]{a}. i =0. El cual. [X] = [1. x. x2 K xn. ]. y. {a} = [a0. a1. a2 K an ]. T. (3.2). Donde n = 1 para interpolación lineal, n = 2 para interpolación cuadrática y así sucesivamente. El grado de libertad ai puede expresarse en términos de valores nodales de φ , que es un valor conocido de x . La relación entre los valores nodales {φ e } y ai es simbolizado como:. {φ e } = [A]{a}. (3.3).

(31) 31 Donde cada fila de [A ] es evaluada a cada localización de nodos [X]. De las ecuaciones 3.1 a 3.3 se obtiene:. φ = [N ]{φ e }. donde. [N ] = [X][A ]−1 = [N1. N 2 K]. (3.4). Individualmente N i de la matriz [N ] es llamado función de forma. Cada N i expresa la interpolación φ = φ ( x) cuando la correspondiente φi es uno y las otras φi son cero. En elementos finitos, el ensamble de estos elementos causan los valores de nodos {φ e } que aparecen en {D} , que es el vector global de los grados de libertad. Por lo tanto {φ e } para cada elemento es determinado resolviendo la ecuación [K ]{D} = {R} .. 3.1.1 GRADOS DE CONTINUIDAD. El símbolo C m es utilizado para describir la continuidad en un campo por segmentos. Un campo C m es continuo hasta sus derivadas e incluso de grado m es la continuidad entre elementos. Por lo tanto una dimensión, φ = φ ( x) es continuidad C 0 solo si φ es continuo y su derivada no lo es y para φ = φ ( x) es continuidad C 1 solo si φ y su primera derivada son continuos , pero con la condición que la segunda derivada no sea continua. La terminología C m se aplica en distintos tipos de elementos, Usualmente C 0 es utilizado para modelación plana y cuerpos sólidos y los tipos C 1 son utilizados para la modelación de vigas, placas y cascarones, debido a que proporcionan una continuidad entre elementos. 3.1.1.1 Interpolación C 0. Se inicia con una interpolación lineal ente dos puntos ( x1 , φ1 ) y ( x 2 , φ 2 ) , de la ecuación 3.2 [X] = [1 x] , evaluando [X] en los puntos 1 y 2 se obtiene ⎧φ1 ⎫ ⎧a 0 ⎫ ⎨ ⎬ = [A ]⎨ ⎬ ⎩φ 2 ⎭ ⎩ a1 ⎭. [A] = ⎡⎢. 1 x1 ⎤ ⎥ ⎣1 x 2 ⎦. (3.5). Si se invierte [A ] y usando la ecuación 3.4 se obtiene. [A] −1=. 1 ⎡ x 2 − x1 ⎤ x 2 − x1 ⎢⎣− 1 1 ⎥⎦. ⎡. [N] = ⎢ x 2 − x. ⎣ x 2 − x1. x − x1 ⎤ ⎥ x 2 − x1 ⎦. (3.6). Las funciones de forma lineales N 1 y N 2 se muestran en la figura 3.1.a. Se muestra una interpolación simple usada en el método del elemento finito. Para formular alguna propiedad de un elemento de dos nodos de largo L , su utiliza x1 = 0 , x 2 = L , grados de libertad nodales φ1 y φ2 ..

(32) 32 Para una interpolación cuadrática se ajusta una parábola a los puntos ( x1 , φ1 ) , ( x 2 , φ 2 ) , ( x3 , φ3 ) ,. [. estos puntos no necesitan ser equidistantes. Ahora [X] = 1 x convierte en ⎧φ1 ⎫ ⎧a 0 ⎫ ⎪ ⎪ ⎪ ⎪ ⎨φ 2 ⎬ = [A ] ⎨ a1 ⎬ ⎪φ ⎪ ⎪a ⎪ ⎩ 3⎭ ⎩ 2⎭. ⎡1 x1 1 [A] = ⎢⎢1 x2 1 ⎢1 x3 1 ⎣. ]. x 2 , de la ecuación 3.2 se. x1 2 ⎤ ⎥ x2 2 ⎥ x3 2 ⎥⎦. (3.7). Las funciones individuales son mostradas en la figura 3.1.b. N1 =. x2 − x x2 − x1. N=. x − x1 x2 − x1. 1. 1. 1. 1. φ1 x1. φ2. φ. x2 2. a). ⎧φ ⎫ φ = [N ]⎨ 1 ⎬ [N ]⎩⎨⎧ φφ 2φ ⎩ ⎭⎬⎫ 2 ⎭. φ1. φ2 x2. x3. 1. 2. 3. (x1 − x)( x3 − x ) ( x1 − x2 )( x3 − x2 ). N3 =. (x1 − x )( x2 − x ) (x1 − x3 )( x2 − x3 ). ⎧φ 1 ⎫ ⎪ ⎪ φ = [N ]⎨φ 2 ⎬ ⎪φ ⎪ ⎩ 3⎭. φ3. x1. N2 =. b). Figura 3.1 a) Interpolación lineal y funciones de forma, b) Interpolación cuadrática y funciones de forma..

(33) 33 3.1.1.2 Interpolación C 1. Se considera una curva cúbica φ = φ ( x) , cuya curva es determinada por 4 elementos. Se toma los elementos para ser la ordenada φi y una pequeña pendiente d φ d x y una longitud L , como se. [. muestra en la figura 3.2.a. Ahora [X] = 1 x ecuación 3.2 se convierte ⎧ φ1 ⎫ ⎧a 0 ⎫ ⎪ dφ ⎪ ⎪a ⎪ ⎪ ⎪ ⎪ d x1 ⎪ ⎪ 1⎪ ⎨ φ ⎬ = [A ]⎨ ⎬ ⎪ 2 ⎪ ⎪a 2 ⎪ d φ ⎪ ⎪ ⎪⎩a3 ⎪⎭ ⎪⎩ d x 2 ⎪⎭. φ. 2. ]. x 3 , evaluando con x = 0 y x = L , La. ⎡1 ⎢0 [A] = ⎢ ⎢1 ⎢ ⎣0. φ. 4. 1. x2. 0 ⎤ 0 ⎥⎥ L L2 L3 ⎥ ⎥ 1 2 L 3 L2 ⎦ 0 1. 0 0. (3.8). dφ d x2. dφ d x1. 3. x. φ2. φ1. x L. 0 a). b). Figura 3.2 a) La línea sólida es una interpolación cúbica C 0 que se ajusta a los 4 puntos de la ordenada de la línea tocada , b) Una curva de Interpolación cúbica fundamentada sobre lo ordenada y información de la pendiente de sus puntos finales. Las funciones de forma son representadas en la figura 3.3.

(34) 34. x=0. x= L L. 3 x 2 2 x2 N1 = 1 − 2 + 3 L L. 1. N2 = x −. 1. 2 x2 x3 + 2 L L. 3 x2 2 x3 N3 = 2 − 3 L L. 1. N4 = −. 1. x2 x3 + L L2. Figura 3.3 Funciones de forma de una curva cúbica ajustada a las ordenadas y a la pendiente en x = 0 y x = L.. 3.2 FUNCIONES DE FORMA CON POLINOMIOS DE HERMITE Las aproximaciones de Hermite son fáciles de calcular, pero no por eso dejan de ser poderosas. Estas se usan para tener una aproximación suave entre puntos. Para calcular una curva de Hermite se necesitan los siguientes vectores . P1 el punto de inicio de la curva. T1 la tangente que deja a la curva en el punto de inicio. P2 el punto final de la curva. T2 la tangente que se reúne con la curva en el punto final. T2. P2. P1. T1. Figura 3.4 Representación de una curva de Hermite y sus componentes..

(35) 35 Estos cuatro vectores son simplemente multiplicados con 4 funciones básicas de Hermite y sumadas al mismo tiempo. H 1 (s) = 2 s 3 − 3 s 2 + 1 H 2 ( s ) = −2 s 3 + 3 s 2. (3.9). H 3 ( s) = s 3 − 2 s 2 + s H 4 (s) = s 3 − s 2. . En la figura 3.5 se presenta dicho sistema de polinomios de tercer grado.. H (s) 1.0 H1. H2. Pendiente = 1 H3. 1. 0. s. H4. Pendiente = 1 Figura 3.5 Funciones de Hermite de primer orden. H 1 inicia en 1 y se aproxima lentamente hasta 0, H 2 inicia en 0 y se aproxima lentamente a 1. H 3 y H 4 son aplicadas a las tangentes de la misma manera, esto se hace para asegurar que la curva se aproxima en la dirección deseada en los puntos de inicio y fin.. Se expresa en forma vectorial y matricial para un mejor entendimiento • • •. Vector S , con potencia de tres. Vector C , los parámetros de la curva de Hermite. Matriz H , los cuatro polinomios de Hermite. ⎧s 3 ⎫ ⎪ 2⎪ ⎪s ⎪ S =⎨ ⎬ ⎪s⎪ ⎪⎩ 1 ⎪⎭. ⎧ P1 ⎫ ⎪P ⎪ ⎪ ⎪ C = ⎨ 2⎬ ⎪T1 ⎪ ⎪⎩T2 ⎪⎭. 1⎫ ⎧ 2 −2 1 ⎪− 3 3 − 2 − 1⎪ ⎪ ⎪ H =⎨ ⎬ 0 1 0⎪ ⎪0 ⎪⎩ 1 0 0 0 ⎪⎭. Para calcular un punto en la curva se logra con P = S ⋅ H ⋅ C. (3.10).

(36) 36. 3.3 FUNCIONES DE FORMA CON POLINOMIOS DE HERMITE MODIFICADOS. La primera propuesta para el desplazamiento w = ( x, y ) fue el uso de las funciones de forma de una viga, la cual extiende las funciones de forma cúbicas de dos dimensiones usadas para una viga a lo largo del eje x . Posteriormente los elementos placas fueron rectangulares de 16 grados de libertad, con un nodo en cada esquina y cuatro grados de libertad por nodo. Consideremos la siguiente placa rectangular de la figura 3.6 que muestra un elemento con 4 nodos y 3 grados de libertad por nodo El vector nodal de desplazamientos de este elemento es. {q}e = [w1. w1 x. w1 y. w2. w2 x. w4. w2 y. w3. w3 x. w3 y. w4. w4 x. w3. w4 x. w4 y. ]. (3.13). w3 x. w4 y. x. w1 y. w1 x. w2 y w2 x. w1. w2. Figura 3.6 Placa rectangular con 12 grados de libertad Para poder desarrollar esta función de forma se utiliza la condición. ∆w = a + b s + c t + d s t. (3.14). Se utiliza el siguiente polinomio de Hermite W (t , s ) = T T ⋅ M HT ⋅ Q ⋅ M H ⋅ S. Se obtiene. (3.15).

(37) 37 T. ⎡6 s ⎤ ⎡6t ⎤ ⎢2⎥ ⎢2⎥ ∆W = ⎢ ⎥ ⋅ M HT ⋅ Q ⋅ M H ⋅ S + T T ⋅ M HT ⋅ Q ⋅ M H ⎢ ⎥ ⎢0⎥ ⎢0⎥ ⎢ ⎥ ⎢ ⎥ ⎣0⎦ ⎣0⎦. (3.16). Se definen los coeficientes de los polinomios de Hermite de la ecuación 3.10. ⎧ 2 −3 0 ⎪− 2 3 0 ⎪ MH = ⎨ ⎪ 1 −2 1 ⎪⎩ 1 −1 0. 1⎫ 0⎪⎪ ⎬ 0⎪ 0⎪⎭. (3.17). Que puede escribirse en su forma matricial. ⎧ w1 w2 w1x w2 x ⎫ ⎪w w w w3x ⎪⎪ ⎪ 3 4 3x Q=⎨ ⎬ ⎪w1y w2 y w1x y w2 x y ⎪ ⎪⎩w3 y w4 y w3x y w4 x y ⎪⎭. (3.18). También se definen ⎡t 3 ⎤ ⎢ 2⎥ t T =⎢ ⎥ ⎢t ⎥ ⎢ ⎥ ⎣⎢ 1 ⎦⎥. ⎡s 3 ⎤ ⎢ 2⎥ s S=⎢ ⎥ ⎢s⎥ ⎢ ⎥ ⎣⎢ 1 ⎦⎥. t=. x a. s=. y b. (3.20). De 3.15 se deben cumplir las siguientes 4 condiciones T. ⎡1⎤ ⎡1⎤ ⎢0⎥ ⎢0⎥ T ⎢ ⎥ ⋅ MH ⋅ Q⋅ MH ⋅ ⎢ ⎥ = 0 ⎢0⎥ ⎢0⎥ ⎢⎥ ⎢⎥ ⎣0⎦ ⎣0⎦. T. ⎡0⎤ ⎡1⎤ ⎢1⎥ ⎢0⎥ T ⎢ ⎥ ⋅ MH ⋅ Q⋅ MH ⋅ ⎢ ⎥ = 0 ⎢0⎥ ⎢0⎥ ⎢⎥ ⎢⎥ ⎣0⎦ ⎣0⎦. (3.21).

(38) 38 T. T. ⎡1⎤ ⎡0⎤ ⎢0⎥ ⎢1⎥ T ⎢ ⎥ ⋅ MH ⋅ Q⋅ MH ⋅ ⎢ ⎥ = 0 ⎢0⎥ ⎢0⎥ ⎢⎥ ⎢⎥ ⎣0⎦ ⎣0⎦. ⎡0⎤ ⎡1⎤ ⎢1⎥ ⎢1⎥ T ⎢ ⎥ ⋅ MH ⋅ Q⋅ MH ⋅ ⎢ ⎥ = 0 ⎢0⎥ ⎢0⎥ ⎢⎥ ⎢⎥ ⎣0⎦ ⎣0⎦. En su formulación tradicional el uso de los polinomios de Hermite requiere de cuatro parámetros por nodo definidos como deflexión ( w) , rotación en x ( wx ) , rotación en y ( w y ) y torsión ( wx y ) . Para poder desarrollar el nuevo elemento se coloca una restricción sobre la función de deflexión w( x, y ) y se expresa como: ∂2 ∂2 w ( x , y ) + w ( x,y ) = Ax + B y + C xy + D ∂ x2 ∂ y2. (3.20). En este caso los momentos flexionantes se aproximan a funciones lineales de coordenadas x y y . De esta manera se obtienen relaciones que permiten expulsar el termino wx y por medio de los parámetros w , w x , w y , reduciendo el número de grados de libertad a 3 por nodo. Se realiza por medio de A ⋅ wx y + B ⋅ w = 0. (3.21). Donde se definenen 1 1 1⎫ 2 2 −4 2 −2 −4 −2 2 4 − 2 − 2⎫ ⎧1 ⎧4 ⎪− 2 − 2 − 1 − 1⎪ ⎪− 6 − 3 − 4 6 − 3 4 6 3 −2 −6 3 2 ⎪⎪ ⎪ ⎪ ⎪ A=⎨ B = ⎬ ⎬ ⎨ 6 4 −3 −6 2 3⎪ ⎪− 2 − 1 − 2 − 1⎪ ⎪− 6 − 4 − 3 6 − 3 3 ⎪⎩ 4 ⎪⎩ 9 2 2 1 ⎪⎭ 6 6 6 3 −6 −9 −6 3 9 − 3 − 3⎪⎭. [. W = w1. w1 x. w1 y. w2. w2 x. w2 y. C = A⋅ B. w3. w3 x. w3 y. w4. w4 x. w x y = −C ⋅ W. w4 y. ]. wx y. ⎡ w1 x y ⎤ ⎢w ⎥ 2x y ⎥ =⎢ ⎢ w3 x y ⎥ ⎢ ⎥ ⎣⎢ w4 x y ⎦⎥. (3.22).

(39) 39 ⎧1 ⎪1 ⎪ C=⎨ ⎪1 ⎪⎩1. 1 0 1 0. 1 1 0 0. −1 −1 −1 −1. 0 −1 −1 −1 0 1 −1 −1 0 0 0 0 −1 −1 1 1 0 −1 0 1. 1 0 0⎫ 1 − 1 0 ⎪⎪ ⎬ 1 0 − 1⎪ 1 − 1 − 1⎪⎭. (3.23). Usando las funciones H (t ) = M H ⋅ (t 3. t2. H ´(t ) = M H ⋅ (3 t 2. t 1). T. 2t 1 0). T. H ( s ) = M H ⋅ (s 3. H ´(s ) = M H ⋅ (3 s 2. s 1). T. s2. 2s 1 0). T. T. H ´´(t ) = M H ⋅ (6 t 2 0 0 ). H ´´(s ) = M H ⋅ (6 s 2 0 0). H ´´´(t ) = M H ⋅ (6 0 0 0). T. H ´´´(s ) = M H ⋅ (6 0 0 0). (3.24). T. T. Siguiendo la siguiente expresión N( x , y ) = {N 1 (s t ), N 2 (s, t ), .. .. . N 12 (s, t )}. (3.25). Se definen las funciones de forma como ⎧ H 1 (t ) ⋅ H 1 ( s ) ⎫ ⎪ H (t ) ⋅ H ( s ) ⎪ 1 ⎪ 3 ⎪ ⎪ H 1 (t ) ⋅ H 3 ( s ) ⎪ ⎪ ⎪ ⎪ H 2 (t ) ⋅ H 1 ( s ) ⎪ ⎪ H 4 (t ) ⋅ H 1 ( s ) ⎪ ⎧ H 3 (t ) ⋅ H 3 ( s ) ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ H (t ) ⋅ H 3 ( s ) ⎪ T ⎪ H 4 (t ) ⋅ H 3 ( s ) ⎪ − C N (t , s ) = ⎨ 2 ⎬ ⎨ ⎬ ⎪ H 1 (t ) ⋅ H 2 ( s ) ⎪ ⎪ H 3 (t ) ⋅ H 4 ( s ) ⎪ ⎪ H 3 (t ) ⋅ H 2 ( s ) ⎪ ⎪⎩ H 4 (t ) ⋅ H 4 ( s )⎪⎭ ⎪ ⎪ ⎪ H 1 (t ) ⋅ H 4 ( s ) ⎪ ⎪ H (t ) ⋅ H ( s )⎪ 2 ⎪ 2 ⎪ ⋅ ( ) H t H ⎪ 4 2 ( s )⎪ ⎪ H (t ) ⋅ H ( s )⎪ 4 ⎩ 2 ⎭. (3.26). Utilizando las funciones siguientes ⎧− 1 1⎫ ⎧t ⎫ S (t ) = ⎨ ⎬⋅⎨ ⎬ ⎩ 1 0⎭ ⎩1⎭ ⎧− 1⎫ S´(t ) = ⎨ ⎬ ⎩1⎭. (3.27).

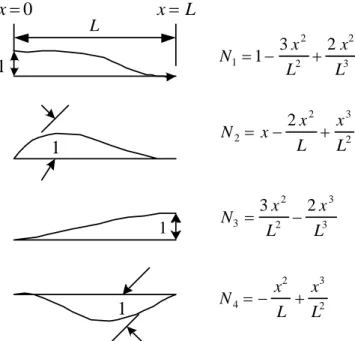
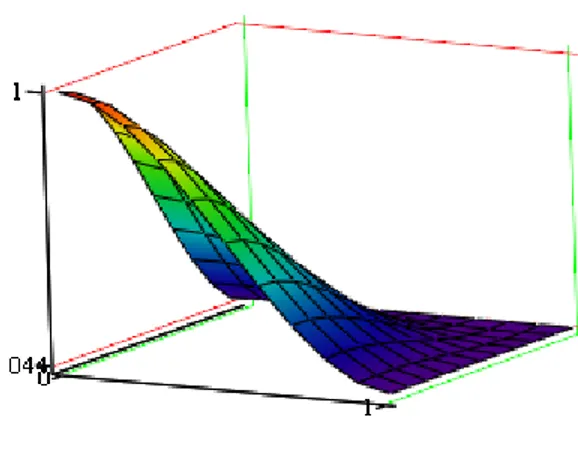
(40) 40 Se obtienen las funciones de forma de los polinomios de Hermite modificados N 1 (s , t ) = H 1 ( s ) ⋅ S1 (t ) − S1 (s ) ⋅ S1 (t ) + S1 (s )⋅ H 1 ( s ) N 2 (s , t ) = H 3 (s )⋅ S1 (t )⋅ a. N 3 (s , t ) = S1 (s )⋅ H 3 (t )⋅ b N 4 (s , t ) = H 2 (s ) ⋅ S1 (t ) − S 2 (s )⋅ S1 (t ) + S 2 (s )⋅ H 1 (t ) N 5 (s , t ) = H 4 (s )⋅ S1 (t )⋅ a N 6 (s , t ) = S 2 (s )⋅ H 3 (t )⋅ b N 7 (s , t ) = H 2 (s ) ⋅ S 2 (t ) − S 2 (s )⋅ S 2 (t ) + S 2 (s )⋅ H 2 (t ) N 8 (s , t ) = H 4 (s )⋅ S 4 (t )⋅ a N 9 (s , t ) = S 2 (s )⋅ H 4 (t )⋅ b N 10 (s , t ) = H 1 (s ) ⋅ S 2 (t ) − S1 (s )⋅ S 2 (t ) + S1 (s )⋅ H 2 (t ) N 11 (s , t ) = H 3 (s )⋅ S 2 (t )⋅ a N 12 (s , t ) = S1 (s )⋅ H 4 (t )⋅ b. La presentación grafica de estos elementos es. Hi( F1). Figura 3.7 Función de forma N 1 .. (3.28).

(41) 41. Hi( F1x). Figura 3.8 Función de forma.. Hi( F1y). Figura 3.9 Función de forma N 3 .. Hi( F2). Figura 3.10 Función de forma N 4 ..

(42) 42. Hi( F1y). Figura 3.11 Función de forma N 5 .. Hi( F3y). Figura 3.12 Función de forma N 6 .. Hi( F3). Figura 3.13 Función de forma N 7 ..

(43) 43. Hi( F2x). Figura 3.14 Función de forma N 8 .. Hi( F4x). Figura 3.15 Función de forma N 9 .. Hi( F4). Figura 3.16 Función de form1 N 10 ..

(44) 44. Hi( F2y). Figura 3.17 Función de forma N 11 .. Hi( F4y). Figura 3.18 Función de forma N 10 .. Se vuelve necesario definir algunas funciones de forma de los polinomio de Hermite que son indispensables para definir y calculo de la matriz de energía, carga, momentos y cortantes.

(45) 45 Primera derivada de N con respecto a s y a t, ecuaciones (3.29) y (3.30). ⎧ H1´ (s) S1 (t ) − S1´ (s) S1 (t ) + S1´ (s) H1 (t ) ⎫ ⎧ H1 (s)S1´ (t) − S1 (s)S1´ (t) + S1 (s)H1´ (t) ⎫ ⎪ ⎪ ⎪ ⎪ ´ ´ H s S t H s S t ( ) ( ) ( ) ( ) 3 1 3 1 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ S1´ (s) H 3 (t ) S1 (s)H1´ (t) ⎪ ⎪ ⎪ ´ ⎪ ´ ´ ´ ´ ´ ⎪ H 2 (s) S1 (t ) − S 2 (s) S1 (t ) + S2 (s) H1 (t ) ⎪ ⎪ H2 (s)S1 (t) − S2 (s)S1 (t) + S2 (s)H1 (t) ⎪ ⎪ ⎪ ⎪ ⎪ H 4´ (s) S1 (t ) H4 (s)S1´ (t) ⎪ ⎪ ⎪ ⎪ S 2´ (s) H 3 (t ) S2 (s)H3´ (t) ⎪ ⎪ ⎪ ⎪ N s (s, t ) = ⎨ ´ ⎬ Nt (s, t) = ⎨ ⎬ ´ ´ ´ ´ ´ ⎪H 2 (s) S 2 (t ) − S 2 (s) S1 (t ) + S 2 (s) H 2 (t )⎪ ⎪H2 (s)S2 (t) − S2 (s)S2 (t) + S2 (s)H2 (t)⎪ ⎪ ⎪ ⎪ ⎪ H 4´ (s) S 2 (t ) H4 (s)S2´ (t) ⎪ ⎪ ⎪ ⎪ ´ ´ S s H t S s H t ( ) ( ) ( ) ( ) ⎪ ⎪ ⎪ ⎪ 2 4 4 2 ⎪ H ´ (s) S (t ) − S ´ (s) S (t ) + S ´ (s) H (t ) ⎪ ⎪ H (s)S ´ (t) − S (s)S´ (t) + S (s)H ´ (t) ⎪ 2 1 2 1 2 2 1 2 1 2 ⎪ ⎪ ⎪ 1 ⎪ 1 ´ ´ H s S t H s S t ( ) ( ) ( ) ( ) ⎪ ⎪ ⎪ ⎪ 3 2 1 4 ⎪ ⎪ ⎪ ⎪ ´ ´ S1 (s) H 4 (t ) S1 (s)H4 (t) ⎭ ⎭ ⎩ ⎩. Segunda derivada de N con respecto a s y t, ecuaciones (3.31) y (3.32). ⎧ H 1´´ ( s ) S1 (t ) ⎫ ⎪ ´´ ⎪ ⎪ H 3 ( s ) S1 (t ) ⎪ ⎪ ⎪ 0 ⎪ ´´ ⎪ ⎪ H 2 ( s ) S1 (t ) ⎪ ⎪ H ´´ ( s ) S (t ) ⎪ 1 ⎪ 4 ⎪ 0 ⎪ ⎪ N s s ( s , t ) = ⎨ ´´ ⎬ ⎪ H 2 ( s ) S 2 (t )⎪ ⎪ H 4´´ ( s ) S 2 (t )⎪ ⎪ ⎪ 0 ⎪ ⎪ ⎪ H ´´ ( s ) S (t )⎪ 2 ⎪ 1´´ ⎪ ( ) H s S ⎪ 3 2 (t ) ⎪ ⎪ ⎪ 0 ⎩ ⎭. ⎧ S 1 ( s ) H 1´´ (t ) ⎫ ⎪ ⎪ 0 ⎪ ⎪ ⎪ S 1 ( s ) H 3´´ (t ) ⎪ ⎪ ⎪ ´´ ⎪ S 2 ( s ) H 1 (t ) ⎪ ⎪ ⎪ 0 ⎪ ⎪ ´´ ⎪ S 2 ( s ) H 3 (t ) ⎪ N t t ( s, t ) = ⎨ ⎬ ´´ ⎪ S 2 ( s ) H 2 (t ) ⎪ ⎪ ⎪ 0 ⎪ ⎪ ´´ ⎪ S 2 ( s ) H 4 (t ) ⎪ ⎪ S ( s ) H ´´ (t ) ⎪ 2 ⎪ 1 ⎪ 0 ⎪ ⎪ ⎪ S ( s ) H ´´ (t ) ⎪ 4 ⎩ 1 ⎭.