U N I V E R S I D A D E D A C O R U Ñ A
E . T . S . D E I N G E N I E R O S D E C A M I N O S , C A N A L E S Y P U E R T O S
T E S I S D O C T O R A L
RESTRICCIONES EN TENSIÓN Y
MINIMIZACIÓN DEL PESO: UNA
METODOLOGÍA GENERAL PARA LA
OPTIMIZACIÓN TOPOLÓGICA DE
ESTRUCTURAS
POR
JOSÉ PARÍS LÓPEZ
DIRIGIDA POR
MANUEL CASTELEIRO MALDONADO
IGNASI COLOMINAS EZPONDA
U N I V E R S I D A D E D A C O R U Ñ A
E . T . S . D E I N G E N I E R O S D E C A M I N O S , C A N A L E S Y P U E R T O S
T E S I S D O C T O R A L
RESTRICCIONES EN TENSIÓN Y
MINIMIZACIÓN DEL PESO: UNA
METODOLOGÍA GENERAL PARA LA
OPTIMIZACIÓN TOPOLÓGICA DE
ESTRUCTURAS
POR
JOSÉ PARÍS LÓPEZ
Ingeniero de Caminos, Canales y PuertosDIRIGIDA POR
MANUEL CASTELEIRO MALDONADO
Dr. Ingeniero de Caminos, Canales y PuertosIGNASI COLOMINAS EZPONDA
Dr. Ingeniero Industrial´
Indice general
´Indice de figuras VII
´Indice de tablas XIII
1. Introducci´on y objetivos 1
1.1. Introducci´on . . . 1
1.2. Evoluci´on de la optimizaci´on de estructuras: la optimizaci´on topol´ogica . . 2
1.3. Objetivos de la tesis . . . 7
1.4. Organizaci´on de la tesis . . . 9
2. Estado actual del conocimiento 11 2.1. Introducci´on . . . 11
2.2. Formulaciones discretas del problema . . . 12
2.2.1. Criterios de Optimalidad (Optimality Criteria) . . . 13
2.2.2. Optimizaci´on Estructural Evolutiva (Evolutionary Structural Optimi-zation) . . . 14
2.2.3. Hierarchical Neighborhood Optimization Method. . . 15
2.2.4. M´etodo de las Curvas de Nivel (Level Set Method) . . . 16
2.2.5. M´etodo de la Burbuja (Bubble Method) . . . 16
2.2.6. Algoritmos gen´eticos o evolutivos (Genetic Algorithms) . . . 17
2.3. Formulaciones continuas del problema . . . 18
2.3.1. T´ecnicas de Homogeneizaci´on (Homogenization) . . . 19
2.3.2. Modelo de material: “hole-in-cell” . . . 20
2.3.3. Modelo de microestructuras formadas por capas (Layered Microstruc-tures) . . . 21
2.3.4. Material S´olido Isotr´opico con Penalizaci´on (SIMP) . . . 22
2.4. Otras aplicaciones de la optimizaci´on topol´ogica . . . 25
2.5. Resumen . . . 27
3. Formulaci´on del problema estructural 29 3.1. Introducci´on . . . 29
3.2.1. Modelo num´erico de Elementos Finitos . . . 31
3.3. An´alisis estructural de material con densidad relativa . . . 33
3.3.1. Modelo num´erico de Elementos Finitos con densidad relativa . . . . 34
3.4. Resumen . . . 36
4. Formulaci´on del problema de optimizaci´on topol´ogica 37 4.1. Introducci´on . . . 37
4.2. Formulaci´on de m´ınimo peso . . . 38
4.3. Funci´on objetivo . . . 39
4.4. Restricciones en tensi´on . . . 40
4.5. Restricciones en tensi´on de tipo local . . . 40
4.5.1. Fen´omenos de singularidad . . . 42
4.6. Restricci´on en tensi´on de tipo global . . . 46
4.7. Reducci´on por bloques de restricciones de tipo local . . . 50
4.8. Planteamiento de condiciones sobre el per´ımetro de la soluci´on . . . 53
4.9. Resumen . . . 57
5. Algoritmos de optimizaci´on 59 5.1. Introducci´on . . . 59
5.2. Algoritmo SLP-QLS (Programaci´on Lineal Secuencial con B´usqueda Unidi-reccional Cuadr´atica) . . . 60
5.2.1. Algoritmo de M´aximo Descenso . . . 61
5.2.2. Algoritmo de Programaci´on Lineal Secuencial . . . 62
5.2.3. Direcci´on de Entrada a la Regi´on Factible . . . 62
5.2.4. B´usqueda del factor de avance . . . 63
5.3. Algoritmo MMA (M´etodo de las As´ıntotas M´oviles) . . . 64
5.4. Funciones barrera . . . 65
5.5. Restricciones laterales . . . 68
5.6. T´ecnicas de refinamiento de la soluci´on . . . 75
5.7. Resumen . . . 77
6. An´alisis de Sensibilidad 79 6.1. Introducci´on . . . 79
6.2. Consideraciones previas . . . 80
6.3. An´alisis de sensibilidad de funciones dependientes de las variables de dise˜no 82 6.4. An´alisis de sensibilidad de funciones dependientes de las variables de estado y de las variables de dise˜no . . . 83
6.4.1. Diferenciaci´on num´erica . . . 83
6.4.2. Diferenciaci´on anal´ıtica directa . . . 84
6.4.3. Diferenciaci´on anal´ıtica por el M´etodo de la Variable Adjunta . . . . 88
6.5. An´alisis de sensibilidad de restricciones en tensi´on . . . 90
6.5.1. An´alisis de sensibilidad de la tensi´on de Comparaci´on de Von Mises 91 6.5.2. An´alisis de sensibilidad del tensor de tensiones . . . 93
6.6. An´alisis de sensibilidad de la funci´on objetivo . . . 95
6.6.2. Derivadas direccionales de primer y segundo orden . . . 95
6.6.3. An´alisis de sensibilidad de la funci´on per´ımetro . . . 95
6.7. An´alisis de sensibilidad de las restricciones en tensi´on locales . . . 97
6.7.1. Derivadas de primer orden completas . . . 97
6.7.2. Derivadas direccionales de primer y segundo orden . . . 99
6.8. An´alisis de sensibilidad de la restricci´on en tensi´on global . . . 100
6.8.1. Derivadas de primer orden completas . . . 101
6.8.2. Derivadas direccionales de primer y segundo orden . . . 102
6.9. An´alisis de sensibilidad de las restricciones en tensi´on por bloques . . . 104
6.9.1. Derivadas de primer orden completas . . . 104
6.9.2. Derivadas direccionales de primer y segundo orden . . . 105
6.10. An´alisis de Sensibilidad de la Funci´on Barrera Inversa . . . 106
6.10.1. Derivadas de primer orden completas . . . 106
6.10.2. Derivadas direccionales de primer y segundo orden . . . 107
6.11. Resumen . . . 108
7. Metodolog´ıa de dise˜no ´optimo e implementaci´on num´erica 111 7.1. Introducci´on . . . 111
7.2. Metodolog´ıa de dise˜no ´optimo . . . 112
7.3. Implementaci´on num´erica y aspectos computacionales . . . 116
7.3.1. An´alisis estructural por Elementos Finitos . . . 116
7.3.2. An´alisis de sensibilidad . . . 117
7.3.3. Implementaci´on del algoritmo SLP-QLS . . . 121
7.4. C´alculo en paralelo . . . 121
7.4.1. Introducci´on . . . 121
7.4.2. T´ecnicas inform´aticas de paralelizaci´on . . . 122
7.4.3. Paralelizaci´on de algoritmos de optimizaci´on . . . 123
7.5. Resumen . . . 125
8. Ejemplos de aplicaci´on 127 8.1. Introducci´on . . . 127
8.2. Ejemplos de validaci´on de la formulaci´on propuesta . . . 130
8.2.1. Soluci´on en arco . . . 130
8.2.2. Problema del voladizo de Michell . . . 137
8.2.3. Problema de la viga en voladizo . . . 146
8.3. Ejemplos pr´acticos de aplicaci´on . . . 157
8.3.1. Viga MBB . . . 157
8.3.2. Viga en forma de L . . . 168
8.3.3. Viga continua de dos vanos . . . 178
8.3.4. Soporte en voladizo . . . 184
8.4. Ejemplos de aplicaci´on combinando t´ecnicas de optimizaci´on y refinamiento de malla . . . 194
8.4.1. Viga con carga centrada de Michell . . . 194
8.4.2. Biela de motor . . . 203
9. Conclusiones y futuras l´ıneas de investigaci´on 219
9.1. Conclusiones . . . 219
9.1.1. Resumen . . . 219
9.1.2. Conclusiones generales . . . 220
9.1.3. Conclusi´on final . . . 222
9.2. Futuras l´ıneas de investigaci´on . . . 223
A. Desarrollo de un algoritmo de Programaci´on Lineal Secuencial 225 A.1. Introducci´on . . . 225
A.2. Planteamiento del problema general de optimizaci´on . . . 226
A.3. Programaci´on Lineal Secuencial (SLP) . . . 227
A.3.1. Planteamiento general . . . 227
A.3.2. El algoritmo Simplex . . . 227
A.3.3. C´alculo de una soluci´on inicial v´alida . . . 235
A.3.4. Aplicaci´on del algoritmo de Programaci´on Lineal Secuencial a la re-soluci´on de problemas estructurales . . . 237
A.4. Implementaci´on num´erica del algoritmo de Programaci´on Lineal Secuencial 243 A.4.1. Aplicabilidad del m´etodo propuesto . . . 245
A.5. Recapitulaci´on . . . 246
A.6. Ejemplo de c´alculo . . . 247
A.6.1. Fase I: C´alculo de la soluci´on inicial v´alida . . . 250
A.6.2. Fase II: Optimizaci´on de la soluci´on obtenida . . . 252
´
Indice de figuras
1.1. Soporte en voladizo. Esquema del problema de optimizaci´on (Zhang [124]) . 4 1.2. Soporte en voladizo. Soluci´on mediante optimizaci´on de formas (Zhang [124]) 5 1.3. Soporte en voladizo. Soluci´on ´optima de m´axima rigidez (Duysinx [18]) . . 6 1.4. Soporte en voladizo. Soluci´on ´optima de m´ınimo peso con restricciones locales
en tensi´on . . . 8
2.1. Esquema de evoluci´on del M´etodo de la Burbuja. . . 17 2.2. Estructura“hole-in-cell” (Olhoff y Eschenauer [71]) . . . 20 2.3. Microestructura bidimensional por capas de rango 3 (Olhoff y Eschenauer [71]) 22 2.4. Microestructura tridimensional por capas de rango 3 (Olhoff y Eschenauer [71]) 22 2.5. Efecto de la penalizaci´on sobre la rigidez en el modelo SIMP . . . 23 2.6. Microestructura correspondiente para el modelo SIMP (p = 3, ν = 1/3)
Bendsøe y Sigmund [7], Eschenauer y Olhoff [26] . . . 24 2.7. Microestructura del modelo SIMP (p= 3, ν= 0), Bendsøe y Sigmund [7] . 25 2.8. Microestructura del modelo SIMP (p= 3, ν= 0.5), Bendsøe y Sigmund [7] 25 2.9. Soluci´on de viga en voladizo con disposici´on en damero (D´ıaz y Sigmund [17]) 26 2.10. Microestructura con coeficiente de dilataci´on negativo (Sigmund,et al.[97],
[98]) . . . 27 2.11. Microestructura con coeficiente de Poisson negativo (Sigmund,et al. [97], [98]) 27
4.1. Exponente de la funci´on objetivo para distintos valores de penalizaci´on. . . 40 4.2. Secci´on de viga con platabandas de densidad variable. . . 42 4.3. Restricci´on en tensiones reales en viga con platabandas paraη= 0.1
(restric-ci´on escalada porbσmax) . . . 43
4.4. Restricci´on en tensiones efectivas en viga con platabandas para η= 0.1 (res-tricci´on escalada porbσmax) . . . 44
4.5. Factor de relajaci´on para diferentes valores de ε. . . 45 4.6. Restricci´on en tensiones reales (izquierda) y en tensiones efectivas (derecha)
para diferentes valores deε. (Restricci´on escalada porσbmax) . . . 45
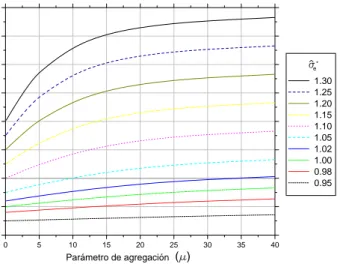
4.8. Funci´on global de restricciones para distintos valores de µ con n´umero de
restricciones violadas creciente . . . 50
4.9. Definici´on de un bloque de elementos de la malla . . . 51
4.10. Funci´on aproximada del valor absoluto. . . 57
5.1. Efecto del par´ametro r sobre la funci´on barrera φ(ρ, r) en un problema 1D conF =x yx∗−x≤0 (Fletcher [27]). . . 67
5.2. Planteamiento del problema de la secci´on a flexi´on pura . . . 69
5.3. Variables de dise˜no del problema de la secci´on a flexi´on pura . . . 71
5.4. Representaci´on gr´afica del problema de optimizaci´on . . . 72
5.5. Regi´on factible del problema de la secci´on a flexi´on pura . . . 73
5.6. Soluci´on sin incorporar las restricciones laterales en la direcci´on de avance . 74 5.7. Soluci´on incorporando las restricciones laterales en la direcci´on de avance . 74 5.8. Refinamiento adaptativo de la malla de Elementos Finitos (Maute y Ramm [51]) . . . 75
5.9. Malla original para el problema de una viga con carga descentrada (450 elementos) . . . 77
5.10. Malla refinada eliminando elementos no necesarios (808 elementos) . . . 77
5.11. Malla refinada por segunda vez eliminando elementos no necesarios (2352 elementos) . . . 77
7.1. Metodolog´ıa de c´alculo para el problema de optimizaci´on topol´ogica . . . . 113
8.1. Arco. Planteamiento del problema (unidades en m) . . . 131
8.2. Arco. Evoluci´on de la soluci´on obtenida con la formulaci´on local . . . 132
8.3. Arco. Soluci´on ´optima obtenida con la formulaci´on local . . . 132
8.4. Arco. Evoluci´on de la soluci´on obtenida con la formulaci´on global . . . 133
8.5. Arco. Soluci´on ´optima obtenida con la formulaci´on global . . . 133
8.6. Arco. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques . . 134
8.7. Arco. Soluci´on ´optima obtenida con la formulaci´on por bloques . . . 134
8.8. Arco. Tensi´on normalizada obtenida con la formulaci´on local . . . 135
8.9. Arco. Tensi´on normalizada obtenida con la formulaci´on global . . . 135
8.10. Arco. Tensi´on normalizada obtenida con la formulaci´on por bloques . . . . 135
8.11. Voladizo Michell. Soluci´on te´orica del problema (Michell [52]) . . . 138
8.12. Voladizo Michell. Planteamiento del problema de optimizaci´on (izqda.) y ma-lla de Elementos Finitos empleada en la resoluci´on (derecha). Unidades en cm . . . 138
8.13. Voladizo Michell. Evoluci´on de la soluci´on obtenida con la formulaci´on local 139 8.14. Voladizo Michell. Soluci´on ´optima obtenida con la formulaci´on local . . . . 140
8.15. Voladizo Michell. Tensi´on normalizada de la soluci´on obtenida con la formu-laci´on local . . . 140
8.16. Voladizo Michell. Evoluci´on de la soluci´on obtenida con la formulaci´on global 141 8.17. Voladizo Michell. Soluci´on ´optima obtenida con la formulaci´on global . . . . 142
8.19. Voladizo Michell. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques . . . 143 8.20. Voladizo Michell. Soluci´on ´optima obtenida con la formulaci´on por bloques 144 8.21. Voladizo Michell. Tensi´on normalizada de la soluci´on obtenida con la
formu-laci´on por bloques . . . 144 8.22. Voladizo. Planteamiento del problema (unidades en m) . . . 147 8.23. Voladizo. Evoluci´on de la soluci´on obtenida con la formulaci´on local . . . . 148 8.24. Voladizo. Soluci´on ´optima obtenida con la formulaci´on local . . . 149 8.25. Voladizo. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
local . . . 149 8.26. Voladizo. Evoluci´on de la soluci´on obtenida con la formulaci´on global . . . . 150 8.27. Voladizo. Soluci´on ´optima obtenida con la formulaci´on global . . . 151 8.28. Voladizo. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
global . . . 151 8.29. Voladizo. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques 152 8.30. Voladizo. Soluci´on ´optima obtenida con la formulaci´on por bloques . . . 153 8.31. Voladizo. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on por
bloques . . . 153 8.32. Voladizo. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques
y penalizaci´on sobre el per´ımetro . . . 154 8.33. Voladizo. Soluci´on ´optima obtenida con la formulaci´on por bloques y
penali-zaci´on sobre el per´ımetro . . . 155 8.34. Voladizo. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on por
bloques y penalizaci´on sobre el per´ımetro . . . 155 8.35. Viga MBB. Planteamiento del problema (unidades en m) . . . 158 8.36. Viga MBB. Soluci´on te´orica (Lewinski,et al. [44]) . . . 158 8.37. Viga MBB. Viga en la secci´on central del fuselaje del avi´on Airbus A380.
(www.diplomatie.gouv.fr/en/album.php3?id article=4375&debut image=2) 159 8.38. Viga MBB. Detalle de viga de fuselaje de Airbus A380. (Aviation Week &
Space Technology, 20 de noviembre de 2006, p´ag. 34) . . . 159 8.39. Viga MBB. Evoluci´on de la soluci´on obtenida con la formulaci´on local . . . 160 8.40. Viga MBB. Evoluci´on de la soluci´on obtenida con la formulaci´on local
(con-tinuaci´on) . . . 161 8.41. Viga MBB. Soluci´on ´optima obtenida con la formulaci´on local . . . 161 8.42. Viga MBB. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
local . . . 161 8.43. Viga MBB. Evoluci´on de la soluci´on obtenida con la formulaci´on global . . 162 8.44. Viga MBB. Evoluci´on de la soluci´on obtenida con la formulaci´on global
(con-tinuaci´on) . . . 163 8.45. Viga MBB. Soluci´on ´optima obtenida con la formulaci´on global . . . 163 8.46. Viga MBB. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
8.48. Viga MBB. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques (continuaci´on) . . . 165 8.49. Viga MBB. Soluci´on ´optima obtenida con la formulaci´on por bloques . . . . 165 8.50. Viga MBB. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
por bloques . . . 165 8.51. Viga MBB. Soluci´on de m´axima rigidez de Duysinx y Bendsøe [20] . . . 166 8.52. Viga en L. Planteamiento del problema (unidades en m) . . . 169 8.53. Viga en L. Evoluci´on de la soluci´on obtenida con la formulaci´on local . . . . 170 8.54. Viga en L. Soluci´on ´optima obtenida con la formulaci´on local . . . 171 8.55. Viga en L. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
local . . . 171 8.56. Viga en L. Evoluci´on de la soluci´on obtenida con la formulaci´on global . . . 172 8.57. Viga en L. Soluci´on ´optima obtenida con la formulaci´on global . . . 173 8.58. Viga en L. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
global . . . 173 8.59. Viga en L. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques 174 8.60. Viga en L. Soluci´on ´optima obtenida con la formulaci´on por bloques . . . . 175 8.61. Viga en L. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
por bloques . . . 175 8.62. Viga en L. Soluci´on ´optima de m´axima rigidez (Duysinx y Bendsøe [20]) . . 176 8.63. Viga 2 vanos. Planteamiento del problema (unidades en m) . . . 178 8.64. Viga 2 vanos. Evoluci´on de la soluci´on obtenida con la formulaci´on local . . 179 8.65. Viga 2 vanos. Soluci´on ´optima obtenida con la formulaci´on local . . . 179 8.66. Viga 2 vanos. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
local . . . 179 8.67. Viga 2 vanos. Evoluci´on de la soluci´on obtenida con la formulaci´on global . 180 8.68. Viga 2 vanos. Soluci´on ´optima obtenida con la formulaci´on global . . . 180 8.69. Viga 2 vanos. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
global . . . 180 8.70. Viga 2 vanos. Evoluci´on de la soluci´on obtenida con la formulaci´on por
bloques . . . 181 8.71. Viga 2 vanos. Soluci´on ´optima obtenida con la formulaci´on por bloques . . 181 8.72. Viga 2 vanos. Tensi´on normalizada de la soluci´on obtenida con la formulaci´on
por bloques . . . 181 8.73. Soporte en voladizo. Planteamiento del problema (unidades en cm) y malla
de elementos finitos utilizada . . . 185 8.74. Soporte en voladizo. Malla de elementos finitos utilizada . . . 185 8.75. Soporte en voladizo. Evoluci´on de la soluci´on obtenida con la formulaci´on
local . . . 186 8.76. Soporte en voladizo. Soluci´on ´optima obtenida con la formulaci´on local . . . 187 8.77. Soporte en voladizo. Tensi´on normalizada de la soluci´on obtenida con la
for-mulaci´on local . . . 187 8.78. Soporte en voladizo. Evoluci´on de la soluci´on obtenida con la formulaci´on
8.79. Soporte en voladizo. Soluci´on ´optima obtenida con la formulaci´on global . . 189 8.80. Soporte en voladizo. Tensi´on normalizada de la soluci´on obtenida con la
for-mulaci´on global . . . 189 8.81. Soporte en voladizo. Evoluci´on de la soluci´on obtenida con la formulaci´on
por bloques . . . 190 8.82. Soporte en voladizo. Soluci´on ´optima obtenida con la formulaci´on por bloques 191 8.83. Soporte en voladizo. Tensi´on normalizada de la soluci´on obtenida con la
for-mulaci´on por bloques . . . 191 8.84. Soporte en voladizo. Soluci´on obtenida mediante optimizaci´on de formas por
Zhang [124] . . . 193 8.85. Viga Michell. Planteamiento del problema (izqda.) y malla de elementos
fi-nitos (dcha.). Unidades en cm . . . 195 8.86. Viga Michell. Evoluci´on de la soluci´on obtenida con la formulaci´on local . . 196 8.87. Viga Michell. Soluci´on ´optima (arriba) y tensi´on normalizada (abajo)
obte-nida con la formulaci´on local . . . 197 8.88. Viga Michell. Malla refinada eliminando los elementos conρe<0.002 . . . . 198
8.89. Viga Michell. Evoluci´on de la soluci´on del problema remallado obtenida con la formulaci´on por bloques . . . 199 8.90. Viga Michell. Soluci´on ´optima del problema remallado obtenida con la
for-mulaci´on por bloques . . . 200 8.91. Viga Michell. Tensi´on normalizada del problema remallado obtenida con la
formulaci´on por bloques . . . 200 8.92. Viga Michell. Soluci´on ´optima te´orica (Michell [52]) . . . 201 8.93. Biela. Planteamiento del problema (unidades en cm) (izqda.) y malla de
Elementos Finitos empleada para su resoluci´on (dcha.) . . . 204 8.94. Biela. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques . . 206 8.95. Biela. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques
(con-tinuaci´on I) . . . 207 8.96. Biela. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques
(con-tinuaci´on II) . . . 208 8.97. Biela. Soluci´on ´optima del problema obtenida con la formulaci´on por bloques
(izqda.) y tensi´on normalizada (dcha.) . . . 209 8.98. Biela. Malla de Elementos Finitos refinada eliminando los elementos conρ <
0.005 . . . 210 8.99. Biela. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques con
penalizaci´on sobre el per´ımetro . . . 211 8.100.Biela. Evoluci´on de la soluci´on obtenida con la formulaci´on por bloques con
penalizaci´on sobre el per´ımetro (continuaci´on) . . . 212 8.101.Biela. Soluci´on ´optima obtenida con la formulaci´on por bloques sin
penaliza-ci´on en el per´ımetro (izqda.), soluci´on ´optima obtenida con penalizaci´on en el per´ımetro (centro) y tensi´on normalizada (dcha.) . . . 213
´
Indice de tablas
8.1. Arco. Resumen de los principales par´ametros y requerimientos computacionales136 8.2. Voladizo Michell. Resumen de los principales par´ametros y requerimientos
computacionales . . . 145 8.3. Voladizo. Resumen de los principales par´ametros y necesidades computacionales156 8.4. Viga MBB. Resumen de los principales par´ametros y necesidades
computa-cionales . . . 167 8.5. Viga en L. Resumen de los principales par´ametros y aspectos computacionales177 8.6. Viga 2 vanos. Resumen de los principales par´ametros y aspectos
computa-cionales . . . 183 8.7. Soporte en voladizo. Resumen de los principales par´ametros y necesidades
computacionales . . . 193 8.8. Viga Michell. Resumen de los par´ametros y aspectos computacionales m´as
Agradecimientos
Siempre he escuchado que es de bien nacido ser agradecido y en este momento no tengo m´as que agradecer toda la ayuda recibida para realizar esta tesis doctoral.
En primer lugar quiero agradecer a los profesores Manuel Casteleiro, Ignasi Colominas y Ferm´ın Navarrina el haberme ofrecido la posibilidad de desarrollar las tareas de investigaci´on que han dado lugar a esta tesis doctoral en un ambiente cordial y agradable. Su esfuerzo y dedicaci´on hacen posible que el Grupo de M´etodos Num´ericos en Ingenier´ıa sea uno de los m´as activos en la Universidade da Coru˜na y un referente a nivel nacional e internacional en investigaci´on sobre M´etodos Num´ericos en Ingenier´ıa.
A Manuel Casteleiro e Ignasi Colominas tengo que agradecerles su especial inter´es e incesante apoyo en las etapas dif´ıciles de esta tesis. Sin cesar en sus objetivos y en sus pretensiones finales me han orientado en los momentos m´as desconcertantes y han sabido sacar lo mejor de m´ı para alcanzar los objetivos planteados. A Ferm´ın Navarrina le agradezco enormemente su constante apoyo y su inestimable colaboraci´on en los temas de optimizaci´on. Su experiencia y sabidur´ıa ha sido fundamental para la consecuci´on de los prop´ositos de esta tesis. Tambi´en tengo que agradecer a Jos´e Luis A˜n´on su eficacia y dedicaci´on. Su ayuda y predisposici´on me han permitido evitar las pesadas tareas administrativas y as´ı poder dedicarme de forma m´as intensiva a las tareas de investigaci´on.
Tambi´en quiero agradecer a Iago Mu´ı˜nos su colaboraci´on en las primeras fases de la realizaci´on de esta tesis. El maravilloso trabajo de investigaci´on desarrollado en su proyecto t´ecnico fue el germen que dio origen a los primeros resultados en optimizaci´on topol´ogica de estructuras para nuestro grupo. Suyo es el m´erito de iniciar esta l´ınea de investigaci´on y de enfrentarse a los retos que ello supone.
No quiero olvidarme tampoco de agradecer el apoyo y asesor´ıa en temas inform´aticos que he recibido por parte del personal del Centro de Supercomputaci´on de Galicia (CESGA). En especial quiero reconocerles a Aurelio Rodr´ıguez y a Carlos Fern´andez su inter´es y colaboraci´on en la depuraci´on de errores de programaci´on.
A mis amigos y compa˜neros tengo que reconocerles la dif´ıcil labor de ayudarme y aguantar mis elucubraciones durante las fases m´as ingratas y duras de la elaboraci´on de esta tesis. Quiero recordar especialmente a mis amigos Diego, Javi, Alberto, Jos´e Enrique y Ton, entre otros muchos, as´ı como a Luis Cueto-Felgueroso, a Xes´us y a todos los compa˜neros del Grupo de M´etodos Num´ericos en Ingenier´ıa.
TESIS DOCTORAL
Esta Tesis Doctoral se present´o el d´ıa 13 de Marzo de 2008 en la Escuela T´ecnica
Superior de Ingenier´ıa de Caminos, Canales y Puertos de A Coru˜na.
El Tribunal de Tesis Doctoral lo compon´ıan los siguientes doctores:
Presidente Dr. Ferm´ın Luis NAVARRINA MART´INEZ
Catedr´atico de Universidad ´
Area de Matem´atica Aplicada Universidade da Coru˜na
Vocal Dr. Gabriel BUGEDA CASTELLTORT
Catedr´atico de Universidad ´
Area de Mec´anica de Medios Continuos y Teor´ıa de Estructuras Universitat Polit`ecnica de Catalunya
Vocal Dr. Pascual MART´I MONTRULL
Catedr´atico de Universidad ´
Area de Mec´anica de Medios Continuos y Teor´ıa de Estructuras Universidad Polit´ecnica de Cartagena
Vocal Dr. Carlos Alberto DA CONCEIC¸ ˜AO ANT ´ONIO
Profesor Asociado ´
Area de Matem´aticas Universidade do Porto
Secretario Dr. Santiago HERN ´ANDEZ IB ´A ˜NEZ
Catedr´atico de Universidad ´
Area de Mec´anica de Medios Continuos y Teor´ıa de Estructuras Universidade da Coru˜na
Resumen
La optimizaci´on topol´ogica de estructuras continuas es una disciplina que pretende obtener la distribuci´on ´optima de material en un dominio predefinido de modo que se cumplan las condiciones resistentes exigidas. Se trata, por lo tanto, de un problema con variables discretas ya que se pretende decidir si en un punto del dominio debe existir o no material resistente. Este planteamiento discreto es muy complejo y por ello, habitualmente, se estudia mediante formulaciones continuas introduciendo el concepto de densidad relativa para identificar el estado material (0=vac´ıo, 1=lleno). Para ello, es necesario definir modelos de microestructura de material que permiten evaluar la respuesta estructural de forma continua para valores de densidad relativa comprendidos entre 0 y 1.
Los problemas de optimizaci´on topol´ogica de estructuras continuas han sido estudia-dos tradicionalmente con formulaciones que maximizan la rigidez de la estructura. Estos modelos pretenden encontrar la estructura de m´axima rigidez empleando un volumen de material prefijado que se distribuye sobre un dominio predefinido. Este tipo de formulacio-nes presenta serios inconvenientes ya que no se impone ninguna restricci´on en tensiones o desplazamientos que garantice la validez de la estructura y adem´as se requiere el uso de t´ecnicas de estabilizaci´on para evitar fen´omenos indeseados como la disposici´on en damero de la soluci´on o la dependencia de la malla. Es m´as, la obtenci´on del dise˜no de m´axima ri-gidez es un problema mal planteado dado que la soluci´on no converge al aumentar el grado de discretizaci´on utilizado.
Abstract
Stress Contraints and Weight Minimization: A General Methodology for Topology
Optimization of Structures
by
Jos´e Par´ıs L´opez
Civil Engineer
University of A Coru˜na
Topology optimization of continuum structures is a technique that pretends to find the optimal distribution of material in a predefined material such that the required structural conditions are satisfied. Thus, the discrete approach of the topology optimization of struc-tures problem tries to decide if at each point of the domain must exist material or not. This approach of the discrete optimization problem is very complicated. So, the discrete approach is usually transformed into a continuous one by introducing the concept of relative density, which means the material state (0=void and 1=solid). In addition, it is necessary to define microstructure models of the material (SIMP,...) that allows to obtain the structural response for intermediate values of the relative densities.
in other structural optimization techniques (dimension or shape optimization). The stated problem is much more realistic from an engineering point of view because it minimizes the economic cost of the structural solution satisfying the mandatory structural norms and laws that correspond nowadays. In addition, minimum weight formulations with stress constraints avoid some difficulties and instabilities of the maximum stiffness approaches like checkerboard, mesh dependency or the previous election of a convenient but unjustified volume of material.
The most usual way of imposing the stress constraints involves to check that the stress of the central point of each one of the elements of the Finite Element mesh does not exceed the maximum stress allowed. Thus, it is very usual to use formulations with constant relative density per element. This way of imposing the stress constraints is usually called local approach of stress constraints. This formulation is very robust and reliable but it also requires a huge computing effort due to the large number of design variables and highly non linear stress constraints. In addition, stress constraints is subjected to some singularity phenomena because they are discontinuous when the relative density tends to zero.
Due to the huge computing effort required by the local approach of the stress constraints two additional formulations that make the optimization problem easier are proposed; the global approach of the stress constraints and a formulation defined over blocks of elements. The global approach of the stress constraints states only one stress constraint that aggrega-tes the effect of all the local ones. This formulation reduces drastically the computing effort but does not strictly guarantee the feasibility of the solution. The formulation that imposes stress constraints over blocks of elements divides the domain of the structure in groups of elements and applies one global stress constraint over the elements of each group. According to that, the computational effort is considerably reduced and the feasibility of the stress constraint is guaranteed with enough accuracy. In addition, this formulation is more general because it includes both previous formulations if the right choice of the number of blocks is applied.
Cap´ıtulo 1
Introducci´
on y objetivos
Las creencias antiguas son dif´ıciles de erradicar incluso aunque sean demostrablemente falsas.
Edward Osborne Wilson (1929)
1.1.
Introducci´
on
Desde los comienzos de la Humanidad el hombre siempre ha pretendido obtener estruc-turas resistentes para mejorar su calidad de vida, lo que se interpretaba como s´ımbolo de progreso y de evoluci´on. Los avances, generalmente, se consegu´ıan realizando pruebas expe-rimentales, a trav´es de procedimientos de prueba y error, basados en deducciones emp´ıricas y a partir de la observaci´on de la naturaleza.
El proceso de evoluci´on ha sido, por este motivo, tremendamente lento aunque continua-do en el tiempo. S´olo en la ´epoca moderna y con el desarrollo de nuevas teor´ıas matem´aticas ha sido posible realizar estudios para determinar el comportamiento de los materiales. Se obtienen as´ı formulaciones para el estudio de la respuesta estructural que permiten conocer los mecanismos de fallo y, en consecuencia, disponer de informaci´on para poder evitarlos o al menos reducir su efecto. Es en el siglo XX y con el espectacular desarrollo de las herramien-tas de c´alculo cuando se proponen distintas formulaciones basadas en los estudios te´oricos precedentes para resolver problemas concretos y as´ı poder predecir la respuesta estructural. Los modelos empleados habitualmente con esta finalidad son, por ejemplo, el M´etodo de Elementos Finitos o el C´alculo Matricial de Estructuras de Barras entre otros.
que reside en el dise˜no de los elementos resistentes se sigue proponiendo, fundamentalmente, seg´un criterios experimentales y personales del dise˜nador. En el mejor de los casos las soluciones que se proponen habitualmente se obtienen mediante un proceso iterativo de prueba y error. Es decir, se establece un dise˜no y se comprueba su factibilidad con las t´ecnicas que se han planteado para, a continuaci´on, modificarlo en funci´on de su respuesta estructural y definir un nuevo dise˜no mejorado. ´Este es uno de los motivos que provocan que se utilicen en la pr´actica distintas soluciones para un mismo problema en funci´on de la persona que se encargue del dise˜no o de las t´ecnicas ingenieriles de construcci´on m´as habituales de cada zona geogr´afica, lo cual no parece en absoluto razonable.
Una vez alcanzado un considerable desarrollo y una amplia difusi´on de las t´ecnicas de c´alculo y comprobaci´on de estructuras, es necesario proponer o estudiar planteamien-tos que, adem´as de garantizar la validez de la soluci´on, propongan modificaciones sobre la misma basados en criterios objetivos previamente definidos. De este modo la fase de dise˜no no quedar´a ligada a criterios subjetivos exclusivamente y se podr´an obtener las solucio-nes m´as adecuadas de un modo riguroso que cumplan las exigencias establecidas en las correspondientes leyes y normas de aplicaci´on.
Esta necesidad de plantear t´ecnicas rigurosas que busquen mejores soluciones a los problemas estructurales dio origen a la optimizaci´on de estructuras. Esta disciplina pre-tende, por tanto, establecer un modelo matem´atico riguroso que permita buscar la mejor soluci´on estructural que cumpla la funci´on para la que ha sido dise˜nada de acuerdo con las necesidades predefinidas.
A pesar de sus enormes ventajas, estos planteamientos de dise˜no ´optimo no han alcan-zado en la actualidad el nivel de desarrollo ni de aplicaci´on en ingenier´ıa que han logrado los m´etodos de c´alculo de estructuras debido a su mayor complejidad y al hecho de que no existe un enfoque ´unico que permita abordar la resoluci´on de diferentes problemas. En general, es necesario utilizar formulaciones y t´ecnicas de optimizaci´on diferentes para cada problema estructural en funci´on de sus caracter´ısticas; a diferencia de lo que ocurre con los m´etodos de c´alculo de estructuras presentados, que pueden ser utilizados directamente en numerosas aplicaciones diferentes.
1.2.
Evoluci´
on de la optimizaci´
on de estructuras: la
optimi-zaci´
on topol´
ogica
una fecha de referencia que fije el nacimiento de esta disciplina. Sin embargo, tienen gran trascendencia en las primeras etapas de desarrollo los trabajos realizados por Michell [52] en 1904 as´ı como los planteamientos utilizados en la industria aeron´autica en los a˜nos 40 del siglo XX motivados en gran medida por la 2a Guerra Mundial1. Posteriormente, en los a˜nos 50 y 60 son Klein [40] y Schmit [93] los que proponen una formulaci´on matem´atica estandarizada as´ı como la aplicaci´on conjunta de estas formulaciones con los m´etodos de c´alculo de estructuras existentes.
A partir de este momento y hasta la actualidad, los problemas de optimizaci´on han ido evolucionando de forma paralela a la evoluci´on de las t´ecnicas y algoritmos de resoluci´on existentes y de la capacidad de c´alculo de las herramientas de computaci´on. A medida que se han ido alcanzando nuevos avances tecnol´ogicos ha sido posible el enunciado y la resoluci´on de problemas de ingenier´ıa m´as complejos y que necesitan, por lo tanto, menos contribuci´on por parte del dise˜nador.
As´ı, en la optimizaci´on de estructuras se han planteado dos l´ıneas de investigaci´on prin-cipales. El primer campo de desarrollo consiste en el estudio de problemas de optimizaci´on de las dimensiones de los elementos que componen la estructura sin modificar la geometr´ıa global de la misma (optimizaci´on de dimensiones oSize Optimization). Esta l´ınea de inves-tigaci´on suele estar ligada, por ejemplo, a la optimizaci´on de estructuras de barras en las que el ´area y/o la inercia de las barras son las variables que el dise˜nador puede modificar. La otra l´ınea de investigaci´on principal consiste en la optimizaci´on de estructuras mediante la modificaci´on de unas ciertas variables geom´etricas de las mismas como pueden ser coor-denadas de nudos de barras o de nodos de las mallas de Elementos Finitos (optimizaci´on de formas o Shape Optimization).
Ambas t´ecnicas plantean el problema de minimizaci´on del coste de la estructura (habi-tualmente expresado en t´erminos del peso de la misma) sujeto a restricciones sobre el dise˜no de tipo tensional o de desplazamientos. Por lo tanto, la funci´on objetivo del problema de optimizaci´on que se pretende minimizar es, habitualmente, el peso de la estructura, y las restricciones se imponen limitando el valor las tensiones o de los desplazamientos.
Estos planteamientos de optimizaci´on de estructuras han sido ampliamente utilizados y han proporcionado soluciones muy adecuadas en problemas reales en ingenier´ıa. Sin embar-go, las formulaciones m´as habituales de optimizaci´on de formas y de dimensiones requieren de la intervenci´on del dise˜nador para definir la tipolog´ıa estructural empleada. Se limitan a obtener el dise˜no ´optimo a partir de la tipolog´ıa estructural que se define inicialmente sin considerar posibles modificaciones en la misma que puedan mejorar su comportamiento. Un
ejemplo de aplicaci´on de las t´ecnicas de optimizaci´on de formas fue utilizado por Zhang [124] para resolver el problema de un soporte en voladizo. La tipolog´ıa estructural de partida de este ejemplo consiste en una soluci´on con tres barras, tal y como se puede apreciar en la figura 1.1, siendo la soluci´on ´optima la propuesta en la figura 1.2. Como se puede apreciar la tipolog´ıa estructural final se mantiene a lo largo del proceso de optimizaci´on asumiendo que es correcta.
Figura 1.1: Soporte en voladizo. Esquema del problema de optimizaci´on (Zhang [124])
En estas formulaciones el ingeniero sigue tomando parte activa en el proceso de con-cepci´on y dise˜no de la estructura. La optimizaci´on de dimensiones y de formas es, en este sentido, incompleta y requiere de otras t´ecnicas para obtener la configuraci´on resistente m´as adecuada. Una vez obtenido el dise˜no inicial de forma rigurosa pueden aplicarse los m´etodos mencionados anteriormente para obtener la soluci´on final m´as adecuada sin perder generalidad y sin necesidad de utilizar hip´otesis de partida en cuanto a tipolog´ıa estructural. Esta necesidad de obtener el dise˜no resistente de partida de forma objetiva y rigurosa provoca la aparici´on de las primeras formulaciones de la optimizaci´on topol´ogica de estruc-turas. El primer planteamiento de este problema fue propuesto por Bendsøe y Kikuchi [3] en 1988 y desde entonces han sido numerosas las contribuciones realizadas en este ´ambito hasta nuestros d´ıas, alcanzando en la actualidad un alto grado de divulgaci´on y formando parte de las materias de desarrollo en numerosos grupos de investigaci´on a nivel mundial.
pre-1.7 : Le modèle initial et la solution du problème obtenue par Zhang
Figura 1.2: Soporte en voladizo. Soluci´on mediante optimizaci´on de formas (Zhang [124])
definido que maximice la rigidez (minimium compliance) imponiendo una limitaci´on sobre la cantidad m´axima de material a emplear. En la pr´actica, este planteamiento consiste en determinar en qu´e elementos de la malla de Elementos Finitos se debe colocar material para que la estructura resultante sea la ´optima. Al contrario de lo que ocurre en la optimizaci´on de formas o de dimensiones no se condiciona el dise˜no con una tipolog´ıa estructural prede-finida de antemano, lo que permite realizar un estudio m´as amplio y general del problema. De acuerdo con esta idea y para comprobar la validez de la soluci´on propuesta por Zhang en la figura 1.2, Duysinx plante´o la resoluci´on del problema de la figura 1.1 con la formulaci´on de m´axima rigidez (minimium compliance). Como se puede apreciar, la soluci´on obtenida con este modelo (figura 1.3) difiere considerablemente de la soluci´on obtenida mediante optimizaci´on de formas (figura 1.2), lo que resalta la importancia de una correcta elecci´on de la configuraci´on resistente inicial para poder obtener buenos resultados mediante las t´ecnicas convencionales de optimizaci´on.
Figura 1.3: Soporte en voladizo. Soluci´on ´optima de m´axima rigidez (Duysinx [18])
mayor parte de los trabajos han estado dirigidos hacia la resoluci´on del problema de m´axima rigidez imponiendo una restricci´on en la cantidad m´axima de material a emplear. Este modelo introduce innecesariamente una serie de par´ametros artificiales en la formulaci´on que no guardan relaci´on alguna con el comportamiento estructural como, por ejemplo, el volumen de material. Habitualmente se utiliza como m´aximo en torno al 25 % del volumen total del dominio de definici´on de la estructura porque los resultados que se obtienen son adecuados, pero no est´a justificado desde un punto de vista ingenieril ya que no tiene porqu´e coincidir con el valor de m´ınimo coste. Adem´as, tampoco se garantiza que la soluci´on final sea factible desde un punto de vista resistente porque no se comprueba el cumplimiento de las tensiones o los desplazamientos de acuerdo con la especificaciones de la normativa correspondiente.
Por otra parte, la formulaci´on de m´axima rigidez presenta inestabilidades que produ-cen soluciones estructurales con disposici´on en damero (checkerboard) as´ı como fen´omenos de dependencia de la malla de Elementos Finitos (mesh dependency) tal y como se puede observar en los trabajos de Bendsøe [5] y Eschenauer y Olhoff [26]. Estas anomal´ıas se re-suelven habitualmente mediante la utilizaci´on de t´ecnicas artificiales de filtrado de imagen y de suavizado (Eschenauer y Olhoff [26]) que, en general, proporcionan resultados adecuados pero que no se basan, de modo alguno, en el comportamiento resistente del problema en estudio.
los inconvenientes m´as notables de los modelos de m´axima rigidez como la necesidad de de-finir una restricci´on en volumen arbitraria, la utilizaci´on de t´ecnicas de filtrado y suavizado para evitar disposiciones en damero, adem´as de garantizar la validez de la soluci´on final desde un punto de vista del estado tensional. La formulaci´on propuesta es general y per-mite la adici´on de nuevas restricciones (por ejemplo, en desplazamientos) de forma sencilla, as´ı como la consideraci´on de varios casos de carga simult´aneamente de forma natural. Otra ventaja muy importante de esta formulaci´on es la utilizaci´on de una funci´on objetivo m´as realista y habitual en ingenier´ıa basada en el coste de la estructura.
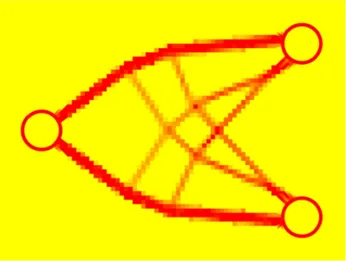
Por lo tanto, esta formulaci´on de m´ınimo peso presenta ventajas considerables frente a los desarrollos de m´axima rigidez para resolver el problema de la optimizaci´on topol´ogica de estructuras continuas y conduce a mejores soluciones. En la figura 1.4 se muestra la distri-buci´on ´optima de material obtenida con la formulaci´on de m´ınimo peso y con restricciones en tensi´on locales que se propone en esta tesis para el problema propuesto por Zhang en la figura 1.1. Como se puede observar la soluci´on obtenida proporciona una configuraci´on resistente muy diferente a la propuesta originalmente por Zhang (figura 1.2) empleando optimizaci´on de formas. Asimismo tambi´en se aprecian diferencias considerables entre la soluci´on de m´axima rigidez obtenida por Duysinx (figura 1.3) y la soluci´on de m´ınimo peso propuesta (figura 1.4). La soluci´on de m´axima rigidez utiliza una cantidad de material su-perior a la formulaci´on de m´ınimo peso debido a la restricci´on en volumen que se establece. La soluci´on de m´ınimo peso (figura 1.4) obtiene una soluci´on que minimiza la cantidad de material a utilizar a la vez que garantiza el comportamiento resistente de la misma frente a las cargas aplicadas, tal y como se plantea habitualmente en otras ramas de la optimizaci´on de estructuras.
1.3.
Objetivos de la tesis
El principal objetivo de esta tesis es desarrollar una metodolog´ıa para la resoluci´on de problemas de optimizaci´on topol´ogica de estructuras continuas basada en la minimiza-ci´on del peso y con restricciones en tensi´on y compararla con las formulaciones habituales de m´axima rigidez que habitualmente se utilizan para resolver este problema. Para ello ser´a necesario prestar especial atenci´on tanto a los aspectos te´oricos de la formulaci´on como a los relativos a la implementaci´on de los algoritmos de forma num´erica en aplicaciones inform´aticas de c´alculo por ordenador. Este objetivo principal se puede desglosar en los siguientes objetivos espec´ıficos:
Figura 1.4: Soporte en voladizo. Soluci´on ´optima de m´ınimo peso con restricciones locales en tensi´on
informaci´on posible para abordar el problema que se plantea y analizar las t´ecnicas y modelos que se han desarrollado hasta la actualidad para resolverlo.
• Plantear y desarrollar un modelo para c´alculo de estructuras basado en una formu-laci´on convencional del M´etodo de los Elementos Finitos que permita incorporar en su formulaci´on el estado material de cada elemento de modo que se pueda realizar el an´alisis estructural en funci´on de la distribuci´on de material existente.
• Formular el problema de optimizaci´on topol´ogica de estructuras de m´ınimo peso con restricciones en tensi´on. Para ello ser´a necesario realizar un estudio acerca de la funci´on objetivo a utilizar y analizar la forma m´as adecuada de imponer las restricciones en tensi´on en el modelo.
• Estudiar algunos aspectos te´oricos fundamentales acerca de las singularidades y par-ticularidades que presentan las restricciones en tensi´on y proponer soluciones para evitarlas.
• Analizar las posibles limitaciones del modelo propuesto y proponer modificaciones que complementen y mejoren su comportamiento.
• Plantear t´ecnicas de refinamiento de malla que permitan resolver problemas de ma-yores dimensiones con un coste computacional reducido.
• Desarrollar algoritmos espec´ıficos para realizar el an´alisis de sensibilidad requerido por los algoritmos de optimizaci´on de forma anal´ıtica teniendo en cuenta la gran relevancia de los aspectos computacionales para su posterior implementaci´on num´erica.
• Llevar a cabo el estudio e implementaci´on eficiente de los algoritmos planteados utili-zando, en la medida de lo posible, las t´ecnicas de programaci´on y c´alculo en paralelo.
• Resolver ejemplos pr´acticos de optimizaci´on habituales en ingenier´ıa y comparar las soluciones obtenidas con las soluciones te´oricas, en el caso de que existan, y con las soluciones de m´axima rigidez propuestas por otros autores.
1.4.
Organizaci´
on de la tesis
Esta Tesis Doctoral est´a organizada en 9 cap´ıtulos incluyendo este cap´ıtulo de intro-ducci´on y consta adem´as de un ap´endice y de las correspondientes referencias bibliogr´aficas. En este primer cap´ıtulo de introducci´on se presenta el problema de la optimizaci´on topol´ogica de estructuras as´ı como su necesidad de estudio en el ´ambito de la optimizaci´on en general. Tambi´en se presentan, adem´as, los principales objetivos que se han acometido en esta tesis.
En el cap´ıtulo 2 se realiza una revisi´on del estado del conocimiento actual, se presentan y describen brevemente los principales m´etodos y formulaciones empleadas en la resoluci´on de distintos problemas de optimizaci´on topol´ogica de estructuras continuas as´ı como algunas aplicaciones m´as espec´ıficas de este tipo de planteamientos.
En el cap´ıtulo 3 se presenta la formulaci´on estructural por Elementos Finitos que nos permitir´a resolver el problema de optimizaci´on topol´ogica de estructuras continuas, teniendo en cuenta la distribuci´on de material existente, a partir de una formulaci´on convencional de Elementos Finitos.
En el cap´ıtulo 5 se presentan los algoritmos de optimizaci´on que se han estudiado para resolver este problema explicando brevemente su funcionamiento as´ı como las ventajas e inconvenientes que presentan.
En el cap´ıtulo 6 se desarrollan las t´ecnicas empleadas para obtener el an´alisis de sensi-bilidad tanto de la funci´on objetivo como de las restricciones de forma anal´ıtica requeridos por los algoritmos de optimizaci´on propuestos en el cap´ıtulo 5.
En el cap´ıtulo 7 se plantea la metodolog´ıa completa a seguir para resolver el problema de optimizaci´on topol´ogica que se presenta en tesis y se realiza un estudio de los aspectos computacionales m´as importantes para la implementaci´on num´erica de esta formulaci´on.
En el cap´ıtulo 8 se presentan los ejemplos num´ericos que se han resuelto con las distintas formulaciones propuestas del problema con la finalidad de validar los resultados obtenidos con el planteamiento de m´ınimo coste y de establecer comparaciones entre las distintas estrategias del problema de optimizaci´on que se proponen.
Por ´ultimo, el cap´ıtulo 9 resume las conclusiones m´as destacables de esta tesis doctoral y propone las futuras l´ıneas de investigaci´on a desarrollar.
En el Ap´endice 1 se presenta una explicaci´on m´as detallada acerca del funcionamiento del algoritmo de Programaci´on Lineal Secuencial que se utiliza en esta tesis.
Cap´ıtulo 2
Estado actual del conocimiento
El conocimiento es de dos clases: O sabemos algo por nosotros mismos, o sabemos donde encontrar informaci´on sobre ello.
Samuel Johnson (1709-1784)
2.1.
Introducci´
on
Desde que en 1988 Bendsøe y Kikuchi [3] presentaron los primeros trabajos del problema de optimizaci´on topol´ogica de estructuras y sentaron las bases de esta nueva disciplina se han realizado numerosas contribuciones en este ´ambito. De forma general, podemos clasificar los modelos propuestos para resolver este problema en discretos o continuos dependiendo de la tipolog´ıa de las variables de dise˜no que se utilicen.
Tal y como se ha comentado en el cap´ıtulo de introducci´on, el problema de optimizaci´on topol´ogica de estructuras pretende obtener la distribuci´on de material m´as adecuada en un dominio predefinido, lo que consiste esencialmente en decidir los puntos del dominio que deben tener material y los que deben permanecer vac´ıos. De acuerdo con esta idea esta formulaci´on es discreta ya que para cada punto del dominio s´olo existen dos configuraciones posibles (con o sin material). Debido a este car´acter discreto, el problema est´a mal planteado ya que la soluci´on var´ıa con el grado de refinamiento de la malla utilizada.
de material discretas (vac´ıo-lleno) basadas en algoritmos de optimizaci´on continuos que presentan una complejidad menor.
Por otra parte, tambi´en se han propuesto t´ecnicas que convierten el modelo discreto original en un problema con variables de dise˜no continuas de modo que se puedan aplicar las t´ecnicas y algoritmos habituales en optimizaci´on de estructuras. De este modo tambi´en se evita el mal planteamiento del problema discreto mediante la introducci´on de modelos de microestructura interna de material para densidades relativas intermedias que reducen los fen´omenos de dependencia de la malla.
Adem´as de estos m´etodos desarrollados para resolver el problema convencional de op-timizaci´on topol´ogica de estructuras continuas tambi´en se han aplicado las formulaciones obtenidas en otros modelos que permiten obtener el dise˜no de microestructuras de materia-les con propiedades definidas (problema inverso) o el dise˜no de mecanismos estructurales, por ejemplo.
A continuaci´on se describen brevemente los desarrollos m´as habituales de las t´ecnicas que se acaban de introducir con la finalidad de presentar el estado del conocimiento actual acerca de la optimizaci´on topol´ogica de estructuras.
2.2.
Formulaciones discretas del problema
La forma m´as evidente de resolver el problema de optimizaci´on topol´ogica de estruc-turas consiste en abordar directamente el problema en su formulaci´on discreta tal y como se plante´o en el apartado de introducci´on. Sin embargo, los problemas de optimizaci´on con variables discretas son mucho m´as complicados que los problemas de optimizaci´on con variables continuas dado que no se pueden utilizar t´ecnicas de programaci´on matem´atica como las que se utilizan habitualmente en otras disciplinas de la optimizaci´on con variables continuas.
Por otra parte, la formulaci´on discreta de las variables de dise˜no presenta algunas ventajas frente a las formulaciones continuas porque la soluci´on presenta distribuciones de material vac´ıo-lleno que facilitan su posterior fabricaci´on. Adem´as, la eliminaci´on de los elementos que no son necesarios supone la desaparici´on de su contribuci´on en el c´alculo estructural de modo que se evitan ciertos problemas num´ericos como los fen´omenos de sin-gularidad en los problemas con restricciones de tipo tensional existentes en las formulaciones continuas.
en su formulaci´on las tensiones (Duysinx y Bendsøe [20], Pereira, et al. [84], Werme y Svanberg [119]).
Los algoritmos m´as habituales que se utilizan para resolver el problema discreto son los criterios de optimalidad, la optimizaci´on estructural evolutiva (ESO), el m´etodo de optimizaci´on jer´arquico de b´usqueda por proximidad as´ı como el m´etodo de las curvas de nivel, el m´etodo de la burbuja o los algoritmos gen´eticos (que est´an adquiriendo gran auge en la actualidad). Estos planteamientos se desarrollan en detalle en los siguientes apartados discutiendo sus principales ventajas e inconvenientes.
2.2.1. Criterios de Optimalidad (Optimality Criteria)
Los criterios de optimalidad son unas t´ecnicas que se han utilizado ampliamente en to-das las ramas de la optimizaci´on estructural y basan su funcionamiento en el establecimiento de una hip´otesis o condici´on de partida que ser´a decisiva y caracterizar´a la soluci´on ´ opti-ma obtenida. Para cada probleopti-ma es necesario definir un criterio de optiopti-malidad apropiado que nos permita obtener la soluci´on ´optima m´as adecuada y realista. Bajo esta hip´otesis de optimalidad el problema original se simplifica de forma considerable y puede resolverse de forma m´as sencilla ya que todos los dise˜nos deben cumplir la exigencia establecida. El problema resultante consiste, por tanto, en
minimizar F(x)
cumpliendo gj(x) j= 1, . . . , J
(2.1)
dondegj es el criterio de optimalidad utilizado yJ es el n´umero de criterios impuestos para
este problema (Hern´andez [36]).
Es obvio, por tanto, que el resultado final depende en gran medida del grado de ade-cuaci´on del criterio de optimalidad empleado para cada problema en particular.
2.2.2. Optimizaci´on Estructural Evolutiva (Evolutionary Structural
Optimi-zation)
Los m´etodos de optimizaci´on estructural evolutiva ESO (Evolutionary Structural Opti-mization) fueron propuestos inicialmente en 1993 por Xie y Steven [120] y consisten, esen-cialmente, en una progresiva eliminaci´on de material del dominio de dise˜no siguiendo unos criterios estructurales prefijados. En la formulaci´on original del m´etodo de la Optimizaci´on Estructural Evolucionaria se eliminan aquellas partes de la estructura que no alcancen un cierto estado tensional previamente definido. Este l´ımite se ir´a incrementando hasta obtener la soluci´on final deseada que corresponder´a a aquellas partes que superen la tensi´on esta-blecida. De forma general, el criterio de eliminaci´on de material se impone tomando como referencia el valor de la tensi´on de comparaci´on de Von Mises.
En la formulaci´on original del algoritmo ESO, Xie y Steven [121] proponen la elimina-ci´on de aquellos elementos en los que se cumple que:
σVM e σVM
max
< RRi (2.2)
donde σVM
e la tensi´on de Von Mises del elementoe,σVMmax el valor m´aximo admisible y RR
el ´ındice de rechazo (Rejection Ratio) de la iteraci´on i, que se actualiza durante el proceso de optimizaci´on como:
RRi+1=RRi+ERi, i= 0,1,2,3, . . . (2.3)
siendoERi el ´ındice de evoluci´on (Evolutionary Rate) yRR el ´ındice de rechazo. El ´ındice
de evoluci´on toma habitualmente el valor ER = 1 % pero en casos m´as complejos puede adquirir valores menores. Asimismo el ´ındice de rechazo inicial tambi´en se toma comoRRo=
1 % en la mayor parte de las aplicaciones pr´acticas.
Con este procedimiento, la topolog´ıa estructural resultante avanza lentamente hacia el ´optimo eliminando aquellas partes que contribuyen en menor medida debido a su bajo estado tensional.
resultar trascendentales cuando la configuraci´on se aproxima a la ´optima. Para evitar este problema, se han planteado otros m´etodos que, al contrario de lo que se propone en el algoritmo original de optimizaci´on evolutiva, incorpora nuevos elementos a la estructura en aquellas zonas donde su existencia reporte un mejor comportamiento estructural. Este m´etodo recibe el nombre de Optimizaci´on Estructural Evolutiva Aditiva (AESO Additive Evolutionary Structural Optimization).
Con posterioridad, se ha propuesto un algoritmo m´as completo que incorpora las dos teor´ıas presentadas anteriormente tanto para eliminaci´on de material (ESO) como para incorporaci´on de nuevas partes o elementos a la estructura (AESO) que recibe el nombre de Optimizaci´on Estructural Evolutiva Bidireccional (BESO Bi-directional Evolutionary Structural Optimization). Con este m´etodo se consigue mejorar considerablemente el proceso de optimizaci´on dado que el algoritmo de eliminaci´on de los elementos resistentes no necesita limitar tanto el ´ındice de rechazo (RRi) porque el algoritmo AESO permite la recuperaci´on
en iteraciones posteriores de elementos eliminados que tienen una relevancia considerable en el comportamiento estructural si fuese necesario.
2.2.3. Hierarchical Neighborhood Optimization Method
El m´etodo de optimizaci´on jer´arquica de b´usqueda por proximidad (Hierarchical Neigh-borhood Optimization Method) es un m´etodo relativamente reciente que han desarrollado Stolpe y Stidsen [110] y Werme y Svanberg [119]. La formulaci´on propuesta plantea una t´ecnica que permite resolver el problema discreto de optimizaci´on topol´ogica de estructuras minimizando el peso y con restricciones en tensi´on.
El algoritmo basa su funcionamiento en la aplicaci´on sucesiva de dos t´ecnicas princi-pales. Por una parte, se busca sobre una malla de elementos bastante gruesa la distribuci´on ´
optima de material. Para ello se modifica el dise˜no colocando o eliminando material en un ´
unico elemento en cada iteraci´on. El elemento a modificar se elige como el m´as adecuado de los adjuntos (vecinos) a los elementos que contienen material de modo que se reduzca la funci´on objetivo y se cumplan las restricciones en tensi´on. Una vez obtenido el dise˜no ´
optimo para este grado de discretizaci´on de la malla se procede a hacer un refinamiento y se comienza de nuevo el proceso de dise˜no ´optimo para esta nueva malla a partir del dise˜no anterior.
de refinamiento y de optimizaci´on de la soluci´on. De esta forma, el c´alculo estructural se realiza con una malla fina garantizando el cumplimiento de las restricciones en tensi´on y la distribuci´on de material se obtiene a partir de una malla m´as gruesa debido al coste computacional tan elevado que requiere.
Este proceso es, en general, muy lento y costoso pero proporciona distribuciones vac´ıo-lleno e incorpora restricciones en tensi´on, lo cual, supone una t´ecnica muy compleja, pero novedosa, para resolver este tipo de problemas desde un punto de vista discreto.
2.2.4. M´etodo de las Curvas de Nivel (Level Set Method)
El m´etodo de las curvas de nivel ha adquirido gran importancia en los ´ultimos a˜nos debido a su facilidad de adaptaci´on en gran variedad de aplicaciones y, en particular, en problemas de optimizaci´on topol´ogica. Los primeros trabajos desarrollados en este ´ambito que empleaban el m´etodo de las curvas de nivel fueron propuestos por Sethian y Wieg-mann [94]. M´as recientemente se han realizado nuevas aportaciones sobre este m´etodo que incorporan otras t´ecnicas adicionales como los propuestos por Alexandrov y Santosa [1], Wang, et al. [117] y Park y Youn [82] para mejorar el comportamiento de estos plantea-mientos.
El m´etodo de las curvas de nivel no es exactamente un algoritmo de optimizaci´on discreto pero proporciona soluciones vac´ıo-lleno. En esencia, el m´etodo consiste en definir la soluci´on del problema de optimizaci´on topol´ogica, es decir la distribuci´on material, mediante una funci´on de muy alto orden de modo que la topolog´ıa final de la soluci´on se obtiene a partir de la curva de nivel de valor cero de esta funci´on. Las partes del dominio que corresponden a curvas de nivel superiores a la curva de nivel cero ser´an zonas con material y las restantes no presentar´an material.
2.2.5. M´etodo de la Burbuja (Bubble Method)
El m´etodo de la burbuja, al igual que ocurre con el m´etodo de las curvas de nivel, no es un m´etodo que trate directamente el problema discreto de optimizaci´on pero, sin embargo, las soluciones obtenidas tambi´en corresponden a distribuciones vac´ıo-lleno.
Si el agujero se incorpora dentro de la regi´on material se ha alcanzado una estructura de “genus” superior y se procede a modificar la geometr´ıa de nuevo considerando el agujero introducido hasta alcanzar la distribuci´on ´optima. Si el agujero infinitesimal se incorpora en el contorno existente, la topolog´ıa de la estructura no cambia y es necesario refinar la malla en esa zona para alcanzar una mejor soluci´on. El proceso se detiene cuando se alcanza el n´umero m´aximo de agujeros que se estima adecuado o cuando el tama˜no de los nuevos agujeros introducidos es menor que un cierto valor predeterminado.
Este procedimiento se puede observar f´acilmente en el esquema 2.1 propuesto por Es-chenauer,et al. [24].
Figura 2.1: Esquema de evoluci´on del M´etodo de la Burbuja.
El m´etodo presenta la ventaja de proporcionar soluciones vac´ıo-lleno pero requiere unos costes computacionales muy elevados debido a la necesidad de redefinir la malla de Elementos Finitos en cada proceso iterativo y de resolver los problemas de optimizaci´on de formas resultantes.
2.2.6. Algoritmos gen´eticos o evolutivos (Genetic Algorithms)
Otra t´ecnica de optimizaci´on que ha adquirido gran difusi´on en los ´ultimos a˜nos son los denominados algoritmos gen´eticos o evolutivos. Reciben este nombre porque basan su funcionamiento en las leyes de la evoluci´on que propuso Charles Darwin en 1859 en su obra “Del origen de las especies por medio de la selecci´on natural” donde se define el fen´omeno de la selecci´on natural como el proceso en el que se preservan diferencias individuales favorables y se erradican aquellas que son perjudiciales para una especie.
El origen de los algoritmos gen´eticos como t´ecnica de c´alculo surge en los a˜nos 50 del siglo XX con los trabajos de autores como Box [8] en 1957 y Friedman [29] en 1959 entre otros. Sin embargo, a pesar de este temprano desarrollo, estas t´ecnicas no han tenido gran difusi´on en el mundo de la optimizaci´on hasta bien entrada la d´ecada de los a˜nos 60 con los trabajos de Rechenberg [90] en 1965 y Fogel, et al.[28] en 1966. Adem´as, su uso en el ´
capacidad de c´alculo que se necesita para poder resolver problemas reales.
El proceso de selecci´on num´erica se realiza a partir de una poblaci´on de individuos suficientemente amplia como para ser representativa del fen´omeno que se pretende estudiar (candidatos a ser la soluci´on de problema) sobre la que se aplican operadores caracter´ısticos de la selecci´on natural y de la evoluci´on gen´etica. Basados en esta idea han ido surgiendo diferentes m´etodos basados en las teor´ıas de Darwin. As´ı, surgen los Algoritmos Gen´eticos propiamente dichos (GA) basados en la supervivencia de los individuos m´as fuertes y las Estrategias Evolutivas que basan su funcionamiento en una serie de operadores gen´eticos como pueden ser la recombinaci´on, la mutaci´on y la selecci´on, entre otros.
Hoy en d´ıa, estas t´ecnicas tienen una gran difusi´on debido a la enorme versatilidad que ofrecen. De ah´ı que se utilicen en la optimizaci´on de estructuras en general y en la opti-mizaci´on topol´ogica en particular atendiendo a formulaciones binarias vac´ıo-lleno e incluso aplicadas sobre formulaciones continuas.
2.3.
Formulaciones continuas del problema
Las formulaciones discretas propuestas presentan algunas ventajas importantes pero requieren, en general, un coste computacional excesivo que limita su capacidad de aplicaci´on en la pr´actica. Por este motivo se han propuesto formulaciones continuas de las variables que simplifican las dificultades de resoluci´on que presentan los modelos discretos.
Por el contrario, la formulaci´on continua introduce ciertas dificultades num´ericas y conceptuales que se analizar´an a lo largo de esta tesis. El primer y principal problema de las formulaciones continuas reside en la necesidad de definir una ecuaci´on constitutiva del material para valores intermedios de las variables de dise˜no. En las formulaciones discretas este an´alisis no es necesario dado que las variables de dise˜no s´olo pueden tomar los valores 0 ´
o 1. Sin embargo, en las formulaciones continuas ´este es un paso imprescindible para poder resolver el problema estructural resultante.
De acuerdo con esta idea es necesario desarrollar una teor´ıa que permita obtener mode-los constitutivos de materiales con variables de dise˜no continuas entre 0 y 1. Estas variables de dise˜no continuas reciben el nombre de “densidades relativas” y representan la porci´on de volumen de material s´olido frente a volumen total, de modo que el valor nulo indica que no existe material y el valor unitario indica que el material es s´olido.
ma-crosc´opico) que caracterice la respuesta estructural para valores intermedios de las variables de dise˜no. Por otra parte, tambi´en tiene especial relevancia el an´alisis de otras magnitu-des, como por ejemplo las tensiones, que tienen interpretaci´on f´ısica sencilla para elementos llenos pero desconocida, a priori, cuando las variables de dise˜no toman valores intermedios.
2.3.1. T´ecnicas de Homogeneizaci´on (Homogenization)
El procedimiento matem´atico de obtenci´on de modelos constitutivos a partir de micro-estructuras resistentes que ha adquirido mayor relevancia en el campo de la optimizaci´on topol´ogica estructural es la t´ecnica de la homogeneizaci´on. Los principios b´asicos fueron propuestos en 1985 por Murat y Tartar [58]. Posteriormente, Lurie y Cherkaev [48] y Kohn y Strang [41] en 1986 continuaron este trabajo encontrando a su vez nuevas dificultades de la formulaci´on continua del problema (dependencia de la malla, disposiciones en damero, ...) en formulaciones de m´axima rigidez.
El mayor auge de estas t´ecnicas surge a partir de 1988 con los trabajos de Bendsøe y Kikuchi [3] en los que se aplica de forma pr´actica la teor´ıa de la homogeneizaci´on a problemas reales y se propone una formulaci´on de m´axima rigidez bajo una restricci´on en el volumen de la estructura. La publicaci´on de estos trabajos supone el nacimiento de la optimizaci´on topol´ogica como una nueva disciplina dentro de la optimizaci´on estructural. Esta t´ecnica de homogeneizaci´on ha sido ampliamente estudiada con posterioridad y es, en la actualidad, el m´etodo habitualmente empleado para obtener modelos constitutivos de materiales con densidades relativas intermedias tal y como queda reflejado directamente en los trabajos de Allaire, et al.[2], Bendsoe y Kikuchi [3], [5], Eschenauer y Olhoff [26], y Suzuki y Kikuchi [112] entre otros. A partir de estos modelos han surgido, de forma paralela, numerosas aplicaciones pr´acticas que utilizan estos modelos de material incorporados en formulaciones continuas del problema de la optimizaci´on topol´ogica de estructuras mediante esquemas de m´axima rigidez o m´ınimo peso, fundamentalmente.
2.3.2. Modelo de material: “hole-in-cell”
El modelo “hole in cell” fue propuesto por Murat y Tartar [58] en 1985 y ha sido el primer tipo de microestructura planteado para resolver el problema de optimizaci´on to-pol´ogica de estructuras continuas. En cada celda o elemento del mismo se introduce un agujero cuadrado de tama˜no variable que se puede orientar en la direcci´on del espacio m´as adecuada, tal y como se puede observar en la figura 2.2. Posteriormente, formulaciones un poco m´as generales de la microestructura“hole-in-cell” propusieron el uso de agujeros con geometr´ıas rectangulares y, por lo tanto, m´as complejas que las originales. Con esta formu-laci´on m´as general el modelo de microestructura queda definido a trav´es de tres par´ametros: las variables µ1 yµ2 y el ´angulo de orientaci´onθ.
Figura 2.2: Estructura“hole-in-cell” (Olhoff y Eschenauer [71])
![Figura 1.3: Soporte en voladizo. Soluci´ on ´ optima de m´ axima rigidez (Duysinx [18])](https://thumb-us.123doks.com/thumbv2/123dok_es/3961829.672458/32.892.255.612.163.432/figura-soporte-voladizo-soluci-optima-axima-rigidez-duysinx.webp)

![Figura 2.9: Soluci´ on de viga en voladizo con disposici´ on en damero (D´ıaz y Sigmund [17])](https://thumb-us.123doks.com/thumbv2/123dok_es/3961829.672458/52.892.218.646.167.420/figura-soluci-viga-voladizo-disposici-damero-ıaz-sigmund.webp)


![Figura 5.1: Efecto del par´ ametro r sobre la funci´ on barrera φ(ρ, r) en un problema 1D con F = x y x ∗ − x ≤ 0 (Fletcher [27]).](https://thumb-us.123doks.com/thumbv2/123dok_es/3961829.672458/93.892.313.651.166.456/figura-efecto-par-ametro-funci-barrera-problema-fletcher.webp)

