Análisis del control de velocidad de un vehículo ante Perturbaciones Externas

Texto completo

(1)UNIVERSIDAD NACIONAL DE SAN AGUSTÍN AREQUIPA ESCUELA DE POSTGRADO UNIDAD DE POSTGRADO DE LA FACULTAD DE INGENIERÍA DE PRODUCCIÓN Y SERVICIOS. TESIS:. “ANALISIS DEL CONTROL DE VELOCIDAD DE UN VEHÍCULO ANTE PERTURBACIONES EXTERNAS” Presentada por el Ingeniero: Christian Humberto, Motta Contreras Para optar el grado académico de Maestro en Ciencias Ingeniería Electrónica con mención en Automatización e Instrumentación ASESOR: Dr. Raúl Sulla Torres. AREQUIPA – PERÚ. 2018.

(2) AGRADECIMIENTOS Gracias a mi Dios por las bendiciones diarias nos brinda; a toda mi familia por su apoyo incondicional. Agradecer también a mi asesor Dr. Raúl Sulla Torres por todo el apoyo brindado.. 2.

(3) Contenido RESUMEN .............................................................................................................................................. 5 INTRODUCCION ................................................................................................................................... 7 CAPITULO I ........................................................................................................................................... 9 MARCO TEÓRICO ................................................................................................................................ 9 1.1 CONTROL DE VELOCIDAD CRUCERO ....................................................................................... 9 1.2 ANTECEDENTES ................................................................................................................................ 10 1.3 PRINCIPIO DE FUNCIONAMIENTO ....................................................................................................... 10 1.4 VENTAJAS Y DESVENTAJAS ............................................................................................................... 11 1.5 CONTROL DE VELOCIDAD INTELIGENTE ............................................................................................ 12 CAPITULO II ........................................................................................................................................ 13 2.1 CONTROL PID................................................................................................................................... 13 ACCIÓN DE CONTROL ........................................................................................................................ 14 2.2 MODO DE CONTROL PROPORCIONAL: .............................................................................................. 14 2.3 PROCESOS DE ORDEN ........................................................................................................................ 17 CAPITULO III ....................................................................................................................................... 37 MODELAMIENTO DEL SISTEMA ...................................................................................................... 37 1.1. 1.1.1. 1.1.2. 1.1.3. 1.1.4. 1.2.. MODELAMIENTO DEL SISTEMA ....................................................................................... 37 ECUACIONES DEL SISTEMA .................................................................................................... 38 PARÁMETROS DEL SISTEMA ................................................................................................... 38 MODELADO DE ESPACIO DE ESTADOS .................................................................................... 38 MODELADO DE FUNCIÓN DE TRANSFERENCIA ....................................................................... 39 MODELAMIENTO DEL SISTEMA ....................................................................................... 39. 1.2.1. MODELO DEL SISTEMA Y PARÁMETROS ................................................................................. 39 1.2.2. ESPECIFICACIONES DE RENDIMIENTO .................................................................................... 40 1.2.3. RESPUESTA DE PASO DE BUCLE ABIERTO ............................................................................... 40 1.2.4. POLOS / CEROS DE BUCLE ABIERTO ........................................................................................ 42 1.2.5. DIAGRAMA DE BODE DE BUCLE ABIERTO .............................................................................. 42 CAPITULO IV ...................................................................................................................................... 44 DESARROLLO DEL CONTROLADOR PID ...................................................................................... 44 1.3. 1.3.1. 1.3.2. 1.3.3. 1.3.4. 1.3.5. 1.3.6. 1.4. 1.4.1. 1.4.2. 1.4.3. 1.4.4. 1.4.5.. DISEÑO DEL CONTROLADOR PID..................................................................................... 44 MODELO DEL SISTEMA Y PARÁMETROS ................................................................................. 44 ESPECIFICACIONES DE RENDIMIENTO .................................................................................... 44 DESCRIPCIÓN GENERAL DE PID ............................................................................................. 44 CONTROL PROPORCIONAL ..................................................................................................... 46 CONTROL PI .......................................................................................................................... 50 CONTROL PID ....................................................................................................................... 55 LUGAR DE RAÍCES (ROOT LOCUS CONTROLLER DESIGN) ..................................... 59 MODELO DE SISTEMA ............................................................................................................ 59 PARÁMETROS DE SISTEMA ..................................................................................................... 59 ESPECIFICACIONES DE RENDIMIENTO .................................................................................... 59 CONTROL PROPORCIONAL ..................................................................................................... 60 CONTROLADOR DE RETARDO ................................................................................................. 65. 1.5. MÉTODOS DE DOMINIO DE FRECUENCIA PARA EL DISEÑO DEL CONTROLADOR .................................................................................................................................... 69 1.5.1. 1.5.2. 1.5.3. 1.5.4.. MODELO DE SISTEMA ............................................................................................................ 69 PARÁMETROS DEL SISTEMA ................................................................................................... 69 ESPECIFICACIONES DE RENDIMIENTO .................................................................................... 69 DIAGRAMA DE BODE Y RESPUESTA DE BUCLE ABIERTO ........................................................ 70. 3.

(4) 1.5.5. 1.5.6.. CONTROLADOR PROPORCIONAL ............................................................................................ 72 COMPENSADOR DE RETRASO ................................................................................................. 75. 1.6. DISEÑO DE UN CONTROLADOR Y UN OBSERVADOR PARA EL SISTEMA DE CONTROL DE CRUCERO UTILIZANDO EL MODELO DE ESPACIO DE ESTADO. .............. 77 1.6.1. 1.6.2. 1.6.3. 1.6.4. 1.7.. ECUACIONES DE ESPACIO DE ESTADOS .................................................................................. 77 REQUERIMIENTOS DE DISEÑO ................................................................................................ 78 DISEÑO DE CONTROL CON COLOCACIÓN DE POLOS ................................................................ 78 ENTRADA DE REFERENCIA ..................................................................................................... 81 DISEÑO DE CONTROLADOR DIGITAL ............................................................................. 82. 1.7.1. MODELO DE SISTEMA ............................................................................................................ 82 1.7.2. PARÁMETROS DEL SISTEMA ................................................................................................... 82 1.7.3. ESPECIFICACIONES DE RENDIMIENTO .................................................................................... 83 1.7.4. FUNCIÓN DE TRANSFERENCIA DE TIEMPO DISCRETO .............................................................. 83 1.7.5. SITIO DE RAÍZ EN EL PLANO Z ................................................................................................ 84 1.7.6. COMPENSACIÓN USANDO UN CONTROLADOR DIGITAL........................................................... 90 CAPITULO V ........................................................................................................................................ 95 ANALISIS Y SIMULACION DEL CONTROL DE VELOCIDAD DEL VEHICULO EN SIMULINK C ............................................................................................................................................................ 95 1.8. 1.8.1. 1.8.2. 1.8.3. 1.9. 1.9.1. 1.9.2. 1.9.3.. MODELADO EN SIMULINK .................................................................................................. 95 CONFIGURACIÓN FÍSICA Y ECUACIONES DEL SISTEMA ........................................................... 95 CONSTRUYENDO EL MODELO ................................................................................................ 96 RESPUESTA DE BUCLE ABIERTO ........................................................................................... 100 DISEÑO DE CONTROL DE SIMULINK ............................................................................. 102 EXTRAYENDO UN MODELO LINEAL EN MATLAB ............................................................... 102 IMPLEMENTANDO EL CONTROL PI ....................................................................................... 105 RESPUESTA DE CIRCUITO CERRADO ..................................................................................... 109. RECOMENDACIÓN ............................................................................................................................. 112 BIBLIOGRAFIA ................................................................................................................................. 113. 4.

(5) RESUMEN El propósito de esta tesis es analizar y simular el sistema de control de un vehículo para mantener su velocidad constante a pesar de las perturbaciones externas, como los cambios en el viento o el grado de la carretera. Esto se logra midiendo la velocidad del vehículo, comparándola con la velocidad deseada o de referencia, y ajustando automáticamente el acelerador de acuerdo con una ley de control. Palabra claves: control de velocidad, control PID, ley de control.. 5.

(6) ABSTRACT The purpose of this thesis is to analyze and simulate a vehicle control system to maintain its constant speed despite external shocks, such as changes in the wind or the grade of the road. This is accomplished by measuring the speed of the vehicle, comparing it with the desired speed or reference, and automatically adjusting the throttle in accordance with a law of control.. Keywords: Speed control, PID control, control law.. 6.

(7) INTRODUCCION. En la presente tesis, se pretende desarrollar el análisis del control de velocidad de un vehículo ante perturbaciones externas a partir del modelo matemático que describe la planta del sistema. Para la formulación de este problema entonces pasaremos directamente a incorporar la incertidumbre en el modelo matemático del vehículo; para conseguir así un modelo dependiente de parámetros físicos del sistema. La simulación del sistema se hará con el software Matlab.. 7.

(8) OBJETIVOS -. Diseñar un Control PID Para El Control del vehículo ante perturbaciones externas. -. Formular Matemáticamente El Problema De Diseño Del Controlador, En el espacio de Estados.. -. Analizar el lugar de raíces del sistema.. -. Simular el sistema de control.. HIPÓTESIS. -. Se puede diseñar un control PID para control de un vehículo ante perturbaciones externas.. 8.

(9) CAPITULO I MARCO TEÓRICO 1. Control de Velocidad de un Vehículo. En los vehículos actuales se utiliza un sistema llamado “control de crucero”, lo que este sistema hace es mantener una velocidad prefijada por el conductor durante un viaje, generalmente en carretera, frenando automáticamente cuando es necesario. El sistema se desactiva cuando el conductor pisa el pedal de freno y en algunos modelos también se puede desactivar con el pedal de embrague. Existen algunos sistemas que permiten aumentar la velocidad al pisar el acelerador y cuando este se suelta la velocidad vuelve a ser la programada previamente. La principal ventaja de este sistema es que le evita al conductor la fatiga de ir manteniendo la velocidad y lo enfoca más en mantener la dirección, lo cual es particularmente útil en viajes muy largos. El control de crucero moderno fue inventado como tal por Ralph Teetor en 1945, el primer automóvil en utilizar este sistema fue el “Imperial” de 1958, llamado autopiloto este sistema calculaba la velocidad del vehículo con base. 1.1 Control de velocidad crucero. El control de velocidad, también conocido como regulador de velocidad o autocrucero (o cruise control en inglés y Tempomat en alemán) es un sistema que controla de forma automática el factor de movimiento de un vehículo de motor. El conductor configura la velocidad y el sistema controlará la válvula de aceleración o throttle del vehículo para mantener la velocidad de forma constante.. 9.

(10) 1.2 Antecedentes Los primeros dispositivos para este propósito basados en un regulador centrífugo se usaron allá por los años 1910, principalmente por Peerless. Peerless hizo una campaña publicitaria en la que explicaba que su sistema "mantendría la velocidad tanto cuesta arriba como cuesta abajo". La tecnología la crearon James Watt y Matthew Boulton en 1788 para controlar el motor de vapor. El controlador ajusta la posición del acelerador a medida que la velocidad del motor varía con cargas diferentes. Los controladores de velocidad modernos se inventaron en 1945 por el inventor ciego e ingeniero mecánico Ralph Teetor. Su idea nació del malestar que le producía ir en el vehículo con su abogado, quien frenaba y aceleraba continuamente según hablaba. El primer vehículo con el sistema de Teetor fue el Chrysler Imperial en 1958. Este sistema calculaba la velocidad sobre la carretera basándose en las rotaciones del palier y usaba una bobina para variar la posición del acelerador según fuera necesario. 1.3 Principio de funcionamiento Los controles de velocidad actuales pueden estar o no activados antes de usarse – en algunos modelos está siempre activo pero no siempre en funcionamiento, en otros hay un interruptor para activarlo, que debe presionarse después de arrancar el motor. En la mayoría de casos hay botones con funciones para activar, continuar, acelerar y "coast". En ocasiones también hay un botón para cancelar. Pisando, indiferentemente, el pedal del freno o del embrague, el sistema es desactivado. El sistema se opera de diferentes formas, según el fabricante, ej. con dos o más botones en los radios del volante o al borde de la rueda del volante como en los vehículos de la marca Honda, o en la manilla de los intermitentes como en algunos modelos de General Motors o con una manilla exclusivamente para este propósito como en modelos de BMW o Toyota. Los modelos iniciales hicieron uso de un dial para regular la velocidad. El conductor debe elevar la velocidad del vehículo de forma manual y entonces usar el control para establecer la velocidad actual como velocidad de crucero. El 10.

(11) control de velocidad calcula la velocidad a partir de un palier rotatorio, velocímetro, sensor de velocidad (situado en las ruedas) o a partir de las rpm del motor. El vehículo mantiene la velocidad tirando del cable del acelerador con una bobina o un servomotor basado en vacío. La mayoría de sistemas pueden desactivarse de forma explícita o automática cuando el conductor pisa el freno o el embrague. El control de velocidad, a menudo, incluye una función de memoria para restablecer la velocidad configurada antes tras frenar el vehículo y una función para disminuir la velocidad apretando un botón. Cuando el control de velocidad esta activo, es posible acelerar el vehículo pisando el acelerador, pero cuando éste se libera, el vehículo reducirá la velocidad hasta alcanzar de nuevo la velocidad de crucero. La última generación de controles de velocidad de forma electrónica pueden integrarse fácilmente en la unidad de control de motor). Los desarrollos actuales incluyen una función para reducir la velocidad de forma automática si el vehículo se aproxima a una cierta distancia del vehículo precedente y cuando se aplica un límite de velocidad (que es registrado por una cámara). Esto es una ventaja especialmente en trayectos que el conductor no conoce. 1.4 Ventajas y desventajas El control de velocidad trae consigo una serie de ventajas y desventajas. Como ventajas cabe destacar: •. Su utilidad para trayectos largos con poco tráfico, pues el desgaste por parte del conductor es menor.. •. Algunos conductores lo usan para no violar de forma inconsciente el límite de velocidad, disminuyendo el riesgo de ser multado. Hay que hacer notar al respecto que el vehículo, en tramos cuesta abajo, puede incrementar su velocidad más allá de la configurada en el control en pendientes pronunciadas.. 11.

(12) Por otro lado, el control de velocidad también puede jugar un papel perjudicial dando pie a accidentes: •. La falta de necesidad de mantener el pie presionando el acelerador puede desembocar en accidentes debido a la denominada hipnosis de la autopista o conductores incapacitados; puede que modelos futuros incluyan un pedal de hombre muerto para evitar este problema.. •. Si se usa en condiciones climatológicas desfavorables, con la calzada mojado o con nieve, el vehículo podría patinar si no cuenta con control de estabilidad. Pisar el freno bajo estas circunstancias para desactivar el control de velocidad, puede resultar en la pérdida de control sobre el vehículo.. Conducir sobre un terreno irregular, con subidas y bajadas, puede hacerse de forma más efectiva en términos de consumo de combustible por parte de un conductor experimentado, manteniendo la válvula del combustible constante. Para ello es necesario adaptarse al terreno y ganar momento en las bajadas, especialmente antes de una subida, y reducirlo durante el tramo ascendente. El control de velocidad trabajará de forma inversa, abriendo la válvula de combustible durante la subida para mantener una velocidad constante y cerrándola durante la bajada para no acelerar el vehículo aún más. 1.5 Control de velocidad inteligente Este sistema (denominado en inglés adaptive cruise control, ACC) está disponible en algunos vehículos de última generación. Se basan en un radar o bien en un láser para permitir mantener la misma velocidad que el vehículo precedente, también a bajas velocidades (ej. vía congestionada por el tráfico). El sistema frena y acelera de forma autónoma para mantener la distancia preestablecida por el conductor. Algunos de estos sistemas disponen de una función denominada forward collision warning (al español "preaviso de colisión") que advierte al conductor de que el vehículo precedente está tan cerca que un frenado por parte de éste desembocaría en un accidente.. 12.

(13) CAPITULO II 2.1 Control PID El ajuste y la implementación de algoritmos de control PID implican diversas tareas, entre las que se incluyen: •. Selección de un algoritmo de control PID apropiado (P, PI o PID).. •. Ajuste de ganancia del controlador.. •. Simulación del control PID con respecto a un modelo de planta.. •. Implementación del controlador en un procesador de ejecución.. El control automático de un proceso requiere de un sistema que ajuste automáticamente una(s) variable(s) del proceso para mantener otra (s) dentro de límites establecidos. Una de las formas más comunes de controlar un proceso es utilizar un sistema de control por retroalimentación, o de lazo cerrado. En este se mide, la variable que se quiere controlar; esta medición va retroalimentada al controlador para compararla con el valor deseado, y determinar la corrección necesaria, en caso de que exista alguna diferencia entre su valor actual y el valor deseado. El comportamiento del sistema de control es evaluado con base en la característica de la respuesta en el tiempo de la variable controlada. Este comportamiento depende del tipo de proceso, del tipo de controlador y de la forma en que es ajustado para producir una determinada señal de control. La relación que existe entre la señal de salida de un controlador y el error en la variable controlada (diferencia entre el valor deseado y el valor instantáneo de la variable controlada) se denomina “Acción de Control”. Por lo tanto, un controlador tendrá una acción de control dada por esta relación. Comercialmente existen controladores que pueden tener una de las siguientes acciones:. 13.

(14) Tabla 2.1. Acciones de los Controladores Comerciales.. Acción de Control Proporcional (P) Proporcional más Integral (PI) Proporcional más Derivativo (PD) Proporcional más Integral más Derivativo (PID) Dos Posiciones (ON – OFF) Estas acciones son las que normalmente encontramos en un controlador, sin embargo, el empleo de controladores programables y dispositivos de control computarizados permiten la programación de acciones de control diferentes a las mencionada anteriormente.. 2.2 Modo De Control Proporcional:. L (s). e(s). +. V a(s). m (s) G c (s). G l (s). +. F (s) G v (s). U (s). G p (s). +. C (s). O (s) H (s). Figura 2.1. Diagrama de Bloques General de un Lazo de Control por Retroalimentación. Un controlador de acción proporcional puede ser descrito por la siguiente ecuación: m(t) = Mo + Kc.e(t). (2-1) 14.

(15) Donde: m(t) : Señal de salida del controlador (Variable Manipulada). Kc. : Ganancia proporcional (parámetro ajustable).. Mo. : Señal de salida del controlador cuando el error es cero (normalmente se le conoce como “bias”).. e(t). : Error.. De la ecuación 2-1, se puede deducir que en un controlador de acción proporcional la señal de salida del controlador (señal de control) es proporcional al error. Al aplicar transformada de Laplace a dicha ecuación se tiene como resultado la función de transferencia representada en la ecuación 2-2, para un controlador de acción proporcional:. Gc(s) =. M(s) = Kc e(s). (2-2). Al igual que la ganancia del proceso, la proporcional generalmente se expresa porcentualmente. Sin embargo, muchos controladores tienen el ajuste proporcional expresado en función de la banda proporcional, la cual puede definirse como el porcentaje de variación en la variable controlada que hace que la señal de salida del controlador cambie desde 0 % a 100 %, como se observa en la ecuación 2-4. Para ilustrar mejor el concepto de banda proporcional supongamos el siguiente ejemplo: En un proceso, con un sistema de control de temperatura, la temperatura puede variar entre 20°C y 100°C. Con un controlador de temperatura que regula el flujo de agua de enfriamiento al proceso, se mantiene la temperatura en 60°C (valor deseado). El controlador esta ajustado de forma tal que cuando la temperatura llega a 40°C la válvula de agua de enfriamiento está completamente cerradas; y cuando la temperatura llega a 80°C, la válvula está completamente abierta. ¿Cuál es la banda proporcional?.. 15.

(16) El porcentaje de variación en la variable controlada, sobre el cual opera el controlador es:. ∆x %Bp = x ∗ 100 ∆y y. (2-3). donde: ∆x : Variación. de. la. señal. de. entrada. ∆y : Variación de la señal de salida X. : Rango de entrada. y : Rango de salida.. Calculando se tiene:. %Bp =. (80 − 40)°C ∗ 100 = 50% (100 − 20)°C. Se tiene que este 50% de variación produce una variación de 100% en la señal de salida del controlador; luego, la banda proporcional es de 50%. También:. %Bp =. 1 ∗ 100 Kc. (2-4). En la figura 2.2, se representa gráficamente la banda proporcional obtenida:. 16.

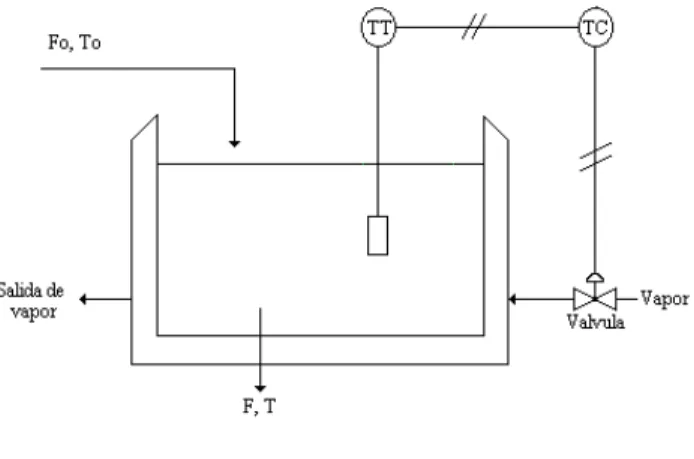
(17) Figura 2.2. Variación de la Señal de Salida. Tanto la banda proporcional como la ganancia son de uso común, sin embargo, en este capítulo, se utilizará la ganancia proporcional como el ajuste proporcional. A continuación, se estudiará el efecto de la acción de control proporcional sobre las características de la respuesta de lazo cerrado. 2.3 Procesos de orden 2.3.1. Proceso de primer orden. Tomando como ejemplo el proceso mostrado en la figura 2.3. Para simplificar el estudio se presume que el proceso es de primer orden, y que la función de transferencia del transmisor de temperatura y la válvula del vapor son iguales a uno.. Figura 2.3. Calentador. El diagrama de bloques para este ejemplo corresponde al mostrado en la figura 2.3a.. Figura 2.3a. Diagrama de bloques completo. La función de transferencia para este caso, es:. 17.

(18) T(s) Gp(s).Gv(s).Gc(s) = Va(s) 1 + Gp(s).Gv(s).Gc(s).H(s). (2-5). Como se presumió que la función de transferencia para el transmisor y para la válvula es de 1, es decir, Gv(s) = H(s) = 1 se tiene:. T(s) Gp(s).Gc(s) = Va(s) 1 + Gp(s).Gc(s). (2-6). Con la que se obtiene el diagrama de bloques de la figura 2.3b Va ( s ). +. e(s). -. Gc(s) = Kc. Gp(s). T(s). Figura 2.3b. Diagrama de bloques con Gv(s) = 1 y H(s) =1. Sustituyendo los parámetros en cada una de las funciones, se obtiene:. Gp(s) =. Kp τ ps + 1. y Gc(s) = Kc.  Kp  Kc  τ ps + 1  T(s)  = Va(s)  Kp  1 + Kc   τ ps + 1 . (2-7). Esta es la función de transferencia de lazo cerrado del ejercicio del calentador, simplificando se tiene:. T(s) KcKp = Va(s) τ ps + (1 + KcKp) dividiendo el numerador y denominador por (1+KcKp), resulta: KcKp KcKp T(s) N 1 + KcKp 1 + KcKp = = = τ ps + (1 + KcKp) τ ps Va(s) +1 D +1 1 + KcKp 1 + KcKp. 18. (2-8).

(19) Donde “N” es la ganancia de lazo cerrado y “D” es la constante de tiempo de lazo cerrado. Observamos que a lazo cerrado la constante de tiempo (τ) del sistema es menor, debido a que la constante Kc es mayor. Como se puede observar el orden de la función de transferencia de lazo cerrado es el mismo que el de la función de transferencia de lazo abierto. Al término “N” se le denomina “ganancia de lazo cerrado”, al término “D” se le llama constante de tiempo de lazo cerrado. Debido a que KcKp es un número positivo, la constante de tiempo de lazo cerrado, “D” siempre será menor que la constante de tiempo de lazo abierto. De este modo, el sistema de lazo cerrado responderá más rápidamente que el sistema de lazo abierto. Por otro lado, la constante de tiempo de lazo cerrado disminuye a medida que la ganancia del controlador aumenta. Así, que una mayor ganancia del controlador implica una respuesta más rápida. La ganancia de lazo cerrado, “N” relaciona los cambios en la variable controlada T(s) con los cambios en el valor deseado Va(s). Usando el calentador de la figura 2-3, como ejemplo, se observará cuál será la variación en la temperatura T, si el valor deseado se incrementa en 10 °C en forma escalón. KcKp 1 + KcKp De la ecuación 2-8 se tiene: T(s) = Va(s) ; sustituyendo Va(s) por su τ ps +1 1 + KcKp. valor: Va(s) =. 10 , se tiene: s. KcKp 1 + KcKp  10  T(s) =   τ ps +1  s  1 + KcKp. 19.

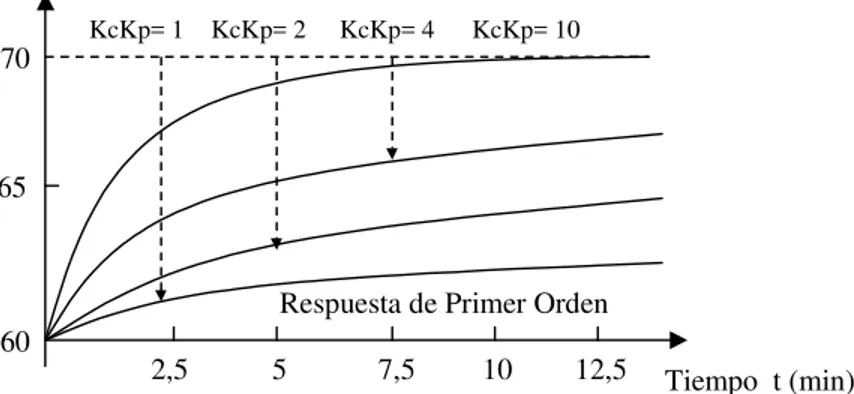
(20) La variación final de la variable controlada T con respecto al nuevo valor deseado es: KcKp     1 + KcKp  10  T = lim s→ 0 sT(s) = lim s→0 s  τ ps  s + 1   1 + KcKp .  1   1   KcKp  ∆T =  + 1 10  10 =   1 + KcKp   KcKp   . (2-9). (2-10). Si KcKp → ∞ => ∆T => 10. Como se puede observar el cambio de la variable controlada depende de la ganancia del controlador Kc. En la figura 2.4 se muestra la respuesta del calentador (donde se presume un comportamiento de primer orden) para diferentes valores de Kc. El valor deseado inicial está fijado en 60 °C. La diferencia entre el cambio en el valor deseado, cambio en la variable controlada se conoce como error. e = 10 ° C - ∆T ° C. (2-. 11).  10KcKp  Sustituyendo: e = 10° C -   °C  1 + KcKp .   10   1   =0 Para Kc→ ∞ , e = 10  1  + 1   KcKp . Se observa que el error solamente está determinado por la ganancia del controlador y por las características de estado estacionario del proceso. La dinámica del proceso no tiene efecto sobre el error. Como se muestra en la figura 2.4, al incrementar la ganancia del controlador se disminuye el error. El error sería cero únicamente cuando Kc → ∞ por este se dice que la acción de control proporcional no elimina el error.. 20.

(21) 70. KcKp= 1. KcKp= 2. KcKp= 4. KcKp= 10. 65. Respuesta de Primer Orden 60. 2,5. 5. 7,5. 10. 12,5. Tiempo t (min). Figura 2.4. Respuesta de un Proceso de Primer Orden, con Acción de Control Proporcional, para un cambio en la referencia. De las curvas de respuesta de la figura 2.4, se puede observar que aumentando la ganancia del controlador, disminuye el error y la respuesta se hace más rápida, siendo estas dos condiciones deseables. Esto sugiere que la ganancia del controlador debería ajustarse lo más alto posible. Desafortunadamente esto solamente es cierto para los procesos de primer orden. En procesos de orden mayor, el aumento de la ganancia del controlador produce otros efectos que limitan los valores aceptables de Kc. 2.3.2. Procesos de segundo orden. La figura 2.5 muestra el diagrama de bloques de un proceso de segundo orden con acción de control proporcional. De la misma forma que en el caso anterior, el diagrama de bloques se obtiene, haciendo Gv(s) = H(s) = 1.. Figura 2.5. Diagrama en bloques de un sistema de segundo orden. En este caso, la función de transferencia de lazo cerrado, con respecto al valor deseado se obtiene de la siguiente manera:. 21.

(22) KcKp (τ p 1s + 1)(τ p 2 s + 1) C(s) = KcKp Va(s) 1+ (τ p 1s + 1)(τ p 2 s + 1). (2-12). C(s) KcKp = Va(s) (τ p 1 s + 1)(τ p 2 s + 1) + KcKp. (2-13). resolviendo el denominador de la función de transferencia: C(s) KcKp = Va(s) τ p 1 τ p 2 s 2 + (τ p 1 + τ p 2 )s + 1 + KcKp. (2-14). dividiendo toda la expresión por 1+KcKp se tiene: KcKp C(s) 1 + KcKp = Va(s)  τ p 1 τ p 2  2  τ p 1 + τ p 2  s +   1 + KcKp   1 + KcKp. El termino:.  s + 1 . (2-15). KcKp es la ganancia del lazo cerrado, y es igual a la expresión 1 + KcKp. obtenida en el caso anterior en un proceso de primer orden, lo cual confirma que el error (offset) no es afectado por la presencia de una segunda constante de tiempo en la función de transferencia (no depende de la dinámica del proceso). Solamente depende de la ganancia del controlador Kc. El efecto de la ganancia del controlador sobre la velocidad de respuesta y sobre la estabilidad del lazo de control se puede deducir, analizando el denominador de la función de transferencia de segundo orden que tiene la forma general, como se muestra a continuación. G(s) =. Y(s) Kp = 2 2 X(s) τp s + 2 δ τp s + 1. De acuerdo a los términos del denominador e igualando se obtiene:. 22.

(23) τ p2 =. τ p 1τ p 2 1 + KcKp. ===> τ p =. τ p 1τ p 2 1 + KcKp. Constante de tiempo en lazo cerrado (frecuencia de resonancia) 2δτ p =. 1 + KcKp. => δ =. τ p1 + τ p 2 τ p1τ p 2. δ= 2. τ p1 + τ p 2. 1 + KcKp. τ p1 + τ p 2 2τ p(1 + KcKp ). (1 + KcKp). =. (2-16). τ p1 + τ p 2. 2 (τ p 1τ p 2 )(1 + KcKp). (2-17). Donde: δ : Coeficiente de amortiguamiento.. Las ecuaciones anteriores muestran que la constante de tiempo de lazo cerrado τp, al igual que en el caso anterior del control de un proceso de primer orden, es. función de la ganancia del controlador. A medida que Kc aumenta, τp es menor, por lo tanto, la respuesta del lazo de control es más rápida. Al analizar la ecuación 2-17, se observa que un aumento de la ganancia del controlador,. produce una disminución en el valor del coeficiente de. amortiguamiento ξ. En el punto anterior se estableció que la estabilidad de un sistema o proceso de segundo orden está estrechamente relacionada con el valor de ξ. En particular, se vio que 0 < ξ < 1, la respuesta sería subamortiguada. Las oscilaciones y el sobreimpulso de la respuesta del lazo de control serán mayores a medida que Kc aumenta. Como se vio anteriormente esto limita el valor máximo de Kc. En la figura 2.6 se pueden observar las curvas de respuesta del sistema de control, del proceso de segundo orden esquematizado en la figura 2.5, frente a una perturbación tipo escalón unitario en el valor deseado, para diferentes valores de Kc. El análisis de las curvas de respuesta confirma lo siguiente. •. El error disminuye al aumentar la ganancia del controlador.. 23.

(24) •. La respuesta es más rápida al aumentar, la ganancia del controlador.. •. El valor de sobreimpulso y las oscilaciones se incrementan al aumentar la ganancia del controlador.. Kc= 10. 1,5 Kc= 4. Respuesta de Segundo Orden Kp=1 %/% tp1= 10 min tp2=2,5 min. 1,0. 0,5. Kc= 2. 0. Kc= 1. 10. 20. Tiempo t (min). Figura 2.6. Respuesta de un Proceso de Segundo Orden con Acción de Control Proporcional, Cambio de Escalón en el Valor Deseado.. Se concluye que un controlador de acción proporcional no elimina el error. Solo una alta ganancia permite reducir el error a un mínimo. En la práctica, la ganancia del controlador se aumenta hasta que el sobreimpulso y las oscilaciones alcanzan un límite aceptable.. 2.4.- MODO DE CONTROL PROPORCIONAL MÁS INTEGRAL (PI). Una de las desventajas de la acción de control proporcional es que no puede eliminar el error. Para compensar esta dificultad, muchos controladores de procesos incorporan una acción de control adicional, llamada acción integral, la cual permite eliminar el error. Como se observara más adelante, la respuesta de la acción integral está basada en la integral del error. 24.

(25) Un controlador de Acción Proporcional más Integral puede describirse por medio de la siguiente ecuación: t. m(t) = Mo + Kce(t) + Kc. 1 e(t) dt τi ∫0. (2-27). Donde, τi es un parámetro ajustable y se denomina “tiempo integral”, normalmente se expresa en minutos. Se observa que el coeficiente de la acción integral disminuye al aumentar el tiempo integral, esto genera una relación inversa entre el tiempo integral y la acción integral (τi = ∞ significa que no hay acción integral). Aplicando la transformada de Laplace a la ecuación 2-27, se obtiene la función de transferencia de un controlador de acción proporcional más integral como se muestra en la ecuación 2-28. M(s) = KcE(s) +. KcE(s) 1   = KcE(s) 1 + τi  τis . (2-. 28). Gc(s) =. m(s) 1  = Kc.1 +  e(s)  τis . (2-29). En las ecuaciones anteriores se observa que la señal de salida de un controlador proporcional más integral consta de dos partes: •. La primera es proporcional al error.. •. La segunda es proporcional a la integral del error.. La figura 2.7, muestra la respuesta de un controlador de acción proporcional más integral ideal frente a un cambio en escalón (∆E) en la señal de error.. 25.

(26) ∆E 0. Tiempo Señal de Error 2Kc∆E Contribución Integral. Señal de Respuesta Kc∆E. 20%. τi. Contribución Proporcional. Tiempo. Figura 2.7. Respuesta de un controlador Proporcional más Integral frente a una entrada escalón. Inicialmente la salida del controlador es del 20%. Cuando el error varia desde 0 hasta ∆E, la acción proporcional inmediatamente cambia la salida en una magnitud igual a Kc∆E y permanece constante. La salida de la acción de control integral no se modifica instantáneamente con el error, sino que varía linealmente con el tiempo.. De la ecuación 2-27 para un error constante ∆E, se tiene que la componente de la ecuación proporcional es una constante igual a Kc.∆E, y la componente de la acción integral es una rampa igual a Kc.∆E.t/τi.. m(t) = Mo + Kc∆E +. Kc t ∫ ∆Edt τi 0. (2-30). t τi. (2-31). m(t) = Mo + KcE + Kc∆E. De la ecuación 2-28, se obtiene:. M(s) 1  = Kc 1 +  E(s) τ is  . (2-32). 26.

(27) De esto se deduce que la acción proporcional actúa primero, respondiendo instantáneamente cuando cambia el error, mientras que la acción integral cambia linealmente en el tiempo proporcional al error.. El tiempo integral τi se define como el tiempo necesario para que la respuesta de la acción integral sea igual a la respuesta de la acción proporcional. La figura 2-7, muestra que, cuando la respuesta de acción integral alcanza el valor Kc.∆E (la respuesta total es Kc.∆E + Kc.∆E 0 2 Kc.∆E), el tiempo transcurrido es igual a τi. Para estudiar las características de la acción de control proporcional más integral, se toma como ejemplo el lazo de control mostrado en la figura 2.8.. Vd (s). +. e (s). -.  1  Kc1 +   τ i∗s . m (s). (τ. Kp ∗s +1 p. ). C (s). b (s). Figura 2.8. Diagrama de bloques de un proceso de primer orden con acción de control PI.. La función de transferencia de lazo cerrado que relaciona la variable controlada C(s) con el valor deseado Va(s) se describe como sigue:.  1  Kp  Kc1 +    τ is   ( τ ps + 1)  C(s)  = Va(s)  1  Kp  1 + Kc1 +    τ is   ( τ ps + 1)  . (2-33). C(s) KcKp(τ is + 1) KcKp(τ is + 1) = = 2 Va(s) τ is(τ ps + 1) + KcKp(τ is + 1) τ i τ ps + τ i (1 + KcKp)s + KcKp. (2-34). 27.

(28) Ahora suponga que sé está interesado en conocer cuál es el error producido por una perturbación tipo escalón, por encima de 10 °C en el valor deseado Va(s). Sustituyendo el valor de Va(s) en la ecuación 2-34, se tiene:. C(s) =. KcKp( τ is + 1) 10 τ i τ ps + τ i (1 + KcKp)s + KcKp s 2. El cambio de la variable controlada respecto al nuevo valor deseado es:.   10 KcKp(τ is + 1) C = lims→0sC(s) = lims→0s 2   τ i τ ps + τ i (1 + KcKp)s + KcKp  s. (2-35). ∆C = 10 °C.. La diferencia entre el cambio que sufre por el valor deseado y el cambio experimentado por la variable controlada es el error. En este caso el error es: Error = 10 °C - ∆C. 10 °C – 10 °C = 0 ⇒ error = 0 . Como se estableció anteriormente, el controlador de acción proporcional más integral tiene la capacidad de eliminar el error. Las características dinámicas de la respuesta de lazo cerrado dependen de las raíces del denominador (polos) de la función de transferencia. Para que el sistema de control sea estable, todos los polos deben ser números reales negativos, o números complejos con parte real negativa. Para hacer un análisis de la estabilidad de lazo de control es convenientes expresar el denominador de la función de transferencia en función del coeficiente de amortiguamiento:. 28.

(29) C(s) KcKp (τ is + 1) = 2 Va(s) τ i τ p s + τ i (1 + KcKp) s + KcKp. (2-37). dividiendo toda la expresión por KcKp se tiene: (τ is + 1) C(s) KcKp = Va(s) τ i τ p s2 + τ i (1 + KcKp) s + 1 KcKp KcKp. (2-37). Por analogía con la ecuación general de un proceso de segundo orden, la ecuación 2-37, puede escribirse como: C(s) (τ is + 1) = 2 2 Va(s) τ p c s + 2ξτ p s + 1. donde: τ p c 2 =. 2 ξ τ pc =. (2-38). τiτp τiτp ⇒ τ pc = KcKp KcKp. (2-39). τ i (1 + KcKp) KcKp. (2-40). La ecuación 2-40 demuestra que el coeficiente de amortiguamiento es función de los dos parámetros del controlador: Kc y τi. El efecto de la ganancia del controlador sobre el valor del coeficiente de amortiguamiento y por consiguiente, sobre la estabilidad del sistema de control fue analizado en la sección de control proporcional de este de este manual. El efecto del tiempo integral τi sobre el valor del coeficiente de amortiguamiento y, por ende, sobre la estabilidad puede ser analizado a partir de la ecuación 240. Un aumento de τi implica un aumento de ξ, lo que hace al sistema más estable. La figura 2.9 muestra la respuesta frente a un cambio escalón unitario en el valor deseado del lazo de control presentado en la figura 2.8 para un valor constante 29.

(30) de la ganancia del controlador (K=2%/%); y para diferentes valores del tiempo integral. C(t). Tiempo Integral ti= 2 min. Respuesta. 1,5. 1,0. 5 10. 0,5. 20 ti= ∞. Kc = 2 %/% Kp = 1 %/% ti = 10 min. 0. 10. 20. Tiempo t (min). Figura 2.9. Respuesta de un sistema de primer orden frente a un escalón unitario en el valor deseado con modo de control proporcional + integral. La figura 2.9 muestra que para valores grandes de τi la respuesta es lenta, y tiende asintóticamente al valor deseado. Para valores pequeños de τi, la respuesta presenta sobreimpulso y es oscilatoria. El ajuste apropiado del tiempo integral depende del criterio utilizado para evaluar el comportamiento del lazo de control. Un criterio de funcionamiento es el del mínimo sobreimpulso, en el cual la forma de la curva de respuesta se determina principalmente por el ajuste proporcional. El tiempo integral se ajusta al valor más bajo, de tal forma que no cambie significativamente el valor del coeficiente de amortiguamiento. Otro criterio de funcionamiento es obtener una curva de respuesta con una razón de amortiguamiento (Ra) igual a 1/4. Este criterio se muestra en las figuras número 2.10 y 2.11. 2.5.- MODO DE CONTROL PROPORCIONAL MÁS DERIVATIVO (PD). Un tercer modo de control es el derivativo. En la practica, el modo derivativo se combina con el proporcional, lo cual da origen al modo de control proporcional más derivativo (PD). En muchos casos, también se usa acción integral formando la acción de control proporcional más integral más derivativo (PID).. 30.

(31) Un controlador proporcional más derivativo se puede representar por la siguiente ecuación:. m(t) = Mo + Kc.e(t) + Kc .τ d. de(t) dt. (2-41). Donde τd es un parámetro ajustable y se denomina “tiempo derivativo”. Expresado normalmente en minutos. Este tipo de controlador es muy sensible al ruido presente en el sistema, por lo que se recomienda no usar la parte derivativa en procesos que tengan mucho ruido. La razón es que la derivada de una señal de ruido (de(t)/dt) genera valores muy altos en la salida del controlador (m(t)), lo que podría originar una salida muy ruidosa o anular la posibilidad de mantener controlado al proceso. Aplicando transformada de Laplace a la ecuación (2-41), se obtiene la función de transferencia de un controlador PD:. Gc(s) =. m(s) = Kc(1 + τ d s) e(s). (2-42). La ecuación anterior es una ecuación ideal. Otra ecuación que puede usarse para describir un controlador PD es:. m(s) Kc(1 +τd s) = e(s) (1 + α τd s). (2-43). La cual representa un circuito de adelanto/atraso. La figura 2.10 muestra la respuesta de un controlador proporcional más derivativo frente a una variación tipo rampa (e(t)=Kt) en la señal de error. Sustituyendo este valor en la ecuación 2-41 se tiene:. m(t) = Mo + Kc.Kt + Kcτd. dKt dt. (2-44). m(t) = Mo + Kc.Kt + KcτdK. (2-45) 31.

(32) La respuesta del controlador es la suma del componente derivativo (KcτdK), más el componente proporcional (KcKt). Cuando a transcurrido un tiempo igual a τd, la respuesta del controlador es igual a dos veces el valor de la respuesta del componente derivativo (2KcdK). De esta forma, el tiempo derivativo se define, como el tiempo requerido para que la respuesta del modo proporcional sea igual a la respuesta del modo derivativo, cuando la entrada sea una función rampa.. Señal de Error. C(t). Pendiente = K. Tiempo. Respuesta. m(t). Contribución Proporcional. Contribución Derivativa. td Tiempo. Figura 2.10. Respuesta de un controlador proporcional más derivativo frente a una señal rampa. Para estudiar las características de la acción de. control proporcional más. derivativo, se toma como ejemplo el lazo de control mostrado en la figura 2.11.. +. e (s). -. Kc (1 + τd s ). m (s). C (s) Kp (τp1 s + 1)(τp2 s + 1). b (s). Figura 2.11. Diagrama en bloques de un proceso de segundo orden con acción de control proporcional más derivativo.. 32.

(33) La función de transferencia de lazo cerrado que relaciona a la variable controlada C(s) con el valor deseado Va, se puede escribir como: C(s) = Va(s). [Kc(1 + τ s)] ( d. [. 1 + Kc(1 + τd s). Kp τp1 s + 1) (τp2 s + 1). ](. Kp τp1 s + 1) (τp2 s + 1). KcKp(1 + τd s) C(s) = Va(s) ( τp1 s + 1) ( τp2 s + 1) + KcKp(1 + τd s). (2-46). (2-47). Suponga ahora se está interesado en conocer cuál es el error producido por una perturbación tipo escalón unitario en el valor deseado Va(s), sustituyendo el valor de Va en la ecuación 2-47 se tiene: C(s) =. KcKp(1 + τd s). 1 ( τp1 s + 1) ( τp2 s + 1) + KcKp(1 + τd s) s. (2-48). La variación de la variable controlada con respecto al nuevo valor deseado es:.  1 KcKp(1 + τd s) C = lim s→0 sC(s) = lim s→0 s    ( τp1 s + 1) ( τp2 s + 1) + KcKp(1 + τd s)  s. C=. (2-49). KcKp 1 + KcKp. La diferencia entre el cambio experimentado por el valor deseado y el cambio experimentado por la variable controlada es el error, en este caso:. error = 1 -. KcK 1 + KcK. (2-50). Como se observa, el error es diferente de cero y al igual que en el caso de acción proporcional, es función de la ganancia del controlador. Si la perturbación es constante, la acción derivativa no tiene efecto sobre el error de estado estacionario.. 33.

(34) La figura 2.12, muestra el efecto de la acción derivativa sobre el proceso de segundo orden mostrado en la figura 2.11. La ganancia del controlador, para este ejemplo, a sido fijada arbitrariamente en 8%/%. En la figura número 2.12, se observa que un argumento del tiempo derivativo (aumento de la acción derivativa) es beneficioso para la estabilidad, pero disminuye la velocidad de respuesta. Kc = 10, τd = 1 min Kc = 5, τd = 1 min Kc = 5, τd = 1 min 1. 0,5. Sistema de Segundo Orden Kp = 1%/%, τp1 = 10 min, τp2 = 1,5 min. 0 0. 10. 20. Tiempo (min). Figura 2.12. Efecto de la acción de control derivativo sobre la respuesta de lazo cerrado.. 2.6.- MODOS DE CONTROL PROPORCIONAL MÁS INTEGRAL MÁS DERIVATIVO (PID). Un controlador PID combina las buenas características de la estabilidad del controlador PD, y la característica de eliminación del error del controlador PI, pero al igual que el controlador PD presenta las mismas desventajas citadas para los procesos donde se tiene altos niveles de ruido. Un controlador PID puede describirse mediante la siguiente ecuación.. m(t) = mo + Kc.e(t) + Kc. 1. t. e(t)dt + Kc τ τ∫. d. i 0. de(t) dt. 34. (2-51).

(35) Aplicando la transformada de Laplace a la ecuación anterior se obtiene la función de transferencia de un controlador de acción PID.. m(s) 1   = Kc(1 + ) + τd s e(s) τi s  . (2-52). La figura 2.13 muestra la respuesta de lazo cerrado del sistema de control de la figura 2.11, al cual se le ha agregado acción integral. Al usar acción de control PID, el ajuste del controlador se complica, ya que hay tres parámetros (Kc, τi, τd) que deben ser ajustados. La figura 2.13 muestra las curvas de respuesta para diferentes ajustes del controlador y en la tabla 2.2 se encuentran los valores de Kp, τi y τd del controlador mostrado en la figura 2.13.. C(t)/∆R. C. K = 1%/%, τ1 = 10 min, τ2 = 2,5 min B A. Respuesta. 1,0. 0,5. 0. 10. 20. Tiempo t (min). Figura 2.13. Respuesta de un Proceso de Segundo Orden, frente a una Perturbación de tipo Escalón Unitario en el Valor Deseado con Acción de Control PID. Tabla 2.2. Valores de los Parámetros del Controlador. Curva. Ganancia Kc. Tiempo Integral. Tiempo Derivativo. %/%. τi (min). τd (min). A. 2. 10. 0. B. 5. 15. 1. C. 10. 15. 1. Para obtener un control adecuado se sugieren los siguientes pasos: 35.

(36) 1. Si la salida del proceso no necesita estar exactamente en el valor de referencia o Set Point, se puede utilizar un controlador proporcional (P). 2. Si se desea tener una salida del proceso con compensación del error se debería utilizar un controlador del tipo Proporcional – Integral (PI) o Proporcional – Integral – Derivativo (PID). 3. Si el proceso presenta mucho ruido, se recomienda no utilizar el componente derivativo del controlador PID. 4. Para mejorar la calidad del controlador se debe utilizar cualquier índice de optimización, tales como el IAE, IAET, ISE.. 36.

(37) CAPITULO III MODELAMIENTO DEL SISTEMA. 1.1. Modelamiento del sistema El control de crucero automático es un ejemplo de un sistema de control de retroalimentación que se encuentra en muchos vehículos modernos. El propósito del sistema de control de crucero es mantener una velocidad constante del vehículo a pesar de las perturbaciones externas, como los cambios en el viento o el grado de la carretera. Esto se logra midiendo la velocidad. del. vehículo,. comparándola. con. la velocidad deseada. o. de referencia, y ajustando automáticamente el acelerador de acuerdo con una ley de control.. Consideramos aquí un modelo simple de la dinámica del vehículo, que se muestra en el diagrama de cuerpo libre (FBD) anterior. El vehículo, de masa m, es actuado por una fuerza de control, u. La fuerza u representa la fuerza generada en la interfaz carretera / neumático. Para este modelo simplificado asumiremos. que. podemos. controlar. esta. fuerza. directamente. y. descuidaremos la dinámica del tren motriz, los neumáticos, etc., que entran en la generación de la fuerza. Se supone que las fuerzas resistivas, bv, debido a la resistencia a la rodadura y al arrastre del viento, varían. 37.

(38) linealmente con la velocidad del vehículo, v, y actúan en la dirección opuesta al movimiento del vehículo. 1.1.1. Ecuaciones del sistema Con estas suposiciones, nos queda un sistema de amortiguador de masa de primer orden . Sumando las fuerzas en la dirección x y aplicando la segunda ley de Newton, llegamos a la siguiente ecuación del sistema: +. =. ( ). Como estamos interesados en controlar la velocidad del vehículo, la ecuación de salida se elige de la siguiente manera =. ( ). 1.1.2. Parámetros del sistema Para este ejemplo, supongamos que los parámetros del sistema son: (m) masa del vehículo 1000 kg (b) coeficiente de amortiguación 50 Ns / m. 1.1.3. Modelado de espacio de estados Los sistemas de primer orden tienen solo un único modo de almacenamiento de energía, en este caso la energía cinética del automóvil, y por lo tanto solo se necesita una variable de estado, la velocidad. La representación de espacio de estado es, por lo tanto: =. =. = 1. −. +. 1. ( ). ( ). Ingresamos este modelo de espacio de estado en MATLAB usando los siguientes comandos:. 38.

(39) 1.1.4. Modelado de función de transferencia. Tomando la transformada de Laplace de la ecuación diferencial gobernante y asumiendo condiciones iniciales cero, encontramos que la función de transferencia del sistema de control de crucero es: ( )=. ( ) = ( ). 1 +. /. ( ). Ingresamos el modelo de función de transferencia en MATLAB usando los siguientes comandos:. 1.2. Modelamiento del sistema 1.2.1. Modelo del sistema y parámetros. El modelo de función de transferencia para el problema de control de crucero se proporciona a continuación.. 39.

(40) ( )=. ( ) = ( ). 1 +. /. ( ). Los parámetros utilizados en este ejemplo son los siguientes: (m) masa del vehículo 1000 kg (b) coeficiente de amortiguación 50 Ns / m (u) fuerza de control nominal 500 N 1.2.2. Especificaciones de rendimiento. El siguiente paso es crear algunos criterios de diseño que el sistema compensado debería lograr. Cuando el motor da una fuerza de 500 Newton, el automóvil alcanzará una velocidad máxima de 10 m / s (22 mph), vea la sección de respuesta de paso de bucle abierto a continuación. Un automóvil debería poder acelerar hasta esa velocidad en menos de 5 segundos. En esta aplicación, es suficiente un 10% de exceso y un 2% de error de estado estable en la velocidad. Teniendo en cuenta lo anterior, hemos propuesto los siguientes criterios de diseño para este problema: Tiempo de subida <5 s Sobregiro <10% Error de estado estable <2% 1.2.3. Respuesta de paso de bucle abierto. La respuesta. de lazo. abierto del. sistema,. sin. ningún. control. de. realimentación, a una fuerza de entrada de paso de 500 Newtons se simula en MATLAB de la siguiente manera:. 40.

(41) Step Response 10 9 8 7 6 5 4 3 2 1 0 0. 20. 40. 60. 80. 100. 120. 140. 160. 180. Time (seconds). Vemos que el sistema de bucle abierto no presenta sobreimpulsos u oscilaciones (características de los sistemas de primer orden) y alcanza la velocidad deseada de estado estacionario de 10 m / s; sin embargo, el tiempo de subida es demasiado lento, ~ 60 s. Por lo tanto, necesitamos diseñar un controlador de retroalimentación que acelere la respuesta significativamente sin afectar negativamente a las otras métricas de rendimiento dinámico.. 41.

(42) 1.2.4. Polos / ceros de bucle abierto. El sistema de control de crucero tiene un solo polo en s = -b / m que podemos ver trazado en el plano s usando los siguientes comandos de MATLAB:. Pole-Zero Map 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 -1. -0.8. -0.6. -0.4. -0.2. 0. 0.2. 0.4. 0.6. 0.8. 1. Real Axis (seconds -1). Observamos que el sistema de circuito abierto es estable y no oscila ya que el polo es real y negativo. Además, la velocidad de respuesta está determinada por la magnitud de este polo, b / m: cuanto mayor es la magnitud, más rápido se acerca el sistema al valor de estado estacionario. Como normalmente no podemos cambiar los parámetros del sistema para cambiar la respuesta dinámica del sistema, debemos diseñar controladores que alteren los polos y ceros del sistema de circuito cerrado para cumplir con las especificaciones de rendimiento deseadas. 1.2.5. Diagrama de Bode de bucle abierto. También estamos interesados en la respuesta de frecuencia de bucle abierto del sistema que encontramos utilizando el siguiente comando MATLAB:. 42.

(43) Bode Diagram -30. -40. -50. -60 0. -45. -90 10 -3. 10 -2. 10 -1. 10 0. Frequency (rad/s). Vemos que las representaciones de Bode exhiben las características definitivas de los sistemas de primer orden , que incluyen una magnitud de 3 dB y una fase de -45 grados a la frecuencia de esquina de w=b/m=0.05 rad / sy -20 dB / dec roll- apagado a altas frecuencias.. 43.

(44) CAPITULO IV DESARROLLO DEL CONTROLADOR PID. 1.3. Diseño del controlador PID. 1.3.1. Modelo del sistema y parámetros. El modelo de función de transferencia para el problema de control de crucero se proporciona a continuación. ( )=. ( ) = ( ). 1 +. /. ( ). Los parámetros utilizados en este ejemplo son los siguientes: (m) masa del vehículo 1000 kg (b) coeficiente de amortiguación 50 Ns / m (r) velocidad de referencia 10 m / s 1.3.2. Especificaciones de rendimiento •. Tiempo de subida <5 s. •. Sobregiro <10%. •. Error de estado estable <2%. 1.3.3. Descripción general de PID. El diagrama de bloques de un sistema de retroalimentación de unidad típico se muestra a continuación.. 44.

(45) La función de transferencia de un controlador PID es ( )=. +. !. +. ". =. ". #. +. +. !. ( ). Podemos definir un controlador PID en MATLAB usando la función de transferencia directamente:. Alternativamente,. podemos. usar. el objeto. del. controlador. PID de. MATLAB para generar un controlador de tiempo continuo equivalente de la siguiente manera:. 45.

(46) 1.3.4. Control proporcional. Lo primero que debe hacer en este problema es encontrar una función de transferencia de bucle cerrado con un control proporcional ( agregado.. =. ). Al reducir el diagrama de bloque de realimentación de unidad, la función de transferencia de bucle cerrado con un controlador proporcional se convierte en: $( ) =. ( ) ( ) %( ) = = &( ) 1 + ( ) ( ). Un controlador proporcional,. +. +. ( ). disminuye el tiempo de subida, lo cual es. deseable en este caso. Por ahora, use. igual a 100 y una velocidad de referencia de 10 m/s.. 46.

(47) 47.

(48) Step Response 10 9 8 7 6 5 4 3 2 1 0 0. 2. 4. 6. 8. 10. 12. 14. 16. 18. 20. Time (seconds). Hemos utilizado el comando de feedback MATLAB para simplificar la reducción del diagrama de bloques del sistema de circuito cerrado. Verifique por sí mismo que el resultado concuerda con la función de transferencia de bucle cerrado, T, derivada anteriormente. Al ejecutar en MATLAB debería dar la respuesta de paso anterior. Como puede ver en la gráfica, ni el error de estado estacionario ni el tiempo de subida satisfacen nuestros criterios de diseño. Se puede aumentar la ganancia proporcional,. '. para reducir el tiempo de. subida y el error de estado estacionario. Cambiamos los datos existentes de modo que sea. '. igual a 5000 y volvemos a ejecutarlo en la ventana de. comandos de MATLAB. Deberíamos ver el siguiente diagrama.. 48.

(49) 49.

(50) Step Response 10 9 8 7 6 5 4 3 2 1 0 0. 2. 4. 6. 8. 10. 12. 14. 16. 18. 20. Time (seconds). El error de estado estacionario ahora es esencialmente cero, y el tiempo de subida se ha reducido sustancialmente. Sin embargo, esta respuesta no es realista porque un sistema de control de crucero real generalmente no puede cambiar la velocidad del vehículo de 0 a 10 m / s en menos de 0,5 segundos debido a las limitaciones de potencia del motor y la transmisión. Las limitaciones de los actuadores se encuentran con mucha frecuencia en la práctica en la ingeniería de sistemas de control y, en consecuencia, siempre se debe considerar la acción de control requerida al proponer un nuevo controlador. Discutiremos este tema mucho más en tutoriales posteriores. La solución a este problema en este caso es elegir una ganancia proporcional más baja. , que dará un tiempo de subida razonable y agregar. un controlador integral para eliminar el error de estado estacionario. 1.3.5. Control PI. La función de transferencia de bucle cerrado de este sistema de control de crucero con un controlador PI (. =. 50. +. !/. ) es:.

(51) $( ) =. ( ) ( ) %( ) = = &( ) 1 + ( ) ( ). #. + ! + ( + ') + '. (. ( ). La adición de un controlador integral al sistema elimina el error de estado estable. Por ahora, dejamos. igual a 600 e. sucede a la respuesta.. 51. !. igual a 1 y vemos qué le.

(52) Step Response 10 9 8 7 6 5 4 3 2 1 0 0. 2. 4. 6. 8. 10. 12. 14. 16. 18. 20. Time (seconds). Ahora ajustamos tanto la ganancia proporcional integral,. !. para obtener la respuesta deseada. Cuando ajustamos la. ganancia integral que una gran y. !. , como la ganancia. !,. se sugiere que comiencemos con un valor pequeño, ya. puede desestabilizar la respuesta. Cuando. es igual a 800. es igual a 40, la respuesta al paso será similar a la siguiente:. 52.

(53) 53.

(54) Step Response 10 9 8 7 6 5 4 3 2 1 0 0. 2. 4. 6. 8. 10. 12. Time (seconds). 54. 14. 16. 18. 20.

(55) 1.3.6. Control PID Para este ejemplo en particular, no fue necesaria la implementación de un controlador derivado para obtener el resultado requerido. Sin embargo, es posible que desee ver cómo trabajar con un control PID para futuras referencias. La función de transferencia de bucle cerrado para este sistema de control de crucero con un controlador PID ( = $( ) =. ( ) ( ) %( ) = = &( ) 1 + ( ) ( ) (. Dejamos. igual a 1,. ". +. igual a 1 e. comandos en un nuevo archivo m.. 55. ". ") ". #. #. +. )* +. + ' + ! + ( + ') +. + (. ". ) es: ( ). igual a 1 e ingresamos los siguientes.

(56) Step Response 10 9 8 7 6 5 4 3 2 1 0 0. 2. 4. 6. 8. 10. 12. 14. 16. 18. 20. Time (seconds). Trazar la respuesta de paso y ajustar todos resultados satisfactorios.. ,. ". y. !. hasta que obtenga. Sugerencia: Por lo general, elegir ganancias apropiadas requiere un proceso de prueba y error. La mejor manera de atacar este proceso tedioso es ajustar una variable (. ,. !. o. "). a la vez y observar cómo cambiar una. variable influye en la salida del sistema.. 56.

(57) 57.

(58) Step Response 12. 10. 8. 6. 4. 2. 0 0. 2. 4. 6. 8. 10. 12. Time (seconds). 58. 14. 16. 18. 20.

(59) 1.4. Lugar de raíces (Root Locus Controller Design) 1.4.1. Modelo de sistema. El modelo de función de transferencia para el problema de control de crucero se proporciona a continuación. ( )=. ( ) = ( ). 1.4.2. Parámetros de sistema. 1 +. /. ( ). Para este ejemplo, supongamos que los parámetros del sistema son (m) masa del vehículo 1000 kg (b) coeficiente de amortiguación 50 Ns / m (r) velocidad de referencia 10 m / s y el diagrama de bloques de un sistema típico de retroalimentación de unidad se muestra a continuación.. 1.4.3. Especificaciones de rendimiento •. Tiempo de subida <5 seg. •. Sobregiro <10%. •. Error de estado estable <2%. 59.

(60) 1.4.4. Control proporcional Recordemos desde la página Introducción: Diseño de controlador de locus de raíz, el gráfico de locus de raíz muestra las ubicaciones de todos los polos de lazo cerrado posibles cuando una única ganancia varía de cero a infinito. Por lo tanto, solo se considerará un controlador proporcional,. para. resolver este problema. La función de transferencia de bucle cerrado se convierte en: %( ) = &( ). +( +. ( ). ). Además, desde la página Introducción: Diseño de controlador de locus de raíz , sabemos que el sgrid de comando de MATLAB se puede usar para mostrar una región aceptable del diagrama de locus de raíz. Para. usar sgrid , primero se deben determinar la relación de amortiguación , , y la frecuencia natural -. . Las siguientes dos ecuaciones se usarán para encontrar la relación de amortiguación y la frecuencia natural: -. ≥. 1.8 $2. ,≥3. dónde • • • •. ( ). ln# (67) 8 # + ln# (67). ( ). -. = Frecuencia natural [rad \ s]. , = Relación de amortiguamiento $2 = Tiempo de subida [s]. 67 = Sobreimpulso máximo. Uno de nuestros criterios de diseño es tener un tiempo de subida de menos de 5 segundos. Desde la primera ecuación, vemos que la frecuencia natural debe ser mayor que 0.36. También utilizando la segunda ecuación, vemos. 60.

(61) que la relación de amortiguamiento debe ser mayor a 0.6, ya que el sobreimpulso máximo debe ser menor al 10%. Ahora, estamos listos para generar un diagrama de locus raíz y usar sgrid para encontrar una región aceptable en el locus raíz. Creamos una nueva m-file e ingresamos los siguientes comandos.. Root Locus. 0.4. 0.36 0.6. 0.2. 0. -0.2 0.6 0.36. -0.4. -0.6 -0.6. -0.5. -0.4. -0.3. -0.2. -0.1. 0. Real Axis (seconds -1 ). Las dos líneas punteadas en un ángulo indican las ubicaciones de la relación de amortiguamiento constante ( = 0.6); la relación de amortiguamiento es mayor a 0.6 entre estas líneas y menos de 0.6 fuera de las líneas. La semi61.

(62) elipse indica las ubicaciones de frecuencia natural constante (. = 0.36); la. frecuencia natural es mayor a 0.36 fuera de la semi-elipse, y más pequeña que 0.36 adentro. Luego podemos encontrar una ganancia para colocar los polos de lazo cerrado en la región deseada mediante el uso del comando rlocfind. Agregue el código [Kp, postes] = rlocfind (P_cruise) al final de su archivo m para ayudarlo a elegir una ganancia de bucle específica. Después de ejecutar en la ventana de comandos, debería ver un mensaje pidiéndole que elija un punto en el diagrama del lugar raíz. Dado que desea elegir un punto entre líneas punteadas ( > 0.6) y fuera de la semielípsula (. > 0.36), haga clic en. el eje real justo fuera de la semi-elipse (alrededor de -0.4) como lo indica la marca cruzada en el siguiente figura. Root Locus. 0.4. 0.36 0.6. 0.2. 0. -0.2 0.6 0.36. -0.4. -0.6 -0.6. -0.5. -0.4. -0.3. -0.2. -0.1. 0. -1. Real Axis (seconds ). Después de hacer esto, debería ver el siguiente resultado en la ventana de comandos de MATLAB.. 62.

(63) Tengamos en cuenta que el valor devuelto por la ventana de comandos de MATLAB puede no ser exactamente el mismo, pero al menos debe tener el mismo orden de magnitud. Este valor devuelto se puede usar como ganancia para el compensador y la respuesta de paso de bucle cerrado se puede generar de la siguiente manera.. 63.

(64) Step Response 9 8 7 6 5 4 3 2 1 0 0. 2. 4. 6. 8. 10. 12. 14. 16. 18. 20. Time (seconds). Con la ganancia Kp que acaba de elegir, el tiempo de subida y los criterios de rebasamiento se han cumplido; sin embargo, permanece un error de estado estable de más del 10%.. 64.

(65) 1.4.5. Controlador de retardo. Para reducir el error de estado estacionario, se agregará un controlador de retardo al sistema. La función de transferencia del controlador de retardo es: ( )=. + 9: + 7:. ( ). La función de transferencia de bucle cerrado (sin incluir. ) ahora se. convierte en: %( ) = &( ). #. + ;: + ( + 7: ) + 7:. Finalmente, incluyendo la ganancia de bucle. (<). , la función de transferencia. de bucle cerrado se convierte en: %( ) = &( ). #. += +. + ;:. 7: +. > + ( 7: +. 9: ). (?). Si lee la sección "Retardador de Lag o Retardo de Fase usando RocusLocus" en la página de Diseño de Compensador de Retardo y Retardo , el polo y el cero de un controlador de rezago deben colocarse muy juntos. Además, establece que el error de estado estable se reducirá por un factor de 9: /7: . Por estas razones, deje 9: igual a 0.3 e 7: igual a 0.03. Crea un nuevo archivo m e ingresa los siguientes comandos.. 65.

(66) Root Locus 0.4 0.6. 0.3 0.2 0.1 0.36. 0 -0.1 -0.2 -0.3 -0.4 -0.6. 0.6. -0.5. -0.4. -0.3. -0.2. -0.1. 0. Real Axis (seconds ). Usando nuevamente el comando rlocfind , podemos elegir una nueva ganancia de bucle. . Ingrese el código [Kp, postes] = rlocfind (C_lag *. P_cruise) en la ventana de comandos y haga clic en el eje real alrededor de. -0.4 como se muestra en la siguiente figura.. Root Locus 0.4 0.6. 0.3 0.2 0.1 0.36. 0 -0.1 -0.2 -0.3 -0.4 -0.6. 0.6. -0.5. -0.4. -0.3. -0.2 -1. Real Axis (seconds ). 66. -0.1. 0.

(67) Después de hacer esto, debería ver el siguiente resultado en la ventana de comandos de MATLAB.. Luego podemos generar la nueva respuesta de paso en bucle cerrado de la siguiente manera.. 67.

(68) Step Response 12. 10. 8. 6. 4. 2. 0 0. 2. 4. 6. 8. 10. 12. 14. 16. 18. 20. Time (seconds). Como puede ver, el error de estado estable se ha reducido a casi cero. El sobreimpulso es el resultado del cero agregado en el controlador de retardo. Por ahora, todos los criterios de diseño se han cumplido y no se necesitan más iteraciones; Sin embargo, usted debe experimentar con diferentes 9: y 7: valores para ver lo que su efecto es sobre la respuesta del sistema de circuito cerrado.. 68.

(69) 1.5. Métodos de dominio de frecuencia para el diseño del controlador 1.5.1. Modelo de sistema. El modelo de función de transferencia para el problema de control de crucero se proporciona a continuación. ( )=. ( ) = ( ). 1.5.2. Parámetros del sistema. 1 +. /. ( ). Para este ejemplo, supongamos que los parámetros del sistema son (m) masa del vehículo 1000 kg (b) coeficiente de amortiguación 50 Ns / m (r) velocidad de referencia 10 m / s (u) fuerza de control nominal 500 N y el diagrama de bloques de un sistema típico de retroalimentación de unidad se muestra a continuación.. 1.5.3. Especificaciones de rendimiento •. Tiempo de subida <5 sec. •. Sobregiro <10%. •. Error de estado estable <2%. 69.

(70) 1.5.4. Diagrama de Bode y respuesta de bucle abierto. El primer paso para resolver este problema utilizando la respuesta de frecuencia es determinar qué función de transferencia de bucle abierto usar. Al igual que para el método de diseño Root-Locus, solo usaremos un controlador proporcional para resolver el problema. El diagrama de bloques y la función de transferencia de bucle abierto se muestran a continuación.. %( ) = @( ). ( ). +. Para usar un diagrama de Bode, la respuesta de bucle abierto debe ser estable. Deje. igual a 1 por ahora y vea cómo se ve la respuesta de bucle. abierto. Creamos una nueva m-file e ingresa los siguientes comandos.. 70.

(71) Step Response 10 9 8 7 6 5 4 3 2 1 0 0. 20. 40. 60. 80. 100. 120. 140. 160. 180. Time (seconds). Como puede ver, el sistema de bucle abierto es estable; por lo tanto, podemos seguir adelante y generar el diagrama de Bode. Cambie la m-file anterior al eliminar el comando step y agregar el siguiente comando.. 71.

(72) Bode Diagram -30. -40. -50. -60 0. -45. -90 10 -3. 10 -2. 10 -1. 10 0. Frequency (rad/s). 1.5.5. Controlador proporcional El error de estado estable se puede encontrar a partir de la siguiente ecuación: A22B2 =. 1 ∗ 100% 1 + 6C→:. ( ). Para este sistema, la ganancia de baja frecuencia es -34dB = 0.02; por lo tanto, el error de estado estacionario debe ser del 98%. Podemos confirmar esto generando una respuesta de paso de bucle cerrado de la siguiente manera.. 72.

(73) Step Response 0.2 0.18 0.16 0.14 0.12 0.1 0.08 0.06 0.04 0.02 0 0. 20. 40. 60. 80. 100. 120. 140. 160. 180. Time (seconds). Necesitamos aumentar la ganancia de baja frecuencia para mejorar el error de estado estacionario. Específicamente, el error debe ser <2%; por lo tanto, 1 / (1+ 6CH: ) <0.02. 6CH: > 49 = 33.8 dB. Dado que, la ganancia de baja. frecuencia es -34 dB y el límite de error de estado estacionario necesita que tengamos una ganancia de baja frecuencia de 33.8 dB, para alcanzar el error de estado estable deseado usando solo control proporcional, se requiere a. > (34 dB + 33.8 dB) = 67.8 dB = 2455. Veamos el diagrama de Bode del. sistema de bucle abierto compensado.. 73.

(74) Como se puede ver en el diagrama de Bode anterior, la magnitud de baja frecuencia es ahora, 34 dB. Ahora simulemos la respuesta escalonada del sistema de ciclo cerrado con esta ganancia.. Step Response 10 9 8 7 6 5 4 3 2 1 0 0. 0.5. 1. 1.5. 2. 2.5. Time (seconds). 74. 3. 3.5. 4.