Empleo de la transformada Wavelet en la reducción del ruido en imágenes de fase

(1)FACULTAD DE INGENIERÍA ELÉCTRICA DEPARTAMENTO DE TELECOMUNICACIONES Y ELECTRÓNICA. TRABAJO DE DIPLOMA. “Empleo de la Transformada Wavelet en la reducción del ruido en imágenes de fase”. Autora: Idelkys Quintana Ramírez. Tutores: MSc. Héctor Cruz Enríquez. Dr. Juan V. Lorenzo Ginori. “Año del 45 Aniversario del Triunfo de la Revolución” 2004.

(2) Hago constar que el presente trabajo fue realizado en la Universidad Central “Marta Abreu” de las Villas como parte de la culminación de los estudios de la especialidad de Telecomunicaciones y Electrónica autorizando a que el mismo sea utilizado por la Institución, para los fines que estime conveniente, tanto de forma parcial como total y que además no podrá ser presentado en eventos, ni publicados sin autorización de la Universidad.. ________________ Firma del Autor. Los abajo firmantes, certificamos que el presente trabajo ha sido realizado según acuerdo de la dirección de nuestro centro y el mismo cumple con los requisitos que debe tener un trabajo de esta envergadura referido a la temática señalada.. ________________ Firma del Tutor. _______________________ Firma del Jefe de Dpto. Donde se defiende el trabajo. ____________________ Firma del Responsable de Información Científico- Técnica.

(3) Resumen.

(4) Las imágenes de fase aparecen en procesos de resonancia magnética (MRI), en imágenes interferométricas de radar de apertura sintética (IFSAR), y en imágenes de densidad de corriente (CDI), entre otros casos. La información de la fase en las imágenes complejas es utilizada para generar datos de fase útiles pero en la mayoría de las ocasiones el ruido presente dificulta la obtención de la imagen de fase con la calidad apropiada. Un ejemplo importante de aplicación de las imágenes de fase se encuentra en la resonancia magnética de imágenes (MRI), que ha adquirido una gran importancia en la actualidad, esencialmente en la rama de la biomedicina para el estudio de diferentes enfermedades. De las imágenes de MRI, se pueden extraer las imágenes de fase, las que presentan un conjunto de aplicaciones que no han sido ampliamente desarrolladas hasta el presente. En este trabajo se aborda el problema de la reducción del ruido o denoising en las imágenes de fase con el empleo de la Transformada Wavelet haciendo uso de las herramientas MATLAB para la simulación de estos algoritmos. Los resultados obtenidos se evalúan fundamentalmente atendiendo al incremento de la relación señal a ruido (SNR) y a la eliminación de los residuos de fase. Se comparan además, con resultados obtenidos de otros estudios sobre esta materia y se comprueba mediante experimentos de simulación la eficacia del método propuesto en este trabajo..

(5) Índice.

(6) Índice. ÍNDICE INTRODUCCIÓN......................................................................................................................... 1 CAPÍTULO I: TÉCNICAS DE FILTRADO DE RUIDO (DENOISING) EN MRI............... 4 1.1. INTRODUCCIÓN........................................................................................................................ 4. 1.1.1 1.2. Transformada Wavelet ........................................................................................................ 5 TÉCNICAS DE DENOISING UTILIZANDO WAVELET .................................................................. 7. 1.2.1. Técnica de umbral empleando denoising Wavelet .............................................................. 7. 1.2.2. Técnica de eliminación del ruido de fondo ......................................................................... 8. 1.2.3. Técnica de denoising Wavelet complejo en MRI............................................................... 10. 1.2.4. Técnica de denoising con filtro Wiener sobre las MRI ..................................................... 11. 1.2.4.1. Algoritmo I: Aproximación de Ruido Gaussiano ..............................................................12. 1.2.4.2. Algoritmo II: Ruido Chi-Cuadrado no central..................................................................15. 1.2.5. Técnica de denoising con filtro Wiener generalizado sobre las MRI complejas............... 16. 1.2.5.1. 1.3. Algoritmo de denoising ........................................................................................................18. TÉCNICA DE DENOISING A LAS MRI DE FASE CON EL EMPLEO DE MÉTODOS NO LINEALES 19. 1.4. APLICACIONES DE LAS MRI DE FASE ................................................................................... 20. CAPÍTULO II: MATERIALES Y MÉTODOS ....................................................................... 23 2.1. IDENTIFICACIÓN DEL PROBLEMA E HIPÓTESIS..................................................................... 23. 2.2. VALIDACIÓN DEL EXPERIMENTO DESDE EL PUNTO DE VISTA ANALÍTICO ........................... 24. 2.3. DESCRIPCIÓN DEL MÉTODO DESDE EL PUNTO DE VISTA EXPERIMENTAL ........................... 27. CAPÍTULO III: RESULTADOS............................................................................................... 32. i.

(7) Índice. 3.1. ANÁLISIS DE LOS RESULTADOS ............................................................................................. 32. 3.2. COMPARACIÓN DE MÉTODOS ................................................................................................ 33. CONCLUSIONES ....................................................................................................................... 47 RECOMENDACIONES ............................................................................................................. 49 REFERENCIAS .......................................................................................................................... 50 BIBLIOGRAFÍA ......................................................................................................................... 56. ii.

(8) Introducción.

(9) Introducción. INTRODUCCIÓN Las imágenes de fase aparecen en procesos de resonancia magnética (MRI), en imágenes interferométricas de radar de apertura sintética (IFSAR), y en imágenes de densidad de corriente (CDI), entre otros casos. La información de la fase en las imágenes complejas es utilizada para generar datos de fase útiles pero en la mayoría de las ocasiones el ruido presente dificulta la obtención de la imagen de fase con la calidad apropiada. Un ejemplo importante de aplicación de las imágenes de fase se encuentra en la resonancia magnética de imágenes (MRI), que ha adquirido una gran importancia en la actualidad, esencialmente en la rama de la biomedicina para el estudio de diferentes enfermedades. La MRI constituye una de las tecnologías de diagnóstico más avanzadas que se están empleando en la actualidad, donde se pueden lograr fotografías de órganos y estructuras internas del ser humano sin necesidad de exponerlo a las radiaciones exigidas en otros procedimientos de imágenes tales como los Rayos X y la observación por Tomografía Computarizada; en su lugar, con el empleo de un fuerte campo magnético, una estructura de gradientes de campo magnético y la emisión de ondas de radio a las que se somete el organismo estudiado, se posibilita la obtención de imágenes tridimensionales de su interior. Esta técnica permite al especialista observar dentro del cuerpo del paciente desde cualquier ángulo con gran claridad, por lo que le ofrece a éste una riqueza de información en forma rápida y en muchos casos menos costosa que otros estudios realizados con este mismo fin. Es un procedimiento que tiene como ventaja el no ser invasivo ni doloroso, y no poseer efectos secundarios. Son muchos los beneficios de la proyección de las MRI, y continuamente se van desarrollando nuevas aplicaciones a través de investigaciones que se están llevando a cabo. Se emplean para diagnosticar enfermedades tales como: los trastornos del sistema nervioso y del cerebro, los desórdenes de los huesos, tejidos y músculos, los tumores, ciertas enfermedades del corazón y de los vasos sanguíneos y el cáncer de los órganos reproductivos, del hígado, de los riñones, de los ganglios linfáticos, de la vejiga, del páncreas y de las cuerdas vocales.. 1.

(10) Introducción. En el proceso de obtención de las imágenes en cuestión aparece la influencia de diferentes ruidos que las afectan y dificultan su interpretación, por lo que se hace necesaria la reducción del ruido para poder realizar un análisis detallado y acertado de las mismas. Se han realizado estudios referentes a este tema pero han estado fundamentalmente orientados a las imágenes de magnitud, dejando a un lado las imágenes de fase, lo que ha provocado que en la actualidad todavía exista un conjunto de facilidades por desarrollar para el tratamiento de estas imágenes, las que permitirían fomentar diversas aplicaciones donde estas pueden ser empleadas. Por lo antes expuesto, en el presente trabajo se pretende desarrollar un algoritmo mediante el empleo de métodos de filtrado en el dominio Wavelet para la reducción del ruido en las imágenes de fase, utilizando como herramienta fundamental el MATLAB, que tiene entre sus aplicaciones la posibilidad de mejorar la calidad de las imágenes MRI de fase. Con la obtención de mayores relaciones señal a ruido, el uso de estas imágenes brindará mejores prestaciones. Finalmente, se aspira a contribuir al desarrollo de la biofísica médica en nuestro país y mejorar los resultados obtenidos en esta rama, ya que con el desarrollo de un algoritmo que realice el denoising de las imágenes de fase podrá existir un grupo de aplicaciones que se llevarán a cabo con mayor efectividad. Además, se puede ofrecer una respuesta a la constante demanda de avances científicos en ese campo tan importante de la vida social con soluciones económicamente factibles, que puedan servir de alternativa al proceso de mejoramiento de las señales obtenidas de los equipos en cuestión (tomógrafos). Para lograr la solución del problema planteado nos trazamos los siguientes objetivos: 1. Realizar una amplia búsqueda de información sobre imágenes de fase y sus aplicaciones, así como de métodos de reducción de ruido en las mismas. 2. Desarrollar algoritmos basados en métodos de filtrado en el dominio Wavelet y probar los mismos mediante la simulación, para la reducción del ruido (denoising) en imágenes de fase. 3. Evaluar los algoritmos desarrollados para medir su eficacia, en términos de la mejora en la relación señal a ruido, velocidad de procesamiento, uso de la memoria y otros parámetros de interés relacionados con la calidad de la imagen.. 2.

(11) Introducción. 4. Realizar una comparación entre el método de filtrado en el dominio Wavelet y el método de filtrado no lineal en cuanto al incremento de la SNR, la reducción de los RES y el tiempo de procesamiento requerido para realizar los algoritmos en igualdad de condiciones. Este informe está dividido en tres capítulos con la siguiente estructura: el primer capítulo está dedicado al estudio y caracterización de las metodologías de denoising de las MRI de magnitud y fase reportadas y al estudio comparativo de estas técnicas, que actualmente se están empleando, aportando las definiciones y métodos que comúnmente se utilizan en la literatura especializada. El segundo capítulo se utiliza para expresar el diseño del experimento que da lugar al desarrollo del algoritmo que realiza el denoising a las imágenes de fase en general y a las de resonancia magnética en particular. Por último, en el tercer capítulo, se expresan los resultados de la validación del algoritmo implementado en un software mediante la comparación con ejemplos prácticos de la efectividad del método y la calidad del mismo.. 3.

(12) Capítulo I.

(13) Capítulo 1. CAPÍTULO I: Técnicas de filtrado de ruido (denoising) en MRI 1.1. Introducción. En los últimos tiempos, la Resonancia Magnética (MR) se ha convertido en parte esencial de la radiología de diagnóstico. Al igual que otros métodos de imagen médica, como el ultrasonido y la tomografía axial computarizada, las imágenes de resonancia magnética, comúnmente denominadas MRI (Magnetic Resonance Imaging) se utilizan para obtener imágenes bidimensionales de secciones del cuerpo humano, pero estas, originalmente están contaminadas con ruido. Existen métodos precedentes en la eliminación de dicho ruido (en lo sucesivo se utilizará para designar este proceso el término del inglés denoising), mas, estos han sido aplicados fundamentalmente a las imágenes de magnitud, y aunque el tema de las imágenes de fase ha sido abordado, existe un conjunto de facilidades para el tratamiento de las mismas que pueden ser desarrolladas en aras de potenciar el desarrollo de diversas aplicaciones. En el proceso de adquisición de una imagen de MR intervienen distintos sistemas que componen el equipo de captura. Cada uno de estos sistemas le adiciona a la señal útil otras señales que, aunque generalmente son de menor intensidad, la interfieren de forma destructiva. La suma de estas señales interferentes forma el ruido que en la imagen recién obtenida afecta su calidad final. Las MRI adquiridas con alta resolución temporal y/o espacial (Ej. microimágenes y angiografía) muestran con frecuencia una pobre relación señal a ruido (SNR). Por lo tanto, la eliminación o reducción del ruido a esas imágenes resulta de gran importancia. Algunos ruidos son originados por el sistema electrónico del equipo como el ruido térmico gaussiano propio de los procesos de recepción de señales débiles de radiofrecuencia, por la influencia ambiental (Ej. línea de 60 Hz, etc.), por procedimientos del software de adquisición que efectúa una normalización de los coeficientes, artefactos debido al muestreo y el resto tienen un origen fisiológico. Esos artefactos de ruido afectan la calidad e interpretación de los datos de imágenes médicas en un grado variable que va a depender de parámetros y modos de adquisición de las imágenes, así como de la región anatómica. 4.

(14) Capítulo 1. bajo escáner. Los artefactos ruidosos se producen por el movimiento de los pacientes, durante el escáner único o durante el escáner de imágenes sucesivas lo que podría degradar seriamente la calidad de los datos. Un método común para reducir el ruido es promediar varias imágenes escaneadas como un intento de mejorar la SNR y el contraste. Sin embargo con la necesidad creciente de una alta resolución temporal en MRI este método se hace impráctico. [1][49][50] El efecto indeseado de los fenómenos y agentes externos como el ruido, descritos anteriormente, puede ser corregido en cierta medida a través de algoritmos que se aplican sobre la imagen recién obtenida para mejorar su calidad final. Esta última se mide directamente con la SNR o con la relación contraste-ruido. El filtrado es un término que se ha impuesto en la literatura para expresar el proceso donde se disminuye el nivel de ruido y artefactos que degradan la calidad de la imagen. En nuestro trabajo se asume este término considerando que en la etapa de post procesamiento de una imagen, el ruido y los artefactos que esta contenga son imposibles de suprimir totalmente. La Transformada Wavelet (WT) ha sido una de las herramientas más empleadas en el filtrado de señales ruidosas y dentro de estas, las señales 2-D como las imágenes de MR [28][39][57]. Aquí presentamos el uso de esta como una alternativa para el filtrado de imágenes de MR que supera los métodos ya existentes basados en la teoría de Fourier. Con este tipo de filtrado al igual que en métodos anteriores, la señal se somete a un proceso de umbral en el espacio de la transformada. Este método resulta novedoso debido a que los coeficientes de la transformada brindan información de las componentes espectrales de la señal y la localización de cada componente dentro de ella. 1.1.1. Transformada Wavelet. La teoría Wavelet tiene su origen alrededor de la década de los `30 del siglo XX, con el trabajo independiente de distintos grupos de investigadores de las más diversas esferas como la predicción sismológica, el análisis de señales, el cálculo matemático, etc.; los cuales se dedicaban a la representación de datos usando bases de funciones de escala variable.. 5.

(15) Capítulo 1. Su desarrollo se nos presenta como algo más que una simple suma de los resultados obtenidos en cada uno de estos campos de investigación donde surge, constituyendo las bases de una teoría sólida. La interrelación entre estos distintos campos de investigación trajo consigo nuevas aplicaciones de la teoría en especialidades como el procesamiento de imágenes, la predicción sismológica, los estudios de turbulencia y la física teórica. [23][36][38][54][57] La Transformada Wavelet (transformada jerárquica o piramidal) proporciona una descomposición no redundante de la señal en términos de desplazamientos y dilataciones de una señal Wavelet, proporcionando una forma muy adecuada para realizar cualquiera de las tareas para las cuales las transformadas en bloque han sido utilizadas tradicionalmente: compresión de datos, análisis de datos y procesamiento de datos (filtros generalizados). Wavelet presenta ciertas ventajas que pueden mejorar la SNR mientras preserva cierto grado de localización en el dominio del tiempo (o espacio). La Transformada Wavelet es una transformación lineal de la señal según el modelo:. ψ ( a ,b ) = a 2ψ (( x − b ) / a ) −1. (1.1). Estas señales representan versiones desplazadas (índice b) y dilatadas (índice a) de una función Wavelet dada. La WT de una señal f∈H (espacio de Hilbert H) es parametrizada por los parámetros de escala (a) y de desplazamiento (b). Un requerimiento básico es que la transformada sea reversible, es decir, que la señal f pueda ser reconstruida de los coeficientes Wavelets TW f (a, b) : TW f ( a, b) = c( a ,b ) = f ,ψ ( a ,b ). (1.2). donde ⟨⋅,⋅⟩ es el producto interno asociado con el espacio de Hilbert. Existe además, una variación no jerárquica, las Wavelets Packets (WP) que constituyen una extensión directa de las transformadas de bloques tradicionales (Transformada de Fourier, Transformada Discreta del Coseno (DCT)). [24]. 6.

(16) Capítulo 1. La distinción entre los diferentes tipos de Transformadas Wavelets depende de la forma en que los parámetros de escala y desplazamiento sean discretizados. La forma más redundante es la Transformada Wavelet Continua (CWT) en la cual los parámetros a y b varían de forma continua. Esta representación ofrece muchas libertades a la hora de realizar el análisis Wavelet. En esencia, la CWT realiza un análisis de correlación, así que podremos esperar que la salida sea máxima cuando la señal de entrada se asemeje más al modelo de análisisψ ( a ,b ) . Existen varios tipos de funciones Wavelets. Resaltan las de tipo discontinuas (Wavelet de Haar), las de estructura de Fractal (Coiflet) y las simétricas (Mexican Hat) por solo citar unos ejemplos. Son varios los métodos y algoritmos empleados para el denoising de las MRI utilizando Wavelets aunque también se han realizado estudios con este mismo propósito haciendo uso de otras técnicas tales como los métodos de filtrado no lineal; debemos señalar, además, que la elección del filtro Wavelet óptimo va a depender de la imagen en cuestión. A continuación exponemos algunas de esas técnicas antes mencionadas. 1.2 1.2.1. Técnicas de denoising utilizando Wavelet Técnica de umbral empleando denoising Wavelet. Una aproximación propuesta por Weaver fue el cálculo de una descomposición Wavelet de las imágenes médicas [59] y la aplicación de una regla de umbral suave sobre los coeficientes c a ,b = f ,ψ a ,b :. cˆa ,b. ⎧ca ,b − t a ⎪ ⎪ = ⎨0 ⎪c + t ⎪⎩ a ,b a. c a ,b ≥ t a c a ,b ≤ t a. (1.3). c a , b ≤ −t a. 7.

(17) Capítulo 1. donde ta es un umbral que depende del nivel de ruido en la i-ésima escala; la imagen es entonces reconstruida por la WT inversa de los coeficientes cˆa ,b . Este es esencialmente el método de denoising utilizando la reducción Wavelet. Recordemos que la técnica de umbral puede ser dura o suave. En el caso de aplicar un umbral duro (método más simple) si t denota el umbral, la señal s de salida conservará el mismo valor que la señal de entrada x si x > t y cero si x ≤ t . La aplicación del umbral suave presenta propiedades matemáticas más adecuadas pues elimina la presencia de discontinuidades presentadas por el umbral duro en x = ±t . En este caso si x > t el valor de la señal de salida será sign( x) ⋅ ( x − t ) y cero si x ≤ t . 1.2.2. Técnica de eliminación del ruido de fondo. El algoritmo que se muestra a continuación, tal vez un poco más robusto que los tradicionales basados en umbrales, ilustra una aproximación de denoising utilizando Wavelet para la eliminación de ruido de fondo en imágenes médicas.. 8.

(18) Capítulo 1. Imagen de entrada. 1) Se aplica la Transformada Wavelet. Directa a la señal original.[63] Transformada Wavelet Directa. 2) Se aplica el umbral suave de Denoho a los. coeficientes. Wavelet. de. la. WT.[10][14][15] Umbral Suave de Wavelet Donoho´s. 3) La Imagen WT-Filtrada es reconstruida mediante la WT Inversa. [63] 4) Se aplica la ALSEC (Adaptative Least. Transformada de Wavelet Inversa. Square Error Clustering o determinación de grupos de píxeles de la imagen en forma. ALSEC. adaptativa siguiendo el criterio del error cuadrático medio) a la imagen reconstruida. Detección de contorno y descripción. para obtener una imagen bi-nivel. [63] 5) El contorno y la máscara de la imagen binivel son obtenidos por un código de los. Operación de Máscara. límites del objeto. [9] [22] 6) Se aplica la máscara a la imagen original. Imagen sin ruido de fondo. y los píxeles fuera de la máscara son estimados. como. ruido. de. fondo. y. eliminados. [63]. 9.

(19) Capítulo 1. 1.2.3. Técnica de denoising Wavelet complejo en MRI. El empleo de algoritmos basados en Wavelets y Wavelet Packets constituye prácticamente un estándar en el denoising de MRI, encontrando funciones básicas de la imagen que concentren la señal respecto al ruido Gaussiano de fondo. En muy bajas SNR (<5) las imágenes de magnitud estándar de las MRI presentan ruido Rician estadístico, el cual limita de cierto modo la realización del denoising. El denoising mediante Wavelets equivale a analizar los componentes principales, es decir, a la selección de las imágenes básicas que concentren la señal respecto al ruido. Como el análisis de los componentes principales supone una distribución de ruido Gaussiano estadístico, cuando nos encontremos en la presencia de una distribución de ruido estadístico no Gaussiano, se observará una degradación significativa. Sin embargo, el ruido en MRI de magnitud es de tipo Rician. La distribución Rician varía dramáticamente en dependencia de los valores asociados a la SNR. Para una SNR igual a cero se observa una distribución Rayleigh altamente asimétrica, mientras que para una SNR>5, la distribución es aproximadamente Gaussiana. El algoritmo de denoising con WP presenta tres conceptos fundamentales: La Transformada Wavelet Packet, la selección de la mejor base, y la selección del umbral a aplicar a los coeficientes. [60] El denoising con WP mejora la SNR de las MRI, a veces de forma significativa sin comprometer los bordes de los objetos. El ruido Rician estadístico de imágenes de magnitud degrada los bordes y la resolución de contraste, el denoising antes de la rectificación de la señal reduce drásticamente ese fenómeno. La media distinta de cero del ruido blanco rectificado, perjudica el fondo de la imagen de magnitud, por lo tanto disminuye el contraste en objetos de baja intensidad [25][60]. A diferencia del denoising de magnitud, el denoising complejo evita este perjuicio y mejora la definición de bordes porque este evita el efecto de distribución no uniforme de ruido a través de la imagen, causado por la rectificación. Algunos resultados obtenidos en el estudio de MRI actuales indican que en el denoising de las imágenes complejas (denoising complejo) se requiere un umbral de compresión. 10.

(20) Capítulo 1. más bajo que en el denoising de las imágenes de magnitud (denoising de magnitud) para alcanzar una mejora comparable de la SNR.[60] Varios métodos empleados en la recuperación de imágenes de los datos ruidosos comienzan por el clásico método de filtrado Wiener [60][61][62] y análisis de los componentes principales hasta los más modernos y usualmente no lineales, tales como Redes Neuronales Artificiales [30], Máxima Entropía [26], o Análisis Wavelet. [11][12][40] 1.2.4. Técnica de denoising con filtro Wiener sobre las MRI. Generalmente las MRI de magnitud son modeladas de acuerdo a una distribución Rician. El ruido Rician no tiene media cero, y la media depende de la intensidad local en la imagen. A diferencia de otros métodos propuestos anteriormente los cuales se basan en el trabajo con los coeficientes Wavelet y la aplicación de métodos de umbrales suaves, una nueva aproximación será expuesta donde se considere explícitamente la naturaleza Rician de los datos [48]. El nuevo procedimiento reduce el ruido Rician mientras preserva los detalles y características claves de la imagen. Este nuevo filtro en el dominio Wavelet, el cual se centra en la reconstrucción de las imágenes de magnitud (Ec. (1.4), método más común), se desempeña mejor que los métodos estándar que utilizan Wavelet para condiciones de baja SNR.. [. x(m, n) ≅ y (m, n) = ( s[m, n] cos(θ ) + η Re [m, n]) 2 + ( s[m, n] sin (θ ) + η Im [m, n]) 2. ]. 1. 2. (1.4). Donde s denota la señal de interés, η Re y η Im denotan el Ruido Blanco Gaussiano con varianza σ2 en los canales real e imaginario, y θ = θ ( m, n) representa el error de fase en el píxel (m, n ) . Debido al error de fase, la magnitud de y es la empleada típicamente para reconstruir la imagen. La imagen de magnitud x( m, n) es un valor real y puede ser utilizado en la inspección visual o para un análisis computarizado automático. Ya que la reconstrucción de la imagen de magnitud es simplemente la raíz cuadrada de la suma de dos variables aleatorias gaussianas independientes, los datos de la imagen de magnitud son descritos por una distribución Rician. En regímenes de baja intensidad de la imagen de magnitud (zonas oscuras), la distribución Rician tiende a una. 11.

(21) Capítulo 1. distribución Rayleigh, y en el caso de alta intensidad (zonas brillantes), la tendencia es a una distribución Gaussiana [42]. Aquí se presenta un método de filtrado para estimar la señal s de la imagen de magnitud de los datos x . 1.2.4.1 Algoritmo I: Aproximación de Ruido Gaussiano Primero calculemos la Transformada Discreta de Wavelet de dos dimensiones (DWT 2D) [42] de una imagen ruidosa x . Tenemos a “c” y “d” que denotan los coeficientes de escala y Wavelet ruidosos de x . El “coeficiente de escala” de la imagen ruidosa x es calculado como: cI = ∑ φI [m]x[m]. (1.5). m. Similarmente el “coeficiente Wavelet” es calculado como: d I = ∑ψ I [m]x[m]. (1.6). m. La meta del filtrado en el dominio Wavelet es obtener un mejor estimado de los coeficientes Wavelet de señales libres de ruido por el filtrado de “d”. El filtrado de la contribución de una Wavelet particular ψ I en la reconstrucción de la imagen está dado por el “peso” de los correspondientes coeficientes d I multiplicados por el valor de αI (0 ≤ αI ≤ 1). Es decir modificar el componente de acuerdo a:. d̂ I = α I ⋅ d1. (1.7). donde d̂ I son los estimados de los coeficientes Wavelet libre de ruido,. d I son los coeficientes Wavelet ruidosos,. α I filtro Wiener propuesto en el dominio Wavelet. [43] Este filtro es aplicado a los coeficientes Wavelet ruidosos obtenidos de la imagen de magnitud representada en (1.4).. 12.

(22) Capítulo 1. La idea es atenuar esos coeficientes Wavelet que contienen más ruido que señal. Si se fija α I = 0 se elimina completamente la contribución de la función Waveletψ I , si en cambio α I = 1 se deja inalterable. Escogiendo 0 ≤ α I ≤ 1 se atenúa la contribución de la función Wavelet consecuentemente. Calculando la Transformada de Wavelet Discreta Inversa (IDWT) de los coeficientes Wavelet filtrados d̂ y de los coeficientes de escala c , se obtiene un estimado de la imagen mejorada la cual se denota como ŝ . La nueva imagen ŝ es conocida como una versión filtrada en el dominio Wavelet de x . El conjunto de pesos α = {α I } es el filtro en el dominio Wavelet. Claramente, la cuestión crucial del filtrado en el dominio Wavelet es el diseño del filtro α. Idealmente el procedimiento de filtrado en el dominio Wavelet debe ser adaptado a la SNR local en cada coeficiente Wavelet, de esta forma coeficientes Wavelet con muy baja SNR pueden ser suprimidos. Se ha considerado que el coeficiente Wavelet ruidoso es un estimado no influenciado de los valores de los coeficientes Wavelet de la señal, con una media δ I = E[d I ] . Es decir, δ I es el coeficiente Wavelet de la señal libre de ruido. Así entonces, los pesos del filtro que minimizan el Error Cuadrático Medio (MSE) de cada coeficiente son:. α I MSE =. δ I2 δ I2 + σ I2. (1.8). donde σ I2 es la varianza del coeficiente ruidoso d I y δ I2 es el coeficiente Wavelet cuadrático libre de ruido. La operación de filtrado puede ser interpretada como una analogía en el dominio Wavelet del clásico filtro Wiener [51]. Desafortunadamente, esos pesos del filtro óptimo requieren conocer a δ I y σ I , y por lo tanto no son factibles en la práctica. Sin embargo, no sería tan ilógico asumir que la varianza σ I2 es conocida, pues excelentes estimados se obtienen con facilidad (Ej.: el estimado MAD [14]). La dificultad se encuentra en el valor desconocido de δ I , entonces, en lugar de utilizar δ I2 que es desconocido, se obtiene un estimado de esta en función del cuadrado del coeficiente Wavelet ruidoso d I . Después de ciertos análisis el filtro propuesto es el siguiente [42]:. 13.

(23) Capítulo 1. ⎛ d I2 − 3σ I2 ⎞ ⎟ 2 ⎝ dI ⎠†. αI = ⎜. (1.9). Esta operación puede ser considerada como un filtro adaptativo en el dominio Wavelet (filtro Wiener). [51] El filtro obtenido en la ecuación (1.9) fija a cero los coeficientes Wavelet pequeños, con magnitud cuadrática menor que tres veces la varianza estimada y deja los coeficientes más grandes prácticamente inalterables. Otras operaciones de filtrado en el dominio Wavelet tales como funciones de umbral (duro y suave) también pueden ser aplicadas [14][59]. Sin embargo, la operación mostrada en (1.9) ha sido lograda para proporcionar mejores resultados de forma significativa con respecto a otros métodos empleados en aplicaciones similares. [43] En altas SNR, la distribución Rician se aproxima muy bien a una distribución Gaussiana, por lo que las MRI de magnitud pueden ser vistas como contaminadas con Ruido Blanco Gaussiano Aditivo con desviación estándar σ , y en consecuencia la separación de la señal del ruido será bastante directa en el dominio Wavelet. Para conformar un filtro en el dominio Wavelet para MRI de alta SNR, asumiremos que el ruido en la MRI de magnitud es Ruido Blanco Gaussiano Aditivo con desviación estándar σ . Basados en esta suposición y el hecho que la DWT es una transformada ortogonal, la varianza en cada coeficiente Wavelet es también σ2. A este procedimiento de filtrado lo llamaremos Algoritmo I. El Algoritmo I trata el ruido de forma independiente a la señal de interés y no se considera la influencia de la imagen. Este algoritmo es bastante efectivo en regímenes de alta SNR. En situaciones de baja SNR, la aproximación Gaussiana sobre los datos tiene un mayor inconveniente. Las componentes real e imaginaria contienen Ruido Blanco Gaussiano Aditivo simple. Si se aplican las técnicas de filtrado que existen en el dominio Wavelet a cada componente por separado se producirán dos problemas con esa aproximación [42]. Para combatirlos se propone un nuevo filtro en el dominio Wavelet el cual opera sobre la magnitud cuadrática en lugar de la magnitud. Los datos de magnitud cuadráticos. 14.

(24) Capítulo 1. obedecen a una distribución Chi-cuadrado no centrada, y esta aproximación permite una estrategia de procesamiento en el dominio Wavelet de forma directa que compensa la influencia inherente. 1.2.4.2 Algoritmo II: Ruido Chi-Cuadrado no central En bajas SNR, los coeficientes de escala y Wavelet (“c” y “d”) de la imagen de magnitud, son influenciados por los coeficientes correspondientes de la señal s libre de ruido. Bajo estas condiciones la aproximación gaussiana no es válida y la distribución Rician tiene dos efectos de degradación: 1. la fluctuación aleatoria de los valores de los píxeles 2. la introducción de una influencia dependiente de la señal por lo que el ruido Rician en este caso es bastante difícil de eliminar. Para solucionar este problema, se analizará una técnica de filtrado [42] que opera sobre las MRI de magnitud cuadrática. Los datos de la imagen de magnitud cuadrática son distribuidos de forma Chi-cuadrado no central. [33] Trabajando con una imagen de magnitud cuadrática, en lugar de una imagen de magnitud se obtienen las siguientes ventajas: 1. los coeficientes Wavelet de la imagen de magnitud cuadrática son estimados no influenciados de los coeficientes Wavelet de la señal cuadrática libre de ruido s2. 2. los coeficientes de escala de la imagen de magnitud cuadrática son casi estimados no influenciados de los coeficientes de escala de s 2 . El valor esperado de cada coeficiente de escala difiere de los coeficientes de escala libres de ruido por un offset constante que no depende de la señal, por tanto, la influencia puede ser fácilmente eliminada. Por lo antes mencionado se infiere que este filtro en el dominio Wavelet elimina el ruido y se ajusta a la influencia de los coeficientes de escala. Este filtro se puede aplicar tanto en régimen de bajas como de altas SNR.. 15.

(25) Capítulo 1. A continuación presentamos el algoritmo final del filtro en el dominio Wavelet para imágenes de magnitud cuadrática: 1. Calcular la DWT y Transformada Cuadrática Wavelet Discreta (DWST) [43] de escala J de la imagen de magnitud cuadrática. La DWST se corresponde con el producto interno de la imagen con las funciones de base Wavelet cuadrática 2. Formar estimados de la varianza σ I2 de cada coeficiente Wavelet d̂ I de acuerdo a:. ⎡⎛. ⎞. ⎤. ⎠. ⎦. σ I2 = 4σ 2 máx ⎢⎜ ∑ψ I2 [m]x 2 [m]⎟ − σ 2 , σ 2 ⎥ ⎣⎝. m. (1.10). 3. Filtrar los coeficientes Wavelet de acuerdo a (1.9) 4. Eliminar la influencia de los coeficientes de escala ĉI substrayéndole c = 2 ( j +1) σ 2 [42] a cada coeficiente, donde σ 2 es un estimado de la varianza de. ruido Gaussiano complejo fundamental 5. Calcular la IDWT de los coeficientes de escala y Wavelet filtrados para obtener un estimado de s 2 6. Calcular la raíz cuadrática a cada píxel (píxel por píxel) de los resultados para obtener un estimado de s 1.2.5. Técnica de denoising con filtro Wiener generalizado sobre las MRI complejas. En epígrafes anteriores se habla de que el ruido Rician en las MRI de magnitud es dependiente de la señal, sin embargo la mayoría de los algoritmos de denoising suponen Ruido Blanco Gaussiano Aditivo, cuando sabemos que la distribución Rician solo parece Gaussiana en altas SNR. Otros algoritmos emplean métodos basados en Wavelet para el denoising de imágenes de magnitud cuadrática, y explícitamente toman en consideración la naturaleza Rician de la distribución de ruido. Analizaremos un algoritmo de denoising basado en Wavelet el cual se aplica directamente a la imagen compleja obtenida como la transformada de Fourier de los datos (real e imaginario). Para retener la imagen compleja, se le aplica el denoising tanto a la imagen de magnitud como a la imagen de fase.. 16.

(26) Capítulo 1. La mayoría de los algoritmos de denoising que han sido desarrollados suponen una distribución de Ruido Blanco Gaussiano Aditivo. La contribución de ruido se produce del escáner electrónico a cada una de las partes real e imaginaria de los datos, de forma aditiva, y se asume no correlacionado y caracterizado por una función de densidad de probabilidad gaussiana con media cero [32][58]. Sin embargo el correspondiente ruido en la MRI de magnitud es Rician [29]. De interés primario para nosotros serán las imágenes de baja SNR, para las cuales la aproximación gaussiana es bastante pobre. El algoritmo presentado en la sección anterior realiza un filtrado en el dominio Wavelet de la imagen de magnitud cuadrática y emplea un esquema de umbral basado en el dominio Wavelet y análogo al clásico filtro Wiener [45][51]. Otros algoritmos aplican el denoising con WP a la parte real e imaginaria de forma independiente [60]. Sin embargo la selección del umbral es diferente y opera en dominios diferentes. El algoritmo de denoising que se presenta [1] es aplicado a la parte real e imaginaria de la señal compleja como una única entidad compleja en lugar de considerarla como dos canales independientes. Una interesante alternativa de aproximación sería utilizar dos Wavelet diferentes para estimar el filtro Wiener [18][51]. La primera Wavelet sería usada para proporcionar un estimado de recorte o reducción Wavelet de la señal, y el filtro Wiener es entonces ejecutado en el segundo dominio Wavelet. El propósito es mejorar el estimado de los coeficientes Wavelet cuya magnitud se encuentra cerca del umbral señal-ruido, los cuales están propensos a una interpretación errónea. Aquí se desarrolla un algoritmo de denoising tipo Wiener en el dominio Wavelet que usa las partes real e imaginaria de los datos MR complejos. El ruido en esos canales es gaussiano, por lo que se puede emplear cualquier método conocido [1][14][31]. El algoritmo requiere que los datos de la imagen de fase y los de magnitud estén disponibles (en la práctica los componentes de la imagen real e imaginaria se derivan de la transformada de Fourier de los datos). Después del denoising, la imagen compleja resultante puede ser mostrada como imagen de magnitud y/o fase. El denoising es logrado usando un umbral en el dominio Wavelet de la imagen compleja, basado en una generalización del filtro empleado en la sección anterior [42][44] al dominio complejo.. 17.

(27) Capítulo 1. 1.2.5.1 Algoritmo de denoising El método de denoising es aplicado en el dominio Wavelet correspondiente al dominio de la imagen compleja. Aquí se emplean solo las bases Wavelets ortogonales, así que la distribución de ruido en los coeficientes Wavelet permanecerá de tipo gaussiana estadística. El denoising es logrado usando un umbral en el dominio Wavelet de la imagen compleja basado en una generalización del filtro de Nowak [42] al dominio complejo. El filtro obtenido es el siguiente [1]:. donde:. ⎡ DI 2 − σ 2 ⎤ αI ≈ ⎢ ⎥ 2 ⎢⎣ DI ⎥⎦ †. (1.11). 2 2 σ 2 = σ Re + σ Im. (1.12). DI. 2. 2 2 = DRe + DIm. (1.13). 2 2 y σ Im son las desviaciones estándar del ruido gaussiano en los canales real e σ Re. imaginario. DI es el coeficiente Wavelet complejo De esta forma α I se asemeja a un factor de atenuación de valor real, con 0 ≤ α I ≤ 1 . Como el clásico filtro Wiener [51], α I no altera la fase de los coeficientes Wavelet, y atenúa su magnitud por una cantidad dependiente de la SNR. La ecuación (1.11) asegura que los coeficientes complejos cuyas magnitudes son menores que la desviación estándar de ruido no den un factor de atenuación negativo, en lugar de eso serán eliminados ( α I = 0 ). El valor de la desviación estándar de ruido. σ es desconocido y debe ser estimado, denotándolo por σ est , entonces:. 18.

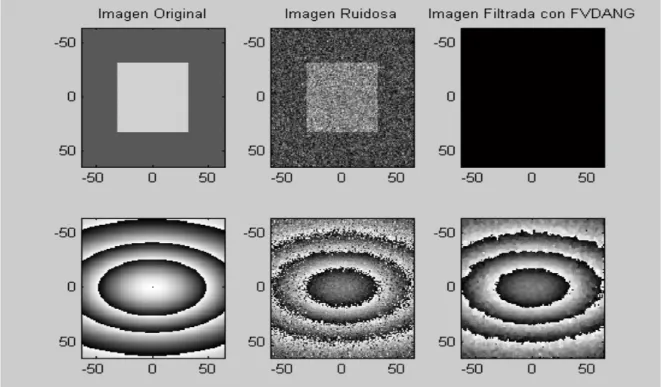
(28) Capítulo 1. α. est I. 2 ⎤ ⎡ DI 2 − σ est =⎢ ⎥ 2 ⎢⎣ DI ⎥⎦ †. (1.14). Para valores de DI bien por encima del ruido, α I ≈ 1 y el método se asemeja a un estimado de umbral duro. Para coeficientes cercanos al nivel de ruido el método se asemeja a un umbral suave. Por lo tanto, anticipemos que el método produce estimados con una pequeña influencia determinada por el umbral duro, y pequeña varianza debido al umbral suave. Existen varios métodos para obtener estimados de σ est .[1][14][31] 1.3. Técnica de denoising a las MRI de fase con el empleo de métodos no lineales. Otras de las técnicas estudiadas para el denoising de las MRI de fase es el empleo del filtros no lineales [37] sobre las imágenes complejas de donde la imagen de fase es extraída. Se emplearon varios filtros vectoriales, los que pueden ser usados en varios ejemplos de procesamiento de señales multicanal como el caso de TV a color. Encontramos más información de estas técnicas en [37][46][47]. Se ha experimentado fundamentalmente con el Filtro de Mediana Vectorial (VMF) [4][37], el Filtro Direccional Vectorial (VDF) [37][55][56], el Filtro de Distancia Direccional (DDF) [34][37] y cuatro ejemplos de Filtros Fuzzy Adaptativo [37][47] para procesar señales complejas simuladas de las cuales la fase es derivada. Las propiedades de supresión de ruido de estos filtros son determinadas para esta aplicación mediante experimentos de simulación extensos. Para evaluar las propiedades de estos filtros en el denoising de las imágenes de fase, se desarrolló una simulación Monte Carlo, utilizando MATLAB como plataforma de cálculo, en el cual la imagen compleja simulada [37] se contaminó de forma sucesiva (20 iteraciones) con seis modelos de ruido diferentes (simulados) [37], luego se aplicó el filtrado para reducir el nivel de ruido y el número de residuos de fase, es decir, la efectividad de los filtros fue determinada por el error cuadrático medio normalizado. 19.

(29) Capítulo 1. (NMSE), la SNR, y la reducción de los residuos de fase, los que se obtuvieron midiendo en cada una de las iteraciones. Los resultados indican una reducción de ruido significativa en términos de la SNR y la supresión de los residuos de fase, especialmente para los filtros no lineales basados en la distancia angular. 1.4. Aplicaciones de las MRI de fase. Las imágenes de fase pueden obtenerse a partir de las imágenes complejas mediante un procesamiento matemático. La información de la fase en las imágenes complejas es utilizada para generar datos de fase útiles, pero en la mayoría de las ocasiones el ruido presente dificulta la obtención de la imagen de fase con la calidad apropiada. Existen numerosas aplicaciones en las que las imágenes de fase poseen un interés particular. Un ejemplo de esto son los equipos de RM llamados tomógrafos, donde se obtienen imágenes mediante la técnica comúnmente denominada MRI. Las imágenes de fase aparecen en procesos de resonancia magnética [53] como ya se había mencionado, en imágenes interferométricas de radar de apertura sintética (IFSAR), en imágenes de densidad de corriente (CDI), entre otros casos [19][52]. Entre las ventajas de las MRI en sentido general, están: poder representar secciones del cuerpo humano en cualquier orientación, lograr altos contrastes en la imagen entre tejidos suaves adyacentes de diferente composición química y la no utilización de radiación ionizante que la hace el método menos invasivo. Las imágenes de fase de MR pueden emplearse para medir el flujo de sangre que atraviesa por las venas del cuerpo humano, permitiendo una caracterización arterial que conlleva a la formación de los arteriogramas con una mejor resolución y alta SNR [35]; al mismo tiempo, son fundamentales para realizar estudios sobre los movimientos de contracción y relajación del corazón [5][27]; su uso permite obtener, bajo ciertas condiciones, información necesaria procedente de nuestro organismo cuando los métodos tradicionales empleados hasta el momento con esos fines, se dificultan, por ejemplo: la diferenciación con una mayor precisión de los adenomas suprarrenales y. 20.

(30) Capítulo 1. sus metástasis [3][16]; y tiene como ventaja que se convierten en un método de investigación rápida y con menos costos que los desarrollados anteriormente. Otra de las aplicaciones de las imágenes de fase de MRI es en la tomografía de impedancia eléctrica (ETI) [7], donde se mide la densidad de flujo magnético por nuestro cuerpo, esta técnica puede emplearse en la ingeniería biomédica: en la búsqueda de soluciones del problema en el campo bioeléctrico [21], en funciones de imagenología o fisiológicas [17], entre otras [41]. Como se mencionó al inicio de este tópico, las imágenes de fase se emplean en las técnicas de radar de apertura sintética (SAR) [20], donde se pueden obtener mapas topográficos de una gran extensión de tierra a partir de las imágenes obtenidas de satélites. También se emplean en la medición de la conductividad nerviosa, específicamente para medir el flujo de corriente a bajas frecuencias con el empleo de las técnicas de Imágenes de Densidad de Corriente de Baja Frecuencia (LF-CDI), donde, después de varios experimentos se llega a demostrar que el flujo de corriente se realiza en una sola dirección y uniformemente a través de la superficie. [13] Igualmente, las imágenes de fase proporcionan información, a escalas nanométricas, acerca de la estructura de la superficie terrestre, la cual no es revelada por otras técnicas [6]. Pueden, además, detectar o descubrir variaciones en la composición y adhesión del terreno, entre otras propiedades de este, que no han sido tratadas con anterioridad. Las aplicaciones de las imágenes de fase en este campo, incluyen la identificación de contaminantes, el descubrimiento de diferentes componentes de los materiales compuestos y la diferenciación de las regiones en cuanto a la alta o baja adhesión de las superficies o su dureza, en fin, todo un estudio de las características del terreno pero con un nivel de resolución mucho mayor a las técnicas empleadas preliminarmente con estos fines. Como se puede observar y a modo de conclusión, las imágenes de fase poseen una amplia gama de aplicaciones: en el estudio del terreno, en radares de apertura sintética y principalmente en la medicina, donde precisamente se centra el objetivo del trabajo. 21.

(31) Capítulo 1. que aquí se realiza dada la gran importancia que representa el empleo de las MRI para el diagnostico y predicción de enfermedades.. 22.

(32) Capítulo II.

(33) Capítulo 2. CAPÍTULO II: Materiales y métodos 2.1. Identificación del problema e hipótesis. Como se mencionó en el capítulo anterior, algunas técnicas de denoising empleando Wavelet como la descrita por Nowak [42] propone dos nuevos filtros en el dominio Wavelet, los cuales centran su trabajo en la reconstrucción de las MRI de magnitud; en el primero, considerado como un filtro adaptativo en el dominio Wavelet (filtro Wiener [51]), se toma el ruido Rician como una aproximación gaussiana y su uso es razonable en altas SNR; el segundo, que opera sobre la MRI de magnitud cuadrática, es más adecuado para bajas SNR, donde los coeficientes de escala y Wavelet son influenciados por los coeficientes correspondientes de la señal libre de ruido. Además, se analizaron otros algoritmos, como el desarrollado por Alexander [1], donde se describe una técnica de denoising basada en Wavelet, la cual se aplica directamente a la imagen compleja, obtenida mediante la Transformada de Fourier, como una única entidad compleja en lugar de considerarla como dos canales independientes pues esto podría originar distorsión de fase y amplitud a la salida, en este caso la imagen de fase nunca se modifica, sólo se le aplica el denoising a la imagen de magnitud. También se han desarrollado algoritmos de denoising de MRI fuera del dominio Wavelet, tal es el caso del experimento realizado por Lorenzo Ginori, donde se aplicaron un conjunto de métodos de filtrado no lineal [37] para el caso particular de las imágenes de fase, las cuales no habían sido tratadas anteriormente con estos tipos de procedimientos. En el presente trabajo se realiza un algoritmo de denoising en el dominio Wavelet pero en este caso sobre las imágenes de fase procedentes de las MRI. El simple hecho de fundamentar y utilizar métodos basados en el filtrado en el dominio Wavelet para el denoising de las imágenes de fase procedentes de MRI, constituye una novedad científica, ya que en ninguno de los métodos desarrollados anteriormente se analiza el problema del ruido en las imágenes de fase utilizando la Transformada Wavelet. Según Nowak [42], debido al error de fase, la magnitud de la señal obtenida es la empleada típicamente para reconstruir la imagen, por lo que se podría pensar en. 23.

(34) Capítulo 2. corregir el error de fase en alguna medida, además si se trabaja solamente con las imágenes de fase la presencia del ruido Rician (presente en las imágenes de magnitud) no sería un problema a la hora de realizarles el denoising. Por otra parte, Alexander [1] plantea que para retener la imagen compleja se le debe aplicar el denoising tanto a la imagen de magnitud como a la de fase. Si se observan las características presentes en el filtro diseñado por Alexander, sale a relucir que el factor de atenuación que se genera del filtro para ponderar cada uno de los coeficientes Wavelet bajo análisis siempre va a tener un valor real y por ende, solo modificará la imagen de magnitud y nunca a la de fase. Alexander expone que la mayoría de los algoritmos de denoising que se han desarrollado hasta ahora siempre suponen para las señales a tratar una distribución de ruido gaussiano aditivo con una contribución de ruido que se produce del escáner electrónico a cada una de las partes real e imaginaria de forma aditiva, esta se supone no correlacionada y caracterizada por una función. de densidad de probabilidad. gaussiana con media cero. Sin embargo, como se ha podido observar, hasta ahora el ruido en la MRI de magnitud es caracterizado por una distribución Rician y como el algoritmo presentado trabaja sobre las imágenes complejas, siendo capaz de evadir el problema de la influencia correspondiente a la señal de magnitud. En resumen, si solo se trabaja con las imágenes de fase simplificando la componente de magnitud el problema de la presencia del ruido con distribución Rician tiende a desaparecer. 2.2. Validación del experimento desde el punto de vista analítico. Se parte de una señal compleja z expresada en su forma cartesiana y polar, la cual representará el caso de estudio que se trata en esta sección:. z = ρ∠ϕ. (2.1). z = a + jb. (2.2). z = ρ cos ϕ + jρsenϕ. (2.3). Donde ρ es el módulo o magnitud y ϕ es el argumento o fase, y se pueden expresar de la siguiente forma: 24.

(35) Capítulo 2. ρ = (a 2 + b 2 ). 1. 2. (2.4). [. ρ = ( ρ cos ϕ )2 + ( ρsenϕ )2. ]. 1. 2. (2.5). ρ = [ρ 2 (cos 2 ϕ + sen 2ϕ )] 2 1. ϕ = tan −1 b a = tan −1. (2.6). ρsenϕ = tan −1 tan ϕ = ϕ ρ cos ϕ. (2.7). Considerando ruido gaussiano aditivo, la señal compleja ruidosa ẑ quedaría como se muestra:. zˆ = (a + η r ) + j (b + η i ). (2.8). donde η = η r + jη i es el ruido gaussiano complejo aditivo. Sustituyendo la Ec. (2.3) en la Ec. (2.8), se obtiene: zˆ = ( ρ cos ϕ + η r ) + j ( ρsenϕ + η i ). (2.9). Expresando la señal compleja ruidosa en su forma polar zˆ = ρˆ∠ϕˆ , la magnitud de dicha señal puede ser representada por la siguiente expresión:. ρˆ = [ρ 2 cos 2 ϕ + 2 ρ cos ϕη r + η r2 + ρ 2 sen 2ϕ + 2 ρsenϕη i + η i2 ]. 1. 2. (2.10). A continuación aparece una disposición de los términos anteriormente representados que permitirá transmitir la idea de este análisis con una mayor claridad. Representando la magnitud cuadrática ruidosa mejor que la magnitud ruidosa y agrupando términos, se llega a:. ρˆ 2 = ρ 2 + 2 ρ (cos ϕη r + senϕη i ) + (η r2 + η i2 ) 144444 42444444 3. (2.11). inf luencia ruidosa. En verdad, lo deseado es que la magnitud cuadrática ruidosa se aproxime lo más posible al primer término del miembro derecho de la Ec. (2.11), es decir que ρˆ 2 ≅ ρ 2 .. 25.

(36) Capítulo 2. Por tanto, el resto de la expresión es considerado como la influencia ruidosa. Aparentemente parece ser un problema fácil de resolver, pues la influencia ruidosa representada aparece como un término aditivo, si fuese así, la utilización de un algoritmo de denoising basado en una aproximación gaussiana sería suficiente para reducir esta componente de ruido y obtener una imagen de magnitud libre de ruido. Sin embargo, el término considerado aquí como influencia ruidosa además de tener las componentes de ruido gaussiano aditivo en la parte real e imaginaria, también está formado por la componente de fase y magnitud de la señal libre de ruido, por ende, la eliminación de este término implicaría un deterioro en la magnitud y la fase de la señal, constituyendo esto una de las limitaciones fundamentales a la hora de obtener una imagen de magnitud libre de ruido. De ahí se puede observar claramente la afectación provocada por el ruido en la magnitud de la señal. Si se trabaja sobre la imagen de fase en cuestión, la fase de la señal compleja ruidosa será: afectacion en la imagen de fase provocada por el ruido } ⎡ ⎤ ⎢ ⎥ ρ ϕ η sen + i ϕˆ = tan −1 ⎢ ⎥ ρ cos ϕ + η{r ⎢ ⎥ Idem ⎣ ⎦. tan ϕˆ =. ρsenϕ + η i ρ cos ϕ + η r. (2.12). (2.13). Expresando nuevamente la señal compleja ruidosa en su forma cartesiana y en función de su magnitud y fase ruidosa, se tiene: zˆ = ( ρ cos ϕ + η r ) + j ( ρsenϕ + η i ). (2.14). Entonces, se aplicará el algoritmo de denoising a cada una de las partes real e imaginarias de la Ec. 2.14 y una vez obtenidas las correspondientes señales reducidas, se introducen estas convenientemente en el numerador y denominador de la Ec. 2.12 respectivamente. En dependencia de la eficacia del algoritmo de denoising empleado, se aproximará en mayor o menor medida la imagen de fase ruidosa a la imagen de fase libre de ruido.. 26.

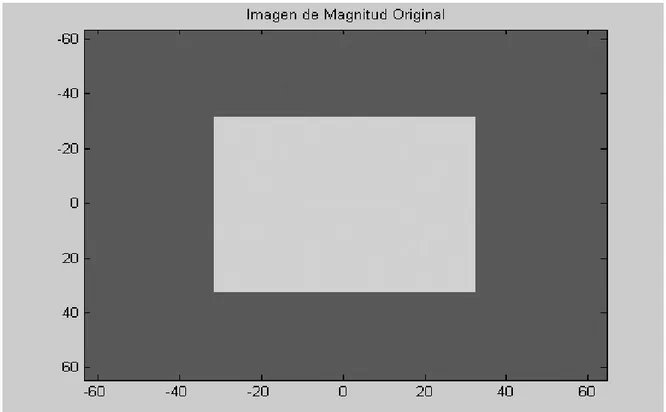
(37) Capítulo 2. 2.3. Descripción del método desde el punto de vista experimental. Uno de los objetivos del presente trabajo plantea realizar una comparación entre el método de denoising basado en el filtrado Wavelet y el método desarrollado con filtros no lineales [37], para lo cual se requiere partir de las mismas condiciones, es decir, emplear la misma imagen y contaminar con los mismos modelos de ruido reiterando el proceso de contaminación y filtrado igual cantidad de veces. Para dar respuesta a las interrogantes mencionadas al inicio de este capítulo, se parte de una imagen simulada, la misma fue construida de acuerdo a una práctica aceptada para este tipo de estudio [1][8], tal y como se implementó en el algoritmo de denoising de las imágenes de fase mediante los métodos de filtrado no lineal. La imagen compleja fue formada por una imagen de magnitud, consistente en un cuadrado de 64x64 píxel de amplitud 210 centrado en otro cuadrado de 128x128 píxel de amplitud 90, y por una imagen de fase “enrollada” (wrapped) original obtenida como una función gaussiana bidimensional dada por:. ϕ uv. ⎛ (u − 64)2 (v − 64)2 = A exp⎜⎜ + 2 σ v2 ⎝ σu. ⎞ ⎟ ⎟ ⎠. (2.15). Donde u y v son las posiciones para los ejes coordenados ( x, y ) . A = 7π , σ u2 = 3500 y. σ v2 = 1000 , son los valores empleados, donde A es la amplitud de la fase y σ u2 y σ v2 son las desviaciones estándar.. 27.

(38) Capítulo 2. Figura 1: Imagen de magnitud de la señal original. Figura 2: Imagen de fase de la señal original. 28.

(39) Capítulo 2. La introducción de los residuos de fase (RES) en las imágenes de fase “enrollada”, las que se obtuvieron de calcular la fase de los datos complejos donde solo se obtienen los valores que están en el intervalo (− π , π ] , es el efecto más negativo del ruido en el problema del “desenrollamiento” (unwrapping) de fase bidimensional. La fase “desenrollada” (unwrapped) se halla para obtener los valores de fase apropiados de la fase “enrollada” y existen diferentes métodos para obtener la fase “desenrollada” . [2][19][36][51] Después de tener la imagen compleja simulada, esta se contaminó con uno de los tres modelos de ruido gaussiano que se muestran a continuación, estos modelos de ruido se emplearon también en el algoritmo de denoising basado en el filtrado no lineal: Tabla 1: Modelos de ruido. MODELOS DE RUIDO 1. STDV=60. 2. STDV=70. 3. STDV=80. En aplicaciones como las de resonancia magnética el modelo gaussiano es ampliamente aceptado para la contaminación de ruido en la parte real e imaginaria de una imagen compleja de donde es obtenida la fase. [2][19] Tanto la imagen compleja simulada como el ruido fueron modelados considerando una resolución de 8 bits para representar sus valores numéricos. La imagen en cuestión se filtró con diferentes bases Wavelets y se escogieron aquellas que mejores resultados aportaron en cuanto al aumento de la SNR y la mayor reducción de los RES. Sin embargo, como se mencionó en el capítulo anterior, la elección del filtro Wavelet óptimo depende de la imagen en cuestión, es decir, las bases Wavelets aquí empleadas no ofrecen las mismas posibilidades para todo tipo de aplicaciones. Las bases Wavelets que aquí se emplearon se nombran a continuación: las Daubechies (DB5), las Symlet (SYM5), las Biortogonales (BIOR2.2, BIOR2.4, BIOR2.6, BIOR3.7) y las Coiflet (COIF5).. 29.

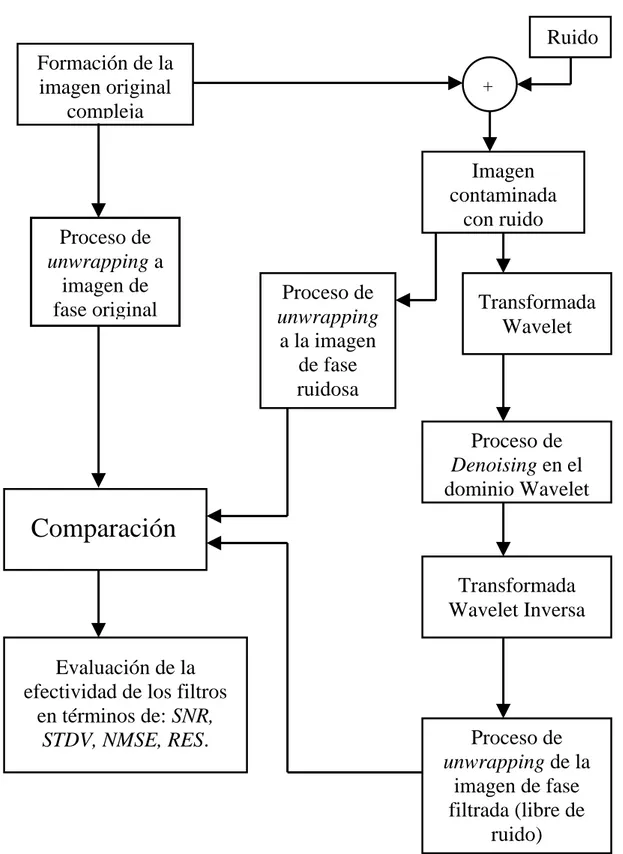
(40) Capítulo 2. Para evaluar las propiedades de los filtros en el domino Wavelet diseñados en el denoising de las imágenes de fase se contaminó con ruido de forma sucesiva la imagen. compleja simulada y luego se aplicaron los filtros para reducir el nivel de ruido y el número de residuos de la MRI de fase. En el desarrollo del filtrado se midieron cuantitativamente los parámetros relacionados con la calidad de la imagen, estos son: relación señal a ruido (SNR), residuos de fase (RES), desviación estándar (STDV) y error cuadrático medio normalizado (NMSE), tal y como se definen a continuación y que coinciden con las expresiones utilizadas en el algoritmo de denoising basado en métodos no lineales. El NMSE fue definido para los cálculos como: ). NMSE =. ∑∑ ϕ (i, j ) − ϕ (i, j ) i. 2. j. ∑∑ ϕ (i, j ) i. 2. (2.16). j. ) donde: ϕ es la fase “desenrollada” original, ϕ es la fase “desenrollada” recuperada. después de filtrar e (i, j ) son los valores de los píxeles en la dirección (u, v ) . La SNR se calculó como: ⎛ 1 ⎞ SNR = 10 log 10 ⎜ ⎟ ⎝ NMSE ⎠. (2.17). Los residuos de fase se calcularon empleando la siguiente expresión sobre la imagen de fase tanto en la ruidosa como en la recuperada después de filtrar [37]:. ϕ (r ) = ∫ ∇ϕ (r ) ⋅ dr = 2 Kπ. (2.18). C. donde: ϕ (r ) es la fase de la señal, ∇ϕ (r ) es el gradiente de la fase, K es un entero que cuenta la cantidad de residuos de fase encerrados en la región C . A continuación se muestra cada una de las etapas que describen el algoritmo de denoising aquí implementado:. 30.

(41) Capítulo 2. Ruido Formación de la imagen original compleja. Proceso de unwrapping a imagen de fase original. +. Imagen contaminada con ruido. Proceso de unwrapping a la imagen de fase ruidosa. Transformada Wavelet. Proceso de Denoising en el dominio Wavelet. Comparación Transformada Wavelet Inversa Evaluación de la efectividad de los filtros en términos de: SNR, STDV, NMSE, RES.. Proceso de unwrapping de la imagen de fase filtrada (libre de ruido). Figura 1: Esquema del algoritmo de denoising general.. 31.

(42) Capítulo III.

(43) Capítulo 3. CAPÍTULO III: Resultados 3.1. Análisis de los resultados. En este capítulo se exponen los resultados obtenidos en el proceso de denoising de las imágenes de fase de MR mediante la Transformada Wavelet y un análisis detallado de cada uno de ellos y se hace una comparación entre los algoritmos empleados para el denoising de estas: los métodos de filtrado no lineal y los realizados en el dominio. Wavelet. Para comenzar, se explica el proceso de generación de la imagen utilizada, su contaminación con los modelos de ruido definidos, el proceso de filtrado como tal y también, los resultados alcanzados al realizar la comparación con los métodos de filtrado no lineal. [37] Anteriormente se había mencionado que una imagen de magnitud y una imagen de fase forman la imagen compleja simulada que es utilizada en este trabajo, la cual se construyó teniendo en cuenta experimentos anteriores, donde se obtuvieron resultados satisfactorios [1][8]. En este caso, la imagen será la misma que se utilizó en el algoritmo de denoising haciendo uso de los filtros no lineales, para de esta forma poder realizar la comparación entre los dos métodos: el aquí desarrollado y el ya mencionado. Luego de tener la imagen compleja simulada, se diseñaron tres modelos de ruido gaussiano con diferentes desviaciones estándar y por ende, diferentes SNR, los cuales se muestran en la Tabla 1. La imagen original que se utilizó se contaminó con cada uno de estos modelos de forma independiente durante veinte veces sucesivas, resultando una imagen compleja contaminada con ruido. Seguido al proceso de contaminación, los canales real e imaginario ruidosos correspondientes a la imagen compleja ruidosa simulada se hicieron pasar por un conjunto de filtros con bases Wavelets (mencionados en el capítulo 2) de forma independiente, es decir, se filtraron las partes real e imaginaria independientemente, luego se formó nuevamente la imagen compleja pero esta vez con sus componentes real e imaginario filtrados.. 32.

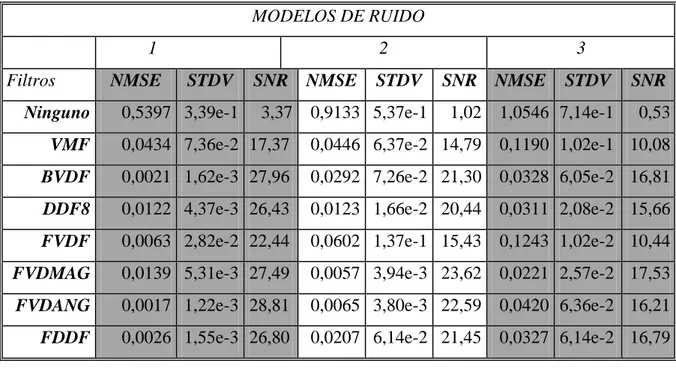
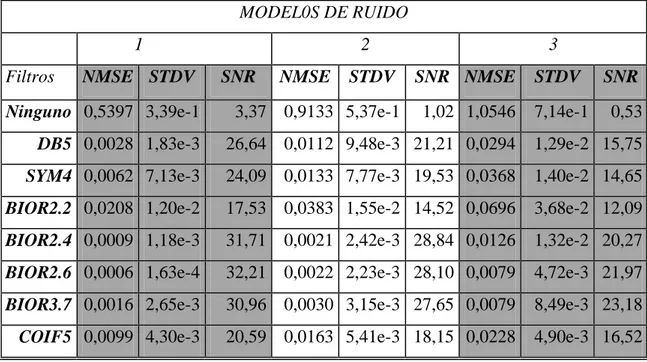
(44) Capítulo 3. Para medir cuantitativamente los parámetros relacionados con la calidad de la imagen de fase (SNR, RES, STDV, NMSE), seguidamente del proceso de denoising ya descrito, se realiza un procedimiento donde se extrae la fase de la imagen compleja filtrada obtenida y a partir de ahí, se hacen los cálculos respectivos. Finalmente se formaron las tablas donde aparecen los resultados obtenidos para cada uno de los tres modelos de ruido presentados y para cada uno de los filtros diseñados. Para hacer la comparación con los métodos de filtrado no lineal desarrollados en [37] se repite este proceso pero en este caso en lugar de emplear los filtros en el dominio Wavelet se usan los filtros no lineales, los modelos de ruido son los mismos al igual que la imagen, el número de iteraciones y la forma de calcular los parámetros antes mencionados. 3.2. Comparación de métodos. Tabla 2: Resultados de los parámetros SNR, NMSE y STDV al aplicar el método de filtrado en el dominio Wavelet.. MODEL0S DE RUIDO 1 Filtros. NMSE STDV. Ninguno 0,5397 3,39e-1. 2 SNR. NMSE. 3. STDV. SNR NMSE. STDV. 3,37 0,9133 5,37e-1. 1,02 1,0546. 7,14e-1. SNR. 0,53. DB5 0,0028 1,83e-3. 26,64 0,0112 9,48e-3 21,21 0,0294. 1,29e-2 15,75. SYM4 0,0062 7,13e-3. 24,09 0,0133 7,77e-3 19,53 0,0368. 1,40e-2 14,65. BIOR2.2 0,0208 1,20e-2. 17,53 0,0383 1,55e-2 14,52 0,0696. 3,68e-2 12,09. BIOR2.4 0,0009 1,18e-3. 31,71 0,0021 2,42e-3 28,84 0,0126. 1,32e-2 20,27. BIOR2.6 0,0006 1,63e-4. 32,21 0,0022 2,23e-3 28,10 0,0079. 4,72e-3 21,97. BIOR3.7 0,0016 2,65e-3. 30,96 0,0030 3,15e-3 27,65 0,0079. 8,49e-3 23,18. COIF5 0,0099 4,30e-3. 20,59 0,0163 5,41e-3 18,15 0,0228. 4,90e-3 16,52. 33.

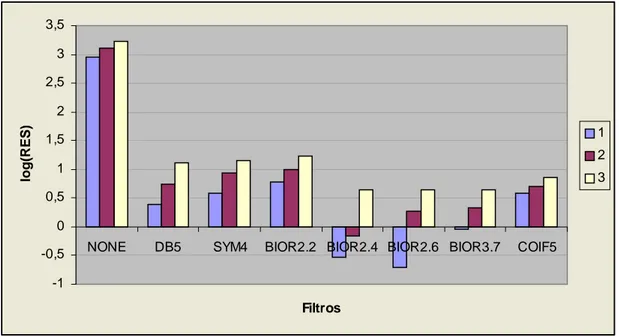
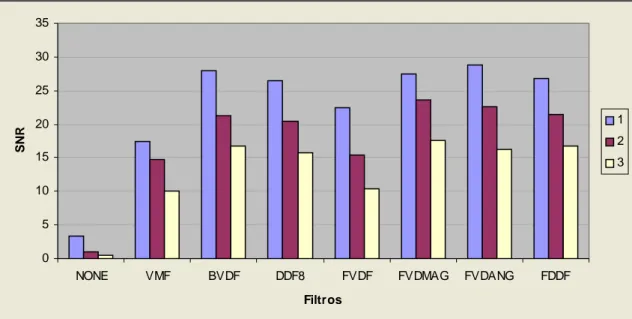
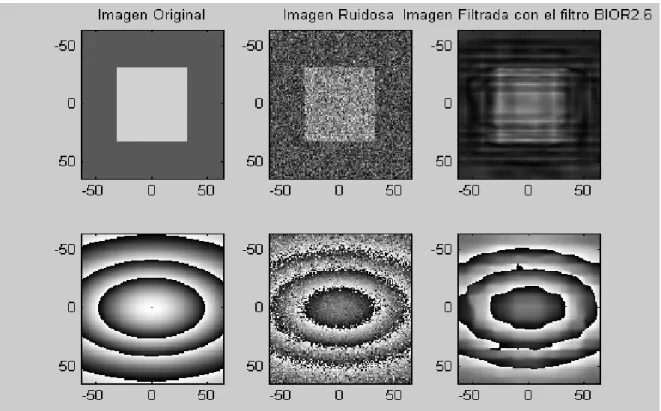
(45) Capítulo 3. Como puede observarse en la Tabla 2 aparecen los resultados correspondiente al experimento que realiza el proceso de denoising utilizando un conjunto de filtros que emplean la Transformada Wavelet. Aquí solo aparecen representado los filtros cuyos resultados fueron los más significativos, aunque en realidad se trabajó con un conjunto de 30 filtros donde además de los mencionados se incluían también el: HAAR, DB1, DB2, DB3, DB4, SYM2, SYM3, SYM5, COIF1, COIF2, COIF3, COIF4, BIOR1.1, BIOR1.3, BIOR1.5, BIOR2.8, BIOR3.1, BIOR3.3, BIOR3.5, BIOR3.9, BIOR4.4, BIOR5.5, BIOR6.8. En la primera línea de cada tabla aparecen los datos. correspondientes a la imagen de fase ruidosa sin filtrar, la cual es tomada como referencia para ilustrar la mejora introducida por cada uno de los filtros aplicados. Los resultados alcanzados al realizar el proceso de denoising a la imagen de fase, en este caso proveniente de una imagen compleja simulada contaminada con ruido, son satisfactorios ya que aumentan considerablemente la SNR con pequeños valores de NMSE, lo que implica que estos filtros constituyen un gran aporte al estudio que se ha estado desarrollando. De ellos, el BIOR2.6 fue el que mejores resultados alcanzó, por lo que se utilizará para realizar las comparaciones pertinentes con los valores obtenidos al emplear los métodos de filtrado no lineal. En la figura siguiente se ve claramente el comportamiento de estos filtros en cuanto al aumento de la SNR para los tres modelos de ruido diferentes, como también se aprecia el filtro que mejor comportamiento presentó.. 34.

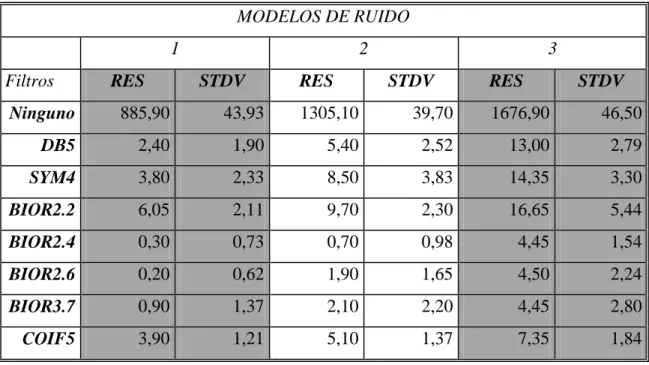
(46) Capítulo 3. 35 30. SNR. 25 1. 20. 2 15. 3. 10 5 0 NONE. DB5. SYM4. BIOR2.2 BIOR2.4 BIOR2.6 BIOR3.7. COIF5. Filtros. Figura 3: Gráfico de barras que muestra los valores de SNR obtenidos para cada uno de los filtros en el dominio Wavelet y para cada modelo de ruido.. Tabla 3: Resultados del parámetro RES, al aplicar el método de filtrado en el dominio Wavelet.. MODELOS DE RUIDO 1 Filtros. RES. 2 STDV. RES. 3 STDV. RES. STDV. Ninguno. 885,90. 43,93. 1305,10. 39,70. 1676,90. 46,50. DB5. 2,40. 1,90. 5,40. 2,52. 13,00. 2,79. SYM4. 3,80. 2,33. 8,50. 3,83. 14,35. 3,30. BIOR2.2. 6,05. 2,11. 9,70. 2,30. 16,65. 5,44. BIOR2.4. 0,30. 0,73. 0,70. 0,98. 4,45. 1,54. BIOR2.6. 0,20. 0,62. 1,90. 1,65. 4,50. 2,24. BIOR3.7. 0,90. 1,37. 2,10. 2,20. 4,45. 2,80. COIF5. 3,90. 1,21. 5,10. 1,37. 7,35. 1,84. En la Tabla 3 se muestran los valores del número de residuos de fase remanentes en cada uno de los procesos de denoising de cada filtro, como se aprecia en este caso, fue el filtro Wavelet BIOR2.6 el que mejores resultados alcanzó, reduciendo en un mayor número los residuos de fase de la señal empleada.. 35.

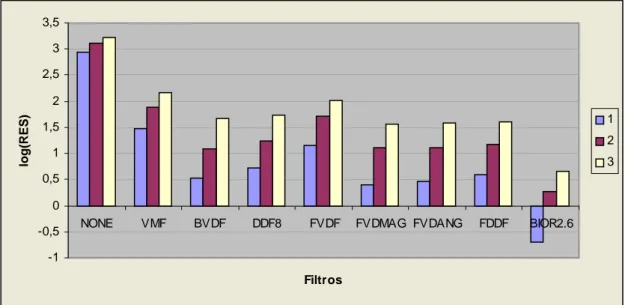
(47) Capítulo 3. En el gráfico que aparece a continuación se muestra los valores obtenidos al filtrar en el dominio Wavelet. Para una mejor comprensión de estos resultados se debe señalar que en lugar de tabular los valores reales, se tabularon los log10 ( RES ) de cada uno de ellos, dando en ocasiones valores negativos, debido a que en algunos filtros los valores de RES se redujeron a un número muy pequeño (< 1), aunque es conocido que el número de residuos de fase se corresponde con un valor entero y ≥ 1 , los resultados obtenidos como valores decimales se deben a la estrategia utilizada en el proceso de contaminación y filtrado de las imágenes complejas donde se incluyen 20 iteraciones cuyo promedio define el resultado final. Con el análisis de la Figura 4 se puede concluir que son varios los filtros que reducen en gran medida la cantidad de residuos de fase, pero para ser consecuentes con lo que se había mencionado antes, tomaremos el filtro BIOR2.6 para realizar las comparaciones con los filtros no lineales desarrollados.. 3,5 3 2,5. log(RES). 2 1. 1,5. 2 1. 3. 0,5 0 -0,5. NONE. DB5. SYM4. BIOR2.2 BIOR2.4 BIOR2.6 BIOR3.7. COIF5. -1 Filtr os. Figura 4: Gráfico de barras que muestra los valores de RES (en este caso se grafica log10 ( RES ) ) obtenidos para cada uno de los filtros en el dominio Wavelet y para cada modelo de ruido.. Seguidamente se muestran los resultados que se obtuvieron al realizar el mismo procedimiento pero en este caso empleando los filtros no lineales que se utilizaron en [37]. Se debe señalar que, como ya se mencionó, la imagen compleja simulada, los modelos de ruido y el número de iteraciones son iguales a los que se usaron para el denoising en el dominio Wavelet.. 36.

(48) Capítulo 3. En [37] se llegó a la conclusión de que el filtro de mejor comportamiento era el FVDANG, tal y como se puede apreciar en la Tabla 4 y Tabla 5. Tabla 4: Resultados de los parámetros: SNR, NMSE y STDV, al aplicar el método de filtrado no lineal.. MODELOS DE RUIDO 1 Filtros Ninguno. 2. NMSE. STDV. 0,5397 3,39e-1. SNR NMSE. 3. STDV. SNR NMSE. 3,37 0,9133 5,37e-1. STDV. SNR. 1,02 1,0546 7,14e-1. 0,53. VMF. 0,0434 7,36e-2 17,37. 0,0446 6,37e-2 14,79 0,1190 1,02e-1 10,08. BVDF. 0,0021 1,62e-3 27,96. 0,0292 7,26e-2 21,30 0,0328 6,05e-2 16,81. DDF8. 0,0122 4,37e-3 26,43. 0,0123 1,66e-2 20,44 0,0311 2,08e-2 15,66. FVDF. 0,0063 2,82e-2 22,44. 0,0602 1,37e-1 15,43 0,1243 1,02e-2 10,44. FVDMAG. 0,0139 5,31e-3 27,49. 0,0057 3,94e-3 23,62 0,0221 2,57e-2 17,53. FVDANG. 0,0017 1,22e-3 28,81. 0,0065 3,80e-3 22,59 0,0420 6,36e-2 16,21. FDDF. 0,0026 1,55e-3 26,80. 0,0207 6,14e-2 21,45 0,0327 6,14e-2 16,79. Tabla 5: Resultados del parámetro RES, al aplicar el método de filtrado no lineal.. MODELOS DE RUIDO 1 Filtros. RES. 2 STDV. RES. 3 STDV. RES. STDV. Ninguno. 885,90. 43,93. 1305,10. 39,78. 1676,90. 46,50. VMF. 29,85. 8,99. 77,50. 12,90. 144,55. 20,22. BVDF. 3,40. 2,98. 12,05. 4,91. 46,80. 9,74. DDF8. 5,40. 3,66. 17,70. 5,07. 52,95. 12,18. FVDF. 14,55. 6,72. 51,20. 8,70. 104,25. 17,04. FVDMAG. 2,45. 2,26. 12,70. 5,35. 36,50. 7,39. FVDANG. 2,90. 2,47. 13,05. 5,37. 38,50. 10,87. FDDF. 4,00. 2,05. 14,75. 6,62. 40,85. 8,50. 37.