´Indice
´Indice I
1. Funciones reales de varias variables 2
1.1. Funciones reales de varias variables . . . 2
1.1.1. Dominio, rango de las funciones reales de varias variables . . . 2
1.1.2. Graficas . . . 3
1.1.3. Curvas de nivel . . . 4
1.1.4. Operaciones con funciones reales de variables variables . . . . 4
1.2. Nociones de topolog´ıa en Rn . . . . 6
1.2.1. Clasificaci´on de los puntos de un conjunto . . . 7
1.2.2. Conjunto abierto . . . 8
1.2.3. Conjunto cerrado . . . 8
1.2.4. Conjunto acotado . . . 8
1.2.5. Conjunto compacto . . . 8
1.2.6. Conjunto conexo . . . 9
1.2.7. Dominio . . . 9
1.3. limites de funciones de varias variables . . . 9
1.3.1. Regla de las dos trayectorias . . . 10
1.3.2. Limites parciales iterados ´o reiterados . . . 12
1.4. Continuidad de funciones de varias variables . . . 14
1.5. Ejercicios Propuestos . . . 15
1.6. Derivadas parciales de funciones reales de varias variables . . . 16
1.6.1. Interpretaci´on geom´etrica de las derivadas parciales . . . 18
1.6.2. Plano tangente . . . 19
1.7. Funciones diferenciables . . . 20
´INDICE 1
1.8. La diferencial . . . 22
1.9. Derivadas parciales de orden superior . . . 24
1.10. Derivaci´on implicita . . . 26
1.11. Funciones compuestas. Regla de la cadena . . . 27
1.12. Derivada direccional . . . 28
1.12.1. Interpretaci´on geom´etrica de las derivadas direccionales . . . . 29
1.12.2. Propiedades de la derivada direccional . . . 30
1.12.3. Relaci´on entre las derivadas parciales, direccionales y la con-tinuidad . . . 31
1.13. Gradiente de una funci´on de varias variables . . . 32
1.13.1. Interpretaci´on geom´etrica del gradiente . . . 32
1.13.2. Plano tangente . . . 32
1.13.3. Propiedades del gradiente . . . 32
1.14. C´alculo de la derivada direccional usando el gradiente . . . 32
1.14.1. El gradiente como direcci´on de m´axima variaci´on . . . 33
1.15. Ejercicios propuestos . . . 35
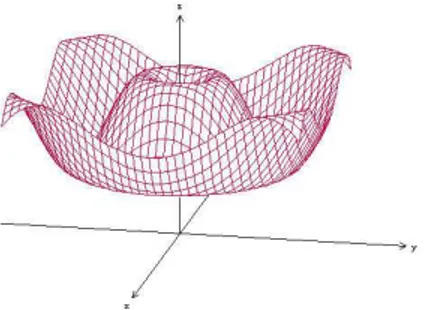
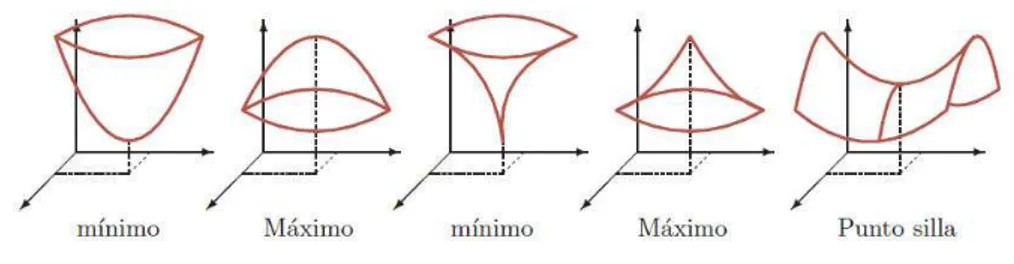
1.16. Extremos de las funciones de varias variables . . . 39
1.17. Formas cuadr´aticas . . . 41
1.18. Extremos condicionados . . . 48
1.19. M´etodo de multiplicadores de Lagrange . . . 49
1.20. Ejercicios propuestos . . . 51
Cap´ıtulo 1
Funciones reales de varias
variables
1.1.
Funciones reales de varias variables
Definici´on 1.1.1. Una funci´on de varias variables definida sobre un D ⊂ Rn es una regla de correspondencia f que asocia a cada punto X = (x1, x2, ...xn)∈D un ´unico n´umero real z =f(x1, x2, ...xn)
Figura 1.1: Funci´on real de varias variables
1.1.1. Dominio, rango de las funciones reales de varias variables
Sea f una funci´on de varias variables de Rn en R. Se define el dominio de f
denotado porDom f como:
Dom f ={X = (x1, x2, ...xn)∈Rn /∃!z ∈R ∧ z =f(X)} ⊂Rn
1.1. FUNCIONES REALES DE VARIAS VARIABLES 3
Se define el rango def denotado por Ran f como:
Ran f ={z ∈R/∃X = (x1, x2, ...xn)∈Rn ∧ z =f(X)} ⊂R
Ejemplo 1.1.1. Sea f(x, y) =psen(x2+y2). Halle el dominio y rango de la
fun-ci´on f y grafique el dominio.
Soluci´on
Se tiene sen(x2+y2)≥0⇒0≤sen(x2+y2)≤1⇒2kπ ≤x2+y2 ≤(2k+ 1)π
para todok = 0,1,2, ... Luego
Domf ={(x, y)∈R2 /2kπ≤x2+y2 ≤(2k+ 1)π , ∀k = 0,1,2, ...}
Por otro lado, como 0≤sen(x2+y2)≤ 1⇒ 0≤psen(x2+y2)≤1 ⇒0≤ z ≤ 1
LuegoRan f = [0,1]
Figura 1.2: Gr´afica del dominio de
f
Figura 1.3: Gr´afica de la funci´on f(x, y) =
p
sen(x2+y2)
1.1.2. Graficas
La grafica de una funci´on f : R2 → R es el conjunto de todos los puntos en el
espacio con coordenadas (x, y, z) que satisface la ecuaci´on z =f(x, y).
1.1. FUNCIONES REALES DE VARIAS VARIABLES 4
Figura 1.4: Gr´afica de la superficie: f(x, y) = 2senpx2+y2+ 3 1.1.3. Curvas de nivel
La intersecci´on del plano horizontal z = k con la superficie z = f(x, y) es la curva de contorno de altura k sobre la superficie. La proyecci´on vertical de esta curva de contorno en el plano XY es la curva de nivelf(x, y) = k de la funci´on f. Las curvas de nivel proporcional una forma bidimensional de representar una superficie tridimensionalz =f(x, y).
Figura 1.5: Curvas de nivel
Ejemplo 1.1.2. Halle las curvas de nivel de la superficie f(x, y) = y2−x2.
Soluci´on
Las curvas de nivel de la superficie f(x, y) =y2 −x2 son: y2−x2 =k para todo
k∈R
1.1.4. Operaciones con funciones reales de variables variables
1.1. FUNCIONES REALES DE VARIAS VARIABLES 5
Figura 1.6: Gr´afica de la su-perficief(x, y) =y2−x2
Figura 1.7: Grafica de las cur-vas de nively2−x2=k
1. (f±g)(X) =f(X)±g(X), ∀X ∈Dom(f±g) = Dom f ∩Dom g
2. (f g)(X) =f(X)g(X), ∀X ∈Dom(f±g) = Dom f ∩Dom g
3. (fg)(X) = fg((XX)) , ∀X ∈Dom(f ±g) =Dom f ∩Dom g− {X/g(X) = 0}
Definici´on 1.1.3. Consideremos f : Rn → R y g : R → R dos funciones con dominios Dom f = D y Dom g = E respectivamente con Ran f ∩ Dom g 6= φ, entonces definamos la funci´on compuesta por:
D⊂Rn f→E ⊂R→g R
(g◦f)(X) =g(f(X)), ∀X ∈Dom(g◦f)
donde
Dom(g◦f) = {X = (x1, x2, ..., xn)/ X ∈Dom f ∧ f(X)∈Dom g}
Ejemplo 1.1.3. Dado g(x) = arc cosx y f(x, y) = px2+y2−16. Halle la
funci´on g◦f y su dominio.
Soluci´on
Primero hallemos el dominio de g◦f.
1.2. NOCIONES DE TOPOLOG´IA ENRN 6
Entonces
Dom(g◦f) = {(x, y)∈R2 / x2+y2 ≥16 ∧ −1≤px2+y2−16≤1}
= {(x, y)∈R2 / x2+y2 ≥16 ∧ 0≤x2 +y2−16≤1}
= {(x, y)∈R2 / x2+y2 ≥16 ∧ 16≤x2+y2 ≤17}
Dom(g◦f) = {(x, y)∈R2 / 16≤x2+y2 ≤17}
Finalmente
Dom(g◦f)(x, y) = g(f(x, y)) =g(px2+y2−16) =arc cospx2+y2−16
para todo (x, y)∈Dom(g◦f)
1.2.
Nociones de topolog´ıa en
R
nDistancia euclidea en Rn
Definici´on 1.2.1. SeanX = (x1, x2, ..., xn)yY = (y1, y2, ..., yn)puntos en Rn. La distancia euclidea de X a Y est´a dada por
d(X, Y) = p(x1−y1)2+ (x2−y2)2+...+ (xn−yn)2 =kX−Yk
Bola abierta
Definici´on 1.2.2. Sea a ∈Rn y r > 0. La bola abierta de centro a y radio r, que se denota B(a, r), es el conjunto
B(a, r) ={X ∈Rn / d(X, a) = kX−ak< r}.
Ejemplo 1.2.1. Sin= 2 ya= (0,0),B(a,2)es el interior del circulo centrado en el origen de coordenadas y radio 2.
Entorno de un punto
Definici´on 1.2.3. Sea a∈ Rn. Un subconjunto A ⊂Rn es un entorno de a si existe una bola abierta de centro a contenida en A.
1.2. NOCIONES DE TOPOLOG´IA ENRN 7
Definici´on 1.2.4. Sea a ∈Rn y r > 0. La bola cerrada de centro a y radio r, que se denota B(a, r)¯ , es el conjunto
¯
B(a, r) ={X ∈Rn / d(X, a) = kX−ak ≤r}.
Ejemplo 1.2.2. Si n = 2 y a = (0,0), B(a,¯ 2) es el interior del circulo de centro (0,0) y radio 2 junto con la circunferencia contorno.
1.2.1. Clasificaci´on de los puntos de un conjunto ConsideremosRn con la distancia euclidea.
Punto interior. Interior de un conjunto
Definici´on 1.2.5. Un punto a ∈ Rn es interior a A si existe r > 0 tal que
B(a, r)⊂A.
Se llama interior de un conjunto A, denot´andose Int A, al conjunto de todos los puntos interiores a A.
Punto exterior. Exterior de un conjunto
Definici´on 1.2.6. Un punto a ∈ Rn es exterior a A si es interior a su com-plementario Ac, o lo que es lo mismo, B(a, r)∩A=φ.
Se llama exterior de un conjunto A, al conjunto de todos los puntos exteriores a A, denotandose Ext A.
Punto frontera. Frontera de un conjunto
Definici´on 1.2.7. Un punto a∈Rn es punto frontera a A si para todo r >0,
B(a, r)∩A6=φ yB(a, r)∩Ac6=φ .
Es decir, un punto es frontera de A si no es ni interior ni exterior a A.
Se llama frontera de un conjunto A al conjunto de todos sus puntos frontera, denot´andose F r A.
Punto adherente. Adherente de un conjunto
Definici´on 1.2.8. Un punto a ∈ Rn es adherente a A si para todo r > 0 se tiene B(a, r)∩A6=φ
1.2. NOCIONES DE TOPOLOG´IA ENRN 8
Punto de acumulaci´on. Conjunto derivado
Definici´on 1.2.9. Un puntoa∈Rn es de acumulaci´on deA si para todo r >0 se tiene
[B(a, r)∩A]− {a} 6=φ
Se llama conjunto derivado deAal conjunto de todos los puntos de acumulaci´on de A, denot´andose A0.
Punto aislado
Definici´on 1.2.10. Un punto a∈Rn es punto aislado de A si existe r >0 tal que B(a, r)∩A={a}
NOTA 1.2.1.
Un punto aislado deApertenece al conjuntoApero no es punto de acumulaci´on deA.
1.2.2. Conjunto abierto
Definici´on 1.2.11. Un conjunto es abierto si todos sus puntos son interiores.
Ejemplo 1.2.3. Las bolas abiertas son conjuntos abiertos pero no todo conjunto abierto es una bola abierta.
1.2.3. Conjunto cerrado
Definici´on 1.2.12. Un conjunto es cerrado si su complemeto es abierto.
Ejemplo 1.2.4. Las bolas cerradas son conjuntos cerrados pero hay conjunto cer-rados que no son bolas cerradas.
1.2.4. Conjunto acotado
Definici´on 1.2.13. Un conjunto A⊂Rn es acotado si y solo si exister >0 tal que
kXk< r para todo X ∈A.
1.2.5. Conjunto compacto
1.3. LIMITES DE FUNCIONES DE VARIAS VARIABLES 9
1.2.6. Conjunto conexo
Definici´on 1.2.15. Un conjunto A ⊂ Rn es conexo si no es posible encontrar dos conjuntos abiertosB yC no vacios, conA∩B 6=φyA∩C 6=φ tales queA⊂B∪C, con C∩B¯ =φ y C¯∩B =φ.
NOTA 1.2.2.
La idea de un conjunto conexo es que sea de una pieza.
1.2.7. Dominio
Definici´on 1.2.16. Un conjunto A ⊂ Rn es un dominio si es que es un conjunto abierto y conexo.
1.3.
limites de funciones de varias variables
Sea f una funci´on definida en un conjunto D ⊂ Rn a valores en R. La idea
intuitiva de limite def cuando X tiende a un punto A ∈ Rn es el de la existencia
de unl ∈Rtal que los valores de f(X) est´en arbitrariamente pr´oximos a l siempre que se tome X ∈D,X 6=A suficientemente pr´oximo aA.
Definici´on 1.3.1. Seaf una funci´on definida en un conjunto D⊂Rn a valores en
R y seaA ∈Rn un punto de acumulaci´on de D. Diremos que el limite def cuando
X tiende aAesl ∈R(denotado porl´ımX→Af(X) =l ) si para cada² >0es posible hallar un δ > 0 tal que | f(X)−A |< ² siempre que X ∈ D y 0 < kX−Ak < δ. Simb´olicamente:
l´ım
X→Af(X) =l ⇔ ∀² >0∃δ >0/ X ∈D ∧ 0<kX−Ak< δ ⇒|f(X)−l |< ²
Ejemplo 1.3.1. Usando definici´on demuestre que:
l´ım
(x,y)→(0,0)
x2+y2 p
x2+y2+ 2−√2 = 2
√
2
Soluci´on
Sea f(x, y) = √ x2+y2
x2+y2+2−√2 con dominioDomf =R
2− {(0,0)}. De la definici´on
se tiene que:
1.3. LIMITES DE FUNCIONES DE VARIAS VARIABLES 10
| x
2 +y2 p
x2 +y2+ 2−√2−2
√
2| = | (x
2+y2) (px2+y2+ 2 +√2)
x2 +y2 −2
√
2|
= |px2+y2+ 2−√2|
= | x
2+y2 p
x2+y2+ 2 +√2 |
= |x2+y2 | | p 1
x2+y2+ 2 +√2 | (∗)
Como 0 < k(x, y) − (0,0)k < δ ⇒ 0 < px2+y2 < δ. Ahora acotemos
| √ 1
x2+y2+2+√2 |.
Dado que √2 ≤ √2 +px2+y2+ 2 ⇒ √ 1
x2+y2+2+√2 ≤
1
√
2 Reemplazando estos
´ultimos resultados en (*) se tiene: | √ x2+y2
x2+y2+2−√2 −2 √
2|< δ2 1√
2 =²
Por lo tanto: δ=p√2²
Teorema 1.3.1. Seaf una funci´on definida en un conjunto D⊂Rn a valores enR y seaA∈Rn un punto de acumulaci´on de D. Si existel´ım
X→Af(X), ´este es ´unico.
Teorema 1.3.2. Sean f y g dos funciones definidas en un conjunto D ⊂ Rn a valores enRy seaA∈Rnun punto de acumulaci´on deD. Si existenl´ım
X→Af(X) =
l1 , l´ımX→Ag(X) = l2 entonces
l´ım
X→A(f±g)(X) =l1 ±l2
l´ım
X→A(f g)(X) =l1l2 Si adem´as g(x) es no nulo para todo X yl2 6= 0,
l´ım
X→A
f(X) g(X) =
l1
l2
1.3.1. Regla de las dos trayectorias
Teorema 1.3.3. Sea la funci´onf :D⊂Rn→R yP
0 = (x01, x02, ..., x0n) un punto de acumulaci´on deD=Domf. Si dos trayectorias, digamosα(t) = (x1(t), x2(t), ..., xn(t)) yβ(t) = (x1(t), x2(t), ..., xn(t))que pasa por P0 =α(t0) = β(t1)producen dos valores
limites diferentes para f entonces l´ım
X→P0
f(X) no existe.
Corolario 1.3.1. Se cumple que l´ım
(x,y)→(x0,y0)
f(x, y) =l si y solo si para toda trayec-toriaα(t) = (x(t), y(t)) que pasa por P0 = (x0, y0), esto es,P0 =α(t0), se tiene
l´ım
(x,y)→(x0,y0)
f(x, y) = l´ım
t→t0
1.3. LIMITES DE FUNCIONES DE VARIAS VARIABLES 11
Ejemplo 1.3.2. Calcule l´ım
(x,y)→(0,0)
3x2y
x4+y2
Soluci´on
Sean las trayectorias:
α(t) = (t,0) ; α(t0) = (t0,0) = (0,0)⇒t0 = 0
l´ım
(x,y)→(0,0)
3x2y
x4+y2 = l´ımt→0
3t2(0)
t4+ 02 = 0
β(t) = (t, t2) ; β(t
0) = (t0, t20) = (0,0)⇒t0 = 0
l´ım
(x,y)→(0,0)
3x2y
x4+y2 = l´ımt→0
3t2t2
t4+t2 =
3 2 Por el teorema anterior, no existe l´ım
(x,y)→(0,0)
3x2y
x4+y2
Ejemplo 1.3.3. Calcule l´ım
(x,y)→(0,0)
x2y
x2+y2
Soluci´on
Consideremos los caminos diferentes que contenga a (0,0). Sea A={(x, y)∈R2/ y =kx , k∈R}
l´ım
(x,y)→(0,0)
x2y
x2+y2 =Ãy=k xÃ= l´ımx→0
k x3
x2(1 +k2) = 0 k ∈R
Esto no prueba en absoluto que el valor del limite sea cero. Un argumento que termina con esta incertidumbre es la definici´on del limite, esto es probemos que
l´ım
(x,y)→(0,0)
x2y
x2+y2 = 0.
Sea f(x, y) = xx2+2yy2 con dominio Domf =R2− {(0,0)}. De la definici´on se tiene
que:
∀² >0∃δ >0/(x, y)∈Domf ∧ 0<k(x, y)−(0,0)k< δ ⇒|f(x, y)−0|< ²
| x2y
x2+y2 | = |x|
2| y
x2+y2 |
≤ |x|2|y| 1
|x|2
= |y|
< δ=²
El ´ultimo resultado se obtiene gracias a que 0 < k(x, y) − (0,0)k < δ implica
|y|<px2+y2 < δ y x2 ≤x2+y2 ⇒ 1
x2+y2 ≤ x12 , ∀(x, y)∈Domf.
Por lo tanto:
l´ım
(x,y)→(0,0)
x2y
1.3. LIMITES DE FUNCIONES DE VARIAS VARIABLES 12
Ejemplo 1.3.4. Calcule, si existe, el valor del siguiente l´ımite:
l´ım
(x,y)→(0,0)
y+senx y+x Soluci´on
Si nos aproximamos al punto (0, 0) mediante rectas y=k x obtenemos l´ım
(x,y)→(0,0)
y+senx
x+y =Ãy=k xÃ= l´ımx→0
k x+senx k x+x
y al ser de una variable podemos aplicar L’Hˆopital, con lo cual l´ım
x→0
k x+senx k x+x =
k+ 1
k+ 1 = 1 para k6=−1
sin embargo, si nos aproximamos al punto (0, 0) mediante la curva y = x3 −x
resulta l´ım
(x,y)→(0,0)
y+senx
x+y =Ãy=x
3−xÃ= l´ım
x→0
x3−x+senx
x3−x+x
y al ser de una variable podemos aplicar L’H’opital, con lo cual l´ım
x→0
x3−x+senx
x3 = l´ımx→0
3x2−1 +cosx
3x2 = l´ımx→0
6x−senx
6x = l´ımx→0
6−cosx
6 =
5 6 Con lo cual podemos afirmar que el l´ımite propuesto no existe.
1.3.2. Limites parciales iterados ´o reiterados Se pueden calcular los siguientes l´ımites:
l´ım
x→x0
[ l´ım
y→y0
x6=x0
f(x, y)]
l´ım
y→y0
[ l´ım
x→x0
y6=y0
f(x, y)]
Si estos dos limites son distintos, entonces la funci´on no tiene l´ımite, pero si son iguales o alguno de ellos no existe, entonces no se puede asegurar nada sobre el l´ımite doble.
Ejemplo 1.3.5. Demuestre que el siguiente l´ımite no existe.
l´ım
(x,y)→(0,0)
x2−y2
x2 +y2
soluci´on
l´ım
x→0[l´ımy→0 x6=0
x2−y2
x2 +y2] = l´ımx→0
x2−0
x2+ 0 = 1
l´ım
y→0[l´ımx→0 y6=0
x2−y2
x2+y2] = l´ımy→0
0−y2
0 +y2 =−1
1.3. LIMITES DE FUNCIONES DE VARIAS VARIABLES 13
Ejemplo 1.3.6. Demuestre que el siguiente l´ımite existe y sin embargo no existen ninguno de los iterados.
l´ım
(x,y)→(0,0)(x sen(
1
y) +y sen( 1 x)) soluci´on
El limite doble existe
l´ım
(x,y)→(0,0)(x sen(
1
y) +y sen( 1
x)) = 0.funci´on acotada + 0.funci´on acotada = 0 Mientras que los l´ımites iterados no existen, en efecto:
l´ım
x→0[l´ımy→0 x6=0
(x sen(1
y) +y sen( 1
x))] = l´ımx→0[no definido + 0] = No definido
l´ım
y→0[l´ımx→0 y6=0
(x sen(1
y) +y sen( 1
x))] = l´ımy→0[0 + no definido] = No definido
Teorema 1.3.4. Relaci´on entre los diferentes tipos de lim´ıtes.
1. Si existe el limite en un punto P ∈D0 de una funci´on f :D ⊂R2 →R y vale
l, entonces existe el l´ımite seg´un cualquier subconjunto en dicho punto P vale
l.
2. Sea f :D⊂R2 →R yP = (x
0, y0)∈D0. Si en P existe el limite y los limites
reiterados de f, entonces los tres coinciden.
NOTA 1.3.1.
Para el c´alculo del l´ımite doble suele ser usual el paso a coordenadas polares con origen en P = (x0, y0).
El cambio a coordenadas polares dado por las relaciones
x=x0+rcosθ , y=y0+rsenθ
convierte l´ım
(x,y)→(x0,y0)
f(x, y) en l´ım
r→0F(r, θ). Si por ejemplo la funci´on F(r, θ) es tal
que verificaF(r, θ) =g(r)h(θ) con l´ım
r→0g(r) = 0 y la funci´onh(θ) est´a acotada para
θ∈[0,2π) entonces podemos asegurar que
l´ım
(x,y)→(x0,y0)
1.4. CONTINUIDAD DE FUNCIONES DE VARIAS VARIABLES 14
Ejemplo 1.3.7. Estudie la existencia del l´ımite:
l´ım
(x,y)→(0,0)
x2y2
(x2+y2)32
Soluci´on
Pasando a coordenadas polares x=x0 +rcosθ , y=y0+rsenθ se tiene
l´ım
(x,y)→(0,0)
x2y2
(x2+y2)32
= l´ım
r→0
r4sen2θ cos2θ
r3 = l´ımr→0r sen
2θ cos2θ = 0
Notemos que la funci´onsen2θ cos2θ est´a acotada y l´ım
r→0r= 0
1.4.
Continuidad de funciones de varias variables
Definici´on 1.4.1. Seaf :D⊂Rn →Runa funci´on definida en el conjunto abierto
D de Rn y sea X
0 ∈D. Se dice que f es una funci´on continua en X0 si,
l´ım
X→X0
f(X) = f(X0).
Observaci´on 1.4.1. .
1. Si no existe f(X0), pero se verifica que el limite existe, l´ım
X→X0
f(X) =l donde
l ∈R, puede prolongarse f por continuidad ampliando el dominio de definici´on de la funci´on f al punto X0 haciendo f(X0) = l. En este caso se dice que la
discontinuidad es evitable.
2. Si l 6= f(X0) se puede redefinir la funci´on en X0 haciendo f(X0) = l y la
funci´on as´ı definida es continua en X0.
3. Se establece que si X0 es un punto aislado de D entonces f es continua en X0.
Ejemplo 1.4.1. Estudie si las funciones,
1. f(x, y) =
(senx)2seny
x2+y2 si (x, y)6= (0,0)
0 si (x, y) = (0,0)
2. g(x, y) = xx32++yy32
son continuas. Estudiar su posible prolongaci´on por continuidad donde no est´en
1.5. EJERCICIOS PROPUESTOS 15
Soluci´on 1. Domf =R2
a) Si (x, y)6= (0,0)
La funci´onf(x, y) es continua, ya que es cociente de funciones continuas.
b) Si (x, y) = (0,0) Se tiene que
l´ım
(x,y)→(0,0)
(senx)2seny
x2 +y2 =(x,yl´ım)→(0,0)
(senx)2
x2
seny y
x2y
x2+y2 =(x,yl´ım)→(0,0)
x2y
x2+y2
y pasando a coordenadas polares,
l´ım
(x,y)→(0,0)
x2y
x2+y2 = l´ımr→0
r3cos2θsenθ
r2 = l´ımr→0r cos
2θ senθ= 0
Entonces f es continua en (0,0).
De a) y b) concluimos que f es continua.
2. Domg =R2−(0,0). Notemos que la funci´on g no est´a definida en (0,0).
Veamos entonces si g se puede prolongar por continuidad al punto (0,0). Para esto, estudiemos el limite de la funci´on g(x, y) en (0,0).
l´ım
(x,y)→(0,0)
x3 +y3
x2 +y2 = l´ımr→0
r3(cos3θ+sen3θ)
r2 = l´ımr→0r(cos
3θ+sen3θ) = 0
Se concluye que g se puede redefinir como
g∗(x, y) =
x3+y3
x2+y2 si (x, y)6= (0,0)
0 si (x, y) = (0,0) de tal manera que es continua.
1.5.
Ejercicios Propuestos
1. Demuestre aplicando la definici´on de limite :
a) l´ım
(x,y)→(0,1)
x2−y2
x2+y2 =−1.
b) l´ım
(x,y)→(0,0)x
2sen(x2+y2) = 0.
c) l´ım
(x,y)→(1,2)((x−1)
2+ (y−2)2) = 0.
1.6. DERIVADAS PARCIALES DE FUNCIONES REALES DE VARIAS VARIABLES 16
a) l´ım
(x,y)→(0,−2)
x3sen(y2−4)
(y+ 2)senx .
b) l´ım
(x,y)→(0,0)
(1−cos(xy))sen(x) x2+y2 .
c) l´ım
(x,y)→(0,0)
exy−1
senx ln(y+ 1).
d) l´ım
(x,y)→(0,0)
tanx seny x2+y2 .
e) l´ım
(x,y)→(0,0)
x2
y−1.
3. Calcule, si existen, los siguientes limites iterados y el limite doble de las fun-ciones:
a) f(x, y) = x
2 −y4
x2+y4 en (0,0)
b) g(x, y) = x
2y2
x4+y4 en (0,0)
c) h(x, y) =y2sen1
x en (0,0) 4. Halle si existe,
a) l´ım
(x,y,z)→(0,0,0)
y2z
x2 +y2+z2 , (x,yl´ım)→(1,1)
Lnx tan(y−1) xy−x−y+ 1
b) l´ım
(x,y,z)→(0,0,0)
y2z
x2 +y2+z2
c) l´ım
(x,y,z)→(0,0,0)
yz x2 +y2+z2
d) l´ım
(x,y,z)→(0,0,0)f(x, y, z) dondef(x, y, z) =
x2 +y2 x≥0
x2 +z2 x <0
1.6.
Derivadas parciales de funciones reales de varias
vari-ables
Definici´on 1.6.1. Seaf :D⊂R2 →Runa funci´on definida en el conjunto abierto
D⊂R2 y P
o = (xo, yo)∈D.
1. La derivada parcial de f con respecto a x en el punto Po denotado por ∂f∂x(Po) ´o D1f(Po), es el limite:
∂f
∂x(xo, yo) = l´ımh→0
f(xo+h, yo)−f(xo, yo)
h
1.6. DERIVADAS PARCIALES DE FUNCIONES REALES DE VARIAS VARIABLES 17
2. La derivada parcial de f con respecto a y en el punto Po denotado por ∂f∂y(Po) ´o D2f(Po), es el limite:
∂f
∂y(xo, yo) = l´ımk→0
f(xo, yo+k)−f(xo, yo)
k
cuando tal limite existe.
La definici´on anterior se puede generalizar de la siguiente manera:
Definici´on 1.6.2. Seaf :U ⊂Rn →Runa funci´on definida en el conjunto abierto
U ⊂ Rn y Q = (a
1, a2, ...an) ∈ U.La i-´esima derivada parcial de f en el punto Q (donde 1≤i≤n) denotado por ∂x∂fi(Q) ´o Dif(Q), es el limite:
∂f ∂xi
(a1, a2, ...an) = l´ım h→0
f(a1, a2, ..ai+h, ...an)−f(a1, a2, ...an)
h
cuando tal limite existe.
La ´ultima expresi´on tambien se puede expresar como: ∂f
∂xi
(Q) = l´ım
h→0
f(Q+h ei)−f(Q)
h dondeei = (0,0, .., |{z}1 i-´esimo lugar
, ...,0,0)
Ejemplo 1.6.1. si
f(x, y) =
x3−y2
1−cosx+y, y 6=cosx−1
0, y=cosx−1
calcule ∂f∂x(0,0) y ∂f∂y(0,0) si existe.
Soluci´on
∂f
∂x(0,0) = l´ımh→0
f(0 +h,0)−f(0,0) h
= l´ım
h→0
h3
1−cosh −0
h
= l´ım
h→0
h2
1−cosh = 2 ∂f
∂y(0,0) = l´ımk→0
f(0,0 +k)−f(0,0) k
= l´ım
k→0
−h2
1−1+k −0
k
= l´ım
h→0
−h2
1.6. DERIVADAS PARCIALES DE FUNCIONES REALES DE VARIAS VARIABLES 18
1.6.1. Interpretaci´on geom´etrica de las derivadas parciales
Sea f : D ⊂ R2 → R una funci´on definida en el conjunto abierto D ⊂ R2 cuya
gr´afica es la superficie:
Graf f ={(x, y, z)∈R3 / z =f(x, y) ∀(x, y)∈D} ⊂R3.
Supongamos que existen ∂f∂x(Po) y ∂f∂y(Po)y donde Po = (xo, yo)∈D.
Figura 1.8:
1. Sea α la curva de intersecci´on del plano y=yo con el gr´afico de f.
La pendiente de la recta secante Ls1 que pasa por P = (x, y, z) y Qo =
(xo, yo, f(xo, yo)) en el plano y=yo es
ms1 =
f(xo+h, yo)−f(xo, yo)
h
entonces cuando h → 0, ms1 → mT1 donde mT1 es la pendiente de la recta
tangente LT1 a la curva α en el punto Qo ∈Graf f. Esto es:
∂f
∂x(xo, yo) = l´ımh→0
f(xo+h, yo)−f(xo, yo)
h =mT1
Luego la ecuaci´on de la recta tangente LT1 es dado por:
z−zo =
∂f
∂x(xo, yo)(x−xo) ∧ y=yo y su forma sim´etrica es:
x−xo =
z−zo ∂f
∂x(xo, yo)
∧ y=yo
El vector direccional de la recta tangente LT1 es −→a = (1,0, ∂f
1.6. DERIVADAS PARCIALES DE FUNCIONES REALES DE VARIAS VARIABLES 19
2. Sea β la curva de intersecci´on del planox=xo con el gr´afico def.
La pendiente de la recta secante Ls2 que pasa por P
0 = (x, y, z) y Q
o =
(xo, yo, zo) en el planox=xo es
ms2 =
f(xo, yo+k)−f(xo, yo)
k
entonces cuando k → 0, ms2 → mT2 donde mT2 es la pendiente de la recta
tangente LT2 a la curva β en el punto Qo∈Graf f. Esto es:
∂f
∂y(xo, yo) = l´ımk→0
f(xo, yo+k)−f(xo, yo)
k =mT2
Luego la ecuaci´on de la recta tangente LT2 es dado por:
z−zo =
∂f
∂y(xo, yo)(x−xo) ∧ x=xo y su forma sim´etrica es:
y−yo =
z−zo ∂f
∂y(xo, yo)
∧ x=xo
El vector direccional de la recta tangente LT2 es − →
b = (0,1,∂f∂y(xo, yo)).
1.6.2. Plano tangente
El plano tangente a la superficie S : z = f(x, y) en el punto (xo, yo, f(xo, yo))
determinado por las rectas tangentes LT1 y LT2 es el plano con vector normal
N =−→a ×−→b =
i j k
1 0 ∂f
∂x(xo, yo)
0 1 ∂f∂y(xo, yo)
= (−
∂f
∂x(xo, yo),− ∂f
∂y(xo, yo),1)
cuya ecuaci´on est´a dada por:
((x, y, z)−(xo, yo, f(xo, yo)))N = 0
luego
∂f
∂x(xo, yo)(x−xo) + ∂f
∂y(xo, yo)(y−yo)−(z−zo) = 0
1.7. FUNCIONES DIFERENCIABLES 20
Figura 1.9:
Soluci´on
Debemos hallar la ecuaci´on del plano tangente P en el punto Qo = (xo, yo, zo)
(ver el grafico). En este caso s´olo nos faltar´ıa hallar el punto Qo que es un punto
que pertenece a la superficie S y al plano P, dado que se puede considerar como vector normalN en el puntoQo al vector (3,8,−5) que es el vector normal del plano
3x+ 8y−5z = 10. Este ´ultimo resultado se debe a que ambos planos deben ser paralelos entonces sus vectores normales son paralelos.
Por otro lado N = (−∂f∂x(xo, yo),−∂f∂y(xo, yo),1) = (−2xo,−2yo,1).
Como N//(3,8,−5) ⇒ N = k(3,8,−5) ⇒ (−2xo,−2yo,1) = k(3,8,−5),
de donde se obtiene k=−1/5, luego xo = 103 y yo = 45.
Dado que Qo ∈ S : z =x2 +y2 se tiene entonces zo = x2o+y2o, luego zo = 10073.
Asi obtenemosQo = (103,45,10073)
Finalmente la ecuaci´on del plano tangenteP es:
((x, y, z)−( 3 10,
4 5,
73
100)).(3,8,−5) = 0 Asi desarollandolo se tiene:
P : 3x+ 8y−5z= 73
20
1.7.
Funciones diferenciables
Intuitivamente, que una funci´on z=f(x,y) sea diferenciable en un punto (x0, y0, z0),
1.7. FUNCIONES DIFERENCIABLES 21
S:z =f(x, y), es decir que la superficie no est´e arrugada en ese punto. En seguida definamos formalmente cuando una funci´on es diferenciable en un punto dado. Definici´on 1.7.1. Sea f : D ⊂ Rn → R y a ∈ D. Diremos que f es diferenciable en el puntoa ∈Dcuando existen las derivadas parciales ∂f
∂x1
(a), ∂f ∂x2
(a), ..., ∂f ∂xn
(a)
y adem´as de esto, para todo vector V = (α1, α2, ..., αn) tal que a+V ∈D se tiene
f(a+V) = f(a) + ∂f ∂x1
(a)α1+ ∂f
∂x2
(a)α2 +...+ ∂f
∂xn
(a)αn+r(V)
donde l´ım
V→0
r(V)
||V || = 0
A r(V) se le llama resto.
Ejemplo 1.7.1. Dada la funci´on f(x, y) =
x2y−y3
x2+y2 , (x, y)6= (0,0)
0, (x, y) = (0,0)
¿Es f diferenciable en (0,0)?
Figura 1.10: gr´afica de la funci´onf(x, y) =xx22y+−yy23
Soluci´on Calculemos:
fx(0,0) = l´ım h→0
f(h,0)−f(0,0)
h = l´ımh→0 0−0
h2 −0
h = 0 fy(0,0) = l´ım
k→0
f(0, k)−f(0,0)
h = l´ımk→0
−k3 k2 −0
k =−1 l´ım
(h,k)→(0,0)
r(h, k)
√
h2+k2 = (h,kl´ım)→(0,0)
f(h, k)−f(0,0)√−fx(0,0)h−fy(0,0)k
h2+k2
= l´ım
(h,k)→(0,0)
2k h2
(h2+k2)√h2+k2
= l´ım
r→0
2r3cos2θ senθ
r3
= cosθ sen(2θ)
1.8. LA DIFERENCIAL 22
Teorema 1.7.1. Si la funci´on f : D ⊂ Rn → R definida en un conjunto abierto
D⊂Rn es diferenciable en el punto P ∈D entonces f es continua en P.
Ejemplo 1.7.2. Sea
f(x, y) =
x2y
x4+y2, (x, y)6= (0,0)
0, (x, y) = (0,0)
¿Es f diferenciable en (0,0)?
Soluci´on
Primero verifiquemos que si f es o no continua en (0,0). l´ım
(x,y)→(0,0)
x2y
x4+y2 =
y=x2
à = l´ım
x→0
x4
x4+x4 =
1
2 6= 0 =f(0,0) De este ´ultimo resultado se concluye quef no es continua en (0,0).
Por el resultado equivalente del ´ultimo teorema se tiene quef no es diferenciable en (0,0).
Teorema 1.7.2. Condici´on suficiente de diferenciabilidad
Sea f : D ⊂ Rn → R una funci´on definida en un conjunto abierto D ⊂ Rn y
a∈D. Si f es continua en a y las funciones ∂f
∂xi
(X) son continuas en a para cada
i= 1,2,3, ..., n entonces f es diferenciable en a.
Ejemplo 1.7.3. Sea f(x, y) =sen(x−2y), ¿es f diferenciable?
Soluci´on
Cuando simplemente se nos pide que f sea diferenciable eso quiere decir que f debe ser diferenciable en todos los puntos de su dominio. En este caso el dominio de f es Domf =R2.
Notemos que f es continua dado que es una funci´on trigonom´etrica. De igual manera las derivadas parciales fx(x, y) = cos(x−2y) y fy(x, y) = −2cos(x−2y)
son continuas. Por el ´ultimo teorema se concluye que f es diferenciable.
1.8.
La diferencial
Sea f : D ⊂ Rn → R una funci´on diferenciable en el conjunto abierto D ⊂ Rn.
Entonces para cadaX ∈D tenemos f(X+V) = f(X) + ∂f
∂x1
(X)α1+
∂f ∂x2
(X)α2+...+
∂f ∂xn
1.8. LA DIFERENCIAL 23
donde l´ım
V→0
r(V)
||V || = 0. Ala parte lineal enα1, .α2, ..., αn de esta expresi´on se le llama
diferencialde la funci´on f enX = (x1, x2, ..., xn) y se denota por df(X). As´ı
df = ∂f ∂x1
α1+
∂f ∂x2
α2+...+
∂f ∂xn
αn
Observemos que si f(x1, x2, ..., xn) =x1 se obtiene df(x1, x2, ..., xn) = dx1 = α1, si
f(x1, x2, ..., xn) = x2 se obtiene df(x1, x2, ..., xn) = dx2 =α2 y si f(x1, x2, ..., xn) =
xn se obtiene df(x1, x2, ..., xn) = dxn=αn. Luego escribimos
df = ∂f ∂x1
dx1+
∂f ∂x2
dx2+...+
∂f ∂xn
dxn.
Volviendo a la definici´on de la diferenciabilidad de la funci´onf podemos escribir f(X+V) =f(X) +df(X) +r(V)
ComoV es peque˜no se tiene
f(X+V)−f(X)≈df(X) Observaci´on 1.8.1. .
Error relativo: ∆ff ≈ dff
Error porcentual: ∆ff 100 %≈ dff 100 %
Ejemplo 1.8.1. La potencia el´ectrica est´a dada por P = E2
R, donde E es el voltaje y R es la resistencia. Aproxime el m´aximo porcentaje de error posible al calcular la potencia para un voltaje de 200 voltios y una resistencia de 4 000 ohms, si los posibles errores en las medidas de E y R son de 2 y 3 %, respectivamente.
Soluci´on Se tiene que d E
E = 0,02 y d RR = 0,03.
Para resolver este problema usemos la diferencial total deP = E2
R y notemos que
P est´a en funci´on de E y R.
d P = 2 E Rd E −
E2
R2d R
d P
P = 2 E
P Rd E− E2
P R2d R
= 2E R E2Rd E−
E2R
E2R2d R
= 2d E E −
1.9. DERIVADAS PARCIALES DE ORDEN SUPERIOR 24
Entonces
¯ ¯ ¯ ¯d PP
¯ ¯ ¯
¯ ≤ 2
¯ ¯ ¯ ¯d EE
¯ ¯ ¯ ¯+ ¯ ¯ ¯ ¯d RR
¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯d PP
¯ ¯ ¯
¯ ≤ 2 0,02 + 0,03 = 0,07
por lo tanto, el m´aximo porcentaje de error posible al calcular la potencia el´ectrica es: 7 %
1.9.
Derivadas parciales de orden superior
Sea la funci´on f : D ⊂ R2 → R definida en el conjunto abierto D ⊂ R2. Si f
es diferenciable, entonces existen las derivadas parciales ∂f∂x y ∂f∂y en cualquier punto (x, y)∈D. Ahora consideremos las funciones
∂f
∂x :D⊂R
2 →R , ∂f
∂y :D⊂R
2 →R
de modo que para cada (x, y) ∈ D se les asocia las derivadas parciales ∂f∂x(x, y) y
∂f
∂y(x, y) respectivamente.
Puede ocurrir a su vez que estas funciones tengan las derivadas parciales ∂
∂x( ∂f ∂x) ,
∂ ∂y(
∂f ∂y) ,
∂ ∂x(
∂f ∂y) ,
∂ ∂y(
∂f ∂x)
en un punto (x, y)∈ D. En este caso diremos que estas son las derivadas parciales de segundo orden de la funci´onf y escribiremos:
∂ ∂x(
∂f ∂x) =
∂2f
∂x2 = fxx = D11f à 2da derivada parcial respecto ax
∂ ∂y(
∂f ∂y) =
∂2f
∂y2 = fyy = D22f à 2da derivada parcial respecto a y
∂ ∂x(
∂f ∂y) =
∂2f
∂x ∂y = fyx = D21f à 2da derivada parcial respecto a y y a x
∂ ∂y(
∂f ∂x) =
∂2f
∂y ∂x = fxy = D12f à 2da derivada parcial respecto a x y a y
Teorema 1.9.1. Teorema de Schwarz(igualdad de derivadas cruzadas). Sea la funci´on f : D ⊂ R2 → R definida en el conjunto abierto D ⊂ R2 y
1.9. DERIVADAS PARCIALES DE ORDEN SUPERIOR 25
1. existen fx , fy en un entorno de a
2. existen fx y en un entorno de a y es continua en a.
Entonces existe fy x(a) y fx y(a) = fy x(a).
NOTA 1.9.1. El teorema es v´alido para derivadas de ordenes mayores, si se verifi-can las condiciones del teorema para las derivadas sucesivas. Si se verifica el teorema de Schwarz s´olo importa el n´umero de veces que se deriva respecto a cada variable. As´ı por ejemplo fxxy =fxyx =fyxx
Ejemplo 1.9.1. Sea
f(x, y) =
x sen y−y sen x
x2+y2 , (x, y)6= (0,0)
0, (x, y) = (0,0)
¿Se cumple, fx y(0,0) =fy x(0,0)?
Soluci´on
fx y(0,0) =
∂
∂yfx(0,0) = l´ımk→0
fx(0, k)−fx(0,0)
k (1.1)
fy x(0,0) =
∂
∂xfy(0,0) = l´ımh→0
fy(h,0)−fy(0,0)
h (1.2)
Ahora calculemos fx(0, k) y fy(h,0)
fx(0, k) = l´ım h→0
f(h, k)−f(0, k) h
= l´ım
h→0
h sen k−k sen h
h(h2+k2) usando L
0Hopitalˆ (para h)se tiene:
= l´ım
h→0
sen k−k cos h 3h2+k2
= sen k−k k2
Tambi´en se tiene:
fx(0,0) = l´ım h→0
f(h,0)−f(0,0)
h = l´ımh→0
0−0 h = 0 fy(h,0) = l´ım
k→0
f(h, k)−f(h,0) k
= l´ım
k→0
h sen k−k sen h
k(h2 +k2) usando L
0Hopitalˆ (para k)se tiene :
= l´ım
k→0
h cos k−sen h h2+ 3k2
1.10. DERIVACI ´ON IMPLICITA 26
Tambi´en se tiene:
fy(0,0) = l´ım k→0
f(k,0)−f(0,0) k = l´ımk→0
0−0 k = 0 De (2.1);
fx y(0,0) = l´ım k→0
sen k−k k2 −0
k = l´ım
k→0
sen k−k
k3 usando L
0Hopital se tieneˆ :
= l´ım
k→0
cos k−1 3k2
= −1
6 De (2.2);
fy x(0,0) = l´ım h→0
h−sen h h2 −0
h = l´ım
h→0
h−sen h
h3 usando L
0Hopital se tieneˆ :
= l´ım
h→0
1−cos h 3h2
= 1 6 Por lo tanto,fx y(0,0)6=fy x(0,0)
1.10.
Derivaci´
on implicita
Definici´on 1.10.1. Sea la funci´onF :U ⊂R3 →Rdefinida en el conjunto abierto
U ⊂ R3. Se dice que la ecuaci´on F(x, y, z) = 0 define z implicitamente como una
funci´on dexey, cuando existe una funci´onf :D⊂R2 →Rdefinida en el conjunto
abierto D⊂R2 tal que:
F(x, y, z) = 0 ⇔ z =f(x, y) , ∀(x, y)∈D
Ejemplo 1.10.1. La ecuaci´on x2 +y2 +z2 −8 = 0 representa implicitamente las
funciones z =f(x, y) =p8−x2−y2 ´o z =g(x, y) = −p8−x2 −y2.
La ecuaci´on x2+y2+z2+ 1 = 0no representa implicitamente ninguna funci´on.
1.11. FUNCIONES COMPUESTAS. REGLA DE LA CADENA 27
Teorema 1.10.1. Teorema de la funci´on implicita.
Sea F : U ⊂ Rn+1 → R una funci´on definida en un conjunto abierto U por
z = F(X) para todo X = (x1, x2, ..., xn, y) ∈ U, de clase Ck (esto es, F tiene derivadas parciales continuas hasta de orden k > 1), y que cumple las siguientes condiciones:
Si P = ( ˙x1,x˙2, ...x˙n, y)∈Rn+1 un punto talque F(P) = 0 y ∂F∂y(P) 6= 0 entonces: la ecuaci´on F(X) = 0 puede resolverse para y en t´erminos de x1, x2, ..., xn y definir as´ı una funci´ony=f(x1, x2, ...xn)dentro de la bolaB(( ˙x1,x˙2, ...x˙n), δ)⊂Rn la cual tiene derivadas parciales continuas en B(( ˙x1,x˙2, ...x˙n), δ) y que se pueden calcularse con las f´ormulas:
∂f ∂xi
(x1, x2, ..., xn) =− ∂F
∂xi(x1, x2, ..., xn, y)
∂F
∂y(x1, x2, ..., xn, y)
, (x1, x2, ..., xn)∈B(( ˙x1,x˙2, ...x˙n), δ)
Ejemplo 1.10.2. Dada la ecuaci´on z+zy =xy una de sus soluciones esP(10,3,2). ¿es cierto que cerca de (10,3), z es funci´on de las otras variables x, y? ¿Cu´al es la derivada de esta funci´on implicita?
Soluci´on
Sea F(x, y, z) =z+zy−x ∀(x, y, z)∈R3− {(a,0,0)} con a∈R
Ahora verifiquemos las condiciones del teorema de la funci´on implicita: 1. F(10,3,2) = 0
2. ∂F
∂z = 1 +y zy−1 ⇒ ∂F∂z(10,3,2) = 1−3.22 6= 0
Como se cumple las condiciones del teorema de la funci´on implicita,z es funci´on de las variables x ey, es decir, existe f(x, y) = z , (x, y)∈B((10,3), δ). Luego
∂f
∂x = −
∂F ∂x ∂F ∂z
= − −1 1+y zy−1
∂f
∂y = −
∂F ∂y ∂F ∂z
= − zyln z
1+y zy−1
1.11.
Funciones compuestas. Regla de la cadena
1.12. DERIVADA DIRECCIONAL 28
las derivadas parciales dew respecto a las variables independientes r y s, se usa la siguente regla, llamada regla de la cadena.
∂w ∂r = ∂w ∂x ∂x ∂r + ∂w ∂y ∂y ∂r ; ∂w ∂s = ∂w ∂x ∂x ∂s + ∂w ∂y ∂y ∂s
En el caso de que x e y fueran funciones de una sola variable independiente t, se escribir´ıa as´ı
d w d t =
∂w ∂x
d x d t +
∂w ∂y
d y d t
x //t
w > > ~ ~ ~ ~ ~ ~ ~ ~ > > ~ ~ ~ ~ ~ ~ ~ ~ Ã Ã @ @ @ @ @ @ @ @
y //t
Ejemplo 1.11.1. Sea f : R3 → R suficientemente diferenciable. Se considera la
funci´on
u(x) = f(x, ϕ(x), ψ(x))
con ϕ yψ sufientemente derivables. Halle d2u dx2
Soluci´on
Consideremosu(x) = f(x, y, z) dondey=ϕ(x) y ψ(x) = z. Luego:
ux =fx+fyϕ0+fzψ0
x f ? ? ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ / / Â Â > > > > > > >
> y //x
z //x
uxx =
∂
∂x(fx) + ∂ ∂x(fyϕ
0) + ∂
∂x(fzψ
0)
= fxx+fxyϕ0+fxzψ0+ (fyx+fyyϕ0 +fyzψ0)ϕ0+fyϕ00
+(fzx+fzyϕ0+fzzψ0)ψ0+fzψ00
= fxx+ 2fxyϕ0 + 2fxzψ0+fyy(ϕ0)2+ 2fzyϕ0ψ0+fyϕ00+fzz(ψ0)2+fzψ00
1.12.
Derivada direccional
Las derivadas parcialesfx(x, y) yfy(x, y), representan, respectivamente, la
1.12. DERIVADA DIRECCIONAL 29
hallar la pendiente en cualquier otra direcci´on se utilizan las derivadas direccionales. Es decir, las derivadas parciales nos dan una medida de la variaci´on de una funci´on solamente en la direcci´on de cada eje coordenado. Es natural buscar un concepto m´as general de derivada a fin de que nuestras consideraciones no queden restringidas a las direcciones particulares de los ejes coordenados y nos permita estudiar la raz´on de incrementos en una direcci´on cualquiera. La derivada direccional responde a este prop´osito.
Definici´on 1.12.1. Sea f : U ⊂ Rn → R una funci´on definida en un conjunto abierto U ⊂ Rn y P
o ∈ U. Sea −→v un vector unitario dado de Rn. Se define la
derivada def enPo, en la direcci´on del vector−→v, denotado porD−→vf(Po) ´o ∂∂f−→v(Po) como el limite
D−→vf(Po) = l´ım
h→0
f(Po+h−→v )−f(Po)
h
si este limite existe.
1.12.1. Interpretaci´on geom´etrica de las derivadas direccionales
Sea f : U ⊂ R2 → R una funci´on definida en el conjunto abierto D ⊂ R2 cuya
gr´afica:
Graf f ={(x, y, z)∈R3 / z =f(x, y) ∀(x, y)∈U} ⊂R3
es una superficie S ⊂ R3. Sea P
o = (xo, yo) ∈ D y −→v = (v1, v2) un vector unitario
Figura 1.11:
de R2, entonces la recta L ={P