III
bloque
Galileo (1564-1642)
Fermat (1601-1665)
Pascal (1623-1662)
Jacob Bernouilli (1654-1705)
Moivre (1667-1754)
Bayes (1702-1761)
Laplace (1749-1827)
De Morgan (1806-1871)
Se publica el primer libro importante Juegos de azar que Cardanoescribió en 1565.(1663).
Pascalpublica el Tratado sobre el triángulo aritmético, la más importante contribución realizada hasta entonces en el campo de la combinatoria.(1665).
Moivrees el primero en enunciar con autoridad el teorema de la multiplicación en Doctrina de las posibilidades.(1711).
Jakob Bernouillienuncia la ley de los grandes números en la obra El arte de predecir,publicada póstumamente.(1713).
Laplaceenuncia la regla para calcular probabi-lidades que lleva su nombre.(1812).
Poisson generaliza la ley de los grandes números.
(1837).
Kolmogorovaxiomatiza la teoría de la probabilidad.
(1937).
Galileocrea la teoría de la medida de errores y pone las bases para el nacimiento de la estadísti-ca. Su obra sobre estadística se publica 14 años después de su muerte.(1656).
Thomas Bayesenuncia el teorema que lleva su nombre.(1763).
Markovcompleta la prueba que generaliza el teorema central del límite.(1887).
Wiener,fundador de la cibernética, formula el
con-•
1605• Sale a la venta la 1.ª edición de D. Quijote de la Mancha.•
1868•Se produce en España la Revolución de 1868 —apodada La Gloriosa— que derrocará a la reina Isabel II.1600
1650
1700
1750
1800
1850
1900
Cantellienuncia la ley fuerte de los grandes números.(1917).
•
1621• Felipe IV se convierte en rey de España y Portugal.•
1762•Inglaterra declara la guerra a España, temerosa del Pacto de Familia entre los Borbones franceses y españoles.•
1665• Comienza el reinado de Carlos II de España.•
1687• Publicación de Philosophiae Naturalis Principia Mathematica,de Isaac Newton.•
1700• Muere Carlos II de España y comienza la Guerra de Sucesión Española.•
1814• Invención de la locomotora de vapor: George Stephenson.Epígrafes
11. Probabilidad
12. Inferencia estadística. Estimación por intervalos
13. Contraste de hipótesis
der calcular riesgos.
Esta teoría está íntimamente relacionada con la estadística que se puede dividir en estadística descriptiva, que recoge, organiza y analiza los datos de un estudio, y estadística inferencial, que con el estudio de muestras intenta inferir o deducir las características de toda la población.
Esta rama de las matemáticas da respuesta a muchas necesidades que la socie-dad actual plantea. Por ejemplo:
Control fiscal de los gobiernos: realización de censos, necesaria para estas actividades de control.
Investigación de mercados:permite saber si un producto cualquiera será bien acogido en el mercado antes de su lanzamiento.
Control de calidad:permite medir la calidad de un producto, compararla con ciertos requisitos y tomar decisiones correctivas si hay diferencias entre el funcio-namiento real y el esperado.
Control de la agricultura y la pesca:con estudios estadísticos aplicados a es-tos sectores se puede estimar el rendimiento obtenido en una cosecha, o encon-trar bancos de peces.
Avances en medicina e investigación farmacológica:la estadística es impres-cindible para probar nuevos tratamientos en grupos de pacientes, o bien para obtener conclusiones sobre ciertas enfermedades.
Estudio de procesos estocásticos (aleatorios):se puede tener una mejor com-prensión de fenómenos de comportamiento aleatorio, como la meteorología, fí-sica nuclear, campañas de seguridad, etc.
Avances en informática:hoy en día, los sistemas de detección de spam a través de Internet se basan en la teoría de Bayes.
Estadística y
Estadística y
pr
pr
obabilidad
obabilidad
Boole (1815-1864)
Florence Nightingale (1820-1910)
Markov (1856-1922)
Pearson (1857-1936)
Borel (1871-1956)
Lebesgue (1875-1941)
11
Probabilidad
El tema comienza con la exposición de los conceptos de espacio mues-tral y de los sucesos asociados a un experimento aleatorio, y con las operaciones entre ellos: contrario, unión, intersección y diferencia.
Luego se exponen la ley de los grandes números, la regla de Laplace y las propiedades de la probabilidad. Se estudian, como estrategia de re-solución de problemas, los diagramas cartesianos, las tablas de contin-gencia y, sobre todo, los diagramas en árbol.
A través del estudio de los diagramas en árbol, se define la probabili-dad condicionada como las segundas y sucesivas ramas de un árbol. Esto da pie a estudiar la probabilidad de un camino, que es la regla del producto o de la probabilidad compuesta. Cuando se estudia la proba-bilidad de varios caminos, se infiere la ley de la probaproba-bilidad de la su-ma o de la probabilidad total. Por último, como aplicación de la proba-bilidad total, se estudia el teorema de Bayes.
Organiza tus ideas
Probabilidad
una medida del azar
estrategias
compuesto simple
experimento aleatorio espacio
muestral
• regla del producto • regla de la suma • teorema de Bayes • diagrama
cartesiano • diagrama
en árbol • tablas de
contingencia
• ley de los grandes números
• regla de Laplace
es
se asocia con se calcula con
como
en éstos se usa la
es éstos se usa la es un
■
Piensa y calcula
En una baraja española de 40 cartas, ¿cuántas figuras hay?
1. Operaciones con sucesos
1.1. Espacio muestral
Ejemplo
Experimento de lanzar un dado de seis caras.
Espacio muestral o suceso seguro: E = {1, 2, 3, 4, 5, 6}
Sucesos elementales: {1}, {2}, {3}, {4}, {5} y {6}
Sucesos: A = {1, 3, 5}, B = {2, 4, 6}, C = {5, 6} …
Suceso imposible:
Ö
= {obtener 8 o 9}
1.2. Operaciones con sucesos
Ejemplo
En el experimento de lanzar un dado de seis caras.
Sea A = {1, 3, 5, 6}
ò
A
—= {2, 4}
Ejemplo
En el experimento de lanzar un dado de seis caras.
Sea A = {1, 2, 3, 4}, B = {2, 4, 6}
ò
A
傼
B = {1, 2, 3, 4, 6}
Ejemplo
En el experimento de lanzar un dado de seis caras.
Sea A = {1, 2, 3, 4}, B = {2, 4, 6}
ò
A
傽
B = {2, 4}
c) Intersección de sucesos
La
intersección de dos sucesos A y B
es el suceso formado por todos los
su-cesos elementales comunes a A y a B, es decir, por aquellos que están en los
dos sucesos a la vez. Se representa por A
傽
B
b) Unión de sucesos
La
unión de dos sucesos A y B
es el suceso formado por todos los sucesos
elementales de A y de B. Se representa por A
傼
B
a) Suceso contrario
El
suceso contrario de un suceso A
está formado por todos los sucesos
ele-mentales que no están en A. Se representa por A
—o por A
CEl
espacio muestral asociado a un experimento aleatorio
está formado por
el conjunto de todos los resultados que se pueden presentar.
En un espacio muestral
E
se definen:
•
Suceso elemental
es cada uno de los resultados del espacio muestral.
•
Suceso
es un conjunto de sucesos elementales. Se representan por letras
mayúsculas, poniendo sus elementos entre llaves y separados por comas.
•
Suceso seguro
es el que siempre se presenta y es igual al espacio muestral
E
•
Suceso imposible
es el que nunca se presenta. Se representa por el símbolo
Ö
1 A
C E
3 5
2
B 4 6
1 E
3 5
2 4 6
1
A A–
E
3 2
5 6 4
1 A
B A 傼 B
E
3 5
2 4 6
1 A
B
A 傽 B E
3 5
2 4 6
Sucesos compatibles e incompatibles
Ejemplo
En el experimento de lanzar un dado de seis caras.
Si A = {1, 2, 3}, B = {1, 3, 5}
ò
A
傽
B = {1, 3}
ò
A y B son compatibles.
Si A = {1, 3, 5}, B = {2, 4}
ò
A
傽
B =
Ö ò
A y B son incompatibles.
Ejemplo
En el experimento de lanzar un dado de seis caras.
Sea A = {1, 2, 3, 4}, B = {2, 4, 6}
ò
A – B = {1, 3}
1.3. Leyes de Morgan
a) Contrario de la unión:
es la intersección de los contrarios:
= A
—»
B
—Ejemplo
En el experimento de lanzar un dado de seis caras.
Si A = {1, 2, 3}, B = {1, 3, 5}
Primer miembro: A
傼
B = {1, 2, 3, 5}
ò
= {4, 6}
Segundo miembro: A
—= {4, 5, 6}, B
—= {2, 4, 6}
ò
A
—»
B
—= {4, 6}
b) Contrario de la intersección:
es la unión de los contrarios:
= A
—傼
B
—Ejemplo
En el experimento de lanzar un dado de seis caras.
Si A = {1, 2, 3}, B = {1, 3, 5}
Primer miembro: A
傽
B = {1, 3}
ò
= {2, 4, 5, 6}
Segundo miembro: A
—= {4, 5, 6}, B
—= {2, 4, 6}
ò
A
—«
B
—= {2, 4, 5, 6}
A
»
B
A
»
B
A
«
B
A
«
B
d) Diferencia de sucesos
El suceso
A menos B
es el suceso formado por todos los sucesos elementales
de A y que no están en B. Se representa por A – B, A | B, o A \ B
Dos sucesos son
compatibles
si se pueden presentar al mismo tiempo, es
de-cir, si A
傽
B
? Ö
; y son
incompatibles
si no se pueden presentar al mismo
tiempo, es decir, si A
傽
B =
Ö
1. Sea el experimento de lanzar un dado de quinielas. Halla: a) el espacio muestral o suceso seguro.
b) los sucesos elementales.
2. En el experimento de lanzar un dado de seis caras nu-meradas del 1 al 6, halla:
a) el espacio muestral o suceso seguro.
b) el suceso A, formado por los números impares. c) el suceso B, formado por los números primos. d) el suceso C, formado por los números pares. e) ¿A y B son compatibles o incompatibles?
f ) ¿A y C son compatibles o incompatibles? g) ¿B y C son compatibles o incompatibles?
3. Sean E = {1, 2, 3, 4, 5, 6, 7, 8, 9 10, 11, 12}, A = {1, 3, 5, 7, 9, 11}, B = {2, 3, 5, 7, 11}. Calcula: a) A 傼B b) A 傽B
c) A— d) B—
4. Sean E = {1, 2, 3, 4, 5, 6, 7, 8},A = {1, 3, 5, 7}, B = {2, 3, 5, 7}. Calcula:
a) A – B b) B – A
c) Comprueba la ley de Morgan: = A—傽—B
d) Comprueba la ley de Morgan: = A—傼—B A »B
A «B
●
Aplica la teoría
2 A
B
A 傽 B E
4 6
1 3 5
A
B E
2 4 6
1 3 5
1 A
3
2 4 B
A – B E
6 5
Equivalencia de la diferencia
■
Piensa y calcula
Se lanzan dos dados de seis caras. ¿Qué suma de puntos tiene la máxima probabilidad?
2. Regla de Laplace
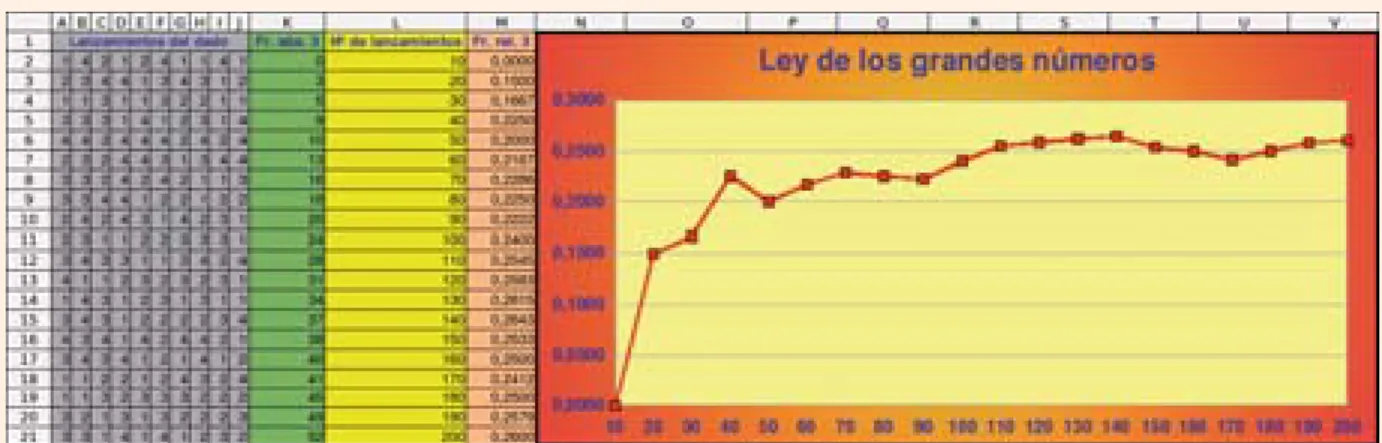
2.1. Ley de los grandes números
Ejemplo
Se repite muchas veces el experimento de lanzar al aire una chincheta y se
anota el número de veces que queda con la punta hacia arriba.
Se puede inferir que: P(
) = 2/3
2.2. Regla de Laplace
Ejercicio resuelto
Halla la probabilidad de obtener un número primo al lanzar un dado de 6 caras.
ò
P(A)
= = =
0,5
2.3. Propiedades de la probabilidad
Ejercicio resuelto
Se sabe que P(A) = 1/3, P(B) = 2/3 y P(A
傽
B) = 1/4. Calcula P(A
傼
B)
P(A
傼
B)
= + – =
= =
3
4
9
12
4 + 8 – 3
12
1
4
2
3
1
3
2
a) La probabilidad del suceso seguro es uno: P(E) = 1
b) La probabilidad del suceso imposible es cero: P(Ø) = 0
c) La probabilidad de cualquier suceso está comprendida entre cero y uno:
0
Ì
P(A)
Ì
1
d) La probabilidad del suceso contrario es P(A
—) = 1 – P(A)
e) Si los sucesos A y B son incompatibles: P(A
傼
B) = P(A) + P(B)
f ) Si los sucesos A y B son compatibles: P(A
傼
B) = P(A) + P(B) – P(A
傽
B)
1
2
3
6
° ¢ £
Espacio muestral: E = {1, 2, 3, 4, 5, 6}
Suceso A = {2, 3, 5}
1
La
regla de Laplace
dice que la probabilidad de un suceso A, de un espacio
muestral E, formado por sucesos elementales
equiprobables
es igual al número
de casos favorables dividido por el número de casos posibles:
Nº de casos favorables al suceso A
P(A) = ——————————————
Nº de casos posibles
La
ley de los grandes números
dice que la frecuencia relativa de un suceso
tiende a estabilizarse hacia una constante a medida que se repite el
experi-mento muchas veces.
La
probabilidad
de un suceso es la constante a la que se aproxima la
frecuen-cia relativa cuando el experimento se repite muchísimas veces.
Nº de lanzamientos
N
10
20
30
40
50
60
70
80
90
100
…
Frecuencia absoluta
n
8
12
20
30
33
37
46
55
59
67
…
Frecuencia relativa
f
0,8
0,6
0,67 0,75 0,66 0,62 0,66 0,69 0,66 0,67
…
Sucesos equiprobables Los sucesos elementales de un es-pacio muestral son equiprobables
si tienen la misma posibilidad de presentarse. Solo en estos casos se puede aplicar la regla de La-place.
Estrategia de resolución de problemas
En los problemas de probabilidad, se debe escribir siempre el espa-cio muestral y el suceso del que se tiene que calcular la probabi-lidad.
P(A 傼B 傼C) = P(A) + P(B) + + P(C) – P(A 傽B) – P(A 傽C) – – P(B 傽C) + P(A 傽B 傽C)
3 –l4 = 4 ab/c
1 –
3 ab/c
2 + 3 ab/c
1
10 20 30 40 50 60 70 80 90 100 0,60
0,65 0,70 0,75 0,80 0,85
Número de tiradas
Lanzamiento de chinchetas
Fr
ecuencia r
e
lativa
E
A B
2.4. Diagrama cartesiano
Ejercicio resuelto
Calcula la probabilidad de que al lanzar dos dados, la suma de los números
obtenidos sea 10. ¿Qué suma es la más probable?
La suma más probable es 7, porque es la que más veces se repite.
2.5. Diagrama en árbol
Ejemplo
Calcula la probabilidad de que al lanzar dos monedas, las dos sean cara.
2.6. Tabla de contingencia
Ejercicio resuelto
En un centro educativo hay 200 alumnos
de bachillerato. De los 120 alumnos de 1º,
62 son chicas, y en 2º hay 36 chicos.
Cal-cula la probabilidad de que, elegido un
alumno al azar, sea una chica de 2º curso.
Se construye la tabla de contingencia del
margen, escribiendo en primer lugar los
datos conocidos, los que están en rojo, y
luego se completa el resto.
4
Una
tabla de contingencia
es una tabla que permite organizar los elementos
de una población según dos características. Se llama tabla de contingencia
porque permite calcular todas las posibilidades o contingencias.
Un
diagrama en árbol
es un gráfico que nace de un tronco, cuyos trazos se
van ramificando como un árbol. Se llama así porque está formado de ramas.
Una
rama
es cada una de las flechas del diagrama. Siempre se debe escribir en
ellas la probabilidad, que corresponde a un experimento simple.
Un
camino
es un conjunto de ramas que van desde el principio al final.
3
Un
diagrama cartesiano
es una tabla de doble entrada, que tiene utilidad en
algunos experimentos compuestos formados por dos simples. En la fila
supe-rior se colocan los sucesos elementales de un experimento simple, y en la
co-lumna de la izquierda, los sucesos elementales del otro experimento simple.
5. Se toman cuatro cartas diferentes de una baraja, dos cincos, un seis y un siete. Las cartas se ponen boca aba-jo sobre una mesa y se mezclan al azar. Determina la probabilidad de que, al darles la vuelta, todas las cartas estén ordenadas en orden creciente si los dos cincos son indistinguibles.
6. Se lanzan dos dados. Calcula la probabilidad de cada uno de los siguientes sucesos:
a) A = Se obtiene cinco en alguno de los dados. b) B = Se obtiene un doble (los dos dados presentan la
misma puntuación).
c) A 傽B d) A 傼B
●
Aplica la teoría
P(Chica de 2º)
= = =
11
0,55
20
44
80
1º
Chicos
58
Chicas
62
Total curso
120
2º
36
44
80
Total chicos/as
94
106
200
1 2 3 4 5 61 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12 10
10
10 7
7
7
7
7
7
P(10) = =
P(7) = = 1 6 6 36
1 12 3 36
Ejemplo
Árbol del lanzamiento al aire de una moneda dos veces.
P(CC) = · = 1 4 1 2 1 2
CC C
CX X
XC C
C
X
XX X
1/2
1/2 1/2
1/2 1/2
■
Piensa y calcula
a) Halla la probabilidad de sacar una carta de copas al extraer una carta de una baraja española de 40 cartas.
b) La carta de copas extraída se deja fuera, y se extrae otra carta. Halla la probabilidad de que esta segunda carta también sea de copas.
3. Probabilidad condicionada
3.1. Sucesos dependientes e independientes
Ejercicio resuelto
Una urna tiene 4 bolas rojas y 5 verdes. Se extrae una bola, se observa el color
y se vuele a introducir; luego se extrae otra bola. ¿Cuál es la probabilidad de
que las dos sean rojas?
P(RR) = P(R) · P(R/R) =
·
=
= 0,20
Cuando se extraen dos bolas de una urna “
con devolución
”, al sacar la segunda
bola se tienen otra vez todas las bolas, y el resultado es independiente de lo que
se haya obtenido anteriormente.
Cuando se extraen dos bolas de una urna “
sin devolución
”, al sacar la segunda
bola, falta la que se ha obtenido anteriormente, y el resultado depende de lo que
se haya obtenido anteriormente.
3.2. Probabilidad condicionada
Ejercicio resuelto
En una urna hay 4 bolas rojas y 5 verdes. Se extraen dos bolas sin devolución.
Halla la probabilidad de que la segunda bola sea roja, con la condición de que
la primera haya sido roja también.
A = “Extraer bola roja la primera vez”
B = “Extraer bola roja la segunda vez”
Hay que hallar P(B/A). En el árbol se observa que P(B/A) = 3/8
Aplicando la fórmula, se obtiene:
ò
P(B/A)
=
= = · = =
3
8
9
24
9
4
1
6
1
—
6
4
—
9
P(A
»
B)
P(A)
° § § ¢ § § £
4 3
12
1
P(A
傽
B) = — · — = — = —
9 8
72
6
4
P(A) = —
9
6
La
probabilidad del suceso B condicionado por el suceso A
es la
probabi-lidad de que se realice B sabiendo que se ha realizado A
P(A
»
B)
P(B/A) = —————
P(A)
Las probabilidades condicionadas son las segundas y sucesivas ramas de los
árboles.
16
81
4
9
4
9
5
Los sucesos A y B son
independientes
si la probabilidad de uno de ellos no
de-pende de que se haya verificado el otro. En otro caso se llaman
dependientes
.
Obser va
Extraer dos bolas al mismo tiem-po o simultáneamente es lo mis-mo que extraer “sin devolu-ción”: primero una, y después la otra.
3 –l8 =
9 ab/c
4 ÷ 6 ab/c
1
R
V 4/9 5/9
4 R 5 V R
V 4/9 5/9
4 R 5 V 4 R
5 V
R
V 3/8 5/8
2 R 5 V R
V 4/9 5/9
3 R 5 V 4 R
3.3. Relación entre las probabilidades
de sucesos independientes
Aplicando la definición de probabilidad condicionada, se tiene que:
P(B/A) =
ò
P(A
傽
B) = P(A) · P(B/A) (1)
Pero si los sucesos A y B son independientes, se tiene que P(B/A) = P(B). Al
sus-tituir en (1), se tiene que: P(A
傽
B) = P(A) · P(B)
Ejercicio resuelto
En un hospital se han producido 60 nacimientos en una
se-mana. De ellos, 35 son varones; y de éstos, 21 tienen el pelo
negro. Asimismo se ha observado que, de las niñas nacidas,
10 no tienen el pelo negro. Basándote en estos datos, razona si
tener el pelo negro depende o no del sexo.
ò
P(V
傽
N) = P(V) · P(N)
ò
P(M
傽
N) = P(M) · P(N)
Se observa que en ambos casos se obtiene el mismo valor, luego son
indepen-dientes.
3.4. Regla del producto o de la probabilidad compuesta
Ejercicio resuelto
Halla la probabilidad de obtener dos copas al extraer sin devolución dos
car-tas de una baraja española de 40 carcar-tas.
P(CC) = P(C) · P(C/C) =
·
=
·
=
3
–l52
=
39
a
b/c9
Ò
40
a
b/c10
3
52
3
13
1
4
9
39
10
40
8
La
regla del producto
o de la
probabilidad compuesta
dice que si A
1,
A
2, …, A
nson sucesos dependientes, entonces:
P(A
1傽
A
2傽
···
傽
A
n) =
= P(A
1) · P(A
2/A
1) · P(A
3/A
1傽
A
2) … P(A
n/A
1傽
A
2···
傽
A
n – 1)
En la práctica, la
regla del producto
o de la
probabilidad compuesta
dice
que la probabilidad de un camino es igual al
producto
de las probabilidades
de las ramas que lo forman.
° ¢ £
P(M
傽
N) = 15/60 = 1/4
P(M) · P(N) = 25/60 · 36/60 = 1/4
° ¢ £
P(V
傽
N) = 21/60 = 7/20
P(V) · P(N) = 35/60 · 36/60 = 7/20
7
P(A
»
B)
P(A)
Si dos sucesos son independientes, entonces la probabilidad de la intersección
es el producto de las probabilidades:
P(A
傽
B) = P(A) · P(B)
7. Sean A y B dos sucesos de un experimento aleatorio tales que P(A) = 0,6; P(B) = 0,4 y P(A—傼—B) = 0,7
a) Calcula P(A 傽B)
b) Razona si los sucesos A y B son independientes.
c) Calcula P(A 傼B)
8. Lanzamos dos veces consecutivas un dado de seis caras numeradas de 1 al 6
a) Calcula la probabilidad de que la suma de los resul-tados sea igual a 4
b) Calcula la probabilidad de que en el primer lanza-miento haya salido un 1, si la suma es 4
●
Aplica la teoría
C
no C 9/39
8 C 30 no C C
no C 10/40
9 C 30 no C 10 C
30 no C
Pelo negro (N)
Niños
(V)
21
Niñas
(M)
15
Total
pelo
36
Pelo no negro
14
10
24
■
Piensa y calcula
Se lanzan al aire dos monedas. Halla la probabilidad de que una sea cara y la otra cruz.
4. Regla de la suma y teorema de Bayes
4.1. Regla de la suma o de la probabilidad total
Se aplica la regla de la suma cuando se pregunta por la probabilidad total de un
suceso, S, de la última experiencia y se conocen las probabilidades condicionadas
de este suceso a los sucesos de la primera experiencia. Es decir, se debe calcular la
probabilidad de un suceso al que se puede llegar por varios caminos del árbol.
Ejercicio resuelto
Una empresa realiza el 50% de sus operaciones en la Unión Europea, el 30%
en América y el 20% en Asia. En la Unión Europea sufren un retraso del
10%, en América del 15% y en Asia del 25%. Halla la probabilidad de que
una operación sufra retraso.
A = Unión Europea, B = América, C = Asia, R = Retraso
P(Retraso) = P(A) · P(R/A) + P(B) · P(R/B) + P(C) · P(R/C)
P(Retraso) = 0,5 · 0,1 + 0,3 · 0,15 + 0,2 · 0,25 = 0,145 = 14,5%
0,145
=
0,25
Ò
0,2
+
0,15
Ò
0,3
+
0,1
Ò
0,5
9
La
regla de la suma
o de la
probabilidad total
dice que si A
1, A
2… A
nes
un sistema completo de sucesos y S es un suceso cualquiera para el que se
co-nocen las P(S/A
i), entonces:
P(S) = P(A
1) · P(S/A
1) + P(A
2) · P(S/A
2) + … + P(A
n) · P(S/A
n)
En la práctica la
regla de la suma
o de la
probabilidad total
dice que la
pro-babilidad de varios caminos es igual a la
suma
de las probabilidades de cada
uno de los caminos.
A1 A1傽 S
S P(A1傽 S
– ) P(A1傽 S) P(S/A1)
P(A1)
P(An) P(Ai)
P(S–/A1)
………
……… S
– S
… …
Ai Ai傽 S … …
An
A1
P(Ai傽 S–) P(Ai傽 S) P(S/Ai)
P(S–/Ai) S– S
Ai P(S)
P(An傽 S–) P(An傽 S) P(S/An)
P(S–/An) S– S An
An傽 S Sistema completo
de sucesos
Un sistema completo de su-cesoses un conjunto de suce-sos:
A1, A2… An tal que:
a) A1傼A2傼… 傼An= E b) A1,A2… Anson incompatibles
dos a dos.
R
R – A
0,1
R
R – B
A B C
0,15
R
R – C
0,25 0,5
0,2 0,3
CC C
CX X
XC C
C
X
XX X
1/2
1/2 1/2
1/2 1/2
1/2
4.2. Teorema de Bayes
Estrategia de resolución de problemas
En la práctica se aplica Bayes cuando se pregunta por la probabilidad de haber
recorrido un determinado camino del árbol para llegar a un suceso, S, de la
se-gunda experiencia, entre todos los caminos posibles que llevan al mismo suceso.
Ejercicio resuelto
Una empresa realiza el 50% de sus operaciones en la Unión Europea, el 30%
en América y el 20% en Asia. En la Unión Europea sufren un retraso del
10%, en América del 15% y en Asia del 25%. Si una operación ha sufrido
re-traso, halla la probabilidad de que se haya realizado en la Unión Europea.
A = Unión Europea, B = América, C = Asia, R = Retraso
P(A/R) =
=
=
0,05
= 0,34
0,145
0,5 · 0,1
0,145
P(A) · P(R/A)
P(R)
10
El
teorema de Bayes
dice que si A
1, A
2… A
nes un sistema completo de
su-cesos y S es un suceso cualquiera para el que se conocen las P(S/A
i), entonces:
P(A
i) · P(S/A
i)
P(A
i/S) = ———————
P(S)
Las P(A
i) se llaman
“probabilidades a priori”
porque se conocen.
Las P(S/A
i) se llaman
“verosimilitudes”
porque se comprenden fácilmente.
Las P(A
i/S) se llaman
“probabilidades a posteriori”
porque son las que hay
que calcular.
9.Se tienen tres cajas iguales. La primera contiene 3 bo-las blancas y 4 negras; la segunda, 5 bobo-las negras; y la tercera, 4 blancas y 3 negras.
a) Si se elige una caja al azar, y luego se extrae una bo-la, ¿cuál es la probabilidad de que la bola extraída sea negra?
b) Si se extrae una bola negra de una de las cajas, ¿cuál es la probabilidad de que proceda de la se-gunda caja?
10. Un día determinado, en una tienda de ropa joven, se han realizado 400 ventas pagadas con tarjeta de
crédi-to V, y 350 ventas pagadas con la tarjeta MC. Las ven-tas restantes del día han sido abonadas en metálico. Se comprueba que 150 de las ventas pagadas con la tarjeta V superan los 150 €, mientras que 300 de las compras pagadas con tarjeta de crédito MC superan esa cantidad. Se extrae al azar un comprobante de las ventas del día pagadas con tarjetas de crédito.
a) ¿Cuál es la probabilidad de que corresponda a una compra superior a 150 €?
b) Si la compra es inferior a 150 €, ¿cuál es la proba-bilidad de que haya sido pagada con la tarjeta MC?
●
Aplica la teoría
A1 A1傽 S
P(A1傽 S–) P(A1傽 S) P(S/A1)
P(A1)
P(An) P(Ai)
P(S–/A1)
………
……… S
– S
… …
Ai Ai傽 S … …
An
A1
P(Ai傽 S–) P(Ai傽 S) P(S/Ai)
P(S–/Ai) S– S Ai
P(An傽 S–) P(An傽 S) P(S/An)
P(S–/An) S– S An
An傽 S
P(S) S
R
R – A
0,1
R
R – B
A B C
0,15
R
R – C
0,25 0,5
Ejercicios y problemas
Ejercicios y problemas resueltos
11.Calcula la probabilidad del su-ceso A—»B sabiendo que la probabilidad de que ocurra al menos uno de los dos sucesos A o B es 0,8 y que P(A) = 0,3
Se aplica la propiedad de la diferencia:
P(A
—»
B) = P(B – A) = P(A
«
B) – P(A) = 0,8 – 0,3 =
0,5
A
—»
B
A
B
Propiedades de la probabilidad12.Sonia y Manuel tiran,cada uno, un dado numerado del 1 al 6. ¿Cuál es la probabilidad de que Sonia saque mayor puntuación que Manuel?
S = Sonia saca mayor puntuación que Manuel.
M = Manuel saca mayor puntuación que Sonia.
I = Ambos sacan la misma puntuación.
Se dibuja un diagrama cartesiano:
P(S) =
=
5
12
15
36
1
Sonia
M
anuel
2 3 4 5 6 1 I S S S S S M I S S S S M M I S S S M M M I S S M M M M I S M M M M M I
2 3 4 5 6
Diagrama cartesiano
13.En una población se ha deter-minado que de cada 100 afi-cionados al fútbol,25 son abo-nados del equipo A, 45 son abonados del equipo B y el res-to son abonados del equipo C. Sabiendo que el 30% de los abo-nados de A, el 40% de los abonados de B y el 50% de los abonados de C tienen menos de 30 años, determina la pro-babilidad de que, selecciona-do al azar, un aficionaselecciona-do al fút-bol en esa población sea menor de 30 años.Justifica la respuesta.
Se resuelve mediante una tabla de contingencia:
El 30% de 25% es 0,3 · 25 = 7,5%
El 40% de 45% es 0,4 · 45 = 18%
El 50% de 30% es 0,5 · 30 = 15%
P(Aficionado menor de 30 años) =
40,5
=
0,405
100
A
Menores 30 años
7,5%
Mayores 30 años
17,5%
Total por equipos
25%
B
18%
27%
45%
C
15%
15%
30%
Total por edades
40,5%
59,5%
100%
Ejercicios y problemas
17.Una caja contiene tres mone-das. Una moneda es normal, otra tiene dos caras y la ter-cera está trucada de forma que la probabilidad de obtener ca-ra es 1/3.Las tres monedas tie-nen igual probabilidad de ser elegidas.
a) Se elige al azar una mone-da y se lanza al aire. ¿Cuál es la probabilidad de que salga cara?
b) Si lanzamos la moneda tru-cada dos veces, ¿cuál es la probabilidad de que salga una cara y una cruz?
N = Moneda normal.
2C = Moneda con dos caras.
T = Moneda trucada.
C = Obtener cara
a) Se aplica la regla de la suma o de la probabilidad total; en cada una de las
ra-mas se aplica la regla del producto o de la probabilidad compuesta:
Diagrama en árbol:
N 2C
T
C X N
1/3
T 1/3
C 1/2
C 1/3 2C
1/3
C 1 C
C
T
Regla del producto o de la probabilidad compuesta y regla de la suma o de la probabilidad total
14.Sean A y B dos sucesos de un mismo espacio muestral. Sabiendo que:
P(A) = 0,5 P(B) = 0,4
P(A «B) = 0,8 determina P(A/B)
15.Sean C y D dos sucesos de un mismo espacio muestral. Sabiendo que:
P(C) = 0,3 P(D) = 0,8
C y D son independientes,de-termina P(C «D)
16.Entre la población de una de-terminada región se estima que el 55% presenta obesidad, el 20% padece hipertensión y el 15% tiene obesidad y es hi-pertenso.
a) Calcula la probabilidad de ser hipertenso o tener obesidad. b) Calcula la probabilidad de tener obesidad condicio-nado a ser hipertenso.
Se aplica la definición de probabilidad condicionada:
P(A/B) =
Se aplican las propiedades de la probabilidad:
P(A
«
B) = P(A) + P(B) – P(A
»
B)
0,8 = 0,5 + 0,4 – P(A
»
B)
ò
P(A
»
B) = 0,1
Sustituyendo en la fórmula anterior:
P(A/B) =
= =
1
0,25
4
0,1
0,4
P(A
»
B)
P(B)
O = Obesidad.
H = Hipertensión.
a) Se aplican las propiedades de la probabilidad:
P(H
«
O) = P(H) + P(O) – P(H
»
O)
P(H
«
O) = 0,20 + 0,55 – 0,15 = 0,60 = 60%
b) Se aplica la definición de probabilidad condicionada:
P(O/H) =
=
0,15
=
0,75 = 75%
0,20
P(O
»
H)
P(H)
Se aplican las propiedades de la probabilidad y la de los sucesos independientes:
P(C
«
D) = P(C) + P(D) – P(C
»
D)
Como C y D son independientes:
P(C
»
D) = P(C) · P(D) = 0,3 · 0,8 = 0,24
Sustituyendo en la fórmula anterior:
P(C
«
D) = 0,3 + 0,8 – 0,24 =
0,86
Sucesos dependientes e independientes y probabilidad condicionada
Te
ma 11.
Pr
oba
bilidad
Ejercicios y problemas
Ejercicios y problemas resueltos
P(C) = P(N) · P(C/N) + P(2C) · P(C/2C) + P(T) · P(C/T) =
= · + ·
1
+ · = + + =
=
b) Se aplica la regla de la suma o de la probabilidad total; en cada una de las
ra-mas se aplica la regla del producto o de la probabilidad compuesta:
Diagrama en árbol:
P(CX) + P(XC) = P(C) · P(X/C) + P(C) · P(C/X) =
= · + · = + =
4
9
2
9
2
9
1
3
2
3
2
3
1
3
C 1/3 X 2/3 C X C 1/3 X 2/3 C X T C 1/3 X 2/311
18
3 + 6 + 2
18
1
9
1
3
1
6
1
3
1
3
1
3
1
2
1
3
18.En un juego consistente en lan-zar dos monedas indistingui-bles y equilibradas y un dado de seis caras equilibrado, un jugador gana si obtiene dos ca-ras y un número par en el da-do,o bien exactamente una ca-ra y un número mayor o igual que cinco en el dado. a) Calcula la probabilidad de
que un jugador gane. b) Se sabe que una persona ha
ganado. ¿Cuál es la proba-bilidad de que obtuviera dos caras al lanzar las monedas?
Definimos los sucesos:
C = Obtener cara en la moneda
P = Obtener par en el dado
M = Obtener mayor o igual que cinco en el dado
G = Ganar
Diagrama en árbol:
a) Se aplica la regla de la suma o de la probabilidad total; en cada una de las
ra-mas se aplica la regla del producto o de la probabilidad compuesta:
P(G) = P(2C, P) + P(CX, M) + P(XC, M)
P(2C, M) = P(C) · P(C/C) · P(M/C
»
C)
= · · =
P(CX, M) = P(C) · P(X/C) · P(M/C
»
X)
= · · =
P(XC, M) = P(X) · P(C/X) · P(M/X
»
C)
= · · =
P(G)
= + + =
b) Se aplica el teorema de Bayes
P(2C/G) =
=
=
3
7
1/8
7/24
P(2C, M)
P(G)
7
24
1
12
1
12
1
8
1
12
2
6
1
2
1
2
1
12
2
6
1
2
1
2
1
8
3
6
1
2
1
2
D C 1/2 P 3/6 C 1/2 X 1/2 M 2/6 M 2/6 D D M 2/6 D C X C 1/2 X 1/2 C X C X X 1/2Ejercicios y problemas
Te
ma 11.
Pr
oba
bilidad
Preguntas tipo test
Dados dos sucesos A y B, sabemos que p(A »B) = 0,1; p(A «B) = 0,7 y p(A|B) = 0,2
Calcula p(A) y p(B)
P(A) = 0,1; P(B) = 0,1
P(A) = 0,2; P(B) = 0,5
P(A) = 0,3; P(B) = 0,4
P(A) = 0,4; P(B) = 0,7
En el problema 1, ¿son independientes los sucesos A y B?
Los sucesos A y B son dependientes.
Los sucesos A y B son independientes.
En el problema 1, calcula p(A—«B), donde A— repre-senta el suceso complementario o contrario de A.
p(A—«B) = 0,2 p(A—«B) = 0,5
p(A—«B) = 0,9
p(A—«B) = 0,8
En un grupo de familias, un 10% ha cambiado de co-che y también ha cambiado de piso; un 50% no ha cambiado de coche y sí de piso. Entre los que han cam-biado de coche, un 25% ha camcam-biado de piso.
¿Qué porcentaje de familias ha cambiado de piso?
P(P) = 0,5
P(P) = 0,6
P(P) = 0,7
P(P) = 0,8
En el problema 4, ¿qué probabilidad hay de que una familia del grupo haya cambiado de coche?
P(C) = 0,4
P(C) = 0,5
P(C) = 0,6
P(C) = 0,7
En el problema 4, de las familias que no han cambia-do de piso, ¿qué porcentaje ha cambiacambia-do de coche?
P(C/ P—) = 0,45
P(C/ P—) = 0,55
P(C/ P—) = 0,65
P(C/ P—) = 0,75
Se consideran dos sucesos A y B de un experimento aleatorio, tales que:
P(A) = 1/4, P(B) = 1/3, P(A »B) = 1/2 ¿Son A y B sucesos independientes?
Los sucesos A y B son dependientes.
Los sucesos A y B son independientes.
En el problema 7. Calcula P(A—/ B—)
P(A—/ B—) = 3/4
P(A—/ B—) = 1/4
P(A—/ B—) = 2/3
P(A—/ B—) = 4/5
Se sabe que el 30% de los individuos de una pobla-ción tienen estudios superiores; también se sabe que, de ellos, el 95% tiene empleo. Además, de la parte de la población que no tiene estudios superio-res, el 60% tiene empleo.
Calcula la probabilidad de que un individuo, elegido al azar, tenga empleo.
P(E) = 0,505
P(E) = 0,605
P(E) = 0,705
P(E) = 0,805
En el problema 9, se ha elegido un individuo aleato-riamente y tiene empleo; calcula la probabilidad de que tenga estudios superiores.
P(S/E) = 0,2
P(S/E) = 0,3
P(S/E) = 0,4
P(S/E) = 0,5
10 9 8 7 6
5 4 3 2 1
Contesta en tu cuaderno:
Ejercicios y problemas
Ejercicios y problemas
Ejercicios y problemas
Ejercicios y problemas propuestos
1. Operaciones con sucesos
11. Sea el experimento de lanzar una moneda al aire.
Halla:
a) el espacio muestral o suceso seguro.
b) los sucesos elementales.
12. En el experimento de extraer una carta de una baraja española de 40 cartas, halla:
a) el espacio muestral o suceso seguro.
b) el suceso A, formado por los oros.
c) el suceso B, formado por las ases.
d) el suceso C, formado por las figuras.
e) ¿A y B son compatibles o incompatibles?
f ) ¿A y C son compatibles o incompatibles?
g) ¿B y C son compatibles o incompatibles?
13. Sean E = {1, 2, 3, 4, 5, 6, 7, 8}, A = {1, 3, 5, 7}, B = {2, 3, 5, 7}
Calcula:
a) A 傼B b) A 傽B
c) A— d) B—
14. Sea E = {1, 2, 3, 4, 5, 6}, A = {1, 3, 5}, B = {2, 3, 5}. Calcula:
a) A – B
b) B – A
c) Comprueba la ley de Morgan:
= A—傽B—
d) Comprueba la ley de Morgan:
= A—傼B—
2. Regla de Laplace
15. Después de haber escuchado tres discos, éstos se guardan al azar. ¿Cuál es la probabilidad de que al me-nos uno de los discos haya sido guardado en su funda?
16. Dado un espacio muestral E, se consideran los sucesos A y B, cuyas probabilidades son:
P(A) = 2/3 y P(B) = 1/2
a) ¿Pueden ser los sucesos A y B incompatibles?¿Por qué?
b) Suponiendo que los sucesos A y B son independien-tes, calcula P(A 傼B)
c) Suponiendo que A 傼B = E, calcula P(A 傽B)
17. El 35% de los estudiantes de un centro practican fútbol. El 70% de los que practican fútbol estudia Ma-temáticas, así como el 25% de los que no practican fút-bol.
Si se elige al azar a un estudiante de este centro, calcu-la calcu-la probabilidad de que éste:
a) estudie Matemáticas.
b) practique fútbol, sabiendo que no es alumno de Ma-temáticas.
18. Supongamos que tras una encuesta se ha concluido que si se elige al azar a una persona, la probabilidad de que esté a favor de la retransmisión de partidos de fútbol es de 0,8; de que esté a favor de la existencia de canales de televisión de pago, de 0,4; y de que esté a fa-vor de la retransmisión de partidos de fútbol y tam-bién de la existencia de canales de pago, de 0,3
a) Calcula la probabilidad de que una persona esté a favor de la retransmisión de partidos de fútbol o de la existencia de canales de televisión de pago.
b) Calcula la probabilidad de que una persona no esté a favor de la retransmisión de partidos de fútbol ni de la existencia de canales de televisión de pago.
3. Probabilidad condicionada
19. La probabilidad de que, en un determinado mes, un clien-te de una gran superficie compre un producto A es 0,6, y la probabilidad de que compre un producto B es 0,5. Se sabe también que la probabilidad de que un cliente compre el producto B no habiendo comprado el pro-ducto A es 0,4
a) ¿Cuál es la probabilidad de que un cliente haya com-prado únicamente el producto B?
b) ¿Cuál es la probabilidad de que un cliente no haya comprado ninguno de los productos?
20. En una ciudad hay un 60% de habitantes aficionados al fútbol, un 30% al baloncesto y un 25% a ambos de-portes.
a) ¿Son independientes los sucesos “ser aficionado al fútbol” y “ser aficionado al baloncesto”.
b) Si una persona no es aficionada al baloncesto, ¿cuál es la probabilidad de que sea aficionada al fútbol?
c) Si una persona no es aficionada al fútbol, ¿cuál es la probabilidad de que no sea aficionada al baloncesto? A »B
Te
ma 11.
Pr
oba
bilidad
Ejercicios y problemas
21. En el experimento aleatorio de lanzar una moneda tres veces al aire se consideran los siguientes sucesos:
A: “sacar, al menos, una cara y una cruz”.
B: “sacar, a lo sumo, una cara”.
a) Determina el espacio muestral asociado a ese expe-rimento, y los sucesos A y B
b) ¿Son independientes ambos sucesos?
22. El temario de una oposición consta de 100 temas. El día del examen éstos se sortean, de manera que solo pueden salir dos temas, a los que debe responder obli-gatoriamente el opositor. Calcula cuántos temas, como mínimo, debe estudiar el opositor para que la probabi-lidad de conocer los dos temas que le toquen sea su-perior a 0,5
4. Regla de la suma y teorema de Bayes
23. En una ciudad, la probabilidad de que uno de sus habi-tantes censados vote al partido A es 0,4; la probabili-dad de que vote al partido B es 0,35 y la probabiliprobabili-dad de que vote al partido C es 0,25. Por otro lado, las pro-babilidades de que un votante de cada partido lea dia-riamente algún periódico son, respectivamente, 0,4; 0,4 y 0,6.
Se elige a una persona de la ciudad al azar:
a) Calcula la probabilidad de que lea algún periódico.
b) La persona elegida lee algún periódico. ¿Cuál es la probabilidad de que sea votante del partido B?
24. Tres máquinas A, B y C fabrican tornillos. En una hora, la máquina A fabrica 600 tornillos, la B 300 y la C 100. Las probabilidades de que las máquinas produzcan tornillos defectuosos son, respectivamente, de 0,01 pa-ra A, de 0,02 papa-ra B y de 0,03 papa-ra C. Al finalizar una hora se juntan todos los tornillos producidos y se elige uno al azar.
a) ¿Cuál es la probabilidad de que no sea defectuoso?
b) ¿Cuál es la probabilidad de que lo haya fabricado la máquina A, sabiendo que no es defectuoso?
25. En un supermercado, las mujeres realizan el 70% de las compras. De las compras hechas por éstas, el 80% supe-ra los 12 €, mientras que de las compras realizadas por hombres, solo el 30% sobrepasa esa cantidad.
a) Elegido un tique de compra al azar, ¿cuál es la proba-bilidad de que supere los 12 €?
b) Si se sabe que un tique de compra no supera los 12€, ¿cuál es la probabilidad de que la compra haya sido hecha por una mujer?
26. Resuelve las siguientes cuestiones:
a) Tenemos tres urnas, cada una de las cuales contiene 2 bolas rojas y 3 bolas negras. Se extrae al azar una bola y se llama xal número de bolas rojas obteni-das. Calcula la probabilidad de que x sea mayor o igual que 1
b) Si cada urna hubiese contenido 5 bolas rojas y 3 bo-las negras y se hubiese extraído una bola de cada urna, ¿cuál hubiese sido la probabilidad de que x hu-biese sido mayor o igual que 1?
c) Justifica la diferencia de los resultados obtenidos.
Para ampliar
27. Se lanzan tres veces consecutivas dos dados equilibra-dos de seis caras:
a) Calcula la probabilidad de que en los tres lanza-mientos salga el seis doble.
b) Calcula la probabilidad de que en los tres lanza-mientos salga un doble distinto del seis doble.
28. Si se escoge un número al azar en la guía telefónica de cierta ciudad española, la probabilidad de que figure a nombre de un hombre es 0,7 y de que figure a nombre de una mujer es 0,3. En dicha ciudad, la probabilidad de que un hombre trabaje es 0,8, y de que lo haga una mujer es 0,7
Se elige un número de teléfono al azar.
a) ¿Cuál es la probabilidad de que corresponda a una persona que trabaja?
b) ¿Cuál es la probabilidad de que corresponda a un hombre, sabiendo que pertenece a una persona que trabaja?
29. Disponemos de tres dados, uno de los cuales está tru-cado. La probabilidad de sacar 5 con el dado trucado es 0,25, siendo los otros resultados equiprobables. Se elige un dado al azar y se realiza un lanzamiento con él.
a) Determina la probabilidad de obtener un 2
Ejercicios y problemas
Ejercicios y problemas propuestos
30. Sean A y B dos sucesos tales que:
P(A) = , P(B) = y P(A 傽B) =
Calcula:
a) P(A | B)
b) P(B | A)
c) P(AC傽B), (ACindica el contrario del suceso A)
31. Se dispone de una baraja española de 40 cartas. Se sa-ca una sa-carta al azar y, sin devolverla a la baraja, se sasa-ca otra, también al azar.
a) Calcula la probabilidad de que ninguna de las cartas extraídas sea una figura (es decir, sota, caballo o rey).
b) Sabiendo que la segunda carta extraída no ha sido una figura, calcula la probabilidad de que tampoco lo haya sido la primera.
32. Una experiencia aleatoria consiste en preguntar a tres personas distintas, elegidas al azar, si son partidarias o no de consumir un determinado producto.
a) Escribe el espacio muestral asociado a dicho experi-mento utilizando la letra S para las respuestas afir-mativas y N para las negativas.
b) ¿Qué elementos del espacio muestral anterior cons-tituyen el suceso “al menos dos de las personas son partidarias de consumir el producto”?
c) Describe el suceso contrario de “más de una perso-na es partidaria de consumir el producto”.
33. Se tienen tres cajas de bombones, A, B y C. La caja A contiene 10 bombones, de los cuales 4 están rellenos; la caja B contiene 8 bombones, de los cuales 3 están rellenos; y la caja C contiene 6 bombones, de los que 1 está relleno.
a) Si se toma al azar un bombón de la caja A, ¿cuál es la probabilidad de que no esté relleno?
b) Si se elige al azar una de las tres cajas y se toma un bombón de la caja elegida, ¿cuál es la probabilidad de que esté relleno?
34. En un centro de enseñanza secundaria se sabe que el 70% de los alumnos practica atletismo, que el 50% jue-ga al fútbol y que el 40% de los que practican atletismo juega al fútbol.
a) Razona si los sucesos “jugar al fútbol” y “practicar atletismo” son independientes.
b) Si se elige al azar a un alumno de ese centro, ¿cuál es la probabilidad de que no participe en ninguno de estos deportes?
35. Se lanza al aire dos veces una moneda.
a) Halla la probabilidad de que en ambas tiradas salga cara.
b) Sabiendo que, al menos, en una de las tiradas sale cara, ¿cuál es la probabilidad de que en ambas sal-ga cara?
36. Un estudiante hace dos pruebas el mismo día. La proba-bilidad de que pase la primera prueba es 0,6; la de que pase la segunda es 0,8 y la de que pase ambas es 0,5
a) Calcula la probabilidad de que no pase ninguna prueba.
b) Calcula la probabilidad de que pase la segunda prue-ba si no ha superado la primera.
37. En un colectivo de 200 personas se ha observado que 120 son hombres y que, de éstos, 54 son fumadores. 44 mujeres de este colectivo no fuman. Con estos da-tos, razona si el suceso “fumar” depende del sexo. 1
4 1
3 1
2
38. Una persona desea jugar en una atracción de feria donde regalan un peluche si al tirar un dardo se acier-ta en un blanco. Si solo se permite tirar tres dardos y la probabilidad de acertar en cada tirada es 0,3 a) ¿cuál es la probabilidad de llevarse el peluche?
b) ¿cuál es la probabilidad de llevarse el peluche exac-tamente en el tercer intento? ¿Y de llevárselo exacta-mente en el segundo?
39. Una urna contiene 7 bolas blancas, 3 bolas rojas y 2 bolas negras. Se considera el experimento aleatorio consistente en extraer tres bolas de la urna, de forma sucesiva y sin reemplazamiento. Sean los sucesos B1: La primera bola es blanca, B2: La segunda bola es blanca y B3: La tercera bola es blanca:
a) Expresa con ellos el suceso “las bolas extraídas en primer y tercer lugar son blancas, y la extraída en se-gundo lugar no”.
b) Calcula la probabilidad del suceso “las tres bolas son del mismo color”.
Te
ma 11.
Pr
oba
bilidad
Ejercicios y problemas
40. Una fábrica produce tres modelos de coche: A, B y C. Cada uno de los modelos puede tener motor de gaso-lina o diésel. Sabemos que el 60% de los modelos son de tipo A y el 30% de tipo B. También sabemos que el 30% de los coches fabricados tienen motor diésel, el 30% de los coches del modelo A son de tipo diésel y el 20% de los coches del modelo B tienen motor diésel. Se elige un coche al azar. Se piden las probabilidades de los siguientes sucesos:
a) El coche es del modelo C
b) El coche es del modelo A, sabiendo que tiene motor diésel.
c) El coche tiene motor diésel, sabiendo que es del modelo C
41. Un examen consiste en elegir al azar dos temas de en-tre los diez del programa, y desarrollar uno.
a) ¿Qué probabilidad tiene un alumno, que sabe seis temas, de aprobar el examen?
b) ¿Qué probabilidad tiene el mismo alumno de saber-se uno de los dos temas elegidos y el otro no?
42. Una empresa emplea tres bufetes de abogados para tratar sus casos legales. La probabilidad de que un caso se deba remitir al bufete A es 0,3; de que se remita al bufete B es 0,5 y de que se remita al bufete C es 0,2. La probabilidad de que un caso remitido al bufete A sea ganado en los tribunales es 0,6; para el bufete B esta probabilidad es 0,8 y para el bufete C es 0,7
a) Calcula la probabilidad de que la empresa gane un caso.
b) Sabiendo que un caso se ha ganado, determina la probabilidad de que lo haya llevado el bufete A
43. De una urna con cinco bolas, dos blancas y tres negras, extraemos dos bolas sin reemplazamiento. Calcula la probabilidad de cada uno de los siguientes sucesos:
a) A = “Las dos bolas extraídas son del mismo color”.
b) B = “Extraemos al menos una bola blanca”.
44. Se dispone de tres urnas: A, que contiene dos bolas blancas y cuatro rojas; B, con tres blancas y tres rojas; y C, con una blanca y cinco rojas.
a) Se elige una urna al azar y se extrae una bola. ¿Cuál es la probabilidad de que esta bola sea blanca?
b) Si la bola extraída resulta ser blanca, ¿cuál es la pro-babilidad de que proceda de la urna B?
45. Los temas objeto de un examen están compuestos por tres temas de máxima dificultad, 5 de dificultad media y 2 de escasa dificultad, de los cuales se elige uno al azar. La probabilidad de que un alumno apruebe el examen si el tema es de máxima dificultad es de 1/8; si es de di-ficultad media, 2/5, y si es de escasa didi-ficultad, 3/4
a) Halla la probabilidad de que el alumno apruebe el examen.
b) Halla la probabilidad de que el tema elegido haya sido de máxima dificultad, si el alumno lo aprobó.
46. Una caja contiene 10 tornillos, de los que dos son de-fectuosos.
a) Si se van extrayendo uno a uno los tornillos hasta localizar los dos defectuosos, ¿cuál es la probabili-dad de necesitar exactamente tres extracciones pa-ra localizarlos?
b) Si extraemos solo dos tornillos, y el segundo ha re-sultado ser defectuoso, ¿cuál es la probabilidad de que el primero también lo haya sido?
47. Tenemos un cofre A con 2 monedas de oro y 3 de pla-ta, un cofre B con 5 monedas de oro y 4 de plapla-ta, y un tercer cofre con 2 monedas de oro. Elegimos un cofre al azar y sacamos una moneda.
a) Calcula la probabilidad de que sea de oro.
b) Sabiendo que ha sido de plata, calcula la probabili-dad de que haya sido extraída del cofre A
48. En un cineclub hay 80 películas: 60 son de acción y 20 de terror. Susana elige una película al azar y se la lle-va.A continuación, Luis elige otra película al azar.
a) ¿Cuál es la probabilidad de que tanto Susana como Luis elijan películas de acción?
Ejercicios y problemas
Ejercicios y problemas propuestos
49. La probabilidad de que un jugador A marque un gol de penalti es de 5/6, mientras que la de otro jugador B es de 4/5. Si cada uno lanza un penalti:
a) halla la probabilidad de que marque gol uno solo de los dos jugadores.
b) halla la probabilidad de que, al menos, uno marque gol.
50. Dos urnas A y B, que contienen bolas de colores, tie-nen la siguiente composición:
A: 5 blancas, 3 negras y 2 rojas.
B: 4 blancas y 6 negras.
También tenemos un dado que tiene 4 caras marcadas con la letra A y las otras dos con la letra B.Tiramos el dado y sacamos una bola al azar de la urna que indica el dado.
a) ¿Cuál es la probabilidad de que esa bola sea blanca?
b) ¿Cuál es la probabilidad de que esa bola sea roja?
c) La bola extraída ha resultado ser blanca. ¿Cuál es la probabilidad de que proceda de la urna B?
51. Una determinada población está formada, a partes igua-les, por hombres y mujeres. La probabilidad de que un individuo de esa población no lea ningún periódico es 0,25. Además, el porcentaje de individuos que o bien leen algún periódico o bien son hombres es el 95%. Se elige, al azar, a una persona.
a) Halla la probabilidad de “ser hombre y leer algún periódico”.
b) Halla la probabilidad de que lea algún periódico, sa-biendo que es hombre.
52. Se dispone de 3 urnas y de 10 bolas, 5 blancas y 5 ne-gras. Distribuimos las bolas de la siguiente forma:
• En la 1ª urna se introducen una bola blanca y una bo-la negra.
• En la 2ª urna se introducen 3 bolas blancas y 2 bolas negras.
• En la tercera urna se introducen 1 bola blanca y 2 bo-las negras.
De una de las urnas, elegida al azar, se extrae una bola. Halla la probabilidad de que la bola elegida sea negra.
53. En un espacio muestral dado se consideran dos sucesos A y B tales que su unión es el suceso seguro, y las pro-babilidades condicionadas entre ellos valen P(A/B) = 1/2 y P(B/A) = 1/3. Halla las probabilidades de A y B
54. Dados los sucesos A y B de un mismo espacio mues-tral, se sabe que:
P(A) = 0,4; P(A 傼B) = 0,8 y P(A—傼B—) = 0,7
a) Comprueba si los sucesos A y B son independien-tes.
b) Calcula la probabilidad de que solo se verifique uno de los dos sucesos.
55. La caja A contiene 40 bolígrafos azules y 30 bolígrafos rojos, la caja B contiene 30 bolígrafos azules y 30 bolí-grafos rojos, y la caja C contiene 30 bolíbolí-grafos azules y 20 rojos. Se elige una caja al azar y, de ella, también al azar, se extrae un bolígrafo. ¿Cuál es la probabilidad de que el bolígrafo extraído sea azul?
56. Se dispone de dos bolsas con bolas numeradas. La 1ª bolsa tiene 7 bolas numeradas del 1 al 7, y la segun-da tres bolas numerasegun-das del 8 al 10. Se realiza el si-guiente experimento compuesto: se saca una bola al azar de la primera bolsa y se introduce en la segunda (antes de introducirla se anota si es par o impar), des-pués se saca al azar una bola de la segunda bolsa –que en este momento tiene 4 bolas– y se anota su número.
a) ¿Cuál es la probabilidad de que las dos bolas extraí-das sean pares?
b) ¿Cuál es la probabilidad de que la segunda bola ex-traída sea impar?
57. El 20% de los tornillos de un gran lote es defectuoso. Se cogen tres tornillos al azar y se pide calcular razo-nadamente:
a) la probabilidad de que los tres sean defectuosos.
b) la probabilidad de que ninguno sea defectuoso.
c) la probabilidad de que solamente uno sea defec-tuoso.
Nota: como son muchos tornillos, se supone que la probabilidad no cambia de sacar un tornillo al sacar el siguiente.
Para profundizar
58. En un videoclub quedan 8 copias de la película A, 9 de la B y 5 de la C. Entran tres clientes consecutivamente y cada uno elige una copia al azar. Calcula la probabili-dad de que:
a) los tres escojan la misma película.
Te
ma 11.
Pr
oba
bilidad
Ejercicios y problemas
59. Con el objetivo de recaudar fondos para un viaje, los alumnos de un centro escolar realizan una rifa con 500 números. Un alumno compra dos números.
a) Si solo hay un premio, ¿qué probabilidad tiene el alumno de que le toque a él?
b) Si hay dos premios, ¿qué probabilidad tiene el alum-no de que le toque, al mealum-nos, ualum-no de ellos?
60. De una urna con 4 bolas blancas y 2 negras se ex-traen dos bolas al azar, sucesivamente y sin reempla-zamiento.
a) ¿Cuál es la probabilidad de que las bolas extraídas sean blancas?
b) Si la segunda bola ha resultado ser negra, ¿cuál es la probabilidad de que la primera también lo haya sido?
61. Se considera una célula en el instante t = 0. En el ins-tante t = 1 la célula puede reproducirse dividiéndose en dos, con probabilidad 3/4; o bien morir, con proba-bilidad 1/4. Si la célula se divide, entonces, en el tiempo t = 2, cada uno de sus dos descendientes puede tam-bién subdividirse o morir, independientemente uno de otro y con las mismas probabilidades de antes.
a) ¿Cuántas células puede haber en el tiempo t = 2?
b) ¿Con qué probabilidad?
62. Dos cajas,A y B, tienen el siguiente contenido:
La A tiene cinco monedas de 1 €y 3 de 2 €
La B tiene cuatro monedas de 1 €, 4 de 2 €y 2 de 50 céntimos.
De una de las cajas elegidas al azar, se extrae una mo-neda.
a) ¿Cuál es la probabilidad de que sea de 1 €?
b) Si la moneda extraída resulta ser de 2 €, ¿cuál es la probabilidad de que proceda de la caja B?
63. La probabilidad de que un conductor no lleve la rueda de repuesto es 0,13, y la de que no lleve lámparas de repuesto es 0,37. Se sabe que el 60% de los conducto-res lleva ambos repuestos.
a) Calcula la probabilidad de que un conductor no lle-ve alguno de los dos repuestos señalados.
b) ¿Son independientes los sucesos “llevar rueda de re-puesto” y “llevar lámparas de rere-puesto”?
64. A un congreso asisten oculistas y pediatras. Se sabe que 240 médicos son andaluces, 135 son navarros y 225 son canarios. El número total de pediatras es 315. De los andaluces, 96 son oculistas; de los navarros, son oculistas 75
a) Se escoge a un asistente al azar. ¿Cuál es la probabi-lidad de que sea un pediatra navarro?
b) Se ha elegido a un médico canario. ¿Cuál es la pro-babilidad de que sea oculista?
c) ¿Son independientes los sucesos “ser andaluz” y “ser oculista”?
65. El 40% de los habitantes de una ciudad va al cine, el 30% va al teatro y el 20% a ambos.
a) Si una persona de esa ciudad no va al cine, ¿cuál es la probabilidad de que tampoco vaya al teatro?
b) Si una persona no va al teatro, ¿cuál es la probabili-dad de que vaya al cine?
66. De los turistas que visitan Málaga, el 60% hace el viaje en avión, el 30% lo hace por carretera y el 10% lo ha-ce en tren. El 70% de los que viajan en avión, el 80% de los que viajan por carretera y el 50% de los que viajan en tren van a las playas de la costa occidental.
a) Si se selecciona al azar un turista que ha visitado Málaga, ¿cuál es la probabilidad de que haya estado en las playas de la costa occidental?
b) Si se selecciona al azar un turista que ha visitado Málaga y que ha estado en las playas de la costa oc-cidental, ¿cuál es la probabilidad de que haya viajado en tren?
67. Se lanzan cinco monedas al aire.
Calcula:
a) la probabilidad de no obtener ninguna cara.
b) la probabilidad de obtener una cara.