UNIVERSIDAD AUTÓNOMA DEL ESTADO DE HIDALGO
INSTITUTO DE CIENCIAS BÁSICAS E INGENIERÍA
ÁREA ACADÉMICA DE MATEMÁTICAS Y FÍSICA
PROCESOS COGNITIVOS QUE MUESTRAN ESTUDIANTES AL UTILIZAR CABRI COMO UN INSTRUMENTO DE RESOLUCIÓN DE PROBLEMAS
TESIS
QUE PARA OBTENER EL GRADO DE:
MAESTRO EN CIENCIAS EN MATEMÁTICAS Y SU DIDÁCTICA
PRESENTA:
Rivelino Meneses Soto Dirigida por:
Dr. Aarón Reyes Rodríguez Dr. Fernando Barrera Mora
Tesis enmarcada en el Proyecto CONACYT: “Bases Teóricas y Conceptuales en la Construcción del Conocimiento Matemático y el Empleo de Herramientas Digitales”, con registro #61996.
RESUMEN
A través de la historia, el desarrollo y evolución de las matemáticas han dependido en gran medida de las herramientas mediante las cuales se representan y operan los objetos matemáticos. Por esta razón, la disponibilidad de software matemático representa nuevas oportunidades de aprendizaje para los estudiantes. ¿Cuáles son las características de los procesos cognitivos que desarrolla un estudiante al utilizar un software dinámico como un instrumento para resolver problemas? Esta pregunta está formulada con la intención de documentar la importancia de utilizar estrategias de instrucción que permitan a los estudiantes incorporar a las herramientas computacionales en sus procesos de reflexión. Se pretende determinar cuáles son las características de las actividades de aprendizaje que pueden permitir a los estudiantes ampliar diferentes elementos del pensamiento matemático (identificar información, encontrar relaciones entre datos e incógnitas, resolver casos particulares, formular conjeturas, proporcionar pruebas, comunicar resultados), cuando resuelven problemas con el uso de las tecnologías digitales.
En esta investigación se analiza la forma en que los estudiantes de un grupo incorporan el uso de las herramientas computacionales en su proceso de aprendizaje de las matemáticas; particularmente, la forma en que a través del desarrollo de tareas de instrucción que promueven el uso sistemático de un software dinámico, los estudiantes construyen conocimiento mediante un proceso de integración de la herramienta, a su estructura cognitiva. En otras palabras, se estudian las características del proceso de transformación de un artefacto en un instrumento (génesis instrumental); así como sus implicaciones en el aprendizaje.
ABSTRACT
Through the history, the developments of mathematics have been related to the tools used to represent and operate mathematical objects. For this reason, the availability of mathematical software represents new learning opportunities for students. What are the features of cognitive processes that students develop when they use dynamic software as a tool to solve problems? This question is formulated with the aim of document the importance of using instructional strategies that allow students to incorporate computational tools as part of their cognitive structure. The aim of this study is to identify the characteristics of learning activities that enable students to improve different elements of mathematical thinking (identifying information, find relationships between data and unknowns, solving individual cases, make conjectures, provide evidence, communicate results) when solving problems with the use of digital technologies.
This study examines how a group of students incorporate the use of computational tools in the learning of mathematics; particularly the way that students construct knowledge through of the use of dynamic software for solving problems and the process of incorporation of the tool to learning processes. In other words, we analyzed instrumental genesis, as well as its implications on student’s learning.
ÍNDICE
Contenido Página
Capítulo 1. El problema de investigación
1.1 Introducción 1.2 Antecedentes 1.3 Objetivos
1.4 Preguntas de investigación
1 4 11 11 Capítulo 2. Marco conceptual
2.1 Introducción
2.2 Mediación instrumental 2.3 Génesis instrumental
2.4 Resolución de problemas como método de aprendizaje
13 15 17 19 Capítulo 3. Metodología
3.1 Introducción
3.2 Participantes en el estudio 3.3 Tarea de aprendizaje
3.4 Técnica de recolección de la información: observación no participante 3.5 Instrumentos de recolección de datos
3.6 Unidad de análisis y procedimiento de análisis 3.7 Criterios para evaluar el diseño de la investigación
23 24 25 30 30 31 32 Capítulo 4. Presentación de resultados
4.1 Introducción
4.2 Potencialidades y restricciones del artefacto 4.3 Fase de instrumentalización
4.4 Fase de instrumentación
4.5 Tipo de esquemas y aspectos del pensamiento matemático que emergieron durante el desarrollo de la tarea
4.6 El papel de las representaciones ejecutables en la construcción del conocimiento
4.7 Orquestación instrumental y su relación con el mantenimiento del nivel de demanda cognitiva
33 33 34 39 42 49 51
Capítulo 5. Discusión y conclusiones
5.5 Implicaciones didácticas 61
Referencias 63
Apéndices
Apéndice A. Guía de la actividad
Apéndice B. Una trayectoria hipotética para la actividad Apéndice C. Cuestionario de salida
Apéndice D. Transcripción de los videos
Apéndice E. Condensado de respuestas a la guía de la actividad Apéndice F. Respuestas del cuestionario de salida
CAPÍTULO 1
EL PROBLEMA DE INVESTIGACIÓN
1.1. INTRODUCCIÓN
El hombre a través de la historia ha utilizado herramientas que han mediado su actividad y pensamiento. Desde sus orígenes, los seres humanos han empleado artefactos para modificar la naturaleza y procurarse mejores formas de vida; por ejemplo, el hombre de la edad de piedra utilizó un artefacto para defenderse y atacar a sus enemigos; tomó una piedra astillada y la convirtió en un instrumento de supervivencia: su primera arma. El mundo se ha transformado desde la aparición de esa piedra astillada hasta los avances tecnológicos que actualmente se encuentran a nuestra disposición.
Hoy en día, los cambios tecnológicos y sociales se desarrollan a un ritmo acelerado, por lo que el manejo o dominio de contenidos matemáticos es una necesidad para los ciudadanos, ya que actividades cotidianas como el cálculo de impuestos, la elaboración de un presupuesto de gastos; la interpretación de la información estadística y financiera de los diarios o de los informes del gobierno, el manejo de créditos bancarios, entre otras, requieren que las personas pongan en práctica diversos niveles de pensamiento o análisis matemático; por tanto, un objetivo fundamental de la educación matemática es lograr que los estudiantes sean capaces de dar significado a los conceptos matemáticos no solamente dentro de la misma disciplina, sino también en otras áreas del conocimiento, además de que establezcan relaciones y conexiones entre esos conceptos (Santos 2001). Así, las herramientas computacionales han llegado a ser un elemento indispensable en la actividad humana; y su incorporación en los proceso de aprendizaje como herramienta didáctica, ha permitido incrementar el número de problemas que un estudiante puede abordar, ya que el uso de la computadora pone a su disposición una amplía variedad de representaciones de objetos matemáticos que se pueden visualizar y operar de forma dinámica.
constantemente busquen y examinen diferentes tipos de relaciones, planteen conjeturas, utilicen distintos sistemas de representación (numéricos, algebraicos, geométricos), establezcan conexiones, empleen diversos argumentos o formas de justificación y comuniquen sus resultados.
Esta perspectiva ha influido notablemente en diferentes propuestas curriculares. En particular, el Consejo Nacional de Profesores de Matemáticas de los Estados Unidos (NCTM, 2000) sugiere, no solamente una reorganización de los contenidos del currículo en términos de líneas generales de pensamiento matemático (números y operaciones, álgebra, patrones y funciones, geometría y relaciones espaciales, medida y análisis de datos y probabilidad), sino también el desarrollo de procesos o acciones cognitivas asociadas con la práctica de la disciplina (resolución de problemas, razonamiento y prueba, comunicación, conexiones y representaciones), además reconoce la importancia de que los estudiantes utilicen distintas herramientas computacionales en el proceso de comprensión de ideas matemáticas. ¿Qué herramientas pueden favorecer el desarrollo de un pensamiento matemático en los estudiantes? ¿Qué tipo de conjeturas y observaciones realizan los estudiantes al resolver problemas con ayuda de alguna herramienta tecnológica? ¿Qué formas de razonamiento desarrollan los estudiantes al emplear artefactos computacionales en la resolución de problemas? ¿Cuál es el papel de las representaciones ejecutables en el proceso de comprensión de ideas matemáticas?, son preguntas que orientan el análisis y reflexión sobre la trascendencia de utilizar a las tecnologías digitales en la instrucción matemática.
El uso educativo de la tecnología ha generado cambios importantes sobre la forma en cómo aprenden matemáticas los estudiantes, porque los ambientes computacionales proporcionan condiciones para que identifiquen, examinen y comuniquen ideas matemáticas (Gamboa 2007). Además, el uso de la tecnología puede llegar a ser una herramienta poderosa para que los estudiantes creen distintas representaciones de ciertas tareas y sirve como un medio para que formulen sus propias preguntas o problemas, lo que constituye un elemento importante en la adquisición de una forma matemática de pensar (Barrera y Santos, 2001).
En este contexto, dado que la tecnología puede modificar sustancialmente la forma en que las ideas matemáticas se desarrollan, es natural preguntar: ¿qué elementos aporta el uso de tecnologías digitales al pensamiento matemático? ¿Qué papel juega el uso de un software en la construcción de demostraciones o justificaciones matemáticas? ¿Cómo contribuye a desarrollar o comprender ideas matemáticas el uso de sistemas computacionales en actividades de aprendizaje? ¿En qué medida cambia la concepción de las matemáticas en los estudiantes que se involucran en procesos de resolución de problemas mediados por el uso de calculadoras o computadoras?
El uso de diversas herramientas computacionales puede aportar elementos variados al proceso de construcción del conocimiento; por ejemplo, el empleo del software dinámico ofrece claras ventajas a los estudiantes para identificar y explorar diversas relaciones matemáticas. Cuando los estudiantes interactúan con construcciones dinámicas, a través del uso del arrastre y las herramientas de medida, pueden identificar relaciones entre los elementos de una configuración, así como discriminar entre la información que puede resultar relevante de aquella que no lo es; por ejemplo, a través de ocultar elementos de una construcción. ¿Qué tipo de recursos necesitan los estudiantes para que el resultado de sus exploraciones incluya relaciones o resultados relevantes en su proceso de aprendizaje? Es una pregunta que se relaciona con la disposición matemática que los estudiantes posean, y está ligada con los valores y creencias que se formen durante sus experiencias de aprendizaje de la disciplina. Una meta importante es que los estudiantes en algún momento identifiquen el uso de la computadora o la calculadora como elementos que les pueden permitir ampliar y reorganizar sus capacidades cognitivas. En este sentido, la tecnología funciona como una lente que permite observar, explorar y analizar situaciones matemáticas desde diversos ángulos o perspectivas.
El software de geometría dinámica es un recurso innovador e importante en el aprendizaje de la geometría y otras áreas, porque permite la exploración, la construcción de figuras con ciertas propiedades, la visualización de relaciones e invariantes entre objetos geométricos y la posibilidad de transformar las construcciones en tiempo real (Arcavi y Hadas, 2000), de esta manera se puede lograr que los estudiantes articulen conceptos matemáticos en redes conceptuales robustas1. Sin embargo, se debe tener en cuenta que “la tecnología no puede sustituir la labor del profesor de matemáticas, ni puede ser utilizada como un reemplazo de conocimientos básicos” (NCTM, 2000, p. 26), por el contrario, al profesor le corresponde tomar la decisión sobre cuándo y cómo un estudiante debe hacer uso de las tecnologías digitales, además de verificar los procesos matemáticos realizados por el estudiante y prestarles ayuda cuando la solución no es la correcta o cuando la observación que realizan no se orienta en la ruta de instrucción planteada. Su función es proponer las actividades y ser un guía de los procesos de aprendizaje (Gamboa, 2007).
¿Cuáles son las características del proceso que sigue un estudiante para transformar un artefacto en un instrumento2 en la resolución de problemas? ¿Cuál es el papel de las
representaciones ejecutables en el proceso de aprendizaje? ¿Qué aspectos del pensamiento matemático se destacan en la resolución de problemas con la ayuda de las tecnologías digitales? ¿Qué características deben poseer las actividades de aprendizaje donde el uso de calculadoras o computadoras propicie en los estudiantes el desarrollo de procesos inherentes del quehacer matemático? Estas preguntas están formuladas con la intención de analizar la importancia de utilizar estrategias de instrucción que permitan a los estudiantes incorporar en su reflexión matemática el empleo de las herramientas computacionales.
Se enfatiza la exploración de aquellos elementos que permitan al estudiante ampliar aspectos del pensamiento matemático con el apoyo de las herramientas tecnológicas: identificar información, encontrar relaciones entre datos e incógnitas, resolver casos particulares, formular conjeturas, proporcionar pruebas, comunicar resultados; de manera que los estudiantes desarrollen recursos y estrategias que les permitan apropiarse de las tecnologías digitales, entendidas como artefactos, y transformarlas en instrumentos para la comprensión de ideas matemáticas (Guin, Ruthven y Trouche, 2005).
La idea principal de este trabajo consiste en observar el desarrollo de actividades de instrucción, en las que se hace uso de las tecnologías digitales, con un enfoque basado en la resolución de problemas, con el objetivo de documentar y analizar el proceso de génesis instrumental (transformación de un artefacto en un instrumento), así como las implicaciones de este proceso en los aspectos pedagógicos, epistemológicos y didácticos del aprendizaje.
1.2. ANTECEDENTES
El proceso que desarrolla un estudiante para transformar un artefacto en un instrumento se denomina génesis instrumental. ¿Cuál es la importancia del proceso de génesis instrumental en el desarrollo cognitivo de los estudiantes? Esta pregunta está encaminada a orientar el problema de investigación. En este sentido, es importante analizar la relación entre las características del artefacto con la actividad del estudiante, sus ideas previas y sus métodos de trabajo. Es decir, se pretende analizar la relación de modificación mutua entre el artefacto y el estudiante, con base en el supuesto teórico de que: el aprendizaje no es fenómeno exclusivo de la mente, sino un producto de la relación entre las estructuras mentales y las herramientas intelectuales originadas por la cultura (Pea, 1987); lo cual implica que el conocimiento del estudiante dirige la manera en que el artefacto es usado y por tanto da forma al instrumento3 (instrumentalización), a la vez que las potencialidades y
restricciones del artefacto influyen en las estrategias de solución de problemas que lleva a cabo el estudiante, así como en las correspondientes concepciones emergentes (instrumentación) (Trouche 2009).
Para los fines que se persiguen en esta investigación, interesa analizar y documentar el proceso de interacción del estudiante con las herramientas tecnológicas cuando resuelve problemas, observando aspectos relacionados con su uso, las representaciones que emplea, el tipo de conjeturas y conclusiones que obtiene y los argumentos que proporciona, con la finalidad de identificar aquellas características de las tareas y de la acción del profesor que pueden ayudar a los estudiantes a obtener una comprensión profunda de los conceptos matemáticos, así como identificar las ventajas y desventajas que se presentan al trabajar con las tecnologías digitales.
¿Qué es una actividad de aprendizaje matemático? ¿Qué objetivos se persiguen al diseñar una actividad? ¿Cuáles son las características de estas actividades? ¿Cómo diseñar actividades de aprendizaje matemático en las que el uso de un software dinámico pueda propiciar en los estudiantes el desarrollo de procesos consistentes con el quehacer de la disciplina? ¿Qué tipo de preguntas pueden formular los estudiantes como resultado de utilizar de forma sistemática Cabri Geometry en la ejecución de las actividades de aprendizaje matemático? ¿En qué medida el software dinámico4 funciona como una herramienta útil para que los estudiantes visualicen, exploren y construyan relaciones matemáticas durante sus experiencias de aprendizaje? Estas son algunas de las preguntas que guían la discusión encaminada a identificar elementos de las actividades de aprendizaje matemático en las que se promueve el uso de herramientas tecnológicas, con el fin de analizar el proceso que siguen los estudiantes al apropiarse de la herramienta para resolver problemas y reestructurar diversos elementos cognitivos en su red conceptual.
A continuación se presenta un análisis de diferentes trabajos de investigación en los que se ha tratado de entender el proceso de génesis instrumental. Esta revisión de la literatura es la base para justificar la relevancia del problema y las preguntas de investigación de este trabajo.
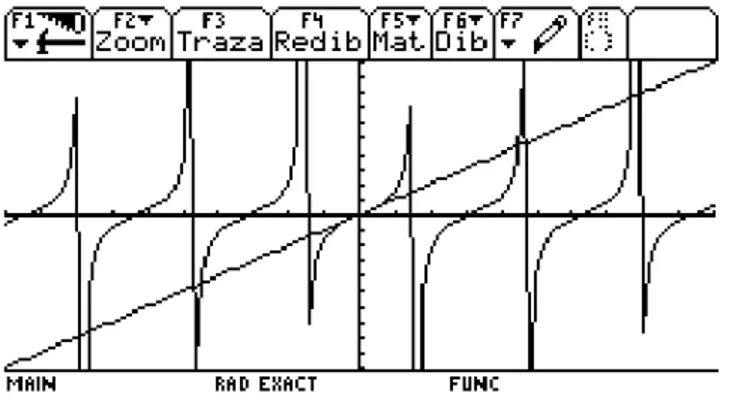
Guin y Trouche (1999), analizaron algunas dificultades que muestran estudiantes al tratar de resolver la ecuación: tan (x) = x (figura 1.1). El estudio se aplicó a 34 alumnos, de los
cuales, cuatro señalaron que existen una infinidad de soluciones. Los demás estudiantes mencionaron un número finito de soluciones.
Figura 1.1. Gráfica de f(x) = tan(x) y f(x) = x. (Guin y Trouche, 1999).
Los autores mencionan que la dificultad estriba en que los estudiantes no consideran a la pantalla como si fuera una ventana en donde solamente se observa una parte de la gráfica. Otra dificultad es interpretar lo que se percibe en esa ventana. Se señala además que algunos alumnos consideran a las asíntotas como parte de la representación gráfica de la función y por tanto, proponen más intersecciones; y otros señalan que la intersección entre las dos funciones cerca del cero se da en una infinidad de puntos. Así, semejantes interpretaciones han permitido preguntarse sobre la matemática creada por el estudiante en actividades donde se emplea el uso de tecnología (Artigue, 2002). ¿Por qué suceden estos fenómenos y cómo afectan el conocimiento matemático del estudiante? Lo anterior es un ejemplo donde se identifica una falta de integración tecnológica en actividades matemáticas.
El uso de recursos tecnológicos existe pero qué pasaría si el problema se representa en un software dinámico y sobre todo si el estudiante realiza la construcción y la manipula. Podría parecer que el propósito es mostrar que el uso de tecnología no es adecuado en el aula de matemáticas, pero más bien, interesa enfatizar la importancia de hacer un uso reflexivo de la misma. La intención es promover habilidades de visualización matemática en un software dinámico en el sentido de Hershkowitz (citado por Arcavi, 2002), que trata la visualización matemática como la habilidad de representar, transformar, generar, comunicar, documentar, y reflexionar sobre información visual.
observará la variación de los parámetros en un contexto gráfico. La finalidad de lo anterior es la integración del artefacto (calculadoras gráficas) a las formas de trabajo del estudiante para que construya conocimiento matemático. En la investigación se consideró como marco referencial a la génesis instrumental, señalando que la problemática tiene que ver con una relación dialéctica técnica-conceptual, es decir, el uso del artefacto (calculadoras) incrementa las técnicas y habilidades, pero ¿de qué manera la herramienta afecta elementos conceptuales en el aprendizaje? Para responder a tal problemática es de utilidad el constructo de génesis instrumental ya que es una herramienta que permite entender la dualidad existente entre instrumentalización (esquemas de uso) e instrumentación (esquemas de acción instrumentada).
En tal investigación se han encontrado avances en cuanto a los diferentes tipos de esquemas mentales que los alumnos desarrollan al resolver la actividad propuesta. Los autores reportan que un alto porcentaje de alumnos responden equivocadamente al usar la calculadora graficadora, cosa que no sucede al trabajar las mismas actividades en un ambiente de papel y lápiz. Por ejemplo, algunos alumnos empiezan a variar el parámetro c de la parábola y observan su comportamiento.
Se observa que la actividad carece de ciertas características que no permiten al estudiante integrar la tecnología en su actividad matemática, ya que es una actividad que solo maneja el uso de la calculadora. ¿Qué pasaría si estas actividades se llevarán a un software dinámico donde el estudiante manipule la construcción? ¿Cuáles son los conocimientos previos que necesita el estudiante para resolver la tarea? Es importante señalar que en esta tarea tampoco se abordan cuestiones relativas a la generalización o extensión de la tarea. Además no se hace mención de la organización de los estudiantes, esto es, si existió el trabajo en equipo o individual.
De la misma manera que el uso de las calculadoras ha conducido a una reflexión sobre su utilización en el desarrollo del sentido numérico de los estudiantes, los sistemas computacionales simbólicos han permitido reflexionar sobre el desarrollo del sentido estructural algebraico, se espera que el empleo del software de geometría dinámica aporte elementos relevantes que permitan diseñar actividades para que los estudiantes desarrollen un pensamiento geométrico (Arcavi y Hadas, 2000).
un estudiante al utilizar y apropiarse de una herramienta (artefacto) (Rabardel, 1995). Las actividades propuestas consistían en presentar ejemplos de aritmética y álgebra, los cuales se abordaron con el software mencionado, como se ilustra a continuación (figura 1.2)
Figura 1.2. Ejemplos de álgebra en un ambiente computarizado (Cedillo, 2006)
El investigador argumenta que los ejemplos anteriores permiten ver las capacidades de procesamiento numérico y simbólico de un Sistema Algebraico Computarizado (SAC); además de que ofrece facilidades para graficar y transitar de la información proporcionada a sus representaciones analítica y tabular.
Las actividades presentadas anteriormente muestran poco o nulo desarrollo de habilidades matemáticas en los usuarios, solo buscan el desarrollo de la manipulación del software, se quedan en lo numérico y algebraico sin tratar de que el estudiante profundice o realice extensiones. El autor menciona que el SAC ayuda a realizar representaciones graficas, pero no presenta actividades que involucren una representación geométrica de un problema que le permita al usuario observar, identificar y conjeturar patrones numéricos o variantes de una gráfica por ejemplo.
Santos Trigo (2008), implementó una actividad con un grupo de estudiantes, que consistía en repartir un terreno de forma cuadrada en dos partes iguales, de manera que cada parte tuviera la misma área. Cabe señalar que, aunque el investigador no hace uso del proceso de génesis instrumental, existe la utilización de tecnología, lo cual permite al estudiante formular conjeturas, justificar y dar una extensión del problema, además de buscar desarrollar en los estudiantes habilidades en la utilización del software dinámico.
matemático. Por ejemplo, la utilización del software dinámico favoreció la construcción y uso de representaciones dinámicas de los objetos matemáticos involucrados en el problema, además de desarrollar algunos aspectos del pensar matemáticamente como búsqueda de conjeturas o relaciones, así como los medios para justificarlas. Por otro lado, el autor menciona que durante el desarrollo de la actividad el estudiante explora comandos dentro de la herramienta (longitud, perímetro, área, lugar geométrico…) que resultaron importantes en la búsqueda de conjeturas que ayudan a solucionar el problema.
Santacruz (2009) desarrolló un proyecto de investigación, donde el problema planteado hace referencia a la actividad mediada por instrumentos y la génesis instrumental, en relación con la noción de orquestación instrumental. En este sentido, reconoce que todo aprendizaje de una noción matemática se encuentra mediado por instrumentos y que dicha mediación influye en la naturaleza transpuesta del saber matemático, las acciones del profesor, la construcción del conocimiento por parte del estudiante y la organización particular de la clase u orquestación instrumental. Así mismo, propone un papel protagónico del profesor como gestor de los sistemas de instrumentos en el contexto de la clase, es decir, como un acompañante en los procesos tanto de construcción de aprendizaje, como de génesis instrumental de los estudiantes. Para el desarrollo de la investigación plantea un diseño metodológico pensado para el diseño de situaciones didácticas cuando se tiene en consideración, alrededor de la noción de actividad, la mediación de instrumentos en el aprendizaje y la enseñanza de las matemáticas, a partir de la metodología de la ingeniería didáctica, a nivel de micro ingeniería. Las situaciones didácticas son diferentes estrategias de aprendizaje que permitan observar los marcos teóricos centrales de la investigación.
Del Castillo y Montiel (2007) analizaron cómo los estudiantes pueden acceder al concepto de función (no sólo mediante representaciones geométricas sino también numéricas) a partir de un entorno de Geometría Dinámica. La investigación se realizó con estudiantes del Nivel Medio Superior de un C. B. T. i. s. de quinto semestre, donde el uso de gráficas, tablas y la dualidad instrumentación-instrumentalización les ayudaría a observar y analizar la integración del instrumento por el estudiante. Así, este trabajo hace uso de la tecnología y toma como marco a la Génesis Instrumental buscando su integración al estudiante para que construya conocimiento matemático (función).
conclusión, los estudiantes responden que la función esta acotada, una razón es que la asocian a funciones trigonométricas (como acotadas) y por la percepción que observan en la pantalla de sus calculadoras. Así, los autores reportan que los estudiantes responden equivocadamente al usar la calculadora gráfica, cosa que no sucede al trabajar las mismas actividades a papel y lápiz.
Al analizar los diferentes reportes de investigación de esta sección, la mayoría no especifican elementos en el diseño e implementación de actividades que podrían ser de utilidad para los profesores de matemáticas. Así, muchas investigaciones solo presentan la actividad, olvidándose: ¿Por qué esa actividad? ¿Qué objetivos de aprendizaje persigue? ¿Para qué estudiantes se recomienda? ¿Qué conocimientos previos se necesitan para abordar el problema? ¿Para qué nivel educativo? Es por ello que en este trabajo se establece que una actividad de aprendizaje matemático debe considerar el conocimiento previo del estudiante y proveerle de elementos para el desarrollo de nuevos conceptos que se articulen con los ya existentes en su red conceptual. Así, es importante que una tarea de aprendizaje cuente con los siguientes elementos: (i) los objetivos de aprendizaje, (ii) los elementos matemáticos estructurados en torno a los objetivos de aprendizaje, (iii) el escenario para desarrollar la tarea y (iv) un proceso inquisitivo para desarrollarla (Barrera, 2008).
Algunas actividades dan a conocer el enunciado de la actividad y solicitan al estudiante que interactué con el software realizando una construcción que represente los datos de la tarea; sin embargo, no se discute con precisión qué principios de la resolución de problemas fueron empleados, además del uso de la tecnología para su diseño, ni cómo fueron utilizados.
En los reportes de investigación, se menciona, como parte de la metodología que los estudiantes tuvieron sesiones previas de entrenamiento para familiarizarse con el uso del software y en otras solo se le presentan al estudiante construcciones fijas, establecidas, donde solo se les pide discutir conceptos matemáticos o propiedades de objetos geométricos que son importantes para resolver la tarea. También se hace mención de la importancia de las características y número de participantes, así como las condiciones del lugar de instrucción, por ejemplo: aula de cómputo, calculadora, software dinámico, cañón, etc. En este sentido, se le da gran importancia al escenario de instrucción, pero no se discute a profundidad la organización del escenario, tampoco se analizan explícitamente los conocimientos matemáticos e informáticos previos necesarios que debe tener el estudiante para que pueda abordar la tarea de aprendizaje.
matemática el uso de las herramientas computacionales, así mismo hacer énfasis en la exploración que le permita ampliar los diferentes elementos del pensamiento matemático; de manera que una herramienta no solamente se maneje para realizar cálculos o procedimientos que con lápiz y papel resultan tediosos para los estudiantes, más bien se espera que puedan integrar la herramienta a su estructura cognitiva para construir conocimiento y organizarlo en una red conceptual robusta. Además se considera que este trabajo pueda ofrecer información que permita completar los resultados de las investigaciones previas.
1.3. OBJETIVO GENERAL
El objetivo general de este trabajo es identificar los diversos elementos cognitivos que tienen lugar en el proceso de transformación de un software dinámico, considerado como artefacto, en un instrumento, en un contexto de resolución de problemas.
OBJETIVOS PARTICULARES Identificar, caracterizar y analizar:
(i) El papel de las representaciones ejecutables en el proceso de transformación de un artefacto en un instrumento.
(ii) La función de una aproximación inquisitiva y la justificación de resultados durante la construcción de conocimiento matemático mediada por el uso de tecnologías digitales. (iii) La relevancia de las actividades de aprendizaje matemático en el proceso de articulación de conceptos matemáticos en redes conceptuales robustas.
Los objetivos planteados tienen como fin, documentar la importancia de utilizar estrategias de instrucción que permitan a los estudiantes incorporar en su reflexión matemática el empleo de distintas herramientas computacionales, así como los aspectos asociados con el diseño de las herramientas que facilitan o dificultan su uso en la comprensión y resolución de problemas por parte de los estudiantes. También sobre el diseño de las actividades y la importancia de la utilización de herramientas computacionales en la construcción del conocimiento matemático mediado por el uso de tales herramientas.
1.4. PREGUNTAS DE INVESTIGACIÓN
estudiantes. Así como, documentar el proceso de transformación de un artefacto en un instrumento de resolución de problemas y las implicaciones de ésta transformación en los procesos didácticos. En particular el software dinámico (Cabri-Geometry) se puede transformar en un instrumento que ayude a los estudiantes a generar representaciones que permiten visualizar elementos claves alrededor de la solución de un problema. Específicamente, interesa detectar en qué momento el estudiante se apropia de la herramienta y la utiliza en la resolución de las actividades matemáticas donde involucra el planteamiento de conjeturas, la construcción y uso de diferentes representaciones, la búsqueda de relaciones, así como la presentación y comunicación de resultados.
2. ¿Qué aspectos del pensamiento matemático se favorecen durante la resolución de problemas con el uso de las tecnologías digitales?
La actividad de aprender no se reduce a memorizar un conjunto de reglas, principios, algoritmos, teoremas, definiciones y procedimientos que pueden aplicarse en la solución de problemas: es una perspectiva en la que existe una conceptualización dinámica de las matemáticas (Santos 2003). Las actividades propuestas pretenden desarrollar en los estudiantes un punto de vista matemático que valore los procesos de matematización y abstracción y tener la tendencia a aplicarlos, mediante un ambiente en donde la reflexión y comunicación de ideas matemáticas jueguen un papel central en los procesos. Con esta pregunta de investigación, se pretende documentar y analizar cuáles procesos del pensar matemáticamente se ven apoyados a través del uso sostenido de la herramienta, es decir, en qué medida el proceso de instrumentación apoya la construcción de una forma matemática de pensar.
3. ¿Qué características de las tareas de aprendizaje y de las herramientas computacionales, propician que los estudiantes estructuren redes conceptuales robustas?
CAPÍTULO 2
MARCO CONCEPTUAL
Las funciones mentales superiores y las acciones humanas en general están mediadas por el uso de herramientas y signos
(Wertsch, 1993, p. 28).
2.1. INTRODUCCIÓN
El Consejo Nacional de Profesores de Matemáticas de los Estados Unidos (NCTM, 1991), reconoce la importancia de que la enseñanza de las matemáticas se lleve a cabo de manera activa, desarrollando una forma matemática de pensar en los estudiantes. El surgimiento de software para la enseñanza y su incorporación al aula, exige que el profesor diseñe actividades apropiadas que ayuden al estudiante en el aprendizaje de conceptos matemáticos, apoyándose en el uso de la computadora o las calculadoras.
La existencia de la computadora plantea a los educadores matemáticos [y a los profesores] el reto de diseñar actividades que tomen ventaja de aquellas características [de las tecnologías digitales] con potencial para apoyar nuevos caminos de instrucción (Arcavi y Hadas, 2000, p. 41).
El logro de los objetivos anteriores requiere de un entendimiento profundo de la forma en que se modifican los procesos de aprendizaje cuando se incorpora el uso de las tecnologías digitales al desarrollo de tareas de instrucción, y esto a su vez, necesariamente requiere de la adopción de una postura teórica que oriente el proceso de comprensión de las complejidades presentes en el entendimiento de ideas matemáticas por parte de los estudiantes. En este trabajo, el fundamento teórico que permitirá dar sentido a los datos obtenidos de experiencias de aprendizaje se organiza en un marco conceptual, el cual está integrado por una estructura de justificaciones que articula diferentes elementos o constructos teóricos, con base en explicaciones de por qué se adoptan esas ideas o conceptos, así como sus posibles relaciones, y no otras, para respaldar las características relevantes del fenómeno analizado (Eisenhart, 1991; Lester, 2005).
El marco conceptual de este trabajo está integrado por tres elementos, el primero es el principio de la mediación instrumental, el cual establece que las características de las herramientas utilizadas en el proceso de aprendizaje determinan la forma en que se adquiere el conocimiento. Los artefactos, como objetos materiales, han influido en el desarrollo de las matemáticas, así como en su aprendizaje. Por ejemplo, en las clases de matemáticas se usan algunos objetos manipulables como el ábaco, o las regletas de Cuisenaire, para ejecutar y aprender a realizar operaciones aritméticas. Asimismo, los sistemas simbólicos (por ejemplo, el sistema decimal de numeración o la notación algebraica) son herramientas que indudablemente influyen en el aprendizaje, desarrollo y avance en la generación de nuevos conocimientos matemáticos. Como parte de este constructo se analiza una característica que distingue a las tecnologías digitales del resto de las tecnologías para aprender matemáticas: la posibilidad de construir y operar con representaciones ejecutables.
Relacionado con el principio de mediación instrumental, se incluye el marco de la génesis instrumental, el cual será utilizado para analizar y tratar de comprender el proceso mediante el cual un artefacto se transforma en un instrumento, es decir, la forma en cómo una herramienta material, a través de la actividad del sujeto al resolver problemas se constituye en una herramienta simbólica, la cual puede integrarse al sistema cognitivo de la persona e influir en la forma en que ésta construye su conocimiento. Completa el marco de la investigación el modelo de resolución de problemas, el cual constituye el escenario en el que se lleva a cabo los procesos de mediación instrumental y génesis instrumental.
describan patrones e invariantes de diversa naturaleza y que desarrollen una actitud inquisitiva, lo cual significa que el objetivo central de resolver un problema no es encontrar una solución, sino el desarrollo de diversos aspectos del pensamiento matemático como la formulación de nuevos problemas, conjeturas, heurísticas o aproximaciones, así como la búsqueda de relaciones y extensiones de los problemas, y diversas formas de justificación de conjeturas.
Las matemáticas revelan patrones escondidos que ayudan a comprender el mundo que nos rodea. El proceso de “hacer” matemáticas es más que cálculos y deducciones; involucra la observación de patrones, la prueba de conjeturas, la estimación de resultados (NRC, 1989, p. 31; citado en Schoenfeld, 1992).
2.2. MEDIACIÓN INSTRUMENTAL
Pea y Roy (1987) desarrollan la idea de que los instrumentos de mediación funcionan como tecnologías cognitivas que ayudan a organizar, amplificar y reorganizar el conocimiento matemático. En esta dirección, Moreno (2002) menciona que no hay actividad cognitiva al margen de la mediación instrumental, en otros términos, toda acción orientada a un aprendizaje, es una acción instrumental. Una tesis central en este marco es que la presencia de los instrumentos de mediación transforma de raíz la estructura cognitiva del estudiante (Werstch, 1993), en forma análoga a lo que ocurre ante la presencia de una herramienta material vinculada a un proceso técnico.
En el desarrollo de la biología. ¿Sería concebible en este momento imaginar el estado actual de esta ciencia sin los recursos tecnológicos que se han desarrollado simultáneamente con sus cuerpos conceptuales? Pensemos en el microscopio; este no solo es un instrumento que ayuda al patólogo experimental, sino que le da acceso a un nivel de estructuración de la realidad imposible de alcanzar sin dicho instrumento. Entonces su acción cognitiva está mediada por el microscopio y el conocimiento producido está afectado de modo sustancial por él (Moreno y Waldegg, 2002, p. 57).
de aprendizaje, es decir que se establezca una relación entre el software y el sujeto (su estructura cognitiva), orientada hacia el aprendizaje y la construcción de ideas matemáticas, de forma análoga a la relación entre el músico y el instrumento, cuando se interpreta una pieza musical.
Cuando un estudiante se auxilia de una calculadora para realizar ciertas operaciones en un problema cuya solución ya ha encontrado, tal vez de forma intuitiva, esa calculadora es un auxiliar de su cognición. En tal caso la calculadora es un artefacto pues se utiliza como un elemento complementario al pensamiento del estudiante, ya que no modifica, sino sólo complementa el pensamiento del estudiante. Por otra parte, es posible que el uso continuo del artefacto produzca cambios a nivel de las estrategias de solución de problemas, en cambios a nivel de la manera en cómo se plantea o entiende el problema, o sobre como se justifican resultados. En otras palabras, puede ocurrir que el pensamiento del estudiante quede afectado radicalmente por la presencia del artefacto, en este caso el artefacto se ha convertido en un instrumento de aprendizaje, ya que la herramienta estructura las acciones que lleva a cabo el estudiante.
Un elemento que caracteriza a las tecnologías digitales son sus sistemas de representación ya que son sistemas ejecutables (procesables, manipulables), que “simulan” funciones cognitivas que anteriormente eran exclusivas de los seres humanos.
En sus versiones informáticas, la forma general de representación tiene una característica central: es ejecutable. Esto significa, dicho de forma simplificada, que una vez instalados en el lenguaje del medio ambiente computacional, las nuevas representaciones son procesables, manipulables. (Moreno, 2002b)
Estos sistemas de representación ejecutables pueden permitir al estudiante trabajar un problema desde diferentes enfoques cognitivos, por ejemplo, tomar un punto de vista concreto al analizar una función. Los sistemas de representación no cumplen tan solo una función de comunicación sino que también ofrecen un medio para el tratamiento de la información y son fuente de generación de significados. El uso de las tecnologías digitales puede permitir a los estudiantes desarrollar nuevos métodos, nuevas estrategias, por ejemplo de graficación, a partir de las capacidades de procesamiento de esas herramientas (Moreno, 2002).
2.3. GÉNESIS INSTRUMENTAL
La génesis instrumental, es un proceso complejo, vinculado al desarrollo de formas de pensar apoyadas en características de un artefacto (potencialidades y limitaciones); a la actividad que un sujeto desarrolla al utilizar un artefacto; así como a sus conocimientos y métodos de trabajo con el mismo (Verillon y Rabaldel, 1995). Este constructo teórico da cuenta del proceso mediante el cual un estudiante integra los esquemas de uso del artefacto en su estructura cognitiva, los cuales pueden apoyarlo en el desarrollo de una forma matemática de pensar (Artigue 2002). Se habla de un instrumento5 cuando hay una relación significativa entre el artefacto (o parte del artefacto) y la estructura mental del estudiante para hacer frente a un determinado tipo de tarea, en nuestro caso actividades matemáticas, que el estudiante resolverá con el uso de software dinámico. Así, “los instrumentos son entidades mixtas, compuestas de una parte de artefacto y de esquemas de uso” (Trouche, 2009, p. 6). Durante el proceso de génesis instrumental, el estudiante desarrolla estructuras mentales que organiza para resolver problemas y entender conceptos con base en los medios que ofrece el uso de un artefacto. Ahora bien, para entender esta construcción, la génesis instrumental debe considerarse como una dualidad “instrumentalización-instrumentación” producto del uso del artefacto, para abordar tareas de aprendizaje por parte del estudiante.
En el proceso de instrumentalización, el estudiante reconoce y se adapta al artefacto, se apropia de sus características; es decir, conoce sus bondades y potencialidades, y en algún momento puede orientar las mismas hacia usos específicos durante la resolución de problemas. El nivel de logro que se obtenga en la fase de instrumentación, estará condicionado por el nivel de manejo operativo y funcional que haga del artefacto (instrumentalización). Durante la génesis instrumental se pueden identificar varias etapas: (i) etapa de descubrimiento y de selección de los comandos relevantes, (ii) etapa de personalización y (iii) etapa de transformación (Trouche, 2005).
Artigue (2002) menciona que en la instrumentación, la génesis instrumental está dirigida hacia el estudiante, conduciendo al desarrollo o la apropiación de los esquemas de acción instrumentada, la cual progresivamente toma forma de técnicas que permiten una respuesta efectiva hacia tareas específicas (búsqueda de patrones, detección de invariantes, etcétera). Es decir, el desarrollo y apropiación de los esquemas de acción instrumentada ayudan al estudiante a entender las ventajas y restricciones del artefacto y así apoyarse en ellas para estructurar una forma matemática de pensar. En otras palabras, la instrumentalización es un reconocimiento de las funciones del artefacto (Cabri-Geometry) y la instrumentación es una construcción que se da cuando el usuario utiliza la herramienta y ésta le permite desarrollar métodos y técnicas para resolver problemas. La instrumentalización elabora esquemas de uso y la instrumentación esquemas de acción instrumentada (Guin y Trouche, 1999).
La primera fase de la génesis instrumental consiste en la producción de esquemas de uso, orientados a la utilización de los comandos e instrucciones básicas de la herramienta. Los esquemas de uso están relacionados con el artefacto, es decir, el estudiante inicia el reconocimiento de la herramienta-artefacto (Cabri-Geometry). A través del uso sostenido de la herramienta, se estabilizan los esquemas de uso, y a partir de ellos se estructuran técnicas que son el antecedente de los esquemas de acción instrumentada; los cuales corresponden a una interacción entre las potencialidades del artefacto y los esquemas mentales del estudiante para originar formas novedosas de pensar o razonar al resolver problemas. Los esquemas de acción instrumentada se construyen con base en los esquemas de uso elementales por medio de la integración de las características de la herramienta en la estructura cognitiva del estudiante.
Artefactos primarios. Se refiere a la herramienta, específicamente a cómo se utiliza ordinariamente.
Artefactos secundarios. Consiste en representaciones de los artefactos primarios y sus acciones al usarlo.
Artefactos terciarios. Corresponde al desarrollo cognitivo por simulación de situaciones matemáticas que desarrollan los estudiantes entrenados.
En esta investigación la orquestación permite analizar la relación entre la idea matemática o concepto que se enseña y las formas en que el artefacto es aplicado para entender esa idea, es decir, a partir de las potencialidades y limitaciones de la herramienta, el estudiante puede generar hipótesis acerca de cómo resolver un problema, crear o modificar técnicas para abordarlo, así como diversas formas de justificación. El papel del profesor durante la orquestación instrumental es el de un guía, de un mediador del aprendizaje (un director de orquesta) (Guin y Trouche, 1999a).
2.4. RESOLUCIÓN DE PROBLEMAS COMO MÉTODO DE
APRENDIZAJE
Con la integración de la resolución de problemas en el marco conceptual, se busca contar con un conjunto de principios que orienten el diseño de actividades de aprendizaje: (i) que motiven al estudiante a quererlas resolver, (ii) que permitan establecer conexiones entre los conocimientos matemáticos presentes en la red conceptual del estudiante y (iii) que permitan abordar y resolver la tarea por distintos medios, además de que promuevan el desarrollo de diversos aspectos del pensamiento matemático a través de la experimentación así como la discusión de ideas. La adopción del marco de resolución de problemas, proporciona también un contexto para la ejecución de las tareas de instrucción en el que el objetivo tradicional de la fluidez algorítmica se sustituye por el objetivo de fluidez procedimental6 y la problematización de las tareas. Esto es, que los estudiantes puedan representar un problema en diversos sistemas de representación y sean capaces de interpretar los resultados del tratamiento que se dé a tales sistemas mediante las herramientas disponibles, aquí el papel de los profesores es proporcionar el contexto para que los estudiantes planteen conjeturas, establezcan conexiones, elaboren argumentos y comuniquen sus resultados.
permita identificar y ampliar los aspectos del pensar matemáticamente? ¿Qué papel juegan las herramientas computacionales en el proceso de formular y validar conjeturas en los procesos del aprendizaje de las matemáticas? ¿Cómo contribuye a desarrollar un punto de vista matemático el uso de sistemas computacionales en actividades de aprendizaje? ¿En qué medida cambia la concepción de las matemáticas en los estudiantes que se involucran en procesos de resolución de problemas mediados por la tecnología? ¿Qué tan confiables son los resultados matemáticos obtenidos con el uso de herramientas computacionales cuando se diseñan actividades de aprendizaje? En este sentido, Santos y Moreno (2002) resaltan que el uso de las tecnologías digitales con el tiempo se van convirtiendo en una herramienta poderosa para que los estudiantes:
(a) den sentido a la información en un problema, (b) realicen conjeturas y
(c) examinen diferentes estrategias en la resolución de problemas.
Un principio fundamental, al considerar la resolución de problemas en el aprendizaje de las matemáticas, es aceptar que la actividad de aprender no se reduce a un conjunto de reglas que pueden aplicarse en la solución de problemas: es una perspectiva en la que existe una conceptualización dinámica de las matemáticas y en la cual es importante identificar elementos que ayuden a desarrollar y promover una disposición matemática en los estudiantes (Santos, 2007, p. 11).
Barrera (2008) menciona que una idea importante en la perspectiva de resolución de problemas, es que el aprendizaje de las matemáticas involucre el desarrollo de cierta disposición de los estudiantes para explorar e investigar relaciones matemáticas, emplear distintas formas de representación al analizar fenómenos particulares, usar diversos tipos de argumentos y comunicar resultados. Aprender matemáticas es ante todo, desarrollar una actitud que valore los procesos del pensar matemáticamente.
Aprender a pensar matemáticamente significa (a) desarrollar un punto de vista que valore el proceso de matematización y abstracción y tener la tendencia a aplicarlos, y (b) desarrollar competencias con las herramientas de trabajo y usarlas para lograr la meta de entender las estructuras y desarrollar el sentido matemático (Schoenfeld, 1994, p. 60).
(i) Un objetivo de aprendizaje. Aquí se establecen los elementos conceptuales a ser desarrollados y articulados por el estudiante durante la realización de la actividad en el aula.
(ii) Elementos matemáticos estructurados por el objetivo de aprendizaje. Se identifican los elementos matemáticos de la actividad para su construcción; los datos, utilizando los conocimientos previos del estudiante y articulándolos para generar nuevos.
(iii) Escenarios para desarrollar la actividad. Es el contexto en el que se ejecuta la actividad, la cual debe incluir infraestructura y equipo necesario. La organización de los estudiantes para realizar la tarea será en forma individual y después en equipo con el fin de que el estudiante platee conjeturas, establezca conexiones y argumente sus resultados para comunicarlos a sus pares y así, fundamenten y propongan una posible solución del problema.
(iv) Un proceso inquisitivo. Consiste en formular preguntas o dilemas en caminados a articular los elementos matemáticos iníciales con aquellos que conduzcan a la consecución de lo planteado en el objetivo de aprendizaje y posibles extensiones. (Barrera, 2008)
En este trabajo se analiza el proceso de implementación de tareas no rutinarias que pueden permitir a los estudiantes adquirir una forma matemática de pensar y, con el empleo de herramientas computacionales, puedan no solo hacer más potentes algunas heurísticas (estrategias de resolución de problemas), sino también desarrollar una disposición y formas de trabajo donde constantemente busquen y examinen diferentes tipos de relaciones, planteen conjeturas, utilicen distintos sistemas de representación, establezcan conexiones, empleen argumentos y comuniquen sus resultados (Santos, 2003).
Figura 2.1: Estructura del marco utilizado en el análisis del proceso de génesis instrumental.
Fluidez Representacional
Artefacto Estudiante
Software dinámico
Instrumentalización Instrumentación
Reconocimiento de
funciones Construcción, entendimiento y
desarrollo de la actividad matemática
Mediación Instrumental
Esquemas de uso
Orientada a un aprendizaje, en un contexto de resolución de problemas
Nuevo potencial
Restricciones Instrumento Estudiante
Génesis Instrumental
CAPÍTULO 3
METODOLOGÍA
3.1 INTRODUCCIÓN
La metodología utilizada en esta investigación es de corte cualitativo. Con base en ella se busca realizar descripciones y análisis del proceso de génesis instrumental ocurrido durante el desarrollo de una tarea de aprendizaje matemático que abordaron estudiantes del nivel superior, haciendo uso del software dinámico Cabri Geometry.
Una de las características especiales del paradigma de investigación cualitativa es el uso del estudio de caso, en el que se determinan las características y circunstancias que subyacen a un caso particular para explorar y analizar aquellos elementos que pueden servir como un ejemplo de algo más general, “no con la precisión de las ciencias exactas, sino sugestivamente como ilustración de una verdad más general y compleja” (Ernest, 1998, p. 34). La investigación cualitativa construye descripciones ricas del caso bajo estudio, de las interrelaciones y contextos de las variables que intervienen en el fenómeno. Esta descripción permite entender el caso a través de la identificación con la realidad de quien lee el reporte de investigación.
De acuerdo con Yin (2003) en una investigación de corte cualitativo se estudia un fenómeno dentro de su contexto. Un estudio de caso se utiliza en situaciones técnicamente distintivas en la cual hay muchas más variables de interés que datos y, como resultado, se basa en múltiples fuentes de evidencia, cualitativas y cuantitativas, con datos que permiten la triangulación. Es decir, se utiliza el estudio de caso cuando el investigador explícitamente aborda situaciones contextuales. Así, el estudio de caso es una búsqueda empírica que investiga un fenómeno contemporáneo dentro de su contexto, especialmente cuando los límites entre el fenómeno y el contexto no se encuentran claramente delimitados.
El estudio de caso es un método que:
(i) Es adecuado para investigar fenómenos en los que se busca conocer cómo y por qué ocurren.
(iii) Permite estudiar los fenómenos desde múltiples perspectivas y no desde la influencia de una sola variable.
(iv) Permite explorar en forma más profunda y obtener un conocimiento más amplio sobre el fenómeno. (Chetty, 1996, citado en Martínez, 2006)
Por las características antes mencionadas, la metodología cualitativa ha ido ganando terreno dentro de las investigaciones que se realizan en el campo de la educación matemática, dadas las posibilidades que ofrece para la explicación de nuevos fenómenos y en la elaboración de teorías. Al utilizar esta metodología, como al utilizar cualquier otra, se deben tener claros cuáles son los objetivos que se quieren conseguir, con qué finalidad se va a recabar e interpretar la abundante información a la que se va a tener acceso, cuál es el objeto de estudio y qué se desea saber del fenómeno que se analiza.
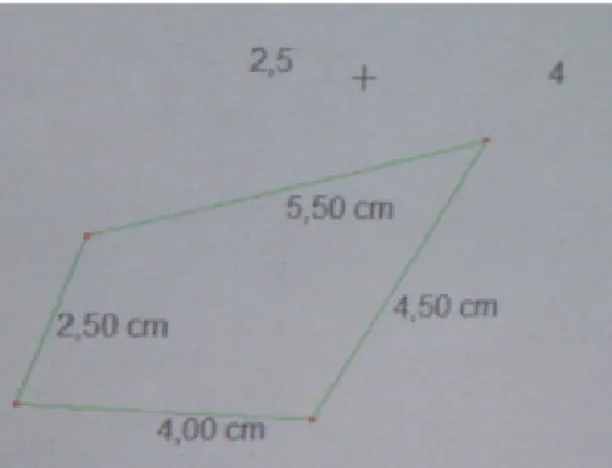
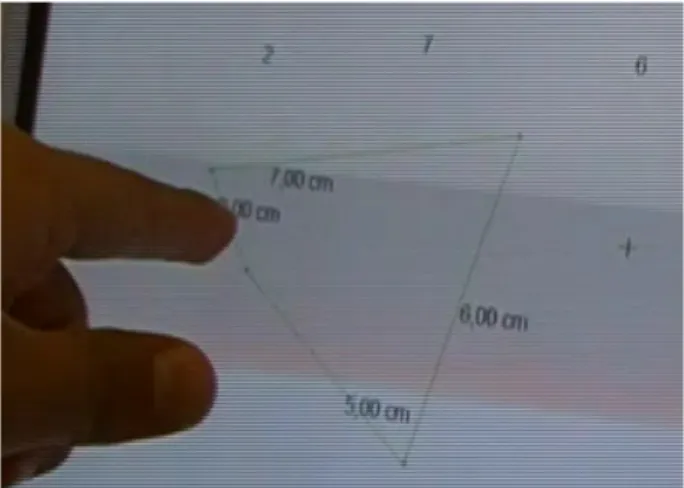
El trabajo de campo de esta investigación consistió en observar el desarrollo de una tarea de instrucción que al ser abordada por un grupo de estudiantes, les permitiera acceder y utilizar una serie de saberes y recursos matemáticos, seleccionar distintas maneras de representar y resolver un problema. Por ejemplo, al representar un cuadrilátero, un estudiante puede pensar en lados de diversos tamaños, ángulos con diferentes medidas, o congruencias de lados y ángulos para describir la figura que desea representar. El proceso de observación de la implementación de esta actividad permitió recolectar información con base en la cual se documenta y caracteriza el proceso de transformación de un software dinámico, considerado como artefacto, en un instrumento de resolución de problemas, así como analizar el papel de las representaciones ejecutables de objetos matemáticos en la aproximación inquisitiva que desarrollaron los estudiantes al abordar la actividad con el uso del software.
3.2. PARTICIPANTES EN EL ESTUDIO
La tarea de aprendizaje se implementó con un grupo de 12 estudiantes que cursaban el segundo semestre de una Licenciatura en Física; sus edades oscilaban entre los 18 y 25 años y sus últimos cursos de matemáticas habían sido: Cálculo, Matemáticas Superiores y Computación, y Geometría Analítica; esta última serviría de apoyo durante la solución de la actividad, ya que en la justificación de resultados la ruta de instrucción propuesta, propone el uso de la ley de cosenos. Los estudiantes no habían trabajado con el software Cabri-Geometry, aunque habían utilizado un software similar, GeoGebra, así como el sistema de álgebra computacional MAPLE.
estudiantes de bachillerato, en su mayoría, manifestaron tener experiencia en el uso del software dinámico Cabri-Geometry.
En la implementación de la actividad; con el grupo de licenciatura, se optó por una sesión de dos horas, debido a que se esperaba que los participantes tuvieran menos dificultades para desarrollar la actividad de aprendizaje que el grupo de bachillerato, con quienes se trabajaron dos sesiones no continuas de dos horas cada una, con la finalidad de que los estudiantes tuvieran tiempo suficiente para la reflexión, discusión e intercambio de ideas.
Estos grupos se eligieron debido a razones circunstanciales, porque los profesores titulares de los mismos, permitieron implementar la actividad de aprendizaje; algunos otros profesores argumentaban que por cuestiones de tiempos en los avances de su programa no les era posible que se trabajara con su grupo.
3.3. TAREA DE APRENDIZAJE
La tarea de aprendizaje utilizada en esta investigación fue diseñada e implementada por un profesor de matemáticas, integrante del equipo de investigación del proyecto en el que se enmarca este trabajo. El profesor que implementó la actividad no era profesor regular de los grupos en que se llevó a cabo la recolección de los datos. El autor de este trabajo solamente actuó como observador del proceso de implementación. La tarea fue diseñada considerando los cuatro elementos establecidos por Barrera (2008): (i) un objetivo de aprendizaje, (ii) un conjunto de elementos matemáticos estructurados en torno al objetivo de aprendizaje, (iii) la determinación de un escenario para desarrollar la tarea, y (iv) un proceso inquisitivo, estructurado a través de una ruta hipotética de instrucción (ver apéndice B).
Figura 3.1: Construcción en Cabri de un mecanismo de Grashof
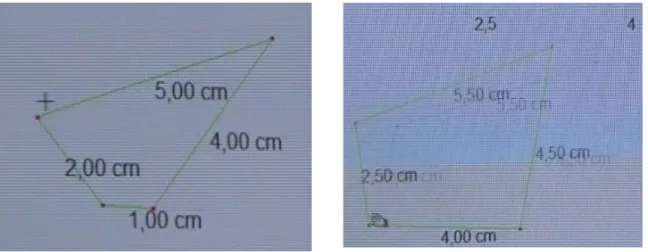
La actividad se desarrolló en dos fases. En la primera fase (preámbulo), los estudiantes trabajaron en forma individual, con la finalidad de reconocer las funcionalidades de diversos comandos del software mediante la construcción de cuadriláteros, dadas las longitudes de sus lados. En la segunda fase (actividad central), los estudiantes trabajaron en parejas, con el propósito de obtener un criterio para determinar si un mecanismo de cuatro barras es un mecanismo de Grashof. La actividad se implementó en una sesión que tuvo una duración de dos horas.
Los elementos de la tarea de aprendizaje, considerados por el profesor en el diseño, son los siguientes:
1. Objetivos de Aprendizaje
(i) Identificar algunas propiedades geométricas de los triángulos y cuadriláteros. (ii) Transitar del pensamiento geométrico al aritmético y algebraico.
(iii) Utilizar distintos registros de representación.
(iv) Incorporar algunos recursos de la geometría analítica a la solución de un problema de geometría sintética.
2. Elementos matemáticos estructurados en torno al objetivo de aprendizaje Conocimientos matemáticos previos
(i) La desigualdad del triángulo.
Conocimientos informáticos previos. Utilización de comandos del software de geometría dinámica Cabri Geometry tales como: segmento, compás, medir longitud, medir ángulo, animación, calculadora, mostrar los ejes y lugar geométrico. Se puede incorporar adicionalmente el uso de una hoja de cálculo como Excel para verificar algunos de los resultados que aparezcan en el software dinámico. Se espera que la interacción del estudiante con el software de geometría dinámica, le permita establecer rápidamente conexiones conceptuales entre las condiciones para poder construir un cuadrilátero, la relación con la desigualdad del triángulo y ley de cosenos, así como observar por medio de la animación el comportamiento que tendría un mecanismo en particular, a partir de las longitudes de sus lados.
3. Escenario para desarrollar la tarea.
Se requiere de un aula con pizarrón, pantalla de proyección, equipos de cómputo con software dinámico para cada estudiante y para el profesor, además de cañón proyector. Los estudiantes serán organizados de la siguiente forma: al inicio de la actividad trabajarán de forma individual, seguirán las indicaciones dadas por el profesor, realizarán las construcciones que éste les solicite, para lo cual será indispensable que se utilice el recurso del cañón proyector como guía para los estudiantes. Posteriormente cuando se pasa a la etapa de tratar de argumentar los criterios o condiciones solicitadas en la actividad y las posibles conjeturas surgidas con la interacción entre estudiante-software-profesor, los estudiantes trabajarán en parejas; se espera que el intercambio de ideas les permita justificar las conjeturas que posiblemente fueron planteadas en la etapa inicial. Se dispondrá de una sesión de dos horas para el trabajo propuesto.
4. Proceso Inquisitivo
Función del instructor. Su función fue guiar al estudiante: (a) en la ejecución de la tarea desde el punto de vista puramente matemático, mediante la formulación de preguntas que lo orientaran en la línea de la ruta hipotética de instrucción que había planeado y, (b) apoyarlo en la problematización de la tarea, con la finalidad de que obtuviera una visión de las matemáticas como un modo de pensar crítico. El docente promovió entre los estudiantes el desarrollo de una actitud inquisitiva, entendiéndose por esto a la formulación sistemática de preguntas encaminadas a entender y proponer soluciones a un problema o tarea (Barrera, 2008).
Configuración del escenario para desarrollar la actividad
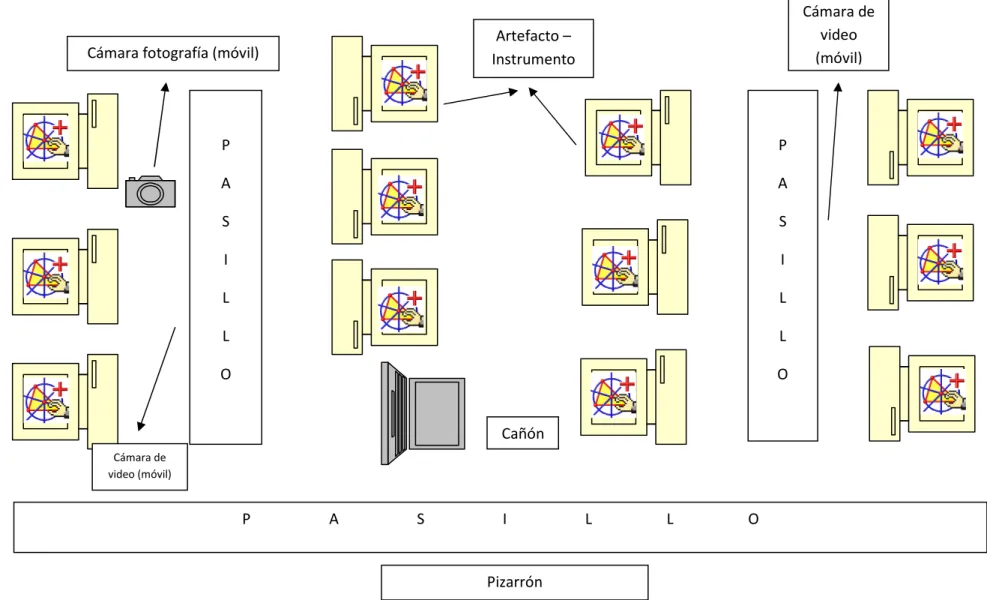
El escenario donde se implementó la actividad de aprendizaje fue un laboratorio de cómputo que contaba con un pizarrón, cañón y pantalla para realizar la proyección; así como de infraestructura (iluminación, ventilación, mobiliario) para la realización de la tarea. El laboratorio de cómputo contaba con una computadora de escritorio por cada estudiante, la cual disponía de acceso a Internet y con el software Cabri-Geometry. Por otra parte, el equipo de investigación utilizó dos cámaras de video y una cámara fotográfica, para obtener evidencia de los diferentes momentos del desarrollo de la tarea de instrucción (Figura 3.2). El instructor utilizó una computadora portátil y un cañón para proyectar y ejemplificar casos particulares de la tarea a los estudiantes.
En una primera etapa los estudiantes trabajaron en forma individual con el fin de que se familiarizaran con los comandos básicos del software de geometría dinámica Cabri-Geometry, para la cual se diseño como parte de la tarea una sección denominada “preámbulo”. En una segunda etapa, se trabajó en grupos de dos (aunque hubo algunos equipos de tres estudiantes), con la finalidad de que compararan y analizaran sus conjeturas realizadas en la primera etapa y así formular nuevas conjeturas con argumentos que justificaran la posible solución del problema y comunicarlos a sus compañeros; es decir, que tuviera lugar un proceso de interacción social que aportara elementos para resolver la tarea y justificar los procedimientos utilizados.
Figura 3.2. Espacio de trabajo y organización de las herramientas durante el desarrollo de la actividad.
Pizarrón Cañón P
A
S
I
L
L
O
P
A
S
I
L
L
O
P A S I L L O Cámara fotografía (móvil)
Artefacto –
Instrumento
Cámara de video
(móvil)
Cámara de
La sesión de trabajo se grabó en video, incluyendo escenas de la actividad del profesor, como de los estudiantes. Asimismo, los investigadores que acudieron a la sesión como observadores tomaron notas de campo durante el desarrollo de misma y al final de la realización didáctica (implementación de la actividad).
3.4. TÉCNICA DE RECOLECCIÓN DE LA INFORMACIÓN: OBSERVACIÓN NO PARTICIPANTE
La técnica de observación proporciona al investigador la oportunidad de conocer el desarrollo de un fenómeno de forma directa y determinar el modo en que el contexto influye sobre las características de la situación. También permite dar cuenta de cosas que de otra forma podrían omitirse de forma inconsciente o de las cuales los involucrados en el fenómeno podrían no hablar libremente en una entrevista. Los datos recolectados mediante esta técnica pueden utilizarse para obtener una visión de la complejidad fenomenológica del “mundo” de los participantes, así como de la forma en que interaccionan las variables de interés, y conocer sus conexiones, correlaciones y causas (Cohen, Manion y Morrison, 2004).
Durante el proceso de recolección de datos se utilizó la técnica de observación no participante, ya que el investigador no participó de manera activa dentro del grupo que se observó, y sólo se limitó a grabar y tomar notas sin relacionarse con los estudiantes. Esta técnica fue de utilidad ya que el objetivo de la investigación es documentar cómo el software dinámico se puede transformar en un instrumento que ayude a los estudiantes a generar distintas representaciones que le permitan visualizar elementos esenciales alrededor de la solución, además de detectar en qué momento el estudiante se apropia de la herramienta y la utiliza en la resolución de la tarea de aprendizaje con el fin de ampliar algunos aspectos del pensar matemáticamente.
En el caso de este trabajo el utilizar esta técnica no causó inconvenientes porque las actividades se desarrollaron en un escenario en el que el instructor que trabajó con los estudiantes para desarrollar la actividad no fue alguno de los profesores de los cursos regulares, razón por la cual no hubo dificultades para que los estudiantes aceptarán la presencia de observadores no participantes.
3.5. INSTRUMENTOS DE RECOLECCIÓN DE DATOS