B sean cualesquiera dos de sus partículas (fig

Se estudian las relaciones existentes entre el tiempo, las posiciones, las

velocidades y las aceleraciones de las diferentes partículas que forman un

cuerpo rígido. Como se verá, los diferentes tipos de movimiento de cuerpo

rígido pueden agruparse de manera conveniente en la forma que sigue

1,-Traslación.

Se afirma que un movimiento será de traslación si toda línea recta dentro del cuerpo mantiene la misma dirección durante el

movimiento. (movimiento de

traslación rectilínea

(a)

, y de

traslación curvilínea (b))

2,-Rotación alrededor de un eje fijo.

En este movimiento, las partículas que forman al cuerpo rígido se mueven en planos paralelos a lo largo de círculos centrados sobre el mismo eje fijo, llamado

eje de rotación.

(a)

_(b)

La rotación no debe

confundirse con ciertos tipos

de traslación curvilínea

3,-Movimiento plano general.

movimientos en los cuales todas las partículas del cuerpo se mueven en planos paralelos. Cualquier movimiento plano que no es ni una rotación ni una traslación se conoce como un movimiento plano general.

4,-Movimiento alrededor de un punto fijo.

El

movimiento tridimensional de un cuerpo rígido unido a un punto fijo O, por ejemplo, el movimiento de un

trompo sobre un piso rugoso, se conoce como movimiento alrededor de un punto fijo.

5,- Movimiento general.

Cualquier movimiento de un cuerpo rígido que no entra en ninguna de las categorías anteriores se conoce como movimiento general.

En general se buscará expresar la velocidad y la aceleración de un punto dado

del cuerpo en términos de su vector de posición, de la velocidad angular y de

la aceleración angular del cuerpo, dependiendo del tipo de movimiento que se

estudie.

Considere un cuerpo rígido en traslación (ya sea rectilínea o curvilinea), y deje que A y

B

sean cualesquiera dos de sus partículas (fig

a).

Al denotar, respectivamente, por

r

_A

y

r

_B los vectores de posición de A y

B

con respecto a un sistema de referencia fijo y

mediante

r

_B

/

_A al vector que une a A y

B,

se escribe

Se diferencia esta relación con respecto a

t.

Hay que resaltar que con la definición pura de traslación, el vector r_B/A debe mantener una dirección constante; su magnitud también debe ser constante, ya que A y B pertenecen al mismo cuerpo rígido. De esta forma:

En consecuencia,

cuando un cuerpo rígido está en traslación, todos

los

puntos el

cuerpo tienen la misma velocidad y la misma aceleración en cualquier instante dado

(figura b y c

).

Considere un cuerpo rígido que gira alrededor de un eje fijo AA'. Sea P un punto del cuerpo y r su vector de posición con respecto de referencia fijo O, (y con

z igual al eje de

rotación) ,P

debe permanecer a una distancia constante de

B y

describirá el círculo de centro

B

y de radio donde denota el ángulo formado por r y

AA’.

La posición de

P

y del cuerpo completo está definida totalmente por el ángulo que forma la línea

BP

con el plano

zx.

El plano se conoce como

coordenada angular

del cuerpo y se define como positivo cuando se ve en sentido contrario al de las manecillas del reloj de A'. La coordenada angular se expresará en radianes (rad) o, en oca-siones, en grados (°) o revoluciones (rev). Recuérdese que

Recuérdese, que la velocidad v =

dr/dt

de una partícula

P

es un vector tangente a la travectoria de

P y

de magnitud v

= ds/dt.

Al observar que la longitud Δs del arco descrito por

P

cuando el cuerpo gira un ángulo Δθ es:

al dividir ambos miembros entre Δt, se obtiene en el límite, cuando Δ, tiende a cero:

Advierta que el ángulo

depende de la posición de

P

dentro del cuerpo, pero que la razón de cambio

es en

La conclusión es que la velocidad v de P es un vector

perpendicular al plano que contiene a AA' y r, y de magnitud

v

Esto es precisamente el resultado que se obtendría al dibujar un vector a lo largo de AA’ y se formara el producto vectorial:

Este vector se llama

velocidad

angular del cuerpo,

su sentido obedece la regla de la mano derecha.

Y la aceleración a de la partícula P es:

y se denomina

aceleración angular del cuerpo

Al diferenciar esta ecuación y recordar que k es constante en magnitud y dirección, se tiene:

Componente tangencial de a.

Componente normal de a.

Supóngase un plano rotando entorno a O en el sentido anti-horario, w es positivo:

Como los vectores k y r son perpendiculares la magnitud v, es:

Sustituyendo

Y se observa que el doble producto cruz r por K origina una rotación de 180º del vector r, se expresa la

aceleración del punto P, como:

Descomponiendo a en las componentes tangencial y normal, se tiene:

Se afirma que se

conoce

el movimiento de un cuerpo rígido que gira alrededor de un eje fijo

AA'

cuando su coordenada angular θ puede expresarse como una función conocida de

t.

Sin embargo, en la práctica la rotación de un cuerpo rígido rara vez se define mediante una relación entre θ y t. Con mayor frecuencia, las condiciones de movimiento se especificarán mediante el tipo de aceleración angular que posea el cuerpo. Por ejemplo, es posible que  se dé como una función de

t,

como una función de  o como una función de w, se escribe:

Y se obtiene:

Con frecuencia se encuentran dos casos particulares de rotación:

1,- Rotación uniforme.

Este caso se caracteriza por el hecho que la aceleración angular es cero. Consecuentemente, la aceleración angular es constante, y la

coordenada angular está da por la fórmula:

2,-Rotación acelerada uniformemente

.

En este caso, la aceleración angular es

constante. Las siguientes fórmulas que relacio-nan la velocidad angular, la coordenada angular y el tiempo pueden obtenerse .La similitud entre las fórmulas deri-vadas aquí y aquellas obtenidas para el movimiento rectilíneo uniformemente acelerado de una

partícula es manifiesta.

El movimiento plano general es un movimiento plano que no es ni una traslación ni una rotación. s _{embargo, como se verá,}

un movimiento plano general siempre puede

considerarse como la suma de una traslación y una rotación.

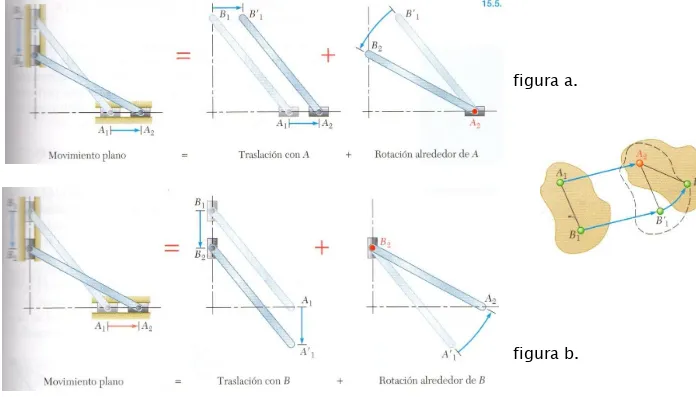
Considere, por ejemplo, una rueda que gira sobre una pista recta. A lo largo de cierto intervalo, dos puntos dados A y B se habrán movido, respectivamente, desde A1 hasta A₂ y

desde

B

₁ hasta

B

₂

.

El mismo resultado podría obtenerse mediante una traslación que llevaría a A y a

B

hacia A₂ y

B’

1 (la línea

AB

se mantiene vertical), se-guida por una

rotación alrededor de A que llevaría a

B

a

B

₂

.

Aunque el movimiento de giro original difiere de la combinación de traslación y rotación cuando estos movimientos se toman en forma sucesiva, el movimiento original puede duplicarse de manera exacta mediante una combinación de traslación y rotación simultáneas.

El movimiento puede sustituirse por una traslación en una dirección horizontal y una rotación alrededor de A (figura

a)

o por una traslación en una dirección vertical y una rotación alrededor de

B

(figura b).

[image:9.720.0.696.51.448.2]

figura b. figura a.

El miembro del lado derecho representa una suma vectorial. La velocidad

v

_A

corresponde a la traslación de la placa con A, mientras que la velocidad relativa

V

_B

/

_A

se asocia con la rotación de la placa en torno a A y se mide con respecto a

ejes centrados en A de orientación fija. Al denotar mediante

r

_B

/

_A

el vector de

posición de

B

relativo a A, y por

wk

la velocidad angular de la placa con

respecto a los ejes de orientación fija, se tiene de

y

Aquí se considera otra vez la varilla

AB

de la figura. Suponiendo que se conoce la velocidad

v

_A del extremo

A, se

propone encontrar la velocidad V_B del extremo

B y

la velocidad angular W de la varilla, en términos de la velocidad v_A, la longitud l y el ángulo

. Al elegir A como un punto de referencia, se expresa que el movimiento dado es equivalente a la traslación con A y una rotación simultánea alrededor de A. La velocidad absoluta de

B

debe entonces ser igual a la suma vectorial:

Si se conoce dirección de

v

_B

/

_A

,

su magnitud es desconocida. Sin embargo, esto se compensa por el hecho de que se conoce la dirección V_B. Por lo tanto, es posible completar el diagrama de la figura. Al despejar las magnitudes de

v

_B

y w

se escribe:

Considere el movimiento plano general de una placa. Se intenta de-mostrar que, en cualquier instante dado, la velocidad de las diversas partículas de la placa es la misma como si la placa girara alrededor de cierto eje perpendicular a su plano, el cual se conoce como

eje de rotación

instantáneo.

Este eje interseca el plano de la placa en el punto C, denominado

centro instantáneo de rotación

de la placa.

Para observar cómo es posible poner en práctica el concepto de centro instantáneo de rotación considere de nuevo la varilla de la figura. Al dibujar la perpendicular a

v

_A a través de A y la perpendicular a

v

_B a través de

B,

se obtiene el centro instantáneo C. En el instante considerado, las velocidades de todas las partículas de la varilla A son las mismas, como si esta última girara en torno a C. Ahora bien, si se conoce la magnitud

v

_A de la velocidad A, la magnitud w de la velocidad angular de la varilla puede obtenerse al escribir

Esto es valido para un determinado tiempo t, para una t+Δt, el centro se habrá movido. Lo que significa que, en general, la partícula C

no tiene aceleración cero

y, por lo tanto, las

aceleraciones

de las diversas partículas de la placa

no pueden

determinarse como si la placa estuviera girando alrededor de C.

Recordando que:

El miembro del lado derecho representa una suma vectorial. La aceleración

a

_A corresponde a la traslación de la placa con

A,

en tanto que la aceleración relativa

A

B/A asocia con la rotación de la placa en tomo a A y se mide con respecto a los ejes centrados en A y de orientación fija. Hay que recordar que la aceleración relativa

A

B

/

A puede descomponerse en dos componentes, una

componente tangencial (

A

B

/

A

)

_t perpendicular a la línea

AB, y

una

componente normal (

A

B/A

)

_n . Denotando por

r

_B

/

_A el vector de posición de

B

relativo a A y, respectivamente, mediante

wk

y k la velocidad angular y la aceleración angular de la placa con respecto a los ejes de orientación fija, se tiene

Si se supone conocido va y aa del

punto A, se puede determinar la aceleración absoluta de B, con:

donde

(a

_B

/

_A

)

_n

tiene la magnitud

Iw

2

_y

_está

_{dirigida hacia A,}

_{en tanto que}

_(a

B

/

A

)

t

tiene la magnitud

l



y

es perpendicular a

AB, no

hay forma de indicar si la

componente tangencial

está

dirigida hacia la izquierda o hacia la derecha y,

por lo tanto, ambas direcciones posibles. De modo similar, se indican ambos

sentidos posibles para

a

_B

,

ya que no se sabe si el punto

B

se acelera hacia

arriba o hacia abajo.

La ecuación se ha expresado de manera geométrica en la figura y es posible

obtener cuatro polígonos vectoriales diferentes, dependiendo del sentido de

a

_A

y

de la magnitud relativa de

a

_A

_y

(a

_B

/

_A

)

_n

.

Si se va a determinar

a

_B

y a

de uno de

estos diagramas, no sólo se debe conocer

a

_A

y



,

sino también w

.

Por

consiguiente, la velocidad angular de la varilla debe determinarse por separado

mediante uno de los métodos indicados anteriormente. Los valores de

a

_B

y



pueden obtenerse de ese modo considerando de manera sucesiva las

componentes

x y y

de los vectores mostrados en la figura. En el caso de un

polígono

a,

por ejemplo, se escribe:

En el caso de ciertos mecanismos, es posible expresar las coordenadas x e y, de todos los puntos importantes del mecanismo por medio de expresiones analíticas simples que contienen un solo parámetro. En estos casos a veces es ventajoso determinar de manera directa la velocidad absoluta y la aceleración absoluta de los diferentes puntos del mecanismo, ya que las componentes de la velocidad y de la aceleración de un punto dado pueden obtenerse diferenciando las coordenadas x e y,de ese punto. Considerando otra vez la varilla AB cuyos extremos se deslizan, de manera

respectiva, en una corredera horizontal y en una vertical. Las coordenadas x_A y y_Bde los extremos de la varilla pueden expresarse en términos del ángulo θ, que forman la varilla con la vertical

Al diferenciar las ecuaciones, dos veces con respecto a t, se escribe

Hay que observar que el signo positivo de v_A o a_A indica que la velocidad v_A o la aceleración a_A está dirigida hacia la derecha; un signo positivo para v_B o a_B indica que v_B o

a_B apunta hacia arriba.

Estas ecuaciones, pueden utilizarse para determinar, por ejemplo, v_B y w,

cuando se conocen v_A y . Sustituir. A sustituir w en estas ecuaciones, se puede determinar entonces a_B y , si se conoce a_A.