Ejercicios detallados del obj 4 Mat III 733

Capitulo III Matemática III (733)

Objetivo 4. Aplicar el cálculo diferencial e integral en curvas dadas en ecuaciones paramétricas y coordenadas polares.

Ejercicio 1

Prueba que la longitud de arco de la curva dada por las ecuaciones paramétricas:

'' '

( ) cos ( )

x= f t t+ f t sent y '' ' ( ) ( ) cos y= −f t sent+ f t t

Entre los puntos correspondientes a t=t1 y t=t2 es igual a

'' ''

2 2 1 1

( ) ( ) ( ) ( )

f t + f t − f t − f t

Solución

Justificación: En el objetivo anterior se dedujo, que la longitud de arco en coordenadas cartesianas era:

2 1 b a dy L dx dx   = +   

∫

Si la curva esta dada en forma paramétrica:

1 2

( ) ( ) x f t

t t t y g t

=  < <  =  Entonces: ' 1 2 ' ( ) ( ) dx f t dt

t t t dy g t dt

 ₌

< < 

= 

Sustituyendo en la ecuación de la longitud de arco, se tiene:

2 1 2 ' ' ' ' ( ) ( )

1 ( ) 1

( )

t

t

g t dt g t dt

L f t dt

f t dt

 

= +  = +

 

∫

'

( ) f t dt

( )

(

)

2 2 1 1 2 2 ' ' ' 2 ' ( )

( ) 1 ( )

( )

t t

t t

g t

f t dt f t dt f t   = +    

∫

∫

(

) ( )

(

)

(

₍

) ( )

₎

2 2 1 1 2 2

2 2 _{' '}

' ' ' ' 2 ₂ ' _' ( ) ( ) ( ) ( ) ( ) ( ) ( ) _{( )} t t t t

f t g t f t g t

L f t dt f t dt

f t _{f t}

+ + =

_∫

=

_∫

(

) ( )

(

) ( )

2 1

2 2 2 2

' ' ' ' ' ' _' ( ) ( ) ( ) ( ) ( ) ( ) _{( )} t t

f t g t f t g t

L f t dt

f t _{f t}

+ +

=

_∫

= 2

1 ' ( ) t t f t

∫

dt

(

) ( )

2 1 2 2 ' ' ( ) ( ) t t

Por lo tanto, si tenemos una curva en coordenadas paramétricas su longitud se puede escribir de cualquiera de las formas:

(

) ( )

( ) ( )

2 2 2

1 1 1

2 2

2 2 2 2

' ' ' '

( ) ( ) ( ) ( )

t t t

t t t

dx dy

L f t g t dt x t y t dt dt

dt dt

   

= + = + =   + 

   

∫

∫

∫

Ahora bien, en nuestro caso, tenemos:

'' '

1 2

'' '

( ) cos ( )

( ) ( ) cos x f t t f t sent

t t t y f t sent f t t

 _{= +}

< < 

= − +



Primero debemos calcular las primeras derivadas de la función paramétrica dada:

Para: '' '

( ) cos ( )

x= f t t+ f t sent se tiene la derivada de 2 productos:

(

)

'

(

)

'

(

)

'

(

)

'

'' '' ' '

( ) cos ( ) cos ( ) ( )

dx

f t t f t t f t sent f t sent

dt = + + +

'' ''' ' ''

( ) ( ) cos ( ) cos ( ) dx

f t sent f t t f t t f t sent

dt = − + + +

'' ( ) dx

f t sent dt = −

''' ' ''

( ) cos ( ) cos ( ) f t t f t t f t sent

+ + +

(

''' '

)

( ) ( ) cos dx

f t f t t dt = +

Para: '' '

( ) ( ) cos

y= −f t sent+ f t t se tiene la derivada de 2 productos:

(

)

'

(

)

'

(

)

'

(

)

'

'' '' ' '

( ) ( ) ( ) cos ( ) cos

dy

f t sent f t sent f t t f t t

dt = − − + +

'' ''' ' ''

( ) cos ( ) ( ) ( ) cos

dy

f t t f t sent f t sent f t t

dt = − − − +

'' ( ) cos dy

f t t dt = −

''' ' ''

( ) ( ) ( ) cos

f t sent f t sent f t t

− − +

(

''' '

)

( ) ( ) dy

f t f t sent dt = − +

Ahora, según la fórmula debemos calcular: 2 dx dt       y

2 dy

dt    

  , entonces:

(

)

(

)

2

2 2

''' ' ''' ' 2

( ) ( ) cos ( ) ( ) cos

dx

f t f t t f t f t t dt   _{ } = + = +   _{ }  

(

)

(

)

2 2 2

''' ' ''' ' 2

( ) ( ) ( ) ( )

dy

f t f t sent f t f t sen t dt

  _{ }

= − + = +

  _{ }

Ahora debemos sumar: 2 2 dx dy dt dt   ₊          :

(

)

2

(

)

2

2

''' ' '''

2

2 ' 2

( ) ( ) cos ( ) ( )

f t f

dx dy

t sen t

dt dt + t f t f t

  ₊  _{= +}

 

 +

 

  

(

_'''

)

2

(

)

2

2 2

' 2

( ) ( ) cos

f t

dx dy

t sen t

dt dt f t

  ₊  _{= +}

 

    +

Como la identidad: 2 2

cos t+sen t =1, se tiene:

(

)

2 2 2 ''' ' ( ) ( ) dx dy

f t f t dt dt

  ₊  _{= +}

   

   

Sustituyendo en la formula de longitud de curva:

(

)

2 2 2

1 1 1

2 2

2

''' ' ''' '

( ) ( ) ( ) ( )

t t t

t t t

dx dy

L dt f t f t dt f t f t dt

dt dt     _{ } = _{ } +_{ } = + = _ + _    

∫

∫

∫

Integrando:

2 2 2

1 1 1

''' ' ''' '

( ) ( ) ( ) ( )

t t t

t t t

L=

∫

_f t + f t dt_ =

∫

f t dt+

∫

f t dt

Pero las integrales son: ''' '' '

( ) ( ) y ( ) ( ) f t dt= f t f t dt= f t

∫

∫

, entonces:

(

) (

)

2

'' '' ''

2 2 1 1

1

( ) ( )t ( ) ( ) ( ) ( )

L f t f t f t f t f t f t t

= + = + − +

Por lo tanto la longitud de la curva es:

'' ''

2 2 1 1

( ) ( ) ( ) ( )

L= f t + f t − f t − f t

l.q.q.d

Respuesta: l.q.q.d = Lo que queríamos demostrar. Ejercicio 2

Calcula el área de la superficie en revolución generada por la curva 4 cos

r= θ al rotar alrededor del eje polar.

Solución

Justificación: Vamos a comentar algunas gráficas conocidas en coordenadas polares, ya que su conocimiento se hace imprescindible para resolver algunos problemas:

[image:4.595.89.503.130.762.2]

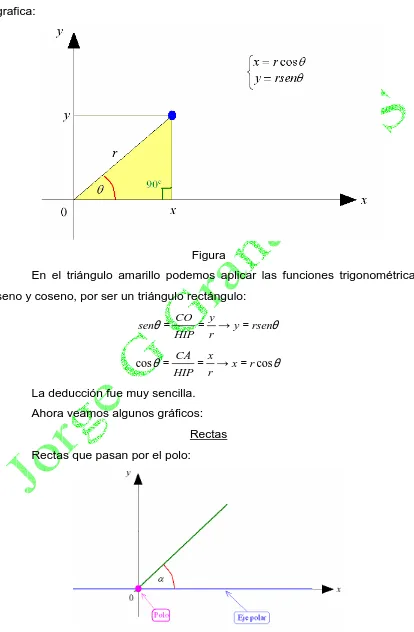
Donde r es la distancia del polo a un punto cualquiera de una curva y θ el ángulo con respecto al eje polar, pero ¿Por qué estas ecuaciones? O más precisamente ¿De dónde salen dichas ecuaciones?, observa la siguiente grafica:

Figura

En el triángulo amarillo podemos aplicar las funciones trigonométricas seno y coseno, por ser un triángulo rectángulo:

CO y

sen y rsen

HIP r

θ = = → = θ

cos CA x x rcos

HIP r

θ = = → = θ

La deducción fue muy sencilla. Ahora veamos algunos gráficos:

La ecuación de una recta que pasa por el origen en coordenadas cartesianas tiene la forma:

y=mx

Donde m es la pendiente, que sabemos vale m=tgα.

Sustituyendo las transformaciones en coordenadas polares, se tiene: y=mx

cos rsenθ =mr θ r senθ =m rcosθ

cos

cos sen

senθ m θ m θ tgθ θ

= ∴ = =

Pero sabemos que: m=tgα, por lo tanto:

tgθ = =m tgα∴tgθ =tgα ⇒θ α=

Por lo tanto la ecuación de la recta que pasa por el polo es:

θ α

=

Circunferencias

La ecuación general de una circunferencia de radio R y centro en el origen es:

2 2 2

x +y =R

Sustituyendo las ecuaciones de transformación polar, se tiene:

(

) (

2

)

2

2 2 2 2 2 2 2 2 2

cos cos

(

)

2 2 2 2

cos

r θ +senθ =R

La identidad fundamental de la trigonometría es:

2 2

cos 1

senθ + θ = Por lo que:

( )

2 2 2 2 2 2

1

r =R →r =R → r = R → =r R

Por lo tanto la ecuación de la circunferencia con centro en el polo es:

r

=

R

Circunferencias tales que contienen al polo y tienen centro en el punto

(

R,

α

)

.

El siguiente grafico ilustra esta situación:

Aplicando la ley del coseno en el triángulo extraído de la derecha, se tiene:

(

)

2 2 2

2 cos R =R + −r rR

θ α

−

2

R = R2 + −r2 2rRcos

(

θ α−

)

(

)

2

0= −r 2rRcos

θ α

−

(

)

2

2

r =2 rRcos

(

θ α

−

)

(

)

2 cos

r

=

R

θ α

−

Analicemos esta última ecuación para algunos casos especiales, que son los más comunes en ejercicios prácticos:

1) Si α =0º se tiene:

(

)

( )

2 cos 0º 2 cos

r= R

θ

− → =r R

θ

(1)

Escribiendo la ecuación r=2 cosR

( )

θ

a su forma cartesiana:

Como: x rcos cos x r

θ θ

= → = (2), además, aplicando Pitágoras en el

triángulo rectángulo de la figura 1, se tiene:

2 2 2

r =x +y (3) Sustituyendo (2) y (3) en (1):

2 2 2 2 2

2 x 2 2 2 0

r R r Rx x y Rx x y Rx

r

= → = → + = → + − =

Completando cuadrados en: 2

(

)

2 2 2

x − Rx= −x R −R

Entonces:

(

)

2

(

)

2

2 2 2 2 2 2

2 0 0

x +y − Rx= → −x R −R +y = → −x R +y =R

Y estas es una circunferencia de radio R y centro en

( )

R, 0

Haciendo un análisis muy semejante al anterior, obtenemos las siguientes gráficas, las cuales debes conocer para resolver ejercicios dond intervengan este tipo de curvas:

2) Si α =180º=π se tiene:

(

)

( )

2 cos 2 cos

r= R

θ π

− → = −r R

θ

Su gráfica es:

3) Si 90º 2 π

α = = se tiene:

( )

2 cos 2

2

r= R _θ −π _→ =r Rsen θ

 

4) Si 270º 3 2

π

α = = se tiene:

( )

3

2 cos 2

2

r= R _θ − π _→ = −r Rsen θ

 

Su gráfica es:

Caracoles

Los caracoles tienen ecuación polar de la forma: r= ±a bcosθ ó de la forma: r= ±a bsenθ .

Consideremos 3 casos:

1.2) r= −a acosθ

1.3) r= +a asenθ

2) Cuando a > b , toman el nombre de LIMACON Ó CARACOL SIN

RIZO.

2.1) r= +6 3cosθ

2.3) r= +6 3senθ

3) Cuando a < b, toman el nombre de LIMACON Ó CARACOL CON

RIZO.

3.1) r= +3 6 cosθ

3.3) r= +3 6senθ

Rosas

Estos lugares geométricos tienen ecuación polar de la forma

( )

cos

r=a n

θ

ó r=asen n

( )

θ

donde n es cualquier número natural mayor que uno.

Consideremos 2 casos:

1) Si n es PAR tenemos una rosa de 2n pétalos.

1.1) r=4sen

( )

2

θ

2) Si n es IMPAR tenemos una rosa de n pétalos.

2.1) r=4 cos 3

( )

θ

Lemniscatas

Tienen ecuación polar de la forma 2

( )

cos 2

r =a

θ

o de la forma

( )

2

2 r =asen

θ

1) r2 =4 cos 2

( )

θ

3) 2

( )

4 2 r = sen

θ

Espirales Consideremos 2 tipos:

1) Espiral de Arquímedes: Ecuación polar de la forma: r=aθ Ejemplo: graficar r =3θ

2) Espiral logarítmica: Ecuación polar de la forma: b

r=aeθ

Retomando nuestro ejercicio, para calcular el área de la superficie en revolución generada por la curva r=4 cosθ al rotar alrededor del eje polar.

En el objetivo anterior, se dedujo la formula que nos permite calcular el área de una superficie en revolución, a saber:

( )

_' 2

2 1

b

a

S =

π

∫

y + y dx

Vamos a encontrar la fórmula que nos permite calcular la superficie de un sólido en revolución en coordenadas polares, cuando gira alrededor del eje polar.

Hagamos uso de las ecuaciones de transformación polar: cos

x r y rsen

θ

θ

=

 

=



Para convertir la expresión:

( )

2 2

'

1 y 1 dy

dx  

+ = + 

  .

Podemos tomar las ecuaciones: x rcos y rsen

θ

θ

=

 

=

 , como una curva dada en forma paramétrica, donde el parámetro es θ, y recordando que en el ejercicio 1 demostramos que una curva en ecuaciones paramétricas viene dada por:

2 2 2

1 dy dx dy

dx d

θ

d

θ

     

+_{ } = _{ } +_{ }

     

Se procede a calcular las derivadas dy y dx

dθ dθ . Sabemos que en las ecuaciones x=rcos y θ y=rsenθ, r depende de θ, es decir, r= f( )θ , entonces, al derivar las ecuaciones polares, debemos aplicar la derivada de un producto:

(

)

'

(

)

' '

cos dy

r sen r sen r sen r dθ = θ + θ = θ+ θ

(

)

'

(

)

' '

cos cos cos

dx

r r r rsen

dθ = θ+ θ = θ− θ Entonces:

(

) (

)

2 2

2 2

' '

cos cos

dx dy

r rsen r sen r

dθ dθ θ θ θ θ

  ₊  _{= − + +}

   

( )

(

)

(

( )

)

2 2

2 2

' 2 ' 2 2 ' 2 ' 2 2

cos 2 cos 2 cos cos

dx dy

r r r sen r sen r sen r r sen r

d

θ

d

θ

θ

θ

θ

θ

θ

θ θ

θ

  ₊  _{= − + + + +}        

( )

2 2 2

' 2 '

cos 2 cos dx dy

r r r sen

dθ dθ θ θ θ

   

+ = −

   

   

(

)

( )

2

2 2 ' 2 '

2 cos r senθ r senθ r r θ θsen

+ +

(

+ 2 2

)

cos r θ +

( )

( )

2 2 2 2

' 2 2 2 ' 2 2 2

cos cos

dx dy

r r sen r sen r

d

θ

d

θ

θ

θ

θ

θ

    + = + + +        

( ) (

) (

)

2 2 2

' 2 2 2 2 2

cos cos

dx dy

r sen r sen

d

θ

d

θ

θ

θ

θ

θ

   

+ = + + +

   

   

Como 2 2

cos 1

senθ+ θ = , se tiene:

( )

2 2 2 ' 2

dx

dy

r

r

d

θ

d

θ









+

=

+

















Como y=rsenθ, se tiene que la fórmula en coordenadas polares para calcular la superficie en revolución de una región que gira alrededor del eje polar:

( )

2

2 '

2

S rsen r r d

β

α

π

θ

θ

=

_∫

+

Si la región gira alrededor de la recta 2 π

θ = , que seria el eje ye en

coordenadas cartesianas, se tendría:

( )

_' 2

2 1

b

a

S=

π

∫

x + x dx

Tomando en cuenta las consideraciones anteriores, se tendría:

2 2 2

1 dx dx dy

dy d

θ

d

θ

     

+  =   + 

   

 

Es decir:

( )

2 2

2

' 2

dx

dy

r

r

d

θ

d

θ









+

=

+

















Y como x=rsenθ se obtiene la fórmula en coordenadas polares para calcular la superficie en revolución de una región que gira alrededor del eje

2

π

θ

= es:

( )

2

2 '

2 cos

S r r r d

β

α

π

θ

θ

En este caso, la superficie a rotar es: r=4 cosθ , es decir la circunferencia:

Como al hacer girar la parte superior de la circunferencia, se obtiene el mismo sólido que hacer girar toda la circunferencia, los límites de integración,

serán de 0 a 2 π

; por otro lado la derivada en este caso de r=4 cosθ , es: '

4

r = − senθ, sustituyendo en la fórmula, se tiene:

(

) (

)

2

2 2

0

2 4 cos 4 cos 4

S sen sen d

π

π

θ θ

θ

θ

θ

=

_∫

+ −

Como

(

cosθ

) (

2+ senθ

)

2 =1, se tiene:

(

) (

)

2 2

2 2

0 0

2 4 cos 16 cos 2 4 cos 16

S sen sen d sen d

π π

π θ θ  θ θ  θ π θ θ θ

=

_∫

_ + _ =

_∫

( )

2

0

2 4 cos 4

S sen d

π

π θ θ θ

=

_∫

2

0 32 cos

S sen d

π

π θ θ θ

La primitiva se obtiene con un sencillo cambio de variable:

2 2

cos cos

cos 2 2

u sen u sen

sen d sen d udu

du d

θ

θ

θ θ θ

→ =

_{θ θ}

→

θ θ θ

= = = = 

∫

∫

∫

Entonces:

(

)

( ) ( )

2

2 2 2

2 _{0 1 0}

1 2

32 2 32 32 32 16

2 2 2 2 2 2

0 sen sen sen

π

π

θ

π

π

π

π

π

_{ }     _{ }   _{= }  _{− =  − =}  ₌     _{ }       _{ }    

A manera de comprobación, resolveré el ejercicio en coordenadas cartesianas:

( )

_' 2

2 1

b

a

S =

π

∫

y + y dx

La ecuación de la circunferencia en este caso es:

(

)

2 2

2 4

x− +y =

(

)

(

)

(

)

' 2 2 _' 2

4 2 2

4 2

2 4 2

x

y x y

x

 _{− −}  ₋

 

= − − → = =

− −

(

2

)

2 x  ₋   

(

)

(

)

(

)

2 2 2

4 2 4 2

x

x x

− − =

− − − −

Sustituyendo en la fórmula del área de la superficie, se obtiene:

(

)

(

)

(

)

2 4 2 2 0 2

2 4 2 1

4 2

x

S x dx

x

π

 − −  = − − +_{ } − −  

∫

(

)

(

₍

)

2

₎

4

2

2 0

2

2 4 2 1

4 2

x

S x dx

x

π

 −  = − − +   _{− −}   

∫

(

)

(

) (

)

(

)

(

)

(

)

2 2 4 4 2 2 2 2 0 0

4 2 2 4

2 4 2 2 4 2

4 2 4 2

x x

S x dx x dx

x x

π

− − + −

π

= − − = − − − − − −

∫

∫

(

)

(

)

(

)

4 2 2 2 0 4

2 4 2 2 4 2

4 2

S x dx x

x

π

π

= − − = − −

− −

∫

(

)

2 2

4− −x 2 4

0

dx

∫

( )

4

(

)

0

2 2 4 4 0 16

S =

π

∫

dx=

π

− =

π

Evidentemente, cuando se hace girar una circunferencia sobre su diámetro, en este caso el eje polar, se obtiene una esfera, y el área de una

esfera es: 2 4

A= πr , como el radio es r=2, se tiene:

( )

2

( )

4 2 4 4 16

A= π = π = π

Respuesta: A=16

π

.

Ejercicio 3

Encuentra el área de la superficie generada por la rotación de la curva dada por las ecuaciones paramétricas:

1

0 2

t

x t

t y e

= +



≤ ≤



=

 Alrededor del eje OX.

Solución

Justificación: Vamos a deducir la fórmula que utilizaremos en coordenadas paramétricas para calcular el área de la superficie en revolución de una región alrededor del eje OX.

Para las ecuaciones paramétricas: ( ) _{1 2} ( )

x f t

t t t y g t

=



< <



=

 , se demostró:

(

) ( )

2

1 2

2 2

' '

1 ( ) ( )

t b

a t

dy

L dx f t g t dt

dx  

= +  = +

 

∫

∫

Por lo tanto la fórmula: 2 1

( )

' 2

b

a

(

) ( )

2 2

' '

2 ( ) ( ) ( )

b

a

S =

π

∫

g t f t + g t dt

Si la curva gira alrededor del eje ye, aplicando el análisis anterior, se tendría:

(

_'

) ( )

2 _' 2

2 ( ) ( ) ( )

b

a

S =

π

∫

f t f t + g t dt

En nuestro ejercicio, se tiene:

( ) 1

0 2 ( ) t

x f t t

t y g t e

= = +  ≤ ≤  = =  Derivando: ' '

( ) 1

0 2 ( ) t

f t

t g t e

 ₌

≤ ≤ 

= 

Sustituyendo en la fórmula correspondiente, se tiene:

(

_'

) ( )

2 _' 2 2

( )

2

( )

2 0

2 ( ) ( ) ( ) 2 1

b

t t

a

S=

π

∫

g t f t + g t dt=

π

∫

e + e dt

Resolviendo esta integral: 2

2 0

2 t 1 t

S =

π

∫

e +e dt

A través de cambio de variable:

Como:

( )

2 2

2 2

0 0

2 t 1 t 2 t 1 t

S=

π

∫

e +e dt=

π

∫

e + e dt

Con el cambio:

t

t

du e d

u e t = =   

Por lo tanto:

( )

2 ₂

1 1

t t

e + e dt= +u du

∫

∫

Hemos llegado a una integral de sustitución trigonométrica, explicada en detalle en el objetivo 1 de Matemática 3 (733).

Con el cambio trigonométrico:

2 2 2 1+u du= 1+tg

α

sec

α α

d

∫

∫

Como: 2 2

1+tg

α

=sec

α

, se tiene:

2 2 2

sec

α

sec

α α

d = sec sec

α

α α

d

∫

∫

Esta última integral es de la forma: 3 sec α αd

∫

Y tal como se explico en detalle en el objetivo 1 de Matemática 3 (733), se debe aplicar el método de integración por partes:

2 2 sec sec sec sec dv d

I α α αd u

α α α = = =  → 

∫

Aplicando la derivada de u y la integral de dv, se tiene:

2 2 sec sec sec sec

sec dv d

dv d

d

v

u tg d

u du tg d

tg α α α α α α α α α α α α     → →     _  = = = = = =

∫

∫

Sustituyendo en la fórmula de integración por parte:

sec s c

.v v. tg . e

u du d

I = −

∫

= α α−

∫

tgα α α αtg

(

)

2 2

sec .sec sec sec 1 .sec

I = α αtg −

∫

tg α α αd = α αtg −

∫

α− α αd

(

3

)

3

sec sec sec .sec sec sec sec

I = α αtg −

∫

α− α α αd = α αtg −

∫

α αd +

∫

α αd

Pero: 3

sec

I =

∫

α αd y de la tabla de integrales:

secα αd =ln secα+tgα +C

∫

Entonces:

sec ln sec

I = α αtg − +I α+tgα

sec ln sec

I+ =I α αtg + α+tgα

2I =secα αtg +ln secα+tgα

3 sec ln sec

sec

2

tg tg

I =

∫

α αd = α α+ α+ α

De donde claramente:

2

sec 1

tg u u α α

=

= +

Por lo tanto:

2 2

1 ln 1

2

u u u u

I

+ + + +

=

Y como t

u=e , se tiene:

(

)

2 2

2

2 2 2

0

1 ln 1 ₂

2 1 2 . 1 ln 1

2 2

t t t t

t t e e e e t t t t

S π e e dt π π e e e e

+ + + +

=

_∫

+ = = + + + +

(

)

2

2 2 2

0

2

2 1 1 ln 1

0

t t t t t t

S= π

∫

e +e dt=π e e + + e + +e

Evaluando esta integral, se tiene:

(

2 4 4 2

) (

0 0 0 0

)

1 ln 1 1 ln 1

S =π_ e e + + e + +e − e e + + e + +e _

 

(

2 4 4 2

)

(

)

1 ln 1 1 1 ln 1 1 1

S =π_ e e + + e + +e − + + + + _

 

(

2 4 4 2

)

(

)

1 ln 1 2 ln 2 1

S=π_ e e + + e + +e − + + _

 

Respuesta:

(

2 4 4 2

)

(

)

1 ln 1 2 ln 2 1

S=π_ e e + + e + +e − + + _

 

Ejercicio 4

a) Dibuja la gráfica de la curva que está dada por las ecuaciones paramétricas:

5 cos 3

0 2

5 1

x t

t

y sent π

= −



≤ ≤



= +



b) Calcula la longitud de la curva de la parte “a” usando integrales. Solución

a) Cuando se nos pide graficar una curva dada en forma paramétrica, podemos eliminar el parámetro para tener la curva en coordenadas cartesianas y saber su naturaleza, por ello para eliminar el parámetro en este caso procedemos así:

1) Despejamos sent y cos t de cada una de las ecuaciones:

5cos 3 3 5 cos

3 co

1

s

1

5

1

5

5 5

x t x t

y sent y sen y

sent

x

t

t

 

= − + =

  

→ →

  

= + − =

 

+ =

− =

 

Ahora hacemos uso de la identidad: 2 2

cos 1

sen t+ t= , entonces:

2 2

cos 1

sen t+ t=

2 2

1

1 5

3 5

x

y  + 



−

 



 



 +

 =



(

) (

2

)

2

(

) (

2

)

2

(

) (

2

)

2

2 2

1 3 1 3 3 1

1 1 1

5 5 25 25 25

y− x+ y− x+ x+ + −y

+ = → + = → =

(

) (

2

)

2

₍

_{) (}

₎

2 2

3 1

1 3 1 25

25

x y

x y

+ + −

= → + + − =

Hemos llegado a la ecuación general de una circunferencia explicada en detalle en el objetivo anterior.

b) Para calcular la longitud de esta curva, hacemos uso de la fórmula:

( ) ( )

2

1

2 2

' '

t

t

L=

∫

x + y dt

Porque la curva esta dada en forma paramétrica, calculemos las derivadas:

' '

5

0 2 5 cos

x sent

t

y t π

 _{= −}

≤ ≤



=

 Por lo tanto:

(

) (

)

2

2 2

0

5 5 cos

L sent t dt

π

=

_∫

− +

Resolviendo la integral:

(

)

2 2

2 2 2 2

0 0

25 25 cos 25 cos

L sen t tdt sen t t dt

π π

=

_∫

+ =

_∫

+

Como 2 2

cos 1

sen t+ t= :

( )

[ ]

(

) ( )

2 2 2

0 0 0

2

25 1 5 5 5 5 2 0 5 2 10

0

L dt dt dt t

π π π

_π

π

π

π

=

_∫

=

_∫

=

_∫

= = − = =

Es fácil verificar este resultado, porque la longitud de una circunferencia es: 2 Rπ y como el radio es 5, se tiene que su longitud es:

( )

2 2 5 10 L=

π

R=

π

=

π

Respuesta:

a) Gráfica de 5 cos 3 0 2

5 1

x t

t

y sent π

= −



≤ ≤



= +



Ejercicio 5

Calcula el área de la superficie de revolución generada al rotar la curva

definida por las ecuaciones cos 0

2 x r t

t y rsent

π

=



≤ ≤



=

 , alrededor del eje OX .

Solución

Justificación: No es necesario dibujar la gráfica para resolver este ejercicio, porque se utilizaría simplemente la fórmula en coordenadas paramétricas para calcular el área del sólido en revolución, sin embargo, al dibujar la gráfica podemos conocer su naturaleza y posiblemente, si es una figura conocida, corroborar el resultado que se obtendrá. Para graficar eliminamos el parámetro t, tal como se ejecuto en el ejercicio inmediato anterior, así:

cos x

t r

y sent r 

=

   ₌ 

Ahora hacemos uso de la identidad: 2 2

cos 1

sen t+ t= , así:

2 2 2 2 2 2

2 2 2

2 2 2

1 1 1

y x y x x y

x y r

r r r r r

+

   

+ = → + = → = → + =

       

Hemos llegado a una circunferencia con centro en el origen y radio

2

R= r =r, entonces su gráfica en el intervalo 0

2 t π

[image:30.595.80.513.159.734.2]

Al rotar esta curva alrededor del eje OX , se obtiene la mitad de una esfera:

Y como sabemos que el área de una esfera es: 2 4

S= πR , tenemos que el área de la mitad de esta esfera generada es:

2

2 4

2 2

r

S =

π

=

π

r

Este sería el resultado esperado.

Ahora bien, aplicando la fórmula para calcular el área de la superficie de

la curva cos 0

2 x r t

t y rsent

π

=



≤ ≤



=

 rotada alrededor del eje OX , se tiene:

( ) ( )

_' 2 _' 2 2

b

a

S =

π

∫

y x + y dt

Calculando las derivadas: '

' 0

2 cos

x rsent t y r t

π  _{= −}

≤ ≤



=



Sustituyendo en la fórmula correspondiente, se tiene:

(

) (

)

2

2 2

0

2 cos

S rsent rsent r t dt

π

π

(

) (

)

(

)

2 2

2 2 2 2 2 2 2

0 0

2 cos 2 cos

S rsent r sen t r t dt rsent r sen t t dt

π π

π

π

=

_∫

+ =

_∫

+

Como 2 2

cos 1

sen t+ t=

(

)

( )

( )

2 2 2

2 2 2 2

0 0 0

2 cos 2 1 2

S rsent r sen t t dt rsent r dt rsent r dt

π π π

π

π

π

=

_∫

+ =

_∫

=

_∫

[

]

[ ]

2

2 2 2 2 2

0

2 2 cos 2 2 cos cos 0 2 0 1 2

2 0

S r sentdt r t r r r

π

_π

π

π

π

π

 

π

π

= = − = _− + _= + =  

∫

Observa que importante fue, conocer el gráfico para corroborar el resultado.

Respuesta: 2 2 S= πr

Ejercicio 6

Calcula el área de la superficie que se obtiene al girar la curva definida en forma paramétrica por las ecuaciones:

cos 0

2

t t

x e t

t y e sent

π

 ₌ ≤ ≤  = 

Alrededor del eje OY.

Solución

Justificación: Tal como se dedujo en el ejercicio 3 de esta guía, como la curva esta dada en forma paramétrica y gira alrededor del eje ye, se aplica la fórmula:

( ) ( )

_' 2 _' 2 2

b

a

S =

π

∫

x x + y dt

Calculemos las derivadas:

(

)

( )

(

)

( )

' ' ' ' ' ' cos cos 0 2 t t t t

x e t e t

t y e sent e sent

π

 _{= +}  ≤ ≤   _{= +}  ' ' cos 0 2 cos t t t t

x e sent e t t y e t e sent

π

 _{= − +} ≤ ≤  = + 

(

)

(

)

' ' cos 0 cos 2 t t

x e t sent

t y e t sent

π

 _{= −}  ≤ ≤  = + 

(

)

(

)

(

(

)

)

2

2 2

0

2 tcos t cos t cos

S e t e t sent e t sent dt

π

π

=

_∫

− + +

(

)

(

)

2 2 2 2 2 0

2 tcos t cos t cos

S e t e t sent e t sent dt

π

π

=

_∫

− + +

(

) (

)

2 2 2 2 0

2 tcos t cos cos

S e t e t sent t sent dt

π

π

  =

_∫

_ − + + _

(

) (

)

2 2 2 2 0

2 tcos t cos cos

S e t e t sent t sent dt

π

π

 

=

_∫

_ − + + _

( ) (

) (

)

2

2 2 2 2

0

2 tcos t cos 2 cos cos 2 cos

S e t e t sent t sen t t sent t sen t dt

π

π

 

=

_∫

_ − + + + + _

( )

2

2 2 2 2

0

2 tcos t cos 2 cos cos 2 cos

S e t e t sent t sen t t sent t sen tdt

π

π

=

_∫

− + + + +

( )

2

2 tcos t cos 2 cos

S=

π

e t e t− sent t +sen t2 +cos2t+ 2sentcost 2 2 0 sen tdt π +

∫

( )

2

2 2 2 2

0

2 tcos t cos cos

S e t e t sen t t sen tdt

π

π

=

_∫

+ + +

Como sen t2 +cos2t=1, se tiene:

2 2 2

2 2

0 0 0

2 t tcos 1 1 2 tcos 2 2 2 tcos

S e t dt e t dt e tdt

π π π

π

+

π

π

=

_∫

+ =

_∫

=

_∫

Observamos que la primitiva 2 cos

t

e tdt

∫

debemos integrar por parte, este tipo de integrales fue explicado en detalle en el objetivo 1 de Matemática 3 (733).

En este caso:

2 2 c cos os t t u e

I e t

t dt dv dt = = →  =  

∫

Aplicando la derivada de u y la integral de dv, se tiene:

2

2 2

cos cos

2 t ₂

t t

dv tdt

dv tdt v sent

du e dt

u e  du e dt

Sustituyendo en la fórmula de integración por parte:

2 2

2

.v v. tsent sen. t

u du e t dt

I = −

∫

= −

∫

e

Esta integral se puede escribir:

2 2

2

t t

I =e sent−

∫

e sentdt

La integral generada, se puede resolver por partes de nuevo, así:

2

2 ₂ 2

2

cos

t

t t

dv sentdt

du e dt

u e du e dt

dv sentdt v t

    → →     _  = = = = = = −

∫

∫

Así:

(

)

2 2 2

cos 2 cos

2

t t t

sent t

e

I = − _−e −

∫

e − t dt_ Desarrollando:

(

)

2 2 2

2 cos 2 2 cos

t t t

I =e sent+ e t+

∫

e − t dt

2 2 2

2 cos 4 cos

t t t

I =e sent+ e t−

∫

e tdt

Observa como se reproduce la integral original, esto sucede en este tipo de integrales y se resuelven como una ecuación, recordando que

2 cos

t

I =

∫

e tdt:

2 2

2 cos 4

t t

I =e sent+ e t− I

(

)

2

4 t 2 cos

I+ I =e sent+ t

(

)

2

5I =e t sent+2 cost

(

)

2

2 cos 5

t

e sent t

I = +

Ahora evaluamos esta integral:

(

)

2

2 cos

2 2 2

5

0

t

e sent t S π π +  =     ( )

(

_{( )}

_{( )}

)

2 2 2 0 2 cos

0 2 cos 0

2 2 2 2 5 5 e sen e sen S π

_π

_π

π

       +   _ _  _{ } ₊      = −      

( )

(

)

0

(

( )

)

1 2 0 0 2 1

( ) ( )

1 2 2 2

2 2 2 2 2 2

5 5 5 5 5

e e e

S

π π π

π

 

π

 

π

 − 

=  − =  − =  

   

 

Respuesta: 2 2 2

5 e S

π

π

 − 

=  

 

Ejercicio 7

Dada la hélice r t( )=

(

3cos , 3t sent, 4t

)

, dar su parametrización en función de la longitud de arco.

Solución

Justificación: Para parametrizar la hélice por medio de la longitud de arco, utilizaremos la definición:

( )

' 0

( ) ( )

t

s t =

∫

r

α

d

α

En este caso, para obtener la derivada de la curva dada, se deriva cada componente, así:

(

)

( ) 3cos , 3 , 4 r t = t sent t

( )

'

(

)

( ) 3 , 3cos , 4 r

α

= − sent t dt

Ahora se usa la definición de módulo de un vector:

( )

'

(

)

(

) (

₂

)

₂

2

( ) 3 , 3cos , 4 3 3cos 4

r

α

= − sent t dt = − sent + t +

( )

'

2 2

( ) 9 9 cos 16

r

α

= sen t+ t+

( )

'

(

)

2 2

( ) 9 cos 16

r

α

= sen t+ t +

Como: 2 2

cos 1

sen t+ t= , se tiene:

( )

'

( ) 9 16 25 5

r

α

= + = =

Sustituyendo en la definición de longitud de arco, se tiene:

[ ]

(

)

0

( ) 5 5 5 0 5

0

t

t

s t =

∫

d

α

=

α

= t− = t

Por lo tanto: 5

5 s

s= ∴ =t t

4

( ) 3cos , 3 , 4 3cos , 3 ,

5 5 5 5 5 5

s s s s s

r s =_{  }  sen_{ }   _{ } _{ }=  _{ } sen _{ } s_

         

   

Respuesta: La curva parametrizada según la longitud de arco es:

4

( ) 3cos , 3 ,

5 5 5

s s

r s =_  _{ } sen _{ } s_

   

 

Ejercicio 8

Calcula el área de la superficie de revolución generada por la curva 2

r= senθ al rotarla alrededor del eje polar. Solución

Justificación: La curva r=2senθ viene dada por la gráfica:

Observa en el grafico que la gráfica de la curva se da en el intervalo

[ ]

0,

π

.

La derivada de la curva r =2senθ , es: r'=2 cosθ

Sabemos que la fórmula para calcular la superficie de un sólido en revolución alrededor del eje polar es:

( )

2

2 '

2

S rsen r r d

β

α

π

θ

θ

=

_∫

+

Sustituyendo, se tiene:

(

) (

2

)

2

0

2 2 2 2 cos

S sen sen sen d

π

π

θ

θ

θ

θ

θ

(

)

2 2 2 2 2 2

0 0

4 4 4 cos 4 4 cos

S sen sen d sen sen d

π π

π

θ

θ

θ θ

π

θ

θ

θ θ

=

_∫

+ =

_∫

+

Como: sen2θ+cos2θ =1, se tiene:

2 2 2

0 0 0

4 4 4 2 8

S sen d sen d sen d

π π π

π θ θ π θ θ π θ θ

=

_∫

=

_∫

=

_∫

Usando la identidad: 2 1 cos 2

( )

2

sen

θ

= −

θ

, se tiene:

( )

₍

_{( )}

₎

_{( )}

0 0 0 0

1 cos 2 8

8 1 cos 2 4 cos 2

2 2

S d d d d

π

_θ

_π

π π π

π

 − 

θ

θ

θ

π



θ

θ θ



=   = − =  − 

   

∫

∫

∫

∫

( )

2

( )

2

(

2 0

( )

)

0 0 2

4 4 0 4 0 4

0

2 2 2 2 2

sen

sen sen

S

π θ

θ

π

π π

π

π π

π

 

  _{ }

=  −  =  − − + = _ − − + _=

 

 

  _{ }

Respuesta: 2 4 S=

π

Ejercicio 9

Calcular el área de una superficie engendrada por el giro alrededor del

eje y, del segmento de parábola 2

y=x , que yace entre x=1 y x=2. Solución

Justificación: para graficar el segmento parabólico 2

y=x se calculan las

ordenadas de cada abscisa, es decir: Par x=1, se tiene, y= = →12 1

( )

1,1 y para x=2, se tiene, 2

( )

2 4 2, 4

y= = → .

Ahora bien, para calcular el área de la superficie en revolución, podemos usar la fórmula:

( )

_' 2

2 1

d

c

S=

π

∫

x + x dy

En este caso: 2 ' 1

2

y x x y x

y

= → = → = , por lo tanto:

2 4

1

1

2 1

2

S y dy

y

π

 

= +_ _

 

∫

4 4 4 4

1 1 1 1

4 1 4 1

1 4 1

2 1 2 2 2

4 4 4 2

y y

y

S y dy y dy y dy y dy

y y y y

π

 

π

+

π

+

π

+

= +  = = =

 

∫

∫

∫

∫

2

S =

π

y 4 1 2

y y

+

4 4 4

1 1 1

2

4 1 4 1

2

dy=

π

y+ dy=

π

y+ dy

Con el cambio de variable:

1 3

1

1 _{2 2} 3 3

2 2 2

4 1 1 1 1 1 1 2 1

4 1 . . .

1 3

4 4 4 4 ₁ 4 4 3 6

2 2

u y u u

y dy udu u du u u

du dy

+

= + 

→ + = = = = = =

 =



∫

∫

∫

₊

Devolviendo el cambio:

(

)

3

2 1

4 1 . 4 1

6 y+ dy= y+

∫

Evaluando la integral:

(

)

3

(

( )

)

3

(

( )

)

3

(

) (

3

)

3

2 2

2 4 2 2

4 1 4 4 1 4 1 1 16 1 4 1

1

6 6 6

S =

π

_ y+ _ =

π

_ + − + _=

π

_ + − + _

     

( ) ( )

3 3

2 2

17 5

6

S =π _ − _

 

Respuesta:

( ) ( )

3 3

2 2

17 5

6

S=π _ − _

 

Ejercicio 10

Calcula el área encerrada por la curva r= −1 senθ. Solución

Para ello se toma un diferencial de área polar que destaque en azul, tal como muestra la figura inmediata anterior, y como sabemos que el área de un

sector circular de radio R y ángulo central θ es:

2 2 R A=

θ

Por lo tanto, si aproximamos a un segmento circular el diferencial de área polar, destacado en verde, se tiene:

2 2 r d dA=

θ

Si sumamos todos los subrectángulos típicos polares, se tiene finalmente que:

2 1 2

A r d

β

α

θ

=

_∫

La curva esta graficada de

[

0, 2

π

]

, por lo tanto el área viene dada por:

(

)

2 2 0 1 1 2

A sen d

π

θ

θ

=

_∫

−

(

)

2 2 2 2

2 2

0 0 0 0

1 1

1 2 2

2 2

A sen sen d d sen d sen d

π π π π

θ

θ θ



θ

θ θ

θ θ



= − + =  − + 

 

∫

∫

∫

∫

(

)

2

( )

2 2

( )

0 0 0

1 cos 2 cos 2

1 1

2 cos 2 cos

2 2 2 2 2

d

A d d

π

_θ

π

_θ

π

_θ

θ

θ

θ

θ

θ

θ

 ₋   

=  − − + =  + + − 



∫

 

∫

∫



( )

2 2

1 1

2 cos .

0

2 2 2 2

sen

A= _

θ

+

θ

+ −

θ

θ

_

π

 

( )

(

2 2

( )

)

( ) ( )

0

(

2 0

( )

)

1 2 1 1

2 2 cos 2 0 2 cos 0 .

2 2 2 2 2 2 2

sen sen

A

π

π

π

π

 

=  + + − − − − + 

 

 

( )

( )

[

]

1 1 0 1 0 1

2 2 1 . 0 2 1 0 . 2 2 0 2 0 0

2 2 2 2 2 2

A= _ π+ + −π − − − + _= π + + − − − +π

 

1

3 2

2

A= π+ − −0 2 0 0 1

[ ]

3 3

2 2

π π

 _{− +} _{= =}

 

Respuesta: 3 2 A= π .

A continuación se te presentaran una serie de ejercicios propuestos, ¿Por qué es importante resolverlos? Por que tú estarás solo en el examen y tu eres quien a las finales debes aprehender para tener éxito en la asignatura. Cualquier duda de los problemas que a continuación se te presentan, déjamelo saber, a través, de mi correo: jorgegranadillomat@gmail.com. Recuerda que en mi página en el apartado “novedades” en la sección “material durante el estudio” se encuentra un programa de nombre Mathype que es un excelente editor de ecuaciones con el cual podrás escribir tus dudas matemáticas, o escanea las páginas de tu cuaderno y envíame las dudas para darte respuesta a la brevedad posible.

Por último recuerda resolver cada ejercicio bajo la estructura, justificación y respuesta, ya que en los exámenes de desarrollo deberás

justificar todas y cada una de tus respuestas, de manera, que es importante

EJERCICIOS PROPUESTOS Ejercicio 1

Calcula la longitud de la curva dada en coordenadas polares 2 2 cos

r= + θ .

Ejercicio 2

Calcula la longitud de la curva dada por las ecuaciones paramétricas:

3 t 1 , 1 t 2 y

2 t 3 x

2 2

≤ ≤

  

− =

+ =

.

Ejercicio 3

Encuentra el área de la superficie generada por la rotación de la curva

dada por las ecuaciones paramétricas: x = t, y = 2 – t2 , 0 ≤ t ≤ 2, alrededor del eje OY.

Ejercicio 4

Calcula el área de la región acotada por la gráfica de r = 2 + cosθ y por

las rectas θ = 0 y θ = 2

π

.

Ejercicio 5

Calcula la longitud de arco de la curva dada en forma paramétrica por

las ecuaciones: ≤ ≤π

  

− =

− =

t 0 con t

2 sen t sen 2 y

t 2 t

2

x cos cos

Ejercicio 6

Calcula la longitud de arco de la función F(t) = ( et, et sen t, et cos t ) con

π ≤

≤ t 2

0 .

Ejercicio 7

Calcula la longitud de arco de la curva dada en forma paramétrica por:

x(t) = t2 , y(t) = (t 3) 3

t 2 _{− entre los puntos de intersección de la curva y el eje x.}

Ejercicio 8

Calcule el área de la superficie de revolución generada al rotar la curva C alrededor del eje 0X, donde C es el menor de los arcos de la circunferencia x2 + y2 = 25 entre los puntos (3,4) y (5,0).

Ejercicio 9