Notas de clase para la UEA
Fundamentos Matemáticos
de Códigos y Criptografía
José Noé Gutiérrez Herrera
Índice general
1. Complejidad 1
1.1. Longitud de números . . . 1
1.2. La notación O grande . . . 4
1.3. P, NP, y NP-completo . . . 7
1.3.1. Problema . . . 7
1.3.2. Las definiciones . . . 8
1.3.3. Reduciendo un problema a otro . . . 9
1.3.4. Problemas NP-completos . . . 9
2. Aritmética modular 11 2.1. Divisibilidad . . . 11
2.2. Congruencias . . . 13
3. Residuos cuadráticos 19 3.1. Conceptos básicos . . . 19
3.2. Reciprocidad Cuadrática . . . 22
3.3. El símbolo de Jacobi . . . 23
4. Álgebra 27 4.1. Grupos . . . 27
4.2. Anillos y Campos . . . 32
4.3. Polinomios . . . 37
5. Campos finitos 43
5.1. Resultados básicos . . . 43
5.2. El grupo multiplicativo . . . 44
5.3. Elementos de un campo finito . . . 44
5.4. Polinomios irreducibles . . . 46
6. Probabilidad 49 6.1. Espacios equiprobables . . . 50
6.2. Probabilidad condicional . . . 51
6.3. Variables Aleatorias . . . 53
6.4. Distribución y Esperanza . . . 53
6.5. Distribución conjunta . . . 55
Prefacio
Estas notas de clase se prepararon como apoyo al curso de Fundamentos Matemáticos de Códigos y Criptografía, que se imparte en la Universidad Autónoma Metropolitana, Unidad Iztapalapa. Dada la diversidad de temas que se abordan el alumno se ve en la necesidad de consultar muchos libros de texto, algunos presentando temas con más profundidad que otros. Esto le dificulta saber si está estudiando un tema con la suficiente profundidad o si está empleando demasiado tiempo en analizar un tema. Con estas notas se espera que el alumno cuente con una guía de los temas más importantes que debe conocer para comenzar el estudio a profundidad de su línea de investigación.
Debe tenerse en cuenta que el presente escrito no es un libro. Además en la mayoría de lo escrito traté de conservar la nota-ción que utilizo en mis manuscritos personales y la que empleo en el salón de clases. Por estas razones es muy importante re-cordar que la notación no es la que se emplearía usualmente en un escrito cualquiera de Matemáticas. La finalidad de la notación empleada aquí es reducir las palabras empleadas pa-ra conservar un aire informal, sin dejar de lado lo riguroso de las proposiciones y demostraciones.
En el primer capítulo se presenta el concepto de número de operaciones de bits al realizar operaciones aritméticas así co-mo la definición de problemas P y NP. En el segundo capítulo se recuerdan los principales conceptos de aritmética modular. En el tercer capítulo, muy relacionado con el segundo, se es-tudia la definición de residuo cuadrático. El cuarto capítulo se
dedica a recordar los conceptos de grupo, anillo, campo, anillo de polinomios y campo de descomposición. El capítulo núme-ro cinco muestra cómo construir campos finitos y algunas de las propiedades de estas estructuras algebraicas. En el último capítulo son presentados algunos de los conceptos básicos de probabilidad.
El curso de Fundamentos Matemáticos de Códigos y Cripto-grafía se pensó principalmente para que los alumnos de nue-vo ingreso tuvieran un lenguaj e común al iniciar el estudio de sus líneas de investigación. Se seleccionaron los conceptos más relevantes por su uso tanto en Teoría de Códigos como en Criptografía. En mi experiencia personal un trimestre es tiempo suficiente para cubrir el material aquí expuesto.
Capítulo 1
Complejidad
1.1.
Longitud de números
Sea b ∈ N, b ≥ 2. Si n ∈ NS{
0} se escribe como n = dk−1bk−1+· · ·+d1b+d0, con 0 ≤ dj ≤ b−1, entonces la
representación de n en base b es
n= (dk−1dk−2· · ·d1d0)b.
Si dk−1 6= 0 llamamos a n un entero con k dígitos en
base b, o bien un entero de longitud k en base b.
Si n satisface bk−1 ≤n < bk entonces es un entero con k
dígitos en base b
Recordemos que si b > 10 entonces se utilizan las letras habituales para representar los números del 10 en adelante.
Para convertirna basebse realizan las siguientes divisiones q0
b n d0
q1
b q0
d1
· · ·
que podemos acomodar en una tabla de la forma siguiente: b
n q0 d0
q1 d1
.. . ... O bien de la siguente forma:
n=bq0+d0, 0≤d0< b
q0=bq1+d1, 0≤d1< b
q1=bq2+d2, 0≤d2 < b
..
. ...
qk−2=bqk−1+dk−1, 0≤dk−1< b
qk−1=b0+dk, 0≤dk< b
Ejemplo 1.1. (103)10 = (2626)7 y (1234)10 = (3412)7 pues
7 103
142 6 20 2 2 6 0 2
7 1234
176 2 25 1
3 4
0 3
Nótese que si bk−1 ≤n < bk entonces k−1 ≤logbn < k por lo tanto el número de dígitos de n en base b es: blogbnc+1= lnn
lnb
+1. Así en base 2:
long(n) =blognc+1.
Por otro lado, en base 2, por una operación de bits enten-deremos una suma de bits como se muestra en la siguiente tabla
AA S1 S2 Suma AS
0 0 0 0 0
1 0 1 0
0 1 1 0
1 1 0 1
1 0 0 1 0
1 0 0 1
0 1 0 1
1 1 1 1
donde AA significa Acarreo Anterior, Si es el sumando i, con i igual a 1 ó 2, y AS es el Acarreo Siguiente.
Ejemplo 1.2. Enseguida se ilustran las operaciones de bits en la suma de dos enteros expresados en base 2
1 1 1 0 0 1
+ 0 1 1 1 0 0
1 0 1 0 1 0 1
Nótese que la suma de dos números, de k bits cada uno, requiere k operaciones de bits.
Es importante conocer el número de operaciones de bits ne-cesarios para realizar una tareas pues la cantidad de tiempo
que una computadora necesita para realizarla es esencialmente proporcional al número de operaciones de bits. Por esta razón para analizar el tiempo de ejecución de un algoritmo se cuen-tan el número de operaciones de bits. Es usual tomar el tiempo para realizar una operación de bits como la unidad de tiempo. En particular tenemos que para a > b
long(a+b)≤long(a) +1 Tiempo(a+b) =long(a)
Ahora se calculará el número de operaciones de bit necesario para calcular la diferencia n−m. Sin pérdida de generalidad podemos suponer que n ≥ m pues en otro caso bastará con agregar un signo negativo al resultado de m−n. Para obtener el resultado de la diferencia 75−22 primero notamos que k= long(75) = blog275c+1 = 7, y 22 = (10110)2. Expresamos la diferencia n−m como
75−22 =75+ 27−22−27
Iniciamos realizando la diferencia 27−22, que puede calcularse
de manera eficiente en dos pasos. Primero se calcula 27−1 − 22, la cual tiene expresión en binario igual al complemento de la correspondiente expresión de longitud k para 22:
27−1
−22= (0010110)2 = (1101001)2,
calcular esta diferencia no tiene costo computacional. Ensegui-da se le debe sumar 1,para esta operación se ubica el bit menos significativo igual a cero de 2k−1−m y se toma el
comple-mento de la subcadena que termina en este bit cero, en nuestro caso que se tiene
27−1
−22
+1= 1101001
2= (1101010)2.
Nuevamente los cálculos puede hacerse sin costo computacio-nal. La suma 75+ 27−22, como vimos antes, se obtiene con k operaciones de bits, de la siguiente manera:
1.1. LONGITUD DE NÚMEROS 3 Dado que n−m≥0 se sigue que n+ 2k−m≥2k, de donde
para obtener la diferencia n+2k−m
−2k basta con omitir
el bit 1 que se encuentra en la posición más significativa. De aquí se concluye que 75−22= (110101)2 =53.
Resumiendo se cumple que Tiempo(n−m) =long(n). Ahora analicemos el número de operaciones de bits que se requieren para multiplicar dos enteros. Supóngase que se desean multiplicar un entero a de k bits y otro b de ` bits.
Si a= (ak−1ak−2· · ·a1a0)2 y b= (b`−1b`−2· · ·b1b0)2 entonces
ab =a b`−12`−1+· · ·+b12+b0
= (ab`−1)2`−1+· · ·+ (ab1)2+ (ab0)
Nótese que abj = a cuando bj = 1, y que abj = 0 si bj =
0. Para multiplicar por dos un entero, expresado en binario, hacemos un corrimiento de su expansión binaria a la izquierda y agregamos un cero al final de la expansión. En consecuencia (abj)2j se obtiene la realizar j corrimientos a la izquierda a la
expansión en binario de abj, y rellenando con j ceros al final
de la expansión. Por último ab será la suma de los enteros (abj)2j, con j=0, . . . , `−1.
Por ejemplo podemos suponer que a = 29 = (11101)2 y que b=13= (1101)2. Entonces
ab020 = (00011101)2,
ab121 = (00000000)2,
ab222 = (01110100)2,
ab323 = (11101000)2.
Se suman sucesivamente los productos parciales pp1:= ab121+
ab020, pp2 :=ab222+pp1, pp3:= ab323+pp2, obteniendo
pp1 = (00011101)2,
pp2 = (10010001)2,
pp3 = (101111001)2,
luego ab=pp3=377.
Analicemos el número de operaciones de bits que se requiren para calcular el producto ab. Ya hemos mencionado que el valor del producto parcial abj2j es 0 si bj=0 y es a recorrido
j lugares a la izquierda si bj =1. Luego para calcular todos los
enteros abj2j, 0≤j < `, se requieren a lo más
0+1+· · ·+ (n−1) = (n−1)n/2
corrimientos, los cuales no consideraremos por no ser opera-ciones de bit (además el tiempo que requiere un corrimiento es despreciable comparado con el tiempo de una operación de bit). Para sumar abj2j desde j = 0 hasta j = `−1 se calculan
su-cesivamente las sumas parciales. Notemos que para cualquier j el entero abj2j tiene a lo más k bits distintos de cero. Luego
para realizar la suma parcial Prj=−01abj2j+abr2r sólo se deben
realizar k operaciones de bits, pues los bits restantes única-mente se copian. Estas sumas parciales de calculan para cada posible valor de j, tal que bj = 1. Resumiendo estas
observa-ciones concluimos que la multiplicación puede realizarse con a lo más ` sumas, y en cada una se realizan k operaciones de bits, por tanto
Tiempo(entero de k bits)×(entero de ` bits)
< k` <(blognc+1) (blogmc+1), esto es Tiempo(mn)≤(logn+1) (logm+1).
Ejemplo 1.3. Como long(mn) = long(m) +long(n) se cum-ple que long(m1· · ·mr) ≤ rlong(mffax{m1, . . . , mr}) de ahí que
long(n!)≤nlong(n).Calculemos una estimación para la lon-gitud de n!. Como todos los factores de n! tienen longitud menor que long(n) se sigue que la longitud de n! es a lo más nlong(n), o equivalentemente, si n es expresable con k bits, entonces n! tiene longitud a lo más de nk (bits).
Supongamos que n es un entero de longitud k bits. En el paso j−1, con 2 ≤ j ≤ n− 1 necesitamos calcular el producto j!(j+1). Por consiguiente en el paso j−1 se realiza el producto de j+1, que tiene longitud a lo más k, y de j!, que por el ejemplo anterior tiene longitud a lo más nk. Como se tienen n−2 pasos para calcular n! se requieren a lo más
knk(n−2) =n(n−2)([log2n] +1)2 operaciones de bits, que es aproximadamente n2[log
2n]2.
Ejemplo 1.5.Encontremos una estimación del número de ope-ración de bits necesarios para calcular mn. Supongamos que n es un entero de k bits. Como mn = n−nm podemos suponer que m≤ n
2. Recordemos que
n m
= n(n−1)(n−2)· · ·(n−m+1) 2·3· · · · ·m .
Para calcular este número se realizan (m−1) multiplicaciones y (m−1) divisiones. El análisis es similar al que se describe en el cálculo de n!. Al realizar los productos se emplean ope-raciones parciales y el resultado se multiplica con el siguien-te número. Los resultados parciales son todos menores que n(n−1)· · ·(n−m+1), el cual tiene longitud a lo más km, y el siguiente número nunca es mayor quen, por lo que los produc-tos parciales tienen longitud a lo máskmk.Se realizanm−1 de estos productos, por lo que el número de operaciones de bits pa-ra realizar los productos es a lo máskmk(m−1). Este mismo análisis es válido para las divisiones, por lo que para calcular
n m
no se requieren más de 2m(m−1)k2 = 2m(m−1)log2n
operaciones de bits. Sim y n son enteros grandes este número es aproximadamente 2m2log2n.
Ejemplo 1.6. Se busca una estimación para el número de operaciones de bits empleadas al multiplicar los polinomios
P
iaix i y P
jbjx
j, cuyos coeficientes son enteros positivos
me-nores o iguales que m, y los grados respectivos de los poli-nomios son n1 y n2 con n2 ≤ n1. El coeficiente de xk en el
producto de los polinomios es:
X
i+j=k
aibj =akb0+ak−1b1+· · ·+ak−n2bn2, 0≤k≤n1+n2,
que requiere a lo más n2+1 multiplicaciones y n2 sumas. Los
números que se multiplican son menores o iguales a m y los números que se suman son menos o iguales a m2. Ya que
necesitamos sumar n2 sumas parcial de estos números cada
sumando parcial es a lo más igual a n2m2. Entonces para
cal-cular el coeficiente de xk el número de operaciones de bits es
a lo más
(n2+1)(log2m+1) 2+n
2[log2(n2m2) +1].
Existen n1+n2 +1 valores para k, por lo que el tiempo para
realizar el producto de los polinomios es menor o igual a (n1+n2+1)
(n2+1)(log2m+1) 2
+n2[log2(n2m2) +1]
.
Si se omiten los sumandos 1 para valores grandes de n1 y n2
se obtiene la cota (n1+n2)
n2(log2m)2+n2log2(n2m2)
=n2(n1+n2)
log22m+2log2m+log2n2
.
1.2.
La notación O grande
Sean f, g:N→(0, ∞) funciones. Se dice quef es O-grande de g, lo que se denota como f(n) =O(g(n)) (o bien como f= O(g)), si ∃ c ∈ R,∃N ∈ N tales que f(n) ≤ cg(n), para todo n > N.
1.2. LA NOTACIÓN O GRANDE 5 proceder como sigue: Para n ≥ 3 se cumple que 8 ≤ n2 y
n≤n2, además como −3≤1 tenemos que −3n≤n ≤n2. De
estas desigualdades se puede concluir que 2n2−3n+8≤2n2+n2+n2.
Como 2n2 −3n−8 ≤ 4n2 para n ≥ 3 podemos afirmar que
2n2−3n+8=O(n2).
Es posible definir el concepto de O-grande para funciones reales positivas en varias variables, pero en este curso no lo consideraremos.
Las notaciones Ω y Θestán estrechamente relacionadas con la notación O-grande, aunque su uso es menos frecuente. Definición 1.1. Seanf, g:N→(0, ∞)funciones.
1. Se dice que f es Ω-grande de g, lo que se denota como
f(n) = Ω(g(n)) (o bien comof = Ω(g)), si ∃ c ∈ R,∃N ∈
Ntales que 0≤cg(n)≤f(n), para todo n > N.
2. Se dice que f es Θ-grande de g, lo que se denota como
f(n) = Θ(g(n))(o bien como f = Θ(g)), si f= O(g) y f= Ω(g).Cuando f=Θ(g) diremos quef y g tienen el mismo orden de crecimiento.
Ejemplo 1.7. Para verificar quef(n) =2n3+4n+1 es O n3 podemos notar que para n > 1 se cumple que n < n2 < n3, por
tanto para n >1 se sigue que 0≤f(n)<2n3+4n3+n3 =7n3. En general de podemos demostrar que si f un polinomio de grado r, cuyo coeficiente del monomio nr es positivo, entonces
f(n) =O(nr).
Ejemplo 1.8. Calculemos el número de sumas y de produc-tos que se requieren para resolver un sistema de n ecuaciones lineales con n incógnitas por el método de eliminación gaus-siana. Se obtiene la forma escalonada de la matriz aumentada
del sistema (A|B), que es una matriz den×(n+1),utilizando operaciones elementales. No contaremos las comparaciones ni los intercambios de renglones por lo que no se mencionarán en el conteo. Dado que se desea una cota superior para el número de operaciones consideraremos el caso en que se realizan todas las sumas y todos los productos.
Para cada renglón i se calcula Ri → cRi, pero sabemos que
las primeras i−1 entradas de Ri son cero y que en la posición
i habrá un 1, así que se calculan n+1−i productos. Enseguida se debe realizar Rj → Rj +djRi para cada uno de los n −i
renglones Rj debajo de Ri,con dj una constante adecuada para
cada j. Como las primeras i−1 entradas de Rj son cero y la
i-ésima también será cero únicamente se calcularán n+1−i productos y el mismo número de sumas. Existenn−i renglones Rj, debajo de Ri, para cada i, por lo que para cada i se deben
realizar (n−i)(n−i+1) = (n−i+1)2 − (n−i+1) sumas y (n−i+1) + (n−i)(n−i+1) = (n−i+1)2 productos.
Así que para llevar la matriz a su forma escalonada se deben hacer
n
X
i=1
(n−i+1)2 = 1 3n
3+ 1
2n
2+ 1
6n productos y
n
X
i=1
(n−i+1)2− (n−i+1) = 1 3n
3− 1
3n
sumas. Por otro lado para la recursión hacia atrás se debe calcular, para cada i desde n hasta 1, una expresión de la forma
xi =βi− n
X
j=i+1
αi,jxj.
de sumas. De esta forma la recursión hacia atrás emplea
n
X
i=1
(n−i) = 1 2n
2− 1
2n
sumas en total, y el mismo número de productos en total. Se tiene así que se puede resolver un sistema de n× n por el método de eliminación gaussiana con
1 3n
3− 1
3n+ 1 2n
2− 1
2n=O n
3 sumas y
1 3n
3+ 1
2n
2+ 1
6n+ 1 2n
2− 1
2n=O n
3 productos.
Ejemplo 1.9. Dado un entero positivo n se cumple que n! =1·2· · · · ·n≤n·n· · · · ·n
de donde n! = O(nn), también es cierto que n! = O(n!). Además como n! ≤ nn se sigue que logn! ≤ nlogn, y de ahí
quelogn! =O(nlogn).
Es posible probar que si existe el límite l´m
n→∞
f(n) g(n),
entonces f(n) =O(g(n)). Además cuando el límite no es cero tenemos g(n) =O(f(n)).
Ejemplo 1.10. Se ilustra el uso de la notación O-grande con los siguientes casos.
a) ∀ >0, lnn=O(n). De hecho: l´m
n→∞
lnn n =0.
b) Si f(n) =dígitos binarios en n; entoncesf(n) =O(lnn).
c) Tiempo(mn) =O(lnnlnm). d) Tiempo(n!) =O((nlnn)2)
Existen algoritmos más eficientes para multiplicar enteros. Uno de ellos utiliza O n1,585
operaciones de bits para multi-plicar dos enteros de n-bits.
Ejemplo 1.11. Es posible verificar que Tiempo(
n1
X
i=0
aixi n2
X
j=0
bjxj) =O(n1n2[(lnm)2+ln m´n(n1, n2)]).
La verificación se deja como ejercicio. Nota 1.1. Se sabe que la expresión
Tiempo((entero dek bits)×(entero de`bits)) = O(klog2klog2log2k) es válida, la cual es mejor que O(k2), e incluso mejor que
O(k1+). Obviamente el tiempo de ejecución de un cálculo
de-pende del algorimo empleado.
Ejemplo 1.12. Encontremos una estimación para el tiempo empleado al convertir un entero n, expresado en binario con k bits, a base 10. Recuerde que de deben realizar sucesivamente las siguientes divisiones
q0
1010 n d0
q1
1010 q0
d1
· · ·
donded0 ∈{0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001}.Este
pro-ceso se repite un número de veces igual al número de dígitos decimales en n, el cual es:
1.3. P, NP, Y NP-COMPLETO 7 Tenemos O(k) divisiones y cada una requiere O(4k) = O(k)
operaciones de bits. Por lo tanto el número total de opera-ciones de bits es O(k)O(k) = O(k2). Pero k = O(logn). Por
consiguiente
Tiempo(convertir na base 10) =O(log2n).
Ejemplo 1.13. El tiempo para convertir un entero n de k bits a base b se calcula de forma similar al del ejemplo anterior. Ahora se deben realizar las divisiones
q0
b n d0
q1
b q0
d1
· · ·
Suponiendo que b tiene ` bits, cada división toma O(k`) ope-raciones de bits. El número dígitos de n en base b es O k`. Por lo tanto el número de operaciones de bits requeridas para realizar todas las divisiones necesarias es
O
k `
·O(k`) =O(k2).
Ejemplo 1.14. Tiempo(n!) = O(n2log2n) y Tiempo mn = O(m2log2n).
1.3.
P, NP, y NP-completo
1.3.1.
Problema
Unproblema P es una descripción general de una tarea, por ejemplo: dado n∈N determinar si es primo. Por otro lado una instancia de un problema es un caso particular de la tarea, por ejemplo ¿573 es primo?
Un problema de decisión es un problema en el que cada una de sus instancias requiere una solución consiste en una
respuesta de sí o no. Si se desea que la respuesta sea más que un sí o un no entonces diremos que el problema es de búsqueda. Para muchos problemas el problema de decisión y el problema de búsqueda son esencialmente equivalentes. Ejemplo 1.15. El problema de búsqueda de factorización en-tera es el siguiente: dado un entero N encontrar un factor no trivial del número o bien probar que es primo. Una vez que N toma un valor particular se tiene una instancia del problema. Ejemplo 1.16. El problema del agente viajero consiste en en-contrar la ruta más corta que comience en una ciudad dada, pase por las otras ciudades exactamente una vez y regrese a la ciudad inicial. Una instancia de este problema es una lista específica de las ciudades a visitar así como de las distancias entre ellas.
Ejemplo 1.17. El problema de la mochila consiste en determi-nar si un entero dado es suma de algunos elementos de una sucesión dada de enteros positivos.
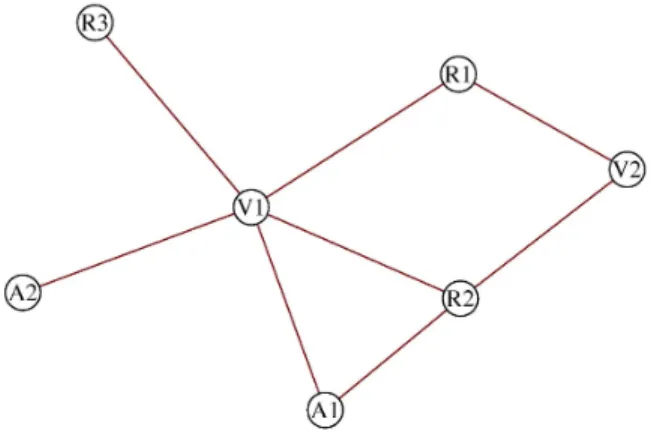
Ejemplo 1.18. El problema de los 3 colores es la tarea de colorear un mapa dado con sólo 3 colores de tal manera que no existan dos regiones vecinas con el mismo color, siempre que sea posible. Este problema puede abstraerse de forma natural y estudiar el problema de colorear una gráfica en lugar de un mapa. En la figura 1.1 se ilustra una coloración donde V,R y A indican los colores verde, rojo y azul respectivamente, y el número que acompaña cada letra sólo se utiliza para distinguir los vértices.
Ejemplo 1.19. Una instancia del problema de decisión de fac-torización entera es la siguiente:
ENTRADA: N, k∈N.
PREGUNTA: ¿Tiene N un factor en [2, k]?.
Figura 1.1: Ilustración del Problema de los Tres Colores
1.3.2.
Las definiciones
Definición 1.2. Un problema de decisión P está en la clase
P de problemas en tiempo polinomial si existe un polinomio
f(n) y un algoritmo tal que si una instancia de P tiene entrada de longitud menor o igual a n, entonces el algoritmo da una respuesta correcta en un tiempo menor o igual a f(n).
Equivalentemente un problema de decisión P está en P si existe una constante c y un algoritmo, tal que si una instancia de P tiene entrada de longitud menor o igual a n, entonces el algoritmo da respuesta al problema en un tiempoO(nc).
Ejemplo 1.20. Un ejemplo de problema en la clase P es el siguiente problema de primalidad:
ENTRADA: N∈N
PREGUNTA: ¿Es N un número primo?
En agosto de 2002 apareció “PRIMES is inP” que resuelve este problema en tiempo O(log7,5+N) para todo >0.
Ejemplo 1.21. Una curva elíptica E es una ecuación en dos variables, de una forma especial, que tiene aplicaciones en Criptografía. Considere el siguiente problema de decisión.
ENTRADA: Una curva elíptica E, un módulo primo p y un entero k.
PREGUNTA:¿Existen al menos k puntos en E sobreZp? El algoritmo de Schoof publicado en 1985 da respuesta a esta pregunta en tiempo O(n8), con n = O(lnp). Existe un
algo-ritmo, en apariencia más eficiente, gracias a Atkin pero nadie conoce una cota para su tiempo de ejecución, ni se sabe si es polinomial.
Definición 1.3. Un problema de decisión P está en la clase NP
si dado cualquier instancia de P un poder ilimitado de cálculo no sólo puede responder el problema, además en el caso de res-puesta afirmativa puede proporcionar evidencia para que otra persona pueda verificar la respuesta en tiempo polinomial. Su evidencia que la respuesta correcta es “sí” es llamada un certi-ficado.
Un problema de decisión P está en la clase co-NP si las con-diciones anteriores se cumplen cuando “sí” se reemplaza por “no”.
En otras palabras la clase NP consiste de los problemas que pueden resolverse por algoritmos no deterministas, cuyas po-sibles soluciones pueden ser verificadas en tiempo polinomial. Así los problemas de la clase NP son resolubles en tiempo po-linomial mediante un número no acotado de cálculos, tal vez realizados en paralelo y de manera independiente.
Ejemplo 1.22. El problema ya mencionado: ENTRADA: N, k∈N.
PREGUNTA: ¿Tiene N un factor en [2, k]?.
Es casi seguro que no esté en P. Pero está en NP, y también en co-NP. Por lo que existen problemas en ambas clases NP y co-NP.
1.3. P, NP, Y NP-COMPLETO 9 PREGUNTA: ¿Existe una subsucesión ai1, ai1, . . . , air de
a1, a2, . . . , ak tal que S=ai1+ai1+· · ·+air?.
Es casi seguro que no esté en P. Pero está en NP, y posible-mente no esté en co-NP.
Ejemplo 1.24. El problema de decisión del agente viajero es casi seguro que no esté en P. Más sin embargo está en NP. De forma similar el problema de los tres colores está en NP.
Es claro que si un problema está en P entonces está en NP, esto es P ⊂NP. Se cree que la clase NP es más grande que la clase P, en el sentido de que existen problemas en la clase NP que no están en la clase P; pero esto no se ha probado. Que NP 6=P es una de las conjeturas más conocidas de la Teoría de la Computación.
1.3.3.
Reduciendo un problema a otro
Definición 1.4. Sean P1 y P2 dos problemas de decisión. Se
dice queP1 se reduce a P2 si existe un algoritmo que corre en
tiempo polinomial como función de la entrada deP1, y que dada
cualquier instanciaP1deP1construye una instanciaP2 deP2 tal
que la respuesta paraP1 es la misma que paraP2.
Ejemplo 1.25. Sea P1 el problema
ENTRADA: Un polinomio cuadrático p(x) con coeficientes en-teros.
PREGUNTA: ¿Tiene p(x) dos diferentes raíces reales? Sea P2 el problema
ENTRADA:N∈Z.
PREGUNTA: ¿N >0?
Entonces P1 se reduce a P2. La reducción permite usar varias
llamadas a instancias de P2 para resolver una única instancia
de P1.
Definición 1.5. SeaP2 un problema de decisión o de búsqueda.
Al describir un algoritmo para algún otro problema P1 siempre
que digamos “llama a un P2-oráculo”, queremos decir que el
algoritmo ha creado una instancia de P2, y suponemos que otro
algoritmo nos da la correspondiente salida para P2. El tiempo
empleado por este algoritmo para P2 no se incluye en el tiempo
de ejecución para el algoritmo que da respuesta aP1.
Definición 1.6. SeanP1yP2 dos problemas ya sea de decisión
o de búsqueda. Decimos que P1 se reduce a P2 en un tiempo
polinomial si existe un algoritmo para P1 que corre en tiempo
polinomial, el cual utiliza a lo más un número polinomial de llamadas a unP2-oráculo.
Ejemplo 1.26. Considere los siguientes problemas
P1 :El problemas de búsqueda de la factorización de enteros.
P2 : El problema de decisión de la factorización de enteros.
Entonces P1 puede resolverse con a lo más n llamadas a un
P2-oráculo, donde n es el tamaño de la entrada. Por lo tanto
P1 se reduce a P2 en tiempo polinomial.
1.3.4.
Problemas NP-completos
Definición 1.7. Un problema de decisiónP enNP se dice que es “NP-completo” si cualquier otro problema Q en NP puede reducirse aP en tiempo polinomial.
Se sabe que el problema del agente viajero y el de la mochila son NP-completos.
Por esta definción si se cuenta con un algoritmo que resuelva en tiempo polinomial un problema NP-completo (es decir a todas sus instancias), entonces todo problema NP puede ser resuelto en tiempo polinomial, probando que NP =P. Se sabe que los problemas del agente viajero y de los tres colores son NP-completos.
Definición 1.8. Un problema de decisión o de búsqueda se dice
Capítulo 2
Aritmética modular
2.1.
Divisibilidad
Comencemos recordando algunos conceptos y propiedades de los enteros que son muy útiles en el estudio de las propiedades de los enteros.
Algoritmo de la división en Z:
Para cualesquiera par de enteros a, b, con a 6= 0, existen q, r∈Z tales que
b=qa+r, con 0≤r <|a|.
El concepto de divisibilidad está entre los más utilizados: Se dice que a6=0 divide a b,lo que se denota como a|b,si existe q∈Z tal que b=aq.
Dos enteros a, b son primos relativos si (a, b) := mcd(a, b) =1.
Si a divide b se también se acostumbra decir que b es divisible por a
Un divisor no trivial de b es un entero c que divide a b y que no es ±1 ni ±b
Llamamos número primo a cualquier entero que tenga exactamente cuatro divisores, es decir tal que no es ±1 y sus únicos divisores son los triviales
Un entero es llamado compuesto si es producto de dos o más primos
Propiedades de la divisibilidad:
Si a|b y b|c entonces a|c.
Si a|b y a|c entonces a|(b+c) y a|(αb+βc), ∀α, β∈Z. Si (a, b) =1 y a|bc entonces a|c.
Si p es un primo y p|ab entonces p|a o p|b. Si m|b, n|a y (m, n) =1 entonces mn|a.
Teorema fundamental de la aritmética: Cualquier en-tero mayor que uno puede expresarse como producto de primos de forma única, excepto tal vez por el orden. Dos consecuencias del teorema fundamental
1. p|ab impica p|a o p|b.
2. Si m|a, n|a y mcd(m, n) =1 entonces mn|a. El algoritmo de Euclides para calcular (a, b) Salida: (a, b)
Entrada : a, b
a = q1b+r1, 0< r1< b
b = q2r1+r2, 0< r2 < r1
r1 = q3r2+r3, 0 < r3< r2
..
. ...
rk−2 = qkrk−1+rk, 0< rk < rk−1
rk−1 = qrk+0, rk+1 =0
Salida : (a, b) =rk
Ejemplo 2.1. Calculemos (2100, 990) 990 = 2100(0) +990 2100 = 990(2) +120
990 = 120(8) +30 120 = 30(4) +0
Así(2100, 990) =30.
Se utilizará con mucha frecuencia la propiedad de que el máximo común divisor de dos números puede expresarse como combinación lineal de ellos. Los pasos que se siguen son los que señala el algoritmo extendido de Euclides. Recordemos este procedimiento con un ejemplo.
Ejemplo 2.2. Encontrar el máximo común divisor de 1617 y 38115. Expresar el resultado como combinación lineal de los números dados.
Solución: En primer lugar se calcula el máximo común divisor de los números dados.
38115 = 1617(23) +924
1617 = 924(1) +693
924 = 693(1) +231
693 = 231(3) +0
Por tanto se concluye que (1617,38115) =231. Ahora se despe-jan los residuos y se realiza una sustitución hacia atrás.
231 = 924−631(1)
= 924− [1617−924(1)]
= 924(2) −1617
= [38115−1617(23)] (2) −1617 = 38115(2) −1617[23(2) +1]
esto es 231=38115(2) +1617(−47), con lo termina el ejemplo. Proposición 2.1. En el algoritmo de Euclides para a > b se cumple
Tiempo(Encontrar(a, b)) =O(log3a).
Demostración. Probemos inicialmente que mientras rj+2 >0 en
el algoritmo de Euclides se cumplirá: rj+2 < 12rj. Si rj+1 ≤ 21rj
entonces rj+2 < rj+1 ≤ 21rj. Supóngase ahora que rj+1 > 21rj, en
este caso rj =1·rj+1+rj+2, de modo que rj+2 =rj−rj+1< 21rj,
pues −rj+1 <−21rj.
Ya que cada 2 pasos da lugar a la reducción de tamaño del residuo por lo menos en la mitad, y como el residuo nun-ca es menor que 1, se deduce que se realizan un máximo de 2blog2ac = O(loga) divisiones. Cada división involucra números no mayores que a, y así requiere de O(log2a) ope-raciones de bits. Por lo que el total de tiempo empleado es O(loga)·O(log2a) =O(log3a).
Se sabe que si se tiene en cuenta la disminución del tamaño de los números en las divisiones sucesivas, se puede mejorar la estimación en el tiempo de cálculo a O(log2a).
Proposición 2.2. Sea d = (a, b), a > b. Entonces existen
u, v ∈ Z tales que d = ua+bv. Pueden encontrarse u, v en
2.2. CONGRUENCIAS 13 Para probar el resultado anterior debe notarse que en cada
etapa del algoritmo extendido de Euclides, al trabajar de abajo hacia arriba, se necesita una multiplicación y una adición o sustracción. Así que el número de operaciones de bits resulta O(log3a).
De aquí en adelante, excepto en el capítulo sobre probabilidad, p denotará un número primo.
2.2.
Congruencias
El concepto de congruencia es uno de los más importantes en la Teoría de los Números. Sus propiedades son muy parecidas a las de las igualdades, lo que facilita su uso. Comencemos con su definición.
Definición 2.1. Sean a, b, m ∈ Z, con m ≥ 2. Diremos que
a es congruente a b módulo m, lo que se denota como a ≡ b (módm), si m|(b−a).
Ejemplo 2.3. 12≡66 (mód 9) pues 9|(66−12), esto es 9|54. Ejemplo 2.4. 11≡66 (mód 5) pues 5|(66−11), es decir 5|55. Proposición 2.3. Dados a, b, m ∈ Z, con m ≥ 2 se cumple la congruencia a ≡ b (módm) si y sólo si existe k ∈ Z tal que
b=a+mk.
Demostración. Inmediata de la definición.
La relación de congruencia es de equivalencia, como lo muestra el siguiente resultado. Se deja al lector probar la vali-dez del resultado.
Teorema 2.1. Sea m∈N.
1. Si a∈Zentonces a≡a (módm).
2. Si a ≡ b (módm) para algunos a, b ∈ Z, entonces b ≡ a (mód m).
3. Si a≡b (módm) y b≡ c (módm)para algunos a, b, c∈
Z,entonces a≡c (módm).
Ahora analicemos lo que sucede si se combinan el algoritmo de la división y la definición de congruencia: Dados enteros a y m, m ≥ 2, se cumple que a = qm+r, para enteros q y r con 0 ≤ r ≤ m−1. Entonces qm = a −r, esto es r ≡ a (mód m). Diremos que r es la reducción a módulo m, lo que representamos como r = a mód m. Por ejemplo 4 = 14 mód 5 pues 4≡14 (mód 5), es decir 5 divide a 14−4.
Dados enteros a y m, m > 0, es posible encontrar q := a mód m y r := a mód m mediante un procedimiento a fuerza bruta: cuando a es positivo restamos m de a tantas veces como sea necesario hasta tener un resultado menor que m. El número de veces que se realiza esta resta es el cociente y el resultado de las restas es el residuo. Para el caso a negativo se encuentra el cociente q y el residuo r cuando |a| se divide por m, cuando r resulta positivo el cociente y el residuo al dividir apor m resultan ser − (q+1) ym−r, respectivamente. Este razonamiento se resume en el siguiente algoritmo.
Algoritmo Cálculo de div y mód
Entrada: a, m enteros con m >0 q:= 0
r:= |a| while r≥m
r:= r−m q:= q+1
q:= −(q+1)
return (q, r) // q es el cociente, r es el residuo
Para m fijo, cada clase de equivalencia, bajo la relación de congruencia, tiene un y sólo un representante entre 0 ym−1. El conjunto de clases de equivalencia (llamadas clases residuales) se representa como Z/mZ o bien como Zm. Cualquier conjunto de representantes de las clases de equivalencia de conoce como conjunto completo de residuos módulo m.
Analicemos algunas propiedades de las congruencias.
1. Si a ≡ b (mód m) y c ≡ d (mód m) entonces a+c ≡ b+d (mód m) y ac≡bd (mód m).
2. Si a ≡ b (mód m) entonces a ≡ b (mód d) para todo d|m, d >0.
3. Si a≡b (mód m), a≡b (mód n) y (m, n) =1 entonces a≡b (mód mn).
Proposición 2.4. Los númerosa∈Z/mZpara los cuales existe
b con ab ≡ 1 (módm) son aquellos que cumplen (a, m) = 1. Además, si(a, m) =1, entonces tal inversobpuede encontrarse enO(log3m)operaciones de bits.
Demostración. Si d = (a, m) > 1, y ab ≡ 1 (mód m) para algún b, tenemos ab ≡1 (mód d) luego d|(ab−1), por con-siguiente d|1 lo cual es una contradicción.
Recíprocamente si (a, m) = 1, supongamos que a < m, en-tonces existen enteros b, e tales que ba+em = 1, los cuales pueden encontrarse enO(log3m) operaciones de bits. Notamos que m|1−ba esto es ab≡1 (mód m).
Ejemplo 2.5. En Z/9Z se cumple 2(5) ≡ 1 (mód 9), sin em-bargo 6 ∈ Z/mZ carece de inverso multiplicativo, como lo
muestra la siguiente tabla
x 0 1 2 3 4 5 6 7 8 6x 0 6 3 0 6 3 0 6 3
Denotamos por Z∗m al conjunto de elementos de Zm que son invertibles bajo el producto. A los elementos del conjunto Z∗m se les llama unidades.
Corolario 2.1. Si p es un número primo, entonces cada clase residual no cero tiene inverso multiplicativo el cual puede ser encontrado enO(log3p) operaciones bits.
Decimos queZ/pZes un campo. Se denota frecuentemente este campo como Fp, el campo finito con p elementos.
Corolario 2.2. Considere la congruencia ax≡b (módm).
Si (a, m) = 1 entonces existe una solución x0, la cual
pue-de encontrarse en O(log3m) operaciones de bits. Además todas las soluciones son de la formax =x0+mt, cont∈Z.
Si(a, m) =dentonces existe solución si y sólo sid|b, y en este caso la congruencia es equivalente a
a dx ≡
b d
mód m d
.
Analicemos un poco la solución a la congruencia ax ≡ b (mód m) cuando (a, m) = d. En este caso podemos es-cribir a = de, m = df, b = dh para algunos enteros e, f, h. La congruencia puede reescribirse como mk = ax −b, para algún entero k. Sustituyendo los valores de a, m y b resulta dfk = dex−dh, es decir fk = ex−h o en términos de con-gruencias ex ≡ h (mód f), que es la última conclusión en el corolario anterior.
Corolario 2.3. Si a ≡ b (módm) y c ≡ d (módm) y si
(c, m) = 1 (en cuyo caso (d, m) = 1) entonces ac−1 ≡
2.2. CONGRUENCIAS 15
Demostración. c(ac−1−bd−1)≡a−b (mód m).
Teorema 2.2. (chino del residuo) Sean m1, m2, . . . , mr ente-ros positivos primos relativos por parejas. Entonces el sistema de congruencias
x≡ak (módmi) 1≤k≤r tienen solución única módulo M=Qimi.
Demostración. Defina Mk = M/mk, 1 ≤ k ≤ r. Entonces
(Mk, mk) = 1 por lo que existe yk ∈ Ztal que Mkyk ≡ 1
(mód mk)
Calcule x0:= a1M1y1+· · ·+arMryr
Como para j 6= k se cumple mk|Mj, se tiene que Mj ≡
0 (mód mk). Por tanto
x0 ≡ akMyyk (mód mk)
≡ ak (mód mk),
esto significa que x0 es una solución al sistema dado.
Resta por probar la unicidad. Para esto tome dos solucio-nes del sistema, digamosx0, x1,entoncesmk|(x0−x1), 1≤
k≤r. Por consiguiente M|x0−x1.
Proposición 2.5. (Pequeño Teorema de Fermat) Sipun pri-mo entonces
ap ≡ a (mód p) para todo a∈Z
ap−1 ≡ 1 (módp) para todo a∈Z, p-a.
Demostración. Nótese que {iamód p:1≤i ≤p−1} =
{1,2, . . . , p−1}. En efecto pues si ax ≡ ay (mód p) en-tonces p|(x−y)a; luego p|x−y, así que x ≡ y (mód p). De
la igualdad de conjuntos se sigue la congruencia
p−1
Y
i=1
(ia)≡
p−1
Y
i=1
i (mód p),
que puede reescribirse como ap−1(p−1)! ≡ (p−1)! (mód p).
Cancelando el factorial se obtiene el resultado deseado.
Corolario 2.4. Si p - a y n ≡ m (módp−1) entonces an ≡
am (módp)
Demostración. Supóngase que n > m. Ya que (p−1)|(n−m) puede escribirsen=m+c(p−1), para unc∈N. Así se cumplen secesivamente las siguientes congruencias
ap−1 ≡ 1 (mód p) am(ap−1)c ≡ am (mód p)
an ≡ am (mód p).
Ejemplo 2.6. Determinemos el último dígito en base 7 del número 2106. En este caso p = 7. Como 10 ≡ 4 (mód6) y 102 ≡ 4 (mód6) se cumple la congruencia 10k ≡ 4 (mód 6),
para todo entero positivo k. Así que 2106 ≡24 (mód 7), esto es 2106 ≡2 (mód 7). Luego del dígito buscado es 2.
En 1750 Euler generalizó el pequeño teorema de Fermat para módulos no primos. En la búsqueda de la generalización se vio en la necesidad de definir lo que hoy se conoce como función de Euler. Recordemos brevemente esta función.
Definición 2.2. Sea n ∈ N. La función de Euler ϕ : N → N
ϕ(1) = 1 ϕ(p) = p−1 ϕ(pk) = pk−pk−1
La función de Euler es multiplicativa en factores primos relativos, como se muestra enseguida.
Teorema 2.3. Si (m, n) =1entonces ϕ(mn) =ϕ(m)ϕ(n). Demostración. Sean A=Z∗mn, B=Z∗m×Z∗
n
a ∈ A implica (a, mn) = 1, por consiguiente (a, m) =
(a, n) = 1. En consecuencia F : A → B, F(a) =
(a mód m, a mód n) es función. Para probar el teorema basta con mostrar que F es biyectiva.
Probemos que F es inyectiva: Si F(a) =F(b) entonces a≡ b (mód m),y a ≡ b (mód n). Por tanto m y n dividen
a b−a, pero (m, n) = 1 en consecuencia mn|b−a. Así
a≡b mód mn) se cumple en A.
F es suprayectiva pues si F(x) = (a, b). Entonces x ≡ a (mód m)
x ≡ b (mód n)
Por el teorema chino del residuo este sistema de congruen-cias tiene solución.
De las propiedades analizadas de la función de Euler se sigue que si p1, . . . , pr son los distintos primos que dividen a
m, entonces
ϕ(m) =m
r
Y
i=1
1− 1
pi
=mY
p|m
1− 1
p
.
Proposición 2.6. Suponga que n = pq es producto de dos primos. Podemos calcular ϕ(n) conociendo p, q en O(logn)
operaciones de bits, y pueden calcularse p, q si se conocen n y
ϕ(n) enO(log3n)operaciones de bits.
Demostración. Sin∈2Zes trivial, p=2, q= n2, ϕ(n) = n2−1. De modo que supongamos que n /∈2Z entonces
ϕ(n) = (p−1)(q−1) =n+1− (p+q).
Recíprocamente consideremos ap, q como desconocidos. Sa-bemos que
pq = n
p+q = n+1−ϕ(n) =:2b De modo que p, q son las raíces de
x2−2bx+n=0.
Por lo tanto p, q =b±√b2−n. El paso más lento es la
eva-luación de la raíz cuadrada, y esto puede hacerse en O(log3n) operaciones de bits.
Teorema 2.4. (Euler) Si (a, m) = 1 entonces aϕ(m) ≡ 1 (mód m).
Demostración. Sean b1, b2, . . . , bϕ(m)los enteros entre 1 y m
primos relativos con m. Como (a, m) =1 se cumple que
{abi mód m:1≤i≤ϕ(m)}={b1, . . . , bϕ(m)}. Por tanto (ab1)· · · abϕ(m)
≡ b1· · ·bϕ(m) (mód m), que puede reescribirse como
aϕ(m)b1· · ·bϕ(m)≡b1· · ·bϕ(m) (mód m).
2.2. CONGRUENCIAS 17 Corolario 2.5. Si (a, m) =1 y si n0 =n mód ϕ(m), entonces
se cumple quean ≡an0(módm).
Recordemos que existe una potencia mínima de a la cual es 1 mód m: a elevado al mínimo común múltiplo de exponentes e tales que ae = 1mód pα, para cada pα|m tal que pα+1
- m.
Por ejemplo a12 ≡1 (mód 105) para (a, 105) =1, ya que 105=
3(5) (7) y 12 es un múltiplo de 3−1, 5−1 y 7−1. Note que
ϕ(105) =48.
Ejemplo 2.7. Calcular 2106
mód 77.
(Primer método) Notemos que 30 = mcm(ϕ(7), ϕ(11)) así que por el comentario hecho justo antes de comenzar el presen-te ejemplo 230 ≡1(mód 77).Ya que 106=30(33333)+10, 2106 ≡
210 ≡23 (mód 77).
(Segundo método) Como 106 = 6(166666) +4 se tiene que
2106 ≡24(mód 7),además como 11−1|106por el pequeño teorema de Fermat se cumple que 2106
≡1(mód 11).Entonces el teorema
chino del residuo encuentra unx∈[0, 76] tal que
x ≡ 2 (mód 7)
x ≡ 1(mód 11)
Tal x satisface x≡2106 (mód 77)como se desea. Exponenciación modular
Para calcular bn mód m, sin pérdida de generalidad puede
suponerse que 0 < b < m. El siguiente algoritmo, conocido como exponeciación rápida o elevar al cuadrado y multiplicar, permite encontrar bn mod m elevando al cuadrado módulo m
ciertas cantidades, de forma sucesiva. El resultado buscado se almacena en el valor a.
Algoritmo ExpRápida(n)
Entrada: n10 = (nk−1nk−2. . . n1n0)2.
a=1
If n0=1, a=b
b1=b2 mód m
for i=1 to k−1 do
if ni =1, a=abi mód m
bi+1=b2i mód m
Salida: a
El algoritmo se basa en la siguiente idea muy sencilla bn= (b2k−1)nk−1(b2k−2)nk−2· · ·(b4)n2(b2)n1(b)n0
Nótese que b2 ≡ b2j ≡ b4 (mód m), en general en el j-ésimo
paso bj ≡b2
j
(mód m). Si ni =1 se incluye bi en el producto
para calcular a como abi mód m.
La siguiente reinterperetación del Teorema Chino del Resi-duo es muy útil en algunas situaciones. Se deja como ejercicio verificar la validez del enunciado.
Teorema 2.5. Sean n1, . . . , nk enteros positivos y primos re-lativos por parejas, y supóngase que n := Qki=1ni. Defina la función
ϕ:Zn→Zn1× · · · ×Znk
a7→(a módn1, . . . , amódnk). 1. ϕestá bien definida
2. ϕes biyectiva
3. Para todo a, b ∈ Zn si ϕ(a) = (a1, . . . , ak) y ϕ(b) =
(b1, . . . , bk)entonces
a) ϕ(a) +ϕ(b) = (a1+b1, . . . , ak+bk)
c) a ∈ Z∗
n si y sólo si ai ∈ Z∗ni para todo i = 1, . . . , k en
cuyo caso ϕ a−1
Capítulo 3
Residuos cuadráticos
Los residuos cuadráticos son muy importantes en Teoría de los Números, en Teoría de Códigos y en Criptografía. Estudia-remos brevemente este concepto.
3.1.
Conceptos básicos
Definición 3.1. Sean a, m ∈ Z, m ≥ 2. (a, m) = 1. Decimos
que a es un residuo cuadrático módulo m si x2 ≡ a (mód
m) tiene solución. Cuando la congruencia carece de solucióna
es llamado no-residuo cuadrático módulo m. Denotaremos
como Qm y NQm a los conjuntos de residuos y no-residuos cuadráticos módulom, respectivamente.
Por ejemplo en Z5 se cumple: 12 = 1, 22 = 4, 32 = 1 y
42 =1; por lo que los residuos cuadráticos módulo 5 son 1 y 4,
mientras 2 y 3 son no-residuos cuadráticos módulo 5.
Ya que a+m ∈ Qm si a ∈ Qm, únicamente se consideran
los residuos o no-residuos cuadráticos no congruentes módulo m.
Definición 3.2. Si p 6=2 y (a, p) = 1, entonces el símbolo de Legendre ap
se define como
a p
=
1, si a∈Qp
−1, si a∈NQp
Teorema 3.1. Sean p6=2, p-a, p-b. Entonces 1. ap ≡a(p−21) (módp),(Criterio de Euler)
2. ap bp= abp,
3. a≡b(módp) implica que ap= bp,
4. ap2=1, p1=1, −p1= (−1)p−21.
Demostración. (1) Si ap = 1 entonces existe un entero x0 tal
que x2
0≡a (mód p). Como x
p−1
0 ≡1 (mód p) se cumple
a(p−1)/2 ≡ x02(p−1)/2≡1 (mód p).
Supongamos ahora que ap = −1. Como p es primo la con-gruencia cx≡a (mód p) tiene solución para cualquier c entre 1 y p−1, además la condición ap= −1 implica que siempre se cumplirá x 6= c. Multiplicando las parejas de elementos en Zp
cuyo producto es a se obtiene a(p−1)/2 ≡ (p−1) ! (mód p). La
conclusión se sigue ahora del Teorema de Wilson. Así que en este caso a(p−1)/2 ≡ a
p
(mód p).
Teorema 3.2. (Lema de Gauss) Sea p 6= 2, p - a. Considere
S={ajmódp:1≤j≤ p−1
2 }y suponga que µ=| {x∈S:x >
p
2} |.
Entonces ap= (−1)µ.
Demostración. Sean
R= {x∈S:x > p2}=: {r1, r2, . . . , rµ}
S−R=: {s1, s2, . . . , sk}
Por lo tanto los ri, sj son todos diferentes, diferentes de cero
y además µ+k= p−21. Se mostrará que
{p−ri :1≤i≤µ}∪{sj:1≤j≤k}={1, 2, . . . ,
p−1 2 }. Nótese que 0 < p−ri < p2, para 1 ≤ i ≤ µ y los p−ri son
distintos. Además si p−ri =si, para i, j fijos entonces como
ri, sj∈S
ri ≡ρa (mód p), sj ≡σa (mód p) con ρ, σ∈
1,p−1 2
.
De donde se obtiene
p−ri ≡ p−ρa (mód p)
≡ sj (mód p)
≡ σa (mód p)
Entonces p−ρa≡σa (mód p), que esquivale a
(ρ+σ)a≡0 (mód p)
lo cuál es una contradicción. Por lo tanto p−ri 6=sj ∀i ∀j
y en consecuencia los números
p−ri, sj, 1≤i≤µ, 1≤j≤k.
son todos distintos, con p−ri, sj ∈[1,p2), y son p−21 elementos.
Luego
({p−ri, sj}µi=1)kj=1=
1, 2, . . . , p−1 2
,
por lo que se cumple sucesivamente "Yµ
i=1
(p−ri)
#Yk
j=1
sj =
(pY−1)/2
i=1
i
"Yµ
i=1
(−rj)
#Yk
j=1
sj ≡
(pY−1)/2
i=1
i (mód p)
(−1)µ
µ
Y
i=1
ri
! k
Y
i=1
sj ≡
(pY−1)/2
i=1
i (mód p)
(−1)µ (pY−1)/2
i=1
(ai) ≡
(pY−1)/2
i=1
i (mód p)
(−1)µap−21 ≡ 1 (mód p).
Pero hemos visto que
a p
≡ap−21 (mód p).
Por tanto
(−1)µ ≡ ap−21 (mód p)
≡ a p (mód p)
3.1. CONCEPTOS BÁSICOS 21 módulo 11. Estos valores respectivamente son 5, 10, 4, 9, 3,
y de ellos sólo el 10 y el 9 son mayores que 112. Entonces
5 11
= (−1)2 =1.Por tanto la congruenciax2 ≡5(mód 11)tiene
solución.
Teorema 3.3. Sean p6=2,y (a, 2p) =1. Entonces
i)
a p
= (−1)t, donde
t =
(pX−1)/2
j=1
ja
p
.
ii) p2= (−1)(p2−1)/8.
Demostración. Con la notación de la demostración al teorema anterior.
({ri, sj}iµ=1)kj=1 =
ja mód p:1≤j≤ p−1 2
({p−ri, sj}µi=1)kj=1 =
1, . . . , p−1 2
Es más
ja=p
ja p
+x, con x=ri ó sk
Entonces (pX−1)/2
j=1
ja= (pX−1)/2
j=1
p ja p + µ X
j=1
rj+ k
X
j=1
sj
y
(pX−1)/2
j=1
j =
µ
X
j=1
(p−rj) + k
X
j=1
sj
= µp−
µ
X
j=1
rj+ k
X
j=1
sj
Restando se obtiene (a−1)
(pX−1)/2
j=1
j=p
(pX−1)/2
j=1
ja p −µ
+2
µ
X
j=1
rj.
La suma a la izquierda es
(a−1)p
2−1
8 . Así
(a−1)p
2−1
8 ≡
(pX−1)/2
j=1
ja
p
−µ (mód 2)
Si a /∈2Z
µ≡ (pX−1)/2
j=1
ja
p
(mód 2)
Si a=2 como 1 ≤j ≤ p−21, se tiene que,p2 ≤ 2pj ≤ p−p1 <1, así ja p =0. Por lo tanto
µ≡ p
2−1
8 (mód 2)
3.2.
Reciprocidad cuadrática
Teorema 3.4. Si py qson primos impares distintos, entonces
p q q p
= (−1)p−21
q−1 2 .
Demostración. Defínase S= 1, p−21
× 1, q−21
, S⊆Z2.
Enton-ces
|S|= p−1 2 ·
q−1 2 .
Supóngase que existe (x, y) ∈ S, qx = py. Así y = qpx, con y∈Z; en consecuecia p|x. Por ende x =kp, para un entero k, sustituyendo y = qpkp = kq. Pero 1 ≤ y ≤ q−1
2 < q, por lo
tanto no existe tal pareja (x, y).
Separemos S = S1 tS2 en dos conjuntos ajenos, definidos
como sigue.
S1 = {(x, y)∈S:qx > py}
= {(x, y)∈S:1≤y < qx p } S2 = {(x, y)∈S:qx < py}
= {(x, y)∈S:1≤x < py q }
Las cardinalidades de estos conjuntos se calculan como
|S1| =
(pX−1)/2
x=1
qx
p
|S2| =
(qX−1)/2
y=1
py
q
Así se tiene
(pX−1)/2
j=1
qj
p
+ (pX−1)/2
j=1
pj
q
= p−1
2 · q−1
2 . Del teorema anterior se deduce la expresión deseada
p q q p
= (−1)p−21
q−1 2 .
Ejemplo 3.2. −4770
= −471 −472 475 477.Calculando cada uno de estos factores se tiene
−1 47
= (−1)462 = (−1)23 = −1,
2 47
= (−1)4728−1 = (−1)276 =1,
5 47
= 475(−1)42 46
2 = 2
5
= (−1)258−1 = −1
7 47
= 477(−1)62 46
2 = 5
7
= 75(−1)42 6 2 = 2
5
= −1
De este forma obtenemos −4770= (−1) (1) (−1)2 = −1.
1. 1317 = 1317= 134= 2132=1
2. 197
= − 197
= − 57
= − 57
= − 25 =1
Ejemplo 3.3. Caractericemos el conjunto {p:3∈Qp}.
Para estos primero suponga que p es impar. Entonces se tiene
3
p
= p3(−1)p−21.Pero
p 3 = 1 3
=1, si p≡1(mód 3)
2 3
= −1, si p≡2(mód 3)
y
(−1)p−21 =
1, si p≡1 (mód 4)
3.3. EL SÍMBOLO DE JACOBI 23 Por lo tanto 3p=1 si y sólo si
p≡1(mód 3)yp≡1(mód 4)o bien p≡2(mód 3)yp≡3(mód 4)
lo que puede reescribirse como
p≡1(mód 12)op≡−1(mód 12).
Por tanto 3p
=1 si y sólo si p≡ ±1 (mód 12) ó p=2.
Enseguida se muestra una aplicación sencilla y construida especialmente para fines de ilustración del resultado del ejem-plo anterior
Ejemplo 3.4. Factorice a 9997 como producto de primos. Co-mo 9997 = 1002 − 3 se cumple que si p | 9997 entonces
1002 ≡ 3 (mód p). Esto es p = 9997 o bien 3
p
= 1. Si este símbolo de Legendre es uno, del ejemplo anterior se sabe que
p≡ ±1(mód 12). Se prueba entonces si un primopes un factor
de 9997,con pque satisface esta última congruencia y sea me-nor que √9997 < 100. Los primos que deben verificarse son: 13,37,61,73,97 y 11,23,47,59,71,83. Se encuentra fácilmente que 9997=13(769), por lo que ahora resta por resolver si 769 es primo, y de no ser así debemos encontrar su factorización. Para este fin debe observarse que sipes un primo que divide a 769 entonces p|9997, por lo quepdebe estar entre los primo de la lista recién construida y que son menores que √768 < 28. Los números con estas características son 13,11,23 y ninguno de ellos divide a 769 por lo que este entero es primo. Así la factorización buscada es 9997=13(769).
3.3.
El símbolo de Jacobi
Definición 3.3. Seanq1, q2, . . . , qkprimos impares no necesa-riamente distintos y b = q1q2· · ·qk. Supóngase que qi - a, 1 ≤
i≤k. Entonces el símbolo de Jacobi ab está definido como
a b = k Y
j=1
a qj
donde qa
j
es el símbolo de Legendre.
Nótese que (a, b) =1.
Nota 3.5. Evidentemente ab=±1. Pero ab=1no implica que
a∈Qb. Por ejemplo
2 9 = 2 3 2 3 =1,
pero x2 ≡ 2 (mód 9) no tiene solución. Por otra parte si x2 ≡
a (mód b) tiene solución entonces ab = 1; en efecto pues si
b= Qjqj, como qj|b entonces x2 ≡ a (mód qj) tiene solución. Por consiguiente qa
j
=1,y así
a b = k Y
j=1
a qj
=1.
Si (a, b) =1 ya∈Qb entonces a∈Qp para todop|b. Si ab
= −1 entonces a /∈Qb.
Teorema 3.6. Supóngase que b, d son enteros impares positi-vos y que se cumple(ac, bd) =1. Entonces
a) ab ad = bda b) ab cb= acb
c) ab2 = ba2
=1 d) ba22cd
= dc
Demostración.
Se prueban sucesivamente los incisos a) Por definición.
b) Por la definición y las propiedades básicas de Legendre. c) De (a) y (b).
d) ba22dc
= ba22d
c
b2d
= bc2
c
d
= dc
e) Sea b=q1q2· · ·qk entonces a≡c (mód qi), para todo i, de
modo que qc
i
= qa
i
. Aplicando la definición se concluye lo que se deseada.
Teorema 3.7. Si b /∈2Z, b >0, entonces
−1
b
= (−1)b−21,
2 b
= (−1)b
2−1 8 .
Demostración. Sea b=Qki=1qi. Entonces
−1 b = k Y
i=1
−1 qi = k Y
i=1
(−1)qi2−1 = (−1)t,
donde t=Pki=1 qi−1
2
. Note que si m, n /∈2Z, entonces
(m−1)(n−1)
2 =
mn−m−n+1 2
= (mn−1) −m+1−n+1
2
= mn−1
2 −
m−1+n−1 2
de ahí que
m−1
2 +
n−1
2 ≡
mn−1
2 (mód 2).
Por lo tanto
k
X
i=1
qi−1
2 ≡
q1q2−1
2
+
k
X
i=3
qi−1
2 (mód 2)
≡ q1q2q3−1
2 +
k
X
i=4
qi−1
2 (mód 2)
.. . ≡ 1 2 k Y
i=1
qi−1
!
(mód 2)
≡ 1
2(b−1) (mód 2). y así
−1
b
= (−1)b−21.
De modo semejante si m, n /∈2Z entonces
(m2−1)(n2−1)
8 =
(m2n2−1)
8 −
(m2−1) + (n2−1)
8 .
Pero (2k−1)2−1=4k2−4k+1−1=4(k2−k)∈4Z, k∈Z. Y por lo tanto
(m2n2−1)
8 ≡
(m2−1) + (n2−1)
8 (mód 8)
luego se cumple
k
X
j=1
q2j −1
2 ≡
b2−1
3.3. EL SÍMBOLO DE JACOBI 25 y de ahí que
2 b = k Y
i=1
2 qi
= (−1)Pkj=1
q2 j−1
2 = (−1)
b2−1 8 .
Teorema 3.8. Si a, b /∈2Z, a, b >0 y (a, b) =1, entonces
a b b a
= (−1)a−21·
b−1 2 .
Demostración. Escribiendo a=Qki=1pi, b=
Q`
j=1qj se tiene
a b = ` Y
j=1
b qj = ` Y
j=1
k
Y
i=1
pi qj = ` Y
j=1
k
Y
i=1
qj
pi
(−1)pi2−1
qj−1 2 = b a
(−1)P`j=1
Pk i=1pi
−1 2
qj−1 2
Pero
`
X
j=1
k
X
i=1
pi−1
2 · qj−1
2
=
k
X
i=1
pi−1
2
! `
X
j=1
qi−1
2 y
k
X
i=1
pi−1
2 ≡
a−1
2 (mód 2)
`
X
j=1
qi−1
2 ≡
b−1
2 (mód 2)
por lo tanto se tiene a b b a
= (−1)a−21·
b−1 2 .
Ejemplo 3.5. 317 es primo, luego 105317
= 105317= 1052 .
Ejemplo 3.6. El valor de 1009713 puede encontrarse de la si-guiente manera:
713 1009
= 231009(31) = 100923 100931 = 100923 100931 = 2023 3117= = 2322 235 3117= 535 1417= 35 172 177
= 53(−1)1728−1 17
7
= 23(−1) 37= (−1)1(−1) 37= 43=1. Se enuncia sin demostración el siguiente resultado sobre el tiempo que requiere el cálculo del símbolo de Jacobi.
Teorema 3.9. Tiempo ab
=O(log2b)3.
Sabemos que si p-a, entonces el criterio de Euler nos dice que ab
≡ ap−21 (mód p). De ahí para verificar si n ∈ Z es
primo podemos elegir a ∈ Z, con (a, n) = 1 y determinar si an−21 ≡ a
n
(mód n). Cuando la congruencia no es válida se concluye que n es compuesto.
Ejemplo 3.7. Analicemos si n=341 es primo.. Elijamos a=2 y calculemos 2170(mód 341) = 1. Como 2
341
= (−1)34128−1 = −1.
Por lo tanto 341 no es primo.
Definición 3.4. Un entero impar n > 0, tal que an−21 ≡ a
n
(módn), para una∈Nes llamado un pseudoprimo de Euler
Capítulo 4
Álgebra
En este capítulo se recuerdan brevemente los conceptos y resultados básicos en Teoría de Grupos, Anillos, Campos, Ani-llos de Polinomios y Campos de Extensión. Estos conceptos se utilizan en el siguiente capítulo para el estudio de los campos finitos, que son una herramienta fundamental en la Teoría de Códigos y la Criptografía.
4.1.
Grupos
Definición 4.1. Ungrupoes una pareja (G,∗) formada por un conjuntoG y una operación binaria ∗ sobreG tal que
1. * es asociativa.
2. Existe e ∈ G con la propiedad de que para todo g ∈ G se cumplee∗g=g∗e=g.(Llamamos aeelementoidentidad
de G.)
3. Para todo g ∈ G existe w ∈ G tal que g∗w = w∗g = e.
Denotamos tal elemento w como g−1. (Llamamos a g−1 un
inversog.)
Cuando la operación binaria∗es conmutativa el grupo se dice
conmutativooabeliano.
Ejemplo 4.1. (N,+), no es un grupo pues por ejemplo 2 ∈ N carece de inverso en el grupo.
En el siguiente ejemplo K es un campo, usualmente Q,R,C o Zp con p primo.
Ejemplo 4.2. Enseguida se muestran algunos ejemplos de gru-pos.
1. (Z,+), (Q,+), (R,+), (C,+), son grupos abelianos.
2. (Q∗,·), (R∗,·), (C∗,·),son grupos abelianos.
3. El conjunto de funciones f : R → R, bajo la operación usual de suma de funciones.
4. (V,+), con V un espacio vectorial.
5. (Mm×n(K),+),el conjunto de matrices de m×n con
en-tradas en el campo K, bajo la suma usual.
6. (Zn,+), los enteros módulo n bajo la suma módulo n.
7. {1,−1}⊂R,bajo el producto usual.