MODELO ANALÍTICO DE LA PROPAGACIÓN DE ONDAS LARGAS LINEALES QUE SE PROPAGAN SOBRE UNA ESTRUCTURA CICLOIDAL

(1)

INSTITUTO POLITÉCNICO NACIONAL

Escuela Superior de Ingeniería Mecánica y Eléctrica

Unidad Zacatenco

“

MODELO ANALÍTICO DE LA PROPAGACIÓN DE

ONDAS LARGAS LINEALES QUE SE PROPAGAN

SOBRE UNA ESTRUCTURA CICLOIDAL

”

T E S I S

QUE PARA OBTENER EL TITULO DE:

INGENIERO EN SISTEMAS AUTOMOTRICES

PRESENTA:

AYRTON ALFONSO MEDINA RODRÍGUEZ

DIRECTOR DE TESIS:

Dr. ERIC GUSTAVO BAUTISTA GODÍNEZ.

(2)

INSTITUTO POLITÉCNICO NACIONAL

ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELECTRLCA

UNIDAD PROFESIONAL "ADOLFO LÓPEZ MATEOS"

TEMA DE TESIS

QUE PARA OBTENER EL TÍTULO INGENIERO EN SISTEMAS AUTOMOTRICES POR LA OPCIÓN DE TITULACIÓN TESIS Y EXAMEN ORAL INDIVIDUAL

DEBERA (N) DESARROLLAR AYRTON ALFONSO MEDINA RODRÍGUEZ

"MODELO ANALÍTICO DE LA PROPAGACIÓN DE ONDAS LARGAS LINEALES QUE SE PROPAGAN SOBRE UNA ESTRUCTURA CICLOIDAL"

CARACTERIZAR LA HIDRODINÁMICA DE ONDAS LARGAS LINEALES USANDO UN MÉTODO NUEVO DE SOLUCIÓN DE ECUACIONES DIFERENCIALES CON COEFICIENTES VARIABLES.

• INTRODUCCIÓN.

• FORMULACIÓN DEL PROBLEMA. • SOLUCIÓN MATEMÁTICA.

• ANÁLISIS DE RESULTADOS. • CONCLUSIONES.

MÉXICO D.F., A 09 DE MARZO DEL 2015.

ASESORES

DR.

A

(3)

´Indice general

Resumen III

Abstract V

Lista de figuras VII

Nomenclatura IX

1. Introducci ´on 1

1.1. Motivaci ´on . . . 1

1.2. Antecedentes . . . 5

1.3. Propuesta . . . 8

1.4. Objetivos . . . 12

2. Formulaci ´on del problema 13 2.1. Modelo f´ısico . . . 13

2.2. Ecuaciones de Gobierno . . . 15

2.3. Hip ´otesis . . . 16

2.4. Variables adimensionales . . . 16

3. Soluci ón matemática 22 3.1. Soluci ón anal´ıtica para el l´ımite deκ2 ∼O(1) . . . 22

3.2. Condiciones de frontera . . . 25

(4)

4. An´alisis de resultados 29

4.1. Cicloide . . . 29 4.2. Semi-cicloide . . . 34 4.3. Cicloide generalizado . . . 37

Conclusiones 43

Referencias 45

A. Teor´ıa de ondas largas 49

(5)

Resumen

(6)

(7)

Abstract

(8)

(9)

´Indice de figuras

1.1. Geotubo como rompelas sumergido. . . 3 1.2. Geotubo de alta resistencia llenado hidr´aulicamente de una

mezcla de arena y agua utilizado para el control de la ero-si ón costera. . . 4 1.3. Representaci ón esquemática de la propagaci ón del oleaje

sobre un fondo variable: (a) propagaci ón del oleaje hacia la transici ón curva, (b) defromaci ón del oleaje sobre la curva, (c) oleaje reflejado y transmitido. . . 9 1.4. Prototipo experimental: (a) vista de la secci ón tranversal, (b)

vista en perspectiva y (c) superposici ón del prototipo ex-perimental, la distribuci ón cicloidal y la soluci ón numérica propuesta por Guoet al.[2]. . . 10

2.1. Diagrama de vista lateral del modelo f´ısico estudiado. La amplitud del oleajeAw para w=I, R y T, representan el

oleaje incidente (viajando de izquierda a derecha), reflejado y transmitido, respectivamente; θ es el ´angulo del circulo generador del arco de cicloide con radio r y θL es el valor

m´aximo de θ en x = L. El modelo f´ısico est´a conformado por tres regionesR1,R2 yR3. . . 13

4.1. Caso 1. Coeficiente de reflexi ´onCRy transmisi ´onCT en

fun-ci ´on del par´ametro adimensional relativo de profundidades

(10)

4.2. Caso 1. Coeficiente de reflexi ´onCRy transmisi ´onCT en

fun-ci ón del parámetro adimensional fun-cinemáticoκ2para valores distintos del parámetroµ.. . . 31 4.3. Caso 1. Amplitud adimensional de las ondas largas en

fun-ci ón del parámetro adimensional θ, con un µ = 0.66 para valores distintos del parámetro cinemáticoκ2. . . 32 4.4. Caso 1. Amplitud adimensional de las ondas largas en

fun-ci ón del parámetro adimensional θ, con un κ2 = 6.3 para valores distintos del parámetroµ. . . 33 4.5. Caso 2. Coeficiente de reflexi ónCRy transmisi ónCT en

µpara valores distintos del parámetro cinemáticoκ2. . . 35 4.6. Caso 2. Coeficiente de reflexi ónCRy transmisi ónCT en

fun-ci ón del parámetro adimensional fun-cinemáticoκ2para valores distintos del parámetroµ. . . 36 4.7. Caso 2. Amplitud adimensional de las ondas largas en

fun-ci ón del parámetro adimensional θ, con un µ = 0.66 para valores distintos del parámetro cinemáticoκ2. . . 37 4.8. Caso 2. Amplitud adimensional de las ondas largas en

fun-ci ón del parámetro adimensional θ, con un κ2 = 6.3 para valores distintos del parámetroµ. . . 38 4.9. Caso 3. Coeficiente de reflexi ónCRy transmisi ónCT en

µpara valores distintos del parámetro cinemáticoκ2. . . 39 4.10. Caso 3. Coeficiente de reflexi ónCRy transmisi ónCT en

fun-ci ón del parámetro adimensional fun-cinemáticoκ2para valores distintos del parámetroµ. . . 40 4.11. Caso 3. Amplitud adimensional de las ondas largas en

(11)

(12)

Nomenclatura

Letras latinas

AI Amplitud del oleaje incidente,[m]

AR Amplitud del oleaje reflejado,[m]

AT Amplitud del oleaje transmitido,[m]

c Velocidad de fase,[m/s]

CR Coeficiente de Reflexi ´on

CT Coeficiente de Transmisi ´on

E Energ´ıa del oleaje,[kgm3_/s3_]

¯

F Flujo de energ´ıa del oleaje,[kgm2/s2]

g Aceleraci ´on de la gravedad,[m/s2_]

h Profundidad del agua,[m]

h1 Profundidad de la regi ´on 1,[m]

h2[x(θ)] Profundidad de la regi ´on 2,[m]

h3 Profundidad de la regi ´on 3,[m]

H Altura del oleaje,[m]

t tiempo,[s]

i √−1

k N ´umero de onda,k = 2π/λ

L Longitud caracter´ıstica de la regi ´on 2,[m]

P Presi ´on hidrost´atica,[N/m2]

PD Presi ´on din´amica,[N/m2]

r Radio del c´ırculo generador del arco de cicloide,[m]

(13)

T Per´ıodo del oleaje,[s]

u Velocidad instant´anea horizontal,[m/s]

U Velocidad media del agua en la direcci ´onx,[m/s]

w Velocidad instant´anea vertical,[m/s]

x Eje de coordenadas horizontal

y Eje de coordenadas lateral

z Eje de coordenadas vertical

S´ımbolos griegos

βI Constante compleja del oleaje incidente

βR Constante compleja del oleaje reflejado

βT Constante compleja del oleaje transmitido

χj Eje coordenado longitudinal adimensional

∆_j₍_χ_,_τ₎ _{Superficie libre adimensional del oleaje}

δj(χ) Superficie libre del oleaje adimensional espacial

θ Angulo del cicloide,´ [rad]

θL Valor m´aximo del ´angulo del cicloide,[rad]

κ2 Par´ametro cinem´atico adimensional

λ Longitud de onda,[m]

µ Relaci ´on de profundidades

ρ Densidad del agua,[kg/m3]

φ Potencial de velocidad

ω Frecuencia angular del oleaje,[1/s] ζ(x, t) Superficie libre del oleaje,[m]

Sub´ındices

I, R, T Incidente, Reflejado y Transmitido, respectivamente

j 1, 2 y 3

(14)

Cap´ıtulo 1

Introducci ´on

1.1. Motivaci ´on

La l´ınea de costa es un espacio dinámico de cambios naturales, en la cual se desarrollan diversas actividades humanas, como son: comerciales, recreativas, de vivienda, entre otras. Ésta ocupa menos del 15 % de la su-perficie terrestre y se estima que 3.1 mil millones de personas viven dentro de un área de 200 kil ómetros de distancia del mar. Para el 2025 se espera que tres cuartas partes de la poblaci ón mundial vivan en una zona cerca-na a la costa [3]. Generalmente, las zocerca-nas costeras son importantes para el buen funcionamiento de muchas naciones, siendo las áreas más desarro-lladas. Además, permiten el intercambio de recursos para la producci ón de bienes y servicios siendo el centro de la mayor´ıa de actividades comer-ciales e industriales.

(15)

Existen diversas formas para combatir la erosi ón, pero son procesos muy costosos para los gobiernos locales. Algunas ciudades reponen sus playas por medio de un proceso, que consiste en importar arena de re-giones alejadas de la playa que reemplace la arena perdida a causa de la erosi ón. Este proceso de regeneraci ón de playas ocurre por lo regular cada 5 a ños [4]. Repetir este proceso puede ser costoso y es una soluci ón que no ayuda a resolver de manera definitiva el problema.

Para proteger las costas, una de las caracter´ısticas hidrodinámicas que se estudia con mayor frecuencia es la reflexi ón del oleaje. Las estructuras naturales y/o artificiales pueden contribuir a modificar su mecánica; una de estas estructuras artificiales son los rompeolas. Éstas brindan protec-ci ón y controlan la erosi ón en las áreas costeras. Generalmente, éstos se dividen en dos grupos: los que s ólo aten úan la energ´ıa del oleaje y los que bloquean totalmente el flujo del oleaje hacia la costa. Los primeros, a su vez se dividen en rompeolas sumergidos, flotantes, neumáticos e hidráulicos.

Los rompeolas sumergidos han llegado a ser más comunes en los a ños recientes. Frecuentemente, son la soluci ón preferida cuando se requiere una protecci ón completa de las costas. Entre las ventajas que proporcio-nan se encuentran que dan una imagen más estética que los rompeolas comunes, que son muy evidentes a la vista. Esta caracter´ıstica estética es importante para mantener el valor tur´ıstico de muchas playas y es usual-mente una de las consideraciones del uso de tales estructuras en la protec-ci ón costera [5]. Éstos, ayudan a reduprotec-cir la erosi ón en las playas causando que una cierta cantidad de la energ´ıa incidente del oleaje se disipe al pasar sobre ellos, en lugar de bloquear totalmente el flujo que se dirige a la cos-ta. Adicionalmente, permiten el tránsito libre de la fauna marina y de los transportes litorales de sedimentos.

(16)

[image:16.595.168.444.219.414.2]

artifi-ciales. Adicionalmente, debido a su costo bajo y a su efectividad en la dis-minuci ón de la energ´ıa del oleaje, los rompeolas sumergidos han cobrado importancia en el área de la hidráulica mar´ıtima. Los rompeolas sumergi-dos presentan una variedad de formas y su rendimiento suele evaluarse con base en los resultados obtenidos en la práctica [7].

Figura 1.1. Geotubo como rompelas sumergido.

(17)

[image:17.595.191.417.166.396.2]

tanto en tierra como en el mar y en ocasiones son apilados para formar diques de mayor altura u otros tipos de estructuras geot´ecnicas.

Figura 1.2. Geotubo de alta resistencia llenado hidr´aulicamente de una mezcla de arena y agua utilizado para el control de la erosi ´on costera.

Los geotubos poseen ventajas con respecto a otras estructuras ya que su impacto es m´ınimo en el ambiente, presentan un bajo costo respecto a otras estructuras tradicionales, as´ı como de mantenimiento, y ostentan una gran resistencia. Su uso es cada vez más extenso y más son los lugares en los cuales se opta por esta opci ón como un medio para conservar y regenerar las playas.

(18)

1.2. Antecedentes

Los geotubos se emplazan en aguas someras, la hidrodinámica del oleaje en estas regiones puede estudiarse con la teor´ıa de ondas largas, la cual tiene la caracter´ıstica de que el campo de velocidades fundamen-talmente es en un plano horizontal y las velocidades verticales se asumen peque ñas, en comparaci ón con las horizontales.

En el pasado, muchos investigadores han desarrollado estudios funda-mentales para caracterizar los efectos geométricos de obstáculos sumer-gidos sobre la reflexi ón del oleaje. Lamb [9] fue uno de los pioneros en desarrollar una soluci ón anal´ıtica para la reflexi ón y transmisi ón de ondas largas que se propagan sobre un escal ón finito, usando condiciones de aco-plamiento para la superficie y el flujo de masa en la frontera [5]. Kreiss [10] investig ó el efecto de la fricci ón de fondo en la deformaci ón de ondas pe-ri ódicas, que se propagan en un canal semi-cerrado. Gallagher et al.[11] analizaron la deformaci ón no lineal de ondas largas en aguas poco pro-fundas causada por los siguientes efectos: la amplitud finita del oleaje, la pendiente en el fondo y la fricci ón. La soluci ón de la ecuaci ón de gobierno se determin ó empleando métodos de perturbaci ón y métodos numéricos.

Aubrey et al. [12] estudiaron experimentalmente la deformaci ón de mareas astron ómicas en estuarios poco profundos durante un tiempo de observaci ón de 29 d´ıas, identificando las interacciones no lineales asocia-das con el equilibrio del océano. Posteriormente, Speeret al.[13] obtuvie-ron la soluci ón de la ecuaci ón de conservaci ón de la cantidad de movi-miento tomando en cuenta efectos geométricos y de fricci ón en el fondo del canal. Con base en estos efectos, determinaron la influencia que tienen en la asimetr´ıa de la elevaci ón de la superficie libre y en la deformaci ón de la velocidad de las part´ıculas del agua.

(19)

y dinámicos que permitieron que su modelo derivara en un problema de perturbaci ón singular. Mead [15] propuso un método anal´ıtico en coorde-nadas lagrangianas, con el prop ósito de trazar la trayectoria de las part´ıcu-las y evitar la generaci ón de malpart´ıcu-las complejas. Lauteret al.[16] presenta-ron una soluci ón anal´ıtica de las ecuaciones de aguas someras, transforma-das de un sistema cartesiano fijo a un sistema cartesiano rotatorio, donde modelaron el campo de velocidades de las part´ıculas del agua. Por otro la-do, Camassaet al.[17] estudiaron la dinámica del oleaje en aguas someras basados en una estructura Hamiltoniana e implementaron un algoritmo, donde el sistema de ecuaciones diferenciales ordinarias tienen soluci ón en un tiempo finito.

La deformaci ón y reflexi ón del oleaje debidas a estructuras naturales (arrecifes de coral, plataformas continentales) y artificiales (rompeolas, di-ques de abrigo) son un importante t ópico en el dise ño de estructuras cos-teras. Ohareet al.[18] estimaron el coeficiente de reflexi ón del oleaje que se propaga sobre un fondo con transiciones variables.

(20)

(21)

con geotextiles.

En la literatura especializada, se pudo identificar que los trabajos re-lacionados con los geotubos, estudian fundamentalmente los esfuerzos a los que está sometida la geomembrana cuando se encuentra en el procedi-miento de llenado con arena, a partir de estas condiciones, se revisan las geometr´ıas que están sometidas a menores cargas por llenado. Otro de los intereses en las investigaciones, es estudiar el comportamiento mecánico de estas estructuras, cuando se encuentran interactuando entre s´ı. Por otra parte, pudo verificarse que la estabilidad de los geotubos se estudia en for-ma experimental y numérica cuando éstos se encuentran bajo la acci ón del oleaje. Cabe precisar que en los trabajos antes mencionados, el objeto de estudio es el geotubo y no el efecto que éste produce en la disipaci ón del flujo de energ´ıa del oleaje, que es el objetivo principal de estas estructuras. Con base en los comentarios anteriores, en esta tesis se propone obtener una soluci ón anal´ıtica que permita analizar la hidrodinámica del oleaje cuando éste se propaga sobre un rompeolas que sigue una distribuci ón cicloidal.

1.3. Propuesta

El fen ómeno de propagaci ón de las ondas largas sobre estructuras su-mergidas en el fondo del mar, se muestra en la Fig. 1.3. Como se observa en la Fig. 1.3 (a), el oleaje proveniente del océano se propaga sobre la re-gi ón 1. En la rere-gi ón 2, el oleaje se deforma a lo largo del obstáculo como se ilustra en la Fig. 1.3 (b). Esto genera que la onda incidente se divida en dos ondas: una onda reflejada que viaja en el sentido contrario de la on-da incidente y una transmition-da que viaja en el mismo sentido de la onon-da incidente hacia la regi ón 3, como se muestra en la Fig. 1.3 (c).

(22)

obe-Ola incidente

Ola reflejada Ola transmitida

a)

b)

c)

Región 1

Región 2

[image:22.595.167.437.129.415.2]

Región 3

Figura 1.3. Representaci ón esquemática de la propagaci ón del oleaje sobre un fon-do variable: (a) propagaci ón del oleaje hacia la transici ón curva, (b) defromaci ón del oleaje sobre la curva, (c) oleaje reflejado y transmitido.

decer, como primera aproximaci ´on, una geometr´ıa cicloidal, la cual sigue las siguientes ecuaciones par´ameticas, Tang [27],

M =r(θ₋sinθ) (1.1)

y

N =r(1₋cosθ), (1.2)

donde(M, N)son las coordenadas del puntoP referenciado a los ejesX¯ y

¯

(23)

Z

X θ= /2π

P(M,N)

θ_L=π

θ_L=3 /2π

r θ c) 0.00 0.01 0.02 0.03 0.04 b) a) H Geometría Cicloidal

Solución numérica Guoet al.[2]

0.02 0.04 0.06 0.08 0.10 0.12 0.00

-0.01

[image:23.595.128.484.124.336.2]

-0.02

Figura 1.4. Prototipo experimental: (a) vista de la secci ón tranversal, (b) vista en perspectiva y (c) superposici ón del prototipo experimental, la distribuci ón cicloi-dal y la soluci ón numérica propuesta por Guoet al.[2].

Para verificar lo anterior, comparamos la transici ón cicloidal, Ecs. (1.1) y (1.2), con la soluci ón numérica para una secci ón transversal de un geo-tubo simétrico, que descansa sobre una base r´ıgida como fue propuesto por Guoet al.[2], la cual está dada por la siguiente ecuaci ón diferencial no lineal de segundo orden

U′′ =−1 T

!

P0+γV "#

1 +U′2$3/2 , (1.3)

con

T = 1 2P0+

1 4γ(H)

4

(1.4)

y las condiciones de frontera

dU!

V = 0"

(24)

y

dU!

V =H"

dV =−∞, (1.6)

dondeH es la altura de la secci ´on transversal,U =X −πryV = 2r−Z

son las cordenadas que definen la geometr´ıa de la secci ón transversal. El origen de las coordenadas anteriores es tomado en la parte superior de la secci ón transversal. La presi ón de bombeo usada para llenar el geotubo con la mezcla esP0. La fuerza de tensi ón circunferencial en el tubo por uni-dad de ancho a lo largo de la secci ón transversal es T y el peso espec´ıfico está denotado porγ.

Adicionalmente, se realiz ó un peque ño prototipo f´ısico de un geotu-bo: éste consiste en llenar a 80 % de su volumen una bolsa rectangular de plástico, la cual tiene un ancho y un largo de 13.5 cm y 30 cm, respec-tivamente, con una mezcla de un 1 kg de yeso y 0.7 L de agua. El peso espec´ıfico de la mezcla esγ = 8335N/m3_.

Cuando la mezcla se endureci ó, se realiz ó un corte transversal al mo-delo experimental, la forma resultante de la secci ón transversal junto con la vista en perspectiva se muestran en la Fig. 1.4-a y Fig. 1.4-b, respecti-vamente. El radio de la secci ón transversal del prototipo tiene el valor de

r = 0.02m

(25)

1.4. Objetivos

Objetivo general:

Caracterizar la hidrodinámica del oleaje, en condici ón de teor´ıa lineal de ondas largas, mediante la implementaci ón de un método nuevo de so-luci ón de ecuaciones diferenciales con coeficientes variables.

Objetivos particulares:

Proponer un modelo matemático adimensional de la propagaci ón del oleaje sobre una superficie con distribuci ón cicloidal.

Determinar una soluci ón anal´ıtica de la deformaci ón de la superficie libre del oleaje que se propaga sobre un fondo con transici ón cicloi-dal.

(26)

Cap´ıtulo 2

Formulaci ´on del problema

[image:26.595.123.484.356.556.2]

2.1. Modelo f´ısico

Figura 2.1. Diagrama de vista lateral del modelo f´ısico estudiado. La amplitud del oleajeAw para w =I, R y T, representan el oleaje incidente (viajando de

izquierda a derecha), reflejado y transmitido, respectivamente;θ_{es el ´angulo del}

(27)

El modelo f´ısico estudiado se muestra en la Fig. 2.1. Consideremos un oleaje largo lineal que se propaga de izquierda a derecha sobre una tran-sici ón cicloidal. En el diagrama, el modelo f´ısico se encuentra divido en tres diferentes regionesR1,R2 yR3. En el sistema de coordenadas que se seleccion ó, el eje x es positivo a la derecha con el origen en la intersec-ci ón de las regiones R1 y R2, mientras que el eje z apunta hacia arriba, normal al nivel medio del agua. El intervalo de transici ón de la regi ónR2 es 0 _≤ x _≤ L, mientras que las regiones R1 y R3 son definidas por los intervalos−∞ ≤x_≤0yL_≤x_{≤ ∞}, respectivamente.

Adicionalmente, asumimos que las profundidades en las regiones R1 y R3 son constantes. En el presente análisis, asumimos que el fondo es impermeable. Sin embargo, las fronteras verticales izquierda y derecha de los extremos del sistema están completamente abiertas al flujo del oleaje. En particular, asumimos que en el lado izquierdo existe oleaje incidente y reflejado y s ólo en el lado derecho hay presencia de oleaje transmitido.

El origen de la geometr´ıa cicloidal, descrito por las Ecs. (1.1)-(1.2) es trasladado al origen del nuevo sistema de referenciax₋z, el cual está lo-calizado en θ = π/2; el máximo valor del ángulo θ es θL, donde π/2 <

θL ≤ 2π. Para el caso particular deθL(= 3π/2),h3 =h1 yh1 =h1−r, res-pectivamente. Tomando en cuenta las consideraciones mencionadas, las profundidades prescritas a lo largo de las tres regiones est´an dadas por las siguientes relaciones

h=

    

   

h1 ; x≤0,

h2[x(θ)] =h1+rcosθ ; 0≤x(θ)≤L, π₂ ≤θ≤θL,

h3 ; x≥L.

(2.1)

y la ecuaci ón paramétrica para la distribuci ón horizontal a lo largo del eje

xen la regi ´onR2, est´a dada por

x(θ) = r#θ₋sinθ+ 1− π

2

$

(28)

De la expresi ´on anterior se puede deducir que la longitudLde la tran-sici ´on cicloidal puede expresarse como

L=r#θL−sinθL+ 1−

π 2

$

(2.3)

y la profundidadh3se obtiene de la Ec. (2.1) y se define como

h3 =h1+rcosθL (2.4)

2.2. Ecuaciones de Gobierno

En el presente trabajo, se usan las ecuaciones de gobierno que descri-ben el movimiento de las ondas largas que presentan densidad constante y viscosidad despreciable. En la aproximaci ón de aguas someras, el movi-miento dominante es en el plano horizontal, debido a que la velocidad ver-tical es débil. El flujo de fluido en la regi ónR2 lo gobiernan las ecuaciones bidimensionales de continuidad y de cantidad de movimiento, Svendsen (2006) [28]

∂ζ

∂t +∇h·[V(h2+ζ)] = 0 (2.5)

y

∂V

∂t + (V·∇h)V+g∇hζ = 0, (2.6)

donde el operador∇hest´a definido como∇h = (∂/∂x,∂/∂y),ζ =ζ(x, y, t)

es es la elevaci ´on de la superficie libre, medida a partir del nivel me-dio del agua en condici ´on de reposo, V es el vector velocidad dado por

V = (U, V)dondeU = )ζ

−h2udz/(ζ+h2)y V =

)ζ

−h2vdz/(ζ+h2)son las velocidades medias en la direcci ´onxyy, respectivamente;u=u(x, y, z, t)

yv =v(x, y, z, t)son las componentes de la velocidad local en la direcci ´on

(29)

2.3. Hip ´otesis

El flujo es irrotacional.

Teor´ıa de ondas con amplitud peque ˜naAI/h(1.

La longitud de onda del oleaje es mucho mayor que la profundidad

h/λ₍1.

La velocidad en direcci ´on vertical es despreciable comparada con la velocidad en direcci ´on horizontal.

El oleaje perturbado se debe ´unicamente al efecto que tiene la geo-metr´ıa ubicada en el fondo del mar.

2.4. Variables adimensionales

Las ecuaciones de aguas someras descritas arriba, Ecs. (2.5) y (2.6), pue-den escribirse de una manera más apropiada usando un análisis de orde-nes de magnitud. Para oleaje de amplitud peque ña, las siguientes relacio-nes se satisfacen:

ζ h2 ∼

AI

h1 (

1, (2.7)

dondeAI es la amplitud del oleaje incidente. Denotanto la escala de

tiem-po caracter´ıstica con el periodoT, la escala de longitud horizontal carac-ter´ıstica es L y para ondas largas lineales no dispersivas la celeridad de onda caracter´ıstica está dada porc=√gh1 =ω/k, donde la frecuencia del oleaje es ω = 2π/T y el n úmero de onda k = 2π/λ. Como una primera aproximaci ón y para aquellas ondas con amplitud peque ña, se considera que U, V yζ son peque ñas; por lo tanto, sus productos también son pe-que ños, Dean (1984) [29, pág. 136]. En este caso y de la Ec. (2.6), la veloci-dad caracter´ısticaUc se determina mediante un balance entre los términos

(30)

Uc

T ∼ gAI

L . (2.8)

Sustituyendo la celeridad caracter´ıstica,c, en la relaci ´on anterior, la ve-locidad caracter´ıstica puede escribirse como,

Uc =

AI

h1

λ

Lc . (2.9)

Del an´alisis anterior, podemos introducir las siguientes variables adi-mensionales

χ2 = _Lx, Y2 = _Ly_y, ˜h= h2[_hx₁(θ)], τ =ωt, ∆2(χ2, Y2,τ) = _Aζ_I,

U2(χ2, Y2,τ) = _Ah_I1_cL_λU y V2(χ2, Y2,τ) = _Ah_I1_cL_λV.

En t´erminos de las variables adimensionales anteriores, las ecuaciones de gobierno, Eqs. (2.5) y (2.6) toman la forma siguiente:

∂∆₂

∂τ +

µ2 1

2π ∂*U2

#

˜

h+ν∆₂$+

∂χ2

+µ1µ2 2π

∂*V2 #

˜

h+ν∆₂$+

∂Y2

= 0, (2.10)

∂U2

∂τ +

νµ2 1

2π U2 ∂U2

∂χ2

+νµ1µ2 2π V2

∂U2

∂Y2

=₋ 1

2π ∂∆₂

∂χ2

(2.11)

y

∂V2

∂τ +

νµ2 1

2π U2 ∂V2

∂χ2

+νµ1µ2 2π V2

∂V2

∂Y2

=₋µ3 2π

∂∆₂

∂Y2

. (2.12)

En las ecuaciones anteriores, los par´ametros adimensionales est´an de-finidos como

µ1 =

λ

L, µ2 = λ Ly

, µ3 =

L Ly

y ν = AI

h1

.

(31)

longitud horizontal caracter´ıstica L son del mismo orden de magnitud, para rompeolas de gran longitud Ly ) λ, normal a la hoja, µ2 ( 1 y

µ3 (1es un par´ametro geom´etrico de esbeltez.

Por lo tanto, como una primera aproximaci ´on, las ecuaciones anteriores se simplifican y pueden ser escritas en la forma:

∂∆₂

∂τ +

µ2 1

2π

∂*U2˜h +

∂χ2

= 0, (2.13)

∂U2

∂τ =−

1 2π

∂∆₂

∂χ2

(2.14)

y

∂V2

∂τ ≈0. (2.15)

La ´ultima relaci ´on, Eq. (2.15), implica que(µ3/2π)∂∆2/∂Y ≈0y por lo tanto, el movimiento a lo largo del ejexes dominante.

De lo anterior, las ecuaciones de gobierno simplificadas para el movi-miento de ondas largas lineales en la regi ´on R2 est´an dadas por las Ecs. (2.13) y (2.14). Ecuaciones similares pueden obtenerse para las regiones

R1 y R3, las cuales son mostradas más adelante. Las ecuaciones de con-tinuidad y de cantidad de movimiento (2.13) y (2.14) pueden combinarse en una única expresi ón. Para este prop ósito, podemos derivar la Ec. (2.13) con respecto al tiempo adimensional, τ, y reemplazar la Ec. (2.14) en la ecuaci ón resultante. El procedimiento anterior nos conduce a la siguiente ecuaci ón,

∂2_∆ 2

∂τ2 =κ

2 2 , ˜ h∂ 2_∆ 2

∂χ2₂ + ∂∆₂

∂χ2

∂˜h ∂χ2

-. (2.16)

Tomando en cuenta las Ecs. (2.1) y (2.3), la Ec. (2.16) escrita en t´erminos del ´anguloθ, se expresa como

1 κ2 2

∂2_∆ 2

∂τ2 =

.

(1 +µcosθ) (1₋cosθ)2

d2_∆ 2

dθ2 −

(1 +µ) sinθ (1₋cosθ)3

d∆₂

dθ

/

(32)

En la ecuaci ón superior, los parámetros adimensionales κ2 y µ están dados por

κ2 =

√

gh1

ωr = λ

2πr y µ= r h1

La Ec. (2.17) requiere para su soluci ón dos condiciones iniciales y dos de frontera, las cuales se obtienen mediante el siguiente procedimiento. La linealidad del problema permite expresar la elevaci ón de la superficie libre adimensional como una funci ón harm ónica en el tiempo. Por lo tanto, tenemos que el oleaje en la regi ónR2 está dado por la siguiente expresi ón

∆₂₍_θ_{, t}_{) = Re}0_δ₂₍_θ₎_e−iτ1

(2.18)

donde∆₂ _{es la amplitud del oleaje en cualquier secci ´on transversal de la}

regi ´onR2,i=√−1y Re indica la parte real del argumento. De la Ec. (2.18), las condiciones iniciales est´an dadas por

∆₂₍_θ_,_{0) =} _Re_[_δ₂₍_θ_)]

∂∆₂₍_θ_,₀₎

∂τ =Re[−iδ2(θ)]

Se debe considerar que las relaciones antes mencionadas son funciones de la amplitd adimensional δ2 del oleaje para cualquier secci ón transver-sal a lo largo del ángulo θ, la cual es una funci ón desconocida y es una parte del problema a resolver. Para oleaje largo lineal la presi ón permane-ce hidrostática, i.e. P(x, t) = ρg(ζ₋z), dondeρes la densidad del agua, la cual en variables adimensionales está escrita como P˜ = (∆_j ₋_z_˜₎_{, con}

˜

P = P/ρgAI yz˜= z/AI. Podemos considerar que la presi ´on es la misma

en cualquier lado de la onda en las interfaces θ = π/2 o θ = θL. Por lo

tanto, las condiciones de frontera de la Ec. (2.17), pueden escribirse como,

(33)

y

θ =θL : ∆2(θL) =∆3(κ3L). (2.20) En el l´ımite deκ2 )1, la Ec. (2.17), se reduce a la siguiente expresi ´on

(1 +µcosθ)∂

2_∆ 2

∂θ2 −(1 +µ) cot

θ 2

∂∆₂

∂θ = 0 (2.21)

donde claramente se puede apreciar en la Ec. (2.21), que el término de la aceleraci ón desaparece, el cual desde una perspectiva f´ısica indica que la elevaci ón de la superficie adimensional ∆₂ _{es desacelerada y que ésta es}

s ólo una funci ón del parametro µ. El modelo anterior puede ser presen-tado para valores peque ños de la frecuencia del oleaje y valores fijos de la profundidad h1 y el radior. Sin embargo, se debe tener en cuenta que la presente formulaci ón es una primera aproximaci ón y para condiciones más realistas deben tomarse en cuenta mecanismos de disipaci ón del olea-je, como son: la fricci ón del fondo y la rotura.

Introduciendo la Ec. (2.18) en la Ec. (2.17), podemos obtener el siguiente problema de valores en la frontera

κ2₂(1 +µcosθ) (1₋cosθ)2

d2_δ 2

dθ2 −

κ2₂(1 +µ) sinθ (1₋cosθ)3

dδ2

dθ +δ2 = 0 (2.22)

con las condiciones de frontera

θ =π/2 : δ2(π/2) =δ1(0) (2.23)

y

θ=θL : δ2(θL) =δ3(κ3L). (2.24)

(34)

cuales se obtienen a continuaci ón. La ecuaci ón de onda para flujo no per-manente en las regionesR1yR3se obtienen por un procedimiento similar al que se describi ó.

Introduciendo las siguiente variables adimensionales para la regi ´onR1

χ1 =k1x, δ1 =

ζ(x)

AI

y para la regi ´onR3

χ3 =k3x y δ3 =

ζ(x)

AI

,

dondek1 = (gh1)1/2/ωyk3 = (gh3)1/2/ωrepresentan los n ´umeros de onda para las regionesR1yR3, respectivamente.

La ecuaciones de gobierno que describen el movimiento del oleaje en las regionesR1 yR3est´an dadas por

d2δj

dχ2_j +δj = 0 paraj = 1y3 (2.25)

Las soluciones a la Ec. (2.25) son triviales y se expresan en la forma siguiente:

Para la regi ´onR1 es

δ1(χ1) =eiχ1 +βRe−iχ1 (2.26)

y para la regi ´onR3 tenemos

δ3(χ3) = βTeiχ3 (2.27)

En las expresiones anterioresβR = AR/AI y βT = AT/AI son

ampli-tudes complejas adimensionales de la reflexi ´on y transmisi ´on del oleaje. Evaluando la Ec. (2.26) en χ1 = 0, podemos obtener que δ1(0) = 1 + βR

y para χ3 = k3L, δ3(k3L) = βTeik3L. Estas relaciones son justamente las

(35)

Cap´ıtulo 3

Soluci ´on matem´atica

3.1. Soluci ´on anal´ıtica para el l´ımite de

κ

2

∼

O

(1)

En esta secci ón, se obtiene una soluci ón anal´ıtica de la ecuaci ón diferen-cial de segundo orden, Ec. (2.22), para el l´ımite del parámetroκ2 ∼O(1). El parámetroκ2 proporciona una medida de la magnitud de los efectos gra-vitacionales(gh1)1/2relativos a los efectos inerciales(ωr)o, de una manera más simple, el parámetroκ2 puede ser definido como la relaci ón entre la longitud de onda(λ)y el radio(r). Por otro lado, el parámetroκ2 no pue-de tomar valores pue-deκ2 (1, porque para este l´ımite la condici ón de ondas largas lineales no es satisfecha.

La presente metodolog´ıa anal´ıtica es capaz de proporcionar una visi ón rápida en c ómo la soluci ón depende de los dos parámetros del problema;

µyκ2. Con la finalidad de obtener la soluci ón anal´ıtica de la Ec. (2.22), se emplea un método efectivo para encontrar soluciones especiales de ecua-ciones diferenciales con coeficientes variables, el cual se basa en encontrar una ecuaci ón diferencial de Bernoulli correspondiente a la ecuaci ón estu-diada, Qin y Fan [1].

(36)

a0(θ)

d2_δ 2(θ)

dθ2 +a1(θ)

dδ2(θ)

dθ +b(θ)δ

m

2 (θ) = 0 (3.1)

donde a0,1(θ)y b(θ)son funciones continuas conocidas, y m += 0 es una constante. Podemos encontrar una soluci ´on, la cual satisfaga la siguiente ecuaci ´on diferencial de Bernoulli

dδ2

dθ =a(θ)δ

α

2 +c(θ)δ2 (3.2)

dondea(θ)yc(θ)son funciones continuas no conocidas y αes una cons-tante a determinar. Sustituyendo la Ec.(3.2) en la Ec.(3.1), obtenemos la siguiente ecuaci ´on

αa0(θ)a2(θ)δ22α−1+b(θ)δ2m+

[a0(a′(θ) + (α+ 1)a(θ)c(θ)) +a1(θ)a(θ)]δ2α+ 0

a0 !

c′₍_θ_{) +}_c2₍_θ₎"

+a1(θ)c(θ) 1

δ2 = 0 (3.3)

Considerando que el exponente m = 2α ₋1en el primer término de la Ec. (3.3), entonces el primer y segundo término del lado izquierdo de la ecuaci ón anterior pueden ser agrupados. Adicionalmente, igualando los coeficientes resultantes con cero, obtenemos el siguiente conjunto de ecua-ciones      m+1

2 a0(θ)a

2₍_θ_{) +}_b₍_θ_{) = 0}

a0 !

a′₍_θ_{) +} m+3

2 a(θ)c(θ) "

+a1(θ)a(θ) = 0

a0(c′(θ) +c2(θ)) +a1(θ)c(θ) = 0

(3.4)

Una comparaci ´on simple entre la Ec. (2.22) y (3.1), nos permite escribir que

a0(θ) =

κ2₂(1 +µcosθ)

(1−cosθ)2 , a1(θ) =−

κ2₂(1 +µ) sinθ

(1−cosθ)3 , b(θ) = 1 y m= 1.

(37)

Sustituyendo las anteriores relaciones en la Ec. (3.4) y resolviendo para el coeficiente variablea(θ)yc(θ), obtenemos que

a(θ) = ± i

κ2

(1₋cosθ)

√

1 +µcosθ (3.6)

y

c(θ) = µsinθ

4 (1 +µcosθ) (3.7)

Ahora, sustituyendo la Ec. (3.6) y (3.7) en la Ec. (3.2), obtenemos la siguiente ecuaci ´on diferencial de Bernoulli

dδ2

dθ =

2

± i

κ2

(1−cosθ)

√

1 +µcosθ +

µsinθ 4 (1 +µcosθ)

3

δ2 (3.8)

Resolviendo la Ec. (3.8), obtenemos fácilmente una soluci ón anal´ıtica paraδ2, la cual está expresada como

δ2 =

1 (1 +µcosθ)14

!

C1ei

Θ

+C2e−i

Θ"

(3.9)

dondeΘ_{est´a definida por}

Θ₌ 2√1+µ

µκ2

*

F #θ

2, 2µ µ+1

$

−E#θ

2, 2µ µ+1

$+

En la Ec. (3.9),F yEson integrales el´ıpticas de primer y segunda espe-cie, respectivamente, definidas como, Zwillinger [30],

F #θ

2, 2µ

1+µ

$

=)θ/2 0

dϕ

!

1−(1+2µµ)

2 sin2_ϕ

E#θ

2, 2µ

1+µ

$

=)θ/2 0

4

1₋#₁₊2µ_µ$2sin2_ϕ_d_ϕ

(38)

3.2. Condiciones de frontera

Para obtener los valores de los coeficientesC1,C2,βRyβT, requerimos

de dos condiciones de frontera adicionales, las cuales pueden obtenerse de la continuidad de la masa en la interfaces de las regionesR1-R2 enθ=π/2 yR2-R3enθ=θL.

En la posici ón χ2 = 0 y en θ = π/2, la versi ón adimensional de la condici ón de frontera de acoplamiento se expresa como

dδ1

dχ1 5 5 5 5_χ

1=0

= κ2

1₋cosθ dδ2

dθ 5 5 5 5_θ =π 2 (3.10)

y paraθ =θLyχ3 =k3L, tenemos

ε1/2_κ 2

1₋cosθ dδ2

dθ 5 5 5 5 θL

= dδ3

dχ3 5 5 5 5

χ3=k3L

(3.11)

De la Ecs. (2.23), (2.24), (3.9), (3.10) y (3.11), podemos obtener fácilmen-te el siguienfácilmen-te sisfácilmen-tema de ecuaciones



   

−1 eiφ _e−iφ ₀

1 eiφ₍₁

−Ω_i₎ ₋_e−iφ_{(1 +}_Ω_i₎ ₀

0 eiΦ

ξ e−iΦ

ξ ₋eiα

0 eiΦ

(ξ₋ψi) ₋e−iΦ

(ξ+ψi) ₋eiα

          βR C1 C2 βT      =      1 1 0 0      (3.12) donde

α= ωL

(gh3)1/2,

Ω₌ µκ2

4 , ξ =

1

(1+µcosθL)1/4, ψ =

κ2µsinθL

4(1+µcosθL)3/4(1−cosθL),

φ= 2√_µ1+_κ µ

2

*

F #π

4, 2µ

1+µ

$

−E#π

4, 2µ

1+µ

$+

y

Φ₌ 2√1+µ

µκ2

*

F #θL

2 , 2µ

1+µ

$

−E#θL

2 , 2µ

1+µ

(39)

Por lo tanto, la soluci ´on al sistema de ecuaciones Ec. (3.12) est´a dado por

βR =

e2iφ_Ω₍_ψ

−2iξ) +e2iΦ

ψ(₋Ω_{+ 2}_i₎

Λ (3.13)

βT = −

4ei(φ+Φ₋α)_ξ2

Λ (3.14)

C1 = −

2eiφ₍₂_ξ₊_i_ψ₎

Λ (3.15)

C2 =

2iei(φ+2Φ)_ψ

Λ (3.16)

conΛ₌_e2iφ₍

−4ξ₋ψΩ_{+ 2}_i₍₋_ψ₊_ξΩ_{)) +}_e2iΦ

ψΩ

3.3. Coeficientes de reflexi ´on y transmisi ´on

En este cap´ıtulo se definen los coeficientes de reflexi ´onCR y

transmi-si ´onCT, que desde un punto de vista f´ısico, ´estos representan el porcentaje

de energ´ıa reflejada y transmitida, como consecuencia de las variaciones de la profundidad en la zona de propagaci ón, la suma de ambos debe corresponder a la energ´ıa total del oleaje incidente, Dean [31]. La impor-tancia de estos coeficientes radica en que permiten cuantificar la amplitud del oleaje que se refleja y transmite. Por lo tanto, en la práctica es posi-ble manipular y obtener alturas de oleaje que permitan en una primera aproximaci ón dise ñar estructuras rompeolas, eficientes y seguras.

Mediante un balance del flujo de energ´ıa entre las regionesR1 −R2 y

R2−R3, obtenemos la expresi ´on siguiente

FI =FR+FT (3.17)

dondeFI,FRyFT son los flujos promedio de energ´ıa incidente, reflejada

(40)

FI =EIc1n1, FR =ERc1n1 y FT =ETc3n3 (3.18)

y EI, ER y ET son las energ´ıas promedio por unidad de superficie

inci-dente, reflejada y transmitida, respectivamente; los productos c1n1 yc3n3 expresan la velocidad a la cual la energ´ıa se propaga en la regiones R1 y

R3, respectivamente. Sustituyendo las expresiones de la Ec. (3.18) en la Ec. (3.17), obtenemos

EIc1n1 =ERc1n1+ETc3n3 (3.19)

con EI = ρgAI2/2, ER = ρgAR2/2 y ET = ρgAT2/2. En ondas largas no

dispersivas, las velocidades de fase est´an dadas por c1 = √gh1 y c3 =

√

gh3. Por otro lado, para condiciones de flujo somero el factor ntiene un valor de1.

Tomando en cuenta las relaciones anteriores, la Ec. (3.19) se escribe co-mo

1 2ρgA

2

I =

1 2ρgA

2 R+ √ gh3 √ gh1 1 2ρgA

2

T, (3.20)

ordenando la expresi ´on anterior, se obtiene

<

AR

AI

=2

+ε1/2

<

AT

AI

=2

= 1 (3.21)

Los t´erminos del lado izquierdo de la Ec. (3.21), representan el porcen-taje de energ´ıa reflejada y transmitida, respectivamente. Estos valores son siempre cantidades positivas, por lo cual la Ec. (3.21) puede definirse en t´erminos de valores absolutos

5 5 5 5 AR AI 5 5 5 5 2

+ε1/2

5 5 5 5 AT AI 5 5 5 5 2

= 1 (3.22)

La Ec. (3.22) en forma simplificada, se escribe en la forma siguiente

(41)

dondeCRyCT son los coeficientes de reflexi ´on y transmisi ´on,

respectiva-mente, dados por

CR=

5 5 5 5 AR AI 5 5 5 5 (3.24) y

CT =

5 5 5 5 AT AI 5 5 5 5 (3.25)

Sustituyendo los valores deβR =AR/AI y βT = AT/AI dados por las

Ecs. (3.13) y (3.14), respectivamente, en las Ecs. (3.24) y (3.25); los coeficien-tes de reflexi ´on y transmisi ´on se reescriben de la forma siguiente

CR=

5 5 5 5

e2iφ_Ω₍_ψ

−2iξ) +e2iΦ

ψ(₋Ω_{+ 2}_i₎ Λ 5 5 5 5 (3.26)

CT =

5 5 5 5

−4ei(φ+Φ₋α)_ξ2

(42)

Cap´ıtulo 4

An´alisis de resultados

Con la finalidad de estudiar el efecto geométrico del rompeolas cicloi-dal en la reflexi ón, transmisi ón y deformaci ón de la superficie libre para ondas largas lineales, se utilizan las siguientes variables f´ısicas: el radio del c´ırculo generador del arco de cicloide y la profundidad son r = 0.6

m y h1 = 0.9 m, respectivamente; el periodo del oleaje es T = 8 s y el n úmero de onda en la regi ónR1 esk = 0.264 m−1, [8]. Adicionalmente, se proponen tres valores más parar(= 0.2,0.3,0.4)m y los siguientes valores para la longitud de ondaλ(= 30,35,40)m; la profundidadh3se calcula a partir de la Ec. (2.4). De los valores mencionados, obtenemos el parámetro adimensional de profundidades µ(= 0.33,0.44,0.55,0.66) y el parámetro cinemáticoκ2(= 6.3,7.95,9.28,10.6).

4.1. Cicloide

Para este caso particular, el rompeolas cicloidal est´a delimitado en el intervalo π/2 _≤ θ _≤ 3π/2, generando profundidades id´enticas en las re-giones R1 y R3 (h1 =h3). En particular, en este caso, considerando que

θL = 3π/2, los coeficientes de reflexi ´on y transmisi ´on dados por Ecs. (3.26)

(43)

CR=

5 5 5 5 5

Ω0

e2iφ₍_Ω_{+ 2}_i_{) +}_e2iΦ

(−Ω_{+ 2}_i₎1

e2iφ₍₂_i₊_Ω₎2₋_e2iΦ_Ω₂

5 5 5 5 5

(4.1)

y

CT =

5 5 5 5

4ei(φ+Φ₋α)

e2iφ₍₂_i₊_Ω₎2₋_e2iΦ_Ω₂

5 5 5 5

[image:43.595.160.484.136.494.2]

(4.2)

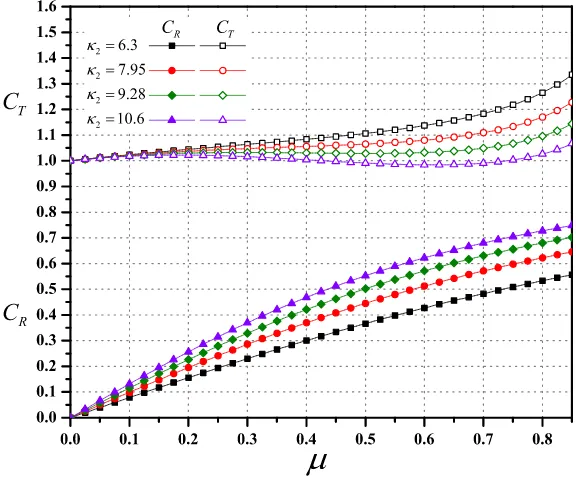
Figura 4.1. Caso 1. Coeficiente de reflexi ónCR y transmisi ónCT en funci ón del

parámetro adimensional relativo de profundidadesµ para valores distintos del parámetro cinemáticoκ₂_.

Los valores de los coeficientes CR y CT, obtenidos en t´erminos del

(44)

estructura es altamente reflejante, esta condici ´on puede presentarse para valores peque ˜nos de la frecuencia del oleaje ω y para valores fijos de la profundidadh1 y el radior.

La Fig. 4.2 muestra los coeficientes de reflexi ón y transmisi ón en fun-ci ón del parámetro fun-cinemático adimensionalκ2y cuatro valores diferentes del parámetro de profundidades µ(= 0.33,0.44,0.55,0.66). Como se ob-serva en la Fig. 4.1, las curvas del coeficiente de reflexi ón CR para ciertos

valores peque ños deκ2 obligan a disminuir la reflexi ón hasta alcanzar un m´ınimo, aunque después los valores de los coeficientes de reflexi ónCR

[image:44.595.161.448.349.583.2]

au-mentan para los distintos valores del parámetroµ. Lo anterior es debido a la influencia de la frecuencia ωen la reflexi ón de la energ´ıa del oleaje que cuanto más peque ña es su magnitud, mayor será la reflexi ón.

Figura 4.2. Caso 1. Coeficiente de reflexi ónC_R y transmisi ónC_T en funci ón del parámetro adimensional cinemáticoκ₂_{para valores distintos del parámetro}_µ_..

(45)

particu-lar se presenta a continuaci ´on. Una vez evaluadas las constantes C1 yC2 cuando θL = 3π/2, se sustituyen en la Ec. (3.9) y se obtiene la siguiente

expresi ´on

δ2 = −

2ei(φ+Θ)!

2 +iΩ!_e2i(Φ₋Θ)

−1""

(1 +µcosθ)14 !e2iφ(2i+Ω)2−e2iΦΩ2"

[image:45.595.162.452.188.489.2]

. (4.3)

Figura 4.3. Caso 1. Amplitud adimensional de las ondas largas en funci ón del parámetro adimensionalθ_{, con un}µ= 0_.66_{para valores distintos del parámetro}

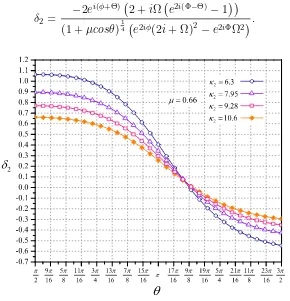
cinem´aticoκ₂_.

Los efectos del parámetro cinemáticoκ2, en la deformaci ón de la ele-vaci ón de la superficie libre se muestran en la Fig. 4.3. En esta figura los valores de δ2 se muestran para valores diferentes del parámetro κ2

(46)

[image:46.595.166.446.127.367.2]

Figura 4.4. Caso 1. Amplitud adimensional de las ondas largas en funci ón del parámetro adimensionalθ_{, con un}κ₂ = 6_.3_{para valores distintos del parámetro}

µ.

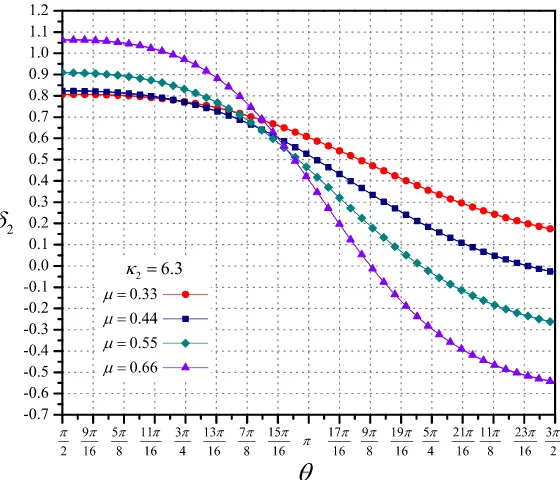
La Fig. 4.4 muestra la elevaci ón adimensional de la superficie de las ondas largas, en funci ón del parámetro adimensionalθ, para cuatro dife-rentes valores de µ(= 0.33,0.44,0.55,0.66) y el parámetro adimensional

κ2 = 6.3. Esta gráfica demuestra la influencia del parámetro µ en la ele-vaci ón de la superficie libre. Cuando µes relativamente grande, debido a quer →h1, la amplitud del oleaje crece fuertemente como se observa con

µ = 0.66. De manera contraria, cuando µ es peque ño, la amplitud de la onda decrece y su comportamiento tiende a ser lineal. Esto último puede observarse a partir de las Ecs. (4.1) y (4.2). Para el l´ımite de µ → 0 la re-laci ónΩ _≈ ₀_{y el denominador de las expresiones mencionadas es} _{≈ −}₄_;

(47)

4.2. Semi-cicloide

Para este caso, el rompeolas cicloidal se encuentra delimitado en el in-tervalo π/2 _≤ θ _≤ π, la profundidad en la regi ´on R3 es h3 = h1 − r. Evaluando en θL = π, se obtienen ξ = ε−1/4 y ψ = 0; los coeficientes de

reflexi ´onCRy transmisi ´onCT en una forma simplificada se expresan en la

forma siguiente

CR=

Ω

√

4 +Ω2 (4.4)

CT =

2ξ

√

4 +Ω2 (4.5)

En la Fig. 4.5 se muestran los efectos del parámetroµen los coeficien-tes CR yCT, para cuatro valores del parámetro cinemático κ2 (= 6.3, 7.95, 9.28, 10.6). En general, los resultados indican que para valores deµ→1la estructura es altamente reflejante; por ejemplo, para un valor de µ = 0.8

y κ2 = 10.6, el valor del coeficiente de reflexi ´on es CR = 0.72, esto

de-muestra la relevancia del parámetro µen la reflexi ón del oleaje. Por otro lado, en la parte superior de la misma figura se presentan los valores del coeficiente de transmisi ón CT, estos resultados ilustran que para valores

de κ2 ∼ O(1), la amplitud del oleaje es fuertemente amplificada, lo cual puede verificarse si comparamos el coeficienteCT para un valor deµ= 0.8

y dos valores del par´ametro κ2(= 6.3y10.6), los coeficientes de transmi-si ´on son CT (= 1.25y1.02), respectivamente, estos valores muestran que

el primer caso es 23 %m´as reflejante que el segundo. Adicionalmente, los resultados mencionados indican que para valores diferentes de la frecuen-cia del oleaje, la configuraci ´on semi-cicloidal es fuertemente reflejante para valores deκ2 ∼O(1).

(48)

[image:48.595.162.450.129.368.2]

oleaje de dos maneras distintas; la primera es el aumento de la magnitud deµque conlleva un incremento del radiorsobre la profundidad enh1; la segunda es el aumento en la reflexi ón que se genera cuando la frecuencia del oleajeωdisminuye y crece el parámetro cinemáticoκ2.

Como caso part´ıcular, cuando µ _→ 0 el par´ametro Ω _→ ₀ _y _ξ _{= 1}_;

por lo tanto, las Ecs. (4.4) y (4.5) recuperan el caso cuando la influencia de la estrutura es pr´acticamente inexistente en el flujo del oleaje, que en los coeficientes se refleja conCR≈0yCT ≈1.

(49)

[image:49.595.163.448.124.366.2]

Figura 4.6. Caso 2. Coeficiente de reflexi ónC_R y transmisi ónC_T en funci ón del parámetro adimensional cinemáticoκ₂_{para valores distintos del parámetro}_µ_.

δ2 =

2iei(Θ₋φ)

(2i+Ω_{) (1 +}_µ_cos_θ₎14

. (4.6)

La Fig. 4.7 muestra la elevaci ón adimensional de la superficie libre pa-ra cuatro valores diferentes del parámetro κ2(= 6.3,7.95,9.28,10.6) y un valor constante de µ = 0.66. Se observa que conforme κ2 disminuye, la deformaci ón del oleaje es menor. Además, un valor menor que µ = 0.66

producirá menor reflexi ón y a medida que la frecuenciaωaumente, la ele-vaci ón del oleaje será menormente deformada y tenderá a una amplitud

δ2 aproximadamente de uno.

(50)

[image:50.595.162.447.129.371.2]

Figura 4.7. Caso 2. Amplitud adimensional de las ondas largas en funci ón del parámetro adimensionalθ_{, con un}µ= 0_.66_{para valores distintos del parámetro}

cinem´aticoκ₂_.

θ =π, presenta un decremento significativo en su magnitud, siempre que

µ _→ 1. Ahora, comparando las alturas de δ2 en la posici ón θ = π, para valores de µ = 0.33 contra µ = 0.66, puede notarse que existe una dife-rencia del23 %. Además, en la misma figura se aprecia que la altura de la elevaci ón adimensional de la superficie libre es menormente deformada siempre queµ _→ 0y para esto la elevaci ón de la superficie libre tiene un valor deδ2 →1.

4.3. Cicloide generalizado

(51)

[image:51.595.162.447.128.370.2]

µ.

conh3 > h1. EvaluandoθL= 7π/4, se obtienen los coeficientes de reflexi ´on

y transmisi ´on particulares para este caso.

Para el presente caso, los coeficientes de reflexi ón y transmisi ón co-mo funci ón del parámetro adimensional µ y con valores distintos de κ2

(= 6.3,7.95,9.28,10.6)son mostrados en la Fig. 4.9. En esta figura, se pue-de notar que el coeficienteCT → 1yCR → 0siempre queµ→ 0, adem´as

muestran que el coeficienteCT presenta un decremento prominente

cuan-doµ _→ 1. En la misma figura, se aprecia que paraµ = 0.85, el valor m´as peque ˜no deCT se presenta paraκ2 = 10.6y este valor esCT = 0.4, as´ı

(52)

[image:52.595.162.451.125.366.2]

La Fig. 4.10 muestra los coeficientes de reflexi ón y transmisi ón en fun-ci ón del parámetro fun-cinemático adimensionalκ2y cuatro valores diferentes del parámetro de profundidades µ(= 0.33,0.44,0.55,0.66). Al igual que en la Fig. 4.9, las curvas del coeficiente de reflexi ón CR presentan un

au-mento en su magnitud cuando µ crece. Se observa que para valores de

µ(= 0.33,0.44,0.55), el aumento del parámetro cinemático κ2 es propor-cional al aumento en el coeficiente de reflexi ón CR. Mientras que en las

curvas mencionadas el aumento del coeficiente de reflexi ón es notorio, en el caso deµ= 0.66sucede de manera inversa, se observa que enκ2 = 5el coeficiente de reflexi ón CR = 0.61y al final, enκ2 = 13, el coeficiente de reflexi ónCRdisminuy ó a0.52

(53)

ma-Figura 4.10. Caso 3. Coeficiente de reflexi ónC_Ry transmisi ónC_T en funci ón del parámetro adimensional cinemáticoκ₂_{para valores distintos del parámetro}_µ_.

nera general la elevaci ón de la superficie libre es la Ec. (3.9). Evaluando al ecuaci ón mencionada y los coeficientesC1yC2, Ecs. (3.15)-(3.16), respecti-vamente, con θL = 7π/4, se obtiene la ecuaci ón que describe la elevaci ón

adimensional de la superficie libre para el presente caso.

La Fig. 4.11 muestra la elevaci ón adimensional de la superficie en fun-ci ón de θ, al pasar sobre la estructura cuandoµ = 0.66y cuatro distintos valores de κ2(= 6.3,7.95,9.28,10.6). La gráfica muestra la semajanza en la amplitud en la superficie libre adimensional cuando µ = 0.66para los distintos valores deκ2que se presentan. La amortiguaci ón de la superficie libre es grande cuando se alcanza el valorθL= 7π/4. La figura demuestra

[image:53.595.163.448.125.365.2]

(54)

[image:54.595.163.447.126.370.2]

Figura 4.11. Caso 3. Amplitud adimensional de las ondas largas en funci ón del parámetro adimensionalθ_{, con un}_µ= 0_.66_{para valores distintos del parámetro}

cinem´aticoκ₂_.

1.47y1.53, mientras que al final enθL= 7π/4los valores est´an dentro del

rangoδ2 ≈ −0.68yδ2 ≈ −0.69.

En la Fig. 4.12 es mostrada la elevaci ón adimensional de la superficie libre como una funci ón del ejeθpara cuatro valores del parámetro de pro-fundidadesµ(= 0.33,0.44,0.55,0.66)y un valor constanteκ2 = 6.3. En esta figura, se observa que la amplitud del oleaje decrece siempre queθ _→θL,

i.e. para el caso de µ = 0.66en la posici ´on θL = 7π/4, la elevaci ´on de la

(55)

[image:55.595.163.446.242.492.2]

(56)

Conclusiones

Con base en la busqueda de una ecuaci ón difencial de Bernoulli corres-pondiente al Problema de Valores en la Frontera estudiado, se deriva una soluci ón anal´ıtica para oleaje largo lineal propagándose sobre un rompeo-las sumergido, el cual obedece una distribuci ón cicloidal. En el presente estudio, se analizan tres diferentes configuraciones geométricas del rom-peolas cicloidal y se presentan f órmulas sencillas para la elevaci ón adi-mensional de la superficie libre,δ2, junto con los coeficientes de reflexi ón,

CR, y transmisi ´on, CT. Con la finalidad de validar el modelo, cada uno

de los casos particulares demostr ó la conservaci ón de la energ´ıa a partir de la expresi ón que define el flujo energ´ıa en aguas someras para ondas largas. Los resultados muestran que el rompeolas sumergido cicloidal es una buena alternativa para el amortiguamiento de oleaje largo lineal y las f órmulas obtenidas para los coeficientes de reflexi ón y transmisi ón cons-tituyen una referencia para aplicaciones ingenieriles, i.e.si consideramos para los tres casos analizados un valor deκ2 = 6.3yµ= 0.85, los coeficien-tes de transmisi ón paraθL = 3π/2,πy7π/4sonCT = 0.805,1.335y0.445,

respectivamente; como se puede notar, el caso de θL = 7π/4 presenta el

menor valor en el coeficiente de transmisi ón y, por lo tanto, esta condici ón puede representar una buena alternativa para la reducci ón en la energ´ıa del oleaje transmitido.

(57)

(58)

Bibliograf´ıa

[1] M. Qin and G. Fan. An effective method for finding special solutions of nonlinear differential equations with variable coefficients. Physics

Letters A, 372:3240–3242, 2008.

[2] W. Guo, C. Jian, and Y. Shuwang. Effect of subgrade soil stiffness on the design of geosynthetic tube.Geotextiles and Geomembranes, 29:227– 284, 2011.

[3] M. Ahmed and R. Anwar. Experimental study on the performance of submerged breakwater as shore protection structure. International

Conference on Environment and BioScience, 21:156–160, 2011.

[4] H. Hanson, A. Brampton, M. Capobianco, H. H. Dette, L. Hamm, C. Laustrup, A. Lechuga, and R. Spanhoff. Beach nourishment pro-jects, practices, and objectives; a european overview. Coastal Enginee-ring, 47:81–111, 2002.

[5] T. H. Junga, K. D. Suh, S. O. Lee, and Y. S. Cho. Linear wave reflection by trench with various shapes.Ocean Engineering, 35:1226–1234, 2008.

[6] C. Sheehan and J. Harrington. An environmental and economic analysis for geotube coastal structures retaining dredge material.

(59)

[7] M. Christou, C. Swan, and O. T. Gudmestad. The interaction of sur-face water waves with submerged breakwaters. Coastal Engineering, 55:945–958, 2008.

[8] E. Alvarez, R. Rubio, and H. Ricalde. Beach restoration with geotex-tile tubes as submerged breakwaters in yucatan, mexico. Geotextiles

and Geomembranes, 25:233–241, 2007.

[9] H. Lamb. Hydrodynamics, sixth Ed. Cambridge University Press, 1932.

[10] H. Kreiss. Some remarks about non linear oscillations in tidal chan-nels. Tellus, 9:53–68, 1957.

[11] B. S. Gallagher and W. H. Munk. Tides in shallow water: spectros-copy. Tellus, 23(4-5):346–363, 1971.

[12] D. G. Aubrey and P.E. Speer. A study of non-linear tidal propagation in shallow inlet/estuarine systems, part i: Observations. Estuarine,

Coastal and Shelf Science, 21:185–205, 1985.

[13] P. E. Speer and D. G. Aubrey. A study of nonlinear tidal propagation in shallow inlet/estuarine systems, part ii: Theory. Estuarine, Coastal

and Shelf Science, 21:207–224, 1985.

[14] A. Ouahsine and P. A. Bois. Mathematical modelling of long ocean waves with a discontinuous density gradient. J. Eng. Math., 40:141– 158, 2001.

[15] J. L. Mead. The shallow water equation in lagrangian coordinates. J.

Comput. Phys., 200:654–669, 2004.

(60)

[17] R. Camassa, J. Huang, and L. Lee. Integral an integrable algo-rithms for a nonlinear shallow-water wave equation.J. Comput. Phys., 216:547–572, 2006.

[18] T. J. Ohare and A. G. L. Davies. A new model for surface wave propa-gation over undulating topography. Coastal Engineering, 18:251–266, 1992.

[19] R. Silva, I. J. Losada, and M. A. Losada. Reflection and transmission of tsunami waves by coastal structures. Applied Ocean Research, 22:215– 223, 2000.

[20] C. J. Bender and R. G. Dean. Wave transformation by two-dimensional bathymetric anomalies with sloped transitions. Coastal

Engineering, 50:61–84, 2003.

[21] Y. Li, G. Dong., H. Liu, and D. Sun. The reflection of oblique incident waves by breakwater with double-layered perforated wall. Coastal

Engineering, 50:47–60, 2003.

[22] P. Lin. A numerical study of solitary wave interaction with rectangu-lar obstacles. Coastal Engineering, 51:35–51, 2004.

[23] H. K. Chang and J. C. Liou. Long wave reflection from submerged trapezoidal breakwaters. Coastal Engineering, 34:185–191, 2005.

[24] I. I. Didenkulova, N. Zahibo, and E. N. Pelinovsky. Reflection of long waves from a nonreflecting bottom profile. J. Fluid Dynamics, pages 22–29, 2002.

(61)

[26] J. Recio and H. Oumeraci. Processes affecting the hydraulic stability of coastal revetments made of geotextile sand containers. Coastal

En-gineering, 56(3):260–284, 2009.

[27] K Tang. Mathematical Methods for Engineers and Scientists 3, 1 edn. Springer, 2007.

[28] Ib. A Svendsen. Introduction to nearshore hydrodynamics. Wold Scienti-fic, Singapore, 2006.

[29] R. G. Dean and R. A. Dalrymple. Water wave mechanics for engineers

and scientists, vol. 2. World Scientific, Singapore, 1984.

[30] Zwillinger D. Standar mathematical tables and formulae. Taylor Francis Group, 2012.

[31] R. G. Dean and R. A. Dalrymple. Water wave mechanics for engineers

(62)

Ap´endice A

Teor´ıa de ondas largas

Las velocidades y el perfil de la superficie libre para una onda progre-siva est´an descritos por las siguientes ecuaciones

u= H 2

gk ω

coshk(h+z)

cosh(kh) cos(kx−ωt) (A.1)

w= H 2

gk ω

sinhk(h+z)

cosh(kh) sin(kx−ωt) (A.2)

ζ = H

2 cos(kx−ωt) (A.3)

dondeurepresenta la componente de velocidad de las part´ıculas del agua en direcci ´on horizontal;w la componente en direcci ´on vertical;ζ el perfil de la superficie libre del oleaje. ρ, g, ω, h, z y t describen la densidad del agua, la gravedad, la frecuencia radial del oleaje, la profundidad del mar, el eje vertical y el tiempo, respectivamente;H es la altura de la onda;

kes el n ´umero de onda dado por2π/λ.

Usando las formas asint óticas en aguas someras de las funciones hi-perb ólicas, podemos llegar a las ecuaciones que describen la velocidad de una part´ıcula de agua en condici ón de ondas largas,k h₍π/10.

us=

H

2

gk

ω cos(kx−ωt) =

ζC

(63)

dondec=√ghes la celeridad de la onda. El sub´ındicesdenota que es en condiciones de aguas someras. Como puede observarse, us no es funci ´on

de la elevaci ón; la velocidad horizontal es uniforme a través de la profun-didad. La velocidad vertical de una part´ıcula de agua está dada por

ws=

H

2

gk

ω [k(h+z)] sin (kx−ωt) = H

2

C h (kh)

#

1 + z

h

$

sin (kx₋ωt) =

−C#1 + z

h

$∂ζ

∂x (A.5)

La velocidad vertical var´ıa linealmente con la profundidad desde cero en el fondo hasta un máximo en la superficie y es mucho más peque ña en magnitud queus. La proporci ón de sus máximos valores es

(u)_s_m´_ax (w)_s_m´_ax =

1

kh (A.6)

dondekhes un valor peque ˜no. La presi ´on bajo ondas largas es

p=₋ρgz+ρgH 2

coshk(h+z)

cosh(kh) cos(kx−ωt) (A.7)

Sustituyendo la Ec. (A.3) para reducir, obtenemos

p=₋ρgz+ζρg 2

coshk(h+z)

cosh(kh) (A.8)

Considerando la relaci ´on de la Ec. (A.6) la expresi ´on anterior se simpli-fica, entonces se obtiene

p=ρg(ζ₋z) (A.9)

(64)

A.1.

Ecuaci ´on de continuidad

La ecuaci ´on tridimensional de conservaci ´on de la masa para un flujo incompresible es

∂u

∂x +

∂v

∂y +

∂w

∂z = 0 (A.10)

Integrando a trav´es de la profundidad, obtenemos

> ζ

−h

<

∂u

∂x +

∂v

∂y +

∂w ∂z = dz = > ζ −h ∂u

∂xdz+

> ζ

−h

∂v

∂ydz+w(x, y,ζ)−w(x, y,−h) = 0 (A.11)

La regla de Leibniz de integraci ón es usada para integrar los primeros dos términos del lado derecho de la expresi ón. En general, se afirma como

∂ ∂x

> β(x)

α(x)

Q(x, y)dy=

> β(x)

α(x)

∂

∂xQ(x, y)dy+Q(x,β(x)) ∂β(x)

∂x −Q(x,α(x)) ∂α(x)

∂x (A.12)

Los l´ımites de la integral son constantes en relaci ón a la variable de integraci ón, el operador diferencial puede ser desplazado dentro o fuera de la integral sin generar términos adicionales. Por lo tanto, la ecuaci ón de continuidad integrada es reescrita como

∂ ∂x

> ζ

−h

udz−u(x, y,ζ)∂ζ

∂x−u(x, y,−h) ∂h

∂x+

w(x, y,ζ)₋w(x, y,₋h) + ∂ ∂y

> ζ

−h

vdz₋

v(x, y,ζ)∂ζ

∂y −v(x, y,−h) ∂h

∂y = 0 (A.13)

(65)

U = 1

h+ζ

)ζ

−hudz y V =

1

h+ζ

)ζ −hvdz

Lo cual es usando la definici ón matemática de promedio (de este modo incorporando cualquier posible variaci ón vertical en la velocidad horizon-tal) o si asumimos queuyvson constantes a través de la profundidad, la ecuaci ón de continuidad puede ser escrita como

∂

∂x[U(h+ζ)] + ∂

∂y[V (h+ζ)]−v(x, y,ζ) ∂ζ

∂y −v(x, y,−h) ∂h ∂y

−u(x, y,ζ)∂ζ

∂x −u(x, y,−h) ∂h

∂x +w(x, y,ζ)−w(x, y,−h) = 0 (A.14)

Una mayor simplificaci ón resultará mediante el uso de condiciones de frontera. La condici ón de frontera cinemática de la superficie libre en tres dimensiones es

∂ζ

∂t +u(x, y,ζ) ∂ζ

∂x+v(x, y,ζ) ∂ζ

∂y =w(x, y,ζ) (A.15)

La condici ´on de frontera del fondo para una superficie fija (en el tiem-po) es

w(x, y,₋h) = ₋u(x, y,₋h)∂h

∂x −v(x, y,−h) ∂h

∂y (A.16)

Sustituyendo estas condiciones dentro de la ecuaci ón de continuidad integrada verticalmente, y reduciendo términos, se obtiene la forma final de la ecuaci ón de continuidad

∂[U(h+ζ)]

∂x +

∂[V (h+ζ)]

∂y =−

∂ζ

∂t (A.17)