Aplicación de los algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada

Texto completo

(1)Departamento de Telecomunicaciones y Electrónica. “Aplicación de los algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada” Autor: Alejandro Javier Llópiz Pérez Tutor: MSc. Yakdiel Rodríguez-Gallo Guerra Cotutor: Dr. C. Rubén Orozco Morales. , Junio de 2018 Año.

(2) Este documento es Propiedad Patrimonial de la Universidad Central “Marta Abreu” de Las Villas, y se encuentra depositado en los fondos de la Biblioteca Universitaria “Chiqui Gómez Lubian” subordinada a la Dirección de Información Científico Técnica de la mencionada casa de altos estudios. Se autoriza su utilización bajo la licencia siguiente: Atribución- No Comercial- Compartir Igual. Para cualquier información contacte con: Dirección de Información Científico Técnica. Universidad Central “Marta Abreu” de Las Villas. Carretera a Camajuaní. Km 5½. Santa Clara. Villa Clara. Cuba. CP. 54 830 Teléfonos.: +53 01 42281503-1419.

(3) Hago constar que el presente trabajo de diploma fue realizado en la Universidad Central “Marta Abreu” de Las Villas como parte de la culminación de estudios de la especialidad de Ingeniería en Telecomunicaciones y Electrónica, autorizando a que el mismo sea utilizado por la Institución, para los fines que estime conveniente, tanto de forma parcial como total y que además no podrá ser presentado en eventos, ni publicados sin autorización de la Universidad.. Firma del Autor Los abajo firmantes certificamos que el presente trabajo ha sido realizado según acuerdo de la dirección de nuestro centro y el mismo cumple con los requisitos que debe tener un trabajo de esta envergadura referido a la temática señalada.. Firma del Tutor. Firma del Jefe de Departamento donde se defiende el trabajo. Firma del Responsable de Información Científico-Técnica.

(4) i. PENSAMIENTO. Lo que sabemos es una gota de agua; lo que ignoramos es el océano. Isaac Newton..

(5) ii. DEDICATORIA. A mi familia, por todo el apoyo que me han brindado en los buenos y en los malos momentos a lo largo de toda mi vida..

(6) iii. AGRADECIMIENTOS. A toda mi familia, que siempre me han apoyado con constancia y han estado junto a mí durante todos estos años. A mi tutor, por la ayuda que me ha ofrecido y por su contribución en mi formación durante la carrera. A todos los profesores, durante estos cinco años, de quienes he podido aprender, gracias a sus conocimientos y experiencias. A todos mis amigos, con quienes he tenido el privilegio de compartir y que me han brindado su apoyo incondicional en todo momento. En fin, a todos con quienes he compartido durante estos magníficos años de universidad..

(7) iv. TAREA TÉCNICA Para lograr la confección del presente trabajo, dar cumplimiento a los objetivos trazados y obtener los resultados esperados, se desarrollan las siguientes tareas técnicas: 1. Revisión bibliográfica de las características de los algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada. 2. Exposición de investigaciones acerca de los algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada realizadas en los últimos años. 3. Caracterización de los algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada. 4. Identificación de la herramienta de simulación para el diseño de los algoritmos. 5. Implementación de los algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada con apoyo del MATLAB. 6. Elaboración del informe final del Trabajo de Diploma.. Firma del Autor. Firma del Tutor.

(8) v. RESUMEN. La contaminación por ruido en las imágenes es un fenómeno que afecta su calidad haciendo que se vean de una forma distorsionada y cambiando los valores reales de los píxeles. Una de las preocupaciones primarias del procesamiento digital es aumentar la calidad y moderar la degradación introducida. Las técnicas de restauración están enfocadas en reconstruir o recuperar una imagen que ha sido deteriorada y los modelos de variación total han sido extremadamente exitosos en esta amplia variedad de problemas, por lo que siguen siendo una de las áreas de investigación más activas en procesamiento de imágenes. En el presente trabajo se abordan las características y aspectos generales de los algoritmos de variación total, la tomografía computarizada y la reducción del ruido. Se realiza la implementación de tres algoritmos de variación total basándose inicialmente en modelos para imágenes que no son del cuerpo humano y luego se modifican. Se muestran las imágenes que fueron manipuladas, evidenciándose mejores valores en su proceso de adquisición. Además, para la obtención de todos los resultados se trabajó con el programa de simulación MATLAB. Finalmente se realiza una comparación de los resultados obtenidos..

(9) vi TABLA DE CONTENIDOS. PENSAMIENTO .....................................................................................................................i DEDICATORIA .................................................................................................................... ii AGRADECIMIENTOS ........................................................................................................ iii TAREA TÉCNICA ................................................................................................................iv RESUMEN ............................................................................................................................. v INTRODUCCIÓN .................................................................................................................. 1 CAPÍTULO 1.. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN. TOTAL Y SU APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA REDUCIR EL RUIDO.............................................................................................................................. 6 1.1. Características fundamentales de la variación total ................................................. 6. 1.1.1 La aproximación bayesiana para el restablecimiento de imágenes ....................... 6 1.1.2 Propiedades principales ......................................................................................... 7 1.1.3 Aplicaciones de la variación total .......................................................................... 9 1.2. Aspectos generales de la tomografía computarizada ............................................. 13. 1.3. El ruido en las imágenes y la contribución de la variación total para su reducción..15. 1.4. Investigaciones acerca de la variación total en la tomografía computarizada ....... 16. 1.5 Conclusiones parciales ................................................................................................ 19 CAPÍTULO 2.. ALGORITMOS. DE. VARIACIÓN. TOTAL. PROPUESTOS. Y. CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS ............................................. 20 2.1 Características principales del algoritmo 1 ................................................................. 20 2.2 Características principales del algoritmo 2 ................................................................. 22 2.3 Características principales del algoritmo 3 ................................................................. 24 2.4 Caracterización de la herramienta de simulación MATLAB ..................................... 26 2.5 Adquisición de las imágenes....................................................................................... 27.

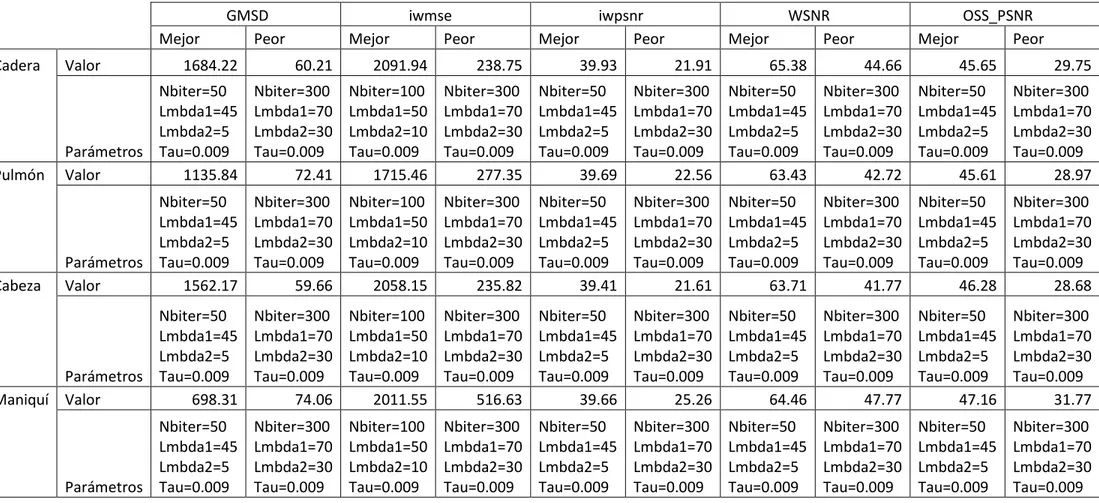
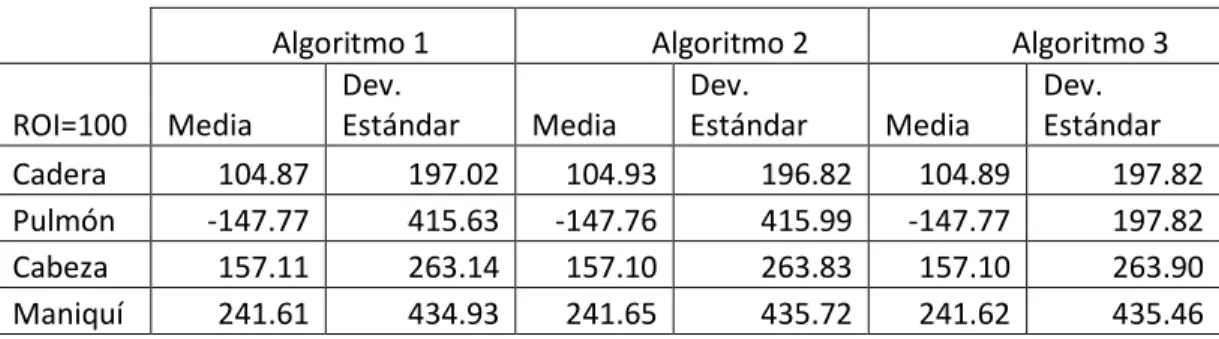
(10) vii 2.6 Análisis de la imagen .............................................................................................. 28 2.6.1 Métricas utilizadas para la evaluación ................................................................. 29 2.7 Conclusiones parciales ................................................................................................ 29 CAPÍTULO 3.. EVALUACIÓN DE LOS ALGORITMOS DE VARIACIÓN TOTAL. PARA LA REDUCCIÓN DEL RUIDO EN IMÁGENES DE CT ...................................... 31 3.1 Parámetros utilizados en la aplicación de los algoritmos ........................................... 31 3.2 Resultados del procesamiento de imágenes utilizando diferentes métricas de calidad objetiva.............................................................................................................................. 32 3.3 Media y desviación estándar de los algoritmos .......................................................... 36 3.4 Evaluación de calidad subjetiva de los radiólogos ..................................................... 36 3.5 Gráficos del tiempo con respecto al número de iteraciones de cada algoritmo .......... 40 3.6 Conclusiones parciales ................................................................................................ 44 CONCLUSIONES ................................................................................................................ 45 RECOMENDACIONES ....................................................................................................... 46 REFERENCIAS BIBLIOGRÁFICAS ................................................................................. 47.

(11) INTRODUCCIÓN. 1. INTRODUCCIÓN. Las imágenes han sido utilizadas por el hombre desde hace varios millones de años, empezando por las primeras personas que habitaron el planeta que las utilizaban para dejar plasmadas en las cuevas sus experiencias del mundo exterior, para representar figuras de personas o deidades en esculturas que se hacían de materiales sólidos dándoles un aspecto tridimensional y palpable; y en pinturas que se creaban en papel o lienzo donde se utilizaron pigmentos para dar colores y así dar una sensación de realismo. Con la invención de la fotografía a mediados del siglo XIX se logró captar imágenes debido a la acción de la luz, estas eran iguales a las mostradas en la vida real. Al pasar los años aparecieron las imágenes digitales a partir de una matriz numérica usando ceros y unos. En la actualidad se utilizan las imágenes para varios propósitos, como la tomografía. Este método es utilizado en ciencias como: Arqueología, Biología, Geofísica, Oceanografía y Medicina [1], [2], [3], [4], [5]. En esta última se utiliza para mostrar el interior del cuerpo humano. Existen diferentes tipos de tomografía [6], pero esta investigación se centrará en la computarizada y su aplicación en la Medicina. El término “tomografía” tiene su origen en la palabra griega tomos, que significa corte y en grafía, que significa representación gráfica. El propósito de esta técnica es la obtención de imágenes correspondientes a cortes del interior de un objeto, sin necesidad de realizar ninguna incisión en él. El procedimiento por el que se obtienen estas imágenes, a partir de las proyecciones tomadas por un escáner, se denomina reconstrucción de imágenes tomográficas [7]. Una imagen médica, es aquella que proviene del conjunto de técnicas y procesos usados para crear imágenes del cuerpo humano o parte de él, con propósitos clínicos, es decir, procedimientos médicos que buscan revelar, diagnosticar, examinar enfermedades con propósitos científicos y médicos tales como el estudio de la anatomía física y metabólica [8]. En Medicina, el diagnóstico basado en la tomografía computarizada (CT) es fundamental para la detección de anomalías. El inicio de la investigación en las imágenes médicas se.

(12) INTRODUCCIÓN. 2. remonta al año 1895 cuando Wilhelm Conrad Rontgen descubrió los rayos X. Él mostró que los huesos podrían ser visualizados al ser atravesados por los rayos X y en consecuencia de este descubrimiento recibió el primer premio Nobel de Física en 1901. Así apareció la radiografía que es una de las modalidades principales para la obtención de imágenes médicas. Desde entonces fueron inventadas diferentes modalidades médicas de obtención de imágenes [9]. En 1971, Godfrey N. Hounsfield presentó el primer escáner de imágenes de tomografía computarizada en el Hospital Atkinson Morley en Wimbledon. En 1972, este escáner fue empleado para realizar la primera medida en un paciente, cuya intervención quirúrgica posterior confirmó el diagnóstico obtenido a partir de la imagen [10]. Las imágenes de CT se emplean habitualmente como prueba con valor diagnóstico y constituyen un procedimiento indicado en caso de hemorragias internas, fracturas de huesos, cáncer, localización de coágulos y búsqueda de cardiopatías. Aunque el examen de CT es de naturaleza no invasiva, no se trata de una prueba inocua puesto que implica la exposición del sujeto a una dosis de radiación ionizante, que en exceso puede provocar efectos nocivos en la salud. Desde su invención, se han realizado avances tecnológicos que han conducido a escáneres más rápidos, a la exposición de una menor dosis de radiación y a una mayor calidad de la imagen. Una parte importante del éxito conseguido por esta técnica reside en el desarrollo de nuevos y eficientes algoritmos de reconstrucción. Aunque el problema de la reconstrucción de la imagen en su forma matemática pura fue resuelto por Johan Radon en 1917, la evolución continua en este campo de estudio ha dado lugar a la aparición de múltiples algoritmos. La reconstrucción de imágenes en CT es un proceso matemático que genera imágenes tomográficas a partir de los datos de proyección de rayos X adquiridos en ángulos diferentes alrededor del paciente. Para una dosis de radiación dada es deseable reconstruir imágenes con el menor ruido posible sin sacrificar la precisión de la imagen y la resolución espacial. Reconstrucciones que mejoran la calidad de la imagen se puede traducir en una reducción de la dosis de radiación porque las imágenes de la misma calidad pueden ser reconstruidas a una dosis menor [11]. En las dos últimas décadas el procesamiento digital de imágenes ha ganado importancia dentro de distintas áreas de la ciencia, debido a que cada día la información visual es más.

(13) INTRODUCCIÓN. 3. importante y abundante. El procesamiento digital de imágenes es un conjunto de modelos y algoritmos que se aplican a imágenes, con el objetivo de mejorar su calidad y facilitar la extracción de algún tipo de información ya sea para la interpretación humana o de máquinas autónomas [12]. A lo largo de los últimos años se han desarrollado varios enfoques para abordar el procesamiento digital de imágenes. Se pueden mencionar los principales métodos basados en: la teoría del filtro, el análisis espectral, o en algunos conceptos básicos de probabilidad y estadística. Otro tipo de herramientas se basa en modelos estocásticos, en ecuaciones con derivadas parciales y en métodos variacionales. Este trabajo se enfocará en los métodos basados en el cálculo de variaciones. Varios modelos basados en métodos variacionales y en ecuaciones con derivadas parciales han sido planteados para el problema del ruido en las imágenes, entre ellos se destaca el modelo de variación total (cuyo acrónimo en idioma inglés es TV debido a su denominación total variation) propuesto por Rudin, Osher y Fatemi (ROF). Este método se presenta como un tipo de algoritmo numérico de optimización restringida para reducir el ruido de las imágenes. Esta técnica no es invasiva pues preserva los bordes de la imagen [13]. El objetivo de aplicar este modelo en las imágenes médicas es contribuir a la obtención de un diagnóstico de mayor certeza a partir de la interpretación de imágenes con mayor precisión. Para el diseño y la implementación de algoritmos se ha utilizado el MATLAB, programa que realiza cálculos numéricos con vectores y matrices, y por tanto se puede trabajar también con números escalares (tanto reales como complejos), con cadenas de caracteres y con otras estructuras de información más complejas [14]. En Cuba son insuficientes las investigaciones sobre los algoritmos de variación total para la reducción del ruido en imágenes médicas, por lo que para su perfeccionamiento es necesario realizar nuevos estudios. En la Universidad Central de Las Villas las investigaciones sobre este tema no abundan, solo dos profesores de la Facultad de Ingeniería Eléctrica lo investigan. De esta manera, la implementación de algoritmos de variación total para la reducción del ruido en imágenes de CT puede brindar información de apoyo para otras investigaciones..

(14) INTRODUCCIÓN. 4. Teniendo en cuenta todo lo antes expuesto, se enuncia el siguiente problema científico: ¿Cómo implementar algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada? Esta investigación tiene como objeto de estudio los algoritmos de variación total y el campo de acción lo constituye la aplicación de diferentes algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada. Para dar cumplimiento al problema de investigación se propone el siguiente objetivo general: Desarrollar algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada. Para resolver el problema científico y dar cumplimiento al objetivo general se plantean los siguientes objetivos específicos: 1. Caracterizar algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada. 2. Exponer algoritmos desarrollados utilizando variación total para la reducción del ruido en imágenes de tomografía computarizada. 3. Implementar algoritmos utilizando variación total para la reducción del ruido en imágenes de tomografía computarizada. 4. Evaluar los algoritmos desarrollados utilizando variación total para la reducción del ruido en imágenes de tomografía computarizada. De los objetivos específicos propuestos surgen las siguientes interrogantes científicas: 1. ¿Qué particularidades presentan los algoritmos de variación total? 2. ¿Cuáles son los algoritmos de variación total? 3. ¿Cómo implementar un algoritmo de variación total para la reducción del ruido en imágenes de tomografía computarizada? 4. ¿Cuál es la evaluación de los algoritmos desarrollados utilizando variación total para la reducción del ruido en imágenes de tomografía computarizada?.

(15) INTRODUCCIÓN. 5. Los resultados de esta investigación permitirán un mejor conocimiento de los algoritmos de variación total en Cuba, debido a su novedad en el mundo. Además, ofrecerá información detallada de los algoritmos para las personas interesadas en el tema, así como un nuevo método para la reducción del ruido en imágenes de tomografía computarizada para ser utilizado en Medicina. El presente trabajo está estructurado de la siguiente forma: resumen, introducción, capítulos, conclusiones, recomendaciones y referencias bibliográficas. En el primer capítulo se exponen aspectos generales de los algoritmos de variación total para la reducción del ruido en imágenes de tomografía computarizada así como sus características y particularidades. En el segundo capítulo se discuten y describen los distintos algoritmos de variación total utilizados. Se caracteriza la herramienta de simulación utilizada y se describe el proceso de adquisición y análisis de las imágenes utilizadas. En el tercer capítulo se muestran los principales parámetros que se pueden emplear para estudiar el desempeño de los algoritmos de variación total, comparación de los resultados obtenidos para cada uno de los algoritmos utilizados y discusión de los mismos..

(16) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 6. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN. TOTAL. Y. SU. APLICACIÓN. EN. TOMOGRAFÍA COMPUTARIZADA PARA REDUCIR EL RUIDO. La tomografía computarizada es una modalidad para representar imágenes por lo que es de gran seguridad en aplicaciones médicas e industriales. Extensos esfuerzos se han realizado para mejorar la calidad de la imagen con fines prácticos [15], [16]. Con base en la teoría de detección de compresión (cuyo acrónimo en idioma inglés es CS debido a su denominación compressed sensing) [17], [18], se desarrollaron algoritmos para reducir el ruido en imágenes para varios problemas de CT, lo que permite una mejor visualización y reducción de la dosis de radiación. Ejemplo de esto es la regularización de la variación total [19], [20]. En este capítulo se describen las principales características de la variación total. Además se presentan las particularidades de la tomografía computarizada y el ruido en las imágenes. También se exhiben investigaciones acerca de la TV en la CT. 1.1 Características fundamentales de la variación total La TV fue introducida para la reducción del ruido y la reconstrucción de imágenes por primera vez en el artículo de 1992 por Rudin, Osher y Fatemi [21]. Desde entonces se han creado y mejorado nuevos algoritmos para perfeccionar la calidad de las imágenes reconstruidas mediante este método. 1.1.1 La aproximación bayesiana para el restablecimiento de imágenes Primero se considera una situación discreta, donde la imagen g = (gi, j) con i ≥1 y j ≤N, limitado por (gi, j ∈ [0,1] o {0,…,255}) para señales 2D. La idea general para resolver problemas lineales es considerar: 1. El siguiente modelo que es la señal perfecta inicial: 𝑔 = 𝐴𝑢 + 𝑛, 𝑢 ∈ ℝ𝑁𝑥𝑁. (1.1).

(17) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 7. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. donde A es alguna transformación (borrosidad, muestreo o un operador lineal más general como la transformada de Radon para la tomografía); n = (ni, j) es el ruido: en situaciones simples se considera normal o Gaussiano con valor medio cero y desviación estándar σ. 2. Una función de densidad probabilística de partida para señales originales perfectas: 𝑃(𝑢)~𝑒 −𝑝(𝑢) 𝑑𝑢. (1.2). Que representa la idea de que se tienen datos perfectos (en otras palabras, el modelo para los datos). Entonces, la probabilidad conjunta para una nueva variable aleatoria g, dado que se observa la variable aleatoria u, según la regla de Bayer, es el producto de la probabilidad condicional P(g|u) multiplicada por la probabilidad marginal de u, P(u); esto es: 𝑃(𝑢|𝑔)𝑃(𝑔) = 𝑃(𝑔|𝑢)𝑃(𝑢). (1.3). Desde que la densidad para la probabilidad de g conociendo u es la densidad para n = g – Au es: 𝑒. −. 1 ∑ 2𝜎2 𝑖,𝑗. 2. |𝑔𝑖,𝑗 −(𝐴𝑢)𝑖,𝑗 |. (1.4). y se deduce de (1.3) que la densidad para P(u|g), la probabilidad de u conociendo la observación g es: 1. e−p(u) e Z(g). −. 1 ∑ 2σ2 i,j. |gi,j −(Au)i,j |. 2. (1.5). con Z(g) como factor de renormalización: 𝑍(𝑔) = ∫𝑢 𝑒. −(𝑝(𝑢)+. 1 2𝜎2. 2. ∑𝑖,𝑗|𝑔𝑖,𝑗 −(𝐴𝑢)𝑖,𝑗 | ). 𝑑𝑢. (1.6). La idea de máxima reconstrucción de la imagen es encontrar la mejor imagen para aumentar esta probabilidad o resolver el problema mínimo [21]: 1. 𝑚𝑖𝑛 𝑝(𝑢) + 2𝜎2 ∑𝑖,𝑗|𝑔𝑖,𝑗 − (𝐴𝑢)𝑖,𝑗 | 𝑢. 2. (1.7).. 1.1.2 Propiedades principales La siguiente definición fué tomada de la referencia [21]. Definición 1.1 La TV de una imagen se define por la dualidad: para 𝑢 ∈ 𝐿1𝑙𝑜𝑐 (Ω) está dado por:.

(18) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 8. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. 𝐽(𝑢) = 𝑠𝑢𝑝{− ∫Ω 𝑢𝑑𝑖𝑣 𝜙 𝑑𝑥 ∶ 𝜙 ∈ 𝐶𝑐∞ (Ω; ℝ𝑁 ), |𝜙(𝑥)| ≤ 1 ∀𝑥 ∈ Ω }. (1.8). Semi-continuidad inferior La definición 1.1 tiene algunas ventajas. Puede ser introducida por cualquier función integrable local (sin requerir ninguna regularidad o derivabilidad). Pero también J(u) se escribe como el supremo de formas lineales: 𝐿𝜙 : 𝑢 ↦ − ∫Ω 𝑢(𝑥)𝑑𝑖𝑣 𝜙(𝑥) 𝑑𝑥. (1.9). que es continuo con respecto a una topología muy débil. Por ejemplo, si un ⇀ u en Lp (Ω) para cualquier p ∈ [1,+∞), o incluso Lp (Ω’) para cualquier Ω’ ∁∁ Ω, entones Lϕun →Lϕu. Pero se escribe de la siguiente manera: 𝐿𝜙 𝑢 = 𝑙𝑖𝑚 𝐿𝜙 𝑢𝑛 ≤ 𝑙𝑖𝑚 𝑖𝑛𝑓 𝐽(𝑢𝑛 ) 𝑛. 𝑛. (1.10). y tomando después el supremo sobre todos los campos ϕ con |ϕ(x)| ≤ 1 en cualquier lugar, se deduce que [21]: 𝐽(𝑢) ≤ 𝑙𝑖𝑚 𝑖𝑛𝑓 𝐽(𝑢𝑛 ) 𝑛→∞. (1.11).. Convexidad Esta es la segunda propiedad fundamental de J que se deduce de la Definición 1.1 donde para cualquier u1, u2 y t ∈ [0,1]: 𝐽(𝑡𝑢1 + (1 − 𝑡)𝑢2 ) ≤ 𝑡𝐽(𝑢1 ) + (1 − 𝑡)𝐽(𝑢2 ). (1.12). Al ser J el supremo de las funciones lineales (por lo tanto convexas) se tiene que: 𝐿𝜙 (𝑡𝑢1 + (1 − 𝑡)𝑢2 ) = 𝑡𝐿𝜙 (𝑢1 ) + (1 − 𝑡)𝐿𝜙 (𝑢2 ) ≤ 𝑡𝐽(𝑢1 ) + (1 − 𝑡)𝐽(𝑢2 ). (1.13). Y tomando el supremo en los prductos del lado izquierdo de (1.12) [21]. Homogeneidad Se plantea por definición que por cada u y t > 0: J(tu) = tJ(u). (1.14).

(19) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 9. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. esto quiere decir que J es uni-homogénea [21]. 1.1.3 Aplicaciones de la variación total Reducción de borrosidad y escalamiento de imágenes El modelo estándar ROF puede ser extendido para reducción de borrosidad y escalamiento en imágenes: λ. min {∫Ω|Du| + 2 ∫Ω(Au − f)2 dx} u. (1.15). donde Ω ∁ ℝ2 es el dominio de la imagen y A es un operador lineal. En el caso de reducción de borrosidad, A es la borrosidad de kernel. En el caso de escalamiento de imágenes, A describe el proceso de reducción de muestreo, que a menudo se supone que es un núcleo difuminado seguido de un operador de submuestreo [21]. La figura 1.1 muestra un ejemplo de reducción de borrosidad mientras que la figura 1.2 muestra uno de escalamiento.. Figura 1.1 Reducción de borrosidad usando variación total. (a) y (b) muestran la imagen limpia y una versión degradada conteniendo borrosidad de aproximadamente 30 píxeles y ruido Gaussiano de desviación estándar σ = 0.02. (c) es el resultado del filtrado estándar de Wiener. (d) es el resultado de la variación total basado en el método de reducción de borrosidad [21]..

(20) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 10. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. Figura 1.2 Escalamiento de imágenes usando variación total. (a) muestra la imagen original y por un factor de 4 versión rebajada. (b) es el resultado del escalamiento por un factor de 4 usando interpolación bicúbica. (c) es el resultado de la TV basado en el modelo de escalamiento [21]. Variación Total con un término de fidelidad de datos L1 El modelo de TV L1 está definido por: min{∫Ω|Du| + λ ∫Ω|u − f| dx} u. (1.16). La figura 1.3 muestra la restauración de una imagen contaminada por ruido impulsivo. Como es de esperar el modelo ROF no puede restaurar la imagen sin perder detalles de fina escala. Mientras que el modelo de TV L1 le da demasiado peso a los valores atípicos y por lo tanto conduce a resultados mucho mejores. Esto muestra la importancia de usar un término de datos que coincide con el modelo de ruido esperado [21]..

(21) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 11. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. Figura 1.3 Reducción de ruido en la imagen en el caso de ruido impulsivo. (a) muestra la imagen limpia y (b) es la versión de ruido que ha sido corrompido por 25% de ruido. (c) es el resultado del modelo ROF. (d) es el resultado del modelo de TV L1. Se nota que este último modelo es capaz de remover el ruido mientras se preservan algunos detalles pequeños [21]. Modelos variacionales con posibilidad de términos no convexos en los datos Regularización cuadrática: Si h(p) = |p|2/2, entones h*(q) = |q|2/2 y se necesita saber cómo proyectar 𝑞0 = (𝑞0𝑥 , 𝑞0𝑡 ) hacia 𝐾 = {𝑞 = (𝑞 𝑋 , 𝑞 𝑡 ): 𝑞 𝑡 ≥ |𝑞 𝑥 |2 /2}. Si q0 no satisface la restricción, o sea, 𝑞0𝑡 < |𝑞0𝑥 |2 /2, se necesita proyectar q0 hacia el paraboloide 𝑞 𝑡 = |𝑞 𝑥 |2 /2. Se necesita resolver el siguiente problema de optimización sin restricciones: min { 𝑞. |𝑞−𝑞0 |2 2. − 𝜆 (𝑞 𝑡 −. |𝑞 𝑥 |2 2. )}. (1.17).

(22) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 12. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. donde λ es un multiplicador Lagrange para la restricción de igualdad 𝑞 𝑡 − |𝑞 𝑥 |2 /2 = 0. Las condiciones óptimas de la ecuación (1.17) están dadas por: 𝑞 𝑥 − 𝑞0𝑥 + 𝜆𝑞 𝑥 = 0 𝑞 𝑡 − 𝑞0𝑡 − 𝜆 = 0 𝑞𝑡 −. |𝑞 𝑥 |2 2. = 0.. (1.18). Después de eliminar qt y qx, se arriba a la siguiente ecuación cúbica para λ: 𝜆3 + 𝜆2 (𝑞0𝑡 + 2) + 𝜆(2𝑞0𝑡 + 1) + 𝑞0𝑡 −. |𝑞0𝑥 |2 2. = 0.. (1.19). En lugar de utilizar una ecuación cúbica para resolver (1.19) se utiliza un método de Newton. Se escoge como punto de partida 𝜆0 = 𝑚𝑎𝑥{0, −(2𝑞0𝑡 + 1)/3} + 1 y para cada n ≥ 0: 𝜆𝑛+1 = 𝜆𝑛 −. (𝜆𝑛 )3 + (𝜆𝑛 )2(𝑞0𝑡 + 2) + (𝜆𝑛 )(2𝑞0𝑡 + 1) + 𝑞0𝑡 − 3(𝜆𝑛 )2. +. 2(𝜆𝑛 )(𝑞0𝑡. + 2) +. 2𝑞0𝑡. |𝑞0𝑥 |2 2. (1.20). +1. Después de computar la solución de (1.19) la solución de la proyección está dada por: [21] 𝑞𝑥. 0 q = (1+𝜆 , 𝑞0𝑡 + 𝜆). (1.21).. Regularización de TV: En el caso que h(𝑝) = |𝑃|, entones h*(q) = 0 para |𝑞| ≤ 1 y el resto para +∞, y la proyección de q0 hacia {𝑞 = (𝑞 𝑥 , 𝑞 𝑡 ): 𝑞 𝑡 ≥ 0, |𝑞 𝑥 | ≤ 1} esta dado por: 𝑞𝑥. 0 𝑡 q = (𝑚𝑎𝑥{1,|𝑞 𝑥 |} , max{0, 𝑞0 }). (1.22).. 0. Regularización Lipschitz: Una ventaja de esta aproximación es que es bastante fácil de que se cumpla. Se considera que h(p) = 0 si |p| ≤ L y el resto para +∞. Entonces el conjugado convexo de h es simplemente ℎ∗ (𝑞) = 𝐿|𝑞| y se necesita saber cómo proyectar q0 hacia el cono convexo {𝑞 𝑡 ≥ 𝐿|𝑞 𝑥 |}. Esta proyección está dada por: 𝑞0𝑥 q = (𝜇 𝑥 , 𝜇𝐿) 𝑞0. (1.22). donde μ está dada por: μ=. 𝑚𝑎𝑥{0,|𝑞0𝑥 |+𝐿𝑞0𝑡 } 1+L2. .. (1.23)..

(23) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 13. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. La figura 1.4 muestra la imagen original y la figura 1.5 muestra la aplicación de diferentes términos de regularidad convexa.. Figura 1.4 Par de imágenes estéreo rectificadas y la disparidad de verdad del suelo, donde los píxeles negros corresponden a valores de disparidad desconocidos [21].. Figura 1.5 Aplicación de diferentes términos de regularidad convexa. Primera columna: regularización cuadrática, segunda columna: regularización de TV, tercera columna: regularización Lipschitz [21]. 1.2 Aspectos generales de la tomografía computarizada Un tomograma es la imagen de un plano o corte dentro del cuerpo. Una radiografía convencional es bidimensional, pero no es un tomograma porque sus datos no provienen de.

(24) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 14. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. un solo plano. La tomografía computarizada es extremadamente popular porque genera imágenes de cortes del cuerpo, eliminando así los artefactos de las estructuras superpuestas que dominan las radiografías convencionales. Un escáner de CT típico se muestra en la Figura 1.6 [22].. Figura 1.6 Escáner típico de CT [22]. El advenimiento de la tomografía computarizada a mediados de la década de 1960 y su desarrollo hasta el presente ha producido un cambio profundo en el papel de la imagen para el diagnóstico en medicina. Hay una gran variedad de condiciones médicas visibles en.

(25) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 15. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. imágenes de CT que no son visibles en las radiografías convencionales. Por lo tanto, el diagnóstico y la monitorización de muchas enfermedades son posibles solo a través de la CT; esto ha reducido la cantidad de cirugía exploratoria previamente requerida para estas enfermedades. Como dispositivo de medición, el escáner de CT también ha recorrido un largo camino desde sus orígenes. Ahora, a través de los procedimientos de calibración estándar, los escáneres de CT miden los números en unidades de Hounsfield, que son constantes que se utilizan en el escaneo y en diferentes escáneres. Por lo tanto, el análisis cuantitativo es posible y es una práctica común en la actualidad [23]. 1.3 El ruido en las imágenes y la contribución de la variación total para su reducción Una de las preocupaciones primarias del procesamiento digital de imágenes es aumentar la calidad de la imagen y moderar la degradación introducida por los sensores y dispositivos de adquisición. Las técnicas de restauración están enfocadas en reconstruir o recuperar una imagen que ha sido degradada. Cuando obtenemos una imagen digital y se ve un poco distorsionada, se dice que la imagen tiene ruido. Esto sucede en el proceso de adquisición, transmisión o almacenamiento cuando la señal sufre una perturbación, y es un defecto de las imágenes no deseado que produce contaminación. Se manifiesta de forma general en píxeles aislados que toman valores distintos de los reales. Los modelos variacionales han sido extremadamente exitosos en una amplia variedad de problemas de restauración, y siguen siendo una de las áreas de investigación más activas en procesamiento de imágenes matemáticas y visión por computadora. Por ahora, su alcance abarca no solo el problema fundamental de la reducción del ruido en imágenes, sino también otras tareas de restauración como reducción de borrosidad, deconvolución ciega y recoloración. Los modelos variables muestran la solución de estos problemas como minimizadores funcionales elegidos de forma apropiada. La técnica de minimización de elección para tales modelos implica rutinariamente la solución de ecuaciones diferenciales parciales no lineales derivando para las condiciones de optimización que sean necesarias [25]. Quizás el problema más básico de restauración de imágenes sea la reducción del ruido. Constituye un paso preliminar significativo en muchas tareas como detección y.

(26) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 16. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. reconocimiento de objetos. También es uno de los problemas más difíciles de resolver desde el punto de vista matemático. Una gran preocupación en el diseño de diferentes modelos de restauración conservan características importantes de la imagen, como aquellos más fáciles de detectar por el sistema visual humano al eliminar el ruido. Una característica importante de la imagen son los bordes; estos son lugares donde hay un cambio brusco en sus propiedades. Se han investigado muchos modelos para reducir el ruido y preservar los bordes. Recientemente también ha sido de gran esfuerzo preservar otras características de la imagen como la textura. Todos los modelos exitosos de reducción de ruido aprovechan el hecho de que hay una regularidad inherente que se encuentra en las imágenes naturales; así es como intentan distinguir el ruido y la información real de la imagen. Los modelos variacionales hacen que sea particularmente fácil imponer reglas geométricas de regularidad en las soluciones obtenidas por lo que esta es una de las razones principales de su éxito [25]. 1.4 Investigaciones acerca de la variación total en la tomografía computarizada En el año 2008 los autores Emil Y. Sidky y Xiaochuan Pan publican “Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization” [26] donde se desarrolla un algoritmo iterativo, basado en el trabajo reciente en detección compresiva para la reconstrucción de imágenes a partir de una exploración circular con haz de cono. El algoritmo minimiza la variación total de la imagen sujeta a la restricción de que los datos de proyección estimados se encuentran dentro de una tolerancia especificada de los datos disponibles y que los valores de la imagen no son negativos. Las restricciones son impuestas por el uso de la proyección en conjuntos convexos (POCS) y el objetivo de la TV se minimiza por la inclinación de descenso con un paso adaptable. El algoritmo se conoce como adaptive-steepest-descent-POCS (ASD-POCS). Parece ser robusto contra los artefactos de haz de cono, y puede ser particularmente útil cuando el rango angular es limitado o cuando la frecuencia de muestreo angular es baja. El algoritmo ASD-POCS se prueba con el disco Defrise y los maniquíes computarizados de la mandíbula. Algunas comparaciones se realizan con los algoritmos POCS y los algoritmos de maximización de expectativas (EM). Aunque el algoritmo se presenta en el contexto de la reconstrucción de imágenes circulares con haz de cono, también se puede aplicar al escaneo de geometrías que involucran otras trayectorias de fuente de rayos X..

(27) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 17. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. En septiembre del 2012 se publica “Low-Dose X-ray CT Reconstruction via Dictionary Learning” [27] por los autores Qiong Xu, Hengyong Yu, Xuanqin Mou, Lei Zhang, Jiang y Ge Wang. En este artículo se presenta un algoritmo basado en la TV en detalle y se evalúa en diferentes experimentos. En este algoritmo, la restricción escasa en términos de un diccionario redundante se incorpora a una función objetivo en un marco de reconstrucción iterativa estadística. El diccionario puede estar predeterminado antes de una tarea de reconstrucción de imagen o definido de manera adaptativa durante el proceso de reconstrucción. Un esquema de minimización alternativo es desarrollado para minimizar la función objetivo. El enfoque se evalúa con proyecciones de dosis bajas de rayos X recogidas en estudios con CT humana y animal, y la mejora asociada con el aprendizaje del diccionario se cuantifica en relación con la retroproyección filtrada y las reconstrucciones basadas en TV. Los resultados muestran que el enfoque propuesto produciría mejores imágenes con menor ruido y características estructurales más detalladas en casos seleccionados. Sin embargo, no hay pruebas de que esto sea cierto para todo tipo de estructuras. En el año 2013 los autores Zhiqiang Chen, Xin Jin, Liang Li y Ge Wang en la publicación “A limited-angle CT reconstruction method based on anisotropic TV minimization” [28] presentan un algoritmo de reconstrucción inspirado en detección comprimida (CS) para tomografía computarizada de ángulo limitado pues actualmente se realiza minimizando la variación total (TV) de una imagen de CT sujeta a la consistencia de los datos. Una clave para obtener una alta calidad de la imagen es optimizar el equilibrio entre el suavizado basado en TV y la fidelidad de los datos. En el caso del problema de CT de ángulo limitado, la fuerza de la consistencia de los datos es angularmente variable. Sin embargo, el proceso de minimización de TV es isotrópico, lo que sugiere que no es apto para CT de ángulo limitado. Aquí se presenta un método anisotrópico de minimización de TV para enfrentar este desafío. La ventaja de este enfoque se demuestra en la simulación numérica que se hace con imágenes de maniquíes e imágenes de CT reales, relativas a la reconstrucción basada en TV. En mayo del 2014 los autores Yi Zhang, Weihua Zhang, Yinjie Lei y Jiliu Zhou publican “Few-view image reconstruction with fractional-order total variation” [29]. Este trabajo presenta un nuevo algoritmo de reconstrucción en la tomografía computarizada para el problema de pocas proyecciones basado en el cálculo fraccional. Para superar las desventajas.

(28) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 18. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. del método de minimización de variación total, se propone un algoritmo de reconstrucción de imágenes basado en la variación total de orden fraccional en lugar de la variación total tradicional. Este algoritmo se obtiene al considerar más vóxeles de imagen vecinos, de modo que el peso correspondiente puede ser determinado de manera adaptativa por el modelo, suprimiendo así el efecto de suavizado excesivo. Los experimentos numéricos y clínicos demuestran que el método logra un mejor rendimiento que los métodos de reconstrucción existentes, incluida filtred back projection (FBP), las proyecciones de variación total basadas en el método de conjuntos convexos (TV-POCS) y el soft-threshold filtering (STH). En marzo del 2016 en el artículo “Statistical iterative reconstruction using adaptive fractional order regularization” [30] los autores Yi Zhang, Yan Wang, Weihua Zhang, Feng Lin, Yifei Pu y Jiliu Zhou donde plantean un modelo de orden fraccional basado en un marco de reconstrucción iterativa estadística. Para mejorar el rendimiento del modelo propuesto, se presenta una estrategia de selección de orden adaptativa, determinando el orden fraccional píxel por píxel. Los experimentos, incluidos los casos numéricos y clínicos, ilustraron mejores resultados que varios métodos existentes, especialmente, en preservación de estructura y textura. En febrero del 2017 se publica “Low-dose CT via convolutional neural network” [31] por los autores Hu Chen, Yi Zhang, Weihua Zhang, Peixi Liao, Ke Li, Jiliu Zhou y Ge Wang. En este documento se propone un nuevo algoritmo de reducción de ruido para dosis bajas de CT a través del aprendizaje profundo sin acceder a los datos de proyección originales. Aquí se usa una red neuronal convolucional profunda para mapear imágenes de CT de baja dosis hacia sus contrapartes correspondientes de dosis normales en forma de parche por parche. Los resultados cualitativos demuestran un gran potencial del método propuesto sobre la reducción de artefactos y la preservación de la estructura. En términos de métricas cuantitativas, el método propuesto ha mostrado una mejora sustancial en PSNR (Peak Signal to noise ratio), RMSE (Root Mean Squared Error) y SSIM (Structural Similarity Index) que los principales métodos existentes. Además, su velocidad es un orden de magnitud más rápido que la reconstrucción iterativa y los métodos de reducción de ruido en imágenes basados en parches..

(29) CAPÍTULO 1. CARACTERÍSTICAS DE LOS ALGORITMOS DE VARIACIÓN TOTAL Y SU. 19. APLICACIÓN EN TOMOGRAFÍA COMPUTARIZADA PARA ELIMINAR EL RUIDO. 1.5 Conclusiones parciales En este capítulo se profundizó en las características de la variación total, desde su aproximación bayesiana, propiedades principales y aplicaciones. También fueron expuestos los aspectos generales de la tomografía computarizada, así como la formación y la calidad de las imágenes mediante este método. Además, fueron abordadas las particularidades del ruido en las imágenes y cómo la variación total contribuye al mejoramiento de imágenes que están contaminadas con dicho fenómeno. Finalmente se presentaron varias investigaciones que se han realizado sobre la variación total y la aplicación en la tomografía computarizada para mejorar imágenes..

(30) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. CAPÍTULO 2. ALGORITMOS PROPUESTOS. DE Y. VARIACIÓN. CARACTERÍSTICAS. 20. TOTAL DE. LAS. IMÁGENES UTILIZADAS. Desde su introducción en el artículo clásico de Rudin, Osher y Fatemi [13], los modelos de minimización de variación total se han convertido en una de las metodologías más populares y exitosas para la restauración de imágenes. Recientemente ha habido un resurgimiento e interés por crear nuevos métodos para eliminar el ruido y restaurar las imágenes. Estos modelos ofrecen mejoras en la preservación del contraste, la geometría y la textura. En el presente capítulo se proponen algoritmos de variación total y para su mejor comprensión se describen de una forma matemática. También se caracteriza la herramienta de simulación MATLAB. Además, se aborda sobre el proceso de adquisición y análisis de cada una de las imágenes que se utilizaron. 2.1 Características principales del algoritmo 1 A lo largo de este algoritmo, Ӿ e ϒ son dos espacios de Hilbert reales. El objetivo principal es resolver el problema de optimización primario: Find 𝑥̂ ∈ 𝑎𝑟𝑔 min[𝐹(𝑥) + 𝐺(𝑥) + 𝐻(𝐿𝑥)], 𝑥∈Ӿ. (2.1). donde: 1. F: X → ℝ es convexo, diferenciable en Ӿ y su gradiente ∇F es β- Lipschitz continuo, para algunos β ∈ [0, + ∞ ]; es decir: ‖∇𝐹(𝑥) − ∇𝐹(𝑥 ′ )‖ ≤ 𝛽‖𝑥 − 𝑥 ′ ‖, 𝑝𝑎𝑟𝑎 𝑐𝑎𝑑𝑎 (𝑥, 𝑥′) ∈ Ӿ2 .. (2.2). 2. G ∈ Ӿ y H ∈ ϒ son simples, en el sentido de que sus operadores de proximidad tienen una representación cerrada, o al menos pueden resolverse de manera eficiente con alta precisión. 3. L: Ӿ → ϒ es un operador lineal limitado con L* adjunto y norma inducida: ‖𝐿‖ = 𝑠𝑢𝑝{‖𝐿𝑥‖ ∶ 𝑥 ∈ Ӿ , ‖𝑥‖ ≤ 1} < +∞.. (2.3).

(31) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. 21. 4. El conjunto de minimizadores de (2.1) se supone que no está vacío [32]. La formulación dual correspondiente del problema primario (2.1) es: Find 𝑦̂ ∈ 𝑎𝑟𝑔 min[(𝐹 + 𝐺)∗ (−𝐿∗ 𝑦) + 𝐻 ∗ (𝑦)], 𝑦∈ϒ. (2.4). donde se nota que (𝐹 + 𝐺)∗ (−𝐿∗ 𝑦) = min[𝐹 ∗ (−𝐿∗ 𝑦 − 𝑥 ′ ) + 𝐺 ∗ (𝑥′)] es una convolución 𝑥′∈Ӿ. ínfima. Sin más suposición, el conjunto de soluciones de (2.4) puede estar vacío. Este algoritmo propuesto es primario-dual, en el sentido de que resuelve el problema primario y dual; (2.1) y (2.4) conjuntamente. Otra formulación de estos dos problemas de minimización más comunes es combinarlos en la búsqueda de un punto en común de la forma [32]: Find(𝑥̂, 𝑦̂) ∈ 𝑎𝑟𝑔 min. max. [𝐹(𝑥) + 𝐺(𝑥) − 𝐻 ∗ (𝑦) + ⟨𝐿𝑥, 𝑦⟩].. 𝑥∈Ӿ 𝑦∈𝑑𝑜𝑚(𝐻 ∗ ). (2.5). La teoría clásica de Karush-Kuhn-Tucker afirma que, si el par (𝑥, ̂ 𝑦̂) es una solución a la inclusión variacional monótona: 𝜕𝐺(𝑥̂) + 𝐿∗ 𝑦̂ + ∇𝐹(𝑥̂) 0 Find (𝑥̂, 𝑦̂) ∈ Ӿ ∗ ϒ tal que ( ) ∈ ( ), −𝐿𝑥̂ + 𝜕𝐻 ∗ (𝑦̂) 0. (2.6). entonces 𝑥̂ es una solución de (2.1), 𝑦̂ es una solución de (2.4) y (𝑥̂, 𝑦̂) es una solución de (2.5). Lo contrario no se cumple en general y el conjunto de soluciones de (2.6) puede estar vacío. Sin embargo, si la siguiente condición de calificación se sostiene: 0 ∈ sri (𝐿(dom(𝐺)) − dom(𝐻)),. (2.7). entonces el conjunto de soluciones de (2.4) no es vacío y para cada solución primaria 𝑥̂ de (2.1) y solución dual 𝑦̂ de (2.4) entonces (𝑥̂, 𝑦̂) es una solución de (2.6). Por lo tanto, a continuación se supone que el conjunto de soluciones a las inclusiones (2.6) no es vacío, teniendo en cuenta que (2.7) es una condición suficiente para que esto se mantenga [32]. La ventaja en la solución de (2.6) en lugar de la inclusión 0 ∈ ∇𝐹(𝑥̂) + 𝜕𝐺(𝑥̂) + 𝐿∗ 𝜕𝐻(𝐿𝑥̂) asociado a (2.1) es doble: (i) la función compuesta H ◦ L se ha dividido; (ii) se obtiene no sólo la solución primaria 𝑥̂, sino también la solución dual 𝑦̂; y el algoritmo propuesto en.

(32) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. 22. realidad utilizan sus propiedades entrelazadas para actualizar el primario y el dual de variables de forma alternativa y eficiente. Se observa que hay espacio en la inclusión dual de (2.6) para un término adicional ∇𝐾 ∗ (𝑦̂), que produce una formulación más simétrica de los problemas primarios y duales. Las inclusiones variacionales obtenidas caracterizan al siguiente problema primario, que incluye una convolución ínfima: [𝐹(𝑥) + 𝐺(𝑥) + 𝐻(𝐿𝑥 − 𝑦 ′ ) + 𝐾(𝑦′)], Find 𝑥̂ ∈ arg min inf ′. (2.8). 𝑥∈Ӿ 𝑦 ∈ϒ. donde la función adicional K ∈ ϒ es tal que K* es diferenciable en ϒ con un gradiente continuo β ' -Lipschitz, para algunos β ' ≥ 0 [32]. 2.2 Características principales del algoritmo 2 La mayoría de las formulaciones matemáticas de los problemas inversos, en particular de los problemas inversos de imágenes, se presentan de la forma: min 𝐹(𝑢) + 𝑅(𝑢) ,. (2.9). 𝑢. donde F representa la fidelidad de los datos y R el término de regularización. Si G denota al operador de modelo directo, entonces el término de fidelidad más común es de la forma: 1. 𝐹(𝑢) = 2 ‖𝐺(𝑢) − 𝑧‖2 ,. (2.10). donde z representa los datos posiblemente propensos a errores y ‖𝐺(𝑢) − 𝑧‖ denota una norma de Hilbert elegida de una forma apropiada. Del mismo modo, el término de regularización elegido con mayor frecuencia viene dado por: ∝. 𝑅(𝑢) = 2 |𝑢|2 ,. (2.11). donde ∝ es el parámetro de regularización y |𝑢| denota una norma de Hilbert. Por lo que se propone y analiza el término de regularización de la forma: 𝑇𝐺𝑉𝛼𝑘 (𝑢) = 𝑠𝑢𝑝 {∫Ω 𝑢 𝑑𝑖𝑣 𝑘 𝑣 𝑑𝑥 | 𝑣 ∈ 𝐶𝑐𝑘 (Ω, 𝑆𝑦𝑚𝑘 (ℝ𝑑 )), ‖𝑑𝑖𝑣 𝑙 ‖ ∞ ≤ 𝛼𝑙 , 𝑙 = 0, … , 𝑘 − 1},. (2.12).

(33) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. 23. donde 𝑆𝑦𝑚𝑘 (ℝ𝑑 ) denota el espacio de tensores simétricos de orden k con argumentos en ℝd y 𝛼𝑙 son parámetros fijos positivos. Se refiere a 𝑇𝐺𝑉∝𝑘 como la variación total generalizada del orden k con el peso ∝∈ ℝ𝑘 . A partir de esta definición queda inmediatamente claro que implica derivados de u de orden i = 1…, k, y que el núcleo de 𝑇𝐺𝑉∝𝑘 es el conjunto de polinomios de grado menor que k. Además, es invariante de forma rotativa y para k = 2. La variación total generalizada de la función de indicador de un conjunto Ω’cc Ω es igual a 𝛼1 𝑃𝑒𝑟Ω′ = 𝛼1 TV(XΩ’) donde 𝑃𝑒𝑟Ω′ denota el perímetro de Ω’ [33]. Como una vista previa adicional se señala que en la dimensión 1, con Ω [0, 𝐿], 𝑘 = 2, ∝0 , ∝1 > 0, tenemos para: 𝑢(𝑥) = ∑2𝑖=1 𝑝𝑖 (𝑥)𝑋Ω𝑖 , con 𝑝𝑖 (𝑋) = 𝑎𝑖 𝑥 + 𝑏𝑖 , para cada 𝑎1 , 𝑎2 , 𝑏1 , 𝑏2 ∈ ℝ y Ω1 = [0, 𝑐], Ω2 = [𝑐, 1]. (2.13). entonces: 𝑇𝐺𝑉∝2 (𝑢) =∝1 |𝑝2 (𝑐) − 𝑝1 (𝑐)| +∝0 |𝑝1′ (𝑐) − 𝑝2′ (𝑐)|. (2.14) ∝. ∝. siempre que el punto de salto c no esté cerca del límite, es decir, 𝑐 ∈ [∝0 , 𝐿 − ∝0 ] . En 1. 1. particular, 𝑇𝐺𝑉∝2 (𝑢) no penaliza la derivada de orden l = 0,1 a menos que salte en c [33]. Esta ecuación se basa en el hecho de que involucra y equilibra las derivadas de mayor orden de u. Como consecuencia, reduce el efecto escalera de la función de variación limitada. El uso de derivadas de orden superior con el objetivo de reducir las escaleras no es nuevo. La función de convolución ínfima: min ∫ |∇𝑢1 | +∝ |∇(∇𝑢2 )| 𝑑𝑥. 𝑢1 +𝑢2 =𝑢 Ω. (2.15). se propone por ser prácticamente eficiente, eliminando el efecto staircasing, para los problemas de reducción del ruido con imágenes que contienen varios niveles de gris, así como bordes y esquinas. Esta idea fue seguida en una forma modificada donde el término de regularización tiene la forma: min ∫ |∇𝑢1 | +∝ |∇𝑢2 | 𝑑𝑥. 𝑢1 +𝑢2 =𝑢 Ω. (2.16). es decir, la segunda derivada es remplazada por el Laplaciano y se deriva un método dual para su realización numérica [33]..

(34) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. 24. Según la función diferencial dada por: ∫Ω|∇𝑢| +∝ 𝛷(|∇𝑢|)(𝐿(𝑢)) 𝑑𝑥. (2.17). donde Φ es una función de valor real que refleja la presencia de bordes en el sentido de que su valor se acerca a 0 cuando el gradiente |∇𝑢 | se es grande y L(u) es un operador elíptico. En términos de regularización de la forma: 𝑅(𝑢) = ∫Ω|𝐷∇𝑙−1 (𝑢)|. (2.18). donde ∫Ω|𝐷∇𝑙−1 (𝑢)| denota la variación total de la derivada (l -1) de 𝑢 ∈ 𝑊 𝑙−1,1 [33]. 2.3 Características principales del algoritmo 3 Para formular el problema de optimización de interés (2.20), primero se proponen algunas definiciones clásicas de optimización convexa [34]. Una función g definida en un espacio real de Hilbert X con valores en ℝ ∪ {+ ∞} es apropiado si su dominio dom (g) = {x ∈ X; g (x) <+ ∞} es no vacío. g es convexa si g (ax + (1 - a) x' ) ≤ ag (x) + (1 - a) g (x' ) para cada x, x' ∈ X y a ∈ [0, 1]. g es semicontinua inferior en x ∈ X si, por cada v ∈[-∞, g (x) ], podemos encontrar una vecindad Ω de x tal que f(Ω) ⊂[v, + ∞] [35]. El conjunto de funciones convexas, correctas, semicontinuas inferiores de X a ℝ ∪ {+ ∞} se denota por Γ0(X). Se va a definir el operador de proximidad de Moreau para g ∈ Γ0(X) dado por: 1. ‖𝑥 − 𝑥′‖2 + 𝑔(𝑥 ′ ). 𝑝𝑟𝑜𝑥𝑔 : 𝑋 ↦ 𝑋, 𝑥 ↦ arg min ′ 2 𝑥 ∈𝑋. (2.19). Existen expresiones explícitas simples para la proximidad de operadores de una gran clase de funciones [36], [37]. Un algoritmo iterativo que tiene como objetivo minimizar una suma de funciones por evaluaciones sucesivas de sus gradientes u operadores de proximidad se llama algoritmo próximo [35]. En este algoritmo el objetivo es resolver el siguiente problema genérico de optimización, formulado en espacios reales de Hilbert X y {𝑈𝑚 }𝑀 𝑚=1 , para M ∈ ℕ: Find 𝑥̂ ∈ arg min 𝑓(𝑥) + 𝑔(𝑥) + ∑𝑀 𝑚=1 ℎ𝑚 (𝐿𝑚 𝑥), 𝑥∈𝑋. (2.20).

(35) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. 25. donde: 1- f, g ∈ Γ0(X), hm ∈ Γ0(U m). 2- Los operadores 𝐿𝑚 : 𝑋 ↦ 𝑈𝑚 son lineales y acotados. 3- f es diferenciable en X y su gradiente ∇𝑓 es 𝛽- Lipschitz continuo, para la constante real 𝛽 > 0, es decir, ‖∇𝑓(𝑥) − ∇𝑓(𝑥′)‖ ≤ 𝛽‖𝑥 − 𝑥′‖. 4- El conjunto de minimizadores se supone que no está vacío. 5- Se cumple la siguiente restricción de calificación:. (0, … ,0) ∈ sri {(𝐿𝑚 𝑥 −. 𝑢𝑚 )1≤𝑚≤𝑀 | 𝑥 ∈ dom(𝑔) y 𝑈𝑚 ∈ dom(ℎ𝑚 ), ∀𝑚 = 1, … , 𝑀 }, donde sri el interior relativo fuerte [35]. Se tiene en cuenta que al permitir que algunas de las funciones en (2.20) sean cero y un operador lineal Lm puede ser el identificador de identidad. También se recuerda que, dado un conjunto convexo cerrado no vacío Ω ⊂ X, se puede definir la función del indicador iΩ ∈ Γ0 (X): x ∈ X ↦ {0 si x ∈ Ω, + ∞ los demás}. Tales funciones son convenientes para aplicar restricciones duras a la solución: el problema de minimizar f ∈ Γ0(X) sobre Ω se puede escribir como la minimización de f + iΩ en todo el espacio X. Dado que el operador de proximidad de una función de indicador es simplemente la proyección en el conjunto, los algoritmos próximos se pueden ver como generalizaciones de algoritmos para encontrar un elemento en la intersección de conjuntos convexos por proyecciones sucesivas (POCS) [34], [36]. La principal dificultad para resolver (2.20) proviene del hecho de que los espacios X y Um son típicamente de gran dimensión, por lo tanto se denomina optimización a gran escala. Por ejemplo, si la solución solicitada 𝑥̂ es una imagen, la dimensión N de X es el número de píxeles en la imagen. Para N = 106 y mayores valores, no es posible manipular, en cada iteración de un algoritmo, matrices de tamaño N × N. Entonces, algoritmos próximos, que solo explotan información de primer orden de las funciones, a menudo son la única forma viable de resolver (2.20) [35]. Ahora se consideran problemas inversos en las imágenes. Entonces, primero hay que colocarlos en el espacio X = ℝNh × Nv de imágenes en escala de grises de tamaño Nh columnas multiplicadas por Nv filas, dotadas con el producto interno euclidiano habitual. Para restaurar o reconstruir una imagen x se resuelve el siguiente problema:.

(36) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS 1. Find 𝑥̂ ∈ arg min 2 ‖𝐴𝑥 − 𝑦‖2 + 𝜆. TV(𝑥) 𝑥∈Ω. 26. (2.21). 1- y representa el dato disponible. 2- A : X → Y es el operador lineal que modela el proceso de adquisición. 3- Ω es un subconjunto cerrado y convexo de X. 4- 𝜆 > 0 es un parámetro para sintonizar, dependiendo de las propiedades de A y el nivel de ruido. La variación total discreta, denotada por TV(x) en (2.21), se define como el operador de gradiente discreto D: X → X2, que asigna una imagen x a un par de imágenes (uh, uv) para todo kh = 1, …,Nh, Kv = 1,…,Nv, 𝑢ℎ = [𝑘ℎ , 𝑘𝑣 ] = {𝑥[𝑘ℎ , 𝑘𝑣 ] − 𝑥[𝑘ℎ − 1, 𝑘𝑣 ] si 𝑘ℎ ≥ 2, 0 para los demás}, 𝑢𝑣 [𝑘ℎ , 𝑘𝑣 ] = {𝑥[𝑘ℎ , 𝑘𝑣 ] − 𝑥[𝑘ℎ , 𝑘𝑣 − 1] si 𝑘𝑣 ≥ 2, 0 para los demás}. Entonces tenemos que: 𝑁 𝑁 TV(𝑥) = ‖𝐷𝑥 ‖1,2 = ‖(𝑢ℎ , 𝑢𝑣 )‖1,2 = ∑𝑘ℎℎ=1 ∑𝑘𝑣𝑣=1 √𝑢ℎ [𝑘ℎ , 𝑘𝑣 ]2 + 𝑢𝑣 [𝑘ℎ , 𝑘𝑣 ]2. (2.22).. 2.4 Caracterización de la herramienta de simulación MATLAB MATLAB es el nombre abreviado de “MATrix LABoratory”, se originó en 1970 como un asistente matemático para el uso en el álgebra de matrices y la computación numérica [38]. Como caso particular puede trabajar con números escalares, tanto reales como complejos, con cadenas de caracteres y con otras estructuras de información más complejas. Una de las capacidades de esta herramienta es realizar una amplia variedad de gráficos en dos y tres dimensiones. Para ciertas operaciones es muy rápido, por ejemplo, cuando puede ejecutar sus funciones en código nativo con los tamaños más adecuados para aprovechar sus capacidades de vectorización [39]. Su entorno utiliza un lenguaje de computación técnico de alto nivel para el desarrollo de algoritmos, la visualización de datos y la computación numérica. Además, puede integrarse bien con otros lenguajes y aplicaciones de terceros. También incluye un ambiente gráfico llamado Simulink. Este es usado para la simulación con múltiples dominios y el diseño.

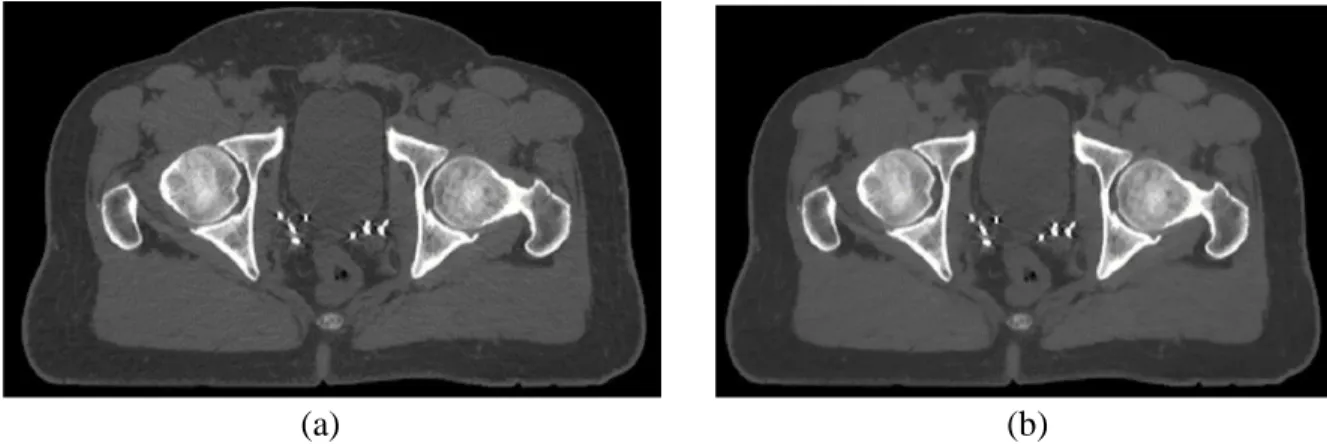
(37) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. 27. basado en modelos. Además, provee interfaces de rutinas externas escritas en otros lenguajes de programación [40]. En MATLAB, así como en cualquier otro conjunto de lenguaje interactivo, el tipo, el rango y la forma de las variables son dinámicamente determinadas. Esta herramienta ofrece varias rutinas especializadas a través de complementos de dominios específicos, llamados “toolboxes” y una interfaz simplificada para bibliotecas de alto rendimiento como BLAS, FFTV y LAPACK. Por ser una herramienta de alto nivel, el desarrollo de programas numéricos con MATLAB puede requerir hasta un orden de magnitud menos de esfuerzo que con lenguajes de programación convencionales, como Fortran, Pascal, C/C++, Java o Visual Basic [41]. Tiene varias ventajas comparadas con los lenguajes de computación convencional para resolver problemas técnicos. Entre ellas se pueden destacar la facilidad de uso, plataforma independiente, funciones predefinidas, compilador, entre otras. Sin embargo, posee dos desventajas fundamentales, la primera es que es un lenguaje interpretado y por eso se ejecuta más lento que los compilados aunque este problema puede ser mitigado estructurando correctamente el programa; la segunda es el costo: una copia completa del MATLAB es cinco a diez veces más cara que un compilador C convencional o Fortran [39]. En este trabajo se utiliza la versión de MATLAB del año 2015. 2.5 Adquisición de las imágenes Los datos de CT se obtuvieron para esta investigación de dos escáneres CT diferentes: un kV on-board imaging (OBI) system integrated en un acelerador lineal médico TrueBeamTM (Varian Medical System, Palo Alto, CA, USA) y un escáner Siemens SOMATOM Sensation 16 scanner CT utilizando la geometría de exploración helicoidal (Santa Clara, Cuba). Los pacientes con empastes dentales se escanearon en un sistema kV OBI con un tipo de filtro “Filtro corporal”, núcleo de convolución “estándar”, corriente del tubo 250mA y 120 kVp; en el caso de pacientes con implantes de cadera y semilla, con "Filtro corporal", núcleo de convolución "estándar", corriente del tubo de 150 mA y 120 kVp . Otros pacientes con empastes dentales se escanearon en un Siemens SOMATOM Sensation 16 scanner CT y fue utilizado un tipo de filtro “WEDGE_2”, convolución kernel “'H31s”, corriente del tubo 226.

(38) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. 28. mA y 120 kVp. La matriz de imágenes reconstruidas es de 512 x 512 píxeles en ambos escáneres. Los tamaños de píxeles correspondientes fueron de 1 mm X 1 mm para OBI y de 0.776 mm X 0.776 mm para Siemens SOMATOM Sensation. La distribución de conjuntos de datos tomados de diferentes regiones anatómicas y CT es la siguiente: tres implantes de semillas, tres implantes de cadera y tres implantes dentales adquiridos de OBI; y once empastes dentales de Siemens SOMATOM Sensation. 2.6 Análisis de la imagen Las imágenes clínicas obtenidas mediante el uso de los algoritmos de variación total fueron evaluadas por dos observadores certificados de forma independiente, cada uno con más de 5 años de experiencia clínica, cegados a todos los datos de los pacientes y los parámetros de la imagen. Las imágenes se visualizaron en las mismas condiciones; se muestra en orden aleatorio y se revisa en la ventana de tejido blando (nivel de ventana 20 HU, ancho de ventana 400 HU) y ventana ósea (nivel de ventana 300 HU, ancho de ventana 2,500 HU). Las imágenes se mostraron con un monitor de 23" con una resolución de 1920 X 1080. Los observadores vieron los monitores desde una distancia de visión aproximada de 2-2.5 altura de pantalla. Los experimentos fueron conducidos en luz ambiental atenuada (menos de 25 lux). Los dos observadores clasificaron 210 imágenes tomográficas generadas (10 originales + 200 modificadas utilizando diferentes algoritmos y parámetros con el propósito de determinar las más óptimas), tanto el ruido como la interpretación diagnóstica en una escala de clasificación de cinco puntos. El grado de calidad en las imágenes se puntuó en una escala de 1 a 5 (1, ruido muy severo; 2, ruido severo; 3, ruido moderado; 4, ruido mínimo; 5, sin ruido). La calidad de la imagen diagnóstica se puntuó de manera similar en imágenes de TC en una escala de 1 a 5 (1, calidad de imagen gravemente reducida, no diagnóstica; 2, calidad de imagen marcadamente reducida, con interpretabilidad diagnóstica deteriorada; 3, calidad de imagen aceptable e interpretabilidad diagnóstica; 4, buena calidad de imagen, con alta confianza de diagnóstico; 5, excelente calidad de imagen, con interpretabilidad de diagnóstico completo) [42], [43]. Con el propósito de evaluar el acuerdo entre observadores, se utilizó el kappa de Cohen. Los valores κ de 0.01-0.20 se consideraron como un leve acuerdo, 0.21-0.40 por acuerdo justo,.

(39) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. 29. 0.41-0.60 por acuerdo moderado, 0.61-0.80 por acuerdo sustancial y 0.81-1.00 por acuerdo casi perfecto. Los análisis estadísticos se realizaron con el software estadístico (SPSS, versión 22.0; IBM, Chicago, IL, USA). Para todos los análisis estadísticos, se consideró que los valores de p inferiores a 0,05 representaban diferencias estadísticamente significativas. Una región de interés (ROI) se le aplicó a cada imagen de CT. Los tamaños utilizados fueron 100 x 100 píxeles con forma cuadrada para un total de 300 ROI. Las ROI se mantuvieron para todas las mediciones. 2.6.1 Métricas utilizadas para la evaluación Este estudio se aplica para cinco métodos de FR (Full Reference) utilizados en muchas aplicaciones como compresión de imágenes, restauración de imágenes, transmisión multimedia y campo de visión por computadora. La desviación de similitud de gradiente (GMSD) [44] es la primera métrica. GMSD emplea mapas de calidad de imagen local basados en la variación global de gradientes para la predicción general de calidad de imagen. Los indicadores segundo y tercero evaluados son relación señal-ruido ponderada por contenido de información (IW-PSNR) y ponderado por contenido de información (IWMSE), propuesto por Wang y Li en [45]. IWPSNR e IWMSE emplean la transformada de pirámide Laplaciana. La cuarta métrica probada es la relación señal / ruido ponderada (WSNR) [46]. Se seleccionó un modelo de selección de escala óptima (OSS) propuesto en [47] y se evaluó el rendimiento de la relación pico señal / ruido (OSS-PSNR). Las métricas analizadas no implican ningún proceso de capacitación. Todas las métricas se implementan con MATLAB y los códigos fuente utilizados en este trabajo están disponibles y programados en Internet por sus autores. Para obtener detalles completos de estos algoritmos, consulte la literatura correspondiente. 2.7 Conclusiones parciales En este capítulo se abordaron las características principales de los algoritmos de variación total utilizados, así como las principales fórmulas matemáticas que utilizan los mismos, y se explica con detalle cada una de las variaciones y despejes matemáticos que tienen. También se caracteriza a la herramienta de simulación que se utiliza para procesar cada una de las imágenes utilizadas. Además, se muestra cómo es el proceso puesto en práctica por los.

(40) CAPÍTULO 2. ALGORITMOS DE VARIACIÓN TOTAL PROPUESTOS Y CARACTERÍSTICAS DE LAS IMÁGENES UTILIZADAS. 30. evaluadores para la adquisición y análisis de las imágenes originales y resultantes visualizadas. Por último se exhiben las métricas propuestas para la valoración de todas las imágenes..