Análisis y diseño de un estabilizador difuso para un robot humanoide utilizando los brazos como medio de control

(1)

“ANÁLISIS Y DISEÑO DE UN ESTABILIZADOR DIFUSO PARA UN ROBOT HUMANOIDE UTILIZANDO LOS BRAZOS COMO MEDIO DE

CONTROL”

T E S I S

QUE PARA OBTENER EL GRADO DE

MAESTRO EN CIENCIAS

C O N E S P E C I A L I D A D EN I N G E N I E R Í A M E C Á N I C A

P R E S E N T A

ING. AURORA ITZEL VENTURA SEPÚLVEDA

DIRECTOR DE TESIS: DR. JESÚS ALBERTO MEDA CAMPAÑA

MÉXICO D.F. 2012 ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA

(2)

(3)

(4)

Dedico este trabajo a las personas que más admiro, mis padres

Nicolás Ventura Barajas y Aurora Sepúlveda Sáenz

Por su amor y enseñanzas que me han formado como persona, brindándome apoyo incondicional, creyendo en mí todo el tiempo, por todos los sacrificios que han hecho para

hacer esto posible, les estaré eternamente agradecida.

A mi hermana

Mayra Nayeli Ventura Sepúlveda

Por la compañía en las buenas y malas, por la ayuda y compresión en cada momento y sobre todo por las palabras de aliento cuando más las necesitaba.

A mis abuelos

Armando, Aurora, Nicolás y Evodia

Aunque ya no están a nuestro lado, su amor, sabiduría, entrega y ejemplo de superación siguen vivas en mi corazón.

A mis amigos

(5)

Al Instituto Politécnico Nacional

Por la oportunidad brindada de formarme como profesionista dentro de esta institución.

A Dr. Jesús Alberto Meda Campaña

Por permitirme trabajar bajo su dirección y tenerme la paciencia necesaria durante el desarrollo de esta tesis.

A Mis profesores:

A todos mis profesores que compartieron sus conocimientos, dentro y fuera del aula de clases forjándome como profesionista

A CONACYT

(6)

Lista de figuras. ... i

Lista de tablas. ... viii

Nomenclatura. ... ix

Resumen. ... xi

Abstract. ... xii

Definición del problema. ... xiii

Objetivos. ... xiii

Justificación. ... xiii

Alcances. ... xiv

Capítulo 1 . Estado del arte. ... 1

1.1 Introducción. ... 1

1.2 Robótica. ... 3

1.2.1 Antecedentes históricos. ... 3

1.3 Aplicación de la lógica difusa en la robótica. ... 8

1.4 Desarrollo de la robótica en México. ... 8

Capítulo 2 . Marco teórico. ... 10

2.1 Robot. ... 10

2.1.2 Clasificación de los robots. ... 10

2.1.3 Elementos de un robot. ... 13

2.2 Dinámica del robot. ... 17

2.2.1 Centro de gravedad... 17

2.2.2 Distribución de la masa. ... 17

2.2.3 Torque... 19

2.2 BIOLOID PREMUM KIT. ... 20

2.3 Lógica difusa. ... 21

2.3.1 Metodología del desarrollo sistemático del modelado de la lógica difusa. ... 23

(7)

2.4 Tipos de funciones de membresía. ... 30

2.4.1 Función de membresía triangular. ... 30

2.4.2 Función de membresía trapezoidal... 30

2.4.3 Función de membresía Gaussiana. ... 31

2.5 Control difuso. ... 31

2.5.1 Base de reglas. ... 32

2.5.2 Mecanismo de inferencia. ... 33

2.6 MATLAB. ... 36

2.7 SIMULINK. ... 37

2.8 SIMMECHANICS... 37

2.8.1 Creación de un modelo de SIMMECHANICS. ... 38

2.9 Fuzzy logic toolbox. ... 42

2.10 SOLIDWORKS. ... 43

Capítulo 3 . Modelado físico y diseño del estabilizador difuso. ... 44

3.1 Modelado físico. ... 44

3.1.1 Modelado del “Torso”. ... 44

3.1.2 Modelado de los “Brazos”. ... 48

3.1.3 Interface entre SimMechanics y SolidWorks. ... 51

3.2 Planteamiento del problema. ... 52

3.3 Diseño del estabilizador difuso. ... 53

Capítulo 4 . Simulaciones. ... 84

Simulación 1, torso en -25° con control. ... 84

Simulación 2, torso en -18°... 87

Simulación 4, torso en -8°. ... 93

Simulación 6, torso en 3°. ... 102

(8)

4.1 Controlador difuso con torque extra. ... 120

4.2 Controlador difuso con restricción la velocidad angular. ... 156

Capítulo 5 . Conclusiones. ... 162

Trabajos futuros. ... 163

Referencias. ... 164

ANEXO A... 167

(9)

Fig. 1.1 Representación a bloques de un sistema. ... 1

Fig. 1.2 Sistema básico de control. ... 2

Fig. 1.3 Sistema básico de control difuso... 2

Fig. 1.4 Escritor automático inventado en 1772 por Pierre Jaquet-Droz. ... 4

Fig. 1.5 Telar de Joseph Jacquard. ... 5

Fig. 1.6 Robot Unimate. ... 5

Fig. 1.7 Robot PUMA de la NASA. ... 6

Fig. 2.1 Clasificación de los robots por su arquitectura. ... 10

Fig. 2.2 Robot de paletizado para carga pesada. ... 11

Fig. 2.3 Robot BR23C. ... 11

Fig. 2.4 Robot Arsen. ... 12

Fig. 2.5 Robot ASIMO. ... 12

Fig. 2.6 Estructura de un robot humanoide. ... 13

Fig. 2.7 Tipos de articulaciones para un robot. ... 14

Fig. 2.8 Servomotor. ... 14

Fig. 2.9 Tipos de sensores internos de Robots. ... 15

Fig. 2.10 Tipos de sensores internos de Robots. ... 16

Fig. 2.11 Descripción del tensor de inercia de la distribución de masa de un objeto, donde el vector AP localiza el elemento de volumen diferencial, dv. ... 18

Fig. 2.12 Bioloid Premium kit. ... 20

Fig. 2.13 Distribución de servomotores en el robot Bioloid Premium kit. ... 21

Fig. 2.14 Diagrama de flujo del modelado de un sistema difuso. ... 23

Fig. 2.15 Ejemplo de conjuntos difusos. ... 26

Fig. 2.16 Unión entre dos conjuntos difusos. ... 27

Fig. 2.17 Intersección entre dos conjuntos difusos. ... 27

Fig. 2.18 Complemento de conjuntos difusos. ... 28

Fig. 2.19 Diferencia de conjuntos difusos. ... 29

Fig. 2.20 Función de membresía triangular. ... 30

Fig. 2.21 Función de membresía trapezoidal... 30

Fig. 2.22 Función de membresía Gaussiana. ... 31

Fig. 2.23 Controlador difuso. ... 32

Fig. 2.24 Mecanismo de inferencia. ... 35

Fig. 2.25 Ejemplo de fusificación. ... 35

Fig. 2.26 Ejemplo de defusificación. ... 36

Fig. 2.27 Librerias de SimMechanics. ... 38

2.28 Bloque de Body. ... 39

Fig. 2.29 Bloque de Ground. ... 39

Fig. 2.30 Constraints & drives. ... 40

Fig. 2.31 Sensors & actuators. ... 41

(10)

Fig. 2.33 Ventana de Fis Editor. ... 42

Fig. 2.34 Bloque de Fuzzy Logic Controller y Fuction Block Parameters. ... 43

Fig. 3.1 Sistema de coordenadas cartesianas. ... 44

Fig. 3.2 Sistema de coordenadas polares... 45

Fig. 3.3 Sistema de coordenadas en el robot BIOLOID PREMIUM KIT. ... 45

Fig. 3.4 Representación del torso del robot. ... 46

Fig. 3.5 Configuración de Block Parameters del torso. ... 47

Fig. 3.6 Visualización del torso en SimMechanics. ... 47

Fig. 3.7 Bloque Joint Initial Condition. ... 48

Fig. 3.8 Péndulo doble. ... 48

Fig. 3.9 Configuración de Block Parameters del eslabón L1 (brazo derecho). ... 49

Fig. 3.10 Configuración de Block Parameters de la del eslabón L2 (brazo derecho). ... 50

Fig. 3.11 Visualización de la parte superior del robot en SimMechanics. ... 50

Fig. 3.12 Visualización del robot en tres dimensiones en SimMechanics. ... 51

3.13 Visualización de la parte superior del robot en SolidWorks. ... 52

3.14 Visualización del robot en tres dimensiones en SolidWorks... 52

Fig. 3.15 Modelo cinemático del robot. ... 53

Fig. 3.16 Diagrama de control difuso. ... 54

Fig. 3.17 Diagrama de control difuso del torso del robot. ... 54

Fig. 3.18 Antecedentes y consecuentes del controlador difuso. ... 55

3.19 Torso en posición inicial de -50° en SolidWorks. ... 55

Fig. 3.20 Torso en posición inicial de -50°. ... 56

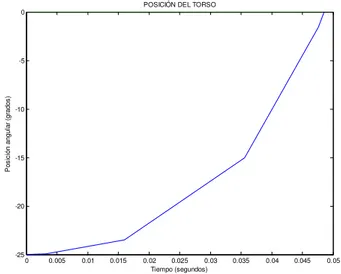
Fig. 3.21 Posición angular del Torso ... 56

Fig. 3.22 Posición angular brazo derecho. ... 57

3.23 Torso en posición inicial de 50° en SolidWorks. ... 57

Fig. 3.24 Torso inicial de 50°. ... 58

Fig. 3.25 Posición angular del torso... 58

Fig. 3.26 Posición angular brazo izquierdo. ... 59

Fig. 3.28Torso en posición inicial de -25°. ... 60

Fig. 3.29Posición angular del torso... 61

Fig. 3.30 Velocidad angular del torso. ... 61

Fig. 3.31 Posición angular del brazo derecho... 62

Fig. 3.33 Torso en posición inicial de -15°. ... 63

(11)

Fig. 3.43 Torso en posición inicial de 5°. ... 68

Fig. 3.48 Torso en posición inicial de 15°... 70

Fig. 3.53 Torso en posición inicial de 25°... 73

Fig. 3.57 Funciones de membresía, entrada1: Posición Angular. ... 75

Fig. 3.58 Funciones de membresía, entrada 2: Velocidad Angular. ... 76

Fig. 3.59 Funciones de membresía, salida1: Torque. ... 76

Fig. 3.60 Interruptor. ... 78

Fig. 3.61 Antecedentes y consecuente del controlador difuso. ... 79

Fig. 3.62 Entrada1: Posición Angular del brazo. ... 80

Fig. 3.63 Entrada 2: Velocidad Angular del brazo. ... 80

Fig. 3.64 Entrada3: Posición Angular del torso... 81

Fig. 3.65 Salida1: Torque. ... 81

Fig. 3.66 Interruptor brazo derecho con control difuso. ... 83

Fig. 3.67 Interruptor brazo izquierdo con control difuso. ... 83

Fig. 4.1 Torso estabilizado a partir de la condición inicial de -25°. ... 84

Fig. 4.2 Posición angular del torso. ... 84

Fig. 4.4 Torque brazo derecho. ... 85

Fig. 4.6 Velocidad angular brazo derecho. ... 86

Fig. 4.7 Simulación con la condición inicial de -18° en el tiempo 0.055095s. ... 87

4.10 Acercamiento de la velocidad angular del torso. ... 88

(12)

Fig. 4.12 Posición del brazo derecho. ... 89

Fig. 4.13 Velocidad del brazo derecho... 90

Fig. 4.14 Simulación con la condición inicial de -13° en el tiempo 0.055095 s. ... 90

Fig. 4.19 Velocidad brazo derecho. ... 93

Fig. 4.20 Simulación con la condición inicial del torso de -8° en el tiempo 0.253 s. ... 93

Fig. 4.25 Velocidad angular brazo derecho. ... 96

Fig. 4.26 Torque brazo izquierdo... 96

Fig. 4.28 Velocidad angular brazo izquierdo. ... 97

4.29 Simulación con la condición inicial del torso de -3° en el tiempo 0.253 s... 98

4.30 Posición angular del torso. ... 98

4.31 Velocidad angular del torso. ... 99

4.32 Torque brazo derecho. ... 99

4.33 Posición brazo derecho. ... 100

4.34 Velocidad brazo derecho. ... 100

4.35 Torque brazo izquierdo... 101

4.36 Posición brazo izquierdo. ... 101

4.37 Velocidad brazo izquierdo. ... 102

4.38 Simulación con la condición inicial del torso de 3° en el tiempo 0.253 s. ... 102

4.39 Posición del torso. ... 103

4.40 Velocidad del torso... 103

Fig. 4.47 Simulación con la condición inicial del torso de 8° en el tiempo 0.253 s. ... 107

(13)

Fig. 4.52 Posición brazo izquierdo. ... 109

Fig. 4.53 Velocidad brazo izquierdo. ... 110

4.57 Simulación con la condición inicial del torso de 13° en el tiempo 0.055095s. ... 112

Fig. 4.60 Torque brazo izquierdo... 113

Fig. 4.63 Simulación con la condición inicial del torso de 18° en el tiempo 0.055095s. .. 115

4.69 Simulación con la condición inicial del torso de 25° en el tiempo 0.055095s ... 118

4.71 Velocidad del torso... 119

4.74 Simulación con la condición inicial del torso de -25° con torque extra en el tiempo 0.055095s ... 120

4.79 Velocidad angular brazo derecho. ... 123

4.80 Simulación con la condición inicial del torso de -18° con torque extra en el tiempo 0.055095s. ... 123

4.84 Posición angular brazo derecho. ... 125

(14)

4.89 Torque del brazo derecho. ... 128

4.99 Posición angular brazo izquierdo. ... 133

4.100 Velocidad angular brazo izquierdo. ... 133

Fig. 4.101 Torso estabilizado a partir de condición inicial del torso de -3° con torque extra. ... 134

Fig. 4.105 Posición brazo derecho. ... 136

Fig. 4.107 Torque brazo izquierdo. ... 137

Fig. 4.110 Torso estabilizado a partir de condición inicial del torso de 3° con torque extra. ... 138

Fig. 4.113 Torque brazo izquierdo. ... 140

Fig. 4.117 Posición brazo derecho. ... 142

4.119Simulación con la condición inicial del torso de 8° con torque extra en el tiempo 0.253s. ... 143

(15)

4.128 Simulación con la condición inicial del torso de 13° con torque extra en el tiempo 0.055095s. ... 147

4.131 Torque brazo izquierdo ... 149

4.132 Posición angular brazo izquierdo. ... 149

4.133 Velocidad angular brazo izquierdo. ... 150

4.137 Torque brazo izquierdo. ... 152

4.138 Posición brazo izquierdo... 152

4.144 Posición brazo izquierdo... 155

4.146 Posición Angular del torso. ... 156

4.149 Simulación con la condición inicial del torso de -3° en el tiempo 0.055095s. ... 157

4.147 Velocidad Angular del brazo. ... 157

4.148 Torque del brazo. ... 157

4.151 Velocidad del torso. ... 158

(16)

Tabla 1.1 Evolución de los prototipos de robots humanoides. ... 7

Tabla 2.1 Información general las aplicaciones de la teoría de sistemas difusos. ... 25

Tabla 2.2 Propiedades de las operaciones difusas. ... 29

Tabla 2.3 Tipos de articulaciones. ... 40

Tabla 3.1 Torques requeridos en los brazos del robot para llevar al torso a 0° a partir de diferentes posiciones angulares iniciales. ... 74

Tabla 3.2 Etiquetas lingüísticas para las funciones de membresía. ... 75

Tabla 3.3 Reglas difusas... 77

Tabla 3.4 Comportamiento de los brazos. ... 79

Tabla 3.5 Etiquetas lingüísticas para las funciones de membresía para el descenso de los brazos... 80

(17)

Θ Posición

Θ̇ Velocidad

Θ̈ Aceleración

( ) Grado de pertenencia

∩ Intersección

∪ Unión

0 Cero

a Aceleración

CAD Diseño Asistido por Computadora

CAM Manufactura Asistida por Computadora

CDM Centro de Masa

CG Centro de Gravedad

COA Centro de Área

CRI Composición de Reglas de Inferencia

CSs Sistemas de Coordenadas

dv Volumen diferencial

e Error

F Fuerza

FAM Memorias Asociativas Difusas

FIS Sistema de Inferencia Difuso

GDL Grado de Libertad

I Inercia

L Lógica proposicional

L1 Eslabón L1

L2 Eslabón L2

m masa

M1 Motor 1

M2 Motor 2

M3 Motor 3

M4 Motor 4

MIMO Múltiples entradas múltiples salidas

MISO Múltiples entradas una salida

NG Negativo Grande

NM Negativo Medio

NP Negativo Pequeño

PG Positivo Grande

PM Positivo Medio

PP Positivo Pequeño

r Referencia

r Vector de posición

S S-norma

T T-norma

u Entrada de control

ui Entradas del mecanismo de inferencia

(18)

ρ Densidad del material

(19)

(20)

(21)

Definición del problema.

El control de los robots industriales y los humanoides es diferente entre sí, la característica que diferencia uno del otro es la naturaleza de su movimiento, ya que el movimiento del humanoide replica el movimiento humano.

Es por esta razón que se busca estabilizar la parte superior humanoide BIOLOID PREMIUN KIT de la compañía ROBOTIS tal como lo hace un ser humano, es decir, cuando existe una perturbación que modifica el estado de reposo, y el cuerpo se desequilibra entran en acción los brazos, en el caso del humanoide se hizo la suposición de que las piernas son inexistentes, partiendo que el torso se encuentra diferentes ángulos con el objetivo de llevarlo al punto de equilibrio de 0° cambiando la posición de los brazos con control difuso y así lograr que se estabilice, identificando además las posiciones en los que no es posible llevarlo al punto de equilibrio con el solo movimiento de los brazos.

Objetivos.

Analizar y diseñar un estabilizador difuso para la parte superior del robot humanoide BIOLOID PREMIUN KIT aplicando control difuso en los brazos.

Modelado del robot Bioloid Premium Kit en Solid Works para obtener las propiedades físicas del robot.

Desarrollo del modelo físico del robot humanoide BIOLOID PREMIUN KIT en SimMechanics con la finalidad de analizar el comportamiento del robot con diferentes posiciones angulares y su comportamiento al introducir diferentes torques en los actuadores ubicados en los brazos del robot.

Aplicación del estabilizador difuso al modelo de SimMechanics para comprobar el funcionamiento del estabilizador sobre el robot.

Justificación.

En la actualidad los robots ocupan un lugar muy importante dentro de la ingeniería y es que la robótica desarrolla en diversos campos. Los robots son utilizados por una diversidad de procesos industriales como lo son: la soldadura de punto y soldadura de arco, pinturas de aerosol, transportación de materiales, molienda de materiales, moldeado en la industria plástica, máquinas-herramientas, entre otros.

(22)

Los robots humanoides son utilizados como una herramienta de investigación en diversas áreas científicas, con la finalidad de entender la estructura y comportamiento del cuerpo humano, por otra parte el intento de simular el cuerpo humano conduce a una mejor comprensión del mismo.

Alcances.

(23)

CAPÍT ULO 1

(24)

Capítulo 1. Estado del arte. 1.1 Introducción.

Cuando se enfrenta un problema en el diseño del control en un proceso físico generalmente se sigue un procedimiento de diseño relativamente sistemático:

1. El desarrollo del modelo dinámico.

2. Diseño del controlador utilizando el modelo matemático.

Básicamente los enfoques tradicionales para el diseño de sistemas control ofrecen una gran variedad de maneras para utilizar la información de los modelos matemáticos y así desarrollar un buen control, por desgracia, cuando se utilizan algunos métodos convencionales y no existe un completo entendimiento de “la planta” esto conduce a la obtención de un modelo matemático erróneo y por lo tanto un controlador no adecuado.

Fig. 1.1 Representación a bloques de un sistema.

El control convencional se basa en modelos matemáticos descritos por ecuaciones diferenciales, resultan simples y fáciles de aplicar en acciones individuales. A medida que aumenta el número de variables, también aumenta su complejidad, tiempo de respuesta y costo computacional.

Para desarrollar el modelo matemático del proceso que será controlado con la finalidad de comprender el problema, existen diferentes procedimientos disponibles. Se pueden utilizar

principios básicos de física para describir un modelo, por ejemplo = , o bien hacer

una “identificación del sistema” a través del uso de datos reales de la planta para producir un modelo del sistema.

A veces, se utiliza un enfoque combinado para escribir una ecuación diferencial que representa el comportamiento de la planta, y después llevar a cabo experimentos en la plata para determinar ciertos parámetros de los modelos.

El modelo matemático se desarrolla para ser lo más preciso posible, pero se debe de Planta

o Proceso

Salida

y

Entrada de Control

(25)

Fig. 1.2 Sistema básico de control.

En la figura 1.2 Se ilustra un sistema básico de control, donde la planta es el objeto que va a ser controlado.

Aunque se considere que el modelo es relativamente preciso a menudo es demasiado complejo para utilizarlo en el desarrollo del controlador, sobre todo cuando se requiere de ciertas restricciones para la planta, es por esta razón que en la práctica los controladores convencionales se han desarrollado a través de modelos simples del comportamiento de las plantas que satisfacen los supuestos necesarios, intentando simplificar el problema.

Fig. 1.3 Sistema básico de control difuso.

A diferencia de los enfoques de control “convencionales” donde la atención se centra en el modelado matemático y el uso de este modelo para la construcción de un controlador que es descrito por las ecuaciones diferenciales, en el control difuso, se centra en profundizar en el conocimiento intuitivo para controlar el proceso[1].

Es importante tomar en cuenta algunas de las características de la lógica difusa.

• Fácil de entender.

• Flexible.

Planta o Proceso Controlador

Medición Entrada de

Control

u

Referencia

r

Salida

y

Controlador Difuso

Planta o Proceso Entrada de

Control

u

Referencia

r

Salida

(26)

• Tolerante con los datos imprecisos.

• Puede modelar funciones no-lineales de complejidad arbitraria.

• Puede ser construido en base a la experiencia de expertos.

• Puede usarse con técnicas de control convencional.

• Se basa en lenguaje natural.

La lógica difusa, se utiliza para la resolución de una variedad de problemas, principalmente los relacionados con control de procesos industriales complejos. Los sistemas de lógica difusa se encuentran presentes en la cotidiana, por ejemplo en robots, cámaras digitales, sistemas de aire acondicionado, lavadoras, etc.

Los sistemas basados en lógica difusa imitan la forma en que toman decisiones los humanos, con la ventaja de ser mucho más rápidos [2].

Por esta razón como principal ventaja, cabe destacar los excelentes resultados que brinda un sistema de control basado en lógica difusa, ya que ofrece salidas de una forma veloz y precisa, disminuyendo así las transiciones de estados fundamentales en el entorno físico que controle.

El uso de la lógica difusa se hace cada vez más extensivo en el campo del control de agentes móviles. La capacidad en tratar con información imprecisa la convierte en una herramienta muy adecuada en el diseño de aplicaciones de control [3].

1.2 Robótica.

La robótica es la ciencia y tecnología de los robots, se ocupa del diseño, manufactura y aplicación de los robots. La robótica combina diversas disciplinas tales como la mecánica, la electrónica, la informática y la ingeniería de control [4,5].

1.2.1 Antecedentes históricos.

Por siglos, el ser humano ha construido máquinas que imitan partes del cuerpo humano. Los antiguos egipcios unieron brazos mecánicos a las estatuas de sus dioses y los griegos construyeron estatuas que operaban con sistemas hidráulicos, los cuales se utilizaban para fascinar a los adoradores de los templos. Durante los siglos XVII y XVIII en Europa fueron construidos muñecos mecánicos tenían algunas características de robots, como moverse de forma autónoma [6].

(27)

La Pianista, es un autómata con forma de mujer que toca el órgano, compuesta por 2.500 piezas podía mover los ojos dirigiendo la mirada del piano a los dedos, inclina el cuerpo, respira y al finalizar cada tema hacía una reverencia.

El Dibujante, está compuesto por unas 2.000 piezas, tiene forma de niño sentado en un pupitre y podía realizar hasta cuatro dibujos distintos.

Fig. 1.4 Escritor automático inventado en 1772 por Pierre Jaquet-Droz.

El más complejo de los autómatas, es “El Escritor”(Figura 1.4), mecanismo compuesto por más de 6.000 piezas, podía escribir utilizando la pluma gracias a una rueda integrada en su mecanismo interno donde se seleccionaban los caracteres uno a uno pudiendo escribir así pequeños textos de unas cuarenta palabras de longitud realizaba movimientos como mojar la tinta y escurrir el sobrante para no manchar el papel, levantar la pluma como si estuviera pensando, respetando los espacios y puntos y aparte, además de seguir con la mirada el papel y la pluma mientras escribe [15].

(28)

Fig. 1.5 Telar de Joseph Jacquard.

Robots totalmente autónomos sólo aparecieron en la segunda mitad del siglo XX.

Son varios los factores que intervienen para que se desarrollaran los primeros robots en la década de los cincuentas.

(29)

Hoy en día los robots industriales y comerciales son utilizados para realizar trabajos de forma más barata y más precisa, también se emplean en trabajos que son peligrosos.

Los robots se usan ampliamente en la fabricación, ensamble, empaque y embalaje, el transporte, exploración, en la medicina, en la industria bélica, la investigación de laboratorio, la seguridad y la producción masiva de bienes de consumo e industriales [8].

En 1973 la compañía KUKA Robot Group desarrolló el primer robot con seis ejes electromecánicos llamándolo “Palletizer”. El robot Palletizer se encuentra en diferentes industrias [9].

Victor Scheinman desarrolló el robot PUMA (Programmable Universal Machine for Assembly, or Programmable Universal Manipulation Arm) en 1975(Figura 1.7) [10].

Fig. 1.7 Robot PUMA de la NASA.

El lanzamiento de un robot capaz de moverse, interactuar con los seres humanos y ayudarles es, sin duda, una de las mayores proezas tecnológicas del siglo XIX.

Honda creó su primer robot bípedo en 1993. El objetivo de Honda es crear un robot humanoide capaz de interactuar con las personas y de ayudarles haciéndoles la vida más fácil y agradable [11].

(30)

Tabla 1.1 Evolución de los prototipos de robots humanoides.

Año Prototipo

1993 Honda Prototype Model 1 (P1). Capaz de apagar y

encender interruptores, agarrar perillas de puertas y llevar objetos.

1996 Honda Prototype Model 2 (P2). Primer robot humanoide

bípedo autorregulable. Camina, sube y baja escaleras y empuja carretillas sin cables.

1997 Honda Prototype Model 3 (P3). Primer robot humanoide

bípedo capaz de andar autónomamente.

1997 HUREL Waseda (Japón). Hadaly-2. Visión, generación

(31)

1998

.

Humanoid Robotics Projects 1. Sofisticada coordinación de las extremidades superiores

2000 Honda ASIMO (acrónimo de "Advanced Step in

Innovative Mobility") tiene 26 grados de libertad. Del año 2000 en adelante han surgido nuevas versiones del humanoide Asimo, incluyendo funcionalidades como reconocimiento facial, incorporación de pulgares opuestos, capacidad para correr, etc., siendo este uno de los robots bípedos mas evolucionado del mundo.

[12]

1.3 Aplicación de la lógica difusa en la robótica.

Al momento de desarrollar un robot se pretende que sea capaz de desenvolverse en un entorno real y que pueda llevar a cabo distintas tareas. Una herramienta muy útil para lograr esto es la lógica difusa, ya que se puede aplicar cuando hay datos imprecisos y en sistemas muy complejos.

Una tendencia actual en el diseño de controladores para robots es el diseño basado en comportamientos, este diseño consiste en dividir las tareas de control en unidades simples [3].

En este proyecto de investigación se muestra cómo la metodología de diseño de control difuso se puede utilizar para la construcción de un estabilizador difuso para una aplicación real como lo es estabilizar el humanoide BIOLOID PREMIUM KIT.

1.4 Desarrollo de la robótica en México.

La difusión de la robótica en México inició a finales de la década de los setenta y se concentró en la en la industria automotriz y en algunas paraestatales como PEMEX y CFE.

(32)

Herramientas de Control Numérico las más utilizadas por sus ventajas frente a las Máquinas Herramienta convencionales y por una reducción de costos[13].

Actualmente la penetración de la robótica en diversos sectores ya es una realidad. Existen diversas aplicaciones a partir del uso de robots, tan diversas, como tareas militares y de seguridad, en el sector salud, en servicios domésticos, en el acceso y exploración de lugares remotos o peligrosos, en la industria manufactura para incrementar la productividad y la eﬁciencia de los factores, en atención de personas con discapacidades, entre otros.

En conjunto, la robótica impulsará el desarrollo de los países que inviertan y se coloquen a

la vanguardia en esta tecnología puesto que va a detonar un importante avance cientíﬁco y

tecnológico en diversas áreas como la mecánica, control, electrónica y computación,

(33)

CAPÍT ULO 2

(34)

Capítulo 2. Marco teórico. 2.1 Robot.

En 1923, el dramaturgo checo Karel Čapek introdujo el término “robot” en su obra RUR

(Robots Universarles de Rossum) para denominar un hombre mecánico.

Un robot es cualquier máquina operada automáticamente que sea usada para efectuar alguna tarea humana. Un robot puede ser definido como una máquina controlada por medio de una computadora y programado para moverse, manipular objetos y realizar trabajos a la vez que interacciona con su entorno [16].

2.1.2 Clasificación de los robots.

Los robots han sido clasificados de acuerdo a su arquitectura (figura 2.1), a su nivel de inteligencia, a su nivel de control, y a su nivel de lenguaje de programación.

Fig. 2.1 Clasificación de los robots por su arquitectura.

Existen distintas clasificaciones para robots, tales como robots industriales, robots móviles, con ruedas y robots móviles con piernas.

Un robot industrial (Figura 2.2) es un manipulador multifuncional reprogramable con varios grados de libertad diseñado para ser utilizado en la producción industrial, los casos

Clasificación de los robots

Robot

industrial Robot móvil

Bípedo

Humanoide

(35)

Fig. 2.2 Robot de paletizado para carga pesada.

Los robots móviles (Figura 2.3) son dispositivos formados por componentes físicos y computacionales dotados de ruedas, orugas o cualquier otro elemento mecánico que les permita desplazarse por un ambiente dinámico, divididos en cuatro subsistemas:

• Locomoción

• Percepción

• Razonamiento

• Comunicación

Fig. 2.3 Robot BR23C.

(36)

Los robots bípedos (Figura 2.4) es un subtipo de robot móvil con piernas, son aquellos robots en los que la locomoción es efectuada por medio de dos piernas. Un bípedo es una cadena cinemática abierta consistente en dos subcadenas llamadas piernas y frecuentemente una subcadena llamada torso, todas conectadas en un punto común llamado cadera

Fig. 2.4 Robot Arsen.

Una subclase de robot bípedo es el robot humanoide (Figura 2.5). Los robots humanoides, son aquellos en el que el diseño físico es semejante a la fisionomía de humana, es decir, pueden poseer piernas, brazos, torso y cabeza, aunque se pueden encontrar algunas formas de robots humanoides con sólo una parte del cuerpo, por ejemplo, la parte superior ó torso [17].

Fig. 2.5 Robot ASIMO.

(37)

El robot humanoide estará formado por una serie de sistemas, cada uno con una función concreta, que son los que le otorgan al conjunto distintas funcionalidades [13], en la figura 2.6 se muestra la estructura de un robot humanoide.

Fig. 2.6 Estructura de un robot humanoide.

2.1.3 Elementos de un robot.

Desde el punto de vista mecánico un robot está formado por una serie de elementos unidos mediante articulaciones las cuales permiten un movimiento relativo entre los eslabones. Cada uno de los movimientos que puede realizar una articulación de forma independiente se denomina grado de libertad. El número de grados libertad de un robot es proporcionado por la suma de los grados de libertad de cada articulación [19].

El movimiento de cada articulación puede ser de desplazamiento, giro, o una combinación de ambos. De este modo son posibles seis tipos diferentes de articulaciones, aunque en la práctica sólo se emplean la de rotación y la prismática (Figura 2.7) [20].

ROBOT

HUMANOIDE

Cuerpo del robot

Sistema de alimentación

Sistema de control

Control remoto Sistema de

visión Sistema de

detección de inclinación

Sistema de detección

(38)

Fig. 2.7 Tipos de articulaciones para un robot.

2.1.3.1 Servomotor.

Un servomotor (Figura 2.8) es un dispositivo similar a un motor de corriente continua que tiene la capacidad de ubicarse en cualquier posición dentro de su rango de operación, y

mantenerse estable en dicha posición.

(39)

2.1.3.2 Actuador.

Los actuadores son los que hacen posible que el robot se mueva según las órdenes dadas por el controlador. Los actuadores utilizados en robótica pueden emplear energía neumática, hidráulica o eléctrica.

2.1.3.3 Sensor.

Para conseguir que un robot realice su tarea de forma adecuada, es necesario que tenga conocimiento tanto de su estado como de su entorno, con esta finalidad, existen sensores internos y externos que miden la posición y velocidad del robot al igual que el ambiente en el que se encuentra [20],[21].

2.1.3.3.1 Sensores internos.

Sensores de posición. Se emplean fundamentalmente para el control de posición angular. Sensores de velocidad. Captan la velocidad, son necesarios para mejorar el

comportamiento dinámico de los actuadores del robot.

Sensores de presencia. Este tipo de sensor es capaz de detectar la presencia de un objeto

dentro de un radio de acción determinado. Esta detección puede hacerse con o sin contacto con el objeto [22].

Fig. 2.9 Tipos de sensores internos de Robots.

Sensores internos

Presencia

Inductivo Capacitivo Efecto Hall Célula Reed

Óptico Ultrasonico

Contacto

Posición

Analógicos

Potenciómetros Resolver

Sincro Inductosyn

LVDT

Digitales

Encoders absolutos Encoders incrementales

Regla óptica

Velocidad

(40)

2.1.3.3.1 Sensores externos.

El empleo de mecanismos de detección exteriores permite a un robot interaccionar con su ambiente de una manera flexible. Esto contrasta con el funcionamiento pre-programado en el que a un robot se le enseña a realizar tareas repetitivas mediante una serie de funciones pre-programadas.

• Sensores táctiles. Son dispositivos que indican el contacto de algún objeto sólido

con ellos mismos. Suelen ser empleados en los extremos de los brazos de robot para controlar la manipulación de objetos.

• Sensores de presencia. Tienen como finalidad determinar la presencia de un objeto

en un intervalo de distancia especificado. Este tipo de sensores se pueden utilizar en relación con la forma de sujetar o evitar un objeto.

• Sensores de alcance. Miden la distancia desde un punto de referencia hasta objetos

que están dentro de un determinado campo de referencia. La detección de alcance se suele usar para esquivar obstáculos [23].

Fig. 2.10 Tipos de sensores internos de Robots.

Sensores externos

Alcance

Triangulación Iluminación

estructural Tiempo de Vuelo

Presencia

Inductivos Capacitivos Efecto Hall Ultrasónicos

Ópticos

Táctiles

(41)

2.2 Dinámica del robot.

La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento que se origina. Por lo tanto, el modelo dinámico de un robot tiene como objetivo conocer la relación entre el movimiento del robot y las fuerzas implicadas en este.

Esta relación se obtiene mediante el denominado modelo dinámico, que relaciona matemáticamente los siguientes puntos.

1. La localización del robot definida por sus variables articulares o por las coordenadas

de localización de su extremo, y sus derivadas: velocidad y aceleración.

2. Las fuerzas pares aplicados en las articulaciones.

3. Los parámetros dimensiónales del robot, como longitud, masa e inercias de sus

elementos [24].

El primer problema es dado por la trayectoria del punto,Θ (posición), Θ̇ (velocidad) y _Θ̈

(aceleración), y se desea encontrar el vector requerido “torque”, τ. El segundo problema es

calcular como se moverá el mecanismo con los torques [25].

2.2.1 Centro de gravedad.

Es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas porciones materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo [26].

2.2.2 Distribución de la masa.

(42)

Fig. 2.11 Descripción del tensor de inercia de la distribución de masa de un objeto, donde el vector AP localiza el elemento de volumen diferencial, dv.

El tensor de inercia puede ser definido en relación a cualquier cuerpo, pero siempre se considera el caso de un tensor de inercia para un cuerpo unido a un cuerpo rígido.

El tensor de inercia del cuerpo {A} es presado en una matriz de 3 × 3.

=

− −

(2.1)

Donde los elementos están dados por:

= ( + ) , (2.2.)

= ( + ) , (2.3)

= ( + ) , (2.4)

= , (2.5)

(43)

En donde el cuerpo rígido está compuesto de elementos de volumen diferencial, dv, contiene la densidad del material ρ.

Los elementos Ixx, Iyy e Izz se llaman momentos de inercia de masas. En cada caso se

integran los elementos de la masa, , multiplicados por los cuadrados de las distancias

perpendiculares al eje correspondiente. Los elementos con índices mezclados se llaman producto de inercia de masas. Este conjunto de seis cantidades independientes dependerá de la posición y orientación del cuerpo. Si se tiene la libertad de elegir la orientación del marco de referencia, es posible hacer que los productos de inercia sean cero.

Los ejes del marco de referencia cuando se encuentran alineados se llaman ejes principales, y los momentos de masas correspondientes son los momentos principales de inercia.

Puntos importantes sobre el tensor de inercia:

1. El producto de la inercia que tiene como índice la coordenada que es normal a la del

plano de simetría será cero.

2. Los momentos de inercia deben de ser siempre positivos.

3. La suma de los tres momentos de inercia es invariante bajo los cambios de

orientación en el marco de referencia. [25]

Tomando en cuenta que la geometría a analizar es compleja se utiliza el programa SolidWorks para obtener el tensor de inercia del torso y brazos del robot Bioloid Premium Kit.

2.2.3 Torque.

El torque también es llamado par o momento de una fuerza, es la tendencia de una fuerza para hacer girar un objeto alrededor de un eje, punto de apoyo o pivote.

En términos generales, es una medida de fuerza de giro sobre un objeto. El símbolo para el torque normalmente es la letra griega tau “τ”. La magnitud del torque depende de tres

cantidades:

• Fuerza aplicada.

• Longitud del brazo de palanca.

• Ángulo entre el vector de la fuerza y el brazo de palanca.

(44)

= × (2.8)

2.2 BIOLOID PREMUM KIT.

Fig. 2.12 Bioloid Premium kit.

Uno de los principales problemas cuando se estudia el comportamiento de un robot humanoide es el modelado de la dinámica del mismo. Esto se debe en gran parte a la gran cantidad de motores que se usan para tratar de simular los puntos móviles del ser humano. Por lo general los robots humanoides que simulan de manera cercana al movimiento real del humano poseen 3 grados de libertad en cada brazo y 6 grados de libertad en cada pierna [17].

Hay muchas cuestiones que implican el desarrollo de un robot humanoide, una de las más complicadas es equilibrar un robot cuando existe movimiento, una de las razones es la que al igual que en los seres humanos, los robots también son afectados por la gravedad [18].

(45)

Fig. 2.13 Distribución de servomotores en el robot Bioloid Premium kit.

En esta tesis se considera sólo parte superior del robot, ya que se desea estabilizar el torso de éste, por lo tanto es posible suponer que las piernas del robot son inexistentes o que siempre poseen una postura rígida.

Aún realizando esta simplificación, el modelo sigue siendo complejo. La siguiente simplificación se realiza tomando los brazos como una estructura rígida, así que se descartan los motores localizados en los codos, semejando su movimiento con el de un péndulo.

2.3 Lógica difusa.

La herramienta matemática de lógica difusa fue introducida por el Dr. Lofti Zadeh en 1965 y es una alternativa a la lógica clásica.

(46)

decisiones, teoría de control, sistemas expertos y redes neuronales. Actualmente, su investigación se centra en la lógica difusa, computación con palabras, y la teoría computacional de nuevo desarrollo de las percepciones y precisiones del lenguaje natural [29].

En un intento de obtener una mayor flexibilidad y una capacidad de manejo más eficaz en el procesamiento de los sistemas mal definidos, el Dr. Zadeh propuso un modelo lingüístico enfocado en el pensamiento humano.

El modelado de un sistema con enfoque lingüístico cuenta con tres características distintivas:

1. El uso de variables lingüísticas en sustitución o complemento a las variables

numéricas.

2. La caracterización de las relaciones entre las variables “SI-ENTONCES” y las

reglas difusas.

3. La formulación de las relaciones complejas de los algoritmos de razonamiento

difuso [30].

La lógica difusa a diferencia de la lógica clásica permite trabajar con información imprecisa y utiliza conceptos de pertenencia parecidos a la manera de pensar humana. Se adapta mejor al mundo real en el que vivimos, ya que provee de un mecanismo para representar los cuantificadores de nuestro lenguaje tales como "mucho", "muy", "un poco", etc. [3].

Hay muchas ideas falsas acerca de la lógica difusa, básicamente la lógica difusa es una lógica precisa de la imprecisión y el razonamiento aproximado, puede ser vista como un intento de mecanización de dos capacidades humanas. Primero la capacidad de conversar, razonar y tomar decisiones racionales en un ambiente de imprecisión, incertidumbre, información incompleta, conflicto de información, parcialidad de la verdad, y en segundo lugar, la capacidad de realizar una amplia variedad de tareas mentales sin ningún tipo de

cálculos [29],[31]. Por lo tanto, la característica central de los sistemas difusos es que se

(47)

2.3.1 Metodología del desarrollo sistemático del modelado de la lógica difusa.

Fig. 2.14 Diagrama de flujo del modelado de un sistema difuso.

Recientemente, las ideas conexiones clásicas han sido refutadas por la nueva teoría de redes neuronales. Esta teoría define cinco principios de cómo es el aprendizaje del cerebro:

1. Un método de aprendizaje en red neuronal debe ser capaz de diseñar una red

adecuada para un problema dado, ya que es una tarea realizada por el cerebro. Una red de pre-diseño nunca debe ser la entrada externa para el método de aprendizaje en redes neuronales, ya que es una entrada externa al cerebro.

2. El método no deberá presentar dificultades aprendizaje caracterizados por

problemas tales como los mínimos locales, oscilación y olvido catastrófico. No es una propiedad de cómputo deseable y no es una propiedad normal del cerebro.

3. El método se debe aprender de forma rápida a partir de sólo unos pocos ejemplos,

como lo hacen los humanos.

4. El método debe ser capaz tanto de diseño y formación una red adecuada en un

tiempo polinómico, el cual es una propiedad de cómputo deseable y tiene su origen en la creencia de que el cerebro no solucionar problemas NP-completos, cuando métodos de aprendizaje más eficaces están disponibles.

5. El método debe ser capaz de generalizar razonablemente de modo que sólo se

utilice una pequeña cantidad de los recursos de la red. Esto significa esencialmente que el método debe hacer un intento explicito de diseñar la red más pequeña

Modelado del sistema difuso

Mecanismo de razonamiento

Sistema de identificación

Identificación de la estructura

Generación de reglas

Selección de entradas y funciones de

membresía

Parámetros de identificación

Ajuste del parámetro de inferencia

Sintonización de las funciones de

(48)

posible. Esta propiedad se basa en la idea de que el cerebro no podría ser un desperdicio de sus recursos [31].

El análisis de los métodos de razonamiento difuso puede dividirse en tres categorías que se superponen: métodos y análisis del razonamiento difuso, el funcionamiento del razonamiento difuso y las aplicaciones del razonamiento difuso.

La primera idea es la composición, esto conduce al método composición de las reglas de inferencia y sus variantes de Zadeh (CRI), la segunda idea es la analogía y similitud y la tercera idea es la interpolación.

El fundamento del razonamiento de la lógica difusa se refiere a los sistemas formales de diversos métodos, no importa que ideas sean adoptadas para determinar los métodos de razonamiento difuso, o en qué áreas se aplica el razonamiento difuso, la filosofía básica del razonamiento difuso es imitar el razonamiento humano y transformar la experiencia humana en términos cuantitativos, de esta manera en la esencia del razonamiento humano puede ser representado en términos matemáticos [32].

2.3.2 Aplicaciones.

La lógica difusa se utiliza cuando proceso en cuestión es muy complejo y no existen modelos matemáticos precisos, para procesos altamente no lineales y cuando se envuelven definiciones y conocimiento no estrictamente definido.

Ejemplos de su aplicación:

• Sistemas de control de acondicionadores de aire.

• Sistemas de foco automático en cámaras fotográficas.

• Electrodomésticos.

• Optimización de sistemas de control industriales.

• Sistemas de escritura.

• Mejora en la eficiencia del uso de combustible en motores.

• Sistemas expertos del conocimiento (simular el comportamiento de un experto

humano).

• Tecnología informática.

(49)

En la tabla 2.1 se presenta información sobre las aplicaciones de sistemas difusos.

Tabla 2.1 Información general las aplicaciones de la teoría de sistemas difusos.

Campo

Clasificación

Administración/ Sociedad

Inteligencia artificial/ información

Ingeniería de control

(1) Modelos

humanos

Planeamiento, evaluación y organización de

las decisiones hechas en las

relaciones humanas.

(2) Imitando la

capacidad humana

Hacer decisiones de sistemas de

soporte para diagnósticos médicos.

Base de datos de sistemas expertos.

Proceso de control de robots.

(3) Interface

humana

Señales/Anuncios para personas con

discapacidad.

Reconocimiento de patrones de voz, letras

y figuras.

(4) Otros Análisis de

predicción de falla.

Predicción de temblores.

Desarrollo de dispositivos de

razonamiento,

(50)

2.1.3 Conjuntos difusos.

Al no contar con datos precisos es necesario hacer una representación matemática de los conjuntos que pueden contener elementos de forma parcial.

Un conjunto difuso es una colección de objetos que pertenecen al mismo grupo, y se mide

la posibilidad de pertenencia a este grupo con un número ( ) llamado grado de

pertenencia.

El grado de pertenencia tiene valores entre 0 y 1, si x es 0 no pertenece a A, si x es 1,

entonces ∈ y si 0 < ( ) < 1, x pertenece a A de forma parcial.

Fig. 2.15 Ejemplo de conjuntos difusos.

2.3.4 Operaciones con conjuntos difusos.

En la teoría de conjuntos difusos se realizan operaciones entre los conjuntos de manera similar que en los conjuntos clásicos, donde se definen también las operaciones de unión, intersección, complemento y diferencia.

2.3.4.1 Unión.

La unión de dos conjuntos A y B, contiene cada elemento que está por lo menos en uno de

ellos [17].

∪ = { | _∈ ó ∈ } _(2.9)

Universo discurso

Conjunto difuso Valor lingüístico

Función de pertenencia

( )

1

0

(51)

Fig. 2.16 Unión entre dos conjuntos difusos.

S-norma: Representa la operación de unión que satisface:

: [0.1] × [0.1] _→ [0.1] (2.10)

∪ ( ) = [ ( ), ( ) ] ∪ ( ) = [1, ( ) + ( ) ]

(2.11) (2.12)

Conmutativa: ( , ) = ( , ) (2.13)

Asociativa: , ( , ) = ( ( , ) ) (2.14)

Monotonía ( , ) _≥ ( , ), _≥ _≥ (2.15)

Condiciones de frontera ( 1,1) = 1, (0, ) = ( ,0) = (2.16)

2.3.4.2 Intersección.

La intersección de dos conjuntos A y B contiene todos los elementos comunes de A y B[17].

∩ = { | _∈ _∈ } (2.17)

Fig. 2.17 Intersección entre dos conjuntos difusos.

T-norma: Generaliza el concepto de intersección.

∪

(52)

: [0.1] × [0.1]_→ [0.1] (2.18)

∩ ( ) = [ ( ), ( ) ] (2.19)

Conmutativa: ( , ) = ( , ) (2.20)

Asociativa: , ( , ) = ( ( , ) ) (2.21)

Monotonía ( , ) ≥ ( , ), ≥ _≥ (2.22)

Condiciones de frontera ( ,1) = (2.23)

[17]

2.3.4.3 Complemento.

El complemento de un conjunto A es el conjunto contiene todos los elementos que no

pertenecen a A [17].

̅( ) = 1− ( ) (2.24)

Para conjuntos difusos:

∪ ̅ ≠ (2.25)

∩ ̅ ≠0 (2.26)

(53)

2.3.4.4 Diferencia.

Fig. 2.19 Diferencia de conjuntos difusos.

La diferencia simétrica de dos conjuntos A y B donde todos los elementos que pertenecen a A o a B, pero no a ambos a la vez.

| = { | _∈ _∉ } (2.27)

2.3.5 Propiedades de las operaciones difusas.

La lógica difusa es la lógica de la imprecisión, las fórmulas de la lógica difusa no son sólo verdaderas o falsas sino también pueden ser parcialmente verdaderas. Las matemáticas en la lógica difusa son un sistema formal como la lógica clásica, en donde el estándar del dominio de los grados de verdad es un intervalo de [0,1], sólo que en la lógica difusa tiene más de dos posibilidades [38].

Las operaciones difusas tienen diferentes propiedades como se puede observar en la tabla 2.2.

Tabla 2.2 Propiedades de las operaciones difusas.

Involución ₌

Conmutativa ∪ = ∪ ∩ = ∩

Asociativa ( ∪ ) ∪ = ∪( ∪ ) ( ∩ )∩ = ∩( ∩ ) Distributiva ∩( ∪ ) = ( ∩ )

∪( _∩ ) ∪

( _∩ ) = ( _∪ ) ∩( _∪ )

(54)

2.4 Tipos de funciones de membresía.

Las formas de las funciones de membresía más típicas son: triangular, trapezoidal y Gaussiana.

2.4.1 Función de membresía triangular.

Se especifica mediante tres parámetros {a, b, c}

Fig. 2.20 Función de membresía triangular.

( : , , )

0

( ₋ ) (_⁄ ₋ )

< ≤ ≤ ( ₋ ) (_⁄ ₋ ) _{≤ ≤}

0 >

(2.28)

2.4.2 Función de membresía trapezoidal.

Se especifica mediante cuatro parámetros {a, b, c, d}

Fig. 2.21 Función de membresía trapezoidal.

1

0

( )

a b c d 1

0

a b c

(55)

( : , , , )

⎩ ⎪ ⎨ ⎪

⎧₍ ₋ _{) (}0_⁄ ₋ ₎ _≤< _< 1

( ₋ ) (_⁄ ₋ ) _{≤ ≤}≤ ≤

0 _≥

(2.29)

2.4.3 Función de membresía Gaussiana.

Se especifica mediante dos parámetros {m, σ}, que denotan el centro y el ancho de la

función, respectivamente.

Fig. 2.22 Función de membresía Gaussiana.

( : , ) = ₋( − ) (2.30)

2.5 Control difuso.

Los controladores clásicos son diseñados con varias técnicas de aplicaciones de sistemas de control, el control difuso se basa en el conocimiento humano [28].

El controlador difuso está compuesto por los siguientes elementos:

1. Base de reglas ( If – Then “Si – Entonces”).

2. Mecanismo de inferencia.

3. Interface de Fusificación.

(56)

Fig. 2.23 Controlador difuso.

La capacidad de la toma de decisiones del modelo difuso depende de la existencia de la base de reglas y del mecanismo de razonamiento difuso. En general, el conocimiento codificado de múltiples entradas y múltiples salidas (MIMO “Multi-Input Multi-Output”) de un sistema puede ser interpretado por los modelos difusos que consisten en reglas Si- Entonces, con múltiples antecedentes y múltiples consecuentes. Un sistema con múltiples salidas independientes puede ser considerado como varios grupos de sistemas de salidas individuales por separado, en consecuencia, la estructura general de un sistema difuso MIMO también se puede representar como un conjunto de múltiples entradas y una sola salida (MISO “Multi-Input Single-Output”). En conclusión la estructura de un sistema difuso MIMO se puede representar con un conjunto de sistemas difusos MISO, aunque se incrementaría el numero de reglas en el nuevo sistema, el modelado es más sencillo [30].

2.5.1 Base de reglas.

La descripción lingüística es desarrollada por un experto, en ella se usan “variables lingüísticas” que describen la variación con respecto al tiempo de las entradas y salidas.

Se utiliza la cuantificación lingüística para crear un conjunto de reglas que capturan el conocimiento del experto acerca de cómo controlar la planta.

El control difuso describe el algoritmo del proceso de control como la relación difusa entre la información acerca de la condición del proceso que será controlado, suponiendo que “x” y “y” son las entradas del proceso y “z”. El algoritmo de control está dado en expresiones “Si – Entonces” como:

Referencia entrada r(t)

Base de

conocimiento Base de _reglas

Fusificación Mecanismo de Defusificación inferencia

Proceso Entrada

u(t)

Salida y(t)

(57)

Las expresiones no sólo incluyen aquellos atributos como pequeño, grande, etc., también incluyen conexiones como si (and) y o (or) [34].

Estas expresiones son conocidas como reglas de control difuso. La condición “Si” es llamada antecedente y el “Entonces” consecuente, la colección de estas reglas a origen a una memoria asociativa difusa conocida como FAM por sus siglas en ingles (Fuzzy Associative Memories).

El universo de discurso de un controlador difuso está pre-definido y cada universo de discurso contiene los conjuntos difusos. Cada conjunto difuso permite que los miembros tengan diferentes grados de membresía, cada uno se encuentra expresado por un número en el intervalo [0,1].

Un subconjunto difuso F del universo de discurso A tiene la función de membresía : _→[0,1] el cual determina el grado de membresía de m(a) en [0,1]. Los tres operadores que operan en los conjuntos difusos A, B de A son:

µ _∩ = min( µ , µ ) : Mínimo (2.31)

µ _∪ = max( µ , µ ) : Máximo (2.32)

µ = 1₋µ : Complemento o cambio de A (2.33)

Las variables difusas que se usan son cuantificadas como Positivo Pequeño, Positivo Medio, Positivo Grande, Cero, Negativo Pequeño, Negativo Medio y Negativo Grande [28].

2.5.2 Mecanismo de inferencia.

El mecanismo de inferencia también llamado “motor de inferencia” o “módulo de inferencia difusa” determina que regla es relevante en cada situación caracterizada por los conjuntos difusos de entrada y genera la salida correspondiente al hacer una interpretación y aplicación del conocimiento del experto acerca de cómo es mejor el control de la planta.

El mecanismo de inferencia tiene dos tareas:

1) Determinando la extensión de cada regla, es relevante ver la situación presente

caracterizada por las entradas , = 1,2,…, .

2) Dibujando las conclusiones usando las entradas ui y la información en la base de

reglas. Para emparentarlas hay que notar que × × … × es el conjunto

difuso representando la premisa de la regla ( , ,…, ; , ) (pueden haber más

de una regla con esta premisa).[1]

(58)

2.5.2.1 Método de inferencia Mamdani.

El método de inferencia difusa Mamdani es el más utilizado en la metodología difusa. Fue propuesto en 1975 por Ebrahim Mamdani como un intento de controlar una máquina de vapor y una caldera mediante la síntesis de un conjunto de reglas de control lingüísticas obtenidas de experimentados operadores [39].

Considerando que existen muchas aplicaciones a la teoría de conjuntos difusos, en este caso, la sintaxis usada en un controlador difuso se aplica en un proceso dinámico. El controlador difuso es análogo al controlador proporcional más el controlador integral.

Para la implementación de las reglas heurísticas usando este método, la fuente de mayor dificultad, es la calidad de las decisiones [35].

Una lógica proposicionalL es determinada en conjunto por una sintaxis, una semántica y

un mecanismo de inferencia [36].

2.5.2.2 Método de inferencia Sugeno.

Las reglas de la base de conocimiento del sistema Sugeno son diferentes a las de los sistemas Mamdani pues el consecuente de estas reglas ya no es una etiqueta lingüística si no es una función de la entrada que tenga el sistema.

En los sistemas Sugeno, los valores de los consecuentes de las diferentes reglas se que se activan en un momento determinado son valores numéricos por lo que no se necesita de la “defusificación” [40].

2.5.2.3 Sistemas difusos de inferencia.

(59)

Fig. 2.24 Mecanismo de inferencia.

2.5.2.4 Interface de fusificación.

Fig. 2.25 Ejemplo de fusificación.

La fusificación es donde el controlador convierte las entradas numéricas en datos difusos que el mecanismo de inferencia puede interpretar fácilmente para aplicar las reglas.

En la fusificación asignan grados de pertenencia a cada una de las variables de entrada con relación a los conjuntos difusos previamente definidos utilizando las funciones de pertenencia asociadas con los conjuntos difusas [40].

Entradas son números limitados

a un rango específico (no

difusas)

Todas las reglas son evaluadas en paralelo usando

razonamiento difuso

El resultado de las reglas es convinado y

desifucado

El resultado es un número (no

difuso)

Entrada 1

Entrada 2

Regla 1

Regla 2

Regla 3

Σ

Salida 1

A B µ

(60)

2.5.2.3 Interface de defusificación.

Fig. 2.26 Ejemplo de defusificación.

La defusificación es el proceso donde se convierten las conclusiones del mecanismo de inferencia en las salidas del proceso.

En la defusificación al momento de escoger una salida concreta a partir de tanta premisa difusa, el método más usado es el del centroide, en el que la salida final será el centro de gravedad del área total resultante [39].

Existen diferentes tipos de métodos defusificación que pueden ser usados para obtener una salida nítida, por ejemplo, centroide, promedio máximo, promedio ponderado y del medio máximo. Para todos estos métodos de defusificación, el conjunto reglas juegan un papel importante [34].

El método del centroide es el más utilizado por los ingenieros de control, este método también es conocido como Centro de Área (COA “Center Of Area”). Este método calcula el centro de gravedad del polígono que se generó en la inferencia [40].

2.6 MATLAB.

Los ingenieros y científicos se valen de la computadora para resolver diversos problemas, desde la evaluación de una función sencilla hasta la resolución de un sistema de ecuaciones. MATLAB se ha convertido en un entorno de computación técnica preferido de muchos ingenieros y científicos porque es un sistema interactivo único que incluye cómputo numérico, cómputo simbólico y. visualización científica [41].

MATLAB tiene varias ventajas:

• Fácil de aprender y usar.

• Potente, flexible y extensible.

• Preciso, robusto y rápido.