Implementation en C/C++ du protocole D'attribute based encryption en utilizant les couplages asymetriques

Mémoire présenté

pour l’obtention du Diplôme de Master Mathématiques et

Applications Ingénierie Mathématique

Parcours Codage Cryptographie Sécurité

Le 16 Septembre 2011

Par : ZAVATTONI Eric

Titre : IMPLEMENTATION EN C/C++ DU PROTOCOLE D'ATTRIBUTE BASED ENCRYPTION EN UTILISANT LES COUPLAGES ASYMETRIQUES

Confidentialité : AUCUNE

Composition du jury des mémoires :

Membres du jury I.S.F.A. Entreprise :CINVESTAV

M. AUGROS Jean-Claude Centro de investigación y de estudios avanzados del Instututo Politécnico Nacional de México

M. CONESA François Avenida Instituto Politécnico Nacional No. 2508 C.P. 07300 MEXICO D.F.

M. GERARD Yves Tuteur entreprise :

M. RODRIGUEZ-HENRÍQUEZ Francisco

Invité : Secrétariat :

UFR DE MATHEMATIQUES

43, Boulevard du 11 Novembre 1918 - 69622 VILLEURBANNE CEDEX et

INSTITUT DE SCIENCE FINANCIERE ET D’ASSURANCES Domaine Scientifique de Gerland

Université Claude Bernard LYON 1 et Institut de Science Financière et

d’Assurance

Centro de Investigación y de Estudios Avanzados del Instituto

Politécnico Nacional Departamiento de computación

Implémentation en C/C++, du protocole

Attribute-Based Encryption , en utilisant les

couplages asymétriques

par :

Eric Zavattoni

eric.zavattoni@etu.univ-lyon1.fr

Maitre de stage :

Dr. Francisco Rodríguez Henríquez

Tuteur universitaire :

Résumé

Implémentation en C/C++, du protocole Attribute-Based Encryption , en utilisant les couplages asymétriques

Eric Zavattoni

MASTER 2 - MAIM - IR - CCS, Septembre 2011 Maître de stage : Dr. Francisco Rodríguez-Henríquez

La première utlisation des couplages dans la cryptographie avait pour but l’attaque d’un cryptosystème, il permettait de transférer le problème du logarithme discret sur les courbes elliptiques au problème du logarithme discret sur les corps finis. La première application a été l’attaque MOV (Menezes A., Okamoto T. and Vanstone S.A.) en 1993, de nos jours les proprits remarquables des fonctions de couplage ont permis la création de nouveaux protocoles cryptographiques, mon travail durant ce stage à été d’implémenter de manière efficiente le protocole d’Attribute-Based Encryption présenté dans les articles [BSW07] ainsi que d’en optimiser son exécution aux niveau de ses 4 étapes qui sont : Setup, Encrypt, KeyGen, Decrypt. Mon implémentation à été effectuée pour une sécurité de 128 bits et utilise les propriétés des courbes Barreto-Naehrig .

Abstract

Implementation of a C library, for the Attribute-Based Encryption , using asymetric pairings

Eric Zavattoni

MASTER 2 - MAIM - IR - CCS, September 2011 Supervisor : Dr. Francisco Rodrìguez-Henrìquez

The first use of pairings in cryptography was an attack against cryptosystems, the prop-erties of the pairing function allow to transfer the elliptic curve discret logarithm problem (ECDLP) to the descret logarithm problem over finite fields. The first application was the MOV attack (Menezes A., Okamoto T. and Vanstone S.A.) in1993 nowadays the remar-quable properties of pairing functions allow the creation of new cryptographic schemes, during this internship, my work consisted in the efficient implementation of the Attribute-Based Encryption scheme explained in the paper [BSW07] as well as the optimization of the 4 steps : Setup, Encrypt, Keygen, Decrypt. My implementation had been done for 128 bits of security and using Barreto-Naehrig curves properties.

Attribute-Based Encryption I

Organisme d’accueil

Le Cinvestav a été créé par un décret présidentiel publié par le président Adolfo Lopez Mateos, le 17 avril 1961, et modifié par le président José López Portillo le 17 Septembre 1982. En conformité avec les dispositions du décret, le Cinvestav est un organisme public décentralisé de la personnalité juridique et de son propre patrimoine.

Pour exercer ses fonctions, le gouvernement fédéral donne une subvention annuelle. Outre la subvention, l’institution est soutenue par des contributions provenant de sources di-verses : agences décentralisées, des institutions étrangères, l’industrie et les particuliers. Les objectifs fondamentaux que le Cinvestav poursuit sont :

Les enseignants et la préparation spécialisée des chercheurs afin de promouvoir l’améliora-tion constante de l’éducal’améliora-tion et créer les condil’améliora-tions pour réaliser des recherches originales dans les domaines scientifiques et technologiques pour élever le niveau de vie et le déve-loppement du pays. Le Centre est composé 28 départements universitaires organisés dans 9 campus, deux d’entre eux sont dans la ville de Mexico et 7 sont réparties dans tout le pays. Les domaines dans lesquels les recherches sont effectuées sont variés et je préfère me référer au site internet du centre [CIN11]

Maître de stage

Durant ce stage de 5 mois et demi, j’ai eu le privilège de tra-vailler avec le Docteur Francisco Rodríguez-Henríquez, il m’a permis de découvrir le milieu de la recherche en cryptogra-phie et réaliser que les avancées scientifiques dans ce domaine, tant au niveau implémentation que nouveaux protocoles, sont légions chaque années . . .

II

Remerciements

Je tiens tout d’abord remercier deux personnes sans qui ma venue au Mexique n’aurait pas été possible : Jonathan Taverne (aka “El Cebolla”) qui a été le premier à se lancer dans l’aventure mexicaine l’année dernière lors de son stage de fin d’études réalisé ici au Cinvestav ainsi que mon tuteur de stage, le docteur Francisco Rodríguez-Henríquez qui m’a permis de travailler dans ce centre d’investigation et de découvrir le milieu de la recherche en cryptographie.

De l’autre côté du monde, je remercie également les docteurs Denis Clot et Yves Gérard pour leur investissement dans ma formation universitaire ainsi que Mme Marie-Christine Brunet pour sa patience et son aide qui a facilité ma venue ici.

Je tiens tout particulièrement à dire un grand merci à ma p’tite femme, “Tu vois, finalement, c’est passé vite”

Enfin skype jajaja

Table des matières

Introduction 2

1 Travail réalisé 3

1.1 Motivation du projet . . . 3

1.2 Objectifs . . . 3

1.3 Organisation du rapport . . . 3

2 Outils cryptographiques 5 2.1 Courbes elliptiques . . . 5

2.1.1 Introduction . . . 5

2.1.2 Représentation . . . 5

2.1.3 Vocabulaire . . . 6

2.1.4 Les courbes elliptiques Barreto-Naehring . . . 6

2.2 Fonctions de hachage . . . 6

2.2.1 Définition . . . 6

2.2.2 Propriétés . . . 7

2.2.3 De chaine de caractères à point sur la courbe elliptique . . . 7

2.3 Les couplages . . . 7

2.3.1 Visualisation . . . 7

2.3.2 Implementation . . . 8

2.3.3 Securité . . . 8

3 Le protocole 10 3.1 CP-ABE . . . 10

3.1.1 L’idée . . . 10

3.1.2 Les étapes . . . 10

3.2 Application du protocole CP-ABE . . . 12

3.2.1 Utilisation . . . 12

3.2.2 Résultats . . . 12

4 Implémentation 13 4.1 Objectifs . . . 13

4.1.1 Les travaux existants . . . 13

4.1.2 Paramètres d’implémentation . . . 13

Attribute-Based Encryption 1

4.2 Implémentation avec Magma . . . 14

4.2.1 Présentation du logiciel . . . 14

4.2.2 Utilisation . . . 14

4.3 Implémentation en C . . . 14

4.3.1 Fonction de hachage . . . 14

4.3.2 Fonction de couplage . . . 14

4.3.3 Résultats . . . 14

Conclusion 15

A SAC Toronto 16

Introduction

blabla du debut

Chapitre

1

Travail réalisé

1.1

Motivation du projet

L’implémentation efficiente d’un protocole cryptographique utilisant les couplages re-présente un challenge passionant. Les propriétés des fonctions de couplages ouvrent des grandes opportunités cryptographiques mais leur conditions d’utilisation imposent de grandes contraintes qu’il a fallut apprendre à gérer tout au long de ce stage.

Implémenter le protocole d’Attribute-Based Encryption ainsi qu’effectuer des modifi-cations pour l’adapter aux couplages assymétriques me permet de manipuler un large éventail d’outils cryptographique tels que les coubres elliptiques, les couplages ou encore les fonctions de hachage. Réaliser un tel projet permet aussi de créer une application utilisant un protocole encore peu connu et peu utilisé de nos jours et qui peut se révéler très utile dans beaucoup de domaines dont l’échange de données doit être sécurisée et accessible pour un groupe d’individus pré-défini.

1.2

Objectifs

Le but de mon stage à été, dans un premier temps, de fournir une implémentation, grâce au logiciel Magma, du protocole d’Attribute-Based Encryption permettant l’accès à des données chiffrées pour les individus possèdant les attributs passant la structure d’accès liée aux données chiffrées puis, une fois le protocole viable, m’interesser à l’efficience de mon implémentation en utilisant un langage plus performant : le C/C++. Le but final étant d’aboutir à un temps d’éxecution des différentes étapes du protocole pouvant rivaliser avec les papiers existant [Bet07, Sco11]

1.3

Organisation du rapport

Ce rapport de stage s’organise de la manère suivante, le chapitre 1 sert d’introduction et prsésente l’une manière globale la motivation et les objectifs de mon travail réalisé ici au Cinvestav, puis dans un second chapitre je fournis les éléments cryptographiques élémentaires indispensables pour la réalisation de ce projet. Le chapitre 3 présente le protocole prsésenté par J. Bethencourt et al. dans l’article [BSW07] implementation et

4 CHAPITRE 1. TRAVAIL RÉALISÉ

resultats

Chapitre

2

Outils cryptographiques

2.1

Courbes elliptiques

2.1.1

Introduction

Une courbe elliptique est une courbe algèbrique particulière. Elle possède une loi d’addition géométrique pour laquelle l’élément neutre est un point à l’infini noté O. Une courbe elliptique et sa loi associée forment un groupe. La première utilisation de ces courbes en cryptographie est due aux travaux de V.S.Miller, il propose alors pour la première fois d’appliquer un protocole cryptographique, l’échange de clés Diffie-Hellman, sur les courbes elliptiques. En effet, les différents protocoles cryptographiques sur les groupes finis peuvent être mis en place sur de telles courbes. L’avantage principal est, que pour un même niveau de sécurité, la taille des éléments utilisés sur une courbe elliptique est plus petite que dans le cas des corps finis.

2.1.2

Représentation

Une courbe elliptiqueE définie sur un corpsK, est une courbe lisse définie par l’équa-tion :

E :y2+a1xy+a3y=x+a2x2+a4x+a6, a1, a2, a3, a4, a5, a6 ∈K

Une courbe est dite lisse si et seulement si ∆6= 0, où ∆ = ∆(E) est la discriminant deE défini par :

          

∆ =−d2

2d8−8d34−27d26+ 9d2d4d6

d2 =a21+ 4a2

d4 = 2a4+a1a3

d6 =a23+ 4a6

d8 =a21a6 + 4a2a6−a1a3a4+a2a23−a24

L’ensemble des point K-rationnels de E, notéE(K) est défini par :

E(K) = {(x, y)∈K2 | y2+a1xy+a3y=x3+a2x2+a4x+a6} ∪ {O}

oùO est la point à l’infini.

6 CHAPITRE 2. OUTILS CRYPTOGRAPHIQUES

2.1.3

Vocabulaire

Il est important de définir quelques notions importantes liées aux courbes elliptiques telles que :

♣ Ordre de la courbe : Soit E une courbe ellitpique définie sur un corps fini F_q. L’ordre de E surF_{q est le nombre d’él’ements de E(}F_{q), noté #E(}F_q)

♣ Ordre d’un point : C’est le plus petit entier k tel que kP = O. Autrement dit le plus petit nombre de fois qu’il faut additionner un pointP avec lui même pour obtenir le zéro de la courbe.

♣ Degré de plongement de la courbe : Soit un sous-groupe de points d’ordre r définis sur une courbe elliptique E(F_{q), la définition standard du degré de plongement k} de la courbe est que k est le plus petit entier tel que :r|qk_−1.

2.1.4

Les courbes elliptiques Barreto-Naehring

En qui concerne la recherche sur les protocoles cryptographiques, l’introduction des courbes elliptiques a permis d’explorer de nouvelles constructions utilisant des couplages, c’est-à-dire des applications bilinéaires particulières.

Les couplages asymétriques utilisés dans mon implémentation utilisent une classe particulière de courbes elliptiques appelées courbes BN qui sont définies par l’équation suivante :

E(F_{p) :y}2 _=x3_{+b, avec b6= 0}

Le degré de plongement k de la courbe est égal à 12

p(z) = 36z4_{+ 36z}3_{+ 24z}2_{+ 6z+ 1}

r(z) = 36z4_{+ 36z}3_{+ 18z}2_{+ 6z+ 1}

z = 2158₋₂128₋₂68_{+ 1}

2.2

Fonctions de hachage

2.2.1

Définition

Une fonction de hachage h est une fonction qui, à partir d’une donnée (document, fichier) de taille quelconque, calcule une chaîne de bitsh(x)d’une taille fixée (m) nommée empreinte (ou haché).

h:{0,1}∗ _{→ {0,1}}m x 7→ h(x)

On ajoute souvent la condition supplémentaire que l’empreinte doit être facile à calculer : ∀x∈ {0,1}∗_{, h(x) facile à calculer.}

De plus, associée à la donnéex, l’empreinte h(x)doit permettre le contrôle d’intègrité du document.

Attribute-Based Encryption 7

2.2.2

Propriétés

Pour un usage cryptographique, une fonction de hachage doit satisfaire les propriétés suivantes :

♣ Résistance au calcul de préimage : pour presque tout y ∈ h({0,1}∗_{), il doit}

être calculatoirement difficile de trouver x∈ {0,1}∗ _{tel que h(x=y).}

♣ Résistance au calcul de seconde préimage : étant donné x ∈ {0,1}∗_{, il doit}

être calculatoirement difficile de trouver x′ _{6=x tel que h(x) = h(x}′₎

Une fonction de hachage satisfaisant ces deux conditions est dite à sens unique, ou “One Way Hash Function” (OWHF)

2.2.3

De chaine de caractères à point sur la courbe elliptique

2.3

Les couplages

2.3.1

Visualisation

Le schéma suivant fournit l’idée du fonctionnement d’une fonction de couplage :

Fonction de couplage (e)

e(P, Q)∈G_T

Q∈G₂ P ∈G₁

Illustration d’un couplage

Plus formellement, un couplage nécessite un environnement bilinéaire que nous définissons comme suit :

Definition 1. Soient G_1,G_2,G_{T trois groupes cycliques d’ordre premier p. Un couplage}

(admissible) est une application e : G_1×G_{2 →}G_{T ayant les trois propriétés suivantes :} Calculable : Pour tout (x, y)∈ G_1×G_{2 , il existe un algorithme efficace pour calculer} e(x, y).

Bilinéaire : Pour tout (x, y)∈G_1×G_{2, et tout (a, b)∈}Z2

p, e(xa, yb) =e(x, y)ab.

Non-dégénérée : Il existe g1 générateur deG1 etg2 générateur deG2 tel que e(g1, g2)6=

1T soit un générateur de GT .

8 CHAPITRE 2. OUTILS CRYPTOGRAPHIQUES

2.3.2

Implementation

Boucle de Miller

Etape 2.3.1 Boucle de miller

Entrée: r,P ∈G_{1, Q∈}G₂

Sortie: fr,P(Q)

1: T ←P 2: f1 ←1

3: Pouri :=n-1 à 0 faire

4: T ←[2]T 5: f1 ←f12×

l1(Q) 1

v1(Q) 2

6: Si ni = 1 Alors

7: T ←T +P 8: f1 ←f1× l2(Q)

3

v2(Q) 4

9: Fin Si 10: Fin Pour 11: Renvoyer f1

Exponentiation finale

Tower Extension Field Arithmetic [BDM+_{10] page 4}

2.3.3

Securité

La sécurité d’un protocole cryptographique repose souvent sur la difficulté de résolu-tion du problème du logarithme discret. Le niveau de sécurité est défini par le nombre d’opérations nécessaires sur le corps de base pour réussir une attaque de logarithme dis-cret. Il est donné en bits, et nous utilisons pour le définir la notion de sécurité équivalente. Par exemple, nous parlons d’un niveau de sécurité de 80 bits s’il faut au minimum 280

opérations pour résoudre le problème du logarithme discret sur les groupes en considéra-tion.

1. l_{1 équation de la tangente au point T}

2. v_{1équation de la droite verticale au point [2]T}

3. l_{2 équation de la droite (TP)}

4. v_{2équation de la droite verticale au point T + P}

Attribute-Based Encryption 9 Niveau de sécurité Taille du sous- Taille du groupe Degré de plongement k

(en bits) groupe r (en bits) étendu qk _{(en bits) ρ≈1 ρ≈2}

80 160 960-1280 6-8 2*,3-4

112 224 2200-3600 10-16 5-8

128 256 3000-5000 12-20 6-10

192 384 8000-10000 20-26 10-13

256 512 14000-18000 28-36 14-14

Table _{2.1 – Taille (en bits) des paramètres des courbes elliptiques et de leur degré} de plongement correspondant pour obtenir le niveau de sécurité désiré (Tableau issu de [FST06]).

Chapitre

3

Le protocole

3.1

Cyphertext-Policy ABE [

BSW07

]

3.1.1

L’idée

Dans le protocole “CP-ABE”, le message est chiffré avec une structure d’accès qui définie quels sont les utilisateurs pouvant accéder au message clair. Les attributs que possèdent un utlisateur servent à définir sa clé privée et si ces attributs passent la structure d’accès, le message clair est obtenu. La principale propriété du protocole “CP-ABE” est sa résistance contre les collusions, ainsi deux ou plusieurs utilisateurs ne peuvent, en unissant leur clé privée, passer la structure d’accès si, individuellement, aucun d’eux ne possède les attributs pour la passer

3.1.2

Les étapes

Le protocole “CP-ABE” est composé de cinq algorithmes fondamentaux : Initialisa-tion, Chiffrement, Génération de clé, Délégation1

et Déchiffrage.

La première étape du protocole est donc l’initialisation au cours de laquelle la clef pu-blique P K et la clef secrète M K sont produites de la manière suivante :

Etape 3.1.1 Initialisation

Entrée: Paramètre de sécurité implicite :k

Sortie: Clé Publique P K et une Clé Principale M K

1: Choisir un groupe bilinéaire G_{0 d’ordre premier r avec un générateur g}

2: Choisir deux exposant aléatoire α, β ∈Z_{r, puis :}

3: Renvoyer P K = (G_{0, g, h=g}β_{, f =g}1/β_{, e(g, g)}α₎

4: Renvoyer M K = (β, gα₎

La partie chiffrement comporte 2 éléments importants, le message à chiffrer M et la structure d’accèsA_{qui définira les droits d’accès au texte clair. Une fois ces deux éléments}

1. L’algorithme Délégation n’a pas été implémenté dans la librairie [Bet07]

Attribute-Based Encryption 11 fournis par l’utilisateur, le programme exécute l’algorithme suivant :

Etape 3.1.2 Chiffrement

Entrée: P K,M K, Structure d’accèsT

Sortie: Texte chiffréCT

1: Paramètrer les polynômes qx correspondants à chaque noeuds de l’arbre T

2: Renvoyer CT = (T,C˜ = M e(g, g)αs_{, C = h}s_{,∀y ∈ Y : C}

y = gqy(0), Cy′ = H(att(y))qy(0)₎

Dans le protocole d’Attribute-Based Encryption , un utilisateur est défini par ses attributs, se sont eux qui vont déterminer ses droits d’accés à tel ou tel message chiffré, lors de la création de sa clef privée, l’utilisateur va donc fournir l’ensemble des attributs le définissant à la partie de confiance afin d’obtenir sa clef de session.

Etape 3.1.3 Création de la clé

Entrée: M K et un ensembleS d’attributs servant à décrire l’utilisateur

Sortie: Une clé privéeSK

1: Choisir au hasard : r ∈Z_{p, et rj ∈}Z_{p ∀j ∈S puis :}

2: Renvoyer SK = (D=g(α+r)/β_{,∀j ∈S :D}

j =gr·H(j)rj, D′j =grj)

Le déchiffrage se déroule de la manière suivante, un utilisateur fournit sa clef privée puis obtient le message M si et seulement si ses attributs passent la structure d’accès T.

Etape 3.1.4 Déchiffrage

Entrée: P K,CT (qui contient la politique d’accès A_{), SK (pour S)}

Sortie: SiS satisfait A_⇒M

1: DecryptNode(CT,SK,x)([BSW07], p.6) 2: Si S passes T Alors

3: Renvoyer C/(e(C, D)/A) = ˜˜ C/(e(hs_{, g}(α+r)/β_{)/e(g, g)}rs_{) =M}

4: Sinon

5: Renvoyer Vous n’avez pas les attributs nécessaires pour accèder à M

6: Fin Si

La propriété de l’algorithme nommé Délégation est de pouvoir, à partir d’une clef privée SK créée avec le jeu d’attributs S, créer une sous-clef formée d’un jeu d’attribut

˜ S ⊆S

Etape 3.1.5 Délégation

Entrée: SK (pour S) et S˜⊆S

Sortie: _SK˜ _{(pour S}˜₎

1: Renvoyer SK˜ = ( ˜D=Dfr˜_{,∀k ∈S˜: ˜D}

k =Dkg˜rH(k)r˜k,D˜′_k=Dk′gr˜k)

12 CHAPITRE 3. LE PROTOCOLE

3.2

Application du protocole CP-ABE [

Bet07

]

3.2.1

Utilisation

Les différentes commandes se font via un terminal, dans un premier temps on initie les paramètres en appelant “cpabe-setup”, ce qui fournit les clés publique et principale du protocole, ensuite on est libre d’encrypter n’importe quelle donnée via la commande “cpabe-enc”, il suffit de fournir les clés générées par la première étapes puis de paramètrer un arbre d’accès qui définira qui pourra déchiffrer le message encrypté. On peut ensuite générer les clés de chaque individu via la commande “cpabe-keygen” suivie de la clé prin-cipale et des attributs de l’utilisateur. Enfin, on peut décrypter le message en fournissant une clé d’utilisateur et la clé publique. Si les attributs de l’utilisateur passent l’arbre d’accès lié au texte chiffré alors, on obtient le message initial, sinon un message s’affiche expliquant que les attributs ne sont pas suffisant pour accèder au message.

Terminal :

eric@linux-john :~> cpabe-setup

eric@linux-john :~> cpabe-enc pub_key data '(cinvestav or UCBL) and (computacion)' eric@linux-john :~> cpabe-keygen -o eric_key pub_key master_key UCBL computacion eric@linux-john :~> cpabe-dec pub_key eric_key data.cpabe

3.2.2

Résultats

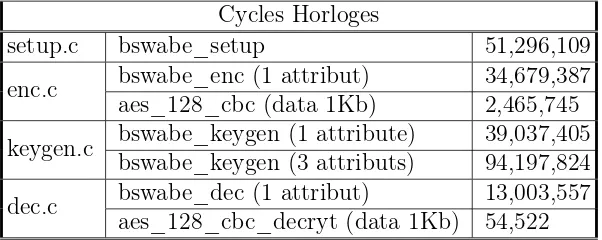
Ce tableau fournit les performances de la librairie de Bethencourt [Bet07], je me suis interressé aux temps d’exécution des fonctions de chiffrages et de déchiffrage utilisées dans ce protocole :

Cycles Horloges

setup.c bswabe_setup 51,296,109

enc.c bswabe_enc (1 attribut) 34,679,387 aes_128_cbc (data 1Kb) 2,465,745

keygen.c bswabe_keygen (1 attribute) 39,037,405 bswabe_keygen (3 attributs) 94,197,824

dec.c bswabe_dec (1 attribut) 13,003,557 aes_128_cbc_decryt (data 1Kb) 54,522

Table _{3.1 – La bibliothèque CP-ABE}

Chapitre

4

Implémentation

4.1

Objectifs

4.1.1

Les travaux existants

Implémentation Bethencourt ou celle de Scott [Bet07, Sco11]

4.1.2

Paramètres d’implémentation

Voici l’implementation du r-ate pairing présenté dans l’article [BDM+_10]

Etape 4.1.1 Couplage Ate optimal sur les courbes Barreto-Naehrig

Entrée: P ∈G_{1, Q∈}G₂

Sortie: aopt(Q, P)

1: écrire s= 6t+ 2 commes =PL−1

i=0 si2i, où si ∈ {−1,0,1}; 2: T ←Q f ←1;

3: Pouri=L−2 à0 faire

4: f ←f2 _·l

T,T(P); T ←2T ;

5: Si si =−1 Alors

6: f ←f ·lT,−Q(P); T ←T −Q;

7: Sinon Si si = 1 Alors

8: f ←f ·lT,Q(P); T ←T +Q;

9: Fin Si 10: Fin Pour

11: Q1 ←πp(Q);Q2 ←πp2(Q);

12: f ←f ·lT,Q1(P); T ←T +Q1;

13: f ←f ·lT,−Q2(P); T ←T −Q2;

14: f ←f(p12_−1)/r

;

15: Renvoyer f;

14 CHAPITRE 4. IMPLÉMENTATION

4.2

Implémentation avec Magma

4.2.1

Présentation du logiciel

Magma est un logiciel conçu pour les calculs algèbriques,la théorie des nombres, la géométrie algébrique et combinatoire. Il fournit un environnement mathématique per-mettant de travailler avec des structures telles que les groupes, les anneaux, les algèbres, les courbes elliptiques et bien d’autres. Magma soutient également un certain nombre de bases de données conçues pour aider la recherche computationnelle dans les domaines mathématiques. Ceci donne un résumé des principales caractéristiques de Magma.

Un des objectifs de développement tout en Magma est de maintenir une documenta-tion complète décrivant les caractéristiques du système.

Magma est distribué par le département d’algèbre computationnelle de l’Université de Sydney.

4.2.2

Utilisation

L’implémentation avec le logiciel Magma a donc été mon premier travail réalisé ici, le but de cette première implémentation n’a pas été l’efficacité mais simplement la fonc-tionalité ainsi que l’ajout de l’algorithme délégation et de la partie “merging pairings” énoncées dans [Bet07]. Cette étape m’a été bien utile pour la compréhension de tous les aspect du protocole Attribute-Based Encryption ainsi que les problèmes rencontrés lors du passage de la théorie à la pratique.

4.3

Implémentation en C

4.3.1

Fonction de hachage

4.3.2

Fonction de couplage

4.3.3

Résultats

Conclusion

blabla de fin

Annexe

A

SAC Toronto

blabla sac

Bibliographie

[BDM+_{10] Jean-Luc Beuchat, Jorge Enrique González Díaz, Shigeo Mitsunari, Eiji}

Oka-moto, Francisco Rodríguez-Henríquez, and Tadanori Teruya. High-speed soft-ware implementation of the optimal ate pairing over barreto-naehrig curves. Cryptology ePrint Archive, Report 2010/354, 2010. http://eprint.iacr. org/.

[Bet07] J. Bethencourt. Cyphertext-policy attribute-based encryption library, 2007.

http://acsc.cs.utexas.edu.cpabe/.

[BSW07] J. Bethencourt, A. Sahai, and B. Waters. Cyhertext-policy attribute-based encryption. Proceedings of the 2007 IEEE Symposium on Security and Pri-vacy, pages 321–334, 2007.

[CIN11] CINVESTAV. domaines de recherche, 2011. http://www.cinvestav.mx/

Investigaci%C3%B3n/L%C3%ADneasdeinvestigaci%C3%B3n.aspx.

[FST06] David Freeman, Michael Scott, and Edlyn Teske. A taxonomy of pairing-friendly elliptic curves. Cryptology ePrint Archive, Report 2006/372, 2006.

http://eprint.iacr.org/.

[Sco11] Michael Scott. On the efficient implementation of pairing-based protocols. Cryptology ePrint Archive, Report 2011/334, 2011. http://eprint.iacr. org/.