Control predictivo basado en modelo aplicado a una planta de evaporación de la Industria Azucarera

Texto completo

(1)Universidad Central “Marta Abreu” de Las Villas Facultad de Ingeniería Eléctrica Departamento de Automática y Sistemas Computacionales. TRABAJO DE DIPLOMA “Control Predictivo Basado en Modelo Aplicado a una Planta de Evaporación de la Industria Azucarera” Autor: Osvaldo Wilfredo Ortega García.. Tutores: Dr. Miguel Ángel Rodríguez Borroto. Ing. Orlando Urquijo Pascual Santa Clara 2014 “Año 56 de la Revolución”.

(2) Universidad Central “Marta Abreu” de Las Villas Facultad de Ingeniería Eléctrica Departamento de Automática y Sistemas Computacionales. TRABAJO DE DIPLOMA “Control Predictivo Basado en Modelo Aplicado a una Planta de Evaporación de la Industria Azucarera” Autor: Osvaldo Wilfredo Ortega García. Email: oortega@uclv.edu.cu Tutor: Dr. Miguel Ángel Rodríguez Borroto. Dpto. de Automática, Facultad de Ing. Eléctrica, UCLV. Email: marodrig@uclv.edu.cu Tutor: Ing. Orlando Urquijo Pascual. Dpto. de Automática, Facultad de Ing. Eléctrica, UCLV. Email: ourquijo@uclv.edu.cu Santa Clara 2014 “Año 55 de la Revolución”.

(3) Hago constar que el presente trabajo de diploma fue realizado en la Universidad Central “Marta Abreu” de Las Villas como parte de la culminación de estudios de la especialidad de Ingeniería en Automática, autorizando a que el mismo sea utilizado por la Institución, para los fines que estime conveniente, tanto de forma parcial como total y que además no podrá ser presentado en eventos, ni publicados sin autorización de la Universidad.. Autor: Osvaldo Wilfredo Ortega García Los abajo firmantes certificamos que el presente trabajo ha sido realizado según acuerdo de la dirección de nuestro centro y el mismo cumple con los requisitos que debe tener un trabajo de esta envergadura referido a la temática señalada.. Firma del Autor. Firma del Jefe de Departamento Dr.C.. Osvaldo Wilfredo Ortega García. Boris Luis Martínez Jiménez. Firma del Responsable de Información Científico-Técnica.

(4) PENSAMIENTO. “Aquel que no ha fracasado es porque nunca ha intentado algo nuevo, En momentos de crisis, sólo la imaginación es más importante que el conocimiento”. A. Einstein. i.

(5) DEDICATORIA. A. todos los que de una forma u otra creyeron en mí y me apoyaron para llegar hasta aquí.. E. specialmente mi madre y a mi abuela por su. apoyo constante y por estar siempre a mi lado incondicionalmente.. sin. ustedes nunca lo hubiera logrado. ii.

(6) AGRADECIMIENTOS. n momentos culminantes siempre miro atrás y pienso en todas las personas que me han ayudado a llegar donde estoy, en cuán diferente sería todo si no hubiesen dejado su marca sobre mí y como nunca tendré la oportunidad de agradecerles suficiente por ello.. Por eso aprovecho este espacio para agradecer: toda Mi familia en especial a tío Kiko, tía Dignora y mi segunda madre: Rosy, por siempre tener los brazos abiertos para recibirme con un abraso y un beso, a ellos les debo gran parte de lo que soy. Mis. vecinos. en especial. a. mi tía. Tata. por. alentarme siempre a seguir adelante y apoyarme en todo el camino. mis amigos de siempre en especial a los que han compartido conmigo estos últimos cinco años, somos y seguiremos siendo la sals. todos los profesores que me han brindado sus enseñanzas. y. educación,. impartieron clases. en. desde. primaria. los hasta. que. me. los del. Departamento de Automática de la UCLV, porque creo modestamente que pueden estar orgullosos de lo que he logrado. En especial a Urquijo por no decir nunca que no a nadie, no cambies. He tratado de ser lo más general posible si se me queda alguien no se lo tomen personal es porque no tengo tiempo para más.. iii.

(7) RESUMEN El presente trabajo se concibe con el objetivo de diseñar un Controlador Predictivo Basado en Modelo de una planta de evaporación de la industria azucarera y evaluar las prestaciones que tendría, comparándolas con las alcanzadas utilizando una estructura de control PID multivariable. A partir de un modelo dinámico en espacio estado de la planta y consideraciones adoptadas, se obtiene el modelo de predicción mediante la técnica de identificación experimental. Este modelo es formulado como un primer orden con retardo, pues se considera que sus parámetros definen perfectamente las particularidades de la planta de evaporación escogida como caso de estudio. A partir del modelo identificado se procede a sintonizar los reguladores a partir de dos estrategias de control fundamentalmente, la primera, típica para este tipo de plantas, en base a la estructura PID multivariable, y la otra basada en el método de control predictivo. Finalmente se simulan los sistemas de control diseñados para observar los resultados del comportamiento transitorio de las variables de salida ante cambios en los valores de consigna. Los resultados de la comparación de estas respuestas transitorias muestran un mejor comportamiento utilizando el Controlador Predictivo Basado en Modelo de la planta de evaporación.. iv.

(8) TABLA DE CONTENIDOS Contenido. PENSAMIENTO ............................................................................................................................ i DEDICATORIA .............................................................................................................................ii AGRADECIMIENTOS ................................................................................................................. iii RESUMEN .................................................................................................................................iv TABLA DE CONTENIDOS ......................................................................................................... v Introducción ................................................................................................................................. 1 Hipótesis ..........................................................................................................................4 Objetivos ..........................................................................................................................4 Objetivo general ...........................................................................................................5 Objetivos específicos ....................................................................................................5 Capítulo 1:. Fundamentos Teóricos del Proceso de Evaporación y del Control Predictivo. ...... 7. 1.1. La Industria Azucarera ...........................................................................................7. 1.2. El Proceso de Producción de Azúcar ......................................................................7. 1.3. El Proceso de Evaporación .....................................................................................8. 1.3.1 Conceptualización y funcionamiento ....................................................................8 1.3.2 Evaporadores de calandria (tipo Robert).............................................................10 1.3.3 Antecedentes del modelado y control de plantas de evaporación ........................11 1.4. El Control Predictivo ............................................................................................14. 1.5. Estrategias del MPC .............................................................................................15. 1.6. Elementos Básicos del MPC .................................................................................17. 1.6.1 Modelo de predicción .........................................................................................17 1.6.2 Función objetivo ................................................................................................18 1.6.3 Obtención de la ley de control ............................................................................19 1.7. Historia, Evolución y Perspectiva Futura del Control Predictivo ...........................19. 1.8. Antecedentes del Control Predictivo en Plantas de Evaporación ...........................23. 1.9. Conclusiones Parciales .........................................................................................25. v.

(9) Capítulo 2: 2.1. Modelo Matemático de la Planta de Evaporación. Identificación y Validación ... 26. Modelo Matemático .............................................................................................26. 2.1.1 Modelo matemático de un evaporador simple efecto ..........................................27 2.1.2 Modelo en el espacio de estados.........................................................................28 2.1.3 Caso de estudio ..................................................................................................31 2.2. Identificación del Sistema ....................................................................................32. 2.2.1 Consideraciones para llevar a cabo la identificación ...........................................34 2.2.2 Identificación del modelo de la planta objeto de estudio .....................................37 2.2.3 Validación del modelo identificado ....................................................................40 El porciento de ajuste ..................................................................................................40 Comprobación física del modelo .................................................................................41 2.3. Conclusiones Parciales .........................................................................................43. Capítulo 3: 3.1. Control de la Planta de Evaporación ..................................................................... 44. Control PID Multivariable ....................................................................................44. 3.1.1 Método de las ganancias relativas ......................................................................45 3.1.2 Síntesis de los reguladores .................................................................................47 3.1.3 Síntesis de desacopladores .................................................................................49 3.2. Diseño del Controlador Predictivo ........................................................................51. 3.2.1 Interfaz de usuario para el diseño del Controlador Predictivo .............................52 3.3. Comparación entre los Sistemas de Control Diseñados .........................................56. 3.3.1 Evaluación de las estrategias de control sintetizadas ...........................................57 3.4. Conclusiones Parciales .........................................................................................59. Conclusiones y Recomendaciones ............................................................................................... 61 Conclusiones ..................................................................................................................61 Recomendaciones ...........................................................................................................62 Referencias Bibliográficas............................................................................................................ 63 ANEXOS. ............................................................................................................................... 67. Anexo I: Generalidades del proceso de producción de azúcar .........................................67 Anexo II: Ecuaciones que describen el comportamiento del evaporador .........................70. vi.

(10)  Linealización...................................................................................................75. Anexo III: Códigos y Modelos ........................................................................................77. vii.

(11) INTRODUCCIÓN. Introducción El azúcar es un producto natural, cuyo nombre técnico es sacarosa. La sacarosa se encuentra en forma natural en algunas plantas; entre las más conocidas está la caña de azúcar que es la materia prima principal de la industria azucarera. El procesamiento de la misma es llevado a cabo en los centrales azucareros, donde a través de una serie de procesos la sacarosa disuelta en el jugo de caña clarificado es concentrada, y se convierte en pequeños cristales de azúcar. El proceso de fabricación de azúcar consta de varias etapas entre las que se destacan: molienda, clarificación, evaporación, cristalización, separación, refino, secado y envasado (Kung, 2002). Siendo el sub-proceso de evaporación el sistema objeto de investigación del siguiente trabajo. La evaporación es una operación empleada para remover agua en forma de vapor de las soluciones líquidas diluidas para obtener un producto concentrado. Esta operación requiere de un evaporador o varios evaporadores dispuestos en serie, los cuales se ajustan a las características fisicoquímicas de la materia prima y del producto terminado requerido. En este sentido es de señalar que este proceso en la industria azucarera es fundamental y juega un valioso papel en la calidad del producto final. En él las variables del sistema: concentración, temperatura, presión y nivel en las distintas etapas deben ser fielmente controladas para obtener a la salida una meladura de calidad y con el mayor ahorro de energía posible en el proceso. El proceso de concentración por evaporación puede ser representado haciendo uso del modelado matemático con la finalidad de facilitar su comprensión, estas técnicas han sido completamente integradas al área de los procesos químicos y como una forma de estimación de parámetros y estudio de diversas situaciones. El control de este proceso reviste una gran importancia desde el punto de vista del desarrollo de productos de calidad y del ahorro de energía, especialmente en la industria azucarera. Sin embargo, se trata de una planta de múltiples entradas y múltiples salidas (MIMO por sus siglas en inglés) con una dinámica compleja para la cual se han realizado diversos intentos por obtener modelos confiables de su desempeño, tanto estacionario como dinámico.. 1.

(12) INTRODUCCIÓN. Una gran proporción de la energía utilizada en la industria es empleada en procesos de secado, los evaporadores juegan un rol importante en el secado industrial de una gran cantidad de productos. Un control preciso de los evaporadores conlleva directamente a un mejor control en procesos subsiguientes, lo que implica una mayor eficiencia energética y una buena calidad del producto final (Russell, Bakker, y otros, 2000). Casi todas las estrategias conocidas hasta el presente para este tipo de plantas están basadas en la estructura clásica de controladores proporcional-integral-derivativo (PID) multivariable con desacoplamiento, las cuales no son capaces de eliminar completamente las consecuencias de los fenómenos que afectan la respuesta transitoria de este sistema como son las fuertes interacciones entre las distintas variables del proceso, retardos significativos, tendencia a la inestabilidad en lazo abierto y severas no linealidades que presenta el proceso (Bordons, 2000). Por ello, y fundamentado en las probadas prestaciones que presentan las modernas estrategias computacionales basadas en el modelo y que se conocen como Control Predictivo Basado en Modelo (Rodríguez, 2008-2009) (identificado por las siglas MBPC o MPC del inglés Model Based Predictive Control o simplemente Model Predictive Control), este trabajo pretende develar las posibilidades de estos métodos para controlar el proceso tecnológico en cuestión. El MPC constituye un campo muy amplio de métodos de control desarrollados en torno a ciertas ideas comunes e integra diversas disciplinas como control óptimo, control estocástico, control de procesos con retardos, control multivariable y control con restricciones. Aunque en un principio se vio limitado, principalmente porque la velocidad de procesamiento de las computadoras de la época no era la adecuada para manejar el cúmulo de datos que significaban estos algoritmos, pero ya en las últimas décadas esto no es un inconveniente y aunque no se prevé que en ningún momento cercano sustituya a los métodos clásicos sí se puede presentar como una opción muy atractiva e innovadora para el control de procesos industriales multivariables. Esto se debe fundamentalmente a que su estructura interna es sustentada en un proceso de optimización que permite predecir el desempeño futuro de las variables de la planta y sus señales de control, basándose fundamentalmente en el conocimiento de las variables que caracterizan el proceso (Rodríguez y León, 2002).. 2.

(13) INTRODUCCIÓN. El Control Predictivo presenta una serie de ventajas:  Se aplica a una gran variedad de procesos, desde las dinámicas más simples hasta las más complejas, incluyendo sistemas con respuesta inversa, grandes retardos y sistemas no estacionarios.  Es particularmente atractivo para practicantes, aún con limitados conocimientos de teoría del control porque es muy intuitivo y de fácil sintonía.  Permite introducir compensaciones por adelanto de la señal de una manera natural para eliminar las perturbaciones.  Permite la compensación del retardo automáticamente y se extiende al caso multivariable de una manera simple.  Es un método totalmente abierto, basado en principios que permiten futuros desarrollos. Desventajas del MBPC:  Su desarrollo e implementación computacional es más complejo que en el clásico PID.  En el control adaptativo todos los cálculos tienen que ser realizados en cada período de muestreo, aunque la dinámica no cambie.  Requiere de un modelo apropiado para ser usado como predictor provocando falta de sistematicidad en cuanto a la robustez de su estabilidad. El esfuerzo y el tiempo de diseño para la estrategia de control en que se basa el MBPC, se emplea principalmente en la obtención del modelo dinámico del proceso. El mismo permite confeccionar el predictor dedicado a evaluar el comportamiento futuro de dicho sistema, y en base a este comportamiento predecir la señal de control futura. Los controladores predictivos permiten tratar problemas complejos de forma óptima, utilizando una serie de parámetros cuyo significado es fácil de comprender y para los que existen reglas de selección que hacen relativamente sencilla la sintonía del controlador MBPC. Una buena selección de estos parámetros, garantiza la efectividad y robustez del control para el evaporador. Todo lo anterior justifica la idea de utilizar esta estrategia para controlar una planta de. 3.

(14) INTRODUCCIÓN. evaporación. Teniendo en cuenta los criterios que se pretenden satisfacer con este trabajo, el caso de estudio seleccionado corresponde a una planta de evaporación operando en simple efecto, ya que el trabajo con el modelado resultará más sencillo, facilitando así la evaluación del desempeño del MBPC. Esto no crea ningún inconveniente para en próximas etapas de investigación extender este estudio a las plantas que operan en múltiple efecto, las cuales son mucho más comunes en las industrias. Con este proyecto se pretende contribuir al desarrollo de la industria azucarera del país, mostrando las potencialidades reales de las técnicas de control predictivo basado en modelo para ser aplicadas en las plantas de evaporación pertenecientes a dicho ambiente industrial. Con esto se posibilita la optimización de este proceso en diferentes aspectos, lo que trae aparejada la reducción de los costos de producción en una de las áreas más importantes para la obtención de un producto final de calidad. Los resultados de esta investigación poseen una aplicación práctica y teórica para todos los especialistas de la industria azucarera, ya que ofrece las novedosas técnicas del control predictivo aplicadas a una planta de evaporación, como una alternativa viable para lograr la optimización de dicho proceso. El diseño de un Controlador Predictivo Basado en Modelo de una Planta de Evaporación perteneciente a la industria azucarera, constituirá una herramienta importante en manos de especialistas e investigadores, en función de aumentar la eficiencia y confiabilidad de una unidad de evaporación real.. Hipótesis Teniendo en cuenta todo lo planteado anteriormente se puede plantear como hipótesis de esta investigación que: La síntesis de un Controlador Predictivo Basado en Modelo de una planta de evaporación de la industria azucarera brindará la posibilidad de mejorar el desempeño y control de las principales variables del proceso en relación a estrategias de control convencionales.. Objetivos Para llevar a cabo el desarrollo de esta tesis se hace necesario fijar los objetivos que guíen y. 4.

(15) INTRODUCCIÓN. enfoquen el trabajo para lograr una metodología adecuada. Objetivo general Sintetizar un Controlador Predictivo Basado en el Modelo de una planta de evaporación de la industria azucarera, con el propósito de mejorar el desempeño y la eficiencia de estos sistemas. Objetivos específicos  Desarrollar un estudio investigativo del proceso de evaporación unitaria de la industria azucarera y de las técnicas modernas de control predictivo basado en modelo.  Estudiar el desempeño de los controladores MPC en los diferentes trabajos consultados, donde se utilizan para el control de procesos industriales multivariables en general y del proceso de evaporación en particular.  Obtener el modelo dinámico de una planta de evaporación unitaria con el propósito de su utilización como modelo de predicción en la estrategia de control predictivo basado en modelo.  Sintetizar una estrategia de Control Predictivo para la planta seleccionada como caso de estudio, que cumpla con las especificaciones de desempeño necesarias para el correcto funcionamiento del sistema.  Evaluar el sistema bajo diferentes regímenes de excitación a través de simulación y comparar con los resultados obtenidos utilizando los métodos clásicos de control, aplicados a la planta objeto de estudio.. Organización del informe Capítulo I: Se realiza un análisis de los fundamentos teóricos del proceso de evaporación y del control predictivo basado en modelo. Capítulo II: Abarca todo lo relacionado con la obtención del modelo de predicción a utilizar para el diseño del Controlador Predictivo Basado en el Modelo de la planta de evaporación. Capítulo III: Está dedicado al diseño del controlador predictivo y de una estrategia de 5.

(16) INTRODUCCIÓN. control en base a PID multivariable para contrastar el desempeño del mismo. Se realiza además, la simulación y evaluación del desempeño del sistema.. 6.

(17) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. Capítulo 1: Fundamentos Teóricos del Proceso de Evaporación y del Control Predictivo. En este capítulo se realiza un análisis crítico de la literatura especializada consultada. Se presentan las principales metodologías que constituyen eje de la investigación sobre el control predictivo y sobre el proceso de evaporación, introduciendo algunos temas relacionados con las principales interioridades del proceso de producción de azúcar. Se plantea la panorámica general existente en torno al control del proceso de evaporación y se exponen estrategias que se usan con este propósito en la actualidad.. 1.1 La Industria Azucarera El azúcar se consume en todo el mundo, puesto que es una de los principales endulzantes en las dietas de todos los países que puede obtenerse principalmente a partir de la caña de azúcar y la remolacha azucarera. Debido a esta demanda, el azúcar es uno de los productos de mayor importancia para el desarrollo comercial principalmente de países con economías emergentes, como India y Brasil, que son actualmente de los principales productores y para los cuales representa un renglón de producción muy importante. Por otra parte, la industria azucarera está muy vinculada al desarrollo de Cuba, esta esfera fue hasta los años 90’ del pasado siglo el principal renglón de la economía, situándola en varios momentos de la historia como el principal exportador de azúcar del mundo, lo que sin dudas impulsó y sostuvo el desarrollo económico desde los últimos siglos de dominación colonial hasta los primeros años de Revolución. Aunque evidentemente ha perdido la importancia de antaño, la producción azucarera sigue siendo una de las principales esferas industriales, por lo que su modernización, en pos de la búsqueda incesante de mayor calidad, productividad y eficiencia del proceso, es aún una prioridad en el sector.. 1.2 El Proceso de producción de azúcar La caña de azúcar (Saccharum officinarum L), es un pasto gigante tropical, rico en azúcar, el cual es sintetizado durante la fotosíntesis. De manera general, la caña contiene una parte. 7.

(18) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. sólida llamada fibra (11-16%) y una parte líquida formada principalmente por agua (7376%) y azúcares simples, sacarosa, glucosa y fructosa (8-15%) (Kung, 2002). La producción de azúcar a partir de la caña se basa en la posibilidad de cristalizar la sacarosa desde un espeso jarabe, obtenido mediante la concentración del jugo de la caña en el proceso de evaporación; mientras la glucosa y la fructosa permanecen disueltas. Para la obtención final de azúcar se requiere de un largo proceso, desde que la semilla de caña germina hasta que el azúcar es comercializada. Un bosquejo muy general del proceso de producción de azúcar se puede apreciar en el Anexo I.. 1.3 El Proceso de Evaporación Uno de los procesos más importantes que se deben llevar a cabo para la obtención final de un producto de calidad en la industria azucarera es la eliminación del exceso de agua contenido en el jugo crudo elevando su concentración de sacarosa, todo esto se lleva a cabo en el proceso de evaporación. Debido a que la optimización de este proceso es el objetivo principal de este trabajo, es necesario profundizar en este tema, exponiendo así sus particularidades y utilidades no solo en la industria azucarera, haciendo énfasis en los principales trabajos que discuten el funcionamiento y el control de este proceso. 1.3.1 Conceptualización y funcionamiento del proceso de evaporación Se comprende por evaporación al proceso en el cual se lleva a cabo el aumento de concentración en una solución, compuesta de un líquido que se denomina solvente y uno o varios solutos sólidos disueltos en dicho solvente, los cuales son prácticamente no volátiles a la temperatura de operación, la cual es la temperatura de ebullición del solvente a la presión de operación. Esta separación se realiza por medio de la adición de calor a la solución, para llevarla a la temperatura de ebullición, de modo que el solvente se volatilice y los solutos permanezcan en la solución, aumentando así la concentración de los mismos. Desde el punto de vista químico se define como una operación unitaria física (Geankoplis, 2005). Se llaman operaciones unitarias a cada una de las acciones necesarias de transporte, adecuación y transformación de la materia en un proceso químico. Los procesos químicos. 8.

(19) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. en general y cada operación unitaria en particular tienen como objetivo modificar las condiciones de una determinada cantidad de materia según ciertos requerimientos. Por definición, las operaciones unitarias físicas son aquellas donde se realiza ya sea transporte de cantidad de movimiento, transferencia de materia, transferencia de energía o transmisión simultánea de materia y energía (Geankoplis, 2005). Es así que la evaporación entra en esta categoría, pues en la misma no se espera que ocurra reacción química y se rige por la transferencia de calor (intercambio de energía), producto de una diferencia de temperatura. La forma más usual en la cual se adiciona calor a un sistema de evaporación es la condensación de vapor de agua de un lado de alguna superficie de contacto, de modo que el calor de la condensación o latente, que es mucho mayor que el calor requerido para el aumento de temperatura de la solución, o calor sensible, sea transferido según los postulados de Reynolds en tres fases: desde el fluido caliente a la superficie metálica, por convección; a través de la superficie metálica, por conducción; y desde la superficie metálica al fluido a calentar, por convección. El calor transportado entre la superficie y el fluido es proporcional a la velocidad con que las partículas se mueven y se difunden, que dependerá de la difusión natural cuando el fluido está en reposo y de los remolinos causados por movimientos que lo mezclan reponiendo continuamente nuevas partículas sobre la superficie, que son proporcionales a la densidad del fluido y a la velocidad de dicho movimiento respecto a la superficie de transferencia. En el caso específico del proceso de evaporación, donde se desea concentrar un líquido, mediante la evaporación de cierta cantidad de agua; el intercambiador de calor recibe el nombre de evaporador, los cuales constituyen una de las estaciones más importantes en los centrales azucareros, ya que en estos equipos se remueve cerca del 80% del agua contenida en el jugo clarificado. Para dicho fin es usada típicamente una configuración de evaporadores en quíntuple o cuádruple efecto, dependiendo del diseño de la planta. La operación es relativamente sencilla debido a que se fijan las condiciones de entrada, salida, nivel de cada evaporador y extracción de vapores hacia el exterior de ser el caso. El jugo entra al primer evaporador y se calienta hasta el punto de ebullición. Al comenzar a bullir. 9.

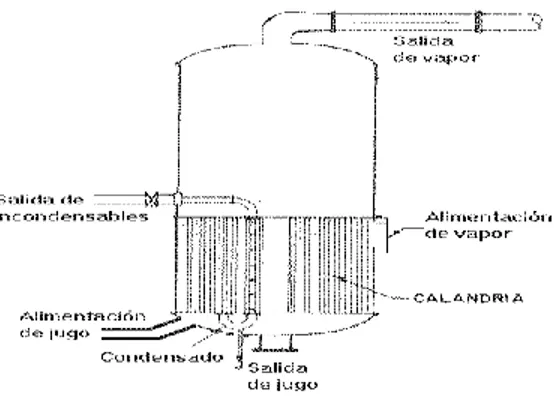
(20) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. se generan vapores los cuales se reutilizan en el siguiente efecto, logrando así el menor punto de ebullición en cada evaporador y una considerable eficiencia. El jugo pasa de un evaporador a otro con bombas denominadas de transferencia. El funcionamiento global de un evaporador se ejecuta a través de la estabilización de siete variables fundamentales: la concentración del producto final, la presión absoluta en el último cuerpo, la alimentación de vapor y jugo al primer evaporador, remoción de condensados y gases, el control de nivel en los vasos de cada evaporador, y el control de incrustación en cada evaporador.. 1.3.2 Evaporadores de calandria (tipo Robert) Los evaporadores tipo Roberts o de calandria (Figura 1.1) son los más utilizados en la industria azucarera, en ellos el vapor y el jugo se encuentran en cámaras separadas que fluyen en el mismo sentido. Este tipo de evaporadores consisten en un haz de tubos verticales, cortos, colocados entre dos espejos que se replican en las bridas del cuerpo del evaporador, recibiendo todo ese conjunto el nombre de calandria. Este consta de una carcasa donde condensa vapor y de una cámara de separación donde tiene lugar la ebullición de la solución a concentrar, la cual, al perder solvente aumenta su proporción de soluto. El vapor fluye por fuera de los tubos en la calandria, habiendo un gran paso circular de derrame en el centro del haz de tubos donde el líquido más frío recircula hacia la parte inferior de los tubos. Dentro de los tubos se produce la evaporación parcial y el producto que está siendo concentrado permanece en íntimo contacto con el vapor que se genera. Los dos fluidos, tanto el producto como su vapor, tienen igual sentido de flujo, por lo que la salida de ambos es por la parte inferior de los tubos, donde se produce la separación de estas dos fases.. Figura 1.1: Esquema de un evaporador tipo Robert o de calandria. 10.

(21) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. El concentrado es tomado por bombas y el vapor se envía al condensador (en un simple efecto), mientras que los sistemas multiefecto utilizan como medio calefactor el vapor generado en el efecto anterior, y por lo tanto el vapor generado en el último cuerpo es el que se envía al condensado. Este tipo de evaporadores son los más difundidos en la industria alimenticia por las ventajas operacionales y económicas que los mismos poseen, entre las cuales se pueden mencionar: altos coeficientes de transferencia térmica, alta eficiencia, economía y rendimiento, alta flexibilidad operativa y limpieza rápida y sencilla. 1.3.3 Antecedentes del modelado y control de plantas de evaporación Como en los objetivos de esta investigación se contempla el modelado y control de una planta de evaporación, a continuación se mencionan diversas referencias importantes dentro de este ámbito. Los métodos de diseño y la operación en estado estable de sistemas de evaporación estuvieron bien documentados gracias a publicaciones realizadas en 1923 y 1963, sin embargo, antes de la década del 60 no existían investigaciones suficientes acerca del comportamiento transitorio de estos sistemas (Andre y Ritter, 1968). El Departamento de Ingeniería Química de la Universidad de Alberta (Canadá), inició un trabajo de investigación notable en el año 1964 con un equipo de planta piloto que dio origen a un grupo importante de publicaciones acerca del modelado dinámico de sistemas de evaporación, ejemplo de ello son los artículos realizados por Andre y Ritter en 1968 y 1970 y el publicado por Newel y Fisher en 1972 (Cesca, 2002). En 1968 Andre y Ritter (Andre y Ritter, 1968; Ritter y Andre, 1970) presentan el modelado mediante balances dinámicos de materia y energía, se evalúa el desempeño del modelo construido mediante la comparación de resultados de simulaciones con datos experimentales y se encuentra que el modelo construido describe el sistema de manera aproximada. A partir del análisis de una forma linealizada del modelo construido, se diseñó una configuración de un control convencional adecuada para un evaporador de dos efectos. En el trabajo realizado por Newell y Fisher en 1972 (Newell y Fisher, 1972) se desarrolla una metodología para expresar el modelo de un tren de evaporadores. Cabe resaltar el trabajo de Pimenta y Feyo de Azevedo que presenta un simulador del 11.

(22) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. comportamiento en estado estable de un sistema de evaporadores de calandria en múltiples efectos, construido con el objetivo de ser aplicado en el diseño, el análisis de diversas formas de operación y el monitoreo de la eficiencia de las unidades en estado estable. Incluye una base de datos con las propiedades termodinámicas y físicas relevantes del soluto, la solución y el solvente. El simulador toma la información necesaria de la base de datos para hacer los cálculos. El modelo general empleado se basa en los balances teóricos de materia y energía (en estado estable) y la información del equilibrio de fases. Ha probado su eficiencia en aplicaciones industriales de evaporación de licor de caña de azúcar (Azevedo y Pimenta, 1993). Entrando ya en el siglo XXI se pueden mencionar algunos trabajos que evalúan el desempeño de diferentes modelos aplicados a sistemas de evaporación, vinculados casi siempre a técnicas computacionales. Estos trabajos aprovechan los avances que, en cuanto a capacidad de procesamiento, han beneficiado a los sectores industriales en la última década, entre ellos se pueden citar los trabajos que se mencionan a continuación. En el artículo realizado en 2003 por Stefanov y Hoo (Stefanov y Hoo, 2003), se modela un sistema de evaporación utilizando parámetros distribuidos como números adimensionales. El modelo se realiza para evaporadores de película descendente en la industria del papel: evaporación de licor negro. En el trabajo desarrollado por Russell, Bakker y Chaplin (Russell, Bakker, y otros, 2000) se compara el desempeño de 3 tipos de modelos en un sistema de evaporación: una red neuronal artificial, un modelo derivado analíticamente y una estructura ARX (siglas del inglés Auto-Regresive with eXogenous inputs) construida utilizando la técnica convencional de mínimos cuadrados. Se encontró que los modelos empíricos tienen un desempeño predictivo superior al del modelo derivado analíticamente. El estudio se realiza para un sistema de planta piloto constituido por 3 evaporadores de película descendente. La concentración del producto no es considerada en este trabajo ya que los experimentos se realizan con agua pura. Las variables de interés en este trabajo son: la temperatura del producto en cada efecto, el nivel de líquido y el flujo de salida de producto en cada efecto.. 12.

(23) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. Una gran proporción de la energía utilizada en la industria es empleada en procesos de secado, los evaporadores juegan un rol importante en el secado industrial de una gran cantidad de productos. Un control preciso de los evaporadores conlleva directamente a un mejor control en procesos subsiguientes, lo que implica una mayor eficiencia energética y una buena calidad del producto final (Russell, Bakker, y otros, 2000). Por otro lado Cardona, Hoyos y Zapata en el 2007 realizaron un trabajo de investigación en la Universidad Tecnológica de Pereira (Colombia) donde presentan el modelo matemático de un proceso de evaporación de doble efecto; caracterizado por ser multivariable, no lineal y con interacciones fuertes entre la entrada y la salida, por lo que proponen un control por redes neuronales en contraste con el control clásico.(Cardona, Hoyos, y otros, 2007) Rojero, Serrano, García, Félix, Ríos de la Universidad Autónoma de Zacatecas en el 2008, realizaron la simulación de un evaporador de doble efecto usado en la producción de jarabe de azúcar. La investigación tuvo como objetivo obtener el área de transferencia necesaria de calor, el gasto (consumo) de vapor de calefacción (W) y la economía de un evaporador de doble efecto. Se obtuvo el modelo matemático a partir de los balances de materia global y para cada uno de los efectos, así como los balances de energía y las ecuaciones de velocidad de transferencia de calor a través del área de intercambio. (Rojero, Serrano, y otros, 2008) Así mismo, Avalo y Varela en el 2008 realizaron el modelado de una unidad de evaporación de triple efecto, utilizada para la concentración de jugo de durazno. Se modeló cada efecto y se obtuvieron las ecuaciones diferenciales representativas del sistema incluyéndose relaciones empíricas en cuanto a las propiedades termo-físicas propias de un equilibrio termodinámico. La simulación permitió variar la concentración a la entrada del primer efecto con presiones constantes, pero distintas en todos los evaporadores, obteniéndose errores relativos bajos comparados con los valores experimentales. (Avalo y Varela, 2008.) Ordoñez, Hernández y Pedraza, de la Universidad Distrital Francisco José de Caldas en Colombia, presentaron en el 2012 un trabajo en el cual realizaron el modelado de un. 13.

(24) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. sistema de evaporación de múltiple efecto para la producción de panela (azúcar no centrifugada), como resultado presentaron un modelo del sistema de evaporización de múltiple efecto mediante una función de transferencia de tercer orden y un control proporcional derivativo. Finalmente muestra que el control de la concentración de azúcar y el nivel del fluido en cada efecto permiten obtener un sistema de evaporación de múltiple efecto más eficiente en términos de tiempos de procesamiento y optimización de recursos. (Ordoñez, C. Hernández, y otros, 2012). 1.4 El Control Predictivo Habiéndose abordado las principales interioridades del proceso de evaporación, se hace necesario discutir los temas relacionados con la técnica de control que se pretende utilizar. El control se aplica con el fin de aumentar la productividad y la eficiencia en cualquier planta de producción, permite además proporcionar estabilidad, seguridad y grandes beneficios económicos. Los métodos tradicionales de control multivariable basados en los algoritmos PID (Proporcional Integral Derivativo) constituyen un baluarte de la ingeniería del control de procesos. Ofrecen muy buenos resultados en el control de sistemas SISO (simple entrada simple salida); pero su éxito en sistemas MIMO (múltiple entrada múltiple salida) ha estado limitado (Rodríguez, 2008-2009). Sin embargo, estos controles aseguran su permanencia gracias a que son fácilmente realizables y poseen gran robustez. El Control Predictivo Basado en Modelo se ha desarrollado considerablemente en las últimas décadas, no solo en investigaciones teóricas sino también con aplicaciones industriales. Este éxito se debe a que el MPC es quizás la forma más general de formular el problema de control en el dominio del tiempo. El control predictivo integra control óptimo, control de procesos con retardos, procesos multivariables, y utiliza las referencias futuras cuando están disponibles. Al utilizar esta estrategia de control con horizonte finito permite además la consideración de restricciones y procesos no lineales (Camacho y Bordons, 2004). El Control Predictivo no es una estrategia de control específica, sino que se trata más bien de un campo muy amplio de métodos de control desarrollados en torno a ciertas ideas comunes. Estos métodos de diseño conducen a controladores lineales que poseen 14.

(25) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. prácticamente la misma estructura y presentan suficientes grados de libertad. Las ideas que aparecen en mayor o menor medida en toda la familia de controladores predictivos son básicamente:  Uso explícito de un modelo para predecir la salida del proceso en futuros instantes de tiempo (horizonte).  Cálculo de las señales de control minimizando una cierta función objetivo.  Estrategia deslizante, de forma que en cada instante el horizonte se va desplazando hacia el futuro, lo que implica aplicar la primera señal de control en cada instante y desechar el resto, repitiendo el cálculo en cada instante de muestreo. Los distintos algoritmos de MPC difieren entre sí casi exclusivamente en el modelo usado para representar el proceso y los ruidos y en la función de coste a minimizar. Aunque las diferencias puedan parecer pequeñas, pueden provocar distintos comportamientos en lazo cerrado, siendo críticas para el éxito de un determinado algoritmo en una determinada aplicación.. 1.5 Estrategias del MPC La metodología utilizada por los controladores de la familia de los MPC se caracteriza por la estrategia mostrada en la Figura 1.2 y 1.3. El MPC se enmarca dentro de los controladores óptimos, es decir, aquellos en los que las actuaciones responden a la optimización de un criterio. El criterio a optimizar o función de coste está relacionado con el comportamiento futuro del sistema, que se predice gracias a un modelo dinámico del mismo denominado modelo de predicción (de ahí el término predictivo basado en modelo). El intervalo de tiempo futuro que se considera en la optimización se denomina horizonte de predicción. Dado que el comportamiento futuro del sistema depende de las acciones que se aplican a lo largo del horizonte de predicción, son éstas las variables de decisión respecto a las que se optimiza el criterio. La aplicación de estas acciones sobre el sistema conduce a un control en bucle abierto. La posible discrepancia entre el comportamiento predicho y el comportamiento real del sistema crean la necesidad de imponer cierta robustez al sistema incorporando realimentación del mismo. Esta realimentación se consigue gracias a la técnica del horizonte deslizante que consiste en aplicar las acciones obtenidas durante un 15.

(26) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. período de tiempo, tras el cual se muestrea el estado del sistema y se resuelve un nuevo problema de optimización. De esta manera el horizonte de predicción se va deslizando a lo largo del tiempo.. Figura 1.2: Uso del horizonte de predicción en cada tiempo de muestreo. Una de las propiedades más atractivas del MPC es su formulación abierta, que permite la incorporación de distintos tipos de modelos de predicción, sean lineales o no lineales, monovariables o multivariables, discretos o continuos y la consideración de restricciones sobre las señales del sistema. Esto hace que sea una estrategia utilizada en muy diversas áreas del control. Además, es una de las pocas técnicas que permiten controlar sistemas con restricciones incorporando éstas en el propio diseño del controlador. Estas características han hecho del Control Predictivo una de las estrategias de control avanzado con un impacto importante en problemas de ámbito industrial (Qin y Badgwell, 1997). Haciendo uso del modelo del proceso se predicen salidas futuras para un horizonte de predicción (Hp) en cada instante k. Para estas salidas futuras es necesario conocer tanto entradas como salidas pasadas, así como señales de mando futuras. que han de ser calculadas y enviadas al. sistema.. Figura 1.3: Estrategia del control predictivo. El conjunto de señales de control futuras se calcula optimizando un determinado criterio en el que se pretende mantener el proceso lo más próximo posible a la trayectoria de referencia 16.

(27) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. Este criterio suele tomar la forma de una función cuadrática de los errores entre la salida predicha y la trayectoria de referencia también predicha, incluyendo en muchos casos el término referente al esfuerzo de control. Debe usarse un método iterativo de optimización con el fin de minimizar la función de costo. En el próximo instante de muestreo se calcula. a partir de la secuencia anterior y de la misma salida medida.. Luego se actualiza de nuevo el mando y se obtiene diferente de. , valor que será. (calculado en el instante anterior).. 1.6 Elementos Básicos del MPC El Control Predictivo se compone básicamente por tres elementos: el modelo de predicción, la función objetivo y la ley de control (Camacho y Bordons, 1999). 1.6.1 Modelo de predicción Es el modelo matemático que describe el comportamiento esperado del sistema. Este modelo puede ser lineal o no lineal, en tiempo continuo o en tiempo discreto, en variables de estado o en entrada salida. Es la piedra angular del MPC, debe captar al máximo el comportamiento dinámico del proceso, ser capaz de permitir el cálculo de las predicciones, además de ser intuitivo y permitir llevar a cabo el análisis teórico del mismo. Su uso se determina por la necesidad de calcular la salida predicha en instantes futuros . Las diferentes estrategias de MPC usan distintos modelos para describir la relación entre las entradas medidas y las salidas. Además tienen en cuenta un modelo de perturbaciones que representa el comportamiento que no aparece reflejado en el modelo del proceso como las entradas no medidas, los ruidos y los errores del modelo. Aunque casi cualquier forma de modelo puede ser usada para la formulación del MPC, los más comúnmente usados son la respuesta al impulso o modelo de convolución, la respuesta al paso, modelo en espacio de estados y en base a funciones de transferencia. Los modelos no lineales pueden ser usados para representar al proceso pero es muy complicado encontrar la respuesta al problema de optimización. Las redes neuronales así como la lógica difusa son otras formas de representación usadas en algunas aplicaciones. El modelo de las señales de perturbación se considera tan importante como el modelo del proceso. El modelo de convolución en base a la respuesta al paso se interpreta como la suma de una serie de 17.

(28) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. cambios tipo paso (ecuación 1.1). (1.1) Entonces el predictor será: (1.2) Donde. son los valores muestreados ante la entrada escalón y. puede tomarse como 0 si. se trabaja con modelos de variación.  Entonces, la predicción viene dada por: (1.3) Donde B y A son polinomios en z. 1.6.2 Función objetivo Los diversos algoritmos de MPC proponen distintas funciones de costo para la obtención de la ley de control. En general se busca que la salida futura una determinada señal de referencia esfuerzo de control. en el horizonte considerado siga. al mismo tiempo que se pueda penalizar el. requerido para hacerlo. La expresión general de esta función. objetivo es: (1.4) Donde:  H1 y HP: horizontes mínimo y máximo de costo o de predicción. Marca los límites de los instantes en que se desea que la salida siga la referencia. Si se toma con un valor grande Hp es porque no importa que exista error en los primeros instantes, lo cual provocará una respuesta suave del proceso. Si un proceso presenta retardo de transporte (td) no tiene sentido que Hp sea menor que este.  HC: horizonte de control, número de acciones de control que serán calculadas en el proceso de optimización para reducir el error. No tiene que coincidir con el horizonte máximo. . : secuencias de factores pesantes de la salida en el funcional.. . : secuencias de factores pesantes del mando que permiten gobernar los esfuerzos 18.

(29) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. de control. Usualmente se consideran valores constantes o exponenciales. Cuando la función de costo a minimizar es cuadrática, por un procedimiento generalizado del método de mínimos cuadrados, se puede encontrar una solución analítica lineal para el vector de los movimientos de la señal de control; pero cuando las restricciones en las variables tanto de salida como de entrada son incluidas en el proceso de optimización, la solución analítica no es posible siendo necesario acudir a un procedimiento de optimización numérica basado en algún método de programación lineal o cuadrática. Para el caso de sistemas descritos por modelos no lineales, este proceso de optimización puede presentar problemas de convergencia, requiriéndose una solución específica para cada caso particular. 1.6.3 Obtención de la ley de control Para obtener los valores de. es necesario minimizar el funcional (1.4). Para ello. se calculan los valores de la salida predicha. en función de los valores pasados. de salidas y entradas y las señales de control futuras, haciendo uso del modelo del proceso que haya sido elegido y se sustituyen en la función de costo obteniendo una expresión cuya minimización conduce a los valores buscados. Para el criterio cuadrático, si el modelo es lineal y no existen restricciones, se puede obtener la solución de forma analítica, en otro caso se debe usar un método iterativo de optimización.. 1.7 Historia El Control Predictivo es un tipo de control de naturaleza abierta dentro del cual se han desarrollado muchos avances, encontrando gran aceptación tanto en aplicaciones industriales como en el mundo académico. En la actualidad existen numerosas aplicaciones de controladores predictivos funcionando con éxito, tanto en la industria de procesos como en control de motores o Robótica. El buen funcionamiento de estas aplicaciones muestra la capacidad del MPC para conseguir sistemas de control de elevadas prestaciones capaces de operar sin apenas intervención durante largos períodos de tiempo. El Control Predictivo surge casi al unísono en Francia y Estados Unidos cuando en 1978 Richalet y otros autores introducen el Control Predictivo heurístico basado en modelo 19.

(30) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. (Richalet y Rault., 1978), más tarde conocido como control algorítmico basado en modelo (MAC por sus siglas en inglés); por otra parte dos ingenieros de la compañía Shell, Cutler y Ramaker presentaron el control con matriz dinámica (DMC por sus siglas en inglés) (Cutler y Ramaker, 1980). Estos no utilizaban modelos determinísticos paramétricos, sino modelos dinámicos del proceso basados en los datos de la respuesta al paso o del impulso del proceso (Rodríguez, 2008-2009). Otra línea de trabajo se desarrolló independientemente en torno a las ideas de control adaptable, desarrollándose estrategias de Control Predictivo para sistemas monovariable y formulada sobre modelos de entrada y salida. El control autosintonizado basado en predictores (Predictor-based Self-Tuning Control) en el trabajo de Peterka en 1984 (Peterka, 1984), el control adaptable de horizonte extendido (Extended Horizon Adaptive Control, EHAC) por Ydstie en 1984 (Ydstie, 1984), el controlador autosintonizado (Extended Prediction Self Adaptive Control, EPSAC) ilustrado por Keyser y Cuawenberghe en 1985 (Keyser y Cuawenberghe., 1985), y el Control Predictivo generalizado (Generalized Predictive Control, GPC) desarrollado por Clarke y Morari en 1987 (Clarke y Morari, 1987) se pueden mencionar en este contexto. El GPC utiliza ideas de los controladores de varianza mínima generalizada (Generalized Minimum Variance, GMV) descritos por Clarke y Gawthrop en 1979 (Clarke y Gawthrop, 1979) y es en la actualidad uno de los métodos más utilizados a nivel académico. Existen numerosas formulaciones de Control Predictivo basadas en las mismas ideas, entre las que se pueden incluir Control Adaptable Multivariable Multipaso (Multistep Multivariable Adaptive Control, MUSMAR) desarrollado y expuesto por Greco y Menga en 1984 (Greco y Menga, 1984) y el Control Predictivo Funcional (Predictive Functional Control, PFC) por Richalet en 1992 (Richalet, 1992). El MPC, también ha sido formulado en el espacio de estados por Moriari en 1994 (Moriari, 1994), lo que permite una utilización de resultados bien conocidos sobre estabilidad y también la generalización a casos más complejos como procesos multivariables, procesos no lineales y sistemas con perturbaciones estocásticas. Los mediados de la década del 90’ marcan la madurez de la teoría sobre el control. 20.

(31) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. predictivo y se da un giro importante hacia la aplicación de la misma en el ambiente industrial principalmente porque los medios de cómputo necesarios ya estaban al alcance de todos. A partir de este momento los principales aportes a la teoría del control predictivo vienen dados por trabajos que utilizan estos métodos para profundizar en aspectos clásicos como el control robusto, lo cual es evidenciado en (Kothare, Balakrishnan, y otros, 1996), y en el trabajo de los autores Lee, Kwon y Lee (Lee, Kwon, y otros, 1996), ambos en el año 1996, y en 1999 el de Bemporad y Morari (Bemporad y Morari, 1999). Todos estos trabajos siguen la misma línea y hacen énfasis en la robustez que ofrece el uso tanto de las restricciones como del horizonte de predicción y control en el MPC. Las técnicas del control predictivo han sido extensamente estudiadas e implementadas en procesos industriales lentos, pero es evidente que solo en la década pasada fue que se alcanzó suficiente poder computacional como para poder pensar en aplicar los métodos del control predictivo en la optimización de sistemas con dinámica rápida, con este objetivo surge la línea más reciente, el control predictivo adaptable. Básicamente esta rama se dedica no solo a estimar y predecir cambios en el comportamiento de las variables de la planta sino que también predice los cambios del modelo de la planta y se adapta al mismo. Las dificultades que conllevaría este MPC adaptativo fueron descritas en el año 2000 por Mayne (Mayne, 2000). Varios autores han aportado a la investigación en este tema, se pueden destacar las conferencias impartidas en 2002 y 2004 por Dunbar y Murray (Dunbar y Murray, 2002; Dunbar y Murray, 2004) sobre MPC de coordinación de formaciones multivehiculares, las que ayudaron a desvelar las verdaderas posibilidades de esta estrategia. También destaca el trabajo de Fukushima, Kim, y Sugie en el 2007, en el que usa el principio de comparación para desarrollar un control predictivo adaptativo para sistemas lineales (Fukushima, Kim, y otros, 2007). Ya en el 2009, Verónica Adetola, Darryl DeHaan, y Martin Guay (Adetola, DeHaan, y otros, 2009) consideran, en su trabajo, los sistemas no lineales linealmente parametrizados y muestran que asegurar que los parámetros iniciales de error están entre límites determinados (restricciones) es una manera de garantizar estabilidad. También en este último tema es significativo el aporte de Aswani en los años 2011 y 2012, en ellos explora y experimenta con el vuelo de cuadrotores (pequeñas unidades que vuelan 21.

(32) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. en base a cuatro aspas contragiratorias) e introduce la noción de safe-MPC (control predictivo seguro en inglés) que consiste en garantizar que las entradas de control son seleccionadas y de acuerdo a esto la evolución del sistema es restringida a una (aproximadamente) invariante salida deseada. Estos trabajos demuestran mediante pruebas realizadas que el control predictivo adaptativo puede mejorar el desempeño del vuelo (Aswani, Sastry, y otros, 2011; Aswani, Bouffard, y otros, 2012). En estos casos el MPC adaptativo es combinado con técnicas de seguimiento espacial con dispositivos ópticos y el uso de redes neuronales. Sobre el tema de MPC aplicado al vuelo de vehículos autónomos a escala, se han realizado investigaciones también en el departamento de Ingeniería en Control y Sistemas Computacionales de la Universidad Central Marta Abreu de las Villas, entre ellas las de (Blanco, 2007) y Yasmany Jesús Martínez Reyes (Martínez_Reyes, 2008), donde emplean el control predictivo del vuelo de un helicóptero y un avión autónomo respectivamente. Hasta ahora se ha evidenciado el control predictivo principalmente como un vasto campo teórico, pero estas estrategias ya han sido aplicadas con buenos resultados en la práctica. Existen aplicaciones y trabajos de MPC en diversos procesos que van desde robots, expuestas por Gómez Ortega y Camacho en 1996 (Gómez_Ortega y Camacho, 1996) hasta la anestesia clínica descrito por Linkers y Mahfonf en 1994 (Linkers y Mahfonf, 1994). Aplicaciones en la industria de cemento, desecadoras, brazos robóticos, se pueden encontrar descritas por Clarke 1988 (Clarke, 1988), mientras que desarrollos para columnas de destilación, plantas de PVC (Policloruro de vinilo), generadores de vapor y servomecanismos se presentan por Richalet en 1993 (Richalet, 1993) y en Richalet y Rault en 1978 (Richalet y Rault., 1978), todos estos ahora podrían ser generalizados en la industria. En 1995, 2000 y 2004 Camacho y Bordons (Camacho y Bordons, 1995; Bordons, 2000; Camacho y Bordons, 2004) elaboran una serie de trabajos en la cual realizan un compendio de los avances del control predictivo en la industria de procesos. Las aplicaciones de MBPC en la industria se encuentran principalmente en el sector petroquímico. Sorprendentemente, MBPC tiene menor impacto en otro tipo de industrias, aunque algunos estudios realizados reflejan que ya a finales de los 90’, unas 20,000. 22.

(33) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. aplicaciones se beneficiaron de esta técnica. La mayoría de las aplicaciones son en procesos multivariables y con dinámica lenta. El éxito actual del MBPC en la industria se debe a tres razones principales:  La incorporación de un modelo explícito del proceso en los cálculos permite al controlador conocer la dinámica del proceso.  La consideración del comportamiento del proceso a lo largo de un horizonte futuro permite tener en cuenta el efecto de las perturbaciones en realimentación y prealimentación, permitiendo al controlador conducir la salida a la trayectoria de referencia deseada.  La consideración de restricciones en la fase del diseño del controlador evita en lo posible la violación de éstas, resultando un control más preciso en torno al punto óptimo de operación. La inclusión de restricciones es quizás la característica que más distingue al MBPC respecto a otras metodologías. Otra de las razones que contribuyeron a que el MBPC se haya convertido en un éxito comercial es el hecho de que existen unos 15 suministradores como: AspenTech, Adersa, Honeywell Profimatics, etc, que instalan el producto llave en mano, con períodos de amortización de entre 3 y 12 meses, permitiendo que medianas empresas puedan tener acceso a esta tecnología. Además, los nuevos sistemas de control distribuido empiezan a ofertar productos MBPC genéricos que ofrecen al usuario la posibilidad de realizar futuras modificaciones sin depender de un producto cerrado.. 1.8 Antecedentes de Control Predictivo en Plantas de Evaporación Como el propósito de esta tesis es lograr la síntesis del controlador predictivo basado en modelo de un evaporador simple efecto perteneciente a la industria azucarera y evaluar su desempeño comparado con las estrategias clásicas de control, es necesario puntualizar que no se ha encontrado explícitamente ningún trabajo que soporte estos fines en la revisión bibliográfica realizada. Sin embargo, se tiene el antecedente del trabajo presentado en la Revista Centro Azúcar, por el tutor del presente, el Dr. Miguel A. Rodríguez Borroto: MPC del Proceso de Cristalización de la Sacarosa en los Tachos al Vacío, proceso con características fisicoquímicas muy similares a las de proceso de concentración en los 23.

(34) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. evaporadores de simple efecto. Además, se pueden mencionar trabajos que de una forma u otra tratan el MPC en éste ámbito, como son los que se exponen a continuación. En (Benne, Grondin-Perez, y otros, 2000) se realiza el modelado de un proceso de evaporación en múltiples efectos utilizando redes neuronales artificiales y se prueba un control predictivo basado en modelo (MPC) para la industria del azúcar de caña, obteniendo resultados satisfactorios. Se afirma también que en vista de los límites de las estrategias de control tradicionales, la aplicación de inteligencia artificial a procesos industriales y de planta piloto ha probado ser efectiva. Un trabajo dentro de la planta Brazilian Klabin Paraná Papéis (KPP) (industria de papel) fue realizado por Costa y Lima en el 2003 (Costa y Lima, 2003). La importancia de la operación de separación estudiada en dicha industria radica en que el licor negro (un efluente contaminante del proceso Kraft), es incinerado tras incrementar su concentración mediante un proceso de evaporación en múltiples efectos. En este trabajo se encontró que un modelo de redes neuronales artificiales dio mejores resultados que un modelo (lineal) ARX, lo que implica que los errores de modelos no lineales ajustados a procesos de evaporación son menores que los errores de los modelos lineales. Se concluyó que la aplicación del control predictivo para controlar únicamente el nivel en el último evaporador es muy prometedora, debido a que el control predictivo tiene la ventaja de utilizar todas las variables manipuladas disponibles para evitar los nocivos efectos de las restricciones duras (Costa y Lima, 2003). También destacan más recientemente el desarrollo de una estrategia de control tolerante a fallas para un evaporador de múltiple efecto en la industria azucarera, llevada a cabo en el Instituto Tecnológico de Minatitlán, México en el 2007, en este trabajo utilizan métodos de control predictivo para limitar la ocurrencia de fallas en los actuadores (Guerrero-Sánchez, 2007); y cabe mencionar un trabajo realizado en la Universidad de Valladolid, que realiza el control predictivo de un evaporador basado en programación multiparamétrica, aplicándolo al simulador de un evaporador usado en la industria azucarera que concluye. 24.

(35) CAPÍTULO 1: FUNDAMENTOS TEÓRICOS DEL PROCESO DE EVAPORACIÓN Y DEL CONTROL PREDICTIVO. que: los parámetros de sintonización confirman que “para tiempos de muestreo grandes se requiere horizontes de predicción también muy grandes, lográndose una complejidad pequeña que se traduce en un instantáneo período de simulación” y además que “el control predictivo explícito, resuelto con programación multiparamétrica da garantía de estabilidad, lo que se comprueba a partir de la funcionalidad incorporada en MPT” refiriéndose a la herramienta de programación multiparamétrica del MathLab (MPT por sus siglas en inglés) (Miranda y Prada, 2010).. 1.9 Conclusiones Parciales  El control preciso de los evaporadores conlleva directamente a un mejor control en los procesos subsiguientes, lo que implica una mayor eficiencia energética y una buena calidad del producto final.  Existen varios trabajos que evidencian las ventajas del MPC como alternativa viable e incluso una mejor opción de control para disímiles procesos industriales en sustitución de las técnicas basadas en controladores clásicos.  El control predictivo abarca una serie de métodos con diferentes algoritmos desarrollados y bien conocidos, pero todos tienen en común el uso explícito de un modelo para predecir la salida del proceso en futuros instantes de tiempo.. 25.

(36) CAPÍTULO 2: MODELO MATEMÁTICO DE LA PLANTA DE EVAPORACIÓN. IDENTIFICACIÓN Y VALIDACIÓN. Capítulo 2: Modelo Matemático de la Planta. de Evaporación. Identificación y Validación El diseño de sistemas de control para un proceso determinado requiere conocer el comportamiento dinámico del mismo, aún más si dicho sistema de control está basado en los métodos de control predictivo, ya que el correcto funcionamiento de los controladores predictivos está condicionado por el conocimiento previo que se tenga de la dinámica del proceso y de un modelado preciso. Para ello hay que contar con un modelo del sistema que consiste en la descripción matemática de las relaciones dinámicas existentes entre las variables a controlar y las variables de entrada, tanto perturbaciones como variables de control. La principal ventaja de la utilización de un modelo radica en que permite la evaluación del sistema sin tener el sistema físico real. El objetivo principal de este capítulo es desarrollar un modelo matemático que caracterice el desempeño dinámico del proceso de evaporación en un evaporador tipo Robert o de calandria, que es el más utilizado en la concentración del jugo de la caña de azúcar en la industria azucarera. En este se pretende exponer explícitamente el modelo representativo de la planta de evaporación escogida como caso de estudio, el cual será validado mediante simulación. Así mismo, se expondrán los resultados de aplicar las técnicas de identificación al modelo obtenido para utilizarlo en la aplicación de la técnica de control predictivo que se pretende diseñar en el próximo capítulo.. 2.1 Modelo Matemático Para poder conocer la dinámica de un sistema se precisa disponer de una descripción matemática del mismo, entiéndase modelo matemático del objeto físico analizado. Por modelo matemático de cualquier sistema se tiene a todo conjunto de ecuaciones matemáticas que caractericen las relaciones existentes entre las variables de entrada y de salida del sistema, considerando al mismo tiempo las variables independientes, de esta manera a través del mismo se puede conocer con cierta precisión el desempeño dinámico del objeto de regulación y control. 26.

(37) CAPÍTULO 2: MODELO MATEMÁTICO DE LA PLANTA DE EVAPORACIÓN. IDENTIFICACIÓN Y VALIDACIÓN. 2.1.1 Modelo matemático de un evaporador simple efecto. Para obtener el modelo matemático de un evaporador industrial simple efecto se utiliza la investigación desarrollada por Alberto Aguado (Aguado, 1980). En la figura 2.1. se. muestra un esquema detallado de un evaporador de simple efecto para el que se desarrolla el modelo.. Figura 2.1: Diagrama de un evaporador de simple efecto. Donde:  M1, C1: flujo volumétrico y concentración de la solución en la entrada.  M2, C2: Flujo volumétrico y concentración de salida.  Ms: Flujo de masa del. vapor de entrada.  Mc: Flujo de masa del vapor de salida.  P1, P2: Presiones en las cámaras superior e inferior respectivamente.  Mv: Flujo másico de vapor producido por el evaporador.  Me: Flujo de masa del vapor de salida en la cámara superior.  h: Nivel equivalente de la solución en los tubos.  Fa: Flujo de masa que entra al condensador. El objetivo fundamental que persigue este equipo tecnológico es que la concentración de una solución sea llevada desde su valor inicial C1 hasta el deseado C2. Para ello el evaporador se compone de dos cámaras separadas que satisfacen distintos propósitos. La. 27.