Rational conchoid and offset constructions: algorithms and implementation

Rational Conchoid and Offset Constructions:

Algorithms and Implementation

J u a n a Sendra1'2, David Gomez2, and Valerio M o r a n3

1 Dpto. de Matematica Aplicada a las TIC, Universidad Politecnica de Madrid,

Madrid, Spain jsendraQetsist.upm.es

2 Research Center on Software Technologies and Multimedia Systems

for Sustainability, Madrid, Spain david.gomezsOupm.es

3 ETSI Sistemas de Telecomunicacion, Universidad Politecnica de Madrid, Spain

vmoranQalumnos.upm.es

A b s t r a c t . This paper is framed within the problem of analyzing the rationality of the components of two classical geometric constructions, namely the offset and the conchoid to an algebraic plane curve and, in the affirmative case, the actual computation of parametrizations. We recall some of the basic definitions and main properties on offsets (see [13]), and conchoids (see [15]) as well as the algorithms for parametrizing their rational components (see [1] and [16], respectively). Moreover, we implement the basic ideas creating two packages in the computer algebra system Maple to analyze the rationality of conchoids and offset curves, as well as the corresponding help pages. In addition, we present a brief atlas where the offset and conchoids of several algebraic plane curves are obtained, their rationality analyzed, and parametrizations are provided using the created packages.

I n t r o d u c t i o n

In this p a p e r we deal with two different geometric constructions t h a t a p p e a r in m a n y practical applications, where t h e need of proving rational p a r a m e t r i z a t i o n s as well as a u t o m a t i z e d algorithmic processes is i m p o r t a n t . O n one side we con-sider offset varieties and on t h e other conchoid varieties. Offsets varieties have been extensively applied in t h e field of computer aided geometric design (see [5],[3],[4]), while conchoids varieties appears in several of practical applications, namely t h e design of t h e construction of buildings, in astronomy [6], in electro-magnetism research [20], optics, physics, mechanical engineering and biological engineering [7], in fluid mechanics [19], etc.

n = 2 or n = 3, and hence C is a curve or a surface). Moreover, although it is

not necessary for the development of the theory, in practice one considers that

C is real (i.e. there exists at least one regular real point on C). The offset variety

to C at distance d (d is a field element, in practice a non-zero real number),

denoted by Od(C), is the envelope of the system of hyperspheres centered at the

points of C with fixed radius d (see Fig.l, left); for a formal definition, see e.g.

[1]. In particular, if C is unirational and V(t), with t = (ti,... ,t

), a rational

parametrization of C, the offset to C is the Zariski closure of the set in C

generated by the expression V(t) ±d

where J\f(t) is the normal vector to

C associated with V(t).

The conchoid construction is also rather intuitive. Given C as above (base

variety) and a fixed point A (focus), consider the line C joining A (in practice

the focus is real) to a point P of C. Now we take the points Q of intersection

of C with a hypersphere of radius d centered at P. The Zariski closure of the

geometric locus of Q as P moves along C is called the conchoid variety of C

from focus A at a distance d and denoted by £^(C) (see Fig.l right); for the

geometric construction of the conchoid and, for a formal definition, see e.g. [15]

and [10]. The Conchoid of Nicomedes and the Limagon of Pascal are the two

classic examples of conchoids, and the best known. They appear when the base

curve is a line or a circle, respectively. Similarly, if C is unirational and V(t) is a

rational parametrization of C, then the conchoid is the Zariski closure of the set

defined by the expression

V(t)±d

V(t) - A

\V(t)-A\\

5-&

4-i &

3

Hk

y

-3 - 2 1

^"P

Fig. 1. Left: Construction of the offset to the parabola, Right: Geometric construction

These two operations are algebro-geometric, in the sense that they create

new algebraic sets from the given input objects. There is an interesting relation

between the offset and the conchoid operations. Indeed, there exists a rational

bijective quadratic map which transforms a given hypersurface F and its offset

Fd to a hypersurface G and its conchoidal Gd, and vice versa (see [11]).

The main difficulty when applying these constructions is that they generate

much more complicated objects than the initial ones. There is a clear explosion

of the degree of the hypersurface, singularity structure and the density of the

defining polynomials (see e.g. [2], [13], [15]). As a consequence, in practice, the

implicit equations are untractable from the computational point of view. This is

one of the reasons why the use of parametric representations of offsets and

con-choids are considered. Let us see an illustrating example. We consider the plane

curve C defined by y

= x

. Its offset has degree 12 and the polynomial defining

it has 65 nonzero terms, and its infinity norm is 300781250. However, the offset

can be parametrized by radicals (see [17], [18]) as ( t

, t

) ± .

(—5t

,4t

) .

On the other, the offset can be rationally parametrized as

/ 1 (t

- 1) ( I 6 t

- 3 2 t

+ 625dt

+ 32t

- 16)

^625 t

(t

+ 1) '

2 - 1 6 t

+ 64t

- 80t

+ 3125dt

+ 80t

- 641

+ 1 6 \

3125 t

(f + 1) ) '

The paper is structured as follows. In Section 1 we recall some of the

ba-sic definitions and main properties on offsets and conchoids of algebraic plane

curves (see [13], [15]). We provide algorithms to analyze the rationality of the

components of these new objects (see [1], [16]), and in the affirmative case,

ra-tional parametrizations are given. In Section 2 we present the creation of two

packages in the computer algebra system Maple to analyze the rationality of

offset and conchoids curves respectively, whose procedures are based on the

above algorithms, as well as the corresponding help pages. Finally, in Section 3,

we illustrate the performance of the package by presenting a brief atlas where the

offset and conchoids of several algebraic plane curves are obtained, with their

ra-tionality analyzed. Furthermore, in case of genus zero, a rational parametrization

is computed. We have not done an theoretical analysis of the complexity of the

implemented algorithms but the practical performance of the implementation

provides answers, in reasonable time for curves of degree less than 5.

1 Parametrization Algorithms: Curve Case

In this section we summarize the results on the rationality of the offsets and

conchoids of curves, presented in [1], [16] respectively, by deriving an algorithm

for parametrizing them. The treatment of surfaces can be found at [1], [12], [14]

(offsets) [8], [9], [10] (conchoids).

The rationality of the components of the offsets is characterized by means of

the existence of parametrizations of the curve whose normal vector has rational

norm, and alternatively by means of the rationality of the components of an

associated curve, that is usually simpler than the offset. As a consequence, one

deduces that offsets to rational curves behave as follows: they are either reducible

with two rational components (double rationality), or rational, or irreducible and

not rational.

For this purpose, we first introduce two concepts: Rational Pythagorean

Hodo-graph and curve of reparametrization. Let V(t) = (Pi(t), P

(t)) G C(t)

be a

ra-tional parametrization of C. Then, V(t) is RPH (Rara-tional Pythagorean Hodograph)

ifits normal vector JV(t) = (N^t), N

(t)) satisfies that N

(t)

+N

(t)

= m(tf ,

with m(t) G C(t). For short we will express this fact writing ||7V(t)|| G C(t). On

the other hand, we define the reparametrizing curve of Od(C) associated with

V(t) as the curve generated by the primitive part with respect to x

of the

nu-merator of x\ P

(x\) — P

(x\) + 2x

P

(xi) , where P

denotes the derivative of

Pi. In the following, we denote by G®(C) the reparametrizing curve of Od(C)

as-sociated with V(t). Summarizing the results in [1], one can outline the following

algorithm for offsets.

Algorithm: offset parametrization

— GIVEN: a proper rational parametrization V(t) of a plane curve C in K

and

dec.

—

— D E T E R M I N E : (in the affirmative rational parametrization of each

component.

1. Compute the normal vector W(t) ofP(i). IF ||W(t)|| G K(£) THEN RETURN

Od(C) has two rational components parametrized by V(t) ± Mn.!,,,Af(t).

2. Determine G-p(C), and decide whether G-p(C) is rational.

3. IF Gp(C) is not rational THEN RETURN no component of Od(C) is rational.

4. Else compute a proper parametrization H(t) = (R(t),R(t)) of G-p(C)

and RETURN that OdiC) is rational and that Q(t) = V(R(t)) +

N,(pm,fpm2

^(R(t)) where W = (JVi, JV

), parametrizes O

(C).

The Conchoid Rationality Problem

In [16], it is proved that conchoids having all their components rational can only

be generated by rational curves. Moreover, it is shown that reducible conchoids to

rational curves have always their two components rational (double rationality).

From these results, one deduces that the rationality of the conchoid component,

to a rational curve, does depend on the base curve and on the focus but not

on the distance. To approach the problem we use similar ideas to those for

off-sets introducing the notion of reparametrization curve as well as the notion of

rdf parametrization. The rdf concept allows us to detect the double rationality

equivalently as t h e conchoid in t e r m s of rationality. As a consequence of these theoretical results [16] provides an algorithm t o solve t h e problem. T h e algo-r i t h m analyzes t h e algo-rationality of all t h e components of t h e conchoid and, in t h e affirmative case, parametrizes t h e m . T h e problem of detecting t h e focuses from where t h e conchoid is rational or with two rational components is, in general, open.

We say t h a t a rational p a r a m e t r i z a t i o n V(t) = (Pi(£), P 2 W ) G K ( t )2 of C

is at rational distance to the focus A = (a, 6) if (Pi(£) — a )2 + (P2(t) — b)2 =

m ( t )2 , with m(t) G K ( t ) . For short, we express this fact saying t h a t V(t) is

rdf or A-rdf if we need t o specify t h e focus. O n t h e other hand, we define t h e

reparametrization curve of the conchoid fi^(C) associated to V(t), denoted by Q!p(C), as t h e primitive p a r t with respect t o x 2 of t h e n u m e r a t o r of—2x2 (Pi ( x i ) —

a) + ( x2- l ) ( P2( x ! ) - 6 ) .

Algorithm: conchoid p a r a m e t r i z a t i o n

— GIVEN: a proper rational p a r a m e t r i z a t i o n V(t) of a plane curve C in K2, a

focus A = (a, 6), and d e C .

— D E C I D E : whether t h e components of t h e conchoid <£j(C) are rational. — D E T E R M I N E : (in t h e affirmative rational p a r a m e t r i z a t i o n of each

component.

1. Compute GpiC).

2. If QJJ{C) is reducible RETURN that <t^(C) is double rational and that •^M ~^~ ±\\v(t)-A\\ (^ffl ~~ A) parametrize the two components.

3. Check whether the genus of QJJ is zero. If not, RETURN that (£d (C) is not

rational.

4. Compute a proper parametrization (</>i(£),</>2(£)) of QJJ and RETURN that C^(C) is rational and that V(4>i(t)) + ^ i m u dtt))-A\\ (^('/MO) — ^ )

para-metrizes (tf(C).

We can note t h a t t h e rationality of t h e b o t h constructions is not equivalent. For instance, if C is t h e p a r a b o l a of equation j/2 = y\, t h a t c a n be p a r a m e t r i z e d

as ( t , t2) , t h e offset at distance d is rational. However, t h e rationality of t h e

conchoid of t h e p a r a b o l a depends on t h e focus.

2 I m p l e m e n t a t i o n of Conchoid and Offset Maple

Packages and Help Pages

In t h e following, we give a brief description of t h e procedures and we show one of t h e help pages for one of t h e Maple functions. T h e procedure codes and packages are available in

h t t p : //www. e u i t t .upm. e s / u p l o a d e d / d o c s - p e r s o n a l e s / s e n d r a . p o n s _ j u a n a / o f f s e t s _ c o n c h o i d s / O f f s e t . z i p

2 . 1 P r o c e d u r e s of t h e C o n c h o i d P a c k a g e

g e t I mpl Conch This procedure determines t h e implicit equation of t h e conchoid

of an algebraic plane curve, given implicitely, at a fixed focus and a fixed distance. For this purpose, we use Grobner basis t o solve t h e system of equations consisting on t h e circle centered at generic point of t h e initial curve C and radius d, t h e straight line from t h e focus A t o t h e generic point of t h e initial curve C, and t h e initial curve C.

getParamConch Firstly this procedure checks whether t h e conchoid of a

ra-tional curve is irreducible or it has two rara-tional components. For this purpose, we analyze whether a proper rational p a r a m e t r i z a t i o n of t h e initial curve is RDF. In affirmative case, t h e procedure o u t p u t s a message indicating reducibil-ity (the conchoid has two rational components) and a rational p a r a m e t r i z a t i o n for each component is displayed. Otherwise, t h e conchoid is irreducible and t h e r e p a r a m e t r i z a t i o n curve is computed in order t o s t u d y its rationality. In t h e affirmative case, it provides a rational p a r a m e t r i z a t i o n by means of a rational p a r a m e t r i z a t i o n of t h e reparametrizing curve and it o u t p u t s a message indicating irreducibility and rationality.

plot I mpl Conch This procedure computes t h e conchoids curve using getlm-plConch procedure, and then it plots b o t h t h e initial curve and its conchoid

within t h e coordinates axes interval \—a, a] x \—a, a].

2 . 2 P r o c e d u r e s of t h e Offset P a c k a g e

ImplicitOFF This procedure determines t h e implicit equation of t h e offset of

a rational algebraic plane curve, given parametrically, at a fixed distance. For this purpose, since t h e algebraic system has three variables and one p a r a m e t e r (namely t h e distance), instead of Grobner basis we simplify t h e c o m p u t a t i o n by using resultants t o solve t h e system of equations consisting on t h e circle centered at a generic point of t h e initial curve C and radius d, and t h e normal line at each point of C.

OFFparametric This procedure analyzes t h e rationality of t h e offset of a

a rational parametrization for each component, using the RPH concept.

Other-wise, it checks whether the offset is rational or not. In the affirmative case, it

provides a rational parametrization by means of a rational parametrization of

the reparametrizing curve.

OFFplot This procedure computes the offset curve at a generic distance, d, and

then replaces d with fixed value, dist. Finally, it plots both the initial curve and

its offset at a distance dist within the coordinates axes interval [—a, a] x [—a, a].

Once we have implemented the Offset/Conchoid procedure in Maple, we have

created two packages containing them, called Conchoid and Offset, respectively.

Theoretically, to compute the implicit equation of either the conchoid or the

offset, we use the incidence varieties introduced in [1] and [15], respectively.

In the definition of this incidence variety an equation, to exclude extraneous

factors, is introduced such that the Zariski closure of the projection is exactly

the offset/conchoid curve. Therefore, by the theorem of the closure, Grobner

basis computation, and resultant when possible, provides the correct equation. In

addition, one has to take into account that we are dealing with generic conchoids

and generic offsets and therefore the specialization of the Grobner basis or the

resultant may fail. Nevertheless, since we have only one parameter there are only

finitely many specializations; In particular, d = 0 generates a bad specialization.

Since d = 0 is not interesting from the geometric construction point of view we

are excluding this case. In addition, we have created the help pages associated

to the procedures.

3 Atlas of Conchoid and Offset Curves

Table 1. Offsets Curves

Base Curve Offset

Degree Rationality & Parametrization

Circle

xl+xj - 4

Double Rational

j_(d+r)2t .^(d±r)(t2-l)

^ t2+l ' + P + l

Parabola

X2 — x\

Rational

( t2- l ) ( - t2 - 1 + 4 dat) t6-t4-t2+ 1 + 32 dt3 a

4at(t2 + l) ' 1 6 a t2( t2 + l)

H y p e r b o l a

2 2

xl 'f2. 1 16 9

Irreducible and non rational

Ellipse

Irreducible and non rational

Cardioid

{x\ + 4x2 +

x22f - 16{xf +

xl)

14

Rational

( - 9 + t2) (tit6-117rit4 + 3456t3-1053rit2 + 729ri)

( 2 4 3 t2+ 2 7 t4+ t6+ 7 2 9 ) ( t2+ 9 ) '

1 8 ( r i t6- 1 6 t5- 2 1 r i t4+ 8 6 4 t3- 1 8 9 r i t2- 1 2 9 6 t + 7 2 9 r i ) t (243t2 + 27t4 + t6 + 729)(t2 + 9)

Three-leaved R o s e

{xj + x\f + x i ( 3 x | - x\) 14 Irreducible and non rational

Trisectrix of Maclau-rin

x\{x\ + xl) - {xl - 3x\)

10 Irreducible and non rational

Folium of Descartes

xl + X% — 3X1X2 14 Irreducible and non rational

Tacnode

2x\-3x\x2+xl-2xl+xi 20 Irreducible and non rational

Epitrochoid

xi + 2x\xl-Uxl+x\ Mxf + 96xi - 63

10 Irreducible and non rational

Ramphoid Cusp

4 , 2 2 o 2 2 , X1-\-X1X2—2x1X2—XlX2 +

xl

20 Irreducible and non rational

Lemniscata oT

Bernoulli 16

( x ? + x i )2- 4 ( x ? - x i )

T a b l e 2. Conchoids Curves

C u r v e C Focus Curve F Focus Conch. A

C o n c h o i d P a r a m e t r i z a t i o n

Circle

A=F=(0,0) A=(-2,0) e C,

A=(-4,0) £ C

- 2 ( - l + t2) ± ( l - t2) 4t±2t

l + *2 l + *2 D R

3 t4- 1 2 t2 + l 2t(-3+5f!) i p

l + 2 t 2+ t4 , l + 2 ( 2+ t4 I « •

N R

P a r a b o l a

A = F = ( 0 , l / 4 ) A e C , A = ( 0 , 0 )

A=(0,-2) £ C

t±

2 t + 2 t3 + l - 2 t2 + t4 2 t ( 2 t + 2 t3 + l ' - 2 t2 + t * ) '\ - p ( - l + t 2 ) ( l + t2 ) , (_1 + t )2( 1 + t )2( 1 + t2 ) I « .

N R

H y p e r b o l a

A=F=(5,0) A=(-4,0) e C

A=(0,0) £ C

- 2 ( 9 + t2) _i_ 2 ( - t - 6 ) ( 2 t + 3 ) 4 5 + 2 4 t + 5 t2 > 3t

f - 9

2t

±

3 ( t2- 9 )

D R

4 5 + 2 4 t + 5 t2

-( 4 5 t6+ 1 2 9 t4+ 3 1 1 t2+ 2 7 ) 2 ( - 6 3 + 8 1 t4- 8 2 t2) t \ p ( l + t2) ( - 9 + t2) ( 9 t2- l ) ' ( l + t2) ( - 9 + t2) ( 9 t2- l ) ^ "•

N R

Ellipse

A=F=(3,0) A=(0,4) e C A=(0,0) £ C

5(f-l) , t2- 4

2 i 1 ±

(2 + 1 t2+ 4 > t2 + l

±

. ( l - r ) ( 1 0 0 t + 1 0 0 t3+ 4 t * + 1 7 r + 4 )

<• ( 4 t4 + 1 7 t 2+4 ) ( l+ t2 ) ,

2 ( - 5 8 t4+ 8 t6- 5 8 t2+ 8 - 4 t5- 1 7 t3- 4 t ) ( 4 t4 + 1 7 t2+ 4 ) ( l + t2)

N R

) R

C a r d i o i d A=(0,0) e C A=(-9,0) £ C

- 1 0 2 4 t3

±

N R

-8t

16*2 + 1 ! - 1 2 8 fi( 1 6 t -i- l ) _|_ l - 1 6 t2 '

( 1 6 * 2 + 1 ) 2 =>= 16(2 + 1, D R

2 ( t4- 6 t2+ 9 ) t2( t - l ) ( t + l ) 4t3(t4-6t2+9) \ -p (t4+2t2+l)2 ' (t4+2t2 + l)2 I ± t

N R

- 2 ( - 5 t2+ 2 t4 + l) - 4 t ( - 5 t2+ 2 t4 + l)^

T h r e e -leaved R o s e

A=(0,0) e C A=(-2,0) £ C T r i s e c t r i x of

M a c l a u r i n

A=(0,0) e C

A=(-4,0) £ C (t4 + 2t2 + l) ' (t_{N R} 4+2t2 + l ) ( t2- l ) R

, ( - 6 t + 6 tb + tt i- 3 t4+ 3 t2- l + 8 t3) ( t - l ) ( t + l ) *• ( t2+ l ) ( t6- 3 t4 + 3 t2- l + 8 t3)

F o l i u m of D e s c a r t e s

A=(0,0) e C A = ( - l , - l ) £ C

(t2+i)(t

2(-6t+6t5 + tb-3t*+3t^

+8t3)

-l+8t3)t

(t2 + l ) ( t6- 3 t4 + 3 t2- l + 8 t3) N R

) R

T a c n o d e A=(0,0) e C A=(0,l) e C

N R N R

, - 7 t * + 2 8 8 t2+ 2 5 6 _i_ 1 6 - t2

<• ( t2 + 1 6 )2 ^ t2 + 16>

±fc§)DR

A=(0,0) £ C - 1 6 t ( 5 t - 1 6 ) ((2 + 16)2

N R R a m p h o i d

C u s p

A=(0,0) e C

A=(-l,-l) £ C

N R N R L e m n i s c a t a

of B e r n o u l l i

A = ( - l , - l ) e C A=(-2,0) e C

N R N R

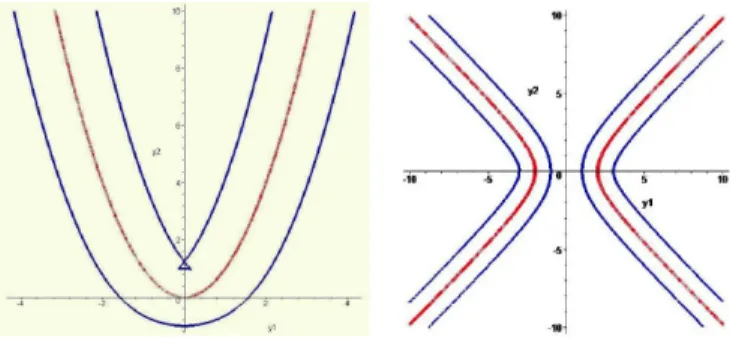
F i g . 2. Left: Parabola and the offset at d = 2. Right: Hyperbola and the offset at d = 1.5.

Fig. 3 . Left: Ellipse and the offset at d = 1. Right: Cardioid and the offset at d = 1.

Fig. 5. Left: Circle and the conchoid at A = (—2,0) and d = 1 (Limacon of Pascal).

Right: Straight line and the conchoid at A = (0, 0) and d = 2 (Conchoid of Nicomedes).

Fig. 6. Left: Conchoid of Sluze and the conchoid at A = (—2,0) and d = 1. Right:

Folium of Descartes and the conchoid at A = (0, 0) and d = 2.

Fig. 7. Left: Leniniscata of Bernoulli and the conchoid at A = (—2,0) and d = 1.

A c k n o w l e d g e m e n t s . Corresponding A u t h o r s u p p o r t e d by t h e Spanish

Minis-terio de Economia y Competitividad under t h e Project MTM2011-25816-C02-01.

References

1. Arrondo, E., Sendra, J., Sendra, J.R.: Parametric Generalized Offsets to Hypersurfaces. Journal of Symbolic Computation 23(2-3), 267-285 (1997)

2. Arrondo, E., Sendra, J., Sendra, J.R.: Genus Formula for Generalized Offset Curves. Journal of Pure and Applied Algebra 136(3), 199-209 (1999)

3. Farouki, R.T., Neff, C.A.: Analytic Properties of Plane Offset Curves. Comput. Aided Geom. Des. 7, 83-99 (1990)

4. Farouki, R.T., Neff, C.A.: Algebraic Properties of Plane Offset Curves. Comput. Aided Geom. Des. 7, 100-127 (1990)

5. Hoffmann, C M . : Geometric and Solid Modeling. Morgan Kaufmann Publis. (1993) 6. Kerrick, A.H.: The limacon of Pascal as a basis for computed and graphic methods

of determining astronomic positions. J. of the Instit. of Navigation 6, 5 (1959) 7. Menschik, F.: The hip joint as a conchoid shape. J. of Biomechanics 30(9)

(Septem-ber 1997) 971-3 9302622

8. Peternell, M., Gruber, D.: Conchoid surfaces of quadrics. Journal of Symbolic Computation (2013), doi:10.1016/j.jsc, 07.003

9. Peternell, M., Gruber, D., Sendra, J.: Conchoid surfaces of rational ruled surfaces. Comp. Aided Geom. Design 28, 427-435 (2011)

10. Peternell, M., Gruber, D., Sendra, J.: Conchoid surfaces of spheres. Comp. Aided Geom. Design 30(1), 35-44 (2013)

11. Peternell, M., Gotthart, L., Sendra, J., Sendra, J.: The Relation Between Offset and Conchoid Constructions. arXiv:1302.1859v2 [math.AG] (June 10, 2013) 12. Peternell, M., Pottmann, H.: A Laguerre geometric approach to rational offsets.

Computer Aided Geometric Design 15, 223-249 (1998)

13. Sendra, J., Sendra, J.R.: Algebraic Analysis of Offsets to Hypersurfaces. Mathematische Zeitschrif 234, 697-719 (2000)

14. Sendra, J., Sendra, J.R.: Rationality Analysis and Direct Parametrization of Gen-eralized Offsets to Quadrics. Applicable algebra in Engineering, Communication and Computing 11, 111-139 (2000)

15. Sendra, J., Sendra, J.R.: An Algebraic Analysis of Conchoids to Algebraic Curves. Applicable Algebra in Engineering, Communication and Computing 19, 413-428 (2008)

16. Sendra, J., Sendra, J.R.: Rational parametrization of conchoids to algebraic curves, Applicable Algebra in Engineering. Communication and Computing 21(4), 413-428 (2010)

17. Sendra, J.R., Sevilla, D.: Radical Parametrizations of Algebraic Curves by Adjoint Curves. Journal of Symbolic Computation 46, 1030-1038 (2011)

18. Sendra, J.R., Sevilla, D.: First Steps Towards Radical Parametrization of Algebraic Surfaces. Computer Aided Geometric Design 30(4), 374-388 (2013)

19. Sultan, A.: The Limacon of Pascal: Mechanical Generating Fluid Processing. J. of Mechanical Engineering Science 219(8), 813-822 (2005) ISSN.0954-4062