1. Usos de la Estadística y conceptos básicos... 1
2. Estadística Descriptiva y Estadística Inferencial... 3
3. Métodos básicos de la Estadística Descriptiva. ... 4
3.1. Recogida de datos ... 4
3.2. Ordenación y tabulación de datos... 5
3.3. Representación de datos ... 7
3.4. Parámetros estadísticos... 14
3.4.1. Medidas de posición o centralización... 14
3.4.2. Medidas de dispersión ... 20
3.4.3. Medidas de forma... 23
4. Métodos básicos de la Estadística Inferencial... 25
4.1. Muestreo ... 25
4.2. Estimación estadística ... 32
4.3. Contrastes de hipótesis... 33
5. Aplicaciones de la estadística ... 35
6. Series estadísticas bidimensionales. ... 40
6.1. Variables estadísticas bidimensionales: tablas estadísticas. ... 40
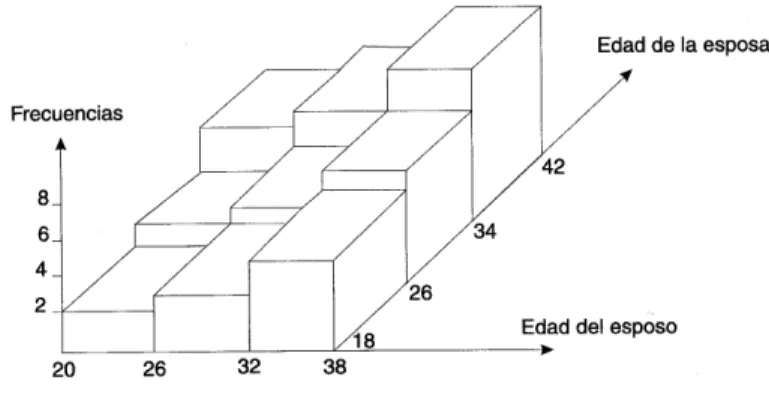
6.2. Representaciones gráficas... 42
6.3. Distribuciones marginales y condicionadas ... 44
6.3.1. Distribuciones marginales ... 44
6.3.2. Distribuciones condicionadas ... 44
6.3.3. Independencia y dependencia funcional ... 45
6.3.4. Características marginales y condicionadas ... 47
6.4. Covarianza ... 48
7. Regresión y correlación lineal... 49
7.1. El problema del ajuste... 49
7.2. Regresión lineal ... 50
8. Coeficiente de correlación ... 53
8.1. Correlación lineal ... 53
8.2. Coeficiente de correlación lineal: propiedades... 54
1 - USOS DE LA ESTADÍSTICA Y CONCEPTOS BÁSICOS
A pesar de los distintos usos de la Estadística, históricamente se la conocía con el único objetivo de recopilar datos, y así fue hasta el siglo XVII, momento en que los matemáticos comenzaron a abordar los problemas relacionados con el recuento de datos analizando las tendencias que se pueden presentar en los sucesivos resultados.
El hecho de entender y usar la Estadística únicamente como colección de datos se debía a que tradicionalmente la Estadística la usaban los gobiernos para establecer registros de nacimientos, defunciones, impuestos,... De hecho, la palabra Estadística tiene el mismo origen que la palabra estado y como puede verse en multitud de documentos históricos, los estados ya sabían como recoger y organizar los datos mucho antes que los métodos científicos les permitiesen un estudio de ellos.
Es a los matemáticos del s. XIX a los que les debemos el uso de la palabra Estadística en todo su sentido técnico ya que fueron ellos los que posibilitaron el paso de la estadística deductiva a la estadística inductiva o inferencial, que es la que actualmente tiene mayor influencia en todos los campos de la ciencia.
La ciencia de la Estadística se divide en dos partes: Estadística descriptiva y Estadística inferencial.
- La estadística descriptiva se encarga de la recogida, ordenación y tabulación de los datos obtenidos en las diferentes observaciones.
- La estadística inferencial cuya función es la de establecer conclusiones y tomar decisiones basadas en ese análisis descriptivo.
Conceptos básicos en un proceso estadístico
Es obvio que toda investigación estadística debe estar necesariamente referida a un conjunto o colección de personas o cosas (realmente existentes o posibles) que verifiquen una definición bien determinada.
Recibe el nombre de población el conjunto de individuos o elementos que tienen unas características comunes. Las personas o cosas que componen una población reciben el nombre de elementos y pueden tener existencia real: un coche, una casa, …, o bien referirse a algo mucho más abstracto: un intervalo de tiempo, un voto, etc..
El tamaño de una población viene dado por el número de elementos que componen dicha población. Puede ser finito o infinito. No siempre es posible analizar cada elemento de una población, ya sea por razones económicas, de tiempo, de personal disponible, por destrucción de los elementos tras el análisis... Por eso, en muchos estudios estadísticos se estudia solo una parte de la población, que denominamos muestra. La operación de tomar una muestra de la población se denomina muestreo.
hace por criterios personales no aleatorios, estamos ante un muestreo no probabilístico que nos da una muestra no representativa.
Las propiedades o cualidades que poseen los elementos de una población se denominan caracteres. Los caracteres de los elementos que componen una población los dividiremos en:
- Cuantitativos o variables. - Cualitativos o atributos.
Los caracteres cualitativos o atributos son los que se describen mediante palabras, tal como el sexo, estado civil, nacionalidad, etc. Un atributo adopta diversas modalidades. Por ejemplo el sexo: hombre o mujer.
Los caracteres cuantitativos o variables son los que se describen mediante números, es decir, son medibles; tales como la estatura, la edad,... Las variables se expresan con símbolos (x, y, z...) que pueden tomar un valor numérico de entre un conjunto de valores posibles que se denomina dominio de la variable.
Distinguimos dos tipos de variables:
- Variable discreta: cuando sus posibles valores son finitos o numerables - Variable continua: cuando sus posibles valores son infinitos no numerables.
La representación de un carácter mediante un número no es un indicador infalible de que se trate de una variable, pues a unos atributos se les asigna un número para indicar la modalidad. Por ejemplo para sexo: 1 para indicar hombre, 2 para indicar mujer. La verdadera diferencia entre un carácter cuantitativo y otro cualitativo es que si se trata de un atributo carece de sentido realizar operaciones algebraicas con los números que representan las modalidades. Además, los atributos se pueden ordenar por modalidades pero no jerarquizar.
Los resultados que se obtienen tras la observación de atributos y variables se denominan datos u observaciones. En el caso de las variables también se les suele llamar valores.
Los métodos de observación de los caracteres de los elementos se denominan:
- Observación exhaustiva: cuando observamos todos los elementos de la población. - Observación parcial: cuando sólo observamos los elementos de una muestra.
2 - ESTADÍSTICA DESCRIPTIVA Y ESTADÍSTICA INFERENCIAL
Cuando se observan exhaustivamente todos los elementos de la población (se supone que la observación se efectúa sin errores), entonces se dispone de todos los datos posibles para aquel estudio. Con tales datos, es posible describir exactamente las regularidades, el comportamiento o las características de la población.
• Estadística descriptiva
La Estadística descriptiva no es otra cosa, pues, que la ciencia dedicada a descubrir las regularidades o características existentes en un conjunto de datos. Pero si la observación no es exhaustiva, sino que se parte de una muestra con la finalidad de conocer, mediante ella, las características de la población, entonces nos enfrentamos con un proceso de inducción, en virtud del cual se aprovecha la información suministrada por la muestra para conocer, aunque sea aproximadamente, aquellas características.
• Estadística inferencial
La Estadística Inductiva, también llamada Inferencia Estadística, tiene, por tanto, como función, generalizar los resultados de la muestra para estimar las características de la población. No obstante, el conjunto de datos muestrales puede describirse o analizarse de la misma forma que una población. Por tanto, el conjunto de observaciones o datos de una muestra puede manejarse en un doble sentido. Primero, para describir el propio conjunto de observaciones, y segundo, para inferir lo que ocurre en la población.
En consecuencia, la fase descriptiva es común a cualquier conjunto de observaciones o datos, ya se refieran éstos a toda la población, a una muestra o incluso a una subpoblación. La Estadística descriptiva, por otro lado, es la parte más clásica y elemental de la ciencia estadística.
Como ya hemos mencionado, una población está constituida por todos los elementos que poseen unos caracteres por cuyo estudio estamos interesados. Una muestra, en cambio, es una parte de los elementos de la población, que, lógicamente, será representativa del total.
Cuando el estadístico puede observar todos los elementos de la población (observación exhaustiva), entonces su tarea se reduce a describir las características y regularidades de la población. Pero si la observación no puede ser exhaustiva, entonces aquellas características hay que estudiarlas a través de una muestra representativa. La información suministrada por la muestra sirve para inducir o inferir, con mayor o menor exactitud, las características de la población.
Conviene que subrayemos, y esto es muy importante, que los conceptos de población y muestra están subordinados al uso que se piensa hacer del conjunto de observaciones disponibles. Si lo único que se pretende es describir las características de dicho conjunto, entonces éste constituye, ciertamente, una población, aun cuando sea una parte de un total más general. Pero si se desea extender la información obtenida de él a otro conjunto mayor para inferir sus características, entonces, evidentemente, el conjunto de observaciones constituye una muestra (se supone que con todas las garantías).
3 - MÉTODOS BÁSICOS DE LA ESTADÍSTICA DESCRIPTIVA
Como hemos indicado, la estadística descriptiva es la que estudia los datos resultantes de una experiencia. En este caso con el término "estudia" nos referimos a recoger los datos, clasificarlos, representarlos y resumirlos en informaciones que ayuden a los interesados en su análisis para poder sacar conclusiones que ayuden a comprender algo o a la toma de decisiones. Por tanto, los métodos básicos que utiliza la Estadística descriptiva para describir e interpretar numéricamente la información obtenida de una gran cantidad de datos son:
- Recogida de datos.
- Ordenación y tabulación datos. - Representación de los datos.
- Calculo de los parámetros estadísticos.
Es importante tener en cuenta que en la estadística descriptiva no nos preguntamos si los datos provienen de una muestra de la población o de toda la población.
Con los datos obtenidos tras la observación y suponiendo ausencia de errores, tanto de medición como de manipulación, trascripción y cálculo, podemos describir perfectamente cuanto acontece en la población o muestra objeto de estudio. La estadística descriptiva es una fase necesaria para luego realizar inferencia.
3.1 - Recogida de datos
Por técnicas de obtención de datos entendemos el conjunto de métodos empleados para recoger una información determinada de una población o muestra. La obtención de datos se realizará de forma que facilite guardar la información con un orden lógico para su posterior estudio y minimizando los errores entre la información inicial dada y el dato final que se analizará. Son justamente el coste de estas técnicas de recogidas de datos, el tiempo necesario para ejecutarlas y el personal disponible, algunos de los motivos que inducen a realizar un muestreo en lugar de analizar cada elemento de la población. Una vez definidas, exactamente, la población, el tipo de muestreo y la muestra se elaborará un documento que permita recoger las respuestas a las preguntas de una manera sencilla y precisa.
Por las razones económicas, de tiempo y de personal antes comentadas, lo primero que se realiza para obtener los datos es buscar si la información que necesitamos ya ha sido trabajada, es decir, si existe alguna fuente que ya la haya estudiado. Una fuente importante son los registros administrativos en donde la información se recoge a nivel de gestión pero que luego se depura de manera que sea una información válida a distintos niveles. Estos trabajos se recogen a nivel oficial en el inventario de operaciones estadísticas del Estado.
En el supuesto de que no exista documentación estadística apropiada y suficiente para el estudio que pretendemos realizar es cuando se lleva a cabo los distintos métodos de recogida, siendo los más usuales:
• Por correo
• Por agentes distribuidores
Se encarece notablemente el método anterior si hay que investigar a una gran masa de población. Este método se realiza mediante agentes debidamente acreditados que recogen el cuestionario una vez efectuado. En esencia, es el mismo método que el anterior.
• Por encuestadores
Son ahora personas especializadas las que formulan las preguntas que aparecen en el cuestionario y anotan las respuestas. Lógicamente, este sistema es el más apropiado, aunque no elimina totalmente los errores, pues pueden darse algunas influencias en las respuestas. Su inconveniente es que puede resultar más caro que los dos primeros métodos. • Por teléfono
Evidentemente mucho más barato que por encuestadores aunque menos fiable. • Por Internet
Método cada vez más generalizado ya que permite minimizar costes, tiempo y personal necesario.
Hoy en día, los estadísticos siguen estudiando formas de mejorar algunos problemas relacionados con las técnicas de recogidas de datos. Estos problemas se centran en conseguir que los elementos de la población o muestra cumplimenten las encuestas necesarias y conseguir que las realicen de un modo que resulte más fiable.
El primero de los problemas, la "participación", se está consiguiendo de dos maneras: compensando de alguna forma al encuestado (regalos, vales descuentos ... ) o haciendo que las encuestas sean de obligado cumplimiento (como son algunas encuestas que el Estado realiza a distintas empresas).
El segundo de los problemas, la fiabilidad, se intenta mejorar implicando al encuestado en la propia encuesta, por ejemplo, enviando los estudios y resultados que se obtienen tras el análisis de los datos de la encuesta que ha realizado o de otras encuestas que lleve la misma empresa y que puedan ser interesantes para el encuestado.
Una de las formas de clasificar los datos para depurarlos y prepararlos para la realización de tablas es organizarlos en montones según una característica determinada aunque actualmente se suelen organizar y representar geográficamente (si los elementos estudiados pertenecen a una provincia, por pueblos; si pertenecen a una ciudad, por barrios ... ) Esta forma de organizar y representar los datos se denomina S.I.G. (Sistema de Información Georeferenciada).
3.2 - Ordenación y tabulación de datos
Todos los datos obtenidos mediante las distintas técnicas de recogida de datos se resumen en tablas, las cuales constituyen una parte fundamental de una investigación estadística. Toda tabla debe ir acompañada de una ficha técnica en donde se especifica el tipo y ámbito de la encuesta, el tipo de muestreo y tamaño de la muestra, el periodo de la referencia de la información, el método de obtención de datos utilizado y los fines de la investigación.
En las tablas estadísticas se introducen las siguientes magnitudes: • Frecuencia absoluta
• Frecuencia relativa
Es la frecuencia absoluta dividida por el número total de datos, que denominamos tamaño de la muestra y representaremos por N. Se suele expresar en tanto por uno, siendo el valor correspondiente al dato i -ésimo, fi, es decir:
N n
f i
i =
La suma de todas las frecuencias relativas es igual a la unidad. • Frecuencia absoluta acumulada
Es la suma de los distintos valores de la frecuencia absoluta tomando como referencia un individuo dado. La última frecuencia absoluta acumulada es el tamaño de la muestra. Si representamos su valor i-ésimo por Ni tenemos:
N1= n1
N2 = n1+n2
... Ni = n1 + n2 + ... + ni • Frecuencia relativa acumulada
Se obtiene al dividir cada frecuencia absoluta acumulada por el tamaño de la muestra, la representaremos por F, y también se puede definir, al igual que la frecuencia absoluta acumulada, como la suma de los distintos valores de la frecuencia relativa, tomando como referencia un individuo dado.
F1= f1
F2 = f1+f2
... Fi = f1 + f2 + ... + fi
La última frecuencia relativa acumulada es igual a la unidad.
Una tabla estadística contiene los datos observados y las distintas frecuencias absolutas y relativas de éstos. Una vez los datos están tabulados, la tabla obtenida ofrece una visión de conjunto de los caracteres que se estudian. Un ejemplo de una tabla estadística para una variable discreta es:
Datos xi
Frecuencia absoluta
ni
Frecuencia absoluta acumulada
Ni
Frecuencia relativa
fi
Frecuencia relativa acumulada
Fi
x1 n1 N1 f1 F1
x2 n2 N2 f2 F2
… … … … …
xn nn Nn = N fn Fn = 1
∑
ni = N∑
fi =1agrupar en intervalos [Li-1, Li) para facilitar la elaboración de la tabla y la comprensión de los
datos.
Antes de ver como se ordenan las frecuencias en una tabla para una variable continua veamos brevemente algunas definiciones propias de la tabla de frecuencia para variables continuas:
• Denominaremos recorrido a la resta entre el valor mayor de los datos y el valor menor y lo representaremos por Re.
• Para operar utilizaremos la marca de clase, el punto medio de un intervalo. La marca de clase se define como la semisuma de los valores extremos del intervalo, esto es, si la marca de clase del intervalo [Li-1, Li) la representamos por xi, entonces:
2 1 i i i
L L x = − +
• Denominaremos amplitud del intervalo a la diferencia entre el extremo superior del intervalo y el extremo inferior, es decir, a la longitud del intervalo, y se representa por:
ai = Li – Li-1
• El número de intervalos que formarán la tabla se obtendrá a partir de la raíz cuadrada del número de datos.
Número de intervalos = el número de datos
• Si los intervalos no son de la misma amplitud para trabajar con ellos obtendremos la densidad de frecuencia del intervalo i-ésimo, como el cociente entre el número total de observaciones de un intervalo, esto es , la frecuencia absoluta, y la amplitud del mismo:
a n
d i
i =
Teniendo en cuenta esto, la ordenación de la tabla será la siguiente:
Intervalo: [Li-1, Li)
Marca de clase: xi
ni Ni fi Fi
3.3 - Representación de datos
Una vez que la masa inicial de datos está tabulada, la tabla obtenida ofrece una visión de conjunto de los caracteres que se están estudiando. Un modo de poner de relieve dicha visión de conjunto consiste en utilizar representaciones gráficas de la tabla obtenida, lo que permite que el impacto visual proporcione una visión global del reparto de las observaciones.
deben considerar las representaciones gráficas como medios útiles de presentación de los datos que, junto con otras medidas numéricas, permitirán un estudio correcto de la masa de datos inicial y, por tanto, de los caracteres de la población que nos interesan.
En general, las representaciones gráficas más utilizadas se basan en un sistema de ejes cartesianos, de forma que en el eje horizontal (o de abscisas) se toman los distintos valores de la variable, y en el eje vertical (o de ordenadas) las frecuencias. Así, el plano queda determinado por cuatro cuadrantes, si bien en estadística la mayor parte de los gráficos pertenecen al primer cuadrante. Debe advertirse también que la graduación de los ejes puede obtenerse aplicando la escala aritmética o de números reales o la escala logarítmica. En el último caso, si se aplica a un solo eje, se dice escala semilogarítmica, y si se aplica a las dos, escala doblemente logarítmica.
Una posible clasificación de los distintos gráficos es respecto al tipo de variable que representa. Esta es la clasificación por la que optamos aunque los gráficos que veremos no tienen que ser exclusivos de un tipo variable concreta, como indicaremos en cada caso. En principio distinguimos dos tipos de gráficos independientemente se trate de una variable discreta o continua, estos gráficos dependen de que queramos representar las frecuencias (absolutas o relativas) o las frecuencias acumuladas.
Se denominan diagramas diferenciales a aquellos gráficos en los que se representan frecuencias absolutas o relativas y se denominan diagramas integrales a aquellos que se realizan a partir de las frecuencias acumuladas, lo que da lugar a gráficos crecientes, y es obvio que este tipo de gráficos no tiene sentido para variables cualitativas.
• Gráficos para variables cualitativas:
Los gráficos más usuales para representar este tipo de variable son los siguientes: a) Diagramas de barras.
Se realizan representando en el eje de ordenadas las variables y en el eje abscisas las frecuencias absolutas relativas.
Si, mediante el gráfico, se intenta comparar varias poblaciones entre sí, existen otras modalidades del diagrama de barras como por ejemplo:
Solteros 4
Casados 5
Viudos 7
Cuando los tamaños de las dos poblaciones son diferentes, es conveniente utilizar las frecuencias relativas, ya que en otro caso podrían resultar engañosas.
b) Diagrama de sectores
Para realizar estos diagramas, también llamados coloquialmente tartas, se divide un círculo en tantos sectores circulares como clases existan, de modo que el área de cada sector sea proporcional a la frecuencia que se quiera representar.Para calcularlo podemos decir que el área depende del ángulo central, mediante la siguiente proporción:
360 α = N ni
Así, siguiendo el ejemplo anterior:
Este diagrama se utiliza para cualquier tipo de variable. c) Pictogramas
d) Cartogramas
Para las distribuciones de tipo geográfico se suelen usar mapas, que se colorean con diferentes tonalidades, cuyas frecuencias equivalentes se explican al margen, o bien se colocan dibujos alusivos si se están estudiando los lugares en que se producen o se encuentran los bienes correspondientes. Estos gráficos se denominan cartogramas y la forma de construirlos se basa en la proporcionalidad con las frecuencias de la misma forma que los pictogramas.
• Gráficos para variables cuantitativas discretas:
a) Diagrama de barras
Para representar las frecuencias absolutas o relativas, acumuladas o no, de una variable cuantitativa discreta se utiliza principalmente el diagrama de barras, aunque se utiliza también para representar otros tipos de variables, como indicaremos en el apartado correspondiente.
En este caso, las barras deben ser estrechas para representar que los valores que toma la variable son discretos. En el eje de abcisas, situaremos los diferentes valores de la variable. En el eje de ordenadas la frecuencia que queramos representar. Levantaremos barras o columnas de altura correspondiente a la frecuencia adecuada.
Así, un ejemplo de diagrama diferencial de barras es:
Variables Frecuencia absoluta
Frecuencia absoluta acumulada
X1 5 5
X2 4 9
X3 6 15
X4 2 17
b) Diagrama integral o acumulado
El diagrama integral o acumulado tiene, por la naturaleza de la variable, forma de escalera.
• Gráficos para variables cuantitativas continuas:
Para variables cuantitativas continuas utilizaremos principalmente como diagramas diferenciales los histogramas y los polígonos de frecuencias.
a) Histograma
Un histograma se construye a partir de la tabla estadística, representando en el eje de abcisas los intervalos y en el eje de ordenadas las frecuencia que queremos representar. Es decir, es igual que el diagrama de barras para el caso discreto pero en este caso representaremos un rectángulo que tiene como base la longitud del intervalo al que hace referencia. El criterio para calcular la altura de cada rectángulo es el de mantener la proporcionalidad entre las frecuencias absolutas o relativas de cada intervalo y el área de los mismos.
El histograma, por tanto, representa las frecuencias de los intervalos mediante áreas y no mediante alturas. Sin embargo, como nos es mucho más fácil hacer representaciones gráficas teniendo en cuenta estas últimas, si todos los intervalos tienen la misma amplitud no es necesario diferenciar entre los conceptos de área y altura. Por ejemplo:
Frecuencia absoluta
[0-2] 2
[2-4] 1
[4-6] 4
[6-8] 3
b) Polígono de frecuencias
El polígono de frecuencias se construye fácilmente si tenemos representado previamente el histograma, ya que consiste en unir mediante líneas rectas los puntos del histograma que corresponden a las marcas de clase. Para representar el polígono de frecuencias en el primer y último intervalo, suponemos que adyacentes a ellos existen otros intervalos de la misma amplitud y frecuencia nula, y se unen por una línea recta los puntos del histograma que corresponden a sus marcas de clase
c) Polígono de frecuencias acumulado
El diagrama integral para una variable continua se denomina también polígono de frecuencias acumulado, y se obtiene como la poligonal definida en abcisas a partir de los extremos de los intervalos en los que hemos organizado la tabla de la variable, y en ordenadas por alturas que son proporcionales a las frecuencias acumuladas.
• Tendenciosidad y errores más comunes
Los errores más comunes y no significativos (por errores no significativos nos referimos a los errores no muestrales) podemos hablar de los siguientes tipos:
1. Errores de planteamiento, que se deben a una investigación mal estructurada o planificada, a definiciones ambiguas o incompletas que no permiten localizar perfectamente los elementos que han de ser observados.
2. Errores de respuesta, originados por un cuestionario poco pensado, por un método de recogida de datos inapropiado, por unos agentes mal instruidos O por no haber previsto el control y depuración de respuestas. Dentro de los errores de respuesta se incluye el «no consta», es decir, el cuestionario no contestado.
3. Errores de manipulación, provocados fundamentalmente por los defectos de organización, pudiendo suceder, incluso, que se pierdan cuestionarios antes de llegar al centro de tabulación.
4. Errores de tabulación y de cálculo, debidos, lógicamente, a la inexistencia de controles de operaciones.
5. Errores en la expresión de los datos, debidos principalmente a la forma como se realiza las gráficas. Es por ejemplo cuando la presentación de la gráfica no es legible.
6. Tendenciosidad, intencionada o no, es probablemente el principal problema que se puede presentar en un estudio estadístico. Consiste en presentar la información, información verdadera, de forma que pueda ser malinterpretada e inducir a error. Un ejemplo es el producido al no tener una escala predeterminada:
Aunque las dos tablas están realizadas con los mismos datos, el crecimiento de la primera parece mucho mayor que el de la segunda. Esto se ha debido, simplemente, al haber utilizado distintas escalas.
Otro ejemplo común es presentar un diagrama de barras con el eje de ordenadas no completo (en vez de comenzar en 0 comenzar en otro valor) mostrando un resultado tendencioso ya que da la impresión de que la diferencia entre las barras es diferente a la real.
3.4 - Parámetros estadísticos
Las tablas estadísticas y la representación gráfica nos dan una idea cualitativa de conjunto de una distribución de frecuencias que no es suficiente, por ejemplo, para comparar dos distribuciones.
Con el fin de obtener un resumen cuantitativo se sustituye el conjunto de valores por números llamados parámetros estadísticos o medidas descriptivas de los datos, que son unos números que nos permitirán, con objetividad y precisión, tener una visión más completa del fenómeno estudiado, comparar distintas distribuciones de frecuencias y valorar con números sus distintas características. Los parámetros estadísticos se clasifican en diversos tipos:
- Medidas de posición o centralización. - Medidas de dispersión.
- Medidas de asimetría y curtosis.
3.4.1 - MEDIDAS DE POSICIÓN O CENTRALIZACIÓN.
Las medidas de centralización son valores que están medidos en las mismas unidades que las observaciones y que nos indican en torno a qué posición se distribuyen las observaciones que disponemos, es decir, cómo se agrupan los datos observados.
Se clasifican en medidas de posición central (medias mediana y moda) y en medidas de posición no central (cuartiles, deciles , percentiles) dependiendo de que estos valores nos orienten sobre el lugar central de la distribución o sobre la posición de una parte cualquiera previamente determinada de la misma.
Todas ellas verifican que su valor está comprendido entre el menor y el mayor valor de los datos disponibles.
1.- Media aritmética de una variable.
Lo que se busca con este parámetro es determinar la posición central de una distribución cualquiera, de modo que su valor represente su centro de gravedad en el sentido de compensar las desviaciones con respecto a él de los valores de la variable en un sentido u otro.
Se define por tanto la media aritmética como la suma de todos los valores de la distribución dividida por el número total de datos y se representa por x . Así pues,
1 2
1 1 N N
i i
x x x
x x
N N =
+ + +
= … =
∑
Si el valor xi de la variable Xi se repite ni veces, hay que considerar estas repeticiones en la
suma, de modo que 1
k i i i
x n x
N
= ⋅
=
∑
; con1
k i i
n N
= =
∑
.La frecuencia relativa del valor xi queda determinada por i i
n f
N
= , por lo que podemos poner
1
k i i i
x x f
= =
∑
⋅supuesto se formulan las hipótesis de que el punto medio del intervalo de clase (marca de clase) representa adecuadamente el valor medio de dicha clase, y se aplicaría la fórmula original de la media simple para dichos valores.
Ventajas e inconvenientes
• Ventajas:
- se utilizan en el cálculo todos los valores de que se dispone en la distribución - está perfectamente determinada de forma objetiva y es única
- es calculable
- es el centro de gravedad de la distribución • Inconvenientes:
- los valores extremos muy dispares influyen de manera notable en su valor, por este motivo puede perder valor representativo
No obstante, la media aritmética, como medida de posición es la forma más adecuada para el resuman estadístico en el caso de distribuciones en escala de intervalos o de proporción, con los cuales dicha medida alcanza su máximo sentido.
2.- Media ponderada.
Cuando es conocido que los valores de la variable no tienen todos la misma importancia con respecto al tratamiento que deben dárseles, suele ser bastante útil utilizar una variable de la media aritmética denominada media ponderada.
Para calcularla se le asocia a cada valor de la variable xi un peso wi que mide su grado de
importancia en la distribución. Dichos pesos wi son valores positivos y representan el número de
veces que sus correspondientes valores xi son más representativos que un valor que tuviese peso
asociado a la unidad.
Se define la media aritmética ponderada de una distribución de valores x x1, 2,…,xk, de pesos
1, 2, , k
w w … w a
1
1
k
i i
i
p k
i i
x w x
w
=
= ⋅
=
∑
∑
Notar que los pesos wi pueden ser números reales positivos cualesquiera.
3.- Media geométrica.
En estas circunstancias, la medida de posición central más utilizada es la media geométrica. Entonces, dada una distribución de frecuencias (xi, ni), se define la Media Geométrica y se
representa por G a la raíz n-ésima del producto de los N valores de la distribución:
1 2
1 2
1
k i
k
n n
n n
N N
k i
i
G x x x x
=
= ⋅ ⋅ ⋅… =
∏
Notar que 1
k i i
n N
= =
∑
. El cálculo de G se facilita empleando logaritmos:1 1
log log
k
i i
i
G n x
N =
=
∑
⋅Ventajas e inconvenientes • Ventajas:
- está definida de forma objetiva y es única.
- considera en su cálculo todos los valores de la distribución.
- los valores extremos tiene menos influencia que en la media aritmética. • Inconvenientes:
- cálculo complicado
- sólo deba aplicarse cuando los valores de la distribución sean todos positivos, ya que si alguno fuese cero anularía la media geométrica y si hubiese valores negativos, se obtendrían valores imaginarios.
Su empleo más frecuente es el de promediar datos de tipo multiplicativo tales como porcentajes, tasas, números índices, etc., es decir, en los casos en que se supone que la variable presenta variaciones acumulativas.
4.- Media Armónica.
Se define la media armónica de una distribución de frecuencias (xi, ni) y se representa por H
como:
1 2
1 1 2
k
k i
i
k i
N N
H
n
n n n
x x x = x
= =
+ + +⋯
∑
Como puede verse, la inversa de la media armónica es la media aritmética de los inversos de los valores de la variable. Se suele utilizar para promediar velocidades, tiempos, rendimientos. Ventajas e inconvenientes
• Ventajas:
- en su cálculo intervienen todos los valores de la distribución. - cálculo sencillo.
- está definida de forma objetiva y es única. • Inconvenientes:
- no debe usarse con valores próximos a cero pues sus inversos pueden crecer en demasía haciendo despreciables frente a ellos la información aportada por valores mayores.
5.- Mediana
La Mediana es el valor de la distribución, supuesta ésta ordenada de menor a mayor, que deja a su izquierda y a su derecha el mismo número de frecuencias. Es decir, divide a la serie estadística ordenada en dos partes iguales, habiendo tantos valores por encima como por debajo de ella. También se puede definir como el valor de la distribución cuya frecuencia acumulada es N/2 (o su frecuencia relativa acumulada es ½).
Si los datos no están agrupados y están numerados de 1 a N, es el valor que ocupa el lugar que ocupa el lugar 1
2 N+
si N es impar. Cuando N es par, la mediana no queda definida y se toma la media de los valores
2 N
y 1
2 N +
.
Representando el polígono de frecuencias acumuladas, bastará con trazar la recta paralela al eje X de ordenadas N/2 y determinar la abcisa del punto en que lo corta. Puede suceder que la recta
2 N
y= tenga un segmento de puntos comunes, entonces se toma como mediana el punto medio del segmento.
N
N/2
M
x1 x2 x3 x5 x6 x7
N
N/2
M
x1 x2 x3 x5 x6 x7
N
N/2
M
x1 x2 x3 x4 x5 x6 x7
N
N/2
M
x1 x2 x3 x4 x5 x6 x7
En el caso de distribuciones agrupadas en intervalos no es necesario distinguir si los intervalos tienen la misma amplitud. Aplicando el método general de búsqueda del valor que ocupa el lugar N/2, en este caso nos encontramos con un intervalo mediano, en lugar de un valor mediano. Como queremos fijar la median en un valor, seleccionaremos un representante del intervalo mediano al que llamaremos mediana.
Suponemos que todos los valores comprendidos dentro del intervalo mediano se encuentran distribuidos uniformemente a lo largo de él. A continuación se considera la poligonal de frecuencias acumuladas correspondientes al intervalo mediano y a sus dos contiguos y determinamos gráficamente la mediana.
N/2
M
ai-1 ai
A B
B’
C C’ Ni
Ni-1
ci m
N/2
M
ai-1 ai
A B
B’
C C’ Ni
Ni-1
Vemos que M =ai−1+m. Determinamos m en base a la hipótesis fijada, que nos permite escribir
' '
AC BC
AC = BC , ya que los triángulos ABC y AB’C’ son semejantes. Por tanto AC=m, ' i
AC =c, BC=(N/ 2)−Ni−1 y B C' '=Ni−Ni−1 =ni.
Sustituyendo en la relación anterior se tiene que: ( / 2) i 1
i i
N N
m
c n
− −
= ,
y por tanto despejando tenemos ( / 2) i 1
i i
N N
m c
n
− −
= ⋅ ,
de modo que: 1
1
( / 2) i
i i
i
N N
M a c
n
− −
−
= + ⋅
Ventajas e inconvenientes
• Ventajas:
- es sencilla de calcular
- no influyen en ella más que los datos centrales de la distribución.
- se puede calcular aún desconociendo los valores extremos de la distribución siempre que contemos con suficiente información respecto de sus frecuencias.
• Inconvenientes:
- no puede expresarse mediante una fórmula matemática sencilla a efectos de realizar con ella grandes desarrollos matemáticos.
A pesar de la fórmula vista para el caso de distribuciones en escala por intervalos, la mediana tiene un mayor sentido en casos de distribuciones en escala ordinal (susceptibles de ser ordenados), de la cual es la medida más representativa por describir la tendencia central de la misma.
6.- Moda
Se llama Moda de una distribución de frecuencias al valor (o valores) de la variable al que corresponde mayor frecuencia. Una distribución de frecuencias puede tener una o varias modas. Si tiene una se llama unimodal, si tiene dos, bimodal, etc.
El cálculo de la Moda resulta sencillo en el caso de datos simples y datos agrupados, pero cuando los datos están agrupados en intervalos no obtendremos el valor exacto de la Moda, sino una aproximación que dependerá de las hipótesis que realicemos sobre las observaciones de cada intervalo considerado. Las hipótesis de partida son:
− Hay una moda en cada intervalo cuya densidad de frecuencia no es superada por ningún otro. − Dentro de los intervalos, la moda es aquel punto que equilibra las densidades de frecuencia de
los intervalos adyacentes, suponiendo que los valores se reparten en el interior de los mismos de manera uniforme.
Sea pues [ai−1,ai) un intervalo cuya densidad de frecuencia no es superada por ningún otro. Estre intervalo recibe el nombre de intervalo modal o clase modal. La densidad de frecuencia hi de
un intervalo i-ésimo es el cociente entre la frecuencia absoluta asociada ni y su amplitud ei: i i i
n h
M0
ai-1 ai
ei b ai+1 ai-2 hi hi+1 hi-1 a M0
ai-1 ai
ei b ai+1 ai-2 hi hi+1 hi-1 a
En la representación gráfica el equilibrio debe darse en el sentido de ser 1 1 i i h a b h + − =
Como la moda M0 será M0 =ai−1+b, tenemos 1 1
1 1 i i i i i e b a
b h h
h− + h− +
−
= ⋅ = ⋅ .
Despejando b h⋅ i−1= ⋅e hi i+1− ⋅b hi+1, y así 1 1 1 i i i i h b e h h + + − = ⋅
+ . Por tanto la expresión de M0 es 1 0 1 1 1 i i i i i h
M a e
h h + − + − = + ⋅ +
Si las amplitudes de los intervalos fuesen constantes, la expresión de la moda será 1 0 1 1 1 i i i i i n
M a e
n n + − + − = + ⋅ +
Ventajas e inconvenientes
• Ventajas:
- fácil interpretación - cálculo sencillo • Inconvenientes:
- no tiene una expresión matemática sencilla para el cálculo algebraico. - no intervienen en su determinación todos los valores de la distribución.
- los cambios en la distribución que se produzcan ajenos al valor modal no son detectados. La obtención de las modas de una distribución tienen una importancia propia derivada del hecho de que sirve para detectar posibles fusiones de distintas poblaciones unidimensionales en la masa de datos. A veces avisa de la necesidad de dividir dicha masa de datos en partes distintas para que el fenómeno que estamos tratando se estudie mejor.
7. - Medidas de posición no centrales.
• Cuartiles: son tres valores de la distribución que la dividen en cuatro partes iguales, es decir, en cuatro intervalos dentro de los cuales están el 25% de los valores de la distr5ibución. Se representan por Ci con i=1,2,3.
• Deciles: son los nueve valores de la distribución que la dividen en 10 partes iguales. Cada parte contendrá el 10% de la distribución. Se representan por Di, con i=1,2,…,9.
• Percentiles: son los 99 valores que dividen a la distribución en 100 partes iguales. Se representan por Pi, con i=1,2,…,99.
Notar que P25=C1; P50=C2=M; P75=C3; P10=D1; P20=D2; …; P90=D9. Su cálculo es análogo
al de la mediana y en general se aplica la expresión 1 / 1
i
r k i i
i
r
N N
k
Q a c
n
− −
⋅ −
= + ⋅ donde
1) para k = 4 y r = 1,2,3 obtenemos los cuarteles 2) para k = 10 y r = 1,2,…,9 obtenemos los deciles 3) para k = 100 y r = 1,2,…,99 obtenemos los percentiles
3.4.2 - MEDIDAS DE DISPERSIÓN.
Las medidas de dispersión tienen por objeto dar una idea de la mayor o menor concentración de los valores de una distribución alrededor de los valores centrales. Las medidas de tendencia central tienen como objetivo sintetizar toda la información de la que se dispone. Por tanto, medir la representatividad de estas medidas equivale a cuantificar la separación de los valores de la distribución con respecto de dicha media. La mayor o menor separación de los valores entre si se llama Dispersión o Variabilidad. Por tanto las medidas de dispersión nos miden el grado de dispersión de la distribución de la variable.
1 - Recorrido
Se llama recorrido a la diferencia entre el mayor y el menor de los valores de la variable y se representa por R: R= −xn x1
Por su sencillez de cálculo se utiliza sobre todo en el control de fabricación industrial, aunque es muy sensible a los valores erróneos.
El recorrido intercuartílico es la diferencia entre los valores P75 y P25 y nos indica el intervalo
de longitud RI donde están comprendidos el 50% central de los valores.
2 - Desviaciones
Consideremos un valor central C y un valor de la variable xi. Al valor xi - C se llama
desviación de xi respecto de C. Al valor xi−C , desviación absoluta.
1 1 k
i i
i
D x C n
N =
=
∑
− ⋅ (en caso de datos agrupados).Las desviaciones medias más utilizadas son respecto a la media y a la mediana, que se obtienen sustituyendo C por x y M, respectivamente.
Las desviaciones medias tienen un significado preciso como promedio de las desviaciones, aunque tienen el inconveniente de no ser adecuadas para el cálculo algebraico.
3 - Varianza y desviación típica
La varianza de una distribución de frecuencias es la media aritmética de los cuadrados de las desviaciones respecto a la media. Es el índice de dispersión más usado y se designa por σ2. Su expresión viene dada por:
(
)
22
1 1 k
i i
i
x x n
N σ
=
=
∑
− ⋅para datos agrupados y xi marcas de clase, siendo x la media aritmética de la distribución de
frecuencias (xi, ni).
A la raíz cuadrada positiva de la varianza se llama desviación típica y se obtiene como
(
)
21
1 k
i i
i
x x n
N
σ
=
=
∑
− ⋅Cálculo abreviado de la varianza y la desviación típica
Desarrollando la expresión anterior:
(
)
2(
)
22 2 2 2
1 1 1 1 1
2 2 2 2 2
1 1
1 1 1 2
2
1 1
2
k k k k k
i i i i i i i i i i
i i i i i
k k
i i i i
i i
x x
x x n x x x x n x n n x n
N N N N N
x n x x x n x
N N
σ
= = = = = = = = − ⋅ = + − ⋅ = ⋅ + − ⋅ = = ⋅ + − = ⋅ −∑
∑
∑
∑
∑
∑
∑
Disponiendo los cálculos en forma de tabla:
i
x n i n xi⋅ i 2
i i
n x⋅
1
x n1 n x1⋅ 1 2
1 1 n x⋅
⋮ ⋮ ⋮ ⋮
i
x ni n xi⋅ i 2
i i
n x⋅
⋮ ⋮ ⋮ ⋮
k
x nk nk⋅xk 2
k k
n ⋅x
i
N =
∑
x∑
n xi⋅ i∑
n xi⋅ i22
2 2
1 1
1 k 1 k
i i i i
i i
n x x n
La varianza medirá la mayor o menor dispersión de los valores respecto a la media aritmética. Si la dispersión es muy grande, la media no será representativa.
Propiedades de la desviación típica
• No tiene un sentido muy concreto en sí misma y tiene significado para comparar dos distribuciones. Dividiendo las desviaciones típicas de ambas se puede obtener cuántas veces una distribución es más dispersa que otra.
• Es más sensible que la media a los valores erróneos, puesto que intervienen al cuadrado. Su cálculo puede resultar pesado, por lo que a veces se prefiere el recorrido.
• Es la menor de todas las desviaciones cuadráticas respecto a un promedio.
• Para distribuciones simétricas o moderadamente asimétricas se cumple de forma aproximada que:
1. Entre x−σ y x+σ están aproximadamente el 68% de las observaciones. 2. Entre x−2σ y x+2σ están aproximadamente el 95% de las observaciones. 3. Entre x−3σ y x+3σ están aproximadamente el 98% de las observaciones.
También podemos utilizar como medida de dispersión respecto a la media la denominada Cuasivarianza:
*2 2
1 N S
N σ
= −
4 - Medidas de dispersión relativas.
Supongamos que se tienen dos distribuciones de frecuencias cuyos promedios son P1 y P2 y
queremos saber cuál de los dos es más representativa. Esta comparación no la podemos efectuar por sus respectivas medidas de dispersión ya que las distribuciones , en general, no vendrán dadas en las mismas unidades de medida. Tampoco, aunque sus unidades de medida sean las mismas, si los promedios son numéricamente diferentes. Por tanto es necesario construir medidas adimensionales. Estas medidas de dispersión, llamadas relativas, siempre vendrán dadas en forma de cociente. Entre ellas destacan:
• Coeficiente de apertura
Es la relación por cociente entre el mayor y el menor valor de una distribución: 1
n
x A
x = . Es muy fácil de calcular pero presenta inconvenientes:
− Mide la dispersión de la distribución, pero no hace referencia a ningún promedio por lo que no resuelve el problema de comparación entre estos.
− Sólo tiene en cuenta dos valores de la distribución (los extremos), lo que dará gran dispersión en el caso de que estén muy separados.
• Recorrido relativo.
Es el cociente entre el recorrido y la media aritmética Rr R x
• Recorrido semiintercuartílico
Es el cociente entre el recorrido intercuartílico y la suma del primer y tercer cuartil: 3 1
3 1
s
C C
R
C C
− =
+
• Coeficiente de variación de Pearson
Con él podemos comparar las medias aritméticas de dos distribuciones que vengan dadas en unidades diferentes. Se define como el cociente entre la desviación típica y la media aritmética:
. . S C V
x x
σ = =
Es una medida adimensional y representa el número de veces que σ contiene a x . Cuanto mayor sea C.V., más veces contendrá σ a x , por lo que a mayor C.V., menor representatividad de
x. El coeficiente se suele expresar en tanto por ciento.
Como tanto en σ como en x han intervenido todos los valores de la distribución, C.V. presenta la garantía de que utiliza toda la información.
La cota inferior de σ es cero (el menor valor que puede tomar σ) y es el valor de C.V. que indica la máxima representatividad de x .
3.4.3 - MEDIDAS DE FORMA
Se han visto hasta ahora las medidas de centralización o posición y las medidas de dispersión, de modo que tenemos una idea de las “forma” que tiene la distribución objeto de nuestro estudio. Pero es necesario definir otra serie de medidas que permitan cuantificar la forma de la distribución en dos sentidos: la mayor o menor simetría y la concentración más o menos acusada de los valores centrales de la distribución en torno a las medidas de posición central que ya conocemos.
Las medidas de forma de una distribución se pueden clasificar en dos grandes grupos: medidas de asimetría y medidas de curtosis.
1 - Medidas de asimetría
Las medidas de asimetría se dirigen a elaborar un indicador que permita establecer el grado de simetría (o asimetría) que presenta una distribución sin necesidad de llevar a cabo su representación gráfica. Diremos que una distribución es simétrica si al representarla gráficamente y trazada una vertical que pase por la media aritmética, deja a ambos lados el mismo número de valores.
Pearson define su índice de simetría como f1 x Mo σ −
= . Así si se verifica que f1 = 0, entonces
x=Mo=Me y la distribución es simétrica. Si f1 > 0 se dice que es asimétrica a la derecha, pues
Otro índice de simetría más general es el de Fisher, que vale
(
)
31
1 2
1 k
i i
i
x x n
N g
σ
=
− ⋅
=
∑
Análogamente como ocurría con el de Pearson, si g1 = 0 la distribución es simétrica, si g1 > 0
presenta asimetría a la derecha y si g1 < 0, asimetría a la izquierda.
2 - Medidas de apuntamiento o Curtosis
Estas medidas se aplican a distribuciones acampanadas, es decir, unimodales, simétricas o con ligera asimetría. Tratan de estudiar la distribución de frecuencias alrededor de la media y en la zona central de la distribución dará lugar a una distribución más o menos apuntada.
Para estudiar la curtosis de una distribución es necesario definir previamente una distribución “tipo” que se toma como modelo de referencia. Esta distribución es la llamada distribución normal, que corresponde a fenómenos muy corrientes en la naturaleza y cuya representación gráfica es una campana de Gauss dada por la fórmula
( )2 2
1 2 1 ( )
2
x x
f x e σ
σ π
− − =
Se trata de ver la deformación existente entre una distribución, en sentido vertical y la normal. Así diremos que una distribución puede ser más apuntada que la normal si es más alta, y recibe el nombre de Leptocúrtica. En caso contrario se la llama Platocúrtica. La propia distribución normal recibe el nombre de Mesocúrtica.
Se define el coeficiente de apuntamiento o curtosis como
(
)
41
2 4
1
3
k
i i
i
x x n
N g
σ
=
− ⋅
=
∑
− .Entonces si g2 = 0 tenemos una distribución mesocúrtica, o asimilable a la distribución normal
de Gauss.
Si g2 > 0 tenemos una distribución Leptocúrtica, más puntiaguda.
Y si g2 < 0, la distribución se llama Platocúrtica y es más aplanada.
4 - MÉTODOS BÁSICOS DE LA ESTADÍSTICA INFERENCIAL
La estadística inferencial establece previsiones y conclusiones sobre la población a partir de los datos obtenidos de una muestra, siguiendo un método basado fundamentalmente en el cálculo de probabilidades. Dicho cálculo busca crear modelos estadísticos teóricos que se ajusten lo más posible a la realidad y cuya función es generalizar los resultados de la muestra para estimar características de la población. Los métodos en los que se basa la Estadística inferencial para poder establecer sus conclusiones son:
- Muestreo.
- Estimación estadística. - Contraste de hipótesis.
4.1. Muestreo
Como ya se ha indicado, en estadística se llama Población o Universo, a cualquier conjunto o colección de individuos o elementos que tienen una característica común. Así son ejemplos de Población los habitantes de una provincia, los árboles de un bosque o los establecimientos comerciales de una ciudad. Lo que interesa en la Población es medir o contar uno o varios caracteres cuantitativos. Por tanto se hace necesario que la Población esté definida para saber qué elementos la componen.
Cuando se pueden observar todos los elementos de la Población, diremos que se está realizando un censo. En este caso la tarea a realizar es describir las características y regularidades de la Población con los métodos de la Estadística Descriptiva y construir el modelo de Distribución de Probabilidad para que pueda ser utilizado en posteriores investigaciones
Pero no siempre es posible analizar cada elemento de la Población debido a diferentes razones como:
- que sea inviable económicamente estudiar la población,
- que el estudio implique la destrucción del elemento (ensayos destructivos) - que la población sea muy difícil de controlar
- que se desea conocer rápidamente ciertos datos de la Población (p.e. encuestas de intención de voto)
por lo que las características de la Población deben ser estudiadas a partir de un subconjunto de esta. Hemos definido muestra de una Población como un subconjunto de elementos de dicha Población. El número de elementos que la componen se llama tamaño de la muestra y el proceso de escoger una muestra de una población, muestreo. Como ya se ha indicado, si la investigación se dirige a toda la población se estará haciendo un censo u observación exhaustiva. Si lo que se recoge es la información de una muestra, una encuesta.
Para obtener conclusiones razonables a partir de una muestra, esta debe estar bien elegida, debe ser representativa de la Población. Esta cualidad depende de dos aspectos fundamentales: el tamaño de la muestra y de cómo se realiza la selección de los individuos que la componen.
Por lo que respecta al tamaño, si la muestra es demasiado pequeña, no se obtendrían conclusiones relevantes y precisas salvo en el caso de poblaciones homogéneas, en las que cualquier subconjunto tiene características análogas al conjunto (p.e. una muestra de sangre). Por otra parte, un aumento del tamaño de la muestra no supone un aumento significativo de la representatividad.
Considerando la selección de los elementos, al sustituir el estudio de la población por el estudio de una muestra se comenten errores. Si la muestra está seleccionada al azar éstos se pueden controlar, pero si está mal elegida, no es representativa y aparecen errores imprevistos e incontrolados. Un ejemplo de estos errores se pueden ver en los estudios de intención de voto en las elecciones a la presidencia de los EEUU en 1936: una revista realizó la encuesta a más de 4 millones de sus lectores obteniendo el resultado de fracaso electoral de Roosevelt. Por otro lado, otra encuesta a 4500 personas adelantó el éxito del Roosevelt con bastante exactitud. La explicación es que el segundo estudio contaba con una muestra más homogénea de la sociedad americana de entonces.
Los integrantes de una muestra han de ser elegidos al azar, eliminando criterios personales. En este caso estamos ante un muestreo probabilístico al que se pueden aplicar métodos de inferencia estadística. Obtenemos así muestras representativas. En caso contrario estamos ante el muestreo opinático o no probabilístico (p.e. encuestas de Internet).
Hay dos tipos de errores en la selección de la muestra.
1. Errores muestrales, que se encuentran latentes en toda muestra representativa pues no proporciona una medida exacta de las características de la población, aun siendo representativa.
2. Sesgos, ocasionados por la falta de representatividad de la muestra, o a errores de observación debidos a definiciones defectuosas, medidas mal efectuadas, etc.
Por este motivo es importante conocer los tipos de muestreo así como la garantía de su representatividad. Para aumentar la representatividad sin necesidad de aumentar el tamaño de la muestra se recurre al muestreo o técnicas de muestreo. En la práctica resuelven el problema de la representatividad. Pero antes de pasar a estudiar los diferentes tipos de muestreo, se presentarán algunos conceptos básicos en el muestreo.
Distribución poblacional
Supongamos que en una Población dada nos interesa estudiar la característica numérica x, y tenemos para cada uno de sus elementos los valores x1, x2,…, xN. Su distribución queda definida
principalmente por los parámetros poblacionales que son:
N : tamaño de la Población;
Media poblacional: 1
N i i
x
N
Varianza poblacional:
2
2 1 1 2
( ) N N i i i i x x N N
µ
σ
= =µ
− =∑
=∑
− ;Desviación típica poblacional:
σ
= +σ
2 Proporción poblacional: AA p
N = ,
con A= nº de elementos de la población con la característica A. Destacar que estos parámetros son valores numéricos
Distribución de la muestra
Medimos en la muestra la característica numérica x que nos interesa. Ahora x es una variable estadística, y se estudia la distribución de sus frecuencias con los métodos de la Estadística Descriptiva. Si x1, x2,…, xn son los valores obtenidos, a partir de estos se calculan los parámetros
estadísticos o muestrales:
n : tamaño de la muestra;
Media muestral: 1
n i i x x n = =
∑
; Varianza muestral: 22 1 1 2
( )
n n
i i
i i
x x x
S x
n n
= =
−
=
∑
=∑
− ;Desviación típica muestral: S = + S2 ; Proporción poblacional: p
n α = ,
con α = nº de individuos de la muestra con la característica A. Destacar que ahora estos parámetros son funciones, pues dependen de la muestra escogida.
Nuestro objetivo es obtener información sobre la Ley de Probabilidad que rige la característica x de la Población a partir de las observaciones de la misma elegidas para formar la muestra, es decir, queremos estimar los parámetros poblacionales a partir de los datos muestrales. Así, se define como estadístico a cualquier función que depende sólo de los valores de la muestra x1, x2,…, xn, y
estimador a aquel estadístico que se utiliza para estimar el valor de un parámetro desconocido de la Población.
Como para cada muestra considerada el estimador toma un valor, este es una variable aleatoria, y por tanto, cada estimador tendrá una distribución que llamaremos Distribución muestral del estimador considerado. Los estadísticos más utilizados son 2
, ,
x S S y un parámetro muestral que se llama Cuasivarianza muestral, definido como:
2 2 1 ( ) 1 n i i C x x S n = − = −
∑
. (Notar queS2 n 1SC2 n
−
= , y 2 2
1 C n S S n = − )
El muestreo probabilístico se caracteriza porque puede calcularse de antemano la probabilidad de obtener cada una de las posibles muestras, para lo cual es necesario que la selección de la muestra pueda considerarse como un experimento aleatorio. Así cada observación xi es una variable
aleatoria que tiene la distribución de probabilidad de la Población: E[xi]=µ, V[xi]=σ2, para todo i =
Este tipo de muestreo es el único que tiene rigor científico y el único que puede darnos el error que cometemos en la inferencia. Dentro del muestreo aleatorio hay varios tipos que se verán a continuación.
I) Muestreo aleatorio simple
Se realiza en poblaciones en las que los datos son homogéneos, es decir, no existen factores que produzcan variabilidad sistemática. En este tipo de muestreos los elementos de la población homogénea se eligen al azar. La representatividad de una muestra obtenida por el muestreo aleatorio simple (MAS) viene garantizada por tener cada elemento la misma probabilidad de ser elegido. Así, si un 40% de la población tiene la característica xi, se obtendrá, por término medio, un
40% de elementos de la muestra con esa característica.
Se distinguen a su vez dos casos de MAS, dependiendo de que los elementos de la población se selecciones con o sin reemplazamiento.
I.1 - MAS sin reemplazamiento
Cuando las sucesivas extracciones de elementos se realizan sin reemplazamiento tenemos un número de muestras posibles dado por N combinaciones tomadas de n en n, por lo que la probabilidad de seleccionar una de ellas es P X( i) 1 / N
n
=
, con Xi muestra cualquiera de n
elementos de las N n
posibles. De este modo, la probabilidad de que la unidad ui pertenezca a la
muestra es ( ) 1 / 1
i
N N n
P u
n n N
−
= − =
.
La distribución que sigue la media muestral x , tiene por esperanza y varianza: Esperanza:
1 1
1 1 1
[ ] [ ]
n n
i i
i i
E x E x E x n
n = n = n
µ µ
= = = ⋅ ⋅ =
∑
∑
Varianza:
(
[ ]
)
2 2
[ ]
1
N n
V x E x E x
N n
σ
−
= − = ⋅
− , donde 1
N n
N −
− se llama factor de corrección para poblaciones finitas.
I.2 - MAS con reemplazamiento
Cuando las sucesivas extracciones de elementos se realiza con reemplazamiento, entonces tenemos un n-upla x1, x2,…, xn de variables aleatorias independientes e idénticamente distribuidas
según la distribución de la población.
Como tenemos Nn muestras posibles, la probabilidad de seleccionar una de ellas es por tanto 1/Nn. En este caso la distribución de la media muestral es:
1 1
1 1 1
[ ] [ ]
n n
i i
i i
E x E x E x n
n = n = n
µ µ
= = = ⋅ ⋅ =
∑
∑
2
2 2
2 2 2
1 1 1
1 1 1 1
[ ] [ ]
n n n
i i
i i i
V x V x V x n
n n n n n
σ
σ
σ
= = =
= = = ⋅ = ⋅ =