Programa de Contaduría Pública Prof. Pedro Quintela
Matemática I
Unidad II. Rectas en el Plano
1. Sistema Coordenado Cartesiano Rectangular
El conjunto de todos los pares ordenados de números reales recibe el nombre de plano numérico, el cual se denota , y cada par ordenado
es un punto del plano numérico.
Asimismo, los puntos de pueden identificarse con los puntos de un plano geométrico (espacio bidimensional) y existir una correspondencia uno a uno entre los mismos. Esta correspondencia se denomina
sistema coordenado cartesiano rectangular y es la base de todo análisis geométrico donde se representa las gráficas de funciones.
El sistema es un plano conformado por dos rectas infinitas perpendiculares entre sí, denominadas ejes de coordenadas. El eje horizontal es el eje de las o eje de las abscisas y el eje vertical es el eje de las o eje de las ordenadas. Estos ejes se intersecan en el punto denominado origen de las coordenadas y dividen el plano en cuatro cuadrantes, las cuales un punto ubicado en cada uno de ellos, las componentes del par ordenado tendrán los signos según los semi-ejes e del cuadrante respectivo.
Figura 2.1. Sistema coordenado cartesiano rectangular.
1.1. Coordenadas de un Punto
Para trazar un punto en el plano, basta trazar las unidades “ ” sobre el eje de las abscisas en la dirección correspondiente , trazar las unidades “ ” sobre el eje de las ordenadas en la dirección correspondiente , y luego, trazar rectas perpendiculares a los ejes de las abscisas y de las ordenadas por las distancias del origen dadas por el punto .
Figura 2.2. Coordenadas de un punto.
2. Distancia entre Dos Puntos
Dos puntos y que no estén en
una misma recta vertical u horizontal, conforman un triángulo rectángulo. La distancia está representada por la hipotenusa del triángulo rectángulo mientras que los catetos vienen dados por la diferencia e . Si se aplica el Teorema de Pitágoras , el cual dice que cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, se tiene que:
Figura 2.3. Distancia entre los puntos y .
3. Punto Medio
Sean los puntos y , el punto medio entre los puntos es .
Figura 2.4. Punto medio.
Como las coordenadas de se ubican en el centro del segmento y en el centro del segmento . Por consiguiente, e vienen dados por los promedios de las abscisas y de las ordenadas respectivamente. Es decir,
Donde
4. La Línea Recta
La línea recta es el lugar geométrico de los puntos del plano real tales que tomados dos puntos diferentes y del lugar, el valor de la pendiente resulta siempre constante.
4.1. Inclinación y Pendiente de una Recta
La inclinación de una recta, es el ángulo formado por el sentido positivo del eje y dicha recta.
Figura 2.5. Inclinación de una recta.
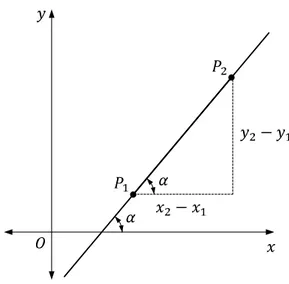
La pendiente o coeficiente angular de una recta es la tangente trigonométrica de su ángulo de inclinación y se denota
Donde,
Si y son dos puntos diferentes de una recta, la pendiente de la recta viene dada por
, si y sólo si Asimismo,
- Si , entonces la recta está inclinada hacia la derecha.
- Si , entonces la recta está inclinada hacia la izquierda.
- Si , entonces la recta está en posición horizontal.
- Si no existe, entonces la recta está en posición vertical.
4.2. Gráfica de una Ecuación
La gráfica de una ecuación en es el conjunto de los puntos de cuyas coordenadas son soluciones de una ecuación.
4.3. Ecuación de una Gráfica
Una ecuación de una gráfica es una ecuación que satisface las coordenadas de aquellos, y sólo aquellos, puntos de la gráfica.
4.4. Ecuación General de la Recta
La ecuación general de una recta es del tipo lineal en dos variables
En donde , y son constantes y teniendo como condición que y no sean nulas simultáneamente. - Si , y , entonces la recta es vertical
en: , donde
- Si , y , entonces la recta es el eje , es decir,
- Si , y , entonces la recta es horizontal en: , donde
- Si , y , entonces la recta es el eje , es decir, .
- Si , y , entonces la recta es de la forma: , donde la pendiente es y ordenada en el origen es .
4.5. Ecuación de la Recta Forma Explícita
Esta forma supone que se conoce la pendiente de la recta y su intersección con el eje en el punto
denominado también ordenada en el origen.
Figura 2.7. Recta dada por la pendiente y la ordenada al origen.
Despejando la ecuación general de la recta, se tiene:
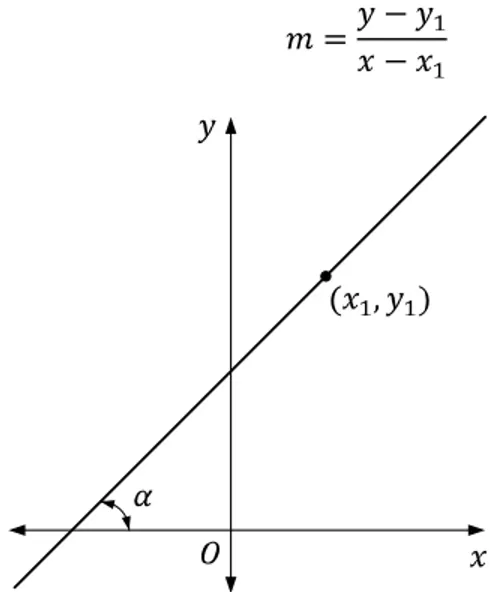
4.6. Ecuación de la Recta Forma Punto – Pendiente
Una recta que pasa por el punto y cuya pendiente es , está completamente determinada, si , es otro punto cualquiera de la recta y , debe cumplirse que la pendiente es
Figura 2.8. Recta dada por las coordenadas de un punto sobre ella y su pendiente.
4.7. Ecuación de la Recta Forma de Dos Puntos
Geométricamente una recta está perfectamente determinada si se conocen dos puntos de ella y analíticamente también lo está si se conocen las coordenadas de dos de sus puntos. De esta forma, la recta que pasa por los puntos y
viene dada por la ecuación:
Figura 2.9. Recta dada por las coordenadas de dos de sus puntos.
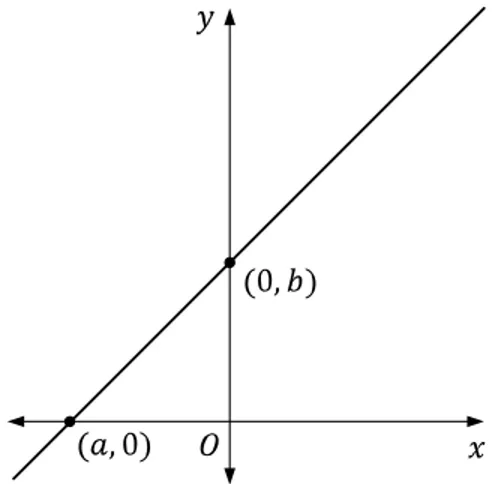
4.8. Ecuación de la Recta Forma Simétrica o Canónica
Si y son las intersecciones de la recta con los ejes e respectivamente, donde y , entonces los puntos y son dos puntos de la recta.
Figura 2.10. Recta dada por las intersecciones con los ejes coordenados.
La ecuación de la recta de la forma simétrica se halla sustituyendo los puntos y en la ecuación de la recta en forma de dos puntos, entonces:
Trasponiendo – al primer término
Dividiendo por se tiene
5. Posiciones Relativas entre Dos Rectas
Se considerarán las condiciones analíticas de cuatro casos específicos de posiciones relativas entre dos rectas, a saber:
- Rectas paralelas - Rectas perpendiculares - Rectas coincidentes - Rectas que se cortan
5.1. Rectas Paralelas
Si dos rectas son paralelas, entonces sus pendientes son iguales.
5.2. Rectas Perpendiculares
Si dos rectas son perpendiculares entre si, entonces la pendiente de una será la opuesta de la inversa de la otra pendiente.
5.3. Rectas Coincidentes
5.4. Rectas que se Cortan
Si dos rectas no son paralelas se cortan en un solo punto. Esta condición establece que las pendientes de ambas rectas son diferentes, es decir, . De esta forma se tiene, que las rectas poseen un punto en común, el cual representa la intersección de ambas rectas.
Para hallar el punto de intersección de dos rectas, se forman un sistema ecuaciones lineales, presentándose de esta forma:
El sistema tiene varias formas de resolverse estando entre ellas:
- Por sustitución - Por igualación - Por reducción - Por determinantes - Por matrices
Al resolverse el sistema se pueden presentar tres casos, a saber:
- Que el sistema sea compatible determinado, es decir, admite una sola solución, lo cual indica que las rectas si son secantes.
- Que el sistema sea, compatible indeterminado, es decir, que admite infinitas soluciones, por lo cual se está en el caso de rectas coincidentes.
- Que el sistema sea, incompatible, por lo cual no tiene solución, estando entonces en el caso de rectas paralelas.
5.4.1.Resolución de Sistemas de Ecuaciones de 2 Ecuaciones y 2 Incógnitas por Determinantes Los determinantes pueden utilizarse en la resolución de sistemas de ecuaciones lineales mediante fórmulas conocidas como la Regla de Cramer. Para un sistema de es
la Regla de Cramer viene dado por las fórmulas
Donde los denominadores de es el determinante de la matriz de los coeficientes de cada una de las variables. Para el valor de , en el numerador se tiene el determinante el cual se obtiene al reemplazar los coeficientes de ( y ) por los términos independientes y , análogamente; para el numerador de se tiene el determinante el cual se obtiene al reemplazar los coeficientes de ( y ) por los términos independientes y .
6. Ángulo entre Dos Rectas
Sean y dos rectas no perpendiculares, con ángulos de inclinación , y pendientes , respectivamente. Siendo , el mayor de los ángulos de inclinación, el ángulo entre ambas rectas es tal que , o sea , de donde:
Luego
Figura 2.11. Ángulo entre dos rectas.
El ángulo se puede calcular mediante la relación equivalente
7. Distancia entre un Punto y una Recta
La distancia de un punto a una recta se debe entender como la distancia más corta del punto a la recta, ésta se obtiene por la perpendicular trazada desde el punto a la recta, y viene dada por
donde son las coordenadas del punto y es la ecuación general de la recta .
Figura 2.12. Distancia de un punto a una recta.
8. Distancia entre Rectas Paralelas
Para calcular la distancia entre dos rectas paralelas se puede usar la fórmula anterior donde es un punto cualquiera sobre una de las rectas y la otra recta. Si las ecuaciones de las rectas son:
A partir de la fórmula de distancia de un punto a una recta se demuestra que la distancia entre ellas viene dada por:
Figura 2.13. Distancia entre rectas paralelas.
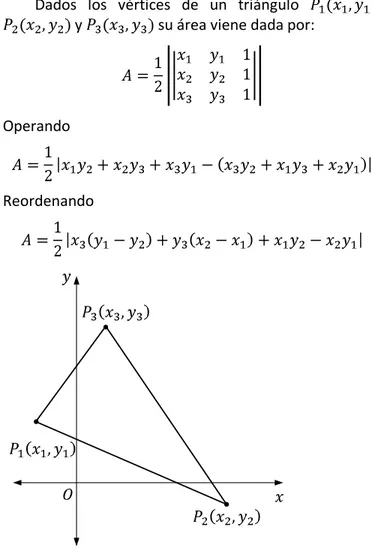
9. Área de un Triángulo
Dados los vértices de un triángulo , y su área viene dada por:
Operando
Reordenando
10. Propiedades Fundamentales de los Triángulos
A continuación se presentan algunos conceptos y propiedades de los triángulos, los cuales se requiere de su conocimiento para la resolución de problemas donde se aplican directamente.
Altura de un triángulo: Es la distancia que hay entre el vértice de un triángulo y su lado opuesto. Las tres alturas del triángulo son perpendiculares a los lados y se cortan en un punto llamado ortocentro.
Mediana de triángulo: Es la recta que pasa por un vértice del triángulo y por el punto medio de su lado opuesto. Las tres medianas de un triángulo se cortan en un punto llamado baricentro o centro de gravedad.
Mediatríz de un triángulo: Es la recta que pasa por el punto medio de un lado del triángulo y es perpendicular a él, las tres mediatrices de un triángulo se cortan en un punto llamado circuncentro puesto que es el centro del cículo que pasa por los tres vértices (círculo circunscrito).
Bisectríz de un ángulo del triángulo: Es la recta que pasa por un vértice del triángulo y divide al ángulo en dos partes iguales. Las tres bisectrices de un triángulo se cortan en un punto llamado incentro puesto que es el centro del círculo inscrito.