Magnitudes escalares y magnitudes vectoriales

Vectores y Trigonometría

1) Vectores

Magnitudes escalares y magnitudes vectoriales

Recordemos que una magnitud es cualquier propiedad de un sistema material que se puede medir. Las magnitudes las podemos clasificar en magnitudes escalares y magnitudes vectoriales. Las escalares son las quedan perfectamente determinadas mediante un número con su unidad. Por ejemplo, la masa de un objeto (2 Kg), o el tiempo que dura la caída de un cuerpo (3 s), o la temperatura a la que se encuentra un líquido (12 ºC), etc.

Las magnitudes vectoriales son aquellas que aparte de especificar su valor (con su unidad), hay que decir hacia dónde. Suelen representarse gráficamente mediante un segmento orientado (una flecha), que apunta hacia la dirección y sentido pertinente y cuyo tamaño (módulo) nos indica el valor. A esta flecha, le llamamos vector.

La velocidad es otra magnitud vectorial. Imaginemos que vamos hacia el norte en una avioneta a 200 km/h (con respecto al aire, que es con respecto a lo que se sostiene), y que hay viento hacia el este a 50 km/h con respecto al suelo. ¿A qué velocidad nos estamos moviendo con respecto al suelo? ¿Y si el viento sopla en otra dirección?

Para que un vector quede perfectamente determinado, es necesario aportar tres datos. Hay que especificar el módulo (con su unidad), que gráficamente representa el tamaño del vector; la dirección, que queda determinada por una recta, en la que se encuentra el vector; y un sentido. Dentro de una recta hay dos sentidos.

A todas las magnitudes vectoriales, hay que dibujarle una flechita encima de la letra que representa dicha magnitud (Figura 1). Así, el vector de la figura 1 lo hemos representado por a. Al módulo de este vector se puede representar de cualquiera de estas tres manera: ∥a∥=∣a∣=a.

Suma vectorial

Las magnitudes vectoriales tienen su propio álgebra, distinto al de las magnitudes escalares.

Como hemos visto en los ejemplos anteriores, el resultado depende de hacia dónde apunten las dos magnitudes vectoriales que vamos a sumar.

¿Y qué hay que hacer para sumar dos vectores? Lo vamos a ver gráficamente sumando el vector ⃗a

al vector ⃗_{b (Figura 2). Se dibuja el vector a, y empezando desde el extremo de a, se dibuja el}

vector _{b. El vector suma es aquel que empieza en el origen de a y termina en el extremo de} _b (Figura 3).



a

Figura 1

Figura 2



a



Hay otra manera de hacerlo. Se unen los dos vectores por sus orígenes, y se forma un romboide con estos dos lados, y dos más paralelos. El vector suma, es el vector que se puede dibujar en el interior del romboide que va desde el origen de los dos vectores hasta el vértice opuesto (Figura 4). Este método no se puede aplicar cuando los dos vectores tienen la misma dirección.

Es fácilmente demostrable, la suma de vectores es una operación conmutativa. Es decir:

⃗

a+⃗b=⃗b+⃗a

Si queremos sumar varios vectores gráficamente, podemos hacerlo sumandolos dos a dos hasta sumarlos todos, o podemos hacerlo de una vez mediante el primer método (Figura 5). En la figura 5 se ve cómo se han sumado los vectores ⃗a, ⃗_{b, ⃗c y d}⃗_.

Ejemplo

Imagínate que vas cruzando un río en una barquita, remando a 5 m/s (con respecto al agua) perpendicularmente a la orilla, y mientras, eres arrastrado por la corriente de agua a una velocidad de 2 m/s. ¿A qué velocidad neta te estarás moviendo? Como ya sabes, no podemos sumar estas velocidades como números; la velocidad no es 7 m/s. Son vectores lo que hay que sumar, y hay que sumarlos como tales.



abcd



a b c



d

Figura 5 Figura 4

⃗ a

⃗ b ⃗ a+ ⃗b

Figura 3

⃗

a

⃗ b

⃗

⃗

v_T= ⃗v₁+ ⃗v₂

Aplicando el Teorema de Pitágoras a uno de los triángulos rectángulos que tenemos (Figura 6), podemos calcular el módulo de la velocidad total o neta.

v=

√

+v2 2

)=

√

Otra posibilidad es medir el módulo del vector suma si tenemos la precaución de dibujarlo todo a escala.

Además, con un transportador de ángulos, podemos medir el ángulo de desviación que tiene la velocidad total con respecto a la dirección a la que remamos. O sabiendo un poco de trigonometría, con la función tangente (tg), podemos calcular ese ángulo, siendo de unos 22º con respecto a v₂.

Producto de un escalar por un vector

De la definición de suma de vectores que hemos visto, se pueden deducir otras operaciones. Por ejemplo, ¿cómo se multiplicará un número por un vector? Por ejemplo, ¿cuánto es 2a? El resultado será un vector con la misma dirección y sentido que a, pero con módulo el doble, ya que

2a es lo mismo que ⃗a+⃗a (Figura 7).

Así, deducimos, que al multiplicar un número cualquiera positivo por un vector, obtenemos otro vector de igual dirección y sentido, pero que su módulo se ha escalado según el número por el que hayamos multiplicado.

Se define el vector opuesto a a, que por ahora escribiremos por op(⃗a), como aquel vector que al sumárselo a a nos da cero. Como vemos gráficamente (Figura 8), op(⃗a) tiene que ser un vector con la misma dirección y sentido que a, pero con sentido opuesto. Si escribimos la ecuación vectorial:

⃗

a+op(⃗a)=0 Podemos despejar el vector opuesto y encontrar:

op(⃗a)=−⃗a

Es decir, el vector op(⃗a) es el vector a multiplicado por -1: op(⃗a)=−1·⃗a 

v₂



v₁ v1 v2

Figura 6

2⃗a ⃗

a ⃗a

En consecuencia, si multiplicamos un vector por un número negativo, obtendremos un vector en la misma dirección pero con sentido opuesto, y cuyo módulo quedará escalado según el valor absoluto del número por el que hemos multiplicado (Figura 9).

Con todo lo visto, ¿cómo se calcularía gráficamente a

3−b? (Figura 10).

Parece una diferencia entre dos vectores. Pero hay que tener muy claro, que restar es sumar el opuesto. Además en el primer vector aparece una división entre un escalar. Pero tampoco hay que olvidar que dividir entre 3 es lo mismo que multiplicar por 1/3.

Componentes de un vector

Podemos utilizar un sistema de ejes para representar los vectores. Desde luego, la situación más fácil es cuando los ejes son perpendiculares entre sí (Figura 11).



a _−3a

−a −a

−a

Figura 9

Figura 10

 a

 b

1 3a

−b

1 3a−b

O Y

P

X

Figura 11 a b

⃗r



a op(⃗a)

Figura 8



a op(⃗a)

Hemos representado el vector ⃗r colocando su origen el el punto O, que es el origen del sistema de coordenadas, y su extremos en P.

Si consideramos los vectores ⃗a y ⃗_{b, como vemos en la figura 12, se cumple que:}

⃗r=⃗a+ ⃗b

A los vectores ⃗a y ⃗_{b se les llama componentes del vector ⃗r respecto al sistema de referencia que} hemos tomado. Si el sistema de ejes hubiera sido otro, las componentes serían distintas.

Coordenadas del vector

Se definen los vectores ̂_{i y} ̂_{j como dos vectores de módulo uno que apuntan en las direcciones y} sentidos de los ejes X e Y respectivamente (Figura 13). Así, podemos representar las componentes del vector de posición como ⃗a=âi y ⃗_b=b̂_{j. A} a y b se les llama coordenadas del vector ⃗r con respecto al sistema de ejes tomado. A los vectores _{i y} _{j se les denomina versores.}

Podemos escribir:

⃗r=⃗a+ ⃗b=â_{i+ b}̂_{j=(a , b)}

Utilizando las coordenadas de los vectores, se puede operar analíticamente más fácilmente. Puede comprobarse que la suma de vectores, se limita a sumar las coordenadas.

Por ejemplo: sea ⃗r=(a , b) y ⃗p=(c , d). Entonces ⃗r+ ⃗p=(a+c , c+d).

El producto de un escalar por un vector, también es más fácil. Si ⃗r=(a , b), y queremos O

Y

P

X

r

Figura 13

_j

_i

b_j

ai

O Y

P

X

Figura 12

⃗

a

⃗

multiplicarlo por e, nos dará e ·⃗r=(e · a , e · b).

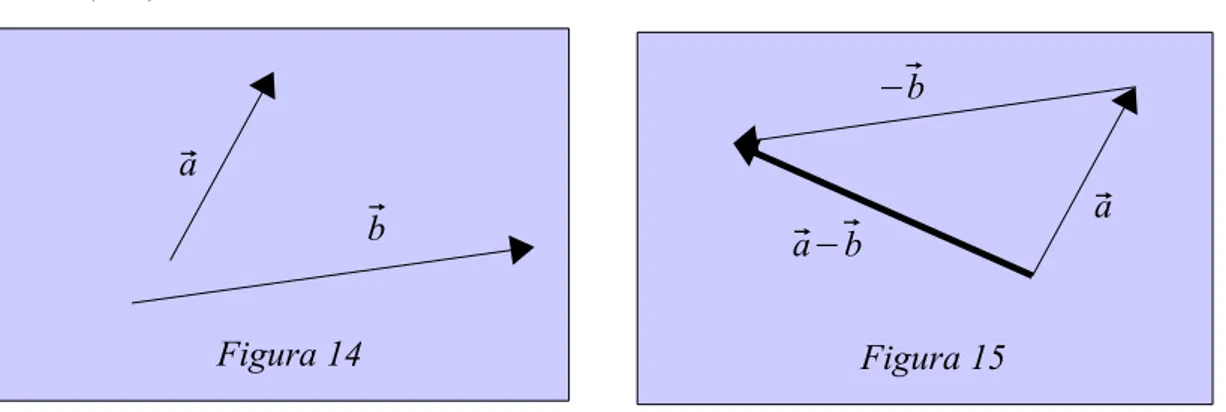
Una operación que no hemos visto es la diferencia de dos vectores. Restar dos vectores es sumar el opuesto. Así, para hacer la diferencia ⃗a−⃗b, lo que hacemos es sumar −⃗b. Es decir:

⃗

a−⃗b=⃗a+(−⃗b) (Figura 14 y Figura 15).

O si queremos, podemos aprendernos la regla de dibujar un vector que sale del extremos del sustraendo y llega al extremo del minuendo (Figura 16).

Si trabajamos con coordenadas, simplemente restamos las coordenadas. Por ejemplo: sea ⃗r=(a , b)

y ⃗p=(c , d). Entonces ⃗r−⃗p=(a−c , c−d).

2) Funciones trigonométricas

Triángulos rectángulos

Como sabemos, un triángulo rectángulo, es un triángulo con un ángulo recto, tal y como el de la figura 17. A los lados a y b se les llama catetos, y al c hipotenusa.

Figura 16

⃗

a

⃗

b

⃗

a−⃗b

Figura 15

⃗ a −⃗b

⃗

a−⃗b

Figura 14

 a

 b

Figura 17

c a

La suma de los dos ángulos agudos nos da 90º. Si nos fijamos en uno de los ángulos agudos, y lo llamamos θ, ya podemos distinguir los dos catetos (Figura 18).

Ahora a es el cateto opuesto, y b el cateto contiguo.

Propiedades de los triángulos rectángulos

Imaginemos dos triángulos rectángulos cualesquiera que sean semejantes. Como los de la figura 19.

Puesto que son semejantes, se cumple que, a a '=

b b '=

c c ' De esta expresión, podemos deducir estas otras dos:

a c=

a ' c ' (1) b

c= b ' c ' (2)

Función seno

Así, la ecuación (1) significa que si tenemos dos triángulo rectángulos con un mismo ángulo θ, si dividimos el cateto opuesto entre la hipotenusa, nos da el mismo valor. Y esto es cierto para cualquier triángulo rectángulo con un ángulo obtuso igual a θ. Evidentemente, esa división dará resultados distintos si cambiamos el valor del ángulo θ. Por tanto, podemos construir una función, que a cada valor de θ le asigne el resultado de hacer el cociente entre el cateto opuesto y la hipotenusa (a/c).

Figura 18 c a

b θ

Figura 19

c a

b θ a ' b '

c '

A esta función, se le llama seno, y se representa por senθ, o en inglés por sinθ.

Por consiguiente, sinθ=a

c . Esta función, viene en las calculadoras científicas, en las que introduciendo un ángulo, nos da el resultado de dicho cociente.

Fíjate que esta función no puede valer más de uno, puesto que un cateto siempre es menor que la hipotenusa.

Tal y como hemos definido la función seno, vemos que podemos poner ángulos desde casi cero hasta casi 90º.

Para que la función seno sea continua, definimos los casos especiales sin 0=0 y sin 90º=1 . Así la función seno, es una función creciente que va desde cero, cuando θ=0 , hasta uno cuando θ=90º.

Función coseno

Totalmente análogo, se puede razonar con la ecuación (2). Y obtenemos una nueva función llamada coseno, cos , definida de la siguiente manera,

cosθ=b

c

Es decir, en esta ocasión, dividimos el cateto contiguo entre la hipotenusa.

Este resultado también es siempre menor que uno, y para hacer continua esta función, definimos cos0=1 y cos90º=0 . La función coseno es una función decreciente, que toma el valor uno cuando θ=0 , y cero cuando θ=90º .

Cuando se estudie estas funciones más ampliamente en la asignatura de matemáticas, el alumno comprobará que las funciones seno y coseno se pueden definir para cualquier ángulo, y que las funciones tomarán valores desde -1 hata 1. Nosotros nos conformaremos con ángulos desde 0 hasta 90º, donce las funciones toman valores desde 0 hasta 1.

Función tangente

Se define la función tangente, tg en español, y tan en inglés, como el cociente entre el seno y el coseno. Es decir,

tanθ=sinθ

cosθ

Como vemos, la tangente, también se puede calcular dividiendo el cateto opuesto entre el cateto contiguo.

tanθ=sinθ

cosθ=

a c b c

=a

b

Funciones inversas

Puesto que estas funciones son estrictamente monótonas, tienen cada una una función inversa. A la inversa del seno, se le llama arcoseno (arcsen o arcsin). Si a esta función le introduces un valor de algún seno, te devuelve el ángulo correspondiente a ese valor de seno.

Análogamente, se definen las funciones arcocoseno ( arccos ), y arcotangente (arctg o arctan ).

Ejemplo

Podemos utilizar cualquiera de estas tres funciones inversas para determinar un ángulo de un triángulo rectángulo.

Consideremos un triángulo rectángulo cuyos catetos miden 3 y 4.

Es decir, a=3 y b=4 . La hipotenusa la calculamos fácilmente mediante el Teorema de Pitágoras.

c=

√

=

√

=5

Vamos a determinar el ángulo θ. Para ello podemos utilizar cualquiera de las funciones inversa. Por ejemplo, vamos a utilizar la función arcoseno.

sinθ=a

c⇒arcsin(sinθ)=arcsin a

c⇒θ=arcsin a

c=arcsin

3

5≈36,9º El ángulo φ es el complementario, θ+ φ =90º⇒ φ=90º−θ=90º−36,9º=53,1º.

Lógicamente, podríamos haber averiguado el ángulo φ utilizando las funciones trigonométricas relacionadas en este ángulo, teniendo en cuenta que con respecto a φ , b es el cateto opuesto, y a

el contiguo.

Figura 20 c a

b θ