INSTITUTO TECNOLÓGICO Y DE ESTUDIOS SUPERIORES DE MONTERREY
PRESENTE.-Por medio de la presente hago constar que soy autor y titular de la obra denominada
, en los sucesivo LA OBRA, en virtud de lo cual autorizo a el Instituto Tecnológico y de Estudios Superiores de Monterrey (EL INSTITUTO) para que efectúe la divulgación, publicación, comunicación pública, distribución, distribución pública y reproducción, así como la digitalización de la misma, con fines académicos o propios al objeto de EL INSTITUTO, dentro del círculo de la comunidad del Tecnológico de Monterrey.
El Instituto se compromete a respetar en todo momento mi autoría y a otorgarme el crédito correspondiente en todas las actividades mencionadas anteriormente de la obra.
Modelado de Juegos Diferenciales Lineales Utilizando Redes
Neuronales -Edición Única
Title Modelado de Juegos Diferenciales Lineales Utilizando Redes Neuronales -Edición Única
Authors Ernesto Manuel Anaya Muedano Affiliation ITESM-Campus Estado de México Issue Date 2007-07-01
Item type Tesis
Rights Open Access
Downloaded 19-Jan-2017 06:12:20
MODELADO DE JUEGOS DIFERENCIALES LINEALES
UTILIZANDO REDES NEURONALES
TESIS QUE PARA OPTAR EL GRADO DE MAESTRO EN CIENCIAS DE LA INGENERÍA PRESENTA
ERNESTO MANUEL ANAYA MUEDANO
Director: DR. DAISHI A. MURANO LABASTIDA
Comité de Tesis:
DR. VIRGILIO VÁSQUES LÓPEZ
DR. JESÚS ULISES LICEAGA CASTRO
MC. GUILLERMO SANDOVAL BENITEZ
A mis padres y hermanos, por su apoyo durante mis estudios...
A Daishi, por su apoyo, amistad y guía durante estos años...
A todos mis amigos y profesores por sus enseñanzas y apoyo durante mi carrera
Cuando existe una interacción entre diferentes sistemas, en ocasiones su
com-portamiento puede verse afectado en su dinámica y en los objetivos que persiguen.
Estos sistemas pueden pertenecer a campos tales como la económica, la política, las
matemáticas, la mecánica, la aeronáutica, etc. El desarrollo de controladores para este
tipo de sistemas, con el n de obtener un comportamiento deseado, ha tenido un avance
notorio en los últimos años, pero éste ha estado basado en el conocimiento total del
modelo matemático que describe a dichos sistemas. El problema identi cado es que
en la mayoría de los casos no se tiene un modelo matemático completo o se carece del
mismo, lo que hace que la tarea de diseño de los controladores sea muy difícil. Este
proyecto de tesis muestra el desarrollo llevado a cabo para obtener el modelo de una
clase de juegos diferenciales lineales mediante el uso de una red neuronal diferencial
y el diseño de un algoritmo de aprendizaje para esta red. Las redes neuronales son
una herramienta que han probado ser efectivas en la identi cación de sistemas cuyo
When different systems interact with each other, sometimes their behavior may
be affected in their dynamics and the objectives they pursue. Such systems may
rep-resent models in elds such as economics, politics, mathematics, mechanics,
aero-nautics, etc. Development of controllers for such types of systems in order to obtain
a desired performance, have had a notorious advance during the last few years, but
such developments have been based in the total knowledge of the mathematical model
which describes such systems. A major problem is that in most cases a complete
mathematical model is not available or there is no mathematical model available at all,
which makes the design of controllers a very dif cult task. This document shows the
development to obtain the model of a class of linear differential games by means of a
differential neural network and the design of a learning algorithm for this net. Neural
networks are tools which have proven to be effective in obtaining the model of systems
1 ANTECEDENTES.
. . .1
1.1 REDES NEURONALES. . . 2
1.1.1 REDES NEURONALES DINÁMICAS. . . 7
1.1.2 IDENTIFICACIÓN DE SISTEMAS LINEALES. . . 9
1.2 TEORÍA DE JUEGOS DINÁMICOS NO-COOPERATIVOS. . . 11
1.2.1 JUEGOS DIFERENCIALES. . . 14
2 PLANTEAMIENTO DEL PROBLEMA.
. . . .16
2.1 ESTADO DEL ARTE. . . 17
2.2 JUSTIFICACIÓN. . . 19
2.3 OBJETIVO GENERAL. . . 20
2.4 OBJETIVOS ESPECÍFICOS. . . 21
2.5 ALCANCES. . . 21
3 MODELADO Y OBTENCIÓN DEL ALGORITMO DE
APRENDIZAJE.
. . . .22
3.1 DESCRIPCIÓN DE LA RED NEURONAL. . . 23
3.2 CONDICIONES DE DISEÑO. . . 28
4.1 JUEGO DIFERENCIAL CON DOS JUGADORES. . . 46
4.2 JUEGO DIFERENCIAL CON TRES JUGADORES. . . 52
4.3 ANÁLISIS EN FRECUENCIA: JUEGO DIFERENCIAL CON DOS JUGADORES. . . 58
4.4 INTERACCIÓN ENTRE LOS JUGADORES: JUEGO DIFERENCIAL CON 3 JUGADORES. . . 68
4.5 ANÁLISIS DE RESULTADOS. . . 74
5 CONCLUSIONES.
. . . .76
5.1 TRABAJO FUTURO . . . 77
REFERENCIAS.
. . .79
A CONSTRUCCIÓN DE LAS REDES NEURONALES
DIFERENCIALES.
. . . .81
A.1 Red Neuronal Diferencial: 2 Jugadores . . . 81
Figura 1.1 Neurona Biológica . . . 3
Figura 1.2 Elementos Básicos de una Neurona Arti cial . . . 6
Figura 1.3 Red Neuronal Dinámica (discreta). . . 8
Figura 1.4 Estructura General de una Red Neuronal Diferencial . . . 11
Figura 3.1 Aprendizaje y Error de Modelado . . . 26
Figura 4.1 Estados del Juego diferencial de 2 Jugadores (Simulación Completa -80s) . . . 48
Figura 4.2 Estados Modelados por la Red Neuronal - 2 Jugadores (Simulación Completa - 80s) . . . 48
Figura 4.3 Estados del Juego Diferencial de 2 Jugadores (Final de la Simulación -últimos 10s) . . . 49
Figura 4.4 Estados Modelados por la Red Neuronal - 2 Jugadores (Final de la Simulación - últimos 10s) . . . 50
Figura 4.5 Error entre Estados del Juego Diferencial y Estados Estimados - 2 Jugadores (Simulación Completa - 80s). . . 51
Figura 4.6 Error Medio Cuadrático - 2 Jugadores (Final de la Simulación - últimos 10s) . . . 51
Figura 4.7 Estados del Juego Diferencial de 3 Jugadores (Simulación Completa -80s) . . . 54
Figura 4.8 Estados Modelados por la Red Neuronal - 3 Jugadores (Simulación Completa - 80s) . . . 55
Figura 4.9 Estados del Juego Diferencial de 3 Jugadores (Final de la Simulación -últimos 10s) . . . 56
Figura 4.12 Error Medio Cuadrático - 3 Jugadores (Final de la Simulación - últimos 10s) . . . 58
Figura 4.13 Estados del Juego Diferencial de 2 Jugadores - f=0.01rad/s (Simulación Completa - 5,000s) . . . 62
Figura 4.14 Estados Modelados por la Red Neuronal de 2 Jugadores - f=0.01rad/s (Simulación Completa - 5,000s) . . . 62
Figura 4.15 Error Medio Cuadrático - 2 Jugadores - f=0.01rad/s (Simulación Completa - 5,000s) . . . 63
Figura 4.16 Estados del Juego Diferencial de 2 Jugadores - f=1rad/s (Final de la Simulación - últimos 100s) . . . 63
Figura 4.17 Estados Modelados por la Red Neuronal de 2 Jugadores - f=1rad/s (Final de la Simulación - últimos 100s) . . . 64
Figura 4.18 Error Medio Cuadrático - 2 Jugadores - f=1rad/s (Simulación Completa - 5,000s) . . . 64
Figura 4.19 Estados del Juego Diferencial de 2 Jugadores - f=1rad/s (Final de la Segunda Simulación - últimos 50s) . . . 66
Figura 4.20 Estados Modelados por la Red Neuronal de 2 Jugadores - f=1rad/s (Final de la Segunda Simulación - últimos 50s) . . . 67
Figura 4.21 Error Medio Cuadrático - 2 Jugadores - f=1rad/s (Segunda Simulación Completa - 5,000s) . . . 67
Figura 4.22 Estados del Juego Diferencial de 3 Jugadores con Interacción
(Simulación Completa - 100s). . . 70
Figura 4.23 Estados Modelados por la Red Neuronal - 3 Jugadores con Interacción (Simulación Completa - 100s). . . 71
Figura 4.24 Estados del Juego Diferencial de 3 Jugadores con Interacción (Final de la Simulación - últimos 10s) . . . 72
Figura 4.27 Error Medio Cuadrático - 3 Jugadores con Interacción (Simulación Completa - 100s) . . . 73
Figura 5.1 Sistema Real - Juego Diferencial de 2 Jugadores . . . 82
Figura 5.2 Subsistema de Sistema Real - Juego Diferencial de 2 Jugadores . . . . 82
Figura 5.3 Programa para Sistema Real - Juego Diferencial de 2 Jugadores . . . 83
Figura 5.4 Modelado de Estados de la Red Neuronal Diferencial - 2 Jugadores 83
Figura 5.5 Subsistema para Sigmoidales de Modelado de Estados - 2 Jugadores 84
Figura 5.6 Subsistema para Aprendizaje de Pesos Sinápticos V1- 2 Jugadores 85
Figura 5.7 Programa para Aprendizaje de Pesos Sinápticos V1 - 2 Jugadores . . 85
Figura 5.8 Subsistema para Aprendizaje de Pesos Sinápticos W1- 2 Jugadores 86
Figura 5.9 Programa para Aprendizaje de Pesos Sinápticos W1- 2 Jugadores . 86
Figura 5.10 Modelado de Dinámica de Jugador 1 - 2 Jugadores . . . 87
Figura 5.11 Subsistema para Sigmoidales de Jugador 1 - 2 Jugadores . . . 87
Figura 5.12 Subsistema de Aprendizaje de Pesos Sinápticos V2 para Jugador 1 - 2
Jugadores . . . 88
Figura 5.13 Programa para Aprendizaje de Pesos Sinápticos V2 para Jugador 1 - 2
Jugadores . . . 88
Figura 5.14 Subsistema para Aprendizaje de Pesos Sinápticos W2para Jugador 1
-2 Jugadores . . . 89
Figura 5.15 Programa para Aprendizaje de Pesos Sinápticos W2para Jugador 1 - 2
Jugadores . . . 89
Figura 5.16 Subsistema para Cálculo de Estados Estimados de la Red Neuronal Diferencial - 2 Jugadores . . . 90
Figura 5.19 Subsistema para Error de Modelado de los Estados - 2 Jugadores . . 92
Figura 5.20 Programa para Error Medio Cuadrado - 2 Jugadores . . . 92
Figura 5.21 Red Neuronal Diferencial para el Modelado de un Juego Diferencial con 2 Jugadores . . . 93
Figura 5.22 Sistema Real - Juego Diferencial de 3 Jugadores . . . 94
Figura 5.23 Subsistema de Sistema Real - Juego Diferencial de 3 Jugadores . . . . 95
Figura 5.24 Programa para Sistema Real - Juego Diferencial de 3 Jugadores . . . 95
Figura 5.25 Modelado de Estados de la Red Neuronal Diferencial - 3 Jugadores 96
Figura 5.26 Subsistema para Sigmoidales de Modelado de Estados - 3 Jugadores 97
Figura 5.27 Subsistema para Aprendizaje de Pesos Sinápticos V1- 3 Jugadores 97
Figura 5.28 Programa para Aprendizaje de Pesos Sinápticos V1 - 3 Jugadores . . 98
Figura 5.29 Subsistema para Aprendizaje de Pesos Sinápticos W1- 3 Jugadores 98
Figura 5.30 Programa para Aprendizaje de Pesos Sinápticos W1- 3 Jugadores . 99
Figura 5.31 Modelado de Dinámica de Jugador 1 - 3 Jugadores . . . 99
Figura 5.32 Subsistema para Sigmoidales de Modelado de Estados - 3
Jugadores . . . 100
Figura 5.33 Subsistema de Aprendizaje de Pesos Sinápticos V2 para Jugador 1 - 3
Jugadores . . . 100
Figura 5.34 Programa para Aprendizaje de Pesos Sinápticos V2 para Jugador 1 - 3
Jugadores . . . 101
Figura 5.35 Subsistema para Aprendizaje de Pesos Sinápticos W2para Jugador 1
-3 Jugadores . . . 101
Figura 5.36 Programa para Aprendizaje de Pesos Sinápticos W2para Jugador 1 - 3
Figura 5.38 Programa para Estados Estimados de la Red Neuronal Diferencial - 3 Jugadores . . . 103
Figura 5.39 Error de Modelado de los Estados - 3 Jugadores . . . 104
Figura 5.40 Subsistema para Error de Modelado de los Estados - 3 Jugadores . 104
Figura 5.41 Programa para Error Medio Cuadrado - 3 Jugadores . . . 105
CAPÍTULO 1
ANTECEDENTES.
Existen sistemas económicos, políticos, matemáticos, mecánicos,
aeronáuti-cos, etc., que poseen interconexiones con otros sistemas, en donde sus
compor-tamientos son inter-afectados tanto en sus dinámicas como en los objetivos que
per-siguen. El desarrollo de controladores para llevar estos sistemas a un desempeño
óptimo han tenido un avance notorio en los últimos años, el problema es que se han
basado en el conocimiento total del modelo matemático que describe a dichos
sis-temas. En la mayoría de los casos no se tiene un modelo satisfactorio, o incluso no
se tiene un modelo, lo que genera un problema para el desarrollo de controladores.
Sin embargo, existe una herramienta, las redes neuronales, que proveen una efectiva
metodología para la obtención de modelos de sistemas en los cuales se desconoce
parte o la totalidad del modelo matemático.
Por otro lado, la teoría de juegos es una ciencia que permite modelar sistemas
de varias personas o jugadores, en donde se utiliza la toma de decisiones de éstos
para que interactúen entre ellos. Cada jugador persigue su propio interés, el cual
puede estar en con icto con los demás. De esta manera, un juego es un sistema o
conjunto de sistemas en donde diversos jugadores interactúan mediante acciones o
controles, que afectan el comportamiento de los otros [9]. Las aplicaciones de la
ingeniería, aeronáutica, con ictos bélicos, etc. Para este tipo de sistemas se busca
un control para encontrar un estado de equilibrio del juego, minimizando pérdidas o
maximizando ganancias. De esta manera, es necesario conocer el modelo matemático
de los juegos, para poder de nir dicho estado de equilibrio, por lo que las redes
neuronales son una herramienta útil para obtener el modelo de diferentes tipos de
juegos.
1.1 REDES NEURONALES.
El cerebro humano trabaja de manera muy diferente a una computadora digital.
El cerebro es complejo, no lineal y es un sistema de procesamiento paralelo, con
la capacidad de organizar sus constituyentes estructurales (neuronas) para llevar a
cabo ciertas tareas. Desde que nacemos, el cerebro tiene la capacidad de generar
sus propias reglas a través de la “experiencia” que se obtiene con el tiempo. De
esta manera, su plasticidad permite al sistema nervioso en desarrollo a adaptarse al
ambiente que lo rodea.
Los sistemas biológicos son la base para el diseño de redes neuronales arti
-ciales. El cerebro se puede considerar como una red neuronal, que recibe
informa-ción de manera constante de los receptores, convirtiéndolos en impulsos eléctricos
que llevan información a la red. Finalmente, la red neuronal envía impulsos
eléc-tricos a los efectores, los cuales convierten dichos impulsos eléceléc-tricos para producir
Receptores Red Neuronal Efectores
Estímulo Respuesta
El sistema nervioso está formado por neuronas, y cada neurona posee una
membrana externa capaz de generar impulsos eléctricos y una sinapsis para
trans-ferir información de una neurona a otra. Cada neurona posee tres regiones:
Cuerpo de la neurona. Recolecta y procesa información proveniente de otras
neuronas.
Axioma. Provee la línea de transmisión mediante la cual se envía información
hacia otras neuronas.
Dendritas. Son extensiones que poseen varias ramas mediante las cuales se
recibe información.
Sinapsis.Uniones del axioma con una dendrita de otra neurona.
Cuando se produce un estímulo en una neurona, la información viaja a lo largo
del axioma hasta llegar a su n, pasando por una sinapsis, que constituye la unión
entre un axioma y una dendrita. En este punto de unión se transmite la
informa-ción de una neurona a otra mediante transmisores químicos. Cada neurona se puede
considerar como un sistema multi-entrada con una sola salida (multi-input,
single-output MISO), y la unión de un gran número de neuronas conforma una red neuronal
biológica.
Las redes neuronales arti ciales son sistemas que poseen la habilidad de
apren-der a medida que adquieren información de las entradas y salidas de un sistema.
Para llevar a cabo el aprendizaje no es necesario conocer el modelo matemático del
sistema analizado. Una red neuronal es un procesador masivamente distribuido de
forma paralela, compuesto de unidades simples de procesamiento, que son
propen-sas a almacenar conocimiento experimental y volverlo accesible para su uso. Las
redes neuronales surgieron como una analogía a las reacciones de las neuronas en el
cerebro humano, de esta manera son similares en dos aspectos principales:
1. El conocimiento se adquiere del ambiente a través de un proceso de aprendizaje.
2. Los pesos sinápticos, que representan la fuerza de conexión inter-neuronal, son
Un algoritmo de aprendizaje, es el procedimiento para llevar a cabo el proceso
de aprendizaje en las neuronas, su función es modi car los pesos sinápticos de la red
en una manera ordenada para lograr un objetivo deseado.
Una neurona, es una unidad de procesamiento fundamental para la operación
de una red neuronal. Cada neurona tiene cuatro elementos básicos:
1. Sinapsis o lazos de conexión. Se caracterizan por un peso o fuerza de
interconexión propia. Una señal en la entrada de una sinapsis j conectada a una
neurona k se multiplica por un peso sináptico . El peso sináptico se encuentra en
un rango que puede incluir valores positivos o negativos.
2. Sumador. Suma las señales de entrada, tiene la función de combinador lineal.
3. Función de activación. Se utiliza para limitar la amplitud de la salida de una
neurona . También es llamada función de límites, ya que limita el rango de
amplitud permisible de la señal de salida .
4. Bias. Tiene el efecto de incrementar o disminuir la entrada neta de la función de
activación, dependiendo si es positiva o negativa. Tiene el efecto de aplicar una
wkm
bk
xm
yk
uk
Función de Activación
Entradas
b Bias,
11
w
12
w
1
x
2
x
()⋅
ϕ Salida
∑
[image:19.612.173.501.118.282.2]Sumador
Figura 1.2: Elementos Básicos de una Neurona Arti cial
En donde x1; :::; xm son las señales de entrada, wk1; :::; wkm son los pesos
sinápticos de la neurona k, yk es la señal de salida de la neurona, bk es el bias y
'( )es la función de activación [7].
En términos matemáticos, una neurona k se describe con el siguiente par de
ecuaciones:
uk= m X
j=1
wkjxj (1.1)
yk ='(uk+bk) (1.2)
Las redes neuronales pueden desarrollarse con una o más capas de neuronas.
El perceptrón es la forma más simple de una red neuronal utilizada para reconocer
tipo de neurona se limita a hacer clasi cación de patrones en sólo dos casos. Si se
expande la capa de salida para tener más de una neurona, se puede ampliar el número
de clases para identi cación. Si se utiliza un mayor número de capas de neuronas se
tienen varios niveles de procesamiento [15].
1.1.1 REDES NEURONALES DINÁMICAS.
Las redes neuronales estáticas son utilizadas normalmente para codi car
informa-ción temporal utilizando un retraso en entradas y salidas. Pero este tipo de redes
requieren de grandes cantidades de memoria, lo que genera sistemas dinámicos de
bajo orden. Para eliminar este problema, se ha explorado el uso de redes neuronales
dinámicas o recurrentes [15]. Este tipo de redes utilizan al menos un lazo de
retroali-mentación, que utilizan elementos de retraso, en el caso de tiempo discreto denotado
porq 1
, tal que: u(k 1) = q 1
u(k), en dondek indica la k-ésima muestra en el
tiempo. El lazo de retroalimentación produce entonces un comportamiento dinámico
no-lineal debido a las funciones de activación no-lineales de las neuronas. Entonces,
además de las entradas de información a las neuronas, se añaden entradas que poseen
1 −
z
Neuronas
Operadores de retardo unitarios
1 −
z z−1
Figura 1.3: Red Neuronal Dinámica (discreta)
Las redes neuronales diferenciales, son el equivalente a las redes neuronales
dinámicas pero en tiempo continuo, éstas se diseñaron para modelar y controlar
sis-temas, y se encuentran representadas por una ecuación diferencial. El aprendizaje de
las redes neuronales se basa en la información que obtiene del entorno, de manera
que no es necesario conocer el modelo matemático para llevar a cabo una identi
-cación del sistema y controlarlo. El modelado mediante el uso de una red neuronal
diferencial se lleva a cabo en línea. Una vez que la red neuronal se ha sometido al
1.1.2 IDENTIFICACIÓN DE SISTEMAS LINEALES.
La identi cación de sistemas lineales es posible mediante redes neuronales
dinámi-cas o diferenciales. La estructura de dichas redes neuronales se basa en la conexión
de neuronas en paralelo, en donde el número de neuronas es seleccionado igual a la
dimensión de los estados del sistema lineal a identi car, que debe ser completamente
medible. Los pesos sinápticos se adaptan en línea para minimizar el error de
identi-cación. El método de análisis de estabilidad de Lyapunov (segundo método), es un
instrumento que además de establecer las condiciones de estabilidad de error de los
pesos sinápticos, es útil para generar un algoritmo de aprendizaje tanto para capas
ocultas como de salida de neuronas.
Las redes neuronales dinámicas utilizan al menos un lazo de retroalimentación
con el n de utilizar la información de los datos de la estructura del sistema. Además
es importante considerar que al utilizar un mayor número de capas ocultas, las
ca-pacidades de aproximación mejoran, así como el uso de funciones de activación
no-lineales para lograr una mejor aproximación de la dinámica de sistemas no-lineales.
La siguiente ecuación representa la estructura del modelo de una red neuronal
diferencial multicapa [15].
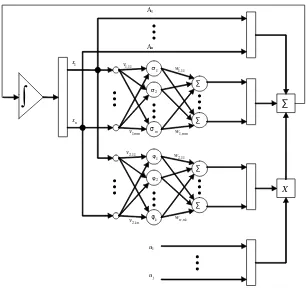
^
x=Ax^t+W1;t (V1;tx^t) +W2;t'(V2;tx^t)ut (1.3)
En donde:
^
ut2 <qes un vector que describe una entrada medible de acción de control,
W1;t2 <n k es la matriz de pesos sinápticos de salida,
W2;t2 <n r es la matriz de pesos sinápticos de salida,
V1;t 2 <m n es la matriz de los pesos sinápticos que describen las conexiones
de capas ocultas,
V2;t 2 <k n es la matriz de los pesos sinápticos que describen las conexiones
de capas ocultas,
A2 <n nes una matriz Hurwitz,
( )y'( )son funciones de activación sigmoidal
El caso más simple de la estructura de red neuronal diferencial es cuando
solamente contiene una capa de entrada y una de salida, es decir, no contiene
An A1 1 σ 2 σ m σ 1 φ 2 φ k φ ∑ ∑ ∑ ∑
∫
∑ j u X 1 u 1 x n x 11 , 1 v 11 , 1 w mmv1, w1,mm
11 , 2 v 11 , 2 w kn
[image:24.612.171.477.119.409.2]v2, ww,nk
Figura 1.4: Estructura General de una Red Neuronal Diferencial
1.2 TEORÍA DE JUEGOS DINÁMICOS
NO-COOPERATIVOS.
La teoría de juegos es una rama de las matemáticas aplicadas, que estudia sistemas
en los que múltiples jugadores o personas toman decisiones para tomar acciones con
el propósito de maximizar o minimizar alguna variable. Su objetivo principal es que
provee una forma de obtener modelos matemáticos de diferentes tipos de sistemas
impor-tante, y no-cooperativa si cada persona que participa busca sus propios intereses, que
pueden ser con ictivos con los intereses de las otras personas. Una situación de
con-icto incluye individuos que toman una decisión, y cada posible decisión lleva a un
resultado diferente, que puede ser valuado de manera distinta por cada individuo. Si
cada individuo valúa las posibles salidas de manera distinta, se genera entonces una
situación de con icto.
Un individuo, también llamado persona o jugador, no siempre tienen control
sobre la salida, en ocasiones existen incertidumbres que in uencian la salida de una
manera impredecible. La salida estará basada entonces por información que no se
obtiene de las decisiones de los individuos, se dice que esta información está bajo el
control de la “naturaleza”.
Existen dos tipos de teoría de juegos, estática y dinámica o diferencial. Cuando
se tiene un solo individuo no se puede hablar de teoría de juegos, sino de un sistema
convencional el cual se soluciona mediante programación matemática en casos
es-táticos o teoría de control en casos dinámicos. Cuando se cuenta con más de un
in-dividuo entonces ya se puede hablar de la teoría de juegos estática y teoría de juegos
dinámica o diferencial. La teoría de juegos diferenciales es aquella en la que la
evolu-ción de los estados de los individuos se describe mediante ecuaciones diferenciales.
Tanto la teoría de juegos estática como la teoría de juegos diferencial se utilizan
prin-cipalmente en situaciones de con ictos en campos tan variados como en economía y
con ictos de guerra, en general se utilizan en el desarrollo de conceptos para describir
y comprender situaciones de con ictos.
En la teoría de juegos existen acciones (controles) y estrategias (reglas de
de-cisión). Las estrategias de nen lo que se va a llevar a cabo, y son utilizadas por los
jugadores. Las consecuencias de las estrategias por parte de los individuos son las
acciones, es decir, las medidas que toman una vez que se conoce la salida de sus
de-cisiones. Las acciones se implementan una vez que se tiene información, en donde la
información puede ser de tipo estocástica o determinística. En el caso estocástico la
acción se basa en datos que no se conocen aún y que no están controlados por otros
jugadores, se determina por la naturaleza (incertidumbre), mientras que en el caso
determinístico la naturaleza no participa, la información es conocida [1].
La teoría de juegos incluye un proceso de toma de decisiones dinámica que
evoluciona en el tiempo, de manera continua o discreta, con más de un individuo
que toma decisiones, cada uno con su función de costo y con la posibilidad de
ac-ceder a información diferente. Un juego es dinámico cuando al menos un jugador
utiliza una estrategia que depende de acciones pasadas y la evolución del proceso
de decisiones, es decir, de la evolución de los estados, que se describe mediante una
ecuación diferencial. Los juegos diferenciales son entonces juegos dinámicos in
1.2.1 JUEGOS DIFERENCIALES.
Existe un tipo de juegos diferenciales denominados juegos dinámicos in nitos. En
este tipo de juegos los conjuntos de acciones de los individuos contienen un número
in nito de elementos o alternativas, y los jugadores adquieren información dinámica
mediante el proceso de toma de decisiones. Este tipo de juegos pueden ser de nidos
de manera discreta (dinámicos) o continua (diferenciales). Los conjuntos de acciones
de los jugadores no son nitos cuando se utiliza una forma extensa de juego, en lugar
de una estructura de árbol. En el caso de formular los juegos de manera extensa se
utilizan ecuaciones diferenciales (en tiempo continuo) para describir la evolución del
proceso de decisión.
Los juegos dinámicos in nitos en tiempo continuo, o juegos diferenciales,
poseen diversos caminos de acción, determinados por las soluciones de las
ecua-ciones diferenciales que los de nen, con el n de determinar el estado en el que se
encuentra el juego. De esta manera, la evolución de los estados del juego
diferen-cial se describen mediante una ecuación diferendiferen-cial y los individuos actúan en un
intervalo de tiempo.
De acuerdo a [1], unjuego diferencial cuantitativo de N-personas de duración
ja o pre-establecidacontiene los siguientes elementos.
2. Un intervalo de tiempo[0; T]especi cado a priori, denotando la duración de la
evolución del juego.
3. Un conjunto in nitoS0 con alguna estructura topológica, llamado espacio
de trayectorias del juego. Sus elementos se denotan de la manera
fx(t);0 t Tgy constituye elestado de trayectoriaspermisible del juego.
4. Un conjunto in nitoUi con alguna estructura topológica, de nida para cada
i2N y que es llamada elespacio de control (acción)dePi.
5. Una ecuación diferencial cuya solución describe latrayectoria de estadosdel
juego.
dx(t)
dt =f t; x(t); u
i(t); :::; uN(t) ; x(0) =x
0 (1.4)
Un juego diferencial no está completamente de nido a menos que se de nan
CAPÍTULO 2
PLANTEAMIENTO DEL PROBLEMA.
Las redes neuronales han probado ser una técnica exitosa para la identi cación
y control de una gran variedad de sistemas tanto lineales como no-lineales,
espe-cialmente en la ausencia de la información del sistema, incluso cuando no se tiene
información de éste [11]. Las redes neuronales pueden ser estáticas o dinámicas. Las
primeras han sido utilizadas para aproximar funciones operativas, en conjunto con
ecuaciones de modelo dinámicos. Pero aún cuando se han implementado de manera
exitosa, presentan algunas desventajas, tal como una taza de aprendizaje lenta y una
alta sensitividad a los datos de entrenamiento en la función de aproximación. A
diferencia de las redes neuronales estáticas, las redes neuronales dinámicas pueden
eliminar estas desventajas y han demostrado que pueden trabajar en la presencia de
sistemas dinámicos que no están modelados, ya que su estructura incluye
retroali-mentación [10].
El problema identi cado, y que se pretende resolver con este proyecto, es el
siguiente:
Aún cuando problemas especí cos de teoría de juegos dinámicos han sido
resueltos por diversos métodos, las redes neuronales diferenciales no han sido
uti-lizadas para este n. En este proyecto se pretende llevar a cabo el modelado de una
diferen-cial. Las redes neuronales presentan un método de solución e caz para este tipo de
problemas, ya que pueden ser utilizadas para la identi cación de sistemas aún en
ca-sos en los que no se cuenta con su modelo matemático, lo que implica que solamente
es necesario el conocimiento de las entradas y salidas de dichos sistemas para poder
modelarlos.
2.1 ESTADO DEL ARTE.
Existen algunas publicaciones que tratan la identi cación o control de procesos
dinámi-cos en donde se desconoce su modelo, mediante redes neuronales. Las redes
neu-ronales diferenciales han sido utilizadas para obtener modelos en aplicaciones de
identi cación de sistemas, mediante el método de identi cación de error para
entre-nar una red, con el n de predecir series caóticas de tiempo generadas por una función
logística y una desmodulación de señales FSK [6]. Otra aplicación de las redes
neu-ronales utilizan un eslabón funcional Chebyschev, con el n de reducir el tiempo
de cómputo que genera un algoritmo de retropropagación, y obtener un mayor
de-sempeño para el perceptrón muti-capa para la identi cación de un sistema dinámico,
incluso en casos en que se añade ruido al sistema [14]. Otro proyecto que utiliza
redes neuronales diferenciales, presenta una red neuronal dinámica que consiste de
una capa completamente conectada con retroalimentación, con el n de describir un
sistema dinámico en una representación de espacio de estados, además se desarrolló
mínima con la dinámica esencial capturada de la medición entrada-salida del sistema
desconocido. Los algoritmos de construcción integran métodos de determinación de
modelo mínimos, inicialización de parámetros y desempeño de optimización para
un trabajo sistemático de procesos de prueba-y-error en la selección de tamaños de
redes y parámetros [17]. Finalmente, hay dos proyectos que proponen el uso de
neuro observadores diferenciales asintóticos. El primero, propone un neuro
obser-vador diferencial asintótico para estimar los estados de un proceso estocástico
con-tinuo con conocimientoa priori de la estructura de la planta. Para el desarrollo de
esta red neuronal diferencial se utilizó un algoritmo de aprendizaje con dos partes,
una que se asemeja al esquema de retropropagación de error y otra proporcional al
error de salida. Para este proyecto además se aplicó un análisis estocástico de
Lya-punov, para probar la existencia de una cota superior para la estimación del error
medio cuadrático [11]. El segundo proyecto propone también un neuro observador
diferencial asintótico para estimar los estados de procesos estocásticos continuos,
pero ahora cuando no se tiene conocimiento a priori de la estructura de la planta
[10]. Sin embargo no se ha desarrollado una red neuronal para el modelado de juegos
diferenciales lineales.
En cuanto a la teoría de juegos se han desarrollado modelos para resolver
problemas especí cos tal como el problema de teoría de juegos diferencial de
evi-tar colisiones de aeronaves, basándose en el con icto de trá co aéreo, mediante
con-siderando que un vehículo que desea evitar la colisión como un “evasor” y uno
no-cooperativo adyacente actúa como “perseguidor”, extendiendo el problema de dos
aeronaves a un problema tridimensional [5]. Otro ejemplo es el de la teoría de
jue-gos diferencial propuesta para resolver problemas de la teoría de juego no-lineal
diferencial no-cooperativa y cooperativa de N-personas. En este proyecto el sistema
lineal estocástico se aproxima utilizando un modelo estocástico difuso, en donde un
controlador con observador difuso se propone para tratar un juego diferencial
no-cooperativo en el sentido de estrategias de equilibrio de Nash o juegos no-cooperativos
en el sentido de estrategias óptimas-Pareto [16]. Sin embargo, no se ha realizado un
modelado de juegos diferenciales mediante redes neuronales, en donde existe la
posi-bilidad de obtener un método generalizado para modelar diversos tipos de problemas
de teorías de juegos.
2.2 JUSTIFICACIÓN.
Las redes neuronales diferenciales son una herramienta mediante la cual es posible
la identi cación y control de sistemas lineales y no-lineales de los que se tiene un
conocimiento parcial o no se tiene conocimiento de su modelo matemático.
Con-siderando que los juegos diferenciales lineales, se modelan mediante ecuaciones
diferenciales que describen la evolución de los estados de un sistema con N
indi-viduos o jugadores, una red neuronal diferencial puede entonces modelar su
Con el desarrollo de una red neuronal diferencial se puede llevar a cabo el
modelado de sistemas de problemas de teoría de juegos diferenciales. El resultado
obtenido de esta red es el modelo matemático del juego diferencial modelado. La red
neuronal diferencial programada no solo modelaría un problema en especí co, sino
que tendría la capacidad de modelar una clase de sistemas, es decir, tendría la
capaci-dad de modelar varios problemas de juegos diferenciales, siempre que éstos cumplan
con las condiciones de diseño. Los sistemas modelados pueden ser tan variados como
sistemas mecánicos, aeronáuticos, matemáticos, económicos, políticos, económicos,
etc., como ha sido mencionado anteriormente, y de esta manera se obtiene un
de-sarrollo que no se ha realizado anteriormente y que posee una gran versatilidad en
solución de problemas de diversos campos.
Mediante el uso de una red neuronal diferencial, el aprendizaje se lleva a cabo
en línea, y mediante el entrenamiento de la red neuronal utilizando un algoritmo
de aprendizaje, la red neuronal se convierte en el modelo matemático, es decir el
modelo que de ne el comportamiento del sistema. Este documento presenta entonces
el desarrollo de un algoritmo de aprendizaje, o ley de aprendizaje para el diseño de
una red neuronal diferencial que modela una clase de juegos diferenciales.
2.3 OBJETIVO GENERAL.
Diseñar una red neuronal del tipo diferencial para el modelado una clase de juegos
2.4 OBJETIVOS ESPECÍFICOS.
Analizar y demostrar la estabilidad del error de modelado.
Obtener un algoritmo de aprendizaje adecuado para la red neuronal.
Generar un modelo matemático aplicado a un problema especí co de teoría de
juegos diferenciales.
2.5 ALCANCES.
Obtener una red neuronal programada en Matlab y Simulink.
Obtener el modelo matemático de algún problema especí co de teoría de
juegos mediante el uso de la red neuronal.
Escribir un artículo para ser publicado en un congreso internacional.
CAPÍTULO 3
MODELADO Y OBTENCIÓN DEL
ALGORITMO DE APRENDIZAJE.
Considerando que los estadosxde un juego diferencial son conocidos y sus
en-tradas y salidas son completamente medibles, se eligió una clase de juegos diferenciales
lineales invariantes en el tiempo para modelarlos mediante una red neuronal
diferen-cial. En primera instancia se eligió una red neuronal diferencial propuesta en [9], y
una clase de juegos diferenciales con una estructura similar a la red neuronal
diferen-cial mencionada. Una vez elegida la red neuronal, fue posible de nir las condiciones
con las que se debe cumplir para poder llevar a cabo el modelo de los juegos. Si el
juego diferencial que se desea modelar cumple con dichas condiciones, es posible
entonces llevar a cabo un análisis de estabilidad de Lyapunov (segundo método),
me-diante el cual se de ne la ley de aprendizaje que actualiza los pesos sinápticos de la
red, así como las condiciones de estabilidad para que el error tienda a cero. A
con-tinuación se muestra la de nición de la red neuronal a utilizar, las condiciones de
diseño y la ley de aprendizaje obtenida de este desarrollo.
La clase de juegos diferenciales que se utilizan en este documento, con el n
general por medio de la siguiente ecuación diferencial,
_
x=Ax+
N X
i=1
Biui (3.2)
en donde,
N es el número de jugadores, en dondei= 1;2;3:::; i2N
x2 <nes el vector de estados,
ui 2 <q es una entrada que describe la acción de control del jugadori(para el
desarrollo de este proyecto se consideraq= 1),i2N
A2 <n nes una matriz estable,
Bi 2 <n q son matrices de constantes de los jugadores,i2N
De esta manera se puede estudiar la interacción entre jugadores utilizando
una ecuación matemática, ya que la ecuación incluye la entrada de control de los
diferentes jugadores y el espacio de estados. Para este proyecto se considera que
to-dos los estato-dos son conocito-dos, y las acciones de control son completamente medibles,
mientras que las matricesAyB son desconocidas, y se determinan mediante el uso
de una red neuronal diferencial para obtener el modelo matemático completo.
3.1 DESCRIPCIÓN DE LA RED NEURONAL.
Del modelo de red neuronal diferencial propuesto en [9] es posible determinar las
propuesta en (3:1). Para poder llevar a cabo el modelado, es importante elegir una
clase de juegos diferenciales que cuenten con una estructura similar a la ecuación de
la red neuronal diferencial mencionada anteriormente.
^
x=W1 (V1x^) +
N X
i=1 Wi
2'i V2ix u^ i (3.1)
En donde,
^
x2 <nes el vector de estados estimados de la red neuronal,
W1 2 <n k es la matriz de pesos sinápticos para la capa de salida de los
estados,
Wi
2 2 <n mson las matrices de pesos sinápticos de la capa de salida para cada
uno de los jugadores,i2N
V1 2 <k n es la matriz de pesos sinápticos para la capa de entrada de los
estados,
Vi
2 2 <m n son las matrices de pesos sinápticos de la capa de entrada para
cada uno de los jugadores,i2N
(V1x^) 2 <k es el vector de evaluación de las entradas de las funciones
sig-moidales de los estados,
'i(Vi
2x^) 2 <m q son las matrices de evaluación de las entradas de las
fun-ciones sigmoidales de los jugadores,i2N
ui 2 <q es el control de entrada de los jugadores (para el desarrollo de este
Esta red neuronal diferencial cuenta con una sola capa de neuronas, con pesos
sinápticos a la entrada y la salida, es decir, una capa de pesos sinápticos ocultos y
una capa de pesos sinápticos a la salida. Para el diseño de esta red neuronal se utiliza
la siguiente forma para las funciones sigmoidales.
(z) ='(z) = 1
1 + exp ( az)
La estabilidad en este proyecto se dirige hacia el error cuadrático de modelado,
y para que la red neuronal lleve a cabo el modelado del sistema de juegos
diferen-ciales deseado, el error entre la salida del sistema real y la salida estimada de la red
neuronal para este proyecto, debe acercarse a cero. Entonces, es necesario demostrar
la estabilidad de error de modelado entre la red neuronal (valor estimado) y el sistema
de juegos (valor real o deseado).
De lo anterior es posible determinar una ley de aprendizaje, cuyo objetivo sea el
de minimizar el error de modelado. La ley de aprendizaje o algoritmo de aprendizaje
deberá incluir la minimización de error entre los estados realesxdel juego diferencial
Figura 3.1: Aprendizaje y Error de Modelado
Como se mostró en (3:2), es necesario veri car que la de nición de la red
neuronal diferencial utilizada cumpla con la forma general de esta clase de juegos
diferenciales. De esta manera se utiliza el error de modelado, expresado como =
^
x x;y considerando que _ = ^x x_, entoncesx^representa el modelo de red neuronal
diferencial yx_ el modelo ideal para el sistema real, cuya dinámica se representa como
sigue,
_
x=W1 (V1x) +
N X
i=1
W2i'i V i
2 x ui (3.3)
en donde,
x2 <nes el vector de estados ideales de la red neuronal,
W1 2 <n k es la matriz de pesos sinápticos iniciales para la capa de salida de
W2i 2 <n mson las matrices de pesos sinápticos iniciales de la capa de salida
para cada uno de los jugadores,i2N
V1 2 <k nes la matriz de pesos sinápticos iniciales para la capa de entrada de
los estados,
V2i 2 <m nson las matrices de pesos sinápticos iniciales de la capa de entrada
para cada uno de los jugadores,i2N
(V1x) 2 <k es el vector de evaluación de las entradas de las funciones
sig-moidales de los estados,
'i V i
2 x 2 <m q son los vectores de evaluación de las entradas de las
fun-ciones sigmoidales de los jugadores,i2N
ui 2 <q es el control de entrada de los jugadores (para el desarrollo de este
proyecto, se consideraq = 1),i2N
Se observa que(3:3)cumple con la forma general de la clase de juegos diferenciales
de(3:2), entonces esta red neuronal diferencial puede ser utilizada para el modelado
de la clase propuesta de juegos diferenciales. Para esto, se considera que W1, V1, W2iyV
i
2 representan matrices de pesos sinápticos iniciales debido a que no se tiene
conocimiento del modelo matemático, en especí co de las matricesAyBi; i2N, y
estos valores iniciales cambiarán cuando se someta a la red neuronal al entrenamiento
y se lleve a cabo el aprendizaje, para nalmente obtener el modelo matemático del
3.2 CONDICIONES DE DISEÑO.
Para de nir las condiciones de diseño de la red neuronal diferencial, se toma en
cuenta que las siguientes suposiciones se cumplen.
Suposición 1.Las funciones sigmoidales ( )y'( )son diferenciables y satisfacen
la condición de Lipschitz y la condición de sector, de tal manera que se cumple lo
siguiente,
~ := (V1x^) (V1x);^ := (V1x^) (V1x^) (3.4)
~
'i :='i V2ix^ '
i
V2ix ;'^
i
:='i V2ix^ '
i
V2ix ; i^ 2N
:= (V1x^); 'i :='i V2ix ; i^ 2N
(0) := 0; 'i(0) := 0; i2N
~
Wi =Wi Wi; V~ i
i =Vi V
i
i ; i2N
~
Wi =Wi Wi; V~ i
i =Vi V
i
i ; i2N
Dado a que las funciones sigmoidales ( ) y '( ) cumplen con la condición de
Lipschitz y la condición de sector, y son diferenciables, se concluye los siguiente de
acuerdo a[15].
^ = D V~1x^+
^
'iui =Di
'V~2ixu^ i+ i'ui; i2N
D =
z (z)jz=V1x^ Di
' = z' i(z)j
z=V2^x; i2N
(~ Aa )
>
1(~ Aa )
>
~
'iui > i
2 '~
iui > i
' u
ui 2 ui; i2N
jj jj21 l1
~
V1x^ 2
; l1 >0
i '
2 i 4
li
2 V~
i
2x^ 2
' ; li
2 >0; i2N
En donde,
2 <nes el vector de error
D 2 <k k es la matriz diagonal de las derivadas de las funciones sigmoidales de
los estados
Di
' 2 <m m es la matriz diagonal de las derivadas de las funciones sigmoidales de
los jugadores,i2N
( )2 <kes el vector de funciones sigmoidales para las neuronas que modelan los
estados
'i( )2 <m q es el vector de funciones sigmoidales para las neuronas de cada uno
de los jugadores (para el desarrollo de este proyecto, se consideraq =1),i2N
Suposición 2.Se utilizan acciones de control acotadasfuig(jjuijj2 ui < constante,
i2N), para cada uno de los jugadores[15].
Suposición 3. Existen matrices 1, 2, , i',Qa,Aa, i3, i4,i2 N y constantes l1; li2, tal que proveen una solución positiva P = P
>
> 0 a la siguiente ecuación
algebraica de Riccati:
RIC :=P A+A>
en donde,
R : =W1 1 1 + 1 2 W > 1 + N X i=1 h W i 2 i 1 3 + i 1 4 W i> 2 i
; i2N
Q : = +
N X
i=1
i 'u
i +Q
a; i2N
A : =W1Aa
1; 2 2 <k k son matrices diagonales positivas,
i
3; i4 2 <m m son matrices diagonales positivas,i2N
2 <n nes una matriz diagonal positiva,
i
' 2 <n n son matrices diagonales positivas,i2N
Qa 2 <n n es una matriz positiva de nida,
l1; li2 2 <son constantes positivas,
Aa 2 <k nes una matriz tal queAes estable,
ui 2 <es una constante positiva,i2N
3.3 OBTENCIÓN DE LA LEY DE APRENDIZAJE Y
ANÁLISIS DE ESTABILIDAD DEL ERROR DE
MODELADO.
El propósito nal es el de de nir el algoritmo de aprendizaje de la red neuronal
diferencial a partir de las condiciones de estabilidad. Para llevar a cabo esto es
nece-sario obtener una expresión matemática de los pesos sinápticosW1,V1,W2i yV2i, en
Pro-poniendo una función candidato de LyapunovV (x), es posible determinar las
condi-ciones que hacen que la función candidato sea positiva de nida, así como su derivada
sea negativa de nida
h
V (x) 0; _V (x)<0i, para garantizar estabilidad. Para
deter-minar el algoritmo de aprendizaje de la red neuronal se utiliza entonces el modelo de
red neuronal diferencial de(3:1)y el error de modelado mencionado anteriormente
para de nir la siguiente función candidato de Lyapunov, de acuerdo a [15],
V ( ) = TP + 1
2tr W~
T
1K 1
1 W~1 +
1
2tr V~
T
1K 1 2 V~1
+1
2
N X
i=1
tr W~
iT 2 K
1i
3 W~2i +
1 2
N X
i=1
tr V~
iT 2 K
1i
4 V~2i ; i 2N (3.5)
en donde
= ^x x;2 <n, es vector de error,
K1; K2; K3i; K4i 2 <son constantes positivas,i2N
P 2 <n n es la matriz positiva de solución de la ecuación de Riccati
~
W1 2 <n k es la matriz de actualización de pesos sinápticos para la capa de salida
de los estados,
~
Wi
2 2 <n m son las matrices de actualización de de pesos sinápticos de la capa de
salida para cada uno de los jugadores,i2N
~
V1 2 <k n es la matriz de actualización de pesos sinápticos para la capa de entrada
~
Vi
2 2 <m n son las matrices de actualización de pesos sinápticos de la capa de
entrada para cada uno de los jugadores,i2N
trf g representa la traza, que en álgebra lineal es la suma de los elementos de la
diagonal principal de una matriz cuadrada [4],
Con , que representa el error, se puede demostrar la estabilidad, considerando para
este proyecto que es estable si tiende a cero. Para llevar a cabo el análisis, se toma la
derivada de la función candidato de Lyapunov.
_
V ( ) = TP _ + _TP +tr
( ~ W T 1K 1
1 W~1+ ~W1TK 1 1 W~1
) +tr ( ~ V T 1K 1
2 V~1+ ~V1TK 1 2 V~1
) + N X i=1 " tr ( ~ W iT 2 K 1i 3 W~
i
2+ ~W
iT 2 K
1i 3 W~
i 2 )# + N X i=1 " tr ( ~ V iT 2 K 1i
4 V~2i+ ~Vi T 2 K
1i 4 V~
i
2
)#
De acuerdo a [4], se tiene la siguiente identidad: x>
Q@x = x>
Q@x > = @x>
Qx,
_
V ( ) = TP _ + TP _ +tr
( ~ W T 1K 1
1 W~1+ ~W
T
1K 1 1 W~1
) +tr ( ~ V T 1K 1
2 V~1+ ~V
T
1K 1 2 V~1
) + N X i=1 " tr ( ~ W iT 2 K 1i 3 W~
i
2+ ~W
iT
2 K 1i 3 W~
i 2 )# + N X i=1 " tr ( ~ V iT 2 K 1i 4 V~
i
2 + ~V
iT
2 K 1i 4 V~
i
2
)#
Finalmente, se obtiene la función que representa a la función candidato de Lyapunov.
_
V ( ) = 2 TP _ +tr
( ~ W T 1K 1 1 W~1
) +tr ( ~ V T 1K 1 2 V~1
) + N X i=1 " tr ( ~ W iT 2 K 1i 3 W~
i 2 )# + N X i=1 " tr ( ~ V iT 2 K 1i 4 V~
i
2
)#
; i2N (3.6)
A continuación se muestra el resultado obtenido acerca del modelado de
jue-gos diferenciales, del cual se deriva la ley de aprendizaje para actualización de
pe-sos sinápticos de la red neuronal. La ley de aprendizaje es un factor importante en
cualquier proceso de modelado de sistemas dinámicos, ya que con la actualización
de sus pesos, se garantiza que la red neuronal logre un modelado satisfactorio del
sistema real. El análisis de actualización de pesos está basado en el análisis de
es-tabilidad de Lyapunov (segundo método), mediante el cual se obtiene dicha ley de
actualización de pesos o algoritmo de aprendizaje, así como los parámetros que
Teorema 1. Sea el juego diferencial lineal invariante en el tiempo dado por(3:2),
el cual será modelado por la red neuronal diferencial dada por (3:1), si las
suposi-ciones 1, 2 y 3 se cumplen, los pesos sinápticos de la red neuronal se ajustan de
acuerdo a la siguiente ley de aprendizaje.
~
W1 = K1 2P
> > (V1x^)
~
V1 = K2
h
2D>W1>P
> ^
x>+l1V~1x^x^
> >i
~
W2 = K3i
h
2P>
ui>
'i>
Vi
2x^
i
; i 2N
~
V2 = K4i
h
2Di>
' W i>
2 P
>
ui>
^
x>
+li
2V~
i
2x^x^
> i>
' u i
; i2N
Y de esto, es posible obtener el siguiente error cuadrático de estimación de estados,
que indica que el error de modelado tiende a cero.
>
Qa !
t!1 0
Prueba. La prueba del teorema anterior se lleva a cabo mediante el análisis de
es-tabilidad del error de estimación de estados, a partir del cual se obtiene la ley de
aprendizaje para la red neuronal.
De acuerdo a la derivada de la función candidato de Lyapunov en (3:6), se trabaja
obtiene,
_ = ^x x_ =
"
W1 (V1x^) +
N X
i=1 Wi
2'
i Vi
2x u^
i #
"
W1 (V1x) +
N X
i=1 W2i'
i V i 2 x u
i #
_ =W1 (V1x^) W1 (V1x) +
N X
i=1 Wi
2'
i Vi
2x u^
i
N X
i=1
W2i'i V i
2 x ui (3.7)
Para analizar las ecuaciones anteriores se utilizarán las siguientes desigualdades.
X>
Y +Y>
X X> 1
X+Y>
Y
2X>
Y X> 1
X+Y>
Y
las cuales son válida para todo X; Y 2 Rm n y cualquier0 < = >
2 Rm m
[15], y
A>
A tr A>
A
Analizando la primera parte de(3:6)se obtiene,
2 TP _ = 2 TP [W1 (V1x^) W1 (V1x)] +
2 TP
" N X
i=1 Wi
2'i V2ix u^ i
N X
i=1
W2i'i V i 2 x ui
#
(3.8)
a) Tomando2 TP _ [W
1 (V1x^) W1 (V1x)], y sumando y restando2 TP W1 (V1x^)
2 TP [W
1 (V1x^) W1 (V1x)] =
2 TP [W1 (V1x^) W1 (V1x) +W1 (V1x^) W1 (V1x^)] =
2 TP [W
1 (V1x^) W1 (V1x)] + 2 TP [W1 (V1x^) W1 (V1x^)] =
2 TP [W
1 ( (V1x^) (V1x))] + 2
TPhW~
1 (V1x^)
i
ahora se suma y resta (V1x^)al término( (V1x^) (V1x))y se obtiene,
2 TP [W
1 ( (V1x^) (V1x) + (V1x^) (V1x^))] + 2 TP
h
~
W1 (V1x^)
i
=
2 TP [W
1~ +W1^] + 2
TP hW~
1 (V1x^)
i
=
2 TP W1~ + 2
T
P W1^ + 2
T
PW~1 (V1x^)
sumando y restando2 TP _W
1Aa(^x x) = 2 TP _W1Aa , en dondeAaes una
matriz tal queW1Aaes estable, considerandoA=W1Aa,
2 TP W
1~ + 2
TP W
1^ + 2
TPW~
1 (V1x^)
+2 TP W1Aa 2 TP W1Aa
= 2 TPW~
1 (V1x^) + 2 TP W1^
+2 TP W
1 (~ Aa ) + 2 TP W1Aa (3.9)
trabajando por separado con cada uno de los términos se obtiene:
1)2 TPW~
1 (V1x^)
2)2 TP W
1^ = 2 TP W1 D V~1x^+ =
2 TP W
2 TP W
1D V~1x^+ TP W1 1 1 W > 1 P > + > 1
2 TP W
1D V~1x^+ TP W1 1 1 W
>
1 P
>
+jj jj21
2 TP W
1D V~1x^+ TP W1 1 1 W
>
1 P
>
+l1 V~1x^
2
2 TP W
1D V~1x^+ TP W1 1 1 W
>
1 P
>
+l1x^
>~
V>
1 V~1x^
2 TP W
1D V~1x^+ TP W1 1 1 W
>
1 P
>
+l1x^x^
>~
V>
1 V~1
3)2 TP W
1 (~ Aa ) TP W1 1 2 W > 1 P > +
(~ Aa )
>
2(~ Aa ) TP W1 1 2 W
>
1 P
>
+jj~ Aa jj
2
2
TP W
1 1 2 W > 1 P > + >
4)2 TP W
1A = T2P A T P A+A
>
P
De(3:9)se obtiene entonces que:
2 TPW~
1 (V1x^) + 2 TP W1^ + 2
TP W
1 (~ Aa ) +
2 TP W1Aa 2 TPW~1 (V1x^) + 2 TP W1D V~1x^+
TP W
1 1 1 W > 1 P >
+l1x^x^
>~
V>
1 V~1+
TP W
1 1 2 W > 1 P > + >
+ T P A+A>
P
T h
P A+A>P +P W1 1 1 +
1 2 W
>
1 P +
i
+
2 TPW~
1 (V1x^) + 2 TP W1D V~1x^+ +l1x^x^
>~
V>
b) Tomando ahora2 TP PN i=1
Wi
2'i(V2ix^)ui
N P
i=1
W2i'i V i
2 x ui , y analizándolo
de la misma manera que (a), sumando y restando2 TP W i
2 'i(V2ix^)ui;
2 TP
" N X
i=1 W2i'
i
V2ix u^
i N X
i=1 W2i'
i
V2ix u
i # = N X i=1 h
2 TP Wi
2'
i Vi
2x u^
i 2 TP W i 2 '
i V i 2 x u
ii=
N X
i=1
n
2 TP hWi
2'
i Vi
2x u^
i W i
2 '
i V i 2 x u
i+W i 2 '
i Vi
2x u^
i
W2i'
i Vi
2x u^
iio= N X
i=1
n
2 T hP hWi
2 W i 2
i
'i Vi
2x u^
i+
W2i
h
'i Vi
2x u^
i 'i V i 2 x u
iiio=
N X
i=1
n
2 TP hW~i
2'
i Vi
2x u^
i+W i 2
h
'i Vi
2x u^
i 'i V i 2 x u
iiio
ahora se suma y resta'i(V
2x^)ui al término
h
'i(Vi
2x^)ui 'i V i 2 x ui
i
y se
ob-tiene,
N X
i=1
n
2 TP hW~2i'
i
V2ix u^
i
+W2i
h
'i V2ix u^
i
'i V2ix u
iiio = N X i=1 n
2 TP hW~2i'
i
V2ix u^
i
+Wh2i'
i
V2ix u^
i
'i V2ix u
i
+'i(V
2x^)ui 'i(V2x^)ui =
N X
i=1
n
2 TP hW~i
2'
i Vi
2x u^
i +W i 2 '
i Vi
2x^ '
i(V
2x^) u
i+
'i(V
2x^) '
i V i 2 x u
iiio=
N X
i=1
n
2 TP hW~i
2'
i Vi
2x u^
i +W i 2 '^
iui+ ~'iui io=
N X
i=1
n
2 TP hW~i
2'
i Vi
2x u^
i +W i 2 '^
iui+W i 2 '~
trabajando por separado con cada uno de los términos se obtiene:
1)
N P
i=1
2 TPW~i
2'i(V2ix^)ui
2)
N P
i=1
2 TP W i
2 '~iui
N P
i=1
TP W i 2 1 3 W i> 2 P > + N P i=1 ~
'iui 2
3
N P
i=1
TP W i 2 1 3 W i> 2 P > + N P i=1 ~
'i 2
3ku
ik2
3
N P
i=1
TP W i 2 1 3 W i> 2 P > + N P i=1 > i
' ui
3)
N P
i=1
2 TP W i
2 '^
i
ui = PN i=1
2 TP W i
2
h
Di
'V~2ixu^ i+ i'ui i = N P i=1 h
2 TP W i
2 D'iV~2ixu^ i + 2 TP W i 2 i'ui
i
N P
i=1
h
2 TP W i
2 D'iV~2ixu^ i + TP W i 2 1 4 W i> 2 P > + i
'ui
2 4 i N P i=1 h
2 TP W i
2 D'iV~2ixu^ i + TP W i 2 1 4 W i> 2 P >
+li
2x^x^
>~
V>i
2 i'V~2iui
i
De(3:11)se obtiene entonces que:
N X
i=1
n
2 TP hW~2i'
i
V2ix u^
i
+W2i'^
i
ui+W2i'~
i
uiio
N X
i=1
n
2 TPW~i
2'
i Vi
2x u^
i+ TP W i 2 1i 3 W i> 2 P > + > i
' u+ 2 T
P W2iD
i 'V~
i
2xu^
i
+
TP W i 2 1i 4 W i> 2 P >
+l2x^x^
>~
Vi>
2 i'V~2iui
o
N X
i=1
n
T hP W i 2 1i 3 + 1i 4 W i>
2 P + i'u
i
+
2 TPW~i
2'
i Vi
2x u^
i+ 2 TP W i 2 D
i 'V~
i
2xu^
i+l
2x^x^
>~
Vi>
2
i 'V~
i
2u
Utilizando(3:10)y(3:12), y sustituyendo en(3:8),
2 TP _ = T hP A+A>
P +P W1 1 1 +
1 2 W
>
1 P +
i
+
2 TPW~1 (V1x^) + 2 TP W1D V~1x^+ +l1x^x^
>~
V>
1 V~1+
N X
i=1
h
T hP W i 2 1i 3 + 1i 4 W i>
2 P + i'u
i
+ 2 TPW~i
2'i V2ix u^ i+
2 TP W i
2 D
i 'V~
i
2xu^
i+l
2x^x^
>~
Vi>
2
i 'V~
i
2u
ii=
T "
P A+A>
P +P
" W1 1 1 + 1 2 W > 1 + N X i=1 h
W2i 1i 3 + 1i 4 W i> 2 i# P+
+ i'u
i
+ 2 TPW~1 (V1x^) + 2 TP W1D V~1x^+ +l1x^x^
>~
V1> V~1+
N X
i=1
h
2 TPW~i
2'i V2ix u^ i+ 2 TP W i
2 Di'V~2ixu^ i+l2x^x^
>~
Vi>
2 i'V~2iui
i
Sumando y restando ahora >
Qa , en donde Qa es una matriz positiva de nida,
Qa >0;
2 TP _ = T P A+A>
P +P RP +Q + 2 TPW~
1 (V1x^) +
2 TP W
1D V~1x^+ +l1x^x^
>~
V>
1 V~1+
" N X
i=1
2 TPW~2i'
i
V2ix u^
i
+ 2 TP W2iD
i 'V~
i
2xu^
i
+
l2x^x^
>~
Vi>
2
i 'V~
i
2u
ii >
Qa (3.13)
En donde:
A = W1A R = W1
1 1 + 1 2 W > 1 + N X i=1 h
W2i 1i 3 + 1i 4 W i> 2 P i
; i 2N
Q = +
N X
i=1
i 'u
i+Q
Sustituyendo ahora(3:13)en(3:6),
_
V ( ) T P A+A>
P +P RP +Q + 2 TPW~
1 (V1x^) +
2 TP W1D V~1x^+l1x^x^
>~
V1> V~1+
N X
i=1
h
2 TPW~2i'
i
V2ix u^
i
+
2 TP W2iD
i 'V~
i
2xu^
i
+l2x^x^
>~
Vi>
2
i 'V~
i
2u
ii
>
Qa +tr n
~
WT
1 K 1 1 W~1
o
+trnV~T
1 K 1 2 V~1
o
+
N X
i=1
trnW~iT 2 K
1i 3 W~
i 2 o + N X i=1
trnV~iT 2 K
1i 4 V~
i
2
o
de donde se obtiene:
_
V ( ) T P A+A>
P +P RP +Q +tr
( ~ W T 1K 1
1 W~1+ 2 (V1x^) TPW~1
) + tr ( ~ V T 1K 1
2 V~1+ 2^x TP W1D V~1+l1x^x^
>~
V>
1 V~1
) + N X i=1 tr ( ~ W iT 2 K 1i 3 W~
i
2 + 2'
i Vi
2x u^
i TPW~i
2 ) + N X i=1 tr ( ~ V iT 2 K 1i 4 V~
i
2 + 2^xu
i T
P W2iD
i 'V~
i
2 +l2x^x^
>~
Vi>
2
i 'V~
i
2u
i )
>
Qa (3.14)
De esto se obtiene lo siguiente:
LW1 = ~W
T
1K 1
1 W~1+ 2 (V1x^) TPW~1
LV1 = ~V
T
1K 1
2 V~1+ 2^x TP W1D V~1+l1x^x^
>~
V>
1 V~1; i2N LW2 = ~W
iT
2 K 1i 3 W~
i
2 + 2'
i
V2ix u^
i T
PW~2i LV2 = ~V
iT
2 K 1i
4 V~2i+ 2^x TP W i
2 Di'V~2iui+l2x^x^
>~
Vi>
2 i'V~2iui; i 2N
Para obtener la ley de aprendizaje diferencial, se conoce que se necesitaV_ ( ) 0,
se cumplan:
LW1 =LV1 =LW2 =LV2 = 0
P A+A>
P +P RP +Q= 0
Entonces se tiene que:
_
V ( ) >
Qa (3.15)
Y comoQa>0, entonces se garantiza la estabilidad, considerando queV_ ( )
siem-pre es menor a cero.
Finalmente, para obtener la ley de aprendizaje se utilizan las expresionesLW1; LV1; LW2; LV2,
igualándolas a cero, de lo que se obtiene:
~
W
T
1K 1
1 W~1+ 2 (V1x^) TPW~1 = 0
~
W
T
1 = K1 2 (V1x^) TP
~
V
T
1K 1
2 V~1+ 2^x TP W1D V~1 +l1x^x^
>~
V>
1 V~1 = 0
~
V
T
1 = K2
h
2^x TP W1D +l1 x^x^
>~
V1>
i ~ W iT 2 K 1i 3 W~
i
2 + 2'
i Vi
2x u^
i TPW~i
2 = 0
~
W
iT
2 = K
i
3 2'
i
V2ix u^
i T
~
V
iT
2 K 1i 4 V~
i
2 + 2^x
TP W i 2 D
i 'V~
i
2u
i +l
2x^x^
>~
Vi>
2
i 'V~
i
2u= 0
~
V
iT
2 = K
i
4
h
2^xui TP W2iD
i
'+l2 i'x^x^
>~
V2i>u
ii
; i2N
De estas expresiones se obtienen entonces las expresiones de actualización de los
pesos de las neuronas en la red,
~
W1 = K1 2P
> >
(V1x^)
~
V1 = K2
h
2D>
W1>P
> ^
xT +l
1V~1x^x^
> >i
~
W
i
2 = K3i 2P
>
'i>
Vi
2x u^ i
>
; i2N
~
V
i
2 = K
i
4
h
2Di>
' W
i>
2 P
>
ui> ^
x>
+l2V~2ix^x^
>
ui i '
i
; i2N (3.16)
Y en donde la ecuación de Riccati queda como sigue,
P A+A>P +P RP +Q= 0 (3.17)
Finalmente, de(3:15), se obtiene lo siguiente,
_
V ( ) >Qa ; Qa >0
Integrando ambos lados la expresión anterior,
1
Z
0
_
V ( )
1
Z
0
>
Qa
Resolviendo la integral del lado izquierdo,
[V (1) V (0)]
1
Z
0
k k2Qa V (0) V (1)
ComoV (0)yV (1)son constantes, y
1
R
0
k k2Qa es una integral nita, menor a una constante, signi ca que el error disminuye hacia cero a medida que pasa el tiempo,
>
Qa ! 0parat <1, es decir, el error cuadrático tiende a cero para sistemas
lineales invariantes en el tiempo.
>
Qa !
t!1 0
De lo anterior se comprueba entonces que el modelo de la red neuronal diseñada es
estable, de acuerdo a la ley de aprendizaje propuesta(3:16), y que el error cuadrático