DESARROLLO DE UNA
CELDA ELECTROMAGNÉTICA TRANSVERSAL
T E S I S
QUE PARA OBTENER EL GRADO DE
MAESTRO EN CIENCIAS EN INGENIERÍA ELECTRÓNICA OPCIÓN INSTRUMENTACIÓN
P R E S E N T A
ING. OSCAR SÁNCHEZ QUINTANILLA
CONTENIDO
Pag.
Nomenclatura. . . . .iv
Lista de figuras. . . .vi
Lista de tablas. . . . .x
Resumen. . . .xi
Abstract. . . . .xii
CAPÍTULO 1. INTRODUCCIÓN 1
1.1.Mediciones de compatibilidad/interferencia electromagnética (siglas internacionales EMC/EMI). . . .1
1.2. Celda electromagnética transversal (TEM). . . . .4
1.3. Objetivo de la tesis. . . . . . .4
1.4. Justificación de la tesis. . . . . . .5
1.5. Organización de la tesis. . . . . . . .6
CAPÍTULO 2. CARACTERÍSTICAS DE LA CELDA TEM 7
2.1. Descripción general de la celda TEM. . . . .7
2.2. Tipos de celdas TEM. . . . . . . .10
2.3. Características mecánicas. . . . . . .17
2.4. Características eléctricas. . . . . . .19
2.4.1. Capacitancia por unidad de longitud e impedancia característica. . . .19
2.4.2. Uniformidad de campo. . . . . . .23
ii
3.2. Ecuaciones y gráficas características para el diseño de la celda TEM . . . .29
3.3. Etapas de diseño. . . .35
3.3.1. Características de la celda TEM. . . . .36
3.3.2. Condiciones de diseño y ecuaciones características. . . .37
3.3.3. Cálculos. . . . .39
CAPÍTULO 4. CONSTRUCCIÓN Y CARACTERIZACIÓN 43
4.1. Geometría de la celda TEM. . . . . . . .43
4.2. Método de construcción. . . . .49
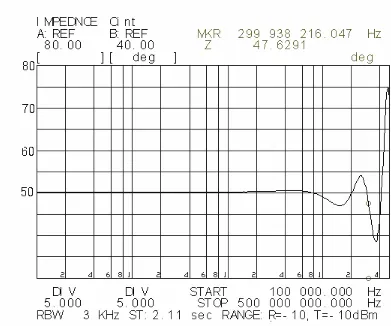
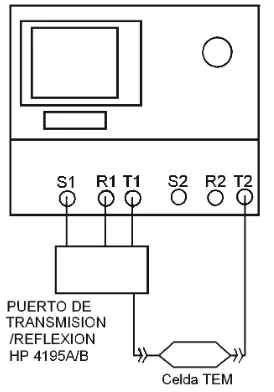
4.3. Medición de la impedancia característica de la celda TEM. . . .52
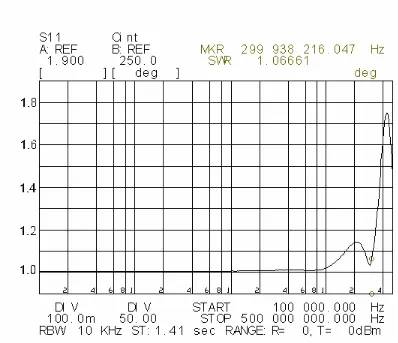
4.4. Medición de la relación de onda estacionaria (SWR), frecuencia de corte y frecuencia de resonancia. . . . . . . .55
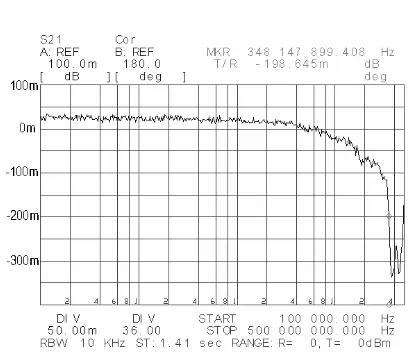
4.5. Medición de las pérdidas de la celda TEM. . . . .57
4.6. Optimización del conductor central (septum). . . . .58
4.7. Medición del campo eléctrico. . . . . . .61
4.7.1. Medición del campo eléctrico al centro de la celda TEM. . . . .61
CAPÍTULO 5. CONCLUSIONES Y RECOMENDACIONES 78
5.1. Características de la celda TEM. . . . . .78
5.2. Comentarios del desarrollo. . . . . . . .79
5.3. Conclusiones. . . .81
5.4. Recomendaciones. . . . .82
BIBLIOGRAFÍA . . . .83
mn
TE Modo eléctrico transversal mn.
( )
fc mn Frecuencia de corte para el modo mn. m, n = 0,1,2,…10
c
f Frecuencia de corte para el modo TE10.
(
)
≅ × ⎢⎣⎡ ⎥⎦⎤ =s m v 12 3 108
0 0ε
µ Velocidad de la luz.
⎥⎦ ⎤ ⎢⎣ ⎡ = − m H 7 0 4π x10
µ Permeabilidad en el espacio libre.
⎥⎦ ⎤ ⎢⎣ ⎡ = − m F 36 10 9 0 π
ε Permitividad en el espacio libre.
0
η = 120π [Ω] Impedancia intrínseca en el espacio libre.
0
z Impedancia característica de la línea en ohms.
0
C Capacitancia de la línea en farads por metro.
L Inductancia de la línea en henrys por metro.
1
f
C Capacitancia de bordes por la parte vertical de una línea rectangular.
2
f
C Capacitancia de bordes por la parte horizontal de una línea rectangular.
w Ancho del conductor interno de la línea rectangular.
h Separación entre el conductor interno y la pared horizontal de una línea rectangular.
E Campo eléctrico en volts por metro.
P Potencia en Watts.
R Parte real de la impedancia característica en ohms.
g
λ La longitud de onda del campo eléctrico en la guía.
K(k) y K(k') Integrales completamente elípticas de primer genero de módulos k y k'
respectivamente
K(λ) y K(λ’) Integrales completamente elípticas de primer genero de módulos λ y λ’ respectivamente.
A Area de sección transversal.
0
ε
C
∆
Factor de corrección de la capacitancia por unidad de longitud de una celda TEM.
b a ,
b w ,
w a ,
a g
Factores de forma de la celda TEM.
2.5. Celda TEM piramidal abierta. . . . . . . .12
2.6. Celda TEM piramidal con absorbedores. . . .13
2.7. Celda GTEM. . . .13
2.8. Celda TEM triple con absorbedores de ferrita. . . . .14
2.9. Celda WTEM. . . .14
2.10. Celda TEM con dos placas conductoras distribuidas hacia los extremos. . . .15
2.11. Celda X-TEM. . . .16
2.12. Celda EUROTEM. . . .16
2.13. Celda TEM rectangular. . . . .17
2.14. (a) Línea rectangular simétrica. (b) Distorsión de campo eléctrico en la esquina de la línea rectangular. . . . .20
2.15. Comportamiento de ε 1 f C o ε 2 f C con respecto a g h o h g . . . .21
2.16. Distribución de campo eléctrico relativo dentro de una celda TEM [3]. . . .24
2.17. Las longitudes de onda limite de algunos modos de orden superior como una función de la geometría de la celda TEM [26]. . . .26
3.1. Sistema de 50Ω. . . . .28
3.2. Transformación del plano complejo z al plano complejo x. . . .30
3.3. Capacitancia por unidad de longitud de una celda TEM como función de la geometría de la celda. . . .35
3.4. Impedancia característica de una línea rectangular coaxial con espesor despreciable del conductor interno. . . .36
3.5. Vistas de la celda TEM. . . . . . .37
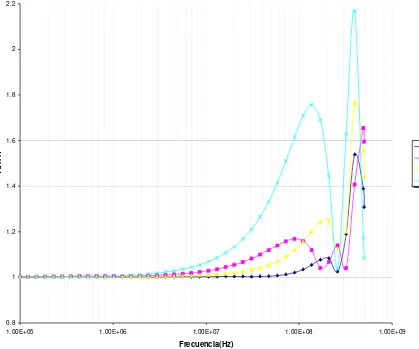
3.6. Impedancia característica de una línea rectangular, a) en escala lineal, b) en escala
logarítmica. . . .38
3.7. Nomenclatura de la celda TEM. . . . . . .39
3.8. Dimensiones de la celda TEM. . . . . . .41
4.1. Factor de forma b a de la parte piramidal de la celda TEM. . . .44
4.2. Factor de forma b w de la sección piramidal de la celda TEM. . . .45
4.3. Vistas lateral y superior de una celda TEM. . . .46
4.4. Variación de la impedancia característica, debido a la variación geométrica de la parte piramidal al implementar el conector coaxial. . . .47
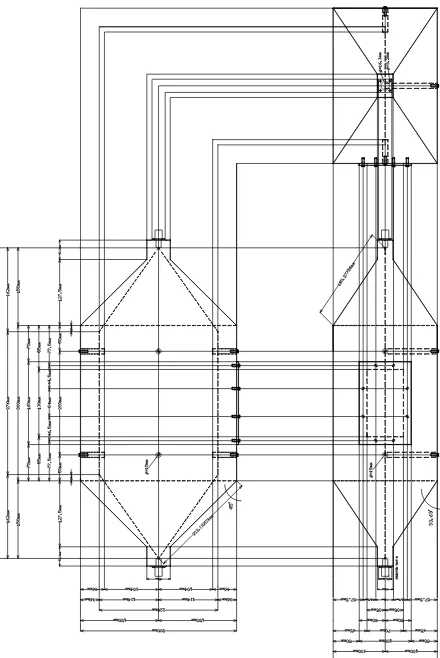
4.5. Plano General de la celda TEM. . . . . . .48
4.6. Espacio de prueba de la celda TEM simétrica. . . . .49
4.7. Partes principales que conforman a la celda TEM. . . .50
4.8. Método de unir las piezas principales de la celda TEM. . . . .50
4.9. Sujeción del conductor interno por medio de barras dieléctricas. . . . .51
4.10. (a) Sujeción del conductor central interno al conector tipo N. (b) Puerta de acceso de la celda TEM. . . .51
4.11. Juego de resistencias tipo “N” empleadas en la calibración del analizador de redes. . .52
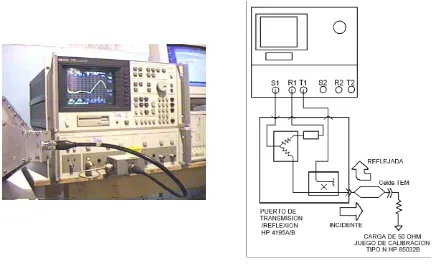
4.12. Impedancia de carga de la celda TEM empleada para medir la impedancia característica de la celda. . . . . . .52
4.13. Configuración para medir la impedancia característica de la celda TEM. . . . . .53
4.14. Gráfica de la impedancia característica de la celda TEM vacía. . . . .54
4.15. Relación de onda estacionaria (SWR) de la celda TEM vacía. . . .56
4.16. Configuración empleada para medir las pérdidas en la celda TEM. . . .57
4.17. Pérdidas en la celda TEM. . . . . . . . .58
4.18. Valor de la impedancia característica para diferentes valores de 2w. . . .59
4.19. Valor de la SWR para diferentes valores de 2w. . . . .60
4.20. Instalación del sensor 904 de EMCO en la celda TEM. . . .61
viii 4.28. Distribución de campo eléctrico vertical para diferentes frecuencias en las cuatro
posiciones verticales de la figura 4.25b. . . .68 4.29. Distribución de campo eléctrico de la figura 4.28. . . .69 4.30. Posiciones de los sensores de campo eléctrico a través de 2w. . . .69 4.31. Distribución de campo eléctrico a través de 2w para diferentes frecuencias en las
cinco posiciones transversales de la figura 4.30. . . .70 4.32. Distribución de campo eléctrico de la figura 4.31. . . .71 4.33. Ubicación de los puntos de medición para medir la distribución de campo
eléctrico transversal de la celda TEM. . . .71 4.34. Distribución de campo eléctrico en los puntos de medición de la tabla 4.7 (f = 100MHz) .72 4.35. Representación en gráfica de superficie de la distribución de campo eléctrico de la
figura 4.34 (f = 100MHz). . . . . . . .73 4.36. Distribución de campo eléctrico de la figura 4.34 (f = 100MHz). . . .74 4.37. Ubicación de los puntos de medición para medir la distribución de campo eléctrico
longitudinal de la celda TEM. . . . . . . .75 4.38. Distribución de campo eléctrico en los puntos de medición de la tabla 4.8 (f = 100MHz) .76 4.39. Representación en gráfica de superficie de la distribución de campo eléctrico de la figura
4.38 (f = 100MHz). . . .76 4.40. Distribución de campo eléctrico de la figura 4.38 (f = 100MHz). . . .77 5.1. Celda TEM construida en el Laboratorio de Compatibilidad Electromagnética del
A3. Sensores de barra y de esfera sensibles al campo eléctrico, altamente insensibles al
campo magnético. . . . . . .88
A4. Esquema de construcción de un sensor de esfera para medir campo eléctrico. . . .88
A5. Esquema de construcción de un sensor de barra para medir campo eléctrico. . . .89
A6. Factor de antena del sensor 901 de EMCO. . . . .91
A7. Factor de antena del sensor 902 de EMCO. . . . .91
A8. Factor de antena del sensor 903 de EMCO. . . . .92
A9. Factor de antena del sensor de esfera 904 de EMCO. . . .92
A10. Factor de antena del sensor de barra 905 de EMCO. . . .93
b
figura 4.2 . . . . .45
4.3. Valores de impedancia característica a diferentes alturas de la sección piramidal de la figura 4.4. . . . .47
4.4. Tabla de valores de campo eléctrico en las cinco posiciones horizontales de la figura 4.25a para diferentes frecuencias. . . . .66
4.5. Tabla de valores de campo eléctrico en las cuatro posiciones verticales de la figura 4.25b para diferentes frecuencias. . . . .68
4.6. Tabla de valores de campo eléctrico en las cinco posiciones transversales de la figura 4.30 para diferentes frecuencias. . . . .70
4.7. Tabla de valores de campo eléctrico transversal de la figura 4.33. . . .72
4.8. Tabla de valores de campo eléctrico longitudinal de la figura 4.37. . . . .75
A1. Características de los sensores de campo cercano EMCO modelo 7405. . . .90
RESUMEN
En esta tesis se describe el desarrollo de una Celda Electromagnética Transversal, la cual se
conoce como celda TEM o Crawford. La celda se construyó y diseñó como un prototipo de
laboratorio para una impedancia de 50 Ohms en un intervalo de frecuencia desde corriente
continua hasta 340 MHz. Las dimensiones de la celda son 0.2x0.3x0.4 m de altura, ancho y largo
respectivamente.
El uso de la celda TEM es para caracterizar sistemas eléctricos, electromecánicos y electrónicos
de acuerdo a las emisiones electromagnéticas y susceptibilidad electromagnética. En la
actualidad, las características de dichos sistemas dan las condiciones de conformidad para la
Compatibilidad Electromagnética (EMC). Las dimensiones máximas del equipo bajo prueba
deben ser 0.04x0.08x0.1 m de alto, ancho y largo. La celda desarrollada se está utilizando en el
laboratorio de EMC de la coordinación del Posgrado en Electrónica de la SEPI-ESIME.
Las características de la celda TEM están determinadas por sus dimensiones, por lo que se
presenta el diseño, problemas de construcción y caracterización. Como aportación original se
presenta un análisis experimental, variando las dimensiones del conductor central (septum), con
lo cual se pueden optimizar las características de la celda dentro de las condiciones de diseño
establecidas.
El prototipo de la celda TEM desarrollado cumple con las características de diseño prefijadas en
el objetivo de la tesis, y de acuerdo con los resultados experimentales su comportamiento
xii The use of the TEM cell is to characterize electrical, electromechanical and electronic systems
according to the electromagnetic emission and the electromagnetic susceptibility. Nowadays, the
characterization of such systems gives the condition of the compliance for Electromagnetic
Compatibility (EMC). Equipment under test, should be 0.04x0.08x0.1 m high, wide and long
respectively as maximum dimensions. The cell is being used in EMC laboratory at the Electronic
Postgraduate Section of SEPI-ESIME.
The characteristics of the TEM cell are determined by mean of its geometry, so in this thesis
design, construction problems and characterization are described. As original contribution an
experimental analysis about septum optimum was done due to the importance of the dimensions
of the septum, with regard to characteristics of the cell.
The prototype of the TEM cell has the design characteristics given in the thesis objective. The
behavior of the developed cell is the same as the one of any commercial cell according to the
CAPÍTULO 1
INTRODUCCIÓN
Cualquier sistema que funciona con energía eléctrica puede comportarse como una fuente de
interferencias, que en forma indeseada contribuye a la contaminación electromagnética del medio
ambiente o puede ser un sistema susceptible a las interferencias existentes en ese ambiente. La
comunidad de la Compatibilidad Electromagnética (EMC) mantiene un gran interés respecto a las
pruebas de emisiones y de susceptibilidad de los sistemas que operan con energía eléctrica, sobre
todo en dispositivos o sistemas de dimensiones pequeñas, donde los niveles de perturbaciones
electromagnéticas son difíciles de cuantificar.
En este capítulo se presenta: La importancia de las mediciones de Compatibilidad/Interferencia
Electromagnética (EMC/EMI); la descripción de una celda electromagnética transversal (TEM),
así como; el objetivo y la organización de esta tesis.
1.1. MEDICIONES DE COMPATIBILIDAD/INTERFERENCIA
ELECTROMAGNÉTICA (SIGLAS INTERNACIONALES EMC/EMI)
Hace más de 15 años en el ambiente de diseñadores, constructores y operadores de sistemas
eléctricos y electrónicos, la palabra Compatibilidad Electromagnética (EMC) no era familiar, se
usaban otros términos como: interferencias de radio frecuencia, ruido electromagnético,
perturbaciones electromagnéticas o Interferencias Electromagnéticas (EMI), para representar los
efectos indeseables que aparecen en todos los lugares donde existe energía eléctrica. En la
actualidad estos términos están bien definidos en la literatura, y la problemática se ha convertido
en una especialidad [1, 2]. Se puede decir que internacionalmente la calidad y eficiencia de
operación de toda una serie de sistemas que funcionan con energía eléctrica se basa en la
2 El primer documento que se tiene respecto a EMI fue realizado en 1927 por la agencia de la
aviación federal de USA. Se reporta perturbaciones en un altímetro debido a interferencias
causadas por el sistema de encendido de un motor. Posteriormente la primera norma respecto a
EMC, de carácter militar, se publico en 1945. Esta especifica las recomendaciones de medición
de EMI en los sistemas de radio en la banda de 150 KHz a 20 MHz.
Algunos sistemas electrónicos se diseñan principalmente para emitir señales, y estos pueden
causar problemas de interferencias a otros sistemas; este es el caso de los sistemas de
radiocomunicación. Otros equipos, que no poseen la función anterior; sin embargo, en muchas
ocasiones causan perturbaciones electromagnéticas, sobre todo aquellos que operan a frecuencias
altas. Idealmente cualquier sistema que funciona con energía eléctrica y no tiene la función de
radiar energía electromagnética no debiera generar perturbaciones electromagnéticas ni radiación
conducidas, ni tampoco debiera ser susceptible a perturbaciones.
El proceso para establecer la compatibilidad electromagnética en cualquier sistema electrónico
requiere de:
1. Identificar la perturbación electromagnética en el sistema. Se requiere hacer mediciones para
determinar el nivel de cualquier señal no deseada, la cual puede ser radiada (EMI radiadas) o
conducida a través de la línea de alimentación, de línea de datos o de las líneas de control
(EMI conducidas).
2. Identificar los niveles de susceptibilidad de los sistemas electrónicos a perturbaciones
electromagnéticas de diferentes niveles, a varias frecuencias, para determinar los niveles a los
cuales pueden operar satisfactoriamente dichos sistemas.
Dentro de las agencias que establecen los límites o requerimientos para las pruebas de
compatibilidad electromagnética están:
1. Federal Communications Commission (FCC), USA.
2. Department of Defense (DoD), EMC Military Standards, USA.
3. Verband Deutscher Elektrotecniker (VDE), Germany.
4. Comisión Federal de Telecomunicaciones (COFETEL), México.
Además de estas existen organizaciones profesionales que aprovechan las experiencias de sus
agremiados para establecer normas respecto a la compatibilidad electromagnética, las más
conocidas internacionalmente son:
1. American National Standards Committee, C63, C95.
2. Institute of Electrical and Electronics Engineers (IEEE).
3. International Special Committee on Radio Interference (CISPR).
4. International Standards Organization (ISO).
Todas las agencias y organizaciones recomiendan una serie de métodos de mediciones que
dependen de las siguientes consideraciones:
1. Tamaño del equipo a probar.
2. Intervalo de frecuencia.
3. Limites de prueba.
4. Tipo de campo (eléctrico o magnético).
4. Cámaras anecoicas.
1.2. CELDA ELECTROMAGNÉTICA TRANSVERSAL (TEM)
La celda electromagnética transversal, conocidas como celda TEM o de Crawford, es una línea
de transmisión coaxial rectangular expandida que opera en el modo electromagnético transversal.
La estructura típica de una celda del tipo TEM se muestra en la figura 1.1, consiste de una caja
metálica rectangular que contiene una placa conductora en su centro. Este tipo de celda es un
recinto blindado aislado, con la ventaja de que no introduce los problemas de reflexión asociados
con los recintos blindados convencionales. Los campos electromagnéticos transversales
generados entre la placa central y las paredes de la celda son estables y uniformes, por lo que se
consideran como estándares para la calibración de medidores de radiación electromagnética y
para pruebas de susceptibilidad y emisión en dispositivos o equipos electrónicos.
1.3. OBJETIVO DE LA TESIS
El objetivo de esta tesis es el diseño y construcción de la una celda TEM con una impedancia
característica de 50 y ancho de banda de 500 MHz, como prototipo de laboratorio para pruebas
de susceptibilidad y de emisiones electromagnéticas en sistemas electrónicos. Este prototipo
formará parte de un sistema automatizado de detección, registro, clasificación y análisis de
perturbaciones electromagnéticas en dispositivos y equipos electrónicos, cuyas dimensiones sean
menores a 5cm de altura, 10cm de ancho y 15cm de largo. El sistema se instalará en el
Ω
laboratorio de Compatibilidad Electromagnética del Programa de Posgrado en Ingeniería
Electrónica de la SEPI-ESIME Zacatenco.
Figura 1.1. Celda TEM típica.
1.4. JUSTIFICACIÓN DE LA TESIS
La celda TEM o de Crawford, se ha convertido en una herramienta básica para la caracterización
de equipos o dispositivos electrónicos desde el punto de vista de EMC. Esta herramienta es
bastante aceptable para la caracterización de radiación y susceptibilidad en los sistemas
electrónicos, porque genera campos electromagnéticos uniformes de alta precisión, además de ser
de bajo costo [11]. También es útil en la calibración de medidores de radiación electromagnética
de alta sensibilidad, así como en la cuantización de los efectos de la radiación electromagnética
no ionizante en medios biológicos [12]. Desde el primer diseño de la celda realizado por
Crawford en 1974 [3] hasta la fecha, se siguen presentando investigaciones al respecto, las cuales
se enfocan a la optimización de la distribución de los campos electromagnéticos dentro de la
celda. Debido a esto se han reportado diferentes construcciones de celdas como generadoras de
6 (resonancias a altas frecuencias), ya que básicamente la celda TEM se comporta como una línea
de transmisión coaxial. Bajo este contexto para realizar investigación de lo antes mencionado se
requiere de una celda TEM típica, que en primera instancia cumpla con las características
mencionadas en le objetivo, las cuales cubren el intervalo de operación (frecuencia e
impedancias) de una gran cantidad de instrumentos y sistemas electrónicos.
1.5. ORGANIZACIÓN DE LA TESIS
Esta tesis se desarrolla en cinco capítulos, el primero corresponde a esta introducción. En el
segundo se describen las características particulares y el desarrollo que han tenido en las últimas
décadas las celdas TEM. En el tercero se desarrolla el diseño de la celda TEM y el cuarto se
describe la construcción y caracterización de esta. En el quinto capítulo se presentan las
conclusiones y recomendaciones, aquí se reportan las aportaciones de la tesis y el planteamiento
CAPÍTULO 2
CARACTERÍSTICAS DE LA CELDA TEM
La celda TEM es uno de los dispositivos esenciales para la caracterización de sistemas
electrónicos en el área de EMC. Este dispositivo permite hacer pruebas de susceptibilidad y de
emisión de campos electromagnéticos y es ampliamente recomendado por el NIST [46]. En este
capítulo se describen las características mecánicas y eléctricas de las celdas TEM más
importantes como son: las dimensiones físicas que determinan los parámetros eléctricos de
operación; impedancia característica y la capacitancia por unidad de longitud.
2.1. DESCRIPCIÓN GENERAL DE LAS CELDAS TEM
Las celdas TEM son instrumentos que se utilizan para la caracterización de la susceptibilidad y la
emisión de radiación electromagnética de sistemas, equipos o elementos eléctricos con gran
precisión, debido a que provee el aislamiento del ambiente electromagnético externo, de igual
manera que las cámaras anecoicas, con la diferencia de que las celdas TEM son portátiles y de
bajo costo. La frecuencia de operación de las celdas TEM está en función de sus dimensiones
físicas, las cuales limitan el tamaño del Equipo Bajo Prueba (EBP). Para pruebas de dispositivos
con dimensiones pequeñas la celda presenta una gran ventaja, ya que se optimiza el espacio
teniendo una distribución de campos uniformes; además para mediciones de susceptibilidad no
requiere ningún aditamento especial que se introduzca dentro de la celda (p. ej. antenas), sino
solamente el EBP. Particularmente es apropiada para mediciones que involucran señales con
anchos de banda grandes, tales como, transitorios, impulsos, o mediciones de barrido en
frecuencia.
Una celda TEM estándar puede ser empleada para la generación de niveles de campos
continua hasta 500MHz, las dimensiones máximas del EBP deben de ser aproximadamente de
5cm de altura, 10cm de ancho y 15cm de largo.
Para pruebas de emisión con la celda TEM se requiere que el EBP se coloque dentro de la celda
con una orientación que permita un acoplamiento apropiado entre los modos de los campos TEM
y el EBP. Normalmente se gira el EBP dentro de la celda para lograr tal objetivo [51, 52, 53].
La celda TEM es una línea de transmisión coaxial expandida que opera en el modo
electromagnético transversal. Consiste de una caja metálica rectangular con un conductor al
centro, terminada en sus extremos en una estructura piramidal en la cual se fijan conectores
coaxiales típicos, tal como se muestra en la figura 2.1. Esta celda es un recinto blindado que no
introduce problemas de reflexión, como normalmente ocurre en los recintos blindados
convencionales. Las dimensiones de la celda y la distribución de la placa central entre las paredes
se fijan para tener un campo TEM relativamente uniforme y estable, el cual se utiliza para
pruebas de susceptibilidad o calibración de sensores de campo eléctrico. También permite hacer
medición de las emisiones de campos electromagnético generados por sistemas, equipos o
dispositivos eléctricos o electrónicos, porque se comporta como una línea de transmisión. Los
campos electromagnéticos se acoplan al conductor central y se miden en las terminales de la
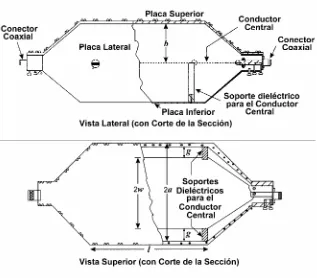
Figura 2.1. Geometría de una celda TEM.
En la tabla 2.1 se resumen algunas características y limitaciones principales de la celda TEM.
Tabla 2.1. Características y limitaciones principales de la celda TEM.
CARACTERISTICAS LIMITACIONES
• Generación de campos eléctricos para
pruebas de susceptibilidad de 10 µV/m a
500 V/m, desde corriente continua hasta
(frecuencia de corte).
10 c
f
• Permite medir emisiones de radiación electromagnética con alta precisión
(±1dB).
• Respuesta de fase lineal desde corriente
continua hasta fc10 (frecuencia de corte).
• Es portátil.
• Es de bajo costo comparado con los recintos blindados como son las cámaras anecoicas.
• Restricción de tamaño del EBP impuestas por las dimensiones de la celda.
• Requiere de un diseño mecánico de alta precisión.
• La frecuencia de operación es función de las dimensiones de la celda (tamaño
inversamente proporcional a la máxima
frecuencia de operación).
• Inexactitud de las mediciones de emisión en dispositivos, equipos o sistemas con
dimensiones casi iguales al volumen para
posteriormente la justifico teóricamente Kanda [11], dando las bases de diseño de celdas de este
tipo. En la figura 2.2 se muestra una celda TEM típica.
Figura 2.2. Celda rectangular (Crawford) TEM.
Las celdas TEM se construyen (sección rectangular con terminaciones de estructura piramidal)
para una impedancia característica nominal de 50Ω, 75Ω, etc., con el fin de asegurar mínima
relación de onda estacionaria. Cuando la celda se alimenta en uno de sus extremos con una señal
de radio frecuencia y en el otro extremo se acopla a la impedancia característica, dentro de la
celda se genera un campo eléctrico uniforme, el cual sirve para medir la susceptibilidad de
dispositivos, equipos o sistemas electrónicos. Estas celdas presentan algunos problemas, los
principales son:
1. Las características de la celda (impedancia, frecuencia de operación, uniformidad de los
2. Por la estructura piramidal en los extremos, se generen reflexiones y resonancias que
corresponden a los modos de alto orden, lo cual hace que el campo eléctrico no sea uniforme.
3. El tamaño del EBP está limitado a las dimensiones de la celda; por ejemplo, para la celda
objeto de este trabajo, los equipos a caracterizar deben tener dimensiones menores de 5cm de
altura, 10cm de ancho y 15cm de largo.
Varios trabajos han reportado modificaciones a la celda TEM, con el fin de mejorar sus
características y evitar los problemas mencionados. En la referencia [13] se propone aumentar el
volumen de prueba, colocando el conductor interno de la línea de transmisión coaxial a 2/3 de la
altura de la sección rectangular hacia la parte superior, en lugar de 1/2 como normalmente se
tiene. Esta celda se le conoce como TEM asimétrica y se muestra en la figura 2.3.
Figura 2.3. Celda TEM asimétrica.
Para compensar algunos de los problemas de resonancia que se presentan en la celda se propone
cubrir la parte interna con material absorbente, tal como se muestra en la figura 2.4. Con esto se
Figura 2.4. Celda TEM con absorbedores.
Con los absorbedores los campos electromagnéticos dentro de la sección transversal de la celda
TEM no se propagan con la misma rapidez, provocando un decremento en la uniformidad del
campo. Esta es una desventaja de los absorbedores. Para resolver este problema se usa solamente
la sección piramidal, colocando en la base una carga (terminal). Esta celda se muestra en la figura
2.5.
Figura 2.5. Celda TEM piramidal abierta.
Si la señal de radiofrecuencia con la que se excita la celda tiene una longitud de onda del mismo
orden de magnitud que la altura de la pirámide, la carga con la que se termina no debe de ser
puramente resistiva, por lo que se utilizan absorbedores [15].
Una combinación de carga resistiva para bajas frecuencias y absorbedores para altas frecuencias
onda abierta con una sola sección piramidal. El desarrollo de una celda TEM piramidal cerrada
con absorbedores se reporta en [18], y es tal como se muestra en la figura 2.6.
Figura 2.6. Celda TEM piramidal con absorbedores.
Otra celda TEM piramidal con conductor interno asimétrico se desarrollo por Brown Boveri
Comp. (BBC) en Suiza y se le dio el nombre de celda GTEM [19]. La estructura de esta celda es
como se muestra en la figura 2.7.
Figura 2.7. Celda GTEM.
Un cambio bastante sustancial en el desarrollo de las celdas TEM, fue el remplazo de los
absorbedores típicos (pirámides de poliuretano con polvo de carbón) por absorbedores de ferrita
tipo mosaico, los cuales son de banda ancha [20]. Como resultado se obtuvo un mayor volumen
en la zona de prueba. Otro adelanto en este desarrollo, es la colocación de un segundo conductor
interno, perpendicular al existente, lo cual genera la polarización de los campos horizontales y
verticales, además con una base giratoria para los EBP se puede irradiar en tres direcciones. Esta
Figura 2.8. Celda TEM triple con absorbedores de ferrita.
Para suprimir los modos longitudinales que se generan dentro de la celda GTEM, los conductores
internos se construyeron con alambres planos paralelos, con esto se obtienen campos más
uniformes. Esta celda se conoce como WTEM [21] y su estructura se muestra en la figura 2.9.
Los trabajos continuaron para mejorar el problema de los absorbedores. En la referencia [22] se
reporta el remplazo de absorbedores resistivos por un conjunto de resistores y capacitores en
combinación con las ferritas. Con esto se suprimieron los modos longitudinales. A esta celda se
le conoce como FRCTEM.
Las celdas TEM asimétricas como se describieron anteriormente, tienen la placa conductora
interna más cercana a la parte superior de la celda que a la parte inferior. Esto es con el fin de
tener mayor volumen para los EBP. En la parte superior de la celda se genera una pantalla
electromagnética, por lo que las emisiones radiadas no son captadas y el campo dentro de la celda
no es adecuado. Para corregir este problema se colocó otra placa conductora hacia la parte
inferior de la celda con una distribución simétrica que permita optimizar el volumen de la celda.
Los conductores internos se alimentan con voltajes de la misma amplitud pero de fases opuestas
para mantener uniformidad en los campos. Esta celda se muestra en la figura 2.10.
Figura 2.10. Celda TEM con dos placas conductoras distribuidas hacia los extremos.
La celda X-TEM [23] se construye haciendo una combinación de las celdas anteriores, la
asimétrica, la triple y la de los absorbedores de ferrita. Las placas conductoras internas se forman
con cables planos y se colocan alrededor de la celda, manteniendo el centro libre para la
Figura 2.11. Celda X-TEM.
En la figura 2.11 las paredes no son el conductor de referencia como en la celda TEM clásica, su
principal función es de blindaje electromagnético. En las celdas que tienen dos conductores
internos y se alimentan de forma balanceada, el blindaje pierde efectividad; en este caso las
paredes se cubren con material absorbedor, tales como mosaicos de ferrita. Los mosaicos de
ferrita producen disminución de los modos longitudinales y mejoran la polarización cruzada. La
celda construida con dos conductores internos simétricos y cubierta con mosaicos de ferrita se le
conoce como EUROTEM [24], la desventaja que presenta es que no tiene la capacidad de
presentar doble polarización. Esta desventaja se elimina con la celda EUROTEM-2, pero a la
fecha no se han publicado sus características globales. La celda EUROTEM se muestra en la
figura 2.12.
2.3. CARACTERÍSTICAS MECÁNICAS
De acuerdo a la figura 2.1 y como se muestra en la figura 2.13, el espacio de prueba de la celda
(recinto de un campo de onda plana uniforme con características bien definidas) corresponde a la
sección central de una Línea de Transmisión Coaxial Rectangular. El conductor central (septum)
es una hoja delgada de metal soportada por medio de barras de material aislante que se fijan a una
de las paredes de la celda. El cuerpo de la celda puede ser rectangular o cuadrado, en el cual se
coloca el conductor central de forma simétrica a las paredes de la celda. La estructura rectangular
es la que genera una mayor uniformidad del campo. En [3] se presenta un análisis de las
geometrías y se realiza una comparación entre el volumen de prueba y la uniformidad de campo.
(a)
(b)
Figura 2.13…continuación. Celda TEM rectangular.
La geometría de la celda define básicamente lo siguiente:
• El máximo volumen para colocar el EBP.
• La máxima frecuencia de operación.
• Las características de uniformidad de campo eléctrico.
• El acoplamiento de los campos electromagnéticos.
• La relación de onda estacionaria (SWR).
• La impedancia del sistema.
Por ejemplo: con relación a la figura 2.13, la expresión que determina la frecuencia superior de
operación de la celda para un modo eléctrico transversal mn (TEmn) es [25, 26]:
( )
b n a m fc mn
2 2 2
1 2 2
+ =
µε …(2.1)
Donde
( )
fc mn = frecuencia de corte para el modo mn.m, n = 0,1,2,…
Como se observa de la ecuación (2.1), la frecuencia máxima de operación de la celda TEM
depende del modo electromagnético transversal y de las dimensiones, que están relacionadas con
el ancho y la altura de la celda (2a y 2b).
2.4. CARACTERÍSTICAS ELÉCTRICAS
Desde su origen la celda TEM se concibió como una línea de transmisión y fue utilizada para la
calibración de dipolos en la medición de campos electromagnéticos, cumpliendo lo siguiente:
a) Máxima transferencia de energía en la celda (mínima desigualdad de impedancia de la línea y
las terminales de entrada y salida).
b) Generación de campos electromagnéticos uniformes en el volumen de prueba.
c) Respuesta en frecuencia específica.
2.4.1. CAPACITANCIA POR UNIDAD DE LONGITUD E IMPEDANCIA CARACTERÍSTICA
La impedancia característica de una celda TEM se determina considerando que se trata de una
línea de transmisión rectangular con conductor central [27, 28]. La capacitancia e inductancia por
unidad de longitud y la impedancia característica de una línea de transmisión se relacionan por
medio de la velocidad de propagación de la onda, a través de:
(
)
12(
)
120 0
0
1 1
LC
v= =
ε
µ …(2.2)
y
0
1
2 1
vC C
L
z ⎟⎟ =
⎠ ⎞ ⎜⎜ ⎝ ⎛
0
z = Impedancia característica de la línea en ohms.
0
C = Capacitancia de la línea en farads por metro.
L = Inductancia de la línea en henrys por metro.
De las ecuaciones anteriores se puede observar que la evaluación de la impedancia característica,
depende de la capacitancia de la línea de transmisión rectangular y de la velocidad de
propagación de la onda electromagnética. La expresión de la capacitancia se determina de la
geometría de la línea de transmisión rectangular con un conductor en el centro, tal como se
muestra en la figura 2.14.
Los efectos capacitivos se han analizado por diferentes metodologías [29, 30], estas coinciden en
que:
a) La capacitancia debida a en los bordes por la parte vertical se puede calcular por:
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = h g arctan g h h h g
Cf 2
4 log 2 2 2 1 π ε …(2.4)
b) La capacitancia debida a los bordes por la parte horizontal se puede calcular por:
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + = g h arctan h g g h g
Cf 2
4 log 2 2 2 2 π ε …(2.5)
Considerando lados grandes del conductor de la figura 2.14 la relación de
ε 1 f C o ε 2 f C , con respecto a g h o h g
esta dada según la figura 2.15.
Figura 2.15. Comportamiento de
ε 1 f C o ε 2 f C
con respecto a
Cuando la línea de transmisión es asimétrica (desplazamiento del conductor central, tanto en la
parte vertical como en la horizontal), la capacitancia entre los conductores puede calcularse por
[31]:
∑
∑
= = = = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + = 2 , 1 2 , 1 2 2 2 2 , 1 2 , 1 2 2 2 2 1 2 1 2 4 log 2 4 log n m n m m n n m n n m n n n m m m n g h arctan h g g h g h g arctan g h h h g h w h w g b g b C π ε π ε ε …(2.7)En la ecuación (2.7) se han involucrados 8 términos de capacitancia debido a los bordes. Por
tanto hay 8 factores de correcciones de longitud que deben de considerarse para determinar la
inductancia de la línea de transmisión.
La impedancia característica de la línea se determina por:
(
)
(
)
∑
∑
∑
∑
= = = = = = ⎥⎦ ⎤ ⎢ ⎣ ⎡ + + + = 2 ,1 1,2
2 , 1 2 , 1 2 2 , 1 2 , 1
1 , ,
2.4.2. UNIFORMIDAD DE CAMPO
Una de las características importantes de una celda TEM es la generación de un campo eléctrico
uniforme entre el conductor central y el cuerpo de la celda. Estudios al respecto se han realizado
en [3, 32] y curvas típicas de la distribución de este se muestran en la figura 2.16. Los datos de
las variaciones del campo son registrados entre el conductor central y las paredes superior e
inferior de la celda TEM.
Resultados dados en [3] demostraron que la geometría rectangular tiene mayor uniformidad en la
distribución de campo eléctrico, con la desventaja de presentar una disminución en su frecuencia
de corte. La geometría cuadrada por el contrario, tiene menor uniformidad de campo eléctrico,
pero con la ventaja de contar con un espacio de prueba y un ancho de banda mucho mayor.
Cuando la potencia es transmitida a través de la celda, el campo eléctrico absoluto (E) en volts
por metro en el centro de la celda (área de prueba) se puede calcular por la expresión (2.9).
b PR
E= …(2.9)
donde:
P = Potencia en Watts
R = Parte real de la impedancia característica en ohms
b = distancia en metros entre el conductor interno y la pared superior (ó la pared interior) que
Parte Inferior
Figura 2.16. Distribución del campo eléctrico relativo dentro de una celda TEM [3].
La medición del campo eléctrico se realiza entre el conductor central y la pared superior (ó
inferior), se normaliza en función de las dimensiones de la celda.
La distribución del campo eléctrico al momento de hacer una medición se modifica, dado que
cualquier dispositivo que se introduzca dentro del área de prueba generara distorsión de este, y
entonces la medición experimental diferirá de la teórica.
Una expresión teórica para determinar la distribución de campo eléctrico dentro de la celda la
desarrollo la NBS (National Bureau of Standards) [11] considerando una celda vacía. La
medición de la distribución de campo se mide con un pequeño dipolo, y se ha determinado que
para despreciar la distorsión del campo dentro de la celda, el EBP debe tener como máximo un
tercio respecto a la distancia entre el conductor central y cualquiera de las paredes horizontales de
la celda [3].
Se han realizado análisis teóricos y experimentales [3, 33] respecto a la distorsión de campo
considerando objetos de metal rectangulares. Spiegel [34] empleó la aproximación cuasi estática
TEM. Sus resultados son acordes a los obtenidos en [32]. También obtuvo expresiones analíticas
para las componentes x y y de campo magnético en la celda.
2.4.3. RESPUESTA EN FRECUENCIA ESPECÍFICA
Una característica muy útil de las celdas TEM es que es una fuente de campo de ondas planas de
radiofrecuencia, con la cual se pueden generar campos desde corriente continua hasta el modo
electromagnético transversal TE10 que corresponde a la frecuencia de corte. Como el nombre de
la celda lo especifica, los campos que se generan están en el modo electromagnético transversal,
y el primer modo de orden superior determina la máxima frecuencia de operación de la celda.
Estos modos dependen de la geometría de la celda y se han determinado teórica y
experimentalmente por un sin número de observaciones dadas en [25, 26, 35]. Tomando como
base la geometría de la celda de la figura 2.13b, se muestra en la figura 2.17 la dependencia del
umbral de la longitud de onda con la geometría para algunos modos de la celda TEM estimadas
por Gruner [25]. Así mismo Weil y Gruner [36] dan una alternativa de los primeros once modos
de alto orden de las frecuencias de corte, y grafican estas como una función de la relación
b a
de
la celda, para algunos valores de impedancia característica.
El comportamiento de la celda se puede determinar alimentándola con un cierto nivel de
potencia, y se observa que al aumentar la frecuencia los modos de orden superior aparecen
superpuestos, degradando la configuración del campo del modo electromagnético transversal
puro. Cuando los primeros modos de orden superior aparecen, estos se comportan como ondas
viajeras que se refleja atrás y adelante dentro de la celda. La reflexión ocurre dentro de las
secciones piramidales de la celda, las cuales forman una guía de onda con frecuencia de corte
Figura 2.17. Las longitudes de onda límite de algunos modos de orden superior como una función de la geometría de la celda TEM [26]
Conforme la frecuencia se incrementa, la longitud de onda λg del campo en la guía de la celda
decrece. Una frecuencia coincidente con una resonancia de la cavidad intensifica los campos de
esta frecuencia. Así, estos modos perturbaran el modo TEM a través de su presencia como ondas
viajeras u ondas estacionarias. Un análisis teórico y experimental de la frecuencia de corte y de
resonancia son dados en [37, 38].
En general, la configuración de campo dentro de la celda, cuando aparecen los modos de orden
superior es suficientemente compleja e imprecisa, por lo que la NIST y otras Corporaciones usan
la calibración de la celda solamente en la región del modo TEM puro abajo de la frecuencia de
corte del primer modo de orden superior. Cuando la celda es usada como una fuente de campo
estándar, el análisis de los modos de orden superior es conveniente solo para predecir la
frecuencia de corte más baja, esto es, la frecuencia más alta a la cual el campo de la celda es
CAPÍTULO 3
DISEÑO DE LA CELDA TEM
En este capítulo se presenta el análisis de una celda TEM y se establecen las características específicas de diseño a partir de ecuaciones aproximadas y gráficas normalizadas.
Como se mencionó en el capítulo anterior, las características eléctricas de la celda TEM las determinan sus dimensiones, y de aquí se puede especificar los límites de utilización de la celda y las dimensiones máximas del EBP. El diseño se realizará bajo los objetivos del capítulo 1 que corresponden al desarrollo de una celda TEM con frecuencia de corte de 500MHz e impedancia característica de 50Ω. Así también considerando las dimensiones del EBP, el cual debe tener como máximo un tercio con respecto a la distancia entre el conductor central y cualquiera de las paredes horizontales de la celda [3].
3.1. CONDICIONES GENERALES DE DISEÑO
Para diseñar una celda TEM primero se requiere establecer sus características eléctricas, que son función de la geometría. En este caso se selecciona la geometría de una celda TEM típica, que es como la que se muestra en la figura 2.13. La selección fue hecha por la simplicidad de construcción y porque aún todavía hay una serie de fenómenos que no han sido totalmente analizados, como por ejemplo la distribución de las corrientes en el conductor central.
De acuerdo a la figura 2.13 las dimensiones de a y b son las que determinan las características de la frecuencia de operación de la celda y desde luego las dimensiones del equipo bajo prueba (EBP).
Otra de las características importantes de la celda es la necesidad de establecer un campo uniforme conocido a través del volumen de prueba (o sea, la región en la cual el dispositivo bajo prueba se coloca). En [11] se menciona un método analítico y experimental para determinar el campo dentro de la celda según la NBS. En capítulo se presentan las ecuaciones básicas de diseño y los resultados experimentales se mencionan en el capítulo 4.
El intervalo de frecuencia seleccionado para la operación de la celda TEM objeto de esta tesis es desde corriente continua hasta 500MHz. La selección se debe a que una gran cantidad de sistemas electrónicos que se utilizan en la instrumentación industrial médica y de propósito general funcionan dentro del intervalo de frecuencia mencionado, y se les está exigiendo caracterización de conformidad de acuerdo a normas establecidas de compatibilidad electromagnética.
La impedancia característica de la celda TEM, puede ser expresada en términos de la capacitancia por unidad de longitud (C0) como [1]:
0 0 0
0 0 0
0 0 0
0
1 1 1
ε η ε η
µ
C C C vC
z = = = = …(3.1)
⎥⎦ ⎤ ⎢⎣ ⎡ = − m F π ε 36 10 9
0 permitividad del espacio libre.
0
η = 120π [Ω] impedancia intrínseca en el espacio libre.
0
µ = 4π× 10-7 permeabilidad del espacio libre.
(
)
≅ × ⎢⎣⎡ ⎥⎦⎤ =s m
v 12 8
0
0ε 3 10
µ velocidad de la luz en el espacio libre.
0
C se da en términos de la geometría de la celda, y se calcula por expresiones exactas y
aproximadas. Las dimensiones de la celda a, b, w y g se muestran en la figura 3.2. Para su
construcción se deben de satisfacer algunas consideraciones, como por ejemplo la relación
w a
que corresponde al ancho de la celda con respecto al ancho del conductor interno, al respecto la NBS da ciertas recomendaciones. También se debe considerar la dependencia de la capacitancia
de la celda por unidad de longitud en función de la relación
b a
. Bajo dichas consideraciones se
determina el ancho del conductor interno necesario para tener una impedancia característica de 50Ω.
3.2. ECUACIONES Y GRAFICAS CARACTERISTICAS PARA EL DISEÑO DE LA CELDA TEM
La celda TEM es básicamente una línea de transmisión coaxial como se muestra en la figura 2.13b. Su capacitancia puede determinarse analíticamente usando el método de Transformaciones Confórmales [40], que consiste en trasladar la estructura de una celda TEM de vista frontal a dos placas en un plano de dos dimensiones que puedan representar el comportamiento de un capacitor típico. Esto se representa en la figura 3.2.
del cual la configuración del plano z de la figura 3.2a será transformada en un plano x
bidimensional que representa un capacitor de dos placas paralelas (figura 3.2b). Para este caso la capacitancia es invariable bajo una transformación conformal [32], por tanto la fórmula que se obtendrá será aplicable para una celda TEM.
Figura 3.2. Transformación del plano complejo z al plano complejo x.
De la figura 2.13b se puede observar que tenemos simetría con respecto al conductor interno. Entonces se podrá calcular la capacitancia entre la pared superior de la celda, cuyas esquinas de la geometría de la pared superior son: A, F, E, y D, y el centro de la placa interna, cuyos extremos son: B y C (plano z de la figura 3.2a). La capacitancia total será entonces el doble de esta capacitancia calculada. Debido a su geometría rectangular, esta región puede ser expresada en términos de funciones elípticas Jacobianas [41].
( )
( )
' 2k K
k K b
a =
( )
( )
' 0 0 λ λ ε K K C= …(3.3)
Donde K(k), K(k'), K(λ) y K(λ') son integrales elípticas completas de primer genero de módulos k,
k', λ y λ', respectivamente y se interpreta como la capacitancia por unidad de longitud. Sin
embargo, la capacitancia total por unidad de longitud L de la celda TEM corresponde al doble de la ecuación anterior, porque la sección transversal inferior de la celda TEM tiene una geometría igual a la del plano z de la figura 3.2a.
0 C
( )
( )
' 2 0 0 λ λ ε K K C= …(3.4)
Utilizando la ec. (3.1) y sustituyendo la ec. (3.4), la impedancia característica es entonces dada por:
( )
( )
λ λ η K K z ' 2 1 00 = …(3.5)
Donde η0 es la impedancia característica en el espacio libre. Las ecs. (3.4) y (3.5) son ecuaciones
exactas que no son fáciles de usar. En vista de que integrales elípticas completas aparecen en las fórmulas anteriores, a continuación se dan formulas que no involucren funciones especiales, cuyos resultados numéricos sean suficientemente precisos desde el punto de vista práctico en ingeniería. La fórmula expresa la capacitancia en términos de las dimensiones a, b, y w de la celda TEM, las cuales puedan ser usadas para diseñar la celda TEM con una impedancia característica dada.
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ > ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + π ≅ 2 1 1 1 2 1 2 2 k k k b a , Ln …(3.7) ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ > ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ≅ 2 1 1 1 2
2 λ2
λ λ π
εo Ln ,
o C
…(3.8)
De acuerdo a la referencia [32], en la ecuación (3.7) la restricción
2 1
2 >
k es equivalente al
requerimiento 1 2a<
b
, considerando
2 1
2 =
k , tenemos que K(k’) = K(k), y se consideramos un
requerimiento más estricto, tenemos que:
1
< a b
…(3.9)
De las ecs. (3.7) y (3.8) se deriva la siguiente expresión aproximada para calcular capacitancia por unidad de longitud de la celda TEM
0 2 2 4 ε ∆ π π ε C b g b a C o o − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −
≅ Ln senh …(3.10)
donde: ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + = k k C o 1 1 1 1
2 2 λ
λ π
ε ∆
Una forma alternativa de la ec. (3.10) puede ser obtenida empleando la siguiente identidad: ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟⎠ ⎞ ⎜ ⎝ ⎛ b g e b g b g 2 1 2 2 π π π coth
senh …(3.12)
dando como resultado:
0 0 0 2 1 2 4 ε ∆ π π ε C b g b w C − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + +
= Ln coth …(3.13)
De esta forma dentro del paréntesis cuadrado de la ec. (3.13), es fácil identificar que el primer término corresponde a la capacitancia entre el conductor central y las paredes horizontales, el segundo término representa la capacitancia entre las orillas del conductor central y las paredes verticales (capacitancia de bordes).
Es interesante notar que el término de la derecha en la ec. (3.13), es idéntico a la fórmula dada por Chen [31] y originalmente derivada por Cohn [29]. La fórmula de Cohn fue derivada suponiendo que el ancho del conductor central 2w, es muy grande comparado con la separación 2b. Que es equivalente a suponer que las orillas del conductor central no interactuan.
De acuerdo a lo anterior, ∆C en la ec. (3.13) puede ser interpretado como un término de corrección, necesario para entender la interacción entre las dos orillas. De la ec. (3.11) se puede observar que ∆C será despreciable, si λ es aproximadamente uno (o en su defecto λ’ es aproximadamente cero) considerando k aproximadamente uno. Esto se logra usando las expresiones aproximadas de k, dada por Anderson [44], donde puede observar que para el modulo λ se reduce a:
b w
e π
λ 2
2
Empleando la ec. (3.1) y la ec. (3.10), la impedancia característica es: 0 0 0 2 2 4 ε ∆ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ π π − η = C b g b a z sen Ln …(3.16)
Ó alternativamente por las ecs. (3.1) y (3.13).
0 0 2 1 2 30 ε ∆ π π π C b g b w z − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = coth Ln …(3.17)
De esta manera se obtienen expresiones aproximadas para la capacitancia por unidad de longitud y la impedancia característica de la celda TEM. Las cuales son las ecs. (3.10) ó (3.13), (3.16) ó (3.17). Debido a las limitaciones de las aproximaciones. Estas fórmulas son válidas, según las relaciones establecidas en (3.9) y (3.15), para
1 ≥ b a y 2 1 ≥ b w …(3.18)
En la figura 3.3 se gráfica la formula exacta (3.4) y la fórmula aproximadas (3.13), para
diferentes factores de forma ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ w a b a
ec. (3.4) se traza con línea continua [11]. Las dos curvas son casi idénticas, excepto cuando
b w
<
2 1
, sin embargo también puede atribuirse esta discrepancia de las curvas al termino ∆C de la
ec. (3.13) que se considero igual con cero al trazar dichas curvas.
La ec. (3.17) para la impedancia característica es trazada en la figura 3.4 [45], para diferentes combinaciones de w y b, así como para diferentes impedancias características, ubicando en la parte superior derecha de la misma un recuadro a detalle para una impedancia de 50 ohms.
Figura 3.3. Capacitancia por unidad de longitud de una celda TEM como función de la geometría de la celda.
3.3. ETAPAS DE DISEÑO
Figura 3.4. Impedancia característica de una línea rectangular coaxial con espesor despreciable del conductor interno.
3.3.1. CARACTERÍSTICAS DE LA CELDA TEM
En detalle, la celda debe cumplir con las siguientes características:
• Una impedancia de 50Ω.
• Una frecuencia de operación: Corriente Continua a 500MHz, ec. (2.1).
• Máximo acoplamiento o Relación de onda estacionaria menor a 1.2, norma dada en [51, 52, 53].
• Una uniformidad de campo según los estándares internacionales (IEC 1000-4-3).
• Conductor central simétrico a la celda TEM.
• Robustez mecánica.
Tamaño EBP
≤
(
)
3 3
2 3
l g a b
× −
× …(3.19)
En la figura 3.5 se muestra la nomenclatura general de las dimensiones de la celda. Observe que la longitud de la celda en el plano superior es 4a, así como la longitud del área rectangular es 2a. El valor de 4a determina la frecuencia de corte de la celda, de acuerdo a la ec. (2.1). Las dimensiones de 2a y 2b en el plano frontal son las que determinan la forma rectangular de la celda, como se indica al inicio del capítulo. El conductor interno no se muestra en la figura 3.5.
3.3.2. CONDICIONES DE DISEÑO Y LAS ECUACIONES CARACTERÍSTICAS
Considérese primeramente las expresiones dadas en (3.18). Se deben cumplir los siguientes factores de forma:
(
a g)
b ba
2 1
≥ −
≥ y ó
2 1
1 ≥
≥ b w b
a
y
Figura 3.5. Vistas de la celda TEM.
Se deben cumplir las condiciones de (3.18) para poder utilizar (3.13) y (3.17), recuérdese también
que el factor
0
ε C
∆
, que es factor de corrección de la capacitancia de bordes entre el conductor
interno y las paredes verticales de la celda, es igual a cero al cumplirse estas condiciones. Así también la impedancia característica de la celda puede ser representada gráficamente (figura 3.6) para diferentes combinaciones de a, b y g, empleando la ec. (3.16). De esta manera una selección
del factor de forma
b a
nos permite seleccionar el espacio correcto entre el conductor central y las
[image:51.612.201.441.400.663.2]paredes verticales.
3.3.3. CÁLCULOS
Del plano frontal de la figura 3.5 obtenemos la figura 3.7. Esta figura servirá para establecer la nomenclatura necesaria en los siguientes cálculos. Se debe de considerar las características dadas en la sección 3.3.1. Además las dimensiones que inicialmente se establecerán son las de a y b. Los criterios para establecer estas dimensiones son: cumplir con las condiciones dadas en la expresión (3.18), proporcionar un espacio de prueba suficiente para las dimensiones máximas del EBP, y establecer un factor de forma tal que la geometría de la celda sea rectangular [3]. Los valores de las dimensiones iniciales se determinan por las condiciones del ancho de banda, hasta una frecuencia de corte de 500MHz, dada por la ec. (2.1) de la cual se despeja el valor de a y se determina b para tener un factor de forma de 1.5 para una geometría rectangular, por lo tanto:
a = 15 cm b = 10 cm
Figura 3.7. Nomenclatura de la celda TEM.
Para el factor de forma:
5 . 1
= b
a ⇒
66 . 0
= a b
Si ubicamos la relación
a b
Por lo tanto: w = 11.4 cm
Se puede observar también de la ec. (3.15) que la condición
b w
también se cumple, es decir
14 . 1 = b w
Si se proyecta este valor en la gráfica de la figura 3.4, el valor en impedancia es aproximadamente 51Ω.
Las dimensiones que dieron los cálculos, son mostradas en la figura 3.8. La ec. (2.1) para el cálculo de la frecuencia de corte involucra la variable 4a, es decir la longitud total de la celda es aproximadamente4a = 60cm. El valor longitudinal del área rectangular se propone de tal manera que l = 2a = 30cm. La finalidad de esta medida es obtener una longitud efectiva de la celda de
2
g λ
. Las secciones piramidales serán de longitud
4
g λ
.
De la ec. (3.13):
7.317 coth
Ln ⎥=
⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + = b g b w C 2 1 2 4 0 0 π π ε
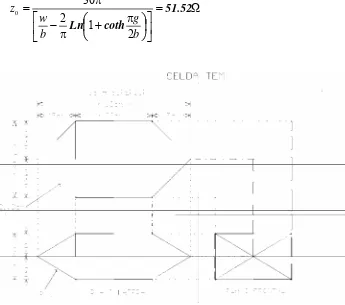
Ω 2 1 2 30 0 51.52 coth Ln = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = b g b w z π π π
Figura 3.8. Dimensiones de la celda TEM.
De la ec. (2.1):
( )
µε
µε b a
n a m f n m c 4 1 2 2 2 1 0 1 2 2
10 = + =
==
( )
= =500MHza c fc
4 10
Es importante hacer notar las siguientes observaciones, que se desprenden de los resultados obtenidos. De la gráfica 3.3, la capacitancia por unidad de longitud para un factor de forma
5 . 1 = b a
y =1.3
w a
es de =7.317
o o
C
ε , cuyo valor es ubicado en la misma gráfica. Algunos autores
CAPÍTULO 4
CONSTRUCCIÓN Y CARACTERIZACIÓN
En el capítulo 4 se desarrolla el diseño de la celda TEM en función de parámetros geométricos.
Se describe el criterio empleado en la construcción de las secciones piramidales para no alterar la
impedancia característica de la celda TEM, así como el método de construcción, planos y
caracterización de parámetros.
4.1. GEOMETRÍA DE LA CELDA TEM
La geometría de la celda, como se observa de la figura 1.1, debe tener dos secciones piramidales
internas perfectamente definidas por las dimensiones dadas en la sección 3.3.3 del capítulo
anterior. El factor de forma
b a
debe permanecer constante a lo largo de la sección rectangular, y
de las secciones piramidales de la celda. Así como el factor de forma
b w
entre el conductor
interno con respecto a la sección rectangular, y a las secciones piramidales de la celda TEM. Las
formas internas de la celda TEM no deben tener protuberancias, o alteraciones físicas que afecten
su funcionamiento, es decir, dobleces del material de manera interna, malas uniones del material,
cabezas de tornillo internos, etc.
Considerando la figura 3.7, y las ecs. (3.16) y (3.17) se puede apreciar la dependencia que existe
entre las ecuaciones de diseño con la geometría de la celda, donde intervienen las dimensiones a,
b, y w. En la figura 4.1 se presentan cortes lateral y frontal de la sección piramidal. De aquí se
obtienen valores de a y b del factor de forma
b a
, cuyo valor es el mismo para diferentes alturas de
la sección piramidal, con lo que se observa una impedancia característica de la celda TEM igual
en cualquier punto de dicha sección. Los parámetros geométricos de las pirámides se muestran en
Figura 4.1. Factor de forma b a
de la parte piramidal de la celda TEM.
Tabla 4.1. Factor de forma b a
a diferentes alturas de la sección piramidal de la celda de la figura 4.1.
Altura (mm) a(mm) b(mm) Factor de Forma
b a
150 150 100 1.5
112.5 112.5 75 1.5
75 75 50 1.5
37.5 37.5 25 1.5
La capacitancia por unidad de longitud en la celda TEM debe mantenerse constante. Esto se logra
de la ec. (3.13) manteniendo constante el factor de forma
b w
(figura 4.1). Así realizando un
procedimiento análogo al anterior se calculan los valores de w y b en la pirámide y se muestran
Figura 4.2. Factor de forma
b w
de la sección piramidal de la celda TEM.
Tabla 4.2. Factor de forma
b w
a diferentes alturas de la sección piramidal de la celda de la figura 4.2.
Altura (mm) w(mm) b(mm) Factor de Forma
b w
162 114 100 1.14
112.5 79.15 75 1.05
75 52.75 50 1.05
37.5 26.35 25 1.05
Es importante que las dimensiones de las pirámides no sufran alteración alguna en su geometría.
En la figura 4.3 se puede observar la disposición del conductor central, el cual es sujeto
simétricamente por medio de barras dieléctricas. Conectores coaxiales son colocados a los
Figura 4.3. Vistas lateral y superior de una celda TEM.
En el proceso de construcción de la celda TEM, al tratar de ajustar la forma de la pirámide (figura
4.4) para la instalación del conector coaxial, la impedancia característica de la celda TEM a
diferentes alturas de la pirámide discrepan del valor calculado. Valores de este factor de forma e
impedancia característica son mostrados en la tabla 4.3. Esto debido a que el factor de forma
b a
es diferente para alturas diferentes en la parte piramidal de la figura 4.4.
Por esta razón, el criterio para instalar los conectores coaxiales, es seguir la forma de la pirámide
![Figura 3.6. Impedancia característica de una línea rectangular, a) en escala lineal, b) en escala logarítmica [46]](https://thumb-us.123doks.com/thumbv2/123dok_es/4990709.76633/51.612.201.441.400.663/figura-impedancia-caracteristica-linea-rectangular-escala-lineal-logaritmica.webp)