Monterrey, Nuevo León a del 200
INSTITUTO TECNOLÓGICO Y DE ESTUDIOS SUPERIORES DE MONTERREY
PRESENTE.-Por medio de la presente hago constar que soy autor y titular de la obra denominada
en los sucesivo LA OBRA, en virtud de lo cual autorizo a el Instituto Tecnológico y de Estudios Superiores de Monterrey (EL INSTITUTO) para que efectúe la divulgación, publicación, comunicación pública, distribución, distribución pública, distribución electrónica y reproducción, así como la digitalización de la misma, con fines académicos o propios al objeto de EL INSTITUTO.
El Instituto se compromete a respetar en todo momento mi autoría y a otorgarme el crédito correspondiente en todas las actividades mencionadas anteriormente de la obra.
De la misma manera, manifiesto que el contenido académico, literario, la edición y en general cualquier parte de LA OBRA son de mi entera responsabilidad, por lo que deslindo a EL INSTITUTO por cualquier violación a los derechos de autor y/o propiedad intelectual y/o cualquier responsabilidad relacionada con la OBRA que cometa el suscrito frente a terceros.
Consideraciones en el Estudio de los Conceptos Matemáticos de
Relación, Función y Educación a Nivel Bachillerato -Edición
Única
Title
Consideraciones en el Estudio de los Conceptos
Matemáticos de Relación, Función y Educación a Nivel
Bachillerato -Edición Única
Authors
Ramón Félix Llanes Fernández
Affiliation
Tecnológico de Monterrey, Universidad Virtual
Issue Date
2009-04-01
Item type
Tesis
Rights
Open Access
Downloaded
19-Jan-2017 00:26:21
Universidad Virtual
Escuela de Graduados en Educación
Consideraciones en el estudio de los conceptos matemáticos
de relación, función y ecuación a nivel bachillerato
Tesis que para obtener el grado de: Maestría en Educación
presenta:
Ramón Félix Llanes Fernández
Asesor tutor:
Mtra. Adriana del Carmen Cantú Quintanilla
Asesor titular:
Dra. Ángeles Domínguez Cuenca
CONSIDERACIONES EN EL ESTUDIO DE LOS CONCEPTOS
MATEMÁTICOS DE RELACIÓN, FUNCIÓN Y ECUACIÓN
A NIVEL BACHILLERATO
Tesis presentada
por
Ramón Félix Llanes Fernández
ante la Universidad Virtual
del Instituto Tecnológico y de Estudios Superiores de Monterrey
como requisito parcial para optar
por el título de
MAESTRO EN EDUCACIÓN
iii
Dedicatorias y Agradecimientos
Para ser justo y coherente, siempre hay que reconocer todas las ayudas recibidas para la elaboración de un trabajo y las primeras personas a agradecer, son:
• La doctora Ángeles Domínguez y la maestra Adriana Cantú. Gracias por la guía
permanente de ambas en este trabajo.
• Mi director de preparatoria, Arturo Delgadillo y mi jefe de departamento, Juan de
Santiago por haberme dado la posibilidad de estudiar esta maestría que ha
contribuido con mi formación profesional y en la realización del presente trabajo.
• Mis compañeros de trabajo y alumnos participantes, que con sus opiniones, apoyo y
aportaciones me ayudaron a salir adelante en esta tarea, muchas gracias a todos.
• Mis familiares y amigos por ayudarme en tantas cosas y sobre todo por las palabras
que me alentaban a continuar y no decaer en mi empeño. Sin el apoyo de ellos el
iv
“
Consideraciones en el Estudio de los Conceptos Matemáticos
de Relación, Función y Ecuación a Nivel Bachillerato
”
Resumen
v
Índice
Introducción .. ………...1
Capitulo 1. Naturaleza y dimensión del tema de investigación 1.1 Introducción… .. ……….…...5
1.2 Marco contextual ... ……….…... .6
1.3 Antecedentes del problema ... 11
1.4 Planteamiento del problema.. ……….….…..17
1.5 Objetivos de la investigación .. ………...19
1.6 Hipótesis de la investigación .. ………...20
1.7 Justificación de la investigación .. ………..…...21
1.8 Limitaciones y delimitaciones .. ………...….22
1.9 Definición de términos .. ……….…...24
Capitulo 2. Revisión de la literatura 2.1 Introducción .. ………...27
2.2 Antecedentes ... ………....……….…...28
2.3 Marco Teórico .. ………...…...44
Capitulo 3. Metodología 3.1 Introducción .. ………...…....….61
3.2 Método de investigación .. …...………..….…...62
3.3 Población y muestra ..……….………...65
3.4 Tema, categorías e indicadores de estudio .. ………...66
3.5 Fuentes de información . ...…..………...69
3.6 Técnica de recolección de datos ... ………...69
3.7 Prueba piloto .. ………...73
3.8 Aplicación de instrumentos .. ……….………...74
3.9 Captura y análisis de datos ... ………76
Capítulo 4. Análisis de resultados 4.1 Introducción ... ……….………...79
4.2Resultados obtenidos ... ………...79
4.3 Análisis de los resultados .. ……….………...88
4.3.1 Cuestionario a profesores y alumnos .. ………...88
4.3.2 Actividad 1: Concepto de función, formas de representación ... ……100
4.3.3 Actividad 2: Solución de problemas típicos y atípicos ... ………...103
4.3.4Observaciones de las visitas a clases ... ………...105
Capítulo 5. Conclusiones y recomendaciones 5.1 Introducción .... ………....111
5.2 Conclusiones ... ………111
5.3 Recomendaciones .... ………...118
5.4 Trabajos futuros ... ...126
vi
Apéndices
Apéndice A: Cuestionario a profesores ...………..136 Apéndice B: Cuestionario a alumnos ... ……….139 Apéndice C: Actividad 1: Concepto de función.... ………142 Apéndice D: Actividad 2: Solución de problemas típicos y atípicos ... ……….145 Apéndice E: Tabla 8: Manual de codificación de cuestionario a profesores ... .147 Apéndice F: Tabla 9: Manual de codificación de cuestionario a alumnos ... ....150 Apéndice G: Tabla 10:Observaciones a clase del profesor A ... ………154 Apéndice H: Tabla 11: Observaciones a clase del profesor B ... ………..156 Apéndice I: Tabla 12: Observaciones y resultados de la actividad 1 ... ……...158 Apéndice J: Tabla 13: Respuestas de profesores a preguntas abiertas del
cuestionario .... ……….………..160 Apéndice K: Tabla 14: Observaciones y resultados de la actividad 2 .... ……..163 Apéndice L: Tabla 15: Matriz de datos de cuestionario a profesores .... ….…..164 Apéndice M: Tabla 16: Matriz de datos de cuestionario a alumnos ... ………..165
vii
Índice de tablas
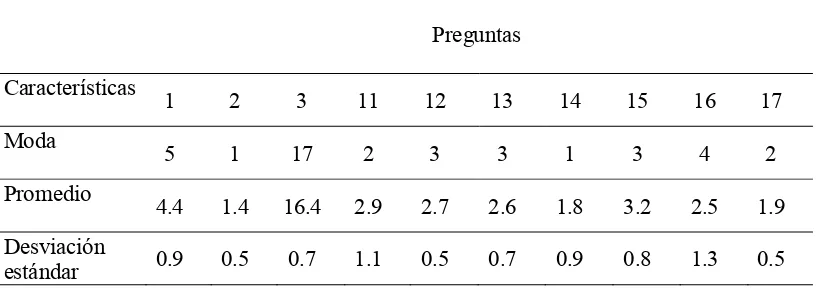
Tabla 1: Resultados de preguntas de cuestionario a profesores ... ….……….….80 Tabla 2: Resultados de las medidas de tendencia central y de dispersión
de preguntas a cuestionario a alumnos ...………..……….……81 Tabla 3: Resumen de observaciones y resultados de la actividad 1 .. ………...83 Tabla 4: Resumen de observaciones y resultados de la actividad 2 .. ……….84 Tabla 5a: Resumen de los resultados de observaciones a clases de profesores ...……....86 Tabla 5b: Ejemplos de actividades desarrolladas en clases por los profesores ... …….…87 Tabla 6: Frecuencias de las respuestas a preguntas del cuestionario
a profesores .... ………..89 Tabla 7: Frecuencias de las respuestas a preguntas del cuestionario
viii
Índice de figuras
Figura 1: Pregunta 7 del cuestionario a profesores …………..………91
Figura 2: Pregunta 8 del cuestionario a profesores …………..………92
Figura 3: Pregunta 9 del cuestionario a profesores …………..………92
Figura 4: Pregunta 5 del cuestionario a alumnos ……….………92
Figura 5: Pregunta 6 del cuestionario a alumnos ………..………...93
Figura 6: Resultados de las preguntas del cuestionario a alumnos que responden a situaciones típicas y atípicas …………..…………..…………..95
Figura 7: Pregunta 10 del cuestionario a alumnos ………..……….…...96
Figura 8: Pregunta 14 del cuestionario a profesores …………..………..96
Figura 9: Pregunta 13 del cuestionario a profesores ….…………..………….………97
Figura 10: Pregunta 15 del cuestionario a profesores ..………..……….…...97
Figura 11: Pregunta 16 del cuestionario a profesores …………..………97
Figura 12: Pregunta 17 del cuestionario a profesores ………...98
Figura 13: Pregunta 17 del cuestionario a alumnos ………..………...98
Figura 14: Pregunta 16 del cuestionario a alumnos …………..…..………...99
Figura 15: Argumentaciones de los alumnos con relación al concepto de función ……….………103
1
Introducción
México ha obtenido importantes avances en la masificación de la enseñanza, el nuevo reto educativo es mejorar la calidad de la formación de los educandos a todos los niveles, dicha mejora debe considerar los elementos de adecuación constante en respuesta a un mundo globalizado, complejo y cambiante que requiere de profesionales competitivos y altamente calificados para encontrar las soluciones a los problemas presentes y futuros.
En lo particular, la educación media superior es básica en la formación de los jóvenes, puesto que es en esta etapa donde se ubica su preparación para continuar estudios superiores. Dicha preparación debe ser integral y contemplar desde la comprensión de conocimientos hasta el desarrollo de destrezas y habilidades para enfrentarse a los retos de la vida profesional de una manera positiva y responsable.
Parte indispensable de estos requerimientos en el ámbito educativo y referente a los programas de nivel bachillerato, está en la enseñanza de las matemáticas, que demandan que sus contenidos se aborden de forma tal, que le resulten más significativos, interesantes y de utilidad a los educandos; para tal propósito, se contempla la posibilidad de cambios en las estrategias y actividades de enseñanza que estén más acorde a las necesidades y
exigencias actuales.
En el estudio de las matemáticas de nivel bachillerato, los alumnos –
2
memorístico y mecanicista. En el tema de las ecuaciones lineales, la enseñanza enfatiza la resolución de ecuaciones lineales con la aplicación de procedimientos basados en las propiedades de la igualdad, pero descuida el aspecto conceptual. Esto propicia que los estudiantes tengan un conocimiento limitado de las ecuaciones y funciones al ser considerado el objeto matemático de estudio desde un sólo punto de vista: el de los procedimientos.
Por otra parte, algunos docentes conciben a las matemáticas como un lenguaje; mismo que por su naturaleza abstracta, dificulta la comprensión y hace que los estudiantes sientan un cierto rechazo hacia las mismas por considerarlas muy difíciles o aburridas, divorciadas de la realidad y sin un significado. Algunas de las causas pueden estar
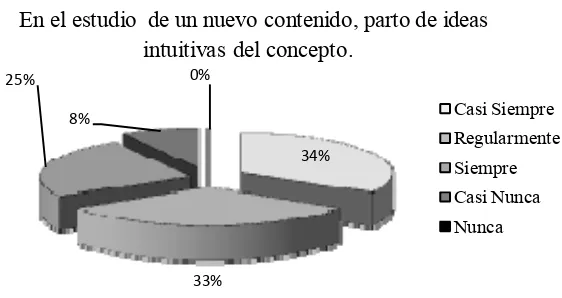
relacionadas con la poca vinculación que se establece entre los conocimientos matemáticos y su utilidad práctica, el no partir de las ideas intuitivas del mismo para descubrir sus propiedades, no relacionar los nuevos contenidos con las ideas previas que tienen los alumnos o lo erróneo de algunas de las estrategias de enseñanza aprendizaje de los profesores relacionadas con sus creencias personales.
Resulta claro que es necesario un equilibrio en el estudio de los contenidos
matemáticos que atienda a los principios formales y de practicidad. El lenguaje matemático permite expresar de manera precisa un concepto y la comprensión de sus propiedades facilita su aplicación en la solución de problemas.
3
investigación al observar la congruencia entre los requerimientos de los contenidos y los métodos de enseñanza así como las soluciones dadas a los problemas.
En el primer capítulo se aborda el problema que se investiga, relacionado con la efectividad de las actividades de enseñanza de las matemáticas que se utilizan en la preparatoria donde se realiza la investigación. Se describe el contexto socio-económico, determinado por la institución privada, situada en el centro de la República Mexicana. Las características de la población, estudiantes que, por lo general, provienen de un nivel socio-económico medio o alto, y maestros, profesionistas de otras ramas que ejercen como profesores y que sus creencias sobre la enseñanza de las matemáticas basadas en la experiencia laboral y en el intercambio con otros profesores, son el fundamento de sus prácticas educativas.
En el segundo capítulo, se hace referencia a los avances teóricos desarrollados y a los estudios realizados a la fecha, que fueron encontrados en la revisión bibliográfica que se hizo en torno a la pregunta de investigación: ¿Las actividades de aprendizaje empleadas por los profesores de matemáticas de nivel preparatoria (de la institución educativa en la que se realiza la investigación) en la enseñanza de los contenidos de relación, función y ecuación, permiten a los estudiantes encontrar los nexos entre las variables que se
presentan en problemas que se modelan por una ecuación o sistema de ecuaciones lineales? Se presenta también, información sobre otras ideas, teorías y conceptos relacionados con la enseñanza de las matemáticas, y consideraciones personales del autor del presente trabajo que llevan a la definición del problema de investigación.
4
observaciones no participativas basadas en simulación. La población y fuentes de
indagación, profesores del departamento de ciencias y alumnos que han recibido o reciben la materia. Las categorías e indicadores están relacionadas con la creencias de los
profesores e ideas previas de los alumnos sobre los contenidos a estudiar, y las estrategias de enseñanza de nuevos contenidos y de solución de problemas. Se indican las fuentes e instrumentos de recopilación de información, los resultados de la prueba piloto, el diseño de los instrumentos y el método de captura y análisis de datos.
El Capítulo 4 está destinado a la presentación y análisis de los resultados de la investigación. Los datos obtenidos mediante las técnicas e instrumentos de investigación (cuestionarios y observaciones no participativas mediante la simulación), se ordenaron, organizaron, interpretaron, evaluaron y analizaron tomando como referencia las categorías definidas en la metodología y en la revisión de la literatura, con los cuales se dio respuesta a la pregunta de la investigación.
5
Capítulo 1
Naturaleza y Dimensión del Tema de Investigación
1.1
Introducción
En este capítulo se abordan los datos generales de la investigación, el problema que se quiere investigar, relacionado con las estrategias de enseñanza de las
matemáticas que se utilizan en la preparatoria donde se realiza la investigación, que no siempre aseguran un aprendizaje adecuado de los conceptos y no preparan a los alumnos para resolver problemas. Se describe sobre el contexto socio-económico, determinado por la institución privada, reconocida por su alto nivel académico y los excelentes resultados obtenidos por varias generaciones de estudiantes, que han trascendido las fronteras del estado situado en el centro de la República Mexicana, las características de la población, estudiantes que por lo general provienen de un nivel socio-económico medio o alto, y maestros, profesionistas de otras ramas que ejercen como profesores y que sus creencias sobre la enseñanza de las matemáticas, basadas en la experiencia laboral y en el intercambio con otros profesores, son el fundamento de sus prácticas educativas.
En la institución no hay estudios relacionados con el tema, pero en la revisión de la literatura se encontró que hay un consenso generalizado de varios autores en cuanto a la importancia de las representaciones semióticas y del tránsito de un registro a otro de un concepto para apropiarse de las propiedades del mismo y en el uso de la
transferencia analógica, es decir se explicita la resolución de un conjunto de problemas en contextos determinados o temas y a continuación se pide a los estudiantes que apliquen lo aprendido en la solución de nuevos problemas.
6
la institución donde se realiza la investigación, no obstante se considera importante el estudio, porque las recomendaciones y principales resultados no sólo serán de utilidad a la entidad donde se realiza la investigación sino a aquellas donde las actividades de aprendizaje utilizadas por los profesores con relación a los contenidos de ecuaciones y funciones lineales, no permitan a los alumnos enfrentar con éxito la solución de problemas.
1.2
Marco contextual
Históricamente la enseñanza y aprendizaje de las matemáticas es una tarea que resulta difícil para alumnos y profesores, por un lado su lenguaje se les hace difícil de comprender a los alumnos, que tampoco logran comunicarse a través de él y por el otro, los profesores no siempre encuentran la forma de expresar las propiedades de los conocimientos matemáticos, que resulte más comprensible a los alumnos. Esta
problemática, también se percibe en la preparatoria donde se desarrolla la investigación y como consecuencia los alumnos manifiestan dificultades primero, en reconocer el conocimiento matemático que está presente en un problema y segundo en encontrar la solución del problema en sí.
7
La preparatoria, que forma parte de esta institución educativa, ofrece un plan de estudios que proporciona una formación integral para desempeñarse en cualquier área de especialidad profesional, además de fomentar valores, habilidades de pensamiento creativo, espíritu emprendedor y liderazgo en cualquiera de sus programas (bicultural o bilingüe). La preparatoria dura seis semestres y las matemáticas están presentes en cada uno de ellos, la frecuencia de las clases es cinco horas semanales y en los contenidos predominan cinco grandes temas: Aritmética, Álgebra (en más de un semestre, relacionándola con el concepto de función), Elementos de Geometría Analítica, Trigonometría y Cálculo Diferencial e Integral.
En el programa bicultural, por lo menos el 60% de las materias son impartidas
en inglés y de acuerdo al resultado del examen de ubicación de inglés el estudiante tendría la posibilidad de estudiar otro idioma diferente. Al término de la preparatoria el alumno deberá presentar el examen de acreditación TOEFL institucional debiendo obtener un mínimo de 600 puntos.
En el programa bilingüe se capacita al estudiante en el manejo del idioma Inglés ofreciendo 14 materias en este idioma y de acuerdo al resultado del examen de
ubicación de inglés también tendría la posibilidad de estudiar otro idioma diferente. Al término de la preparatoria el alumno presenta el examen de acreditación TOEFL institucional debiendo obtener un mínimo de 550 puntos.
8
15 y 18 años de edad). No se incluyen en el estudio a los alumnos de 1er semestre por no haber sido instruidos en los contenidos objetos de estudio del presente trabajo.
La misión y visión de esta institución están definidas de manera centralizada, y es uno de los más de treinta campus que la conforman alrededor de la República
Mexicana. En el 2005 se definieron la Visión, la Misión, las Estrategias y los Principios que los habrán de regir hasta el 2015.
En cuanto a la visión se señala que el año 2015, la institución educativa será la más reconocida de América Latina por el liderazgo de sus egresados en los sectores privado, público y social; y por la investigación y desarrollo tecnológico que realiza para impulsar la economía basada en el conocimiento, generar modelos de gestión e
incubación de empresas, colaborar en el mejoramiento de la administración pública y las políticas públicas, y crear modelos y sistemas innovadores para el desarrollo sostenible de la comunidad.
Es misión de la institución formar personas íntegras, éticas, con visiones humanísticas y competitivas internacionalmente en su campo profesional, que al mismo tiempo sean ciudadanos comprometidos con el desarrollo económico, político, social y cultural de su comunidad y con el uso sostenible de los recursos naturales. Hasta el momento cuenta con 900 alumnos a nivel bachillerato y 400 en niveles superiores.
9
creado programas de apoyo para la mejora continua de sus profesores y más del 90% está certificado en el programa ASESORE (Programa de Asesoría y Orientación Educativa) y en el de programas de PDHD (Programa de Desarrollo de Habilidades Docente). Sólo dos profesores del departamento cuentan con capacitación en la técnica didáctica de solución de problemas.
La tendencia de los profesores es considerar las matemáticas como instrumento a ser utilizado por otras materias en la solución de problemas, se descuida el aspecto conceptual y se hace énfasis en los conocimientos procedimentales. Muchos profesores aún ven su tarea como la transmisión de un conocimiento acabado y abstracto, tienden a adoptar un estilo expositivo. Su enseñanza está plagada de definiciones, en abstracto y
de procedimientos algorítmicos; pocas veces aparece un problema contextualizado como aplicación de lo que supuestamente se ha aprendido en clase. Por lo general los problemas no guardan una relación real con la práctica y se tiende a que los alumnos utilicen las ideas aplicadas en un ejercicio en la solución de otros por transferencia, creando la falsa expectativa en los estudiantes de esquemas para la solución de problemas.
Aunque la institución plantea en su currículo que el modelo educativo se basa en fundamentos constructivistas, en el currículo real hay todavía elementos del teoricismo y el tecnicismo, aunque la mayor tendencia es hacia el procedimentalismo, modelo docente que relaciona dos momentos de la actividad matemática: el exploratorio y el del trabajo de la técnica (Chevallard, Bosch y Gascón, 1997).
10
Provienen de diversas instituciones educativas de nivel secundario (privado y público), ubicadas en diversas regiones del estado, aunque en su mayoría son de la capital. Se considera que hay diferencias a veces significativas en los planes de estudio de las escuelas de donde proceden y en los conocimientos que traen los alumnos.
Para ingresar a esta institución se les aplica un examen de ingreso donde deben alcanzar un mínimo de 980 puntos de 1600 posibles y deben tener promedio superior a los 80 puntos. A los alumnos que obtengan bajos resultados en el examen de
matemáticas, se les ofrece un curso de nivelación con una duración aproximada de tres semanas con frecuencia de cinco veces a la semana en el área de aritmética.
Se considera importante incluir la opinión de los alumnos sobre las actividades
que los maestros desarrollan en las clases respecto del tratamiento de los conocimientos matemáticos y formarán parte del experimento de propuesta de la metódica para la enseñanza aprendizaje de conceptos relacionados con los temas ecuaciones, funciones y sistemas de ecuaciones lineales; y es por ello que son incluidos dentro de los sujetos a investigar.
En las diferentes generaciones que han pasado por esta preparatoria, siempre se han presentado dificultades en cuanto a la comprensión por parte de los alumnos de los aspectos conceptuales de los conocimientos matemáticos (no identifican si una relación es o no función, no hay comprensión de los conceptos de ecuación, sistemas de
11
1.3. Antecedentes del problema
No hay evidencia de que en este centro educativo se hayan realizado
investigaciones en Matemática Educativa y los antecedentes que se puedan tener sobre el problema a tratar, se fundamentan en la experiencia de los profesores que imparten la materia.
Al juntarse las academias siempre se escuchan los mismos comentarios sobre el problema que tienen los estudiantes cuando se les plantean problemas, aunque sencillos, en donde se les presentan situaciones relacionados con la realidad (con frecuencia son ejercicios con texto extraídos de los libros de texto, que pueden no tener un significado real para los alumnos) y las cosas que los rodean y que involucran los conceptos de función, dominio, rango, ecuación y/o sistemas de ecuaciones lineales. El problema por lo general se manifiesta en dos sentidos: son capaces de enunciar las propiedades de un conocimiento matemático, pero no las reconocen en el contexto de un ejercicio o problema o demuestran no tener un significado para ellos. Los estudiantes pueden enunciar todas las leyes que se les presenten en clases, pero cuando deben usarlas, no llegan a poder expresarse.
Los profesores identifican como las causas al poco interés de los alumnos, que no estudian, que no realizan sus tareas, etc., pero pocas veces se cuestionan sobre sus propias estrategias de enseñanza. El diseño de actividades de aprendizaje tiene su fundamento en la experiencia personal e intercambio con otros docentes y se centra en la exposición de problemas típicos del texto que favorece los procedimientos, pero descuida los conceptos.
12
tener claridad de los conocimientos previos que traen los alumnos, se enuncian las propiedades del concepto empleando la simbología matemática y se pasa a su aplicación en la solución de ejercicios. Un ejemplo podríamos encontrarlo en una clase
(presentación con empleo de la tecnología utilizada por los profesores) diseñada para impartir el tema de las relaciones y funciones:
• Se define el concepto de relación como un conjunto de pares ordenados (x,
y), del plano cartesiano. Definición del concepto
• Se determina que una función es una relación que cumple determinadas
propiedades (se enuncian en el lenguaje matemático)
• Se procede a analizar si determinadas relaciones definidas en lenguaje
matemático son o no funciones y a determinar su dominio y rango. Con relación a la literatura revisada y que guarda afinidad con este problema, resulta importante lo señalado por Parra (2005) en el sentido de que las creencias personales de los profesores deben tenerse en cuenta en el contexto educativo, ya que forman parte de una red de creencias bien constituidas en torno a la institución escolar y cualquier intento por modificarlas conlleva a plantearse acciones que consideren el conjunto de actores que en ella intervienen.
Bagni (2004), Socas, Camacho y Hernández (1998) concuerdan en la importancia de las representaciones semióticas (diferentes registros) de un concepto matemático, para apropiarse de las propiedades del mismo, pero sin llegar a
identificarlos con alguna de ellas. Las propiedades abstractas de un conocimiento matemático como el de funciones y/o ecuaciones son independientes de sus
13
El trabajo de Panizza, Sadovsky y Sessa (1999) ilustra con ejemplos, la
apropiación que de manera parcial hacen los alumnos de un conocimiento matemático, cuando no se trabaja con diferentes representaciones semióticas del mismo ni se establece el tránsito entre ellas.
La definición de problema en el contexto pedagógico dada por Pérez (2006) en lo fundamental se ajusta a lo que se requiere en el presente estudio y resalta tres rasgos esenciales:
• El sujeto desconoce la vía de solución.
• Es una tarea docente con un nivel de complejidad, que exige de un esfuerzo
cognoscitivo, y a veces también práctico para su solución.
• Tiene un carácter relativo, porque para algunos puede ser un problema
mientras que para otros, con mayor experiencia, habilidades, conocimientos o cultura en general, puede ser considerado un ejercicio.
A estas características hay que agregar que debe existir diversidad en las vías de solución, no debe suscribirse al marco estrecho de una clase y que para estudiantes de este nivel educativo, la colaboración en pequeños grupos con aportaciones individuales de sus integrantes podría ser una forma adecuada de afrontar su solución. Aliprantis y Carmona (2003) con relación a esto, señalan que los estudiantes demuestran sus conocimientos matemáticos, cuando se los pueden comunicar a los demás y que este proceso no sólo les permite conversar con otras personas, sino que también promueve en el estudiante el desarrollo y perfeccionamiento de estas y otras ideas.
14
científicos y ampliación de los conocimientos, resulta prácticamente imposible alcanzar resultados positivos en la solución de problemas sin la formación de equipos
multidisciplinarios y puede ser un marco adecuado la preparatoria para cultivar esta forma de trabajo.
Las ideas previas que tienen los alumnos respecto a un conocimiento matemático, deben ser tomadas en cuenta por los profesores en el diseño de sus
actividades de aprendizaje, (Flores, et al, 2004). El trabajo de exploración que realice el profesor en este sentido puede resultar beneficioso. Es importante destacar algunas prescripciones que indican en su trabajo Scott, Asoko, Driver y Emberton (1994) y que actualmente son comunes entre las estrategias de enseñanza aprendizaje de las ciencias
y que toman en cuenta las ideas previas de los estudiantes:
• Desde una perspectiva constructivista, no existe un solo método o vía
instruccional para enseñar un conocimiento científico particular.
• El aprendizaje de las ciencias, no implica solamente la organización de
conceptos en una nueva estructura, sin darles una nueva justificación y/o fundamentación.
• Los profesores deben reconocer que tanto las actividades experimentales,
como las discusiones, serán interpretadas por los estudiantes de manera diferente de aquélla que se pretende educativamente.
• La enseñanza debe involucrar el tratamiento de argumentos científicos de
15
Independientemente de los conocimientos previos que tengan los alumnos sobre un concepto matemático, cobra gran importancia lo señalado por Duval (1993) en el sentido de que un objeto algebraico difícilmente puede interiorizarse sin reunir diversas representaciones del mismo. En observaciones hechas a actividades de aprendizaje relacionadas con los conceptos algebraicos, los profesores recurren con frecuencia a la traducción entre los sistemas de representación verbal y algebraico, aunque sin darle un significado real (el doble de un número se identifica con 2x), pero poco se recurre a otros sistemas de representación como el geométrico, el aritmético y al tránsito entre ellos.
Estas ideas también se destacan en el trabajo de Segura (2004) al señalar que en
la adquisición del objeto sistema de ecuaciones, algunos libros de texto y profesores insisten en el estudio de los métodos de solución analíticos (sustitución, suma y resta, igualación, determinantes), que implican un procedimiento algorítmico, y no trabajan los pasajes del registro algebraico al verbal, ni del gráfico al algebraico, aunque es considerado el paso entre registros de representación semiótica necesario para acceder a un objeto matemático. Se consideran los ejemplos de pasaje del registro verbal al algebraico que ella maneja, como los clásicos ejercicios con texto que aparecen en los libros de texto o creados por el profesor, que por lo general no tiene un significado real para los estudiantes. Estos ejemplos se consideran de utilidad, pero no suficientes para lo que se aspira lograr en el tema de solución de problemas.
Un antecedente importante a esta investigación y que va más allá de la solución de ejercicios con textos de aritmética, es el estudio relacionado con la didáctica en la solución de problemas de Rizo y Campistrous (s.f.) donde formulan un procedimiento que está relacionado con los tres momentos reconocidos para toda actividad:
16
propuestas de fases en la resolución de problemas propuestas por Polya (1957): comprender el problema, búsqueda de la vía de solución, resolución y control, vista y perspectiva y con el modelo educativo del modernismo, que se caracteriza por conceder una preeminencia absoluta al momento exploratorio (Chevallard, Bosch & Gascón, 1997). En el marco teórico se hace referencia a las principales ideas y recomendaciones que hacen estos autores en la solución de problemas.
A manera de conclusión, se señalan las cuestiones que se consideran importantes respecto a los antecedentes:
• Los estudiantes enuncian las propiedades de un concepto, pero no las pueden reconocer en un problema, por su parte los profesores relacionan las causas con
el hecho de que los alumnos no estudian, olvidan lo aprendido, etc., pero no cuestionan sus propias estrategias de enseñanza.
• El diseño de actividades de aprendizaje tiene su fundamento en la experiencia personal e intercambio con otros docentes, centrada en la exposición de problemas típicos del libro que favorecen los conocimientos procedimentales pero no los conceptuales.
• Los profesores de esta institución educativa, de manera general, basan sus
17
• En las academias los profesores no siempre analizan ni discuten propuestas didácticas para el estudio de los conocimientos matemáticos. Se enfocan por lo general en conocer los resultados académicos de los grupos y en las medidas de apoyo a los estudiantes rezagados a través de asesorías y el cumplimiento de los planes analíticos.
La literatura revisada con relación al tema de investigación refleja algunas propuestas que pueden ayudar al mejoramiento del aprendizaje de conocimientos matemáticos en general y de aspectos a tener en cuenta en la solución de problemas, desde las perspectivas de los autores (creencias y modelos educativos con los que se identifican). Pero no se considera un problema resuelto, ni agotado y las causas y
propuestas de solución varían de un contexto educativo a otro.
1.4 Planteamiento del problema
Unos de los principales problemas que se presentan en la materia de
matemáticas a nivel bachillerato, es la falta de imaginación, entendimiento, poder de resolución de los problemas que se presentan en los libros de texto, relacionados con el aspecto conceptual o de aplicación de los conocimientos matemáticos estudiados. Al leer los problemas, los alumnos normalmente no saben identificar con claridad los datos presentados en el mismo, la ecuación o función que relaciona las variables o si el objeto de análisis cumple con las propiedades relacionadas con los conocimientos matemáticos estudiados (pueden enunciar las propiedades por ejemplo del concepto de función, pero no siempre logran establecer si una relación entre dos magnitudes constituye o no una función).
18
suficientes, y en algunas ocasiones puede ser cierto, pero se puede identificar un problema más importante, los alumnos no están entendiendo los conceptos que se les enseñan en clase y por tanto no pueden emplearlos en la solución de ejercicios y problemas. ¿Y cómo el docente se puede percatar de que un conocimiento matemático no quedo claro?, cuando se pone a los alumnos a analizar algún ejemplo donde deben identificar las propiedades de un concepto o explicar algún fenómeno que simula una situación de la vida real, y no logran alcanzar el éxito esperado.
Se conoce que los profesores que imparten la materia de matemática en la institución en donde se realiza la investigación están capacitados en la estrategia de aprendizaje colaborativo, pero se limitan a utilizarla en clases de resolución de
ejercicios típicos con el empleo de algoritmos (conocimientos procedimentales). Estos profesores como se ha señalado no cuentan con una formación básica como maestros de matemáticas y sus estrategias en el diseño de actividades de aprendizaje se fundamentan en sus paradigmas educativos, forjados en su experiencia como docentes y del fruto del intercambio con otros profesores.
Algunos de los temas a tratar en esta investigación, son los relacionados con los conceptos de ecuación, función y/o sistemas de ecuaciones. El concepto de función es uno de los conceptos matemáticos más importantes por su relación con otros
conocimientos matemáticos (ecuaciones, derivada, límite, integrales, cónicas, funciones trigonométricas, sistemas de ecuaciones lineales y otros) y con problemas relacionados con otras materias como la Física, la Química y la Biología.
19
forma se puede llegar a una mejor construcción del conocimiento. Lo anterior se encuentra muy relacionado con las consideraciones de Filio (2007) cuando señala la importancia de las nociones que los alumnos tienen del concepto, para ampliarlas y aplicar una estrategia de aprendizaje que asegure que no se rompan las cadenas cognitivas de un conocimiento matemático.
Dado lo anterior y con las características que se cuentan, se planteo la siguiente pregunta de investigación: ¿Las actividades de aprendizaje empleadas por los profesores de matemáticas de nivel preparatoria (de la institución educativa en la que se realiza la investigación) en la enseñanza de los contenidos de relación, función y ecuación, permiten a los estudiantes encontrar los nexos entre las variables que se presentan en
problemas que se modelan por una ecuación o sistema de ecuaciones lineales?
1.5 Objetivos de la investigación
Si bien entre las múltiples tareas que desempeña el profesor y dentro de las expectativas educativas e institucionales, se encuentra la de diseñar actividades de aprendizaje con un enfoque constructivista que permitan el desempeño escolar eficiente de sus alumnos en la comprensión de los conocimientos matemáticos y en su utilización en la solución de problemas, no siempre logra el profesor cumplir con dichas demandas. El objetivo de la investigación es hacer recomendaciones a los maestros respecto al diseño de actividades que puedan favorecer la comprensión y aprendizaje de conceptos matemáticos tales como relación, ecuación, función y su aplicación en la solución de problemas.
Derivado del problema de investigación y del objetivo general, se plantean los siguientes objetivos específicos:
• Examinar información de cómo conciben diferentes autores el estudio de las
20
• Formular algunas recomendaciones para el estudio de los temas de ecuación y función lineal.
• Determinar la validez de las estrategias de los maestros de la institución educativa donde se realizó la investigación al observar la congruencia entre los requerimientos de los contenidos y los métodos de enseñanza así como las soluciones dadas a los problemas.
En este estudio se pretende plantear algunas actividades de aprendizaje con un enfoque constructivista para ser desarrolladas en pequeños grupos, con indicaciones de las tareas a cumplir por los alumnos. En ellas se tratará de profundizar tanto en las ideas previas que traen los estudiantes respecto de determinados conceptos matemáticos
(entiéndase ecuación, relación y función), en distintos sistemas de representación de esos conocimientos matemáticos y sugerencias de estrategias a emplear en la solución de problemas modelados por una ecuación y/o sistemas de ecuaciones lineales.
Las propuestas de actividades se aplicarán de manera experimental en un grupo de estudiantes de tercer semestre, y de esta forma determinar los saberes de los estudiantes respecto a los contenidos objetos de estudio en el presente trabajo. Para poder realizar esto, se pedirá ayuda a uno de los profesores que imparten la materia para que aplique las mismas y se harán observaciones a las clases donde se implementen. Es importante considerar además los puntos de vistas de los alumnos por medio de cuestionarios, y los reportes estadísticos de los resultados de las actividades que permitan avalar el trabajo.
1.6
Hipótesis de la investigación
A partir de los análisis que se realizan en las academias sobre las estrategias de enseñanza –aprendizaje de las matemáticas, de las actividades que utilizan los
21
relación, función y ecuación lineal y su empleo en la solución de problemas modelados mediante ecuaciones y/o sistemas de ecuaciones lineales, no resulta aventurado afirmar que las actividades de enseñanza de los profesores de matemáticas de esta institución educativa sobre el aprendizaje de los conceptos de relación, función y ecuación lineal, no siempre favorecen la comprensión de los mismos, creando una visión, que no ayuda en la aplicación e identificación de estos conceptos por parte de los estudiantes, en la solución de problemas.
1.7 Justificación de la investigación
La importancia de esta investigación radica en que los conocimientos
matemáticos permiten encontrar la solución de innumerables problemas relacionados con la vida real, pero si los alumnos no demuestran una comprensión de las propiedades de los conceptos matemáticos implicados en los mismos, difícilmente podrán utilizarlos en su solución. Las matemáticas son consideradas por muchos investigadores como una herramienta a utilizar para resolver problemas de otras ciencias y como base de muchos estudios profesionales.
Por otra parte, es una de las materias más rechazada por los estudiantes y en donde existe un índice de calificaciones bajas o de reprobación considerado
significativo por la institución educativa. Se trata de buscar una mejora en la enseñanza de las matemáticas que permita a los alumnos adquirir conocimientos que les resulten significativos y les permita resolver problemas relacionados con el área de las
matemáticas y de otras ciencias. Desde la trinchera del bachillerato podemos contribuir a motivar a los estudiantes al estudio de las ciencias exactas y a mejorar sus métodos de enseñanza– aprendizaje.
22
de las ciencias exactas como un proceso mecánico y trivial, totalmente controlable por el profesor. (Gascón, 2001). Con esa concepción de la enseñanza se ha identificado enseñar y aprender matemáticas con enseñar y aprender teorías, que ignora las tareas dirigidas a elaborar estrategias de resolución de problemas complejos, modelo con tendencia al teoricismo o con enseñar y aprender técnicas o algoritmos, modelo con tendencia al tecnicismo, (Gascón, 2001). Estas concepciones de la enseñanza han formado parte de las estrategias de los profesores, determinan sus actividades de instrucción y frenan y limitan un aprendizaje adecuado de los conocimientos
matemáticos y de su utilización en la solución de problemas y sería importante lograr avances en revertir este proceso.
Esta investigación también podría contribuir a tener estudiantes que se encuentren más interesados en las ciencias y en particular en las matemáticas, ya que por el efecto de las actividades de aprendizaje que realizaron le encuentran una razón, un sentido y se den cuenta de que sabiendo ciencias pueden llegar a ayudar mucho a su país. Que no sólo se necesitan abogados, contadores, administradores, sino también de otros profesionales con inventiva, con creatividad y los profesores en bachillerato tienen mucho que ver para que este cambio ocurra. En la actualidad el país necesita de
ingenieros capaces de contribuir al desarrollo y fortalecimiento económico, el desarrollo de la tecnología y la globalización hacen necesario formar profesionales altamente competitivos que puedan insertarse de manera eficiente en el mundo laboral.
1.8 Limitaciones y delimitaciones
23
y/o ecuación y su aplicación en la solución de problemas modelados mediante
ecuaciones y/o sistemas de ecuaciones lineales u otros conceptos como los de derivada, integrales, donde también es frecuente hacer énfasis en los conocimientos
procedimentales, y se descuida el aspecto conceptual.
La institución educativa, por los amplios recursos tecnológicos y materiales con que cuenta, no es representativa de las instituciones educativas del resto del estado o país, y esto podría ser una limitante en la generalización de los resultados. Por otro lado, independientemente de que la mayoría de los maestros son profesionistas que no ejercen la carrera estudiada, la institución educativa ha creado y fomentado diversos programas de capacitación, para elevar el nivel de su personal docente, aunque resulta a veces
insuficiente sobre todo en el área de las matemáticas, donde las creencias de los profesores pueden constituir un freno en la implementación de otras ideas no compatibles con su concepción de la enseñanza- aprendizaje de las mismas.
La población estudiantil tiene características muy similares (educación familiar, nivel socio-económico de medio a alto, admitidos con los más altos promedios, en su mayoría proceden de instituciones educativas privadas con características similares en su misión y visión), lo que pudiera favorecer la implementación de las ideas propuestas, cuestión que no ocurre con la población de estudiantes del resto de las escuelas del estado y el país en las que es posible, que sea necesario tomar en cuenta otras variables.
Parte del estudio se realizará en una muestra de estudiantes obtenida de manera no probabilística por cuotas lo que constituye una limitación para la generalización de algunos de los resultados que se lograrán de la información de los alumnos.
24
búsqueda de las soluciones particulares a problemas generales en el contexto educativo donde se desarrolle la enseñanza de las matemáticas.
El trabajo hace énfasis en algunas consideraciones sobre el estudio de los conceptos de ecuación, función y sistemas de ecuaciones lineales, que pueden ayudar a la comprensión de las propiedades de estos contenidos y su correcta utilización en la solución de problemas.
1.9 Definición de términos
El glosario que se presenta a continuación permitirá conocer los conceptos que se utilizarán en forma continua en este trabajo.
Aprendizaje: Es un proceso activo de construcción de nuevas ideas o conceptos basados en el conocimiento previo o actual.
Actividades de aprendizaje: Se entiende por actividades de aprendizaje el conjunto de procedimientos que un aprendiz emplea en forma consciente, controlada e intelectual como instrumentos flexibles para aprender significativamente.
Aprendizaje colaborativo: Técnica didáctica que propicia una situación de aprendizaje en la que los alumnos con diferentes niveles de conocimientos y
habilidades, aprenden y trabajan juntos para llegar a una meta u objetivo común. Las técnicas de aprendizaje colaborativo son muy variadas; van desde una simple discusión en pequeños grupos intercalada con breves exposiciones por parte del profesor, hasta aquéllas más complejas, como la controversia, el debate, la deliberación, la simulación y la argumentación, orientadas todas al desarrollo de la toma de decisiones.
25
Creencias matemáticas: El conjunto de conocimientos, valores e ideologías que posee el docente acerca de las matemáticas y la manera como entiende todo lo referente a su enseñanza y aprendizaje.
Definición en matemáticas: Es una convención que formaliza un concepto de manera unívoca y por lo tanto, es la que fundamenta la estructura matemática.
Ideas previas: Son construcciones que los sujetos elaboran para dar respuesta a su necesidad de interpretar fenómenos naturales, porque sea necesaria para la vida cotidiana o para mostrar cierta capacidad de comprensión que les son solicitadas.
Modelo educativo: Conjunto de prácticas docentes compartidas que permiten organizar y gestionar el proceso de enseñanza- aprendizaje en una institución
determinada.
Modelo docente teoricista: A los que se sustentan en una concepción del saber matemático que pone el acento en los conocimientos acabados y cristalizados en teorías y deja en un segundo plano a la actividad matemática.
Modelo docente tecnicista: Enfatizan los aspectos más rudimentarios del momento del trabajo de la técnica. Tiende a olvidar los auténticos problemas, que son aquellos cuya dificultad principal consiste en escoger las técnicas adecuadas para construir una estrategia de solución.
Modelo docente modernista: Se tiende a identificar la actividad matemática con la exploración de problemas no triviales, es decir, con las tareas que se realizan cuando todavía no se sabe gran cosa de la solución (tantea técnicas diversas, buscar problemas semejantes, formular conjeturas, buscar contraejemplos, etc.).
26
Noción: Es una forma de conocimiento primitivo que se tiene de las cosas, de la que se puede hablar sin tener que precisarla y aun así, no perder una cierta comprensión de éstas.
Objeto matemático: Es todo (lenguaje, situaciones, conceptos, acciones, argumentos, propiedad o atributo) lo que es indicado, señalado, nombrado cuando se construye, se comunica o se aprende matemáticas.
Problema: Toda situación en la que hay un planteamiento inicial y una
exigencia que obliga a transformarlo. La vía para pasar de la situación o planteamiento inicial a la nueva situación exigida tiene que ser desconocida y la persona debe estar motivada en hacer la transformación.
Representaciones semióticas: Representaciones que se hacen de los objetos matemáticos (no son directamente accesibles a la percepción humana), para poder comprender y apropiarse de sus propiedades.
Transferencia analógica: A partir de los métodos y estrategias empleados en la resolución de un conjunto de problemas en contextos determinados o temas, los
alumnos deben ser capaces de aplicar lo aprendido en la solución de nuevos problemas, usualmente no idénticos a los problemas ejemplos.
27
Capítulo 2
Revisión de la literatura
2.1 Introducción
En esta etapa de la investigación se hace referencia a los avances teóricos desarrollados y a los estudios realizados a la fecha, que fueron encontrados en la
revisión bibliográfica que se hizo en torno a la pregunta de investigación: ¿Las actividades de aprendizaje empleadas por los profesores de matemáticas de nivel preparatoria (de la institución educativa en la que se realiza la investigación) en la enseñanza de los contenidos de relación, función y ecuación, permiten a los estudiantes encontrar los nexos entre las variables que se presentan en problemas que se modelan por una ecuación o sistema de ecuaciones lineales?
A través del análisis de diferentes investigaciones y artículos se muestran algunos estudios relacionados con este tema, donde se señala desde el punto de vista y resultados de las investigaciones de los autores, la manera de lograr que los estudiantes aprendan las nociones conceptuales de determinados objetos matemáticos (ecuación, función y/o sistemas de ecuaciones lineales), ideas sobre la utilización de los mismos en la solución de problemas, causas de la ruptura de la relación entre estos conceptos y con la aritmética y sobre la capacitación que requiere el profesor y su disposición a aceptar y estudiar sobre las estrategias didácticas en la enseñanza de las matemáticas que se manejan en la actualidad para el estudio de conceptos y la solución de problemas.
28
otras ideas, teorías y conceptos relacionados con la enseñanza de las matemáticas, y consideraciones personales del autor del presente trabajo que llevan a la definición del problema de investigación.
2.2. Antecedentes
A continuación se presenta una breve síntesis de algunos trabajos de
investigación relacionados con la pregunta de investigación y que fueron realizados por diferentes autores. En estos trabajos, se tratan aspectos relacionados con la transferencia del conocimiento, las creencias de los profesores respecto de la enseñanza de las
matemáticas, las representaciones de un concepto y el tránsito entre ellas y las
dificultades de los alumnos con el lenguaje algebraico, que deben ser tomados en cuenta por los docentes en el diseño de las actividades, aunque no signifique que sean las únicas.
En el trabajo de investigación Vicente Sanjosé, Tomás Valenzuela, María del Carmen Fortes y Joan Josep Solaz-Portales (2007) proponen determinar si es adecuada o no la asunción de varios profesores de matemáticas en el sentido de que las relaciones analógicas entre problemas resueltos y los problemas propuestos es sencilla de
comprender y establecer. Estos autores atribuyen el fracaso a la falta de dominio de los procedimientos matemáticos de resolución.
29
especiales que los distinguieran de manera significativa de la población, fueron objeto del experimento 83 estudiantes.
Los principales resultados dentro de las limitantes de este experimento, son que las dificultades detectadas por los profesores a la hora de aprender a resolver problemas con enunciado, no provienen de conocimiento inadecuado para el uso de las
herramientas matemáticas (el 87.3% de los estudiantes tuvo éxito en la resolución del sistema de ecuaciones), pero sólo el 50% fue capaz de formular correctamente el sistema que representaba la situación del problema. Por tanto, señalan que las dificultades deben proceder de la falta de comprensión de la situación descrita en el enunciado o del proceso de traducción entre un lenguaje natural del enunciado y el
lenguaje matemático.
Concluyen que los sujetos demuestran saber resolver las ecuaciones, pero manifiestan problemas graves de comprensión de los problemas algebraicos con
enunciado. Para facilitar la comprensión de los significados algebraicos, sugieren que en las clases se deberían contemplar más problemas con texto. Así mismo, se debería dedicar más trabajo a establecer analogías estructurales entre diversas situaciones planteadas para generalizar las representaciones y codificaciones de los problemas. Consideran que las matemáticas deben ser algo más que rutina para ser lenguaje y que requiere de un contenido semántico referido al mundo.
30
maestros con relación al significado de transferencia (se identifica con resolver problemas similares a un ejercicio típico) y la forma en que son introducidas las definiciones de los conceptos matemáticos. También se considera importante la
inclusión de un mayor número de ejercicios con diversidad de textos y vías de solución. En el estudio realizado en el año 1999 por Mabel Panizza, Patricia Sadovsky y Carmen Sessa, se busca identificar condiciones de apropiación del álgebra elemental en alumnos de la escuela media. Se inscribe el trabajo en el marco teórico y metodológico de la teoría de situaciones de Brousseau (1986), y de la ingeniería didáctica de Artigue (1988). Consideran los aportes que diferentes investigadores utilizan para caracterizar la ruptura del pasaje de la aritmética al álgebra y describir los elementos esenciales de la
actividad algebraica.
Los autores realizaron el estudio mediante el empleo de un análisis cualitativo. Aplicaron una encuesta exploratoria destinada a indagar sobre las representaciones de los alumnos acerca de las ecuaciones, variables e incógnitas. Realizan observaciones de las clases en un curso de primer año de matemáticas relacionadas con el tema,
entrevistan a profesores y alumnos. La escuela fue seleccionada tomando en cuenta su prestigio en la zona.
Concluyen como resultado de su trabajo, que la ecuación lineal en dos variables no es reconocida por los alumnos como un objeto que define un conjunto de infinitos pares ordenados. Los estudiantes adaptan bien la concepción de la letra como incógnita a la resolución de sistemas de ecuaciones con solución única. La noción de incógnita, en cambio, no resultó eficaz para interpretar el rol de las letras en una ecuación en dos variables.
31
los puntos de la recta y las soluciones de la ecuación correspondiente. Consideran que avanzar en el conocimiento de la relación que existe entre el aprendizaje de la noción de incógnita y el de la noción de variable parece ineludible para desentrañar la compleja y desafiante relación entre la aritmética y el álgebra.
Aquí también se aprecian dificultades en la comprensión de las propiedades de conocimientos matemáticos (ecuación) y de la forma parcializada o limitada en que algunos son estudiados, cuestiones que no permiten a los alumnos establecer nexos entre diferentes formas de representación de un concepto y de su utilización en la solución de problemas. Parece ser que las actividades de enseñanza de los profesores respecto a estos contenidos deben ser modificadas, pero ¿qué se debe tener en cuenta?,
¿las recomendaciones hechas por estos autores son suficientes para revertir la situación? Martín Socas, Erika Matías Camacho y Josefa Hernández publicaron un trabajo relacionado con el lenguaje algebraico en 1998. A partir de un análisis breve de las principales características que los currículos de matemáticas poseen, se concretan los aspectos más significativos que el conocimiento didáctico debe aportar al profesor y se analiza el lenguaje algebraico en la enseñanza secundaria a partir de organizadores como los modos y situaciones de enseñanza, los contenidos en términos de capacidades y los sistemas de representación semióticos, materiales, recursos, dificultades, errores y obstáculos.
Con base en una investigación documentada, se hacen sugerencias sobre la enseñanza del álgebra y recomendaciones a los profesores tomando como base los organizadores descritos anteriormente y las aportaciones teóricas al respecto de otros autores.
Enuncian como aceptable que la apropiación de un objeto matemático
32
recursos tecnológicos amplían la consideración habitual del álgebra como un lenguaje. Caracterizan en dos grupos las causas de los errores en el aprendizaje del álgebra, los que tiene su origen en un obstáculo y los que lo tienen en una ausencia de significado.
Proponen que la enseñanza del álgebra sedé en términos de traducción entre los cuatro sistemas de representación: habitual (entiéndase la expresión en el lenguaje natural de situaciones reales que involucran cantidades o relaciones), aritmético, algebraico y geométrico. En la formación de profesores debe concederse prioridad a las actividades prácticas con participación activa de los alumnos, proporcionándoles una información clara de los medios a utilizar, pasando por los organizadores del currículo antes mencionados.
Estas recomendaciones se consideran importantes, pero no suficientes, se deben tomar en cuenta además: los conocimientos previos de los alumnos, la forma en que deben ser introducidos conceptos tan importantes como: ecuación, sistemas de ecuaciones, relación y función que aseguren poder construir una cadena de esos conocimientos. En México, por lo general, los docentes no son maestros de profesión y basan sus actividades de enseñanza en la experiencia personal y fruto del intercambio con otros profesores, las creencias no son fáciles de modificar y pueden frenar cualquier cambio significativo en el currículo y la forma de implementarse. La capacitación del profesor en temas de la didáctica de las matemáticas pudiera ayudar en ese sentido.
El autor Hugo Parra en un artículo publicado en el año 2005, aborda la
33
El enfoque metodológico asumido fue la etnografía educativa, específicamente el estudio de casos. Se realizaron observaciones en las clases que impartían los pasantes y entrevistas a los mismos y profesora colaboradora. Los hechos muestran que hay una fuerte vinculación entre las creencias de los pasantes y las de los actores más próximos a ellos dentro del contexto escolar. Se incorporaron tímidamente actividades de
resolución de problemas a las actividades de aprendizaje, motivados por las limitaciones que en este sentido estableció la profesora colaboradora. En cuanto a los objetivos se observo cierta tendencia hacia la mecanización de destrezas básicas. El estudio evidenció que las creencias personales no estaban aisladas.
El trabajo concluye que las creencias personales deben considerarse en el marco
de un contexto, ya que ellas forman parte de una red de creencias bien constituidas en torno a la institución escolar y cualquier intento por modificarlas conlleva a plantearse acciones que consideren el conjunto de actores que en ella interviene.
Este estudio confirma la influencia de las creencias personales de los maestros en el diseño de las actividades de aprendizaje. La tendencia de la profesora colaboradora en el énfasis de los conocimientos procedimentales creó limitantes en el tema de la solución de problemas y en los aspectos conceptuales de los contenidos abordados, aspectos que deben ser considerados importantes en el estudio de conceptos matemáticos. Pocas veces son cuestionadas las creencias de los profesores y su influencia en las actividades de enseñanza en las investigaciones revisadas.
34
propiciar comportamientos matemáticos y cognitivos en el quehacer de los alumnos, haciendo que el tratamiento y pasaje de registros de representación sea el eje sobre el cual gire la construcción de las actividades de aprendizaje.
La metodología utilizada es la ingeniería didáctica, que se caracteriza por tener un esquema experimental, basado en las realizaciones didácticas en clase (concepción, realización, observación y análisis de secuencias de enseñanza). Se apoya en la comparación de los análisis a priori y a posteriori de la secuencia. El experimento se llevo a cabo durante seis jornadas de dos horas cada una en un grupo de 29 alumnas acostumbradas a la enseñanza tradicional.
Diseñaron una secuencia de aprendizaje para el objeto matemático: sistema de
ecuaciones lineales, que previera desarrollos en el campo matemático y en el cognitivo, seleccionando los elementos necesarios de diferentes teorías e investigaciones. Al no contar la docente con formación didáctica en la enseñanza de las matemáticas, creo limitantes en el desarrollo del experimento. Durante el desarrollo de la secuencia la mayoría de las estudiantes pasaron satisfactoriamente por las fases de acción, formulación y validación que proponen para el proceso de aprendizaje.
35
Respecto a la solución de problemas, la autora no hace referencias explícitas a la necesidad de que los estudiantes demuestren conocimientos de los conceptos
involucrados en su solución, ni en la forma en que deben ser abordados para su estudio. El autor del presente estudio considera además, que para la solución de problemas hay que lograr formar en los estudiantes la capacidad de lograr la transferencia del
conocimiento y se debe lograr un equilibrio en el tratamiento de los conocimientos procedimentales y conceptuales estrechamente relacionados con situaciones que describan situaciones reales, para que los alumnos puedan encontrarle un sentido y un significado a las matemáticas.
Estas publicaciones no hacen referencia a la importancia del estudio de los
conceptos a partir de las nociones que tienen los estudiantes de los mismos, ni sobre la posible influencia que puede tener el dominio de las propiedades de un conocimiento matemático en su aplicación en la solución de ejercicios y/o problemas que exijan de la transferencia del conocimiento.
Los autores de las investigaciones sintetizadas, coinciden en que en el estudio de las matemáticas de nivel bachillerato con frecuencia los profesores se encuentran con la dificultad que presentan los alumnos en la comprensión de los conceptos matemáticos y su aplicación en la solución de problemas. Ejemplo de ello lo vemos en la traducción de la información de un problema (lenguaje verbal) al modelo matemático que representa la solución del problema con ayuda de las herramientas algebraicas (lenguaje
algebraico) que puede ser una ecuación o función lineal o cuadrática, o un sistema de ecuaciones lineales.
36
lineales con la aplicación de un algoritmo que implica la aplicación de las propiedades de una igualdad y que por lo general conlleva a la obtención de una solución), pero descuidan el aspecto conceptual. Esta forma de concebir la enseñanza de las
matemáticas se identifica con elementos de los modelos educativos del tecnicismo y el procedimentalismo (Gascón, 2001) y por lo general el objeto matemático de estudio es considerado desde un sólo punto de vista, el procedimental.
Hay otro grupo de profesores que conciben a las matemáticas como un lenguaje y en este sentido el maestro guiará sus tareas en el aula buscando que el estudiante vea a las matemáticas como un instrumento de comunicación y de expresión de ideas
acabadas, se hace énfasis en enseñar y aprender teorías, sin ver su utilización en la
solución de problemas. Ésta forma de enseñar las matemáticas se identifica con elementos del teoricismo (Gascón, 2001).
Este lenguaje en su grado de generalización para expresar los conceptos es muy abstracto y esto hace que los estudiantes sientan un cierto rechazo hacia las mismas, por considerarlas muy difícil o aburridas y divorciadas de la realidad (no le encuentran un significado porque el profesor no fue capaz de relacionar o hacerles ver la relación de los contenidos matemáticos con situaciones reales). Una de las causas puede estar relacionada con la poca vinculación que se establece entre los conocimientos
matemáticos y su surgimiento y desarrollo histórico. Se debe lograr un equilibrio en el estudio de los contenidos matemáticos que no descuide ninguno de los dos puntos de vista, señalados.
37
Los profesores de Matemáticas, sin importar el nivel de enseñanza, siempre se enfrentan a retos sumamente difíciles para poder lograr un avance significativo en los alumnos. Uno de los principales problemas que se enfrentan, son las ideas previas que poseen los estudiantes sobre un determinado concepto, estas pueden deberse a lo que ellos están sometidos desde pequeños, determinadas en ocasiones por explicaciones erróneas dadas por los padres, amigos y hasta por las concepciones de los profesores en la enseñanza de los mismos. Flores, et al. (2004) mencionan que las ideas previas son construcciones que los sujetos elaboran para dar respuesta a su necesidad de interpretar fenómenos naturales, ya sean de la vida diaria o porque se quiera demostrar cierta capacidad de entendimiento.
El tema del tratamiento de nuevos contenidos y los conocimientos previos que deben tener los alumnos, es un tema cotidiano en las academias de matemáticas, los profesores con frecuencia se quejan de que los alumnos no dominan las operaciones básicas con los polinomios, las factorizaciones y no pueden resolver entonces ecuaciones lineales de 1er ó 2do grado (aquí entra el problema de la solidez de los conocimientos, porque los alumnos aprenden a resolver determinados ejercicios, siguiendo reglas dadas por el profesor, pero no le han dado un significado a lo aprendido y lo olvidan con facilidad).
Es recomendable que cuando un profesor diseñe una actividad de aprendizaje, prevea la exploración de las ideas previas sobre el tema a estudiar. Para poder realizar esto se deben de considerar los siguientes puntos:
• Desde la perspectiva constructivista no existe un solo método para enseñar
un tema en específico (Flores, et al., 2004).
• En el aprendizaje de la ciencia deben de tomarse en cuenta tanto la
38
les debe de dar ciertas justificación y fundamentación a los mismos (Flores, et al., 2004).
• La enseñanza debe de involucrar el tratamiento de argumentos científicos,
para que así el alumno se vaya acostumbrando a esta manera de ver el conocimiento (Flores, et al., 2004).
• Una concepción de enseñanza debe reconocer que tanto las actividades
experimentales, como las discusiones, pueden ser interpretadas de manera diferente a como se pretendieron educativamente (Flores, et al., 2004). Lo anterior puede ser válido para las ciencias en general, en este trabajo, se considera de utilidad en la enseñanza de conceptos y procedimientos matemáticos.
Otro problema que señalan los profesores de preparatoria con frecuencia, es que los alumnos ya estudiaron un concepto y no son capaces de aplicarlo en otro contexto, por ejemplo ya se instruyeron en resolver ecuaciones lineales y cuadráticas, pero no son capaces de solucionar ecuaciones trigonométricas, exponenciales o logarítmicas (no las
identifican como ecuaciones, no pueden establecer analogías entre ambas o no
reconocen las incógnitas) ¿Cuáles pueden ser las causas? Pudiera entre otras, deberse a que no tienen el significado de lo que significa una ecuación, resolver la misma, no reconocer sus propiedades al cambiar de contexto y/o por una rotura de las cadenas cognitivas en la enseñanza del concepto.
Filio (2007) considera que en matemáticas hay conceptos tan complejos y simbología tan difícil de comprender, que se incorporan en los currículos de estudio de manera dosificada. En un principio de un modo simple e impreciso y se van
39
frecuencia se observa que ese aprendizaje se logra de manera parcializada y si el alumno no ha podido comprender un concepto y eso significa identificar sus propiedades en cualquier pasaje en que aparece, difícilmente pueda utilizarlo en la solución de
problemas o de aplicarlos a situaciones similares dentro del contexto de las matemáticas o de otras ciencias.
Chevallard (1991) al referirse a la enseñanza de conocimientos matemáticos manifiesta la necesidad de adaptación del conocimiento matemático para transformarlo en conocimiento para ser enseñando, que define como transposición didáctica y así mismo resalta la importancia de las nociones, al indicar que en la primera fase de esta transposición se debe pasar, del saber matemático al saber enseñar y de la descripción
de los empleos de la noción a la descripción de la misma noción.
En un curso normal de matemáticas se presentan los dos tipos de problemas, en unos se les pide a los alumnos que en base a sus conocimientos den una explicación a algún fenómeno de la vida real, o por lo menos lo más cercano a la realidad (por ejemplo el concepto de ecuación para modelar una situación dada) y lo apliquen a la solución de problemas. En cuanto a los otros, que son tal vez, dos terceras partes de los ejercicios que se realizan en clase (ejercicios con texto de solución de ecuaciones y/o sistemas de ecuaciones lineales, que por lo general no tienen que ver con la realidad: la suma de dos números es 106 y el mayor excede al menor en 8. Hallar los números. Baldor, 1977), se busca medir las destrezas de los alumnos para utilizar herramientas de las matemáticas para resolver ejercicios y problemas dentro de su propio contexto.