Diseño de un Control Digital Desacoplante para el Control de Nivel y Temperatura-Edición Única

BIBLIOTECAS DEL TECNOLÓGICO DE MONTERREY

PUBLICACIÓN DE TRABAJOS DE GRADO

Las Bibliotecas del Sistema Tecnológico de Monterrey son depositarias de los trabajos recepcionales y de

grado que generan sus egresados. De esta manera, con el objeto de preservarlos y salvaguardarlos como

parte del acervo bibliográfico del Tecnológico de Monterrey se ha generado una copia de las tesis en

versión electrónica del tradicional formato impreso, con base en la Ley Federal del Derecho de Autor

(LFDA).

Es importante señalar que las tesis no se divulgan ni están a disposición pública con fines de

comercialización o lucro y que su control y organización únicamente se realiza en los Campus de origen.

Cabe mencionar, que la Colección de

Documentos Tec,

donde se encuentran las tesis, tesinas y

disertaciones doctorales, únicamente pueden ser consultables en pantalla por la comunidad del

Tecnológico de Monterrey a través de Biblioteca Digital, cuyo acceso requiere cuenta y clave de acceso,

para asegurar el uso restringido de dicha comunidad.

El Tecnológico de Monterrey informa a través de este medio a todos los egresados que tengan alguna

inconformidad o comentario por la publicación de su trabajo de grado en la sección Colección de

Documentos Tec

del Tecnológico de Monterrey deberán notificarlo por escrito a

Diseño de un Control Digital Desacoplante para el Control de

Nivel y Temperatura-Edición Única

Title

Diseño de un Control Digital Desacoplante para el Control

de Nivel y Temperatura-Edición Única

Authors

Gerardo de Jesús Olvera Martínez

Affiliation

Tecnológico de Monterrey, Campus Monterrey

Issue Date

1996-12-01

Item type

Tesis

Rights

Open Access

Downloaded

19-Jan-2017 01:52:14

INSTITUTO TECNOLÓGICO Y DE ESTUDIOS

SUPERIORES DE MONTERREY

C A M P U S M O N T E R R E Y

D I V I S I Ó N D E G R A D U A D O S E

I N V E S T I G A C I Ó N

E N INGENIERÍA

D I S E Ñ O D E U N C O N T R O L DIGITAL

D E S A C O P L A N T E PARA EL C O N T R O L D E

N I V E L Y T E M P E R A T U R A

T E S I S

P R E S E N T A D A C O M O REQUISITO PARCIAL

PARA O B T E N E R EL GRADO A C A D É M I C O DE:

M A E S T R O E N CIENCIAS

ESPECIALIDAD E N INGENIERÍA D E CONTROL'

PRESENTA

INSTITUTO TECNOLÓGICO Y DE ESTUDIOS SUPERIORES DE MONTERREY CAMPUS MONTERREY

DIVISIÓN DE GRADUADOS E INVESTIGACIÓN PROGRAMA DE GRADUADOS EN INGENIERÍA

Los miembros del comité de tesis recomendamos que la presente tesis del Ingeniero Químico y de Sistemas Gerardo de Jesús Olvera Martínez, sea aceptada como requisito parcial para obtener el grado académico de Maestro en Ciencias con especialidad en :

INGENIERÍA DE CONTROL

APROBADO

Director del Programa de Graduados en Ingeniería

DEDICATORIA

Quiero dedicar esta tesis a mis padres Gerardo y María Tayde ; a mis hermanas Alejandra , María Tayde, y a mi novia Maricarmen por su apoyo incondicional que me brindaron para que yo empezara y terminara mi maestría.

AGRADECIMIENTOS

DISEÑO DE UN CONTROL DIGITAL

ÍNDICE

CAPITULO 1. INTRODUCCIÓN 1

1.1 Introducción 1 1.2 Antecedentes del Problema 2

1.3 Alcance y Objetivo 4

CAPITULO 2. DESACOPLADORES DINÁMICOS CONVENCIONALES 7

2.1 Bases Teóricas 7

2.2 Ejemplo 9

2.2.1 Solución del Ejemplo con Desacopladores Parciales 10

2.2.2 Desacopladores Completos Continuos 15 2.2.3 Desacopladores Completos Discretos 19

CAPITULO 3. CONTROL DESACOPLANTE 23

3.1 Bases Teóricas 23 3.2 Ejemplo 26

3.2.1 Solución del ejemplo en modo continuo 26 3.2.2 Solución del ejemplo en modo discreto 28

CAPITULO 4. IDENTIFICACIÓN DEL PROCESO 31

4.1 Introducción 31 4.2 Estrategia de Identificación 31

4.3 Arreglo actuador-proceso 32

CAPITULO 5. IMPLEMENTACIONDESACOPLADORES COMPLETOS 34

5.1 Introducción 34 5.2 Estrategia de Control 34

5.3 Diseño de los Desacopladores Continuos 34 5.3.1 Sintonización de los Controladores PID 36 5.4 Diseño de los Desacopladores Discretos 38

5.5 Ecuación discreta a implementar 39

CAPITULO 6. IMPLEMENTACION CONTROL DESACOPLANTE 41

6.1 Introducción 41 6.2 Estrategia de Control 41

6.3 Diseño de los Controladores Continuos 41 6.4 Diseño de los Controladores Discretos 43 6.5 Ecuación discreta a implementar 44

CAPITULO I INTRODUCCIÓN 1.1 Introducción

En la industria es común encontrarse con procesos automatizados en los cuales se encuentren dos o más variables involucradas en el lazo de control; a estos procesos se les conoce como sistemas M.I.M.O (múltiple inputs múltiple outputs). La características de dichos sistemas es que necesitan dos o más variables manipuladoras, que son las encargadas de realizar acciones de control para mantener en un valor deseado a dos o más variables de control (variables de salida).

Los sistemas desacoplantes son estrategias de control ampliamente usadas para tratar de controlar un sistema M.I.M.O; su característica principal se basa en que anula o desacopla la interacción de una variable manipuladora con respecto a las salidas que no son de su interés, para que de esta manera el proceso entero no se vea perturbado. Debido a lo anterior, es posible su aplicación en la industria química para el monitoreo y control de procesos industriales, en los cuales generalmente se involucran sistemas M.I.M.O como pueden ser procesos de destilación, separación, reacción, temperatura, concentración, secado, etc.

En los procesos químicos en donde la concentración y temperatura de un producto al final de la línea de producción son importantes para cumplir con las normas de calidad, se hace necesario un monitoreo y control en donde por lo menos dos variables ya están involucradas: la concentración y temperatura. Es por ello que las estrategias de control por medio de sistemas desacoplantes se vuelven atractivas para ser implementadas, y es en este tipo de proceso en donde se concentrará la atención de este trabajo.

El equipo que se utilizará como estación de trabajo se encuentra en el Laboratorio de Control Discreto ubicado en aulas IV del ITESM campus Monterrey.

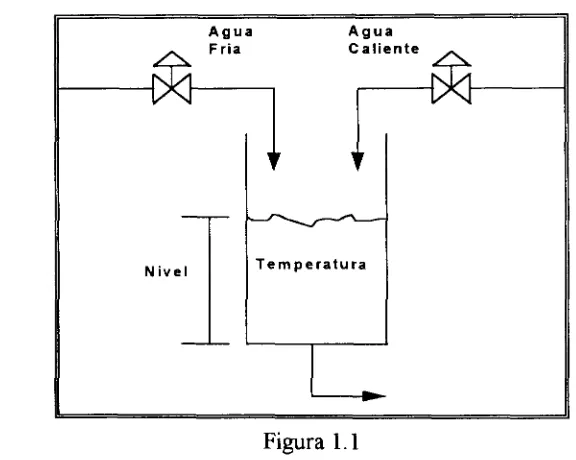
El proceso a controlar se muestra en la figura 1.1 [Lucía Hanger]. Este cuenta con dos variables a controlar que son nivel y temperatura en la descarga.

A g u a F r í a

A g u a C a l i e n t e

N i v e l

t t

T e m p e r a t u r a

Figura 1.1

Una característica que cabe mencionar es la no linealidad en el comportamiento de las válvulas, la cual se tomará en consideración para el desarrollo del trabajo.

1.2 Antecedentes del Problema

Desde sus inicios el hombre por su naturaleza innovadora ha venido aplicando sus conocimientos y experiencias en beneficio del desarrollo tecnológico. Ya desde los tiempos de la antigua Babilonia las puertas del gran templo eran accionadas por un ingenioso mecanismo en base a vapor de agua. Posteriormente, la invención del molino hizo mas fácil la molienda del trigo. Con la llegada de la revolución industrial a finales del siglo XVIII, la automatización de las fábricas, aunque mecánicamente rudimentaria, trajo con sigo un gran despegue económico entre los principales países europeos al producir más y a menor costo. Hoy en día la automatización ha llegado a puntos extremadamente complejos, ya que con la invención de las computadoras digitales ha sido posible controlar procesos multivariables y no lineales, como en este trabajo se pretende realizar.

Existe mucha bibliografía referente a control multivariable acoplado, encontrándose una gran cantidad de metodologías matemáticas para resolver el problema, ya sea utilizando funciones de transferencia o variables de estado. La primera forma en que se comenzó a atacar este tipo de procesos fue mediante funciones de transferencia [1], en donde al diagrama de bloques original se le agregaban compensadores de adelanto atraso comúnmente llamados lead-lags, cuya función era antealimentar la perturbación de una variable sobre la otra y de esta manera desacoplarlas. Después se fue inclinando más la

balanza hacia las variables de estado, debido a que el acelerado desarrollo tecnológico de las computadoras hizo más fácil la implementación de los algoritmos matriciales.

Grizzle y Shor [2] desarrollaron un sistema de muestreo, ceros infinitos y desacoplamiento de sistemas lineales a partir de la representación clásica en variables de estado: Zx = ZAx + ZBu + ZDw

(1.1) Zy = ZCx

donde x son los estados (n), u son las entradas (m), w las perturbaciones, y las salidas (p), A es la matriz de estados (nxn), B la matriz de entrada (nxm), C la matriz de salida (pxn) y D casi siempre vale cero, y en base a la definición (Wonham, 1979) de que un sistema se dice ser desacoplable si uno puede encontrar una retroalimentación en variables de estado u = Fx + v (en tiempo continuo o discreto), tal que en el sistema de lazo cerrado resultante las perturbaciones no afecten a la salida. Dejando a V como el máximo subespacio invariante-controlado contenido en ker C, entonces se conoce que la ecuación 1.1 puede ser desacoplada si y solamente si Im D c : V . Por lo tanto en base al número de ceros infinitos definidos como:

p** :=dim(Im B o V*1

"!) - dim(Im B o V*) del sistema muestreado ZS(T); entonces el

mismo procedimiento puede aplicarse a un subsistema: ZJ

x = ZÍAx + ZÍBu + Z b w (1.2)

z y = z i d x

donde C1

y y1

son matrices del subsistema, además si se cumple el lema Z pjl = pl el sistema es dinámicamente desacoplable.

Commault, Dion y Torres [3] por su parte aplicaron criterios de estabilidad al problema de desacoplamiento, donde el sistema del compensador desacoplado es estable y no ocurren cancelaciones de polos y ceros. Para ello caracterizaron el mínimo grado de McMillan del sistema y de la ecuación (1.1) T(s) = C(sl - A )_ 1

B usaron un compensador combinado de la forma:

u = Fx + C(s)v

donde x es el estado mínimo realizable, F cualquier retroalimentación de estados y C(s) es un precompensador, donde se debe cumplir para que el sistema sea desacoplable si:

rang T(s) = Z rang Tˇ(s)

área más estudiada del control multivariable utilizando desacopladores, es el control de torres de destilación binaria. Como lo muestran Castro y Alvarez [10], en su trabajo del control desacoplante de perturbaciones no lineales en una columna de destilación binaria. En él consideraron un sistema no lineal del tipo:

x = fíx) + Xgi(x)uj + Zdj(x)wj, x° = x(0),

(1.3) y = hi(x) (i= l,....,m)

donde el estado x e U, un subconjunto abierto de Rn

, mientras los componentes m u,j,...,u,m de la entrada, los componentes d w^.^w^ de la perturbación externa y los

componentes y i , . , ym de la salida son funciones reales. En seguida proponen para el

problema del desacoplamiento de la perturbación, modificar el sistema 1.3 vía retroalimentación de estados de la forma (Moog y Glumineau, 1983):

u, = a(x) + P(x)v + y(x)w (1.4)

donde a(x) es un vector m-dimensiones, 3(x) es una matriz de n x m dimensiones y y(x) es una matriz m x d, de tal manera que la perturbaciones wl v. . w ż no tienen influencia en las

salidas y i , . . , ym. Además si y(x) = 0 el problema se vuelve del tipo DDPM (disturbance

decoupling problem with partial measurement) y la solución local para este tipo de sistemas es:

A* cz Kerndth Tx R n

y cumpliendo con ciertas condiciones de varianza, el sistema 1.4 podrá resolverse.

Como estas metodologías matemáticas existen muchas más, centrándose la mayoría en atacar al problema vía retroalimentación de estados, y una vez encontrados los parámetros y matrices correspondientes, programarlos en una computadora digital e implementar el control.

1.3 Alcance y Objetivo

En el presente estudio se tiene como alcance el diseño de un control multivariable de 2x2 del proceso de nivel y temperatura mencionado, en donde se utilizarán dos estrategias de control:

a) Desacopladores completos de proceso actuando sobre controladores P.I.D.

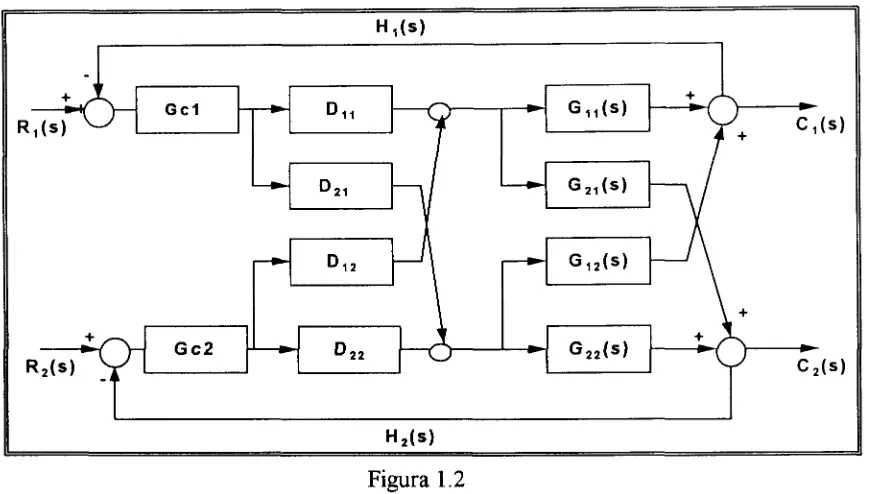
- Esta estrategia propone utilizar un controlador para cada variable de control (salida), y desacoplar la interacción entre ellas, como lo muestra la figura 1.2:

b) Utilizando un control digital desacoplante.

- A diferencia de la estrategia anterior, esta técnica propone utilizar un solo compensador digital para todo el proceso, realizando la cancelación de los acoplamientos y control como se muestra en la figura 1.3:

c^s)

C2( s )

H2( s )

Figura 1.3

El objetivo del trabajo es desarrollar las estrategias de desacopladores completos y control digital desacoplante para el proceso de nivel y temperatura, simular los resultados obtenidos mediante el paquete "CC", e implementar su funcionamiento en la estación del laboratorio.

CAPITULO H DESACOPLADORES DINÁMICOS CONVENCIONALES

2.1 Bases Teóricas

Como ya se mencionó anteriormente, un desacoplador es una estrategia que elimina la interacción entre las variables de control y las manipulaciones, cambiando estas últimas de tal manera que solamente la variable controlada cambie [11].

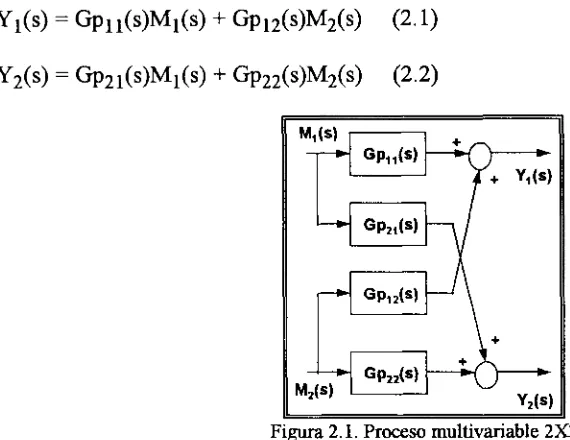
Si se considera un sistema un sistema interactuante de 2x2 variables, como se muestra en la siguiente figura 2.1, se puede escribir:

Y,(s) = Gp1 1(s)M1(s) + Gp1 2(s)M2(s) (2.1)

Y2(s) = Gp2 1(s)M1(s) + Gp2 2(s)M2(s) (2.2)

M,(s) M,(s)

GPn(s) GPn(s)

f*

f*

Gp21(s)

X

Gp12(s)

-A

V

Gp22(s)

M2(s)

Gp22(s)

M2(s)

Y2(s)

Figura 2.1. Proceso multivariable 2X2

Las entradas al desacoplador son las variables manipuladoras Mi y M2 , y sus salidas son

las variables manipuladoras llamadas ahora ui y u2 , como se muestra en la figura 2.2. Se

puede diseñar el desacoplador de tal manera que M j afecte solamente a Y[ y M2 afecte

solamente a Y2.

I

H,(s)

De la figura 2.2 se puede ver que las ecuaciones del desacoplador pueden escribirse como:

Yi = UlGpn + U2G p1 2

(2.3)

Y2 = U1G p2 1 + U2G p2 2

(2.4)

U i = M1D1 1 + M2D2 2

(2.5)

u

(2.6)

En teoría, al menos un desacoplador puede ser construido con hardware análogo, particularmente cuando modelos de primer orden son usados. Sin embargo, el éxito no esta ligado siempre a modelos sencillos, entonces hay que aplicar modelos más complejos en donde la computadora digital es usada para el desarrollo de algoritmos en línea.

En el diseño de las ecuaciones para un desacoplador general de un sistema nxn, es conveniente sintetizar usando notación matricial. El diagrama de bloques para un sistema multivariable general se muestra en la figura 2.3.

u

M — • D _— Gp

Figura 2.3. Diagrama de bloques

Los términos son definidos de la siguiente manera:

Gp =

GP l 1( s ) . . . Gp1 n(s)

Gpn 1(s) . . . Gpn n(s)

D =

Dn(s)

D„,(s)

Di n(s)

Dm(s)

Donde M y U son vectores de nxl, por lo tanto de las ecuaciones 2.3, 2.4 y 2.5, 2.6 se pueden rescribir como:

GPii(s) Gp12(s) 11,(8)

_Y2(s)_ _GP2i(s) Gp^® JJ2(S)_

~Üi(sr

D

(s)

D

(s)

"Mi

(sT

JJ2(s)_ _ D2 1( S ) D22(S)_ jyi2(s)_

(2.7)

(2.8)

o en forma compacta:

Y = G p U (2.7')

U = D M (2.8')

entonces Y = Gp D M (2.9)

Además de realizar un desacoplamiento de variables, es factible especificar también un cierto comportamiento del sistema en lazo abierto, o sea definir una planta deseada (Gd) y entonces la salida queda de la siguiente manera:

Y = G d M

Gd = G d ^ s ) 0 l_ 0 Gd2 2(s]_l

(2.10)

(2.11)

donde Gd es una matriz diagonal principal ya que se quiere que las plantas 1 y 2 estén desacopladas.

Se puede observar si se comparan las ecuaciones 2.9 y 2.10 que:

Gd = Gp D (2.12)

Qd«(s) 0 GPii(s) Gp12(s) Duís) D12(s)

_ 0 G d ^ s ^ _Gp2i(s) Gp^g)

obteniéndose un sistema de cuatro ecuaciones con cuatro incógnitas,

Gdn = QpnI>n + Qp12D2l (2.13)

0 = G p2 1D1 1 + G p2 2D2 1 (2.14)

0 = G p1 1D1 2 + G p1 2D2 2 (2.15)

G d2 2 = G p2 iD 1 2 + G p2 2D2 2 (2.17)

De estas ecuaciones se obtienen las expresiones de los desacopladores que en notación matricial queda de la siguiente manera:

D = G p - ! G d (2.18)

2.2 Ejemplo

Se tiene un sistema de 2x2 tomado de Smith y Corripio [1] en donde las expresiones de las plantas en tiempo continuo son las siguientes:

GPu(s) =

0.36 e ­0.15í

Gp2l(s)

Gpu(s) =

-0.144 e~0As

1.655+1

0.72 e~03s

2.75 + 1

Gp22(s) =

-0.336 < T0 1 5 í

1.055 + 1

Se desea diseftar desacopladores completos (en CC) para el sistema en tiempo discreto, de tal manera que permitan un mejor desempeño tanto en el desacoplamiento de variables como en el comportamiento de las plantas.

2.2.1 Solución del ejemplo con Desacopladores Parciales

Primero los modelos continuos de las plantas se discretizan por medio de la transformada Z, usando un retenedor de orden cero (ZOH) con un tiempo de muestreo de 0.1 seg.

G pn( z ) = -0.00199ÍZ - 8.3206) (2.19)

(Z - 0.9668)(Z - 0.2635)

Gp2 1(z) = 0.004826UZ- 1.6903) (2.20)

(Z-0.9411)(Z- 0.6065)

G p1 2( z ) = -0.011957ÍZ- 2.0652) (2.21)

(Z-0.9636)(Z-0.5134)

Gp2 2(z) = 0.002847CZ- 8.8951) (2.22)

(Z - 0.9091)(Z - 0.2635)

Una vez realizado esto, como primera opción se diseña un sistema desacoplante en donde los desacopladores T>n y D2 2 se suponen uno. Entonces de las ecuaciones 2.14 y 2.15 se

obtiene una expresión para D1 2 y D2 1:

D2 1 = ­Gp2i (2.23) D1 2 = - Gpi2 (2.24)

Gp22 Gpn

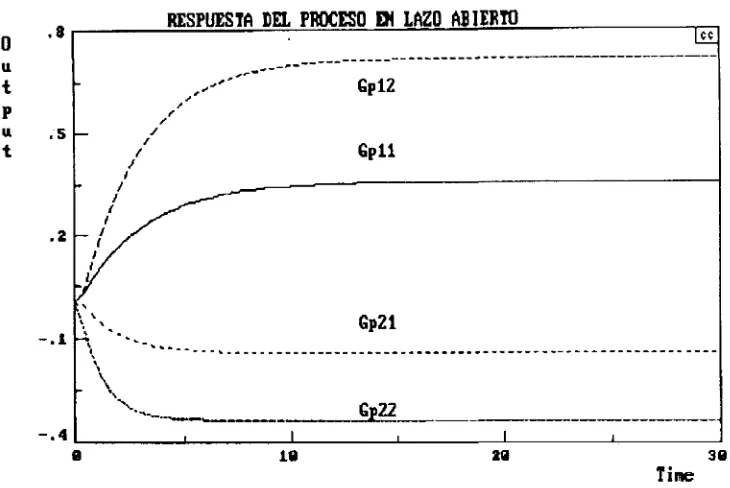
Con la ayuda del paquete CC se grafican primero las cuatro plantas por separado para saber el comportamiento natural de las que se quieren desacoplar (Gpii(z) y Gp2 2(z)), su

R E S P U E S T A B E L PROCESO EM L A Z O A B I E R T O

I ce

/

f _ y

/

/

GP12

GP11

/

/ .

/ ^

— 1

/ 1 / 1 / 1 / ¡/

; ^

\ V

\ \

s Gp21

\

- \

GP22

• l i l i

0 10 20 30

Tinte

Figura 2.4. Respuesta del proceso en lazo abierto ante un escalón unitario

De las ecuaciones 2.19 y 2.20:

D2 1 = -1.695UZ - 0.9091ĄZ - 0.2635)(Z - 1.6903) (2.25)

(Z - 8.8951)(Z - 0.9411)(Z - 0.6065)

D1 2 = -9.973(Z - 0.9668)ÍZ - 0.2635)fZ - 2.0652) (2.26)

(Z - 8.3206)(Z - 0.9636)(Z - 0.5134)

40 50

n, Tine=n*T

4 8

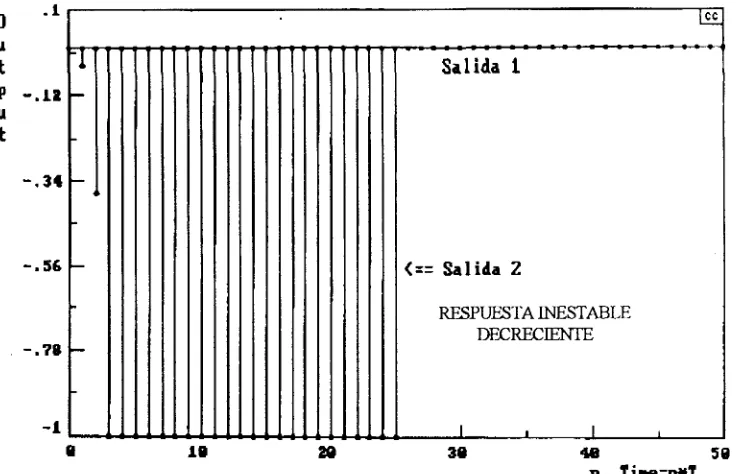
TI, Time=n*T Figura 2.7. Desacopladores parciales en lazo abierto ante un escalón unitario a la entrada 2

En las figuras 2.6 y 2.7 se observa que el comportamiento de las salidas se hace inestable, esto se debe a que en ellos existe un polo que lo provoca. Para eliminarlo, en los polos inestables de las ecuaciones 2.21 y 2.22 Z se pone igual a uno. De esta forma:

D2 1 = -0.1482CZ - 0.9091VZ - 0.2635) (2.27)

(Z-0.9411)(Z-0.6065)

D1 2= -1.4511(Z - 0.9668VZ - 0.2635) (2.28)

(Z - 0.9636)(Z - 0.5134)

n, Tine=rr*T

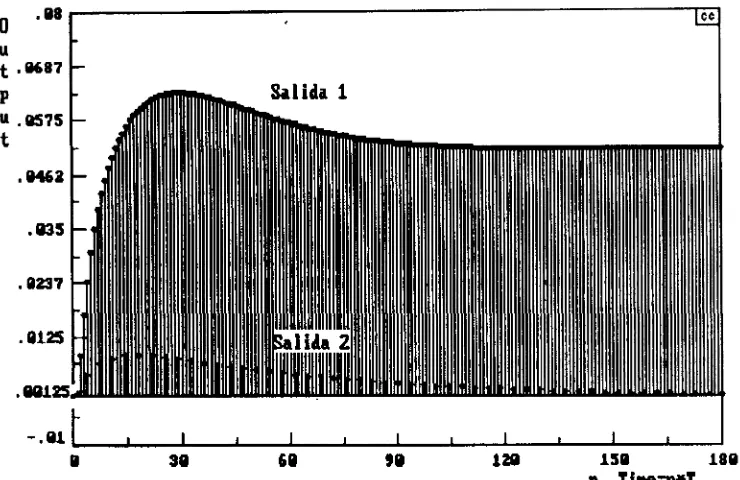
Figura 2.9. Desacopladores parciales continuos en lazo abierto ante un escalón unitario a la entrada 2

2.2.2 Desacopladores Completos Continuos

Como se puede ver en las salidas de las plantas Gpu(z) y Gp22(z_{) (salidas 1 y 2) el}

comportamiento no es el mismo con respecto al de la figura 2.4, ya que su respuesta original es un sistema de primer orden y el obtenido con los desacopladores parciales D21 y D12 s e

parece mas bien a un sistema de segundo orden bajo amortiguado. Para evitar estos resultados se necesita diseñar un sistema de desacopladores completos definiendo también el comportamiento del lazo, es decir, definiendo las salidas deseadas en lazo abierto (Gd),tal como lo muestra la ecuación 2.12. Para fines de ejemplo, las salidas deseadas se plantearán iguales a las plantas Gpi ˇ(s) y

Gp22(s)-Primero se diseña el sistema desacoplante en tiempo continuo, donde las salidas deseadas son:

036 Gdl(s) = 2.975 + 1

-0.336 e~°1 5 í

GdJs)

2 _{1.055 + 1}

Sustituyendo las salidas deseadas junto con las plantas en la ecuación 2.18, se llega a las

siguientes ecuaciones:

A , <*m'*>- ( Z 2 9 )

GpnGp22 - GpnGp2l

Gd.GP2.

D21 = - — (2.30)

GpnGp22 - Gp12Gp2l

Gd2GR2

Dn=

2

-—* (2.31)

GpnGp22 - GpnGpu

Gd2GPu

D22 =

2

-—ü (2.32)

GpnGp22 - Gpl2Gp21

Que dando finalmente las siguientes funciones de transferencia:

_ 0.78197(^ + 0.37037)(ż' + 0.60606)(^ + 5)(S + 6.6666)

1 1 _{~ [(S + 0.22155)}2 _{+ (0.060331)}2_{](S + 1.8843)(S +8.4132)}

_ -0.079977(^ + 0.37037)(^ + 0.9523)(S + 6.6666){S + 13.3333)

21

~ [(S + 0.22155)2 _{+(0.06033 l)}2

-0.860207(5 4­ 0.3367)(5 + 0.60606)(5 + 5)(5 + 13.3333) [(5 + 0.22155)2

+ (0.06033 \)2

](S + 1.8843X5 + 8.4132)

0.78197(5 + 0.3 703 7)(5 + 0.60606)(5 + 5)(5 + 6.6666) [(5 + 0.22155)2

+ (0.060331)2

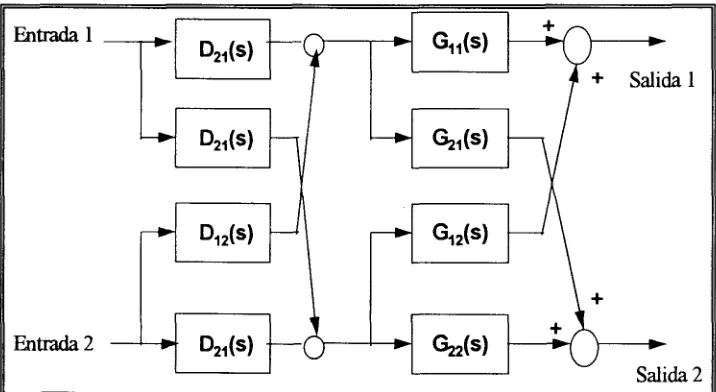
](5 + 1.8843)(5 + 8.4132)

Se grafican los resultados ante un escalón unitario en lazo abierto según la figura 2.10 y se puede ver el nuevo desempeño en las figuras 2.11 y 2.12. Como se puede observar, las salidas 1 y 2 representan las variables a controlar, y ahora el comportamiento de las plantas es el mismo al de la figura 2.4, debido al desempeño pedido al lazo.

Figura 2.10. Lazo abierto usando desacopladores completos continuos

Ice

Salid» 1

Salida 2

1 ... 1 . 1 , 1 , 1 . 1 , 1 .

0 1 0 8 0 3 0 « 0 5 0 G 0 7 8 8 0 Tine

Figura 2.11. Desacopladores completos continuos en lazo abierto ante un escalón unitario a la entrada 1

O 10 20 3 0 48 38 ' 0

Figura 2.12. Desacopladores completos continuos en lazo abierto ante un escalón unitario a la entrada 2

El siguiente paso es cerrar el lazo y controlarlo. Para esto se utilizarán dos controladores PID diseñados en base a los parámetros de las plantas

G p u

( s )

método de síntesis. Los controladores quedan de la siguiente forma:

Gci (s) = 2.6442[2.97s + ll[0.075s +1] 2.97s[0.07139s+l]

Gc2(s) = -2.6041[1.05s+ l][0.075s+ll

1.05s[0.06562s+l]

(2.37)

(2.38)

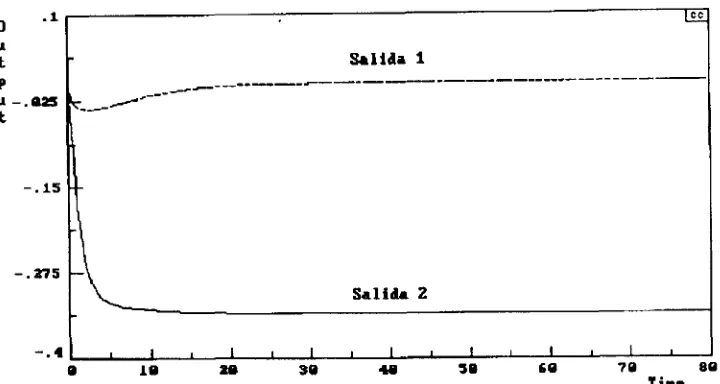
Las respuestas del lazo cerrado de acuerdo a la figura 2.13 aparecen en las figuras 2.14 y 2.15, donde se le dio una referencia de uno al lazo para Gci(s). Lo mismo se hizo para Gc2(s).

Se observa que ambas gráficas existe un pequeño offset en la señal que debe permanecer cero, esto debido a la pérdida de decimales que provoca la cancelación de polos inestables.

Ti «o

Figura 2.14. Respuesta para una entrada de uno para la referencia uno

Figura 2.15 Respuesta para una entrada de uno para la referencia dos

NOTA: El offset que se observa en las figuras 2.14 y 2.15 es debido a errores de redondeo el paquete CC.

2.2.3 Desacopladores Completos Discretos

Para implementar la solución de desacoplamiento total en un proceso real, es necesario discretizar el lazo.

Una manera de aproximar el tiempo muerto es por medio de la aproximación de Pade, esto con el fin de simplificar el número de polos y ceros de las funciones de transferencia, porque si se tomase las expresión de la función de transferencia pulso:

Gp(z) = Transf(z)[Z-N

[Gp(s)/s]]

la Z "N

daría un orden de magnitud muy grande en la ecuación característica de cada una de las plantas del proceso; en cambio si se usa la aproximación de Pade de primer orden una función de transferencia con tiempo muerto quedaría como sigue:

Kp(\-?-s) G(s) = ^ j

-( „ + 1X1 + - J )

Y de esta manera las N raíces solo serían un polo y un cero.

De las ecuaciones 2.19 a 2.22, y siguiendo el mismo criterio de comportamiento de la planta, los desacopladores ya con sus polos inestables cancelados quedan de la siguiente manera:

D - ° -8 5 9 2 7

(Z

~ 0-S134XZ-.6065XZ-.9411XZ-.9636)

1 1 ~ (Z-.43268)(Z - 0.82816)(Z2 - 1.95602Z + 0.95653)

_ -0.12735(Z - 0.2635)(Z - 0.5134)(Z - 0.909l)(Z-.9636)

2 1

~ (Z-.43268)(Z - 0.82816)(Z2

-1.95602Z +0.95653)

_ -1.24685(Z - 0.263 5)(Z - 0.6065)(Z - 0.941 l)(Z-.9668)

1 2

~ (Z-.43268)(Z - 0.82816)(Z2

-1.95602Z +0.95653)

_ 0.85927(Z-0.5134)(Z-.6065)(Z-.9411)(Z-.9636)

2 2

~ (Z-.43268)(Z - 0.82816)(Z2

- 1.95602Z + 0.95653) ^ '

Con los nuevos desacopladores el sistema de la figura 2.16 ante una entrada escalón unitario responde como lo muestran las figuras 2.17 y 2.18, en donde se observa el comportamiento según el desempeño deseado ahora para

G p u

( z )

Gcx =

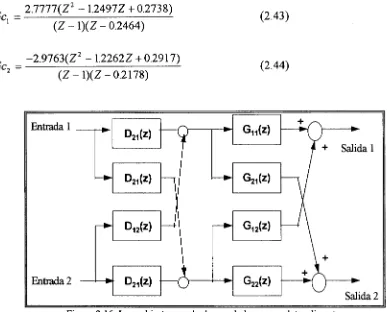
21111 {Z2 _{- \2491Z + 0.2738)}

(Z - 1)(Z - 0.2464) (2.43)

Ge, -2.9763(Z

2 _{- 1.2262Z + 0.2917)}

( Z - 1 ) ( Z - 0 . 2 1 7 8 ) (2.44)

Figura 2.16. Lazo abierto usando desacopladores completos discretos

n, Tine=n*T

Figura 2.17. Desacopladores completos discretos en lazo abierto ante un escalón unitario a la entrada 1

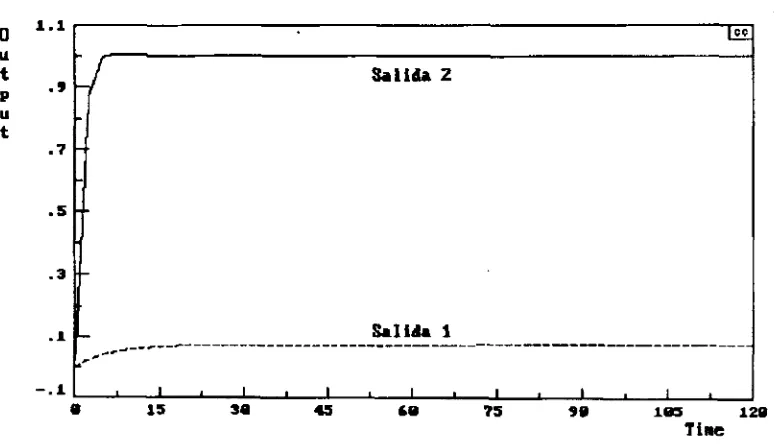
El lazo cerrado discreto se muestra en la figura 2.19 y su comportamiento ante una referencia de uno en el lazo para Gci(z), se observa en la figura 2.20, y se aprecia que el lazo responde bien con excepción de la salida 2, ya que esta tiene algo de offset debido a la cancelación de polos en los desacopladores. Lo mismo se hizo para Gc2(z) y Gp22(z

) en la figura 2.21.

0 lflfl 20a 300

Figura 2.21. Respuesta para una entrada de uno para la referencia dos

NOTA: El offset de las figuras 2.17, 2.18, 2.20 y 2.21 es debido a errores de redondeo del paquete CC.

CAPITULO m CONTROL DESACOPLANTE

3.1 Bases Teóricas

En el capítulo anterior se mostró que para controlar dos variables de un sistema de 2x2, la estrategia era desacoplar primero las variables de interés en el lazo abierto, y una vez hecho esto controlarlas con un controlador para cada una. El objetivo ahora es realizar una estrategia que desacople y controle al mismo tiempo los mismos procesos pero con un desempeño específico para el lazo cerrado.

De nuevo, si se considera un sistema interactuante de 2x2 variables como se muestra en la figura 3.1 se puede escribir:

Y,(s) = Gp1 1(s)M1(s) + Gp1 2(s)M2(s) (3.1)

Y2(s) - Gp2 1(s)M1(s) + Gp2 2(s)M2(s) (3.2)

Figura 3.1 Sistema Interactuante de 2X2

En donde las manipulaciones M^(s) y M2(s) son el resultado del error por la acción del controlador según lo muestra la figura 3.2

De la figura 3.2 se puede compactar en diagrama de bloques para un sistema multivariable general de la siguiente manera:

Figura 3.3 Diagrama de Bloques

En donde los términos están definidos como:

Donde M y E son vectores de nxl, por lo tanto el sistema queda de la siguiente manera:

(3.3)

M ( 5 ) '

M2(s)

Gcu(s)..Gcn(s)

Gc2l(s)..Gc22(s) E2(s)

(3.4)

o en forma compacta:

Y = GpM (3.3')

M = GcE (3.4')

entonces sustituyendo la ecuación 3.4 en la 3.3 se deduce que.

Y = GpGcE (3.5)

donde el error es igual a.

E = R - Y (3.6)

En este caso, se desea obtener un respuesta deseada en el lazo de control, o lo que es lo mismo especificar ciertos parámetros para que la salida del lazo sea predecible, por lo tanto, es necesario definir un planta deseada y entonces la salida queda de la siguiente manera:

Y = GdR (3.7)

Gd Gdn(s) 0 "

0 Gd22(s\

donde Gd es una matriz diagonal principal ya que se quiere que las plantas G pn y G p2 2

estén desacopladas, si sustituimos la ecuación 3.6 en 3.5:

Y = GpGc(R - Y)

Y = GpGcR - GpGc Y

Y + GpGc Y = GpGcR

( I + GpGc)Y = GpGcR

Y = ( I + GpGc)_ 1

GpGcR (3.8)

y sustituyendo 3.7 en 3.8

Gd = ( I + G p G c ^ G p G c

GpGc = ( I + GpGc)Gd

GpGc = Gd + GpGcGd

GpGc( I - Gd) = Gd

Ge = Gp-kjd( I - Gd)"1

(3.9)

3.2 Ejemplo

Tomando el mismo ejemplo del capítulo anterior del sistema de 2x2 del Smith y Corripio [1] las expresiones de las plantas vuelven a ser:

Gpu(s) =

Gp2](s) =

Gpu(s) =

Gp22(s) =

0.36 e ­0.15í

2.975+1

-0.144 e~0As

1.655+1

0.72 e~°3 í

2.75 + 1

-0.336 g ^1 5

' 1.055 +1

Se desea diseñar un control desacoplante para las plantas G p i ^ s ) y Gp22(s) de tal

manera que se rompa el acoplamiento para poder ejercer control entre ellas.

3.2.1 Solución del ejemplo en modo continuo

De acuerdo a la ecuación 3.9' las ecuaciones de los controladores son las siguientes:

Gp22Gd,

Gcu

l-Gd,

G C _M

Gc2X

Gc22

G PnG

Pn -G PuG

Pn

-GpnGd2

l-Gd2

GPnGp22-GPnGp2X

-Gp2lGdx

l-Gd,

G PuG

Pn ~G PnG

Pix

G P nG d

2 l-Gd2

G PnG

Pii - G PuG

Pii

Ahora hay que definir las características de las plantas deseadas, se especifica la misma dinámica de las plantas G pn( s ) y Gp22(s) con ganancias unitarias:

Gd}(s) =

2.975 + 1 (3.10)

­0.15 s

Gd2(s)

1.055 + 1 (3.11)

Sustituyendo las ecuaciones 3.10 y 3.11 en la 3.9 los controladores del lazo son:

0.665(5 + 0.3367)(5 + 0.3703)(5 + 5)(5 + 6.6666)

Ge,, =

Gcu =

Gc2] =

Gc22 =

5 ( 52

+ 0.44315+ 0.05272)(5 +8.4132)

-2.2641(5 + 0.3367)(5 + 0.6060)(5 + 5)(5 - 6.6666) 5 ( 52

+ 0.44315 + 0.05272)(5 + 8.4132)

0.285(5 + 0.3367)(5 + 0.3703)(5 - 5)(5 + 6.6666) 5 ( 52

+ 0.44315 + 0.05272)(5 + 8.4132)

-1.02917(5 + 0.3703)(5 + 0.6060)(5 + 5)(5 + 6.6666) 5 ( 52

+ 0.44315 + 0.05272)(5 + 8.4132)

(3.12)

(3.13)

(3.14)

(3.15)

De acuerdo al diagrama de bloques de la figura 3.4 se hicieron dos pruebas en cambio en referencia de uno para cada planta, como lo muestran las figuras 3.5 y 3.6, observándose un buen desempeño del lazo.

3.2.2 Solución del ejemplo en modo discreto

Debido a que en un proceso real se utilizarán microprocesadores para los controladores, es necesario al igual que en el capítulo anterior, discretizar el lazo de control. De nuevo se

utilizará un retenedor de orden cero (ZOH) y la aproximación de Pade, quedando las plantas del proceso y deseadas de la siguiente manera:

-0.001199(Z-8.3206)

Gp,, - (316)

Gp,, = ( 3 1 / )

^2 1

(Z - 0.9411)(Z - 0.6065)

-0.0! .957(7-2.0652) (Z-0.9636)(Z-0.5134)

= 0.002847(2-8.8951)

^2 2

( Z - 0 . 9 0 9 1 ) ( Z - 0.2635)

-0.0033305(2-8.3206)

1

(Z - 0.9668)(Z - 0.2635)

-00084732(2-8.895!) 2

¿ / ^7 c\r\r\ i\ / 'r_{7 r\ s\ s~ ~* t-\ ^ '}

CAPITULO TV IDENTIFICACIÓN DEL PROCESO

4.1 Introducción

En la mayoría de los procesos la dinámica de su comportamiento es representada por un modelo de primer orden con tiempo muerto, esto con fines prácticos, por lo cual en este trabajo el proceso de nivel-temperatura será representado por procesos de primer orden con tiempo muerto cuya estructura es la siguiente:

Gp = Kpe

­es

r s + 1 (4.1)

4.2 Estrategia de Identificación

El proceso a controlar se muestra en la figura 4.1. Este cuenta con dos variables a controlar que son nivel y temperatura en la descarga.

Las variables de manipulación son el porcentaje de abertura de la válvula de flujo de agua fría y de agua caliente. Por lo tanto para la realización de la prueba de identificación se pondrá a oscilar en un rango de mas menos 5% de abertura a la válvula de agua fría mientras que la otra se mantendrá fija, de esta manera se registrarán los valores de nivel y temperatura para la obtención de los parámetros de los modelos de primer orden con tiempo muerto que están relacionados con las manipulaciones de la válvula oscilante; después la válvula de agua caliente se pone a oscilar en el mismo rango de abertura mientras que la de agua fría se deja fija para obtener los parámetros de los modelos relacionados con la válvula de flujo de agua caliente.

Figura 4.1. Proceso multivariable acoplado

F _{2205 + 1 3805 + 1}

i n sP -5 s

1 43e"3 4 1 s

G p i 2

= B

5

_f_

(4.4) Gp2 2 = - ^ — (4.5)

F _{1075 + 1 495 + 1}

Donde:

Gpn es el la dinámica del nivel al manipular la válvula de agua fría.

G p 2 i es el la dinámica de la temperatura al manipular la válvula de agua fría. G p i 2 es el la dinámica del nivel al manipular la válvula de agua caliente.

Gp22 es el la dinámica de la temperatura al manipular la válvula de agua caliente.

4.3 Arreglo actuador­proceso

Ahora el siguiente paso es definir con que válvula se controlará el nivel y la temperatura. Por lo tanto se tiene que realizar un análisis de ganancias relativas, en donde se asegura si el sistema está acoplado o no, además de conocer que manipulación debe controlar a la temperatura para que el nivel no cambie.

Del análisis de ganancias relativas del apéndice B5, se obtuvieron los siguientes resultados:

0.2198 0.7801 0.7801 0.2198

Donde se puede ver que el proceso está acoplado, debido a X, es menor que 0.8 (cuando

X=l no hay acoplamiento). Por lo tanto como Xn y X21 son las más cercanas a uno, la temperatura deberá controlarse con la válvula de agua fría, y el nivel con la del agua caliente, redefiniéndose las funciones de transferencia de la siguiente manera:

10 5 e"5s

1 43e'3 4 1 s

G p u = • 6

(4.6) Gp2>= — (4.7)

1075 + 1 495+1

5.503c-6 3 2 8

, .Q. _ -2.66e" 2 3 3 5 s

, . m

Gpi2

= (4.8)

Gp22

= (4.9)

2205 + 1 3805 + 1

De las expresiones 4.6 a la 4.9 se pueden obtener sus equivalentes en Z usando la aproximación de Pade y T= 1 seg, cuyas ecuaciones son las siguientes:

-0.063281(z-1.50885) / A „ _ -0.0165396(z-1.68722)

Gpn = ^ ¿—(4.6) Gp2i = ^ — ( 4 . 7 )

(z-0.99069)(z-0.67032) (z -0.97979)(z-0.60653)

CAPITULO V IMPLEMENTACION DESACOPLADORES COMPLETOS

5.1 Introducción

Para la implementación primero se deben realizar los diseños de desacopladores y

controladores a nivel simulación para su posterior implementación en el proceso real.

En este capítulo se describen los cálculos y la estrategia de desacoplamiento para el diseño de un control con desacopladores completos, para el proceso mencionado en el capítulo uno.

5.2 Estrategia de Control

Para realizar control utilizando desacopladores completos, se seguirá la estrategia mostrada en la figura 5.1, donde el acoplamiento del proceso es muy fuerte por lo que se diseña un desacoplador de proceso [1]. Una vez desacoplado se utilizarán para cada lazo dos controladores PID clásicos con constante de filtro cada uno.

Figura 5.1. Lazo de un proceso 2X2 usando desacopladores completos

En donde se propone una función de transferencia deseada para cada lazo, en este trabajo la función deseada es igual a las plantas Gi i y G2 2 como se mencionó en el capítulo dos.

5.3 Diseńo de los Desacopladores Continuos

De acuerdo a la ecuación 2.18 los desacopladores de proceso en el dominio de Laplace son los siguientes:

_ 0.2217(5 + 0.0045454)0 + 0.02040816)0 + 0,3333)0 + 0.5)

(s + 0.0040833)(5 + 0.01 5)(s + 0.17428)0 + 0.41156)

_ -0.0470942(s + 0.0093457)(s + 0.020408 l)(s + 0.4)(s + 0.5) (s + 0.0040833)(s + 0.015)(s + 0.17428)(s + 0.41156)

_ 5.3148(s + 0.0026315)(s + 0.0045454)(s + 0.086956)(s + 0.3333) 3

(s + 0.0040833)(s + 0.015)(s + 0.17428)(s + 0.41156)

_ 0.2217(5 + 0.0045454)p + 0.02040816)p + 0.3333)p + 0.5)

(5 + 0.0040833)(5 + 0.015)(5 + 0.17428)(5 + 0.41156)

Una vez calculados los desacopladores se cuenta con un sistema desacoplado en lazo abierto como lo muestra la figura 5.2, donde para comprobar que funcionan se obtienen las respuestas de Cl(s) y C2(s) (salidas del proceso) ante una entrada escalón, primero con Ul(s) igual a uno y U2(s) cero cuyo comportamiento se ve en la figura 5.3; después con U2(s) igual a uno y Ul(s) cero figura 5.4. Donde se puede ver que el proceso ya está desacoplado, porque la señal de entrada que es cero tiene una salida con el mismo valor.

Figura 5.2. Proceso 2X2 desacoplado en lazo abierto

Donde: Cl es el nivel del tanque. C2 es la temperatura del agua.

Figura 5.4 Respuesta ante un escalón unitario en la entrada dos en lazo abierto

5.3.1 Sintonización de los Controladores PID

En la mayoría de los casos cuando se tienen desacopladores de proceso se utiliza un controlador para cada variable de control, como en este caso son dos las variables de interés (nivel y temperatura) serán dos controladores. Por lo tanto para fines prácticos se escogió la estructura del PID clásico con filtro:

Gc{s) - K c ( T ¡ s ) ( T a s + l ) (5.5)

Donde:

T a es la constante del filtro

Las funciones de los controladores a simular son las siguientes:

Gc<s) =

0.090986 (

' + + Q

( 5 6 )

(1075X2.3883*+1)

Gciís) =

­0.3536^

' (380í)(l0.84365+1)

(5.7)

Ya sintonizados los controladores se puede cerrar el lazo como en la figura 5.1 y realizar pruebas de control.

Estas pruebas de control consisten en una estrategia de simulación parecida a la realizada en lazo abierto, solo que aquí las entradas (Ul(s) y U2(s)) serán sustituidas por las referencias Rl(s) y R2(s), y sus respuestas se encuentran en las figuras 5.5 y 5.6.

DESACOPLADORES CONTINUOS EN LAZO CEBRADO

Figura 5.5 Respuesta ante un escalón unitario para la referencia uno

DESACOPLADORES CONTINUOS EN LAZO CERRADO

5.4 Diseńo de los Desacopladores Discretos

Como se mencionó con anterioridad en el ejemplo del capítulo dos, para implementar físicamente una estrategia de control es necesario tener las funciones de transferencia en modo discreto por los sistemas digitales que existen para llevar a cabo el control. Por lo tanto una vez que se comprobó que el lazo esta desacoplado y se puede controlar, el siguiente paso es transformar al dominio de Z todas las funciones de transferencia involucradas utilizando la técnica del retenedor de orden cero (ZOH) y T= 1 seg.

Usando la aproximación de Pade de primer orden las funciones de los desacopladores y

controladores en el dominio de Z son:

= -0.86605(z - 0.60653)(z - 0.97979)(z -1.09097)

(z - 0.66268)(z - 0.84016)(z - 0.98511)

D 0- 2645 l(z - 0.67032)(z - 0.99069)(z -1.40461)

(z - 0.66268)(z - 0.84016)(z - 0.98511)

-2.2382(z-0.91671)(z-0.99737)(z-1.68722)

Di\ = (5.10)

(z - 0.66268)(z - 0.84016)(z - 0.98511) _-0.95733(z-0.71653)(z-0.99546)(z-1.50885)

Ul2 (5.11)

(z - 0.66268)(z - 0.84016)(z - 0.98511) _ 0.0952413(z2 _{-1.6639z + 0.66696)}

G a ( z ) = ^ - (5.12)

V _{' ( z - l ) ( z - 0 . 6 5 7 8 9 )} V _'

_ . . -0.375004(z2_{-1.9143z +0.91452)}

t F

Gc2(z) = ^ - (5.13)

( z - l ) ( z - 0.91190) V _'

Con estas funciones se vuelven a realizar las pruebas en cerrado como se hicieron anteriormente en el dominio de Laplace, cuyas respuestas aparecen en la figura 5.7.

, , DESAOOPLADORES COMPLETOS EN LAZO CERRADO

En la figura 5.7 se encuentran empalmadas las dos pruebas, cuando Cl vale uno y C2

vale cero, y viceversa.

5.5 Ecuación Discreta a Implementar

Se observa que en lazo cerrado la respuesta ya esta desacoplada y controlada por los PLD's, el siguiente paso es entonces calcular las ecuaciones de diferencias que serán programadas para su implementación en el proceso real.

La manipulación que se programó resulta de la siguiente ecuación:

M = DGc (5.14)

Donde de manera individual queda como sigue:

M i = D l l G c l E l + Dl2Gc2E2 (5.15) M2 = D 2 l G c l E l + D22Gc2E2 (5.16)

De las ecuaciones 5.8 al 5.11, y usando las expresiones 5.15 y 5.16 las manipulaciones discretas (Apéndice B l ) que fueron implementadas en un programa computacional (Apéndice B2) quedaron de la siguiente manera:

M l n = 5.0577Mln­l ­ 10.6004Mln­2 + 11.7817Mln­3 ­ 7.3222Mln­4

+ 2.4112Mln­5 ­ 0.328Mln­6 ­ 0.08248Eln + 0.43329Eln­l ­ 0.94075Eln­2 + 1.07996Eln­3 ­ 0.69093Eln­4 + 0.23344Eln­5 ­ 0.03253Eln­6

­ 0.09919E2n + 0.55922E2n­l ­ 1.29509E2n­2 + 1.57795E2n­3 ­ 1.06723E2n­4 + 0.38E2n­5 ­ 0.05566E2n­6

M2n = 5.0577M2n-l - 10.6004M2n­2 + 11.7817M2n­3 - 7.3222M2n­4

+ 2.4112M2n­5 - 0.328M2n­6 - 0.21316Eln + 1.31677Eln-l - 3.32636Eln­2

+ 4.41061Eln­3 - 3.24337Eln­4 + 1.25552Eln­5 - 0.20001Eln­6

+ 0.359E2n - 2.07971E2n-l + 4.93805E2n­2 - 6.16E2n­3 + 4.26213E2n­4

- 1.55193E2n­5 + 0.23246E2n­6

Con estas expresiones discretas se probó el proceso real mediante el programa antes mencionado, estabilizando al proceso en 16.58cm y 48.8°C.

El proceso se mantuvo estable por unos segundos, pero al incrementarse el nivel la válvula de agua fría se abrió para mantener estable la temperatura, aumentando con esto el nivel y saturando las manipulaciones con el fin de corregir el error, mas sin embargo este nunca se corrigió llegando el nivel al máximo de 40cm con una temperatura de 54°C.

Los resultados se muestran en el Apéndice B3.

CAPITULO VI IMPLEMENTACION CONTROL DESACOPLANTE

6.1 Introducción

Como en el capítulo anterior primero se deben realizar los diseños de los controladores a nivel simulación para su posterior implementación en el proceso real.

En este capítulo se describen los cálculos y la estrategia de desacoplamiento y control por medio de control desacoplante, para el proceso mencionado en el capítulo uno.

6.2 Estrategia de Control

Para realizar un control desacoplante, se seguirá la estrategia mostrada en la figura 6.1, para el control de nivel y temperatura. Donde se diseñan controladeres capaces de desacoplar cualquier señal perturbante que llegase a afectar el valor de las variables de control (Cl(s) o C2(s)).

II

Figura 6.1. Lazo de un proceso 2X2 usando control desacoplante

En donde se propone una función de transferencia deseada para cada lazo, en este trabajo la función deseada es igual a las plantas Gi i y G2 2 pero con ganancias unitarias.

6.3 Diseńo de los Controladores Continuos

De acuerdo a la ecuación 3.9' y usando la aproximación de Pade en las plantas, los controladores en el dominio de Laplace son los siguientes:

0.02115(s + 0.004545)(s + 0.009345)(s+0.0204)(s + 0.3333)(s + 0.4)(s + 0.5)

Gen = (6.1)

s(s+0.00408Xs + 0.015)(s + 0.17428Xs + 0.4115)(s + 0.4186)

0.0177(s + 0.00263)(s + 0.009345)(s + 0.0204)(s + 0.0869)(s + 0.4)(s + 0.5)

GC21: 0.5061(s + 0.00263)(s+0.004545)(s + 0.009345)(s + 0.0869)(s + 0.3333)(s+0.4)

s(s + 0.00408Xs + 0.015)(s + 0.1742)(s + 0.4115)(s + 0.4186) (6.3) -0.0833(s+0.00263j(s + 0.00454^(s+0.020408Xs+0.0869)(s+0.3333)(s+0.5)

s(s + 0.00408Xs+0.015)(s+0.0922 í)(s+0.1742)(s+0.4115)

Una vez calculados los controladores se cuenta con un sistema desacoplado en lazo cerrado como lo muestra la figura 6.1, donde para comprobar que funcionan se obtienen las respuestas de Cl(s) y C2(s) (salidas del proceso) ante una entrada escalón, primero con Ul(s) igual a uno y U2(s) cero cuyo comportamiento se ve en la figura 6.2; después con

U2(s) igual a uno y Ul(s) cero figura 6.3. Donde se puede ver que el proceso ya controla y desacopla, porque la señal de entrada que es cero tiene una salida con el mismo valor.

1.81 CONTROL BKSftCOPLAHTE CONTINUO

Figura 6.2 Respuesta ante un escalón unitario para la referencia uno

Donde: Cl es el nivel del tanque. C2 es la temperatura del agua.

CONTROL DESACOPLANTE CONTINUO

­ . l l . . ; ... i , i B 1000 2B0O 3000 4000

Time

Figura 6.3 Respuesta ante un escalón unitario para la referencia dos

6.4 Diseńo de los Controladores Discretos

Al igual que en el capítulo anterior y por razones ya explicadas en él, el siguiente paso es discretizar el lazo. Por lo tanto una vez que se comprobó que el lazo esta desacoplado y se puede controlar, todas las funciones de transferencia involucradas se transforman al dominio de Z utilizando la técnica del retenedor de orden cero (ZOH), eliminando los polos inestables y partiendo de la ecuación 3.9'(según la solución del capítulo 3).

Las funciones de los controladores en el dominio de Z son:

_ -0.002706(z - 0.6065)(z - 0.6703)Q - 0.7165)(z - 0.9797)(z -1.0909)

0 0 , 1

~ (z - l)(z - 0.6549)(z - 0.6626)(z-0.840 l)(z-0.9851) ( 6 5 )

_ -6.64le - 4(z - 0.6065)(z - 0.6703)(z - 0.9167)(z - 0.9906)(z - 1.404)

G C

1 2 ~ ( z - l)(z-0.6626)(z-0.8401)(z-0.9116)(z-0.9851) ( 6 6 )

-6.995e - 3(z - 0.6703)(z - 0.7165)(z - 0.9167)(z - 0.9973)(z -1.687)

Ge = (6.7)

2 1

(z - l)(z - 0.6549)(z - 0.6626)(z - 0.8401)(z - 0.9851)

2.403e - 3(z - 0.6065)(z - 0.7165)(z - 0.9167)(z - 0.9954)(z - 1.5088)

Ge = (6.8)

22 (z - l)(z-0.6626)(z-0.840 l ) ( z - 0.9116)(z- 0.9851)

4~

- . 5 | : : ; J , ; , | . i

e íeaa 2aea aaaa 4aea saaa

n j T i m e = n * T

Figura 6.4 Respuesta ante un escalón unitario para la referencia uno

CONTROL DESACOPLANTE DISCRETO ENTRADA R2

1000 2000 3808 4000 5000

ri, Time=n*T

Figura 6.5 Respuesta ante un escalón unitario para la referencia dos

6.5 Ecuación Discreta a Implementar

Se puede ver que en Z las respuestas del lazo ya están desacopladas y controladas, por lo tanto solo falta calcular las manipulaciones, estas ecuaciones discretas resultan de la siguiente ecuación:

M i = G c l l E l + Gcl2E2 (6.9)

M2 = GC21E1 + GC22E2 (6.10)

De las ecuaciones 6.5 a la 6.8 y las expresiones 6.9 y 6.10 las manipulaciones que se deben de programar son las siguientes:

Mln = 5.0546Mln-l - 10.5867Mln­2 + 11.7579Mln-3 - 7.3015Mln­4

+ 2.4032Mln­5 - 0.3275Mln­6 - 0.0027Eln + 0.01346Eln-l - 0.02767Eln­2

+ 0.03004Eln­3 - 0.018185Eln­4 + 0.005817Eln­5 - 0.000762Eln­6

- 0.000664E2n + 0.003482E2n-l - 0.007457E2n­2 + 0.008361E2n­3

- 0.005183E2n­4 + 0.001687E2n­5 - 0.000226E2n­6

M2n = 5.0546M2n-l - 10.5867M2n­2 + 11.7579M2n­3 - 7.3015M2n­4

+ 2.4032M2n­5 - 0.3275M2n­6 - 0.00699Eln + 0.04127Eln-l - 0.09909Eln­2

+ 0.12443Eln­3 - 0.08640Eln­4 + 0.03151Eln­5 - 0.00473Eln­6

+ 0.00240E2n- 0.01297E2n-l + 0.02852E2n­2 - 0.03275E2n­3

+ 0.02076E2n­4 - 0.006905E2n­5 + 0.000945E2n­6

Con estas expresiones discretas se probó el proceso real mediante el programa computacional mencionado en el capítulo pasado.

El proceso se estabilizó en 21cm de nivel y 48.4°C de temperatura, así se mantuvo hasta que se cambió la referencia de nivel a 25 cm, entonces la válvula de agua caliente que es la que gobierna el nivel (ver Apéndice B4) empezó a abrirse para corregir el error, mientras que la válvula de agua fría empezó a cerrarse, cuando el nivel llegó a su nueva referencia, la válvula no se cerró provocando que la temperatura creciera y el nivel se desbordara.

Los resultados fueron los siguientes representados en Apéndice B4.

CONCLUSIONES

Como se puede ver en las gráficas del proceso real (pruebas en la estación de nivel-temperatura) de los capítulos 5 y 6, las variables de control (nivel y temperatura) se salen de sus referencias ocasionando que las manipulaciones se saturen y entren en un ciclo sin fin.

En el caso de los desacopladores completos sin haber hecho algún cambio, el nivel se salió de referencia tratando el controlador de nivel de realizar la corrección, pero al hacer esta corrección la temperatura también cambió, y la interacción de las dos válvulas de control ocasionó que el nivel y temperatura se descontrolaran.

Algo similar a la descrito en el párrafo anterior sucedió con el control desacoplante, solo que este sí se mantuvo en su referencia de estado estable por un tiempo, haciéndose después un cambio en el set-point de 21 a 25cm. Cuando se abrió la válvula de control correspondiente al nivel, este se fué corrigiendo poco a poco, pero al llegar al valor deseado la válvula no cerró a tiempo ocasionando que la temperatura aumentara y el controlador tratara de corregir el error saturando las dos válvulas del proceso.

Se puede concluir entonces que el proceso de nivel y temperatura del laboratorio de control posee un alto nivel de no linealidad en su dinámica, porque la temperatura y flujos de alimentación nunca son constantes y la capacidad de desagüe del tanque es mucho menor que la capacidad de llenado, además las válvulas instaladas no son iguales ni en tamaño, ni en características, ocasionando histéresis que afectan directamente a la no linealidad del proceso. Por lo tanto el tratar de implementar un control desacoplante lineal en un proceso como este no es recomendable por carecer de robustez.

RECOMENDACIONES

De acuerdo a las conclusiones, se recomienda en este escrito lo siguiente: 1.- Hacer modificaciones físicas al proceso por ejemplo:

a) Instalar nuevas válvulas que sean iguales o similares en tamaño y características. b) Sustituir el boiler de gas como medio de calentamiento del agua, por una resistencia eléctrica para de esta manera tener la temperatura de entrada lo más constante posible.

c) Instalar manómetros antes de las válvulas de control para estar seguros de que la presión del agua es la misma con la que se identificó el proceso.

d) Hacer el desagüe del tanque más ancho, para que el flujo de salida sea lo más cercano posible al de entrada, y de esta manera facilitarle al controlador el llenar o vaciar el tanque.

2.- Si con las modificaciones realizadas en el punto uno el proceso se vuelve lineal, entonces sí se puede implantar un control desacoplante como en el que este escrito se realizó, si no hacer lo que dice el punto tres.

APÉNDICE A l

- PRUEBAS ESCALÓN AL PROCESO REAL MULTIVARIABLE ACOPLADO

TJ £ 3

n>

CD

3

CD —<

s.

0

APÉNDICE B l

- ECUACIONES DE LAS MANIPULACIONES DISCRETAS

5:

1?

I O

Sν 3

1?

i

p

§ *

^Ώ ^ I

P

'i

oo o

3 I

"?r °

0 v o VO ' t T

1 O í o VO

0 0 "

3 I

? §

m

o

P

o

oo

o

P

3

3

1?

0 ^

'SÍ

3

I

1 P

0 ^

S s

y ' N

P §

0 0 w

I

3 o

1 _{v o}

p

n

N 'Os

oí I X O

N o \

APÉNDICE B2

- LISTADO DEL PROGRAMA QUE LMPLEMENTA CONTROL AL PROCESO REAL

- Este programa implementa físicamente las manipulaciones que salieron de los cálculos de los desacopladores completos (capítulo 5) y control desacoplante (capítulo 6), así como las manipulaciones de dos PID's sin estar desacoplados.

PROGRAM CTRL2X2;

uses crt,dos,graph,util4b; var

OPCIÓN:INTEGER;

REFO, REF1,histO , voltminO , ot,MANSS,MANO ,MANÍ,R,T,NIV,TEM,TEMP, AB, AB1:REAL; bandhistO, bandhistl, voltmaxO, voltminl, voltmaxl, histl, mancamO, mancaml: REAL ;

PROCEDURE PORTADA; BEGIN CLRSCR; TEXTBACKGROUND(WHITE) WINDOW(1,1,80,25); CLRSCR; TEXTBACKGROUND(BLUE); TEXTCOLOR(LIGHTGRAY); GOTOXY(20,3); GOTOXY(20,4); GOTOXY(20,5); GOTOXY(18,10) GOTOXY(18,11) GOTOXY(18,12) GOTOXY(17,16) GOTOXY(17,17) GOTOXY(17,18) GOTOXY(17,19) WRITE('éééééééééééeééééééeéééééééééééééééééééE');

WRITE('n CONTROL DIGITAL DESACOPLANTE a ' ) ;

WRITE('áéééééééeéééééééééééeéeééééééééééééééé¥');

WRITE (' éeééééééééééééééééééééééééééééééééééééééééé(¿£ ') ;

WRITE('0 CONTROL DE NIVEL Y TEMPERATURA a ' ) ;

WRITE('áééééééeééééééééééééééééééééééééééééééééééée¥'); WRITE('éeééeéééééééeeééééééééeeééeééeééeéééééeéeeeéeééeE')

WRITE('n Autor: Gerardo J. Olvera MartÁnez # 15567 0 n ' )

WRITE('a D ' )

WRITE('áééééééeéééééééééééééééeéeéééééééééeéééééééééééé¥/ ) TEXTBACKGROUND(LIGHTGRAY); TEXTCOLOR(RED); GOTOXY(59,23) GOTOXY(59,24) GOTOXY(59,25) TEXTCOLOR(22) GOTOXY(60,24) WRITE('Presione Enter') READLN; END; WRITE('éééééééééééééeéeeE') WRITE('n a') WRITE('áéééééeéééééééééé¥') .Procedure Menú; begin TEXTCOLOR(WHITE); CLRSCR; TEXTBACKGROUND(WHITE)

WINDOW(lf1,80,25);

CLRSCR; TEXTBACKGROUND(BLUE); TEXTCOLOR(LIGHTGRAY) GOTOXY(13,4) GOTOXY(13,5) GOTOXY(13,6) GOTOXY(13,7) GOTOXY(13,8) GOTOXY(13,9) GOTOXY(13,10) GOTOXY(13,11) GOTOXY(13,12) GOTOXY(13,13)

G O T O X Y( 1 3, 1 4 )

GOTOXY(13,15) WRITE( WRITE( WRITE( WRITE( WRITE( WRITE( WRITE( WRITE( WRITE( WRITE(

W R I T E (

WRITE( ééééééeéééééééééeééeéééééééééééeéeééééeeéééééeéeéééééeE'

1)

M e n E

Manual

Procedure DefineVoltDAO(VoltminimoO,VoltmaximoO,HisteresisO:real); begin

VoltminO:=VoltMinimoO; VoltmaxO: =VoltmaximoO ; HistO :=HisteresisO; end;

procedure EscribirDAO(var man:real; canalDA:integer); var

vlr : integer; dif,manchist : real; begin

if man>100 then man:=100; if man<0 then man:=0; manchist:=man;

if h i s t o o o then begin

dif:=man-mancamO;

if abs(dif)>(0.09) then begin

mancamO:=man;

if (bandhistO*dif)<0 then bandhistO:=-bandhistO; end;

manchist:=man*(1-histO/100);

if bandhist0=l then manchist:=manchist+hist0; end; volt:=voltmin0+manchist/100*(voltmaxO-voltminO); vlr:=round(volt/10*4095); port[dirbase+drgecan+hbyte]:=canalDA; port[dirbase+drgane]:=lo(vlr); port[dirbase+drgane+hbyte]:=hi(vlr); snd; Procedure DefineVoltDAl(Voltminimol,Voltmaximol,Histeresisl:real); begin Voltminl:=VoltMinimol; Voltmaxl:=Voltmaximol; Histl :=Histeresisl; end;

procedure EscribirDAl(var man:real; canalDA:integer); var

vlr : integer; dif,manchist : real; begin

if man>100 then man:=100; if man<0 then man:=0; manchist:=man;

if h i s t l o o then begin

dif:=man-mancaml;

if abs(dif)>(0.09) then begin

mancaml:=man;

if (bandhistl*dif)<0 then bandhistl:=-bandhistl; end;

manchist:=man*(1-histl/100);

volt:=voltminl+manchist/100* (voltmaxl-voltminl) ; vlr:=round(volt/10*4095) ; port[dirbase+drgecan+hbyte]:=canalDA; port[dirbase+drgane]:=lo(vlr) ; port[dirbase+drgane+hbyte]:=hi(vlr) ; end; FUNCTION LEERNIVEL:REAL; VAR SUMA:REAL; I:INTEGER; BEGIN SUMA:=0;

FOR I:=l TO 50 DO SUMA:=SUMA+LEERAD(1); LEERNIVEL:=-7+4.7244*(SUMA/50); END; FUNCTION LEERTEMP:REAL; VAR SUMA1:REAL; II:INTEGER; BEGIN SUMA1:=0;

FOR Il:=l TO 5 DO

SUMA1:=SUMA1+LEERAD(2); LEERTEMP:=(SUMAl/5)*11.0553; END; PROCEDURE ENVIARMAN; BEGIN AB:=0.6*MAN0; AB1:=MAN1; ESCRIBIRDAO(AB,0); ESCRIBIRDA1(AB1,1); END; Procedure Pantgraf; begin GD:=9; GM:=1; INITGRAPH(GD,GM,'');

MARCOGRAFICO(3,0,TRUNC(GETMAXX* 0.5),0,TRUNC(GETMAXY* 0.5),0,100,0,40, 'NIVEL DEL TANQUE','TIEMPO','SEG','NIVEL','CM',true);

MARCOGRAFICO(4,0,TRUNC(GETMAXX*0.5)+2,TRUNC(GETMAXY*0.5)+2,GETMAXY,0,100,0 'MANIPULACIONES','TIEMPO','SEG','Avertura','%',true);

MARCOGRAFICO(5,TRUNC(GETMAXX*0.5)+2,GETMAXX,0,TRUNC(GETMAXY*0.5),0,100,0,1

'TEMPERATURA DEL TANQUE' , 'TIEMPO', 'SEG' , 'Temperatura' , ' C ,true) ; {A VECES TIENE QUE DEJARSE FIJO, POR LA MEMORIA}

end;

•PROCEDURE LETRAS; BEGIN

outtextxy(325,200,'<== Rojo válvula de agua caliente'); outtextxy(325,210,'<== Mangenta válvula de agua fria'); outtextxy(450,3 30,'Esc para cancelar');

BEGIN

GRAFICA(TIEMPO,NIV,3,5,'C'); GRÁFICA(TIEMPO,TEM,5,4,'D'); GRÁFICA(TIEMPO,REFO,3,7,'C); GRÁFICA(TIEMPO,REF1,5,7,'D'); GRÁFICA(TIEMPO,MANO,4,5,'D') ; GRÁFICA(TIEMPO,MANÍ,4,4,'D'); END;

(

*

PROCEDURE GRAFICAR; BEGIN

GRÁFICA(TIEMPO,NIV,1,5,'C); GRÁFICA(TIEMPO,TEM,2,4,'D'); esgrafxy(550,170,TIEMPO,6); END;

Procedure PortManual; begin

outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy outtextxy end; (445,240 (445,245 (445,250 (445,255 (445,260 (445,265 (445,270 (445,275 (445,280 (445,285 (445,290 (445,295 (525,215 (525,255 (535,255 (525,290 (445,215 (580,215 (455,255 (525,215 (575,245 (455,275 (525,275 (575,275 (490,130 (490,310 (490,140 (490,320 (470,170 ' 0 'o ' 0 'o 'a ,₀ 'a 'o 'o 'o

0 o 0 ' )

0 0 B ' j 0 0 0 ' )

0 0 F 0 ' )

0 0 0 ' )

'aééééééóééééééeóéééééé¿')

o 0 o')

o n n') o o o')

X 0 o V o')

o o o') 'áééééééóééeééééóééeééé¥')

'E') ; chr(27) chr(26)

C ) ; 0 %' 100 %' + 10 %' + 1 %' +0.1%' -10 %' - 1 %' -0.1%' MAN:') MANÍ:' NIVEL: TEMP:'. TIEMPO:'); Procedure Pantalla(i:integer); begin GD:=9; GM:=1;

INITGRAPH(GD,GM, " ) ; case i of

1:begin

MARCOGRAFICO(1,0,TRUNC(GETMAXX*0.65),0,TRUNC(GETMAXY*0.5),0,100,0,40, 'NIVEL DEL TANQUE','TIEMPO','SEG','NIVEL','CM',true);

MARCOGRAFICO(2,0,TRUNC(GETMAXX*0.65),TRUNC(GETMAXY*0.5)+2,GETMAXY,0,100,0, 'TEMPERATURA DEL TANQUE','TIEMPO','SEG','Temperatura','C,true);

end; 2:begin

MARCOGRAFICO(3,0,TRUNC(GETMAXX*0.5) ,0,TRUNC(GETMAXY*0.5) ,0,100,0,40, 'NIVEL DEL TANQUE','TIEMPO','SEG','NIVEL','CM',true);

MARCOGRAFICO(4,0,TRUNC(GETMAXX*0.5)+2,TRUNC(GETMAXY*0.5)+2,GETMAXY,0,100,0 'MANIPULACIONES','TIEMPO','SEG','Avertura','%',true);

MARCOGRAFICO(5,TRUNC(GETMAXX* 0.5)+2,GETMAXX,0,TRUNC(GETMAXY* 0.5),0,100,0,1 'TEMPERATURA DEL TANQUE','TIEMPO','SEG','Temperatura','C,true);

end; end;

* {A VECES TIENE QUE DEJARSE FIJO, POR LA MEMORIA} end;

PROCEDURE LCP; var

ch