Simulación del sensor tubo recto para la medición de flujo másico por Efecto Coriolis

Texto completo

(1)UNIVERSIDAD NACIONAL DE SAN AGUSTÍN ESCUELA DE POSGRADO UNIDAD DE POSGRADO DE LA FACULTAD DE INGENIERÍA DE PRODUCCION Y SERVICIOS. SIMULACIÓN DEL SENSOR TUBO RECTO PARA LA MEDICIÓN DE FLUJO MÁSICO POR EFECTO CORIOLIS. TESIS PRESENTADO POR BACHILLER CARMELO MAYTA OJEDA PARA OPTAR AL GRADO DE MAGISTER EN CIENCIAS INGENIERÍA ELECTRÓNICA CON MENCIÓN EN AUTOMATIZACIÓN E INSTRUMENTACIÓN. ASESOR: Dr. GERMÁN ALBERTO ECHAIZ ESPINOZA. Arequipa, 2018.

(2) Jurados dictaminadores. ___________________________. Dr. RAUL SULLA TORRES Presidente. ___________________________. Mg. RUBEN MATHEOS HERRERA Secretario. ___________________________. Dr. GERMAN ECHAIZ ESPINOZA Asesor. I.

(3) Dedicatoria. Al Dr. Germán Alberto Echaiz Espinoza Por su contribución al logro de la presente Investigación.. II.

(4) Resumen. El análisis del fundamento teórico del sensor de Coriolis del tipo tubo recto, para la medición del flujo de masa por efecto Coriolis es muy importante, porque permite hacer simulaciones por la computadora para que se pueda determinar los parámetros de diseño del sensor como son: la frecuencia angular de resonancia según las características del material de trabajo, el ángulo de desfase que se origina por el efecto Coriolis, el flujo de masa que se puede medir. Se. ha sistematizado el trabajo (previo análisis teórico) para el. material acero inoxidable para una longitud de 0,75 m , ½” x3/4” de diámetro interno y externo respectivamente a través del cual el flujo del agua fluye a velocidad de 5,0 m/s, para el cual se ha determinado una frecuencia angular de resonancia de 723,6 rad/s y con los datos obtenidos se calcula el flujo de masa que se transporta, los datos obtenidos para velocidad 0,5 m/s corresponde 0,036 kg/s y para velocidad hasta 25 m/s el flujo de masa es 1,783 kg/s.. III.

(5) Abstract. The analysis of the theoretical basis of the Coriolis sensor of the straight tube type, for the measurement of the mass flow by Coriolis effect is very important, because it allows to make computer simulations to determine the sensor design parameters such as: resonance angular frequency according to the characteristics of the working material, the angle of phase shift that is originated by the Coriolis effect, and the. mass flow that can be. measured. The work has been systematized (prior theoretical analysis) for the material stainless steel for a length of 0.75 m, ½"x3/4" of internal and external diameter respectively through which the flow of water flows at a speed of 5.0 m/s, for which an angular resonance frequency of 723.6 rad/s has been determined and with the data obtained the mass flow that is transported is calculated, the data obtained for speed 0.5 corresponds to 0.036 kg/s and for speed up to 25 m/s the mass flow is 1,783 kg/s.. IV. m/s.

(6) Índice general Jurados dictaminadores ........................................................................................................ I Dedicatoria ..........................................................................................................................II Resumen ............................................................................................................................ III Abstract ............................................................................................................................. IV Capitulo I: INTRODUCCIÓN ........................................................................................... 1 1.1.. Análisis situacional del problema y su relevancia ................................... 1. 1.2.. Definición del problema .................................................................................... 2. 1.3.. Justificación ............................................................................................................ 2. 1.4.. Delimitación de la frontera del trabajo ........................................................ 3. 1.5.. Objetivo general ..................................................................................................... 3. 1.6.. Objetivos específicos ........................................................................................... 3. 1.7.. Hipótesis ..................................................................................................................... 4. 1.8.. Variables ..................................................................................................................... 4. 1.9.. Aspecto teórico ....................................................................................................... 5. 1.10.. Metodología .......................................................................................................... 8. Capítlo II: FUNDAMENTACIÓN TEÓRICA .................................................................. 9 2.1.. Efecto Coriolis ......................................................................................................... 9 V.

(7) 2.2.. Método de elementos finitos ............................................................................. 16. 2.3.. Formulación de fuerzas que actúan sobre un tubo recto que vibra .. 17. 2.4.. Deducción de la función de forma ................................................................. 21. Capítulo III:. PROCESO DE SIMULACIÓN ................................................................ 29. 3.1.. Características de los materiales para simular ........................................ 29. 3.2.. Elaboración del programa script ................................................................... 31. 3.3.. Resultados del programa ejecutado ............................................................ 32. Capítulo VI: ANÁLISIS DE RESULTADOS ................................................................. 36 4.1.. Análisis de resultados del programa .......................................................... 36. 4.2. Flujo de masa aplicando la ecuación de continuidad. ................................................... 47. Conclusiones y recomendaciones ..................................................................................... 50 Bibliografía ....................................................................................................................... 52 Apéndice A .......................................................................................................................... 56 1.Cálculo de los elementos de la matriz [A] [6] y [9] .............................................................. 56 2.Cálculo de los elementos de la matriz [B] ........................................................................... 62 3. Cálculo de los elementos de la matriz [C] .......................................................................... 68 4. Cálculo de los elementos de la matriz [D] ............................................................................ 74 Apéndice B .......................................................................................................................... 80 Apéndice C ....................................................................................................................... 101. VI.

(8) Capitulo I: INTRODUCCIÓN. 1.1.. Análisis situacional del problema y su relevancia. En el contexto del mundo industrial moderno, la instrumentación es uno los pilares del avance tecnológico en el campo de la medición de magnitudes de físicas, la capacidad para desarrollar los instrumentos de medición con alto grado de precisión, que permita contar con instrumentos con la que puedan realizar las mediciones con bajos niveles de error. Así mismo adquirir los conocimientos para construir instrumentos de medición con alto grado de precisión que garantice la seguridad del proceso de medición de flujo de masa en distintas actividades humanas como: en transporte, distribución y comercialización, etc. La industria moderna exige una gama de instrumentos de medición, una de las cuales es la medición de flujo másico que ofrezca una alta precisión, en el proceso de medición por lo que es muy necesario desarrollar los fundamentos teóricos y su simulación respectiva del dicho instrumento de medición para medir el caudal de un fluido, para que la región sea competitiva en dicho campo tecnológico, que hasta el presente no se ha desarrollado.. 1.

(9) 1.2.. Definición del problema. En la medición del flujo másico, hay un principio físico que se puede aplicar, dicho principio es el Efecto Coriolis, que se efectúa sobre la circulación de un fluido en oscilación a través de una tubería que transporta el fluido a una velocidad dada. Por lo que en el presente trabajo se propone desarrollar los fundamentos teóricos que intervienen sobre la circulación del flujo circulante y hacer la simulación correspondiente, para determinar el tipo de geometría apropiada, en este caso se considera el tubo recto de sección circular, fijo en ambos extremos a través del cual circula un fluido, que puede funcionar de la mejor manera el instrumento es necesario calcular en primer lugar la frecuencia de resonancia, para la medición del caudal másico.. 1.3.. Justificación. El trabajo se justica ya que se tendría que desarrollar el fundamento teórico y su simulación correspondiente, posteriormente serviría para construir el prototipo, según las características que el proceso de simulación lo pueda determinar la frecuencia de resonancia del sensor tubo recto y el flujo en el proceso de medición, el mismo que dará el inicio del desarrollo instrumental para la medición del flujo másico, hecho que podría concretar la capacidad de los tecnólogos locales en la aplicación de los conocimientos teóricos adquiridos, en beneficio de la región o el país. En la medición del flujo de masa como de gases, líquidos como el petróleo y otros basado en el principio del Efecto Coriolis.. 2.

(10) 1.4.. Delimitación de la frontera del trabajo. El trabajo se delimita a desarrollar las básicas teóricas del sistema de medición propuesta a llevarse a cabo la simulación para la medición del flujo másico en un tubo que conduce líquido, en este caso el agua o gas, así mismo desarrollar un programa en script en GNU Octave para la simulación y calcular la frecuencia de resonancia ω para determinado tipo de geometría, en este caso es el sensor tubo recto y la posible respuesta que se obtendrá en la medición flujo másico cuando se desarrolle el prototipo del dicho instrumento.. 1.5. Objetivo general. Establecer los fundamentos teóricos para generar el Efecto Coriolis que será el principio físico del sensor de caudal másico del flujo. Determinar el tipo de geometría y el flujómetro másico basado en el principio del Efecto Coriolis, según las características de los materiales utilizados en la construcción. Determinar la frecuencia de resonancia del flujómetro másico de la geometría determinada, tubo recto de sección circular, según las características de los materiales a utilizarse.. 1.6.. Objetivos específicos. Estudiar el tubo recto de sección circular de material acero inoxidable, de longitud determinada, fijo en ambos extremos como sensor del caudal f l ui d o .. 3.

(11) Deducir las ecuaciones básicas que intervienen la aplicación del Efecto Coriolis, que gobiernan el caudalímetro del flujo másico. Determinar mediante la simulación en GNU Octave la frecuencia de resonancia del sistema tubo- fluido según las propiedades del material. Calcular el flujo másico que puede registra el tubo sensor en el sistema tubo-fluido por el efecto Coriolis.. 1.7.. Hipótesis. Mediante los mecanismos de electromagnéticos, es posible generar el Efecto Coriolis mediante la inducción de un movimiento oscilatorio externo, previamente calcular la frecuencia de resonancia ω entre el sistema, el sensor tubo recto y fluido. Dicho principio está basado en la propiedad de la elasticidad del material [1] que se utiliza como sensor en el flujo másico. Sobre el que ejerce una vibración armónica externa y en cuyo interior del sensor tubo recto, circula un fluido a una velocidad. En tales circunstancias se experimenta un fenómeno llamado Efecto Coriolis [2]. Dichos principios de vibración y circulación del fluido permiten medir el caudal del flujo másico cuando oscila en la frecuencia de resonancia correspondiente.. 1.8.. Variables. Las variables que se calculan en la simulación son la frecuencia de resonancia ω, entre el sistema sensor tubo-fluido para una velocidad ⃗⃗ del fluido que circula dentro del tubo recto, que permitirá calcular el caudal Q del flujo de masa. 4.

(12) circulante. El ángulo de desfase. que se origina por el efecto de aceleración de. Coriolis. Otros parámetros intervienen permaneciendo constantes como módulo de Young, la densidad del tubo, densidad del líquido y el radio de la sección circular.. 1.9.. Aspecto teórico. Se propone simular el diseño de un sensor tubo recto (flujómetro lineal), es decir, un tubo recto de longitud L, de sección circular y fijo en los extremos. Deducir las ecuaciones diferenciales basados en el Efecto Coriolis lo gobiernan su movimiento, debido a las fuerzas que se ejercen sobre el fluido (gas o líquido) que circula con una velocidad lineal V dentro del tubo recto. Las ecuaciones que gobiernan están basadas en la vibración de un tubo o viga de sección transversal circular f i ja en ambos extremos y que cuyas soluciones de las ecuaciones diferenciales son estandarizadas en [3], [4] y [5]. que cuya expresión. matemática tiene la forma de la ecuación que sigue a continuación. (. ). (1.1). Con las condiciones de contorno impuestas en ambos extremos, en el extremo inicial y el extremo final. (. ). (. ). (. ). (1.2). En la literatura científica la Ec.(1.1) es ampliamente conocida y se denomina método. 5.

(13) Euler-Bernoulli, [6]-[9] cuyo proceso de tratamiento matemático es estándar y muy aplicado a vibración de vigas de sección circular empotrados en ambos extremos, el mismo que se aplica en diversos campos tecnológicos. Por otro lado, se dan las condiciones de contorno en cada uno de los extremos como son las deformaciones que experimenta el tubo y las pendientes que se forman como consecuencia del movimiento, por consiguiente, se forman un conjunto de cuatro grados de libertad (dos grados de libertad por ambos extremos) para un tubo-fluido que vibra. Cada uno de los factores que intervienen en la Ec.(1.1) se identifican como se indican. a. continuación: (. ): elongación instantáneo de oscilación en la dirección transversal a la. circulación del fluido con relación al eje de simetría horizontal. : definida como el coeficiente de rigidez a la flexión del tubo. Proviene del producto de módulo de Young y el segundo momento de área. V: velocidad lineal del fluido dentro del tubo. : masa por unidad de longitud del fluido.. : masa por unidad de longitud del. tubo. La ecuación Ec.(1.1) es en el estado de régimen estacionario, cada uno de los términos están expresados a nivel de ecuaciones diferenciales se denominan [10]-[12]: : fuerza elástica almacenada por la rigidez flexional del tubo recto. : fuerza centrípeta que se origina debido al movimiento del fluido. : fuerza de Coriolis o efecto Coriolis que se evidencia sobre el fluido. (. ). : fuerza inercial de masa del fluido y la masa de la. sección del tubo oscilante.. 6.

(14) Se plantea su solución de la Ec.(1.1), por el método de elementos finitos [6]-[7], discretizando en nodos o nudos y en elementos y luego se ensamblan o se globalizan, para lo cual asume una solución de la forma:. (. ). (. ). (1.3). Que a partir del desarrollo de la función de forma correspondiente se obtiene una función globalizada de tal manera que la Ec.(1.1) se pueda reescribir de la forma:. [. ]. [. ]. [. ]. (1.4). donde las matrices [Mg], [Eg] y [Kg] son globalizadas y cuadradas que describen el problema en función de la variable x. La fuerza externa de régimen permanente o estacionaria que mantiene la oscilación armónica de tipo senoidal. (. ). (1.5). En donde lo que interesa es la frecuencia de resonancia ω, el cual se determina mediante la simulación en GNU Octave en este caso el sensor tubo recto de longitud L, cuyo tratamiento matemático se dan en [8]-[13].. 7.

(15) 1.10.. Metodología. Para fundamentar el funcionamiento del sensor del medidor de Coriolis se consideran los siguientes aspectos metodológicos como se detalla a continuación: se considera la deducción el principio del efecto Coriolis, como una fuerza ficticia que se origina sobre sistemas en movimiento, para luego aplicar a la vibración de un tubo recto de sección circular empotrado en ambos extremos. Se hace una exploración bibliográfica de ecuaciones diferenciales y sistemas de ecuaciones diferenciales ordinarias y su solución con condiciones de contorno impuestas en los extremos. Se calculan cada uno de los elementos de las matrices y a partir de ellos, mediante el Método de Elementos Finitos se calcula fundamentalmente la frecuencia de resonancia |ω| tubo y fluido del flujómetro. La simulación del comportamiento del sistema del sensor tubo recto y fluido se realiza mediante el GNU Octave el que permite calcular el flujo de masa que puede medir el sistema, según sus propiedades del material de que está hecho.. 8.

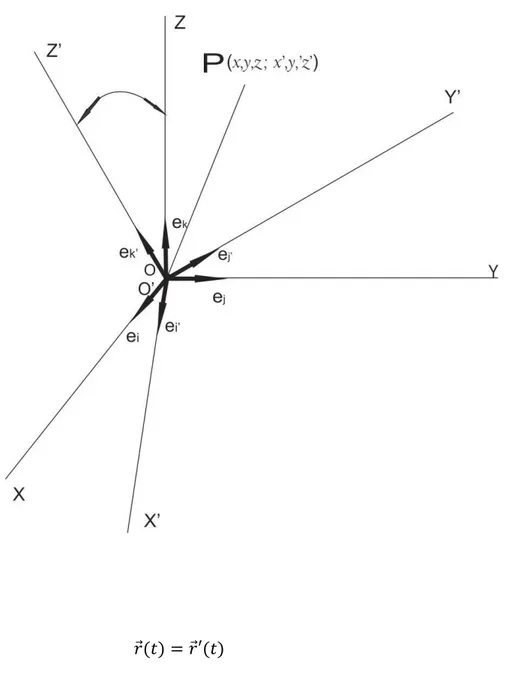
(16) Capítlo II: FUNDAMENTACIÓN TEÓRICA. En este capítulo se analiza el movimiento de una partícula, considerándola como un cuerpo puntiforme, que en realidad no existe, por lo tanto, es una idealización matemática de un objeto físico en la que cuyas dimensiones y orientaciones en el espacio son despreciable para la descripción particular de su posición, velocidad y aceleración que son de interés, en el estudio del movimiento. La forma que toman las cantidades vectoriales depende de los sistemas de coordenadas en función de las cuales se describen y del sistema de coordenadas con respecto al cual se miden dichas cantidades para describir el movimiento de la partícula. La elección del sistema de coordenadas es completamente arbitraria, con la condición de que los vectores bases no sean coplanares.. 2.1.. Efecto Coriolis. El vector de posición de una partícula queda determinado por el radio vector desde el origen O del sistema al punto P en el que está situada la partícula [2].. 9. que va.

(17) Figura 2.1: Sistema de ejes fijo y rotado. ( ). ( ). Considerando dos observadores O y O’ Fig.2.1 en el que un sistema de referencia rota con respecto al otro sistema de referencia, pero sin el movimiento de traslación relativa. Cada uno de ellos utilizan un sistema de referencia y así mismo tienen el origen común, por lo tanto, sus vectores de posición se escriben como a continuación se describen. Para el observador en posición. ( ) en sistema de referencia fija. 10.

(18) ( ). ⃗⃗. ⃗⃗. ⃗⃗⃗⃗. (2.1). Para el observador en sistema referencia rotatorio las ⃗⃗⃗ ( ) coordenadas que especifican son primadas. ⃗⃗⃗ ( ). ⃗⃗⃗⃗. ⃗⃗⃗⃗⃗. ⃗⃗⃗⃗. (2.2). Las ecuaciones (2.1) y (2.2), representan la posición de un punto P con respecto a los dos sistemas de coordenadas ( ). ⃗⃗ ( ), únicamente son distintos sus componentes. Los. vectores unitarios que son constantes en un sistema sin rotación, no son constantes en el otro sistema rotatoria son primadas, sino que gira a una velocidad angular ⃗⃗ , cuyas direcciones y sentidos varían y es definido convencionalmente como dextrógiro, es decir, positivo si el avance es contrario a las manecillas del reloj. Para una partícula A ubicado en dicho punto P cuyo vector de posición. ( ) referido al. sistema XYZ y su velocidad instantánea es la derivada con respecto al tiempo es. ( ). ⃗⃗. ⃗⃗. ⃗⃗⃗⃗. (2.3). en donde los vectores unitarios ⃗⃗ , ⃗⃗ y ⃗⃗⃗⃗ se mantienen fijos según el observador O. Mientras que el observador O’ del sistema X’Y’Z’ está en rotación y por consiguiente los vectores unitarios ⃗⃗⃗⃗ , ⃗⃗⃗⃗ y ⃗⃗⃗⃗⃗ no tienen la misma dirección ya que tienen una rotación. 11.

(19) relativa respecto al origen del sistema O con una velocidad angular ⃗⃗ , por lo que su derivada con respecto al tiempo es como sigue. ⃗⃗⃗ ( ). ⃗⃗⃗⃗. ⃗⃗⃗⃗⃗. ⃗⃗⃗⃗⃗. ⃗⃗⃗⃗. ⃗⃗⃗⃗⃗. ⃗⃗⃗⃗⃗⃗. (2.4). en la ecuación (2.4) analizando cada uno de los términos del segundo miembro, el primer término. ⃗⃗⃗⃗ es la magnitud de cambio de la posición en la componente ⃗⃗⃗⃗⃗. el segundo término. mientras que. es el cambio de la orientación y de manera similar en las otros. componentes, por lo tanto Ec. (2.4) se pueden reagrupar como. ⃗⃗⃗ ( ). ⃗⃗⃗⃗. ⃗⃗⃗⃗. ⃗⃗⃗⃗⃗. ⃗⃗⃗⃗⃗. ⃗⃗⃗⃗⃗. ⃗⃗⃗⃗⃗⃗. (2.5). de las ecuaciones (2.3) y (2.5), se establece que las derivadas temporales en ambos sistemas no son iguales [2]. ( ). |. ⃗⃗⃗ ( ). |. (2.6). a partir de la ecuación (2.5) se llega a un operador que establece la relación de velocidades entre los sistemas de coordenadas fijas y giratorias. |. |. ⃗⃗. 12. (2.7).

(20) la ecuación (2.7) es la relación de velocidades entre los sistemas fija y giratoria dada por. ⃗⃗⃗. ⃗⃗. (2.8). Por otro lado la Ec.(2.7) establece un operador diferencial entre el sistema fijo y el sistema giratorio. |. ⃗⃗. |. (2.9). La ecuación (2.9) es una identidad que se puede aplicar para obtener otras magnitudes en sistemas fijos y giratorios. Para hallar la relación de aceleración entre los sistemas, se aplica la identidad Ec.(2.9) sobre la Ec. (2.8) que es la velocidad obtenida. ⃗. ⃗. |. ⃗⃗. |. (2.10). y sustituyendo la ecuación (2.8) en la Ec.(2.9) se tiene. ⃗. |. (⃗⃗⃗. ⃗⃗. ). |. ⃗⃗. (⃗⃗⃗. ⃗⃗. ). (2.11). desarrollando el operador diferencial con respecto al tiempo a cada uno de los términos. 13.

(21) del segundo miembro se tiene. ⃗. |. ⃗. ⃗⃗. |. ⃗. ⃗⃗. |. ⃗⃗⃗. ⃗⃗. |. ⃗⃗. ⃗. escribiendo el sistema de giro por sistema primado. |. ⃗⃗. ). ⃗⃗⃗. y. (2.12). |. ⃗⃗ en. la Ec.(12) ⃗⃗⃗. ⃗⃗. ⃗⃗. ⃗⃗⃗. ⃗⃗. ⃗⃗⃗. ⃗⃗. ⃗⃗. ⃗⃗. (2.13). agrupando los términos en el segundo miembro se establece la relación de aceleraciones entre el sistema referencia fijo y el sistema de referencia giratorio. ⃗⃗⃗. ⃗⃗. ⃗⃗. ⃗⃗⃗. ⃗⃗. ⃗⃗. ⃗⃗. (2.14). se identifica cada uno de los términos de la Ec.(2.14) en el primer miembro corresponde a la aceleración referida al sistema de referencia fijo, en el segundo miembro, el primer término es la aceleración con respecto al sistema giratorio, el segundo es la aceleración lineal o tangencial si la velocidad angular es variable con el tiempo, el tercer término se denomina la aceleración de Coriolis descubierta por J. G. Coriolis (1835) y el cuarto término se identifica como la aceleración centrípeta. Si la velocidad angular es constante. ⃗⃗. ⃗⃗. observador móvil es. 14. luego la aceleración que experimenta el.

(22) ⃗⃗⃗. ⃗⃗. ⃗⃗. ⃗⃗⃗. ⃗⃗. ⃗⃗. La aceleración de Coriolis ⃗⃗⃗⃗. ⃗⃗⃗. (2.15) que es una aceleración ficticia que. experimenta un observador en un sistema en rotación con una velocidad angular ⃗⃗ , que geométricamente ésta siempre es perpendicular a la dirección del eje de rotación y a la dirección del movimiento de la partícula el cual se desprende del producto vectorial según el segundo término del segundo miembro en la Ec.(2.15). Para el caso en el que la velocidad angular está definida en una dirección ⃗⃗⃗⃗ , no habrá aceleración de Coriolis si el movimiento es paralelo al eje de rotación. ⃗⃗ ⃗⃗⃗⃗. en la que tangencial y. ⃗⃗. ⃗⃗⃗⃗. |. |. (2.16). es la componente perpendicular el eje de rotación, es la componente es la componente paralela al eje rotación.. Ahora bien, si sobre una partícula de masa m en movimiento con respecto al eje en rotación, esta aceleración causará una fuerza denominada la fuerza de Coriolis. ⃗⃗⃗. ⃗⃗⃗⃗. ⃗⃗. ⃗⃗⃗. (2.17). La fuerza de Coriolis es una fuerza ficticia que se origina en sistemas giratorias y que es directamente proporcional a la masa del objeto m, la velocidad lineal ⃗⃗⃗ que lleva y la velocidad angular ⃗⃗ con que, rota el sistema, multiplicado por factor 2. Otra alternativa. 15.

(23) para expresar la fuerza de Coriolis es mediante el momento lineal, definiendo. ⃗⃗⃗ y. permutando el producto vectorial, luego la Ec. (2.17) queda como sigue. ⃗⃗⃗. ⃗⃗⃗⃗. ⃗⃗. ⃗⃗. ⃗⃗⃗. (2.18). Dicho efecto fue demostrado experimentalmente por Jean Leon Foucault (1851) [2], el efecto que se puede aprovechar para la medición del flujo de masa, el cual es el tema de interés del presente trabajo.. 2.2.. Método de elementos finitos. Desde los inicios de la década de 60 [6]-[7], el Método de Elementos Finitos (MEF) es hoy en día ampliamente usado para analizar los problemas de ingenierías como en ingeniería civil, aeronáutica, mecánica, oceanografía, minería, nuclear, biomédica, etc. En el presente trabajo se formula, mediante el Método de Elementos Finitos para el análisis de la estructura en forma lineal a desplazamientos pequeños a los materiales con propiedades elásticos lineales que cumplen con la ley de Hooke y por consiguiente la ley de Newton. El Método de Elementos Finitos, es un procedimiento numérico que consiste en la idealización del sistema en la discretización del fenómeno continuo en cuestión, es decir, es la representación de un cuerpo o estructura por un ensamble de subdivisiones llamados elementos que se interconectan entre sí a través de dos puntos llamado nodos, de tal manera que la agrupación de dichos elementos representa al cuerpo o estructura sistema original. Las soluciones que se obtienen para cada elemento finito se combinan o se. 16.

(24) globalizan para obtener la solución total. En los elementos se establecen las ecuaciones que gobiernan según las leyes físicas y con la reunión de los elementos individuales se forma la matriz de rigidez y a partir de esto se obtiene la solución que gobierna el sistema. Para Hallar la solución se elabora el algoritmo en GNU Octave [29], el mismo que permite la simulación por computadora. Por lo general se analizan los matrices simétricos y variables escalares que determinar los autovalores, los mismos que permiten hallar los autofunciones que caracterizan el sistema. Con la interpretación física de los resultados obtenidos de la solución se conduce a una explicación moderna y efectiva para una aplicación de uso práctico [7]-[12].. 2.3.. Formulación de fuerzas que actúan sobre un tubo recto que vibra. A partir de la Ec.(1.1) se tiene que una fuerza aplicada externamente. (. ) se. estable la ecuación dinámica en donde cada uno de los términos del primer miembro son ecuaciones diferenciales tal como se expresan a continuación, que es una ecuación diferencial estándar que se aplica a la teoría de vibración de vigas, propuesta por EulerBernoulli. [12], [21] y [22] que son muy tradicionales en las aplicaciones prácticas. (. ). (. ). Con las siguientes condiciones de contorno impuestas en los ambos extremos, que son. 17. (2.19).

(25) (. (. ). (2.20). ). (2.21). (. ). (. (2.22). ). (2.23). para empezar, se considera que el tubo tiene una longitud L de densidad lineal homogénea y de sección transversal circular uniforme a lo largo de su longitud. La figura 2.2, es una representación esquemática no a escala del sistema tubo-fluido en el que se especifican los aspectos más resaltantes: 1. Longitud del tubo, 2. Espesor, 3. Diámetro interno del tubo que transporta el fluido, 4 y 5 son velocidades de entrada y salida del fluido, 6. Extremos inicial y final empotrados, las regiones m y n de la zona de entrada y salida respectivas del fluido dentro del tubo que circula a una rapidez uniforme → En ausencia de alguna carga externa sobre el tubo (incluyendo su propio peso) da una curva que une los centroides de todas las secciones transversales, es una línea recta llamada eje de simetría. Si una carga es aplicada sobre el tubo conteniendo en un plano vertical del eje de simetría, somete a una distorsión y la curva que contiene todos los centroides de la sección transversal se llama curva de deflexión de la curva elástica, la curva de deflexión. 18.

(26) Figura 2.2: Esquema general del sensor Coriolis tubo recto. se aproxima a la forma del tubo. Ahora suponemos que el eje x coincide con el eje de simetría y que la deflexión (. ) medido desde su eje que es considerado positiva hacia. abajo. En teoría de la elasticidad se muestra que el momento de flexión. ( ) en el punto. x a lo largo del tubo está relacionada con la carga por unidad de longitud por la ecuación [1]. ( ). además, el momento. ( ). (2.24). ( ) es proporcional a la curvatura κ de la curva elástica, donde E. 19.

(27) y. son constantes, E es el módulo de elasticidad del material utilizado y. momento de área de la sección transversal del tubo circular. El producto. es el segundo se llama. rigidez de flexión. Ahora según los cálculos, la curvatura es dado por [4], . en donde la deflexión de ( ) es muy pequeña y la pendiente de la. por lo tanto. , así la ecuación. , expresa la curvatura. para pequeñas deflexiones. La segunda derivada de esta expresión Ec.(2.24) es. ( ). Se ve que la deflexión. (2.25). ( ) satisface la ecuación diferencial de cuarto orden es una. ecuación diferencial de cuarto orden con respecto a la variable x, que tiene la forma de la ecuación que sigue. ( ). (2.26). las condiciones asociadas con la ecuación dependen de cómo están los extremos del tubo, si en ambos extremos están empotrados o fijos, entonces las condiciones de contorno que se establecen, constituyen los grados de libertad y son: ( ) ( ). : expresa la deflexión en el extremo inicial : la curva de deflexión es tangente al eje x, es decir, la pendiente de la curva. que forma la viga. En el extremo. las condiciones son similares. 20.

(28) ( ) ( ). 2.4.. : deflexión en el extremo final : la curva de deflexión es tangente al eje x, la pendiente en el extremo final.. Deducción de la función de forma. Consideremos la Ec.(1.3), es decir, (. ). (. ). en el que. las constantes [6], C1, C2, C3 y C4 son constantes arbitrarias desconocidas por determinarse. Las cuales se determinan aplicando las condiciones de contorno. En el extremo. ,. así mismo la derivada de la función en. ( ). ( ). ,. |. , es decir,. |. de manera similar en el otro extremo en. ,. (2.27). |. (2.28). 21.

(29) de las ecuaciones Ec.(2.27) y Ec.(2.28) se obtienen un sistema de ecuaciones para determinar los constantes desconocidas C3 y C4. Resolviendo el sistema se tiene que la constante C3. y de la misma manera la constante C4. y ahora se escribe la función ( ) para obtener un arreglo sustituyendo cada uno de los constantes. ( ). 22.

(30) agrupando los términos y factorizando. ( ). (. ). (. ). ( (. ) ). (2.29). haciendo un arreglo a la Ec. 2.29 se obtiene una matriz columna de elementos son [6]. [X. (2.30) [. ]. por otro lado, la matriz columna de. de condiciones iniciales. (2.31) [. ]. de donde la Ec.(1.3), ( ) matricialmente expresado es. (. ). (2.32). 23. en el que cuyos.

(31) La obtención de la matriz. [6], es muy importante ya que a partir de ella se calculan. los elementos de las matrices. Por otro lado, es importante notar que se han obtenido solo para dos nodos y un elemento, según la teoría de método de elementos finitos, cuyos elementos de la matriz que a continuación se deducen. Ver el apéndice A, deducción de los elementos las matrices.. Se calculan los elementos de cada uno de los matrices según el operador diferencial que actúan sobre la función (. ), los mismos que se evalúan para un segmento de elemento. con dos nudos, así mismo se minimizan los errores por el método de Galerkin. El procedimiento que se sigue es, primero, se aplica el operador diferencial correspondiente según la Ec.(2.19) para el régimen permanente, es decir, el segundo miembro es igual a cero. Las primeras derivadas de los elementos de la matriz. Las segundas derivadas de los elementos de la matriz son. 24. son:.

(32) Se calculan los elementos para cada matriz, los mismos que están desarrollados en el Apéndice A. Los elementos de cada matriz contribuyen a los coeficientes del sistema de tubo recto y fluido en estudio, según las condiciones fijas en ambos extremos del mismo. Los elementos de la matriz. se obtienen del operador. es un producto. no definido de matrices que da origen a una matriz de orden 4x4 para un elemento discreto. Se observa que son derivadas con respecto a la variable. , a lo largo de la. longitud del tubo-fluido, que se expresa por la matriz, globalizado para dos elementos [9]-[14]. 6 L  12 6 L 0 0   12  6 L 4 L2  6 L 2 L2 0 0    12  6 L 24 0  12 6 L    2 2 0 8L  6 L 2 L2   6L 2L  0 0  12  6 L 12  6 L    0 6 L 2 L2  6 L 4 L2   0. 25. (2.33).

(33) El siguiente término, cuyo operador diferencial es. que da una. matriz de orden 4x4, que también son derivadas con respecto a la variable x, se denomina matriz [Bg], globalizado para dos elementos es..  6  5L  1   10  6  5L  1   10  0    0. El operador. 1 10 2L 15 1  10 L  30. . 0. . 0. 6 5L 1  10 12 L 5. 1 10 L  30 0 4L 15 1  10 L  30. 0 6 5L 1 10. 0 0 6 5L 1  10 6 5L 1  10. .  0   0   1  10  L   30  1   10  2L  15 . (2.34). corresponde a la fuerza de Coriolis que es una derivada mixta con. respecto a las variables t y x, da origen a una matriz orden 4x4 que denomina matriz [Cg], se obtiene para dos elementos globalizados.  1 2  L   10  1 2  L   10   0   0 . L 10 0 L 10 L2 60. . 0 0. 1 2 L 10 0 2L  10 1  2 L 10. L 10 L2  60 2L 10 . 0 L 10 L2 10. . 26. 0 0 1 2 L 10 1 2 L  10.  0   0   L   10 L2    60  L  10   0  . (2.35).

(34) El último operador diferencial es (. ). es una derivada segundo orden con. respecto al tiempo que da origen a la matriz de masas, [Dg], globalizado para dos elementos es.. (.  13L  35  2  11L  210  9L  )  70 2  13L  410   0   0 . 11L2 210 L3 105 13L2 420 L3  140 0 0. 9L 70 13L2 420 26 L 35 0 9L 70 13L  410. 13L2 420 L3  140. . 0 2 L3 105 13L 420 L2  140. 0 0 9L 70 13L2 420 13L 35 11L2  210.    0   2 13L   420  L2   140  11L2    210  L3  105  0. (2.36). Las matrices elementales, cuyos elementos son calculados en el Apéndice A,. ,. son del mismo orden 4x4 en cada caso. Teniendo en cuenta que las matrices son derivadas respecto a través de la matriz. y luego se pueden sumar matricialmente. ,. y y que a. está relacionada con las propiedades de tubo recto, por lo que en la. literatura especializada lo denominan la matriz de rigidez. Escribiendo de la manera más compacta la Ec.(2.19), para el régimen permanente toma la forma de:. (2.37). En donde aparece en la frecuencia angular ω de oscilación que viene a ser la frecuencia. 27.

(35) de resonancia del sistema de oscilación del sensor tubo recto que transporta el fluido agua. El paso siguiente es hallar dicha frecuencia angular de resonancia que caracteriza el sistema para el que se utiliza el Método de Elementos Finitos.. 28.

(36) Capítulo III: PROCESO DE SIMULACIÓN. 3.1.. Características de los materiales para simular. El material que se requiere es básicamente el tubo recto de acero inoxidable que existe en el mercado cuyas características a considerarse son: la resistencia a las oxidaciones, la resistencia a la temperatura. Para lo cual existen aceros inoxidables de distintas variedades, por mencionar algunos, como por ejemplo, acero inoxidable Stainless Steel cuyos códigos son: SS 304, SS 316, SS 316L [28] y otros. Sus características o especificaciones mecánicas se encuentran en sus respectivos catálogos y/o en el handbook, los mismos que ya son estandarizadas. Para el caso de la simulación, según las Ec.(2.33) o la Ec.(2.36) [15]-[19]. a) los parámetros mecánicos básicos que se requieren en el proceso de simulación son: : Módulo de Young de tubo recto, [N/m2] : Densidad del fluido, [kg/m 3] : Densidad del tubo, [kg/m3] : Diámetro externo del tubo, [m] : Diámetro interno del tubo, [m]. b) Los siguientes datos que se suministran, son arbitrarios : Velocidad del fluido, [m/s] ,. : Longitud del tubo, [m]. 29.

(37) : amplitud de del tubo de oscilación [m]. c) Con los datos suministrados en a) y b) se calculan los siguientes parámetros , para utilizar posteriormente en los cálculos [16]: : segundo momento de área del tubo, [m4] : masa del fluido distribuida por unidad de longitud, [kg/m] : masa del tubo distribuida por unidad de longitud, [kg/m] : el espesor del tubo, [m] : radio medio del tubo, [m]. : área del fluido, [m2]. : Área del tubo, [m2].. d) Los parámetros antes mencionados en c) se definen mediante las relaciones que siguen a continuación: espesor del tubo transporta el líquido o el fluido [15]-[20]. (3.1) Radio medio del tubo (3.2) Sección por donde se transporta o se conduce el fluido (3.3) Área de la sección del tubo recto (3.4) El segundo momento de área del tubo (3.5). 30.

(38) Masa del tubo distribuida por unidad de longitud por donde circula el fluido. (3.6). Masa del fluido distribuida por unidad de longitud. (3.7). Con los datos suministrados en a) y b) y los cálculos realizados en c) se resuelve la Ec.(2.37). para hallar la frecuencia de resonancia |ω| de oscilación para el sistema tubofluido, mediante el Método de Elementos Finitos, MEF, para ello se discretiza el tubo recto en elementos finitos, en mayor número posible de subdivisiones y luego se globalizan de manera que la frecuencia de resonancia y el modo de vibración correspondiente que represente al sistema tubo-fluido.. 3.2.. Elaboración del programa script. Para calcular los parámetros arriba indicados se ha elaborado un programa en script en GNU Octave [29] para el cual, solo es necesario suministrar longitud, módulo de Young, densidad del tubo, densidad el fluido, diámetro exterior y el diámetro interior, velocidad del fluido y el número de iteraciones que se han de realizar, es decir, en cuántos elementos finitos se va fraccionar el tubo recto de acero inoxidable que conduce el fluido. El programa calcula las magnitudes como el espesor del tubo, área de la sección del fluido, el segundo momento de área del tubo, la masa por unidad de longitud del tubo, la. 31.

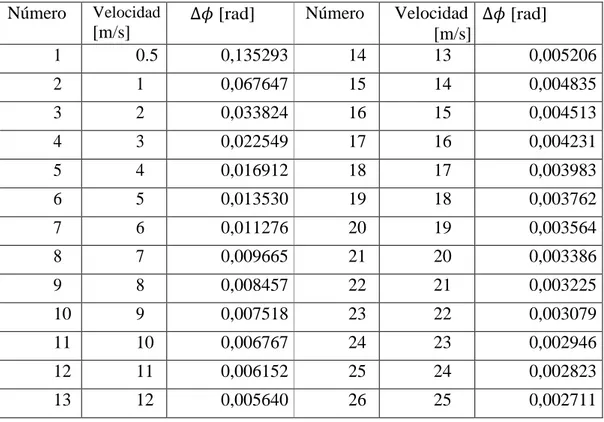
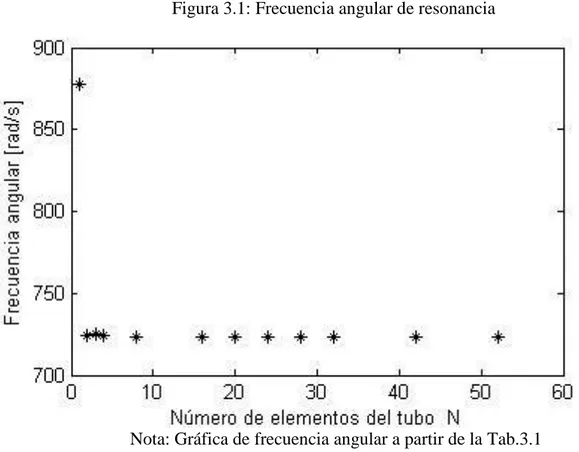
(39) masa por unidad de longitud del fluido. El desarrollo se encuentra en el Apéndice B. En donde el primer programa es para leer los parámetros mecánicos del sensor tubo recto y fluido, con dichos parámetros calcula los otros parámetros definidos. El segundo programa es para calcular la frecuencia angular de resonancia en módulo | | para el tubo de acero inoxidable, utilizando los elementos de las matrices calculados en el Apéndice A. El tercer programa calcula la frecuencia angular de resonancia según la longitud del tubo para optimizar el tipo de geometría del tubo sensor y el cuarto programa calcula el cambio de fase que se genera con el cual luego se calcula el flujo de masa por el método de Coriolis, simultáneamente se calcula el flujo de masa por el método de ecuación de continuidad para hacer las comparaciones en el cálculo del flujo de masa, [18]-[21].. 3.3.. Resultados del programa ejecutado. Los resultados del programa se calculan por comando norma de GNU Octave, para hallar la frecuencia angular | | [rad/s] [21]-[23], puesto que los valores que dan son número complejos, los resultados se dan en la Tab.3.1, en donde en la primera columna se dan el número de elementos en que se ha dividido el sensor tubo recto de acero inoxidable. En la segunda columna se presentan la cantidad de elementos de cada matriz, que en este caso son matrices cuadradas en conjunto son cuatro matrices. La tercera columna representa los valores de la frecuencia angular de resonancia calculado en módulo. En la tabla 3.1, y la figura 3.1 se muestra la tendencia de la frecuencia angular de resonancia a un valor 723.6 rad/s para el sensor tubo recto dado para los diferentes elementos finitos, en este caso se ha tomado hasta 52 subdivisiones, cuya convergencia se observa en la figura 3.1. La interpretación física correspondiente está en el capítulo siguiente.. 32.

(40) Tabla 3.1: Frecuencia angular de resonancia por MEF Número elementos. Orden matriz. Frecuencia angular |ω| [rad/s]. 1. 4x4. 878.05. 2. 6x6. 724.4. 3. 8x8. 724.89. 4. 10x10. 723.91. 8. 18x18. 723.48. 16. 34x34. 723.61. 20. 42X42. 723.62. 24. 50x50. 723.67. 28. 58x58. 723.63. 32. 66x66. 723.63. 42. 86x86. 723.64. 52. 106x106. 723.64. Nota: Tab. 3.1,.Muestra los resultados de la Ec. (2.37), para frecuencia angular. Es necesario calcular qué frecuencia angular de resonancia se alcanza para diferentes longitudes del tubo, por lo que se ha simulado para diferentes longitudes del tubo desde 0.25 metros hasta 0.85 metros de longitud manteniendo constante la velocidad del fluido y los otros parámetros del tubo y fluido cuyos resultados se dan en la tabla 3.2. en donde la frecuencia angular para longitudes cortos como de 0.25 metros es muy alta, alcanza hasta alrededor de 6512.3 rad/s y conforme aumenta la longitud del tubo, la frecuencia. 33.

(41) Figura 3.1: Frecuencia angular de resonancia. Nota: Gráfica de frecuencia angular a partir de la Tab.3.1 angular de resonancia va disminuyendo hasta un valor apropiado por lo que se toma como frecuencia angular de resonancia 723.6 rad/s, para continuar con el trabajo. Ver la tabla 3.2 y la figura 3.2. A partir de la frecuencia angular de resonancia, se calcula el ángulo del desfasaje, manteniendo constantes la velocidad del fluido, longitud del tubo, área de la sección por donde transporta el fluido, [22]-[27].. Tabla 3.2: Frecuencia angular de resonancia por MEF Longitud [m] F.resonancia [rad/s]. 0.25. 0.35. 0.45. 0.55. 6512.3 3322.6 2010.0 1345.5. 34. 0.65. 0.75. 0.85. 963.4. 732.6. 563.4.

(42) Figura 3.2: Frecuencia angular de resonancia vs longitud. Nota: Gráfica de la Tab.3.2, frecuencia angular para diferentes longitudes del tubo. 35.

(43) Capítulo VI: ANÁLISIS DE RESULTADOS. 4.1.. Análisis de resultados del programa. Las Ec. (1.4) y Ec. (2.37) que expresan matricialmente la mecánica de vibración del sensor tubo-líquido, en donde aparece la frecuencia angular de resonancia ω como autovalores de las matrices por determinar. A partir del desarrollo de las matrices que ya han sido evaluados mediante el programa Script en GNU Octave [29] y que después de haber calculado dichos valores, resaltan los siguientes aspectos importantes: Conforme se incrementa el número de elementos finitos de discretización del sensor tubo-fluido, el tamaño del rango de las matrices aumentan el orden (2xelemento+2) x (2xelemento+2), es decir, para los 52 elementos finitos, el rango de la matriz. es 2x52+2 =106, luego el tamaño de las matrices es del orden de. 106x106 =11236 elementos. Para cada una de las cuatro matrices cuadradas dadas, los elementos de las cuatro matrices en total dan 44944 elementos (elementos de matrices), constituyéndose la parte más laboriosa del trabajo, en si. La frecuencia angular de resonancia de las matrices cuadrados en cuyo diagonal está el cuadrado de la frecuencia angular al cuadrado, de tal manera que una matriz de dos elementos finitos discretos 2x2+2=6 que es el rango de la matriz, por lo. 36.

(44) tanto, las matrices de [6x2] elementos generan doce raíces y así mismo la matriz de [106x2] tiene 212 raíces en total. La cantidad de raíces aumentan según el número de elementos finitos en que se discretiza el tubo y luego el rango de las matrices también aumentan, por lo tanto, no todas las raíces son de interés físico, a pesar de que provienen del problema de origen físico. Las raíces que se obtienen son autovalores en todos los casos y son de carácter de números complejos, luego para obtener un valor real, se tiene que hallar la norma dos a las raíces a los autovalores obtenidos para determinar la frecuencia angular de resonancia |ω|. La obtención de números complejos como resultado es muy importante puesto que implica que el sistema es oscilatorio. Según los cálculos realizados con los primeros uno o dos elementos finitos, el valor de la frecuencia angular de resonancia que se obtiene es muy incierta, como se observa en la Fig 3.1 o la Tab. 3.1, A partir de un número, por ejemplo, cuatro elementos finitos, aparece la frecuencia angular de resonancia y converge conforme se aumentan el número de elementos finitos en que se divide el tubo sensor. Por lo tanto, es necesario discretizar el sensor tubo recto en varios elementos finitos, dichos cálculos se ejecutan por Método de Elementos Finitos mediante programa en GNU Octave, que según los investigadores, el uso del comando Polyeig es el método más recomendable. [21]. De todas las raíces posibles se toma el menor autovalor convergente, en el presente trabajo se ha tomado |ω| =723,6 rad/s y para propósitos prácticos | |. rad/s. para una longitud de 0,75 m y con una rapidez del fluido de V=5,0 m/s. Ahora bien, si se aplica una vibración externa a un sensor de tubo recto que conduce el fluido como se muestra en la Fig.4.1, una frecuencia angular de. 37.

(45) resonancia |ω|, cuyo sentido positivo se considera convencionalmente en el sentido contrario a las manecillas de las agujas del reloj, en este caso se considera sentido negativo en el punto medio el sensor, el sentido de la frecuencia angular. El tubo sensor se distorsiona como muestra el esquema de la Fig.4.1 en donde el fluido que ingresa por la zona m entra a una velocidad ⃗ experimenta una descomposición de velocidades en ⃗. y una velocidad ⃗. los que originan una aceleración de Coriolis. que de manera general se expresa como fuerza de Coriolis. ⃗. ⃗ el mismo que genera una. sobre la masa del líquido que circula a una velocidad ⃗ a lo. largo del tubo que conduce fluido, cuya expresión es la fuerza vectorial de Coriolis sobre la masa del fluido en la zona de entrada m tiene dos componentes, figura 4.2,. Figura 4.1: Sensor tubo recto con fluido sometido a vibración. 38.

(46) ⃗ | | [. (4.1) ]. | |. | |. (4.2). de manera análoga, la fuerza de Coriolis sobre la masa del fluido en la región n también tiene dos componentes ⃗ | | [. (4.3) ]. | |. | |. (4.4). Figura 4.2: Fuerzas en el sensor tubo con fluido sometido a vibración. 39.

(47) Figura 4.3: Momento de fuerza que se origina. Nota: en la Fig. 4.3 se observa el efecto de los momentos de fuerza ejercida sobre el sensor tubo recto.. las fuerzas de Coriolis que se origina a lo largo de las zonas de entrada m y salida n causan dos efectos importantes sobre el fluido en movimiento. El primer efecto es el momento de fuerzas que se generan sobre el tubo describe como sigue. Considerando el momento de fuerza Mk con respecto al eje. 40.

(48) ⃗ ⃗⃗. (4.5) [. ]. A partir del cual surge un momento de fuerza resultante. ⃗. ⃗⃗⃗⃗. en la zona m. (4.6). en la zona de salida n, de manera análoga se tiene el momento de fuerza correspondiente como se puede ver en la Figura 4.3 ⃗ ⃗⃗. (4.7) [. ⃗⃗. ]. ⃗. (4.8). En la Fig. 4.3 se observa el efecto de los momentos de fuerza ejercida sobre el sensor tubo recto, expresado por las ecuaciones Ec.(4.6) y Ec.(4.8).. 41.

(49) Figura 4.4: desfasaje en las pendientes. Nota: Desfasaje producido por los efectos de momentos de fuerza sobre el sensor tubo recto. 42.

(50) Tabla 4.1: Cambio de fase Número. Velocidad. vs velocidad Ec.(4.9). Número. [rad]. [m/s]. Velocidad [m/s] 13. [rad]. 1. 0.5. 0,135293. 14. 0,005206. 2. 1. 0,067647. 15. 14. 0,004835. 3. 2. 0,033824. 16. 15. 0,004513. 4. 3. 0,022549. 17. 16. 0,004231. 5. 4. 0,016912. 18. 17. 0,003983. 6. 5. 0,013530. 19. 18. 0,003762. 7. 6. 0,011276. 20. 19. 0,003564. 8. 7. 0,009665. 21. 20. 0,003386. 9. 8. 0,008457. 22. 21. 0,003225. 10. 9. 0,007518. 23. 22. 0,003079. 11. 10. 0,006767. 24. 23. 0,002946. 12. 11. 0,006152. 25. 24. 0,002823. 13. 12. 0,005640. 26. 25. 0,002711. tubo recto y el fluido, en donde la componente de momento de fuerza en la zona n es la Ec.(4.8). El segundo efecto es que la diferencia de momentos de fuerza que se originan, según las Ec.(4.6) y Ec.(4.8), producen una diferencia fase de ángulos con respecto al punto medio del tubo, el cual se mide mediante una magnitud llamado diferencia de fase dado en radianes. La diferencia de fase o el ángulo de desfasaje. se. calcula con la expresión propuesta por [22] que se expresa a continuación y otros [23], [24], [25] y [26]. (. )(. ). (. 43. (. ). (. ). (. ). (. ). ). (4.9).

(51) Esta diferencia de fase entre los ángulos que se forman debido al momento de fuerza neta que resulta sobre el tubo que conduce el fluido, donde dicho momento es resultante del efecto Coriolis en el que están involucrados varios parámetros, algunos de ellos son constantes que provienen de la solución general [22] como son:. ,. y otros como diferencia de frecuencias al. cuadrado (. ) que es la frecuencia de sensores ubicados en punto críticos se. puede expresar como frecuencia angular. y. , es una. diferencia de modos de vibración entre modo uno y modo dos cuya diferencia es despreciable de manera que se puede aproximar la frecuencia de resonancia, además es proporcional a la distribución de masa del fluido por longitud. Es inversa a la longitud del tubo, inversa a la suma de la distribución de masa de fluido y del tubo, al cuadrado de frecuencias. Por otro lado en Ec.(4.9) interviene la posición de la ubicación de sensores que son simétricos al punto medio del tubo sensor. La diferencia de fase en la Ec. (4.9) es directamente proporcional. , es decir, si es mayor velocidad (rapidez) mayor es. la diferencia de fase. pero intervienen las frecuencias que están en función de la velocidad. Se presenta un programa script en GNU Octave, ver Apéndice B, para calcular la diferencia de fase. cuyos resultados se presentan en la Tab.4.1 y Fig.4.5 respectivamente en función de velocidad.. 44.

(52) Figura 4.5: Cambio de fase. vs velocidad. Nota: Gráfica de cambio de fase en función de velocidad a partir de Tab. 4.1. Tabla 4.2: Flujo de masa de Coriolis vs velocidad Número. [kg/s]. 1. Velocidad [m/s] 0,5. 0,035675. 14. 13. 0,927297. 2. 1. 0,071331. 15. 14. 0,998628. 3. 2. 0,142661. 16. 15. 1,069959. 4. 3. 0,213992. 17. 16. 1,141289. 5. 4. 0,285322. 18. 17. 1,212619. 6. 5. 0,356653. 19. 18. 1,283950. 7. 6. 0,427983. 20. 19. 1,355281. 8. 7. 0,499314. 21. 20. 1,426611. 9. 8. 0,570645. 22. 21. 1,497942. 10. 9. 0,641975. 23. 22. 1,569272. 0,713306. 24. 23. 1,640603. 11 10. Número. Velocidad [m/s] [kg/s]. 12. 11. 0,784636. 25. 24. 1,711934. 13. 12. 0,855967. 26. 25. 1,783264. Nota: Flujo de masa obtenido a partir de la ejecución de Ec.(4.10). 45.

(53) Flujo de masa calculado por el método de Coriolis [22]. ̇. Una vez calculado. (. ). (4.10). , Ec.(4.10) se elabora un programa Script en GNU Octave y. se calculan los resultados y se obtiene la Tab. 4.2 y Fig. 4.6 correspondientes. como expresa la (4.10), el flujo de masa depende de varios parámetros que intervienen, algunos son valores constantes y otros parámetros en función de la velocidad definido según la Ec. (4.10). Fundamentalmente lo que más afecta al flujo de masa es el cambio de fase que se estable, en este caso se ha calculado como consecuencia de efecto de momentos de fuerza causado por el efecto Coriolis. Con todos los parámetros involucrados se calcula el flujo de masa, se denomina flujo de masa por el método de efecto Coriolis, como se observa en la Tab.4.2 y Fig.4.6 en donde se observa en función de la velocidad del fluido ⃗ .. 46.

(54) Figura 4.6: Flujo de masa por efecto Coriolis vs velocidad. Nota: gráfica de flujo de masa a partir de la tabla 4.2. 4.2. Flujo de masa aplicando la ecuación de continuidad. Considerando un tubo recto de sección circular constante. por el que circula un. fluido a una velocidad constante ⃗ , prescindiendo de otros efectos, el flujo de masa que se transporta se obtiene por la ecuación de continuidad en donde se calcula volumen por unidad de tiempo,. ⃗. (4.11). Cuyo análisis dimensional es [m ].[m/t] = [m ]/[t], luego el flujo de masa se calcula considerando la densidad del fluido. ̇. constante. (4.12). 47.

(55) Otra alternativa para calcular el flujo de masa es por la ecuación de continuidad que consiste en multiplicar la distribución de masa por unidad de longitud de tubo y por la velocidad con se transporta el fluido por dicha sección.. Tabla 4.3: Flujo de masa por continuidad vs velocidad Número Velocidad [m/s]. [kg/s]. 1. 0,5. 0,035675. Nú me ro 14. 2. 1. 0,071331. 3. 2. 4. Velocidad [m/s] [kg/s]. 13. 0,927297. 15. 14. 0,998628. 0,142661. 16. 15. 1,069959. 3. 0,213992. 17. 16. 1,141289. 5. 4. 0,285322. 18. 17. 1,212619. 6. 5. 0,356653. 19. 18. 1,283950. 7. 6. 0,427983. 20. 19. 1,355281. 8. 7. 0,499314. 21. 20. 1,426611. 9. 8. 0,570645. 22. 21. 1,497942. 10. 9. 0,641975. 23. 22. 1,569272. 11. 10. 0,713306. 24. 23. 1,640603. 12. 11. 0,784636. 25. 24. 1,711934. 13. 12. 0,855967. 26. 25. 1,783264. Nota: resultados de flujo masa obtenido de la Ec.(4.13). ̇. (4.13). En el cálculo de flujo de masa por este método, solo se utilizan dos parámetros: la velocidad del fluido. y la distribución de masa por unidad de longitud,. 48. . Los.

(56) otros parámetros no intervienen en el cálculo como los que se utilizan a largo de este trabajo, es decir, en el método de Coriolis. Por otro lado, tampoco es necesario emplear relaciones matemáticas a nivel de ecuaciones diferenciales y otras consideraciones matemáticas a diferencia de método de Coriolis que en cuyo caso involucran varios aspectos como la característica del tubo, longitud, radio externo y radio interno, frecuencia de resonancia de vibración, determinación de diferencia de fase producido por efecto de Coriolis y otros. Sin embargo, los resultados calculados por ambos métodos son sorprendentemente iguales, ver la Tab. 4.3 y la Fig.4.7, respectivamente, en el que los valores de flujo de masa calculados coinciden exactamente.. Figura 4.7: Flujo de masa por continuidad vs velocidad. Nota: flujo de masa a partir de la tabla 4.3. 49.

(57) Conclusiones y recomendaciones. Durante la investigación, mediante la revisión de la literatura especializada en la medición del flujo de masa por efecto Coriolis, en paralelo a la realización del presente trabajo de investigación y después de haber hecho una simulación en programa script en GNU Octave para un sensor tubo de acero inoxidable, se ha determinado que la geometría de un solo tubo recto, sería el más apropiado que otros como el doble tubo recto que puede por efecto de taponamiento en uno de ellos podría causar el desbalance en la medición del flujo másico o que causaría el efecto de contrapresión en caso de otra geometría de forma U, que afectaría la medición de flujo de masa. Dentro del objetivo planteado en la realización de la presente invesetigación, fue la determinación de la frecuencia angular de resonancia para el sistema apropiado, en este caso sensor tubo recto de acero inoxidable y utilizando como sustancia de trabajo las propiedades del agua. Para alcanzar tal propósito se ha organizado la secuencia de pasos que sería más adecuado, por lo que es considerado primero la base teórica, seguido de algoritmos matemáticos apropiados para simular la frecuencia de angular de resonancia de oscilación el cual conduce al efecto de Coriolis, mediante el transporte del fluido. Para una geometría de tubo recto con agua de longitud 0,75 m y velocidad 5,0 m/s, es calculado una frecuencia angular de resonancia de. 732,6 rad/s, para el tubo de material acero inoxidable y agua.. 50.

(58) Con los datos obtenidos y mencionados antes, en el proceso de simulación se ha llegado a calcular el flujo de masa que mediría, que según los resultados es de 0,356653 kg/s.. Es recomendable con los avances que se tiene hasta el presente investigación, en nuestro medio sobre la medición de masa por efecto Coriolis, se continúe hasta implementar un laboratorio en El se podría concretar una consolidación de la teoría y práctica,. hasta alcanzar la madurez e las innovaciones correspondientes y. asimismo en el futuro conducir hacia una transferencia tecnológica a la región.. 51.

(59) Bibliografía [1] L. D. Landau and E.M. Lifshitz. Teoría de la Elasticidad, Curso de Física Teórica. Vol. 7, Reverté S. A. Barcelona, 1969. [2] Walter Hauser. Introducción a los Principios de Mecánica. Unión Tipográfica Editorial Hispanoamericana, México, 1969. [3] Steven C. Chapra, Reymond P. Canale. Métodos Numéricos para Ingenieros. 3ra. Edición, McGraw-Hill, México, 2000. [4] Dennis G. Zill, Warren S. Wright. Advanced Engineering Mathematics. Fourth edition. The Jones and Bartlett Publishers, USA, 2011. [5] C. R. Wylie. Advanced Engineering Mathematics. Third edtion., McGrawHill, USA, 1966. [6] Saeed Moaveni. Finite Element Analysis Theory and Applications whit ANSYS. Prentice-Hall. Inc. USA, 1999. Disponible en: <http://www1.gantep.edu.tr/ er- klig/me408/kitap.pdf>. [Consultado 23/04/2014] [7] K. J. Bathe. Finite Element Procedures. Prentice-Hall1, 1996. Disponible en:<http://ftp.demec.ufpr.br/disciplinas/EME748/Textos/Bathe, [Consultado 23/04/2014]. [8] Young W. and Hyochoong Bang. The Finite Element Methods Using MatLab. CRC Press LLC USA, 1997.. 52.

(60) [9] Lisandro Massera, Mauro Podoreska and Mónica Romero. Mecánica Computacional. Córdoba, Argentina, 2007. Disponble <http://www.oilproduction.net/files/caudalimetro_masico_coriolis.pdf> [Consultado 0 2 / 1 1 / 2016]. [10] Samer Guirguis and Fan ShangChun. Modeling of Coriolis mass flow meter of general plane-shape pipe. Flow Measurement and Instrumentation, Elsevier Ltd. 2009. Disponible en: <http://stu. olomo.de/imat/allgemeine_rohrform.pdf>, [Consultado mayo 2015]. [11] G. Bobovnik, J. Kutin and I. Bajsic. The effect of flow conditions on the sensitivity of the Coriolis flowmeter. Flow Meas. Instrum. 15, 2004. Págs. 69-76. [12] G. Bobovnik, J. Kutin and I.n Bajsie. The effect of different inlet-velocity profile on the performance of a Coriolis flowmeter. Procedencia: XVII IMKO World Congress Metrology in the 3rd. Millennium, June 22-27 2003, Dubovnik, Croatia. Disponible en:<http://www.imeko.org/publications/wc2003/PWC-2003-TC9-005.pdf>. [13] Stephanie Enz. Factors Affecting Coriolis Flowmeter Accuracy, Precision and Robustness. [PhD. Thesis] (online). DCMM Special Report No. S119, Technical University of Denmark, September 2010, [Consultado, 2014.] [14] J. Kutin, and I. Bajsié. Stability-Boundary Effect in Coriolis Meters. Elsevier Science Ltd. 2001. [15] G. Sultan, J. Hemp. Modelling of the Coriolis mass flowmeter. Journal of Sound and Vibration. 1989. 132(3): Págs. 473-489.. 53.

(61) [16] G. Sultan. Single straight-tube Coriolis mass flowmeter. Flow Measure Instrument. Vol.3 N° 4, 1992, Págs. 241-246. [17] G. Sultan, J. Hemp. Modelling of the Coriolis mass flowmeter. Journal of Sound and Vibration. 1989. 132(3): Págs. 473-489. [18] J. Dominick, F. Durst, H. Raszillier and H. Zeisel. A method to measure mass and volume flow rates of two-phase flows. Int. J. Multiphase Flow. Vol. 13 N° 5, 1987, Págs. 685-698. [19] U. Langue, A. Levient, T. Pankratz and H. Raszillier. Effect of detector masses on calibration of Coriolis flowmeters. Flow Measurement and Instrumentation Vol.5 N° 4, 1994. Págs. 255-262. [20] J. Ruo, W. Gauchel, H. Kuck. Advances in signal acquisitions and signal processing of Coriolis flow meters. Procedencia: Engineering 87, 2014, Págs. 1585-1588. [21] R. Chessewright, S. Shaw. Uncertainties associated with finite element modelling of Coriolis mass flow meters. Flow Measurement and Instrumentation 17, 2006. Págs. 335-347. [22] R. Chessewright and C. Clark. The effect of flow pulsations on Coriolis mass flow meters. Journal of Fluid and Structures 12, 1998. Págs. 1025-1039. [23] A. Belhadi, R. Chessewright and C. Clark. The simulation of Coriolis meter response to pulsating flow using a general purpose. Journal of Fluid and Structures 14, 2000. Págs. 613-634. [24] H. Raszillier, and V. Raszillier. Dimensional and symmetry analysis of Coriolis mass flowmeters. Flow Measurement and Instrumentation 2(3), 1991. Págs. 180-184.. 54.

(62) [25] Jian Guo Zhang, Ke-Juan Xu, Shuai Dong Zheng Liu, Qi-Li Hou, Zheng-Yu Fang. [para ser publicado] Mathematical model of time difference for Coriolis flow sensor output signals under gas-liquid flow. Measurement 05, 2017, Págs. 345-354. [26] A. A. Yaushev, P. A. Taranenko, V. A. Longinovsky. Study of the oscillation modes of a Coriolis flowmeter using a parametric finite element model, verified by the results of modal. Procedia Engineering 150, 2016, Págs. 336340. [27] Dezhi Zheng, Shuai Wang, Bei Liu, Shangchun Fan. Theoretical analysis and experimental study of Coriolis mass flow sensor sensitivity. Journal of Fluids and Structures 65, 2016, Págs. 295-312. [28] James F. Shackelford, William Alexander. Material and science and engineering handbook, third Edition CRC press LLc. USA, 2001. Disponible <http://www.resheji.com/uploads/bbsfile/Thermal_Properties_of_Materials53.pdf>. Consultado [17 abril 2017] [29] John W.Eaton. GNU Octave 4.4.0 Released. 1996-2018, (30 de abril 2018). Disponible en <https://www.gnu.org/software/octave/news/release/2018/04/30/octave-4.4.0-released.html>. 55.

(63) Apéndice A. 1.Cálculo de los elementos de la matriz [A] [6] y [9]. (. (. (. ). ). )(. ). (. ) (. ) (. ) (. ). (. ) (. ) (. ) (. ). ∫ (. )(. ∫ (. ). ). ∫ (. )(. ∫ (. ). ). 56.

(64) ∫ (. )(. ). ∫ (. ). ∫ (. )(. ∫ (. ). ). ∫ (. )(. ∫ (. ). ). 57.

(65) ∫ (. )(. ∫ (. ∫ (. ). ). )(. ). ∫ (. ). ∫ (. )(. ∫ (. ). ). ∫ (. )( 58. ).

(66) ∫ (. ). ∫ (. )(. ∫ (. ). ). ∫ (. )(. ∫ (. ). ). ∫ (. )(. ∫ (. ). ). 59.

(67) ∫ (. )(. ∫ (. ). ). ∫ (. )(. ∫ (. ). ). ∫ (. )(. ∫ (. ). ). 60.

(68) ∫ (. )(. ∫ (. ). ). 61.

(69) 2.Cálculo de los elementos de la matriz [B]. Definición de los elementos de la matriz. *(. ) (. ) (. ) (. )+. *(. ) (. ). ) (. )+. ∫ (. )(. ∫ (. ∫ (. (. ). ). )(. ∫ (. ). ). 62.

(70) ∫ (. )(. ∫ (. ∫ (. ). )(. ∫ (. ∫ (. ). ). ). )(. ∫ (. ). ). 63.

(71) ∫ (. )(. ). ∫ (. ∫ (. ). )(. ∫ (. ∫ (. ). ). )(. ∫ (. ). ). 64.

(72) ∫ (. )(. ∫ (. ∫ (. ) ). )(. ). ∫ (. ∫ (. ). )(. ∫ (. ∫ (. ). ). )( 65. ).

(73) ∫ (. ). ∫ (. )(. ∫ (. ∫ (. ). ). )(. ). ∫ (. ∫ (. ). )(. 66. ).

(74) ∫ (. ). ∫ (. ). ∫ (. ). 67.

(75) 3. Cálculo de los elementos de la matriz [C]. Definición de los elementos de la matriz. (. *(. ) (. ). ) (. ( ( ). ). (. ). (. ). [(. ∫ (. ) (. ) ]. )(. ). ∫ (. ∫ (. ). )(. 68. ). )+.

(76) ∫ (. ∫ (. ). )(. ). ∫ (. ∫ (. ). )(. ). ∫ (. ∫ (. ). )(. ∫ (. ). ). 69.

(77) ∫ (. )(. ). ∫ (. ∫ (. ). )(. ∫ (. ∫ (. ∫ (. ). ). )(. )(. 70. ). ).

(78) ∫ (. ∫ (. ). )(. ). ∫ (. ∫ (. ). )(. ∫ (. ∫ (. ). ). )(. ∫ (. ). ). 71.

(79) ∫ (. )(. ∫ (. ∫ (. ). ). )(. ). ∫ (. ∫ (. ). )(. ∫ (. ). ). 72.

(80) ∫ (. )(. ∫ (. ). ). 73.

(81) 4. Cálculo de los elementos de la matriz [D] Definición de los elementos de la matriz. ( )( ). ( ). *(. ). (. ) (. ( ). ) (. (. ). (. ) (. ). [ (. ) ]. ∫ (. ). ∫ (. ). ∫ (. )(. ∫ (. ). ). 74. )+.

(82) ∫ (. )(. ). ∫ (. ). ∫ (. )(. ∫ (. ∫ (. ). ). )(. ∫ (. ). ). 75.

(83) ∫ (. )(. ). ∫ (. ). ∫ (. )(. ∫ (. ). ∫ (. )(. ∫ (. ∫ (. ). ). ). )(. ). 76.

(84) ∫ (. ). ∫ (. )(. ). ∫ (. ∫ (. ). )(. ∫ (. ∫ (. ). ). )(. ∫ (. ). ). 77.

(85) ∫ (. )(. ). ∫ (. ). ∫ (. )(. ). ∫ (. ∫ (. ). )(. ∫ (. ). ). 78.

(86) ∫ (. )(. ∫ (. ). ). 79.

(87) Apéndice B. Primer programa %% DATOS PARA EL TUBO ACERO INOXIDABLE UTILIZANDO COMO FLUIDO EL. AGUA %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % INGRESA Y/O LEE DATOS AL PROGRAMA EN FORMA MANUAL % CALCULA LOS PARAMETROS CON LOS DATOS DE "CRC" [28] % LOS PARÁMETROS QUE SE REQUIEREN SON: % MÓDULO DE YOUNG DEL TUBO % DIÁMETRO EXTERNO DEL TUBO % DIÁMETRO INTERNO DEL TUBO % LONGITUD DEL TUBO % DENSIDAD DEL TUBO % DENSIDAD DEL FLUIDO % INICIA LA LECTURA DE DATOS E INGRESAR MANUALMENTE LOS DATOS clear all format longeng display('. '). display('. *** POR FAVOR INGRESAR LOS DATOS QUE SE. PIDEN:. ***') display ('MÓDULO DE YOUNG'). E=input('E=') [28] display('INGRESAR DIAMETRO EXTERNO ') Dext=input('Dext=') 80.

(88) display('INGRESAR DIÁMETRO INTERNO ') Dint=input('Dint=') display('INGRESAR DENSIDAD DEL TUBO') rhot=input('rhot=') display('INGRESAR DENSIDAD DEL FLUIDO') rhof=input('rhof=') display('LONGITUD DEL TUBO RECTO CIRCULAR') long=input('long=') display('NÚMERO DE ELEMENTOS DE ITERACIÓN') N=input('N=') L=long/N ; display('INGRESE FRECUENCIA ANGULAR DE RESONANCIA') ommega=input('ommega='). % FRECUENCIA ANGULAR. 81.

(89) display('INGRESE AMPLITUD DE RESONANCIA') C=input('C=') display('INGRESAR VELOCIDAD DEL FLUIDO') V=input('V=') %display('VARIABLES. x'). %x=input('x=') %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% display('. '). display(' %display('. &&& LOS PARAMETROS CALCULADOS SON : '). L=long/N V display(' EL ESPESOR DEL TUBO. ES:. '). Et=(Dext-Dint)/2 display('RADIO MEDIO DEL TUBO') Rm=(Dext+Dint)/2 display('ÁREA DE LA SECCION CIRCULAR DEL TUBO') At=(pi*(Dext^2-Dint^2))/4 display('MASA DEL TUBO POR UNIDAD DE LONGITUD') Mt=rhot*At display('SEGUNDO MOMENTO DE ÁREA DEL TUBO') It=pi*(Dext^4-Dint^4)/64, [15]-[17] 82. &&& ').

(90) display('ÁREA DE LA SECCION CIRCULAR PARA EL FLUIDO') Af=(pi*Dint^2)/4 display('MASA DEL FLUIDO POR UNIDAD DE LONGITUD ') Mf=rhof*Af %display(' display('. ') &&&. SE TERMINARON LOS CÁLCULOS DE LOS PARÁMETROS DE. ENTRADA &&& '). Segundo programa % LA FRECUENCIA ANGULAR DE RESONANCIA SE CALCULAN % DESDE UN ELEMENTO HASTA 52 ELEMENTOS % LOS VALORES PROPORCIONADOS SON PARA PARA EL TUBO. ACERO. INOXIDABLE % LOS VALORES CONSTANTES SON VELOCIDAD DE FLUIDO Y LONGITUD DEL TUBO clear all % ARCHIVO:acero_inox3.m. 83.

(91) % ** POR FAVOR INGRESAR LOS DATOS QUE SE PIDEN: % MÓDULO DE YOUNG format longe E=1.93e11; % INGRESAR DIÁMETRO EXTERNO Dext=0.0127; % INGRESAR DIÁMETRO INTERNO Dint=9.53000000000000e003 % INGRESAR DENSIDAD DEL TUBO rhot=7900; % INGRESAR DENSIDAD DEL FLUIDO rhof=1000; % LONGITUD TOTAL DEL TUBO long=0.75; % NÚMERO DE ELEMENTOS DE ITERACION N=1; L=long/N ; % INGRESAR VELOCIDAD DEL FLUIDO V=5; % ***LOS RESULTADOS SON :*** % EL ESPESOR DEL TUBO ES : et=1.58500000000000e003; % RADIO MEDIO DEL TUBO 84. **.

(92) Rm=11.1150000000000e003; % ÁREA DE LA SECCIÓN CIRCULAR DEL TUBO At=55.3463017162711e-006; % MASA DEL TUBO POR UNIDAD DE LONGITUD Mt=437.235783558542e003; % SEGUNDO MOMENTO DE AREA DEL TUBO It=872.087871085041e-012; % ÁREA DE LA SECCIÓN PARA EL FLUIDO Af=71.3305680581033e-006; % MASA DEL FLUIDO POR UNIDAD DE LONGITUD Mf=71.3305680581033e-003; % II. LAS MATRICES [A],[B],[C] Y [D] Y ELEMENTOS CORRESPONDIENTES [A]=[12 6*L -12 6*L;6*L 4*L.^2 -6*L 2*L.^2;-12 -6*L 12 -6*L;. 85.

(93) 6*L 2*L.^2 -6*L 4*L.^2] [B]=[6/5*L 1/10 -6/5*L 1/10;1/10 2*L/15 -1/10 -L/30; -6/5*L -1/10 6/5*L -1/10; 1/10 -L/30 -1/10 2*L/15]; [C]=[-1/2 L/10 1/2 -L/10;-L/10 0 L/10 -L.^2/60; -1/2 -L/10 1/2 L/10;L/10 L.^2/60 -L/10 0]; [D]=[13*L/35 11*L.^2/210 9*L/70 -13*L.^2/420; 11*L.^2/210 L.^3/105 13*L.^2/420 -L.^3/140; 9*L/70 13*L.^2/420 13*L/35 -11*L.^2/210; -13*L.^2/410 -L.^3/140 -11*L.^2/210 L.^3/105]; % III. DEFINICIÓN DE LOS COEFICIENTES DE LAS MATRICES h1=(E*It)/(L.^3); COEFICIENTES DE LA MATRIZ DE REGIDEZ h2=Mf*V.^2;. COEFICIENTES. DE LA MATRIZ DE REGIDEZ h3=2*Mf*V; COEFICIENTES DE LA MATRIZ DE CORIOLIS h4=(Mf+Mt);. COEFICIENTES DE LA. MATRIZ DE MASAS % IV MATRICES GLOBALIZADOS Y CON SUS FACTORES RESPPECTIVOS [Kg]=h1*[A]+ h2*[B]; [Eg]=h3*[C]; [Mg]= h4*[D]; % V. SE CALCULA POR EL MÉTODO DE COMANDO :. polyeig, en GNU Octave. display('[x,e]=polyeig(Kg,i*Eg,-Mg)') [x,e]=polyeig(Kg,i*Eg,-Mg); disp('TERMINÓ DE UN ELEMENTO') % VI. RESULTADOS CALCULADOS HASTA 52 ELEMENTOS FINITOS. 86.

(94) Tercer programa. DADA LA VELOCIDAD, CALCULA EL ÁNGULO DE DESFASE PARA TUBO DE ACERO INOXIDABLE ARCHIVO: CálculoDesfase_acero_inox.m clear all % I. PARÁMETROS Y UNIDADES % E : MÓDULO DE YOUNG. [N/m^2]. % G : MÓDULO DE CORTE. [N/m^2]. % V : VELOCIDAD DEL FLUIDO. [m/s]. % As: ÁDEL SECCION TRANSVERSAL DEL TUBO [m^2]. % Af: ÁREA DEL SECCIÓN TRANSVERSAL DEL FLUIDO[m^2] % Mt: MASA POR UNIDAD DE LONGITUD DEL TUBO. 87. [kg/m].

(95) % Mf: MASA POR UNIDAD LONGITUD DEL FLUIDO % rhot:DENSIDAD DEL TUBO. [kg/m^3]. % rhof:DENSIDAD DEL FLUIDO. [kg/m^3]. [kg/m]. % It: SEGUNDO MOMENTO DE ÁREA DEL TUBO [m^4] % L, long: LONGITUD DEL TUBO RECTO. [m]. % ommega: FRECUENCIA ANGULAR DE RESONANCIA [1/rad] % C: AMPLITUD DE OSCILACIÓN. [m]. II. RANGO DE VALORES PROPIOS Y DEFINICIÓN MODO DE. VALORES i=1:1:5;. VARIABLE DE ITERACIÓN PARA. VALOR PROPIO %lai=(2*i+1)*pi/2;. FÓRMULA PARA CALCULAR. VALOR PROPIO lan1=4.73; PRIMER MODO FUNDAMENTAL [21]-[23] lan2=7.853;. SEGUNDO MODO. f21=3.399;. FACTOR. the1=1.0359;. THETA1. the2=0.9984;. THETA2. xi11=-12.74;. FACTOR11. xi22=-45.98;. FACTOR22. III. VALORES DE LOS PARÁMETROS DE ENTRADA DEL TUBO. ACERO INOXIDABLE INCLUIR LA ENTRADA DE DATOS EL ARCHIVO: ACEROP0_1 MODULO DE YOUNG E=1.93e11; INGRESAR DIÁMETRO EXTERNO Dext=0.0127; 88.