Mediciones e Incertidumbres
Introducción
Todas las medidas vienen condicionadas por Incertidumbres experimentales (accidentales o sistemáticas) y por la apreciación del instrumento. Es imposible conocer el "valor verdadero" (x) de una magnitud. La teoría de Incertidumbres acota los límites entre los que debe estar dicho valor, x.
La incertidumbre en las medidas tiene un significado distinto a "equivocación": la incerteza es inherente a todo proceso de medida.
Magnitudes:
Una magnitud es todo aquello que se puede medir de un cuerpo material o un fenómeno físico, que se puede representar por un número y que puede ser estudiado en las ciencias experimentales.
Ejemplos de magnitudes: velocidad, fuerza, temperatura, energía física (no la energía espiritual), etc.
Para obtener el número que representa a la magnitud debemos medirla y al medir surgen las Incertidumbres.
Para medir debemos utilizar el instrumento de medida apropiado y si dicho instrumento no existe, deberemos inventarlo.
Unidades:
Una unidad es una cantidad de magnitud que se toma como patrón para compararla con la cantidad de magnitud que tiene “eso” que queremos medir
Para medir la masa, por ejemplo, tomamos (arbitrariamente) como unidad una cantidad materia a la que llamamos kilogramo. Para medir la longitud, tomamos una cantidad de longitud que se llama metro, etc
La Medida es el resultado de medir, es decir, de comparar la cantidad de magnitud que queremos medir con la unidad de esa magnitud. Este resultado se expresará mediante una cantidad (número) seguida de la unidad que hemos utilizado: 4m, 200 Km , 5 Kg ...
Las unidades deben ser:
La idea de cómo deben ser las unidades, surge como una consecuencia de la Revolución Francesa.
Reproducibles por cualquiera en cualquier parte del mundo.
Universales y contrastables: utilizadas por todos los países y accesibles para el que quiera calibrar con ellas otros patrones de medida.
Inalterables por las condiciones atmosféricas, el uso, etc.
Coherentes: Para que se puedan basar unas en o otras y tener múltiplos y submúltiplos.
Sistema Internacional de unidades (S.I.)
El Sistema Internacional de unidades (S.I.) establece siete unidades básicas con sus múltiplos y submúltiplos (Sistema Internacional ampliado) correspondientes a siete magnitudes fundamentales.
A las unidades fundamentales le corresponden las Magnitudes fundamentales siguientes:
Longitud, Masa, Tiempo, Intensidad de corriente eléctrica, Temperatura absoluta, Intensidad luminosa y Cantidad de materia
Para cada magnitud se define una unidad fundamental. Longitud: metro; Masa: kg ; etc,
A estas siete magnitudes fundamentales hay que añadir dos magnitudes complementarias: Ángulo plano y Ángulo sólido.
Las demás magnitudes que se relacionan con las fundamentales mediante fórmulas matemáticas reciben el nombre de Magnitudes derivadas.
Cada uno de los países desarrollados ha establecido, por ley, un sistema de unidades coherente, basado en el S.I., de uso obligatorio en la industria y en el comercio. En nuestro país se denomina SIMELA (Sistema Métrico Legal Argentino)
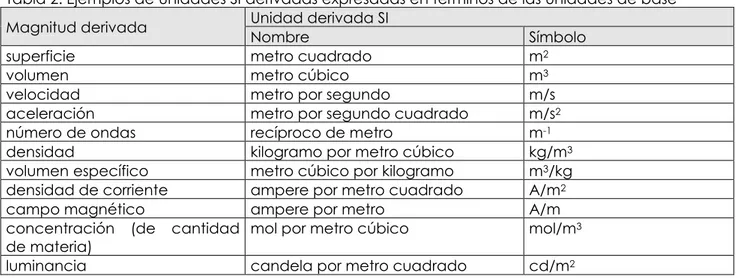
Tabla 1. Unidades de base SI
Magnitud de base Unidad de base SI
Nombre Símbolo
longitud metro m
masa kilogramo kg
tiempo segundo s
corriente eléctrica ampere A
temperatura termodinámica kelvin K
cantidad de materia mol mol
intensidad luminosa candela cd
Tabla 2. Ejemplos de unidades SI derivadas expresadas en términos de las unidades de base Magnitud derivada Unidad derivada SI Nombre Símbolo
superficie metro cuadrado m2
volumen metro cúbico m3
velocidad metro por segundo m/s
aceleración metro por segundo cuadrado m/s2
número de ondas recíproco de metro m-1
densidad kilogramo por metro cúbico kg/m3
volumen específico metro cúbico por kilogramo m3/kg
densidad de corriente ampere por metro cuadrado A/m2
campo magnético ampere por metro A/m
concentración (de cantidad
de materia) mol por metro cúbico mol/m
3
luminancia candela por metro cuadrado cd/m2
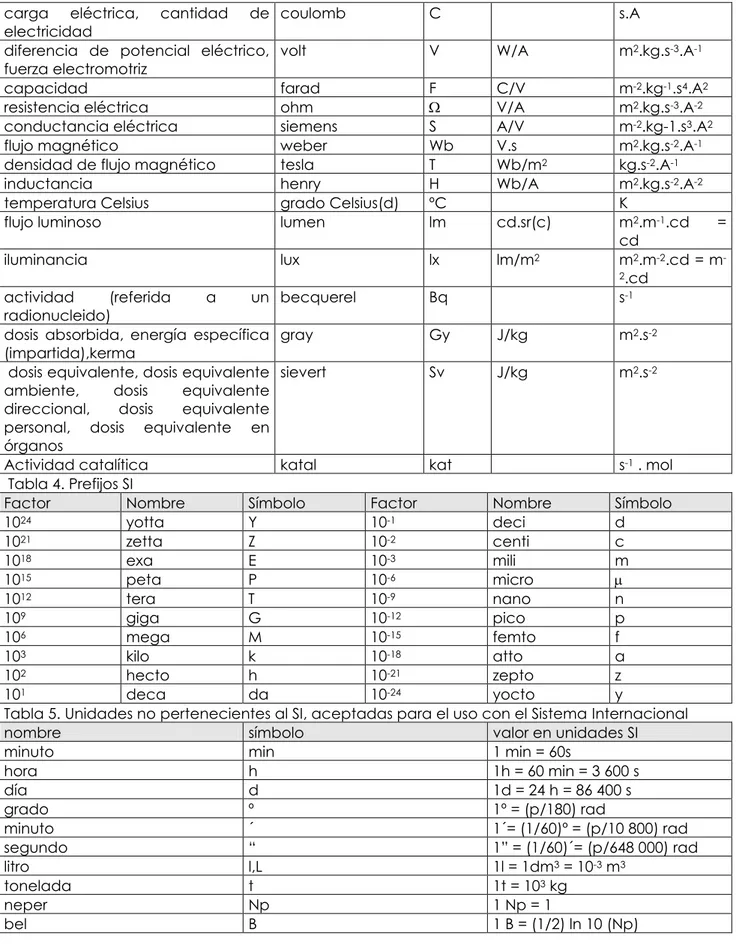
Tabla 3. Unidades SI derivadas con nombres y símbolos especiales
magnitud derivada
unidad derivada SI
nombre símbolo
expresada en término de otra unidad SI
Expresada en término de unidades SI de base
ángulo plano radian rad m.m-1 = 1
ángulo sólido estereoradián sr m2.m-2 = 1
frecuencia hertz Hz s-1
fuerza newton N m.kg.s-2
presión, tensión pascal Pa N/m2 m-1.kg.s-2
energía, trabajo, cantidad de calor joule J N.m m2.kg.s-2
carga eléctrica, cantidad de
electricidad coulomb C s.A
diferencia de potencial eléctrico,
fuerza electromotriz volt V W/A m
2.kg.s-3.A-1
capacidad farad F C/V m-2.kg-1.s4.A2
resistencia eléctrica ohm
V/A m2.kg.s-3.A-2conductancia eléctrica siemens S A/V m-2.kg-1.s3.A2
flujo magnético weber Wb V.s m2.kg.s-2.A-1
densidad de flujo magnético tesla T Wb/m2 kg.s-2.A-1
inductancia henry H Wb/A m2.kg.s-2.A-2
temperatura Celsius grado Celsius(d) ºC K
flujo luminoso lumen lm cd.sr(c) m2.m-1.cd =
cd
iluminancia lux lx lm/m2 m2.m-2.cd = m
-2.cd
actividad (referida a un radionucleido)
becquerel Bq s-1
dosis absorbida, energía específica
(impartida),kerma gray Gy J/kg m
2.s-2
dosis equivalente, dosis equivalente ambiente, dosis equivalente direccional, dosis equivalente personal, dosis equivalente en órganos
sievert Sv J/kg m2.s-2
Actividad catalítica katal kat s-1 . mol
Tabla 4. Prefijos SI
Factor Nombre Símbolo Factor Nombre Símbolo
1024 yotta Y 10-1 deci d
1021 zetta Z 10-2 centi c
1018 exa E 10-3 mili m
1015 peta P 10-6 micro
1012 tera T 10-9 nano n
109 giga G 10-12 pico p
106 mega M 10-15 femto f
103 kilo k 10-18 atto a
102 hecto h 10-21 zepto z
101 deca da 10-24 yocto y
Tabla 5. Unidades no pertenecientes al SI, aceptadas para el uso con el Sistema Internacional
nombre símbolo valor en unidades SI
minuto min 1 min = 60s
hora h 1h = 60 min = 3 600 s
día d 1d = 24 h = 86 400 s
grado º 1º = (p/180) rad
minuto ´ 1´= (1/60)º = (p/10 800) rad
segundo “ 1” = (1/60)´= (p/648 000) rad
litro l,L 1l = 1dm3 = 10-3 m3
tonelada t 1t = 103 kg
neper Np 1 Np = 1
bel B 1 B = (1/2) ln 10 (Np)
Incertidumbres sistemáticas
Pueden ser debidos a un mal calibrado del instrumento, a la utilización de fórmulas incorrectas, al manejo del instrumento de forma no recomendada por el fabricante, etc. Estas Incertidumbres sólo se eliminan mediante un análisis del problema y una "auditoria" de un técnico más calificado que detecte lo erróneo del procedimiento.
Incertidumbres accidentales o aleatorias
No es posible determinar su causa. Afectan al resultado en ambos sentidos y se pueden disminuir mejorando el instrumento de medida y por tratamiento estadístico: realizando varias medidas para que las desviaciones, por encima y por debajo del valor que se supone debe ser el verdadero, se compensen.
Los instrumentos de medida
Los instrumentos de medida pueden introducir una Incertidumbre sistemática en el proceso de medida por un defecto de construcción o de calibración. Sólo se elimina el Incertidumbre cambiando de instrumento o calibrándolo bien.
Debemos conocer el rango de medida del instrumento, es decir, entre que valores, máximo y mínimo, puede medir.
Los instrumentos deben indicar el límite de protección (por ejemplo un amperímetro que tenga una protección frente a corrientes de hasta 1 A mediante un fusible).
Deben tener las siguientes cualidades: Rapidez
Es rápido si necesita poco tiempo para su calibración antes de empezar a medir y si la aguja o cursor alcanza pronto el reposo frente a un valor de la escala cuando lanzamos la medida. La aguja no oscila mucho tiempo.
Sensibilidad
Es tanto más sensible cuanto más pequeña sea la cantidad que puede medir. Una balanza que aprecia mg es más sensible que otra que aprecia gramos.
El umbral de sensibilidad es la menor división de la escala del instrumento de medida La sensibilidad con que se fabrican los instrumentos de medida depende de los fines a los que se destina. No tendría sentido fabricar una balanza que aprecie mg para usarla como balanza de un panadero.
Fidelidad
Un instrumento es fiel si reproduce siempre el mismo valor, o valores muy próximos, cuando medimos la misma cantidad de una magnitud en las mismas condiciones.
Es fiel si la aguja se coloca en el mismo punto de la escala (o muy próximo) cuando repetimos la medida con la misma cantidad de magnitud.
Es fiel si dispersa poco las medidas.
Precisión
Un Instrumento es preciso si las incertidumbres absolutas (desviación de lo que mide del "valor verdadero") que se producen al usarlo son mínimos. El valor que da en cada medida se desvía poco del "valor verdadero".
Un instrumento es preciso si es muy sensible y además es fiel (produce poca dispersión de las medidas). Naturalmente debe estar previamente bien calibrado.
Proceso de medida.
El proceso de medida casi siempre perturba lo que vamos a medir y en consecuencia obtenemos un valor real alterado.
Por ejemplo: al colocar un termómetro más frío que la muestra, ésta se enfría por efecto del termómetro y lo que leemos es el resultado de la interrelación muestra/ termómetro, y no sólo de la temperatura de la muestra que queríamos medir.
Al intercalar un instrumento de medida en un circuito eléctrico introducimos un componente que no tenía y el resultado de la medida reflejará la alteración.
Para realizar una medición debemos seguir los siguientes pasos:
Comprobar la calibración del instrumento.
Cumplir las normas de utilización del fabricante del instrumento en cuanto a conservación y condiciones de uso.
Conocer y valorar la sensibilidad del instrumento para dar los resultados con la correspondiente imprecisión.
Anotar cuidadosamente los valores obtenidos en tablas.
Realizar la gráfica que corresponda o la de distribución de medidas.
Hallar el valor representativo, su Incertidumbre absoluta, su Incertidumbre relativa y porcentual.
Mediciones directas e indirectas
Medición directa: es aquella que se obtiene por la lectura directa del instrumento utilizado para medir la magnitud, por ejemplo, medir una longitud con una cinta métrica.
Medición indirecta: Son aquellas que se obtienen a partir de un cálculo entre mediciones directas. Es decir, no medimos directamente la magnitud que queremos conocer, si no que medimos en forma directa otras magnitudes y mediante la aplicación de un ecuación matemática obtenemos el valor de la magnitud deseada. Un ejemplo sería calcular el volumen de una caja midiendo el largo, el ancho y el alto.
Resultado de una medición directa
Supongamos que se desea medir la longitud de un cuerpo y se utiliza una regla centimetrada como se muestra en la figura:
Podemos observar claramente que el valor de la longitud del cuerpo se encuentra entre las marcas de 23 cm y 24 cm. A estos valores los denominaremos cota mínima y máxima de la medición: Lmin=23 cm ; Lmax=24cm
Valor representativo de la medición:
Denominaremos valor representativo de una medición a la suma de las cotas mínima y máxima divididas por 2:
0
24
23
23 5
2
2
max min
,
L
L
cm
cm
L
cm
verdadero que nunca podremos conocer. Para cuantificar dicha incertidumbre, definiremos lo que llamaremos “Incertidumbre experimental o absoluta”
Incertidumbre experimental o absoluta:
La incertidumbre absoluta de la medición es la diferencia entre la cota máxima y la mínima dividida por 2:
24
23
0 5
2
2
L
L
cm
cm
L
cm
max min
,
Es decir, la incertidumbre absoluta nos indica cuánto se puede apartar el valor verdadero de la medición, del valor representativo que obtuvimos.
Resultado de una medición:
El resultado de la medición se expresa de la siguiente forma: 0
23 5
,
0 5
,
L
L
L
L
cm
cm
Esto significa que el valor verdadero de la longitud del cuerpo se encuentra entre 23cm y 24cm.
Lo mismo se hace cuando se mide cualquier otra magnitud: tiempo, temperatura, etc. Cuando el instrumento de medición es de lectura directa sobre una escala fija (reloj analógico, termómetro de mercurio, amperímetro analógico, etc.
Si el instrumento es digital, o no permite apreciar el espacio entre dos marcas consecutivas, se toma como incertidumbre absoluta la apreciación del instrumento.
Incertidumbre relativa:
Al cociente entre la Incertidumbre absoluta y el valor representativo se lo denomina Incertidumbre relativa:
L
0,5 cm
L
0,021
L
23,5cm
0
Obsérvese que la incertidumbre relativa nos da la relación que existe entre la incertidumbre absoluta y el valor representativo, es decir, cuántas veces entra una en el otro.
Incertidumbre porcentual
Si se multiplica la Incertidumbre relativa por cien se obtiene la Incertidumbre porcentual:
ε%L=εL×100=0,021×100=2,1%
Esto significa que de cada cien unidades medidas me estoy equivocando a lo sumo en 2,1.
Fidelidad vs. sensibilidad
Los instrumentos analógicos tienen, normalmente, una escala con divisiones frente a la que se mueve una aguja. En teoría la aguja pasa frente a los infinitos puntos de la escala.
¿Es indicio de haber realizado una buena medida que al repetirla obtengamos el mismo valor?
Obtener exactamente el mismo valor al repetir la medida es un indicio de que el instrumento es muy "fiel", pero tanta fidelidad lo que pone de manifiesto es una falta de "sensibilidad".
Ejemplo: Si medimos la longitud de una mesa con una regla graduada en cm (no tiene divisiones de mm) y obtenemos 80,0 cm, el resultado será: 80,0 ± 0,5 cm.
Si medimos la mesa con una regla tan poco sensible no vamos a notar diferencia entre una medida y otra, obtendremos siempre 80 cm.
del instrumento aumenta y su fidelidad disminuye las incertidumbres accidentales que afectan a cada medida.
Un instrumento muy fiel es, casi siempre, poco sensible
En estos casos, la incertidumbre de una medición, claramente supera la apreciación del instrumento, pues la diferencia entre una medición y otra puede ser mucho mayor que la apreciación del mismo. Para evaluar la medición y su incertidumbre, podemos hacer un tratamiento estadístico realizando un gran número de mediciones para una misma medida.
Valor más probable de una medida
Supongamos que se realiza un gran número n de mediciones de una magnitud X obteniéndose los valores: x1, x2, x3, x4, x5, x6, …….., xn. Es claro que no podemos saber cuál de las
mediciones xi se aproxima más al valor verdadero. Podríamos obtener un valor para la medida
calculando la media aritmética (promedio) de todas las mediciones. A este resultado lo llamaremos valor más probable x.
i n i i 1
x
x
n
Podemos pensar que si el número de mediciones n tiende a infinito, el valor más probable x será muy próximo al valor verdadero.
Para evaluar la incertidumbre, tendremos que seguir pensando un poco más.
Desviación Estándar:
Podríamos evaluar la incertidumbre en una de las mediciones haciendo la diferencia entre el valor más probable y el valor de dicha medición.
i
x x
i
Este valor nos indica cuánto se aparta del valor más probable, el valor de la medición considerada. Al valor de este apartamiento, lo denominaremos desviación de la medición xi.
Obviamente, tendremos tantas desviaciones como mediciones realizadas ¿cuál sería más adecuada tomar para tener una idea de de la incertidumbre que corresponde al valor más probable?
Un criterio podría ser calcular el promedio de todas las desviaciones, pero esto no sería muy adecuado ya que habrá algunas desviaciones positivas y otras negativas y al hacer la sumatoria de todas, si son muchas, tenderá a cero ya que se irán compensando.
Para solucionar este problema, podríamos elevar cada una de las desviaciones al cuadrado, de modo que toras se hagan positivas y entonces calcular el promedio de estos valores.
i n 2 i i 1
x x
promedio
n
Pero este valor no tiene las mismas unidades que la medición, ya que las desviaciones fueron elevadas al cuadrado. La solución es calcular la raíz cuadrada y de este modo obtener lo que denominaremos desviación estándar de la medición.
i n 2 i i 1
x x
x
n
Este valor, puede tomarse como incertidumbre estadística para la medición:
x
x
x
n
Donde claramente, si el numero de mediciones es pequeño, la incertidumbre se parece mucho a la desviación estándar, pero si n es grande, la incertidumbre será mucho menor. Si el número Por lo tanto el resultado de la medición podrá expresarse como:
x x
x
En rigor de verdad, la incertidumbre experimental vendrá dada por la suma de la apreciación del instrumento utilizado y el valor de la incertidumbre estadística.
Ejemplo:
Se mide el diámetro de una pieza cilíndrica con un calibre digital a la centésima de milímetro obteniéndose los siguientes calores:
X1=34.89 mm ; X2=34.82 mm ; X3=34.88 mm ; X4=34.88 mm ; X5=34.86 mm ; X6=34.88 mm ; X7=34.80
mm ; X8=34.89 mm ; X9=34.87 mm ; X10=34.89 mm
Primero calcularemos el valor más probable:
i n i
1 2 3 4 5 6 7 8 9 10
i 1
x
x
x
x
x
x
x
x
x
x
x
x
34,87mm
n
10
Calculamos ahora la desviación estándar:
La incertidumbre estadística será:
x
x
0,03mm
0,03mm
0,01mm
3,16
n
10
La incertidumbre experimental vendrá dada por la suma de la apreciación del instrumento, en este caso, A=0,01mm y la incertidumbre estadística.
x A
x
0,01mm 0,01mm 0,02mm
Cálculo de una medición indirecta
Como dijimos, una medición indirecta se obtiene de un cálculo realizado a partir de mediciones directas. Este cálculo siempre implica operaciones matemáticas. En dichas operaciones deben tenerse en cuenta los valores representativos y sus respectivas Incertidumbres. El resultado de estas mediciones también debe ser expresado por un valor representativo y su Incertidumbre absoluta.
Para tal fin se siguen las siguientes reglas:
Incertidumbre en la suma:
Sean las medidas:
a= a0
a
i n 2
2 2 2 2 2 2 2 2 2 2
i
1 2 3 4 5 6 7 8 9 10
i 1
x x x x x x x x x x x x x x x x x x x x x x
x
n 10
i n 2
2 2 2 2 2 2 2 2 2 2
i i 1
x x 0,02 0,05 0,01 0,01 0,01 0,01 0,07 0,02 0,00 0,02
x 0,03mm
b= b0
b
Se desea realizar la suma
S=a+b
El valor representativo de la suma se obtiene como la suma de los valores representativos:
S0=a0+b0
La Incertidumbre absoluta de la suma se obtiene como la suma de las incertidumbres absolutas:
S=
a+
b
El resultado de la medición se expresa como:
S=S0
S
Incertidumbre en la resta:
Sean las medidas:
a= a0
a
b= b0
b
Se desea realizar la resta
R=a-b
El valor representativo de la resta se obtiene como la resta de los valores representativos:
R0=a0-b0
La Incertidumbre absoluta de la resta se obtiene como la suma de las incertidumbres absolutas:
R=
a+
b
El resultado de la medición se expresa como:
R=R0
R
Incertidumbre en el producto:
Sean las medidas:
a= a0
a
b= b0
b
Se desea realizar el producto
M=a.b
El valor representativo del producto se obtiene como el producto de los valores representativos:
M0=a0.b0
Para calcular la Incertidumbre absoluta del producto no pueden sumarse las incertidumbres absolutas de las mediciones (obsérvese que tendríamos problemas con las unidades). Por esta razón, se deben sumar las incertidumbres relativas. La Incertidumbre relativa del producto es igual a la suma de las Incertidumbres relativas de cada medición:
M=
a+
b
Por lo tanto:
0 0 0
M
a
b
M
a
b
0 0
0
0 0
0 0a
b
a
b
M
M
a b
a
b
a
b
El resultado de la medición se expresa como:
M=M0
M
Incertidumbre en el cociente:
Sean las medidas:
a= a0
a
b= b0
b
Se desea realizar el cociente
C=a/b
El valor representativo del cociente se obtiene como el cociente de los valores representativos:
Para calcular la Incertidumbre absoluta del cociente no pueden sumarse las incertidumbres absolutas de las mediciones (obsérvese que, al igual que en el producto, tendríamos problemas con las unidades). Por esta razón, se deben sumar los Incertidumbres relativas. La Incertidumbre relativa del cociente es igual a la suma de las Incertidumbres relativas de cada medición:
C=
a+
b
Por lo tanto:
C
a
b
C
a
b
0 0 0
a
a
b
a
b
C
C
a
b
0a
b
b
00 0 0 0 0
El resultado de la medición se expresa como:
C=C0
C
Incertidumbre en la potencia:
Sea la medida:
a= a0
a
Se desea realizar la potencia
P=a
nEl valor representativo de la potencia se obtiene como la potencia del valor representativo:
P0=a0n
Para calcular la Incertidumbre absoluta de la potencia debemos tener en cuenta que no es otra cosa que un producto por si mismo.
P=n.
a
Por lo tanto:
P
n
a
P
a
0 0
n
n 10 0 0
0 0
a
a
P n
P
n
a
n a a
a
a
El resultado de la medición se expresa como:
P=P0
P
Incertidumbre en la raíz:
Dado que la raíz no es otra cosa que una potencia fraccionaria, se procede exactamente igual que en la potencia:
Sea la medida:
a= a0
a
Se desea realizar la raíz
n
T
a
El valor representativo de la raíz se obtiene como la raíz del valor representativo:
n
10 0 0
T
a
a
nPara calcular la Incertidumbre absoluta de la raíz:
T=1/n .
a
Por lo tanto:
T
a
T
0n a
01
T
a
T
n a
00
1
El resultado de la medición se expresa como:
Ejemplo de cálculo de una medición indirecta
Se desea medir la superficie de una chapa rectangular y para ello se miden su largo y su ancho obteniéndose los siguientes resultados:
L = 25,4 cm ± 0,1 cm
a = 16,8 cm ± 0,1 cm
Para obtener el valor representativo, simplemente se realiza la operación matemática necesaria entre los valores representativos de las mediciones directas,
Como la superficie del rectángulo se calcula multiplicando el largo por el ancho, el valor representativo de la superficie será:
2 0 0 0
S = L . a = 25,4 cm . 16,8 cm = 426,72 cm
Para obtener la Incertidumbre absoluta aplicaremos las reglas estudiadas en este caso para el producto:
S=
L+
a
Por lo tanto:
S
L
a
S
0L
0a
0
L
a
S
S
L
a
00 0
Ahora remplazamos por los datos correspondientes:
,
,
S
, cm
,
,
,
2
0 1
0 1
426 72
4 22
25 4
16 8
Los resultados obtenidos se aproximarán con el siguiente criterio:
La Incertidumbre se redondea en la primera cifra significativa (primera cifra que no sea cero) y siempre al valor inmediatamente mayor, en nuestro caso:
S = 4,22 cm
2≈ 5 cm
2En la misma cifra se redondea el valor representativo, si la siguiente cifra mayor o igual a 5, se redondea al valor inmediatamente mayor y si es menor que 5, se deja el mismo valor.
En nuestro caso:
S = 426,72 cm
2≈ 427 cm
2El resultado de la medición es entonces:
2
2Criterios para expresar los resultados de las mediciones:
Medición directa con instrumento analógico:
Se toma como incertidumbre la apreciación del instrumento.
Cuando el instrumento es de lectura sobre escala fija (por ejemplo regla milimetrada, voltímetro analógico, probeta graduada), y se aprecia claramente el espacio entre dos marcas consecutivas, puede tomarse como incertidumbre la mitad de la menor división del instrumento, siempre que se esté seguro de que el valor verdadero se encuentra dentro del intervalo adoptado (apreciación del instrumento).
Cuando el instrumento tiene escala fija y móvil, como el Vernier o el Palmer, se toma como incertidumbre la apreciación del instrumento, que se obtiene haciendo el cociente entre menor división de la escala fija dividido el número de divisiones de la escala móvil. (Apreciación del instrumento).
Se expresa con igual número de decimales el valor representativo y la incertidumbre: Ejemplo 1: Regla milimetrada
X=38mm ± 1 mm
Ejemplo 2: Probeta graduada cada 2 cm3
V= 26 cm3 ± 2 cm3
Ejemplo 3: Calibre a la media décima X= 12,20 mm ± 0,05 mm
(Nótese que al valor representativo se lo completa con ceros a la derecha, hasta tener el mismo número de cifras que en la incertidumbre)
Ejemplo 4: Palmer: X= 14,23 mm ± 0,01mm
Medición directa con instrumento digital:
Se toma como incertidumbre la apreciación del instrumento. Ejemplo 5: Voltímetro digital a la décima:
V= 24,3V ± 0,1 V
Medición directa con instrumento digital:
Se toma como incertidumbre la apreciación del instrumento. Ejemplo 5: Voltímetro digital a la décima:
V= 24,3V ± 0,1 V
Mediciones indirectas:
El valor representativo se redondeará en la misma cifra que la incertidumbre teniendo en cuenta que si la siguiente cifra es 5 o mayor, se pasa al valor inmediatamente superior y si es menor de cinco, no se modifica.
Ejemplo 6: Finalizado un cálculo de valor representativo e incertidumbre de un volumen se obtuvo el siguiente resultado:
V= 25,5468 cm3 ± 0,26586 cm3
El resultado de la medición se expresa como: V= 25,5 cm3 ± 0,3 cm3
Ejemplo 7: Finalizado un cálculo de valor representativo e incertidumbre de una presión se obtuvo el siguiente resultado:
p= 14476,34456 Pa ±142,25365 Pa
Guía de ejercicios y problemas de mediciones e Incertidumbres
1) ¿Qué es una magnitud?
2) ¿Qué es una unidad de medida? 3) ¿Una medición puede ser exacta?
4) ¿Cómo se puede mejorar la precisión de una medición?
5) ¿Cuál es la diferencia entre una medición directa y una indirecta? Dé tres ejemplos de cada una.
6) Se mide el espesor (e) de una pieza de madera con una regla milimetrada y se aprecia que el valor más aproximado de la medición es 34 mm. Indicar:
a) valor representativo de la medición. b) Incertidumbre absoluta.
c) Resultado de la medición. d) Cota mínima.
e) Cota máxima.
f) Incertidumbre relativa. g) Incertidumbre porcentual.
7) Se mide el diámetro (d) de un pistón de una moto con un calibre que aprecia la décima del milímetro y se observa que el valor más aproximado de la medición es 22,9 mm. Indicar:
a) valor representativo de la medición. b) Incertidumbre absoluta.
c) Resultado de la medición. d) Cota mínima.
e) Cota máxima.
f) Incertidumbre relativa. g) Incertidumbre porcentual.
8) Se mide la longitud (X) de un tornillo con un micrómetro que aprecia la centésima del milímetro y se observa que el valor más aproximado de la medición es 16,28 mm. Indicar: a) valor representativo de la medición.
b) Incertidumbre absoluta. c) Resultado de la medición. d) Cota mínima.
e) Cota máxima.
f) Incertidumbre relativa. g) Incertidumbre porcentual.
9) Se mide la temperatura (t) de un líquido con un termómetro cuya menor graduación es 1 ºC y se aprecia que el valor más aproximado de la medición es 45,0 ºC. Indicar:
a) valor representativo de la medición. b) Incertidumbre absoluta.
c) Resultado de la medición. d) Cota mínima.
e) Cota máxima.
f) Incertidumbre relativa. g) Incertidumbre porcentual.
10)Se mide la masa (m) de una piedra con una balanza electrónica al gramo y se aprecia que el display indica 106 g. Indicar:
a) valor representativo de la medición. b) Incertidumbre absoluta.
c) Resultado de la medición. d) Cota mínima.
e) Cota máxima.
11)Durante un experimento se mide la altura desde la que se deja caer un cuerpo y el tiempo que tarda en llegar al piso, obteniéndose los siguientes resultados:
h = 4,90 m 0,05 m t = 1,10 s 0,02 s
Calcular para cada medición: a) Incertidumbre relativa. b) Incertidumbre porcentual.
c) Indicar qué medición es más precisa.
12)¿Cuál de las siguientes mediciones es más precisa? Justifique la respuesta. a) m = 246 g ± 2g
b) t= 2,26 s ± 0, 05 s c) h= 2,32 m ± 0,12 m
13) Se miden los lados de una chapa rectangular con la intención de medir su superficie, obteniéndose los siguientes resultados:
A= 12,4 cm ± 0,1 cm B= 9,0 cm ± 0,1 cm Calcular:
a) Valor representativo de la superficie. b) Incertidumbre absoluta da la superficie. c) Resultado de la medición de la superficie. d) Incertidumbre porcentual de la superficie
14)Se mide el diámetro de una placa circular con la intención de medir su superficie, siendo d= 8,2 m ± 0,1 m. Teniendo en cuenta que
2
.
4
d
S
Calcular:
a) Valor representativo de la superficie. b) Incertidumbre absoluta de la superficie. c) Resultado de la medición de la superficie. d) Incertidumbre porcentual de la superficie
15)Se miden las arista de un prisma rectangular con la intención de medir su volumen, obteniéndose los siguientes resultados:
A= 8,40 mm ± 0,05 mm B= 27,10 mm ± 0,05 mm C= 49,35 mm ± 0,05 mm Calcular:
a) Incertidumbre porcentual de cada medición. b) Valor representativo del volumen.
c) Incertidumbre porcentual del volumen. d) Incertidumbre absoluta del volumen. e) Resultado de la medición del volumen.
16)Se mide el diámetro de una pieza cilíndrica con un calibre a la décima y la altura con una regla milimetrada con la intención de medir su volumen, obteniéndose los siguientes valores representativos:
d0= 31,2 mm y h0=96 mm. Teniendo en cuenta que
2
.
.
4
d h
V
Calcular:
a) Incertidumbres porcentuales de las mediciones del diámetro y la altura. b) ¿Qué medición sería conveniente mejorar?
17)Se mide el volumen de un pequeño prisma triangular por dos métodos.
I- Utilizando una probeta graduada en cm3 que contiene 30 cm3 de agua y se observa
que cuando se introduce el prisma el nivel de agua llega a 46 cm3
II- Utilizando un calibre a la décima obteniéndose para la base b0=22,4 mm, la altura
h0= 26,3 mm y la longitud L0=55,0 mm.
. .
2
b h L
V
Calcular:
a) Resultado de la medición con probeta.
b) Incertidumbre porcentual de la medición con probeta. c) Resultados de las mediciones de b, h y L
d) Incertidumbres porcentuales de las mediciones de b, h y L e) Valor representativo del volumen medido con calibre. f) Incertidumbre porcentual del volumen.
g) Incertidumbre absoluta del volumen. h) Resultado de la medición del volumen.
i) ¿Por qué método la medición fue más precisa?
18) Sabiendo que : b = bo b c = co c d = do d e = eo
e
Para la magnitud
2 3
.
c
b
A
Calcular:
I.
Valor representativo
II.
Cota máxima
III.
Cota mínima
IV.
Indeterminación absoluta o experimental
V.
Indeterminación relativa
VI.
Indeterminación relativa porcentual
Ídem anterior para:
A
b
c
Ídem anterior para:
A
a b
a
b
.
Ídem anterior para:
A
b
2
c
2Ídem anterior para:
A
c
2
d
3Ídem anterior para:
A
b
c
d
e
219) Se mide el diámetro de una pieza cilíndrica con un calibre digital que tiene una apreciación de 0,01 mm. La medición se repite 10 veces y se obtienen los siguientes valores para cada medición: 12,08mm ; 12,09mm ; 12,05mm ; 12,04mm ; 12,10mm ; 12,08mm ; 12,07mm ; 12,07mm ; 12,09mm ; 12,06mm.
Respuestas
6) e0 = 34mm; e = 0,5mm; e = 34,0mm 0,5 mm; emin = 33,5mm; emax = 34,5mm; e = 0,015; e =
21,5%
7) d0=22,9mm; d=0,1mm; d=22,9mm 0,1mm; dmin=22,8mm; dmax=23,0mm; d =0,0044; d=0,44%
8) X0=16,28mm; X=0,01mm; X=16,28mm0,01mm; Xmin=16,27mm; Xmax=16,29mm; X=0,0006;
X=0,06%
9) t0 = 45,0ºC; t = 0,5ºC; t = 45,0ºC 0,5ºC; tmin =44,5ºC ; tmax =45,5ºC; t = 0,011; t = 1,1%
10) m0 = 106g; m = 1g; m = 106g 1g; mmin = 105g; mmax = 107g; m = 0,0094; m = 0,94%
11) h = 0,010; h = 1,0%; t = 0,018; t = 1,8% la da la altura es más precisa porque tiene menos Incertidumbre porcentual.
12) %m =0,8%; %t = 2,2%; %h =5,1% La de la masa es más precisa porque su Incertidumbre porcentual es menor.
13) S0 =112 cm2 ; S =3cm2 ; S =112 cm2 3cm2 ; %S =1,9%
14) S0=53 m2 ; %S=3,8% ; S=53 m2 2 m2; S =2 m2
15) V0 =11200 mm3 ; V = 100 mm3 ; V = 11300 mm3 100 mm3; %V=0,88%
16) %d =0,32% ; h =1,10% ; habría que mejorar la de la altura ; V0 =74000 mm3 ; %V =1,74% ;
V =2000 mm3 ; V=73000 mm3 2000 mm3
17) V =16cm31cm3 ó V= 16000 mm3 1000 mm3 ; %V =6.25% ; b=22,4mm 0,1 mm ; h=26,3 mm
0,1 mm ; L= 55,0 mm 0,1 mm ; %b= 0,45% ; %h= 0,38% ; %L= 0,18% ; V0= 16200 mm3 ; %V= 1,01% ;
V =200 mm3 ; V =16200 mm3 200 mm3 ; Por el método indirecto porque tiene menor
Incertidumbre porcentual.