Guía 11: Ángulos en la circunferencia y teoremas

(1)

GUÍA TEÓRICO PRÁCTICA Nº 13 UNIDAD: GEOMETRÍA

ÁNGULOS EN LA CIRCUNFERENCIA Y TEOREMAS DEFINICIONES

CIRCUNFERENCIA: Dado un punto O y una distancia r, se llama circunferencia de centro O y radio r al conjunto de todos los puntos del plano que están a la distancia r del punto O.

RADIO: Trazo cuyos extremos son el centro de la circunferencia y un punto de ésta ( OA ).

CUERDA: Trazo cuyos extremos son dos puntos de una circunferencia ( DE ).

DIÁMETRO: Cuerda que contiene al centro de la circunferencia, mide 2 radios, es decir d = 2r en la figura, ( BC ).

SECANTE: Recta que intersecta en dos puntos a la circunferencia (PQ)

TANGENTE: Recta que intersecta a la circunferencia en un solo punto (TM). T punto de tangencia.

ARCO: Es una parte de la circunferencia determinada por dos puntos distintos de ella, por ejemplo arco CE (CE).

ÁNGULO DEL CENTRO:Es todo ángulo interior cuyo vértice es el centro de la circunferencia (EOD).

EJEMPLOS

1. ¿Cuál de las siguientes opciones es falsa?

A) El radio de una circunferencia mide la mitad del diámetro.

B) Dos cuerdas son congruentes si los arcos que subtienden son congruentes. C) En circunferencias congruentes los diámetros son congruentes.

D) Al cortarse dos cuerdas en el centro de la circunferencia forman ángulos del centro. E) Por tres puntos en el plano siempre pasa una circunferencia.

r

O 1

0: Centro r: Radio C(O,r) = (O,r)

C

u

r

s

o

:

Matemática

Material N° 16

cuerda

diámetro

secante

tangente radio

arco C A Q

M P

B

D E

T

(2)

2. Dos circunferencias son concéntricas

A) si una pasa por el centro de la otra. B) sólo si sus radios son congruentes. C) sólo si tienen el mismo centro.

D) sólo si tienen dos cuerdas congruentes.

E) si el radio de una es el doble del radio de la otra.

3. ¿Cuál de las siguientes opciones es verdadera?

A) Una cuerda no puede pertenecer a una secante. B) La mayor secante es el diámetro.

C) La tangente corta en dos puntos a la circunferencia. D) Toda cuerda pasa por el centro.

E) El diámetro es la cuerda de mayor longitud.

4. En la circunferencia de centro O de figura 1, AC y BD son diámetros. Si OD = 4x – 2 y AC = 6x + 4, entonces OC =

A) 8 B) 10 C) 12 D) 14

E) 16

5. En la circunferencia de centro O de la figura 2, AB es diámetro y AO = CD . ¿Cuál(es) de las siguientes afirmaciones es (son) siempre verdadera(s)?

I) AB // CD II) AB = 2 CD

III) ∆OCD es equilátero.

A) Sólo I B) Sólo II C) Sólo III D) Sólo II y III E) I, II y III

D A

O

fig. 1

C B

fig. 2

B

C D

(3)

MEDIDA ANGULAR DE UN ARCO

En toda circunferencia la medida angular de un arco es igual a la medida del ángulo del centro que subtiende dicho arco.

ÁNGULO INSCRITO: Es todo ángulo cuyo vértice es un punto de la circunferencia y parte de sus rayos son cuerdas de ésta (FHG).

TEOREMA

Todo ángulo inscrito en una circunferencia, tiene como medida la mitad del ángulo del centro, que subtiende el mismo arco.

EJEMPLOS

1. En la circunferencia de centro O de la figura 1, AB y CF son diámetros. ¿Cuál(es) de las siguientes relaciones es (son) siempre verdadera(s)?

I) 2ODC = DOF

II) AE OE≅ III) AB DC⊥

A) Sólo I B) Sólo II

C) Sólo III D) Sólo I y III E) I, II y III

2. Si en la circunferencia de centro O de la figura 2, AC es diámetro, la medida del ángulo x es

A) 26,5º

B) 27º

C) 63,5º

D) 64º

E) 90º

DE = _{EOD =}_α_α_α_α

E D

O

α

G

H

F

B

A

O

fig. 1 D

C E

F

x

O

A

B C

fig. 2 53º

O centro de la circunferencia

α 2

(4)

3. En la circunferencia de centro O de la figura 3, ¿cuánto mide el suplemento de β?

A) 4º B) 64º C) 86º D) 116º E) 180º

4. En la circunferencia de centro O de la figura 4, 2α + β = 120º. Entonces, el valor de β es

A) 15º B) 30º C) 45º D) 60º E) 75º

5. En la figura 5, CD es un diámetro de la circunferencia de centro O. Si el AOD = 40º,

AD y DB

son congruentes, entonces ¿cuál(es) de las siguientes afirmaciones es (son) falsa(s)?

I) CAO = 20º

II) CBO = BOD

III) 2AOB = ACB

A) Sólo I B) Sólo II C) Sólo I y II D) Sólo II y III E) I, II y III

6. En la circunferencia de centro O y diámetro BC de la figura 6, ¿cuánto mide el AOC?

A) 14º B) 34º C) 56º D) 90º

E) 112º _56º

O C

A B

fig. 6

β

O

fig. 4

α x + 30º

x

fig. 3 3x + 10º

O

β

A

B

O _C

(5)

TEOREMA

Todos los ángulos inscritos en una circunferencia que subtienden un mismo

arco tienen igual medida.

TEOREMA

Todo ángulo inscrito en una semicircunferencia es recto, (subtiende un arco de 180º).

TEOREMA

En todo cuadrilátero inscrito en una circunferencia, los ángulos opuestos son suplementarios.

TEOREMA

La recta tangente a una circunferencia es perpendicular al radio en el punto de tangencia.

EJEMPLOS

1. Si en la figura 1, TQ es diámetro, RPQ = 40º y 2QRP = 50º. ¿Cuánto mide el TQR?

A) 20º B) 25º C) 30º D) 40º E) 50º

2. Si en la circunferencia de la figura 2, α + β + 3γ = 100°, entonces el valor de β es

A) 15º B) 20º C) 25º D) 33,3º E) 60º

O

P Q r

⇒ _⊥

QP tangente en P QP OP α

αα

α = ββββ α β

α α α

α + γγγγ = 180º

β β β

β + δδδδ = 180º

A

C

γ

α δ

β

B D

_{BCA = 90º}

O

A

B

C

O: centro de la circunferencia

P Q

R T

fig. 1

β α

γ fig. 2

(6)

3. En la figura 3, el cuadrilátero ABCD está inscrito en la circunferencia. Entonces, x =

A) 35º B) 40º C) 45º D) 85º

E) faltan datos.

4. En la figura 4, AC es diámetro de la circunferencia de centro O. ¿Cuánto mide el ángulo BCA?

A) 15º B) 25º C) 35º D) 55º E) 70º

5. En la figura 5, PT es tangente a la circunferencia de centro O, en T. ¿Cuánto mide el PTQ?

A) 20º B) 50º C) 90º D) 110º

E) Faltan datos.

6. En la circunferencia de centro O de la figura 6, PB es tangente en B, ¿cuánto mide el ángulo BCO?

A) 20º B) 30º C) 40º D) 50º E) 100º

7. En la figura 7, el cuadrilátero ABCD está inscrito en la circunferencia. Si β = 115° y α = β – δ, entonces γ =

A) 100° B) 125° C) 130° D) 135°

E) 140° _β γ _C

B D

fig. 7

α δ

A

fig. 3

35º x

40º

A B

D C

60º

T

P

O

fig. 5 40º

Q

B O

A C

fig. 4 55º

B

P O

fig. 6

C

(7)

ANGULO INTERIOR DE LA CIRCUNFERENCIA

El ángulo interior de la circunferencia es aquel que se forma al cortarse interiormente dos cuerdas, como se muestra en la figura 1, y su medida corresponde a la semisuma de los arcos que subtiende.

ANGULO EXTERIOR EN LA CIRCUNFERENCIA

El ángulo exterior, está formado por dos rectas secantes, o tangentes o una recta secante y una tangente, que se intersectan en un punto exterior a la circunferencia, como se muestra en la figura 2, y su medida corresponde a la semidiferencia de los arcos que subtiende.

ANGULO SEMI INSCRITO

Es el ángulo δ formado por una recta tangente a la circunferencia y una cuerda que pase por el punto de tangencia, como se muestra en la figura 3, su medida corresponde a la del ángulo inscrito que subtiende el mismo arco ε.

EJEMPLOS

1. En la circunferencia de centro O de la figura 4, AD es diámetro, DE = 90º y L es tangente en E. ¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s)?

I) β – α = 25º II) δ + α = 90º III) β + α = δ – β + 50º

A) Sólo I B) Sólo II C) Sólo III D) Sólo I y II E) I, II y III

fig. 2

β

P

A

B

C

D

fig. 3

δ ε

A B

C B

fig. 1 A

C

D

α

B

α α α α =

BA + CD 2

β ββ β =

DC AB

2

− − − −

δ δδ δ = εεεε

C α O

δ δ β

L D

E A B

65º

(8)

EJERCICIOS

1. En la circunferencia de centro O de la figura 1, si α + β = 56º, entonces el valor del ángulo λ es

A) 28º B) 56º C) 74º D) 112º

E) no se puede determinar.

2. En la circunferencia de centro O de la figura 2, el ángulo ONM mide 48º. ¿Cuál es la medida del ángulo LON?

A) 24º B) 48º C) 96º D) 132º E) 156º

3. En la circunferencia de centro O de la figura 3, BC

= 1 3

DA. Si DOA mide 90º, ¿cuánto

mide BEA?

A) 60º B) 90º C) 100º D) 120º E) 130º

4. En la figura 4, AB es el diámetro de la circunferencia de centro O. Si BC

= 3CA

, ¿cuál es la medida de α?

A) 75º B) 67,5º C) 45º D) 30º E) 22,5º

O

α

β λ

fig. 1 A

B

C

D

fig. 2 O

M

N L

fig. 4 O

A B

C

α

fig. 3 A

B

C

D E

(9)

5. En la figura 5, AB ≅ BC y O es el centro de la circunferencia. Si AD

= EB

, entonces la medida del ángulo α es

A) 10º B) 20º C) 40º D) 60º E) 80º

6. En la figura 6, AB es el diámetro de la circunferencia con centro en O. Si L es tangente a la circunferencia en B, la medida del _ε es

A) 22,5º B) 35º C) 55º D) 72,5º

E) faltan datos.

7. En la circunferencia de la figura 7, AB

= 80º y α = 20º, luego la medida de β es

A) 80º B) 60º C) 40º D) 30º E) 20º

8. En la circunferencia de centro O de la figura 8, E es punto de tangencia, EOH = 110º,

¿cuál es la medida del ángulo ε?

A) 110º B) 90º C) 75º D) 60º E) 55º

α

A

B

β

C

D

fig. 7 C E

α

30º

• fig. 5

A

B O

D

α

A

B C

ε

55º

fig. 6 O

L

H E

O

fig. 8

(10)

9. Si en la circunferencia de centro O de la figura 9, AC es el diámetro, FB AC⊥ , FB

= 80º

y CE

= 40º, ¿cuánto mide el ángulo ACB?

A) 50º B) 25º C) 20º D) 15º

E) Faltan datos.

10. El ∆ABC está inscrito en la circunferencia la figura 10, y A’, B’ y C’ son los puntos en que la circunferencia es cortada por las bisectrices de los ángulos α, β y γ. Entonces, el ángulo β mide

A) α + γ

B) + 2

α γ

C) 2(α + γ)

D) + 4

α γ

E) 2( + ) 3

α γ

11. En la circunferencia de centro O de la figura 11, AD y BE son diámetros. Si DE

= BC

y el β = 72º, entonces la medida del α es

A) 9º B) 18º C) 36º D) 72º E) 108º

12. Si en la circunferencia de centro O de la figura 12, AB es un diámetro y el ABD = 37º,

entonces el BCD mide

A) 53º B) 74º C) 84º D) 90º

E) faltan datos.

A _C

D

B fig. 9

E

O F

fig. 10

A B

C

A’ B’

C’

α

β γ

O A

B

E

D

C

α

β

fig. 11

C D

A B

O

(11)

13. En la circunferencia de centro O de la figura 13, BC = OA . Si OBC = 30º, ¿cuánto

mide α?

A) 60º B) 80º C) 90º D) 120º

E) Falta información.

14. En la circunferencia de la figura 14, BD y BC son tangentes a la circunferencia en los puntos C y D, respectivamente. Si BCD = 65º, entonces α – β es igual a

A) 180º B) 165º C) 65º D) 55º E) 30º

15. Si en la circunferencia de la figura 15, L es tangente en P y QP : RQ : PR

= 4 : 3 : 2, entonces la medida del ángulo x

A) 80º B) 120º C) 160º D) 170º

E) ninguna de las anteriores.

16. En la figura 16, los arcos AB, BC y CD son congruentes. Si el ángulo AFD mide 84º, la medida del ángulo BEC es

A) 168º B) 84º C) 42º D) 28º E) 14º

F

A

B

C D 84º

x

E

fig. 16 O

A B

D

C

α

E

fig. 13

L P

Q R

x

fig. 15 A

B

fig. 14

α β

C

(12)

17. En la circunferencia de centro O de la figura 17, OA // BC , AOB = 62º. Entonces, la

medida del ángulo x es

A) 31º B) 62º C) 83º D) 87º E) 128º

18. En la circunferencia de centro O de la figura 18, AC es diámetro. Entonces, el ángulo x en función de αααα mide

A) 90º – 2

α

 

 

 

B) 90º + α

C) 90º – α

D) 180º – α

E) 180º – 2

19. Si en la figura 19, A, B, C y D son puntos que pertenecen a la circunferencia y el _{BCD = 80º, entonces el ángulo x mide}

A) 80º B) 100º C) 160º D) 200º E) 280º

20. En la circunferencia de centro O de la figura 20, está inscrito un hexágono regular, cuyos vértices son A, B, C, D, E y F. Si unimos A con D y D con F, entonces la medida del ángulo ADF es

A) 30º B) 60º C) 90º D) 120º

E) faltan datos.

A

B

C D

x

fig. 19 fig. 17

A O

B C

x

D

A B

C

x

α

fig. 18 O

F

A B

C

fig. 20 O

(13)

21. De las afirmaciones siguientes, es falsa

A) en todo cuadrilátero inscrito en una circunferencia sus ángulos opuestos son suplementarios.

B) el ángulo semi-inscrito mide lo mismo que el ángulo del centro que subtiende el mismo arco.

C) el ángulo exterior es equivalente a la semi-diferencia de los arcos que subtiende. D) el ángulo interior es equivalente a la semi-suma de los arcos que subtiende.

E) al inscribir polígonos regulares en una circunferencia, tendrá mayor ángulo interior, aquel que tenga un mayor número de lados.

22. En la circunferencia de la figura 21, el DEC es

A) 10º B) 20º C) 40º D) 60º E) 120º

23. Los puntos A, B y C pertenecen a la circunferencia de centro O de la figura 22. Entonces, el ángulo α mide

A) 120º B) 160º C) 180º D) 240º E) 300º

24. Los puntos A, B, C, D y E son puntos de la circunferencia de la figura 23. Si 2ED = AE , entonces el ángulo ACE mide

A) 13,5º B) 27º C) 54º D) 81º E) 108º

D

A C

E _60º

80º

fig. 21

A

C E

B 81º D

fig. 23 A

B

C

α

70º

50º

fig. 22

(14)

25. En la circunferencia de la figura 24, la medida del ángulo exterior AGC es

A) 120º B) 100º C) 80º D) 40º E) 20º

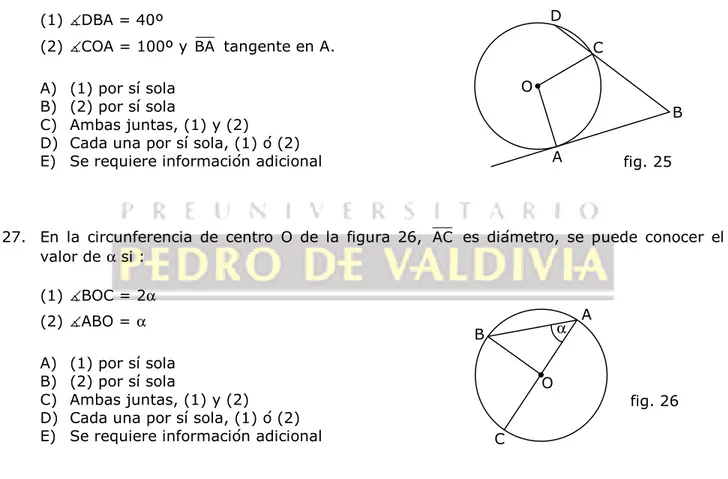
26. Siendo A, C y D puntos que pertenecen a la circunferencia de centro O de la figura 25, se puede conocer el valor del ángulo DCO si :

(1) DBA = 40º

(2) COA = 100º y BA tangente en A.

A) (1) por sí sola B) (2) por sí sola

C) Ambas juntas, (1) y (2)

D) Cada una por sí sola, (1) ó (2) E) Se requiere información adicional

27. En la circunferencia de centro O de la figura 26, AC es diámetro, se puede conocer el valor de α si :

(1) BOC = 2α

(2) ABO = α

28. En la circunferencia de centro O de la figura 27, _{AC y BD son diámetros. Se puede} conocer el valor del ángulo x si :

(1) CD = 120º

(2) CDB + BAC = 60º

fig. 27

A B

C D

x O 20º

60º

fig. 24

A

B C

D

O

fig. 25

C

α

B

A

O

fig. 26 A

B

C

D

G E

(15)

29. Si AB es diámetro de la circunferencia de centro O y L es tangente en C (fig. 28). La medida del CBA se puede determinar si :

(1) AB = 2 AC (2) ACL = 150º

30. En la figura 29, el cuadrilátero ABCD está inscrito en la circunferencia. Se puede determinar la medida del CDA si :

(1) BCD = 120º

(2) DAB = 60º

DMDMA16

Puedes complementar los contenidos de esta guía visitando nuestra web

http://www.pedrodevaldivia.cl/

D C

B

A

fig. 29 C

O

A

B

fig. 28