Tema 2

(1)

Ecuaciones diferenciales lineales de

primer orden

2.1 Introducci´

on y definiciones

Definición 2.1. Una ecuación diferencial lineal de primer orden, en forma impl´ıcita, es una ecuación del tipo

(2.1) a₀(t)x!(t) +a₁(t)x(t) +a₂(t) = 0,

donde las funciones a0, a1 ya2 son conocidas y est´an definidas en un intervalo I de R.

Véase que (2.1) es una ecuación del tipo F(t, x(t), x!(t)) = 0, que es la forma general de una ecuación diferencial ordinaria (EDO) de primer orden impl´ıcita. La ecuación diferencial

tx!(t)₋x(t) + sent= 0

es un ejemplo de (2.1), en el que las tres funciones: a₀, a₁ ya₂ est´an definidas en _R.

Si la funci´on a0 no se anula en el intervalo I est´a claro que podremos despejar la primera

derivadax!(t) en (2.1) y escribir la ecuaci´on en la forma expl´ıcita o normalx!(t) =a(t)x(t) +b(t).

Definición 2.2. Una ecuación diferencial lineal de primer orden, en forma expl´ıcita, es una ecuación del tipo

(2.2) x!(t) =a(t)x(t) +b(t),

donde las funciones a y b son conocidas y est´an definidas en un intervalo I de _R.

La ecuaci´on (2.2) es del tipo x!(t) = f(t, x(t)) (forma general de una EDO de primer orden expl´ıcita), donde f: I ×R → R,(t, x) $→ f(t, x) = a(t)x+b(t). De forma reducida (abreviada) escribiremos la ecuaci´on como x!=a(t)x+b(t). Tres ejemplos de (2.2) son

x! =tx+ 1, x! = 3tx₋cos_tt, x! = 1_tx₋logt.

(2)

En el primer ejemplo las funcionesaybest´an definidas en_R, en el segundo, los intervalos maximales dondeaybest´an definidas sonI = (∞,0) eI = (0,∞) y, en el tercero, el intervalo maximal donde

aybestán definidas esI = (0,_∞).Obsérvese que el ejemplo dado en el caso impl´ıcito no se podr´ıa escribir expl´ıcitamente en un intervalo que contenga a t = 0. Ahora bien, si únicamente estamos interesados en soluciones definidas en I = (0,∞), la ecuación s´ı ser´ıa equivalente a la ecuación expl´ıcita:

x!= 1_tx₋ sen_tt.

La ecuaciones lineales en forma expl´ıcita son las que vamos a estudiar en este tema. A partir de ese estudio se podr´a, a veces, obtener conclusiones sobre ciertas ecuaciones impl´ıcitas (como la del ejemplo anterior).

Definición 2.3. Cuando en la ecuación (2.2) la funciónb es idénticamente nula en el intervalo

I, se dice que la ecuación diferencial lineal es homogénea, pero cuando bno es la función nula se dice que la ecuación no es homogénea o es completa.

Las ecuaciones lineales son muy útiles (poseen interesantes aplicaciones) y vienen a dar, como modelo matemático, una primera aproximación de ciertos problemas reales (f´ısicos).

El estudio de estas ecuaciones es muy instructivo pues sirve de referencia para el estudio de ecuaciones lineales de orden superior y de sistemas diferenciales ordinarios de primer orden.

Sin m´as que suponer que las funciones aybson continuas en I, vamos a ver lo siguiente:

• Podremos resolver la ecuación (2.2) en el sentido de que podremos dar una fórmula, dependien-te de un parámetroC, que nos proporcione las expresiones expl´ıcitas de todas las soluciones. En la práctica, el único problema con el que nos podremos encontrar será con el cálculo de primitivas.

• Probaremos adem´as que todas las soluciones est´an definidas en el intervalo I donde a y b

son continuas. Esto es algo casi privativo de las lineales pues veremos que no sucede as´ı en la mayor´ıa de las ecuaciones diferenciales de primer orden (recu´erdese el caso x! = 2tx2, visto en el tema anterior).

• Por otra parte, podremos probar que cualquier problema de valor inicial (problema de Cauchy) asociado posee una ´unica soluci´on en el intervalo I (existencia y unicidad).

Obsérvese que la única suposición que hacemos: a, b ∈ C(I,R) implica que la función de dos variables f:I _×R_→R,(t, x)_$→f(t, x) =a(t)x+b(t),escontinua en I_×R.

A través de este tema, veremos diversos motivos para llamar “lineales” a estas ecuaciones (con-sideraciones de tipo algebraicos), aunque, para ser más riguroso, las que verdaderamente deber´ıan llamarse lineales son las ecuaciones homogéneas.

(3)

2.2 La ecuaci´

on diferencial lineal homog´

enea:

x

'

(

t

) =

a

(

t

)

x

(

t

)

Una ventaja inicial que plantea una ecuación diferencial lineal homogénea respecto de una completa, es que la homogénea siempre tiene una solución trivial: la función nulax(t) = 0, válida en cualquier intervalo I donde la función a esté definida; por ejemplo, la ecuación x!(t) = (logt)x(t) tiene a la función nula como solución en el uintervalo I = (0,_∞). Esto no sucede con la ecuación no homogénea. En esta sección supondremos únicamente que la función a:I _→ _Res continua en el intervalo I.

El caso visto en la introducci´on de la asignatura, el delmodelo malthusiano x!(t) =rx(t), donde

r _∈R, es un caso particular de ecuación lineal homogénea donde la función aes constante y este caso nos debe servir de referencia. Vimos all´ı que todas las soluciones de la ecuación, definidas en

R, son las funciones de la forma: x_C(t) =Cert, donde C es cualquier número real. Obsérvese que la función que aparece en la exponencial es una primitiva de la función constantea(t) =r.

Al serauna función continua enI posee primitivas en este intervalo. Notemos por!a(t)dtuna primitiva (enfatizamos que, en adelante, y en contra del uso tradicional, con el s´ımbolo anterior estamos notando una primitiva y no el conjunto de todas las primitivas de la función a). Es evidente, por simple comprobación, que para cada constanteC_∈R, la función definida por

x_C(t) =Ce!a(t)dt

es solución de la ecuación lineal homogénea (entre ellas está considerada la solución nula para el caso C= 0), pues

x!_C(t) =Ce!a(t)dt d dt(

!

a(t)dt) =e!a(t)dt_a₍_t_{) =}_a₍_t₎_x

C(t).

Veamos que las funciones anteriores son las únicas soluciones de la ecuación homogénea. Para esto procederemos como en el caso del modelo malthusiano. Supongamos que x: I _→ R es cualquier solución y consideramos la función derivable y:I →R,definida por

y(t) =x(t)e−!a(t)dt.

Sin m´as que derivar esta funci´on tenemos:

y!(t) =x!(t)e−!a(t)dt₋x(t)a(t)e−!a(t)dt="x!(t)₋a(t)x(t)#e−!a(t)dt = 0, para cadat_∈I,

por lo que, al ser I un intervalo, la funci´on y es constante en I y as´ı existe C _∈ R tal que

x(t) =Ce !

a(t)dt

para cada t_∈I. De esta forma hemos concluido el siguiente resultado:

Proposición 2.1. Si I es un intervalo en Ry a:I _→R una función continua enI, la ecuación diferencial lineal homogénea x!(t) =a(t)x(t) posee infinitas soluciones definidas en el intervaloI. Concretamente, si !a(t)dt es una primitiva de la función a en I, las soluciones de la ecuación son todas las funciones x_C:I _→R definidas por

(2.3) x_C(t) =Ce!a(t)dt donde C∈R.

(4)

Por otra parte, obs´ervese que, si en lugar de tomar la primitiva t _$→ !a(t)dt, tomamos otra, que ser´a de la forma: t $→ !a(t)dt+k, con k constante, el conjunto de funciones que aparecer´ıa en (2.3) ser´ıa el mismo.

En muchos textos (donde el rigor matemático brilla por su ausencia) llevan a cabo el siguiente procedimiento para resolver la ecuación homogénea:

x!(t) =a(t)x(t) =_⇒

(1)

x!(t)

x(t) =a(t) =(2)⇒

$ _x_!₍_t₎

x(t) dt=

$

a(t)dt+k =_⇒

(3) log|x(t)|= $

a(t)dt+k

=_{⇒ |}x(t)_|=e!a(t)dt+k =_⇒ x(t) =_±eke!a(t)dt =Ce!a(t)dt.

El paso incorrecto es el (1) pues se está suponiendo que no hay un punto de I donde la solución de la ecuación se anula. Sabemos por la proposición anterior, que salvo la función nula, esto es cierto, pero a priori no se puede suponer. De hecho, la constante C que sale al final del proceso anterior no es nula, por lo que la solución nula ha sido excluida. La aparición de la constante k, que aparece en el paso (2), no queda muy clara aunque esto se podr´ıa solventar de otra forma. A veces, ni siquiera ponen valor absoluto dentro del logaritmo en el paso (3), lo que es un error pues sólo tiene sentido logaritmos de números positivos. De todas formas, el proceso anterior no está mal tenerlo en cuenta como regla mnemotécnica por si se nos olvida la expresión (2.3).

Afrontamos ahora el estudio de un problema de valor inicial, tambi´en llamado problema de Cauchy:

(P) :

%

x!(t) =a(t)x(t)

x(t₀) =x₀ t0 ∈I, x0 ∈R, a:I →R continua enI,

es decir, estudiar cuantas soluciones x:I → R de la ecuación diferencial, si existen, verifican la condición inicial x(t₀) = x₀ y, en tal caso, determinarlas. Para esto es conveniente, no elegir cualquier primitiva de la función a, sino la primitiva definida por P(t) = !_tt

0a(s)ds, que tiene

la particularidad de que verifica P(t0) = 0. Seg´un (2.3) las soluciones de la ecuaci´on diferencial

estar´ıan dadas por las funciones x_C(t) = Ce

!t

t0a(s)ds, donde C ∈ R, pero obs´ervese que s´olo hay

una de ellas que verifica la condici´on inicial, que es la que corresponde a la constanteC =x0.De

esta forma concluimos el siguienteresultado de existencia y unicidad.

Proposici´on 2.2. Sean I un intervalo en R, t₀ _∈I, x₀ _∈R ya:I _→R una funci´on continua en

I. El problema de valor inicial

(P) :

%

x!(t) =a(t)x(t)

x(t0) =x0

posee una única solución en el intervalo I, que es la funciónx:I →R definida por

(2.4) x(t) =x₀e

!t t₀a(s)ds_.

En la práctica, salvo en casos excepcionales, no es necesario recordar la expresión (2.4). Basta con recordar (es fácil y de comprobación inmediata) que la solución general de la ecuación es de la forma x(t) = Ce!a(t)dt _{y se determina la constante} _C _{imponiendo que se verifique la condición}

x(t0) =x0.

(5)

Ejemplo 2.1. Soluciones de la ecuaci´on diferencial x!(t) =tx(t).

La ecuaci´on escrita en forma abreviada esx! =tx.

En este caso I =_R y la función a: _R_→ _R, a(t) =t es continua en _R. Por tanto, la ecuación diferencial posee infinitas soluciones definidas enR.Para cadaC∈R tenemos la solución definida por x_C(t) =Ce!t dt, es decir, x_C(t) =Cet

2

2 . Estas son las ´unicas soluciones.

Ejemplo 2.2. Soluci´on del problema de valor inicial (P) :

%

x!(t) +1_tx(t) = 0

x(1) = 13

En este caso a(t) = −1_t y el intervalo maximal I al que pertenecet0 = 1 y donde la funci´on a

está definida y es continua es I = (0,_∞). Por tanto, el problema (P) tiene solución y solamente una definida en ese intervalo. Para encontrar la solución lo hacemos primeramente usando la fórmula (2.4) y obtenemos que la solución de (P) es la función definida por

x(t) = 13e!1t−s1ds = 13e(−logt+log 1)= 13

t .

Si no queremos recordar la fórmula (generalmente eso es lo más conveniente), determinamos todas las soluciones de la ecuación diferencial definidas en el intervaloI = (0,_∞),que son las funciones de la formax(t) =Ce!(−1/t)dt₌_e−logt₌ C

t y, ahora, basta con determinar la constanteCimponiendo

la condici´on x(1) = 13, de lo que resulta trivialmente C = 13. De cualquier forma se obtiene la soluci´on x(t) = 13/t.

%

x!(t) =₋1_tx(t)

x(1) = 0

Planteamos la solución de este problema con el único objetivo de hacer ver que en este caso no es necesario hacer cálculos ya que vemos quela función nula es solución y, teniendo en cuenta el resultado de la proposición 2.2, esta es la única solución. Esto mismo saldr´ıa de aplicar directamente la expresión (2.4).

%

x!(t) =et2 x(t)

x(3) = 0

En este ejemplo, el único objetivo es hacer ver que en este caso no podr´ıamos dar expl´ıcitamente las soluciones de la ecuación diferencial por el problema de cálculo que tenemos con la primitiva

!

(6)

2.3 La ecuaci´

on diferencial lineal no homog´

enea (completa)

Nos planteamos ahora el estudio de la ecuaci´on diferencial

x!(t) =a(t)x(t) +b(t).

Suponemos que las funciones ayb son conocidas y continuas en un intervalo I y que la funci´on b

no es la función nula. Obsérvese que ahora la función nula x(t) = 0 no es solución de la ecuación. Vamos a dar aqu´ı dos métodos para su estudio. El primero es más elemental y más técnico y es un adelanto de algo que veremos en el tema 5 sobreel método de los factores integrantes. El segundo método es más algebraico, más fácil de recordar y llevar a la práctica, con la ventaja adicional de que posteriormente se generalizará a ecuaciones diferenciales lineales de orden superior y a sistemas diferenciales lineales. Este segundo método se basa fundamentalmente en el conocimiento que ya tenemos sobre la ecuación homogénea asociada. El primero también usa (en menor medida) lo ya visto para ecuaciones homogéneas.

Aprovecharemos el primer m´etodo para estudiar un problema de valor inicial asociado a una ecuaci´on diferencial lineal completa.

2.3.1 Primer m´etodo: Uso de un “factor integrante”

En este método no exclu´ımos el caso en que b sea la función nula, aunque este caso de lugar a una ecuación homogénea, ya estudiada. De hecho los resultados que obtendremos generalizarán los vistos en la sección anterior.

En primer lugar sscribimos la ecuaci´on diferencial as´ı:

(2.5) x!(t)₋a(t)x(t) =b(t).

Si µ es una funci´on definida en I tal que µ(t) ₎= 0 para cada t_∈ I, la ecuaci´on anterior se puede escribir de forma equivalente como

(2.6) µ(t)[x!(t)₋a(t)x(t)] =µ(t)b(t).

La idea es encontrar (veremos que existe) una funci´onµderivable (y que no se anule) enI tal que

(2.7) d

dt[µ(t)x(t)] =µ(t)[x

!₍_t₎₋_a₍_t₎_x₍_t_)] _{para cada} _t_∈_I _{y cada funci´on}_x,

pues, en tal caso, tendr´ıamos que la ecuaci´on (2.5) podr´ıamos escribirla de forma equivalente as´ı:

(2.8) d

dt[µ(t)x(t)] =µ(t)b(t).

La ventaja de (2.8) respecto de (2.5) es que de (2.8) es muy fácil deducir la expresión de x. En efecto, (2.8) nos dice que la función productoµxes una primitiva de la funciónµben el intervaloI. Por tanto, si !µ(t)b(t)dt denota una primitiva de tal función (la que sea), existirá una constante

C tal que

µ(t)x(t) =

$

µ(t)b(t)dt+C

y, por tanto, cualquier soluci´onx de la ecuaci´on (2.5) ser´ıa de la forma:

(2.9) x(t) = 1

µ(t)

& $

(7)

(Obsérvese que se necesita que seabcontinua enI para que tenga sentido la expresión!µ(t)b(t)dt). Rec´ıprocamente, si x es una función definida por la expresión anterior, donde C ∈ R, entonces obviamente x es derivable y verifica la condición (2.8) y, por tanto, x ser´ıa solución de (2.5). Es decir, que en tal caso, (2.9) nos dar´ıa la expresión de cualquier solución de la ecuación completa.

Veamos que efectivamente existe una función µque no se anula y es derivable enI, que verifica la condición (2.7) y, al mismo tiempo, obtendremos una expresión deµ. Obsérvese que

(2.7) _⇐⇒ µ!(t)x(t) +µ(t)x!(t) =µ(t)x!(t)₋µ(t)a(t)x(t) _⇐⇒ µ!(t)x(t) =₋µ(t)a(t)x(t),

por lo que ser´ıa suficiente con determinar una µque no se anule enI y verifique la condici´on

µ!(t) =₋a(t)µ(t) para cada t_∈I.

Lo anterior es una ecuación diferencial lineal homogénea en la función incógnitaµ, cuyas soluciones vienen dadas porµ(t) =Ce−!a(t)dt_{, con}_C_{cualquiera en} _R_{. A nosotros nos basta con una solución}

que no se anule en I y est´a claro que una adecuada es la funci´on definida por µ(t) = e−!a(t)dt.

Usando estaµen la expresi´on obtenida en (2.9), concluimos que las soluciones de la ecuaci´on lineal completa son las funciones definidas por

(2.10) x_C(t) =e!a(t)dt&C+

$

b(t)e−!a(t)dtdt'.

Cuando b es la función nula en I, la expresión que se obtiene de (2.10) es la ya conocida para la solución general de la ecuación homogénea. En conclusión, hemos obtenido el siguiente resultado:

Teorema 2.1. Si I es un intervalo en R y a, b:I _→ R son dos funciones continuas en I, la ecuaci´on diferencial lineal completa x!(t) =a(t)x(t) +b(t) posee infinitas soluciones definidas en el intervalo I. Las soluciones de la ecuaci´on son las funciones x_C:I _→ R definidas por (2.10), donde C _∈R.

Una vez visto c´omo son todas las soluciones de la ecuaci´on diferencial, abordamos un problema de valor inicial

(P) :

%

x!₍_t_{) =}_a₍_t₎_x₍_t_{) +}_b₍_t₎

x(t₀) =x₀

Suponemos l´ogicamente que el punto inicial t₀ se encuentra en el intervalo I, donde las funciones

ay b son continuas. Buscamos, si es que existe, una solución de la ecuación diferencial lineal que verifica la condición inicial x(t0) =x0. En (2.10) tenemos las expresiones de todas las soluciones

de la ecuación, pero en este caso, de la misma forma que vimos en el caso homogéneo, no es conveniente tomar primitivas cualesquiera en tal expresión. Por ejemplo, para la función a ser´ıa conveniente elegir la primitiva definida por P(t) = !_tt

0a(s)ds, que tiene la particularidad de que

verifica P(t₀) = 0. Esto mismo hacemos con el resto de las primitivas, es decir, tomar t₀ como l´ımite inferior de cada integral que aparece en (2.10). De esta forma, el conjunto de soluciones de la ecuaci´on lineal podemos escribirlo as´ı:

(2.11) x_C(t) =e

!t

t₀a(s)ds&_C₊ $ t

t0

b(s)e−

!s

t₀a(r)dr_ds'_.

Observemos, que la ventaja de la expresión (2.11) es que la evaluación de x_C en el punto t₀ es trivial, concretamentex_C(t0) =C. Esto nos confirma que existe una y solamente una solución para

(8)

Teorema 2.2. Sean I un intervalo en R, t₀ _∈I, x₀ _∈Rya, b:I _→Rdos funciones continuas en

I. El problema de valor inicial

(P) :

%

x!(t) =a(t)x(t) +b(t)

x(t0) =x0

posee una única solución en el intervalo I, que es la función definida por

(2.12) x(t) =e

!t t0a(s)ds

&

x0 +

$ t

t0

b(s)e−

!s

t0a(r)drds

'

.

Véase que la expresión obtenida para la solución de (P) generaliza la obtenida en (2.4) para el caso homogéneo. En la práctica no es aconsejable, salvo en casos excepcionales, usar las fórmulas (2.10) y (2.12), pues la memorización de estas es dif´ıcil y es fácil equivocarse. Para conseguir las soluciones de la completa, lo mejor es recordar el razonamiento seguido en la prueba del teorema 2.1 y para la resolución de un problema de Cauchy, al igual que en el caso homogéneo, en general aconsejo que se resuelva la ecuación diferencial y después se calcule el valor de la con-stante C que hace que se verifique la condición inicialx(t0) =x0. Ponemos en práctica estas ideas

en el siguiente ejemplo.

Ejemplo 2.5. Soluciones de la ecuaci´on diferencial: x!(t) = 2tx(t) +t y la soluci´on, definida

en R, del problema de valor inicial(P) :

%

x!(t) = 2tx(t) +t x(0) = 0

Observemos que las funciones dadas por a(t) = 2tyb(t) =test´an definidas y son continuas en

R. Por tanto, la ecuación diferencial posee infinitas soluciones definidas en R, cuyas expresiones difieren en un parámetro C ∈ R. Por otra parte, el teorema 2.2 nos asegura que el problema de Cauchy planteado posee una única solución definida enR.

Si µ es una funci´on definida en R tal que µ(t) ₎= 0 para cada t_∈R, la ecuaci´on diferencial se puede escribir de forma equivalente como

µ(t)"x!(t)₋2tx(t)#=tµ(t).

La idea es determinar una funci´on µ, derivable y que no se anule en_R, que verifique

(2.13) d

dt[µ(t)x(t)] =µ(t)

"

x!(t)−2tx(t)#

para que nuestra ecuaci´on diferencial sea equivalente a la ecuaci´on

(2.14) d

dt[µ(t)x(t)] =tµ(t).

Derivando y desarollando la expresi´on (2.13) resulta

µ!(t)x(t) =−2tµ(t)x(t),

para lo cual será suficiente con que µno se anule y sea solución de la ecuación lineal homogénea

(9)

lo que nos lleva a elegir

µ(t) =e!−2t dt=e−t2.

Llevando esta expresi´on a la ecuaci´on (2.14) obtenemos

d dt[e

−t2

x(t)] =te−t2

y as´ıx debe verificar que existec∈Rtal que

e−t2x(t) =

$

te−t2 +C para cada t∈I

y, por tanto,

x(t) =et2

$

te−t2dt+Cet2 =et2"₋1₂e−t2#+Cet2 para cada t_∈I.

En definitiva, las soluciones de la ecuaci´on diferencial son las funcionesx_C:R→Rdefinidas por

x_C(t) =Cet2 ₋1₂ dondeC _∈_R.

Se suele decir que x(t) = Cet2

− 12 es la solución general de la ecuación. Obsérvese que, si en

lugar de la función b(t) =t tuviésemos la función nula, la ecuación resultantex!(t) = 2tx(t) ser´ıa homogénea y sus soluciones vendr´ıan dadas porx_C(t) =Cet2

, expresi´on que ´unicamente difiere de la nuestra en el sumando₋1₂.

Para determinar la solución del problema (P) sólo tenemos que calcular el único valor de C

tal que x_C(0) = 0, lo que nos lleva trivialmente al valor C = 1/2 y, as´ı, la soluci´on de (P) en el intervalo R es la funci´on definida por x(t) = 1₂(et2 −1) . Siempre es aconsejable comprobar los resultados obtenidos.

Observación: De pedir directamente la solución de (P) (sin pedir las demás soluciones de la ecuación), lo conveniente es llevar a cabo el procedimiento anterior; es decir, determinar todas las soluciones de la ecuación y, posteriormente, calcular la constante C imponiendo la condición inicial.

Una vez resuelta la ecuación x! = 2tx+t se plantea otra muy parecida, aparentemente más fácil que la anterior, pues cambiamos la función b(t) = t por la función constante b(t) = 1.

Ejemplo 2.6. Resolver la ecuaci´on diferencial: x!(t) = 2tx(t) + 1.

Vamos a ver que, a veces, las apariencias engañan (y esto es algo que sucede con asiduidad con las ecuaciones diferenciales). De entrada tenemos asegurado que la ecuación posee infinitas soluciones definidas en R, cuyas expresiones difieren en un parámetro C_∈R.En este caso, procediendo de la misma forma que en el ejemplo anterior escribimos

µ(t)"x!(t)−2tx(t)#=µ(t)

y necesitamos encontrar una funci´on µ, derivable y que no se anule, que verifique la misma condici´on (2.13) del ejemplo anterior

d

"

(10)

y, por tanto, µ(t) =e−t2

,pero, al llevar esta expresi´on a la ecuaci´on (equivalente a la inicial)

d

y al despejar x(t) nos encontramos con la desagradable sorpresa

(2.15) x(t) =et2

$

e−t2dt+Cet2,

es decir, con el cálculo de una primitiva,!e−t2dt,que no se conoce. Este problema no se dió en el caso anterior donde nos encontramos con la primitiva trivial !te−t2dt. En este caso, no hay más remedio que dejar la expresión de la solución general como aparece en (2.15).

Obs´ervese el problema que ha surgido con unos coeficientes tan simples como a(t) = 2t y

b(t) = 1. Incluso en los casos en que las correspondientes primitivas pueden explicitarse, el trabajo de cálculo puede ser bastante laborioso. Interesa entonces disponer de métodos alternativos que permitan, eventualmente, llegar a las soluciones por caminos más cortos, aunque eso no siempre será posible.

2.3.2 Segundo m´etodo

Vamos a ver un segundo método de resolución más fácil de recordar en la práctica y generaliza-ble a ecuaciones lineales de orden superior y sistemas lineales de primer orden. Este método se basa fundamentalmente en el conocimiento de las soluciones de una ecuación lineal homogénea. Aunque no es estrictamente necesario, vamos a enfocarlo bajo ciertas consideraciones algebraicas, aprovechando que ya se conocen conceptos como espacios vectoriales, subespacios vectoriales y aplicaciones lineales. De hecho, estas consideraciones son las que realmente justifican que a tales ecuaciones diferenciales se les llamen lineales y, por otra parte, sus generalizaciones al caso de ecuaciones lineales de orden superior serán fundamentales en el estudio de éstas.

Dada una ecuación diferencial lineal de primer orden (E) : x!(t) =a(t)x(t) +b(t) diremos que (H) : x!(t) =a(t)x(t) es la ecuación homogénea asociada a la ecuación (E). En lo que sigue en esta sección suponemos siempre queaybsoncontinuas en un intervaloI y, por tanto, las soluciones de ambas ecuaciones están definidas en el intervaloI.

Consideraciones algebraicas sobre la ecuación homogénea y la ecuación completa.

La ecuación homogénea (H) tiene la siguiente propiedad, trivial pero importante, que no posee la ecuación completa (E) ni otro tipo de ecuación diferencial.

Proposición 2.3. Six ey son soluciones de la ecuación homogénea yα∈R, las funcionesx+y

y αx también son soluciones de la ecuación homogénea.

Véase que lo afirmado en el resultado anterior no sucede con la simple ecuación lineal no homogénea: x! =x+ 1.

Observemos que las soluciones de la ecuación (E) y las soluciones de la ecuación (H) son funciones derivables en I que, además, tienen derivadas continuas en I (ya que suponemos que

(11)

El conjunto de soluciones de la ecuaci´on (H) tiene la siguiente particularidad:

Proposición 2.4. El conjunto de soluciones de la ecuación homogénea es un subespacio vectorial de C1(I,R) de dimensión igual a 1.

Prueba. El que el conjunto de soluciones de (H) sea un subespacio vectorial de _C1(I,_R) se sigue inmediatamente del resultado de la proposición 2.3. El que este espacio sea unidimensional es consecuencia inmediata del resultado de la proposición 2.1, pues éste nos confirma que el espacio de soluciones está generado por el elementox₁, dondex₁ es la función definida porx₁(t) =e!a(t)dt_.

Observación: La solución nula (solución trivial) de la ecuación homogénea es el elemento nulo del subespacio de soluciones.

En las ecuaciones diferenciales lineales de orden superior veremos que los conjuntos de soluciones de las ecuaciones homogéneas asociadas también tienen estructuras de espacios vectoriales, de dimensión finita, donde la dimensión, en cada caso, coincide con el orden de la ecuación diferencial.

Resulta útil y cómodo usar el siguiente operador (aplicación)

L:C1(I,R)→ C(I,R), x$→Lx=x!−ax.

Es trivial comprobar queL eslineal. En efecto, six, y_{∈ C}1(I,_R), λ, µ_∈_R, se verifica:

L(λx+µy) = (λx+µy)!₋a(λx+µy) =λx!+µy!₋aλx₋aµy

= λ(x!₋ax) +µ(y!₋ay) =λLx+µLy.

En términos de este operador podemos escribir de una forma muy simple cuándo una función es solución de (H) o de (E). Concretamente:

1. x es solución de la homogénea si, y sólo si, Lx=θ, donde θ representa la función nula (elemento nulo del espacio vectorial ). Dicho de otra forma, el conjunto de soluciones de la homogénea es elnúcleo del operador lineal L.

2. x es solución de la ecuación completa si, y sólo si, Lx=b.

Teniendo en cuenta lo anterior y que L es lineal es muy f´acil comprobar el siguiente resultado, que es la clave de nuestro segundo m´etodo.

Proposición 2.5. Sixp es una solución (particular) de la ecuación completa (E), se verifica que

x es solución de (E) si, y sólo si, x es de la forma x=xh+xp , donde xh es solución de la homogénea (H).

Prueba. En efecto, six =xh+xp se tiene que Lx=Lxh+Lxp=θ+b=b y as´ıx es soluci´on de

(E). Rec´ıprocamente, si x es soluci´on de (E), podemos escribir x=xh+xp, dondexh=x−xp y

resulta quexh es soluci´on de (H) puesLxh=Lx−Lxp=b−b=θ.

Conclusión: Si conocemos las soluciones xh de la ecuación homogénea asociada y una solución particular xp de la ecuación completa, conocemos todas las soluciones de la completa. Este conjunto

de soluciones es

(12)

En el lenguaje del Algebra Lineal podemos decir queel espacio de soluciones de la ecuaci´on completa es un espacio af´ın asociado al espacio vectorial de las soluciones de la homog´enea.

Lo visto anteriormente se puede contrastar con lo que obtuvimos en el primer m´etodo. Vimos en el teorema 2.1 que las soluciones de la ecuaci´on completa son de la forma

x(t) =e!a(t)dt&C+

$

b(t)e−!a(t)dtdt',

lo que se puede escribir como

x(t) =Ce!a(t)dt + xp(t),

donde

(2.16) xp(t) =e

!

a(t)dt$ _b₍_t₎_e−!a(t)dt_dt.

Obs´ervese quexpes soluci´on de la completa (casoC = 0) yxh(t) =Ce

!

a(t)dt _{representa la soluci´on}

general de la ecuaci´on homog´enea.

Ejemplo 2.7. Soluciones de la ecuaci´on diferencial x!(t) =x(t)−t+ 1.

Esta ecuación posee infinitas soluciones definidas en_R. Se ve a ojo una solución particular de la completa, que esxp(t) =t, por lo que la resolución de la ecuación es casi inmediata. Las soluciones

de la ecuación homogénea asociadax!=xson las definidas porx_C(t) =Cet, conC _∈R. Por tanto, las soluciones de ecuación completa son las funciones de la forma x_C(t) =Cet+t, dondeC _∈R.

2.3.3 M´etodos para determinar una soluci´on particular de la completa

En pocos casos se puede determinar a ojo una solución particular por lo que se hace necesario un método general para conseguir esto. Por suerte, hay uno muy fácil de recordar y de llevar a la práctica (salvo eventuales cálculos de primitivas), que fue propuesto por el matemático J.L. Lagrange y se conoce de la siguiente forma:

A): Conjetura de Lagrange o método de variación de las constantes (parámetros).

Observemos que las soluciones de la ecuación homogénea asociada a una ecuación completa son las definidas por x_C(t) = Ce!a(t)dt_, _siendo _C _{cualquier constante (real). Por tanto, es muy fácil}

acordarse del siguiente resultado, pues en él se conjetura que hay soluciones de la ecuación completa que son como las anteriores pero cambiando la constante C por una función t _$→ k(t) derivable y con derivada continua (de ah´ı el discutido nombre del método de variación de las constantes).

Proposici´on 2.6. Hay soluciones de la ecuaci´on completa x!(t) =a(t)x(t) +b(t) del tipo

(2.17) xp(t) =k(t)e

!

a(t)dt_,

donde k∈ C1(I,R).

Prueba. Realmente la solución particular (2.16), obtenida por el primer método, confirma esta con-jetura, ya que all´ı obtuvimos una solución particular como la propuesta, dondek(t) =!b(t)e−!a(t)dt

(13)

primer método y vamos a llevar a cabo un simple razonamiento, que es el que hay que seguir en la práctica, para obtener la función k sin necesidad de recordar fórmulas. Consiste en suponer que, fijada una primitiva!a(t)dtde la funciónaen el intervaloI, la función dada por (2.17) es solución de la ecuación y llegar fácilmente a una expresión de k(t).Finalmente la expresión que se obtiene de xp es la misma que en (2.16).

En efecto, si suponemos que la funci´on definida porxp(t) =k(t)e

!

a(t)dt_{, donde}_k_{es derivable, es}

solución de la ecuación completa, derivando tal expresión e imponiendo que sea solución, obtenemos:

x!_p(t) =k!(t)e!a(t)dt+k(t)a(t)e!a(t)dt,

k!(t)e!a(t)dt+k(t)a(t)e!a(t)dt=a(t)k(t)e!a(t)dt+b(t)

y, por tanto,

k!(t)e!a(t)dt=b(t), es decir, k!(t) =b(t)e−!a(t)dt.

De esta forma, la obtención de la función kse reduce a un cálculo de primitiva:

k(t) =!b(t)e−!a(t)dtdt.

(Obsérvese que la funciónkobtenida tiene derivada continua enI.) Una vez obtenida una de estas primitivas (la que sea) obtenemos la expresión de una solución particular as´ı:

xp(t) =& !b(t)e−

!

a(t)dt_dt'&_e!a(t)dt'_,

que es exactamente, la misma expresión que se obtuvo en (2.16). Por tanto, de existir tal solución particular debe tener la expresión descrita anteriormente. Ahora, lo único que habr´ıa que hacer es derivar y comprobar que, efectivamente, la función obtenida es solución de la ecuación diferencial, lo que nos podr´ıamos ahorrar por tenerlo asegurado por el primer método, pero la comprobación es as´ı de simple

x!_p(t) =b(t)e−!a(t)dte!a(t)dt+& !b(t)e−!a(t)dtdt'a(t)e!a(t)dt=b(t) +a(t)xp(t).

Ponemos en pr´actica el m´etodo anterior con cuatro ejemplos, donde cada uno de ellos presenta una peculiaridad distinta.

En el primer ejemplo resolvemos la misma ecuación que se vio con el primer método para poder comparar ambos métodos.

Ejemplo 2.8. Soluciones de ecuaci´on diferencial x!(t) = 2tx(t) +t.

.

La ecuación homogénea (H) asociada a nuestra ecuación completa esx! = 2tx, cuyas soluciones son las funciones, definidas en R, por xh(t) = Cet

2

, siendo C cualquier constante real. Seg´un la conjetura de Lagrange, hay soluciones particulares del tipo xp(t) = k(t)et

2

, donde k _{∈ C}1(R,R).

Para obtener una función k adecuada procedemos como en la prueba del resultado anterior; es decir, imponemos que tal función xp es solución de la ecuación diferencial completa y, si no nos

(14)

En efecto, derivando xp obtenemos: x!p(t) = k!(t)et

2

+ 2tk(t)et2

y ahora imponemos que sea soluci´on:

k!(t)et2 + 2tk(t)et2 = 2tk(t)et2 +t.

Por tanto, quedak!(t)et2 =ty, de esta forma, k!(t) =te−t2. Determinamosk mediante el c´alculo de la primitiva trivialk(t) =!te−t2 =−1

2e−t

2

.Llevando esta expresi´on de la funci´on k a la de xp,

se obtiene finalmente xp(t) =−1/2.

Las soluciones de la ecuaci´on completa son las funciones de la formax=xh+xp, dondexh son

las soluciones de la hom´enea (H) asociada. Por tanto, las soluciones de la ecuaci´on dada son las funcionesx_C:R→Rdadas por las expresiones

x_C(t) =Cet2 ₋1

2 dondeC∈R.

Obsérvese que hemos tenido el mismo resultado que el que vimos con el primer método y las primitivas que han aparecido son las mismas que aparecieron all´ı. Sin embargo, esta forma de proceder es más fácil de recordar.

Indicamos a continuación la resolución de la ecuación diferencial usando el programa Mathe-matica. En principio vamos a indicar la entrada y salida con la versión 5.0 del programa y anteriores. En la primera l´ınea aparece lo forma en que se introduce la expresión de la ecuación diferencial en este programa. En la segunda aparece la respuesta que da Mathematica.

DSolve[x’[t] == 2 t x[t] + t, x[t], t] {{x[t] -> -(1/2) + E^t^2 C[1]}}

La forma de introducir la ecuación es bastante natural. Dentro del corchete donde actúa la ins -trucciónDSolveescribimos la ecuación diferencial x’[t] == 2 t x[t] + t y después, separados por comas, indicamos quién es la función incógnita, en este caso x[t], y quién es la variable independiente, en este caso t. Nótese que usamos el doble igual == , que se usa en general para ecuaciones para distinguirlo del=de asignaciones. La solución que da el programa tiene un aspecto algo raro: aparece C[1], que indica simplemente el parámetro C de la solución general (está pensado para que en ecuaciones de orden superior, donde aparecen varios parámetros, aparezcan estos numerados). El s´ımbolo ^ se usa para las potencias y E indica la función exponencial; as´ı E^t^2 indica et2.Algo más raro son las dos llaves que rodean la expresión de la solución general. Esto tiene su explicación, que no vamos a comentar aqu´ı.

En las versiones 6.0 y posteriores de este programa (actualmente tenemos la versión 8.0) las expresiones de las soluciones aparecen con mejores aspectos, análogos al que utilizamos en estos apuntes. As´ı, en nuestro ejemplo, una versión posterior a la 5.0 dar´ıa la solución as´ı:

((

x[t]_{→ −}1 2+e

t2 C[1]

))

.

Por otra parte, tenemos la posibilidad de introducir las expresiones de las ecuaciones mediante una paleta de caracteres, lo que nos facilita la tarea y, al mismo tiempo, en muchos casos, expresa la ecuaci´on de una forma m´as agradable.

En los pr´oximos ejemplos escribiremos los resultados que da Mathematica usando versiones posteriores a la 5.0.

(15)

Ejemplo 2.9. Estudiar y resolver el problema (P) :

%

x!(t) = cost₋1_tx(t)

x(π) = 1

En primer lugar, podemos afirmar que (P) tiene solución única en el intervalo I = (0,_∞) ya que las funciones definidas por a(t) =−1/t yb(t) = cost son continuas en ese intervalo (el mayor intervalo donde a y b son continuas y que contiene al punto t = π). En segundo lugar, vamos a determinar todas las solucionesxc de la ecuación diferencial definidas en el intervaloI = (0,∞) y,

por ´ultimo, determinamos la soluci´on de (P) buscando una constanteC para la que se verifica que

xc(π) = 1.

La ecuaci´on homog´enea asociada (H) es x! =₋1_tx,cuyas soluciones son las funciones definidas en el intervalo I = (0,_∞) por xh(t) = Ce

!

−1

tdt =C/t, siendo C ∈ R. Por tanto, hay soluciones

particulares del tipo xp(t) = k(t)/t, donde k ∈ C

1

(I,R). Determinamos la función k imponiendo quexp sea solución de la ecuación completa. Esto nos lleva a la igualdad

k!₍_t₎

t − k(t)

t2 =−

k(t)

t2 + cost,

de donde se sigue que k!(t) = tcost. Llevando a cabo una integraci´on por partes, obtenemos

k(t) =!tcost dt=tsent+ cost y, finalmente,xp(t) = sent+cos_tt.

Por tanto, las soluciones de la ecuaci´on diferencial son las funciones x_C definidas en el intervalo

I = (0,∞) por

x_C(t) = C_t + sent+cos_tt, dondeC_∈R.

Resoluci´on de la ecuaci´on diferencial con Mathematica:

DSolve[x’[t] == Cos[t] - (1/t) x[t], x[t], t]

**

x[t]_→ C[1]_t +Cos[t]+_ttSin[t]++

Determinamos la solución del problema (P) entre las funciones anteriores sin más que imponer la condición inicial x_C(π) = 1, lo que nos lleva a C = 1 +π. Por tanto, la solución del problema (P) es la función x: (0,_∞)_→_Rdefinida por

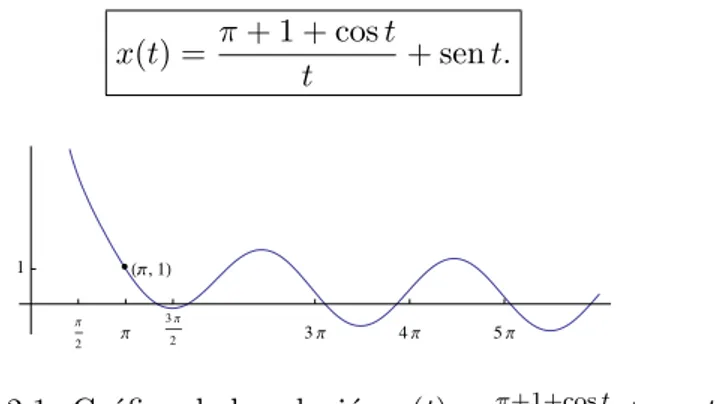
x(t) = π+ 1 + cost

t + sent.

!!, 1"

Π

2 Π

3Π

2 3Π 4Π 5Π

1

Figura 2.1: Gr´afica de la soluci´onx(t) = π+1+cos_t t+ sent.

(16)

DSolve[{ x’[t] == Cos[t]-x[t]/t, x[Pi]==1}, x[t], t]

**

x[t]_→ 1+π+Cos[_tt]+tSin[t]++

En el siguiente ejemplo proponemos una EDO lineal de primer orden no expl´ıcita (impl´ıcita), muy especial, con el fin de hacer ver que los resultados vistos para las ecuaciones expl´ıcitas no son v´alidos para las impl´ıcitas. De paso veremos que cierto tipo de ecuaciones propiamente impl´ıcitas se pueden resolver usando ecuaciones expl´ıcitas.

Ejemplo 2.10. Soluciones de ecuaci´on diferencial tx!(t) + 2x(t)₋4t2_{= 0} _{y soluciones de los} problemas de Cauchy

(P) :

%

tx!(t) + 2x(t)₋4t2 = 0

x(0) = 0 y (Q) :

%

tx!(t) + 2x(t)₋4t2= 0

x(0) = 1

En principio tendr´ıa sentido que una solución de esta ecuación diferencial estuviese definida en un intervaloI tal que 0∈I, pero para poder estudiarla tenemos que escribir de forma equivalente esta ecuación como una ecuación expl´ıcita, en este caso:

x!(t) =₋2_tx(t) + 4t

y esto solo sucede si consideramos soluciones definidas en los intervalos I = (_−∞,0) e I = (0,_∞) (o intervalos contenidos en estos). Vamos a determinar las soluciones de la expl´ıcita por el segundo m´etodo para intentar, a partir de ´estas, estudiar lo que sucede con la impl´ıcita.

Las ecuaci´on homog´enea asociada es (H) : x! =₋2_tx,cuyas soluciones vienen definidas por

xh(t) =Ce

!

(−2/t)dt ₌_Ce−2 log|t|₌ C

t2, dondeC∈R.

Existen soluciones particulares de la ecuaci´on completa de la forma xp(t) = k_t(2t), siendok de clase

uno en I. Determinamos kimponiendo que xp sea soluci´on de la completa as´ı:

k!(t)

t2 −2

k(t)

t3 =−

2

t k(t)

t2 + 4t,

lo que nos lleva a k!(t) = 4t3 y, por tanto, k(t) = t4. Por tanto, una soluci´on particular de la completa es la dada por xp(t) = t2. Se concluye que las soluciones de la ecuaci´on diferencial

expl´ıcita son todas las funciones definidas en los intervalosI por

x_C(t) =t2+ C

t2, donde C∈R.

Resoluci´on de la ecuaci´on diferencialx!=₋2_tx+ 4tconMathematica:

DSolve[x’[t] == -(2/t) x[t] + 4 t, x[t], t]

**

x[t]_→t2+ C_t[1]2

++

En principio, las soluciones obtenidas son soluciones de la ecuación diferencial impl´ıcita en los intervalos I = (_−∞,0) e I = (0,_∞). Curiosamente sólo una de éstas, concretamente la solución particular x(t) = t2, tiene sentido como función en todo R. Las otras, las definidas por xc(t) =

t2₊C

t2,siendoC)= 0,no se pueden extender de forma continua a funciones definidas enRpues no

(17)

Si x:_R_→_R fuese soluci´on de la ecuaci´on impl´ıcita, distinta dex(t) =t2_{, entonces} _x_:_I _→_R_,

siendoI = (−∞,0) o I = (0,∞),ser´ıa soluci´on de la expl´ıcita y, por tanto, xvendr´ıa definida por

xc(t) =t2+_tC2,parat)= 0.Pero esta situaci´on es imposible, puesx debe ser derivable y, por tanto,

continua en t= 0, lo cual no sucede pues x no posee l´ımite finito en ese punto. Un razonamiento análogo se puede usar para ver, que salvo la dada por x(t) =t2, no puede haber otra solución de la ecuación impl´ıcita definida en un intervaloI que contenga a t= 0.

Comprobamos que efectivamente la función definida por x(t) =t2 es solución de la impl´ıcita enRy el razonamiento anterior nos lleva a que es la única solución de la ecuación impl´ıcita válida en _R. Esto tiene como consecuencia que el problema de Cauchy (P) tendr´ıa solución válida en_R, que es la función definida por x(t) =t2 (parece ser que es la única) peroel problema (Q) no tiene solución. Esto supone un comportamiento muy distinto al caso de ecuaciones expl´ıcitas pues véase que nuestra ecuación lineal impl´ıcita es de la forma generala₀(t)x!(t) +a₁(t)x(t) +a₂(t) = 0,donde las funcionesa0(t) =t, a1(t) = 2 y a3(t) =−4t2 están definidas y son continuas enR.

C ! 0

C " 0

C" 0

!0, 0"

!0, 1"

#4 #2 2 4

#20

#10 10 20 30 40

Figura 2.2: Gr´aficas de las solucionesx_C para C= 1,3,0,₋3,₋1.

Si le damos a Mathematica la ecuaci´on lineal impl´ıcita nos da las mismas soluciones de la expl´ıcita asociada; es decir, las que hemos obtenido anteriormente:

DSolve[t x’[t] + 2 x[t] - 4 t^2 == 0, x[t], t] **x[t]_→t2₊C[1]

t2

++

y si le pedimos la soluci´on del problema (Q) no nos sabe responder.

(18)

Ejemplo 2.11. Soluciones de la ecuaci´on diferencial x!(t) + 5x(t) =t3et.

Escribimos la ecuaci´on comox!(t) =₋5x(t)+t3_et_._{En este caso una de las funciones coeficientes}

es constante (a(t) =−5) y la otra es la definida porb(t) =t3et.Ambas son continuas enR y, por tanto, las soluciones de la ecuaci´on diferencial est´an definidas en R.

La ecuación homogénea (H) asociada a nuestra ecuación completa es x! = ₋5x, cuyas solu-ciones son las funsolu-ciones definidas por xh(t) = Ce−5t, siendo C cualquier constante real. Según la

conjetura de Lagrange, hay soluciones particulares del tipo xp(t) = k(t)e−5t, donde k ∈ C

1

(R,R).

Para obtener una función k adecuada imponemos que tal función xp sea solución de la ecuación

diferencial completa y obtenemos k!(t) = t3_e6t_{. El problema con el que nos encontramos aqu´ı es}

la determinación de la primitiva k(t) =!t3e6tdt, lo cual exige tres integraciones por partes. En la primera integración por partes tomamos u(t) = t3 y v!(t) = e6t y de forma análogav!(t) = e6t en las otras dos integraciones por partes. Con un poco de paciencia obtenemos:

!

t3

,-./ u(t)

e6t

,-./ v!(t)

dt = 1₆t3e6t₋₂1!t2e6tdt= 1₆t3e6t₋1₂01₆t2e6t₋1₃!te6tdt1

= 1₆t3e6t₋₁₂1t2e6t+1₆!te6tdt= 1₆t3e6t₋₁₂1t2e6t+ 1₆01₆te6t₋1₆!e6tdt1

= e6t21₆t3₋₁₂1 t2+₃₆1t₋ ₂₁₆1 3,

obteniendo finalmente la soluci´on particular

(2.18) xp(t) =et

& 1

6t3−121t2+ 361t−2161 '

= ₂₁₆1 et(36t3₋18t2+ 6t₋1).

En definitiva, las soluciones de la ecuaci´on vienen dadas por

x_C(t) =Ce−5t+₂₁₆1 et(36t3₋18t2+ 6t₋1), dondeC _∈_R.

A la vista de la dificultad de cálculo que se ha tenido para obtener la solución particular (2.18), nos planteamos si la resolución de esta ecuación es más cómoda por el primer método (el del factor integrante). La respuesta es negativa, tanto en este ejemplo como en cualquier otro, si tenemos en cuenta la expresión (2.16); es decir, usando el primer método nos vamos a topar con las mismas primitivas y, por lo tanto, con la misma dificultad. Para ratificar esto (por si alguien no queda convencido), vamos a intentar resolver la ecuación de este ejemplo con ese método y, de paso, vemos un ejemplo más.

Siµ:R→R no se anula en ning´un punto de R, la ecuaci´on diferencial es equivalente a

µ(t)"x!(t) + 5x(t)#=µ(t)t3et.

La idea es determinar una funci´on µ, derivable y que no se anule enR, que verifique

(*) d

"

x!(t) + 5x(t)#

para que nuestra ecuaci´on diferencial sea equivalente a la ecuaci´on

d

dt[µ(t)x(t)] =µ(t)t

(19)

de donde es trivial “despejar” x as´ı:

x(t) = 1

µ(t)

0

C+!µ(t)t3_et1_.

Derivando y desarollando la expresi´on (*) resulta

µ!(t)x(t) = 5µ(t)x(t),

para lo cual ser´a suficiente con que µno se anule y verifiqueµ!(t) = 5µ(t),lo que nos lleva a elegir

µ(t) =e5t,para finalmente obtener

x(t) =Ce_{, -. /}−5t

xh(t)

+e−5t!t3e6tdt

, -. / xp(t)

.

Como era de esperar, en el primer sumando de la expresi´on anterior aparece xh(t), expresi´on de

la solución general de la ecuación homogénea y, en el segundo, la misma solución particularxp(t)

que surgió con el método de variación de los parámetros y, por tanto, con el mismo problema de cálculo de la primitiva!t3e6tdt.

Resoluci´on de la ecuaci´on diferencial con Mathematica:

DSolve[x’[t] + 5 x[t] == t^3 Exp[t], x[t], t]]

44

x[t]_→ ₂₁₆1 et"₋1 + 6t₋18t2+ 36t3#+e−5tC[1]55

El ejemplo anterior es una buena excusa para explicar el siguiente m´etodo para determinar una soluci´on particular.

(B): M´etodo de los coeficientes indeterminados

Este es un método que se usa para determinar una solución particular de una ecuación lineal completa, pero que sólo se puede aplicar en ciertos casos; concretamente, cuando la función a es

constante, es decir, la ecuaci´on es de la forma

x!(t) =ax(t) +b(t)

y, además, la función b es de unos tipos especiales. Cuando este método se puede llevar a cabo, la ventaja que tiene respecto al anterior (método de Lagrange) es la simplicidad de cálculos; de hecho, no requiere cálculos de primitivas.

El método de los coeficientes indeterminados se desarrollará con todo detalle cuando veamos las EDO lineales de segundo orden; aqu´ı sólo vamos a considerar, con poco formalismo, el caso especial en que la función bes de la forma:

b(t) =Pm(t)eαt, dondePm(t) es un polinomio de gradom)= 0 en ty α∈R.

El ejemplo visto anteriormente es un caso particular de esta situaci´on. Al ser aconstante, como queremos una funci´onxp que verifiquex!p(t)−axp(t) =b(t),parece factible buscarxp as´ı:

xp(t) =Qm(t)eαt, dondeQm(t) es otro polinomio de grado m en t.

¿Es esto posible? En principio podr´ıa serlo si α₎=aya que

(20)

y el factor que acompa˜na aeαt _{en la expresi´on anterior es un polinomio de grado} _m _{siempre que}

α−a)= 0 (se puede probar que, en este caso, efectivamente existe tal soluci´on particular).

Ponemos en práctica esta idea con la ecuación ya vista anteriormente: x!(t) + 5x(t) =t3et. Observemos que aqu´ıα= 1)=a=−5, por lo que puede existir una solución particular de la forma

xp(t) =Q3(t)et= (At3+Bt2+Ct+D)et, dondeA, B, C, D∈R.

Veamos si existen coeficientes A, B, C, D que verifiquen que xp es realmente soluci´on y, en tal

caso, los determinaremos; de ah´ı que el m´etodo reciba el nombre de m´etodo de los coeficientes indeterminados.

La función xp será solución de la ecuación si y sólo si, al imponer esa condición el sistema de

ecuaciones que resulta en las incógnitasA, B, C yDes compatible. De hecho, vamos a comprobar que al imponer que tal función xp sea solución llegamos a un sistema lineal de ecuaciones con

solución única y de resolución inmediata, pues sale un sistema triangular donde se obtiene inmedia-tamente el coeficiente A; a partir del valor de A se obtiene el valor de B y as´ı sucesivamente. Finalmente veremos que sale la misma solución particular que se obtuvo mediante el método de variación de las constantes.

En efecto, derivando la expresi´on de xp y escribiendo adecuadamente x!p+ 5xp obtenemos

x!_p(t) =&At3+ (3A+B)t2+ (2B+C)t+C+D'et

5xp(t) = &

5At3+ 5Bt2+ 5Ct+ 5D'et

x!_p(t) + 5xp(t) = &

6At3+ (3A+ 6B)t2+ (2B+ 6C)t+C+ 6D'et.

Puesto que se debe verificar que x!_p(t) + 5xp(t) =t3et para cada t∈R, resulta que, xp es soluci´on

de la ecuaci´on diferencial si y s´olo si, los coeficientes verifican

            

6A = 1

6B+ 3A = 0

6C+ 2B = 0

6D+C = 0.

Lo anterior es un sistema lineal de cuatro ecuaciones con cuatro incógnitas, compatible determinado y de resolución trivial. De la primera ecuación se obtieneA= 1/6. Llevando este valor a la segunda ecuación se obtiene B = −1/12. Sustituyendo el valor de B en la tercera se tiene C = 1/36 y, por último, de la cuarta ecuación se sigue D = ₋1/216, obteniendo as´ı la misma solución particular (2.18) que obtuvimos con el método de variación de las constantes, pero de una forma más simple.

Obsérvese que cuando α = 0 tenemos el caso particular en el que la función b es polinómica

y en este caso se busca una solución particular que también sea polinómica y del mismo grado (α =asólo se dar´ıa en el caso en el que ecuación fuese de la forma x!(t) =Pm(t), ecuación que es

trivial). Se propone como ejercicio la resolución de la ecuación x!+x=t4 .Otro caso particular deb(t) =Pm(t)eαtesb(t) =λeαt(casom= 0), pero éste no da problemas de cálculo con el método

de Lagrange.

(21)

ecuaciones. Una de las propiedades más significativas de las ecuaciones linealesx! =a(t)x+b(t) es que poseen soluciones (infinitas) en cualquier intervaloI donde las funcionesaybsean continuas. Por otra parte, un problema de Cauchy posee solución única en un intervaloI donde las funciones

ayb sean continuas yt₀ _∈I. As´ı por ejemplo, el problema lineal

(P) :

%

x!(t) =x(t)

x(0) = 1

posee solución única válida en todo R. Otra cuestión a destacar es que las expresiones de las soluciones se han obtenido de una forma expl´ıcita.

A partir de ahora, en el tratamiento del resto de las ecuaciones, a priori no podremos conocer los intervalos de existencia de la soluciones. Por ejemplo, un problema tan parecido a (P) como

%

x!(t) =x2(t)

x(0) = 1

no posee solución válida en R. La solución de este problema, que es x(t) = ₁₋1_t,sólo es válida en el intervalo I = (−∞,1). La ecuación no es lineal; es de un tipo que estudiaremos en el próximo tema. En muchas de las ecuaciones diferenciales, que trataremos en este curso, las expresiones de las soluciones se obtendrán, en principio, de una forma impl´ıcita y, en muchos casos, no se podrán obtener expresiones expl´ıcitas.

2.4 Algunos modelos matem´

aticos usando ecuaciones diferenciales

lineales de primer orden

Este tema se acaba con la exposición de algunos modelos matemáticos en el que aparecen ecuaciones lineales de primer orden. Uno de ellos ya se vio en la introducción de la asignatura (tema 1), que es el

modelo de población malthusiano, que dio lugar a una simple ecuación diferencial lineal homogénea:

x!(t) =rx(t). Exponemos a continuaci´on otros dos ejemplos muy interesantes.

2.4.1 La ley de desintegraci´on radioactiva

Hay ciertos átomos cuyos núcleos poseen un número excesivo de neutrones y esto los hace inesta-bles. Los átomos tienden entonces a desintegrarse, liberando part´ıculas que les sobran y adquiriendo configuraciones más estables. Las sustancias con este tipo de átomos se llaman radioactivas (o ra-diactivas). Se suele suponer que todos los átomos de una sustancia radiactiva tienen la misma probabilidad de desintegrarse en la unidad de tiempo y que esa probabilidad no depende del mo-mento en que tiene lugar la desintegración.

Experimentalmente se ha establecido quela velocidad de desintegraci´on de una sustancia radiac-tiva es directamente proporcional a la cantidad de sustancia existente. Esto se conoce comoley de desintegraci´on radioactiva y fue formulada por E. Rutherford y F. Soddy en 1902 (premios Nobel de qu´ımica en 1908 y 1921 respectivamente).

La ley de desintegración anterior se puede expresar en términos de una simpl´ısima ecuación diferencial lineal homogénea (análoga a la del modelo malthusiano). Si para cada instante de tiem-pot,x(t) denota la cantidad de materia radioactiva existente en ese instante, lo que nos dice la ley de desintegración es que existe una constante K >0 tal que